1 introduction

Quantum electrodynamics in 2+1 dimensions(QED\(_3\)) has been studied as a theoretical laboratory for many years. Due to its similarities to quantum chromodynamics(QCD) such as chiral symmetry breaking(CSB) and confinement [1,2,3,4], QED\(_3\) is considered to be a simple model that has a great significance in understanding fundamental characteristics of QCD, which is hard to be investigated for its non-Abelian nature. On the other hand, QED\(_3\) has been found applications in condensed matter physics, and it could serve as an effective model for high-\(T_c\) superconductors [5,6,7,8] and graphene [9]. For these reasons, there should be great interest in the study of features of QED\(_3\).

The earliest significant progress in chiral phase transition (CPT) of QED\(_3\) is conducted by Appelquist et al. [10] who found a critical number \(N_c\) of fermion flavors when the system undergoes CPT at zero temperature. But their technical approach was questioned by Pennington and co-workers because of their neglect of wave function renormalization of the fermion propagator. Further investigation was conducted by other groups using improved methods, and the results are qualitatively similar which are between 3 and 4 [2, 11,12,13], and also the critical flavor number depend on the infrared cutoff [14]. As the research of QED\(_3\) at zero temperature has achieved a wealth of results, a natural thought is extending the theory to finite temperatures. The N-flavor thermal QED\(_3\) was first studied by Dorey and Mavromatos [15] who found a non-zero critical temperature above which chiral symmetry gets restored at all numbers of flavors. Later on, more conditions that may have an effect on CPT of QED\(_3\) were taken into account, such as chemical potential [16,17,18], and find that, at high temperature, the system demonstrates a second-order phase transition characteristic in the chiral limit and illustrates a crossover beyond the chiral limit, while in the high density region it exhibits a first-order transition when the fermion mass is small but always reveals a crossover when the fermion mass exceeds a critical value \(m_c\) [19].

The above conclusions are obtained from the infinite volume and will be changed when the volume becomes finite. A breakthrough in the study of CPT in QED\(_3\) at finite volume was achieved in the paper of [20], which shows that the critical value depends apparently on the size of system, where \(N_c\) decreases with the reduction of the system size and exhibits an abnormal feature of phase transition [14]. The conclusion is arrived by numerically solving the truncated Dyson-Schwinger equation (DSE) for the propagators. Based on the same spirit and the temperature field technique, it is found a similar result in thermal QED\(_3\): the critical temperature \(T_c\) apparently decreases with the reduction of the system size [21]. Then, an interesting question will be risen: what is the nature of thermal QED\(_3\) with finite volume at \(T_c\)? Since the analysis of effective pressure is an suitable framework to study the feature of phase transition [22], in this paper, we shall adopt CJT effective potential to indicate the nature of thermal QED\(_3\) at finite volume.

In QED\(_3\), the previous works illustrated that QED\(_3\) at \(N=1\) undergoes CPT into a chiral symmetric phase when the temperature reaches a critical value \(T_c\). Later, the authors of Ref. [23] studied an improved truncated scheme for DSE to study the CPT and reveal that the correctional contribution to the factor only slightly changes the value of \(T_c\). These conclusions suggest that the lowest-order DSE for the fermion propagator is a suitable approximation to investigate CPT of thermal QED\(_3\). In the rainbow approximation, the Cornwall-Jackiw-Tomboulis (CJT) effective potential provides us with a useful tool to analyze the phase structure of QED\(_3\). So in this paper, we shall try to answer the question by employing the effective potential model [24] to explore the characteristic of the phase transition of thermal QED\(_3\) both in the chiral limit and beyond chiral limit.

2 Model of chiral phase transition

2.1 CJT’s framework

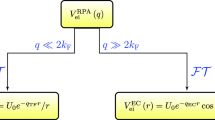
In Euclidean space, the Lagrangian of massive QED\(_3\) with a general covariant gauge is given by

$$\begin{aligned} \mathcal {L}=\bar{\psi }(\not \!{\partial }+i\mathrm {e}\not \!\!{A}-m)\psi +\frac{1}{4}F^{2}_{\sigma \nu }+\frac{1}{2\xi }(\partial _{\sigma }A_{\sigma })^2, \end{aligned}$$
(1)

where the 4-component spinor \(\psi \) is the fermion field, \(\xi \) is the gauge parameter. In infinite volume, the order parameter with chiral limit for CPT is defined as the vacuum expectation value of the fermion chiral condensate

$$\begin{aligned} \langle \bar{\psi } \psi \rangle ={\text {Tr}}[S(x \equiv 0)]=\int \frac{\mathrm {d}^{3} p}{(2 \pi )^{3}} \frac{4 B\left( p^{2}\right) }{A^{2}\left( p^{2}\right) p^{2}+B^{2}\left( p^{2}\right) }. \end{aligned}$$

The two functions \(A(p^{2})\) and \(B(p^{2})\) are related to the inverse fermion propagator

$$\begin{aligned} S^{-1}(p)=i \gamma \cdot p A\left( p^{2}\right) +B\left( p^{2}\right) , \end{aligned}$$
(2)

which reduces to the free form in high energy region

$$\begin{aligned} S^{-1}_0(p)=i \gamma \cdot p+m. \end{aligned}$$
(3)

The unknown function \(A(p^2)\) and \(B(p^2)\) can be obtained by the DSE for the fermion propagator

$$\begin{aligned} S^{-1}(p)=S^{-1}_0(p)+\int \frac{\mathrm {d}^{3} k}{(2 \pi )^{3}} \gamma _\mu S(k)\Gamma _\nu (p,k)D_{\mu \nu }(q). \end{aligned}$$
(4)

with \(q=p-k\) and the nature unit \(e^2=1\) are used. Beyond the chiral limit, the order parameter is not well-defined. Since the condensate is the phenomenon in low energy region, one can remove the free part to give an renormalized value

$$\begin{aligned} \langle \bar{\psi } \psi \rangle&={\text {Tr}}[S(x \equiv 0)-S_0(x \equiv 0)]\nonumber \\&=\int \frac{\mathrm {d}^{3} p}{(2 \pi )^{3}}\left[ \frac{4 B\left( p^{2}\right) }{A^{2}\left( p^{2}\right) p^{2}+B^{2}\left( p^{2}\right) }-\frac{4m}{p^2+m^2}\right] . \end{aligned}$$
(5)

As we all know, the parameter can not reveal the nature of phase transition. To answer our question, we first write the expression of effective pressure, which is the negative value of the CJT effective potential:

$$\begin{aligned} \mathcal {P}'= & {} -Tr\left[ \ln (SS_0^{-1})+\frac{1}{2}(1-SS^{-1}_0)\right] \nonumber \\&+\frac{1}{2}Tr[\ln (DD^{-1}_0)+(1-DD_0^{-1})], \end{aligned}$$
(6)

where the \(D,D_0\) denote the full and free boson propagator, respectively. Because of the divergent integral, the differential pressure between the chiral symmetry breaking phase (b) and chiral symmetry phase (c) is often written as

$$\begin{aligned} \mathcal {P}=\Delta \mathcal {P}'=\mathcal {P}'_b-\mathcal {P}'_c. \end{aligned}$$
(7)

In the lowest-order approximation of DSE for the propagators, the propagator in chiral symmetry phase gives its free form and the differential pressure reduces to

$$\begin{aligned} \mathcal {P}=2\int \frac{\mathrm {d}^3p}{(2\pi )^3}\left[ \ln \left( \frac{p^2+B^2}{p^2+m^2}\right) -\frac{B^2}{p^2+B^2}+\frac{m}{p^2+m^2}\right] . \end{aligned}$$
(8)

Apart from zero temperature, the \(\mathcal {O}(3)\) symmetry of the system reduces to \(\mathcal {O}(2)\), and the corresponding inverse fermion propagator can be written as

$$\begin{aligned} S^{-1}(T, P)=i \mathbf {\gamma } \cdot \mathbf {P} +i \varpi _{n} \gamma _{0} +B\left( P^2\right) , \end{aligned}$$
(9)

where \(\varpi _{n}=(2n+1)\pi T\). The effective pressure at finite temperature can be written as

$$\begin{aligned} \mathcal {P}(T)=\frac{1}{\mathcal {V}} {\text {Tr}}\left[ \ln \left( \frac{1}{TS}\right) -\frac{1}{2} B S\right] . \end{aligned}$$
(10)

According to the discussion in Ref. [25], during the model calculation, the integral of pressure is divergent. In order to eliminate this problem, a little trick is used to deal with the divergence, and the pressure is given as

$$\begin{aligned} \mathcal {P}(T)= & {} \mathcal {P}(T)-\mathcal {P}_{0}(T)+\mathcal {P}_{0}(T) \nonumber \\= & {} 2 \int \frac{\mathrm {d}^{2} P}{(2 \pi )^{2}}\left[ \mathcal {E}_{p}-\mathcal {E}_{p 0}+2 T \ln \frac{e^{-\beta \mathcal {E}_{p}}+1}{e^{-\beta \mathcal {E}_{p 0}}+1}\right. \nonumber \\&\left. -\frac{B^{2}}{2 \mathcal {E}_{p}} \tanh \frac{\mathcal {E}_{p}}{2 T}+\frac{m^{2}}{2 \mathcal {E}_{p0}} \tanh \frac{\mathcal {E}_{p0}}{2 T}\right] +\mathcal {P}_{0}(T) , \end{aligned}$$
(11)

where \(\mathcal {E}_{p}=\sqrt{P^{2}+B^{2}(P^{2})}, \mathcal {E}_{p0}=\sqrt{P^{2}+m^2}\), \(\mathcal {P}_{0}(T)\) is the pressure for free fermion, and \(\mathcal {P}_{0}(T)\approx 0.573T^3\) at small mass. When T \(\rightarrow \) 0, Eq. (11) will reduce to Eq. (8), and in the high temperature limit, it will reduce to its free value, which meet our expectations.

As we can see from Eq. (11), once the fermion self-energy is known, we can obtain the effective pressure promptly. In the lowest order approximation of DSE for the fermion propagator, the fermion self-energy in infinite volume can be obtained

$$\begin{aligned}&B\left( P^{2}\right) \nonumber \\&\quad =m+ \sum _{n} \int \frac{\mathrm {d}^{2} K}{(2 \pi )^{2}} \frac{2 T B\left( K^{2}\right) }{\left[ \varpi _{n}^{2}+\mathcal {E}^{2}\left( K^{2}\right) \right] \left[ Q^{2}+\Pi \left( Q^{2}\right) \right] } \nonumber \\&\quad =m+ \int \frac{\mathrm {d}^{2} K}{(2 \pi )^{2}} \frac{B\left( K^{2}\right) \tanh \frac{\mathcal {E}\left( K^{2}\right) }{2 T}}{\mathcal {E}\left( K^{2}\right) \left[ Q^{2}+\Pi \left( Q^{2}\right) \right] }, \end{aligned}$$
(12)

where \(Q=P-K,~ \mathcal {E}\left( K^{2}\right) =\sqrt{K^{2}+B^{2}\left( K^{2}\right) }\) and the Matsubara frequency summation is used analytically. The corresponding photon polarization is given as

$$\begin{aligned} \Pi (Q^{2})=\frac{T}{\pi } \int _{0}^{1} \mathrm {d} x\left\{ \ln \left( 4 \cosh ^{2} \frac{X(x)}{2 T}\right) -\frac{m^{2} \tanh \frac{X(x)}{2 T}}{T X(x)}\right\} , \end{aligned}$$
(13)

where \(X^{2}(x)=m^{2}+x(1-x)Q^{2}\). As the fermion self-energy is obtained, we can adopt the pressure Eq. (11) to analyze the natural of thermal QED\(_3\) at \(T_c\).

2.2 Effect of finite volume

Taking the finite volume effect into account, we consider a system with limited boundary, which is constrained in a potential well in spatial directions, and the length of the well is \(L_{1}=L_{2}=L\). Based on the discussion in Refs. [21, 24], we adopt the antiperiodic boundary conditions for the fermion fields and write the momentum integral as a sum of Matsubara modes. Then we can obtain the fermion self-energy function at finite volume

$$\begin{aligned} B\left( \omega _{m_1}^{2}, \omega _{m_2}^{2}\right)= & {} m+\frac{1}{L^{2}} \sum _{n_{1}, n_{2}=-M}^{M} \nonumber \\&\times \frac{B\left( \omega _{n_1}^{2}, \omega _{n_2}^{2}\right) \tanh \frac{\mathcal {E}\left( \omega _{n_1}^{2}, \omega _{n_2}^{2}\right) }{2 T}}{\mathcal {E}\left( \omega _{n_1}^{2}, \omega _{n_2}^{2}\right) \left[ Q_{v}^{2}+\Pi \left( Q_{v}^{2}\right) \right] }, \end{aligned}$$
(14)

where \(\omega _{n}=(2n+1) \pi / L\) and \(Q_{v}^{2}=\left( \omega _{m_1}-\omega _{n_1}\right) ^{2}+\left( \omega _{m_2}-\omega _{n_2}\right) ^{2}\). The expression of the dynamical fermion self-energy shows a natural infrared cutoff \(\pi /L\), which is a typical finite size effect. This cutoff also implies that a system with finite volume will reveal some anomalous properties which is different from that in finite volume. In order to obtain the self-energy through numerical iteration method, the behavior of boson polarization should be investigated first.

Let us recall the one-loop order boson polarization tensor in infinite volume

$$\begin{aligned} \Pi _{\sigma \nu }(q)=- \int \frac{\mathrm {d}^{3} k}{(2 \pi )^{3}} {\text {Tr}}\left[ \frac{\gamma _{\sigma }(m-i \not \! k) \gamma _{\nu }(m-i \not \! p)}{\left( k^{2}+m^{2}\right) \left( p^{2}+m^{2}\right) }\right] , \end{aligned}$$
(15)

where \(q=p-k\). When the temperature and the volume become finite, the zero frequency boson polarization with massive fermion reduces to

$$\begin{aligned} \Pi (Q_{v}^{2})= & {} \Pi (\omega _{m_1}'^{2},\omega _{m_2}'^{2}) \nonumber \\= & {} \frac{2}{L^{2}} \sum _{n_1,n_2 = -M}^{M} \int _{0}^{1} \mathrm {d} x \Bigg [\frac{\tanh \left[ \frac{Y}{2 T}\right] }{Y} -\frac{U^{2}+m^{2}}{Y^{2}} \nonumber \\&\times \left( \frac{\tanh \left[ \frac{Y}{2 T}\right] }{Y}-\frac{{\text {sech}}^{2}\left[ \frac{Y}{2 T}\right] }{2 T}\right) \Bigg ], \end{aligned}$$
(16)

where \(Q_{v}^{2}=\omega _{m_1}'^{2}+\omega _{m_2}'^{2},~U^{2}=\omega _{n1}^{2}+\omega _{n2}^{2},\) and \(Y^{2}=U^{2}+m^{2}+x(1-x)Q_{v}^{2}\). Unlike the fermion fields, the boson fields is periodic at finite volume, and the Matsubara mode gives \(\omega '_{n}=2\pi n/L\).

In the chiral limit, the behavior of boson polarization and fermion self-energy were illustrated in Ref. [21]. Beyond the chiral limit, we make a extended investigation as demonstrated in Fig. 1. The results are consistent with that in the chiral limit, as we can find that lower system sizes fit the fixed upper bound better, which means that, with the increasing of system sizes, we should select a larger value of upper bounds. On the other hand, we find that as the upper limit of the summation increases, \(\Pi (Q^2_v)\) approaches the polarization value of the infinite system. Therefore, we expect that the description of boson polarization can agree well with that in the case of infinite volume, but the momentum here is not continuous, while is discrete.

Fig. 1
figure 1

The behaviors of boson polarization with different summation upper bounds (Left) and range of volume(with \(M=300\)) at \(T=0.01,m=0.01\) (Right), and the solid line \(L_{inf}\) illustrates the behavior of Eq. (13)

Full size image

The next step is to investigate the fermion self-energy beyond the chiral limit by numerical iteration method and choose a size-related sum of the upper limit \(M=M_1 =\frac{L}{2\pi }\), which can be seen in Fig. 2.

Fig. 2
figure 2

The behaviors of fermion self-energy with different summation upper bounds and range of volume and temperature(with \(L=300\)) at \(T=0.01,m=0.01\)

Full size image

It is shown that \(M_1\) is large enough to satisfy our upper summation limit and the fermion self-energy shrinks with the decrease of the size. Apart from the discussion of massless fermion in Ref. [21], when the mass of fermion increases, the fermion self-energy increases disproportionately as plotted in Fig. 3, which reveals a peculiar phenomenon and will be confirmed in the next section.

Fig. 3
figure 3

The value of fermion self-energy with different mass of \(L=300,T=0.01\)

Full size image

3 Numerical results

3.1 Massless fermion

To distinguish the characteristics of chiral phase transition in thermal QED\(_3\) at finite volume, we investigate the typical order parameter entropy and specific heat, and the procedure is conducted by numerical iteration method. In the actual calculation, we choose a size-related sum of the upper limit \(M_1\), which is large enough to ensure accuracy. Then, we obtain the dependence of \(\mathcal {P}\) on T and L, as well as the behavior of fermion chiral condensate, which can be seen in Fig. 4. With the increasing of temperature, the chiral fermion condensate diminishes gradually but does not suddenly jump to zero at a critical temperature \(T_{c}\), which increases with the increasing of system size. Over the critical temperature, the system switch from chiral symmetry breaking phase to chiral symmetric phase, and the pressure tends to converge, in spite of the fact that it behaves differently in different sizes under the chiral symmetry breaking phase, but this result does not reveal any information for the nature of CPT.

Fig. 4
figure 4

The dependence of the fermion chiral condensate (left) and pressure (right) on the temperature with several volume size

Full size image

It has commonly been assumed that the discontinuous of entropy indicates a first-order phase transition occur, whereas its continuous may show a higher-order phase transition. We can define the entropy as following trivially via the pressure

$$\begin{aligned} s(T)=\frac{\partial \mathcal {P}(T)}{\partial T}. \end{aligned}$$
(17)

We can calculate entropy directly through the pressure, and as plotted in the Fig. 5, the entropy also tends to converge in the symmetry phase and manifest an inflection point at \(T_c\) where CPT happens.

Fig. 5
figure 5

The dependence of entropy on the temperature with several volume size in the chiral limit

Full size image

To further study the nature, a typical order parameter to indicate a second-order phase transition can be depicted by specific heat, which is defined as

$$\begin{aligned} C_{v}=\frac{\partial s(T)}{\partial T}=\frac{\partial ^{2} \mathcal {P}(T)}{\partial T^{2}}. \end{aligned}$$
(18)

Derived from Eq. (11), we can obtain the specific heat as plotted in Fig. 6.

Fig. 6
figure 6

The behavior of special heat with several volume size in massless QED\(_3\)

Full size image

The values in chiral symmetry phase and chiral symmetry broken phase are continuous separately, but there is a skip at critical temperature \(T_{c}\), which exhibits a typical signal for second-order phase transition.

3.2 Massive fermion

Beyond the chiral limit, the fermion has a small nonzero mass m. In this section, we consider the system with different mass and investigate the characteristic of CPT in thermal massive QED\(_3\). For the purpose of comparison with massless fermion, we choose the same parameters as selected in the previous section, and the calculation process is similar, we plot the figures in Fig. 7.

Fig. 7
figure 7

The values of thermal parameters with different volume while \(m=10^{-4}\)

Full size image

It is clearly illustrated that, with a small mass, the chiral condensate with some size still vanishes at critical temperature, which is apparently different from that in infinite volume, which increases with the increasing of system size. Additionally, the pressure and the entropy still tend to converge in the chiral symmetry phase while they behave inconsistently in the chiral symmetry broken phase. The specific heat in chiral symmetry phase and chiral symmetry broken phase are continuous separately, and the leap at critical temperature \(T_{c}\) still releases a signal for second-order phase transition.

Fig. 8
figure 8

The values of thermal parameters with different mass at \(L=300\)

Full size image

Nevertheless, as the mass of fermion increases, this situation slowly but surely changes as we can see in Fig. 8. The chiral condensate enlarge as the mass increases, and stay at a small value but do not vanish, whereas the value of specific heat switching from jumping to continuous changing, which indicates a crossover. When the fermion mass surpass its critical value \(m_{c}\approx 5\times 10^{-4}\) at small volume, the specific heat changes continuously and hence CPT disappears. Just as we mentioned before, when the mass of fermion increases, the fermion self-energy changes atypically, which leads to the disappearance of CPT, this has not been discovered before. The phase diagram with fermion mass can be found in Fig. 9.

Fig. 9
figure 9

The phase diagram of thermal QED\(_3\) with several fermion mass (The solid line represents the phase boundary, and the undrawn part near the temperature axis illustrates a crossover)

Full size image

From Fig. 9, we find that, for a fixed fermion mass, the system, with the increasing temperature, undergoes a phase transition at critical size and reveals a crossover when the size is larger than its critical value. It is clearly show that the critical size depends on the fermion mass. Moreover, the dependence of the critical fermion mass on the volume size is shown in Fig. 10.

Fig. 10
figure 10

The dependence of critical fermion mass and volume size

Full size image

It is found that the value \(m_c\) decreases with the increasing volume size, and vanishes at \(1/L\rightarrow 0\) which means the system reveals a crossover with the increasing T for any nonzero fermion mass. This conclusion is consistent with that obtained in the previous analysis in the infinite volume [19].

4 Conclusions

In this paper, we adopt the truncated Dyson-Schwinger equation to study chiral phase transition in thermal QED\(_3\) under the influence of finite size effect. Our model study is based on the CJT effective potential framework and shows that, as the rise of temperature, the chiral condensate in chiral limit vanishes at a critical temperature \(T_{c}\), around which the entropy changes continuously, while the specific heat undergoes a jump from chiral symmetry broken phase to chiral symmetry phase, which exhibits a second-order phase transition. On the other hand, in the case of massive fermion with finite volume, the system also performs a second-order phase transition at small fermion mass, while it switches to a crossover when fermion mass exceeds its critical value \(m_c\), which reduces to zero in the infinite volume. This result shows that the effect of finite volume will cause the system to exhibit some abnormal feature. Since QED\(_3\) has many features, similar to QCD, we expect that the phase transition will occur in the thermal QCD with a small quark mass at finite volume.

We note that the adopted model in the present work is of course schematic and might be discrepant from reality (for example, we have neglected the effect of the wave function renormalization factor \(A\ne 1\) and the nonzero frequency of boson polarization). Nevertheless, this is the first time that one observes crossover and critical fermion mass \(m_c\) in thermal QED\(_3\) at finite volume. In order to further confirm this observation, we need to study this problem in more realistic models [26].