1 Introduction

Since Hawking reveals the thermal radiation of a scalar field on a collapsing black hole [1], the Hawking radiation is considered in different black hole systems, such as, the Hawking radiation of a spherical collapsing shell and of the Kerr–Newmann black hole [2,3,4], the Hawking radiation in the Hořava–Lifshitz gravity [5], and the Hawking radiation in the Einstein-dilaton-Gauss–Bonnet black hole [6]. The Hawking radiation is also considered for various kinds of fields, such as, the Hawking radiation of the Dirac particle in the Kerr black hole via tunneling [7], the Hawking radiation of spin-1 particles in a rotating hairy black hole and spin-2 particles in a static spherical black hole [8, 9], and the Hawking radiation of type-II Weyl fermions [10]. The Hawking radiation is also verified by different methods. The density matrix method is used in Refs. [11,12,13]. A path-integral calculation of the Hawking radiation is developed by Hawking and Hartle [14]. Based on the discontinuous jump of the field on the horizon, Ruffini and Damour provide a method to calculate the Hawking radiation in the Schwarzschild black hole [15], which is also called the tunneling mechanism [16]. The Hawking radiation may cause the information loss problem which is widely discussed in the black hole physics [17,18,19,20,21,22,23,24] .

The spacetime background of a real black hole is complicated, so we usually consider the asymptotic behavior of a quantum field on the horizon and at the null infinity in stead of the exact solution. Besides, there are few works which consider boundary conditions at the singularity and on the horizon. In our previous work [25, 26], we provide an exact solution of both scattering states and bound states of the scalar field on the Schwarzschild spacetime and the R-N spacetime. We also provide a new method for the scalar scattering problem in the Schwarzschild spacetime [27]. However, we have to deal with complicated special functions caused by the Schwarzschild spacetime background.

The universal property of a quantum field on a black hole spacetime deserves more discussions. There are some toy models about the Hawking radiation and the Unruh effect. The advantage of the toy model is that the spacetime is simple enough so that we can calculate the quantum field exactly on the entire spacetime with proper boundary conditions. Though the geometry is simple, the universal property of the spacetime is nontrivial. The best known model is the moving mirror model which is first considered by Davies and Fulling [28, 29]. The moving mirror model attracts renewed interests because of experimental developments [30,31,32] and the information loss problem of black holes [30, 33,34,35].

A black hole or a white hole is a universal geometry structure of the spacetime, which is irrelevant to local details of the metric. In this paper, we construct a toy black hole and a toy white hole by setting proper boundaries in the Minkowski spacetime. In the model, the local metric is trivial, but the universal structure is nontrivial.

We calculate the thermal effect in the black hole spacetime with the tunneling mechanism. The tunneling mechanism indicates the thermal effect should be regarded as the Hawking radiation.

The simplicity of the toy black hole allows us to concentrate on universal properties rather than local behaviors. Universal properties are closely related to boundary conditions. In this paper, the influence of the boundary condition at the singularity and the influence of the periodic boundary conditions in the Euclidean time method are discussed. We also suggest a classification scheme of states of the field by the behavior of the field on the horizon.

In addition, we show that the white hole has a thermal absorption.

In Sect. 2, we review the modern definitions of a black hole and a white hole and introduce the toy black hole model and the toy white hole model in the Minkowski spacetime. In Sect. 3, we calculate the thermal effect on the black hole spacetime and discuss the relation between the Hawking radiation and the Unruh effect. In Sect. 4, we discuss the role of boundary conditions. The results in this section are used to discuss the information loss problem in conclusions. In Sect. 5, we show that a white hole has a thermal absorption. Conclusions are presented in Sect. 6.

2 Black hole and white hole in Minkowski spacetime

2.1 Modern definition of black hole and white hole: brief review

In this section, we introduce the modern definitions of a black hole and a white hole.

The black hole is first recognized as a region of a spacetime where the gravity is so strong so that nothing can escape. The boundary of a black hole is called the event horizon. Later on, physicists realize that a black hole is a global structure of a spacetime which is irrelevant to the local metric structure. The notion of a black hole is not properly captured by the strength of the gravity. According to the equivalence principle, the gravity disappears in a comoving frame and there is no observable effect for a freely falling observer passing the horizon. The curvature on the horizon of a supermass black hole can be very small. The notion that nothing can escape should also be carefully treated since any point cannot escape from its causal future. The above viewpoint provides a global definition (or a geometrical definition) of a black hole. The black hole is defined as a region that nothing in it can escape to the future null infinity [36]

$$\begin{aligned} B=M-J^{-}\left( \mathcal {J}^{+}\right) , \end{aligned}$$
(2.1)

where M is the entire spacetime, \(\mathcal {J}^{+}\) is the future null infinity, and \(J^{-}\left( \mathcal {J}^{+}\right) \) is the causal past of \(\mathcal {J}^{+}\). One can find more details of the definition in Ref. [36].

Similarly, we can construct a white hole in the Minkowski spacetime. A white hole is defined as a region [36]

$$\begin{aligned} W=M-J^{+}\left( \mathcal {J}^{-}\right) , \end{aligned}$$
(2.2)

where M is the entire spacetime, \(\mathcal {J}^{-}\) is the past null infinity, and \(J^{+}\left( \mathcal {J}^{-}\right) \) is the causal future of \(\mathcal {J}^{-}\).

2.2 Model of black hole and white hole

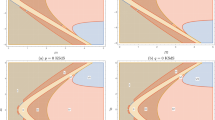
According to the definition (2.1), we construct a black hole by setting a boundary in the Minkowski spacetime.

For simplicity, we consider the 1+1-dimensional case. The metric of the Minkowski spacetime reads

$$\begin{aligned} ds^{2}=-dt^{2}+dx^{2}. \end{aligned}$$
(2.3)

We set a boundary at

$$\begin{aligned} t=\sqrt{x^{2}+\eta ^{2}},\quad t>0, \end{aligned}$$
(2.4)

as shown in Fig. 1. By the definition (2.1), the region II in Fig. 1 is a black hole. The boundary \(t=\sqrt{x^{2}+\eta ^{2}}\) is the spacetime singularity and \(t=x\) between the region I and the region II is the event horizon.

Similarly, the white hole can be constructed by setting a boundary at

$$\begin{aligned} t=-\sqrt{x^{2}+\eta ^{2}},\text { }t<0 \end{aligned}$$
(2.5)

as shown in Fig. 2. The boundary \(t=-\sqrt{x^{2}+\eta ^{2}}\) is the spacetime singularity and \(t=-x\) between the region I and the region IV is the horizon.

The black hole and the white hole constructed in the Minkowski spacetime are toy models, they are used to clarify theoretical properties of the black hole. Since the singularity in the spacetime is spacelike, we cannot simulate them with moving mirrors in reality.

Fig. 1
figure 1

Toy black hole

Full size image
Fig. 2
figure 2

Toy white hole

Full size image

3 Thermal effect in black hole spacetime

In this section, we discuss the thermal effect in the toy black hole spacetime. We show that the thermal effect can be regarded as both the black hole radiation and the Unruh effect. For simplicity, we consider a massless scalar field \(\phi \)

$$\begin{aligned} \left( -\frac{\partial ^{2}}{\partial t^{2}}+\frac{\partial ^{2}}{\partial x^{2}}\right) \phi =0. \end{aligned}$$
(3.1)

In Refs. [15, 16, 37,38,39] , the authors show that the field has a discontinuous jump on the horizon of a black hole which should be regarded as a scattering. The scattering implies the creation of particles on the horizon which is the black hole radiation.

We calculate the thermal effect with the tunneling mechanism so that the thermal effect of the black hole in this paper should be regarded as the black hole radiation.

We introduce new coordinates \(\left( \tau ,\xi \right) \). In the region I,

$$\begin{aligned} t&=\frac{1}{a}e^{a\xi }\sinh \left( a\tau \right) ,\nonumber \\ x&=\frac{1}{a}e^{a\xi }\cosh \left( a\tau \right) , \end{aligned}$$
(3.2)

with \(\tau \in \left( -\infty ,\infty \right) \) and \(\xi \in \left( -\infty ,\infty \right) \). In the region II,

$$\begin{aligned} t&=\frac{1}{a}e^{a\xi }\cosh \left( a\tau \right) ,\nonumber \\ x&=\frac{1}{a}e^{a\xi }\sinh \left( a\tau \right) , \end{aligned}$$
(3.3)

with \(\tau \in \left( -\infty ,\infty \right) \) and \(\xi \in \left( -\infty ,\frac{1}{a}\ln \left( a\eta \right) \right) \). The coordinates \(\left( \tau ,\xi \right) \) in the region I is the comoving coordinates of an uniformly accelerated observer with a proper acceleration a. Without loss of generality, we require \(a>0\). The equation of a massless field in coordinates \(\left( \tau ,\xi \right) \) is

$$\begin{aligned} \left( -\frac{\partial ^{2}}{\partial \tau ^{2}}+\frac{\partial ^{2}}{\partial \xi ^{2}}\right) \phi =0. \end{aligned}$$
(3.4)

Defining

$$\begin{aligned} \phi =T\left( \tau \right) X\left( \xi \right) , \end{aligned}$$
(3.5)

with the separation of variables, we have

$$\begin{aligned} -\frac{\partial ^{2}}{\partial \tau ^{2}}T\left( \tau \right) =-\frac{\partial ^{2}}{\partial \xi ^{2}}X\left( \xi \right) =k^{2}, \end{aligned}$$
(3.6)

where k is the eigenvalue.

For each \(k>0\), we denote the out-going wave by

$$\begin{aligned} \phi _{k}^{\text {out}}=e^{ik\left( \tau -\xi \right) } \end{aligned}$$
(3.7)

and the in-going wave by

$$\begin{aligned} \phi _{k}^{\text {in}}=e^{ik\left( \tau +\xi \right) }. \end{aligned}$$
(3.8)

With Eqs. (3.2) and (3.3), we have

$$\begin{aligned} \phi _{k}^{I\text { out}}&=e^{ik\left( \tau -\xi \right) }=e^{-i\frac{k}{a}\ln \left( ax-at\right) },\nonumber \\ \phi _{k}^{II\text { out}}&=e^{ik\left( \tau -\xi \right) }=e^{-i\frac{k}{a}\ln \left( at-ax\right) }. \end{aligned}$$
(3.9)

There exists a scattering on the horizon and the amplitude is

$$\begin{aligned} \lim _{t\rightarrow x}\frac{\phi _{k}^{I\text { out}}}{\phi _{k}^{II\text { out}} }= & {} \lim _{t\rightarrow x}\frac{e^{-i\frac{k}{a}\ln \left( ax-at\right) } }{e^{-i\frac{k}{a}\ln \left( at-ax\right) }}\nonumber \\= & {} \lim _{t\rightarrow x} \frac{e^{-i\frac{k}{a}\left[ \ln \left( at-ax\right) +\ln \left( -1\right) \right] }}{e^{-i\frac{k}{a}\ln \left( at-ax\right) }}=e^{-\frac{\pi k}{a}}. \end{aligned}$$
(3.10)

The superscripts “I” and “II” denote the field in corresponding regions. In the above calculation, \(\ln \left( -1\right) =-i\pi \) is used. By the standard procedure in Refs. [15, 39], the scattering probability is

$$\begin{aligned} P_{k}=\left( \lim _{t\rightarrow x}\frac{\phi _{k}^{I}}{\phi _{k}^{II}}\right) ^{2}=e^{-\frac{2\pi k}{a}}. \end{aligned}$$
(3.11)

The probability of creating n particles is

$$\begin{aligned} p_{n}=CP_{k}^{n}, \end{aligned}$$
(3.12)

where C is the normalization constant. With the normalization of the probability

$$\begin{aligned} \sum _{n=0}^{\infty }p_{n}=1, \end{aligned}$$
(3.13)

we obtain

$$\begin{aligned} C=1-e^{-\frac{2\pi k}{a}}. \end{aligned}$$
(3.14)

The average particle number

$$\begin{aligned} \left\langle N\right\rangle =\sum _{n=0}^{\infty }np_{n}=\frac{1}{e^{\frac{2\pi k}{a}-1}} \end{aligned}$$
(3.15)

satisfies a bose distribution. That is, the horizon have a temperature

$$\begin{aligned} T=\frac{a}{2\pi }. \end{aligned}$$
(3.16)

The scattering does not happen for in-going waves. With Eqs. (3.2) and (3.3), we have

$$\begin{aligned} \lim _{t\rightarrow x}\frac{\phi _{k}^{I\text { in}}}{\phi _{k}^{II\text { in}} }=\lim _{t\rightarrow x}\frac{e^{i\frac{k}{a}\ln \left( at+ax\right) } }{e^{i\frac{k}{a}\ln \left( at+ax\right) }}=1. \end{aligned}$$
(3.17)

With the tunneling mechanism, we see that the black hole radiates thermally while absorbs all in-going waves. In a word, the thermal effect is a black hole radiation.

On the other hand, the region I is the Rindler spacetime and one can calculate the thermal effect with the Bogolyubov transformation method [40] or the Euclidean time method [41] as the Unruh effect. In addition, we find that the temperature \(T=\frac{a}{2\pi }\) is irrelevant to the sole parameter \(\eta \) of the black hole.

The thermal effect can be regraded as both the black hole radiation and the Unruh effect in the model. This fact indicates that the black hole radiation has the same physical mechanism with the Unruh effect in the model.

Actually, the Bogolyubov transformation method and the Euclidean time method are also used to calculate the Hawking radiation of a black hole in a curved spacetime. The Bogolyubov transformation in a black hole spacetime only involves a inertial frame at infinity and a uniform acceleration frame (a freely falling frame) on the horizon, which is the same with the Unruh effect.

4 Role of boundary condition

In this section, we discuss the role of boundary conditions. The boundary conditions will influence universal properties of the field on a black hole spacetime.

For simplicity, we use following boundary conditions in the black hole spacetime.

First, the field \(\phi \) vanishes at the singularity

$$\begin{aligned} \left. \phi \right| _{t=\sqrt{x^{2}+\eta ^{2}}}=0. \end{aligned}$$
(4.1)

Second, the field \(\phi \) is continuous on the horizon

$$\begin{aligned} \lim _{t-x\rightarrow 0^{+}}\phi =\lim _{t-x\rightarrow 0^{-}}\phi . \end{aligned}$$
(4.2)

Third, the field \(\phi \) is finite everywhere.

In addition, we point that a periodic boundary condition is applied in the Euclidean time method.

4.1 Boundary condition at singularity

In this section, we show the role of the boundary condition at the singularity.

The general solution of Eq. (3.1) is

$$\begin{aligned} \phi =f\left( t-x\right) +h\left( t+x\right) , \end{aligned}$$
(4.3)

where f and h are arbitrary functions representing out-going modes and in-going modes, respectively. Substituting the boundary condition (2.4) into Eq. (4.3), we get

$$\begin{aligned} f\left( \sqrt{x^{2}+\eta ^{2}}-x\right) +h\left( \sqrt{x^{2}+\eta ^{2} }+x\right) =0. \end{aligned}$$
(4.4)

Equation (4.4) can also be expressed as

$$\begin{aligned} h\left( z\right) =-f\left( \frac{\eta ^{2}}{z}\right) , \quad z>0 \end{aligned}$$
(4.5)

with \(z\equiv \sqrt{x^{2}+\eta ^{2}}-x\). That is, the boundary condition at the singularity is a constraint for the field.

We emphasize that in Eq. (4.4), variables of f and h are positive. That is, as a restriction, Eq. (4.4) is not effective on all in-going modes and out-going modes.

Inside the horizon (region II) \(t-x>0\) and \(t+x>0\), so \(f\left( t-x\right) \) and \(h\left( t+x\right) \) must satisfy the relation (4.4). This means that each out-going mode \(f\left( t-x\right) \) equals to an in-going mode \(h\left( t+x\right) =-f\left( \frac{\eta ^{2}}{t+x}\right) \). When \(f\left( t-x\right) =0\), we have \(h\left( t+x\right) =-f\left( \frac{\eta ^{2}}{t+x}\right) =0\).

Conversely, outside the horizon (region I) \(t+x>0\) and \(t-x<0\), so the in-going mode \(h\left( t+x\right) \) is restrained by the relation (4.4) while the out-going mode \(f\left( t-x\right) \) is no longer restrained by the relation (4.4). That is, outside the horizon, even though \(h\left( t+x\right) =0\), \(f\left( t-x\right) \) may still be nonvanishing. So there may exist more out-going modes than in-going modes. The extra out-going modes can only exist outside the horizon (region I). Since the horizon is thermal, extra out-going modes in the region I satisfy the thermal distribution. Extra out-going modes come from the horizon and go to the future null infinite, which is the physical picture of the Hawking radiation.

4.2 Boundary condition in Euclidean time method

The thermal effect can also be obtained by the Euclidean time method. A periodic boundary condition is imposed on the field in the Euclidean time method. That is, the imaginary time have a period of \(2\pi \). In this section, we show that the periodic boundary condition leads to the divergence of the field, which means we should be more careful with the Euclidean time method.

We introduce new coordinates \(\left( r,\theta \right) \) in the region I

$$\begin{aligned} t&=r\sinh \theta ,\nonumber \\ x&=r\cosh \theta \end{aligned}$$
(4.6)

with \(r\in \left( 0,\infty \right) \) and \(\theta \in \left( -\infty ,\infty \right) \). With coordinates \(\left( r,\theta \right) \), the metric in the region I reads

$$\begin{aligned} ds^{2}=-r^{2}d\theta ^{2}+dr^{2}. \end{aligned}$$
(4.7)

The coordinate \(\theta \) should be regarded as the time coordinate. We introduce the imaginary time

$$\begin{aligned} \tau =i\theta \end{aligned}$$
(4.8)

and the metric becomes

$$\begin{aligned} ds^{2}=dr^{2}+r^{2}d\tau ^{2}. \end{aligned}$$
(4.9)

There is no singularity in the region I, so \(\tau \) should have a period \(2\pi \).

The field equation of the massless scalar field in coordinates \(\left( r,\theta \right) \) (4.6) is

$$\begin{aligned} \left( -\frac{\partial ^{2}}{\partial \theta ^{2}}+r^{2}\frac{\partial ^{2} }{\partial r^{2}}+r\frac{\partial }{\partial r}\right) \phi =0. \end{aligned}$$
(4.10)

Defining

$$\begin{aligned} \phi =R\left( r\right) \Theta \left( \theta \right) , \end{aligned}$$
(4.11)

with the separation of variables, we have

$$\begin{aligned} -\left( r^{2}\frac{\partial ^{2}}{\partial r^{2}}+r\frac{\partial }{\partial r}\right) R\left( r\right) =-\frac{\partial ^{2}}{\partial \theta ^{2}} \Theta \left( \theta \right) =k^{2}, \end{aligned}$$
(4.12)

where k is the eigenvalue.

For a single k, the solution is

$$\begin{aligned} \phi _{k}\left( r,\theta \right) =\left( A_{k}e^{ik\ln r}+B_{k}e^{-ik\ln r}\right) e^{ik\theta }. \end{aligned}$$
(4.13)

When we apply the periodic boundary condition on \(\phi _{k} \), we have

$$\begin{aligned} \phi _{k}\left( r,\theta \right)&=\phi _{k}\left( r,\theta +2\pi i\right) ,\nonumber \\ e^{ik\theta }&=e^{ik\left( \theta +2\pi i\right) },\nonumber \\ k&=im, \quad m\in Z \end{aligned}$$
(4.14)

However, when \(k=im\), \(e^{ik\ln r}\) diverges at \(r=0\) while \(e^{-ik\ln r}\) diverges at \(r\rightarrow \infty \).

That is, the Euclidean time method will lead to the divergence of the field. Actually, we can define the complex time

$$ T\equiv t+i\tau . $$

If we require that the field is finite everywhere, the field must be periodic along the t direction. On the other hand, we require the field is periodic along the \(\tau \) direction so that the field of \(\psi \left( T\right) \) is double periodic. That is impossible for a function \(\psi \) on the complex plane.

4.3 Classification of state by boundary condition on the horizon

With the asymptotic behavior at spacelike infinity, the field can be classified as bound states and scattering states. In our previous work, we develop the gravitational wave scattering theory without large-distance asymptotics [42]. When we concern bound states and scattering states, only the field outside the horizon (region I) is considered. The classification of bound states and scattering states is irrelevant to the black hole.

In this section, we classify states of the field by the behavior of field on both sides of the horizon. Generally, a particle can stay inside the black hole, stay outside the black hole or stay both outside and inside the black hole. If a continuous field does not vanish inside the black hole while vanishes outside the black hole, we call it a confined state. If a continuous field does not vanish both inside the black hole and outside the black hole, we call it an entanglement state.

We first provide bound states and scattering states of the massless field and the massive field on the black hole.

It is convenient to use coordinates \(\left( \tau ,\xi \right) \) defined in Eq. (3.2) (\(\tau \in \left( -\infty ,\infty \right) \), \(\xi \in \left( -\infty ,\infty \right) \), \(a>0\)) outside the horizon. Field equations of the massless field and the massive field are

$$\begin{aligned} \left( -\frac{\partial ^{2}}{\partial \tau ^{2}}+\frac{\partial ^{2}}{\partial \xi ^{2}}\right) \phi _{\text {nm}}^{I}&=0, \end{aligned}$$
(4.15)
$$\begin{aligned} \left( -\frac{\partial ^{2}}{\partial \tau ^{2}}+\frac{\partial ^{2}}{\partial \xi ^{2}}-m^{2}e^{2a\xi }\right) \phi _{\text {m}}^{I}&=0, \end{aligned}$$
(4.16)

where \(\phi _{\text {nm}}^{I}\) represents the massless field outside the horizon and \(\phi _{\text {m}}^{I}\) represents the massive field outside the horizon.

Defining

$$\begin{aligned} \phi _{\text {nm}}^{I}&=T_{\text {nm}}^{I}\left( \tau \right) X_{\text {nm} }^{I}\left( \xi \right) , \end{aligned}$$
(4.17)
$$\begin{aligned} \phi _{\text {m}}^{I}&=T_{\text {m}}^{I}\left( \tau \right) X_{\text {m}} ^{I}\left( \xi \right) , \end{aligned}$$
(4.18)

and with the separation of variables, we have

$$\begin{aligned} -\frac{\partial ^{2}}{\partial \tau ^{2}}T_{\text {nm}}^{I}\left( \tau \right)&=-\frac{\partial ^{2}}{\partial \xi ^{2}}X_{\text {nm}}^{I}\left( \xi \right) =k^{2}, \end{aligned}$$
(4.19)
$$\begin{aligned} -\frac{\partial ^{2}}{\partial \tau ^{2}}T_{\text {m}}^{I}\left( \tau \right)&=\left( -\frac{\partial ^{2}}{\partial \xi ^{2}}+m^{2}e^{2a\xi }\right) X_{\text {m}}^{I}\left( \xi \right) =k^{2}, \end{aligned}$$
(4.20)

where k is the eigenvalue. Solutions for single k are

$$\begin{aligned} \phi _{\text {nm }k}^{I}&=\left( A_{\text {nm }k}^{I}e^{ik\tau }+B_{\text {nm }k}^{I}e^{-ik\tau }\right) \left( C_{\text {nm }k}^{I}e^{ik\xi }+D_{\text {nm }k}^{I}e^{-ik\xi }\right) , \end{aligned}$$
(4.21)
$$\begin{aligned} \phi _{\text {m }k}^{I}&=\left( A_{\text {m }k}^{I}e^{ik\tau }+B_{\text {m } k}^{I}e^{-ik\tau }\right) \left( C_{\text {m }k}^{I}\tilde{I}_{k}\left( \frac{m}{a}e^{a\xi }\right) +D_{\text {m }k}^{I}\tilde{K}_{k}\left( \frac{m}{a}e^{a\xi }\right) \right) , \end{aligned}$$
(4.22)

where \(A_{\text {nm }k}^{I}\) (\(A_{\text {m }k}^{I}\)), \(B_{\text {nm }k}^{I}\) (\(B_{\text {m }k}^{I}\)), \(C_{\text {nm }k}^{I}\) (\(C_{\text {m }k}^{I}\)) and \(D_{\text {nm }k}^{I}\) (\(D_{\text {m }k}^{I}\)) are expansion coefficients, \(\tilde{I}_{k}\), and \(\tilde{K}_{k}\) are defined as [43]

$$\begin{aligned} \tilde{I}_{k}\left( x\right)&\equiv {\text {Re}}\left( I_{ik}\left( x\right) \right) ,\\ \tilde{K}_{k}\left( x\right)&\equiv K_{ik}\left( x\right) \end{aligned}$$

with \(I_{ik}\) and \(K_{ik}\) modified Bessel functions of the first kind and the second kind.

Now, we show that \(\phi _{\text {nm }k}^{I}\) is a scattering state and \(\phi _{\text {m }k}^{I}\) is a bound state.

When k is pure imaginary, such as \(k=i\nu \) and \(\nu >0\), the field diverges either at \(\tau \rightarrow \infty \) or at \(\tau \rightarrow -\infty \). That is, k must be a real number.

The massless field \(\phi _{\text {nm }k}^{I}\) is nonvanishing at \(\xi \rightarrow +\infty \), that is, \(\phi _{\text {nm }k}^{I}\) is a scattering state. With [43]

$$\begin{aligned} \lim _{x\rightarrow +\infty }\tilde{I}_{k}\left( x\right)&=\frac{1}{\sqrt{2\pi x}}e^{x}\left( 1+O\left( \frac{1}{x}\right) \right) ,\nonumber \\ \lim _{x\rightarrow +\infty }\tilde{K}_{k}\left( x\right)&=\sqrt{\frac{\pi }{2x}}e^{-x}\left( 1+O\left( \frac{1}{x}\right) \right) , \end{aligned}$$
(4.23)

\(\tilde{I}_{k}\left( \frac{m}{a}e^{a\xi }\right) \) diverges at \(\xi \rightarrow +\infty \). So we must choose

$$ C_{\text {m }k}^{I}=0. $$

When \(\xi \rightarrow +\infty \),

$$\begin{aligned} \phi _{\text {m }k}^{I}\sim \tilde{K}_{k}\left( \frac{m}{a}e^{a\xi }\right) \rightarrow 0. \end{aligned}$$
(4.24)

That is, \(\phi _{\text {m }k}^{I}\) is a bound state.

Now, we talk about the confined state and the entanglement state.

To obtain a confined state, we need

$$\begin{aligned} \phi ^{I}&=0,\nonumber \\ \left. \phi ^{II}\right| _{\text {horizon}}&=0. \end{aligned}$$
(4.25)

When we choose

$$ C_{\text {nm }k}^{I}=D_{\text {nm }k}^{I}=C_{\text {m }k}^{I}=D_{\text {m }k} ^{I}=0, $$

we have \(\phi ^{I}=0\) for both the massless field and the massive field.

Now we consider the field inside the horizon. It is convenient to use coordinates \(\left( \tau ,\xi \right) \) (\(\tau \in \left( -\infty ,\infty \right) \), \(\xi \in \left( -\infty ,\frac{1}{a}\ln \left( a\eta \right) \right) \), \(a>0\)) defined in Eq. (3.3). The horizon locates at \(\xi \rightarrow -\infty \). Inside the horizon (region II), field equations of the massless field and the massive field are

$$\begin{aligned} \left( -\frac{\partial ^{2}}{\partial \tau ^{2}}+\frac{\partial ^{2}}{\partial \xi ^{2}}\right) \phi _{\text {nm}}^{II}&=0, \end{aligned}$$
(4.26)
$$\begin{aligned} \left( -\frac{\partial ^{2}}{\partial \tau ^{2}}+\frac{\partial ^{2}}{\partial \xi ^{2}}+m^{2}e^{2a\xi }\right) \phi _{\text {m}}^{II}&=0, \end{aligned}$$
(4.27)

where \(\phi _{\text {nm}}^{II}\) represents the massless field and \(\phi _{\text {m}}^{II}\) represents the massive field.

Defining

$$\begin{aligned} \phi _{\text {nm}}^{II}&=T_{\text {nm}}^{II}\left( \tau \right) X_{\text {nm}}^{II}\left( \xi \right) , \end{aligned}$$
(4.28)
$$\begin{aligned} \phi _{\text {m}}^{II}&=T_{\text {m}}^{II}\left( \tau \right) X_{\text {m} }^{II}\left( \xi \right) , \end{aligned}$$
(4.29)

and with the separation of variables, we have

$$\begin{aligned} -\frac{\partial ^{2}}{\partial \tau ^{2}}T_{\text {nm}}^{I}\left( \tau \right)&=-\frac{\partial ^{2}}{\partial \xi ^{2}}X_{\text {nm}}^{I}\left( \xi \right) =k^{2}, \end{aligned}$$
(4.30)
$$\begin{aligned} -\frac{\partial ^{2}}{\partial \tau ^{2}}T_{\text {m}}^{I}\left( \tau \right)&=-\left( \frac{\partial ^{2}}{\partial \xi ^{2}}+m^{2}e^{2a\xi }\right) X_{\text {m}}^{I}\left( \xi \right) =k^{2}, \end{aligned}$$
(4.31)

where k is the eigenvalue. Solutions for single k are

$$\begin{aligned} \phi _{\text {nm }k}^{II}&=\left( A_{\text {nm }k}^{II}e^{ik\tau }+B_{\text {nm }k}^{II}e^{-ik\tau }\right) \left( C_{\text {nm }k}^{II} e^{ik\xi }+D_{\text {nm }k}^{II}e^{-ik\xi }\right) , \end{aligned}$$
(4.32)
$$\begin{aligned} \phi _{\text {m }k}^{II}&=\left( A_{\text {m }k}^{II}e^{ik\tau }+B_{\text {m }k}^{II}e^{-ik\tau }\right) \left( C_{\text {m }k}^{II}\tilde{J}_{k}\left( \frac{m}{a}e^{a\xi }\right) +D_{\text {m }k}^{II}\tilde{Y}_{k}\left( \frac{m}{a}e^{a\xi }\right) \right) . \end{aligned}$$
(4.33)

where \(A_{\text {nm }k}^{II}\) (\(A_{\text {m }k}^{II}\)), \(B_{\text {nm }k}^{II}\) (\(B_{\text {m }k}^{II}\)), \(C_{\text {nm }k}^{II}\) (\(C_{\text {m }k}^{II}\)) and \(D_{\text {nm }k}^{II}\) (\(D_{\text {m }k}^{II}\)) are expansion coefficients, \(\tilde{J}_{k}\) and \(\tilde{Y}_{k}\) are defined as [43]

$$\begin{aligned} \tilde{J}_{k}\left( x\right)&\equiv {\text {sech}}\left( \frac{1}{2}k\pi \right) {\text {Re}}\left( J_{ik}\left( x\right) \right) ,\nonumber \\ \tilde{Y}_{k}\left( x\right)&\equiv {\text {sech}}\left( \frac{1}{2}k\pi \right) {\text {Re}}\left( Y_{ik}\left( x\right) \right) \end{aligned}$$
(4.34)

with \(J_{ik}\) and \(Y_{ik}\) Bessel functions of the first kind and the second kind.

When k is pure imaginary, such as \(k=i\nu \) and \(\nu >0\), the field diverges either at \(\tau \rightarrow \infty \) or at \(\tau \rightarrow -\infty \). That is, k must be a real number.

The massless field \(\phi _{\text {nm }k}^{II}\) is oscillating on the horizon so that there is no confined states for the massless field. With [43]

$$\begin{aligned} \lim _{x\rightarrow 0^{+}}\tilde{J}_{k}\left( x\right)&=\sqrt{\frac{2\tanh \left( \frac{1}{2}\pi k\right) }{\pi k}}\cos \left( k\ln \left( \frac{1}{2}x\right) -\gamma _{k}\right) +O\left( x^{2}\right) ,\\ \lim _{x\rightarrow 0^{+}}\tilde{Y}_{k}\left( x\right)&=\sqrt{\frac{2\coth \left( \frac{1}{2}\pi k\right) }{\pi k}}\sin \left( k\ln \left( \frac{1}{2}x\right) -\gamma _{k}\right) +O\left( x^{2}\right) , \end{aligned}$$

where \(\gamma _{k}\) is the Euler’s constant, the massive field \(\phi _{\text {m }k}^{II}\) is also oscillating on the horizon. That is, there is no confined states for the massive field neither.

We provide another simpler method to show that there is no confined states for the massless field. The general solution of the massless field inside the black hole is present in Eq. (4.3)

$$ \phi =f\left( t-x\right) +h\left( t+x\right) . $$

Substituting the boundary condition of the confined state (2.4) and (4.25) into Eq. (4.3), we have

$$ \phi =0. $$

That is, there is no confined states for the massless field.

In a word, there is no confined state on the black hole. This result means that a particle coming into the horizon either collapses into the singularity or stays in an entanglement state.

5 White hole thermal absorption

In this section, we show that a white hole possesses a thermal absorption. First, we show that the white hole should possess an absorption rather than a radiation qualitatively. Second, we calculate the white hole thermal absorption quantitatively.

In order to show the white hole absorption, we consider a massless scalar field \(\phi \) in Eq. (3.1) on the white hole spacetime.

For simplicity, we use the following boundary condition in the white hole spacetime

$$\begin{aligned} \left. \phi \right| _{t=-\sqrt{x^{2}+\eta ^{2}}}=0. \end{aligned}$$
(5.1)

The general solution of Eq. (3.1) is Eq. (4.3)

$$ \phi =f\left( t-x\right) +h\left( t+x\right) , $$

where f and h are arbitrary functions representing out-going modes and in-going modes, respectively. Substituting the boundary condition (5.1) into the general solution, we obtain

$$\begin{aligned} \phi =f\left( -\sqrt{x^{2}+\eta ^{2}}-x\right) +h\left( -\sqrt{x^{2}+\eta ^{2}}+x\right) =0. \end{aligned}$$
(5.2)

Equation (5.2) can also be expressed as

$$\begin{aligned} h\left( z\right) =-f\left( \frac{\eta ^{2}}{z}\right) ,\text { }z<0 \end{aligned}$$
(5.3)

with \(z\equiv -\sqrt{x^{2}+\eta ^{2}}-x\).

In Eq. (5.2), variables of f and h are negative. That is, as a restriction, Eq. (5.2) is not effective on all in-going modes and out-going modes.

Inside the white hole (region IV), \(t-x<0\) and \(t+x<0\), so \(f\left( t-x\right) \) and \(h\left( t+x\right) \) must satisfy the relation (5.2). This means that each out-going mode \(f\left( t-x\right) \) equals to an in-going mode \(h\left( t+x\right) =-f\left( \frac{\eta ^{2} }{t+x}\right) \). When \(f\left( t-x\right) =0\), we have \(h\left( t+x\right) =-f\left( \frac{\eta ^{2}}{t+x}\right) =0\).

Conversely, outside the white hole (region I) \(t+x>0\) and \(t-x<0\), so the out-going mode \(f\left( t-x\right) \) is restrained by the relation (5.2) while the in-going mode \(h\left( t+x\right) \) is no longer restrained by the relation (5.2). That is, outside the white hole, even though \(f\left( t-x\right) =0\), \(h\left( t+x\right) \) may still be nonvanishing. So there may exist more in-going modes than out-going modes. Extra in-going modes come from the null infinity and go into the white hole, which indicates that the white hole has a absorption.

The fact that the white hole absorption is thermal can be deduced by the tunneling mechanism.

We introduce new coordinates \(\left( \tau ,\xi \right) \) in region IV,

$$\begin{aligned} t&=-\frac{1}{a}e^{a\xi }\cosh \left( a\tau \right) ,\nonumber \\ x&=-\frac{1}{a}e^{a\xi }\sinh \left( a\tau \right) , \end{aligned}$$
(5.4)

with \(a>0\), \(\tau \in \left( -\infty ,\infty \right) \) and \(\xi \in \left( -\infty ,\frac{1}{a}\ln \left( a\eta \right) \right) \). Coordinates \(\left( \tau ,\xi \right) \) in region I are defined in Eq. (3.2)

$$\begin{aligned} t&=\frac{1}{a}e^{a\xi }\sinh \left( a\tau \right) ,\\ x&=\frac{1}{a}e^{a\xi }\cosh \left( a\tau \right) , \end{aligned}$$

with \(\tau \in \left( -\infty ,\infty \right) \) and \(\xi \in \left( -\infty ,\infty \right) \).

For each \(k>0\), we denote the out-going wave by

$$\begin{aligned} \phi _{k}^{\text {out}}=e^{ik\left( \tau -\xi \right) } \end{aligned}$$
(5.5)

and the in-going wave by

$$\begin{aligned} \phi _{k}^{\text {in}}=e^{ik\left( \tau +\xi \right) }. \end{aligned}$$
(5.6)

With Eqs. (3.2) and (5.4), we have

$$\begin{aligned} \phi _{k}^{I\text { in}}&=e^{ik\left( \tau +\xi \right) }=e^{i\frac{k}{a} \ln \left( at+ax\right) },\nonumber \\ \phi _{k}^{IV\text { in}}&=e^{ik\left( \tau +\xi \right) }=e^{i\frac{k}{a}\ln \left( -at-ax\right) }. \end{aligned}$$
(5.7)

There exists a scattering for the out-going wave on the horizon and the amplitude is

$$\begin{aligned} \lim _{t\rightarrow x}\frac{\phi _{k}^{I\text { in}}}{\phi _{k}^{IV\text { in}} }=\lim _{t\rightarrow x}\frac{e^{i\frac{k}{a}\ln \left( at+ax\right) } }{e^{i\frac{k}{a}\ln \left( -at-ax\right) }}=\lim _{t\rightarrow x} \frac{e^{i\frac{k}{a}\ln \left( at+ax\right) }}{e^{i\frac{k}{a}\left[ \ln \left( at+ax\right) ++\ln \left( -1\right) \right] }}=e^{-\frac{\pi k}{a}}. \end{aligned}$$
(5.8)

The superscript “I” and “IV” denote the field in corresponding regions. In the above calculation, \(\ln \left( -1\right) =-i\pi \) is used. By the standard procedure [15, 39], we find the in-going modes on the horizon satisfies the bose distribution with a temperature

$$ T=\frac{a}{2\pi } $$

which means that the white hole absorbs thermally.

The scattering does not happen for out-going waves. With Eqs. (3.2) and (5.4), we have

$$\begin{aligned} \lim _{t\rightarrow x}\frac{\phi _{k}^{I\text { out}}}{\phi _{k}^{IV\text { out}} }=\lim _{t\rightarrow x}\frac{e^{-i\frac{k}{a}\ln \left( ax-at\right) } }{e^{-i\frac{k}{a}\ln \left( ax-at\right) }}=1. \end{aligned}$$
(5.9)

Actually, a white hole spacetime can be regarded as the time reversal of the corresponding black hole spacetime. If the black hole radiates thermally, the white hole will absorb thermally.

6 Conclusion and outlook

The black hole is a universal structure of a spacetime. It is irrelevant to details of the local metric structure of the spacetime. When considering a quantum field on a black hole spacetime, we should concern the universal property rather than the local property of the field. However, the spacetime background of a real black hole is complicated so that we have to investigate local asymptotic behaviors of a quantum field on the horizon or at the null infinity.

In this paper, we build toy models of a black hole and a white hole by setting proper boundaries in the Minkowski spacetime. The advantage of the toy model is that the local spacetime background is simple enough. The simplicity of the spacetime structure allows us to get rid of complicated details of the spacetime and concentrate on the physical picture of the quantum field.

We calculate the thermal effect with the tunneling mechanism. The tunneling mechanism indicates that the thermal effect should be regarded as the black hole radiation. On the other hand, the spacetime outside the black hole (the region I) is the Rindler spacetime. We can also calculate the thermal effect with the Bogolyubov transformation method or the Euclidean time method as the Unruh effect. This fact indicates that the black hole radiation and the Unruh effect have the same mechanism in the model.

We consider several boundary effects on the black hole spacetime. (1) With the boundary condition at the singularity, we show qualitatively that outside the black hole there exist more out-going modes than in-going modes. Extra out-going modes outside the black hole serve as the black hole radiation. (2) A periodic boundary condition is imposed in the Euclidean time method. We point out that the periodic boundary condition leads to the divergence of the field, which means we should be more careful with the Euclidean time method. (3) We suggest a classification scheme of states of the field: the confined state and the entanglement state. The confined state and the entanglement state are more closely related to the property of a black hole, comparing with the bound state and the scattering state. We show that there is no confined state on the black hole in the model. If we suppose that the field of any particle will never collapse into a Dirac-delta function, a particle will be in an entanglement state. That is, the field of a particle can be divided into two entangled parts: the field inside the black hole and the field outside the black hole. The event horizon of the black hole plays a role similar to the boundary of a potential well of finite depth. One can always test the field outside the black hole to get the information of the field inside the black hole. In a word, the information of the black hole in the model is never lost. We suppose that this result holds true for real black hole systems. In addition, we show that a white hole has a thermal absorption. Since the spacetime background is fixed, the backreaction of the radiation particle to the black hole is not considered in this paper. The readers can refer to Refs. [44,45,46,47].

Once we get rid of the complicated local spacetime structure, there are a lot of interesting problems in a black hole system beyond the thermal effect.