Bulk observables at 5.02 TeV using quasiparticle anisotropic hydrodynamics

Abstract

We compare predictions of 3+1D quasiparticle anisotropic hydrodynamics (aHydroQP) for a large set of bulk observables with experimental data collected in 5.02 TeV Pb–Pb collisions. We make predictions for identified hadron spectra, identified hadron average transverse momentum, charged particle multiplicity as a function of pseudorapidity, the kaon-to-pion ($K/\pi$) and proton-to-pion ($p/\pi$) ratios, identified particle and charged particle elliptic flow, and HBT radii. We compare to data collected by the ALICE collaboration in 5.02 TeV Pb–Pb collisions. We find that, based on available data, these bulk observables are well described by aHydroQP with an assumed initial central temperature of $T_0=630$ MeV at $\tau _0 = 0.25$ fm/c and a constant specific shear viscosity of $\eta /s=0.159$, which corresponds to a peak specific bulk viscosity of $\zeta /s = 0.048$. In particular, we find that the momentum dependence of the kaon-to-pion ($K/\pi$) and proton-to-pion ($p/\pi$) ratios reported recently by the ALICE collaboration are extremely well described by aHydroQP in the 0–5% centrality class.

1 Introduction

At high-temperatures one expects hadronic matter to undergo a phase transition to a quark–gluon plasma (QGP) in which the appropriate degrees of freedom are quarks and gluons rather than hadrons. The phase transition from hadronic matter to QGP is associated with both the restoration of chiral symmetry and deconfinement of the quarks and gluons. Direct numerical calculations of the QGP phase transition temperature using lattice quantum chromodynamics (QCD) have found that the transition is a smooth crossover with a crossover temperature of $T_c \sim 155$ MeV [1, 2]. To produce the QGP in the lab, experimentalists at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) collide ultrarelativistic nuclei in order to create a short-lived QGP with a lifetime on the order of 12 fm/c in central 5.02.TeV Pb–Pb collisions. Analysis of the data produced in the last decades has shown that many aspects of the collective behavior observed in high-energy heavy-ion collisions are well-described by relativistic viscous hydrodynamics with an equation of state that takes into account the transition between hadronic and partonic degrees of freedom [3,4,5,6,7,8,9].

In viscous hydrodynamics approaches one typically starts from the assumption that the non-equilibrium corrections to the dynamics, e.g. shear and bulk viscous tensors, are small relative to the equilibrium contributions to the energy-momentum tensor. One of the challenges such approaches face is that at early times, $\tau < 1$ fm/c, the QGP created in heavy-ion collisions can suffer from quite large deviations from thermal equilibrium. These deviations can be large enough that the resulting one-particle distributions become negative in large regions of phase space [10, 11]. Additionally, one finds that in such models the diagonal components of the energy-momentum tensor (anisotropic local rest frame pressures) can become negative even in cases where the underlying model being described by viscous hydrodynamics can never possess negative pressures, e.g. kinetic theory in relaxation time approximation. These problems are particularly worrisome at early-times and near the transverse/longitudinal edges of the system [12, 13].

The emergence of these problems is related to the fact the viscous hydrodynamics equations of motion are typically truncated at second-order in an expansion in terms of the inverse Reynolds number and Knudsen numbers of the system. While it is formally possible to go beyond second order viscous hydrodynamics to third and higher orders in order to improve the treatments, an alternative idea was introduced in Refs. [14, 15] called anisotropic hydrodynamics (aHydro) in which no truncation in the inverse Reynolds number is performed. This non-perturbative treatment of the response of the system to large gradients has been seen to result in better agreement between aHydro and exact solutions than seen with traditional second-order approaches [16,17,18,19,20,21,22,23,24,25,26,27,28,29].

Since its inception, the original anisotropic hydrodynamics framework proposed in Refs. [14, 15] has been extended to full 3+1-dimensional (3+1D) hydrodynamics including a realistic equation of state taken from lattice QCD calculations. In addition, both shear and bulk viscous correction plus an infinite set of implicit higher-order transport coefficients are included, as there is no truncation in inverse Reynolds number [11, 30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46] (for a recent review, see Ref. [47]). In Refs. [45, 46, 48,49,50,51] the resulting 3+1D quasiparticle anisotropic hydrodynamics code (aHydroQP) was used to make model to data comparisons for 2.76 TeV Pb–Pb collisions and 200 GeV Au–Au collisions. These prior studies found quite good agreement between aHydroQP and many heavy-ion observables such as the identified hadron spectra, mean transverse momentum of identified hadrons, multiplicities, the elliptic flow, and the HBT radii. For all of these observables, the aHydroQP model was able to describe the data quite reasonably over a broad range of centrality bins.

In this work, we continue our comparisons with heavy-ion experimental data, this time for 5.02 TeV collisions. We present predictions for identified hadron spectra and their ratios, the charged particle multiplicity, identified hadron average transverse momentum, and the elliptic flow, and HBT radii. We compare our aHydroQP predictions with data collected by the ALICE experiment and find that the agreement with data is quite good. In particular, we find that the momentum dependence of the kaon-to-pion ($K/\pi$) and proton-to-pion ($p/\pi$) ratios reported recently by the ALICE collaboration are extremely well described by aHydroQP in 0–5% centrality collisions out to transverse momentum of 2.5 GeV. The resulting initial temperature extracted for the QGP in 5.02 TeV collisions is $T_0 = 630$ MeV at $\tau _0 = 0.25$ fm/c and the specific shear viscosity found to give best agreement with the data is $\eta /s = 0.159$ (assumed to be constant), with a corresponding peak specific bulk viscosity of $\zeta /s = 0.048$ as can be seen in Fig. 1. The results presented here provide a standard point of reference for using aHydroQP in the calculation of other heavy-ion observables. Even prior to this manuscript the results of this tuning have been used, e.g. to study the nuclear modification factor $R_{AA}$ and elliptic flow $v_2$ of bottomonium states in 5.02 TeV Pb–Pb collisions [54, 55].

The structure of our paper is as follows. In Sect. 2, we review the basics of the 3+1D quasiparticle anisotropic hydrodynamics model. In Sect. 3, we present the predictions of the aHydroQP model for 5.02 TeV collisions and compare them to experimental data for many heavy-ion observables. Section 4 contains our conclusions and an outlook for the future.

2 Model

The evolution of the aHydro macroscopic variables are obtained by taking the first and second moments of Boltzmann equation for a system with temperature-dependent quasiparticle masses [40]

$$\begin{aligned} p^\mu \partial _\mu f(x,p)+\frac{1}{2}\partial _i m^2\partial ^i_{(p)} f(x,p)=-C[f(x,p)] . \end{aligned}$$

(1)

The first and second moments of Eq. (1) give

$$\begin{aligned} \partial _\mu T^{\mu \nu } =0\, , \end{aligned}$$

(2)

$$\begin{aligned} \partial _\alpha I^{\alpha \nu \lambda }- J^{(\nu } \partial ^{\lambda )} m^2 =-\int \!dP\, p^\nu p^\lambda {{{\mathcal {C}}}}[f]\, , \end{aligned}$$

(3)

where

$$\begin{aligned} J^\mu = \int dP \, p^\mu f , \end{aligned}$$

(4)

$$\begin{aligned} T^{\mu \nu } = \int dP \, p^\mu p^\nu f , \end{aligned}$$

(5)

and

$$\begin{aligned} I^{\mu \nu \lambda } = \int dP \, p^\mu p^\nu p^\lambda f , \end{aligned}$$

(6)

with $\int dP = N_\text {dof} \int \frac{d^3\mathbf{p}}{(2\pi )^3} \frac{1}{E}$ being the Lorentz invariant integration measure.

Fig. 1

Quasiparticle model bulk viscosity over entropy density as a function of temperature. For details concerning the method used to obtain this result see Refs. [46, 52, 53]

In the aHydroQP approach, the mass is a function of temperature which can be obtained from lattice QCD calculations of the entropy density in order to enforce a realistic equation of state [40]. The collisional kernel C[f(x, p)] in aHydroQP is taken in the relaxation-time approximation (RTA).

$$\begin{aligned} C[f] = - \frac{p \cdot u}{\tau _{\mathrm{eq}}(T)} [ f - f_\text {eq}(E/T) ] , \end{aligned}$$

(7)

where $u^\mu$ is the four-velocity of the fluid local rest frame and $\tau _{\mathrm{eq}}(T)$ is the temperature-(and hence time-)dependent relaxation time. We note here that the equilibrium distribution function is taken to be of the form $f_{\mathrm{eq}}(x)=\exp (-x)$ and $E = \sqrt{p^2 + m^2}$.

We obtain the necessary dynamical equations by taking projections of the Boltzmann equation. For this purpose, one needs to first specify the form of the underlying one-particle distribution function. In aHydroQP, the distribution function is taken to be anisotropic in momentum space, with only diagonal momentum-space anisotropy parameters, and having, in the local rest frame, the form

$$\begin{aligned} f(x,p) = f_{\mathrm{eq}}\!\left( \frac{1}{\lambda }\sqrt{\sum _i \frac{p_i^2}{\alpha _i^2} + m^2}\right) . \end{aligned}$$

(8)

Note that the anisotropies $\alpha _i(t,\mathbf{x})$ and temperature-like scale $\lambda (t,\mathbf{x})$ are both functions of space and time, however, we have suppressed their arguments for compactness. This distribution function reduces back to an equilibrium distribution function with temperature T when $\alpha _i(t,\mathbf{x})=1$ and $\lambda (t,\mathbf{x})$ = T. Evaluating the necessary moments of this distribution function, one can obtain dynamical equations for the evolution of the aHydro macroscopic parameters from the first and second moments of the Boltzmann equation. For details of the derivation of the dynamical equations for aHydroQP we refer readers to Refs. [11, 36, 40, 47].

Using the aHydroQP dynamical equations we allow the system to evolve until reaching the freeze-out temperature $T_{\mathrm{FO}}=130$ MeV where a hypersurface is constructed at a constant energy-density. On this hypersurface we convert the underlying hydrodynamic evolution results for the flow velocity, the anisotropy parameters, and the scale $\lambda$ into explicit ‘primordial’ hadronic distribution functions using a generalized Cooper–Frye prescription [47]. For this purpose, we use a customized version of THERMINATOR 2 [56] to perform the production and necessary decay(s) of the primordial hadrons. Both the aHydroQP and modified THERMINATOR 2a codes are publicly available [57]. Note that the freeze-out temperature used herein and all other parameters besides $T_0$ and $\eta /s$ were assumed to be the same as in our prior 2.76 TeV study [45, 46]. Similarly, in order to have a meaningful comparison to results obtained previously at 200 GeV and 2.76 TeV, we use smooth Glauber type initial conditions with the central energy density scaling with the nuclear overlap profile which is taken to be a linear combination of the profile obtained from the number of participants and the number of binary collisions . Here we assumed the system to initially have Bjorken flow in the longitudinal direction and zero transverse flow ($u_x(\tau _0)=u_y(\tau _0)=0$). In the transverse plane, the initial energy density is computed from a linear combination of smooth Glauber wounded-nucleon and binary-collision profiles [45, 46]. In the longitudinal direction, we used a tilted profile with a central plateau and Gaussian wings. More details can be found in [46]. For the initial condition for the anisotropy parameters, $\alpha _i(\tau _0,\mathbf{x})$, we take these to be equal to unity at all points in the three-volume.

2.1 Interferometry

In the results section we will present predictions for the Hanbury Brown–Twiss (HBT) radii extracted from pion correlations. These radii provide information about the size of the QGP. Following Ref. [56], we review below the basics of the HBT interferometry. In principle, two-particle interference is a direct result of correlations that exist between pairs of particles due to their quantum nature. The correlation function, which reduces to unity in the absence of quantum correlations, is defined as

$$\begin{aligned} C(\mathbf {p}_{1},\mathbf {p}_{2})=\frac{W_{2}(\mathbf {p}_{1},\mathbf {p}_{2})}{W_{1}(\mathbf {p}_{1})W_{1}(\mathbf {p}_{2})} , \end{aligned}$$

(9)

where $W_{1}$ is a one-particle distribution (the probability of emission of a particle with momentum $\mathbf {p}$) and $W_{2}$ is the two-particle distribution function. Both $W_{1}$ and $W_{2}$ are obtained by the space-time integral of the source emission function S(x, p)

$$\begin{aligned} W_{1}(\mathbf {p})= E_{p}\frac{dN}{d^3p} \int d^4x \, S(x,p) , \end{aligned}$$

(10)

and

$$\begin{aligned} W_{2}(\mathbf {p}_{1},\mathbf {p}_{2})= E_{p1}E_{p2}\frac{dN}{d^3p_1d^3p_2} \int S(x_1,x_2,p_1,p_2) d^4x_1 d^4x_2 . \end{aligned}$$

(11)

The emission function is usually parameterized as a 3-D ellipsoid with a Gaussian profile

$$\begin{aligned} S(r)= N \, \mathrm{exp}\!\left( -\frac{r^{2}_{\mathrm{out}}}{2R^{2}_{\mathrm{out}}}-\frac{r^{2}_{\mathrm{side}}}{2R^{2}_{\mathrm{side}}}-\frac{r^{2}_{\mathrm{long}}}{2R^{2}_{\mathrm{long}}} \right) , \end{aligned}$$

(12)

with N as a normalization constant and r is the relative space-time separation of the pair decomposed into three components (${r_{\mathrm{out}}}$, ${r_{\mathrm{side}}}$, ${r_{\mathrm{long}}}$). The radii $R_{\mathrm{out}}$, $R_{\mathrm{side}}$ and $R_{\mathrm{long}}$ are the HBT radii where the $\mathrm{out}$, $\mathrm{long}$, and $\mathrm{side}$ directions are defined parallel to the mean transverse momentum of the pair $k_T$, parallel to the beam axis, and perpendicular to both $\mathrm{long}$ and $\mathrm{out}$, respectively.

Using Eq. (12), the correlation function can be parametrized following Bertsch–Pratt parameterization in terms of three Gaussians [58, 59] where Coulomb repulsion between similar pairs is ignored

$$\begin{aligned} C(q,k)= 1+\lambda \, \mathrm{exp}\!\left( -R^{2}_{\mathrm{out}}q^{2}_{\mathrm{out}}-R^{2}_{\mathrm{side}}q^{2}_{\mathrm{side}}-R^{2}_{\mathrm{long}}q^{2}_{\mathrm{long}}\right) . \end{aligned}$$

(13)

Here, $0 \le \lambda \le 1$ is the incoherence parameter where chaotic sources have $\lambda =1$ and totally coherent sources have $\lambda =0$. The relative momenta $\mathbf {q}=\mathbf {p}_1-\mathbf {q}_2$ is decomposed into three components similar to the HBT radii. Finally, the HBT radii are obtained by fitting to the correlation function as a function of $k_T$. Once the HBT radii found, they provide information about the homogeneity of the system, e.g., the product $R_{\mathrm{out}} \, R_{\mathrm{side}} \, R_{\mathrm{long}}$ gives the homogeneity volume. For more details about the analysis of the HBT interferometry, one can refer to Refs. [60,61,62,63]. We note here that we used THERMINATOR 2 as an event generator to extract the HBT interferometry [64,65,66,67,68].

3 Results

In this section, we present comparisons of aHydroQP predictions with 5.02 TeV Pb–Pb collision data collected by the ALICE collaboration. We consider only two free parameters, the initial central temperature $T_0$ and the specific shear viscosity $\eta /s$.¹ We fix these two parameters by fitting the spectra of pions, kaons, and protons in both the 0–5% and 30–40% centrality classes. The parameters obtained from the spectra fit were: $T_0=630$ MeV and $\eta /s=0.159$. The initial temperature obtained is higher than found at 2.76 TeV, $T_0^\text {2.76~TeV} = 600$ MeV, by 5% [46]. The best fit value for $\eta /s$ is the same as was found at 2.76 TeV [46].

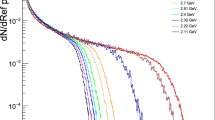
We begin by presenting aHydroQP predictions for the transverse momentum distribution of identified hadrons in 5.02 TeV Pb–Pb collisions. We will compare our aHydroQP predictions with experimental data from the ALICE collaboration [69, 73]. In Fig. 2, we show the combined spectra of pions, kaons, and protons as a function of transverse momentum in six different centrality classes. In more central collisions, aHydroQP shows very good agreement with the data as shown in Fig. 2a. On the other hand, for more peripheral collisions the agreement is good only for $p_T \lesssim 1$ GeV as can be seen in, e.g., Fig. 2.

In Fig. 3, the $K/\pi$ (left column) and $p/\pi$ (right column) ratios are shown as a function of $p_T$ in three different centrality classes and once again compared to experimental data. The agreement between aHydroQP and the data at $p_T \lesssim 1$ GeV is very good in all centrality bins. In the 0–5% centrality class, for the $K/\pi$ ratio, the agreement between aHydroQP and the data extends up to $p_T \sim 2.5$ GeV, while for $p/\pi$ it extends up to $p_T \sim 1.5$ GeV. The aHydroQP predictions for the $K/\pi$ and $p/\pi$ rations as a function of centrality are shown in Fig. 4, in the left and right panels, respectively. In both panels, we see that aHydroQP is able to describe the ratios reported by the ALICE collaboration well over a broad range of centralities.

In Fig. 5, we present the aHydroQP prediction for the charged-particle pseudorapidity density in Pb–Pb collisions at 5.02 TeV along with data provided by the ALICE collaboration [70]. In all centrality bins shown, aHydroQP describes the data quite well over a broad range of pseudorapidity. At high rapidities we notice some differences from the data where there are indications of a more slow decrease. This was not the case at 2.76 TeV where, in the most central class, the agreement between aHydroQP and experimental data extended out to $|\eta | \sim 5$. Overall, however, we see good agreement at central rapidities in all centrality classes considered in Fig. 5.

Next we turn to the left panel of Fig. 6 in which present aHydroQP predictions for the mean transverse momentum $\langle p_T \rangle$ of pions, kaons and protons. The aHydroQP results are compared to experimental data from the ALICE collaboration [69]. For both pions and kaons, we see good agreement between aHydroQP and the experimental data at all centralities, however, aHydroQP seems to underestimate the mean $p_T$ for protons. This discrepancy is consistent with the proton spectra, but one needs to plot the spectra on a linear scale to clearly see it instead of the log plot scale shown in Fig. 2. We have no immediate explanation for why there is such a discrepancy, but we do note that a similar discrepancy exists in state-of-the-art second-order viscous hydrodynamics calculations [74].

In Fig. 6 (right panel), we present the aHydroQP predictions for the integrated flow as a function of centrality. Since we used smooth initial conditions, the event plane is known and we computed $v_2$ using the $\langle \cos (2\phi ) \rangle$ for all hadrons. The aHydroQP predictions are compared to ALICE data for $v_2\{2\}$ and $v_2\{4\}$ reported in Ref. [71]. As can be seen from this comparison, the aHydroQP predictions agree well with the experimentally measured $v_2\{4\}$ in the most central bins ($< 25 \%$) and are closer to $v_2\{2\}$ at higher centralities.

In Fig. 7, we show the elliptic flow as a function of transverse momentum $v_2(p_T)$ for identified particles for various centrality classes in the range 10–50% (10% bins). The solid lines are obtained by 3+1D aHydroQP where the data are from the ALICE Collaboration [72]. As shown in Fig. 7a, 3+1D aHydroQP was able to describe the $v_2(p_T)$ for $\pi ^{\pm }$, $K^{\pm }$, and $p+{\bar{p}}$ quite well up to intermediate $p_T \sim 2.5$ GeV. For larger centrality classes, as can be seen in panel d, the agreement holds only to lower $p_T \sim 1$ GeV. This disagreement is related to the use of smooth Glauber initial conditions. In all cases, 3+1D aHydroQP was able to capture the mass ordering of $v_2(p_T)$. In Fig. 8, the elliptic flow $v_2(p_T)$ for charged particles in 30–40% centrality class is shown. Again the solid line is the predictions of 3+1D aHydroQP and the points are the experimental results from the ALICE Collaboration [71]. As can be seen from this figure, aHydroQP predictions agrees quite well with the data up to $p_T \sim 2$ GeV.

Fig. 2

Combined transverse momentum spectra of pions, kaons and protons for 5.02 TeV Pb–Pb collisions in different centrality classes. The solid lines are the predictions of 3+1D aHydroQP and the points are experimental results from the ALICE Collaboration [69]

Fig. 3

The $K/\pi$ (left) and $p/\pi$ (right) ratios as a function of $p_T$ measured in Pb–Pb collisions at 5.02 TeV in different centrality classes. Solid lines are predictions of aHydroQP model where symbols with error bars are experimental data from Ref. [69]

Fig. 4

Transverse-momentum integrated $K/\pi$ (left) and $p/\pi$ (right) ratios as a function of centrality measured in Pb–Pb collisions at 5.02 TeV. Solid lines are predictions of aHydroQP model where symbols with error bars are experimental data from Ref. [69]

Fig. 5

The charged-particle pseudorapidity density in Pb–Pb collisions at 5.02 TeV obtained by aHydroQP model (solid lines) as a function of pseudorapidity $\eta$. In panel a, the centrality classes correspond to 0–5, 5–10, 10–20, 20–30, and 30–40% from top to bottom and, in panel b, correspond to 40–50, 50–60, 60–70, 70–80, 80–90%, respectively, again from top to bottom. Data are from ALICE Collaboration Ref. [70]

Fig. 6

In panel a, identified particle mean transverse momentum vs. centrality is shown in 5.02 TeV Pb+Pb collisions where data are from ALICE Collaboration Ref. [69], while in panel b, the centrality dependence of the elliptic flow $v_2$ of charged particles in 5.02 TeV Pb–Pb collisions is shown where data are from Ref. [71]

Fig. 7

Identified elliptic flow as a function of transverse momentum for 5.02 TeV Pb–Pb collisions in different centrality classes. The solid lines are the predictions of 3+1D aHydroQP and the points are experimental results from the ALICE Collaboration [72]

Fig. 8

The elliptic flow $v_2$ for charged particles in 30–40% centrality class is shown where the solid line is the prediction of 3+1D aHydroQP and the points are the experimental results from the ALICE Collaboration [71]

Fig. 9

HBT radii are shown as a function of $k_T$ for $\pi ^+ \pi ^+$ in the 0–5, 5–10, 10–20, and 20–30$\%$ centrality classes. The left, middle, and right columns show $R_{\mathrm{out}}$, $R_{\mathrm{side}}$, and $R_{\mathrm{long}}$, respectively. All results are for 5.023 TeV Pb–Pb collisions

Fig. 10

Ratios of HBT radii as a function of $k_T$ for $\pi ^+ \pi ^+$ in the 10–20, and 20–30$\%$ centrality classes. The left, middle, and right columns show $R_{\mathrm{out}}/R_{\mathrm{side}}$, $R_{\mathrm{out}}/R_{\mathrm{long}}$, and $R_{\mathrm{side}}/R_{\mathrm{long}}$, respectively. All results are for 5.023 TeV Pb–Pb collisions

Finally, we turn to the aHydroQP predictions for HBT radii determined from pion correlations. In Fig. 9, the HBT radii, $R_{\mathrm{out}}$, $R_{\mathrm{side}}$, and $R_{\mathrm{long}}$ are shown as a function of $k_T$ in panels a, b, and c, respectively. In each panel, four centrality classes are presented 0–5, 5–10, 10–20, and 20–30% using black, blue, red, and green colors, respectively. In all panels, we see first that radii decreases as a function of $k_T$ with the maximum values at low $k_T$. Second, the radii also decrease as a function of centrality with the highest at more central collisions. This is consistent with the changing size of the freeze-out volume as one varies centrality. In Fig. 10, we present aHydroQP predictions for the HBT ratios, $R_{\mathrm{out}}/R_{\mathrm{side}}$, $R_{\mathrm{out}}/R_{\mathrm{long}}$, and $R_{\mathrm{side}}/R_{\mathrm{long}}$ as a function of $k_T$ in panel a, b, and c, respectively. To the best of our knowledge, there are no experimental results to compare our model predictions against, making this a prediction that can be tested in the future. We note that the trends shown here are similar to what was found by us previously [46] at 2.76 TeV. It is also similar to what had been presented in Ref. [75] where the HBT radii at 5.023 TeV collision energy were computed using (3+1)D viscous hydrodynamics.

4 Conclusions and outlook

In this work, we continued our comparisons of aHydroQP with experimental data. In the past, we presented comparisons with data at 2.76 TeV Pb–Pb collisions [45, 46] and 200 GeV Au–Au collisions [48, 51]. Herein we made theory to data comparisons between aHydroQP and data collected by the ALICE collaboration using 5.02 TeV Pb–Pb collisions. We presented aHydroQP predictions for a large set of bulk observables and found quite reasonable agreement with experimental data using a central temperature of $T_0 = 630$ MeV at $\tau = 0.25$ fm/c and a specific shear viscosity of $\eta /s = 0.159$. Comparing to our previous studies at 2.76 TeV [45, 46], all other parameters besides $T_0$ and $\eta /s$ were assumed to be the same.

Fig. 11

In panel a, b, and c, the spatial profile of anisotropy parameters $\alpha _x$, $\alpha _y$, and $\alpha _z$, respectively, is shown as a function of x at $\tau =1.25$ fm/c for a collision in the 40–50% centrality class

We made aHydroQP predictions for identified hadron spectra, identified hadron average transverse momentum, charged particle multiplicity as a function of rapidity, the kaon-to-pion ($K/\pi$) and proton-to-pion ($p/\pi$) ratios, elliptic flow, and HBT radii. In all of these comparisons, aHydroQP was quite successful in describing the experimental data in 5.02 TeV Pb–Pb collisions when data was available. In particular, we found that the momentum dependence of the kaon-to-pion ($K/\pi$) and proton-to-pion ($p/\pi$) ratios reported recently by the ALICE collaboration are extremely well described by aHydroQP in the most central collisions. Our predictions for the HBT radii will hopefully soon be confronted with experimental data.

We note, in closing, that the initial state model (Glauber model) and assumed collision kernel (RTA) used herein are rather simple. As a result of the smooth initial condition assumed, we do not correctly reproduce the $v_2^{\mathrm{chg}}$ in the most central collisions. The aHydroQP code allows for fluctuating initial conditions and we plan to report on the results of such simulations in a forthcoming paper. One of the challenges with using, e.g. IPGlasma-type, fluctuating initial conditions is that these types of initial conditions can possess large numbers of cells in which there are negative total pressures in the local rest frame, which is incompatible with the kinetic-theory based assumptions underpinning aHydroQP. With respect to the collision kernel, a framework for including realistic collisional kernels in the aHydro framework was introduced in Refs. [76, 77]. It will be interesting to see if aHydroQP results are sensitive to the choice of the collisional kernel.

Finally, we mention that another assumption made herein was that the anisotropy tensor is diagonal in the local-rest frame. Although this is justified by the smallness of the off-diagonal contributions, it is desirable to have a complete treatment which includes the off-diagonal contributions in a non-perturbative manner. Such a scheme was introduced in Ref. [78] and is currently being implemented.

Appendix A: Typical momentum-space anisotropies

As a bit of additional information about the underlying parameter values, in Fig. 11 we present a three panel figure showing $\alpha _x$ (left) , $\alpha _y$ (middle), and $\alpha _z$ (right) at $\tau = 1.25$ fm/c. As can be seen from this figure, the transverse anisotropies are similar and within 30% of unity, however, the longitudinal anisotropy is markedly different and can differ substantially from unity. In particular, we emphasize that in the dilute regions $|x| > 5$ fm, there exist quite large momentum-space anisotropies and one has $\alpha _z \ll \alpha _{x,y}$. It is in such regions that typical viscous hydrodynamics codes must regulate the viscous shear tensor, whereas, no such regulation is required in aHydroQP.