1 Introduction

The picture of \(\pi _1\) resonances with spin-exotic quantum numbers \(I^G(J^{PC})\) = \(1^-(1^{-+})\) in the light-meson sector is poorly understood and the experimental indications of various resonances are controversially discussed. Lattice QCD calculations [1,2,3,4] and phenomenological QCD studies [5, 6] predict only one state at a mass of 2 GeV\(/c^2\) or slightly below. Experimentally, three different resonances with \(I^G(J^{PC})\) = \(1^-(1^{-+})\) quantum numbers have been reported. The lightest one, the \(\pi _1(1400)\), has only been seen in the \(\pi \eta \) decay mode by several experiments [7,8,9,10,11,12,13]. In contrast, for the \(\pi _1(1600)\) no coupling to \(\pi \eta \) has been found, but it has been observed in several other channels, namely \(\pi \eta ^\prime \), \(\rho \pi \), \(f_1(1285) \pi \) and \(b_1(1235) \pi \) [14,15,16,17,18,19]. The third state which has the poorest evidence, and is thus listed in the Review of Particle Physics (RPP) as a further state, is the \(\pi _1(2015)\) seen by the BNL E852 experiment decaying into \(f_1(1285) \pi \) and \(b_1(1235) \pi \) [17, 18]. A weak point in various of these previous analyses is the extraction of the resonance parameters using Breit-Wigner parameterizations. The outcome of an analysis performed by the JPAC group likely sheds more light on the understanding of the lightest \(\pi _1\) states [20]. Utilizing the N/D method to model the reaction process, it turned out that the two candidates for a spin-exotic state, \(\pi _1(1400)\) and \(\pi _1(1600)\), that are listed in the RPP, can be described by only one pole with a separate coupling to \(\pi \eta \) and \(\pi \eta ^\prime \).

The Crystal Barrel Collaboration observed a significant \(\pi _1\) contribution in \({{\bar{p}}p}\) annihilations in flight for the first time with a coupling to \(\pi \eta \) in the reaction \({{\bar{p}}p}\,\rightarrow \,\pi ^0\pi ^0\eta \) [21] using a coupled-channel analysis. In this paper, the analysis has been extended by considering not only the channels \({{\bar{p}}p}\,\rightarrow \,\pi ^0\pi ^0\eta \), \({\pi ^0\eta \eta }\) and \({K^+K^-\pi ^0}\) at a beam momentum of 900 \(\mathrm {MeV/}c\)  and data from 11 different \(\pi \pi \)-scattering channels but also the P- and D-waves in the \(\pi \eta \) and \(\pi \eta ^\prime \) systems measured at COMPASS [22, 23]. The dynamics is treated slightly differently compared to [20]. The K-matrix approach was used by taking into account the analyticity with Chew-Mandelstam functions [24].

2 Partial-wave analysis

The partial-wave analysis has been performed with the software package PAWIAN (PArtial Wave Interactive ANalysis Software) [25] and with the same algorithms as described in [21].

Description of the \({{\bar{p}}p}\) channels:   We analyzed data of the three \({{\bar{p}}p}\) annihilation channels \({\pi ^0\pi ^0\eta }\), \({\pi ^0\eta \eta }\) and \({K^+K^-\pi ^0}\) at a beam momentum of 900 \(\mathrm {MeV/}c\) measured with the Crystal Barrel detector at LEAR. The full description of the reconstruction and event selection can be found in [21].

The complete reaction chain starting from the \({{\bar{p}}p}\) initial state down to the final-state particles is fitted. The description for the angular part of the amplitudes is based on the helicity formalism. The amplitudes are further expanded into the LS-scheme which guaranties that also the orbital angular momentum dependent barrier factors for the production and the decay are properly taken into account. In addition to \(\pi _1\pi ^0\), the sub-channels \(f_0\eta \), \(f_2\eta \), \(a_0\pi ^0\) and \(a_2\pi ^0\) are contributing to \({{\bar{p}}p}\,\rightarrow \,\pi ^0\pi ^0\eta \). The contributing isovector states \(a_0\) and \(a_2\) exhibit a similar decay pattern as the \(\pi _1\)-wave amplitude with a strong coupling to the \(\pi ^0\eta \) system. Therefore, it is not straightforward to properly disentangle these waves from each other. In this case, the simultaneous fit of the channels \({\pi ^0\eta \eta }\) and \({K^+K^-\pi ^0}\) helps considerably. It ensures a strong control on the production of \(a_0\pi ^0\) and \(a_2\pi ^0\) by directly sharing the relevant amplitudes between the two channels \({\pi ^0\pi ^0\eta }\) and \({K^+K^-\pi ^0}\). Apart from the two isolated resonances \(\phi (1020)\) and \(K^*(892)^\pm \), which are described by Breit-Wigner functions, the K-matrix formalism with P-vector approach is used for the dynamics [21, 26, 27].

For each partial wave with defined quantum numbers \(I^G(J^P)\), the mass-dependent amplitude \(F^{p}_i(s)\) is parametrized as follows:

$$\begin{aligned} F^{p}_i(s) \; = \; \sum _j (I \; + \; K(s) \; C(s))_{ij}^{-1} \cdot P^p_j(s), \end{aligned}$$
(1)

where i and j represent the two-body decay channels like \(\pi \pi \), \(\pi \eta \) or \(K^+K^-\) and s is the invariant mass squared of the respective two-body sub-channel. The analyticity is taken into account by using the Chew-Mandelstam function C(s) [24, 28]. \(P^p_{j}(s)\) represents one element of the P-vector taking into account the production process p:

$$\begin{aligned} P^p_j(s) = \sum _{\alpha } \left( \frac{\beta ^p_{\alpha _p} \; g^{{\text {bare}}}_{\alpha _j} }{{m^{{\text {bare}}}_\alpha }^2 -s} +\sum _k c_{kj} \cdot s^k \right) \cdot B^l(q_j,q_{\alpha _j}),\nonumber \\ \end{aligned}$$
(2)

where \(\beta ^p_{\alpha _p}\) is the complex parameter representing the strength of the produced resonance \(\alpha \). \(g^{{\text {bare}}}_{\alpha _j}\) and \(m^{{\text {bare}}}_\alpha \) are the bare parameters for the coupling strength to the channel j and for the mass of the resonance \(\alpha \). \(B^l(q_j,q_{\alpha _j})\) denotes the Blatt-Weisskopf barrier factor of the decay channel j with the orbital angular momentum l, the breakup momentum \(q_j\) and the resonance breakup momentum \(q_{\alpha _j}\). This factor was chosen such that the centrifugal barrier is explicitly included and is normalized at \(q_{\alpha _j}\) [29, chap. 49]. It is worth mentioning that the production barrier factors are already taken into account separately in the production amplitude as described in [21]. The s-dependent polynomial terms of the order k with the parameters \(c_{kj}\) describe background contributions for the production.

The elements of the K-matrix for the two-body scattering process with orbital angular momentum l are given by

$$\begin{aligned} K_{ij}(s) = \sum _{\alpha } B^l(q_i,q_{\alpha _i}) \cdot \left( \frac{g^{{\text {bare}}}_{\alpha _i} \; g^{{\text {bare}}}_{\alpha _j} }{{m_\alpha ^{{\text {bare}}}}^2 -s} + {\tilde{c}}_{ij} \right) \cdot B^l(q_j,q_{\alpha _j}), \end{aligned}$$
(3)

where i and j represent the input and output channels, respectively. The parameters \({\tilde{c}}_{ij}\) stand for the constant terms of the background contributions, which are allowed to be added to the K-matrix without violating unitarity. In addition to the form given in Eq. (3), the K-matrix elements for the description of the \(f_0\)-wave amplitude are multiplied with an Adler zero term \((s - s_0) / s_{\text {norm}}\) as outlined in detail in [21].

Also the K-matrix descriptions of the \(f_0\)-, \(f_2\)-, \(\rho \)-, \(a_0\)- and \((K\pi )_S\)-waves are the same as outlined in [21]. A slightly different K-matrix for the \(\pi _1\)- and \(a_2\)-wave is employed for the following reasons:

  • the \(\pi _1\)-wave amplitude consists of one K-matrix pole and the two channels \(\pi \eta \) and \(\pi \eta ^\prime \). Constant background terms for the K-matrix and the P-vector for the \({{\bar{p}}p}\) channel have been used. Due to the fact that the t-channel exchange plays an important role for the \(\pi ^-p\)-scattering process, a first-order polynomial is needed for the relevant background terms of these P-vector elements.

  • the K-matrix of the \(a_2\)-wave is parametrized by two poles, \(a_2(1320)\) and \(a_2 (1700)\), and by the three channels \(\pi \eta \), \(\pi \eta ^\prime \) and \(K {\bar{K}}\). Constant background terms for the K-matrix are used. No background terms for the P-vector are needed for the \({{\bar{p}}p}\) channels while also here first-order polynomial background terms are required for the production in \(\pi ^-p\). This is due to the fact that the COMPASS data are simultaneously fitted, which contain not only the \(\pi \eta \) but also the \(\pi \eta ^{\prime }\) channel as discussed below.

Description of the \({\pi \pi }\) -scattering data:  The mass-dependent terms of each partial wave describing the \({\pi \pi }\)-scattering reactions are parametrized by the T-matrix

$$\begin{aligned} T(s) = (I \, + \, K(s) \; C(s))^{-1} \; K(s), \end{aligned}$$
(4)

where s is the total energy squared of the \(\pi \pi \) system. For elastic channels, phase and inelasticity are compared with the data. For inelastic channels, such as \(\pi \pi \rightarrow \eta \eta \), the moduli squared of the T-matrix are taken. As in [21], the following data for the I = 0  S- and D-wave and the I = 1 P-wave for energies below \(\sqrt{s} \, <\,1.9\,\) GeV were included in the analysis:

  • the phases and inelasticities of the reaction \(\pi \pi \rightarrow \pi \pi \) for the \(I=0\) S- and D-wave and for the \(I=1\) P-wave,

  • the intensities of the inelastic channels \(\pi \pi \rightarrow K{\bar{K}}\) and \(\pi \pi \rightarrow \eta \eta \) for the \(I=0\) S- and D-wave and

  • the intensity of the inelastic channel \(\pi \pi \rightarrow \eta \eta ^\prime \) for the \(I=0\) S-wave.

Description of the COMPASS data:  The COMPASS data are taken from the mass-independent analysis of \(\pi p \rightarrow \eta ^{(\prime )} \pi p\) with a 191 \(\mathrm {GeV/}c\) pion beam integrated over the transferred momentum squared \(-t\) between 0.1 and 1.0 \(\mathrm {GeV}^2\) [22, 23]. Only the intensities of the P- and D-wave and their relative phases for the two channels \(\pi \eta \) and \(\pi \eta ^\prime \) are considered. The choice of these waves for the coupled-channel analysis ensures strong constraints in particular for the channel \({\pi ^0\pi ^0\eta }\), where large contributions of the \(\pi _1\)- and \(a_2\)-waves are found.

The description of the reaction \(\pi p \rightarrow R p \rightarrow (\eta ^{(\prime )} \pi ) p\) with R being the produced \(\pi _1\) or \(a_2\) partial wave is approximated via the exchange of a Pomeron with \(J^P\) = 1\(^-\) and an effective transferred momentum squared of \(t_{\text {eff}} = -0.1\, \mathrm {GeV}^2\). The intensities \(I^{\pi p \rightarrow R p}_{\pi \eta ^{(\prime )}}\) of the COMPASS data for the P- and D-partial-wave are described by:

$$\begin{aligned} I^{\pi p \rightarrow R p}_{\pi \eta ^{(\prime )}} = p^{2J-2}_{\pi \eta ^{(\prime )}} \cdot q_{\pi \eta ^{(\prime )}} \cdot \left| F^{\pi p \rightarrow R p}_{\pi \eta ^{(\prime )}} \right| ^2, \end{aligned}$$
(5)

where J stands for the spin associated to the relevant wave, \(q_{\pi \eta ^{(\prime )}}\) for the \(\pi \eta ^{(\prime )}\) breakup momentum representing the behavior of the phase space for the decay and \(p_{\pi \eta ^{(\prime )}}\) is the \(\pi \) beam momentum in the \(\pi \eta ^{(\prime )}\) rest frame, where

$$\begin{aligned} p_{\pi \eta ^{(\prime )}}= \frac{\sqrt{\lambda (s, m^2_\pi , t_{\text {eff}})}}{2\,\sqrt{s}} \end{aligned}$$
(6)

is the production breakup momentum with \(\lambda \) being the Källén triangle function. \(F^{\pi p \rightarrow R p}_{\pi \eta ^{(\prime )}}\) is taken as given in Eq. (1) and the production barrier factor is taken into account by \(p^{2J-2}_{\pi \eta ^{(\prime )}}\) according to [20, 30].

The relative phases of the \(\pi _1\)- and \(a_2\)-wave amplitudes for the channels \(\pi \eta \) and \(\pi \eta ^\prime \) are modeled as defined in Eq. (1) by subtracting the relevant F-vectors according to \( F^{\pi p \rightarrow a_2 p}_{\pi \eta ^{(\prime )}} - F^{\pi p \rightarrow \pi _1 p}_{\pi \eta ^{(\prime )}}\).

Fits to all data:  A combined minimization function is used for the fit, in which all data sets are taken into account. For the \({{\bar{p}}p}\) data, for each event the full information of the multi-dimensional phase space is used. The other data sets are provided as data points with uncertainties. The construction of the complete negative log-likelihood function to be minimized is performed in analogy to [21] and described in detail therein.

Different hypotheses have been tested by systematically adding and removing the potentially contributing resonances. For the selection of the best fit hypothesis the Bayesian and the Akaike information criterion have been used in the same way as in [21]. The significantly best fit result was achieved with the same contributing resonances as in our previous paper [21]. All tested hypotheses with the obtained information criteria are summarized in Table 1 of the supplemental material.

Fig. 1
figure 1

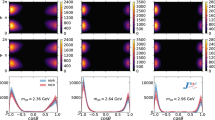
Invariant mass distribution (upper left) and selected angular distributions for the production (upper right) and decay (lower left and right) of the \({\pi ^0\pi ^0\eta }\) channel in the \({{\bar{p}}p}\) data. The red markers with error bars show the efficiency-corrected data with two entries per event, while the black curve represents our best fit and the colored curves show the individual contributions of the \(\pi _1\)- and \(a_2\)-waves

Full size image
Fig. 2
figure 2

Fits to the \(\pi \eta \) (upper row) and \(\pi \eta ^\prime \) (lower row) data from COMPASS. The intensities of the P- (left), D-wave (center), and their relative phases (right) are shown. The data are represented by the red points with error bars. The black curve illustrates our best fit to the data, while the yellow and gray bands represent the statistical and systematic uncertainty, respectively

Full size image

3 Fit result

Reasonably good agreement is achieved between the fit based on the model described in Sect. 2 and all data samples. Exemplarily for all \({{\bar{p}}p}\) channels, the result for \({\pi ^0\pi ^0\eta }\) is shown in Fig. 1. The invariant \(\pi ^0\eta \) mass as well as the production and decay angular distribution of the subsystems where the \(a_2\)- and \(\pi _1\)-wave are directly contributing are very well described. In analogy to [21] also here a non-parametric goodness of fit test has been performed for all three \({{\bar{p}}p}\) channels by utilizing a multivariate analysis based on the concept of statistical energy [31]. The obtained p-values of 0.405, 0.519 and 0.832 for the channels \({\pi ^0\pi ^0\eta }\), \({\pi ^0\eta \eta }\) and \({K^+K^-\pi ^0}\), respectively, demonstrate that the quality of the fit is as good as the one without considering the COMPASS data yielding strong constraints for the \(\pi _1\)- and \(a_2\)-wave. In \({\pi ^0\pi ^0\eta }\), the contribution of the \(\pi _1\)-wave with (11.9 ± 1.6 ± 1.9)%, of the \(a_2\)-wave with (30.8 ± 2.7 ± 1.9)% and also of all other waves are in the ballpark of the fractions obtained by the fit without the COMPASS data (supplemental material, Table 2). Also the individual contributions in the channels \({\pi ^0\eta \eta }\) and \({K^+K^-\pi ^0}\) are similar to the old results.

The results for the 11 different \({\pi \pi }\)-scattering data sets are shown in the supplemental material (Fig. 5) and there are no major differences visible in comparison to [21].

Table 1 Obtained masses, total widths and ratios of partial widths for the pole of the spin-exotic \(\pi _1\)-wave and for the two poles in the \(a_2\)-wave, the \(a_2(1320)\) and the \(a_2(1700)\). The first uncertainty is the statistical and the second the systematic one
Full size table

The comparison between our fit result and the COMPASS data is shown in Fig. 2. All data are described remarkably well. It is worth mentioning that the K-matrix of the \(\pi _1\)-wave consisting of only one pole can reproduce the shapes of the intensities in \(\pi \eta \) and \(\pi \eta ^\prime \) even though there is a shift of roughly 200 \(\mathrm {MeV/}c^2\) of the peak position between both channels [Fig. 2 (upper left) and (lower left)]. A significantly worse fit result based on the information criteria was achieved for the scenario in which the \(\pi _1\)-wave in the channel \({{\bar{p}}p}\,\rightarrow \,\pi ^0\pi ^0\eta \) has been removed from the model. The negative log-likelihood value increases by more than 125 with only 20 free parameters less. Similar to the results obtained in [21] also here the \(\pi _1\)-wave amplitude is definitely needed for this \({{\bar{p}}p}\)-annihilation channel. Contrary to the outcome without the \(\pi _1\) contribution, the fit taking into account two individual \(\pi _1\)-poles does not yield significantly worse results. Based on the chosen Bayesian and Akaike information criteria [21] the two-pole scenario cannot be completely excluded.

The pole positions for the individual resonances described by the K-matrix are extracted in the complex energy plane of the T-matrix on the Rieman sheet located next to the physical sheet. To some extent also partial widths have been derived from the residues calculated from the integral along a closed contour around the pole. The procedure for the extraction of these properties are explained in detail in [21]. The extracted resonance parameters for the \(\pi _1\) and the two \(a_2\) states are summarized in Table 1. The \(\pi _1\)-mass is significantly higher compared to the one published in [21]. This is compatible with all other findings attributing a lower mass to \(\pi _1\), if only \(\pi \eta \) decays are analyzed. One conjecture is that the requirement of unitarity cannot be strictly fulfilled for all analyses that take into accout only one decay channel with a weak coupling to the resonance. Apart from a larger width of more than 400 MeV/\(c^2\) obtained for the \(a_2(1700)\) resonance, all other masses and widths are comparable with the ones obtained in [20]. The absolute coupling strengths have not been determined because the non-negligible decay channel \(\rho \pi \) is not covered by the fitted data samples. Instead, the ratios \(\varGamma _{\pi \eta ^\prime }/\varGamma _{\pi \eta }\) for all three poles and \(\varGamma _{KK}/\varGamma _{\pi \eta }\) for the \(a_2\) resonances have been determined which should deliver more reasonable results. The obtained quantities of the remaining resonances can be found in Table 4 of the supplemental material. The results are in the ballpark of other individual measurements [29] and the ones published in [21], except the \(f_2\) state with the highest mass, which is located far beyond the phase space of the \({{\bar{p}}p}\) and \({\pi \pi }\) data. A general reason for the slight inconsitencies compared to the outcome of [21] is that a large correlation was found between the two waves with \(\pi _1\) and \(a_2\), which are mainly driven by the COMPASS data, and the remaining waves representing the \({{\bar{p}}p}\) data. The results are not meant to supersede the previous ones obtained by [21], which use fewer channels and thus less parameters. Here a different analysis is presented, where in particular the inclusion of the \(\pi p\) data leads to much stronger constraints for the description of the \(\pi _1\) and \(a_2\) amplitudes. The fit in [21] did not include any data for the \(\pi \eta ^\prime \) decay channel. Also the representation of the K-matrix for the \(a_2\)-wave has been extended by adding the \(\pi \eta ^\prime \) decay channel.

4 Statistical and systematic uncertainties

The statistical uncertainties are estimated by the boostrap method [32, 33]. Due to the fact that the coupled-channel fits require a lot of CPU time, only 100 pseudo-data samples are generated and refitted. However, with this limited number of datasets it is still possible to determine the standard deviations for each quantity with relative uncertainties of less than 10%. The obtained statistical uncertainties related to the properties of the \(\pi _1\) and \(a_2\) resonances are slightly larger than the ones published in [20], although additional \({{\bar{p}}p}\) data are used. This is caused by more free parameters needed for the description of the two waves. In particular the \(a_2\)-wave here consists of a three channel scenario with the coupling to \(\pi \eta \), \(\pi \eta ^\prime \) and \({\bar{K}}K\), while in [20] the decay to \({\bar{K}}K\) was not taken into accout.

The systematic uncertainties listed in Table 1 are derived from the outcome of alternative fits which deliver reasonably good results compared to the one with the best hypothesis by applying the same criteria as in [21]. Also the impact of the K-matrix and P-vector background terms of the \(\pi _1\) pole was investigated and is included in the systematic uncertainties. In addition the effective transferred momentum squared of \(t_{\text {eff}}= -\,0.1\) \(\hbox {GeV}^2\) for the description of the COMPASS data has been varied in the range between \(-\,0.1\) \(\hbox {GeV}^2\) and \(-\,0.5\) \(\hbox {GeV}^2\). Only slight differences are obtained which are also considered as systematic uncertainty.

One of the main systematic effects seems to be caused by a strong correlation between the widths of the \(\pi _1\) and of the \(a_2(1700)\) pole which accounts for the relevant large uncertainties listed in Table 1.

5 Conclusion

A coupled-channel analysis of the \({{\bar{p}}p}\) annihilation channels \({\pi ^0\pi ^0\eta }\), \({\pi ^0\eta \eta }\) and \({K^+K^-\pi ^0}\) measured at Crystal Barrel, of 11 different \({\pi \pi }\)-scattering data sets and of the P- and D-waves in the \(\pi \eta \) and \(\pi \eta ^\prime \) system measured at COMPASS has been performed. The analysis was mainly focused on the investigation of the spin-exotic \(I^G(J^{PC})\) = \(1^-(1^{-+})\) wave recently observed in the \(\pi \eta \) system of the \({{\bar{p}}p}\) channel \({\pi ^0\pi ^0\eta }\) and in the \(\pi \eta \) and \(\pi \eta ^\prime \) systems of the high-energy \(\pi ^- p \)-scattering data [22, 23]. For a sophisticated description of the dynamics the K-matrix approach with Chew-Mandelstam functions has been used which ensures an appropriate consideration of analyticity and unitarity conditions. The fit can reproduce all 20 different data samples reasonably well. Only one pole is needed for an appropriate description of the \(\pi _1\)-wave amplitude in the two subsystems \(\pi \eta \) and \(\pi \eta ^\prime \), but a 2-pole scenario cannot be completely excluded. The mass and width of this single \(\pi _1\)-pole are measured to be \((1623 \, \pm \, 47 \, ^{+24}_{-75})\, \mathrm {MeV/}c^2\) and \((455 \, \pm 88 \, ^{+144}_{-175})\, \mathrm {MeV}\), respectively. This result is in good agreement with [20] even though a slightly different description for the dynamics has been chosen and a much larger data base has been exploited. The outcome of the study here confirms the statement that the two \(\pi _1\) resonances listed in the RPP, the \(\pi _1(1400)\) and \(\pi _1(1600)\), might originate from the same pole. The shift of the pole with respect to [21] shows that the influence of the \(\pi \eta ^\prime \) channel plays an essential role and is in agreement with all previous findings.