1 Introduction

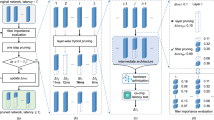
In this work, we explore the implementation of deep convolutional neural networks in FPGAs, leveraging on several model compression and simplification techniques (quantization, knowledge distillation, input-fragmentation).

We adopt as use-case a Level-0 trigger system of one of the Large Hadron Collider (LHC) experiments for the high luminosity phase of the LHC (HL-LHC), whose trigger logic will be implemented on FPGAs. Starting from the expected specs, we have implemented a toy simulation of the detector and trigger response that includes realistic effects related to resolution and noise. We train state-of-the-art deep neural network architectures on these examples for different tasks (identification and prediction of the particle parameters), optimizing with respect to physics performance. The learned knowledge of these models (Teachers) is then transferred to light and simple architectures (Students) using Knowledge Distillation by soft labels [1,2,3]. During the training of the Student models, pruning and quantization techniques are also applied.

We demonstrate that it is possible to reach marginal occupation of the FPGAs resources and sub microseconds latency in muon reconstruction and identification, with minimal performance loss.

2 Related work

Machine Learning (ML) inference on FPGAs has received increasing interest in the context of high energy physics (see for example: [4,5,6,7]). In this work, we get inspiration from these and other similar studies, evolving and extending them with the novel idea of exploiting knowledge transfer methods to achieve high level of simplification in the Neural Network model architectures, crucial to meet the tight constraints due to the limited hardware resources and latency in practical HEP real-time applications.

3 Datasets

Networks able to be deployed as trigger algorithm in a typical HEP experiment at the LHC have been investigated as benchmark scenario for this work. Trigger systems typically collect information from specific detector sub-systems and regions and analyze them in order to infer properties of potential interesting particles.

As an example case, it is possible to think at the hardware level muon trigger system of the ATLAS experiment [8]. The system aims to collect all the particle hit information from the fast RPC detectors in a given sector (i.e. a solid angle region of the detector) and tries to find a muon candidate – a collection of hits identified as a track in the detector – and measure its properties. The interesting quantities are the muon track spatial parameter inside the experiment (typically represented in terms of pseudorapidity \(\eta \)) and the transverse momentum of the muon \(p_{\mathrm {T}}\).

One can think to arrange the RPC detector strips into image-like objects, to be used as input for ML models, specifically convolutional architectures, particularly suitable to find patterns like the muon tracks in this test scenario.

Using published estimates of the particle rate during the so-called future Phase-II of the ATLAS experiment [9], together with well-known detector geometry and resolution as well as its magnetic field map, it is possible to generate toy events with muon tracks in the RPC system together with a random hit background, emulating the expected particle rate conditions in the future phases of the experiment during the HL-LHC.

The background is generated only accounting for the average hit rate in the spectrometer RPCs, therefore it does not consider correlated backgrounds. We did not aim to perfectly reproduce the experimental conditions, but to give a proof of principle of the compression and simplification chain in the context of a high energy physics experiment. An example of a toy event is reported in Fig. 1. Each bin of the vertical axis corresponds to a detector layer (from the bottom: 3 detector layers for the inner trigger station, 4 for the middle and 2 for the outer station). The horizontal axis linearly maps the pseudorapidity \(\eta \) of the RPC strips in a given range, corresponding to physical edges of the detector subsystem. The number of bins on the horizontal axis is set to 384, a realistic average number of ATLAS RPC strips. This provides a convenient representation for the RPC hits data, in which an infinite momentum muon appears in the image as a vertical pattern of pixels, independently of the pseudorapidity \(\eta \), while lower momentum muons appear ideally as tilted pixel patterns with slopes inversely proportional to the muon \(p_{\mathrm {T}}\). A total of 700 thousand images with muons in the range 3–20 GeV \(p_{\mathrm {T}}\) (half of which with just background and no muon) has been generated and used in this work, properly divided in training, validation and testing sets (450k images for training, 50k images for validation 200k images for testing). We checked that the generated sample size is enough to allow a stable training results by increasing the number of training events without observing significant differences in the results.

Fig. 1
figure 1

Example of RPC event image used to train the CNN: an event with one low-\(p_{\mathrm {T}}\) muon (\(p_{\mathrm {T}} \simeq 6\) GeV, \(\eta \simeq 0.3,\) \(\eta \) index \(\simeq 110\)) plus background noise due to pileup and cavern background. The image shows the complete \(9\times 384\) strips toy detector; each row corresponds to one of the nine RPC layers, while the \(\eta \) index is a rescale of the pseudorapidity

Full size image

4 Teacher model

In the context of Knowledge Distillation (discussed in Sect. 5.2) we started from the development of a relatively complex model which we will refer to as “Teacher”. As Teacher model we decided to deploy a ML-based approach using a conventional CNN architecture that fits well the muon identification task. All the models defined thereafter have been built using TensorFlow and Keras [10, 11].

In particular, the chosen CNN model is based on state-of-the-art floating-point CNN implementation, a simplified version of the VGG architecture [12].

The Neural Network architecture is illustrated in Fig. 2 and its structure detailed in Table 1. The model is composed of two convolutional blocks and two dense layers. The first convolutional block is constituted of two Convolutional bi-dimensional (Conv2D) layers with 10 filters each, followed by a Max-Pooling layer of pooling size (1,2). The second block is made of three Conv2D layers with 17 filters each and a Max-Pooling layer of pooling size (2,2). For all Conv2D layers we use square filters (3,3), the activation function is ReLU and the padding is put to “same”. This means that a zero-padding is added to the borders of the layer input to perform the convolution centering the filters on each of the image pixels, even the ones belonging to the borders. After the convolutional kernel, a flatten layer bridges to two dense layers with 10 neurons each and a ReLU activation function. A linear activation is used for the output layer, in order to describe continuous values in output. The network is trained to predict a two-component vector \( (p_{\mathrm {T}},~\eta \) index). The Mean Squared Error (MSE) is chosen as loss function and minimized using the Adam algorithm [13].

Fig. 2
figure 2

Schematic view of the network architecture that has been adopted. The numbers next to “Conv 2D” and to “Dense” represent respectively the number of filters and the number of neurons of that layer

Full size image

5 Model compression and simplification

Several different and somehow competing constraints have origin from the particular experimental condition:

  • Fit within the FPGA resources: the ML model obviously needs to fit within the resources of the specific hardware (a Virtex UltraScale\(^+\) 13 [14]). While this is the minimum requested, a lower occupancy would allow to use in parallel either the same algorithm, or also different algorithms with different specific targets, a much needed feature in nowadays HEP experiments triggers.

  • Latency: due to the high event-rate of the experiment, to keep-up the algorithm needs to run in less than \(\sim \)400 ns.

  • Efficiency: the Level-0 RPC muon trigger has to reconstruct muons with a momentum resolution that allows to select muons with efficiency > 90% for \(p_{\mathrm {T}}>\) 20 GeV as far as concerns single-lepton triggers, and to select muons with \(p_{\mathrm {T}}>\) 10 GeV for multi-lepton triggers with a rate smaller than approximately 40 kHz [9]. To take into account this requirement, we choose a threshold of 10 GeV in this study as nominal \(p_{\mathrm {T}}\) trigger threshold, to define the energy scale where to measure the resolution of the trigger turn-on and the plateau efficiency.

  • Fake Efficiency: We define “Fake Efficiency” the percentage of background events (i.e. events with no muons) that pass the nominal 10 GeV trigger threshold. Fake Efficiency needs to be less than \(\sim \) 2‰ in order for the background rate not to overflow the maximum data bandwidth.

These key-points have been the red thread which guided the choices taken in the development of this project and regulated the trade-off between compression and performance.

5.1 Compression by fragmentation of the input

In order to reduce the algorithm complexity, as first step in the data processing pipeline, we applied a procedure of pruning of the input information that we have called Fragmentation of the Input.

The number of parameters of the model, the number of loop cycles and therefore time interval the Neural Network needs to process an event (i.e. latency) in our framework are dominated by the size of the input images.

Since on average the horizontal curvature of low-\(p_{\mathrm {T}}\) muons inside the image is \(\sim 30\) pixels, we progressively fragmented the initial image into smaller ones, drastically reducing the model number of multiplications with minimal loss in performance. We split each image of the dataset into \(9\times 32\) pixels images scanning over the x-axis with variable stride. Then, the \(9\times 32\) image with the highest number of non-empty pixels is selected, being the most likely to contain the muon track (the background is indeed uniformly distributed through the image). The target quantity muon \(\eta \) is shifted as follow:

$$\begin{aligned} \qquad \qquad \qquad \quad \eta _{small} = \frac{\eta - \eta _{bin}^i}{\eta _{bin}^f - \eta _{bin}^i} \end{aligned}$$
(1)

with \(\eta _{bin}^i\), \(\eta _{bin}^f\) being respectively the initial and final pixel \(\eta \) of the image sector considered. \(\eta _{smalll}\) is used as target for the CNN instead of \(\eta \), since it represents the position of the muon in the sub-image which is the only predictable quantity once a single specific sector is selected. After the Network prediction, the output is reconverted to a global \(\eta \).

Figure 3 shows the result of this procedure in terms of fraction of images which contain at least a certain fraction of the true muon track as a function of the stride. Since we verified that our network is able of reconstruct images which contain as low as 50% of the track with no significant reconstruction efficiency loss, 16 pixels has been reasonably chosen as stride.

Fig. 3
figure 3

Stride comparison. When splitting the original \(9\times 384\) image into smaller \(9\times 32\) ones with fixed stride, inevitably part of the muon track gets lost. The blue, yellow, green and red points represent the fraction of \(9\times 32\) images which include respectively the 50, 80, 90 and 100% of the muon track

Full size image

The \(9\times 32\) images have been further compressed: feeding them to an Average-Pooling (pool size (1,2)) layer, the final image comes out as a \(9\times 16\) pixels with no significant information loss from the previous step. The Input Fragmentation procedure results in a reduction of the original image size by a factor of 24, with enough information for the model to produce correct predictions. Figure 4 shows the same event shown in Fig. 1 after the Fragmentation.

Fig. 4
figure 4

Same event of Fig. 1 after the Fragmentation procedure described in Sect. 5.1 (muon \(\eta _{small} \simeq 0.88\)). The black (grey) pixels of the bottom image represent the result of two (one) turned-on contiguous pixels after the Average-Pooling step

Full size image

5.2 Compression by knowledge distillation

Knowledge Distillation (KD) is a rather recent model compression and acceleration technique that has been developed to be able to deploy large deep-learning models on devices with limited resources (for example mobile phones and embedded devices). The general idea of KD is to effectively build a small Student model from a large one with strong capability, called Teacher model. The Teacher model is used to teach the Student model by transferring to it a significant amount of knowledge during the training phase [1,2,3].

Teacher-Student KD in deep neural networks has been successfully employed in several types of applications with different level of complexity and Neural Network architectures. In the specific context we are interested, it is possible to mention three principal benefits arising from implementing Teacher-Student distillation techniques:

  • it allows to deploy very light and streamlined CNN models that meet the constraints in computational and power resources imposed by the real-time HEP environments;

  • it allows to preserve as much as possible the neural network model performance while reducing resources and without increasing the size of the training samples;

  • providing a simplified architecture for the neural network, in general may simplify the study and optimization of model performance, for example by making it easier to understand the dependence of the network response on the characteristics of the input.

Applying distillation techniques to our specific regression task, in contrast to the typical classification in which KD has demonstrated excellent improvements, is more challenging since in the regression task it is not possible to take advantage from the softened softmax output of the teacher [1], and also because the real valued regression outputs are unbounded. We addressed this challenge by implementing an end-to-end trainable framework with Adaptation layers for hint learning, that allows the Student to better learn from the distribution of neurons in intermediate layers of the Teacher. It has been indeed demonstrated in [15], that using the intermediate representation of the Teacher as hint can help the training process and improve the final performance of the Student.

Fig. 5
figure 5

Schematic view of the Student model training, receiving hints from the Teacher model. Adaptation layer are present in each of the hint loss blocks

Full size image

Figure 5 reports a schematic view of the implemented Teacher-Student model relationship. The Student model receives hints from the Teacher after each of the two convolutional blocks and after the first dense layer. An additional layer called Adaptation layer is added in these positions to match the size of the Teacher and Student output (the latter being smaller) making possible the computation of a distance between the two. The Adaptation layer is represented by a Dense layer when it connects two dense layers and a Convolutional layer (1x1) when it connects two convolutional layers.

Since the regression outputs are real valued and not bounded, the Teacher can provide misleading guidance to the Student model. To mitigate this effect we bounded the Teacher contribution to the regression loss, so that the Teacher guidance is not provided to the Student once the quality of the Student surpasses that of the Teacher with a certain margin.

The explicit definition of the loss is reported in Eq. 2:

$$\begin{aligned} \begin{aligned}&L(y, y_S, y_T) \\&\quad = {\left\{ \begin{array}{ll} \Vert y - y_S\Vert ^2 +\sum _{i = 1}^{3} \gamma _iH_i &{} \text {if }\Vert y - y_T\Vert ^2 < \Vert y - y_S\Vert ^2\\ \Vert y - y_S\Vert ^2 &{} \text {Otherwise} \end{array}\right. } \\&H_i = \Vert A_i-T_i^H\Vert ^2 \end{aligned} \nonumber \\ \end{aligned}$$
(2)

with y being the truth labels vector, \(y_S\) the Student predictions, \(y_T\) the Teacher predictions, \(A_i\) the output of the i-th Adaptation layer, \(T_i^H\) the output of the i-th Teacher layer used as hint, and \(\gamma _i\) a tuned hyper-parameter, weighting in respect to the standard MSE the contribution of each hint term to the total loss.

5.3 Compression by quantization

Since most of the state-of-the-art deep neural network architectures are built and trained on powerful and power-hungry devices, the availability of resources or latency constraints at run-time are sometimes left-behind problems. A very effective technique to reduce and limit the models footprint is the quantization of weights and activations: while in fact the typical choice is to use 32 or 64 bits precision floating-point arithmetic, it has been demonstrated that it is possible to reduce the number of bits per weight in order to greatly decrease the model occupancy and improve its computational efficiency with marginal loss in performance [16].

A widespread approach is to compress an already trained model rounding the parameters to fixed precision values; procedure that most of the times especially for particularly aggressive quantization leads to a great degradation of the accuracy. In our work, to overcome this problem and to fully investigate end exploit the benefits of KD, we use a Quantization-Aware Training (QAT) approach: this means that the quantization is applied before the training of the model. We report in Sect. 6 how the benefits of KD are more evident with increasing quantization. All the architectures we will present are completely quantized (both weights and activation functions) beside the last layer which uses Floating Point 32 bits weights (FP32), in order to perform regression on a continuous output.

Table 1 Specifics of the CNN models used for the Teacher with input image size of \(9\times 384\) and for the Teacher and the Student with \(9\times 16\) images. The numbers reported in the “output shape” column represent respectively the height, width and depth of the output of each layer
Full size table

6 Performance

In this section, the result of the various techniques described in Sect. 5 are presented.

It is not obvious to build an unambiguous definition for a figure of merit against which to measure the performance of a hardware trigger for an experiment at a hadron collider. The complex constraints linked to the available data bandwidth allocated to each trigger and the presence of multiple selection chains designed for different physical processes, lead to competing requests. In order to obtain performance estimates that are sufficiently general and applicable to different types of physical processes, in this study we decided to focus on a limited number of proxies related to the performance of a generic muon trigger algorithm, able to capture the fundamental characteristics of the ATLAS muon trigger. We define the trigger efficiency turn-on curve as a function of the muon \(p_{\mathrm {T}}\) considering a nominal transverse momentum trigger threshold for the muon of 10 GeV, which corresponds to the planned multi-muon threshold for the muon in the ATLAS TDAQ TDR [9]. The main proxy to evaluate trigger performances is the plateau value of the efficiency turn-on curve, which is the relevant parameter for the efficiency to select muons from interesting high-\(p_{\mathrm {T}}\) physics at the LHC (e.g. W/Z/Higgs/top physics). In addition to the plateau efficiency, we also considered as additional proxies the fake efficiency, defined as the probability to reconstruct an event with no muons as containing a muon with \(p_{\mathrm {T}}\) above the nominal threshold, and the \(p_{\mathrm {T}}\) resolution (”\(\sigma _{p_{T}}\) around threshold”) around the nominal threshold, that is a proxy for the overall trigger rate driven by low-\(p_{\mathrm {T}}\) physics.

Figure 6 shows the comparison between using the entire images as input vs applying the Fragmentation strategy. While a slight decrease in performance is observed, Input Fragmentation is essential for the FPGA implementation (as will be clear in Sect. 7).

Fig. 6
figure 6

Trigger efficiency comparison. The curves have been realized with a nominal threshold at 10 GeV. The ideal case would shows as a step function with efficiency equal to 0 before threshold and to 1 after threshold. Statistical uncertainties computed as binomial confidence intervals are shown as well. If not visible, they’re smaller than the markers size. In orange (diamonds) the model taking as input \(9\times 384\) pixels images. In indigo (circles) the same model architecture taking as input \(9\times 16\) pixels images (the model adopted afterward as “Teacher”)

Full size image

Figure 7 shows the advantages of using KD. The improvement is clearly visible both over-threshold (higher plateau efficiency) and under-threshold (better \(\sigma _{p_{T}}\) around threshold, resulting in an efficiency curve that goes faster to zero when \(p_{\mathrm {T}} \rightarrow 0\)).

Fig. 7
figure 7

Efficiency curves (realized as for Fig. 6). Statistical uncertainties computed as binomial confidence intervals are shown as well. If not visible, they’re smaller than the markers size. Here in indigo (circles) the performance of the Teacher model. In light green (triangles) the performance of the Student trained without any help from the Teacher. In red (squares) the performance of the Student trained with hints from the Teacher

Full size image

In Fig. 8 we show the effect of different levels of quantization on the Teacher model. The quantized model weights are always (i.e. in this case and for all the models presented thereafter) fixed point numbers, with 0 bits reserved to the integer part and \(n_{bits}\) for the decimal part. The performance degradation starts to become visible with less than 5 bits per weight. The 2-bits model curve (orange) is flat since, no matter what, the network remains stuck in a local minimum, always predicting the same value for the \(p_T\).

Fig. 8
figure 8

Teacher efficiency curves (realized as for Fig. 6) for different levels of quantization. Each weight is a fixed point number whom integer part is described using 0 bits and the decimal part using \(n_{bits}\). Statistical uncertainties computed as binomial confidence intervals are shown as well. If not visible, they’re smaller than the markers size

Full size image

Figures 9 and 10 show the result of quantization for models with 4 and 3 bits per weight respectively.

Interestingly we report how the knowledge extracted through KD increase with increasing quantization aggressiveness.

Fig. 9
figure 9

Efficiency curves (realized as for Fig. 6). Statistical uncertainties computed as binomial confidence intervals are shown as well. If not visible, they’re smaller than the markers size. Here in indigo (circles) the performance of the Teacher model. In light green (triangles) the performance of the Quantized Student (4 bits per weight) trained without any help from the Teacher. In red (squares) the performance of the Quantized Student (4 bits per weight) trained with hints from the Teacher

Full size image
Fig. 10
figure 10

Efficiency curves (realized as for Fig. 6). Statistical uncertainties computed as binomial confidence intervals are shown as well. If not visible, they’re smaller than the markers size. Here in indigo (circles) the performance of the Teacher model. In light green (triangles) the performance of the Quantized Student (3 bits per weight) trained without any help from the Teacher. In red (squares) the performance of the Quantized Student (3 bits per weight) trained with hints from the Teacher

Full size image

In Fig. 11 we compare the effect of using a quantized-Teacher for the training of the students. Noticeably we observe how using a quantized-Teacher generally leads to worse results.

Fig. 11
figure 11

Efficiency curves (realized as for Fig. 6). Statistical uncertainties computed as binomial confidence intervals are shown as well. If not visible, they’re smaller than the markers size. Red triangles (cyan diamonds) represent the performance of the 4-bit Student trained with the hints from the (quantized-)Teacher. Orange circles (blue squares) represent the performance of the 3-bit Student trained with the hints from the (quantized-)Teacher

Full size image

In Figs. 12, 13, 14 some quantities relative to physics performance which we used to compare different algorithms are reported; respectively \(\sigma _{p_{\mathrm {T}}}\) (resolution) around trigger threshold, Plateau Efficiency and Fake Efficiency. The improvements coming from the KD are clearly visible with all the adopted metrics. It is also worth to notice that thanks to KD, for all possible choices for quantization (down to 3 bits) the CNN is capable of a Fake Efficiency lower than 2‰ (one of the stringent requirements presented in Sect. 5). Without the help from the Teacher (whom Fake Efficiency remains 0 for all level of quantization) the model would otherwise break the limit imposed by the experimental framework. A curious feature is represented by the increasing Fake Efficiency for higher numbers of bits for the Student models. By observing the wrongly-triggered images, characterized by low-density of non-empty pixels and accidental vertical patterns, we speculate the reason for this is that the deeper accuracy reached by higher precision Students collides with their lower generalization power (caused by their small architecture) causing a higher fraction of random pattern (ignored by the lower precision counterparts) to be triggered.

Fig. 12
figure 12

\(\sigma _{p_{\mathrm {T}}}\) computed in a true \(p_{\mathrm {T}}\) interval around threshold \((7.5~\hbox {GeV}<p_{\mathrm {T}}<12.5\) GeV) as a function of the number of bits per weight. In indigo (circles) the performance of the Teacher model. In light green (triangles) the performance of the Student trained without any help from the Teacher. In red (squares) the performance of the Student trained with hints from the Teacher

Full size image
Fig. 13
figure 13

Plateau Efficiency computed as the mean efficiency in a true \(p_{\mathrm {T}}\) interval well above threshold (\(p_{\mathrm {T}}>17\) GeV) as a function of the number of bits per weight. In indigo (circles) the performance of the Teacher model. In light green (triangles) the performance of the Student trained without any help from the Teacher. In red (squares) the performance of the Student trained with hints from the Teacher

Full size image
Fig. 14
figure 14

Fake Efficiency for events with no muon tracks but only background as a function of the number of bits per weight. In indigo (circles) the performance of the Teacher model. In light green (triangles) the performance of the Student trained without any help from the Teacher. In red (squares) the performance of the Student trained with hints from the Teacher. The Teacher Fake Efficiency remains 0 for all level of quantization

Full size image
Table 2 Resources occupancies for different FPGA components and latencies in clock cycles (2.38 ns requested clock in synthesis)
Full size table

7 Implementation on FPGA

The implementation of the different architectures has been performed using the HLS4ML library [17], which in combination with the Vivado HLS package translate a Tensorflow model into VHDL code.

Table 2 shows synthesis-level estimations for the latency and the occupancy in terms of FPGA components usage of different CNNs. The design implementation has been tested with different clock frequencies to verify the minimum clock the model is able to sustain with no timing-violation. The minimum value proved to be 2.38 ns (maximum frequency: \(f_{max}=\) 420MHz) corresponding to a latency of 435 ns for the Qstudent 3-bit model. Table 3 shows the same numbers as percentages relatively to the total FPGA available resources. While the Teacher architecture wouldn’t even fit, it is clear that with quantization and compression the occupation of FPGA resources becomes almost irrelevant.

The numbers are referred to models with \(9\times 16\) pixels inputs solely, since for \(9\times 384\) pixels inputs the software implementation pipeline always crashed during the unrolling of the outer loops. Given the results for the “Teacher (\(9\times 16\))”, we think it is safe to assume that bigger input models would not fit within the FPGA resources nor the latency constraint.

Table 3 Percentage occupancy relative to the total FPGA available resources (model xcvu13p-fhga2104-2L-e [14])
Full size table

8 Conclusions

Machine learning alternatives to conventional trigger algorithms require the ability to deploy Deep Neural Networks highly compressed and with the appropriate simplicity. We have developed a multi-stage compression approach based on a mix of conventional compression strategies and knowledge transfer techniques, crucial to streamline the DNN models and simplifying the synthesis phase in the FPGA firmware. The approach has been successfully applied to a realistic use-case of one of the triggers for the Phase-II of the ATLAS detector at the LHC, showing that a deep neural network-based algorithm can be effectively implemented in the trigger FPGA, within the latency requirements of the ATLAS trigger, and with competitive performance.