1 Introduction

Gravitational collapse is an important phenomenon in astrophysics in which the theory of General Relativity (GR) may be applied and studied. The gravitational potentials involved are in general, both space and time dependent and so the full time-dependent Einstein Field Equations (EFEs) are utilized. Off diagonal elements of the energy–momentum tensor due to shearing, viscosity and most notably heat flux, are also invoked and this provides a physically rich scenario for thermodynamic analyses, otherwise limited in static, time-independent GR. Physical problems involving gravitational collapse have been well studied since the pioneering work of Oppenheimer and Snyder [1] in which the collapse of a spherically symmetric cloud of dust was studied with an empty space exterior as described by the Schwarzschild solution. The inclusion of radiation within the exterior spacetime was made by Vaidya [2] and this allowed for more accurate models of gravitational collapse in which radiation transfer is necessary. An important step forward was also made by Misner and Sharp [3]. A connection was made with the Oppenheimer–Volkoff equations for hydrostatic equilibrium, allowing for more realistic equations of state in the case of adiabatic collapse and the inclusion of neutrino flux for a non-adiabatic scenario [4]. Other notable researchers include Bonnor et al. [5], Santos [6] and Chan et al. [7]. Bonnor et al. gave an extensive review of radiating spherical collapse. Herrera, Santos and Chan have looked into various aspects of the dynamics of gravitational collapse, augmenting models to include viscous effects, imperfect fluids and anisotropy.

Gravitational collapse is the physical phenomenon which occurs during the birth or death of stellar objects. Protostar formation begins with the self-gravitational collapse of interstellar clouds in a process which can take hundreds of thousands to millions of years. Relativity theory is not required for the most part of such a collapse process. At the other end of the spectrum, so to speak, and more relevant to applications of GR is the formation of supernova remnants such as neutron stars and black holes. These processes are probably about sixteen orders of magnitude more rapid than say protostar formation, yet gravity provides the key driving force, dominating all other forces if a black hole is the final state of collapse. Computation of the timescales involved in the formation of neutron stars or black holes from the progenitors of core-collapse supernovae necessitates the use of GR or higher gravity theories. Such computations suggest collapse processes of the order of tens of milliseconds [8]. The release of gravitational binding energy in supernovae is typically of the order of \(10^{51}\) ergs [9] and in the more extreme case of neutron star collapse, perhaps as high as \(10^{54}\) ergs [10]. In complementing such luminosity data which is accessible to both theoretical and experimental methods, an investigation of the dynamical forces at work might help elucidate the time-dependent structural properties of collapsing neutron star material up until horizon formation. At the present time, such investigations remain computationally based using GR or extended gravity theories.

An alternative to black hole formation, due to a core-collapse supernova of sufficient magnitude, could be the collapse of a neutron star which has become unstable. Such a scenario might arise as a result of accretion, eventually leading to a core with a critical density, or in the more spectacular event in which two stars merge. Such events are actively studied with the inclusion of gravitational wave research. A recent theoretical study investigates the collapse of an unstable neutron star with initial conditions derived from realistic equations of state [11]. A detailed analysis of the radial oscillation modes was used to establish instability. Other methods for determining instability include evaluation of the adiabatic index [12, 13], however this might not guarantee stability with respect to radial oscillations.

The Tolman–Oppenheimer–Volkoff (TOV) equation for hydrostatic equilibrium provides insight into the internal forces present in compact stellar objects [14, 15]. Originally developed using the time-invariant field equations for spherically symmetric bodies of isotropic matter in static gravitational equilibrium, it is then linked to an equation of state to provide a definite internal structure of the body. Since its original inception, the TOV equation has been augmented to include pressure anisotropy [16] which naturally arises if a non-perfect fluid scenario is assumed. Such assumptions are supported by investigations into strong magnetic fields, solid cores and other properties likely to be inherent in compact objects [17, 18]. Further work has provided the so-called dynamical Tolman–Oppenheimer–Volkoff equation, developed via the scheme of Misner and Sharp [19]. This dynamical TOV equation is suitable for monitoring gravitational collapse processes such as the collapse of an unstable neutron star [20].

In our study, we make use of the Vaidya–Tikekar gravitational potential in setting up an initial configuration representing an unstable neutron star. This gravitational formalism has been shown to be well-suited to modelling superdense compact objects [21]. The potential incorporates a spheroidal parameter which allows for the enhancement of physical features associated with superdense matter such as high core densities, required as a precursor to gravitational collapse. We take as our initial configuration, the example of an unstable neutron star of appropriate mass and radius as given by [11]. Instability analysis is disregarded for the time being, in order to focus on the implementation of the dynamical TOV equation which is the aim of this study.

2 The field equations

In modelling gravitational collapse, we consider the matter distribution to be shear-free and spherically symmetric. This is a reasonable assumption when modelling a relativistic, radiating star. In this case there exist coordinates for which the line element may be expressed in a form that is simultaneously isotropic and comoving. We make use of a line element similar to that originally proposed by de Oliveira et al. [22] and modified by Sharma and Das [23] for studying radiating, gravitational collapse. With the coordinates \(({x}^a ) = (t, r, \theta , \phi )\) this line element, for the interior spacetime of the stellar model, takes the form

$$\begin{aligned} ds^2= & {} -A_0^2(r)dt^2 + f^2(t)\nonumber \\&\times \left[ B_0^2(r)dr^2 + r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2)\right] , \end{aligned}$$
(1)

where the metric functions are to be determined according to physically viable gravitational potentials. We consider a model which represents a spherically symmetric, shear-free fluid configuration with heat flux. For our model, the energy–momentum tensor for the stellar fluid takes the form

$$\begin{aligned} T_{ab}= & {} (\rho + p_t)u_a u_b + p_t g_{ab} + (p_r - p_t)\chi _a\chi _b\nonumber \\&\quad + q_a u_b + q_b u_a \,, \end{aligned}$$
(2)

where \(\rho \) is the energy density, \(p_r\) and \(p_t\) are the radial and tangential stresses respectively and \(q^a = (0, q, 0, 0)\) is the heat flux vector assumed to flow in the radial direction due to spherical symmetry. The fluid four-velocity \(\mathbf{u}\) is co-moving and is given by

$$\begin{aligned} u^a = \displaystyle \frac{1}{A} \delta ^{a}_0 \,. \end{aligned}$$
(3)

and \(\chi ^a\) is a unit space-like four-vector along the radial direction. The following relations need to be satisfied

$$\begin{aligned} u^au_a = -1, u^aq_a = 0, \chi ^a\chi _a = 1, \chi ^au_a = 0. \end{aligned}$$

The fluid collapse rate \(\Theta = u^a_{;a}\) of the stellar model is given by

$$\begin{aligned} \Theta = 3\frac{\dot{B}}{AB} \,, \end{aligned}$$
(4)

where dots represent differentiation with respect to t.

The nonzero components of the Einstein field equations for the line element (1), in geometrized units, are

$$\begin{aligned} 8\pi \rho= & {} \frac{1}{f^2}\left[ \frac{1}{r^2}-\frac{1}{r^2B_0^2}+\frac{2B_0'}{r B_0^3}\right] +\frac{3\dot{f^2}}{A_0^2f^2} \,, \end{aligned}$$
(5)
$$\begin{aligned} 8\pi p_r= & {} \frac{1}{f^2}\left[ -\frac{1}{r^2}+\frac{1}{r^2B_0^2}+\frac{2A_0'}{r A_0B_0^2}\right] \nonumber \\&- \frac{1}{A_0^2}\left[ 2\frac{\ddot{f}}{f}+\frac{\dot{f^2}}{f^2}\right] , \end{aligned}$$
(6)
$$\begin{aligned} 8\pi p_t= & {} \frac{1}{f^2}\left[ \frac{A_0''}{A_0B_0^2}+\frac{A_0'}{r A_0B_0^2}-\frac{B_0'}{r B_0^3}-\frac{A_0'B_0'}{A_0B_0^3}\right] \nonumber \\&-\frac{1}{A_0^2}\left[ 2\frac{\ddot{f}}{f}+\frac{\dot{f^2}}{f^2}\right] , \end{aligned}$$
(7)
$$\begin{aligned} 8\pi q= & {} -\frac{2A_0'\dot{f}}{A_0^2B_0^2f^3} \,, \end{aligned}$$
(8)

We rewrite Eqs. (5)–(7) in the form

$$\begin{aligned} \rho= & {} \frac{\rho _s}{f^2}+\frac{3\dot{f^2}}{8\pi A_0^2f^2} \,, \end{aligned}$$
(9)
$$\begin{aligned} p_r= & {} \frac{(p_r)_s}{f^2}-\frac{1}{8\pi A_0^2}\left[ 2\frac{\ddot{f}}{f}+\frac{\dot{f^2}}{f^2}\right] , \end{aligned}$$
(10)
$$\begin{aligned} p_t= & {} \frac{(p_t)_s}{f^2}-\frac{1}{8\pi A_0^2}\left[ 2\frac{\ddot{f}}{f}+\frac{\dot{f^2}}{f^2}\right] , \end{aligned}$$
(11)

where \(\rho _s\), \((p_r)_s\) and \((p_t)_s\) denote the energy density, radial pressure and tangential pressure respectively of the initial static configuration. These are given by

$$\begin{aligned} 8\pi \rho _s= & {} \left[ \frac{1}{r^2}-\frac{1}{r^2B_0^2}+\frac{2B_0'}{r B_0^3}\right] \,, \end{aligned}$$
(12)
$$\begin{aligned} 8\pi (p_r)_s= & {} \left[ -\frac{1}{r^2}+\frac{1}{r^2B_0^2}+\frac{2A_0'}{r A_0B_0^2}\right] \,, \end{aligned}$$
(13)
$$\begin{aligned} 8\pi (p_t)_s= & {} \left[ \frac{A_0''}{A_0B_0^2}+\frac{A_0'}{r A_0B_0^2}-\frac{B_0'}{r B_0^3}-\frac{A_0'B_0'}{A_0B_0^3}\right] \,. \end{aligned}$$
(14)

Equations (6) and (7) can be used to calculate the anisotropy parameter, defined as

$$\begin{aligned} \delta \left( r,t \right) = \left( p_t - p_r \right) \end{aligned}$$
(15)

This is similar to a definition given by [23]. In order to construct a static model of the initial configuration, Sharma and Das assumed that the anisotropy parameter, \(\delta \), was separable in r and t, i.e.

$$\begin{aligned} \delta \left( r , t \right) = \frac{\delta _s (r)}{f^2 (t)} \end{aligned}$$
(16)

Then Eq. (15) reduces to

$$\begin{aligned} \delta _s (r)= & {} \frac{1}{8\pi }\bigg [\frac{A''_0}{A_0 B^2 _0} - \frac{A'_0}{rA_0 B^2 _0} - \frac{B' _0}{rB^3 _0} - \frac{A' _0 B' _0}{A_0 B^3 _0} \nonumber \\&- \frac{1}{r^2 B^2 _0} + \frac{1}{r^2} \bigg ] \end{aligned}$$
(17)

which is clearly independent of t. They further utilized the Finch and Skea ansatz which has been successfully used to model compact stars [24]. In order to solve (17), Sharma and Das assumed a particular profile for the anisotropy parameter based on physically reasonable behaviour. Equation (17) reduces to a second order equation in \(A_0\) for which they obtained the general solution. Hence the initial static configuration could be fully specified.

In this paper, we adopt a different approach. We begin with an initial static configuration described by a Vaidya–Tikekar (V–T) model which is suitable for modelling superdense compact objects. The V–T ansatz, together with a linear equation of state has been used recently by Sharma et al. to generated new and viable solutions for describing pulsars [25]. We make further use of this work by setting up initial static configurations which represent an unstable neutron star. Gravitational collapse then ensues in which heat is dissipated and a black hole remnant is formed.

3 Junction conditions

Since the interior is radiating energy, the exterior spacetime is described by Vaidya’s outgoing solution [2] given by

$$\begin{aligned} ds^2 = - \left( 1 - \frac{2m(v)}{\textsf {r}}\right) dv^2 - 2dvd\textsf {r} + \textsf {r}^2 \left( d\theta ^2 + \sin ^2\theta d\phi ^2 \right) \,. \end{aligned}$$
(18)

The quantity m(v) represents the Newtonian mass of the gravitating body as measured by an observer at infinity, as a function of the retarded time v. The metric (18) is the unique spherically symmetric solution of the Einstein field equations for radiation in the form of a null fluid. The Einstein tensor for the line element (18) is given by

$$\begin{aligned} G_{ab} = -\frac{2}{\textsf {r}^2}\frac{dm}{dv} \delta ^0_a \delta ^0_b \,.\end{aligned}$$
(19)

The energy momentum tensor for null radiation assumes the form

$$\begin{aligned} T_{ab} = {\Phi }w_{a}w_{b} \,,\end{aligned}$$
(20)

where the null four-vector is given by \(w_a = (1, 0, 0, 0)\). Thus from (19) and (20) we have

$$\begin{aligned} {\Phi } = -\frac{2}{\textsf {r}^2}\frac{dm}{dv} \,,\end{aligned}$$
(21)

for the energy density of the null radiation. Since the star is radiating energy to the exterior spacetime we must have \(\displaystyle \frac{dm}{dv}\le 0 \).

The necessary conditions for the smooth matching of the interior spacetime to the exterior spacetime was first presented by Santos [6] in his seminal paper. The junction conditions for the line elements (1) and (18) are given by

$$\begin{aligned} \left( p_r\right) _{\Sigma }= & {} \left( q B_0 f\right) _{\Sigma } \end{aligned}$$
(22)
$$\begin{aligned} m(v)= & {} \left[ \frac{r f}{2} \left( 1 - \frac{1}{B_0^2} + \frac{(r \dot{f})^2}{A_0^2}\right) \right] _{\Sigma } \end{aligned}$$
(23)

4 A Vaidya–Tikekar static configuration

Vaidya and Tikekar [21] have developed realistic compact stellar models according to the gravitational potential formulation given by

$$\begin{aligned} B_0^2(r) = \frac{1 - K(r^2/L^2)}{1 - (r^2/L^2)} \end{aligned}$$
(24)

where K is a spheroidal parameter which allows for departure from spherical symmetry with respect to the radial coordinate. This formulation has been shown to be suitable for modelling superdense stellar matter and is less prone to instability due to anisotropy in pressure towards the surface. A linear equation of state, \(p_r = \alpha \rho - \beta \), together with the standard time-independent field equations are used to generate the gravitational potential,

$$\begin{aligned} A_0^2(r) = J \left( 1 - r^2/L^2\right) ^n \left( 1 - K r^2/L^2 \right) ^\alpha e^{K\left( L^2 - r^2\right) \beta /2} \end{aligned}$$
(25)

where

$$\begin{aligned} n = \frac{1}{2}\left( -1 - 3\alpha + L^2 \beta + K(1 + \alpha - L^2 \beta ) \right) \end{aligned}$$
(26)

and J is a constant to be determined through matching of both potentials at the boundary. Matching of the internal metric to a Schwarzschild exterior at the boundary provides

$$\begin{aligned} L^2 = \frac{R^2 \left( 2KM - KR + R\right) }{2M} . \end{aligned}$$
(27)

The surface energy density is given by

$$\begin{aligned} \rho _s = \frac{\left( 1 - K\right) \left( 3 - K R^2 /L^2 \right) }{L^2 \left( 1 - K R^2 /L^2 \right) ^2} \end{aligned}$$
(28)

and

$$\begin{aligned} \beta = \alpha \rho _s . \end{aligned}$$
(29)

We choose \(\alpha = 1/3\) which then sets \(\rho _s = 4\mathcal {B}\) where \(\mathcal {B}\) is the MIT Bag constant.

5 Non-adiabatic collapse process

In order to develop the temporal dependence for the collapse process, the boundary condition \((p_r)_\Sigma = (q B)_\Sigma \) is used. Making use of (8) and (10) with the static part set to zero, we obtain

$$\begin{aligned} 2 f \ddot{f} + \dot{f}^2 - 2 a \dot{f} = 0 \end{aligned}$$
(30)

where

$$\begin{aligned} a = \left( \frac{A_0' }{B_0}\right) _\Sigma \end{aligned}$$
(31)

which sets the temporal dependence of the model.

An integral of (30) is given by

$$\begin{aligned} \dot{f} = 2a\left( 1 - \frac{1}{\sqrt{f}} \right) \end{aligned}$$
(32)

in which the integration constant was set so that \(f = 1\) represents the initial static configuration at \(t = - \infty \). This can be further integrated to obtain

$$\begin{aligned} t = \frac{1}{a}\left[ \frac{f}{2} + \sqrt{f} + \ln (1 - \sqrt{f}) \right] \end{aligned}$$
(33)

A similar result was originally obtained by Bonnor et al. [5] and subsequently used in a model incorporating pressure anisotropy by Govender et al. [26]. Recently, Pretel and da Silva [11] obtained a similar result with a temporal function defined to be the square of the one we have defined, and Veneroni and da Silva [27] also displayed similar results. We also express the second derivative of f as

$$\begin{aligned} \ddot{f} = -\frac{2a^2}{f^2}\left( 1 - \sqrt{f}\right) \end{aligned}$$
(34)

which is clearly directed towards the centre of the gravitationally collapsing system.

It is necessary to determine the lower limit of f at which the event horizon is formed. This is determined by examining the asymptotic behaviour of the surface redshift, given by

$$\begin{aligned} z_\Sigma = \left[ \frac{dv}{d\tau }\right] _\Sigma - 1 = \left[ \frac{1}{B_0} + r\dot{f}\right] ^{-1}_\Sigma - 1 \end{aligned}$$
(35)

where \(\tau \) is the proper time defined on the surface boundary. Divergence of \(z_\Sigma \) leads to

$$\begin{aligned} f_{bh} = \left( \frac{2M}{R}\right) ^2 \end{aligned}$$
(36)

which gives the time of formation of the black hole.

6 A dynamical model

We follow a model similar to that used by Pretel and da Silva [11] describing an unstable neutron star with radius \(R = 9.384 \) km and mass \(M = 2.015 M_\odot \) which undergoes gravitational collapse to form a black hole. We investigate various settings of the spheroidal parameter and associated parameters required for the models, as shown in Table 1. Vaidya and Tikekar [21] initially proposed a value of \(K = -2\) for the spheroidal parameter although the suitability of larger negative values (more radially asymmetric potentials) has been investigated, with \(K = -20\) of particular interest [25]. Values of the MIT Bag constant \(\mathcal {B}\) are calculated from \(\rho _s = \rho (r = R)\) and are a bit higher than the more common value of \(60\, \mathrm{MeV/fm}^3\). Higher MIT Bag constants have been utilised in studies of strange stars [28] wherein it is noted that a higher value softens the equation of state. Studies of semiempirical mass-radius relationships for strange stars also required the use of large values (\(\mathcal {B} \approx 110\, \mathrm{MeV/fm}^3\)) [29]. We note that the temporal dependence parameter, a, is related to the surface gravity by

$$\begin{aligned} a = \frac{M}{R^2} = g_s \sqrt{1 - 2M/R}. \end{aligned}$$
(37)

For our model, the parameter which sets the temporal dependence is calculated to be \(a = 0.03377 \,\mathrm{km}^{-1}\). This gives a surface gravity of \(g_s = 0.05582 \,\mathrm{km}^{-1} c^2 = 5.02 \times 10^{14} \, \mathrm{cm/s}^2\) for the initial configuration. This is about twice the surface gravity of a typical neutron star but within an upper bound as given by Bejger and Haensel [30].

Table 1 Model parameters of initial unstable static configuration
Full size table

The mass function (23) is given by

$$\begin{aligned} m(r,f) = f m_0 (r) + 2 r^3 \frac{a^2}{A_0(r)^2}\left( 1 - \sqrt{f} \right) ^2 \end{aligned}$$
(38)

where

$$\begin{aligned} m_0(r) = 4\pi \int {\rho _0(r) r^2}dr = r^3 \left[ \frac{R^3}{M} + \frac{2K}{1 - K}\left( R^2 - r^2 \right) \right] ^{-1} \end{aligned}$$
(39)

is the mass of the initial configuration. The temporal function, evaluated at the time of horizon formation, gives \(f_{bh} = 0.4018\). At horizon formation, the mass function gives \(m(R,f_{bh}) = 1.277 M_\odot \) which corresponds to the mass of the black hole remnant. The radius of the horizon is \(\textsf {r}_{bh} = R \times f_{bh} = 3.770\) km. The time-dependent field equations allow for the evaluation of physical quantities at important points in spacetime, in particular the central densities (\(\rho _c\)) and pressures (\(p_c\)). Results of these calculations are given in Table 2 for comparison and integration with models in similar studies.

Table 2 Core densities and pressures at initial and final stages
Full size table

7 Dynamical Tolman–Oppenheimer–Volkoff equations

A generalized Tolman–Oppenheimer–Volkoff (TOV) equation, incorporating heat-flux, may be obtained from the divergence of the energy–momentum tensor and the Einstein field equations [31]. Within our formalism, we obtain

$$\begin{aligned} \frac{\partial }{\partial r}p_r= & {} -(\rho + p_r)B_0^2 f \left[ \frac{m}{(r f)^2} + 4\pi (r f) p_r + \frac{r}{A_0^2}\ddot{f}\right] \nonumber \\&+ \frac{2}{r}(p_t - p_r) - \frac{B_0^2 f^2}{A_0}\left[ \dot{q} + 5 q \frac{\dot{f}}{f} \right] . \end{aligned}$$
(40)

This equation can be re-arranged as

$$\begin{aligned} \left( \rho + p_r \right) \frac{r}{A_0^2}\ddot{f}= & {} F_g + F_h + F_a + F_q \end{aligned}$$
(41)

where the gravitational, hydrostatic, anisotropic and heat-flux forces are defined as

$$\begin{aligned} F_g= & {} -(\rho + p_r)\left[ \frac{m}{(r f)^2} + 4\pi (r f) p_r \right] \end{aligned}$$
(42)
$$\begin{aligned} F_h= & {} -\frac{1}{B_0^2 f}\left[ p_r' \right] \end{aligned}$$
(43)
$$\begin{aligned} F_a= & {} \frac{1}{B_0^2 f}\left[ \frac{2}{r}(p_t - p_r)\right] \end{aligned}$$
(44)
$$\begin{aligned} F_q= & {} - \frac{1}{A_0}f\left[ \dot{q} + 5 q \frac{\dot{f}}{f} \right] . \end{aligned}$$
(45)

Equation (41) has the form of Newton’s second law and the forces identified therein correspond to those found in similar studies [20, 32]. The resultant force is given by

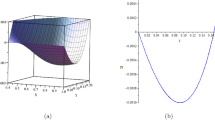
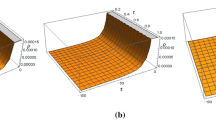
$$\begin{aligned} F_s = \left( \rho + p_r \right) \frac{r}{A_0^2}\ddot{f} \end{aligned}$$
(46)

We plot the temporal dependence at the boundary in Fig. 1 for the models determined by spheroidal parameters of \(K = -2\) and \(K = -20\). The normalized spatial profiles are shown in Figs. 2, 3, 4 and 5 at various stages of collapse, namely at \(f = 1\) which corresponds to the initial static configuration, then at \(f = 0.7\), \(f = 0.5\) and finally at \(f = f_{bh} = 0.4018\) which corresponds to the time of formation of the black hole.

Fig. 1
figure 1

Temporal progression of surface forces for \(K = -2\) (solid) and \(K = -20\) (dashed)

Full size image
Fig. 2
figure 2

Force profiles at \(f = 1\) for \(K = -2\) (solid) and \(K = -20\) (dashed)

Full size image
Fig. 3
figure 3

Force profiles at \(f = 0.7\) for \(K = -2\) (solid) and \(K = -20\) (dashed)

Full size image
Fig. 4
figure 4

Force profiles at \(f = 0.5\) for \(K = -2\) (solid) and \(K = -20\) (dashed)

Full size image
Fig. 5
figure 5

Force profiles at \(f = f_{bh}\) for \(K = -2\) (solid) and \(K = -20\) (dashed)

Full size image

8 Discussion

We now provide further discussion of the trends and physical viability of our dynamical gravitational collapse model. Figure 1 shows the effect of the spheroidal parameter K on the magnitudes of the forces generated at the surface boundary, with respect to the time measurement parameter f. At early times \((f \approx 1)\), the stellar configuration is in an unstable, quasi-static equilibrium with a resultant force close to zero. Initially, heat dissipation to the exterior and the associated heat-flux force are zero. As the star collapses and radiates, the component forces grow in magnitude, most notably at late times \((f_{bh}< f < 0.5)\). The gravitational force is increasingly negative and is clearly the dominant driving force. We observe that the force due to anisotropy is positive, indicating that the tangential pressure dominates the radial pressure. This gives rise to a repulsive force which tends to counteract the effect of the gravitational force. Similar trends are observed for the forces at the surface for the more aspherical settings of the spheroidal parameter \((K = -20)\). Apart from the anisotropy-free hydrostatic component, we observe that radial asymmetry tends to diminish slightly the magnitudes of the forces at the surface boundary. Figures 2, 3, 4 and 5 display the radial profiles and show the progression of the internal stresses. The initial, quasi-static equilibrium is shown in Fig. 2 where there is no resultant force throughout the configuration. Gravitational collapse could be initiated due to the extreme and hostile environment of compact objects such as neutron stars which most likely have marked seismological activity. Accretion of material could also assist in inducing collapse. There appears to be competition between the inwardly driven gravitational force and the outwardly directed hydrostatic force, with the difference being enhanced with larger deviations from spherical symmetry i.e., a larger magnitude of the spheroidal parameter, K. Figures 3, 4 and 5 show the evolution of the forces as the star collapses. As time progresses (decreasing values of f), we note that the magnitudes of the competing forces increase with the largest effects occurring at a comoving radial distance of about 2/5 of the surface boundary \(r_b\). While the forces due to gravity, aniosotropy and the hydrostatic interaction exhibit similar behaviour, the force due to the heat-flux changes sign. During the initial stages of collapse (Fig. 3), we see that the force due to heat flux (\(F_q\)) promotes the collapse although it is relatively small in magnitude, dominated by the other forces. During the later stages (Figs. 4, 5), the heat flux has a retarding effect. As the core collapses, its density increases leading to a larger output of energy. Although the heat flux is directed outwards, the inertia associated with it has a tendency to ’stall’ the collapse process. The effect of the spheroidal parameter, K, is more noticeable within the interior of the collapsing fluid than at the surface and we note that aspheroidicity generally promotes instability.

9 Conclusion

In this work we investigated the stability of a collapsing, radiating star by focussing on the forces at play within the stellar fluid. We employed a dynamical Tolman–Oppenheimer–Volkoff equation which allowed us to take snapshots of the various forces at work as functions of the temporal and radial coordinates. We observed that the magnitudes and behaviours of the various forces are altered as the collapse proceeds. This in turn drives the fluid to greater instability. We further showed that the spheroidal parameter, K, in the Vaidya–Tikekar superdense stellar model is well suited and plays a key role in the evolution of the forces within the stellar material. Our work confirms earlier findings by Sharma et al. [25] that deviation from spherical geometry can influence the stability of the fluid. For the more asymmetric case \((K = -20)\) we noted a local minimum of the resultant force within the interior. Such minima, generated within short timeframes, might produce shock waves which could result in material being ejected from the surface, a likely consequence of such a collapse process. Radial asymmetry also appears to promote inhomogeneity within the matter distribution which could in turn affect the opacity and resulting heat flow properties of the collapsing medium. Inhomogeneity might arise due to string fields as recently investigated [33]. Although outside the scope of the present study, heat transport properties of the medium would further enhance the description of gravitational collapse problems with the theoretical framework already having been set up by Herrera et al. [34]. Nevertheless, we have already observed the dynamics of the heat flux which is the novel finding of our study. As the star collapses, the heat generated from the conversion of gravitational potential energy appears to initiate towards the surface, thus promoting the collapse process. During the later stages, heat within the core seems to stall the collapse process although the net force promotes continued collapse into a black hole. We believe that our approach is novel within the framework of General Relativity theory and demonstrates for the first time the connection between dynamical and structurally fundamental quantities (forces) and the spacetime geometry via the spheroidal parameter, K, of the gravitational formalism used.