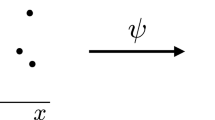Abstract
The purpose of this article is to construct an explicit relation between the field operators in Quantum Field Theory and the relevant operators in Quantum Mechanics for a system of N identical particles, which are the symmetrised functions of the canonical operators of position and momentum, thus providing a clear relation between Quantum Field Theory and Quantum Mechanics. This is achieved in the context of the non-interacting Klein–Gordon field. Though this procedure may not be extendible to interacting field theories, since it relies crucially on particle number conservation, we find it nevertheless important that such an explicit relation can be found at least for free fields. It also comes out that whatever statistics the field operators obey (either commuting or anticommuting), the position and momentum operators obey commutation relations. The construction of position operators raises the issue of localizability of particles in Relativistic Quantum Mechanics, as the position operator for a single particle turns out to be the Newton–Wigner position operator. We make some clarifications on the interpretation of Newton–Wigner localized states and we consider the transformation properties of position operators under Lorentz transformations, showing that they do not transform as tensors, rather in a manner that preserves the canonical commutation relations. From a complex Klein–Gordon field, position and momentum operators can be constructed for both particles and antiparticles.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since its inception, Quantum Field Theory suffered from a number of problems, perhaps most notably: it inherited the conceptual problems already present in the interpretation of Quantum Mechanics; the theory is plagued with infinities – despite the successes of renormalization, the situation is uncomfortable – ; and the theory is not “dynamical”, i.e., it does not provide for a picture of the spacial and temporal evolution of a system.
None of these problems have had up to now a satisfactory resolution. Nevertheless, no one questions the validity of both theories, Quantum Mechanics and Quantum Field Theory, as their successes have been so overwhelming, and many people believe that the resolution of these problems shall come someday. Even if these theories are not “correct”, it is legitimate to believe that they must be correct in “some limit”, as their validity has been solidly proven experimentally in many domains.
Given the proximity between Quantum Mechanics in first and second quantisation, it would be sensible too to find the “limit” when Quantum Field Theory can be approximated by Quantum Mechanics, that is, Quantum Mechanics should be contained in Quantum Field Theory, because the former deals with quantum systems with fixed number of particles while the latter deals with arbitrary numbers of particles. While there are some methods that allow one to recover single particle Quantum Mechanics from Quantum Field theory (see [1] for an extensive review on propagator methods and [2, Chap. 33], for approximative methods in the context of effective field theories), it would be interesting to construct an explicit relation between the two. Such a task seems formidable for interacting field theories.
Here we propose a method by which from a theory for a free quantum field (the Klein–Gordon field, for simplicity) one can construct all the quantum mechanical systems with fixed numbers of particles in first quantization. In particular, we construct the algebra of operators in first quantisation (that is, the x’s and p’s, or rather their symmetrized combinations, for systems with more than one particle) from the field operators in second quantisation. We find it rewarding that, at least for free theories, the reduction of Quantum Field Theory to Quantum Mechanics can be done - and can be done for any number of particles.
We should note that while completing this article we became aware of the work of Pavšič [3] where very similar conclusions were withdrawn. However, we use a different approach to some of problems which are tackled in both works, and made some improvements on the results.
It is rewarding to find out that, independently of the statistics of the quantum field (that is, whether they obey commutation or anticommutation relations), the operators for position and momentum always obey commutation relations. This is possible because these latter operators are even combinations of the former.
We show that the position operators constructed are the Newton–Wigner operators (which were an early attempt to build localised states in Relativistic Quantum Mechanics [4]), that they do not transform as components of tensors under Lorentz transformation but rather in a manner that preserves the canonical commutation relations, and that localized states are indeed present in relativistic field theories, though they do not have an invariant meaning: like the position operators they are frame dependent concepts.
We finish by showing that in the case of a complex Klein–Gordon field, a duplicate of all the N-particle operators is generated for antiparticles.
2 The Klein–Gordon field
We make a brief review the classical Klein–Gordon field, which can also be found in most textbooks. The Lagrangian is
The momentum conjugate to \(\phi \) is (we use a \(\left( +,-,-,-\right) \) metric)
and one can solve the Klein–Gordon equation with the result
where the \(a_{k}\) are complex constants. Here
and both x and k are to be understood as 3-dimensional quantities, e. g., kx stands for \(\varvec{k}\cdot \varvec{x}\). Energy and linear momentum are given by
Quantization is performed replacing the classical fields \(\phi \left( x,t\right) \) by operators and imposing the commutation relations
which translate to replacing the classical coefficients \(a_{k}\) by operators and imposing the commutation relations
We should note that the normalization of the coefficients \(a_{k}\) can be chosen at will. Frequently the weighting factor in (3) and (4) is chosen to be \(\left( 2\omega _{k}\right) ^{-1}\) rather than \(\left( 2\omega _{k}\right) ^{-1/2}\) because \(d^{3}k\left( 2\omega _{k}\right) ^{-1}\) is Lorentz invariant; then the commutator \(\left[ a_{k},a_{q}^{+}\right] \) becomes \(2\omega _{k}\delta \left( k-q\right) \) which is again Lorentz invariant. This is the preferred normalization in many textbooks in Field Theory (see, e. g., [5] or [6]). Here we chose a different normalization, which we find more practical for our purpose of getting Quantum Mechanics from Quantum Field Theory, as the former is constructed in a language which is not manifestly covariant.
That said, we immediately face a problem of operator ordering since the two alternative expressions for energy and linear momentum in (6)–(7) are not equivalent, given the ambiguity in the ordering of operators. For instance,
We shall adopt the right hand side of (6)–(7) as our definitions of energy and linear momentum, that is, normal ordering, thus skipping the issue of zero-point infinities. In terms of the Klein–Gordon field they are
Here the operator
is non-local and can be understood in the sense of an infinite power series
or in the form
with
Clearly expressions (14)–(15) coincide with the classical limit (6)–(7) for commuting fields.
We can also compute the number of particles operator
Curiously, in the classical limit
which can be easily checked to be a constant of motion. There is therefore a semiclassical sense of “number of particles”, in accordance with [7, 8], its semiclassical nature being noticeable in the emergence of Planck’s constant. However, this expression involves the non-local operator \({\mathcal {W}}^{n}\), meaning that one cannot define the “density of particles”, the number of particles being a strictly global concept.
The states that describe N identical particles with sharply defined momenta
form a basis for the Hilbert space \({\mathcal {H}}_{S}^{N}\) of Quantum Mechanics for a system with N identical particles. The complete space of states for the field theory is the direct sum
It is our purpose to show that it is possible, within each \({\mathcal {H}} _{S}^{N}\), to reconstruct the usual canonical variables of Quantum Mechanics out of the field operators \(\phi \) and \(\pi \). However, since we are dealing with identical particles, the operators that act on \({\mathcal {H}}_{S}^{N}\) cannot be usual canonical variables \(X_{i}\) and \(P_{i}\), since they are not permutation invariant. We shall therefore first revisit the spaces \({\mathcal {H}}_{S}^{N}\).
3 Systems of N identical particles
The states (22) can be constructed without the use of creation operators from the direct products of one-particle basis states for each particle
by summing over permutations
Here we introduced the index S to remind that the creation and annihilation operators obey commutation relations (11)–(12). Had we used instead anticommutation relations
and the order p of the permutation should have been taken into consideration,
This would be the space \({\mathcal {H}}_{A}^{N}\) of antisymmetric wavefunctions. Both \({\mathcal {H}}_{S}^{N}\) and \({\mathcal {H}}_{A}^{N}\) are subspaces of the space \({\mathcal {H}}^{N}\) generated by the kets (24).
The only operators that map states in \({\mathcal {H}}_{S}^{N}\) into states in \( {\mathcal {H}}_{S}^{N}\) and states in \({\mathcal {H}}_{A}^{N}\) into states in \( {\mathcal {H}}_{A}^{N}\) are permutation invariant operators, which can be constructed from any operator \(O\left( X_{1},P_{1},\ldots ,X_{N},P_{N}\right) \) by summing over permutations
We shall show that such operators can also be written using creation and annihilation operators.
For that purpose we start by reminding that any polynomial operator in a canonical pair, of order m in X and n in P, can be written as a sum of monomials with X ordered to the left of the P. That happens because, using the commutation relations \(\left[ X,P\right] =\mathrm {i}\hbar \), one can always write a monomial of order m in X and n in P in the form
For example
For N particles this result generalizes to the statement that any polynomial operator of order \(m_{i}\) in \(X_{i}\) and \(n_{i}\) in \(P_{i}\) can be written as a sum of monomials with \(X_{i}\) ordered to the left of the \( P_{i}\)
Therefore all polynomial operators for identical particles can be written as sums of parcels of the type
Now we note that sums over permutations can always be written as combinations of ordinary sums. We start by writing
And use the identity
For \(N=2\) in (34) this produces (omitting the sum signs, for convenience)
For \(N=3\), eq. (34) can be used successively to get
And so on for higher N.
Hence, all polynomial operators for identical particles can be obtained from parcels of the type
or with a lesser number of sums. These parcels, in turn, can be obtained from the building blocks
by multiplication. As for the parcels with a lesser number of sums, they again can be written using these building blocks, as it is evident by the following example
In conclusion, if we find a representation for the operators (39), we can construct all permutation invariant operators in either \({\mathcal {H}} _{S}^{N}\) or \({\mathcal {H}}_{A}^{N}\) by summing and multiplying them.
4 Fock space
Indeed we can see that the operators of the type (39) can be written in the form
independently of N and independently of whether commutation or anticommutation relations are used. This can be done by computing the spectra of the operators on the left and on the right sides of (41 ) and checking that they match for all basis states using (25) or ( 28) on the left hand side and (22) on the right hand side. For example, for two-particle states
and it is easy to check that
Notice that the result is valid irrespectively of whether one uses commutation or anticommutation relations, that is, either in \({\mathcal {H}} _{S}^{2}\) or in \({\mathcal {H}}_{A}^{2}\). The generalization to higher N is straightforward.
The cross terms between \({\mathcal {H}}^{M}\) and \({\mathcal {H}}^{N}\) with \(M\ne N \) cannot be computed for the operator on the left hand side of (41) but for the operator on right hand side they can, and they vanish identically. One should therefore look upon the right hand side of (41) as an extension of its left hand side which is valid for the whole of Fock space.
In three-dimensional space it is easy to generalize the building blocks (41) to
Let us have a look at the expressions for the operators “total momentum” and “sum of positions”
derived using (44)
One can compute the commutator of this two operators
where we have used the identity
which is valid for commutators (− sign) and anticommutators (\(+\) sign). The commutator (48) gives the expected result for both types of statistics, being proportional to the number of particles operator.
5 Creation and annihilation of particles at fixed points in space
The Fourier transform of the set of creation operators for particles with fixed values of momentum
can be seen as a set of creation operators for particles at fixed positions x since its action on the vacuum produces precisely what is interpreted in Quantum Mechanics as a localized state at position x. Multiparticle states of N localized particles can be constructed from these operators in the same manner as it is done with states of N particles with definite momenta
The position creation operators obey similar commutation or anticommutation relations to the momentum creation operators,
The inverse relations are
The building blocks (44) become
Using position creation operators, the operators (46)–(47) become
We see that a complete symmetry is provided by the Fourier transform which allows one to use either position or momentum creation and annihilation operators.
The following conclusions can be withdrawn from these results:
-
It is possible to construct all operators involving permutation invariant combinations of the canonical variables which act in each of the \({\mathcal {H}} _{S}^{N}\) and \({\mathcal {H}}_{A}^{N}\) spaces for all N using the set of creation and annihilation operators obeying respectively commutation and anticommutation relations
-
Whichever statistics is used for the creation and annihilation operators, the resulting operators obey commutation relations.
-
These operators are extensions to the whole Fock space. They map \({\mathcal {H}}^{N}\) onto \({\mathcal {H}}^{N}\) and therefore have vanishing cross products for different values of N.
-
Using the transformations (50) and (54) one can freely switch between the momentum and the position representations and describe the Hilbert state either in terms of basis states of particles with “well defined momenta” or with “well defined positions”.
6 Non-relativistic Quantum Field Theory
We should note that in Sects. 2, 3 and 4 we dealt only with the structure of the space of states and the operators that act on it, and not with the dynamics of the system. Therefore, the results of these sections are equally applicable to relativistic and to non-relativistic theories.
The quantisation of the Schrödinger equation (that is, when the field \(\psi \) is treated as an operator and not as a wavefunction) is treated in detail in [10] or [11], where the construction of creation and annihilation operators at fixed points in space is performed, as we did in Sect. 4.
In this article we went further, in Sects. 2 and 3, by providing the construction of the symmetrised combinations of position and momentum operators from the fields, which was one of our goals. These results are not provided either in relativistic texts, such as [12] or [13], though the latter does show the general result that any operator acting on Fock space can be constructed out of combinations of creation and annihilation operators.
In [14] the quantisation of non-relativistic and relativistic fields can be compared. The main difference between the quantisation of the Schrödinger equation and of the Klein–Gordon equation is that while in the former the relation between the annihilation operator at a fixed point in space and the field operator is trivial, \(\psi \left( x\right) =a_{x}\), in the latter it is given by (3). This difference will show up in the next section when we construct the position operator from the fields (59) in the fact that this operator cannot be written as a volume integral of a local operator.
7 Position operator in Quantum Field Theory
As we have seen, the set of creation and annihilation operators allows us to construct all states in Fock space and all the relevant operators for identical particles, whichever the statistics that they obey. It is interesting to go back to the Klein–Gordon field and see what do these operators look like when expressed in terms of the fields \(\phi \left( x,t\right) \) and \(\pi \left( x,t\right) \) using the inverse relations to (3)–(4)
Doing so for the “sum of momenta” (47), or total momentum, one gets back to (15). And for the “sum of positions” (46), one gets
Again we see that in the classical limit one gets a non-local operator
We can use the Hamiltonian (6) to compute the time evolution of operators, with the result
Going back to our identification of operators (44), the last operator can be identified with
as it should for a collection of non-interacting relativistic particles.
We should also remark that commutation relations (11)–(12) for the a’s are compatible with the canonical relations (8)–(10) for the fields. Anticommutation relations (26)–( 27) for the a’s would imply the following anticommutation rules for the fields
These functions do not vanish for spacelike separations and this is precisely one of the features showing up in the spin-statistics theorem [9] (see [15] for a complete review on this theorem) which excludes Fermi-Dirac statistics for integer spin fields, as is the case of the Klein–Gordon field. We included here the case of anticommuting variables because they can be used for semi-integer spin fields and their treatment is analogous to the one performed here.
8 Behaviour of operators under Lorentz transformations
Classically one can use the energy-momentum tensor \(T^{\mu \nu }\) to construct the momentum four-vector
where the integration is done on a spacelike three-surface. At first sight such a quantity should depend on the specific surface on which it is calculated (Fig. 1). In particular, for a given Lorentz frame, on each constant time three surface (that is, on a space volume for a given time) this four vector should have a different value \(P^{\mu }\left( t\right) \), which in turn should be different from any constant time three surface on another Lorentz \(P^{\mu }\left( t^{\prime }\right) \). It is the fact that \(T^{\mu \nu }\) satisfies a conservation law
that guarantees that \(P^{\mu }\left( t_{1}\right) =P^{\mu }\left( t_{2}\right) \) for \(t_{1}\ne t_{2}\) and that \(P^{\mu }\left( t\right) =P^{\mu }\left( t^{\prime }\right) \) (see [16]).
Operators constructed by integrating local fields over spacelike surfaces cannot in general have simple transformation properties under Lorentz transformations since \({\mathcal {O}}(0)\) transforms to \(\tilde{{\mathcal {O}}}(0)\) and not to \(\tilde{{\mathcal {O}}}({\tilde{0}})\), which is the transform of \({\mathcal {O}}({\tilde{0}})\). That will happen only if \({\mathcal {O}}(0)={\mathcal {O}}({\tilde{0}})\)
That \(P^{\mu }\left( t\right) \) does not depend on t and that it behaves like a four vector under Lorentz transformations can be seen easily using the creation and annihilation operators formalism where one can write the field in the form (3). Since this expression is valid in one frame \( x^{\mu }\), it must be valid in another frame
for some other operators \({\tilde{a}}_{k}\)
Equality of the two expressions implies that
where \({\tilde{k}}_{\nu }=k_{\mu }\Lambda _{\;\nu }^{\mu }\). Had we used the covariant normalization suggested after eqs. (11)–(12) and this transformation law would have had a simpler form, with no \(\sqrt{\omega }\) factors. Now we have from (6)–(7)
Following the same procedure, the number operator is shown to behave as a scalar
However, no such type of transformation should be expected for the position operators \(X^{i}\left( t\right) \), and indeed for any operator that is not constant in time. Of course any operator constructed for \({\tilde{t}}\) constant can be expressed in terms of operators constructed for t constant but the transformation law shall typically be complicated, e. g.,
The fact that the position operators do not behave under Lorentz transformations as tensors should not be seen as a drawback, but rather as what should be expected: they are frame-dependent concepts and are constructed so that they obey canonical commutation relations with the momentum operators, can be verified from (70) and (72)
In fact, the canonical commutation relations would not retain its form under Lorentz transformations if the position operators transformed like tensors.
However, for rotations \(\omega _{{\tilde{k}}}=\omega _{k}\), \({\tilde{t}}=t\) and, since \({\tilde{k}}^{j}\) depends linearly on \(k^{i}\),
where \(R_{\;j}^{i}\) is a rotation matrix. Hence, Eq. (72) becomes
9 Localization in relativistic quantum mechanics
It is the case that one can indeed construct position operators and find states with sharply defined values for the position for the Klein–Gordon field, in contrast with a common saying that “it is not possible to localize a relativistic particle”. One should therefore clarify this point. In a famous article [4] Newton and Wigner studied the concept of localization in Quantum Mechanics while attempting to satisfy the requisites of Special Relativity too. Their work, together with the important work of Foldy and Wouthuysen [17,18,19,20] generated some discussion on the literature regarding position operators in Relativistic Quantum Mechanics and their physical meaning lasting to these days [3, 21,22,23,24,25].
Newton and Wigner worked outside the context of Quantum Field Theory, rather they searched for one-particle localized relativistic wavefunctions, starting from momentum space \(\psi \left( p\right) \) where an inner product can be constructed using a relativistic invariant measure
And they assumed that the wavefunction in position space should be given by the Fourier transform of \(\psi \left( p\right) \) computed using the same invariant measure
Here we use the letter \(\chi \) for position rather than x for, as we shall see, it cannot be interpreted as a position variable at all.
Then they imposed a set of physically reasonable assumptions on the properties that localized states should obey and they found out that the wave function describing a particle localized at position x at \(t=0\) is given by
or, using (77),
which is in fact spread in space at distances of the order of the Compton wavelength, and not a delta function. This has been sometimes erroneously interpreted as non-localizability of particles in the Theory of Relativity. In fact it is not possible to interpret simultaneously \(\left\langle \chi |\psi \right\rangle \) as the “wavefunction in position space” and \( \left\langle p|\psi \right\rangle \) as the “wavefunction in momentum space” as long as \(\left| \chi \right\rangle \) and \(\left| p\right\rangle \) are respectively the eigenkets of operators X and P which obey canonical commutation relations among themselves, as we shall show.
Assuming that the sets of eigenkets of X and P, respectively \(\left| x\right\rangle \) and \(\left| p\right\rangle \), are complete, one can write the following normalizations and partitions of unity
and the inner product is
The point is that the canonical commutation relations impose further that
which, together with the partitions of unity (82) leads to
Now we see that Eqs. (83) and (76) imply \(g_{P}\left( p\right) \propto \omega _{p}\) while Eqs. (86) and (77) imply that \(g_{P}\left( p\right) \propto \omega _{p}^{2}\). Therefore, if \( \psi \left( p\right) \) is the wavefunction in momentum space, \(\psi \left( \chi \right) \) cannot be the wavefunction in position space. In which space is it a representation, that is, which operator has \(\left| \chi \right\rangle \) as its eigenkets? Using the partition of unity (82) one can compute
The states \(\left| \chi \right\rangle \) are not orthogonal to each other and therefore cannot even correspond to the eigenstates of a hermitian operator. The wavefunction \(\psi \left( \chi \right) \) is a representation to which no observable is associated. Ref. [1] gives a clear presentation of this point.
The eigenstates of the position operator are naturally the localized states themselves, \(\left| x\right\rangle \equiv \left| \psi _{x}\right\rangle \), for which (78) and (84) are compatible. In this representation the wave function is given by (86) and not (77)
and localized states are indeed delta functions. Reference [3] provides us with a detailed exposition of the \(\psi \left( \chi \right) \) and \(\psi \left( x\right) \) representations and how to transform between the two.
We should call the reader’s attention to the reason why we could choose the measure either as \(\omega _{p}^{-1/2}\) or \(\omega _{p}^{-1}\) in (3) but not in (88). The reason is that in (3) the choice of the measure amounts only to a redefinition of the creation and annihilation operators while in (88) the choice of the measure amounts to a redefinition of the basis kets \(\left| x\right\rangle \) – and they are not free to choose, they have to be the eigenkets of an operator satisfying canonical commutation relations with P. In summary, what Newton and Wigner showed was that it is not possible to implement the canonical commutation relations in a covariant manner. But that should not be surprising since the canonical commutation relations are not covariant if we insist in transforming the position operator with Lorentz transformations.
However, with the definition of position operator used here and with the transformation law (72) the canonical commutation relations become covariant.
10 Antiparticles
We make a brief incursion into the complex Klein–Gordon field, described by the Lagrangian
in order to address the issue of antiparticles. The solution to the complex Klein–Gordon equation involves two sets of creation and annihilation operators
The space of states becomes the cross product between the Fock spaces generated by each set of creation operators
The number of particles operator splits into two parcels, each one of them acting in each one of the factor spaces, and each one of them being independently conserved
Their difference is the charge operator
The energy, momentum, and position operators also split into two parcels each one of them acting in each one of the factor spaces,
It should be pointed out that antiparticles do not disappear in the transition from Quantum Field Theory to Quantum mechanics: all subspaces with fixed numbers of particles show up, be it one particle, two particles, one antiparticle, one particle plus one antiparticle, etc. One last observation is that we do not agree with the conclusion withdrawn in [1] that “...the consistent description of the NRQM limit of QFT requires us to work with a pair of fields, corresponding to a particle and its antiparticle”. In fact we have done it here for the real Klein–Gordon field, and this could also have been done in [1] too if in his section 6 the author had defined \(\phi \left( x\right) =A\left( x\right) +A^{+}\left( x\right) \) rather than introducing a new field \(B\left( x\right) \) and defining \(\phi \left( x\right) =A\left( x\right) +B^{+}\left( x\right) \).
11 Conclusions
In this work, we have analysed the non-interacting Klein–Gordon field as a tool to construct the algebra of operators acting on the Hilbert spaces of Quantum Mechanics for systems of N identical particles from the field operators acting in the Fock space of Quantum Field Theory. This is achieved by relating the position and momentum quantum operators with the field operators.
The main point is that all polynomial operators on the positions and momenta acting on any of the N-particle subspaces of Fock space can be constructed out of the field operators. The position operators so constructed turn out to be the Newton–Wigner operators. Under Lorentz transformations, they do not transform as tensors, rather in a manner that preserves the canonical commutation relations.
As a by-product, we showed that regardless of the Fermi-Dirac or Bose–Einstein statistics of field, the position and momentum operators obey commutation relations.
Finally we showed that, contrary to what is claimed in [1], the transition from Quantum Field Theory to Quantum Mechanics can be obtained without resource to antiparticles. However, if the field theory describes particles and antiparticles, then two single particle quantum mechanical systems can be extracted from it: one with one particle and one with one antiparticle; as well as all possible combinations of numbers of particles and antiparticles.
In interacting field theories, linear momentum often retains the some form as in its non-interacting counterpart. For example, in \(\phi ^4\) theory it is still given by (15). The operator N defined by (20) no longer is a constant of motion but equation (48) is still valid if \(\varvec{X}\) is defined by (59). That this equation holds in an interacting field theory comes out immediately from that fact that in its derivation no use was made of the dynamics of the system; only the definitions of N and \(\varvec{X}\) were used, plus the canonical commutation (or anticommutation) relations for the fields. It is tempting to try to use the same definitions of particle number and position in interacting field theories. However, even though such operators can be constructed, their physical interpretation as number and position operators seems to get lost, as can be checked by applying them to the toy models presented in [26]. This is a consequence of the known fact that interactions do not really switch off when particles are separated, rather they manifest themselves in the need for renormalisation.
It is not clear to us whether the results in this article could be helpful for interacting fields. An exact match between an interacting field theory and a set of quantum mechanical theories, as was done here, is certainly out of question when particle numbers are not conserved. Any such correspondence must be, if possible, achieved through a limiting procedure.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This work is entirely theoretical and has no associated data either from experimental work or from simulations.]
References
T. Padmanabhan, Obtaining the non-relativistic quantum mechanics from quantum field theory: issues, folklores and facts. Eur. Phys. J. C 78, 563 (2018)
M. Schwartz, Quantum Field Theory and the Standard Model (Cambridge UP, Cambridge, 2014)
M. Pavšič, Localized states in quantum field theory. Adv. Appl. Clifford Algebras 28, 89 (2018)
Newton, E. Wigner, Localized states for elementary systems. Rev Mod. Phys. 21, 400 (1949)
M. Peskin, D. Schroeder, An Introduction to Quantum Field Theory (Perseus Books Publishing, New York, 1995)
C. Itzykson, J.-B. Zuber, Quantum Field Theory (McGraw-Hill, New York, 1980)
B. Feintzeig, J. Librande, R. Soiffer, Localizable particles in the classical limit of quantum field theory. Found. Phys. 51, 49 (2021)
T. Browning, B. Feintzeig, R. Gates-Redburg, J. Librande, R. Soiffer, Classical limits of unbounded quantities by strict quantization. J. Math. Phys. 61, 112305 (2020)
W. Pauli, The connection between spin and statistics. Phys. Rev. 58, 716 (1940)
A. Fetter, J. Walecka, Quantum Theory of Many-Particle Systems (Dover, New York, 2003)
G. Baym, J. Librande, R. Soiffer, Lectures on Quantum Mechanics (CRC Press, Boca Raton, 2018)
L. Horwitz, Relativistic Quantum Mechanics (Springer, Berlin, 2015)
S. Weinberg, The Quantum Theory of Fields, vol. I (Cambridge UP, Cambridge, 2005)
D. Lurié, Particles and Fields (Wiley, New York, 1968)
I. Duck, E. Sudarshan, Pauli and the Spin-Statistics Theorem (World Scientific, Singapore, 1997)
H. Goldstein, C. Poole, J. Safko, Classical Mechanics (Addison-Wesley, Boston, 2002)
L. Foldy, S. Wouthuysen, On the Dirac theory of spin 1/2 particles and its non-relativistic limit. Phys. Rev. 78, 29 (1950)
B. Bakamjian, L. Thomas, Relativistic particle dynamics. Phys. Rev. 85, 868 (1952)
B. Bakamjian, L. Thomas, Relativistic particle dynamics. Phys. Rev. 92, 1300 (1953)
B. Bakamjian, L. Thomas, Relativistic particle dynamics. Phys. Rev. 121, 1849 (1961)
G. Fleming, Covariant position operators, spin, and locality. Phys. Rev. 137, 188 (1965)
J. Ingall, The Newton–Wigner and Wightman localization of the photon. Found. Phys. 26, 1003 (1996)
G. Fleming, Reeh–Schlieder meets Newton–Wigner. Philos. Sci. 67, 495 (2000)
P. Schwartz, D. Giulini, Classical perspectives on the Newton–Wigner position observable. Int. J. Geom. Methods Mod. Phys. 17, 2050176 (2020)
B. Feintzeig, J. Librande, R. Soiffer, Localizable particles in the classical limit of quantum field theory. Found. Phys. 51, 49 (2021)
N. Bogoliubov, D. Shirkov, Quantum Fields (Addison-Wesley, Boston, 1982)
Acknowledgements
Cláudio Gomes is supported by “Fundo Regional para a Ciência e Tecnologia” through Azores Government Grant No. M3.2DOCPROF/F/008/2020.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Barros e Sá, N., Gomes, C. From quantum field theory to quantum mechanics. Eur. Phys. J. C 81, 931 (2021). https://doi.org/10.1140/epjc/s10052-021-09742-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09742-0