Elucidating cosmological model dependence with $H_0$

Abstract

We observe that the errors on the Hubble constant $H_0$, a universal parameter in any FLRW cosmology, can be larger in specific cosmological models than Gaussian processes (GP) data reconstruction. We comment on the prior mean function and trace the smaller GP errors to stronger correlations, which we show precludes all well studied dynamical dark energy models. We also briefly illustrate cosmographic expansions as another model independent cosmological reconstruction. Our analysis suggests that “cosmological model independence”, especially in the statement of Hubble tension, has become a misnomer.

Introduction

Cosmology rests upon assumptions. When one works with assumptions, timely contradictions are inevitable and these seed progress. Over two decades ago, the concordance flat $\varLambda$CDM model emerged from a set of contradictions. Today, cosmological tensions [1] point to problems with the assumption that the Universe is flat $\varLambda$CDM. Moreover, some assumptions underlying supernovae are in a state of flux [2,3,4], and even the assumption that the Universe is isotropic and homogeneous is being called into question [5,6,7,8,9,10]. This perpetual cycle of assumptions and contradictions is integral to cosmology. Recently, Gaussian Processes (GP) has become a staple of data-driven cosmology [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. In this letter, using the Hubble constant $H_0$, we chip away at the widespread assumption that GP data reconstruction is cosmological model independent.

Cosmology strives to make robust statements across a host of cosmological models and this drives the “model independence” narrative. Working within parametric models, it is well established that Taylor expansion, or cosmography [60, 61], offers one a glimpse of model independence, but the Cauchy-Hadamard theorem [62] (see [63]) confines one to low redshifts, $z \lesssim 1$. Nevertheless, even within these restrictions, the Hubble constant $H_0$ can be determined in a bona fide model independent manner [64, 65]. In contrast, GP reconstruction is a non-parametric technique that in principle allows one to extend “model independence” to higher redshifts. In practice, one reconstructs data through an assumption on the covariance matrix, or “kernel”, and its “hyperparameters”.

The commonly held belief that GP is model independent may be misleading for largely two reasons. First, cosmological inferences of $H_0$ from GP [66,67,68,69,70,71] at the percent level can be discrepant with local $H_0$ determinations [72] (see also [73]).¹ These local determinations are largely independent of the background cosmological model and only rely on the assumption of homogeneity and isotropy, which is needed to identify the observed rate of expansion with $H_0$. If true, since the two determinations of $H_0$ are independent of the cosmological model, it is an immediate corollary that Hubble tension has no cosmological resolution, at least within the Friedmann–Lemaître–Robertson–Walker (FLRW) framework.

Admittedly, this may be true, so there may be no contradiction. Nevertheless, more seriously, Table 1 shows the average errors for $300+$ flat $\varLambda$CDM mock realisations with forecasted DESI data [74], where GP based on commonly used kernels in the Matérn covariance matrix class with positive parameter $\nu$ (e.g. see [75]) is compared against the ubiquitous Chevallier–Polarski–Linder (CPL) model [76, 77] for dynamical dark energy (DDE). As we argue later, similar results should hold for all parametric DDE models. The obvious question is how does a putative “model independent” technique outperform a specific model on errors? Recall that typically, where there’s smoke, there’s fire.

Table 1 Average values of $H_0$ for different GP kernels vs. the CPL dark energy model. These results are based on 300+ mock flat $\varLambda$CDM realisations of forecasted DESI data through a process explained in Sects. 3.2 and 4. The key point is that GP leads to smaller errors than a representative model, here CPL, and this is unexpected for any putatively “model independent” technique

In essence, the overt problem with non-parametric techniques, such as GP, is that the implications for parametric models are far from transparent. Obviously, in its simplest setting with observational Hubble data (OHD), one assumes a kernel, either extremises or marginalises over hyperparameters in a likelihood and outputs a mean $H(z_i)$ at redshifts $z_i$, as well as an associated covariance matrix. In contrast, when one fits a parametric model, one recovers the best-fit parameters and their covariance, typically from a Markov Chain Monte Carlo (MCMC) chain. In principle, one can infer $H(z_i)$ from the MCMC chain and this facilitates a direct comparison. Alternatively, one can strip away the errors in $H(z_i)$ in both cases and directly compare the correlation matrix.

In this note, we focus on $H_0$, which, as remarked in [78], is an integration constant in the Friedmann equations, so it is universal to all FLRW cosmologies. Concretely, we show that while the correlations in simpler models such as flat $\varLambda$CDM and wCDM are typically stronger than the GP output, in turn correlations from GP are generically stronger than DDE models. As a result, GP represents a restriction on the parameter space of DDE models. This explains the smaller errors in Table 1 and highlights the problem with the assumption that GP is model independent.

Taylor expansion

We warm up by highlighting commonly propagated misconceptions regarding model independence of cosmography [60], which may or may not echo previous studies in this direction [79,80,81,82,83,84,85,86,87,88,89,90]. Let us begin with two relevant math theorems (see for example [62, 91]).

Taylor’s Theorem: Let $n \ge 1$ be an integer and the let the function $f: {\mathbb {R}} \rightarrow {\mathbb {R}}$ be n times differentiable at the point $z_0 \in {\mathbb {R}}$. Then there exists a function $f_{n}: {\mathbb {R}} \rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} f(z)= & {} f(z_0) + f'(z_0) (z-z_0) + \frac{f''(z_0)}{2!} (z - z_0)^2 + \cdots \nonumber \\&+ \frac{f^{(n)}}{n!} (z_0) (z-z_0)^n + f_{n} (z) (z-z_0)^n, \end{aligned}$$

(1)

and $\lim _{z \rightarrow z_{0}} f_n(z) = 0$.

Cauchy–Hadamard Theorem: Consider the formal power series in $z \in {\mathbb {C}}$ of the form $f(z) = \sum _{n=0}^{\infty } c_n (z - z_0)^{n}$, where $z_0, c_{n} \in {\mathbb {C}}$. Then the radius of convergence R of f at the point $z_0$ is given by

$$\begin{aligned} \frac{1}{R} = \limsup _{n \rightarrow \infty } ( |c_n|^{1/n} ). \end{aligned}$$

(2)

Observe that Taylor’s theorem simply guarantees that provided the Hubble parameter H(z) is differentiable, which is usually the case, the remainder function $f_n(z)$ exists and approaches zero as z approaches $z_0$. While one could perform this expansion at any redshift, it is natural to consider expansions around $z = 0$, and this is the basis for cosmographic (Taylor) expansions [60, 61]. Note, working in the vicinity of $z=0$ is also sufficient for determining $H_0$.

Taylor expansions can be regarded as truly model independent reconstructions of H(z) to a given order in the vicinity of $z_0$, only if they can cover all models to that order and precision. In practice, this is an impractical definition and usually one simply demands that the Taylor expansion covers a suitably large class of models. This is essentially the regime that Riess et al. [64] operate in to make local determinations of $H_0$ (see also [65]). The farther one goes from $z=z_0$, the fewer models that are accurately described by the Taylor expansion.

As observed in [61], recalling the definition of the Hubble parameter in terms of the scale factor, $H \equiv {\dot{a}}/a$, and the usual expression for a in terms of redshift z, $a = 1/(1+z)$, it is clear that the scale factor becomes singular at $z = -1$. We can extend z into the complex plane, where in the Cauchy–Hadamard language (2), this singularity corresponds to at least one of the $c_n$ becoming large at $z \approx -1$. This in turn ensures $R \rightarrow 0$ in its vicinity. For this reason, as stated in [61], the radius of convergence of any FLRW cosmology is at most $|z| =1$. It should be clear that Taylor’s theorem does not apply to expansions in $(1+z)$ about $z=0$, e. g. [92, 93], only expansions about $z=-1$, and there the radius of convergence is strictly zero. Together, these theorems make expansions in $(1+z)$, or $\log _{10} (1+z)$ [94, 95] completely random in the sense that adding higher order terms does not improve convergence (see [96,97,98]).

Gaussian processes

GP is a method to smooth a given (sparse) dataset. In essence, given n observational real data points ${\mathbf {y}} = (y_1, \ldots y_n)$ at redshifts ${\mathbf {z}} = (z_1, \ldots z_{n})$ with a covariance matrix C, one wishes to reconstruct a function ${\mathbf {f}}^* = (f(z_1^*), \ldots f(z_N^*))$ underlying the data at N new points ${\mathbf {z}}^{*} = (z_1^*, \ldots , z_{N}^*)$, where typically $N \ge n$. Obviously, attempting to reconstruct data far outside the range of the original data will lead to questionable results.²

In implementing GP, one has to make an assumption on how the reconstructed data points are correlated, and to do so, one introduces a new covariance matrix $K({\mathbf {z}}^*, {\mathbf {z}}^*)$, typically called a kernel. The kernel K is a function of some hyperparameters, which in cosmological applications are usually taken to be two ($\sigma _f, \ell _f)$. The most commonly used kernel is Gaussian,

$$\begin{aligned} K (z, {\tilde{z}}) = \sigma _f^2 \exp \left( - \frac{(z-{\tilde{z}})^2}{2 \ell _f^2} \right) . \end{aligned}$$

(3)

The other kernels that are commonplace in cosmological settings are the Matérn covariance functions, e.g. see [75],

$$\begin{aligned} K_{\nu }(z, {\tilde{z}}) = \sigma _f^2 \frac{2^{1-\nu }}{\varGamma (\nu )} \left( \frac{\sqrt{2 \nu (z- {\tilde{z}})^2 }}{\ell _f}\right) ^{\nu } {\tilde{K}}_{\nu } \left( \frac{\sqrt{2 \nu (z- {\tilde{z}})^2 }}{\ell _f }\right) ,\nonumber \\ \end{aligned}$$

(4)

where $\varGamma$ is the gamma function and ${\tilde{K}}_{\nu }$ is a modified Bessel function. We refer the reader to [75] for a discussion on the optimal covariance matrices for cosmology. Here $\nu$ is a positive parameter and in the $\nu \rightarrow \infty$ limit one recovers the Gaussian kernel (3). It should be noted that the Matérn kernels are only mean square n-differentiable provided $\nu > n$. This differentiability property is important when one is interested in the derivatives of H(z), but as we work here with OHD, this is less of a concern. In addition to the Gaussian, following [75], we will largely focus on $\nu = p +\frac{1}{2}$, where $p=0, 1, 2, 3, 4$.

Since we are only interested in H(z), the mean $\overline{f^*}$ and the covariance cov($f^*)$ from the GP reconstruction can be easily constructed through a few lines of linear algebra [14]:

$$\begin{aligned} \overline{f^*}= & {} \mathbf {\mu }({\mathbf {z}}^*) + K({\mathbf {z}}^*, {\mathbf {z}}) [ K({\mathbf {z}}, {\mathbf {z}}) + C]^{-1} \left( {\mathbf {y}} - \mathbf {\mu }({\mathbf {z}}) \right) , \nonumber \\ \text {cov}{(f^*)}= & {} K({\mathbf {z}}^*, {\mathbf {z}}^*) - K({\mathbf {z}}^*, {\mathbf {z}}) [ K({\mathbf {z}}, {\mathbf {z}}) + C]^{-1} K({\mathbf {z}}, {\mathbf {z}}^*),\nonumber \\ \end{aligned}$$

(5)

where $\mathbf {\mu }({\mathbf {z}})$ is a prior mean function that one commonly sets to zero, $\mathbf {\mu }({\mathbf {z}}) = 0$ [14] (see also [66,67,68,69,70,71]).

The only problem now is to identify the hyperparameters and this is done through the following log normal likelihood:

$$\begin{aligned} \ln {\mathcal {L}}= & {} - \frac{1}{2} ({\mathbf {y}} - \mu ({\mathbf {z}}))^{T} [ K({\mathbf {z}}, {\mathbf {z}}) + C]^{-1} ({\mathbf {y}} - \mu ({\mathbf {z}})) \nonumber \\&- \frac{1}{2} \ln | K({\mathbf {z}}, {\mathbf {z}}) +C| - \frac{n}{2} \ln 2 \pi . \end{aligned}$$

(6)

In a strict Bayesian sense, one should marginalise over the hyperparameters through an MCMC routine, e. g. [99]. However, this is computationally more expensive, so in practice it is common to simply optimise (6), by setting to zero the gradient of $\ln {\mathcal {L}}$,

$$\begin{aligned} \nabla (\ln {\mathcal {L}} )= & {} \frac{1}{2} ({\mathbf {y}} - \mu ) ^{T} (K + C)^{-1} \nabla K ( K + C)^{-1} ( {\mathbf {y}} - \mu ({\mathbf {z}}) ) \nonumber \\&- \frac{1}{2} \text {tr} [ (K+C)^{-1} \nabla K]. \end{aligned}$$

(7)

Mean function

Going through the GP literature in cosmology, one can identify two schools of thought, or viewpoints, on how to deal with the mean function $\mu (z)$. Here, we follow Seikel et al. [14], where the zero mean function, $\mu (z) = 0$, is imposed. This choice is closer to our interests, as it represents the methodology that has led to curiously small errors on $H_0$ [66,67,68,69,70,71]. When $\mu (z) = 0$, irrespective of whether one optimises (6) or marginalises over the hyperparameters, there is very little difference to the results [68, 75]. As is clear from (6) or (7), since ${\mathbf {y}}^2 \gg \sigma _{{\mathbf {y}}}^2 \sim C$, the hyperparameter $\sigma _f$ is a large number. As a result, $K \gg C$, which is clear from the values in Table 2. With this difference in scales, one can approximate

$$\begin{aligned} (K + C)^{-1} \approx K^{-1} - K^{-1} C K^{-1} + \cdots , \end{aligned}$$

(8)

and the mean and covariance matrix become to leading order:

$$\begin{aligned} \begin{aligned} \overline{f^*}&= \mathcal{D}({\mathbf {z}}^*, {\mathbf {z}}) \ {\mathbf {y}} + \cdots , \\ \text {cov}{(f^*)}&= \mathcal{D}({\mathbf {z}}^*, {\mathbf {z}})\ C\ \mathcal{D}( {\mathbf {z}}, {\mathbf {z}}^*) + \cdots , \end{aligned} \end{aligned}$$

(9)

where $\mathcal{D}({\mathbf {z}}^*, {\mathbf {z}}):=K({\mathbf {z}}^*, {\mathbf {z}}) K({\mathbf {z}}, {\mathbf {z}})^{-1}$ is the “dressing matrix” which essentially dresses the original data ${\mathbf {y}}$ and covariance matrix C. It is a matrix of O(1) numbers. It should be clear from the leading order expressions that GP implemented with zero mean $\mu ({\mathbf {z}})$ is a mapping from data ${\mathbf {y}}$ into the mean $\overline{f^*}$, and a mapping from the covariance matrix C into the reconstructed covariance matrix $\text {cov}{(f^*)}$.

The other school, primarily Shafieloo et al. [13], maintains that the prior on the mean is important. As is clear from (6) or (7), a reasonably competitive guess for the mean should lead to a small ${\mathbf {y}} - \mu ({\mathbf {z}})$, which makes $\sigma _f$ a small number, $\sigma _f \sim K \sim O(1)$. For this reason, one just recovers the input mean if one optimises the likelihood (6) and one must marginalise over the hyperparameters. This marks a key distinction between the two approaches. The other important difference is that one expects marginalisation to lead to a distribution of $\sigma _f$ peaked in the vicinity of $\sigma _f \approx 0$. Therefore, one is working in the opposite regime to (9) where now $C \gg K$. In this case, the mean and the covariance to leading and sub-leading order are,

$$\begin{aligned} \begin{aligned} \overline{f^*}&= \mu ({\mathbf {z}}^*) + K({\mathbf {z}}^*, {\mathbf {z}}) C^{-1} ( {\mathbf {y}} - \mu ({\mathbf {z}}) ) + \cdots , \\ \text {cov}{(f^*)}&= K({\mathbf {z}}^*, {\mathbf {z}}^*) - K({\mathbf {z}}^*, {\mathbf {z}}) C^{-1} K({\mathbf {z}}, {\mathbf {z}}^*) + \dots . \end{aligned} \end{aligned}$$

(10)

It should be clear that these expressions are trivial at leading order: one gets out what one puts in. So, the sub-leading terms have to matter and this is where marginalisation helps. Nevertheless, the better the guess on the mean, which is typically inferred from specific models, the smaller the sub-leading terms, and hence the less relevant the GP becomes. Clearly, choosing a prior is a balancing act that represents additional modeling in this “model independent” approach and for this reason, we adopt the $\mu (z)=0$ viewpoint.

Data

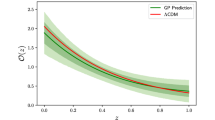
We use OHD, which serves as the basis for mock realisations. More precisely, we make use of cosmic chronometer (CC) [100,101,102,103,104,105,106,107] and homogenised BAO [108,109,110,111,112,113,114,115,116,117,118,119] data. It should be stressed that the CC data largely comprises statistical errors only, and the systematic errors on H(z) are a work in progress [120]. A further caveat is that, as pointed out in [121], some of the cosmic chronometer data may be less reliable. That being said, this OHD will only serve as the basis for mock realisations of the flat $\varLambda$CDM cosmological model with the canonical parameters $(H_0, \varOmega _{m0}) = (70, 0.3)$. Furthermore, we are not interested in the absolute value of $H_0$, but the errors and only their relative values. We present the OHD in Fig. 1. From the real data, we extract the redshifts $z_i$ and the errors in the Hubble parameter $\sigma _{H(z_i)}$. To perform the mocks, at each $z_i$ we choose a new $H(z_i)$ value from a normal distribution about the flat $\varLambda$CDM value with standard deviation $\sigma _{H(z_i)}$.

Fig. 1

The real CC and BAO data serving as the basis for mock realisations

Analysis

In this section we focus on $H_0$ extracted from the GP reconstruction. This is arguably the simplest cosmological parameter that one can reconstruct from the data since it just involves an extrapolation beyond the last data point ($z=0.07$ in our study) to $z = 0$. Before beginning, it is instructive to remove the BAO data and run the GP analysis for the CC data with a Gaussian kernel, just to validate our GP code. We find $H_0 = 67.55^{+4.75}_{-4.68}$ km/s/Mpc, which reproduces the result of Yu et al. [67], $H_0 = 67.42 \pm 4.75$ km/s/Mpc, so there is no indication that our GP code is doing anything unusual. In particular, the errors are the same size. It should be stressed again that GP is simple linear algebra (5).

Here, we begin exploring the GP whereby the likelihood (6) is minimised. This represents a simplification, but it has been confirmed in [68, 75] that this make little difference. In Table 2 we show how the inferred Hubble constant $H_0$ depends on the kernel for the full redshift range of the data $0 \lesssim z \lesssim 2.5$. It should be stressed that we are using OHD, namely CC and BAO data, but since we average over a large number of mocks, we are reporting general trends. We find that errors on $H_0$ decrease with increasing $\nu$, and our analysis shows that the smallest $H_0$ error is achieved for the Gaussian kernel. Our findings are in line with Table 1 of [66], where we have included the $\nu = 1/2$ and $\nu = 3/2$ entries just to fill out the picture. Note that results are kernel dependent. This trend is expected. The reason being that as $\nu$ increases one is increasing the differentiability of the kernel. This means that the class of reconstructed functions, here H(z), should be smoother, since their derivatives have to be continuous to a greater order. Ultimately, smoother functions enjoy stronger correlations and smaller errors.

Table 2 Average values of $H_0$ and hyperparameters ($\sigma _f, \ell _f$) for different kernels and 500 mock realisations of the data. There is a descending trend in the errors on $H_0$ as we increase the GP kernel parameter $\nu$, so the final result is kernel dependent

Observe that the central $H_0$ values are all biased lower than the mock value $H_0 = 70$ km/s/Mpc. Independently, we have performed some fits with Taylor expansions and one observes the same phenomenon, which suggests that this biasing is down to the data. As is evident from Fig. 1, the error bars increase at low redshifts, but the slope of H(z) is fixed by the BAO data, making it less likely that the visibly poorer quality CC data can affect the central value.

It is instructive to fit the same data to concrete models in order to compare the errors in $H_0$. The result is reported in Table 3. Evidently, the errors on $H_0$ for both $\varLambda$CDM and wCDM are within the GP errors, but for CPL we find that the error on $H_0$ is larger. In order to ascertain if this is a fluke, we replace our OHD with the DESI H(z) determination forecasts in the extended redshift range $0.05 \le z \le 3.55$ [74], where we assume the optimistic outcome that the five-year survey covers 14,000 deg$^2$. Repeating the mocking exercise outlined in Sect. 3.2, we can see from Table 1 that even with the forecasted data, GP outperforms the CPL model by leading to smaller errors on $H_0$.³ We conclude that this is not an artifact of the dataset and that GP produces smaller errors on $H_0$ than CPL.

Table 3 Average values of $H_0$ for different models based on $\sim 300$ mock realisations of the data in Fig. 1. This is to be compared with the GP results, in particular the $\nu =\infty$ case, quoted in Table 2. As expected, $\varLambda$CDM has smaller error, while wCDM has comparable error, but CPL leads to a larger error

Correlations

Recall that the output from GP is a mean and a covariance matrix and that any covariance matrix $C_{ij}$ is simply a dressing of the correlation matrix $D_{ij}$ through the errors $\sigma _i$, $C_{ij} = \sigma _i \sigma _j D_{ij}$ (no summation). It is an easy task to take the output covariance matrix from GP and identify the underlying correlation matrix. Concretely, we have

$$\begin{aligned} \text {cov}{(f^*)} (z_i, z_j) = \sigma _{H(z_i)} \sigma _{H(z_j)} D ( z_i, z_j). \end{aligned}$$

(11)

Fig. 2

Correlations between $H(z=0)$ and $H(z_i)$ across a host of Matérn class kernels. The increase in the strength of correlations is directly reflected in the decreasing errors in Table 2 as $\nu$ is increased

Next, one can fix $z_i = 0$ and the first row of the correlation matrix gives us an indication of the correlations between $H(z =0)$ and $H(z_i)$. These are shown in Fig. 2, where it is clear that the $\nu = \frac{1}{2}$ kernel has the weakest correlations with redshift, whereas the Gaussian kernel ($\nu = \infty$) exhibits the strongest. It can also be observed that beyond $\nu = \frac{3}{2}$, the differences in the correlations are not so pronounced. This explains not only the trend in the $H_0$ errors in Table 2, but also why the difference in the $H_0$ errors beyond $\nu = \frac{3}{2}$ is not so great. It is an undeniable fact that stronger correlations lead to smaller errors.

One can then extend this analysis to parametric models, so that a direct comparison can be made. In fitting parametric models, one typically ends up with an MCMC chain for the parameters, which within the two-parameter family of dynamical dark energy (DDE) models we study, amounts to a maximum of four parameters $(H_0, \varOmega _{m0}, w_0, w_a)$. Concretely, we make use of a redshift model [122, 123], the CPL model [76, 77], as well as models due to Efstathiou [124], Jassal–Bagla–Padmanabhan (JBP) [125] and Barboza–Alcaniz (BA) [126]. See Table 4 for explicit expressions for the corresponding equations of state w(z) and dark energy densities $X(z):={\rho _{\text {de}}(z)}/{\rho _{\text {de}, 0}}= \exp \left( 3 \int _0^{z} \frac{1 + w(z')}{1+z'} \text {d}z' \right)$. As observed recently in [127], focusing on any particular DDE parametrisation risks biasing the search for DDE, so here we analyse a broad class of models (see also [128]). We will see that our conclusions are robust to the parametrisation.

From the MCMC chain, one can infer $H(z_i)$ at the same redshifts as the GP. From there one can make a direct comparison by plotting H(z) and the confidence intervals. However, since the mean values can be displaced, it may be difficult to quantify the difference through plots. Nevertheless, one can boil any distinction down to numbers. Viewing $H(z_i)$ as parameters in their own right, one can infer the corresponding covariance matrix and strip away the errors to leave the correlation matrix. In Fig. 3 we plot the correlations across the parametric models.

Table 4 DDE parametrisations/models

Fig. 3

Correlations between $H(z=0)$ and $H(z_i)$ across a host of DDE models. As expected, a model induces certain correlations between values of observables at different redshifts and as depicted in FIG. 2, so do GP kernels. The Gaussian kernel is added for comparison

In line with expectations, the flat $\varLambda$CDM model exhibits the strongest correlations, next wCDM, while any of the DDE models, including the CPL model, are less strongly correlated. This is more or less the content of Table 3, though, over a large number of mocks; here we only use the real data in Fig. 1. Ultimately, since the data is the same, these correlations are simply an artifact of the number of parameters in the model. However, for DDE models, the correlations are also in line with observations made in [127], which is yet another consistency check. There it was noted that the errors on $w_a$, which propagate to all parameter errors, including $H_0$, are larger for the JBP and CPL models, while the Efstathiou, BA and redshift models lead to smaller errors. Once again, this is evident from Fig. 3. As explained the figures are only for a single realisation of the data, while Tables 1 and 3 represent repeated mock realisations, so the conclusion that the errors on $H_0$ differ should be beyond doubt. So while Figs. 2 and 3 are based on real data including BAO, which assumes a fiducial flat $\varLambda$CDM cosmology, the fact that mocks return results consistent with smaller (larger) errors, or alternatively stronger (weaker) correlations, should convince readers that Figs. 2 and 3 are representative.

Finally, the reader will note that we have mocked up on flat $\varLambda$CDM. However, we have checked that if one mocks up on one of the DDE models, for example the CPL model, and dials $(w_0,w_a)$ so that the CPL model fits the data better than flat $\varLambda$CDM, GP still leads to smaller errors than the best fitting DDE model. We expect our findings here are generic in nature.

Conclusions

“Model independence” has casually slipped into the cosmology lexicon. Here, our interest in the claims were piqued by notably small errors in $H_0$ that are even comparable in size to flat $\varLambda$CDM errors [66,67,68,69,70,71].⁴ We started with some observations on Taylor expansion and the regime where the corresponding cosmographic expansion may be regarded as model independent in a bona fide sense. As explained, these observations are rooted in 18th and 19th century math theorems, but this is routinely overlooked with dire consequences. Importantly, beyond the radius of convergence $|z|=1$, higher order terms in any expansion no longer converge.

We also explained the difference between the two schools in the GP method [13, 14]. Clearly, an assumption on the mean function, as advocated in [13], can lead to very different expressions at leading order. In particular, a competitive guess on the mean, not only represents extra modeling, but risks triviliasing the GP. Moreover, one can add a “nugget” or noise contribution to $K+C$ [11, 13], but this again is extra modeling. While these observations may not settle the debate, we believe they constitute progress.

We analysed the correlations relevant for the inferred $H_0$ values with $\mu (z) = 0$ [14]. Consistent with observations on the errors, we found that GP leads to stronger correlations and thus smaller errors than well known parametric DDE models. If this is confirmed by the community, one must conclude that GP analysis is tantamount to fitting the wCDM model to the same data. While this may seem counter-intuitive, it is worth noting that GP has a myriad of applications, but in cosmology, H(z) is to first approximation a simple monotonically increasing function of redshift. Therefore, it is possible that the optimal kernels for cosmology have yet to be identified. It is also possible that a hybrid approach that involves inference from both data and a prior on the kernel is required, e. g. [130, 131].

Finally, let us emphasise again that we have only analysed $H_0$. Our motivation was that competing discrepant “model independent” $H_0$ determinations immediately lead to the conclusion that Hubble tension has no resolution in an FLRW cosmology. It is imperative to extend our results to other cosmological parameters, e. g. [47, 49,50,51,52,53,54,55,56,57,58,59, 132], to ascertain the level of implicit or hidden model dependence in the GP approach. It is worth recalling again our comments on Taylor expansions, namely that a Taylor expansion beyond the strict vicinity of $z \sim 0$ corresponds to a class of models. In essence, GP should be the same. The responsibility is on the GP community to properly define the class of models in a transparent manner.