Abstract
We argue that high-quality data on the reaction \(e^+e^-\rightarrow \pi ^+\pi ^-\eta \) will allow one to determine the doubly-virtual form factor \(\eta \rightarrow \gamma ^*\gamma ^*\) in a model-independent way with controlled accuracy. This is an important step towards a reliable evaluation of the hadronic light-by-light scattering contribution to the anomalous magnetic moment of the muon. When analyzing the existing data for \(e^+e^-\rightarrow \pi ^+\pi ^-\eta \) for total energies squared \(k^2>1\,\text {GeV}^2\), we demonstrate that the effect of the \(a_2\) meson provides a natural breaking mechanism for the commonly employed factorization ansatz in the doubly-virtual form factor \(F_{\eta \gamma ^*\gamma ^*}(q^2,k^2)\). However, better data are needed to draw firm conclusions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Transition form factors contain important information about the properties of the decaying particles. Additional interest in meson decays with one or two virtual photons in the final state comes from the fact that the theoretical precision of the Standard Model calculations for the anomalous magnetic moment of the muon is significantly affected by the one of hadronic light-by-light (HLbL) scattering, where the latter appears as a sub-amplitude; see Fig. 1. A few years ago, the Bern group reported on important progress towards a model-independent determination of the HLbL contribution based on dispersion theory [1,2,3]. In principle this allows for an analysis of similar rigor as commonly applied for the hadronic vacuum polarization [4].Footnote 1 The updated experimental value for \((g-2)_\mu \), combining the BNL measurement [6] with the first Fermilab results [7, 8], shows a \(4.2\sigma \) tension as compared to the current theory consensus on the Standard Model value [4, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33] and the upcoming improvement in the experimental statistics [34] demands further efforts to reduce the theoretical uncertainty. Reference [4] identifies the \(\eta \) and \(\eta '\) pole terms as major outstanding contributions in the dispersive approach to HLbL, next to axial vectors [35, 36] and the matching to short-distance constraints [21, 29,30,31, 37,38,39,40]. A refined understanding of the doubly-virtual \(\eta \) transition form factor is the object of this article; see also the review Ref. [41].
In Ref. [42] the isovector contribution of the singly-virtual form factor \(F_{\eta \gamma ^*\gamma }(q^2) \equiv F_{\eta \gamma ^*\gamma ^*}(q^2,0)\) was calculated for virtualities \(q^2\ll 1\,\text {GeV}^2\) from data on \(\eta \rightarrow \pi ^+\pi ^-\gamma \) and the pion vector form factor via a dispersion integral. This was done with the help of a convenient parameterization of the corresponding \(\pi \pi \) invariant-mass distribution derived in Ref. [43], see also Ref. [44]. In particular, it was demonstrated that when the high-statistics data of Ref. [45] were used to fix the \(\eta \rightarrow \pi ^+\pi ^-\gamma \) input, this procedure leads to a determination of \(F_{\eta \gamma ^*\gamma }(q^2)\) with an accuracy higher than that of the most recent direct measurements [46,47,48,49]. Especially this is the case since the isoscalar contribution is negligibly small.
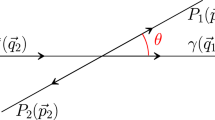
In this article, the program to pin down the \(\eta \) transition form factor with high accuracy will be extended to the doubly-virtual form factor \(F_{\eta \gamma ^*\gamma ^*}(q^2,k^2)\) in the kinematic regime \(q^2\ll 1\,\text {GeV}^2\) and \(k^2>1\,\text {GeV}^2\). The analysis is based on input from the reaction \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\), see Fig. 2, which plays a very similar role to data on \(e^+e^-\rightarrow 3\pi \) for the \(\pi ^0\) transition form factor [26, 27, 50]. The method provides access to the doubly-virtual form factor in a kinematic regime where it is yet unknown. In particular it allows for a test whether the factorization ansatz
for the normalized form factor \(\bar{F}_{\eta \gamma ^*\gamma ^*}(q^2,k^2)= F_{\eta \gamma ^*\gamma ^*}(q^2,k^2)/F_{\eta \gamma ^*\gamma ^*}(0,0)\) is still valid in the kinematic regime specified above.Footnote 2 It should be stressed that although a direct measurement of the doubly-virtual form factor via \(e^+e^-\rightarrow \eta e^+e^-\) is in principle possible, we still expect our method to lead to higher accuracy, simply because the hadronic rates for \(\gamma ^*\rightarrow \eta \pi ^+\pi ^-\) are a factor \(1/\alpha _{\mathrm{em}}^2\) larger than those for \(\gamma ^*\rightarrow \eta e^+e^-\).
In Ref. [51] it was argued that the \(a_2(1320)\), a tensor resonance with \(I^G (J^{PC}) = 1^- (2^{++})\), should provide the leading left-hand-cut contribution to the decay amplitude for \(\eta \rightarrow \pi ^+\pi ^-\gamma \), and accordingly distort the spectra significantly, however, only beyond the kinematic region accessible in the direct measurement of the decay. Interestingly all necessary parameters can be fixed from data directly. The claim was corroborated by an analysis of the data for \(\eta '\rightarrow \pi ^+\pi ^-\gamma \) [52, 53]. In this work we therefore also include the \(a_2\) contribution. Diagrammatically this amounts to including \(a_2\) crossed-channel exchange as shown in Fig. 2b, in addition to the structureless vertex of Fig. 2a.
Unfortunately, the differential data presently available for the reaction \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\) from the BaBar [54, 55], SND [56], and CMD-3 [57] collaborations are rather limited: only BaBar and CMD-3 provide \(\pi \pi \) spectra, and both with the shortcoming that they are not given at a fixed value of \(k^2\), but for \(\sqrt{k^2}\) integrated in ranges from 1.0–4.5 GeV [54], 1.4–1.8 GeV [55], or 1.3–1.8 GeV [57]. As we argue below, analyzing the two BaBar data sets, this integration limits the extraction accuracy of the form factor, since changes in the \(\pi \pi \) spectrum cannot only be induced by changes in the explicit dependence of the amplitude on the \(\pi \pi \) invariant mass, but also by changes in the parameterization of the line shape of the \(\rho '\). The latter is the first excited resonance of the \(\rho \) meson and dominates the total cross section.
The paper is structured as follows. In Sect. 2 we generalize the formalism of Ref. [42] to the doubly-virtual \(\eta \) transition form factor, based on amplitudes for \(\eta \rightarrow \pi ^+\pi ^-\gamma ^*\). Subsequently, we show how the dispersive representations for \(\eta \rightarrow \pi ^+\pi ^-\gamma \) discussed in Refs. [43, 51] can be extended to the virtual-photon case of interest here. In Sect. 3 we discuss the parameterization used for virtualities beyond \(1\,\text {GeV}^2\), which are beyond the range of applicability of the dispersive approach employed in this work. In Sect. 4 we present and discuss the results of our analysis of \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\) total and differential cross section data, without and with the inclusion of the \(a_2\) contribution. Section 5 reflects on the impact of our findings for the \(\eta \) transition form factor. We close with a summary and discussion; some technicalities are relegated to an appendix.
2 Dispersive representations
2.1 Transition form factor of the \(\eta \) meson
The \(\eta \rightarrow \gamma ^*\gamma ^*\) transition form factor (TFF) \(F_{\eta \gamma ^*\gamma ^*}(q^2,k^2)\) is defined by the matrix element
where \(j_\mu = (2{\bar{u}}\gamma _\mu u-{\bar{d}}\gamma _\mu d-\bar{s}\gamma _\mu s)/3\) denotes the electromagnetic current, q and k are the photon momenta, and the convention \(\varepsilon ^{0123}=+1\) is used. The decay into two real photons is driven by the chiral anomaly [58, 59], which fixes the normalization \(F_{\eta \gamma \gamma } \equiv F_{\eta \gamma ^*\gamma ^*}(0,0)\) of the TFF,
where \(\alpha _{\text {em}} = e^2/(4\pi )\) is the fine-structure constant.
Isospin symmetry allows us to decompose \(F_{\eta \gamma ^*\gamma ^*}(q^2,k^2)\) into an isovector–isovector (\(I=1\)) and an isoscalar–isoscalar (\(I=0\)) part, which, for the normalized doubly-virtual TFF \(\bar{F}_{\eta \gamma ^*\gamma ^*}(q^2,k^2)\equiv F_{\eta \gamma ^*\gamma ^*}(q^2,k^2)/F_{\eta \gamma \gamma }\), can be written according to
As vector-meson-dominance estimates demonstrate, the isoscalar part is strongly suppressed [41, 42], such that for the TFF’s low-energy properties, its contribution is within the isovector part’s uncertainty.
Diagrammatic representation of the dispersion relation for the isovector part of the \(\eta \) TFF; see Eq. (5)
A single-variable dispersion relation for the isovector part is at low energies dominated by the two-pion intermediate state, see Fig. 3, which yields
where \(F_\pi ^V(t)\) is the pion vector form factor, and \(F_{\eta \pi \pi \gamma ^*}(t,k^2)\) denotes the projection of the \(\eta \rightarrow \pi ^+\pi ^-\gamma ^*\) amplitude onto the pion–pion P-wave, to be defined formally below. We expect the dispersion relation Eq. (5) to hold up to \(q^2 \sim 1\,\text {GeV}^2\), even for a much wider range in the second argument \(k^2\). We will briefly comment on the extent to which two pions alone saturate this isovector dispersion relation below in Sect. 5.
2.2 Dipion amplitudes
The decay amplitude for \(\eta (p_\eta ) \rightarrow \pi ^+(p_+)\pi ^-(p_-)\gamma ^{(*)}(k)\) can be written as
with the Mandelstam variables given as \(s=(p_{\eta }-p_+)^2\), \(t=(p_+ + p_-)^2\), and \(u=(p_\eta -p_-)^2\), \(s+t+u=\Sigma \equiv M_\eta ^2+2M_\pi ^2+k^2\). An expansion of \({\mathcal {F}}(s,t,u,k^2)\) in pion–pion partial waves proceeds in odd waves only, and is totally dominated by the P-wave [51], denoted by \(F_{\eta \pi \pi \gamma ^*}(t,k^2)\) in the following,
where
and the Källén function is defined by
In the real-photon case \(k^2=0\), the \(\eta \rightarrow \pi ^+\pi ^-\gamma \) differential decay rate with respect to t can be written as [43]
On the other hand, for \(k^2 > (M_\eta +2M_\pi )^2\), the matrix element (6) can be assessed in the reaction \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\). We write the differential cross section as
where the normalization is kept unspecified due to the BaBar differential cross sections being provided in arbitrary units [54, 55]. The total cross section data sets used, however, are provided in meaningful units. Hence, for the total cross section we use
A central element of the amplitude \(F_{\eta \pi \pi \gamma ^*}(t,k^2)\) is the universality of the elastic pion–pion P-wave final-state interactions as encoded in the Omnès function [60]
where \(\delta _1^1 (t)\) denotes the pion–pion P-wave phase shift. In particular, \(\Omega (t)\) contains the physics of the \(\rho (770)\) resonance. One of the most obvious applications to make use of the Omnès function is the pion vector form factor, which can be extracted directly from data on \(e^+e^-\rightarrow \pi ^+\pi ^-\) or \(\tau ^-\rightarrow \pi ^-\pi ^0\nu _\tau \). It can be written as
where R(t) is a function free of cuts up to inelastic effects, which can in practice be approximated by a linear function up to \(t \sim 1\,\text {GeV}^2\) [42, 52]. Utilizing the phase shift parameterization specified in Appendix A.1 and fitting to \(\tau \) decay data [61], this linear function is found to be \(R(t) = 1 + 0.126(2)\,\text {GeV}^{-2} t\). Comparable parameterizations [62, 63] were used in previous studies of the \(\eta \) TFF [42, 43]. Similarly,
is a function free of right-hand cuts in t up to inelastic thresholds. In Refs. [43, 45] it was shown that for the real-photon case, the function P(t, 0) is sufficiently well approximated as a linear polynomial
where \(A_{\pi \pi \gamma }^{\eta }\) is a normalization constant, to describe the high-accuracy \(\eta \rightarrow \pi ^+\pi ^-\gamma \) decay data obtained by the KLOE collaboration [45]. The slope parameter \(\alpha _\Omega \) is found to be [51]
with only the statistical uncertainty included.Footnote 3
As P(t, 0) is not expected to grow for large t on fundamental grounds, the representation Eq. (16) is unlikely to hold beyond the small range in t accessible directly in the decay \(\eta \rightarrow \pi ^+\pi ^-\gamma \). Indeed, high-statistics data for the analogous decay \(\eta '\rightarrow \pi ^+\pi ^-\gamma \) require a polynomial of second order [52, 53] instead, motivating an alternative parameterization
that we will also test below. A possible physical motivation for such a curvature term was given in Ref. [51], where it was demonstrated that the left-hand cut induced by the \(a_2(1320)\) distorts the linear behavior of P(t, 0) significantly beyond \(t \le M_\eta ^2\). In order to include the left-hand-cut contribution, we need to generalize the dispersive representation of \(F_{\eta \pi \pi \gamma ^*}(t,0)\) according to [51]
with
where \({\mathcal {F}}_{a_2} (s,t,u,0)\) comprises the \(a_2\) s- and u-channel exchange amplitudes (for real photons), see Ref. [51] for details. The subtraction constant \(\alpha _\Omega [a_2]\) that takes over the role of the slope parameter \(\alpha _\Omega \) is shifted only marginally: extracted from a fit to \(\eta \rightarrow \pi ^+\pi ^-\gamma \) (where \(t<0.25\,\text {GeV}^2\)), it reads [51]
We define the function
as a straightforward generalization of Eq. (15) (for \(k^2=0\)). This function is still free of right-hand cuts, but now contains the left-hand cut due to \(a_2\) exchange. \(P^{(a_2)}(t,0)\) can be approximated by
in the range \(4M_\pi ^2 \le t \le 1\,\text {GeV}^2\). It turns out that with \(\alpha _{a_2}=0.28\,\text {GeV}^{-2}\) and \(\beta _{a_2}=-0.66\,\text {GeV}^{-4}\), this approximation works to better than 1% accuracy. The constant \(A_{\pi \pi \gamma }^\eta [a_2]\) is chosen such that \(F_{\eta \pi \pi \gamma ^*}(t,0)\) is normalized to the experimental rate for \(\eta \rightarrow \pi ^+\pi ^-\gamma \). Note that if the \(a_2\) left-hand-cut contribution is turned off, the constants \(A^\eta _{\pi \pi \gamma }\) and A, see Eq. (20), coincide. The overall strength of the \(a_2\) contribution is phenomenologically known from \(a_2\) branching fractions to better than 10% accuracy [51]. Given the size of the errors in the data analyzed in the present study, we will neglect this source of uncertainty in what follows.
The same method that allowed us to connect \(\eta \rightarrow \pi ^+\pi ^-\gamma \) to the isovector component of \(\eta \rightarrow \gamma ^*\gamma \) permits to connect \(\gamma ^*\rightarrow \eta \pi ^+\pi ^-\) to the isovector component \(\gamma ^*\rightarrow \eta \gamma ^*\) and thus to the doubly-virtual \(\eta \) transition form factor. To this end, we need to generalize the dispersion relation Eq. (5), and hence the description of \(F_{\eta \pi \pi \gamma ^*}(t,k^2)\), to an off-shell photon with invariant mass squared \(k^2\). We begin by noting that the left-hand-cut contribution of Eq. (19) changes naturally for \(k^2\ne 0\) due to the changed kinematics. We define
The angular integral over the \(a_2\) exchange amplitudes can be done analytically and yields the hat function (cf. Appendix A.2 for details on the analytic continuation)
where the coupling constant \(g_T\) (\(c_T\)) has been determined from the branching ratio of \(a_2 \rightarrow \pi \eta \) (\(a_2 \rightarrow \pi \gamma \)) [51] and \(F_\pi =92.28(10)\,\text {MeV}\) [64] is the pion decay constant. The dispersion integral contained in
can be carried out numerically via path deformation into the complex plane in order to circumvent the singularities of the integrand, inspired by the methods of Ref. [65]. Due to the need to deform the integration path into the complex plane, we utilize a \(\pi \pi \) phase shift \(\delta _1^1\) calculated via the inverse-amplitude method (we employ an approximation to the two-loop representation of Ref. [66]), which provides us with an analytic expression; see Appendix A.1. Equations (25) and (26) encode a nontrivial entanglement of the dependences on t and \(k^2\) that clearly does not factorize in a simple manner.
We now make the following ansatz for the complete \(\gamma ^* \rightarrow \eta \pi ^+ \pi ^-\) form factor:
i.e., any additional \(k^2\) dependence is assumed to be multiplicative (or factorizing). Note that \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2)\) cannot be treated within the formalism of Ref. [42] for an application to \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\) data, since with \(k^2>1\,\text {GeV}^2\) it is to be evaluated in a kinematic regime where the original method, relying on elastic unitarity, is no longer applicable. However, as will be shown in Sect. 3, for the analysis aimed at here we only need a convenient parameterization of \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2)\). Alternatively, we will revert to the simpler approach to replace \(F_{\eta \pi \pi \gamma ^*}^{(a_2)}(t,k^2)\) by \(F_{\eta \pi \pi \gamma ^*}(t,0)\), given by either the linear or the quadratic approximations \(P^{(1,2)}(t,0)\). In these limits, \(F_{\eta \pi \pi \gamma ^*}^{(a_2)}(t,k^2)\) and, via the dispersion integral (5), the (isovector part of the) doubly-virtual TFF, become factorizing in their dependences on the two respective variables, and we can check the consistency of the assumption by testing to which extent the linear subtraction constants of Eqs. (20) and (26) fulfill \(\alpha _\Omega [a_2] = \alpha ^*_\Omega [a_2]\), i.e., to which extent \(\alpha ^*_\Omega [a_2](k^2)\) can (on average) be approximated by a constant consistent with the value for the real-photon case. In this limit (only), \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2)\) also corresponds to the normalized singly-virtual \(\eta \) TFF \(\bar{F}_{\eta \gamma \gamma ^*}(k^2)\).
In order to fix \(\alpha ^*_\Omega [a_2](k^2)\) and \(\tilde{F}_{\eta \gamma \gamma ^*}(k^2)\), which provide the input for the calculation of the doubly-virtual transition form factor \(F_{\eta \gamma ^*\gamma ^*}(q^2,k^2)\), data on \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\) need to be analyzed, with particular attention to the distributions with the dipion invariant masses. However, data for the \(\pi \pi \) spectrum are available only with a simultaneous integration over the initial energy \(k^2\). Therefore it is not possible to extract values for \(\alpha ^*_\Omega [a_2](k^2)\) as a function of \(k^2\), but only to extract some averaged value \({{\bar{\alpha }}}^*_\Omega [a_2]\). Moreover, since the value of \({{\bar{\alpha }}}^*_\Omega [a_2]\) also influences the shape of the total cross section for \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\), a combined fit to the \(\pi \pi \) spectrum and the total cross section is mandatory, which calls for a parameterization of the data in kinematic regimes that cannot be captured by the dispersion integrals employed in this work. We describe this parameterization in the following section.
3 Form factor parameterization above \(1\,\text {GeV}\)
3.1 Inclusion of excited isovector vector resonances
For the fit to the total cross section we need to parameterize the function \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2)\) for \(k^2>1\,\text {GeV}^2\). As one can see from Fig. 4, the total cross section for \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\) shows a very prominent contribution from an excited \(\rho \) resonance, the \(\rho '\) or \(\rho (1450)\). It turns out that the low-energy side of the spectrum calls for an inclusion of the \(\rho (770)\) resonance, which enters through its upper tail. Moreover, the addition of a higher resonance, the \(\rho ''\) or \(\rho (1700)\), improves the data fit significantly. Note that most experimental or phenomenological analyses of the reaction \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\) employ two or three vector resonances [67,68,69,70]. It should be stressed that what is crucial for the analysis is not that we have the correct physics optimally built into the parameterization of the function \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2)\), but all we need is a convenient representation that describes the data for the quantity of interest for this analysis: the \(k^2\)-integrated \(\pi \pi \) spectrum. Since \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2)\) enters here as a weight factor – cf. Eq. (11) – it is sufficient to parameterize \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2)\) by a sum of Breit–Wigner functions. Clearly in doing so we should not expect the resonance parameters to agree with those of the Particle Data Group (PDG), since Breit–Wigner parameters are reaction dependent and a sum of Breit–Wigner functions violates unitarity. More explicitly, the Breit–Wigner (BW) functions we employ are given by
with \(j \in \lbrace \rho ,\rho ',\rho '' \rbrace \) and the energy-dependent widths written as [71]
where the center-of-mass momentum is given by
Additionally, we employ another variant, in which the \(\rho '\) and \(\rho ''\) widths are parameterized by the decay into the \(\omega \pi \) final state:
We parameterize the function \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2) \propto \sum _{j} c_j M_j^2 BW_j(k^2)\), where \(j \in \lbrace \rho ,\rho ',\rho '' \rbrace \). Through the normalization constraint \({\tilde{F}}_{\eta \gamma \gamma ^*}(0){=}1\) we eliminate the coupling \(c_{\rho }\):
The remaining couplings are used as fit parameters. While the (large) Breit–Wigner coupling to the \(\rho '\) is taken to be real as required by unitarity, we see a substantial improvement in the fit quality if the (small) coupling to the \(\rho ''\) is allowed to take complex values, which likely subsumes the effects of yet higher resonances and the more complicated coupled-channel structure in that energy region. Additionally, the masses \(M_{\rho '}\) and \(M_{\rho ''}\) as well as the widths \(\Gamma _{\rho '}(M_{\rho '}^2)\) and \(\Gamma _{\rho ''}(M_{\rho ''}^2)\) of the \(\rho '\) and \(\rho ''\) are fitted to the data. For the \(\rho \) we use the PDG values for mass and width.
Since we do not expect the form factor ansatz in Eq. (24) to hold up to arbitrarily high energies, we employ the following prescription for a certain cutoff value \(s_c\):
Fit to the total cross section from BaBar 2007 [54] and 2018 [55] up to \(\sqrt{k^2}={1.9}{\,\text {GeV}}\) for \(s_c={3}{\,\text {GeV}^2}\) (see Eq. (33) for details). The gray band around the central black-dashed curve represents the full model with \(\pi \pi \) widths (cf. Eq. (29)) used in the Breit–Wigner parameterizations, while the red line corresponds to the central value of the full model with \(\omega \pi \) widths (cf. Eq. (31)) for \(\rho '\) and \(\rho ''\). The error band of this curve is very close to the gray one. The central values of both variants display only tiny differences between each other
with
and the dispersion integral
This continuation ensures that the form factor drops off like 1/t and \(1/k^2\) for high energies and is continuous everywhere when going from one region to another. Through treating the cutoffs in t and in \(k^2\) in the same way, it reflects a symmetry that is important for a later application in the \(\eta \) transition form factor in the HLbL contribution to the muon \(g-2\). We test the independence of the choice of continuation point \(s_c\) by varying it in the fits according to \(s_c \in \lbrace 3,\,4,\,5 \rbrace \,\,\text {GeV}^2\).
3.2 Finite-width effects in the \(a_2\) exchange
In the tensor model used to describe the \(a_2\)-exchange diagrams, the \(a_2\) meson is assumed to have no width. However, in reality the \(a_2(1320)\) has a width of about \({100}{\,\text {MeV}}\), and in the reaction \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\), where the \(a_2\) can be produced quasi on-shell, this effect is surely not negligible. To cure this caveat, we define a dispersively improved Breit–Wigner function \({\overline{BW}}(s)\), using the imaginary part of BW(s) as in Eq. (28) as the spectral function above a certain threshold \(s_\text {thr}\) [72, 73],
where in the last step we have written the Cauchy kernel as a Breit–Wigner function with mass parameter \(\sqrt{x}\) and width zero. We therefore generalize both dispersion integral \(D(t,k^2)\) and hat function \({\hat{F}}_{a_2}(t,k^2)\) with the \(a_2\) mass dispersed according to this spectral function,
where \(C \in \lbrace D, {\hat{F}}_{a_2} \rbrace \). We employ the parameterization [74, 75]
where \(M_\rho \) (\(M_\eta \)) is the mass of the \(\rho \) (\(\eta \)) meson, \(\Gamma _{a_2}\) the total \(a_2\) width, and the barrier factor is given by \(R = {5.2}{\,\text {GeV}^{-1}}\) [75]. This energy-dependent width explicitly takes into account the \(a_2\) decays into \(\pi \eta \) and \(\pi \rho \) with branching ratios \(p_\eta = {0.17}\) and \(p_\rho = {0.83}\).
We evaluate \(C(t,k^2;M_{a_2}^2)\) for 20 different values of \(M_{a_2}^2\) in the range \(\left[ s_\text {thr},{2.3}{\,\text {GeV}^2}\right] \), where \(s_\text {thr} = (M_\eta + M_\pi )^2\). For D we use a grid of \({107} \times {150}\) values for \(t,k^2 \in [4M_\pi ^2,{3}{\,\text {GeV}^2}]\). The integral of Eq. (37) was then carried out using the trapezoidal rule for each point of the \((t,k^2)\) grid. In the fitting routine we make the replacements
4 Data analysis of \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\)
In the following, we analyze the \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\) data by the BaBar collaboration [54, 55] in three successively refined models for the \(\pi \pi \) invariant mass distribution: assuming a linear or a quadratic polynomial multiplying the final-state interactions as parameterized by the Omnès function, and using the full-fledged description of left-hand cuts due to the \(a_2\), which automatically generates breaking of the factorization assumption. We fit to data from BaBar published in 2007 [54] and 2018 [55]. The differential cross section data from 2007 are integrated over \(\sqrt{k^2}\) in \([1.0,\, 4.5]\,{\,\text {GeV}}\), the ones from 2018 in the range \(\sqrt{k^2} \in [1.4,\, 1.8]\,{\,\text {GeV}}\). The \(\pi \pi \) spectrum is dominated by the \(\rho \), we choose to fit the differential cross section data up to \(\sqrt{t}={1}{\,\text {GeV}}\). The tail of the Breit–Wigner parameterization of \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2)\) is rather uncontrolled for larger \(k^2\), thus we fit the total cross section data up to \(\sqrt{k^2}={1.9}{\,\text {GeV}}\) only.
4.1 Linear model
As in the first dispersive attempts that dealt with the \(\eta \) TFF [42, 43] we employ a linear function as part of \(F_{\eta \pi \pi \gamma ^*}(t,k^2)\), which does not include any effects of the \(a_2\)-exchange left-hand-cut contribution:
For values of the \(\pi \pi \) invariant mass squared larger than a certain cutoff parameter \(s_p\) we let the form factor fall off like 1/t by setting the linear polynomial to a constant. The constant term in the polynomial part of Eq. (40) is fixed by fitting the corresponding linear representation to \(\eta \rightarrow \pi ^+ \pi ^- \gamma \) data measured by KLOE [45] to \({A} = 18.0(4){\,\text {GeV}^{-3}}\). The results of these fits with cutoff parameter \(\sqrt{s_p} \in \lbrace 0.9,\, 1.0,\, 1.2 \rbrace \,\text {GeV}\) are shown in Table 1. The central finding is that the extracted values for \(\alpha _\Omega ^*\) are consistently and significantly smaller than those found for \(\alpha _\Omega \), see Eq. (17).
4.2 Quadratic model
Fit to the differential cross sections from BaBar 2007 [54] and 2018 [55] up to \(\sqrt{t}={1}{\,\text {GeV}}\) for \(s_c={3}{\,\text {GeV}^2}\) (full). The results shown here correspond to the fits employing the full model, with \(\pi \pi \) width parameterizations for the \(\rho '\) and \(\rho ''\) resonances in the total cross section. For comparison, the central value of the fit of the quadratic model (quad.) with \(s_p={1}{\,\text {GeV}^2}\) and \(\pi \pi \) width is also shown
As noted in Ref. [51] for the real-photon case, the inclusion of the \(a_2\)-induced left-hand-cut contribution adds a curvature part to the form factor \(F_{\eta \pi \pi \gamma ^*}(t,k^2)\). In the quadratic model, we do not use the explicit form of the \(a_2\) exchange amplitudes, but restrict ourselves to the approximation in Eq. (23). The fit of this representation to \(\eta \rightarrow \pi ^+ \pi ^- \gamma \) decay data yields \(A={17.4(4)}{\,\text {GeV}^{-3}}\). Note that this form omits all the \(k^2\)-dependence in \(F_{\eta \pi \pi \gamma ^*}(t,k^2)\) other than through the multiplicative factor \({{\tilde{F}}}_{\eta \gamma \gamma ^*}(k^2)\), cf. Eq. (32):
where the linear coefficient \({\bar{\alpha }}^*_\Omega [a_2]\) is used as a fit parameter and the parameters \(\alpha _{a_2}\) and \(\beta _{a_2}\) are held fixed at their respective values given below Eq. (23). For values of the \(\pi \pi \) invariant mass squared larger than a certain cutoff parameter \(s_p\) we, again, let the form factor fall off like 1/t by the prescription
The fit results for cutoff parameter \(\sqrt{s_p} \in \lbrace 0.9,\, 1.0,\, 1.2 \rbrace \,\text {GeV}\) are displayed in Table 2. Compared to the results of the linear model, the linear parameter \({\bar{\alpha }}^*_\Omega [a_2]\) comes out substantially closer to the value of the linear subtraction constant \(\alpha _\Omega [a_2]\) for all tested values of \(s_p\), cf. Eq. (21), which has been obtained from \(\eta \rightarrow \pi ^+\pi ^- \gamma \) decay data, and compatible within uncertainties throughout. The sizable shift of the slope between the linear and quadratic model can be understood in the following manner: in the real-photon case, the main impact of the \(a_2\) contribution on the \(\pi \pi \) spectrum is to provide a downward curvature, with the quadratic coefficient \(\beta _{a_2}\) being sizable and negative. Accordingly, a fit with a linear term only must find a reduced strength in order to reproduce the data in the region of the \(\rho \) resonance.
4.3 Full model
Here, the full representation of \(F_{\eta \pi \pi \gamma ^*}(t,k^2)\) in Eq. (27) is used for the \(e^+ e^- \rightarrow \eta \pi ^+ \pi ^-\) fits, i.e., including the \(k^2\)-dependent \(a_2\)-induced left-hand-cut contribution. The parameter \(A={17.2(4)}{\,\text {GeV}^{-3}}\) in Eq. (26) is fixed by fitting the representation in Eq. (19) to \(\eta \rightarrow \pi ^+\pi ^- \gamma \) decay data measured by KLOE [45]. The fit results for cutoff parameters \(s_c \in \lbrace 3,\, 4,\, 5 \rbrace {\,\text {GeV}^2}\) according to the high-energy prescription in Eq. (33) are summarized in Table 3. We observe that the \(\omega \pi \) parameterizations of the \(\rho '\) and \(\rho ''\) widths result in a slightly better fit quality. The mass and width parameters of the \(\rho '\) and \(\rho ''\), which must not be confused with pole parameters, vary strongly between both descriptions of the energy-dependent width, most prominently for the \(\rho '\). A comparison with the PDG parameters (\(M_{\rho '}^\text {PDG}={1465(25)}{\,\text {MeV}}\), \(\Gamma _{\rho '}^\text {PDG}={400(60)}{\,\text {MeV}}\)) is therefore not particularly meaningful. However, the linear subtraction constant, the central result for our investigation of potential factorization breaking, only varies within the error margins between the two fits. Additionally, the resulting spectra for cutoff parameter \(s_c = 3 \,\text {GeV}^2\) are shown in Figs. 4 and 5, where the error bands are generated by the fit uncertainties taking their correlations into account. The description of differential spectra turns out to be slightly worse than for the linear/quadratic models. Those, however, do not capture the nontrivial \(k^2\)-dependence of the amplitude illustrated in Fig. 6: the change of the left-hand-cut contribution with \(k^2\) is seen to be quite significant. In Fig. 5 the fit result of the full model can be compared to the central value of the quadratic one. Differences between the two curves can only be seen at the lower flank of the \(\rho \) resonance. Moreover, if the uncertainty band were added, it would overlap with the curve of the full model almost everywhere. The large values of the reduced \(\chi ^2\) of the differential cross section in the full model fit are primarily caused by the flanks of the \(\rho \) resonance, as one can see in Fig. 5. Especially below the \(\rho \) peak, the \(\chi ^2\) receives a large contribution. The tension specifically for these \(\pi \pi \) invariant masses is surprising, as the dispersive representation should be perfectly reliable there. Doubly-differential data (in the variables t and \(k^2\)) would be highly desirable to better understand the origin of this discrepancy.
The Breit–Wigner coupling of the \(\rho '\) resonance comes out consistently in all fits; in particular, in contrast to mass and width, it only changes mildly between the two different parameterizations of the energy-dependent width. Moreover, to good accuracy it fulfills the expectation
(where in our convention Eq. (32), \(c_\rho =1\)), derived from a superconvergence relation for \(V \rightarrow P\) transition form factors that are expected to drop \(\propto k^{-4}\) asymptotically [76,77,78,79]. The coupling to the \(\rho ''\) resonance comes out complex, however it is two orders of magnitude suppressed compared to the \(\rho \) and more than one order of magnitude with respect to the \(\rho '\) coupling. Also the mass and width parameters of the \(\rho ''\) deviate somewhat from the PDG values, \(M_{\rho ''}^\text {PDG} = {1720(20)}{\,\text {MeV}}\) and \(\Gamma _{\rho ''}^\text {PDG} = {250(100)}{\,\text {MeV}}\), which may be explained by the occurrence of higher resonances in the spectrum that are not included in our parameterization.
The function \(P(t,k^2)\), cf. Eq. (15), of the full model for \(s_c = {3}{\,\text {GeV}^2}\) for different \(k^2\)
Comparison of the functions \(P(t,k^2=0)\), cf. Eq. (15), extrapolated from \(e^+e^- \rightarrow \eta \pi ^+\pi ^-\) using both the full and the quadratic model, and the one directly obtained from \(\eta \rightarrow \pi ^+\pi ^- \gamma \). The band for the full model includes the uncertainty due to \({\bar{\alpha }}_\Omega ^*[a_2]\) as well as the different values for \(s_c \in \lbrace 3,\, 4,\, 5 \rbrace \, {\,\text {GeV}^2}\); see Table 3. In the same way the band for the quadratic model comprises the uncertainty due to \({\bar{\alpha }}_\Omega ^*[a_2]\) as well as \(\sqrt{s_p} \in \lbrace 0.9,\, 1.0,\, 1.2 \rbrace \, {\,\text {GeV}}\); see Table 2. The onset of the high-energy prescription can be seen in the quadratic band around \(t = {0.81}{\,\text {GeV}^2}\)
Results for the normalized singly-virtual \(\eta \) transition form factor. The very small isoscalar contribution has been omitted. We show \(\eta \rightarrow e^+ e^- \gamma \) data from the A2 (squares [47], triangles [49]) and \(\eta \rightarrow \mu ^+ \mu ^- \gamma \) data from the NA60 (circles [46], diamonds [48]) collaborations. The insert magnifies the low-\(q^2\) region. The gray band shows the result from the full model for \(s_c = {3}{\mathrm{GeV}^2}\). The red (yellow) band represents the outcome of the quadratic (linear) model for \(s_p = {1}{\,\text {GeV}^2}\). Additionally, for comparison, the result derived from \(\eta \rightarrow \pi ^+ \pi ^- \gamma \) is shown as the blue band. The central results are represented by dashed lines colored accordingly throughout
The linear subtraction constant \({\bar{\alpha }}^*_\Omega [a_2]\) comes out consistently for different cutoff parameters \(s_c\), but deviates from the linear constant found in the polynomial part fitted to \(\eta \rightarrow \pi ^+\pi ^- \gamma \) decay data of \(1.42(6){\,\text {GeV}^{-2}}\). This is illustrated in Fig. 7, where the \(e^+e^- \rightarrow \eta \pi ^+\pi ^-\) form factor in the extrapolation to \(k^2=0\) is compared to the representation in Eq. (19) fitted to \(\eta \rightarrow \pi ^+\pi ^- \gamma \) decay data. This is in contrast to the quadratic model, which allows for a smooth connection between the extrapolated \(e^+e^- \rightarrow \eta \pi ^+\pi ^-\) and the \(\eta \) decay data. We therefore have to conclude that the dominant left-hand-cut contribution of the \(a_2\) exchange provides a factorization breaking mechanism that is too strong compared to the available data, and likely calls for further effects that mitigate this to some extent.
5 Consequences for the \(\eta \) transition form factor
The observations made on the different models for \(F_{\eta \pi \pi \gamma ^*}(t,k^2)\) in the previous section immediately translate into the \(\eta \) transition form factor. Figure 8 shows the results for the normalized \(\eta \rightarrow \gamma \gamma ^*\) transition form factor based on a once-subtracted variant of Eq. (5) in the time-like regime (thus enforcing the correct normalization by hand), compared to experimental data [46,47,48,49]. Here, the dispersion integral has been truncated [42], with the upper limit of integration varied between \(M_{\eta '}^2\) and \({2}{\,\text {GeV}^2}\). The error bands in Fig. 8 are generated from the error of the linear subtraction constant \({\bar{\alpha }}_\Omega ^*[a_2]\), the variation of the integration upper limit, the pion vector form factor, and the errors of the branching ratios entering the result. The central results shown as the dashed lines stem from evaluating the integral with cutoff \({1}{\,\text {GeV}^2}\). Not surprisingly, the transition form factor based on the extrapolated quadratic model agrees well with the direct calculation based on \(\eta \rightarrow \pi ^+\pi ^-\gamma \), while the extrapolated linear and full models yield a form factor significantly below the others. This is also illustrated by the \(\chi ^2/\text {dof}\), where \(\chi ^2\) as usual refers to the weighted sum of residuals between data and the central values of the predictions and \(\text {dof}\) stands for the number of data points (as there are no fit parameters to be adjusted). The full model yields \(\chi ^2_\text {full}/\text {dof} = 2.09\), when compared to the linear model with \(\chi ^2_\text {lin.}/\text {dof} = 1.54\) and the quadratic model with \(\chi ^2_\text {quad.}/\text {dof} = 0.48\). This is to be compared to \(\chi ^2_{\pi \pi \gamma }/\text {dof} = 0.78\) for the TFF calculated directly based on \(\eta \rightarrow \pi ^+\pi ^-\gamma \) decay data. In particular the data from Refs. [46, 48] disfavor the TFF based on the extrapolated full model rather strongly.
These differences are also reflected in the slope parameter of the TFF defined by
According to Eq. (5), its isovector part fulfills a sum rule
The slope parameters of the respective models are listed in Table 4. The isoscalar contribution \(b_\eta ^{(I=0)}=-{0.022}{\,\text {GeV}^{-2}}\) [42] is inside the quoted uncertainties throughout.
Comparison of the normalized isovector \(\eta \) transition form factor \(\bar{F}_{\eta \gamma ^*\gamma ^*}^{(I=1)}(q^2,k^2)\) in the singly-virtual limits \(k^2=0\) and \(q^2=0\). Results are shown from the full model for \(s_c = {3}{\,\text {GeV}^2}\). The error band for the \(k^2=0\) case is generated as described before, whereas the error band of the \(q^2=0\) curve additionally takes the fit errors of the parameters in \({\tilde{F}}_{\eta \gamma \gamma ^*}(k^2)\) and their correlations into account
Bose symmetry requires the TFF as well as its isovector part to be symmetric under the exchange of the two arguments \(q^2\) and \(k^2\). This symmetry is by no means manifest in our model, which in contrast is built onto information in two disjoint kinematic ranges: the dispersion relation (5) is designed for the region \(q^2\le 1\,\text {GeV}^2\), while the dependence on the second variable is fitted in the range \(1\,\text {GeV}^2 \le k^2 \le (1.9\,\text {GeV})^2\). Indeed, Fig. 9 demonstrates that the two different singly-virtual limits \({\bar{F}}_{\eta \gamma ^*\gamma ^*} ^{(I=1)}(q^2,k^2=0)\) and \({\bar{F}}_{\eta \gamma ^*\gamma ^*}^{(I=1)}(q^2=0,k^2)\) do not coincide in the region of the \(\rho (770)\) peak, although the disagreement hardly exceeds the combined width of the two uncertainty bands. Obviously, in order to calculate and predict the limit \(q^2=0\), we are required to use the unsubtracted dispersion relation (5), without the integral being cut off. Instead, the high-energy prescription in Eq. (33) has been used above a certain cutoff varied between 1 and \({2}{\,\text {GeV}^2}\). Note that the TFF shown in Fig. 9 is normalized using \(F_{\eta \gamma \gamma }\) based on the physical value of the two-photon partial width. \({\bar{F}}_{\eta \gamma ^*\gamma ^*}^{(I=1)}(0,0)\) is hence a test of the hypothesis that two-pion intermediate states saturate the isovector dispersion relation to a large extent: indeed, the normalization is reproduced to \(90(8)\%\). Figure 9 suggests that the remaining deficit, which is due to omitted heavier intermediate states (such as \(4\pi \), \(\pi \omega \), \(K{\bar{K}}\), etc.), likely increases somewhat around the \(\rho (770)\), but not dramatically so.
6 Summary and discussion
In this article, we have investigated the consistency of pion–pion spectra in the closely related reactions \(\eta \rightarrow \pi ^+\pi ^-\gamma \) and \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\), which serve as central input to dispersion-theoretical analyses of the singly- and doubly-virtual \(\eta \) transition form factor, respectively. This comparison has been quantified in terms of the residual dependence on the \(\pi \pi \) invariant mass squared t that multiplies universal elastic rescattering, as encapsulated in the Omnès function. While the small phase space available in the decay \(\eta \rightarrow \pi ^+\pi ^-\gamma \) is sufficiently accurately described by a residual linear t-dependence [43, 45], both a study of the dominant left-hand cuts, induced by crossed-channel exchanges of the \(a_2\) tensor meson [51], and data on the closely related \(\eta '\rightarrow \pi ^+\pi ^-\gamma \) decay [52, 53] demonstrate that at least a quadratic polynomial is required to describe the \(\pi \pi \) spectra up to \(1\,\text {GeV}^2\).
The present analysis of the pion–pion distributions in \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\) confirms that, indeed, a linear parameterization is insufficient to describe these with a universal slope parameter independently of the dilepton squared invariant mass \(k^2\). On the other hand, a quadratic polynomial, with the quadratic term in t fixed from the size of curvature induced by the left-hand cut at \(k^2=0\), seems well compatible with a naïve factorization assumption for the t and \(k^2\) dependences, and as a result, for the doubly-virtual \(\eta \) transition form factor varying with its two arguments according to Eq. (1). The somewhat puzzling observation is that the natural breaking of factorization, induced by the nontrivial \(k^2\) dependence of the \(a_2\) exchange contribution, is too strong to be consistent with the data: the amplitude we have built on this physically well-motivated picture does not link the available \(e^+e^-\rightarrow \eta \pi ^+\pi ^-\) data to those for the \(\eta \) decay in a consistent manner; factorization breaking has to be mitigated significantly by other mechanisms not investigated so far.
One way how such a damping might be achieved is through different \(k^2\)-dependences of the two considered isobar components in the \(\gamma ^*\rightarrow \eta \pi ^+\pi ^-\) amplitude: we have implicitly assumed that the dominant “\(\eta \rho \)” and the supplementary \(a_2\pi \) contribution responsible for the left-hand cut evolve with \(k^2\) in parallel. The only way to understand deviations from this simple picture is to analyze differential distributions in \(\eta \pi ^+\pi ^-\) in different bins of \(k^2\), as opposed to the \(k^2\)-integrated \(\pi \pi \) spectra available to date [54, 55, 57]. Such information, combined with a doubly-dispersive construction based on a \(\eta \rightarrow 2(\pi ^+\pi ^-)\) amplitude at low energies (cf. the corresponding \(\eta '\rightarrow 2(\pi ^+\pi ^-)\) decays [80, 81] and the discussion in Ref. [41]), would then pave the way towards a more complete understanding of the doubly-virtual \(\eta \) transition form factor.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: There is no data because this work is of theoretical nature.]
Notes
See also the alternative approach to analyze the muon’s Pauli form factor dispersively [5].
Strictly speaking, we test factorization for the isovector–isovector part of the transition form factor, as the isoscalar–isoscalar contribution is small unless one of the virtualities hits a narrow isoscalar resonance, \(q^2, k^2 \approx M_\omega ^2\), \(M_\phi ^2\).
The analyses [43,44,45] employ Eq. (15) with \(\Omega (t)\) replaced by \(F_\pi ^V(t)\), due to the observation that the linear slope in R(t) relating both quantities is small. The analogously defined parameter \(\alpha \) was then determined to be \(\alpha = 1.32(13) \,\text {GeV}^{-2}\), combining statistical and systematic errors, which is slightly shifted compared to Eq. (17).
References
G. Colangelo, M. Hoferichter, M. Procura, P. Stoffer, JHEP 09, 091 (2014). arXiv:1402.7081 [hep-ph]
G. Colangelo, M. Hoferichter, B. Kubis, M. Procura, P. Stoffer, Phys. Lett. B 738, 6 (2014). arXiv:1408.2517 [hep-ph]
G. Colangelo, M. Hoferichter, M. Procura, P. Stoffer, JHEP 09, 074 (2015). arXiv:1506.01386 [hep-ph]
T. Aoyama et al., Phys. Rep. 887, 1 (2020). arXiv:2006.04822 [hep-ph]
V. Pauk, M. Vanderhaeghen, Phys. Rev. D 90, 113012 (2014). arXiv:1409.0819 [hep-ph]
G.W. Bennett et al., [Muon \(g-2\) Collaboration], Phys. Rev. D 73, 072003 (2006). arXiv:hep-ex/0602035
B. Abi et al., [Muon \(g-2\) Collaboration], Phys. Rev. Lett. 126, 141801 (2021). arXiv:2104.03281 [hep-ex]
T. Albahri et al., [Muon \(g-2\) Collaboration], Phys. Rev. D 103, 072002 (2021). arXiv:2104.03247 [hep-ex]
T. Aoyama, M. Hayakawa, T. Kinoshita, M. Nio, Phys. Rev. Lett. 109, 111808 (2012). arXiv:1205.5370 [hep-ph]
T. Aoyama, T. Kinoshita, M. Nio, Atoms 7, 28 (2019)
A. Czarnecki, W. J. Marciano, A. Vainshtein, Phys. Rev. D 67, 073006 (2003). arXiv:hep-ph/0212229, [Erratum: Phys. Rev. D 73, 119901 (2006)]
C. Gnendiger, D. Stöckinger, H. Stöckinger-Kim, Phys. Rev. D 88, 053005 (2013). arXiv:1306.5546 [hep-ph]
M. Davier, A. Hoecker, B. Malaescu, Z. Zhang, Eur. Phys. J. C 77, 827 (2017). arXiv:1706.09436 [hep-ph]
A. Keshavarzi, D. Nomura, T. Teubner, Phys. Rev. D 97, 114025 (2018). arXiv:1802.02995 [hep-ph]
G. Colangelo, M. Hoferichter, P. Stoffer, JHEP 02, 006 (2019). arXiv:1810.00007 [hep-ph]
M. Hoferichter, B.-L. Hoid, B. Kubis, JHEP 08, 137 (2019). arXiv:1907.01556 [hep-ph]
M. Davier, A. Hoecker, B. Malaescu, Z. Zhang, Eur. Phys. J. C 80, 241 (2020). arXiv:1908.00921 [hep-ph], [Erratum: Eur. Phys. J. C 80, 410 (2020)]
A. Keshavarzi, D. Nomura, T. Teubner, Phys. Rev. D 101, 014029 (2020). arXiv:1911.00367 [hep-ph]
B.-L. Hoid, M. Hoferichter, B. Kubis, Eur. Phys. J. C 80, 988 (2020). arXiv:2007.12696 [hep-ph]
A. Kurz, T. Liu, P. Marquard, M. Steinhauser, Phys. Lett. B 734, 144 (2014). arXiv:1403.6400 [hep-ph]
K. Melnikov, A. Vainshtein, Phys. Rev. D 70, 113006 (2004). arXiv:hep-ph/0312226
P. Masjuan, P. Sánchez-Puertas, Phys. Rev. D 95, 054026 (2017). arXiv:1701.05829 [hep-ph]
G. Colangelo, M. Hoferichter, M. Procura, P. Stoffer, Phys. Rev. Lett. 118, 232001 (2017). arXiv:1701.06554 [hep-ph]
G. Colangelo, M. Hoferichter, M. Procura, P. Stoffer, JHEP 04, 161 (2017). arXiv:1702.07347 [hep-ph]
I. Danilkin, M. Hoferichter, P. Stoffer, Phys. Lett. B 820, 136502 (2021). arXiv:2105.01666 [hep-ph]
M. Hoferichter, B.-L. Hoid, B. Kubis, S. Leupold, S.P. Schneider, Phys. Rev. Lett. 121, 112002 (2018). arXiv:1805.01471 [hep-ph]
M. Hoferichter, B.-L. Hoid, B. Kubis, S. Leupold, S.P. Schneider, JHEP 10, 141 (2018). arXiv:1808.04823 [hep-ph]
A. Gérardin, H.B. Meyer, A. Nyffeler, Phys. Rev. D 100, 034520 (2019). arXiv:1903.09471 [hep-lat]
J. Bijnens, N. Hermansson-Truedsson, A. Rodríguez-Sánchez, Phys. Lett. B 798, 134994 (2019). arXiv:1908.03331 [hep-ph]
G. Colangelo, F. Hagelstein, M. Hoferichter, L. Laub, P. Stoffer, Phys. Rev. D 101, 051501 (2020). arXiv:1910.11881 [hep-ph]
G. Colangelo, F. Hagelstein, M. Hoferichter, L. Laub, P. Stoffer, JHEP 03, 101 (2020). arXiv:1910.13432 [hep-ph]
T. Blum, N. Christ, M. Hayakawa, T. Izubuchi, L. Jin, C. Jung, C. Lehner, Phys. Rev. Lett. 124, 132002 (2020). arXiv:1911.08123 [hep-lat]
G. Colangelo, M. Hoferichter, A. Nyffeler, M. Passera, P. Stoffer, Phys. Lett. B 735, 90 (2014). arXiv:1403.7512 [hep-ph]
J. Grange et al. [Muon \(g-2\) Collaboration], arXiv:1501.06858 [physics.ins-det]
M. Hoferichter, P. Stoffer, JHEP 05, 159 (2020). arXiv:2004.06127 [hep-ph]
M. Zanke, M. Hoferichter, B. Kubis, JHEP 07, 106 (2021). arXiv:2103.09829 [hep-ph]
M. Knecht, JHEP 08, 056 (2020). arXiv:2005.09929 [hep-ph]
J. Lüdtke, M. Procura, Eur. Phys. J. C 80, 1108 (2020). arXiv:2006.00007 [hep-ph]
J. Bijnens, N. Hermansson-Truedsson, L. Laub, A. Rodríguez-Sánchez, JHEP 10, 203 (2020). arXiv:2008.13487 [hep-ph]
J. Bijnens, N. Hermansson-Truedsson, L. Laub, A. Rodríguez-Sánchez, JHEP 04, 240 (2021). arXiv:2101.09169 [hep-ph]
L. Gan, B. Kubis, E. Passemar, S. Tulin, arXiv:2007.00664 [hep-ph]
C. Hanhart, A. Kupść, U.-G. Meißner, F. Stollenwerk, A. Wirzba, Eur. Phys. J. C 73, 2668 (2013). arXiv:1307.5654 [hep-ph], [Erratum: Eur. Phys. J. C 75, 242 (2015)]
F. Stollenwerk, C. Hanhart, A. Kupść, U.-G. Meißner, A. Wirzba, Phys. Lett. B 707, 184 (2012). arXiv:1108.2419 [nucl-th]
P. Adlarson et al., [WASA-at-COSY Collaboration], Phys. Lett. B 707, 243 (2012). arXiv:1107.5277 [nucl-ex]
D. Babusci et al., [KLOE Collaboration], Phys. Lett. B 718, 910 (2013). arXiv:1209.4611 [hep-ex]
R. Arnaldi et al., [NA60 Collaboration], Phys. Lett. B 677, 260 (2009). arXiv:0902.2547 [hep-ph]
P. Aguar-Bartolome et al., [A2 Collaboration], Phys. Rev. C 89, 044608 (2014). arXiv:1309.5648 [hep-ex]
R. Arnaldi et al., [NA60 Collaboration], Phys. Lett. B 757, 437 (2016). arXiv:1608.07898 [hep-ex]
P. Adlarson et al., [A2 Collaboration], Phys. Rev. C 95, 035208 (2017). arXiv:1609.04503 [hep-ex]
M. Hoferichter, B. Kubis, S. Leupold, F. Niecknig, S.P. Schneider, Eur. Phys. J. C 74, 3180 (2014). arXiv:1410.4691 [hep-ph]
B. Kubis, J. Plenter, Eur. Phys. J. C 75, 283 (2015). arXiv:1504.02588 [hep-ph]
C. Hanhart, S. Holz, B. Kubis, A. Kupść, A. Wirzba, C.-W. Xiao, Eur. Phys. J. C 77, 98 (2017). arXiv:1611.09359 [hep-ph], [Erratum: Eur. Phys. J. C 78, 450 (2018)]
M. Ablikim et al., [BESIII Collaboration], Phys. Rev. Lett. 120, 242003 (2018). arXiv:1712.01525 [hep-ex]
B. Aubert et al. [BaBar Collaboration], Phys. Rev. D 76, 092005 (2007). arXiv:0708.2461 [hep-ex], [Erratum: Phys. Rev. D 77, 119902 (2008)]
J.P. Lees et al., [BaBar Collaboration], Phys. Rev. D 97, 052007 (2018). arXiv:1801.02960 [hep-ex]
M.N. Achasov et al., Phys. Rev. D 97, 012008 (2018). arXiv:1711.08862 [hep-ex]
S.S. Gribanov et al., [CMD-3 Collaboration], JHEP 01, 112 (2020). arXiv:1907.08002 [hep-ex]
J. Wess, B. Zumino, Phys. Lett. B 37, 95 (1971)
E. Witten, Nucl. Phys. B 223, 422 (1983)
R. Omnès, Nuovo Cim. 8, 316 (1958)
M. Fujikawa et al., [Belle Collaboration], Phys. Rev. D 78, 072006 (2008). arXiv:0805.3773 [hep-ex]
F.-K. Guo, C. Hanhart, F.J. Llanes-Estrada, U.-G. Meißner, Phys. Lett. B 678, 90 (2009). arXiv:0812.3270 [hep-ph]
C. Hanhart, Phys. Lett. B 715, 170 (2012). arXiv:1203.6839 [hep-ph]
P.A. Zyla et al. [Particle Data Group], PTEP 2020, 083C01 (2020)
J. Gasser, A. Rusetsky, Eur. Phys. J. C 78, 906 (2018). arXiv:1809.06399 [hep-ph]
M. Niehus, M. Hoferichter, B. Kubis, J. Ruiz de Elvira, Phys. Rev. Lett. 126, 102002 (2021). arXiv:2009.04479 [hep-ph]
R.R. Akhmetshin et al., [CMD-2 Collaboration], Phys. Lett. B 489, 125 (2000). arXiv:hep-ex/0009013
L.-Y. Dai, J. Portoles, O. Shekhovtsova, Phys. Rev. D 88, 056001 (2013). arXiv:1305.5751 [hep-ph]
M.K. Volkov, A.B. Arbuzov, D.G. Kostunin, Phys. Rev. C 89, 015202 (2014). arXiv:1310.8484 [hep-ph]
W. Qin, L.-Y. Dai, J. Portoles, JHEP 03, 092 (2021). arXiv:2011.09618 [hep-ph]
N.N. Achasov, V.A. Karnakov, JETP Lett. 39, 342 (1984)
E. L. Lomon, S. Pacetti, Phys. Rev. D 85, 113004 (2012). arXiv:1201.6126 [hep-ph], [Erratum: Phys. Rev. D 86, 039901 (2012)]
B. Moussallam, Eur. Phys. J. C 73, 2539 (2013). arXiv:1305.3143 [hep-ph]
F. von Hippel, C. Quigg, Phys. Rev. D 5, 624 (1972)
G.M. Beladidze et al., [VES Collaboration], Phys. Lett. B 313, 276 (1993)
G.R. Farrar, D.R. Jackson, Phys. Rev. Lett. 35, 1416 (1975)
A.I. Vainshtein, V.I. Zakharov, Phys. Lett. B 72, 368 (1978)
G.P. Lepage, S.J. Brodsky, Phys. Lett. B 87, 359 (1979)
G.P. Lepage, S.J. Brodsky, Phys. Rev. D 22, 2157 (1980)
F.-K. Guo, B. Kubis, A. Wirzba, Phys. Rev. D 85, 014014 (2012). arXiv:1111.5949 [hep-ph]
M. Ablikim et al. [BESIII Collaboration], Phys. Rev. Lett. 112, 251801 (2014), arXiv:1404.0096 [hep-ex], [Addendum: Phys.Rev.Lett. 113, 039903 (2014)]
I. Caprini, G. Colangelo, H. Leutwyler, Eur. Phys. J. C 72, 1860 (2012). arXiv:1111.7160 [hep-ph]
J. Gasser, H. Leutwyler, Ann. Phys. 158, 142 (1984)
M. Dax, T. Isken, B. Kubis, Eur. Phys. J. C 78, 859 (2018). arXiv:1808.08957 [hep-ph]
S. Aoki et al., [FLAG Collaboration], Eur. Phys. J. C 80, 113 (2020). arXiv:1902.08191 [hep-lat]
A. Bazavov et al. [MILC Collaboration], PoS LATTICE2010, 074 (2010). arXiv:1012.0868 [hep-lat]
S. Borsányi, S. Dürr, Z. Fodor, S. Krieg, A. Schäfer, E.E. Scholz, K.K. Szabó, Phys. Rev. D 88, 014513 (2013). arXiv:1205.0788 [hep-lat]
S. Dürr et al., [BMW Collaboration], Phys. Rev. D 90, 114504 (2014). arXiv:1310.3626 [hep-lat]
P.A. Boyle et al., Phys. Rev. D 93, 054502 (2016). arXiv:1511.01950 [hep-lat]
S.R. Beane, W. Detmold, P.M. Junnarkar, T.C. Luu, K. Orginos, A. Parreño, M.J. Savage, A. Torok, A. Walker-Loud, Phys. Rev. D 86, 094509 (2012). arXiv:1108.1380 [hep-lat]
A. Dobado, M.J. Herrero, T.N. Truong, Phys. Lett. B 235, 134 (1990)
T.N. Truong, Phys. Rev. Lett. 67, 2260 (1991)
A. Dobado, J.R. Peláez, Phys. Rev. D 47, 4883 (1993). arXiv:hep-ph/9301276
Acknowledgements
We are grateful to the anonymous referee who pointed out a conceptual inconsistency in the first version of this manuscript. We would like to thank Eugeny P. Solodov and Simon Eidelman for helpful discussions and advice, and Evgeny A. Kozyrev for providing us with the data of Ref. [55]. Furthermore, we are grateful to Peter Stoffer for help with the pion–pion phase shift solution of Ref. [82]. This work is supported in part by the DFG and the NSFC through funds provided to the Sino–German Collaborative Research Center TRR110 “Symmetries and the Emergence of Structure in QCD” (DFG Project-ID 196253076, NSFC Grant No. 12070131001). The project that gave rise to these results received the support of a fellowship from “la Caixa” Foundation (ID 100010434), fellowship code LCF/BQ/IN17/11620037.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Technical implementation
Appendix A: Technical implementation
1.1 A.1: P-wave phase shift
As mentioned in the main text, the \(\pi \pi \) phase shift employed in this work is calculated via the inverse-amplitude method (IAM) from an approximation of the two-loop representation of Ref. [66]. The amplitude for \(\pi \pi \rightarrow \pi \pi \) scattering in chiral perturbation theory (ChPT) up to next-to-leading order (NLO), projected onto the P-wave, can be written as
where \(t_i\) labels the contribution of chiral order \(p^i\). The P-wave projected amplitudes up to NLO are given by [83, 84]
where
and \(\sigma = \sigma _\pi (s)\). In those expressions F represents the pion decay constant in the chiral limit, which can be extracted from the ratio \(F_\pi /F = 1.062(7)\) [85,86,87,88,89,90]. The combination of low-energy constants \(\bar{l}_2 - \bar{l}_1\) is later used as a free parameter. Utilizing the IAM, we write the unitarized amplitude as [91,92,93]
Now the \(\pi \pi \) P-wave phase shift can be extracted from this expression as \(\delta _1^1 = {\text {arg}}\, t_\text {IAM}(s)\). However, in order to enforce the phase to converge to \(\pi \) for \(s \rightarrow \infty \), we add terms, inspired by the next-to-next-to leading order amplitude, to \(t_4\) by hand:
where two additional parameters \({\hat{l}}_s\) and \({\hat{l}}_\pi \) have been introduced. In order to fix the three parameters, we fit the phase parameterization from the IAM amplitude to the solution of the Roy-equation analysis of \(\pi \pi \) scattering [82]. The fit up to \(\sqrt{s} = {1.3}{\,\text {GeV}}\) is displayed in Fig. 10. The parameters resulting from this fit are \(\bar{l}_2-\bar{l}_1 = {4.47(3)}\), \({\hat{l}}_s = {1.74(3)}{\,\text {GeV}^{-2}}\), and \({\hat{l}}_\pi = {560(20)}{\,\text {GeV}^{-2}}\).
Fit of the IAM phase to the phase of Ref. [82] (“Bern analysis”, with the dashed curve as the central result) up to \(\sqrt{s} = {1.3}{\,\text {GeV}}\)
1.2 A.2: Hat function
The analytical hat function obtained through the angular integral over the \(a_2\) exchange amplitudes in Eq. (25) is implemented in a smooth way by choosing the correct sheets of the logarithm appearing in Q(y), explicitly given by
where
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Holz, S., Plenter, J., Xiao, C.W. et al. Towards an improved understanding of \(\varvec{\eta \rightarrow \gamma ^*\gamma ^*}\). Eur. Phys. J. C 81, 1002 (2021). https://doi.org/10.1140/epjc/s10052-021-09661-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09661-0