Abstract
Double-differential yields of \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) resonances produced in p+p interactions were measured at a laboratory beam momentum of 158 \(\text{ GeV }\!/\!c\). This measurement is the first of its kind in p+p interactions below LHC energies. It was performed at the CERN SPS by the NA61/SHINE collaboration. Double-differential distributions in rapidity and transverse momentum were obtained from a sample of \(26\times 10^6\) inelastic events. The spectra are extrapolated to full phase space resulting in mean multiplicity of \({\Xi \left( 1530\right) ^{0}} \) (\(6.73 \pm 0.25\pm 0.67)\times 10^{-4}\) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) (\(2.71 \pm 0.18\pm 0.18)\times 10^{-4}\). The rapidity and transverse momentum spectra and mean multiplicities were compared to predictions of string-hadronic and statistical model calculations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Double-differential yields of \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) resonances were measured in inelastic p+p interactions at laboratory beam momentum of 158 \(\text{ GeV }\!/\!c\). The measurement was performed at the CERN SPS by the NA61/SHINE collaboration [1].
The description of strange quark production in hadron–hadron interactions and their subsequent hadronization are challenging tasks for QCD-inspired and string-based phenomenological models. This applies especially to doubly strange hyperons and their resonances. No experimental results are available from measurements of p+p interactions in the CERN SPS energy range.
At higher energy, \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) resonances were studied in p+p interactions at the CERN LHC [2]. Microscopic string/hadron transport models are widely used to describe and understand relativistic heavy-ion collisions. Data on strangeness production and especially on doubly strange resonances in p+p interactions provide important input data for these models.
The paper is organised as follows. The NA61/SHINE detector system is presented in Sect. 2. Sections 3–7 are devoted to the description of the analysis method. The results are shown in Sect. 8 and compared to published data and model calculations in Sect. 9. Section 10 closes the paper with a summary and outlook.
The following variables and definitions are used in this paper. The particle rapidity y is calculated in the p+p center of mass system (cms), \(y=0.5ln[(E+cp_L)/(E-cp_L)]\), where E and \(p_L\) are the particle energy and longitudinal momentum, respectively. The transverse component of the momentum is denoted as \(p_T\). The momentum in the laboratory frame is denoted \(p_{lab}\) and the collision energy per nucleon pair in the centre of mass by \(\sqrt{s_{NN}}\). The unit system used in the paper assumes \(c=1.\)
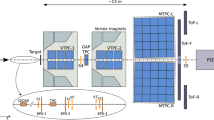
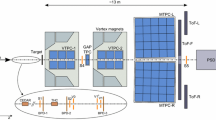
Schematic layout of the NA61/SHINE experiment at the CERN SPS (horizontal cut, not to scale) showing the detectors used in the data taking. The orientation of the NA61/SHINE coordinate system is shown in the picture. The nominal beam direction is along the z-axis. The magnetic field bends charged particle trajectories in the x–z plane. The electron drift direction in the TPCs is along the y (vertical) axis
2 Setup of NA61/SHINE experiment
Data used for the analysis were recorded at the CERN SPS accelerator complex with the NA61/SHINE fixed target large acceptance hadron detector [1]. The schematic layout of NA61/SHINE detector system is shown in Fig. 1. The NA61/SHINE tracking system consists of 4 large volume time projection chambers (TPCs). Two of the TPCs (VTPC1 and VTPC2) are within superconducting dipole magnets. Downstream of the magnets, two larger TPCs (MTPC-R and MTPC-L) provide acceptance at high momenta. The fifth small TPC (GAP-TPC) is placed between VTPC1 and VTPC2 directly on the beamline. The interactions were measured in the H2 beamline in the North Experimental Hall with a secondary beam of 158 \(\text{ GeV }\!/\!c\) positively charged hadrons impinging on a cylindrical Liquid Hydrogen Target (LHT) of 20 cm length and 2 cm diameter. This beam was produced by 400 \(\text{ GeV }\!/\!c\) protons hitting a Be-target. The primary protons were extracted from the SPS in a slow extraction mode with a flat-top lasting about 10 seconds. Protons and other positively charged particles produced in the Be-target constitute the secondary hadron beam. Two Cherenkov counters identified the protons, a CEDAR (either CEDAR-W or CEDAR-N) and a threshold counter (THC). A selection based on signals from the Cherenkov counters identified the protons with a purity of about 99% [3]. The beam momentum and intensity was adjusted by proper settings of the H2 beamline magnet currents and collimators. A set of scintillation counters selects individual beam particles (see inset in Fig.1). Their trajectories are precisely measured by three beam position detectors (BPD-1, BPD-2, BPD-3) [1].
3 Event selection
A total of 53 million minimum bias p+p events were recorded in 2009, 2010, and 2011 and analysed. Interactions in the target are selected with the trigger system by requiring an incoming beam proton and no signal from the counter S4 placed on the beam trajectory between the two vertex magnets (see Fig. 1).
Inelastic p+p events were selected using the following criteria:
-
(i)
no off-time beam particle detected within a time window of \(\pm 2~\upmu \)s around the time of the trigger particle,
-
(ii)
beam particle trajectory measured in at least three planes out of four of BPD-1 and BPD-2 and in both planes of BPD-3,
-
(iii)
the primary interaction vertex fit converged,
-
(iv)
z position of the interaction vertex (fitted using the beam trajectory and TPC tracks) not farther away than 9 \(\text{ cm }\) from the centre of the LHT,
-
(v)
events with a single, positively charged track with laboratory momentum close to the beam momentum (see Ref. [3]) were rejected, eliminating most of the elastic scattering reactions.
After the above selection, 26 million inelastic events remain for further analysis.
4 Reconstruction and selection of \({\Xi \left( 1530\right) ^{0}}\) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) candidates
Reconstruction started with pattern recognition, momentum fitting, and the formation of global track candidates. These track candidates generally span multiple TPCs and are generated by charged particles produced in the primary interaction and at secondary vertices.
The \(\Lambda \) \(\pi ^-\) (\({\overline{\Lambda }}\) \(\pi ^+\)) invariant mass spectrum of \(\Xi ^-\) (\({\overline{\Xi }}^+\)) candidates are shown in the left panel (right panel). Filled areas indicate the mass range of the selected candidates. The vertical dashed black line shows the nominal PDG \(\Xi \) mass
Particle identification was performed via measurement of the specific energy loss (\({\text {d}} E\!/\!{\text {d}} x\)) in the TPCs. The achieved \({\text {d}} E\!/\!{\text {d}} x\) resolution is 3–6% depending on the reconstructed track length [1, 4]. The dependence of the measured \({\text {d}} E\!/\!{\text {d}} x\) on velocity was fitted to a Bethe–Bloch type parametrization.
The \({\Xi \left( 1530\right) ^{0}}\) is produced in the primary interaction and decays strongly into \(\Xi ^-\) and \(\pi ^+\). Then the \(\Xi ^-\) travels for some distance, after which it decays into a \(\Lambda \) and a \(\pi ^-\). Subsequently, \(\Lambda \) decays into a proton and a \(\pi ^-\). A schematic drawing of the \({\Xi \left( 1530\right) ^{0}}\) decay chain is shown in Fig. 2.
The first step in the analysis was the search for \(\Lambda \) candidates, which were then combined with a \(\pi ^-\) to form the \(\Xi ^-\) candidates. Next, the \({\Xi \left( 1530\right) ^{0}} \) was searched for in the \(\Xi ^-\) \(\pi ^+\) invariant mass spectrum, where the \(\pi ^+\) originates from the primary vertex. An analogous procedure was followed for the antiparticles.
The \(\Lambda \) candidates are formed by pairing reconstructed and identified tracks with appropriate mass assignments and opposite charges. These particles are tracked backwards through the NA61/SHINE magnetic field from the first recorded point, which is required to lie in one of the VTPC detectors. This backtracking is performed in 2 cm steps in the z (beam) direction. Their separation in the transverse coordinates x and y is evaluated at each step, and a minimum is searched for. A pair is considered a \(\Lambda \) candidate if the minimum distance of the closest approach in the x and y directions is below 1 cm in both directions. Using the track parameters and the distances at the two neighbouring space points around the point of the closest approach, a more accurate \(\Lambda \) decay position is found by interpolation. This position, together with the momenta of the tracks at this point, is used as the input for a 9 parameter fit using the Levenberg–Marquardt fitting procedure [5].
\(\Xi ^-\) candidates were assembled by combining all \(\pi ^-\) with those \(\Lambda \) candidates having a reconstructed invariant mass within ±15 \(\text{ MeV }\) of the nominal [6] mass. A fitting procedure is applied using as parameters the decay position of the \(V^{0}\) candidate, the momenta of both the \(V^{0}\) decay tracks, and the momentum of the \(\Xi ^- \) daughter track. The z position of the \(\Xi ^- \) decay point is the intersection of the \(\Lambda \) and \(\pi ^-\) trajectories. The x and y coordinates of the \(\Xi \) decay position are not subject to the minimization, as they are determined from the fitted parameters using momentum conservation. This procedure yields the decay position and the momentum of the \(\Xi ^- \) candidate.
Imposed cuts increase the significance of the \(\Xi ^-\) signal. As the combinatorial background is largely due to particle production and decays close to the primary vertex, a distance of at least 12 cm was required between the primary and the \(\Xi ^-\) vertices. Furthermore, the distance of the closest approach between the extrapolated \(\pi ^-\) track from the \(\Xi ^-\) decay and the primary vertex was required to be larger than 0.2 cm in the non-bending plane. To remove spurious \(\Xi ^-\) candidates, their trajectory was required to have a distance of closest approach to the main vertex of less than 2 cm (1 cm) in the (non) bending plane. The resulting \(\Lambda \) \(\pi ^-\) invariant mass spectrum is shown in Fig. 3 (left), where the \(\Xi ^-\) peak is clearly visible. The \(\Xi ^-\) candidates were selected within ±15 \(\text{ MeV }\) of the nominal \(\Xi ^-\) mass. Only events (95%) with one \(\Xi ^-\) candidate were retained. Precisely the same procedure was applied for the antiparticles, and the resulting \({\overline{\Xi }}^+\) peak is shown in Fig. 3 (right).
To search for the \({\Xi \left( 1530\right) ^{0}}\) (\({\overline{\Xi }\left( 1530\right) ^{0}}\)), the selected \(\Xi ^-\) (\({\overline{\Xi }}^+\)) candidates were combined with primary \(\pi ^+\) (\(\pi ^-\)) tracks. To select pions originating from the primary vertex, their impact parameter \(|b_y |\) was required to be less than 0.5 cm, and their \({\text {d}} E\!/\!{\text {d}} x\) to be within 3\(\sigma \) of the nominal Bethe–Bloch value.
5 Signal extraction
For each \({\Xi \left( 1530\right) ^{0}} \) candidate, the invariant mass was calculated assuming the \(\Xi \) and pion masses for the reconstructed candidate daughter particles and then histogrammed in \({y}\),\(p_{\text {T}}\) bins. Examples of invariant mass distributions of \(\Xi ^-\) \(\pi ^+\), \({\overline{\Xi }}^+\) \(\pi ^-\) combinations are plotted in Fig. 4. The grey shaded histograms show the mixed-event background normalized to the number of real combinations, shown as red data points. The mixed background is determined by combining \(\Xi ^-\) (\({\overline{\Xi }}^+\)) candidates with 1000 \(\pi ^+\) (\(\pi ^-\)) candidates from different events. The mixed background distributions were calculated for each y-\(p_{\text {T}}\) bin separately. The signal is determined by subtracting this normalized mixed-event background (shaded histogram) from the experimental invariant mass spectrum. The background-subtracted signal was fitted to a Lorentzian function:
where mass \(m_\Xi \), width parameter \(\Gamma \) and normalization constant are the fit parameters. The raw multiplicity of \({\Xi \left( 1530\right) ^{0}}\) and \({\overline{\Xi }\left( 1530\right) ^{0}}\) is calculated as the sum of the signal bins in a mass window whose width is defined as 3\(\Gamma \) around the \({\Xi \left( 1530\right) ^{0}} \) mass of the fitted signal function [see Eq. (1)] to limit the propagation of statistical background fluctuations.
The fitted value of \(\Gamma \) is larger than the PDG width due to the finite resolution of the detector. The width is close to expectations given by the analysis of inelastic p+p interactions generated by Epos 1.99 with full detector simulation and standard track and \({\Xi \left( 1530\right) ^{0}} \) reconstruction procedures. The invariant mass distributions obtained experimentally and from simulations agree well, as shown for a selected \({y}\),\(p_{\text {T}}\) bin as examples in Fig. 5 for \({\Xi \left( 1530\right) ^{0}}\) and \({\overline{\Xi }\left( 1530\right) ^{0}}\), respectively. The fitted mass value of \({\Xi \left( 1530\right) ^{0}} \) equals \(1532.36 \pm 0.94\) \(\text{ MeV }\) and agrees within uncertainty with 1531.80 \(\pm 0.32\) \(\text{ MeV }\) provided by PDG [6]. More detailed verification of the stability of the fitted mass \(m_\Xi \) was performed in the rapidity range \(-0.25< y <0.25\), as shown in Fig. 6 where the masses are shown as a function of \(p_{\text {T}}\). The fit results on \({\Xi \left( 1530\right) ^{0}} \) for both the real data and simulation are seen to agree with the PDG values.
Background-subtracted invariant mass distribution of \({\Xi \left( 1530\right) ^{0}}\) (left panel) and \({\overline{\Xi }\left( 1530\right) ^{0}}\) (right panel) in the rapidity range \(-0.25< y <0.25\) and transverse momentum range \(0.30~\text{ GeV }\!/\!c< p_{\text {T}} < 0.60~\text{ GeV }\!/\!c \) from data (red points), and from Epos 1.99 with full detector simulation and standard track and reconstruction procedures (gray histogram)
Mass of \({\Xi \left( 1530\right) ^{0}}\) (left panel) and \({\overline{\Xi }\left( 1530\right) ^{0}}\) (right panel) fitted at mid-rapidity \(-0.25< y <0.25\) as function of \(p_{\text {T}}\) for data (red points) and simulations (blue points). The red horizontal band presents the uncertainty of the fitted mass of \({\Xi \left( 1530\right) ^{0}}\) and \({\overline{\Xi }\left( 1530\right) ^{0}}\) using the events of the full data set (combining all y, \(p_{\text {T}}\) bins) and the grey bands the PDG values [6]
6 Corrections factors for yield determination
A set of corrections was applied to the extracted raw results to determine the actual hyperons produced in inelastic p+p interactions.
Interactions may contaminate the triggered and accepted events with the target vessel and other material in the target’s vicinity. About 10% of the data were collected without the liquid hydrogen in the target vessel to estimate the fraction of those events. After applying the event selection criteria described in Sect. 3 and scaling to the same number of incoming beams, only 1% of \({\Xi \left( 1530\right) ^{0}}\) were found compared to the full target event sample. The correction was not applied for this contamination.
A detailed Monte-Carlo simulation is performed to quantify the losses due to acceptance limitations, detector inefficiencies, reconstruction shortcomings, analysis cuts, and re-interactions in the target. This simulation used complete events produced by the Epos 1.99 [7] event generator using a hydrogen target of appropriate length. The generated particles in each Monte-Carlo event are tracked through the detector using a GEANT3 [8] simulation of the NA61/SHINE apparatus. They are then reconstructed with the same software as used for real events. Numerous observables were confirmed to be similar to those of the data, such as residual distributions, widths of mass peaks, track multiplicities and their differential distributions, the number of events with no tracks in the detector, the cut variables and others.
A correction factor is computed for each (\({y} \), \(p_{\text {T}}\)) bin:
where \(n_{rec}^{MC}\) is the number of reconstructed, selected, and identified \({\Xi \left( 1530\right) ^{0}} \)s normalized to the number of analyzed events, and \(n_{generated}^{MC}\) is the number of \({\Xi \left( 1530\right) ^{0}} \) generated by Epos 1.99 normalized to the number of generated inelastic interactions. The raw multiplicity of \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) are multiplied by \(C_{F}\) to determine the true \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) yields. These correction factors also include the branching fraction (66.7%) of the \({\Xi \left( 1530\right) ^{0}}\) and \({\overline{\Xi }\left( 1530\right) ^{0}}\) decays into charged particles as well as the decay branching fraction of the \(\Lambda \).
Transverse momentum spectra of \({\Xi \left( 1530\right) ^{0}} \) (left) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) (right) in rapidity slices produced in inelastic p+p interactions at 158 \(\text{ GeV }\!/\!c\). Rapidity values given in the legends correspond to the middle of the corresponding interval. Statistical uncertainties are shown as vertical bars, and shaded bands show systematic uncertainties. Spectra are scaled for better visibility. Lines represent the fitted function [Eq. (3)]
7 Statistical and systematic uncertainties
Statistical uncertainties of the yields receive contributions from the finite statistics of both the data and the correction factors derived from the simulations. The contribution from the statistical uncertainty of the data is much larger than that from the correction factors \(C_{F}\). The statistical uncertainty of the ratio in Eq. (2) was calculated assuming that the denominator \(n_{rec}^{MC}\) is a subset of the nominator \(n_{generated}^{MC}\) and thus has a binomial distribution.
Possible systematic uncertainties of final results (spectra and mean multiplicities) are due to the Monte Carlo procedure’s imperfectness, e.g. the physics models and the detector response simulation - used to calculate the correction factors.
Several tests were performed to determine the magnitude of the different sources of possible systematic uncertainties:
-
(i)
Methods of event selection.
Not all events which have tracks stemming from interactions of off-time beam particles are removed. A possible uncertainty due to this effect was estimated by changing by \(\pm 1~\upmu s\) the width of the time window in which no second beam particle is allowed with respect to the nominal value of \(\pm 2~\upmu \)s. The maximum difference of the results was taken as an estimate of the uncertainty due to the selection. It was estimated to be 1–6%.
Another source of a possible bias are losses of inelastic events due to the interaction trigger. The S4 trigger selects mainly inelastic interactions and vetoes elastic scattering events. However, it will miss some of the inelastic events. To estimate the possible loss of \(\Xi \)s, simulations were done with and without the S4 trigger condition. The difference between these two results was taken as another contribution to the systematic uncertainty. The uncertainty due to the interaction trigger was calculated as half of the difference between these two results, which is 4–6%.
The next source of systematic uncertainty related to the normalization came from the selection window for the z-position of the fitted vertex. To estimate the contribution of this systematic uncertainty, the selection criteria for the data and the Epos 1.99 model were varied from \(\pm 9\) to \(\pm 10\), and \(\pm 11\) \(\text{ cm }\). The uncertainty due to the selection window for the z-position of the fitted vertex was estimated to be smaller than 2%.
-
(ii)
Methods of \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) candidates selection. To estimate the uncertainty related to the \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) candidate selection, the following cut parameters were varied independently:
-
the distance cut between primary and decay vertex of \(\Xi ^-\) (\({\overline{\Xi }}^+\)) was changed by \(\pm 1\) and \(\pm 2\) \(\text{ cm }\) yielding a possible bias of 1–6%,
-
the extrapolated impact parameter of \(\Xi \)s in the y direction at the main vertex z position was changed from 0.2 to 0.1 \(\text{ cm }\) and 0.4 \(\text{ cm }\), yielding a possible bias of up to 10%,
-
the DCA of the pion (\(\Xi \)) daughter track to the main vertex was changed from 0.5 to 0.25 cm and 1 cm, yielding a possible bias of up to 9%.
-
-
(iii)
Signal extraction.
The uncertainty due to the signal extraction method was estimated by varying the invariant mass range used to determine the \({\Xi \left( 1530\right) ^{0}} \) yields by a change of ±7 \(\text{ MeV }\) with respect to the nominal integration range and yielded a possible uncertainty up to 7%.
The systematic uncertainty was calculated as the square root of the sum of squares of the described possible biases, assuming uncorrelated. The uncertainties are estimated for each (\({y} \), \(p_{\text {T}}\)) bin separately.
8 Experimental results
This section presents results on inclusive \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) production by strong interaction processes in inelastic p+p interactions at beam momentum of 158 \(\text{ GeV }\!/\!c\).
8.1 Spectra and mean multiplicities
Double differential yields constitute the primary result of this paper. The \({\Xi \left( 1530\right) ^{0}} \) (\({\overline{\Xi }\left( 1530\right) ^{0}} \)) yields are determined in 4 (4) rapidity and between 5 (3) and 6 (5) transverse momentum bins. The former is 0.5 units and the latter 0.3 \(\text{ GeV }\!/\!c\) wide. The resulting (\({y} \), \(p_{\text {T}}\)) yields are presented at the function of \(p_{\text {T}}\) in Fig. 7. The following exponential function can describe the transverse momentum spectra [9, 10]:
where m is the \({\Xi \left( 1530\right) ^{0}} \) mass, \(m_{T}\) is the transverse mass defined as \(m_{T} = \sqrt{m^2 + (cp_{T})^2}\) and c is the speed of light. The yields S and the inverse slope parameters T are determined by fitting the function to the data points in each rapidity bin. The \(p_{\text {T}}\) spectra from successive rapidity intervals in Fig. 7 are scaled for better visibility. Statistical uncertainties are shown as error bars, and shaded bands correspond to systematic uncertainties. Tables 1 and 2 list the numerical values of the results shown in Fig. 7. The resulting inverse slope parameters are listed in Table 3.
The yields as function of rapidity were then obtained by summing the measured transverse momentum spectra and extrapolating them into the unmeasured regions using the fitted functions given by Eq. (3). The resulting rapidity distributions are shown in Fig. 8. The statistical uncertainties are shown as error bars. They were calculated as the square root of the sum of the squares of the statistical uncertainties of the contributing bins. The systematic uncertainties (shaded bands) were calculated as the square root of squares of systematic uncertainty as described in Sect. 7 and half of the extrapolated yield. The numerical values of the rapidity distribution dN/dy and their errors are listed in Table 3.
A correction factor based on the Epos model is calculated and used to extrapolate into the unmeasured regions. The correction factor is defined as the ratio of the \({\Xi \left( 1530\right) ^{0}}\) (\({\overline{\Xi }\left( 1530\right) ^{0}}\)) multiplicity from the Epos model in the measurement region to the total Epos \({\Xi \left( 1530\right) ^{0}}\) (\({\overline{\Xi }\left( 1530\right) ^{0}}\)) multiplicity and equals 1.52 (1.27). Summing the data points and multiplying by the obtained correction factor allows to obtain the mean multiplicities \({\Xi \left( 1530\right) ^{0}} =\) (\(6.73 \pm 0.25\) ± 0.67)\(\times 10^{-4}\) and \({\overline{\Xi }\left( 1530\right) ^{0}} = \) (\(2.71 \pm 0.18\) ± 0.18)\(\times 10^{-4}\). In addition a systematic error of 50% of the extrapolated yield was included.
The rapidity densities (\(dn/d{y} \)) at mid-rapidity of \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) produced in inelastic p+p interactions at \(\sqrt{s_{NN}}=17.3\) \(\text{ GeV }\) collisions can be compared with results from ALICE at CERN LHC measured at \(\sqrt{s_{NN}}\) = 7 \(\text{ TeV }\) [2]. The ratios of \(\Xi (1530)\) to \(\Xi \) [11, 12] at mid-rapidity in p+p interactions at 17.3 \(\text{ GeV }\) and 7 \(\text{ TeV }\) are shown in Table 4. The ratio of \(\Xi (1530)\) to \(\Xi \) at these two energies are similar: \(0.294 \pm 0.017\) ± 0.047 at 17.3 \(\text{ GeV }\) and \(0.3241 \pm 0.0053\) \(^{+0.0325}_{0.0275}\) at 7 \(\text{ TeV }\), while the yields of \({\Xi \left( 1530\right) ^{0}}\) increase with collision energy by an order of magnitude from (2.75\(\pm 0.18\pm \)0.58)\(\times 10^{-4}\) at 17.3 \(\text{ GeV }\) to (2.56\(\pm 0.07^{+0.40}_{-0.37}\))\(\times 10^{-3}\) at 7 \(\text{ TeV }\).
Rapidity spectra of \({\Xi \left( 1530\right) ^{0}} \) (blue squares) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) (red circles) produced in inelastic p+p interactions at 158 \(\text{ GeV }\!/\!c\). Statistical uncertainties are shown by vertical bars, and shaded bands correspond to systematic uncertainties of the measurements. Full symbols show measured points, open symbols values reflected around mid-rapidity
8.2 Anti-baryon/baryon ratios
The NA61/SHINE measurement of \({\Xi \left( 1530\right) ^{0}} \) hyperon production allows to determine anti–baryon/baryon ratios at central rapidity and ratios of total mean multiplicities in p+p collisions. The systematic uncertainties of \({\Xi \left( 1530\right) ^{0}}\) and \({\overline{\Xi }\left( 1530\right) ^{0}}\) are correlated. Therefore the systematic uncertainty of \({\overline{\Xi }\left( 1530\right) ^{0}}/{\Xi \left( 1530\right) ^{0}} \) had to be determined separately (following the procedure described in Sect. 7). The \({\overline{\Xi }\left( 1530\right) ^{0}}/{\Xi \left( 1530\right) ^{0}} \) ratios as a function of rapidity and transverse momentum are listed in Table 5. The ratio of the rapidity spectra are listed in Table 6 and drawn in Fig. 10c. The small value of the ratio of mean multiplicities \(\left\langle {\overline{\Xi }\left( 1530\right) ^{0}} \right\rangle / \left\langle {\Xi \left( 1530\right) ^{0}} \right\rangle = \) \(0.40 \pm 0.03\) ± 0.05 emphasizes the strong suppression of \({\overline{\Xi }\left( 1530\right) ^{0}} \) production at CERN SPS energies. This effect disappears, as expected, at the much higher LHC energies [2].
9 Comparison with models
The new NA61/SHINE measurements of \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) production are essential for understanding multi-strange particle production in elementary hadron interactions.
Measurements of multi-strange hyperon production at intermediate energies possibly provide new insight into string formation and decay. In the string picture, p+p collisions create string “excitations”, which are hypothetical objects that decay into hadrons according to longitudinal phase space. Multi-strange baryons and their anti-particles play a special role in this context. Their pairwise production in string decays will increase the anti-strange-baryon to the strange-baryon ratio significantly compared to the anti-baryon to baryon ratio. Indications of this expectation are observed in the \(\Xi \) and \({\overline{\Xi }}\) yields obtained from the Urqmd model shown below.
The experimental results of NA61/SHINE are compared with predictions of the Epos 1.99 [13] and Urqmd 3.4 [14, 15] models. In Epos, the reaction proceeds from the excitation of strings according to Gribov–Regge theory to string fragmentation into hadrons. Urqmd starts with a hadron cascade based on elementary cross sections for the production of states, which either decay (mostly at low energies) or are converted into strings that fragment into hadrons (mostly at high energies). These are the only models that provide the history of the produced particle needed to extract the \({\Xi \left( 1530\right) ^{0}}\) and \({\overline{\Xi }\left( 1530\right) ^{0}}\) yields. The model predictions are compared with the NA61/SHINE measurements in Figs. 9 and 10. Epos 1.99 describes well the \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) transverse momentum and rapidity spectra. The comparison of the Urqmd 3.4 calculations with the NA61/SHINE measurements reveals significant discrepancies for the \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) hyperons. The model strongly overestimates \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) yields. The ratio of \({\overline{\Xi }\left( 1530\right) ^{0}} \) to \({\Xi \left( 1530\right) ^{0}} \) cannot be described by the Urqmd model but is well reproduced by Epos 1.99 (see Figs. 9 and 10).
Transverse momentum spectra at mid-rapidity of \({\Xi \left( 1530\right) ^{0}} \) (left) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) (right) produced in inelastic p+p interactions at 158 \(\text{ GeV }\!/\!c\). Shaded bands show systematic uncertainties. Urqmd 3.4 [14, 15] and Epos 1.99 [13] predictions are shown as magenta and blue markers, respectively
Rapidity spectra of \({\Xi \left( 1530\right) ^{0}} \) (left), \({\overline{\Xi }\left( 1530\right) ^{0}} \) (middle) and \({\overline{\Xi }\left( 1530\right) ^{0}}/{\Xi \left( 1530\right) ^{0}} \) ratio (right) measured in inelastic p+p interactions at 158 \(\text{ GeV }\!/\!c\). Shaded bands show systematic uncertainties. Urqmd 3.4 [14, 15] and Epos 1.99 [13] predictions are shown as magenta and blue points, respectively
Mean multiplicities of \(\pi ^+\), \(\pi ^-\), \(K^+\), \(K^-\), p, \({\overline{p}}\), \(K^*(892)^0\), \(\Lambda \), \(\phi (1020)\), \(\Xi ^-\), \({\overline{\Xi }}^+ \), \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}}\) produced in p+p interactions at 158 \(\text{ GeV }\!/\!c\) [3, 4, 12, 17,18,19,20] measured by NA61/SHINE are compared with mean multiplicities obtained from the HRG model based on the Canonical Ensemble with fixed \(\gamma _s = 1\) (i) and fitted \(\gamma _s\) (ii). Uncertainties of the measurements are smaller than the size of the markers
The statistical model of particle production in various versions has been in use for many years to fit experimental results on particle production in p+p as well as N+N interactions (see, e.g. Ref. [16]). The new measurements by NA61/SHINE of \({\Xi \left( 1530\right) ^{0}}\) and \({\overline{\Xi }\left( 1530\right) ^{0}}\) produced in inelastic p+p interactions at 158 \(\text{ GeV }\!/\!c\) as well as previously obtained results for \(\pi ^+\), \(\pi ^-\), \(K^+\), \(K^-\), p, \({\overline{p}}\), \(K^*(892)^0\), \(\Lambda \), \(\phi (1020)\), \(\Xi ^-\) and \({\overline{\Xi }}^+ \) (see Refs. [3, 4, 12, 17,18,19,20]) were compared to two versions of the Hadron Resonance Gas Model (HRG) using the software package THERMAL-FIST 1.3 of Ref. [21]. For the small p+p system, the appropriate approach is to use the Canonical Ensemble. The following HRG versions were considered:
-
(i)
Canonical Ensemble with fixed strangeness saturation factor, \(\gamma _{s} = 1\). The fit parameters are the freeze-out temperature of the particle composition T and the fireball radius at freeze-out R
-
(ii)
Canonical Ensemble with the free \(\gamma _{s}\) parameter. The fit parameters are \(\gamma _{s}\) and R.
Figure 11 compares the measured multiplicities of particles produced in inelastic p+p interactions at 158 \(\text{ GeV }\!/\!c\) with predictions of the two versions of HRG model.
The version with \(\gamma _s\) fixed to one shows unacceptably large \(\chi ^2\)/NDF = 29. The version with free \(\gamma _s\) yields the best fit for \(\gamma _s = 0.434 \pm 0.028\). The description of the data improves, but the \(\chi ^2\)/NDF = 11 is still large.
10 Summary
Measurements by NA61/SHINE of double-differential spectra and mean multiplicities of \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) resonances produced in inelastic p+p interactions were presented. The results were obtained from a sample of 26\(\cdot 10^6\) minimum-bias events at the CERN SPS using a proton beam of 158 \(\text{ GeV }\!/\!c\) momentum (\(\sqrt{s_{NN}}\) = 17.3 \(\text{ GeV }\)). The measured rapidity and transverse momentum distributions were extrapolated to full phase space, and mean multiplicities of \({\Xi \left( 1530\right) ^{0}} \) (\(6.73 \pm 0.25\) ± 0.67)\(\times 10^{-4}\) and of \( {\overline{\Xi }\left( 1530\right) ^{0}} \) (\(2.71 \pm 0.18\) ± 0.18)\(\times 10^{-4}\) were obtained. The \({\overline{\Xi }\left( 1530\right) ^{0}} \)/\({\Xi \left( 1530\right) ^{0}} \) ratio at mid-rapidity was found to be \(0.54 \pm 0.07\) ± 0.08.
The NA61/SHINE results were compared with predictions of two hadronic models Urqmd and Epos. Epos describes well the experimental results. However, Urqmd overestimates the yields by a factor of 2.5. Results were also compared with predictions of the hadron-resonance gas model in the canonical formulation. The equilibrium version of the model is in strong disagreement with the data. This disagreement is slightly reduced by allowing for out-of-equilibrium strangeness production.
Data Availability Statement
This manuscript has associated data in a data repository. [Authors’ comment: Data will be uploaded to the Hepdata repository.]
References
N. Abgrall et al. (NA61/SHINE Collab.), JINST 9, P06005 (2014). https://doi.org/10.1088/1748-0221/9/06/P06005. arXiv:1401.4699 [physics.ins-det]
B.B. Abelev et al. (ALICE Collab.), Eur. Phys. J. C 75(1), 1 (2015). https://doi.org/10.1140/epjc/s10052-014-3191-x. arXiv:1406.3206 [nucl-ex]
N. Abgrall et al. (NA61/SHINE Collab.), Eur. Phys. J. C 74, 2794 (2014). https://doi.org/10.1140/epjc/s10052-014-2794-6. arXiv:1310.2417 [hep-ex]
A. Aduszkiewicz et al. (NA61/SHINE Collab.), Eur. Phys. J. C 77(10), 671 (2017). https://doi.org/10.1140/epjc/s10052-017-5260-4. arXiv:1705.02467 [nucl-ex]
W. Press, S. Teukolsky, W. Vetterling, B. Flannery, Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd edn. (Cambridge University Press, Cambridge, 1992)
P.A. Zyla et al. (Particle Data Group Collab.), PTEP 2020(8), 083C01 (2020). https://doi.org/10.1093/ptep/ptaa104
T. Pierog, K. Werner Nucl, Phys. Proc. Suppl. 196, 102–105 (2009). https://doi.org/10.1016/j.nuclphysbps.2009.09.017. arXiv:0905.1198 [hep-ph]
R. Brun, F. Bruyant, M. Maire, A.C McPherson, P. Zanarini. GEANT 3: user’s guide Geant 3.10, Geant 3.11; rev. version (CERN, Geneva, 1987). https://cds.cern.ch/record/1119728
R. Hagedorn, Nuovo Cim. Suppl. 6, 311–354 (1968)
W. Broniowski, W. Florkowski, L.Y. Glozman, Phys. Rev. D 70, 117503 (2004). https://doi.org/10.1103/PhysRevD.70.117503. arXiv:hep-ph/0407290
B. Abelev et al. (ALICE Collab.), Phys. Lett. B 712, 309–318 (2012). https://doi.org/10.1016/j.physletb.2012.05.011. arXiv:1204.0282 [nucl-ex]
A. Aduszkiewicz et al. (NA61/SHINE Collab.), Eur. Phys. J. C 80(9), 833 (2020). https://doi.org/10.1140/epjc/s10052-020-8381-0. arXiv:2006.02062 [nucl-ex]
K. Werner, Nucl. Phys. Proc. Suppl. 175–176, 81–87 (2008). https://doi.org/10.1016/j.nuclphysbps.2007.10.012
S. Bass et al., Prog. Part. Nucl. Phys. 41, 255–369 (1998). https://doi.org/10.1016/S0146-6410(98)00058-1. arXiv:nucl-th/9803035
M. Bleicher et al., J. Phys. G 25, 1859–1896 (1999). https://doi.org/10.1088/0954-3899/25/9/308. arXiv:hep-ph/9909407
F. Becattini, J. Manninen, M. Gazdzicki, Phys. Rev. C 73, 044905 (2006). https://doi.org/10.1103/PhysRevC.73.044905. arXiv:hep-ph/0511092
A. Aduszkiewicz et al. (NA61/SHINE Collab.), Phys. Rev. C 102(1), 011901 (2020). https://doi.org/10.1103/PhysRevC.102.011901. arXiv:1912.10871 [hep-ex]. https://www.hepdata.net/record/ins1772241
A. Aduszkiewicz et al. (NA61/SHINE Collab.), Eur. Phys. J. C 80(5), 460 (2020). https://doi.org/10.1140/epjc/s10052-020-7955-1. arXiv:2001.05370 [nucl-ex]. https://www.hepdata.net/record/ins1775731
A. Aduszkiewicz et al. (NA61/SHINE Collab.), Eur. Phys. J. C 80(3), 199 (2020). https://doi.org/10.1140/epjc/s10052-020-7675-6. arXiv:1908.04601 [nucl-ex]. https://www.hepdata.net/record/ins1749613
A. Aduszkiewicz et al. (NA61/SHINE Collab.), Eur. Phys. J. C 76(4), 198 (2016). https://doi.org/10.1140/epjc/s10052-016-4003-2. arXiv:1510.03720 [hep-ex]
V. Vovchenko, H. Stoecker, Comput. Phys. Commun. 244, 295–310 (2019). https://doi.org/10.1016/j.cpc.2019.06.024. arXiv:1901.05249 [nucl-th]
Acknowledgements
We would like to thank the CERN EP, BE, HSE and EN Departments for the strong support of NA61/SHINE. This work was supported by the Hungarian Scientific Research Fund (grant NKFIH 123842/123959), the Polish Ministry of Science and Higher Education (grants 667/N-CERN/2010/0, NN 202 48 4339 and NN 202 23 1837), the National Science Centre Poland(grants 2014/ 490 14/E/ST2/00018, 2014/15/B/ST2 / 02537 and 2015/18/M/ST2/00125, 491 2015/19/N/ST2 /01689, 2016/23/B/ST2/00692, DIR/WK/ 2016/2017/ 492 10-1, 2017/ 25/N/ ST2/ 02575, 2018/30/A/ST2/00226, 2018/31/G/ 493 ST2/03910, 2019/34/H/ST2/00585), WUT ID/UB, the Russian Science Foundation, grant 16-12-10176 and 17-72-20045, the Russian Academy of Science and the Russian Foundation for Basic Research (grants 08-02-00018, 09-02-00664 and 12-02-91503-CERN), the Russian Foundation for Basic Research (RFBR) funding within the research project no. 18-02-40086, the National Research Nuclear University MEPhI in the framework of the Russian Academic Excellence Project (contract No. 02.a03.21.0005, 27.08.2013), the Ministry of Science and Higher Education of the Russian Federation, Project “Fundamental properties of elementary particles and cosmology” No 0723-2020-0041, the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 871072, the Ministry of Education, Culture, Sports, Science and Technology, Japan, Grant-in-Aid for Scientific Research (grants 18071005, 19034011, 19740162, 20740160 and 20039012), the German Research Foundation DFG (grants GA 1480/8-1 and project 426579465), the Bulgarian Nuclear Regulatory Agency and the Joint Institute for Nuclear Research, Dubna (bilateral contract No. 4799-1-18/20), Bulgarian National Science Fund (grant DN08/11), Ministry of Education and Science of the Republic of Serbia (grant OI171002), Swiss Nationalfonds Foundation (grant 200020117913/1), ETH Research Grant TH-01 07-3 and the Fermi National Accelerator Laboratory (Fermilab), a U.S. Department of Energy, Office of Science, HEP User Facility managed by Fermi Research Alliance, LLC (FRA), acting under Contract No. DE-AC02-07CH11359 and the IN2P3-CNRS (France).
Author information
Authors and Affiliations
Consortia
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Acharya, A., Adhikary, H., Allison, K.K. et al. Measurements of \({\Xi \left( 1530\right) ^{0}} \) and \({\overline{\Xi }\left( 1530\right) ^{0}} \) production in proton–proton interactions at \(\sqrt{s_{NN}}\) = 17.3 \(\text{ GeV }\) in the NA61/SHINE experiment. Eur. Phys. J. C 81, 911 (2021). https://doi.org/10.1140/epjc/s10052-021-09631-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09631-6