1 Introduction

The recent astrophysical observations indicate the accelerated rate of universe expansion but general relativity (GR) is unable to explain it properly. The existence of an unknown form of matter is suggested by gravitational lensing in the universe named dark matter (DM) while the accelerated expansion is caused due to the existence of dark energy (DE). Einstein’s theory is also unable to illustrate the flat rotation curves of galaxies as well as the expansion rate of the universe without invoking DM and DE, which together account for \(96\%\) of the universe’s total energy content. Modified gravity theories have been discovered to be one of the most appealing mathematical methods for exploring the universe’s rapid expansion. These theories were recently reviewed in the literature to explain various dynamical phases of the universe evolution, particularly the early and late time acceleration eras determined from recent observations. By changing the gravitational part of the standard Einstein–Hilbert action, various dark energy theoretical models are proposed. The f(R) theory is the most fascinating because it offers a viable alternative to DE without taking into consideration DM. The inclusion of the generic function f(R) in the standard Einstein–Hilbert action is the simplest modification of GR knows as f(R) gravity and applying variational principle to the modified Einstein–Hilbert action gives rise to different formalisms of f(R) gravity. The formalism in which we consider the metric and connection as an independent quantity is known as Palatini formalism while the other is known as metric formalism. The Palatini formalism produces a second-order nonlinear differential equation but in the case of metric formalism, we have fourth-order field equations. Some suitable forms of the f(R) model have been developed to describe the accelerated expansion by SnIa data at late times. The Palatini version of f(R) theory generates second-order field equations and present a simple gravitational alternative in the absence of any matter content. Furthermore, the significant advantages of this version are, it provides correct Newtonian limit, it is free of instabilities. Also, the Palatini f(R) vacuum solutions are comparable with GR solutions with a cosmological constant. It is observed that by applying Palatini formalism to the f(R) theories, we can create models with the radiation-dominated, and late-time acceleration phases that are compatible with the recent observations.

The modification of standard Einstein–Hilbert action in order to study the f(R) gravity is manifested as [2]

$$\begin{aligned} S_{f(R)}=S_{m}+\frac{1}{2\kappa } \int d^{4}x \sqrt{-g} f(R), \end{aligned}$$
(1)

here \(S_{M} \) and \( \kappa \) are the matter action and coupling constant and f(R) denotes the non-linear Ricci scalar function, while g represents the determinant of \( g_{\alpha \zeta }\). The contraction of Ricci tensor \( R_{\alpha \zeta } \) associated with connection symbols is used to construct R in the modified action, meaning that R is the product of geometrical connections. One can get the following equations of motion by applying the variation on the action integral given in (1) with respect to connection symbols \( \Gamma ^{\mu }_{\alpha \zeta } \) and metric tensor \( g_{\alpha \zeta } \) as

$$\begin{aligned} F(R)R_{\alpha \zeta }-\frac{1}{2}g_{\alpha \zeta }f(R)&=\kappa T_{\alpha \zeta }, \end{aligned}$$
(2)
$$\begin{aligned} \nabla _{\mu }(g^{\alpha \zeta }\sqrt{-g}F(R))&=0, \end{aligned}$$
(3)

where \( T_{\alpha \zeta } \) represents the standard energy momentum tensor that is independent of connection symbols and \( F(R)=\frac{df(R)}{dR}\). The equation that compares R (Ricci scalar) with T (Trace of the energy momentum tensor) is obtained by multiplying (2) with conjugate metric tensor \( g^{\alpha \zeta } \) as

$$\begin{aligned} RF(R)=\kappa T+2f(R), \end{aligned}$$
(4)

tells us that the energy-momentum tensor is dependent on R. For second-order field equations, a standard expression can be obtained by solving (2) and then utilizing the obtained value in (3) of the following form

$$\begin{aligned}&R_{\alpha \zeta }-\frac{1}{2}g_{\alpha \zeta }R=\frac{\kappa }{F}T_{\alpha \zeta }+\frac{1}{2}g_{\alpha \zeta }\left( \frac{f}{F}-R\right) +\frac{1}{F} (\nabla _{\alpha }\nabla _{\zeta }-g_{\alpha \zeta }\Box )F\nonumber \\&\qquad +\frac{3}{2F^2}\left[ \frac{1}{2}g_{\alpha \zeta }(\nabla F)^{2}-\nabla _{\alpha }F \nabla _{\zeta }F\right] . \end{aligned}$$
(5)

The f(R) field equations can be expressed in alternate form as

$$\begin{aligned} G_{\alpha \zeta }=\frac{\kappa }{F} \left( T_{\alpha \zeta }+T^{(D)}_{\alpha \zeta }\right) , \end{aligned}$$
(6)

where \( G_{\alpha \zeta }\equiv R_{\alpha \zeta }-\frac{1}{2} g_{\alpha \zeta } R \) and \( \Box \) is the d Alembert operator and can be defined as \( \Box \equiv g^{\alpha \zeta }\nabla _{\alpha } \nabla _{\zeta } \) whereas \(\nabla _{\zeta }\) indicates the covariant derivative. Moreover

$$\begin{aligned} T^{(D)}_{\alpha \zeta }&=\frac{1}{\kappa } \left[ \nabla _{\alpha }\nabla _{\zeta } F-g_{\alpha \zeta } \Box F-\frac{F}{2} g_{\alpha \zeta } R+\frac{f g_{\alpha \zeta }}{2}\right. \nonumber \\&\quad \left. +\frac{3}{2F}\left( \frac{1}{2} g_{\alpha \zeta }(\nabla F)^2-\nabla _{\alpha }F\nabla _{\zeta }F\right) \right] , \end{aligned}$$
(7)

is the Palatini f(R) energy–momentum tensor that describes a gravitational contribution.

Bhatti et al. [3] examined the stability of charged neutron stars in the presence of modified gravity and constructed the generalized Tolman–Oppenheimer–Volkoff (TOV) equations. They deduced that if uniform entropy and chemical composition are taken under consideration then generalized TOV equations represent stable star configurations that are independent of the generic feature of modified gravity. With the Palatini approach of f(R) gravitation, Kainulainen and co-workers [2] determined the mass equation for the interior geometry and structure of stars. They demonstrated that in general, combining the interior and exterior geometry yield a connection between the density profile of star and gravitational mass that differs from the one found in general relativity. Bamba et al. [4] investigated the thermodynamics of the apparent horizon using equilibrium and non-equilibrium constraints in f(R) gravity. They concluded that understanding the horizon entropy in the equilibrium system is more straightforward than in the non-equilibrium one. They also exhibited that the second law of thermodynamics could be verified from both phantom and non-phantom stages as long as the temperature of the universe outside and inside the apparent horizon stays unchanged. Sharif and Yousaf [5] examined the stability of spherical collapse using the Palatini approach of f(R) gravity. They used Bianchi’s identities of energy-momentum tensor to construct the collapse equation and investigated the instability ranges in the Newtonian and post-Newtonian patterns. They deduced that adiabatic index \( \Gamma _{1} \) managed the stability of the star.

Bhatti and Yousaf [6] determined the inhomogeneity factors using the dissipative fluid under the influence of electromagnetic field in Palatini f(R) gravity for plane topology. To examine the corresponding inhomogeneity causes, some specific cases are examined with and without dissipation. They investigated anisotropic, dust, and isotropic matter in the presence of charge in a non-radiating scenario. They examined the inhomogeneity factor for a dissipative fluid in the presence of a dust cloud. They inferred that the electromagnetic field raises the matter inhomogeneity, while the additional curvature terms make the system more homogeneous as time passes. Yousaf et al. [7] studied the consequences of charged gravastar models in f(R, T) gravity using metric formalism. They used the equation of state to investigate the exact models and stable regions of gravastar under the influence of electromagnetic field and taking into account the Reissner–Nordström spacetime to match the exterior geometry with the interior at the hypersurface. They also examined the realistic character of charged gravastar model using a graphical representation. Bhatti et al. [8] examined the impact of density inhomogeneity and local anisotropy on the gravitational collapse in f(R) gravity under the influence of charge. They explored modified Maxwell field equations and established a connection between Weyl tensor and local anisotropy. They acquired an expression for Tolman mass which plays a significant role to study the impact of charge and extra curvature terms on the physical variables, as well as the study of their role in gravitational collapse.

Bhatti and Tariq [9] studied the dynamics of an anisotropic sphere in the presence of charge within the context of f(R) gravity. They used the general pattern provided by Herrera and Barreto to examine the primitive properties of polytropic spheres and constructed physical restrictions for polytropes. They tested the consistency of polytropes through Tolman mass by using conformally flat conditions. They inferred that the electromagnetic field plays the same function as anisotropic pressure. Tremblay and Faraoni [10] investigated the initial value problem of f(R) gravity using the dynamical correspondence with Brans–Dicke gravity for metric and Palatini formalisms. They concluded that the Cauchy problem is well-defined for metric formalism as compared to Palatini formalism under the influence of matter. Sharif and Siddiqa [11] studied the self-gravitating source under the influence of charge in f(R, T) gravity explaining the situation of expansion and collapse process. They calculated the expansion scalar to examine the process of collapse and expansion and discussed the impact of charge and model parameters on physical variables with the help of graphical representations. They noticed that physical variables changes with time in case of expansion while the charge effects during the collapse process and the model parameters have the same effects in both cases. Garfinkle [12] examined that for type Ia supernova data inhomogeneous spacetimes are used as a cosmological model. They inferred that the model is found to match the data as well as the regular CDM cosmology with certain choices.

Herrera et al. [13] investigated the physical significance of structure scalars for dissipative and dust fluids under the influence of charge. They highlighted the importance of these factors in the scalar functions and addressed their physical outcome. They inferred that the evolution of kinematical variables and modifications in the inhomogeneity factor provided by the above-described factors requires special attention. Sharif and Yousaf [14] examined the dynamical features of cylindrical self-gravitating structures by considering the f(R) model undergoing the process of dissipative collapse and observed the consequences of higher-order curvature terms appeared in the scalar functions. They used the transport equation to study the impact of relaxation time on the evolution of collapsing structure and developed eight modified scalar functions, three Weyl, and two shear scalars that are needed to address the dynamics of cylindrically symmetric spacetime, in contrast to spherical systems. Sharif and Bhatti [15] developed the structure scalars for planer symmetry in the presence of charge and associated them with the fluid variables. They established a connection between Weyl scalar and kinematical quantities with the help of Taub mass formalism and discussed the consequences of the charge on the evolution of matter variables. Yousaf [16] investigated how f(G, T) terms affect the formation of scalar functions as well as evolution equations. They dealt with a geometry linked with viscous dissipative matter content and established the relationship between Misner–Sharp mass and curvature scalar. They also developed the relation for f(G, T) scalar functions by decomposing the Riemann tensor and investigating their consequences.

LTB models are the most ancient and fascinating Einstein equation solutions. They define a spherically symmetric distribution of non-dissipative dust that is inhomogeneous and have been used in the study of quantum gravity and gravitational collapse as a cosmological model. LTB spacetimes have the drawback that they do not allow dissipative fluxes. Yousaf et al. [17] examined the evolution of LTB spacetime under the influence of charge in Palatini f(R) gravity. They established the relationship between comoving and tilted observers by considering the effects of charge for dust and imperfect fluid respectively and also studied the f(R) models in LTB geometry in the presence of dissipative fluid. They inferred that dynamics of LTB spacetime have been modified due to the existence of charge and Palatini f(R) correction terms. Bhatti and Yousaf [18] analyzed the impact of f(R) terms for the collapse of LTB spacetime in the presence of the charged field. They examined the apparent horizons to study their consequence during the process of collapse and noticed that the area of horizons reduces by the presence of charge. They also inspected that the impedance in the gravitational collapse is caused by the presence of charge due to which the process slows down and observed that due to a significant role of higher-order terms in the collapse process, the system becomes more consistent. Chakraborty and Saha [19] discussed the dynamics of different horizons in the context of inhomogeneous LTB geometry. They analyzed that the comparison of these horizons reveals that the apparent horizon has a different character from the other horizons and if the apparent horizon accelerates, it will become a trapping horizon. They also described the Kodama vector with a causal character similar to that of the FRW model. Fernandes et al. [20] examined the behavior of LTB spacetime on the massive electromagnetic models and estimated the physical quantities like density and scale factor for Podolsky models and discovered a new type of singularity. Herrera et al. [21] applied the technique of Misner and Sharp to examine the gravitational collapse for dissipative fluids. They linked the transport equation with the dynamical equation in the background of Israel-steward theory together with thermodynamics coefficients and compare the results with previous calculations where these coefficients were ignored. Herrera et al. [22] discussed the properties of dissipative fluids under the influence of shear-free conditions and demonstrated the purpose of dissipative fluxes. They concluded that the magnetic part of the Weyl tensor disappears for geodesic fluid implying that gravitational waves do not emit during the evolution. In this manuscript, we investigate the generalization of LTB spacetime for charged fluid in Palatini f(R) gravity and consider the spherically symmetric spacetime along with dissipative dust fluid by following the strategy deployed by Herrera et al. [1]. In Sect. 2, we formulate the field equations coupled with f(R) gravity and matter variables in the presence of charge. Section 3 includes the structure scalars obtained from the orthogonal decomposition of Riemann tensor and evolution equations. In Sect. 4, we study the properties of LTB spacetime and analyze the behavior of the evolution equation by considering the masses of compact objects with the help of graphical representations. In the same section, we discuss the GLTB spacetime and its symmetric properties using diffusion and streaming-out approximations. Finally, our main results are mentioned in the last section.

2 Inhomogeneous LTB geometry coupled with kinematical variables

The diagonal non-static inhomogeneous and irrotational LTB line element is given by the following form

$$\begin{aligned} ds^2=-dt^2+C^2(d\theta ^2+sin^2\theta d\phi ^2)+B^2 dr^2, \end{aligned}$$
(8)

where B is a dimensionless metric coefficient and C has similar dimension as r while both depend on t and r. The interior region of the metric is filled by dissipative dust fluid using heat and null radiation. The energy-momentum tensor describes such matter fields as follows

$$\begin{aligned} T_{\alpha \zeta }=\mu V_{\alpha } V_{\zeta }+V_{\alpha } q_{\zeta }+\epsilon l_{\alpha } l_{\zeta }+q_{\alpha } V_{\zeta }, \end{aligned}$$
(9)

where \( l^{\alpha },~\mu ,~\epsilon ,~V_{\alpha },~q_\alpha \) correspond to the null four-vector, energy density, radiation density, four-velocity and the heat flux respectively. The null four vector \( l^{\alpha }= \delta ^{\alpha }_0+B^{-1}\delta ^{\alpha }_1\), four velocity \( V^{\alpha }=\delta ^{\alpha }_0\), heat flux \( q^{\alpha }=q B^{-1}\delta ^{\alpha }_1\), and unit four-vector \( \chi ^{\alpha }=B^{-1} \delta ^{\alpha }_1\), in a comoving coordinate system satisfy the following relationships

$$\begin{aligned} V^{\alpha } V_{\alpha }&=-1, \quad l^{\alpha } V_{\alpha }=-1, \quad V^{\alpha } q_{\alpha }=0, \quad l^{\alpha } l_{\alpha }=0, \nonumber \\ \chi ^{\alpha } V_{\alpha }&=0, \quad \chi ^{\alpha } \chi _{\alpha }=1. \end{aligned}$$
(10)

The relativistic matter distribution is fully explained by matter variables like shear tensor, four-acceleration, and expansion scalar. The four-acceleration is defined as \( a_{\alpha }=V_{\alpha ;\zeta } V^{\zeta } \) and its non-vanishing components are given by

$$\begin{aligned} a_{0}=\frac{\dot{F}}{2F}, \quad a_{1}=\frac{F'}{2F}, \end{aligned}$$
(11)

as seen from (11), the occurrence of four acceleration components is completely dependent on Palatini f(R) formalism. The shear tensor is defined as

$$\begin{aligned} \sigma _{\alpha \zeta }=V_{(\alpha ;\zeta )}-\frac{1}{3} \Theta h_{\alpha \zeta }+a_{(\alpha }V_{\zeta )}, \end{aligned}$$
(12)

where \( h_{\alpha \zeta }=g_{\alpha \zeta }+V_{\alpha } V_{\zeta } \) is the projection tensor and the non vanishing elements of shear tensor in f(R) gravity are given by

$$\begin{aligned} \sigma _{11}&=-\frac{\dot{F}B^2}{6F}+\frac{2}{3} B^2 \sigma , \quad \sigma _{01}=\frac{F'}{4F}, \nonumber \\ \sigma _{22}&=-\frac{1}{3} C^2 \sigma -\frac{\dot{F}C^2}{6F}=\frac{\sigma _{33}}{sin^2 \theta }. \end{aligned}$$
(13)

The shear scalar appeared in the above equation is defined as \( \sigma =\frac{\dot{B}}{B}-\frac{\dot{C}}{C}\), while its value in f(R) gravity becomes

$$\begin{aligned} \sigma _{eff}=\left( \left( -\frac{\dot{C}}{C}+\frac{\dot{B}}{B}\right) ^2+\frac{\dot{F}^2}{8F^2}-\frac{3F'^2}{16F^2 B^2}\right) ^{\frac{1}{2}}. \end{aligned}$$
(14)

The fractional rate of change in volume at the center of a spherical cloud to proper time is determined by expansion tensor and its trace is known as the expansion scalar and its value in Palatini f(R) gravity takes the form

$$\begin{aligned} \Theta _{eff}=2\frac{\dot{F}}{F}+2\frac{\dot{C}}{C}+\frac{\dot{B}}{B}. \end{aligned}$$
(15)

The Modified field equations in the form of Einstein tensor under the influence of electromagnetic field can be written as

$$\begin{aligned} G_{\alpha \zeta }=\frac{8\pi }{F} \left( T_{\alpha \zeta }+T^{(D)}_{\alpha \zeta }+E_{\alpha \zeta }\right) . \end{aligned}$$
(16)

The electromagnetic tensor for the comoving coordinate system can be used to assess the influence of charge and defined as:

$$\begin{aligned} E_{\alpha \zeta }=\frac{1}{4\pi }\left( F^{\mu }_{\alpha } F_{\zeta \mu }-\frac{1}{4} F^{\mu \nu } F_{\mu \nu } g_{\alpha \zeta }\right) , \end{aligned}$$
(17)

where \( F_{\alpha \beta }=-\phi _{\alpha ,\beta }+\phi _{\beta ,\alpha } \) is the Maxwell strength tensor that satisfies the Maxwell field equations.

$$\begin{aligned} F^{\alpha \beta }_{;\beta }=\mu _{0} j^{\alpha }, \quad F_{[\alpha \beta ;\gamma ]}=0, \end{aligned}$$
(18)

where \( \phi _{\mu },~j^{\mu }\) and \( \mu _{0} \) represents the four-potential, four-current and magnetic permeability. For the solution of the Maxwell field equations, we take \( \phi _{\mu }=\phi \delta _{\mu }^{0},\) and \( j^{\mu }=\sigma U^{\mu } \) while charge density and scalar potential are denoted by \( \sigma \) and \( \phi \), respectively, which are functions of t and r. We obtain two independent equations while solving the Maxwell field equations of the following form

$$\begin{aligned}&\frac{\partial ^2 \phi }{\partial r^2}-\left( -2\frac{F'}{F}+\frac{B'}{B}-2\frac{C'}{C}\right) \frac{\partial \phi }{\partial r}=4 \pi \sigma B^2, \end{aligned}$$
(19)
$$\begin{aligned}&\frac{\partial ^2 \phi }{\partial r \partial t}-\left( -2\frac{\dot{F}}{F} \frac{\dot{B}}{B}-2\frac{\dot{C}}{C}\right) \frac{\partial \phi }{\partial r}=0. \end{aligned}$$
(20)

Equation (19) is integrated with respect to r to provide

$$\begin{aligned} \phi '=\frac{B s}{C^2 F^2}, \end{aligned}$$
(21)

where \( s= 4 \pi \int _0^r \sigma C^2 B F^2 \) represents the total charge carried by non-interacting particles in a region of radius r. The non-vanishing components of the electromagnetic stress tensor are given by

$$\begin{aligned} E_{00}&=\frac{1}{8\pi } \frac{s^2}{C^4 F^4}, \quad E_{11}=-\frac{1}{8\pi } \frac{B^2 s^2}{C^4 F^4}, \nonumber \\ E_{22}&= E_{33}=\frac{1}{8\pi } \frac{s^2}{C^2 F^4}. \end{aligned}$$
(22)

The Palatini f(R) field equations with charged field are given by

$$\begin{aligned}&\frac{\dot{C}}{C} \left( \frac{\dot{C}}{C}+\frac{2 \dot{B}}{B}\right) -\left( \frac{1}{B^2}\right) \nonumber \\&\qquad \times \left[ -\frac{2 C' B'}{B C}-\frac{B^2}{C^2}+\left( \frac{C'}{C}\right) ^2+\frac{2C''}{C}\right] \nonumber \\&\quad =8\pi \left( \tilde{\mu }_{eff}+\frac{1}{8\pi } \frac{s^2}{C^4 F^5}\right) , \end{aligned}$$
(23)
$$\begin{aligned}&-2\left( -\frac{\dot{B} C'}{B C}+\frac{\dot{C'}}{C}\right) =-8\pi \tilde{q}_{eff} B , \end{aligned}$$
(24)
$$\begin{aligned}&\left( \frac{C'}{C}\right) ^2-\left[ \left( \frac{\dot{C}}{C}\right) ^2 +\frac{2\ddot{C}}{C}\right] B^2-\left( \frac{B}{C}\right) ^2\nonumber \\&\quad =8\pi \left( B^2 \epsilon _{eff}-\frac{1}{8\pi } \frac{B^2 s^2}{C^4 F^5}\right) , \end{aligned}$$
(25)
$$\begin{aligned}&-\left( \frac{\dot{B}\dot{C}}{B C}+\frac{\ddot{C}}{C}+\frac{\ddot{B}}{B}\right) C^2+\left( -\frac{B' C'}{B C}+\frac{C''}{C}\right) \left( \frac{C}{B}\right) ^2\nonumber \\&\quad =\chi _{22}+\frac{s^2}{C^2 F^5}, \end{aligned}$$
(26)

where \( \tilde{\mu }_{eff},~\epsilon _{eff} \) and \( \tilde{q}_{eff}\) each contain the Palatini f(R) extra as well as usual terms whose values are given below

$$\begin{aligned} \tilde{\mu }_{eff}&=\frac{1}{F} (\tilde{\mu }+\chi _{00}), \quad \epsilon _{eff}=\frac{1}{F}\left( \frac{\chi _{11}}{B^2}+\epsilon \right) , \nonumber \\ \tilde{q}_{eff}&=\frac{1}{F}\left( \tilde{q}+\frac{\chi _{01}}{B}\right) , \end{aligned}$$
(27)

here \( \chi _{00},~\chi _{11},~\chi _{01}, \) and \( \chi _{22} \) are the extra curvature terms appeared in the field equations and are addressed in Appendix C, while prime denotes r differentiation and dot denotes t differentiation.

The formula for calculating the mass function m(t, r) in the presence of charge to determine the amount of matter inside a self-gravitating system is provided by Misner–Sharp [23], which is given by

$$\begin{aligned} m=\frac{(C^3)}{2} R_{23}^{~~23}=\frac{C}{2}\left[ \dot{C}^2-\left( \frac{C'}{B}\right) ^2+1\right] +\frac{s^2}{2C}, \end{aligned}$$
(28)

so Eq. (28) can be rewritten as

$$\begin{aligned} E=\frac{C'}{B}=\left[ 1+U^2+\frac{s^2}{C^2}-\frac{2m(t,r)}{R}\right] ^{\frac{1}{2}}. \end{aligned}$$
(29)

The radial variation of the mass function yields the following equation.

$$\begin{aligned} m'=&4\pi \left( \tilde{q}_{eff}\frac{U}{E}+\tilde{\mu }_{eff}\right) C'C^2 +\frac{s^2 C'}{2C^2 F^5}-\frac{s^2 s'}{2 C^2}+\frac{s s'}{C}, \end{aligned}$$
(30)

where U indicates the collapsing matter velocity and can be specified as \( U=D_{T} C \) where \( D_{T}=\frac{\partial }{\partial t}\), it is assumed to be negative in the case of collapsing spheres. While \( \tilde{q}=q+\epsilon \), \( \tilde{\mu }=\mu +\epsilon \). Integrating partially the Eq. (30), with a Palatini f(R) context reveals the relationship between matter variables and mass function given below

$$\begin{aligned}&\frac{3m}{C^3}=4\pi \tilde{\mu }_{eff}+\frac{3}{C^3} \int _0^r \frac{s^2 C'}{2C^2 F^5}dr\nonumber \\&\quad -\frac{4\pi }{C^3} \int _0^r C^3 \left( \tilde{\mu }_{eff}'-3\tilde{q}_{eff}\frac{C' U}{C E}\right) dr+\frac{3 s^2}{2 C^4}. \end{aligned}$$
(31)

The Weyl tensor can be manifested in the context of its electric part for spherically symmetric matter distributions while its magnetic part vanishes and the electric part is defined as

$$\begin{aligned} E_{\alpha \zeta }=C_{\alpha \mu \zeta \nu } V^{\mu } V^{\nu }, \end{aligned}$$
(32)

in terms of unit four-vector, metric tensor and unit four-velocity, the electric part of Weyl tensor may be granted as

$$\begin{aligned} E_{\alpha \zeta }=\varepsilon (\chi _{\alpha } \chi _{\zeta }-\frac{1}{3} (V_{\alpha } V_{\zeta }+g_{\alpha \zeta })), \end{aligned}$$
(33)

where

$$\begin{aligned} \varepsilon&=-\frac{1}{2C^2}+\frac{1}{2}\left[ -\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}-\frac{\dot{C}}{C}\left( \frac{\dot{C}}{C}-\frac{\dot{B}}{B}\right) \right] \nonumber \\&\quad +\left[ \frac{C'}{C}\left( \frac{B'}{B}+\frac{C'}{C}\right) -\frac{C''}{C}\right] \frac{1}{2B^2}. \end{aligned}$$
(34)

is the scalar enwraping the products of spacetime curvature. Now, using Eqs. (23), (25), (26), (28) and (34) we have

$$\begin{aligned} 4\pi (\tilde{\mu }_{eff}-\epsilon _{eff})-\varepsilon =\frac{3m}{C^3}-\frac{3 s^2}{2 C^4}-\frac{\chi _{22}}{2C^2}-\frac{3 s^2}{2 C^4 F^5}. \end{aligned}$$
(35)

The equation describes the dependence of the Weyl scalar on the matter variables and the mass function under the influence of charge as well as dark source terms.

2.1 The matching conditions

We consider the exterior spacetime [24] given by the following equation in order to derive the junction conditions for exterior and interior spacetime.

$$\begin{aligned} ds^2&=-\left[ 1-\frac{2M(\nu )}{r}-\frac{R r^2}{12}+\frac{Q^2}{r^2}\right] d\nu ^2-2dr d\nu \nonumber \\&\quad +r^2 (d\theta ^2+sin^2\theta d\phi ^2), \end{aligned}$$
(36)

where the symbols r and \( \nu \) referred to the null and retarded time coordinates while M is a function of retarded time coordinate. Darmois junction conditions are used to match smoothly the interior and exterior geometry at the surface which produces

$$\begin{aligned}&M+\frac{r^3 R}{24}\overset{\Sigma }{=}m(t,r), \end{aligned}$$
(37)
$$\begin{aligned}&q+\frac{R}{2 \kappa }\left( F-\frac{f}{R}\right) -\frac{r R}{12}\overset{\Sigma }{=}0, \end{aligned}$$
(38)

where \( \overset{\Sigma }{=} \) signify that both quantities are calculated on the boundary surface.

$$\begin{aligned} q_{eff}\overset{\Sigma }{=}s. \end{aligned}$$
(39)

3 Dynamical equations and structure scalars

Here, we define the tensors \( Y_{\alpha \zeta } \) and \( X_{\alpha \zeta } \) and dynamical variables in the context of f(R) gravity. We also manifested a connection between curvature scalar and fluid parameters in the presence of electromagnetic field and Palatini f(R) terms by formulating the modified Ellis equations. Bel [25] studied the orthogonal decomposition of Riemann curvature tensor \( R_{\alpha \gamma \zeta \delta } \) which has been applied to describe the evolution and structure formation of self-gravitating objects in the background of different Astrophysical scenarios. We introduce the tensors \( Y_{\alpha \zeta } \) and \( X_{\alpha \zeta } \) by adopting the pioneer work of Bel, which are the elements of the orthogonal splitting to obtain structure scalars in Palatini f(R) gravity as

$$\begin{aligned}&Y_{\alpha \zeta }=R_{\alpha \gamma \zeta \delta } V^{\gamma } V^{\delta },\nonumber \\ X_{\alpha \zeta }=~^{*}R^{*}_{\alpha \gamma \zeta \delta }&V^{\gamma } V^{\delta }=\frac{1}{2} \eta _{\alpha \gamma }^{~~\epsilon \rho } R^{*}_{\epsilon \rho \zeta \delta } V^{\gamma } V^{\delta }, \end{aligned}$$
(40)

where the right and double dual of the Riemann tensor can be expressed as \( R^{*}_{\alpha \zeta \gamma \delta }=\frac{1}{2} \eta _{\epsilon \gamma \rho \delta } R_{\alpha \zeta }^{~~\epsilon \rho } \) and \( ~^{*}R^{*}_{\alpha \gamma \zeta \delta }=\frac{1}{2} \eta _{\alpha \gamma }^{~~\epsilon \rho } R^{*}_{\epsilon \rho \zeta \delta } \) and the Levi–Civita tensor is denoted by \( \eta _{\epsilon \rho \gamma \delta } \). The tensors \( Y_{\alpha \zeta } \) and \( X_{\alpha \zeta } \) can be written as

$$\begin{aligned} Y_{\alpha \zeta }&=E_{\alpha \zeta }+\frac{\kappa }{2F}(\tilde{\mu } h_{\alpha \zeta }-\epsilon \chi _{\alpha } \chi _{\zeta })+\frac{\kappa }{3F}(-\tilde{\mu }+\epsilon )h_{\alpha \zeta }\nonumber \\&\quad -\frac{1}{2F}\left[ (\nabla _{\alpha } \nabla _{\zeta } F -g_{\alpha \zeta }\Box F)+(\nabla _{\gamma } \nabla _{\zeta } F \right. \nonumber \\&\quad -g_{\gamma \zeta } \Box F) V_{\alpha } V^{\gamma }+(\nabla _{\alpha } \nabla _{\delta } F-g_{\alpha \delta } \Box F) V_{\zeta } V^{\delta }\nonumber \\&\quad \left. -(\nabla _{\gamma } \nabla _{\delta } F -g_{\gamma \delta } \Box F) g_{\alpha \zeta } V^{\gamma } V^{\delta }\right] +\frac{3}{4F^2} \nonumber \\&\quad \times \left[ \nabla _{\alpha } F \nabla _{\zeta } F +\nabla _{\gamma } F \nabla _{\zeta } F V_{\alpha } V^{\gamma }+\nabla _{\alpha } F \nabla _{\delta } F V_{\zeta } V^{\delta }\right. \nonumber \\&\quad \left. -\nabla _{\gamma } F \nabla _{\delta } F g_{\alpha \zeta } V^{\gamma } V^{\delta }\right] -\frac{1}{2F^2}\nonumber \\&\quad \times (g^{\alpha \zeta } \nabla _{\alpha } F \nabla _{\zeta } F-\Box F)h_{\alpha \zeta }+\frac{1}{6} (f-F R)h_{\alpha \zeta }\nonumber \\&\quad +\frac{1}{4} (\nabla F)^2 h_{\alpha \zeta }+\frac{\kappa s^2}{8 \pi C^4 F^5} \chi _{\alpha } \chi _{\zeta }, \end{aligned}$$
(41)
$$\begin{aligned} X_{\alpha \zeta }&=-E_{\alpha \zeta }+\frac{\kappa \epsilon }{2F}(\chi _{\alpha } \chi _{\zeta }-h_{\alpha \zeta })+\frac{\kappa }{3 F}(-\tilde{\mu }+\epsilon )h_{\alpha \zeta }\nonumber \\&\quad +\frac{1}{8} \epsilon ^{\epsilon \rho }_{\alpha }\left[ \epsilon _{\pi \rho \zeta }\left( \nabla ^{\pi } \nabla _{\epsilon } F-\frac{3}{2F} \nabla ^{\pi } F \nabla _{\epsilon } F\right) \right. \nonumber \\&\quad -\epsilon _{\pi \epsilon \zeta }\left( \nabla ^{\pi } \nabla _{\rho } F-\frac{3}{2F} \nabla ^{\pi } F \nabla _{\rho } F\right) -\epsilon _{\rho \theta \zeta }\left( \nabla ^{\theta } \nabla _{\epsilon }\right. \nonumber \\&\quad \left. F-\frac{3}{2F} \nabla ^{\theta } F \nabla _{\epsilon } F\right) +\epsilon _{\epsilon \theta \zeta }\left( \nabla ^{\theta } \nabla _{\rho } F \right. \nonumber \\&\quad \left. \left. -\frac{3}{2F} \nabla ^{\theta } F \nabla _{\rho } F\right) \right] -\frac{3}{2F^2} \nabla _{\alpha } F \nabla _{\zeta } F +\frac{1}{F}\left( \frac{1}{4 F} (\nabla F)^2\right. \nonumber \\&\quad \left. +\frac{(f-R F)}{6}\right) h_{\alpha \zeta } +\frac{3 \kappa s^2}{8 \pi C^4 F^5} h_{\alpha \zeta }. \end{aligned}$$
(42)

The tensors \( Y_{\alpha \zeta } \) and \( X_{\alpha \zeta } \) can be decomposed in their trace and trace-free parts. Each of these terms in its turn (in the spherically symmetric case) may be expressed through a single scalar function (named as the structure scalars). These variables were firstly introduced, defined and discussed in detail for the first time by Herrera et al. [26]. Following the same scheme as developed in [26], we can find \( Y_{T},~X_{T},~Y_{T F} \) and \( X_{T F} \) as

$$\begin{aligned} Y_{T}&=4\pi (\epsilon _{eff}+\tilde{\mu }_{eff})+\frac{s^2}{C^4 F^5}+M^{(D)}_{1}, \end{aligned}$$
(43)
$$\begin{aligned} Y_{T F}&=\varepsilon -4\pi \left( \epsilon _{eff}-\frac{s^2}{8\pi C^4 F^5}\right) +\frac{4\pi }{F} \chi _{11}+\frac{3 s^2}{2 C^4 F^5}\nonumber \\&\quad +M^{(D)}_{2}, \end{aligned}$$
(44)
$$\begin{aligned} X_{T}&=8\pi \left( \tilde{\mu }_{eff}+\frac{s^2}{8\pi C^4 F^5}\right) -\frac{8\pi }{F} \chi _{00}-\frac{10 s^2}{C^4 F^5}+M^{(D)}_{3}, \end{aligned}$$
(45)
$$\begin{aligned} X_{T F}&=-\varepsilon -4\pi \left( \epsilon _{eff}-\frac{s^2}{8\pi C^4 F^5}\right) +\frac{4\pi }{F} \chi _{11}+\frac{s^2}{2 C^4 F^5}\nonumber \\&\quad +M^{(D)}_{4}, \end{aligned}$$
(46)

where

$$\begin{aligned} M^{(D)}_{2}=\frac{M^{(D)}_{\alpha \zeta }}{\chi _{\alpha } \chi _{\zeta }-\frac{1}{3} h_{\alpha \zeta }} \quad M^{(D)}_{4}=\frac{N^{(D)}_{\alpha \zeta }}{\chi _{\alpha } \chi _{\zeta }-\frac{1}{3}h_{\alpha \zeta }}, \end{aligned}$$
(47)

using Eqs. (31), (35) and (44), we obtain

$$\begin{aligned} Y_{T F}&=-8\pi \epsilon _{eff}dr-\frac{3}{C^3} \int _0^r \frac{s^2 C'}{2C^2 F^5}dr+\frac{4\pi }{C^3}\\&\quad \times \int C^3\left( -3\tilde{q}_{eff}\frac{C' U}{C E}+\tilde{\mu }'_{eff}\right) dr+\frac{2 s^2}{C^4 F^5}\\&\quad +\frac{\chi _{22}}{2C^2}+\frac{4\pi }{F} \chi _{11}+M^{(D)}_{2}, \end{aligned}$$

where the values of \( M^{(D)}_{\alpha \zeta },~N^{(D)}_{\alpha \zeta },~M^{(D)}_{1},\) and \( M^{(D)}_{3},\) are mentioned in Appendix A. The null radiation and dissipative variables as well as the correction terms can be used to express the scalar \( Y_{TF} \). In [26], it was also stated that there is a relation between the structure scalar \( Y_{TF} \) and Tolman mass. In literature, it has been shown that for geodesic case, the scalar \( Y_{TF} \) supervise the stability of the shear-free condition and the trace part of Riemann second dual tensor is found to be dependent on the energy density with extra curvature terms due to f(R) Palatini gravity, while the remaining scalar functions are dependent on the anisotropic stress tensor.

We can construct a couple of differential equations to continue our investigation and to examine the expansion and motion of particles by using the method addressed by Ellis [27]. These equations describe a relationship between fluid variables and the Weyl tensor along with Palatini f(R) terms and can be found as

$$\begin{aligned}&\dot{\Theta }_{eff}+\frac{2}{3} \sigma _{eff}^2+\frac{1}{3} \Theta _{eff}^2=-4\pi (\epsilon _{eff}+\tilde{\mu }_{eff})\nonumber \\&\quad -\frac{\chi _{22}}{C^2}-\frac{s^2}{C^4 F^5}+D_{1}, \end{aligned}$$
(48)
$$\begin{aligned}&\dot{\sigma }_{eff}+\frac{2}{3} \Theta _{eff} \sigma _{eff}+\frac{1}{3} \sigma _{eff}^2=T_{1}(4\pi \epsilon _{eff}+T_{2}-\varepsilon )\nonumber \\&\quad -\frac{s^2}{C^4 F^5}+D_{2}, \end{aligned}$$
(49)
$$\begin{aligned}&[\varepsilon -4\pi (-\epsilon _{eff}+\tilde{\mu }_{eff})]'+(4\pi \epsilon _{eff}+\varepsilon )\frac{3C'}{C}\nonumber \\&\quad =-12\pi B \frac{\dot{C}}{C} \tilde{q}_{eff}+\frac{\chi _{22} C'}{2C^3}+\frac{\chi '_{22}}{2C^2}+\frac{2C's^2}{C^5 F^5}+\left( \frac{s^2}{C^4 F^5}\right) '\nonumber \\&\qquad +\frac{1}{2C^2}\left( \frac{s^2}{C^2 F^5}\right) '. \end{aligned}$$
(50)

Here \(2\left( \frac{\dot{B}}{B}-\frac{\dot{C}}{C}\right) =T_{1} \) and \(-\frac{\dot{B}^2}{3B^2}+2\frac{\dot{B}\dot{C}}{BC}-\frac{\dot{C}^2}{3C^2}=T_{2}\) here \( D_{1} \) and \( D_{2} \) emerge as extra curvature ingredients and their values are given in appendix B. The independent components of the Bianchi identities [28] with ordinary and efficient matter fields yields a couple of equations for energy and momentum conservation.

$$\begin{aligned}&(\tilde{\mu }_{eff}+\epsilon _{eff})\frac{\dot{B}}{B}+\dot{\tilde{\mu }}_{eff} +\frac{2\dot{C}}{C} \tilde{\mu }_{eff}+2\frac{C'}{C B} \tilde{q}_{eff}+\frac{\tilde{q}'_{eff}}{B}\nonumber \\&\quad +\frac{5\dot{F}}{2F} \tilde{\mu }_{eff}+\frac{\dot{F}}{2F} \epsilon _{eff}+\frac{3F'}{F B} \tilde{q}_{eff}\nonumber \\&\quad +\frac{s^2}{4\pi C^4 F^5}\left( \frac{\dot{F}}{F}+\frac{\dot{C}}{C}\right) +\frac{1}{8\pi }\dot{\left( \frac{s^2}{C^4 F^5}\right) }=0, \end{aligned}$$
(51)
$$\begin{aligned}&2\left( \frac{\dot{C}}{C}+\frac{\dot{B}}{B}\right) \tilde{q}_{eff}+\dot{\tilde{q}}_{eff}+\frac{\epsilon '_{eff}}{B}+\frac{2C'}{C B} \epsilon _{eff} +\frac{3\dot{F}}{F} \tilde{q}_{eff}\nonumber \\&\quad +\frac{F'}{2F B}\tilde{\mu }_{eff}+\frac{5F'}{2F B} \epsilon _{eff}+\frac{s^2}{8\pi C^4 F^5}\nonumber \\&\quad \times \left( \frac{2B'}{B^2}-\frac{2C'}{C B}-\frac{2 F'}{F B}\right) -\frac{1}{8\pi B^3}\left( \frac{B^2 s^2}{C^4 F^5}\right) '=0. \end{aligned}$$
(52)

Structure scalars (43)-(46) for line element (8), in terms of metric coefficients are given by

$$\begin{aligned} Y_{T}&=-\frac{\ddot{B}}{B}-2\frac{\ddot{C}}{C}-\frac{\chi _{22}}{C^2}+\frac{s^2}{C^4 F^5}+M^{(D)}_{1}, \end{aligned}$$
(53)
$$\begin{aligned} X_{T}&=\frac{\dot{C}}{C}\left( \frac{\dot{C}}{C}+2\frac{\dot{B}}{B}\right) +\frac{1}{C^2}-\frac{1}{B^2}\nonumber \\&\quad \times \left[ \frac{C'^2}{C^2}-2\frac{B' C'}{B C}+2\frac{C''}{C}\right] -\frac{8\pi }{F} \chi _{00}-\frac{10 s^2}{C^4 F^5}+M^{(D)}_{3}, \end{aligned}$$
(54)
$$\begin{aligned} Y_{T F}&=\frac{\ddot{C}}{C}-\frac{\ddot{B}}{B}-\frac{\chi _{22}}{C^2}+\frac{4\pi }{F} \chi _{11}+\frac{3 s^2}{2 C^4 F^5}+M^{(D)}_{2}, \end{aligned}$$
(55)
$$\begin{aligned} X_{TF}&=\frac{1}{C^2}+\frac{\dot{C}}{C}\left( -\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right) +\frac{1}{B^2}\nonumber \\&\quad \times \left[ -\frac{C'}{C}\left( \frac{B'}{B}+\frac{C'}{C}\right) +\frac{C''}{C}\right] -\frac{\chi _{22}}{2C^2}+\frac{4\pi }{F} \chi _{11}\nonumber \\&\quad +\frac{s^2}{2 C^4 F^5}+M^{(D)}_{4}. \end{aligned}$$
(56)

These structure scalars are interlinked with the simulation of compact objects in f(R) gravity and also in that scenario, we use the Raychaudhuri equation for investigating the consequences of \( \epsilon R^2 \) terms. In the absence of Palatini f(R) extra curvature and charge terms, we obtain the dynamical variables as mentioned in [1] from the Eqs. (53)–(56). Equations (48), (49) and (50) in the form of dynamical variables may be written as

$$\begin{aligned} \dot{\Theta }_{eff}+\frac{2}{3} \sigma ^2_{eff}+\frac{1}{3} \Theta ^2_{eff}&=-Y_{T}-\frac{\chi _{22}}{C^{2}}+D_{1}+M^{(D)}_{1}, \end{aligned}$$
(57)
$$\begin{aligned} \dot{\sigma }_{eff}+\frac{2}{3} \Theta _{eff} \sigma _{eff}+\frac{1}{3} \sigma ^2_{eff}&=T_{1}\Bigg (-Y_{T F}+\frac{4\pi }{F}\chi _{11}\nonumber \\&\quad +T_{2}+M^{(D)}_{2}\Bigg )+D_{2}. \end{aligned}$$
(58)

The Eq. (57) explains the expansion evolution with the help of the f(R) structure scalar \( Y_{T} \) with the addition of dark source terms while Eq. (58) describes the connection between the structure scalar \( Y_{T F}\) and shear scalar \( \sigma _{eff} \) which illustrate the impact of electromagnetic field and Palatini f(R) gravity on the shearing motion. Moreover, the relationship between Weyl tensor and fluid variables in terms of dynamical variables can be found as

$$\begin{aligned} (X_{T F}+4\pi \tilde{\mu }_{eff})'&=-3\frac{C'}{C} X_{T F} +4\pi \tilde{q}_{eff}(\Theta -\sigma )B\nonumber \\&\quad -\frac{\chi '_{22}}{2C^2}+\frac{\chi _{22} C'}{2C^3}\nonumber \\&\quad + \left( \frac{4\pi }{F} \chi _{11}+\frac{s^2}{C^4 F^5}+M_{4}^{(D)}\right) '+\frac{2C's^2}{C^5 F^5}\nonumber \\&\quad +\left( \frac{4\pi }{F} \chi _{11}+\frac{s^2}{C^4 F^5}+M_{4}^{(D)}\right) \frac{3C'}{C}\nonumber \\&\quad +\left( \frac{s^2}{C^4 F^5}\right) '+\frac{1}{2C^2}\left( \frac{s^2}{C^2 F^5}\right) '. \end{aligned}$$
(59)

Now, the Eq. (59) is reduced to the following form for non-dissipative dust fluid

$$\begin{aligned} (X_{T F}+4\pi \tilde{\mu }_{eff})'&=-3\frac{C'}{C} X_{T F}-\frac{\chi '_{22}}{2C^2}+\frac{\chi _{22} C'}{2C^3}\nonumber \\&\quad +\left( \frac{4\pi }{F} \chi _{11}+\frac{s^2}{C^4 F^5}+M_{4}^{(D)}\right) '\nonumber \\&\quad +\left( \frac{4\pi }{F} \chi _{11}+\frac{s^2}{C^4 F^5}+M_{4}^{(D)}\right) \frac{3C'}{C}\nonumber \\&\quad +\frac{2C's^2}{C^5 F^5}+\left( \frac{s^2}{C^4 F^5}\right) '+\frac{1}{2C^2}\left( \frac{s^2}{C^2 F^5}\right) ', \end{aligned}$$
(60)

if \( \tilde{\mu }'_{eff}=0 \) then Eq. (60) becomes

$$\begin{aligned}&(X_{T F})' =-3\frac{C'}{C} X_{T F}-\frac{\chi '_{22}}{2C^2}+\frac{\chi _{22} C'}{2C^3}\nonumber \\&\quad +\left( \frac{4\pi }{F} \chi _{11}+\frac{s^2}{C^4 F^5}+M_{4}^{(D)}\right) '\nonumber \\&\quad +\left( \frac{4\pi }{F} \chi _{11}+\frac{s^2}{C^4 F^5}+M_{4}^{(D)}\right) \frac{3C'}{C}\nonumber \\&\quad +\frac{2C's^2}{C^5 F^5}+\left( \frac{s^2}{C^4 F^5}\right) '+\frac{1}{2C^2}\left( \frac{s^2}{C^2 F^5}\right) ', \end{aligned}$$
(61)

integrating Eq. (61), which produces

$$\begin{aligned} X_{T F}&=\frac{f(t)}{C^3}-\int \frac{1}{X_{T F}}\left[ \frac{\chi '_{22}}{2C^2}+\frac{\chi _{22} C'}{2C^3}\right. \nonumber \\&\quad +\left( \frac{4\pi }{F} \chi _{11}+\frac{s^2}{C^4 F^5}+M_{4}^{(D)}\right) '\nonumber \\&\quad +\left( \frac{4\pi }{F} \chi _{11}+\frac{s^2}{C^4 F^5}+M_{4}^{(D)}\right) \frac{3C'}{C}\nonumber \\&\quad \left. +\frac{2C's^2}{C^5 F^5}+\left( \frac{s^2}{C^4 F^5}\right) '+\frac{1}{2C^2}\left( \frac{s^2}{C^2 F^5}\right) '\right] dr. \end{aligned}$$
(62)

The energy density is being regulated by the structure scalar \( X_{T F} \) for non-dissipative dust fluid as observed from the Eq. (62). This is also true for an isotropic fluid as described in [26].

4 Lemaître–Tolman–Bondi spacetime and its generalization

In this section, we address the properties of LTB spacetime and analyze the behavior of the evolution equation under the influence of charge by considering the masses of compact objects. We generalize our LTB spacetime by incorporating the heat flux and acquire structure scalars for that generalized spacetime. To find similarities between LTB and generalized spacetime, we match the structure scalars corresponding to LTB and GLTB. While on the other hand, we discuss symmetric properties of generalized spacetime based on the assumption that they correspond to LTB properties using two cases: diffusion and streaming out limit. We consider the non-dissipative dust fluid to obtain the general mechanics for LTB spacetime. By substituting \( q=0 \) in Eq. (24) and then integrating we obtain

$$\begin{aligned} B(t,r)&=\frac{C'}{(1+\kappa (r))} \end{aligned}$$
(63)

where \( C'=exp\left[ \int \frac{\frac{1}{2F}\left( \dot{F'}-\frac{5\dot{F}F'}{2F}\right) -\frac{\dot{C'}}{C}}{\left( \frac{F'}{2F}-\frac{C'}{C}\right) }dt\right] \), where \( \kappa \) serves as a constant for integration. We get the Lemaitre–Tolman–Bondi-metric in the following form by substituting the Eq. (63) in (8).

$$\begin{aligned} ds^2=-dt^2+\frac{C'^2}{(1+\kappa (r))^2} dr^2+C^2 (d\theta ^2+sin^2\theta d\phi ^2). \end{aligned}$$
(64)

The LTB spacetime is generally coupled with an inhomogeneous dust source but it is important to mention that the general source corresponding to the metric appeared in (64) is an anisotropic fluid [29]. Now the element of Bianchi identities take the simplified form for non-dissipative dust fluid

$$\begin{aligned}&\left( \mu _{eff}+\frac{s^2}{8\pi C^4 F^5}\right) ^{.}=-\left( \mu _{eff}+\frac{s^2}{8\pi C^4 F^5}\right) \nonumber \\&\quad \times \left( \frac{\dot{B}}{B}+2\frac{\dot{C}}{C}+\frac{5\dot{F}}{2F}\right) -\frac{s^2}{8\pi C^4 F^5}\left( \frac{\dot{B}}{B}+\frac{\dot{F}}{2F}\right) , \end{aligned}$$
(65)

integrating Eq. (65), we get

$$\begin{aligned} \mu _{eff}=\frac{h(r) D_{5}}{B C^2 F^{\frac{5}{2}}}-\frac{s^2}{8\pi C^4 F^5}, \end{aligned}$$
(66)

where \( D_{5}=\exp \left[ \int \frac{s^2}{8\pi C^4 F^5 \left( \mu _{eff}+\frac{s^2}{8\pi C^4 F^5}\right) }\right] \) and h(r) is an integration constant. Now using the Eqs. (28) and (63) we obtain

$$\begin{aligned} \dot{C}^2=\frac{2m}{C}-\frac{s^2}{C^2}-1+\frac{C'^2}{B^2}, \end{aligned}$$
(67)

where

$$\begin{aligned} B(t,r)=\frac{1}{(1+\kappa (r))} exp\left[ \int \frac{\frac{1}{2F}\left( \dot{F'}-\frac{5\dot{F}F'}{2F}\right) -\frac{\dot{C'}}{C}}{\left( \frac{F'}{2F}-\frac{C'}{C}\right) }dt\right] , \end{aligned}$$
(68)

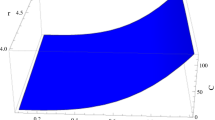
which is known as evolution equation and there are different solutions depending on the values of s, m and \( \kappa \). These solutions describe the different phases of the universe (Figs. 1, 2, 3).

Fig. 1
figure 1

The plot is for \( \kappa < 0, m = 1.4\) and \( s=0.5 \) that corresponds to closed universe which explains that after expanding to maximum size, the universe falls into itself known as big cruch

Full size image
Fig. 2
figure 2

The plot is for \( \kappa > 0, m = 1.4\) and \( s=0.5 \) which corresponds to open universe that expands exponentially and expansion increases due to f(R) and charge terms

Full size image
Fig. 3
figure 3

The plot is for \( \kappa = 0, m = 1.4\) and \( s=0.5 \) which corresponds to flat universe

Full size image

The scalar functions \( X_{T F}, Y_{T}, X_{T},\) and \( Y_{T F} \) for line element (64) are given by

$$\begin{aligned} Y_{T F}&=-\frac{\ddot{C'}}{C'}+\frac{\ddot{C}}{C}-\frac{\chi _{22}}{C^2}+\frac{4\pi }{F} \chi _{11}+M^{(D)}_{2}+\frac{3 s^2}{2 C^4 F^5}, \end{aligned}$$
(69)
$$\begin{aligned} Y_{T}&=-\frac{\ddot{C'}}{C'}-2\frac{\ddot{C}}{C}-\frac{\chi _{22}}{C^2}+M^{(D)}_{1} +\frac{s^2}{C^4 F^5}, \end{aligned}$$
(70)
$$\begin{aligned} X_{T}&=\frac{\dot{C}^2}{C^2}+\frac{2\dot{C} \dot{C'}}{C C'}-\frac{\kappa }{C^2}-\frac{\kappa '}{C C'}-\frac{8\pi }{F} \chi _{00}+M^{(D)}_{3}\nonumber \\&\quad -\frac{10 s^2}{C^4 F^5}, \end{aligned}$$
(71)
$$\begin{aligned} X_{T F}&=-\frac{\dot{C} \dot{C'}}{C C'}+\frac{\dot{C}^2}{C^2}-\frac{\kappa }{C^2}+\frac{\kappa '}{2C' C}-\frac{\chi _{22}}{2C^2}\nonumber \\&\quad +\frac{4\pi }{F} \chi _{11}+M^{(D)}_{4}+\frac{s^2}{2 C^4 F^5}. \end{aligned}$$
(72)

The structure scalars \( Y_{TF} \) and \( Y_{T} \) do not incorporate the term \( \kappa \) in their formulation as shown in Eqs. (69) and (70). Now again integrating the Eq. (24), by including the heat effects we obtain

$$\begin{aligned} B(t,r)=\frac{C'}{(1+K(t,r))^{\frac{1}{2}}}, \end{aligned}$$
(73)

where

$$\begin{aligned} 1+K(t,r)=\left[ C(r)+\int 4\pi \tilde{q}_{eff} R dt\right] ^2. \end{aligned}$$
(74)

In the absence of dissipation Eq. (74) reduces to

$$\begin{aligned} C(r)=(1+\kappa (r))^{\frac{1}{2}}, \end{aligned}$$
(75)

we acquired the GLTB spacetime by using Eqs. (73) and (8) in the following form

$$\begin{aligned} ds^2&=-dt^2+\frac{ (C')^2}{\left[ C(r)+\int 4\pi \tilde{q}_{eff} C dt\right] ^2} dr^2\nonumber \\&\quad +C^2(d\theta ^2+sin^2\theta d\phi ^2). \end{aligned}$$
(76)

Structure Scalars \( Y_{T F}, X_{T F}, Y_{T} \) and \( X_{T} \) for the line element (76) are given by

$$\begin{aligned} Y_{T}&=-\frac{\ddot{C'}}{C'}-2\frac{\ddot{C}}{C}+\frac{\dot{K}}{1+K} \left( -\frac{3\dot{K}}{4(1+K)}+\frac{\dot{C'}}{C'}\right) \nonumber \\&\quad +\frac{\ddot{K}}{2(1+K)} +\frac{s^2}{C^4 F^5}-\frac{\chi _{22}}{C^2}+M^{(D)}_{1}, \end{aligned}$$
(77)
$$\begin{aligned} Y_{T F}&=-\frac{\ddot{C'}}{C'}+\frac{\ddot{C}}{C}+\frac{\dot{K}}{1+K} \left( -\frac{3\dot{K}}{4(1+K)}+\frac{\dot{C'}}{C'}\right) \nonumber \\&\quad +\frac{\ddot{K}}{2(1+K)}-\frac{\chi _{22}}{C^2}+\frac{4\pi }{F} \chi _{11}+\frac{3 s^2}{2 C^4 F^5}+M^{(D)}_{2}, \end{aligned}$$
(78)
$$\begin{aligned} X_{T}&=\frac{2\dot{C} \dot{C'}}{C C'}+\frac{\dot{C}^2}{C^2}-\frac{K'}{C C'}-\frac{K}{C^2}-\frac{\dot{C} \dot{K}}{C (1+K)}-\frac{8\pi }{F} \chi _{00}\nonumber \\&\quad -\frac{10 s^2}{C^4 F^5}+M^{(D)}_{3}, \end{aligned}$$
(79)
$$\begin{aligned} X_{T F}&=\frac{\dot{C}^2}{C^2}-\frac{\dot{C} \dot{C'}}{C C'}+\frac{K'}{2C C'}-\frac{K}{C^2}+\frac{\dot{C} \dot{K}}{2C(1+K)}-\frac{\chi _{22}}{2C^2}\nonumber \\&\quad +\frac{s^2}{2 C^4 F^5}+\frac{4\pi }{F} \chi _{11}+M^{(D)}_{4}. \end{aligned}$$
(80)

To continue our analysis and obtain some specific solutions, we need to impose some constraints. The criteria for choosing such constraints will be based on how similar the obtained solutions to LTB geometry so we shall regard the extensions of LTB geometry based on symmetric properties and structure scalars to analyze the impact of charged fluid and modified gravity. We shall study the transport equation to obtain the temperature profile for the diffusion case.

4.1 Transport equation

To calculate the temperature of the self-gravitating system under the diffusion approximation \( (\tilde{q}_{eff}=q_{eff}, \epsilon _{eff}=0) \), we will apply a transport equation for dissipative fluids derived from the Muller–Israel–Steward second-order phenomenological theory. The heat flux transport equation can be written as

$$\begin{aligned} q^{\alpha }_{eff}+\zeta h^{\alpha \rho } V^{\gamma } q_{\rho ;\gamma }&=-K h^{\alpha \rho }(T a_{\rho }+T_{,\rho })\nonumber \\&\quad -\frac{1}{2}K T^2 \left( \frac{\zeta V^{\rho }}{K T^2}\right) _{;\rho } q^{\alpha }_{eff}, \end{aligned}$$
(81)

where the heat flow, thermal conductivity, temperature, and relaxation time are represented by \( q_{eff}, K, T, \) and \( \zeta \), respectively. Set \( \zeta =0 \) to restore the Eckart–Landau equation. In the case of a spherically symmetric distribution, the transport equation has only one independent element which is given by

$$\begin{aligned} q_{eff}+\zeta \dot{q}_{eff}-\zeta \frac{\dot{F}}{2F} q_{eff}&=-\frac{1}{2} \zeta q_{eff} \Theta _{eff}\nonumber \\&\quad -\frac{K}{B} T'+\zeta \frac{\dot{T}}{T} q_{eff}, \end{aligned}$$
(82)

in the shortened edition of the theory, the last term in Eq. (81) is absent. As a result, Eq. (82) implies

$$\begin{aligned} \zeta \dot{q}_{eff}+q_{eff}-\zeta \frac{\dot{F}}{2F} q_{eff}=-\frac{K}{B} T', \end{aligned}$$
(83)

if \( \epsilon _{eff}=0 \) then we obtain from Eq. (52)

$$\begin{aligned} q_{eff}=\frac{g(r)D_{3}}{B^2 C^2 F^3}, \end{aligned}$$
(84)

where

$$\begin{aligned} D_{3}&=exp\left[ -\int \frac{F'}{2F B q_{eff}}\left( \mu _{eff}+\frac{s^2}{8\pi C^4 F^5}\right) dt\right. \nonumber \\&\quad -\int \frac{1}{B^3 q_{eff}}\left( \left( \frac{-B^2 s^2}{8\pi C^4 F^5}\right) '+\left( \frac{2C'}{C}\right. \right. \nonumber \\&\quad \left. \left. \left. -\frac{2B'}{B}+\frac{5F'}{2F}\right) \frac{-B^2 s^2}{8\pi C^4 F^5}\right) \right] , \end{aligned}$$
(85)

where g(r) is an arbitrary function, and the temperature of the matter distribution can be determined in terms of metric coefficients using Eqs. (82) and (83).

4.2 Extension through scalar functions

We have drawn the following conclusions from our analysis of structure scalars. The structure scalars \( Y_{T F} \) and \( Y_{T} \) entirely determine the evolution of expansion and shear scalar in the case of dissipative dust fluid and the difference between their terms is the same. In the case of LTB spacetimes, the term \( \kappa \) is absent from the expressions of \( Y_{T} \) and \( Y_{T F} \). Next we examine the structure scalars \( Y_{T} \) and \( Y_{T F} \) by keeping in view the above conclusions and maximal similarity condition occur between LTB and its generalized spacetime(GLTB). Therefore by comparing Eqs. (69) and (78), we have

$$\begin{aligned} \frac{\dot{K}}{1+K} \left[ -\frac{3\dot{K}}{4(1+K)}+\frac{\dot{C'}}{C'}\right] +\frac{\ddot{K}}{2(1+K)}=0, \end{aligned}$$
(86)

which exactly match with Eq. (103) of [1] but in expression (86), the value of K(t, r) contains the extra f(R) terms and its value is mentioned in (74). integrating Eq. (86) produces

$$\begin{aligned} \frac{C' \dot{K}^{\frac{1}{2}}}{(1+K)^{\frac{3}{4}}}=C_{1}(r), \end{aligned}$$
(87)

where \( C_{1}(r) \) is a constant of integration. Using Eqs. (74) and (75), we have

$$\begin{aligned} C_{1}(r)=\frac{(8\pi \tilde{q}_{eff} C)^{\frac{1}{2}} C'}{(1+\kappa (r))^{\frac{1}{2}}+\int 4\pi \tilde{q}_{eff} C dt}, \end{aligned}$$
(88)

integration of Eq. (87) yields

$$\begin{aligned} K+1=\frac{4}{ \left[ C_{2}(r)+C_{1}(r)^2 \int \frac{dt}{C'^2}\right] ^2}, \end{aligned}$$
(89)

where \( C_{2}(r) \) is another arbitrary constant of integration. Taking t Derivative of Eq. (88), we obtain

$$\begin{aligned} \dot{K}=- \frac{8C_{1}^2(r)}{(C')^2 \left[ C_{2}(r)+C_{1}^2(r) \int \frac{dt}{C'^2}\right] ^3}, \end{aligned}$$
(90)

comparing the Eqs. (74) and (90), we have

$$\begin{aligned} 2\pi \tilde{q}_{eff}=\frac{C_{1}^2(r)}{ (C')^2 C \left[ C_{2}(r)+C_{1}^2(r) \int \frac{dt}{(C')^2}\right] ^2}. \end{aligned}$$
(91)

The relation between integration constants C(r) and \( C_{2}(r) \) can be found by comparing the Eqs. (88) and (91)

$$\begin{aligned} C_{2}(r)=\frac{2(1-4\pi \tilde{q}_{eff} C C'^2)}{C(r)+\int 4\pi \tilde{q}_{eff} C dt}. \end{aligned}$$
(92)

Based on the suppositions put on \( Y_{T} \) and \( Y_{T F} \), we can obtain a GLTB. Taking the temporal and radial dependence of R from (91), the dissipative flux of GLTB may be derived up to two functions of r. The regularity condition \( C_{1}(0) = 0\) must be satisfied by the function \( C_{1}(r)\), and its disappearance returns to the original LTB solution. The rest of the physical variables are presented by the field equations. To explain the procedure described earlier, we consider an example from the parabolic subclass of LTB which corresponds with Eq. (110) of [1] because we are following the strategy mention in [1]. Therefore, we take:

$$\begin{aligned} C(r,t)=(-t+T(r))^{\frac{2}{3}} f(r). \end{aligned}$$
(93)

The parameters for parabolic LTB solution are f(r) and T(r) . Using Eq. (93), we manifest the integral \( \int \frac{dt}{(C')^2} \) as

$$\begin{aligned} I=\int \frac{dt}{(C')^2}=\int \frac{(T(r)-t)^{\frac{2}{3}}dt}{[\frac{2}{3} T'(r)f(r)+(T(r)-t)f'(r)]^2}, \end{aligned}$$
(94)

plugging \( \tau ^3 = -t+T(r) \) in Eq. (94) and integration yields:

$$\begin{aligned} I=-3\int \frac{\tau ^4d\tau }{(a\tau ^{3}+b)^{2}}, \end{aligned}$$
$$\begin{aligned} I&=\frac{\tau ^2}{a^{2}\tau ^{3}+ab}+\frac{1}{3\root 3 \of {ba^{5}}}\nonumber \\&\times \left[ 2\sqrt{3}\arctan \left( \frac{1-2\root 3 \of {\frac{a}{b}\tau }}{\sqrt{3}}\right) -\ln \left( \frac{a\tau ^{3}+b}{(\root 3 \of {a}\tau +\root 3 \of {b})^{3}}\right) \right] , \end{aligned}$$
(95)

where \( b=\frac{2}{3}T'(r)f(r) \) and \( a=f'(r) \). Putting Eq. (95) in (91) and then utilizing (93) we obtain

$$\begin{aligned} 2\pi \tilde{q}_{eff} = \frac{C^{2}_{1}(r)f(r)^{-1}}{\left( C^{2}_{1}(r)\left[ \frac{\tau ^{2}}{a}+\frac{a\tau ^{3}+b}{3\root 3 \of {ba^{5}}} \left[ 2\sqrt{3}\arctan \left( \frac{1-2\root 3 \of {\frac{a}{b}\tau }}{\sqrt{3}}\right) -\ln \left( \frac{a\tau ^{3}+b}{(\root 3 \of {a}\tau +\root 3 \of {b})^{3}}\right) \right] \right] +C_{2}(r)(a\tau ^{3}+b)\right) ^{2}}. \end{aligned}$$
(96)

This expression exactly corresponds with Eq. (113) of [1] but the term \( \tilde{q}_{eff}\) contains the extra curvature terms and its value is mentioned in Eq. (27). When we desired LTB perturbations then the amplitude of dissipation is being regulated by the function \( C_{1}(r) \), which can be adjusted as little as desired. The results have shown that these GLTB can be transformed into LTB when we rule out dissipative fluxes. For a smaller value of \( C_{1}(r) \) associated with LTB geometry, the physical features of GLTB have logical consequences.

4.3 Symmetric properties

In this subsection, we present another way to obtain a GLTB spacetime under the impact of Palatini f(R) gravity and electromagnetic field. This study is based on the assumption that the symmetric properties of GLTB spacetime correspond to LTB. The Lie derivative of stress tensor w.r.t. \( \xi \) is defined as

$$\begin{aligned} {\L }_{\xi } T_{\alpha \zeta }=0, \end{aligned}$$
(97)

Taking the Lie derivative of the effective energy–momentum tensor in the presence of charge using (97) we get the following equations:

$$\begin{aligned}&\xi ^{1} \tilde{\mu }'_{eff}+\xi ^{0} \dot{\tilde{\mu }}_{eff}+2\tilde{\mu }_{eff} \xi ^{0}_{,0}-2\tilde{q}_{eff} B \xi ^{1}_{,0}+\frac{1}{4\pi }\frac{s^2}{C^4 F^5} \xi ^{0}_{,0}\nonumber \\&\quad +\frac{\xi ^{0}}{8\pi }\left( \frac{s^2}{C^4 F^5}\right) +\frac{\xi ^{1}}{8\pi }\left( \frac{s^2}{C^4 F^5}\right) =0, \end{aligned}$$
(98)
$$\begin{aligned}&-\xi ^{1} \tilde{q}'_{eff}-\xi ^{0} \dot{\tilde{q}}_{eff}+\tilde{\mu }_{eff} \frac{\xi ^{0}_{,1}}{B}-\tilde{q}_{eff}\nonumber \\&\quad \times \left( \xi ^{0}_{,0}+\xi ^{0} \frac{\dot{B}}{B}+\xi ^{1}\frac{B'}{B}+\xi ^{1}_{,1}\right) \nonumber \\&\quad +\epsilon _{eff} B \xi ^{1}_{,0}+\frac{1}{8 \pi }\frac{s^2}{C^4 F^5 B}\xi ^0_{,1} -\frac{1}{8 \pi }\frac{s^2}{C^4 F^5} B \xi ^1_{,0}=0, \end{aligned}$$
(99)
$$\begin{aligned}&\xi ^1 \epsilon '_{eff}+\xi ^0 \dot{\epsilon }_{eff}-2\tilde{q}_{eff} \frac{\xi ^0_{,1}}{B}+2\epsilon _{eff}\nonumber \\&\quad \times \left( \xi ^0 \frac{\dot{B}}{B}+\xi ^1 \frac{B'}{B}+\xi ^1_{,1} \right) \nonumber \\&\quad -\frac{\xi ^0}{8 \pi B^2}\left( \frac{s^2 B^2}{C^4 F^5}\right) -\frac{\xi ^1}{8 \pi B^2}\left( \frac{s^2 B^2}{C^4 F^5}\right) '\nonumber \\&\quad -\frac{\xi ^1_{,1}}{4\pi }\left( \frac{s^2}{C^4 F^5}\right) =0. \end{aligned}$$
(100)

We will describe two strategies for generalizing LTB based on symmetry in the presence of charge and Palatini extra curvature terms. Diffusion approximation \( ( q_{eff}\ne 0, \epsilon _{eff}=0, \tilde{q}_{eff}=q_{eff}) \) and streaming out limit \( (q_{eff}=0, \epsilon _{eff}\ne 0, \tilde{q}_{eff}=\epsilon _{eff})\).

4.3.1 Diffusion approximation

Following the same strategy as deployed by Herrera et al. [1], we use Eqs. (24) and (73) for the case of heat flux \( ( \epsilon _{eff}=0, q_{eff}\ne 0, \tilde{q}_{eff}=q_{eff}) \), we get

$$\begin{aligned} 8\pi q_{eff} B= \frac{C'}{C} \frac{\dot{K}}{1+K}, \end{aligned}$$
(101)

using Eqs. (73), (84) and (101), we get the following

$$\begin{aligned} 8\pi g(r)= \frac{\dot{K}}{(1+K)^{\frac{3}{2}}} \frac{C C'^2 F^{3}}{D_{3}}. \end{aligned}$$
(102)

Now, Eq. (100) suggests that \( \xi ^0 =F(t) \) in the case of LTB spacetime and by applying this result in Eqs. (98) and (99), we have

$$\begin{aligned}&F(t) \dot{\mu }_{eff}+\xi ^1 \mu '_{eff}+2\mu _{eff} \dot{F}(t) -2q_{eff} B \xi ^1_{,0}\nonumber \\&\quad +\frac{\dot{F}(t)}{4 \pi } \frac{s^2}{C^4 F^5} +\frac{F(t)}{8\pi } \left( \frac{s^2}{C^4 F^5}\right) \nonumber \\&\quad +\frac{\xi ^1}{8\pi } \left( \frac{s^2}{C^4 F^5}\right) '=0, \end{aligned}$$
(103)
$$\begin{aligned}&F(t) \dot{q}_{eff}+\xi ^1 q'_{eff}+q_{eff} \left( \dot{F}(t)+F(t)\frac{\dot{B}}{B}+\xi ^1 \frac{B'}{B}+\xi ^1_{,1}\right) \nonumber \\&\quad +\frac{B \xi ^1_{,0}}{8\pi } \left( \frac{s^2}{C^4 F^5}\right) =0. \end{aligned}$$
(104)

The Eq. (104) can be manifested in the following form

$$\begin{aligned}&F(t)\left[ \ln (q_{eff} B F(t))\right] ^{.}+\xi ^1\left[ \ln (q_{eff} B \xi ^1)\right] '\nonumber \\&\quad +\frac{B \xi ^1_{,0}}{8\pi } \left( \frac{s^2}{C^4 F^5}\right) =0, \end{aligned}$$
(105)

multiplying Eq. (105) by \( q_{eff}B \), we get

$$\begin{aligned} (q_{eff} F B)^{.}+(q_{eff} B \xi ^1)'+\frac{B \xi ^1_{,0}}{8\pi } \left( \frac{s^2}{C^4 F^5}\right) =0, \end{aligned}$$
(106)

now, from Eq. (106) we may write as

$$\begin{aligned} q_{eff} B F(t)=\psi '(t,r), \end{aligned}$$
(107)

using Eqs. (101) and (107), we get:

$$\begin{aligned} \psi '(t,r)=\frac{F(t)}{8\pi }\frac{C'}{C}\frac{\dot{K}}{1+K}. \end{aligned}$$
(108)

Now using the Eqs. (84), (107) and (108), we have

$$\begin{aligned} 8\pi g(r)=\frac{\dot{K}}{(1+K)^{\frac{3}{2}}} \frac{C C'^2 F^3}{D_{3}}, \end{aligned}$$
(109)

which exactly corresponds with Eq. (102). Integration of Eq. (102) yields

$$\begin{aligned} \frac{1}{(1+K)^{\frac{1}{2}}}= - 4\pi g(r) \int \frac{D_{3}dt}{C C'^2 F^3}+C'(r), \end{aligned}$$
(110)

where \( C'(r) \) denotes the integration constant. For a specific situation, using the value of C(t, r) by using Eq. (93), we obtain

$$\begin{aligned}&\frac{1}{(1+K)^{\frac{1}{2}}}=C'(r)+4\pi g(r)\nonumber \\&\quad \times \int \frac{3\dot{F} F^2}{[\frac{2}{3} T'(r) f(r)+(T(r)-t)f'(r)]} \nonumber \\&\quad +\frac{-4\pi g(r)}{F^3[\frac{2}{3} T'(r) f(r)+(T(r)-t)f'(r)]f(r) f'(r)}, \end{aligned}$$
(111)

inserting Eq. (111) in (84), we get the following relation

$$\begin{aligned} q_{eff}&=\frac{g(r)}{f^{2}(r)F^{3}(T(r)-t)^{\frac{2}{3}}}\left[ -\frac{4\pi g(r)}{f(r)F^{3}f'(r)}\right. \nonumber \\&\quad +\left( 4\pi g(r)\int \frac{3\dot{F} F^2}{(\frac{2}{3} T'(r) f(r)+(T(r)-t)f'(r))}\right. \nonumber \\&\quad \left. \left. +C'(r)\right) \left( \frac{2}{3} T'(r) f(r)+(T(r)-t)f'(r)\right) \right] ^{-2}. \end{aligned}$$
(112)

The GLTB spacetime derived using diffusion approximation is defined by four functions of r, although one function vanishes due to radial coordinate invariance. Two functions may be discovered using the LTB seed model, and the remaining one can be determined using the Eq. (106) under the assumption that the LTB solution has the same radial dependence as \( \xi \). Moreover, Eq. (112) is used to calculate the temperature profile using the transport equation for diffusion case. These results are compatible with those of [1].

4.3.2 Streaming out approximation

The Bianchi identities take the following form in the case of streaming out approximations \( (q_{eff}=0, \epsilon _{eff}\ne 0) \) as obtained by Herrea et al. in the case of GR [1].

$$\begin{aligned}&\left( \mu _{eff}+\frac{s^2}{8\pi C^4 F^5}\right) ^{.}-\frac{1}{B^3} \left[ \left( -\frac{B^2 s^2}{8\pi F^5 C^4}\right) ^{'}\right. \nonumber \\&\quad \left. -\frac{B^2 s^2}{8\pi F^5 C^4}\left( \frac{2B'}{B}-\frac{2C'}{C}-\frac{5F'}{2F}+\frac{\dot{F}B}{2F} +\dot{B}\right) \right] \nonumber \\&\quad +\left( \mu _{eff}+\frac{s^2}{8\pi C^4 F^5}\right) \left( \frac{\dot{B}}{B}+2\frac{\dot{C}}{C}+\frac{5\dot{F}}{2F}-\frac{F'}{2F B}\right) =0, \end{aligned}$$
(113)

integrating Eq. (113), we have

$$\begin{aligned} \mu _{eff}+\frac{s^2}{8\pi C^4 F^5}=\frac{j(r)D_{6}}{B C^2 F^{\frac{5}{2}}}, \end{aligned}$$
(114)

using Eqs. (73), (74), (75) and (114), we obtain

$$\begin{aligned} \mu _{eff}=\frac{3j(r)D_{6}[\int 4\pi \epsilon _{eff}Cdt+(1+\kappa (r))^{\frac{1}{2}}]}{(C^{3})'F^{\frac{5}{2}}}, \end{aligned}$$
(115)

where

$$\begin{aligned} D_{6}&=\exp \left[ \int \frac{F'}{2F B}dt+\int \frac{1}{B^3 \left( \mu _{eff}+\frac{s^2}{8\pi C^4 F^5}\right) }\right. \nonumber \\&\quad \times \left[ \left( -\frac{B^2 s^2}{8\pi F^5 C^4}\right) ^{'}-\frac{B^2 s^2}{8\pi F^5 C^4}\left( \frac{2B'}{B}-\frac{2C'}{C}-\frac{5F'}{2F}\right. \right. \nonumber \\&\quad \left. \left. \left. +\frac{\dot{F}B}{2F}+\dot{B}\right) \right] \right] =0, \end{aligned}$$
(116)

and j(r) is an integration constant function. Now the Eqs. (98)–(100) turn into the following form by keeping in view the assumption \( (\epsilon _{eff}\ne 0, q_{eff}=0) \) [1],

$$\begin{aligned}&\xi ^0(\mu _{eff}+\epsilon _{eff})^{.}+\xi ^1 (\mu _{eff}+\epsilon _{eff})'+2(\mu _{eff}+\epsilon _{eff})\xi ^0_{,0}\nonumber \\&\quad -2\epsilon _{eff} B \xi ^1_{,0}+\frac{\xi ^0_{,0}}{4 \pi } \frac{s^2}{C^4 F^5}+\frac{\xi ^0}{8\pi } \left( \frac{s^2}{C^4 F^5}\right) +\frac{\xi ^1}{8\pi } \left( \frac{s^2}{C^4 F^5}\right) '=0, \end{aligned}$$
(117)
$$\begin{aligned}&\xi ^0 \dot{\epsilon }_{eff}+\xi ^1 \epsilon '_{eff}-(\mu _{eff}+\epsilon _{eff})\frac{\xi ^0_{,1}}{B}\nonumber \\&\quad +\epsilon _{eff} \left( \xi ^0_{,0}+\xi ^0 \frac{\dot{B}}{B}+\xi ^1 \frac{B'}{B}+\xi ^1_{,1}\right) -\epsilon _{eff} B \xi ^1_{,0}\nonumber \\&\quad -\frac{\xi ^0_{,1}}{8\pi B}\frac{s^2}{C^4 F^5} +\frac{B \xi ^1_{,0}}{8\pi }\frac{s^2}{C^4 F^5}=0, \end{aligned}$$
(118)
$$\begin{aligned}&\xi ^0 \dot{\epsilon }_{eff}+\xi ^1 \epsilon '_{eff}-2\epsilon _{eff} \frac{\xi ^0_{,1}}{B}+2\epsilon _{eff}\left( \xi ^0 \frac{\dot{B}}{B}+\xi ^1 \frac{B'}{B}+\xi ^1_{,1}\right) -\frac{\xi ^0}{8\pi B^2} \left( \frac{B^2 s^2}{C^4 F^5}\right) \nonumber \\&\quad -\frac{\xi ^1}{8\pi B^2} \left( \frac{B^2 s^2}{C^4 F^5}\right) ' -\frac{\xi ^1_{,1}}{4\pi } \frac{s^2}{C^4 F^5} =0. \end{aligned}$$
(119)

Solving Eqs. (117), (118) and (119), we have

$$\begin{aligned}&\xi ^0 \dot{\mu }_{eff}+\xi ^1 \mu '_{eff}+2 \mu _{eff} \xi ^0_{,0}+2 \mu _{eff} \frac{\xi ^0_{,1}}{B}+\frac{1}{4\pi } \frac{s^2}{C^4 F^5}\nonumber \\&\quad \times \left( \xi ^0_{,0} +\frac{\xi ^0_{,1}}{B}-\xi ^1_{,0} B-\frac{\xi ^1_{,1}}{2}-\xi ^0 \frac{\dot{B}}{B}-\xi ^1 \frac{B'}{B}\right) =0. \end{aligned}$$
(120)

To indulge the property of maximal similarity between LTB geometry and GLTB, we assume that \( \xi ^0=F(t), \) and in this scenario, the Eqs. (117)–(119) take the form [1]

$$\begin{aligned}&F(t)(\mu _{eff}+\epsilon _{eff})^{.}+\xi ^1 (\mu _{eff}+\epsilon _{eff})'\nonumber \\&\quad +2 \left( \mu _{eff}+\epsilon _{eff}+\frac{1}{8\pi }\frac{s^2}{C^4 F^5}\right) \dot{F}(t)-2\epsilon _{eff} B \xi ^1_{,0}\nonumber \\&\quad +\frac{F(t)}{8\pi }\left( \frac{s^2}{C^4 F^5}\right) ^{.}\nonumber \\&\quad +\frac{\xi ^1}{8\pi }\left( \frac{s^2}{C^4 F^5}\right) =0, \end{aligned}$$
(121)
$$\begin{aligned}&F(t) \dot{\epsilon }_{eff}+\xi ^1 \epsilon '_{eff}+\epsilon _{eff} \left( \dot{F}(t)+F(t)\frac{\dot{B}}{B}+\xi ^1 \frac{B'}{B}+\xi ^1_{,1} \right) \nonumber \\&\quad -\epsilon _{eff} B \xi ^1_{,0}+\frac{B\xi ^1_{,0}}{8\pi } \frac{s^2}{C^4 F^5}=0, \end{aligned}$$
(122)
$$\begin{aligned}&F(t) \dot{\epsilon }_{eff}+\xi ^1 \epsilon '_{eff}+2\epsilon _{eff} \left( F(t) \frac{\dot{B}}{B}+\xi ^1 \frac{B'}{B}+\xi ^1_{,1} \right) \nonumber \\&\quad -\frac{F(t)}{8\pi B^2}\left( \frac{B^2 s^2}{C^4 F^5}\right) ^{.}-\frac{\xi ^1}{8\pi B^2}\left( \frac{B^2 s^2}{C^4 F^5}\right) '-\frac{\xi ^1_{,1}}{4\pi }\frac{s^2}{C^4 F^5}=0. \end{aligned}$$
(123)

The Eq. (123) may be written as

$$\begin{aligned}&F(t) \left[ \ln (\epsilon _{eff} B^2 )\right] ^{.} + \xi ^1 \left[ \ln (\epsilon _{eff} (B \xi ^1)^2 ) \right] '+\frac{F(t)}{8\pi B^2 \epsilon _{eff}}\left( \frac{B^2 s^2}{C^4 F^5}\right) ^{.}\nonumber \\&\quad +\frac{1}{8\pi B^2 \epsilon _{eff} \xi ^1}\left( \frac{(B s \xi ^1)^2}{C^4 F^5}\right) '=0, \end{aligned}$$
(124)

or Eq. (123) may also be rewritten as

$$\begin{aligned}&F(t) (\epsilon _{eff} B^2)^{.} +\frac{1}{\xi ^1} (\epsilon _{eff} (B \xi ^1)^2 )'+\frac{F(t)}{8\pi }\left( \frac{B^2 s^2}{C^4 F^5}\right) ^{.}\nonumber \\&\quad +\frac{1}{8\pi \xi ^1}\left( \frac{(B s \xi ^1)^2}{C^4 F^5}\right) '=0, \end{aligned}$$
(125)

under these assumptions the Eq. (46) becomes

$$\begin{aligned}&\left[ \ln (\epsilon _{eff}(B F C)^2 ) \right] ^{.} +\frac{1}{B} \left[ \ln (C^2 \epsilon _{eff}) \right] '+\frac{3 F'}{B}+\frac{\dot{F}}{F} \nonumber \\&\quad +\frac{F'}{2BF} \left( \frac{\mu _{eff}}{\epsilon _{eff}}\right) +\frac{1}{8\pi B \epsilon _{eff}}\left( \frac{3F'}{F}+\frac{2B'}{B}-\frac{2C'}{C}\right) \frac{s^2}{C^4 F^5}\nonumber \\&\quad -\frac{1}{8\pi B^3 \epsilon _{eff}}\left( \frac{B^2 s^2}{C^4 F^5}\right) '=0, \end{aligned}$$
(126)

Or Eq. (126) may be rewritten as

$$\begin{aligned}&\left[ \epsilon _{eff} (B F C)^2 \right] ^{.}+B F^2 (\epsilon _{eff} C^2)'+B^2 F \dot{F} C^2 \epsilon _{eff}\nonumber \\&\quad +\frac{F' B C^2 F}{2} \mu _{eff}+3B F^2 F' C^2 \epsilon _{eff} -\frac{B}{8\pi }\left( \frac{s^2}{C^2 F^3}\right) '=0. \end{aligned}$$
(127)

The following approach can be used to obtain GLTB based on LTB (in the streaming out approximation) in the presence of f(R) gravity and electric charge:

Assume that the radial dependence of the LTB solution is comparable to the vector field \( \xi ^{1} \). Take the value of \( (\epsilon _{eff} B^2) \) from Eq. (127) and insert it into Eq. (125).

Using a definite LTB model with a specified vector field \( \xi \), assuming \( F(t)=1 \) and integrating Eq. (125), we obtain the effective radiation density with respect to r. These results are compatible with those of GR under usual limit [1].

5 Discussion

The observations of type Ia supernovae have motivated the researchers to study the inhomogeneous LTB spacetime for determining the accelerated rate of the universe expansion. In this article, we have studied the inhomogeneous LTB geometry and its properties in the framework of f(R) gravity. The f(R) gravity enables us to a better understanding of the inflationary era and late-time accelerated rate of the universe expansion. We have considered the dissipative dust fluid along with spherically symmetric spacetime to study the consequences of charge and f(R) terms. To continue further, we have evaluated the Maxwell-field equations for compact objects and have seen that the field equations contain the higher-order terms due to the Palatini formulation. We have computed the matter variables in the context of f(R) gravity which has a substantial role in the field of relativistic astrophysics and found that the four acceleration components appear only due to the Palatini version. To observe the amount of matter inside the geometrical object, we utilized the interpretation for mass function presented by Misner and Sharp and devised the Darmois junction conditions for smooth fitting of the solutions. We have established an expression for Weyl scalar in terms of fluid variables along with dark source terms that demonstrated the consequences of the charge. The method used by Ellis has been adopted to investigate the evolution equations to examine the inhomogeneities that arise due to the presence of the Weyl tensor.

Herrera et al. [26] computed a set of scalar functions using the orthogonal decomposition method to express the physical behavior of the matter variables and these scalars are known as structure scalars. We set up the expressions for tensors \( Y_{\alpha \zeta } \) and \( X_{\alpha \zeta } \) in f(R) gravity and further break down into their trace and trace-free parts. The energy density of the fluid is addressed by the scalar \( X_{T} \) with extra curvature terms that identify the outcomes of an unknown form of energy and matter. The scalar \( Y_{T} \) carried the information about the pressure anisotropy with higher-order terms due to modified gravity that signifies the existence of DM and DE. These scalars are also served to express the solutions of field equations using a static spacetime and we have associated them with metric coefficients using field equations. The previously attained differential and evolution equations are expressed in the form of scalar functions through modified field equations.

We generalized LTB spacetime by following the strategy as mentioned in [1] in the background of Palatini f(R) gravity and electric charge. We studied the properties of LTB geometry and analyzed the behavior of evolution equation by considering the masses of compact objects through graphical representation and found the structure scalars for LTB geometry using (63). The LTB spacetime has been extended for dissipative fluid which is known as generalized LTB spacetime (GLTB) and we have calculated the scalar functions for GLTB with the inclusion of charge and curvature terms. We compared the structure scalars obtained from LTB and GLTB to achieve the maximum similarity between two spacetimes and studied the symmetric properties of LTB and GLTB geometry using two techniques. we have estimated a transport equation to obtain the temperature profile for the diffusion case. In this article, the generalization of LTB spacetime has been modified and our calculation has generalized the previously obtained results under the influence of charge in f(R) gravity. Our results are compatible with those of GR [1] under the usual limit.