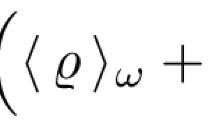1 Introduction

In recent years, there has been a growing interest in non-trivial spacetime topologies in Einstein’s General Theory of Relativity (GR). The wormholes in GR allow topological passage through hypothetical tunnel connecting two distant regions of a universe or two different universes. In 1957 Wheeler and Misner [1, 2] coined the term wormhole, a number of interesting features of the traversable wormholes led to a spurt in activities in theoretical physics [3, 4]. Visser [5,6,7,8,9] elegantly constructed traversable wormhole based on surgical modified solution of the Einstein’s field equations. The observed features of the wormhole solutions may be taken up for constructing hypothetical time machine [10, 11]. In the literature [12, 13], it is found that astrophysical accretion of ordinary matter could convert wormholes into black holes. Hayward [14] shown that black holes and wormholes are interconvertible structures and stationary wormholes may be the final stage of a evaporating black hole. The stability of the wormhole solutions in GR are also analysed in the presence of matter [15,16,17,18,19,20,21,22,23,24] and in some generalized theories of gravity (see, e.g. , [25]). Considering the end-state of stellar mass binary black hole merger in GW150914 as a possible wormhole candidate, it is shown [26] that their properties can be measured from the distinct signatures imprint in the gravitational waves as they settle down in the post merger phase from an initially perturbed state.

It is known that in GR, Lorentzian wormhole solution exists when the matter energy condition is violated. The matter sector of the Einstein gravity supporting such geometries violates the null energy condition (NEC) at the throat of the wormhole [27, 28] for its existence. The matter violating NEC \((\rho + p)_{eff}|_{r_0} <0\) (\(r_0\) is the wormhole throat radius) is called exotic matter. The exotic matter at the throat signifies that an observer who moves through the throat with a radial velocity approaching the speed of light will observe presence of negative energy density. The necessity of exotic matter or modification of the matter sector in GR is also felt to understand the recent discovery of the astronomical observations that the universe is experiencing a phase of accelerated expansion. It is a challenging job in theoretical physics, to accommodate the phase of expansion of the universe in GR modifying the matter sector which violates the energy conditions. The prediction that the universe may be composed of unknown cosmic fluids in addition to normal matter led to scrutiny for cosmological models for a realistic scenario with dark energy (DE), phantom, Chaplygin gas [29,30,31,32] etc.. The phantom field [33,34,35], Chaplygin gas [36], DE [37,38,39] are employed to obtain wormholes. Böhmer et al. [40] obtained a class of wormhole solutions systematically with exotic matter restricted to the throat neighbourhood and with a cutoff of the stress energy tensor at a junction interface, in addition to the asymptotically flat exact solutions. Thus there is an amazing and unexpected overlapping between the two different topics.

It is known that the wormhole solutions mediating spatial topology change by absorption and production of baby universes provided a mechanism for realizing a vanishing cosmological constant [41,42,43,44,45,46, 48, 49]. The topology-changing amplitudes in classical and quantum gravity and their association with degenerate metrics, creation of a universe from nothing, kinematic possibilities for existence of spinors, cobordism theory, etc. have been reported in Ref. [50]. In this context gravitational instantons which are the Euclidean solutions with finite action in wide classes of theories can be employed to understand in a better way. The Euclidean wormholes [51, 52] play a significant role in understanding origin of the universe without singularity which however, contributes to the Euclidean path integral formulation of quantum gravity. A consistent theory of quantum gravity is not yet known. However, the superstring theory is considered to be a promising candidate for quantum gravity which requires 10 dimensions for its consistent formulation. The advent of string theory led a paradigm shift in higher-dimensional cosmology. Consequently astrophysical and cosmological issues in GR find wide attention in higher dimensions.

The original Morris-Thorne wormhole can be generalized by inducting a time dependent scale factor that gives an evolving relativistic wormhole. The evolving relativistic wormholes or rather dynamical wormholes are not very popular in the literature. However, various work on dynamical wormholes speculated their existence with matter satisfying weak energy condition (WEC) and dominated energy condition (DEC) [53,54,55]. Also there are other works [56, 57] speculating that matter threading the wormhole violates NEC. Recently dynamical wormholes have been explored in the presence of two different fluids [58, 59] for realizing expanding universe that accommodates the present accelerating phase [60,61,62,63] and in the presence of dissipation due to particle creation in non-equilibrium thermodynamics [64].

A higher-dimensional dynamical wormhole satisfying NEC was obtained by Zangeneh et al. [65] for a spatially homogeneous Ricci scalar to obtain power law or de Sitter expansion. In this paper we extend the analysis of dynamical wormholes in a higher dimensional GR with non-linear equation of state (nEoS) to explore the origin of an emergent universe [66] The EU model is free from Big Bang singularity assuming that the universe originated from an Einstein static universe (ESU) which will be explored. A closed EU model [66,67,68] can be obtained assuming the universe originated from ESU with no singularity in GR making use of particular scalar field potential which also admits the present accelerating phase. It is shown subsequently that such potential is admissible in \(R+ \alpha R^2\) gravity [67]. Subsequently, a flat EU model was obtained with nEoS in GR [69]. Flat EU model is also implemented in different theories of gravity [70,71,72,73,74,75,76] with the observed features [77,78,79,80,81,82,83]. The nEoS [69] \(p = A \rho - B \sqrt{\rho _o \rho }\) that admits an EU model, permits three different barotropic fluids determined by A and B. The fluids are identified with exotic matter, dark energy and normal matter. For a given A, the non-interacting cosmic fluids are identified which however fails to describe the observed universe because the composition of fluids are fixed, the changing phases of the universe with matter cannot be realized. However, a viable cosmological scenario can be obtained taking into account interaction among fluids that originates at a later epoch [84, 85]. We obtain EU model using dynamical wormhole solutions permitted in the GR with nEoS. It accommodates ESU in the infinite past at the throat. The gravitational instanton in Euclidean gravity will be also considered here to investigate the possibility and naturalness of EU scenario in four and in higher dimensions.

The paper is organized as follows: In Sect. 2, the Einstein field equation in higher dimensions with wormhole geometry is discussed. In Sect. 3, Emergent Universe models are obtained in flat, open and closed universes and study their origin with dynamical wormholes using the shape functions obtained from a homogeneous Ricci scalar. The higher dimensional flat EU model is discussed with nEoS. We also discuss the new EU solutions obtained here in closed universe. In Sect. 4 considering interacting cosmic fluid we discuss EU scenario. In Sect. 5 we discuss gravitational instantons that permits a flat emergent universe. In Sect. 6 we summarise the result.

2 Einstein field equation in higher dimensions and wormhole geometry

We consider a higher dimensional gravitational action which is given by

$$\begin{aligned} I= - \frac{1}{16 \pi G_D} \; \int \sqrt{-g} \;d^Dx \;R +I_m \end{aligned}$$
(1)

where R is the Ricci scalar, \(G_D\) is the D-dimensional gravitational constant and \(I_m\) represents the matter action. The Einstein field equation is given by

$$\begin{aligned} R_{AB} -\frac{1}{2} g_{AB}R = \kappa ^2 T_{AB} \end{aligned}$$
(2)

where \(A, B = 0,1, \ldots , D-1\) and \(T_{AB }= ( \rho , P_r, P_t, \ldots )\) the energy-momentum tensor, \(\rho \) the energy density, \(P_r\) the radial pressure, \(P_t\) transverse pressure, \(\kappa ^2=8 \pi G_D\) and \( c=1\). The D dimensional spacetime metric for expanding wormholes is given by

$$\begin{aligned} ds^{2}= - dt^{2} + S(t) ^2 \left[ \frac{dr^{2}}{1- \alpha (r) } + r^2 d\varOmega ^2_{D-2} \right] \end{aligned}$$
(3)

where \( d\varOmega ^2_{D-2}= d\theta _1^2+ sin^2 \theta _1 d\theta _2^2 +sin^2 \theta _2 (d\theta _3^2 + \cdots +sin^2 \theta _{D-3} \; d\theta _{D-2}^2)\), S(t) is scale factor, \(\alpha (r)\) is an unknown dimensionless function. We consider \(\alpha (r)= \frac{b(r)}{r}\), where b(r) is the shape function [4,5,6,7,8, 10,11,12,13]. The metric is a generalization of the FRW metric but less symmetric than the FRW metric. However, it is still isotropic about the center of the symmetry but may not be homogeneous. For the vanishing shape function i.e.,  \(\alpha (r) \rightarrow 0\), the metric reduces to a flat Robertson-Walker (RW) metric and approaches to a static wormhole metric for \(S(t) \rightarrow const.\). The wormhole form of the metric is preserved with time for an embedding \(t=const.\) and \(\theta _{1}=\frac{\pi }{2}\) and setting others \(\theta _{D-4}= \frac{\pi }{2} \), slices of the spacetime given by Eq. (3) in a flat three dimensional Euclidean space given by

$$\begin{aligned} ds^2=d{\bar{z}}^2+d{\bar{r}}^2+{\bar{r}}^2 d\phi ^2. \end{aligned}$$
(4)

The metric of the wormhole slice is

$$\begin{aligned} ds^{2}= S(t) ^2 \left[ \frac{dr^{2}}{1- \alpha (r) } + r^2 d\phi ^2 \right] . \end{aligned}$$
(5)

Now, comparing Eq. (4) with Eq. (5) we can write

$$\begin{aligned} d{\bar{r}}^2 = S^2(t) dr^2|_{t=const.}, \quad {\bar{r}} = S(t) r|_{t=const.}, \end{aligned}$$
(6)

it can be regarded as the rescaling of the radial coordinate r on each \(t=const.\) slice [86]. The “wormhole” form of the metric will be preserved with respect to the \({\bar{z}}\), \({\bar{r}} \) and \(\phi \) coordinates, if the embedded slice has the following metric given by

$$\begin{aligned} ds^{2}=\frac{d{\bar{r}}^{2}}{1- {\bar{b}}({\bar{r}})/{\bar{r}} } + {\bar{r}}^2 d\phi ^2, \end{aligned}$$
(7)

where \({\bar{\alpha }} ({\bar{r}}_{0})=1\), i.e. \({\bar{b}} ({\bar{r}})\) has a minimum at \({\bar{b}} ({\bar{r}}_{0})={\bar{r}}_{0}\) and \({\bar{\alpha }} ({\bar{r}}) = S(t) \alpha (r)\). Now the Eq. (5) can be written in the form of Eq. (7) using the Eq. (6) and we get

$$\begin{aligned} {\bar{a}} ({\bar{r}}) = S(t) \; a (r) \end{aligned}$$
(8)

where S(t) is a constant at \(t=const. \;\) surface. The evolving wormholes will have the same size and shape relative to the \({\bar{z}} \), \({\bar{r}}\), \(\phi \) coordinate system, as the initial wormhole is described by the coordinates of the initial embedding space at \(t=constant\). Following the embedding procedure prescribed in Ref. [6] we obtain the following equation from Eqs. (4) and (7)

$$\begin{aligned} \frac{d{\bar{z}}}{d{\bar{r}}} = \pm \left( \frac{{\bar{r}}}{{\bar{b}}({\bar{r}})} -1 \right) ^{-\frac{1}{2} }= \frac{dz}{dr} \end{aligned}$$

it is now easy to see that

$$\begin{aligned} {\bar{z}}({\bar{r}})= & {} \pm \int \frac{d{\bar{r}}}{\sqrt{ \frac{{\bar{r}}}{{\bar{b}}({\bar{r}}) }-1}}\\= & {} \pm S(t) \int \sqrt{ \frac{b(r)}{r-b (r) } } \; dr= \pm S(t) z(r). \end{aligned}$$

Thus we obtain the initial embedding space at \(t=t_0\) and the embedding space at any time t making use of the above equation with the Eq. (6) which is given by

$$\begin{aligned} ds^{2}= d{\bar{z}}^2 + d{\bar{r}}^2 + {\bar{r}}^2 d\phi ^2 = S^2(t) ( dz^2 +dr^2 +r^2 d\phi ^2 ),\nonumber \\ \end{aligned}$$
(9)

where

$$\begin{aligned} {\bar{b}}({\bar{r}}) = S(t) b(r). \end{aligned}$$
(10)

The wormhole will change size relative to the initial embedding space. The flaring out condition for the evolving wormhole at or near the throat is \(\frac{d^2 {\bar{r}} ({\bar{z}})}{d{\bar{z}}^2} > 0\). Using Eqs. (6) and (9) we get

$$\begin{aligned} \frac{d^2 {\bar{r}} ({\bar{z}})}{d{\bar{z}}^2} = \frac{1}{S(t)} \left( - \frac{\alpha '}{2 \alpha ^2} \right) = \frac{1}{S(t)} \frac{d^2r(z)}{dz^2} > 0. \end{aligned}$$
(11)

where \(()'\) represents derivative w.r.t r at or near the throat and \(\alpha ' <0\). From Eqs. (6), (10), and (11) we get

$$\begin{aligned} \frac{d^2 {\bar{r}}({\bar{z}})}{d{\bar{z}}^2} = \frac{1}{S(t)} \frac{b-b'r}{2b^2} = \frac{1}{S(t)} \frac{d^2r(z)}{dz^2} >0 \end{aligned}$$
(12)

at or near the throat. Using Eqs. (6) and (10) it follows

$$\begin{aligned} {\bar{b}}'({\bar{r}}) = \frac{d{\bar{b}}}{d{\bar{r}}} = b'(r)=\frac{db}{dr} \end{aligned}$$
(13)

and from Eq. (12) relative to the coordinate system \({\bar{z}}\), \({\bar{r}} \) and \(\phi \) in the embedding space can be rewritten as

$$\begin{aligned} \frac{d^2 {\bar{r}}({\bar{z}})}{d{\bar{z}}^2} =\left( \frac{{\bar{b}}- {\bar{b}}' {\bar{r}}}{2b^2} \right) > 0, \end{aligned}$$
(14)

at or near the throat. Thus the flaring out condition in the barred coordinate has the same form as for a static wormhole.

2.1 Gravitational field equations

For the D-dimensional metric (3) and the anisotropic energy momentum tensor given by \(T^{A}_{A} = (- \rho \), \( P_r, P_t, P_t, \ldots , P_t\)), where \(\rho \) the energy density, \(P_r \) and \(P_t \) are radial and transverse pressures respectively. The components of the Einstein field equation yields

$$\begin{aligned}&\frac{ (D-2)(D-3) \alpha (r)}{2 S^2(t) r^2} + \frac{(D-2) \alpha '(r)}{2 S^2(t) r} \nonumber \\&\quad +\frac{(D-1)(D-2)}{2} \frac{ {\dot{S}}^2(t)}{S^2(t)}= \kappa ^2 \rho (r, t), \end{aligned}$$
(15)
$$\begin{aligned}&- (D-2) \left[ \frac{ {\ddot{S}}(t)}{S(t)} + \frac{D-3}{2} \frac{ {\dot{S}}^2(t)}{S^2(t)} \right] \nonumber \\&\quad - \frac{(D-2)(D-3) \alpha (r)}{2 r^2 S^2(t)} = \kappa ^2 P_r (r, t), \end{aligned}$$
(16)
$$\begin{aligned}&- (D-2) \left[ \frac{ {\ddot{S}}(t)}{S(t)} + \frac{D-3}{2} \frac{ {\dot{S}}^2(t)}{S^2(t)} \right] \nonumber \\&\quad - \frac{(D-3)(D-4) \alpha (r)}{2 r^2 S^2(t)}- \frac{(D-3) \alpha '(r)}{2 r S^2(t)} = \kappa ^2 P_t (r, t) .\nonumber \\ \end{aligned}$$
(17)

Note that the Eqs. (15)–(17) are the Einstein field equations with anisotropic fluids in D dimensions. The Ricci scalar for the metric corresponding to the metric Eq. (3) is given by

$$\begin{aligned} R= & {} 2 (D-1) \frac{ {\ddot{S}}(t)}{S(t)} + \frac{(D-1)(D-2)}{2} \frac{{\dot{S}}^2(t)}{S^2(t) } \nonumber \\&+ \frac{(D-2)(D-3) \alpha (r)}{r^2 S^2(t)} + \frac{(D-2) \alpha '(r)}{r S^2(t)} \end{aligned}$$
(18)

here R is a function of r and t. For a homogeneous Ricci scalar, \(\left( \frac{\partial R}{\partial r} =0 \right) \), we obtain a second order differential equation in \(\alpha \) which is given by

$$\begin{aligned} r^2 \alpha ''(r) + (D-4) r \alpha '(r) -2 (D-3) \alpha (r) =0. \end{aligned}$$
(19)

The solution of the Eq. (19) is given by

$$\begin{aligned} \alpha (r) = C_1 \; r^{3-D} \pm C_2 \; r^2, \end{aligned}$$
(20)

where \(C_1\) and \(C_2\) are constants. Using \(C_2=k\) and basic need of wormhole \(\alpha (r_0)=1\), we determine other constant, which is \(C_1=\left( 1- k r_0^2 \right) r_0^{D-3}\), therefore, we get

$$\begin{aligned} \alpha (r) = \frac{ r_0^{D-3} -k \; r_0^{D-1}}{r^{D-3} } + k\; r^2 \end{aligned}$$
(21)

although k is a continuous variable, we have used the fact that the spacetime is asymptotically RW and applied the normalization to make it convenient to identify the curvature index of RW metric, \(k=0 \;(flat), \; -1\; (open)\). The above expression admits only \(k=0\) and \(-1\) as it is necessary to satisfy the constraints for wormholes,

$$\begin{aligned} \alpha (r_0)=1, \quad \alpha (r)< 1 \quad \mathrm{and} \quad \alpha '(r) <0. \end{aligned}$$
(22)

Now we set \(c_2=-k\) in Eq. (20) and obtain

$$\begin{aligned} \alpha (r) = \frac{ r_0^{D-3} + \; r_0^{D-1}}{r^{D-3} } -\; r^2 \end{aligned}$$
(23)

where \(k=1\) closed universe and it satisfies the criterion mentioned in Eq. (22). Using Eqs. (15)–(17), the energy density and the pressure corresponding to a flat dynamical universe are (we consider \(\kappa ^2=1\))

$$\begin{aligned} \rho (t)= & {} \frac{(D-1)(D-2)}{2} \frac{ {\dot{S}}^2(t)}{S^2(t)}, \end{aligned}$$
(24)
$$\begin{aligned} p(t)= & {} - (D-2) \left[ \frac{ {\ddot{S}}(t)}{S(t)} + \frac{D-3}{2} \frac{ {\dot{S}}^2(t)}{S^2(t)} \right] . \end{aligned}$$
(25)

The radial and transverse null energy conditions (NEC) are determined from the Eqs. (15)–(17) which are

$$\begin{aligned} \rho (r,t) + P_r (r,t)= & {} \rho (t) + p(t) + \frac{(D-2) \alpha '}{2 S^2 (t) r}, \end{aligned}$$
(26)
$$\begin{aligned} \rho (r,t) + P_t (r,t)= & {} \rho (t) + p(t) + \frac{(D-3) \alpha }{S^2 (t) r^2} + \frac{\alpha '}{2 S^2 (t) r}. \end{aligned}$$
(27)

We study the variation of the NEC in this case with the shape function that determines \(\alpha \) for a given wormhole structure.

3 Emergent universe scenario in \(D \ge 4\) dimensions and dynamical wormholes

3.1 EU in flat background

In this section we consider construction of an emergent universe with nEoS given by \(p(t)= A \rho (t) - B {(\rho _o \rho (t))}^{\gamma } \) where A, B and \(\rho _o\) are arbitrary parameters. It is interesting to note that \(\gamma < 0\) represents modified Chaplygin gas [87, 88] which will not be considered here. In the usual 4-dimensional Einstein gravity a flat emergent universe is obtained with \(\gamma > 0\) (i.e. \(\gamma =1/2\)). Thus we choose here \(\gamma = \frac{1}{2}\) in a \(D \ge 4\) dimensional universe to construct the EU scenario in four and in other dimensions. The objective is to explore the existence of Einstein static universe in the infinite past from which EU emerged in higher dimensional GR with nEoS. The important feature of the EU model is that there is no Big Bang singularity. EU model also accommodates the observed universe fairly well [69]. In the literature [70,71,72,73,74,75,76,77,78,79,80,81,82,83], EU model is implemented in a number of gravitational theories and found to work satisfactorily. We demonstrate here the emergent universe [69] model in the usual 4 and in higher dimensions making use of the nEoS with \(\gamma =\frac{1}{2}\) which is given by

$$\begin{aligned} p(t) = A \; \rho (t) -B \sqrt{\rho _o \; \rho (t)}. \end{aligned}$$
(28)

where A and B are constant and \(\rho _o\) is a dimensional constant. Using the dynamical field Eqs. (24) and (25) in flat background with the EoS given by Eq. (28) we construct a second order differential equation which is given by

$$\begin{aligned} \frac{{\ddot{S}}}{S} + \frac{A \; (D-1) +(D-3)}{2} \; \frac{{\dot{S}}^2}{S^2} - \beta \; \frac{{\dot{S}}}{S} =0 \end{aligned}$$
(29)

where \( \beta = B \sqrt{ \frac{(D-1) \rho _o}{2(D-2)} } \). On integrating once it yields

$$\begin{aligned} {\dot{S}} S^{\frac{A(D-1)+(D-3)}{2}} = \chi e^{\beta t} \end{aligned}$$

where \(\chi \) is an integration constant and once again integrating the differential equation we obtain the solution

$$\begin{aligned} S(t) = \left[ \frac{(A+1)(D-1)}{2} \left( a_o + \frac{\chi }{ \beta } \; e^{\beta t}\right) \right] ^{\frac{2}{(A+1)(D-1)}} \end{aligned}$$
(30)
Table 1 Composition of universal matter with A, \(\omega _2\) corresponds to exotic matter (EM), \(\sigma = \frac{(D-1) (A+1)}{2}\)
Full size table

where \(a_0\) is an integration constant. We discard \(B < 0\) as it represents a singular cosmology. A singularity free solution is obtained for \(B >0\) and leads to an emergent universe (EU) scenario. In the EU scenario [66,67,68,69] one of the basic assumption is that the present universe emerged from an Einstein static universe (ESU) in the infinite past. We demonstrate that such a early Einstein static universe at infinite past exists and it may be the throat of the wormhole which evolves very slowly to encompass the present universe. In this case the size of the Einstein static universe is given by

$$\begin{aligned} S_0=\left( \frac{1}{2} (A+1)(D-1) a_0\right) ^{\frac{2}{(A+1)(D-1)}} \end{aligned}$$
(31)

which is the size of the static universe (ESU) at \(t \rightarrow - \infty \) follows from the Eq. (30). As the universe evolves the size of the universe increases and at \(t=0\) we obtain

$$\begin{aligned} S(t=0)= \left[ \frac{1}{2} (A+1)(D-1) \left( a_o+ \frac{ \chi }{\beta } \right) \right] ^{\frac{2}{(A+1)(D-1)}}>S_0. \end{aligned}$$

The conservation equation in D-dimensions is given by

$$\begin{aligned} \frac{d \rho }{dt} + (D-1) (\rho +p) \; \frac{{\dot{S}}}{S} =0. \end{aligned}$$
(32)

Here p is replaced by the nEOS given by Eq. (28) and integrating once yields the energy density given by

$$\begin{aligned} \rho (S)= \left( \frac{1}{1+A} \right) ^2 \left( B \sqrt{\rho _o} + \frac{K}{S^{\frac{(D-1)(1+A)}{2}}}\right) ^2 \end{aligned}$$
(33)

where K is an integration constant. Therefore, the energy density from Eq. (33) can be expressed

$$\begin{aligned} \rho (t)= & {} \left( \frac{B}{1+A} \right) ^2 \rho _o + \frac{2\;B K\sqrt{\rho _o}}{(1+A)^2} \frac{1}{S^{\sigma }}.\nonumber \\&+ \left( \frac{K}{1+A} \right) ^2 \frac{1}{S^{2\sigma }}. \end{aligned}$$
(34)

Now using Eq. (34) in Eq. (28) we determine the pressure which is expressed in the form

$$\begin{aligned} p (t)= & {} - \left( \frac{B}{1+A} \right) ^2 \rho _o + \frac{B K (A-1) \sqrt{\rho _o}}{(1+A)^2} \frac{1}{S^{\sigma }} \nonumber \\&+ A \left( \frac{K}{1+A} \right) ^2 \frac{1}{S^{2\sigma }}. \end{aligned}$$
(35)

for simplicity we denote \( \frac{(D-1) (1+A)}{2} = \sigma \). The energy density and pressure are determined by the EoS parameters A, B, spacetime dimension D and the constant K. Thus there are three different model parameters both in the energy density and pressure for a given spacetime dimensions. Now we compare the energy density \(\rho =\rho _1+\rho _2+\rho _3\) and pressure \(p=p_1+p_2+p_3\) with the barotropic equation: \(p_i= \omega _i \; \rho _i\), where \(i=1, \; 2, \; 3\) and identified that \(\omega _1 =-1, \; \; \omega _2=\frac{A-1}{2}, \;\; \omega _3=A\). The composition of fluid is determined once A is given and found that the cosmological constant \(\varLambda = \left( \frac{B}{A+1} \right) ^2\rho _o \) at the early epoch. The distribution of cosmic fluids of the universe for a given A is tabulated in Table 1. We identify the composition of the cosmic fluids for a given A. For a given value of the EoS parameter A, the matter composition of the universe gets determined which remains fixed. Thus the EU model does not work well, it is not possible to describe the evolution of the different phases of the universe. Recently it is shown that a realistic EU scenario emerged when we assume interaction among the cosmic fluids that might have originated at a later epoch [84] which will be studied in Section IV in the usual four and in higher dimensions.

3.2 Dynamical wormhole for EU

The dynamical wormhole solutions for EU are obtained assuming a homogeneous Ricci scalar. We impose the following conditions on the shape function \(b(r) = r \; \alpha (r)\) which are:

  • the radial coordinate \(r_{0} \le r \le \infty \), where \(r_{0}\) is throat radius,

  • \(b(r_{0})=r_{0}\) at the throat and away from the throat \(b(r) < r\),

  • it satisfies the flaring out condition \(b'(r_{0})<1\),

  • for an asymptotic flatness of the spacetime \( \frac{b(r)}{r} \rightarrow 0 \ \ \ as \ \ \ |r| \rightarrow \infty \).

In the usual four and in higher dimensions, the NEC [87] is \(T_{AB} u^{A} u^{B} \ge 0\) where \(u^{A}\) the null vector. The radial NEC and transverse NEC are \( \rho + P_r \ge 0, \; \; \rho + P_t \ge 0\) which will be studied here. Using the energy density and pressure given by Eqs. (34), (35) and \(\alpha (r)\) from Eq. (21) we rewrite Eq. (26) in EU model which is given by

$$\begin{aligned} \rho (r,t) + P_r (r,t)= & {} - \frac{(D-2)(D-3) r_0^{D-3} }{2 S^2 (t) \; r^{D-1}} + \frac{B K \sqrt{\rho _o}}{(1+A) S^{\sigma }} \nonumber \\&\quad + \left( \frac{K}{1+A}\right) ^2 \frac{A+1}{S^{2\sigma }}, \end{aligned}$$
(36)

where \(\sigma = \frac{(D-1) (1+A)}{2}\), we use the above expression to test the validity of the radial NEC. For an example, we set the size of the initial Einstein static universe with that of the wormhole neck radius (i.e., \(S_0 =r_0\)) in \(D=4\) dimensions and \(A= \frac{1}{3} \) which yields \(\sigma =2\), then NEC reduces to

$$\begin{aligned} \rho (r,t) + P_r (r,t)= \frac{3B K\sqrt{\rho _o} }{4S_0^2} - \left( 1 - \frac{3K^2}{4} \right) \frac{1}{S_0^4}. \end{aligned}$$
(37)

Thus NEC is obeyed right from the wormhole throat for an ESU satisfying the lower bound \(S_0^2 \ge \frac{4-3K^2}{3BK\sqrt{\rho _o}}\). For a positive EoS parameter B, one gets a lower limiting value \( K \ge \frac{2}{\sqrt{3}}\). The transverse NEC obtained from the Eq. (27) is given by

$$\begin{aligned} \rho (r,t) + P_t (r,t)= & {} \frac{(D-3) r_0^{D-3}}{2S^2 (t) r^{D-1}} + \frac{B K \sqrt{\rho _o}}{(1+A) S^{\sigma }} \nonumber \\&+ \left( \frac{K}{1+A}\right) ^2 \frac{A+1}{S^{2\sigma }} >0. \end{aligned}$$
(38)

Thus a realistic EU model can be realized in the GR with matter described by a nEOS. The non-linear part of the EoS is analogous to the viscous term in the fluid. It is interesting to note that the nEoS led to three different fluids that can be identified with the matter composition of the universe. In an EU at \(t \rightarrow - \infty \) in Eq. (30), the initial size of the ESU gets determined which is \(S_0= ( \sigma a_0)^{\frac{1}{ \sigma }}\), and we set the wormhole throat radius \(r_0=S_0\). Thus the throat radius is a function of A, \(a_0\) and D. It is noted that for \(D=4\), maximum size of the initial static phase of the universe is obtained with \(A=\frac{1}{3}\) in 4 dimensions corresponding to radiation.

The wormhole will sustain with normal matter and admits an EU. For \(r \ge r_0\), the total radial NEC \(\rho +P_r\) is obeyed when the energy density at the throat of the wormhole satisfies a lower bound

$$\begin{aligned} \rho \ge \left( \frac{\sqrt{\varLambda }}{2} + \sqrt{ \frac{\varLambda }{4}+ \frac{ (A+1) (D-3)(D-2)}{2 (A+1)^2 r_0^2 \;S_0^2}} \right) ^2 \end{aligned}$$

where \(\varLambda = \left( \frac{B}{A+1} \right) ^2 \rho _o \). For \(D=3\), the density at the throat, \(\rho (r_0)|_{D=3} \ge \varLambda \). However, in the usual 4 dimensions, we note that the lower limit of density \(\rho (r_0)|_{D=4}\) is shifted towards a higher value compared to \(D=2+1\) dimensions. In the EU model

$$\begin{aligned} N_{fb}= (D-2) \left[ A(D-1) \frac{{\dot{S}}^2}{S^2}- \beta \frac{{\dot{S}}}{S} \right] \ne 0 \end{aligned}$$
(39)

which is not valid in an expanding universe namely, de Sitter universe where \(N_{fb}=0\) always as the universe evolves. It is shown in Ref. [65] that the NEC in five dimensions is obeyed always with barotropic fluid \(p=\omega \rho \) when \(\omega >-1\). In the EU model, we note that the radial NEC obeys at or near the throat when the wormhole neck radius is same as that of the ESU if \(S_0^2 \ge \frac{4-3K^2}{3BK\sqrt{\rho _o}}\). The transverse NEC is always valid, to test the matter that sustains the dynamical wormholes for EU we study temporal variation of the radial NEC which is plotted in Fig. 1 for \(D=4, \;5, \;10\). It is evident that as the flat EU emerged out from Einstein static phase in the infinite past, NEC satisfies initially, thereafter it violates before reaching \(t=0\) and then obeys once again. The temporal variation of NEC is plotted in Fig. 2 for different EoS parameter B (\(B>0\)) in \(D=4\), the behaviour is found same as that obtained in Fig. 1. The temporal variation of radial NEC is plotted in Fig. 3 for different values of A in \(D=4\) dimensions. In the later case we note that at the beginning NEC is obeyed thereafter emerged two branches with the following features: (i) for \(A <0\), NEC obeys and then violates, (ii) for \(A > 0\) , NEC violate and then obeys again. Thus the sign of A is important which predicts the matter present in the universe. The violation of NEC near \(t=0\) predicts onset of interaction that sets in which transforms normal matter to exotic matter and vice versa subsequently to matter phase. For negative A, initially NEC is obeyed later it began to violate indicating origin of exotic matter at a later stage. For \(A >0\), we found exotic matter that transforms to matter. We note that in \(D=2+1 \) dimensions, a flat EU with normal matter emerged out from a dynamical wormhole.

Fig. 1
figure 1

Temporal variation of \(\rho + p_r\) with \(D= 4 \; (red), \; 5 \; (blue), \; 10\; (green)\) with \(A=1, \; B\sqrt{\rho _o}=1\)

Full size image
Fig. 2
figure 2

Temporal variation of \(\rho + p_r\) with \(B= 1 \; (red), \; 5 \; (blue), \; 10\; (green)\) for \(D=4\)

Full size image
Fig. 3
figure 3

Temporal variation of \(\rho + p_r\) with \(A=-1/3 \; (red), \; -0.8 \; (dashed), \; 1/3 \; (green), \;1\; (blue)\) for \(D=4\)

Full size image

3.3 EU in closed/open background

Using the field Eqs. (15)–(16) and (23), in a closed universe we obtain the NEC for analyzing the cosmological model, which is given by

$$\begin{aligned} \rho +P_r = N_{fb} - \frac{D-2}{2S^2}\left[ 1 + \frac{(D-3) \; r_0^{D-3}(r_0^2+1)}{2r^{D-1}} \right] ,\nonumber \\ \end{aligned}$$
(40)

Using the field Eqs. (15)–(16) and (21) in an open universe NEC is given by

$$\begin{aligned} \rho +P_r= & {} N_{fb}- \frac{D-2}{ S^2}\nonumber \\&\times \,\left[ 1 + \frac{(D-3) \; r_0^{D-3}(r_0^2+1)}{2r^{D-1}} \right] , \end{aligned}$$
(41)

where \(N_{fb}\) is given by Eq. (39). The radial NEC is same for closed universe as well as open universe. Selecting the neck size of the wormhole equal to that of the size of the ESU and \(A= \frac{1}{3}\) in \(D=4\), radial NEC reduces to

$$\begin{aligned} \rho +P_r = \frac{3}{4S_0^2} (BK\sqrt{\rho _o}-2) - \frac{1}{4S_0^2} (2-3K^2). \end{aligned}$$
(42)

It is evident that the NEC respects at the throat when \(S_0^2 \ge \frac{2-3K^2}{3(BK\sqrt{\rho _o}-2)}\). For \( B=0\), we get a lower bound on \(K^2 > \frac{2}{3}\). In the case of non flat universe background NEC is violated near \(t=0\) indicating existence of exotic matter although the universe emerged out from the dynamical throat at infinite past with normal matter satisfying the EoS. We study the temporal variation of NEC as depicted in Figs. 2 and 3. NEC in \(D=4\) is plotted in Fig. 3 for \(r \ge r_0\), we note that NEC is satisfied in the infinite past indicating existence of normal matter at the throat. However, as it evolves near \(t=0\) the NEC is violated. In Fig. 3 it is evident that there exists two scenarios (i) with \(A<0\) where NEC obeys initially, subsequently at \(t=0\) it does not respect NEC, (ii) with \(A> 0\) where NEC violates near \(t=0\) but afterwards it obeys.

4 Interacting cosmic fluids in higher dimensions

The nEoS is equivalent to three different cosmic fluids which are given in Eqs. (34)–(35) and the cosmic fluid is non-interacting at the beginning. Assuming onset of interaction among the components of fluids (\(\rho = \rho _1 + \rho _2 +\rho _3\)) at \(t \ge t_i\) here \(t_i\) is the time when interaction originates, and the energy conservation Eq. (32) in the presence of interaction are

$$\begin{aligned}&\frac{d \rho _1 }{dt} + (D-1) H \; (\rho _1 + p_1) = Q, \end{aligned}$$
(43)
$$\begin{aligned}&\frac{d \rho _2 }{dt} + (D-1) H \; (\rho _2 + p_2) = -Q', \end{aligned}$$
(44)
$$\begin{aligned}&\frac{d \rho _3 }{dt} + (D-1) H \; (\rho _3 + p_3) = Q' - Q, \end{aligned}$$
(45)

where \(H=\frac{{\dot{S}}}{S}\), Q and \(Q' \) represent the interaction terms which can have arbitrary form, \(\rho _1\), \(\rho _2\), \(\rho _3\) are DE density, exotic matter (EM) and normal matter respectively. For, \(Q < 0 \) energy transfer from EM sector to two other constituents, \(Q' > 0 \) energy transfer from DE sector to the other two fluids, and \(Q' < Q \) energy loss for the normal matter sector. In the above the limiting case \(Q = Q' \) represents that DE interacts only with EM. The equivalent effective uncoupled equations are

$$\begin{aligned} \frac{d \rho _i }{dt} + (D-1) H \; \left( 1+ \omega _i^{eff} \right) \rho _i =0 \end{aligned}$$
(46)

the effective parameters are \( \omega _1^{eff} = \omega _1 -\frac{Q}{(D-1) H \rho _1} \), \(\omega _2^{eff} = \omega _2 + \frac{Q'}{(D-1) H \rho _2} \) and \( \omega _3^{eff} = \omega _3 + \frac{Q-Q'}{(D-1) H \rho _3}\). Consider an interaction as \(Q - Q' = -\beta H \rho _3,\) where \(\beta \) is the strength of interaction. The effective state parameter for the normal fluid can be expressed as \(\omega _3^{eff} = \omega _3 - \frac{\beta }{(D-1)} \). In Fig. 4, we plot the effective EoS parameter with \( \omega _3=A\) for different strengths of interaction determined by \(\beta \). It is evident that for a given dimension of the universe, say \(D=10\), the universe attains matter dominated phase faster then that with smaller interaction. However, for a given interaction the matter in the universe is determined by an effective EoS parameter and \(\omega _3^{eff}=0\) in higher dimensions faster than the usual four dimensional universe [84]. It is found that the on set of matter domination phase in the universe depends on the spacetime dimension. When the interaction sets a transition of cosmic fluids lead to \(\omega _{eff} \rightarrow - 1\) with change in interaction incorporated in \(Q' \) due to energy transference from one sector of matter to another sector where \(A^{eff} = A- \frac{\beta }{D-1} \). Consequently the effective cosmological constant \(\varLambda ^{eff}\) decreases as \(\omega _1^{eff}\) decreases accommodating a small value of the cosmological constant at the present time. In the next section we explore gravitational instanton which permits EU.

Fig. 4
figure 4

Variation of \(\omega _3^{eff} \) with \( \omega _3\) for \(\beta =10 \) (Blue), \( \beta =5\) (Green), \(\beta =0.1\) (Red) for \(D=10\), \(\beta =0.1 \) (Cyan) and \(\beta =5 \) (Yellow) for \(D=4\)

Full size image

5 Gravitational instantons

Gravitational instantons are the sinusoidal solutions of the Einstein field equation in Euclidean gravity with a finite Euclidean gravitational action. In this section we consider a transformation of Lorentzian time to Euclidean time by Wick rotation \(t=i \tau \) in Eq. (3). The D dimensional Euclidean metric is given by

$$\begin{aligned} ds^2=d\tau ^2+S^2 (\tau ) \; d\varOmega _{D-1}^2. \end{aligned}$$
(47)

The time-time component of the Einstein field equation in Lorentzian time given by Eq. (15)

$$\begin{aligned} \frac{{\dot{S}}^2}{S^2} + \left[ \frac{(D-3) \alpha }{(D-1) r^2} + \frac{\alpha '(r)}{(D-1) r} \right] \frac{1}{S^2} = \frac{2 }{(D-1)(D-2)} \; \rho \nonumber \!\!\!\!\!\\ \end{aligned}$$
(48)

where as denoted earlier \(\dot{()}\) is the derivative w.r.t t. In the Euclidean gravity the field equation is obtained by using \(t=i \tau \), where \(\tau \) is the Euclidean time. The Eq. (48) in the Euclidean gravity yields

$$\begin{aligned} \left( \frac{dS}{d\tau }\right) ^2 = \xi - \frac{2 \; S^2}{(D-1)(D-2)} \rho \end{aligned}$$
(49)

where (\(\tau \)) is the Euclidean time and \(\xi = \frac{(D-3) \alpha }{(D-1) r^2} + \frac{\alpha '(r)}{(D-1) r} \). To begin with we consider the energy density given by Eq. (34), \(\rho = \left( \frac{K}{1+A} \right) ^2 \frac{1}{S^{2 \sigma }}+ \frac{2\;B K}{(1+A)^2} \frac{1}{S^{\sigma }} + \left( \frac{B}{1+A} \right) ^2 \) in the above equation which can be written as

$$\begin{aligned} \left( \frac{dS}{d\tau }\right) ^2 = \xi -\mu S^2 - \sum _{\sigma =1}^{N} \frac{\nu _{\sigma }}{S^{2\sigma } } \end{aligned}$$
(50)

where \(\mu \) and \(\nu _{\sigma }\) are coefficients with powers of \(S^{-2\sigma }\) and \(\sigma = \frac{1}{2} (A+1)(D-1) \). We now look for gravitational instanton solutions [88, 89] from the above equation. In this case one finds a functional form

$$\begin{aligned} P_{N+1} (S^2)= S^{2N} \left[ \xi - \mu S^2 -\sum _{n=1}^{N} \frac{\nu _{\sigma }}{S^{2\sigma } } \right] \end{aligned}$$
(51)

which is a (N+1)th order polynomial in \(S^2\). Defining a radial variable \({\mathfrak {R}} =S(\tau )\) so that \(d {\mathfrak {R}}^2= \left( \frac{dS}{d\tau }\right) ^2 d\tau ^2\) we can rewrite the metric (47) as follows

$$\begin{aligned} ds^2= \frac{{\mathfrak {R}}^{2N}}{P_{N+1} ({\mathfrak {R}}^2) } d {\mathfrak {R}}^2 + {\mathfrak {R}}^2 d\varOmega _{D-1}^2 \end{aligned}$$
(52)

The metric (52) will be used for obtaining instantons. The polynomial \(P_{N+1} ({\mathfrak {R}}^2) \) has \((N+1)\) roots and it is important to consider only the range of \({\mathfrak {R}}^2\) values between two real positive consecutive roots so that \(P_{N+1} (S^2) >0\) on the range, commensurate with Euclidean signature to permit a non-singular metric. Different instantons for different pairs of roots are permitted satisfying the criteria. The search for instantons essentially reduces to finding the polynomial \(P_{N+1} (S^2) = \left( \frac{dS}{d\tau }\right) ^2 S^{2N}\) satisfying the Euclidean field equations and then the Euclidean metric. Thus analytically continued into the Lorentzian signature by Wick rotation \(\tau = i t\), finally describes an emergent universe. In this case a dynamical wormhole with a contracting universe \(\frac{dS}{d\tau }<0\) and an expanding universe \(\frac{dS}{d\tau } >0\) connected by a neck of radius \(S=S_0\) is permissible when \(\xi >0\) at the throat. It is evident that at the throat \(r=r_0\), we get \(\xi =k\), and a dynamical instanton solution exists for a closed universe \(k=1\) only in any dimension. For non-interacting fluid permitted by the non-linear EoS, the Euclidean field equation becomes

$$\begin{aligned} \left( \frac{dS}{d\tau } \right) ^2= & {} k - \left( \frac{K}{\sqrt{3}(1+A)} \right) ^2 \frac{1}{S^{1+3A}} \nonumber \\&-\frac{2}{3} \left( \frac{BK \sqrt{\rho _o}}{(1+A)^2 \rho _o} \right) \frac{1}{S^{\frac{3A-1}{2}}} - \left( \frac{B}{\sqrt{3}(1+A)} \rho _o\right) ^2 S^2.\nonumber \\ \end{aligned}$$
(53)

We note that a new gravitational instanton is obtained in a flat universe (\(k=0\)), when \(B=0\) with \(A= - \frac{2}{3} \), i.e.,  a universe filled with quintessence matter, where the solution is given by

$$\begin{aligned} S(\tau ) = S_0 \; cos \sqrt{3} K \; \tau \end{aligned}$$
(54)

thus a gravitational instanton solution is obtained in a flat universe that admits an expanding universe in the Lorentzian time. A flat emergent universe can be realized with a big size of the universe when \(B \rightarrow 0\) as the contribution of the second term \({\mathcal {O}}(S^{3/2})\) and the third term \({\mathcal {O}}(S^2)\) are small compared to the first term (for a flat universe \(k=0\)) in Eq. (53). In the case of \(B\ne 0\) and neglecting the terms \({\mathcal {S}}^{2 \sigma }\) (which is legitimate for a large size of ESU) and \({\mathcal {S}}^{2 \sigma -2}\), we obtain instanton solution integrating Eq. (53) which is given by

$$\begin{aligned} S(\tau ) = \sqrt{ \frac{\xi }{\mu }} \; sin \;(\sqrt{\mu }\tau + \tau _0) \end{aligned}$$
(55)

we denote \(\mu = \frac{2 }{(D-1)(D-2)} \left( \frac{B}{1+A} \right) ^2\rho _o\) and \(\tau _0\) an integration constant. The gravitational action is finite in this case as the curvature scalar is \(R= -\frac{(D-1)(D-6)\mu }{2}+ \frac{(D-2)(D-4)\xi }{S^2}\). However, the instantons obtained with \(B\ne 0\) admits a closed emergent universe [66, 67] for \(D\ge 4\). The finite Euclidean action can be obtained evaluating the integral

$$\begin{aligned} I_E= \frac{1}{16 \pi G_D} \int \sqrt{g} \;d^Dx R. \end{aligned}$$
(56)

For \(D=4\), the wave function of the universe is \(\varPsi \sim e^{- I_E}\) which is real. As one transforms from Euclidean to Lorentzian region, \(\tau = i t\) and \(\tau _0=\frac{\pi }{2}\), the Eq. (55) yields

$$\begin{aligned} S(t) = \sqrt{ \frac{\xi }{\mu }} \; cosh \; \sqrt{\mu } t \end{aligned}$$
(57)

where \(\sqrt{\frac{\xi }{\mu }}\) is initial size of the ESU and comparable to the size of the instanton given by Eq. (55). A dynamical wormhole obtained in the sec. III permits a flat emergent universe which however cannot be realized with gravitational instanton as \(k=0\) admits a new solution which is not EU. The gravitational instanton in higher dimensions however permits a closed emergent universe including \(D=4\) dimensions [66, 67]. In this scenario the Lorentzian universe is realized from the Euclidean solution by a Wick rotation \(\tau =it\). In the above we choose \(\tau _0=0\) and \(\mu \rightarrow 0\) (as \(B \rightarrow 0\)) so that \(\tau \) is very large indicating existence of a static universe phase for a long time and it indicates also a universe with a big size which in the Lorentzian time accommodates an emergent universe senario [69]. Away from the throat \(\alpha (r)\) decreases which leads to a decreasing \(\xi \). However, for \(k=0\) the differential equation permits solution that are relevant only in the Lorentzian universe but no gravitational instanton.

6 Discussion

We present a new class of dynamical wormhole solutions which permit emergent universe scenario in the usual four or in higher dimensions (\(D > 4\)) with a non-linear EoS in Einstein gravity. The flat EU is obtained with a dynamical wormhole naturally assuming shape functions permitted by a homogeneous Ricci scalar. The EU is basically based on the assumption of the existence of a ESU in the infinite past. We note the following :

  1. (i)

    Dynamical wormholes that are relevant for describing the origin of EU scenario are obtained for a flat, closed and open universe. The throat of the wormhole is considered as the seed of the EU with its size same as the radius of the neck. The shape function b(r) for the wormhole is obtained considering a homogeneous Ricci scalar (R) i.e., \(\frac{dR}{dr} =0\) in the flat, closed and open background.

  2. (ii)

    The size of the ESU is determined by the EoS parameter A. The EoS parameters A and B determine the initial cosmological constant \(\varLambda =\left( \frac{B}{1+A}\right) ^2 \rho _o\). The size of the ESU is determined by the D but its maximum size is independent of the spacetime dimensions.

  3. (iii)

    NEC is found to obey at the neck of the wormhole (in the infinite past i.e., \(t \rightarrow -\infty \)), as the universe evolves NEC violates near \(t=0\). In the case of flat EU, the NEC is obeyed at the throat for a neck size \(r_0=S_0 \ge \frac{4-3K^2}{3BK\sqrt{\rho _o}}\) and in closed or open universe the limiting value is \(r_0=S_0 \ge \frac{2-3K^2}{3(BK\sqrt{\rho _o}-2)}\) imposed with \(A=\frac{1}{3}\) in \(D=4\).

  4. (iv)

    In the case of a flat universe background, EU emerged out from the wormhole throat (\( t \rightarrow - \infty \)) with NEC that obeys. Away from the throat and near \(t=0\) the NEC does not obey for \(A=1\) and \(B=\frac{1}{\sqrt{\rho _o}}\) say, \(D=4, \; 5,\) and 10 dimensions as shown in Fig. 1, but after \(t=0\) NEC obeys once again. The temporal variation of NEC in \(D=4\) for different B (with \(B > 0\)) are plotted in Fig. 2, the feature is same as found in Fig. 1. In Fig. 3, temporal variations near \(t=0\) permits two branches : (a) NEC is satisfied for \(A < 0\) and (b) NEC is violated for \(A> 0\). In case (a) NEC violates always after \(t=0\) but in case (b) NEC obeys once again.

  5. (v)

    NEC with different A are plotted in Fig. 3, the interesting aspect of A is that it takes the role of the EoS parameter \(\omega \), the change in the behaviour of NEC near \(t=0\) indicates a transition from normal matter to exotic matter phase. The late accelerating phase of the universe in the EU model can be described satisfactorily [77,78,79,80,81,82,83]. The nEoS is equivalent to a composition of three different types of fluids namely, dark energy (DE), dark matter (DM) and normal matter, which later transform from one sector to the other due to interaction that sets in among them accommodating observed universe which is discussed in Sect. 4. The observed universe can be realized satisfactorily in the EU scenario. The smallness of the cosmological constant at the present time can be addressed here with a given strength of the interactions. It is also noted that in \(2+1\) dimensions, wormhole solution exists with normal matter always.

  6. (vi)

    An EU model with non-interacting fluids is not a realistic cosmological model as for a given A, the composition of the fluid in the universe is fixed shown in Table 1. It is not possible to correlate the present observed universe or the different phases of evolution. For this we consider interaction that sets in the fluid at \(t=t_i\) for a realistic scenario and found that it leads to a satisfactory description of the observed universe in \(D=4\) dimensions. Assuming interaction at \(t=t_i\), an expanding EU with a cosmological constant \(\varLambda =\left( \frac{B}{1+A}\right) ^2 \rho _o\) in the beginning is found to decrease as the universe evolves to an effective cosmological constant : \(\varLambda ^{eff} < \varLambda \) which is given in the Eq. (43). The effective value depends on the strength of interaction Q and \( Q'\), which also determines a transition from one sector of matter to the other sector.

  7. (vii)

    The EU model can be implemented in the usual four and in higher dimensional Einstein gravity with non-linear EoS making use of the dynamical wormhole obtained with the shape function permitted by a homogeneous Ricci scalar. The results obtained here in a flat background is different from that obtained by Zangeneh et al. [65] with a linear equation of state \(p= \omega \rho \), where it is shown that in five dimensions wormhole structures can be realized satisfying NEC always when \(\omega > -1\). It was also shown that dynamical wormholes can be found in flat and open background. We obtain here dynamical wormholes in flat, open and closed background to realize EU and determined the different criterion for the model parameters. The wormhole structure for EU can be realized satisfying NEC under a restriction of the throat size satisfying the inequality \( S_0^{4-3(1+A)} + \left( \frac{B \sqrt{\rho _o}}{K} \right) S_0^{4-\frac{3(1+A)}{2}} > \frac{1+A}{K^2} \). in flat background. The size of the neck in flat or open universe are also determined in \(D=4\) dimensions. Thus we get a limited access of the wormhole solutions that respects NEC at the throat.

  8. (viii)

    The existence of the initial Einstein static universe from which the EU emerged is also explored in the Einstein gravity in the framework of gravitational instantons with a modification of the matter sector. It is found that a flat EU model in 4 dimensions cannot be realized via gravitational instantons. In higher dimensional EU scenario the gravitational instanton mechanism works well to permit the EU scenario satisfactorily.

  9. (ix)

    The gravitational instanton has a limited applicability, it permits closed EU in \(D\ge 4\) but does not permit a flat EU. The Lorentzian universe is obtained from the gravitational instanton by transforming the Euclidean time to Lorentzian time by Wick rotation (\(\tau = i t\)). Thus dynamical wormhole mechanism to construct EU model is better than the gravitational instanton.

  10. (x)

    Superstring theory is realistic in higher dimensions and it is not known the spacetime dimensions, the analysis presented here is academically interesting in dimension \(D>4\). We study the gravitational instanton and dynamical wormholes in cosmology to explore the origin of the initial phase and subsequent phases of the observed universe in the usual four and in higher dimensions. The modified theories of gravity will be taken up elsewhere in understanding the EU scenario.