1 Introduction

Non-minimal coupled scalar field models are often used to explain various cosmological observations. These models naturally arise from the quantum corrections to the scalar field theory and motivated by high energy physics such as superstrings and grand unified theories [1]. Further, these models provide a natural solution to the problem associated with the energy scale difference between inflation and the Universe’s dark energy (DE) era [2].

Most of the cosmological model’s governing equations are nonlinear and pose a severe impediment to extract exact analytical solutions. However, one can infer the global asymptotic behavior described by the cosmological equations using the advanced tools of dynamical systems. The main advantage is that we can represent the Universe’s history geometrically. One can also predict the sensitivity of the solution to initial conditions. Dynamical system methods have been used extensively in cosmology; see [3,4,5,6,7,8,9,10,11,12,13,14,15] for relevant work and [16] for a comprehensive review.

The dynamical system of most cosmological models usually contains parameters. One can determine the system’s global dynamics for fixed values of parameters using the formal stability analysis. On the other hand, to understand how the global dynamics changes with a change of parameters, the bifurcation theory plays a crucial role (see Refs. [17,18,19] for detailed information). The dynamical system’s nonlinear nature usually leads to vital structures of the solutions, such as bifurcations and chaos. A more in-depth analysis of such forms is interesting from an observational perspective (e.g., see [20]).

One of the bifurcation theory’s novelties is that we can use it to classify the Universe’s evolution into two categories: generic and non-generic evolution [21]. While the former occurs for various solutions over a wide range of initial conditions, the latter corresponds to a particular solution for a given initial condition. The parametric relation associated with a non-generic scenario forms a bifurcation boundary between regions of different generic cases in the parameter space. Non-generic evolution is also exciting but requires fine-tuning of initial conditions. In some cases, generic evolution emerges from non-generic one in the form of bifurcation. Therefore, bifurcation theory can help extract a class of models describing the observed dynamical evolution irrespective of initial conditions for a wide range of parameters. To have a clear picture of how the bifurcation phenomenon depends on model parameters, one has to use bifurcation diagrams. These diagrams stratify the parameter space into different regions, each with distinct dynamical behavior. The steps involved in the bifurcation analysis are two-fold. Initially, we extract the range of parameters for both the generic and the non-generic evolution. Then, we analyze different qualitative behaviors that arise from each scenario.

Another novelty of bifurcation theory is that it allows us to identify a structural stable model’s emergence from a structurally unstable one. For instance, Szydlowski and Tambor showed that the notion of bifurcation and structural instability could be instrumental in detecting the emergence of the structurally stable \(\Lambda \)CDM model from the structurally unstable CDM model [22]. Kokarev further extended a similar analysis to various Friedmann–Robertson–Walker (FRW)-models [23]. Usually, structurally stable models are physically viable and hence fit with most observations. In a 2-dimensional system, Peixoto’s theorem completely characterizes the structurally stable vector fields, which guarantee their generic behavior. Identifying structurally stable models is useful when the prediction of model parameters from the empirical analysis is unsettled. Thus, bifurcation theory helps in finding observationally viable models and further endows the usual stability analysis.

In most of the dynamical analysis for the non-minimal coupled scalar field models, the dynamical variables are constructed for a specific case of coupling or potential functions in flat or curved spacetime [12, 24,25,26,27,28,29,30,31]. However, the analysis for a general non-minimal coupled scalar field model will certainly help us to identify classes of viable models. The extension to a broad class of scalar field potentials and couplings might help us to connect the phenomenological models with some high-energy physical theories. Therefore, it will be scientific and economical to carry out the dynamical analysis for a broad class of coupling functions and potentials.

We find in the literature that bifurcation phenomena arise naturally in cosmological models. For instance, Ref. [32] shows that in FRW-models with perfect fluids and the cosmological constant, the expanding and contracting deSitter Universe arise as bifurcation. It is worth mentioning that interesting bifurcation scenarios were reported in the Randall–Sundrum braneworld model [33], interacting Veneziano ghost DE [34], Brans–Dicke model [35], non-minimal coupled scalar field model [31, 36] etc. Recently, bifurcation scenarios and chaos were discussed in the context of Hořava–Lifshitz gravity [37], non-minimal coupled scalar field with Ratra–Peebles potential [21], interacting f(T) gravity [38] and bulk viscous cosmology [39]. These recent work show that the study of bifurcation is important in cosmology, giving rise to interesting scenarios.

In the non-minimal coupled scalar field context, interesting bifurcation scenarios were reported for a specific coupling and potential function. For instance, Hrycyna et al. [31] obtained a particular bifurcation value of a coupling constant for the case of a constant potential. Then, Szydlowski et al. in [36] analyzed the phase space’s structural stability of a specific coupling model for a broad class of potentials. They found that an exponential potential constitutes a structurally stable model. Using the bifurcation methods, Humieja et al. in [21] extract the conditions of model parameters under which a specific non-minimal coupling with Ratra–Peebles potential generically evolve from an early de Sitter to a late time de Sitter state. The analysis in [21] was performed in the absence of a matter component. We extend the analysis for general coupling and potential functions along with the matter component in the present work. To meet our objective, we consider a different choice of dynamical variables to encompass a broad class of models. By employing bifurcation methods, we obtain a class of models and pinpoint the range of parameters capable of describing a cosmic evolution over a wide range of initial conditions from an early radiation era towards a late time DE era. We also found that the system undergoes a transcritical type of bifurcation, which predicts how to tune our models to have certain desired dynamics.

The bifurcation theory’s concrete tools have been used extensively in various fields. However, they have not been applied systematically in many cosmological systems, particularly for the non-minimal coupled scalar field. Thus, it is imperative to use bifurcation theory to identify a class of scalar field models describing some of the main generic cosmic evolution. Therefore, the present work serves as an introductory analysis for scalar field models required to test against interesting observational signatures.

The paper’s order is as follows: in Sect. 2, we briefly discuss the framework of a non-minimal coupled scalar field model. We follow this by a dynamical system analysis of a non-minimal coupled scalar field model for a broad class of coupling function and potential in Sect. 3. In Sect. 4, we demonstrate the dynamics by an example using the quadratic coupling functions and the power-law form of potentials. Within this section, we perform the stability analysis of critical points in Sect. 4.1 and the discussion on bifurcation scenarios in Sect. 4.2. Lastly, we summarized the work in Sect. 5.

2 Non-minimal coupled scalar field model

We consider a model of a non-minimal coupled scalar field and a barotropic fluid in the present work. Here the non-minimal coupled scalar field is playing the role of DE, while a barotropic fluid is the matter component of the Universe. The total action is given by [40,41,42]

$$\begin{aligned} S&=\frac{1}{\kappa ^2}\int d^4 x \sqrt{-g} \Bigg [ \frac{F(\phi )}{2} R-\frac{1}{2}\nabla ^a \phi \nabla _a \phi -\ell ^{-2}\,V(\phi ) \nonumber \\ {}&\quad +\kappa ^2 {\mathscr {L}}_m \Bigg ], \end{aligned}$$
(1)

where the integration is taken over a 4-dimensional Lorentzian curved spacetime manifold. In the above action, \(\kappa ^2\) is the gravitational constant, R is the Ricci scalar, g is the determinant of the spacetime metric \(g_{ab}\) (\(a, b=0, 1, 2, 3\)), F is the coupling function, V is the potential of a scalar field \(\phi \) and \({\mathscr {L}}_m\) is the matter Lagrangian. We have used the units where \(c=1\) and \(\ell \) is the positive parameter having the dimension of length. For a fixed scalar field, the above action reduces to the case of general relativity (GR) with a potential playing the role of a cosmological constant. While the case \(F(\phi )=1\) of (1) corresponds to the minimal coupled scalar field, \(F(\phi )=\frac{\phi ^2}{\omega }\) reduces to the Brans–Dicke gravity limit, with \(\omega \) as the Brans–Dicke parameter [27, 43,44,45]. On varying the action (1) with respect to the metric \(g_{ab}\), one can obtain the modified Einstein’s field equation as

$$\begin{aligned}&F(\phi ) G_{ab}+\frac{1}{2} \nabla _a \phi \nabla _b \phi -\frac{1}{4} g_{ab}\nabla ^c\phi \nabla _c\phi +\frac{1}{2} g_{ab}\, \ell ^{-2}\,V(\phi )\nonumber \\&\quad -\nabla _a\nabla _b F(\phi )+g_{ab} \square F(\phi )=-\kappa ^2 T_{ab} \, , \end{aligned}$$
(2)

where \(G_{ab}\) is the Einstein tensor, \(\square \equiv \nabla _a \nabla ^a\) with \(\nabla _a\) as the covariant derivative with respect to the metric and \(T_{ab}\) is the matter energy-momentum tensor given by

$$\begin{aligned} T_{ab}=p_m\,g_{ab}+(\rho _m+p_m) u_a u_b\, . \end{aligned}$$
(3)

In the above equation, \(\rho _m\) and \(p_m\) are respectively the energy density and pressure of the barotropic fluid, and \(u_a\) is a four-velocity vector of the fluid. One interesting feature of the action (1) is that the effective Newton’s gravitational parameter depends on the coupling function F, i.e., on the scalar field as

$$\begin{aligned} G_{\mathrm{eff}}=\frac{\kappa ^2}{F(\phi )}. \end{aligned}$$
(4)

The negative values of \(G_{\mathrm{eff}}\) and hence of F indicates the ghost instability in the theory [46]. On varying the action with respect to the scalar field \(\phi \), we get

$$\begin{aligned} \square \phi + \frac{1}{2}RF_{,\phi }- \ell ^{-2}\,V_{,\phi }=0, \end{aligned}$$
(5)

where the notation \((\cdot )_{,\phi }\) denotes a derivative with respect to \(\phi \). Note that the second term of (5) arises from the non-minimal coupling of scalar field to gravity. At a very large scale, consistent with the observed data, we assume the homogeneous and isotropic Universe whose evolution is determined by the scale factor a(t) associated with the FRW metric

$$\begin{aligned} ds^2=-dt^2+a^2(t)(dx^2+dy^2+dz^2), \end{aligned}$$
(6)

where t is the coordinate time and x, y, z are the Cartesian coordinates. Under this metric, the field equations (2) and the Klein Gordon equation (5) can be reduced to the ordinary differential equations

$$\begin{aligned} 3H^2 F+3H {\dot{\phi }}F_{,\phi }-\frac{1}{2} {\dot{\phi }}^2-\ell ^{-2}\,V= & {} \kappa ^2 \rho _m, \end{aligned}$$
(7)
$$\begin{aligned} 2 F {\dot{H}}+{\dot{\phi }}^2F_{,\phi \phi }+(\ddot{\phi }-H{\dot{\phi }})F_{,\phi }+{\dot{\phi }}^2= & {} -\kappa ^2 \rho _m (1+w), \end{aligned}$$
(8)
$$\begin{aligned} \ddot{\phi }+3H {\dot{\phi }}+\ell ^{-2}\,V_{,\phi }-3 F_{,\phi }(2 H^2+{\dot{H}})= & {} 0. \end{aligned}$$
(9)

In the above equations, w is an equation of state (EoS) defined by a relation \(p_m=w \rho _m\) and the upper dot denotes derivative with respect to t. The scalar field describes DE and for simplicity, we shall consider for matter a single barotropic fluid with a constant w, constrained to be between 0 and 1. While a non-relativistic dust fluid corresponds to \(w = 0\), relativistic radiation fluid corresponds to \(w =\frac{1}{3}\). We note here that one needs to consider a two-fluid model containing radiation and dust fluids for a more phenomenologically interesting case. Further, on assuming the conservation of the matter energy-momentum tensor i.e., \(\nabla _a T^{ab}=0\), under a metric (6), one can obtain the conservation equation

$$\begin{aligned} {\dot{\rho }}_m+3 H (1+w) \rho _m=0. \end{aligned}$$
(10)

To determine the energy density contribution of each component, we introduce the relative energy densities of the scalar field and that of the barotropic fluid, respectively as

$$\begin{aligned} \Omega _\phi= & {} \frac{\rho _\phi }{3H^2 F}=\frac{{\dot{\phi }}^2}{6F H^2}-\frac{F_{,\phi } {\dot{\phi }}}{H F}+\frac{\ell ^{-2}V}{3H^2 F}, \end{aligned}$$
(11)
$$\begin{aligned} \Omega _m= & {} \frac{\kappa ^2\rho _m}{3 F H^2}. \end{aligned}$$
(12)

These energy densities are connected by the Friedmann constraint (7) as

$$\begin{aligned} \Omega _m+\Omega _\phi =1. \end{aligned}$$
(13)

While we can identify the first two terms of (11) as the kinetic component of the relative energy density of the scalar field, the last term corresponds to the relative potential energy density component of the scalar field. From (13), we can define the matter domination as a scenario where \(\Omega _m \approx 1 \) and \(\Omega _\phi \approx 0\). Similarly, we can also define from (13), a kinetic dominated solution or potential dominated solution when the first two terms or the last term in (11) dominate over the others, respectively.

As expected, the above quantities (11) and (12) reduce to the familiar relative energy densities of a scalar field and matter for the minimal coupled case (i.e., \(F(\phi )=1\)) respectively. Further, the quantity (11) reduces to the relative energy density of the cosmological constant for a non-dynamical scalar field (i.e., the GR case). In the context of minimal coupling, the above relative energy densities are usually bounded within the interval [0, 1]. However, this is not necessarily true in non-minimal coupling due to coupling function F. Under the physical assumption \(\rho _m \ge 0\) and an attractive gravitational force, \(F(\phi )> 0\), the problem of negative \(\Omega _m\) does not arise. Nonetheless, due to the second term in the right-hand side of the Eq. (11) for \(\Omega _\phi \), there is also a possibility for \(\Omega _\phi \) to be negative. Thus taking into account the above conditions, the relation (13) implies that in the matter domination, the dust fluid can be relatively overdense (i.e., \(\Omega _m>1\)) compared to the corresponding \(\Lambda \)CDM case.

The cosmological equations (7) and (8) can be rewritten in the form

$$\begin{aligned} 3H^2= & {} \kappa ^2 \rho _{\mathrm{eff}}, \end{aligned}$$
(14)
$$\begin{aligned} 3H^2+ 2{\dot{H}}= & {} -\kappa ^2 p_{\mathrm{eff}}, \end{aligned}$$
(15)

where \(\rho _{\mathrm{eff}}\) is the effective energy density and \(p_\mathrm{eff}\) is the effective pressure of all the components which are respectively given by

$$\begin{aligned} \rho _{\mathrm{eff}}= & {} \frac{\rho _m+\rho _\phi }{F(\phi )}\,\nonumber \\= & {} \frac{\rho _m}{F(\phi )}+ \frac{1}{\kappa ^2 F(\phi )} \left[ \frac{{\dot{\phi }}^2}{2} -3H F_{,\phi }(\phi ) {\dot{\phi }} +\ell ^{-2} V(\phi ) \right] ,\nonumber \\ \end{aligned}$$
(16)
$$\begin{aligned} p_{\mathrm{eff}}= & {} \frac{p_\phi +p_m}{F(\phi )}\, \nonumber \\= & {} \frac{1}{\kappa ^2F(\phi )} \left[ \frac{{\dot{\phi }}^2}{2}+2 H F_{,\phi }(\phi ) {\dot{\phi }} + F_{,\phi \phi }(\phi ){\dot{\phi }}^2 + F_{,\phi }(\phi )\ddot{\phi } \right. \nonumber \\&\left. - \ell ^{-2}\,V(\phi ) +\kappa ^2 p_m\right] . \end{aligned}$$
(17)

Using Eq. (7), the effective EoS of all the components \(w_{\mathrm{eff}}\) defined as \(\frac{p_{\mathrm{eff}}}{\rho _\mathrm{eff}}\) is given by

$$\begin{aligned} w_{\mathrm{eff}}= & {} \frac{1}{3 F(\phi ) H^2} \left[ \frac{{\dot{\phi }}^2}{2}+2 H F_{,\phi }(\phi ) {\dot{\phi }} + F_{,\phi \phi }(\phi ){\dot{\phi }}^2 \right. \nonumber \\&\left. + F_{,\phi }(\phi )\ddot{\phi }- \ell ^{-2}\,V(\phi ) \right] +w\, \Omega _m. \end{aligned}$$
(18)

While for the accelerated behavior of the Universe, one requires the condition \(w_{\mathrm{eff}}<-\frac{1}{3}\), super-accelerated Universe or phantom dominated Universe demands \(w_{\mathrm{eff}}<-1\). It is worth noticing from (18) that in the GR limit, within the matter domination epoch, we have \(w_{\mathrm{eff}}=w\) and under the scalar field potential dominated epoch (i.e., cosmological constant epoch) \(w_{\mathrm{eff}}=-1\).

The above Eqs. (7)–(10) are complicated to solve analytically, yet, by recasting them into a dynamical system, one can still obtain important information on the characteristics of solutions. Therefore, in the next section, we shall analyze the dynamics of a general class of non-minimal coupling scalar fields using dynamical system techniques.

3 Dynamical system analysis

In order to qualitatively analyze the background cosmological dynamics of the present model, we shall convert the cosmological equations (7)–(10) into a dynamical system using the following set of normalized variables [16]:

$$\begin{aligned} x= & {} \frac{{\dot{\phi }}}{H\sqrt{F}},~~~~~~~y=\frac{\ell ^{-2}\,V}{3H^2F}, \nonumber \\ \lambda _F= & {} -\frac{F_{,\phi }}{\sqrt{F}},~~~~~~~ \lambda _V=-\frac{V_{,\phi }}{V}\sqrt{F}. \end{aligned}$$
(19)

We note here that the chosen variables are well-defined for \(F>0\), i.e., attractive gravity, which is also free from any ghost instability, even though the case \(F<0\) may lead to physically interesting scenarios [47]. From the cosmological equations (7)–(10), we see that there are basically four variables \(H, \phi , {\dot{\phi }}, \rho _m\). As we have considered the usual H-normalized variables, the variable H is being absorbed by other variables, so we are left with three variables [16]. Since the H-normalized variables are connected by the Friedmann constraint (7), the number of independent variables reduces to two. The extra variables \(\lambda _F\), \(\lambda _V\) are introduced to monitor the overall effect of coupling function and potential on the dynamics. It is important to note here that the above choice of variables fails for static Universe \(H=0\). However, these variables are of physical interest as the energy density of each component can be easily tracked in terms of these variables. In this work, we shall focus on the case of an expanding Universe i.e., \(H>0\) as favored by various present observational data. Therefore, we can choose the above normalized variables without any extra concern. Employing the variables (19), the cosmological equations (7)–(10) can be re-written as the following dynamical system:

$$\begin{aligned} x'= & {} \frac{1}{6\,{\lambda _F}^{2}+4}\Big [{x}^{3} \left( 2\, \Gamma _F \,{\lambda ^2_{F}}-w+1 \right) +{x}^{2}\lambda _F\, \left( 3\,\lambda _F\, \left( 2\, \Gamma _F \,{\lambda _F}\right. \right. \nonumber \\&\left. \left. +\lambda _F \right) -9\,w+7 \right) -x \left( 6(3\,{\lambda ^2_F}w-w+1) +6\,y \left( \lambda _F\,\lambda _V \right. \right. \nonumber \\&\left. \left. +w+1 \right) \right) +y \left( 12\,\lambda _V -18\, \left( w+1 \right) \lambda _F \right) \nonumber \\&+6\, \left( 3\,w-1 \right) \lambda _F \Big ], \end{aligned}$$
(20)
$$\begin{aligned} y'= & {} \frac{y}{3\,{\lambda ^2_F}+2} \Big [ 12\,{\lambda _F}^{2}+6\,w+6+x \left( \lambda _F\, \left( 3 \,{\lambda ^2_F}-6\,w+4 \right) \right. \nonumber \\&\left. - \left( 3\,{\lambda ^2_F}+2 \right) \lambda _V \right) +{x}^{2} \left( 2\,{\lambda ^2_F} \Gamma _F -w+1 \right) \nonumber \\&-6\,y \left( \lambda _F\,\lambda _V +w+1 \right) \Big ] , \end{aligned}$$
(21)
$$\begin{aligned} \lambda _F'= & {} \frac{1}{2} x \lambda _F^2 \left( 1-2 \Gamma _F\right) , \end{aligned}$$
(22)
$$\begin{aligned} \lambda _V'= & {} -\frac{1}{2} x \lambda _V \left[ \lambda _F+2 \left( \Gamma _V-1\right) \lambda _V\right] , \end{aligned}$$
(23)

where \(\Gamma _F=\frac{FF_{,\phi \phi }}{F^2_{,\phi }}\) and \(\Gamma _V=\frac{VV_{,\phi \phi }}{V^2_{,\phi }}\). The prime notation denotes the differentiation with respect to the number of e-folds \(N=\ln a(t)\). We note that the above system (20)–(23) reduces to the minimal coupling case for \(\lambda _F=0\) [48].

For the above dynamical system to represents an autonomous system of equations, we consider a class of coupling function F and potential V where \(\Gamma _F\), \(\Gamma _V\) can be written as functions of \(\lambda _F\), \(\lambda _V\) respectively [49]. If \(\lambda _F=\lambda _F(\phi )\) is invertible, then we can express \(\phi \) as function of \(\lambda _F\). As \(\Gamma _F\) is a function of \(\phi \), therefore, we can also express \(\Gamma _F\) as a function of \(\lambda _F\). Similarly, one can express \(\Gamma _V\) as a function of \(\lambda _V\). In general, the quantities \(\Gamma _F\), \(\Gamma _V\) may not be a functions of variables \(\lambda _F\), \(\lambda _V\). In such a case, one has to consider the higher derivatives of the scalar field function [50] or consider new dynamical variables [51]. We note that the above system has an invariant submanifold \(y=0\), as \(y'\) vanishes when \(y=0\). This submanifold corresponds to a scenario where the scalar field potential vanishes. Physically, it means that if there is no potential source, the scalar field will not evolve. Further, depending on F and V (hence in the form of \(\Gamma _F\) and \(\Gamma _V\)), the system also contains \(\lambda _F=0, \lambda _V=0\) as invariant submanifolds. Therefore, a global attractor (if exists) should lie at an intersection of all these invariant submanifolds [16]. On the other hand, the absence of a global attractor makes the application of bifurcation theory more appealing as the evolution depends on the values of parameters and initial conditions.

Using the dynamical variables (19), one can express various cosmological parameters viz., the relative energy density parameter of the scalar field (\(\Omega _\phi \)) and of matter (\(\Omega _m\)), the EoS of the scalar field (\(w_\phi \)) and the effective EoS (\(w_{\mathrm{eff}}\)) respectively as

$$\begin{aligned} \Omega _\phi= & {} \frac{x^2}{6}+y+x \lambda _F, \end{aligned}$$
(24)
$$\begin{aligned} \Omega _m= & {} 1- x \lambda _F-\frac{x^2}{6}-y, \end{aligned}$$
(25)
$$\begin{aligned} w_\phi= & {} \frac{p_\phi }{\rho _\phi }= \frac{1}{ \left( 3 \,{\lambda _F}^{2}+2 \right) \left( 6\,x\lambda _F+{x}^{2}+6\,y \right) } \Big (\left( 3\,{\lambda _F}^{2}w \right. \nonumber \\&\left. +4\,{\lambda _F}^{2}\Gamma _{{F}}+2 \right) {x}^{2}+6\,{\lambda _F}^{2} \left( 3\,x\lambda _F\,w+3\,wy \right. \nonumber \\&\left. -3\,w+1\right) -12\,y \left( \lambda _F\,\lambda _V +1 \right) +4\,x\lambda _F \Big ), \end{aligned}$$
(26)
$$\begin{aligned} w_{\mathrm{eff}}= & {} \frac{p_{\mathrm{eff}}}{\rho _{\mathrm{eff}}}= \frac{1}{3 (3\,{\lambda _F}^{2}+2)}\,\left( (2 \Gamma _F {\lambda ^2_F}-w+1){x}^{2}+\lambda _F (3\,{\lambda _F} \right. \nonumber \\&\left. +2\,x-6\,w x) -6\,y\,(\lambda _V \lambda _F +w+1) +6\,w\right) . \end{aligned}$$
(27)

Notably the coupling term \(H {\dot{\phi }} F_{,\phi }\) of (7) can steer the value of \(w_\phi \) to \(\pm \infty \) during the matter domination epoch. However, this does not cause any physical singularity problem as the effective EoS \(w_{\mathrm{eff}}\) remains smooth and finite. The divergence behavior of \(w_{\phi }\) reduces as the value of \(\lambda _{F}\) approaches zero i.e., as the model approaches the minimal coupling case.

By imposing the physical constraint \(\rho _m \ge 0\) on the relation (13), the dynamical variables (19) obey the constraint

$$\begin{aligned} x \lambda _F+\frac{x^2}{6}+y \le 1. \end{aligned}$$
(28)

Hence, the phase space of the system is given by

$$\begin{aligned} \Psi =\left\{ (x, y, \lambda _F, \lambda _V) \in {\mathbb {R}}^4 ~\vert ~ x \lambda _F+\frac{x^2}{6}+y \le 1 \right\} . \end{aligned}$$
(29)

From the cosmological equations (7)–(10), one can solve the scale factor a(t) evaluated at the critical point by re-writing the equations in terms of the dynamical variables as

$$\begin{aligned} \beta {\dot{H}}+ H^2=0, \end{aligned}$$
(30)

where

$$\begin{aligned} \beta= & {} \Bigg [\frac{3}{2}+\frac{1}{2 (3\,{\lambda _F}^{2}+2)}\,\left( ({\lambda ^2_F}-w+1){x}^{2}+\lambda _F (3\,{\lambda _F}\right. \\&\left. +2\,x -6\,w x) -6\,y\,(\lambda _V \lambda _F +w+1) +6\,w\right) \Bigg ]^{-1}. \end{aligned}$$

Integrating Eq. (30), we get

$$\begin{aligned} a=a_i (t-t_i)^\beta , \end{aligned}$$
(31)

where \(a_i\) and \(t_i\) are constants of integration. We recall that \(0<\beta <1\) corresponds to a decelerated expanding Universe, while \(\beta >1\) corresponds to an accelerated expanding Universe.

Table 1 Critical points of the system (20)–(23)
Full size table
Table 2 Eigenvalues of the critical points of the system (20)–(23) presented in Table 1. Here: \(x_k\) denotes the corresponding x-component of a critical point
Full size table

In order to extract the dynamics of the above system, we will carry out the standard procedures of the dynamical system analysis [16]. The critical points (\(A_1, A_{2\pm }, A_3, A_4\)) of the system (20)–(23) for the general case of F and V are presented in Table 1 along with the corresponding values of the cosmological parameters. The corresponding eigenvalues of the perturbed matrix of each critical point are presented in Table 2. The existence and stability of each critical point can be determined without specifying the potential and coupling function by treating \(\lambda _{F_*}\) and \(\lambda _{V_*}\) as parameters. Therefore, there are as many critical points of the system (20)–(23) as the number of parameters \(\lambda _{F_*}\) and \(\lambda _{V_*}\). Note here that \(\lambda _{F_*}\) and \(\lambda _{V_*}\) denote the solutions of the equations \(2 \Gamma _F(\lambda _{F})-1=0\) and \(\lambda _{F}+2 \left( \Gamma _V(\lambda _V)-1\right) \lambda _V=0\) respectively. The quantities \(\Gamma \,^\prime _F\) and \(\Gamma \,^\prime _V\) denote the derivatives of \(\Gamma _F\) and \(\Gamma _V\) with respect to \(\lambda _F\) and \(\lambda _V\) respectively. In Tables 1 and 2, we have

$$\begin{aligned}&x_{2\pm }=-3 \lambda _{F_*}\pm \sqrt{9\lambda _{F_*}^2+6},\\&y_3=\frac{1}{2}\,{\frac{3\,{\lambda ^2_{F_*}}w-3\,\lambda _{F_*}\,\lambda _{V_*}\,w+3\,{\lambda ^2_{F_*}}+\lambda _{F_*}\,\lambda _{V_*}-3\,{w}^{2}+3}{{\lambda _{V_*}}^{2}}},\\&y_4= \frac{ \left( 5\,{\lambda ^2_{F_*}}+4\,\lambda _{F_*}\,\lambda _{V_*}-{\lambda ^2_{V_*}}+6 \right) \left( 3 {\lambda ^2_{F_*}}+2 \right) }{3\,({\lambda ^2_{F_*}}+\lambda _{F_*}\,\lambda _{V_*}+2)^2},\\&\Xi = \frac{3\,w \left( w+1 \right) {\lambda ^2_{F_*}}+\lambda _{V_*}\, \left( 3\,{w}^{2}+5\,w-2 \right) \lambda _{F_*}+6\,w \left( w+1 \right) }{3\, \left( w+1 \right) {\lambda ^2_{F_*}}+\lambda _{V_*}\, \left( 3\,w+7 \right) \lambda _{F_*}+6\,w+6},\\&G(\lambda _{F_*},\lambda _{V_*}) =\left( {\lambda _{V_*}^2} \Gamma \,^\prime _V(\lambda _{V_*}) +2 (\lambda _{F_*}+2(\Gamma _V-1) \lambda _{V_*}) \right) ,\\&\Delta =(81\,{\lambda ^4_{F_*}}{w}^{2}+18\,{\lambda ^3_{F_*}}\lambda _{V_*}\,{w}^{2}-63\,{\lambda ^2_{F_*}}{\lambda ^2_{V_*}}{w}^{2}+162\,{\lambda ^4_{F_*}}w \\&\quad +192\,{\lambda ^3_{F_*}}\lambda _{V_*}\,w-210\,{ \lambda ^2_{F_*}}{\lambda ^2_{V_*}}w-72\,{\lambda ^2_{F_*}}{w}^{3}+48\,\lambda _{F_*}\,{\lambda ^3_{V_*}} w \\&\quad -72\,\lambda _{F_*}\,\lambda _{V_*}\,{w}^{3}+81\,{\lambda ^4_{F_*}}+174\,{\lambda ^3_{F_*}}\lambda _{V_*}+17 \,{\lambda ^2_{F_*}}{\lambda ^2_{V_*}} \\&\quad +78\,{\lambda ^2_{F_*}}{w}^{2}-16\,\lambda _{F_*}\,{\lambda ^3_{V_*}}-300\,\lambda _{F_*}\,\lambda _{V_*}\,{w}^{2}+54\,{\lambda ^2_{V_*}}{w}^{2}\\&\quad +372\,{\lambda ^2_{F_*}}w -24\,\lambda _{F_*}\,\lambda _{V_*}\,w-12\,{\lambda ^2_{V_*}}w-144\,{w}^{3}+222\,{\lambda ^2_{F_*}}\\&\quad +204\,\lambda _{F_*}\,\lambda _{V_*}-42\,{\lambda ^2_{V_*}}-144\,{w}^{2}+144\,w+144). \end{aligned}$$

The behavior of the system (20)–(23) might change dramatically due to a small change of the parameters emerges from potential and coupling. Consequently, it will lead to a change in the phase space’s topological structure and gives rise to bifurcation. To have a general information on the effect of various parameters on the dynamics of a system (20)–(23), we present the bifurcation diagrams for each critical point in Fig. 1. These diagrams comprise of finite number of regions in the parameter space \((\lambda _{F_*},\lambda _{V_*})\). Each region in a bifurcation diagram corresponds to parameter values with distinct dynamical behavior [18]. Bifurcation curves separating different regions in a diagram corresponding to the specific relation between parameters in which the perturbed matrix evaluated at a critical point has at least one zero real part eigenvalue. When the perturbed matrix evaluated at a critical point has at least one zero real part eigenvalue, a critical point is said to be non-hyperbolic. Otherwise, it is hyperbolic. For a hyperbolic point, we can use linear stability analysis to determine the stability of a point. However, for non-hyperbolic point, one has to analyze beyond the linear stability analysis via sophisticated tools of dynamical systems such as the center manifold theory (see Ref. [19] for details). Thus along the bifurcation curves, one has to investigate the nature of points by the center manifold theory. However, we shall postpone such analysis to a concrete model in Sect. 4 and refrain from the general case analysis as the equations involved are complicated and not very illuminating. In what follows, we summarize each critical point’s nature and identify the possible bifurcation scenarios:

Fig. 1
figure 1

Bifurcation diagrams in \((\lambda _{F_*}, \lambda _{V_*})\) parameter space exhibiting the local stability of points \(A_1\) in a, \(A_{2+}\) in b, \(A_{2-}\) in c, \(A_3\) in d and \(A_4\) in e for the case of \(w=0\). In all panels, the yellow shaded regions represent the regions where the corresponding critical points are saddle. Black colored line \(\lambda _{V_*}=0\) in d and curve C8 in e corresponds to the non-existence of a point \(A_3\) and \(A_4\) respectively. A green colored curve in d represents the curve where \(\Delta =0\). Black colored curves C1 to C7 separating each region represent non-hyperbolic curves. The curve C7 is \(2\lambda _{F_*}=\lambda _{V_*}\). For the expressions corresponding to curves C1 to C6, we refer to the text in Statement 1

Full size image

  • Point \(A_1\) corresponds to a solution with a vanishing potential component. For this point, the exponent for the solution (31) is given by

    $$\begin{aligned} \beta _{A_1}=\frac{2({\lambda }^{2}_{F_*}-w+1)}{4\,{\lambda }^{2}_{F_*}-3\,{w}^{2}+3}. \end{aligned}$$
    (32)

    It can be checked that \(0<\beta _{A_1}<1\) for \(0 \le w \le 1\) and any choice of \(\lambda _{F_*}\). Hence, this point corresponds to a decelerated expanding solution for any choice of model parameters even though the scalar field can possibly behave as the quintessence field (\(-1<w_{\phi }<-\frac{1}{3}\)). This point can be either stable or saddle depending on the values of \(\lambda _{F_*}\), \(\lambda _{V_*}\) and w. For instance, as shown in Fig. 1a for \(w=0\) case, this point behaves as stable node in region I only if \(\Gamma \,^\prime _F(\lambda _{F_*})>0\) and \(G(\lambda _{F_*},\lambda _{V_*})>0\). Region III represents the region of stable node only if \(\Gamma \,^\prime _F(\lambda _{F_*})<0\) and \(G(\lambda _{F_*},\lambda _{V_*})<0\); otherwise all regions in the \((\lambda _{F_*},\lambda _{V_*})\) parameter space represent the regions of saddle for any choice of coupling function F and potential V. However, for the case of radiation (\(w=\frac{1}{3}\)), it is always saddle. Further, for \(\lambda _{F_*}=0\), this point corresponds to a usual decelerated matter dominated solution of the minimal coupled case (\(\Omega _m=1, w_{\mathrm{eff}}=w\)).

  • Points \(A_{2\pm }\) correspond to kinetic dominated solutions which exist for any choice of model parameters. In this case, we have

    $$\begin{aligned}&\beta _{A_{2+}}={\frac{\lambda _{F_*}\,\sqrt{9\,{\lambda }^{2}_{F_*}+6}+3\,{\lambda }^{2}_{F_*}+3}{12\,{ \lambda }^{2}_{F_*}+9}}, \end{aligned}$$
    (33)
    $$\begin{aligned}&\beta _{A_{2-}}={\frac{-\lambda _{F_*}\,\sqrt{9\,{\lambda }^{2}_{F_*}+6}+3\,{\lambda }^{2}_{F_*}+3}{12\,{\lambda }^{2}_{F_*}+9}}, \end{aligned}$$
    (34)

    which are both positive and less than one and hence, correspond to decelerated expansion. The bifurcation diagrams for these points are given in Fig. 1b, c. These points can be either unstable node or saddle depending on the form of potential and coupling function. For example, region I in Fig. 1b represents region of unstable node of point \(A_{2_+}\) if \(\Gamma \,^\prime _F(\lambda _{F_*})<0\) and \(G(\lambda _{F_*},\lambda _{V_*})<0\); region II in Fig. 1c represents the region of unstable node of \(A_{2_-}\) if \(\Gamma \,^\prime _F(\lambda _{F_*})>0\) and \(G(\lambda _{F_*},\lambda _{V_*})>0\). Otherwise, they are saddle in nature for any choice of parameters. When \((\lambda _{F_*},\lambda _{V_*})=(0, \sqrt{6})\) and \((0, -\sqrt{6})\), points \(A_{2+}\) and \(A_{2-}\) correspond to stiff matter dominated solutions (\(\Omega _\phi =1, w_{\mathrm{eff}}=1\)) of the minimal coupled scalar field.

  • Point \(A_{3}\) corresponds to a scaling solution and exists for all values of the model parameters except when \(\lambda _{V_*}=0\). This point can either be a stable node or stable focus or behaving as a saddle. The bifurcation diagrams for this point for \(w=0\) case is given in Fig. 1d. In this plot, when \(\Gamma \,^\prime _F(\lambda _{F_*})>0\) and \(G(\lambda _{F_*},\lambda _{V_*})>0\), region II represents region of stable focus, regions VI and X represent regions of stable node and the remaining regions represent the regions where this point behaves as saddle. However, when \(\Gamma \,^\prime _F(\lambda _{F_*})<0\) and \(G(\lambda _{F_*},\lambda _{V_*})<0\), region I represents region of stable focus, regions V and IX represent regions of stable node and the remaining regions represent the regions where this point behaves as saddle. It is important to note that as the parameters values change across the bifurcation curves C5 and C6 of Fig. 1d, the property of the Universe changes from a decelerated scaling solution (\(w_{\mathrm{eff}}>-\frac{1}{3}, \Omega _m>0\)) to a decelerated scalar field dominated solution (\(w_{\mathrm{eff}}>-\frac{1}{3}, \Omega _m=0\)). For this point, the exponent \(\beta \) in (31) is given by

    $$\begin{aligned} \beta _{A_3}=\frac{2}{3}\,{\frac{ \lambda _{V_*}}{ \left( w+1 \right) \left( \lambda _{V_*} - \lambda _{F_*}\right) }}. \end{aligned}$$
    (35)

    Therefore, it represents a decelerated expansion when \(0<\frac{\lambda _{V_*}}{\lambda _{V_*}-\lambda _{F_*}}< \frac{3}{2}(w+1)\) and an accelerated expanding Universe when \(\frac{\lambda _{V_*}}{\lambda _{V_*}-\lambda _{F_*}}> \frac{3}{2}(w+1)\). When \(\lambda _{F_*}=\lambda _{V_*}\), it corresponds to an effective cosmological constant behavior (\(w_\mathrm{eff}=-1\)), but it is unphysical as \(\Omega _m<0\). Further, from the bifurcation diagram of this point, we have checked that within the unstable (or saddle) accelerated regions of the parameter space, this point is unphysical.

  • Point \(A_4\) corresponds to a scalar field dominated solution (\(\Omega _\phi =1\)). This point disappears for values of \(\lambda _{F_*}, \lambda _{V_*}\) satisfying \({\lambda _{F_*}}^{2}+\lambda _{F_*}\,\lambda _{V_*} +2=0\). It can either be a stable node or unstable node or saddle depending on the choice of model parameters (see Fig. 1e). For \(\Gamma \,^\prime _F(\lambda _{F_*})>0\) and \(G(\lambda _{F_*},\lambda _{V_*})>0\), while region I represents a region of unstable node, regions III and VIII represent regions of stable node. The remaining regions represent the regions where this point behaves as a saddle. For \(\Gamma \,^\prime _F(\lambda _{F_*})<0\) and \(G(\lambda _{F_*},\lambda _{V_*})<0\), region II represents a region of unstable node, regions IV and VII represent regions of stable node and the remaining regions represent the regions where this point behaves as a saddle. The corresponding exponent for the scale factor solution (31) is given by

    $$\begin{aligned} \beta _{A_4}=\frac{{\lambda }^{2}_{F_*}+\lambda _{F_*}\,\lambda _{V_*}+2}{2\,{\lambda }^{2}_{F_*}-3\,\lambda _{F_*}\,\lambda _{V_*}+\lambda ^2_{V_*}}. \end{aligned}$$
    (36)

    This point exhibits an accelerated expanding Universe or decelerated expanding Universe for some parameter values. We have checked that this point is stable from the bifurcation diagram when it corresponds to an accelerated expansion. Hence, this point can describe the late time Universe. Further, depending on coupling function and potential, this point can correspond to an accelerating Universe when it is a saddle. Therefore, we can also use this point to model the graceful exit phenomenon. We have verified numerically that this point exhibits different behavior of the Universe when this point undergoes a bifurcation. For example, this point describes a decelerated Universe and an accelerated expanding Universe as this point changes from a saddle (some parts of regions V and VI of Fig. 1e) to a stable node (some parts of regions VII and VIII of Fig. 1e). It is worth mentioning that this point corresponds to an effective cosmological constant behavior (\(w_\mathrm{eff}=-1\)) when \(\lambda _{F_*}=\lambda _{V_*}\) or \(\lambda _{F_*}=\frac{\lambda _{V_*}}{2}\). The solution corresponds to \(\lambda _{F_*}=\frac{\lambda _{V_*}}{2}\) is of interest as it is identical to the de Sitter solution in GR (since \(\phi \) is constant in time). From the bifurcation diagram (i.e., Fig. 1e), one could confirm that there is a possibility that this point is stable when \(\lambda _{F_*}=\frac{\lambda _{V_*}}{2}\). This point’s stable nature explains the possible late time convergence behavior of the scalar-tensor theory towards GR. In other words, such a model converges towards a structurally stable GR-based model. For coupling function \(F(\phi )=1+\xi \phi ^2\) and \(V =V_0 \phi ^n\), this condition is met for \(n=4\). Also when \(\lambda _{F_*}< \lambda _{V_*}< 2\lambda _{F_*}\), this point behaves as a stable phantom-like attractor. A similar result for a particular potential case has been reported in [52]. Therefore, our present work provides a framework for choosing proper coupling and potential functions to get interesting dynamics for a broad class of non-minimal coupled scalar field models.

As there is no stable critical point lying on the intersection of invariant sub-manifolds \(y=0, \lambda _F=0, \lambda _V=0\), therefore, the above system does not contain any global attractor. Further, from the above analysis, one can see that the present model exhibits interesting solutions that can describe various cosmological eras of the Universe. For instance, the decelerated scalar field dominated solution can describe the early radiation era, the matter scaling solution that can describe the intermediate dark matter (DM), and the late time scalar field dominated solution describing the DE dominated era. Numerically, we observe that the local stability behavior of critical points changes for the coupling and potential parameters (Fig. 1), and hence the system as a whole undergoes bifurcation. Using the bifurcation diagrams of various critical points, we can classify the parameters for which the evolution corresponds to the generic evolution and non-generic evolution. Geometrically, when an orbit evolves from an unstable point and then settles in a stable point, it is called generic evolution. However, if the initial or final point is a saddle, it is called non-generic evolution. From the above analysis, we found that only class of models where the parameters \(\lambda _{V_*}, \lambda _{F_*}\) belong to the common region of region I of Fig. 1b and region VII of Fig. 1e; and also in the common region of region II of Fig. 1c and region VIII of Fig. 1e can possibly lead to physically interesting generic evolutionary scenarios. These correspond to the evolution from a decelerated kinetic dominated unstable node point \(A_{2+}\)/\(A_{2-}\) to an accelerated potential dominated stable point \(A_4\) via a matter scaling solutions \(A_1\) or \(A_3\). However, solutions evolving near an intermediate point \(A_3\) correspond to unphysical solutions (\(\Omega _m<0\)). Therefore, the sequence of generic cosmic viable evolution is given by \(A_{2\pm } \rightarrow A_1 \rightarrow A_4\). Thus, bifurcation diagrams allow us to classify the coupling and potential functions, describing interesting cosmological dynamics.

Table 3 Critical points of the system (37)–(38)
Full size table

Further from the bifurcation diagrams of each point, we see that there is an occurrence of transcritical bifurcation between critical points. For example, critical points \(A_1\) and \(A_3\) undergo transcritical bifurcation (Fig. 1a, d), \(A_{2+}\) and \(A_4\) (Fig. 1b, e), \(A_{2-}\) and \(A_4\) (Fig. 1c, e), \(A_{3}\) and \(A_4\) (Fig. 1d, e). This type of bifurcation occurs when two critical points interchange their stability properties at the bifurcation curve [18]. We can summarize these bifurcation scenarios as follows:

Statement 1

(Existence of transcritical bifurcation) A system (20)–(23) undergoes a transcritical bifurcation when

  1. 1.

    Critical points \(A_1\) and \(A_3\) interchange a saddle and stable node behavior along the bifurcation curve \(\lambda _{V_*}=\frac{3(1+\lambda ^2_{F_*}-w)(1+w)}{(3w-1)\lambda _{F_*}}\) for fixed w. In particular, for \(w=0\), the above curve is represented geometrically by two branch curves C1 and C2 of Fig. 1a, d.

  2. 2.

    Critical points \(A_{2+}\) and \(A_4\) interchange a saddle and unstable node behavior along a bifurcation curve \(\lambda _{V_*}=2\lambda _{F_*}+ \sqrt{9 \lambda _{F_*}^2+6}\), represented geometrically by curve C3 of Fig. 1b, e. Also, critical points \(A_{2-}\) and \(A_4\) interchange a saddle and unstable node behavior along a bifurcation curve \(\lambda _{V_*}=2\lambda _{F_*}- \sqrt{9 \lambda _{F_*}^2+6}\), represented geometrically by curve C4 of Fig. 1c, e.

  3. 3.

    Critical points \(A_{3}\) and \(A_4\) interchange a saddle and stable node behavior along the bifurcation curves

    $$\begin{aligned} \lambda _{V_*}= & {} \frac{1}{4}(3\,\lambda _{F_*}\,w+7) \\&+ \frac{1}{4}\,\sqrt{9\,{\lambda _{F_*}}^{2}{w}^{2}+66\,{\lambda ^2_{F_*}}w+73\,{\lambda ^2_{F_*}}+48\,w+48} \end{aligned}$$

    and

    $$\begin{aligned} \lambda _{V_*}= & {} \frac{1}{4}(3\,\lambda _{F_*}\,w+7) \\&- \frac{1}{4}\,\sqrt{9\,{\lambda _{F_*}}^{2}{w}^{2}+66\,{\lambda ^2_{F_*}}w+73\,{\lambda ^2_{F_*}}+48\,w+48} \end{aligned}$$

    for fixed value of w. In particular, for \(w=0\), the above curves are represented geometrically by curves C5 and C6 of Fig. 1d, e.

Note that one can prove the existence of transcritical bifurcation analytically by using the Sotomayor’s theorem [17,18,19]. However, since the bifurcation parameters \(\lambda _{V_*}, \lambda _{F_*}\) do not appear explicitly on the system (20)–(23), therefore, we postpone the analytical proof to a concrete example of coupling function F and scalar field potential V. Even though we can determine the general properties without specifying the concrete model, to understand the cosmological applications of a general model and better investigate its dynamics, we must assume a concrete example. Therefore, in the next section, we consider a specific model and analyze its cosmological dynamics in detail.

Fig. 2
figure 2

Bifurcation diagrams in \((\xi , n)\) parameter space exhibiting different local stability regions of points \(B_1\) in a, \(B_{2+}\) in b, \(B_{2-}\) in c, \(B_3\) in d and \(B_4\) in e for the case of \(w=0\). In each panel, the yellow color regions correspond to saddle regions, red color regions correspond to regions of stable node, blue color regions correspond to regions of stable focus, magenta color regions correspond to regions of unstable node. Black colored curves D1–D5 (see statements 2, 3, 4 for their expressions) separating different regions represent the non-hyperbolic curves. The curves D6 and D7 represent the curves where point \(B_3\) changes between a stable node and stable focus nature. Line \(n=0\) in d and curve D8 represents non-existence of points \(B_3\) and \(B_4\) respectively

Full size image

4 Example: quadratic coupling along with power-law potential

4.1 Stability analysis

Here, we shall examine the case where the non-minimal coupling is of the form \(F(\phi )= \xi \phi ^2\) and the scalar field potential is of form \(V(\phi )=V_0 \phi ^n\) (power-law). For this example, we have \(\lambda _F=-2 \sqrt{\xi }\), \(\lambda _V=-n\sqrt{\xi }\) and hence they are constants. This particular example is inspired physically by the string-dilaton, Brans Dicke actions and several effective quantum field theories [53]. Mathematically, this form of coupling and potential agrees with the Noether symmetry approach of the Lagrangian given by (1) and hence, leads to physically interesting exact solutions [54, 55]. This model is also compatible with the solar system constraint test [56]. Various cosmological data constrain the value of \(\xi \) to be \( \lesssim 10^{-2}\) at 95% confidence limit. However, a degeneracy between the value of \(\xi \) and the present Hubble constant \(H_0\) allows a larger value of \(\xi \) [57, 58].

Stability analysis for this particular example has been performed earlier in [27] where the main focus is on the hyperbolic points. However, a discussion on the condition for non-hyperbolicity of points has not been performed. The non-hyperbolic nature of the critical point is important to analyze the bifurcation scenarios. Since for this concrete example, \(\lambda _F\) and \(\lambda _V\) are fixed, the system (20)–(23) reduces to following two-dimensional system:

$$\begin{aligned} x'= & {} \frac{1}{4(6\,\xi +1)} \Big [{x}^{3} \left( 4\,\xi -w+1 \right) -2\,{x}^{2}\sqrt{\xi } \left( 24\,\xi -9\,w+7 \right) \nonumber \\&-6 x \left( 12\,w\xi - \,w+1+y \left( 2 \,n\xi +w+1 \right) \right) +12 \sqrt{\xi } y \nonumber \\&\left( - n+3\, \left( w+ 1 \right) \right) -12\, \left( 3\,w-1 \right) \sqrt{\xi } \Big ], \end{aligned}$$
(37)
$$\begin{aligned} y'= & {} \frac{y}{2(6\,\xi +1)} \Big [ 6(8\,\xi + w+1) +2\,\sqrt{\xi }x \left( -2(6\,\xi -3\,w+2) \right. \nonumber \\&\left. + \left( 6\,\xi +1 \right) n \right) -{x}^{2} \left( -4\,\xi +w-1 \right) \nonumber \\&-6\,y \left( 2\,n\xi +w+1 \right) \Big ]. \end{aligned}$$
(38)

The physical phase space of the reduced system is

$$\begin{aligned} \Psi =\left\{ (x, y) \in {\mathbb {R}}^2 ~\Big \vert ~\frac{(x-6\sqrt{\xi })^2}{6}+y \le (1+6 \xi ) \right\} . \end{aligned}$$
(39)

The critical points for the above system are given in Table 3. We note that critical points \(B_1, B_{2\pm }, B_3, B_4\) correspond to points \(A_1, A_{2\pm }, A_3, A_4\) respectively for this concrete example of coupling function and potential. The existence and stability behavior of these critical points are similar to the general case (see Table 3). The bifurcation diagrams exhibiting the stability regions of critical points are given in Fig. 2. It is worth noting that each critical point shows a non-hyperbolic behavior for different values of parameters (represented by black colored curves in Fig. 2). As analyzed in the general case (see Sect. 3), critical points \(B_1\) and \(B_3\) coincide along the curve D1 in which both of them are non-hyperbolic. Therefore, in this case, it is sufficient to analyze the non-hyperbolic nature only for a point \(B_1\). The analysis of center manifold theory for this case is performed in the appendix A and it is found that point \(B_1\) behaves as a saddle. For a detailed mathematical background on the center manifold theory, we refer to [19]. Further, points \(B_{2+}\) and \(B_{2-}\) coincide with point \(B_4\) and are non-hyperbolic along the curves D2 and D3 respectively. Also, critical points \(B_3\) and \(B_4\) are non-hyperbolic and coincide along the curves D4 and D5. Therefore, in each case, we shall analyze the non-hyperbolic property for a point \(B_4\) only. The analysis performed in the appendix B reveals that point \(B_4\) behaves as a saddle along each bifurcation curve.

As the phase space (39) is in general not compact, for the sake of completeness, we analyze the nature of the system (37)–(38) at infinity by employing the Poincaré’s projection method involving the following transformation [19]:

$$\begin{aligned} x_r=\frac{x}{\sqrt{1+x^2+y^2}},~~~~y_r=\frac{y}{\sqrt{1+x^2+y^2}}. \end{aligned}$$
(40)

The compactified phase space of the resulting system is therefore given by

$$\begin{aligned} \Psi _r&=\left\{ (x_r, y_r) \in {\mathbb {R}}^2 \Big | -1 \le x_r, y_r \le 1, x_r^2+y_r^2\le 1, \right. \nonumber \\&\quad \left. \frac{\left( \frac{x_r}{R}-6 \sqrt{\xi }\right) ^2}{6}+\frac{y_r}{R} \le 1+6 \xi \right\} , \end{aligned}$$
(41)

with \(R=\sqrt{1-x_r^2-y_r^2}\) . The critical points near infinity i.e., \(\sqrt{x^2+y^2} \rightarrow \infty \) correspond to points on the circle

$$\begin{aligned} \left\{ (x_r, y_r) \in {\mathbb {R}}^2 : x_r^2+y_r^2= 1 \right\} . \end{aligned}$$
(42)

We should take due care in applying the Poincaré compactification method, resulting in a wrong phase space topology, and hence false properties of the solutions [59]. However, in this case, the above choice of the dynamical variables does not destroy the phase space’s global structure since \(H>0\) [60]. The method’s advantage is to capture the possible critical points hidden at infinity that cannot be detected by the finite analysis. On employing this method, we found that there are four critical points near infinity viz., \((x_r, y_r)=(\pm 1,0), (0,\pm 1)\) lying on the equator of the Poincaré’s sphere. The analysis shows that points \(P_{1}^\infty \,(1,0)\), and \(P_{3}^\infty \,(-1,0)\) are saddle in nature. Points \(P_{2}^\infty \, (0,1), P_{4}^\infty \, (0,-1)\) are non-hyperbolic and hence the stability needs to be checked with an extra effort by the center manifold theory. However, by using a quick numerical check, we found that point \(P_2^\infty \) is saddle and \(P_4^\infty \) is stable for various values of model parameters \(n, \xi \) and \(w=0\). We note that of all critical points at infinity, only a saddle point \(P_2^\infty \) corresponds to an accelerated solution, but it is unphysical. Thus, critical points at infinity cannot describe either late time or early time behavior of the Universe and hence are not phenomenologically interesting. Therefore, here we do not present a detailed calculation of the analysis at infinity. In the next section, we discuss the possible bifurcation scenarios occurring at the non-hyperbolic condition of each critical point.

4.2 Bifurcation scenarios

In this section, we shall discuss the occurrence of local bifurcation of the system (37)–(38) with respect to parameters \(\xi \) and n. Then we extract the condition on \(\xi \) and n under which the present model describes the generic evolution of the Universe. In the case of a two-dimensional system, we can completely characterize the structural stability by Peixoto’s theorem. However, we cannot extend the theorem to a system of dimensions greater than two [19]. As a result of Peixoto’s theorem, a structurally stable system guarantees an open dense subset of initial conditions leading to a generic evolution (see appendix C).

In general, the necessary condition for the occurrence of bifurcation of the system is the non-hyperbolicity of the critical point. However, in the two-dimensional system, according to Peixoto’s theorem, the existence of non-hyperbolic critical points also implies the structural instability of the system [19]. As we have seen in the previous section, the system (37)–(38) contains non-hyperbolic points \(P_2^\infty \) and \(P_4 ^\infty \) on the Poincaré sphere, therefore, the vector field of the system is structurally unstable. Moreover, finite critical points can be non-hyperbolic for some values of \(\xi \), n and w. In what follows, similar to the general case, we again prepare the bifurcation diagrams (Fig. 2) for each critical point in the \((\xi ,n)\) parameter space and then apply the Sotomayor’s theorem (see the appendix C for the statement). The theorem’s main aim is to analytically investigate and specify the types of bifurcation.

The local bifurcation diagram for point \(B_1\) is given in Fig. 2a. A topological change occurs as this point changes from stable node to saddle along the curve D1 via a non-hyperbolic saddle node.

Another bifurcation occurs for points \(B_{2+}\) and \(B_{2-}\) along the curves D2 and D3 respectively, where both the points undergo an upheaval from unstable node to saddle via a non-hyperbolic saddle node (see Fig. 2b, c).

Point \(B_{3}\) changes its stability from a stable node to a saddle along the bifurcation curves D1, D4, D5 of Fig. 2d. For a particular case, \(n=2\), this point exhibits an effective cosmological constant behavior and for \(n=6\), the point’s dynamics change from an unaccelerated to an accelerated behavior.

Out of the above mentioned critical points, point \(B_{4}\) is an interesting point which can explain the late time behavior of the Universe. This point undergoes a stability change from an unstable node to a saddle along the curves D2 and D3 of Fig. 2e. Again, a change from a stable node to a saddle occurs when the point passes through the bifurcation curves D4 and D5 of Fig. 2e. As this point can represent interesting late time Universe, using bifurcation diagram (Fig. 2e), we summarize the stability property of this point for different range of \(\xi ,n, w\) as follows:

  • Point \(B_4\) is not stable when

    1. (i)

      \(n > \frac{3\,w+7}{2} +\frac{\sqrt{9\,{w}^{2}{\xi }^{2}+66\,w{\xi }^{2}+12\,w\xi +73\,{\xi }^{2}+12\,\xi }}{2\xi }\,\) (regions I and II of Fig. 2e), or,

    2. (ii)

      \(\frac{4 \xi -\sqrt{6 \xi +36 \xi ^2}}{\xi }<n<\) \(\frac{3\,w+7}{2} -\frac{\sqrt{9\,{w}^{2}{\xi }^{2}+66\,w{\xi }^{2}+12\,w\xi +73\,{\xi }^{2}+12\,\xi }}{2\xi }\,\)       (regions IV and V of Fig. 2e).

  • It is stable when

    1. (iii)

      \(4\le n < \frac{3\,w+7}{2} +\frac{\sqrt{9\,{w}^{2}{\xi }^{2}+66\,w{\xi }^{2}+12\,w\xi +73\,{\xi }^{2}+12\,\xi }}{2\xi },\)    or,            \(2\le n \le 4,\) or,     \(\frac{3\,w+7}{2} -\frac{\sqrt{9\,{w}^{2}{\xi }^{2}+66\,w{\xi }^{2}+12\,w\xi +73\,{\xi }^{2}+12\,\xi }}{2\xi }\,<n \le 2\,\)    (region III of Fig. 2e), or,

    2. (iv)

      \(n<\frac{4 \xi -\sqrt{6 \xi +36 \xi ^2}}{\xi }\,\) (region VI of Fig. 2e).

Table 4 Conditions on parameters \(\xi , n, w\) for which dynamics of Universe governed by the system (37)–(38) undergoes a generic evolution. Here, \(Q_{\pm }=\frac{3\,w\xi +7\,\xi \pm \sqrt{9\,{w}^{2}{\xi }^{2}+66\,w{\xi }^{2}+12\,w\xi +73\,{\xi }^{2}+12\,\xi }}{2\xi }\)
Full size table

It is worth mentioning that independent of the value of \(\xi \), this point describes a stable phantom attractor behavior for \(2<n<4\). Also, when \(n=4\), point \(B_4\) belongs to a stable region of parameter space. Therefore, as discussed in Sect. 3 (i.e., model with the condition \(\lambda _{F_*}=\frac{\lambda _{V_*}}{2}\)) this point corresponds to a deSitter solution in GR for \(n=4\). Similar result also holds for model considered in [21] with biquadratic potential.

From the above discussion on the bifurcation diagrams, we found the possibility of transcritical bifurcation exhibited by the system (37)–(38). In what follows, we summarize the occurrence of bifurcation and mathematically analyze the transcritical bifurcation with \(\xi \) as the bifurcation parameter using Sotomayor’s theorem.

Statement 2

The system (37)–(38) undergoes a transcritical bifurcation of critical points \(B_1\) and \(B_3\) along a curve

$$\begin{aligned} \xi =\frac{3}{2}\,{\frac{1-{w}^{2}}{n(3w-1)-6\,(w+1)}}, \end{aligned}$$

for fixed w.

Proof:

In this case, the bifurcation value is

$$\begin{aligned} \xi =\xi _0=\frac{3}{2}\,{\frac{1-{w}^{2}}{n(3w-1)-6\,(w+1)}}, \end{aligned}$$

in which the points \(B_1\) and \(B_3\) coincide and the real part of the eigenvalue corresponding to common critical point vanishes.

The eigenvector corresponding to a simple eigenvalue \(\lambda =0\) (i.e., multiplicity is 1) of the Jacobian matrix \(D\mathbf{f}(B_1,\xi _0)\) evaluated at a point \(B_1\) when \(\xi =\xi _0\) is

$$\begin{aligned} \mathbf{v}=\left[ \frac{\sqrt{6(1-w^2)} \sqrt{n(3w-1)-6(1+w)}}{(3w-1)(w-1)}~~~~~1 \right] ^T, \end{aligned}$$

where T stands for transpose and f is the vector field of the system (37)–(38).

Also, the eigenvector corresponding to a simple eigenvalue \(\lambda =0\) of the transpose of the Jacobian matrix is \(\mathbf{w}=\left[ 0~~1 \right] ^T.\)

After, few simple algebraic calculations one could easily verify that when \(\xi =\xi _0\), we have

$$\begin{aligned}&\mathbf{w}^T \mathbf{f}_\xi (B_1, \xi _0) = 0, \end{aligned}$$
(43)
$$\begin{aligned}&\mathbf{w}^T [\mathbf{Df}_\xi (B_1, \xi _0) \mathbf{v}] =\frac{1}{\left( 3\,{w}-1 \right) (w-1) {n}^{2}} \Big ( \left( (3w-1)n(n+2) \right. \nonumber \\&\quad \left. -24\,(w+1) \right) \left( 3\,nw-n-6\,w-6 \right) \Big ), \end{aligned}$$
(44)
$$\begin{aligned} \text {and}\nonumber \\&\mathbf{w}^T [\mathbf{D^2 f}(B_1, \xi _0) (\mathbf{v, v})] = -\,{\frac{ 6 \left( w+1 \right) n}{3\,w-1}}, \end{aligned}$$
(45)

where vector \(\mathbf{f}_\xi \) denotes the partial derivative of \(\mathbf{f}\) with respect to \(\xi \). Note here that the right hand side of (44), (45) is non-zero for any admissible value of n and w, otherwise \(\xi \) is undefined or negative. Hence, by the Sotomayor’s theorem, the system (37)–(38) undergoes a transcritical bifurcation when \(\xi =\frac{3}{2}\,{\frac{1-{w}^{2}}{n(3w-1)-6\,(w+1)}}\), which is represented by a curve D1 of Fig. 2a, d for \(w=0\). In a similar manner, one could also verify the following statements. \(\square \)

Statement 3

The system (37)–(38) undergoes a transcritical bifurcation of critical points \(B_{2\pm }\) and \(B_4\) along a curve

$$\begin{aligned} \xi =\frac{6}{n^2-8n-20}. \end{aligned}$$

For \(w=0\), the above equation is represented by two branch curves D2, D3 of Fig. 2b, c, e.

Statement 4

The system (37)–(38) undergoes a transcritical bifurcation of critical points \(B_3\) and \(B_4\) along a curve

$$\begin{aligned} \xi =\frac{3(w+1)}{{n}^{2}-3\,nw-7\,n-6\,w-6}. \end{aligned}$$

for fixed w.

For \(w=0\), the above equation is represented by two branch curves D4 and D5 of Fig. 2d, e.

Fig. 3
figure 3

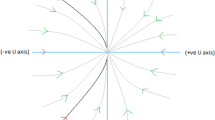
A global phase portrait of the system (37)–(38) for the generic scenario (II) with \(w=0, n=4, \xi =0.1\). The grey shaded region represents the non-physical region (i.e., \(\Omega _m<0\)). The yellow shaded region corresponds to the phantom like solution (\(w_{\mathrm{eff}}<-1\)) and the blue shaded region corresponds to a quintessence like solution (\(-1<w_{\mathrm{eff}}<-\frac{1}{3}\))

Full size image
Fig. 4
figure 4

Time evolution of the scalar field energy density \(\Omega _\phi \), matter energy density \(\Omega _m\), effective EoS \(w_{\mathrm{eff}}\) and EoS of scalar field \(w_\phi \) for a generic scenario (II). In a we have taken \(w=0, n=4, \xi =0.1\), b A closer look on the evolution of \(w_{\mathrm{eff}}\) given in a at late time, c \(w=0, n=4, \xi =0.001\)

Full size image

The above bifurcation scenarios help us to properly separate the Universe’s evolution into generic and non-generic evolution. In Table 4, we present the conditions satisfied by the model parameters to describe the Universe’s possible generic cosmological evolution. This type of evolution is interesting as it can determine the initial phase and the final phase of the Universe’s cosmological evolution for a wide range of initial conditions. Out of all the scenarios presented in Table 4, only scenarios II and IV are of cosmological interest as they could explain the late-time behavior of the Universe and fits with various CMB and BAO observational data [57]. In Fig. 3, we present the global phase space diagram for a particular choice of n and \(\xi \) which corresponds to a generic evolution of scenario II where the model exhibits a late-time acceleration (similar dynamics is exhibited by scenario IV). It is important to remark here that for the parameters within the range of generic scenario II, there is no bifurcation, so it is sufficient to present only one phase portrait for this scenario. Furthermore, in Sect. 5, we will discuss the evolution of cosmological quantities described by this model for parameters corresponding to scenario II.

5 Discussion and conclusion

In this work, we studied the global qualitative cosmological dynamics of a non-minimal coupled scalar field for a general class of coupling function and potential. We focused on the bifurcation analysis to investigate the effect of varying the model parameters on the global dynamics. The main objective of applying bifurcation theory is to determine the existence of generic evolutionary scenarios. It will help us identify the Universe’s initial and final phases for a wide range of initial conditions. The bifurcation theory also allows us to understand how physics described by the phase space changes with parameters.

The general model described by the system (20)–(23) contains different interesting cosmological solutions for different model parameters. For instance, the present model exhibits a scalar field dominated solution \(A_{2\pm }\), resembling a stiff matter Universe or radiation Universe for some choice of coupling and potential parameters. The scalar field’s sole contribution to an early radiation epoch is an interesting scenario missing in a minimal coupled canonical scalar field within the GR context. For some choice of coupling function and potential, the general model also shows the presence of DM-DE scaling solutions \(A_1\) and \(A_3\) describing an intermediate matter epoch. Lastly, the present model exhibits a late time acceleration of the Universe via a critical point \(A_4\). Thus, from the analysis presented in Sect. 3, one can select a class of non-minimal coupled scalar field models describing a viable sequence of cosmic evolution. In particular, for models with \(\lambda _{F_*}=\frac{\lambda _{V_*}}{2}\), point \(A_4\) corresponds to a late time de Sitter solution of the GR case. Hence, such a class of scalar-tensor theories converges towards a structurally stable GR-based model, i.e., the \(\Lambda \)CDM model. This is a common feature of the scalar-tensor gravity which has been verified numerically and analytically [61,62,63,64,65,66]. Therefore, the present analysis identifies a broad class of scalar-tensor models generically possessing this property. Further, it is possible that the point \(A_4\) corresponds to a late time super-accelerated phase (\(w_{\mathrm{eff}}<-1\)) when \(\lambda _{F_*}<\lambda _{V_*}<2 \lambda _{F_*}\). Hence, in the presence of a non-minimal coupling, the model can explain a super-accelerated phase (\(w_{\mathrm{eff}}<-1\)) without the need for the introduction of a phantom field. Depending on the potential and coupling function, point \(A_4\) is a saddle in nature and hence can also describe the possible inflationary exit phenomenon.

In Sect. 4, we illustrate the global dynamics in detail by considering a simple example corresponding to a quadratic coupling function and a power-law form potential. For this particular example, we find the range of parameters n and \(\xi \) describing a generic evolution scenario (see Table 4). In Fig. 4, we have plotted the evolution of cosmological parameters against the redshift \(\mathrm z\) for a choice of parameters corresponding to one of the generic scenarios, i.e., scenario (II) which starts from an unstable decelerated solution (\(B_{2\pm }\)) towards a deSitter like solution \(B_4\) (a similar evolution is obtained for scenario IV). Recall that redshift \(\mathrm{z}=-1+\frac{1}{a}\) where the present value of the scale factor taken to be unity, with \(\mathrm{z}=0\) corresponds to the present Universe and \(\mathrm{z}=-1\) corresponds to its infinite future. It is worth mentioning here that only the parameters’ values corresponding to the generic evolution of scenarios II or IV satisfy various observational constraints coming from Planck and BAO datasets [58]. Therefore, mathematically, stability analysis and bifurcation theory help us to locate various physically rich models. For instance, we can find the parameter’s range which can generically describe the thermal history of the Universe starting from an early radiation domination (\(w_{\mathrm{eff}} \simeq \frac{1}{3}\)) or stiff matter solution (\(w_{\mathrm{eff}} \simeq 1\)) represented by points \(B_{2\pm }\) towards a DE dominated solution \(B_4\) (\(w_{\mathrm{eff}} \simeq -1\)) via a matter like solution \(B_1\) (\(w_{\mathrm{eff}} \simeq 0\)) i.e., \(B_{2\pm } \rightarrow B_1 \rightarrow B_4\) (see Figs. 3, 4).

The possibility that \(\Omega _m>1\) and \(w_{\phi }\) diverges at the onset of a matter-dominated era (as explained in paragraphs after Eqs. (13) and (27)) can also be confirmed from Fig. 4a. The divergence of \(w_\phi \), however, does not cause any issue to the evolution behavior of \(w_{\mathrm{eff}}\), as this corresponds to the vanishing of scalar field energy density. The overdensity of matter component is not a surprise in cosmological models where interaction between different components occurs [67]. Such behavior is more visible by comparing a change in the behavior of \(\Omega _m\) and \(w_\phi \) to \(\xi \) (i.e., \(\lambda _F\)) from Fig. 4a, c (the range of divergence of \(w_\phi \) reduces and \(\Omega _m \rightarrow 1\) as \(\xi \rightarrow 0\)). Interestingly, the behavior is consistent with the result of [56], that the background dynamics of the present model approach GR with the cosmological constant in the limit \(\xi \rightarrow 0\). For a generic scenario (II), there is also a possibility of crossing the phantom divide line and eventually the solution settles down towards a cosmological constant behavior (see Fig. 3). We can confirm it by taking a closer look at the late time evolution of \(w_{\mathrm{eff}}\) (see Fig. 4b). In Fig. 4, we choose initial conditions such that the Universe agrees with the current observational data i.e., \(\Omega _m \approx 0.3, w_{\mathrm{eff}} \approx -0.8\) [68].

Our analysis shows that the non-minimal coupled scalar field model describes a rich cosmological history of the Universe. For instance, the model exhibits the transition: radiation \(\rightarrow \) matter \(\rightarrow \) DE and the possible crossing of phantom divide line but avoiding the big rip singularity. It is worth noting that only by using the stability analysis, one can determine such a transition. However, bifurcation tools help us locate the parameter values describing such dynamics without a fine-tuning of initial conditions. With the present choice of variables (19), this model can explain the graceful exit scenario and the late time DE era separately. Such a result is a common feature of many classes of scalar-tensor theories. Therefore, it is of interest to extend the analysis to the case where the scalar field is coupled non-minimal with gravity and matter, as discussed in [69]. Such discussion is beyond the scope of the present work.