1 Introduction

As it is well known, the development of Riemannian geometry led to the rigorous mathematical formulation of general relativity (GR). In spite of the great success and solid predictive power of GR in many contexts, it still falls short in explaining some of the current cosmological data. It does not properly explain the cosmological evolution at early times and is unable to predict a late time accelerated expansion. Consequently, diverse alternative modified theories of gravity have been proposed [1]. Among the various proposals, a particularly well motivated and promising setup in the spirit of gravity geometrization is that of non-Riemannian geometry [2, 3], where the Riemannian assumptions of metric compatibility and torsionlessness of the connection are released and therefore non-vanishing torsion and nonmetricity are allowed along with curvature. Non-Riemannian effects, induced by the presence of torsion and non-metricity, are nowadays believed to have played a key role in particular in the very early Universe (see [4, 5] and references therein).

Different restrictions of non-Riemannian geometry provide distinct frameworks for gravity theories formulations and the inclusion of torsion and non-metricity in gravitational theories has led to many fruitful applications in various areas of both mathematics and physics, among which, for instance, the ones recently presented in [6,7,8,9,10,11,12,13,14,15]. In particular, in the cosmological context, in [15] the most general form of acceleration equation in the presence of torsion and non-metricity was derived and conditions under which torsion and non-metricity accelerate/decelerate the expansion rate of the Universe were discussed. Let us also mention that imposing the vanishing of torsion and non-metricity one gets metric theories of which GR is a special case, whereas by demanding the vanishing of the curvature and non-metricity one is left with the standard teleparallel formulation [16]. Moreover, one could either set the curvature and torsion to zero while allowing for a non-vanishing non-metricity, which yields the symmetric teleparallel scheme [17, 18], or fix just the curvature to zero getting a generalized teleparallel framework involving both torsion and non-metricity [19]. On the other hand, one may also impose no constraint on such geometric objects. This is the non-Riemannian scenario where Metric-Affine Gravity (MAG) theories are developed. The literature on the subject is huge. For an exhaustive review of the geometrical theoretical background on MAG we refer the reader to e.g. [20,21,22]. In the metric-affine approach the metric and the connection are considered as independent fields and the matter Lagrangian depends on the connection as well. In this framework, the theory is assumed to have, in principle, a non-vanishing hypermomentum tensor [23] encompassing the microscopic characteristics of matter such as spin, dilation, and shear [20].

What is more, in the framework of non-Riemannian geometry, where the presence of extra degrees of freedom with respect to GR is due to torsion and non-metricity of spacetime which are linked to the microstructure of matter, fluid carrying hypermomentum turns out to be very appealing. In particular, diverse hyperfluid models have proved to have relevant applications especially in cosmology, such as the ones given in [24,25,26,27,28,29,30,31,32,33]. In particular, in [33] the perfect (ideal) hyperfluid model representing the natural generalization of the classical GR perfect fluid structure has been formulated and analyzed.

Motivated by the prominent and intriguing role of non-Riemannian geometry and hyperfluids in the cosmological scenario, in the present paper we study the cosmology of a quadratic torsionful gravity theory given by the Einstein–Hilbert (EH) contribution plus all the admitted quadratic parity even torsion scalars (see also [34]) and in the presence of a perfect hyperfluid. We restrict ourselves to the case of vanishing non-metricity while allowing for a non-vanishing torsion and let the matter action also exhibit a dependence on the connection.

The remaining of this paper is structured as follows: in Sect. 2 we briefly review the geometric setup and in Sect. 3 we give a short account of energy–momentum and hypermomentum tensors. Subsequently, in Sect. 4 we write our quadratic torsionful gravity theory and derive its field equations. We work in a first order formalism, where the metric and the affine connection are treated as independent variables. The theory and the aforementioned general analysis is developed in n spacetime dimensions, whereas we restrict ourselves to the case \(n=4\) when studying solutions. Section 5 is devoted to the study of the cosmology of the theory. Here we first discuss the torsion degrees of freedom in a Friedmann–Lemaître–Robertson–Walker (FLRW) spacetime and recall the notion of perfect hyperfluid together with its properties. Then we analyze the field equations, conservation laws, and torsion modified Friedmann equations for our torsionful model. Finally, in Sect. 6 we provide exact analytic solutions for such torsionful cosmology. In Sect. 7 we discuss our results and possible future developments. Useful formulas and conventions are collected in Appendix A.

2 Review of the geometric setup

Let us start with a brief review of the geometric setup. We will adopt the same notation and conventions of Ref. [22], to which we refer the reader for more details. We consider the framework of non-Riemannian geometry, endowed with a metric \(g_{\mu \nu }\) and an independent affine connection \({\Gamma ^\lambda }_{\mu \nu }\). The generic decomposition of an affine connection reads

$$\begin{aligned} {\Gamma ^\lambda }_{\mu \nu } = {\tilde{\Gamma }}^\lambda _{{\lambda }\mu \nu } + {N^\lambda }_{\mu \nu }, \end{aligned}$$
(1)

where the distortion tensor \({N^\lambda }_{\mu \nu }\) (non-Riemannian contribution to the affine connection) and the Levi–Civita connection \({\tilde{\Gamma }}^\lambda _{{\lambda }\mu \nu }\) (Riemannian contribution) are respectively given by

$$\begin{aligned} {N^\lambda }_{\mu \nu }= & {} \underbrace{\frac{1}{2} g^{\rho \lambda }\left( Q_{\mu \nu \rho } + Q_{\nu \rho \mu } - Q_{\rho \mu \nu }\right) }_{\text {deflection {(or disformation)}}}\nonumber \\&- \underbrace{g^{\rho \lambda }\left( S_{\rho \mu \nu } + S_{\rho \nu \mu } - S_{\mu \nu \rho }\right) }_{\text {contorsion} \, := \, {K^\lambda }_{\mu \nu }}, \end{aligned}$$
(2)
$$\begin{aligned}&{\tilde{\Gamma }}^\lambda _{{\lambda }\mu \nu } = \frac{1}{2} g^{\rho \lambda }\left( \partial _\mu g_{\nu \rho } + \partial _\nu g_{\rho \mu } - \partial _\rho g_{\mu \nu }\right) . \end{aligned}$$
(3)

In Eq. (2), \({S_{\mu \nu }}^\rho \) is the Cartan torsion tensor,

$$\begin{aligned} {S_{\mu \nu }}^\lambda := {\Gamma ^\lambda }_{[\mu \nu ]}, \end{aligned}$$
(4)

whose trace is given by

$$\begin{aligned} S_\mu := {S_{\mu \lambda }}^\lambda . \end{aligned}$$
(5)

On the other hand, \(Q_{\lambda \mu \nu }\) is the nonmetricity tensor, defined as

$$\begin{aligned} Q_{\lambda \mu \nu }:= -\nabla _\lambda g_{\mu \nu } = -\partial _\lambda g_{\mu \nu } + {\Gamma ^\rho }_{\mu \lambda } g_{\rho \nu } + {\Gamma ^\rho }_{\nu \lambda }g_{\mu \rho }. \end{aligned}$$
(6)

In the sequel we will focus on the case of a metric-compatible torsionful affine connection, namely we will consider vanishing non-metricity and non-vanishing torsion. Our definition for the covariant derivative \(\nabla \), associated with a metric-compatible torsionful affine connection \(\Gamma \), acting on a vector is

$$\begin{aligned} \nabla _\mu u^\lambda = \partial _\mu u^\lambda + {\Gamma ^\lambda }_{\nu \mu } u^\nu . \end{aligned}$$
(7)

The curvature tensor is defined by

$$\begin{aligned} {R^\mu }_{\nu \alpha \beta } := 2 \partial _{[\alpha } {\Gamma ^\mu }_{|\nu |\beta ]} + 2 {\Gamma ^\mu }_{\rho [\alpha } {\Gamma ^\rho }_{|\nu |\beta ]} \end{aligned}$$
(8)

and we also have the following contractions:

$$\begin{aligned}&R_{\nu \beta } := {R^\mu }_{\nu \mu \beta }, \end{aligned}$$
(9)
$$\begin{aligned}&{\hat{R}}_{\alpha \beta } := {R^\mu }_{\mu \alpha \beta } = 0, \end{aligned}$$
(10)
$$\begin{aligned}&{\check{R}}^\lambda _{{\lambda } \alpha } := {R^\lambda }_{\mu \nu \alpha } g^{\mu \nu } . \end{aligned}$$
(11)

The tensor in (9) is the Ricci tensor of \(\Gamma \), while in (10) we have the so-called homothetic curvature which vanishes for metric-compatible affine connections, and in (11) we have introduced a third tensor that is sometimes referred to as the co-Ricci tensor in the literature. In particular, for metric-compatible affine connections we have \({\check{R}}_{\mu \nu }=-R_{\mu \nu }\) (see also [22] for details). A further contraction gives us the Ricci scalar of \(\Gamma \), which is uniquely defined, since

$$\begin{aligned} R := R_{\mu \nu } g^{\mu \nu } = - {\check{R}}_{\mu \nu } g^{\mu \nu }. \end{aligned}$$
(12)

Let us also mention that plugging the decomposition (1) into the definition of the curvature tensor (8) one can prove that

$$\begin{aligned} {R^\mu }_{\nu \alpha \beta } = {\tilde{R}}^\mu _{{\mu } \nu \alpha \beta } + 2 {\tilde{\nabla }}_{[\alpha } {N^\mu }_{|\nu |\beta ]} + 2 {N^\mu }_{\lambda |\alpha } {N^\lambda }_{|\nu |\beta ]}, \end{aligned}$$
(13)

where \({\tilde{\nabla }}\) denotes the Levi–Civita covariant derivative. Moreover, the torsion can be derived from the distortion tensor through the relation

$$\begin{aligned} S_{\mu \nu \alpha } = N_{\alpha [\mu \nu ]}. \end{aligned}$$
(14)

The variation of the torsion with respect to the metric and the connection (see e.g. [22]) reads, respectively,

$$\begin{aligned}&\delta _g {S_{\mu \nu }}^\alpha = 0, \end{aligned}$$
(15)
$$\begin{aligned}&\delta _\Gamma {S_{\alpha \beta }}^\lambda = \delta ^{[\mu }_{\alpha }\delta ^{\nu ]}_{\beta } \delta {\Gamma ^\lambda }_{\mu \nu }. \end{aligned}$$
(16)

These formulas are particularly useful to reproduce the calculations in the sequel.

3 Hypermomentum and energy–momentum tensors

In this section we give a short account of energy–momentum and hypermomentum tensors, following the same lines of [31]. Here we shall restrict ourselves to the metric-compatible torsionful case.

In our setup we consider the action to be a functional of the metric, the independent metric-compatible torsionful connection, and the matter fields, that is to say

$$\begin{aligned} S[g,\Gamma ,\varphi ] = S_{\text {G}}[g,\Gamma ] + S_{\text {M}}[g,\Gamma ,\varphi ], \end{aligned}$$
(17)

where

$$\begin{aligned} S_{\text {G}}[g,\Gamma ] = \frac{1}{2\kappa } \int d^n x \sqrt{-g} {\mathcal {L}}_{\text {G}} (g,\Gamma ) \end{aligned}$$
(18)

and

$$\begin{aligned} S_{\text {M}}[g,\Gamma ,\varphi ] = \int d^n x \sqrt{-g} {\mathcal {L}}_{\text {M}} (g,\Gamma ,\varphi ) \end{aligned}$$
(19)

represent, respectively, the gravitational sector and the matter one. In the former \(\kappa =8\pi G\) is the gravitational constant, while in the latter \(\varphi \) collectively denotes the matter fields. Let us mention that the action (17) also depends on the derivatives of the metric and connection. Here we are suppressing the aforesaid dependence for simplicity.

Then, we define as usual the metrical (symmetric) energy–momentum tensor (MEMT)

$$\begin{aligned} T_{\mu \nu } := - \frac{2}{\sqrt{-g}} \frac{\delta S_{\text {M}}}{\delta g^{\mu \nu }} = - \frac{2}{\sqrt{-g}} \frac{\delta (\sqrt{-g} {\mathcal {L}}_{\text {M}})}{\delta g^{\mu \nu }} \end{aligned}$$
(20)

and the hypermomentum tensor (HMT) [23]

$$\begin{aligned} {\Delta _\lambda }^{\mu \nu } := - \frac{2}{\sqrt{-g}} \frac{\delta S_{\text {M}}}{\delta {\Gamma ^\lambda }_{\mu \nu }} = - \frac{2}{\sqrt{-g}} \frac{\delta (\sqrt{-g} {\mathcal {L}}_{\text {M}})}{\delta {\Gamma ^\lambda }_{\mu \nu }}, \end{aligned}$$
(21)

which encompasses matter microstructure [20]. Now, note that if one works in the equivalent formalism based on the vielbeins \({e_{\mu }}^c\) and spin connection \(\omega _{\mu a b}\), then the so-called canonical energy–momentum tensor (CEMT) is defined by

$$\begin{aligned} {t^\mu }_c := \frac{1}{\sqrt{-g}} \frac{\delta S_{\text {M}}}{\delta {e_\mu }^c}, \end{aligned}$$
(22)

which, in general, is not symmetric. Here we use Latin letters to denote Lorentz indices, that is tangent indices. The usual relation \(g_{\mu \nu }= {e_\mu }^a {e_\nu }^b \eta _{ab}\) connecting metric and vielbeins holds, where \(\eta _{ab}\) is the tangent space flat Minkowski metric. Our conventions are given in Appendix A. The CEMT is not independent of the MEMT and HMT (see also [20]). Indeed, one can prove that the following relation holds:

$$\begin{aligned} {t^\mu }_\lambda := \frac{1}{\sqrt{-g}} \frac{\delta S_{\text {M}}}{\delta {e_\lambda }^c} {e_\lambda }^c = {T^\mu }_\lambda - \frac{1}{2 \sqrt{-g}} {\hat{\nabla }}_\nu \left( \sqrt{-g} {\Delta _\lambda }^{\mu \nu } \right) ,\nonumber \\ \end{aligned}$$
(23)

where we have also exploited the identity

$$\begin{aligned} \nabla _\nu {e_\mu }^a = 0 = \partial _\nu {e_\mu }^a - {\Gamma ^\rho }_{\mu \nu } {e_\rho }^a + \omega ^{{\nu } a}_{\nu {a} b} {e_\mu }^b, \end{aligned}$$
(24)

connecting the two formalisms, and we have defined

$$\begin{aligned} {\hat{\nabla }}_\nu := 2 S_\nu - \nabla _\nu . \end{aligned}$$
(25)

Observe that for matter with no microstructure (\(\Delta _{\alpha \mu \nu }\equiv 0\)) the CEMT and MEMT coincide. Furthermore, note that from Eq. (23) one can obtain the conservation law for spin [35], which, in the metric-compatible torsionful case, reads

$$\begin{aligned} 2 t_{[\mu \nu ]} = \frac{1}{\sqrt{-g}} {\hat{\nabla }}_\alpha \left( \sqrt{-g} {\tau _{\mu \nu }}^\alpha \right) , \end{aligned}$$
(26)

where

$$\begin{aligned} {\tau _{\mu \nu }}^\alpha := {\Delta _{[\mu \nu ]}}^\alpha . \end{aligned}$$
(27)

Additionally, upon contraction of \(\mu ,\lambda \) in (23), one gets the trace relation

$$\begin{aligned} t = T + \frac{1}{2 \sqrt{-g}} \partial _\nu \left( \sqrt{-g} \Delta ^\nu \right) , \end{aligned}$$
(28)

with

$$\begin{aligned} t := {t^\mu }_\mu , \quad T := {T^\mu }_\mu , \quad \Delta ^\nu := {\Delta _\lambda }^{\lambda \nu }. \end{aligned}$$
(29)

From Eq. (28) one can notice that for specific matter types the following relations hold true:

$$\begin{aligned} T = 0 \quad&\leftrightarrow \quad 2t = \frac{1}{\sqrt{-g}} \partial _\nu \left( \sqrt{-g} \Delta ^\nu \right) , \end{aligned}$$
(30)
$$\begin{aligned} t = 0 \quad&\leftrightarrow \quad 2T = - \frac{1}{\sqrt{-g}} \partial _\nu \left( \sqrt{-g} \Delta ^\nu \right) , \end{aligned}$$
(31)
$$\begin{aligned} t = T \quad&\leftrightarrow \quad \partial _\nu \left( \sqrt{-g} \Delta ^\nu \right) = 0, \end{aligned}$$
(32)

corresponding, respectively, to the case of conformally invariant, frame rescalings invariant, and special projective transformations invariant theories (see [36] for details on such models).

4 The theory

We consider an extension of the Einstein–Cartan theory, including also the three torsion (parity even) quadratic terms that are allowed by dimensional analysis.Footnote 1 As we shall show, their presence is rather essential in order to obtain non-trivial dynamics for the torsion variables.Footnote 2 Then, our extended quadratic torsionful action involves three parameters and reads

$$\begin{aligned} S[g,\Gamma ,\varphi ]= & {} \frac{1}{2 \kappa }\int d^{n}x \sqrt{-g} \Big [ R+ b_{1}S_{\alpha \mu \nu }S^{\alpha \mu \nu } \nonumber \\&+ b_{2}S_{\alpha \mu \nu }S^{\mu \nu \alpha } + b_{3}S_{\mu }S^{\mu } \Big ] +S_{\text {hyp}}, \end{aligned}$$
(33)

where \(b_{1}\), \(b_{2}\), and \(b_{3}\) are dimensionless parameters. \(S_{\text {hyp}}\) denotes the matter part which we assume to be that of a perfect hyperfluid. Note that the above action is a special case of the more general gravitational theory involving both torsion and non-metricity quadratic parity even and parity odd terms [22]. Moreover, the action (33) has been considered also in [34] in a different context and in the presence of a cosmological constant. In this regard, let us mention here that the inclusion of a cosmological constant term in (33) would just imply a further contribution to the metric field equations we are going to analyze, while the connection field equations would not be modified.

Let us now derive the field equations of the theory (33). Variation with respect to the metric gives

$$\begin{aligned} R_{(\mu \nu )}-\frac{R}{2}g_{\mu \nu }-\frac{{\mathcal {L}}_{2}}{2}g_{\mu \nu } + B_{\mu \nu }=\kappa T_{\mu \nu }, \end{aligned}$$
(34)

where we have defined

$$\begin{aligned} B_{\mu \nu }= & {} B_{\nu \mu }:=b_{1}(2S_{\nu \alpha \beta }{S_{\mu }}^{\alpha \beta }-S_ {\alpha \beta \mu }{S^{\alpha \beta }}_{\nu })\nonumber \\&-b_{2}S_{\nu \alpha \beta }{S_{\mu }}^{\beta \alpha } +b_{3}S_{\mu }S_{\nu } \end{aligned}$$
(35)

and

$$\begin{aligned} {\mathcal {L}}_{2}:= b_{1}S_{\alpha \mu \nu }S^{\alpha \mu \nu } + b_{2}S_{\alpha \mu \nu }S^{\mu \nu \alpha } + b_{3}S_{\mu }S^{\mu }. \end{aligned}$$
(36)

In addition, varying the action with respect to the metric-compatible but torsionful connection \({\Gamma ^\lambda }_{\mu \nu }\) we get the field equations

$$\begin{aligned} {P_{\lambda }}^{\mu \nu }+{\Psi _{\lambda }}^{\mu \nu }=\kappa {\Delta _{\lambda }}^{\mu \nu }, \end{aligned}$$
(37)

where

$$\begin{aligned} {P_{\lambda }}^{\mu \nu }=2(S_{\lambda }g^{\mu \nu }-S^{\mu }\delta _{\lambda }^{\nu }+g^{\mu \sigma }{S_{\sigma \lambda }}^{\nu }) \end{aligned}$$
(38)

is the metric-compatible torsionful Palatini tensor, which fulfills \({P_{\mu }}^{\mu \nu }\equiv 0\), and where we have defined

$$\begin{aligned} {\Psi _{\lambda }}^{\mu \nu }:= 2 b_{1}{S^{\mu \nu }}_{\lambda }+2 b_{2}{S_{\lambda }}^{[\mu \nu ]}+2b_{3}S^{[\mu }\delta ^{\nu ]}_{\lambda }. \end{aligned}$$
(39)

In what follows we will analyze the cosmology of this quadratic torsionful gravity theory.

5 Cosmology with quadratic torsion terms

In this section we move on to the study of the cosmology of the theory (33). To pursue this aim, we shall consider a flat FLRW spacetime with the usual Robertson-Walker line element

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}\delta _{ij}dx^{i}dx^{j}, \end{aligned}$$
(40)

where a(t) is the cosmic scale factor and \(i,j=1,2,\ldots ,n-1\). In addition we let \(u^\mu \) represent the normalized n-velocity field of a given fluid which in co-moving coordinates is expressed as \(u^\mu = \delta ^\mu _0=(1,0,0,\ldots ,0)\), \(u_\mu u^\mu =-1\). Accordingly, we define in the usual way the projector tensor

$$\begin{aligned} h_{\mu \nu }:= g_{\mu \nu } + u_\mu u_\nu , \end{aligned}$$
(41)

which project objects on the space orthogonal to \(u^\mu \). We also define the temporal derivative

$$\begin{aligned} \dot{}=u^\alpha \nabla _\alpha . \end{aligned}$$
(42)

The projection operator (41) and the temporal derivative (42) constitute together a \(1+(n-1)\) spacetime split.

5.1 Perfect cosmological hyperfluid

As we have already mentioned in the introduction, a hyperfluid is a classical continuous medium carrying hypermomentum. The general formulation of perfect hyperfluid generalizing the classical perfect fluid notion of GR has been recently presented in [33] by first giving its physical definition and later using the appropriate mathematical formulation in order to extract its energy tensors by demanding spatial isotropy. In our study we consider such perfect hyperfluid model in a homogeneous cosmological setting.Footnote 3

As shown in [33], the description of the perfect hyperfluid is given by the energy related tensors

$$\begin{aligned} T_{\mu \nu }= & {} \rho u_\mu u_\nu + p h_{\mu \nu }, \end{aligned}$$
(43)
$$\begin{aligned} t_{\mu \nu }= & {} \rho _c u_\mu u_\nu + p_c h_{\mu \nu }, \end{aligned}$$
(44)
$$\begin{aligned} \Delta ^{(n)}_{\alpha \mu \nu }= & {} \phi (t) h_{\mu \alpha } u_\nu + \chi (t) h_{\nu \alpha } u_{\mu } + \psi (t) u_{\alpha } h_{\mu \nu } \nonumber \\&+ \omega (t) u_\alpha u_\mu u_\nu + \delta ^n_4 \varepsilon _{\alpha \mu \nu \rho } u^\rho \zeta (t), \end{aligned}$$
(45)

all of them respecting spatial isotropy and subject to certain conservation laws (see discussion below). In the hyperfluid MEMT (43), \(\rho \) and p are, as usual, the density and pressure of the perfect fluid component of the hyperfluid, while, in the hyperfluid CEMT (44), \(\rho _c\) and \(p_c\) are, respectively, the canonical density and canonical pressure of the hyperfluid. On the other hand, the variables \(\phi \), \(\chi \), \(\psi \), \(\omega \), and \(\zeta \) in the hypermomentum (45) characterize the microscopic properties of the fluid which, upon using the connection field equations, act as the sources of the torsionful non-Riemannian background. The aforementioned conservation laws for the perfect hyperfluid in the case in which the non-metricity is set to zero while the torsion is non-vanishing read as follows:

$$\begin{aligned}&\frac{1}{\sqrt{-g}} {\hat{\nabla }}_\mu \left( \sqrt{-g} {t^\mu }_\alpha \right) = \frac{1}{2} \Delta ^{\lambda \mu \nu } R_{\lambda \mu \nu \alpha } + 2 S_{\alpha \mu \nu } t^{\mu \nu } \quad \nonumber \\&\quad \rightarrow {\tilde{\nabla }}_\mu {t^\mu }_\alpha = \frac{1}{2} \Delta ^{\lambda \mu \nu } R_{\lambda \mu \nu \alpha }, \end{aligned}$$
(46)
$$\begin{aligned}&{t^\mu }_\lambda = {T^\mu }_\lambda - \frac{1}{2 \sqrt{-g}} {\hat{\nabla }}_\nu \left( \sqrt{-g} {\Delta _\lambda }^{\mu \nu } \right) , \end{aligned}$$
(47)

Recall that \({\tilde{\nabla }}\) denotes the Levi–Civita covariant derivative. Notice that (47) is exactly the same relation (23) we have previously obtained connecting the three energy related tensors.Footnote 4 In addition, as we can see from (46), the canonical energy–momentum tensor naturally couples to torsion. Equations (46) and (47) will be fundamental in the study of the cosmology of our theory.

5.2 Cosmology with torsion

Now we need the most general form of torsion that can be written in a homogeneous and isotropic space. In such a space the torsion has at most two degrees of freedom in \(n=4\) and a single one for \(n \ne 4\) [37], and it can be written in an explicitly covariant fashion as (see also [15, 31])

$$\begin{aligned} S_{\mu \nu \alpha }^{(n)}=2u_{[\mu }h_{\nu ]\alpha }\Phi (t)+\varepsilon _ {\mu \nu \alpha \rho }u^{\rho }P(t)\delta ^n_4, \end{aligned}$$
(48)

where \(\varepsilon _{\mu \nu \alpha \rho }\) is the Levi–Civita tensor and \(\delta ^{n=4}_4=1\), otherwise it is zero. Here the upper label (n) is used to denote that we are considering n spacetime dimensions. Eq. (48) also implies

$$\begin{aligned} S_\alpha = (n-1) \Phi u _\alpha , \end{aligned}$$
(49)

and the following relations hold:

$$\begin{aligned}&S_{\mu \nu \alpha } S^{\mu \nu \alpha } = - 2 (n-1) \Phi ^2 + 6 P^2 \delta ^n_4, \end{aligned}$$
(50)
$$\begin{aligned}&S_{\mu \nu \alpha } S^{\alpha \mu \nu } = (n-1) \Phi ^2 + 6 P^2 \delta ^n_4, \end{aligned}$$
(51)
$$\begin{aligned}&S_\mu S^\mu = - (n-1)^2 \Phi ^2, \end{aligned}$$
(52)

which imply, in particular,

$$\begin{aligned} (n-1) S_{\mu \nu \alpha } S^{\mu \nu \alpha } - (n-1) S_{\mu \nu \alpha } S^{\alpha \mu \nu } - 3 S_{\mu } S^{\mu } = 0, \end{aligned}$$
(53)

indicating that actually only two out of the three torsion scalars are independent.

Consequently, the distortion tensor takes the form

$$\begin{aligned} N_{\alpha \mu \nu }^{(n)}= & {} -\left( S_{\alpha \mu \nu }^{(n)} + S_{\alpha \nu \mu }^{(n)}-S_{\mu \nu \alpha }^{(n)}\right) =X(t)u_{\alpha }h_{\mu \nu }\nonumber \\&+Y(t)u_{\mu }h_{\alpha \nu } +\varepsilon _{\alpha \mu \nu \lambda }u^{\lambda }W(t)\delta ^n_4. \end{aligned}$$
(54)

Note that the functions determining the distortion are linearly related with the functions of torsion. This can be shown by using the fact that

$$\begin{aligned} S_{\mu \nu \alpha }^{(n)}=N_{\alpha [\mu \nu ]}^{(n)}, \end{aligned}$$
(55)

which results in the relations

$$\begin{aligned} 2(X+Y)=0, \quad 2\Phi = Y, \quad P = W, \end{aligned}$$
(56)

or, inverting them,

$$\begin{aligned} W=P, \quad Y=2\Phi , \quad X=-2\Phi . \end{aligned}$$
(57)

Therefore, non-Riemannian effects driven by torsion can be parametrized using either the set \(\lbrace \Phi , P \rbrace \) or the set \(\lbrace X,Y,W \rbrace \rightarrow \lbrace Y,W \rbrace \) (in fact, notice that we have \(Y=-X=2\Phi \)). Both of these sets will be related to the set of hypermomentum sources by means of the connection field equations of the theory. Nevertheless, in what follows we shall use the former, which provides a more transparent geometrical meaning with respect to the latter.

Let us also recall that the hyperfluid energy related tensors take the form (43), (44), and (45). Moreover, since we are considering a metric-compatible setup (that is to say vanishing non-metricity), we will also have \(\omega =0\), since \(\omega u_\alpha u_\mu u_\nu \), being totally symmetric, can only excite non-metric degrees of freedom, which are absent here.

5.3 Analysis of the connection field equations

Using the information collected above and contracting the connection field equations (37) independently in \(\mu ,\lambda \), then in \(\nu ,\lambda \), and finally with \(g_{\mu \nu }\), we get the following three equations:

$$\begin{aligned}&-\Big [ 2b_{1} -b_{2} +(n-1)b_{3} \Big ] (n-1) \Phi =\kappa \Big [ (n-1)\phi -\omega \Big ], \nonumber \\\end{aligned}$$
(58)
$$\begin{aligned}&\Big [ -2(n-2)+2 b_{1}- b_{2}+(n-1)b_{3} \Big ](n-1)\Phi \nonumber \\&\quad =\kappa \Big [ (n-1)\chi -\omega \Big ], \end{aligned}$$
(59)
$$\begin{aligned}&2(n-2)(n-1)\Phi =\kappa \Big [ (n-1)\psi -\omega \Big ]. \end{aligned}$$
(60)

Moreover, the contraction of the connection field equations with \(u^{\lambda }u_{\mu }u_{\nu }\) gives the constraint \(\omega =0\), which we already anticipated, since this part of hypermomentum, being totally symmetric, can only excite the non-metric degrees of freedom which are absent here. In addition, the pseudo-scalar torsion mode is obtained by taking the totally antisymmetric part of (37), which yields

$$\begin{aligned} 2(b_1 +b_2 -1)P =\kappa \zeta . \end{aligned}$$
(61)

Let us observe that the assumption \(b_1 + b_2 \ne 1\) is crucial here, since otherwise one would face the constraint \(\zeta (t)=0\) on the sources which would then make P(t) arbitrary, signaling a problematic (unphysical) theory. It is therefore natural to assume that \(b_{1} + b_2 \ne 1\). Combining the above equations we have

$$\begin{aligned}&\kappa \phi =-\Big [ 2b_{1} -b_{2} +(n-1)b_{3} \Big ]\Phi , \nonumber \\&\kappa \psi = 2(n-2)\Phi , \nonumber \\&\kappa \chi =-2(n-2)\Phi +\Big [ 2b_{1}-b_{2}+(n-1)b_{3} \Big ]\Phi \nonumber \\&\qquad =-\psi -\phi , \nonumber \\&\omega =0, \nonumber \\&2(b_1 + b_2 -1)P =\kappa \zeta . \end{aligned}$$
(62)

Note that the latter imply that the hypermomentum variables are related to each other, since it is evident that the following relations hold true:

$$\begin{aligned} \chi= & {} \left[ \frac{2(n-2)}{2 b_{1} -b_{2} +(n-1)b_{3}}-1\right] \phi , \end{aligned}$$
(63)
$$\begin{aligned} \psi= & {} - \frac{2(n-2)}{2 b_{1} -b_{2}+(n-1)b_{3}}\phi , \end{aligned}$$
(64)

with

$$\begin{aligned} \chi +\psi =-\phi . \end{aligned}$$
(65)

The dynamics is therefore contained in \(\phi \). In the above the assumption \(2 b_{1}-b_{2}+(n-1)b_{3}\ne 0\) has been made. The latter is crucial in order to obtain non-trivial solutions. Moreover, note that if the quadratic terms are switched off, that is if \(b_{1}=0=b_{2}=b_{3}\), it follows that both \(\phi =0\) and \(\omega =0\), as seen from the above. Then, in such a case, there are no evolution equations for the hypermomentum variables and subsequently \(\Phi \) remains undetermined (this was in fact the case in [11]).

5.4 Conservation laws

Using (43), (44), and (45), one can easily prove that the continuity equation from (46) in the present case readsFootnote 5

$$\begin{aligned} {\dot{\rho }}_{c}+(n-1)H(\rho _{c}+p_{c})=\frac{1}{2}(\psi -\chi )R_{\mu \nu }u^{\mu }u^{\nu }, \end{aligned}$$
(66)

where, as usual, \(H:= \frac{\dot{a}}{a}\) is the Hubble parameter. On the other hand, taking the 00 and ij components of the conservation law (47) we obtain the evolution equations for the hypermomentum variables, which result to be given by

$$\begin{aligned}&{\dot{\omega }}+(n-1)H(\chi +\psi +\omega )+(n-1)( \psi X-\chi Y)\nonumber \\&\quad =2(\rho _{c}-\rho ), \end{aligned}$$
(67)
$$\begin{aligned}&{\dot{\phi }}+(n-1)H \phi +H(\chi +\psi ) +\psi X- \chi Y=2 (p_{c}-p). \nonumber \\ \end{aligned}$$
(68)

Moreover, since in our case \(\omega =0\), the first becomes

$$\begin{aligned} (n-1)(\psi +\chi )(H-Y)=2 (\rho _{c}-\rho ), \end{aligned}$$
(69)

where we have also used the fact that \(Y=-X\).

Let us now see what happens if we assume that our hyperfluid is of the hypermomentum preserving type [31]. In this case the metrical and canonical energy momentum tensors coincide and as a result \(\rho _{c}=\rho \) as well as \(p_{c}=p\). Then, the above equation becomes

$$\begin{aligned} (n-1) (\psi +\chi )(H-Y)=0 \end{aligned}$$
(70)

and therefore it follows that either

$$\begin{aligned} \psi +\chi =0 \end{aligned}$$
(71)

or

$$\begin{aligned} H-Y=0. \end{aligned}$$
(72)

Remarkably, each of the above constraints has a direct physical interpretation. Indeed, as it can be seen from the hypermomentum decomposition (45), the combination \(\psi +\chi \) appears in the shear part of hypermomentum. Therefore, Eq. (71) is related to the vanishing of one of the shear sources. On the other hand, one can trivially verify that

$$\begin{aligned} \nabla _{i}u^{i}=(n-1)(H-Y). \end{aligned}$$
(73)

Hence, Eq. (72) turns out to imply that the hyperfluid is incompressible, \(\nabla _{i}u^{i}=0\). Thus, we see that Eq. (70) has a very clear interpretation, meaning that the fluid must either have one shear part vanishing or it should be incompressible.

Let us now go back to the analysis of Eq. (68). Using (70) and continuing to consider the case of hypermomentum preserving hyperfluid, Eq. (68) simplifies to

$$\begin{aligned} {\dot{\phi }}+(n-1)H \phi =0. \end{aligned}$$
(74)

Had we not assumed hypermomentum preserving configuration, this would generalize to

$$\begin{aligned}&{\dot{\phi }}+(n-1)H \phi =\frac{2}{(n-1)}\nonumber \\&\quad \times \Big [ -(\rho _{c}-\rho )+(n-1)(p_{c}-p) \Big ]. \end{aligned}$$
(75)

In order to keep the following discussion as general as possible, we shall not assume, at this point, that the hyperfluid is of hypermomentum preserving type. We will further come back to this special case with some observations at the end of Sect. 6, where we will study solutions of our model.

5.5 Torsion modified Friedmann equations

We are now in a position to derive the torsionful Friedmann equations. Taking the 00 components of the metric field equations (34), after some calculations (see Appendix A for a collection of useful formulas we have derived and exploited in our computations), we finally find

$$\begin{aligned} H^{2}= & {} -\frac{1}{(n-2)}\Big [ 2b_{1}-b_{2}+(n-1)b_{3}+4(n-2) \Big ]\Phi ^{2}\nonumber \\&+4 H\Phi +(1-b_{1}-b_{2})P^{2}\delta ^n_4 + \frac{2 \kappa }{(n-1)(n-2)}\rho . \nonumber \\ \end{aligned}$$
(76)

Note that when the quadratic torsion terms are absent the above reduces to

$$\begin{aligned} H^{2}=-4 \Phi ^{2}+4 H\Phi +P^{2}\delta ^n_4 +\frac{2 \kappa }{(n-1)(n-2)}\rho , \end{aligned}$$
(77)

which is in perfect agreement with [11, 31], as expected. The second Friedmann equation (also known as acceleration equation) can be obtained by combining the 00 and the ij components of the metric field equations. This would require some cumbersome calculations, but eventually there exists a much simpler road. Indeed, in [15] the most general form of the acceleration equation was derived and, in the case of vanishing non-metricity we are considering, it takes the form

$$\begin{aligned} \frac{\ddot{a}}{a}=-\frac{1}{(n-1)}R_{\mu \nu }u^{\mu }u^{\nu }+2 \left( \frac{\dot{a}}{a} \right) \Phi +2{\dot{\Phi }}. \end{aligned}$$
(78)

Therefore, we can find the second Friedmann equation by just computing the piece \(R_{\mu \nu }u^{\mu }u^{\nu }\) from the metric field equations in the present case (see Appendix A for details). We get

$$\begin{aligned} \frac{\ddot{a}}{a}= & {} -\frac{\kappa }{(n-1)(n-2)}\Big [ (n-3)\rho +(n-1)p \Big ]\nonumber \\&+\Big [ 2b_{1}-b_{2}+(n-1)b_{3}\Big ]\Phi ^{2}+2 H \Phi +2 {\dot{\Phi }}. \end{aligned}$$
(79)

Observe that in the case \(n=3\) the \(\rho \) contribution disappear. On the other hand, in \(n=4\) all terms survive, and this is the case we will restrict to in the following, where we are going to discuss solutions of our cosmological theory.

6 Solutions

In this section we derive exact analytic solutions of our torsionful cosmological model. Before proceeding in this direction, let us just recall that, as we have shown, since (53) holds true not all the three quadratic torsion invariants are linearly independent. This means that we may set one of the \(b_a\) (\(a=1,2,3\)) to zero, which would amount to a renaming of the \(b_a\) as they appear in (33). We choose to set \(b_{2}=0\). Then, our cosmological set of equations now reads

$$\begin{aligned} H^{2}= & {} -\frac{1}{(n-2)}\Big [ 2b_{1}+(n-1)b_{3}+4(n-2) \Big ]\Phi ^{2}\nonumber \\&+4 H\Phi +(1-b_{1})P^{2}\delta ^n_4+\frac{2 \kappa }{(n-1)(n-2)}\rho , \end{aligned}$$
(80)
$$\begin{aligned} \frac{\ddot{a}}{a}= & {} -\frac{\kappa }{(n-1)(n-2)}\Big [ (n-3)\rho +(n-1)p \Big ]\nonumber \\&+\Big [ 2b_{1}+(n-1)b_{3}\Big ]\Phi ^{2}+2 H \Phi +2 {\dot{\Phi }}, \end{aligned}$$
(81)

where \(\Phi \) is related to the source field \(\phi \) through

$$\begin{aligned} \kappa \phi =-\Big [ 2b_{1}+(n-1)b_{3} \Big ]\Phi , \quad \chi +\psi =-\phi , \end{aligned}$$
(82)

and we also have that (63) and (64) hold true, together with \(2b_1+(n-1)b_3 \ne 0\). In addition, the sources are subject to the conservation laws

$$\begin{aligned}&{\dot{\rho }}_{c}+(n-1)H(\rho _{c}+p_{c})=\frac{1}{2}(\psi -\chi )R_{\mu \nu }u^{\mu }u^{\nu }, \end{aligned}$$
(83)
$$\begin{aligned}&(n-1)(\psi +\chi )(H-Y)=2 (\rho _{c}-\rho ), \end{aligned}$$
(84)
$$\begin{aligned}&{\dot{\phi }}+(n-1)H \phi =\frac{2}{(n-1)}\nonumber \\&\quad \times \Big [ -(\rho _{c}-\rho )+(n-1)(p_{c}-p) \Big ]. \end{aligned}$$
(85)

Let us now consider \(\zeta =0\) and disregard the pseudo-scalar mode, setting \(P=0\) (which is consistent with (61), as we can see from our previous analysis). This does not modify the qualitative analysis and the general results we are going to provide. Indeed, by allowing \(P\ne 0\) one would have to introduce a barotropic equation connecting P to \(\Phi \) of the form \(P \propto \Phi \) and the presence of P would just introduce a shift in coefficients.Footnote 6

In order to study the physical cosmology of our Universe, we shall fix \(n=4\). With the assumption that the perfect fluid variables of the hyperfluid are related through barotropic equations of state of the usual form,

$$\begin{aligned} p_{c}= & {} w_{c}\rho _{c}, \end{aligned}$$
(86)
$$\begin{aligned} p= & {} w \rho , \end{aligned}$$
(87)
$$\begin{aligned} \rho _{c}= & {} {\tilde{w}}\rho , \end{aligned}$$
(88)

where \(w_c\), w, and \({\tilde{w}}\) are the associated barotropic indices, we will now obtain general exact and analytic solutions of the above system. To start with, we first observe the emergence of a perfect square in (80), which, defining

$$\begin{aligned} \xi :=H-2 \Phi \end{aligned}$$
(89)

and

$$\begin{aligned} b_{0}:=2b_{1}+3b_{3}, \end{aligned}$$
(90)

simplifies to

$$\begin{aligned} \xi ^{2}=-\frac{1}{2}b_{0}\Phi ^{2}+\frac{\kappa }{3}\rho . \end{aligned}$$
(91)

Furthermore, recalling that \(Y=2\Phi \) and using (82), Eq. (84) can be expressed as

$$\begin{aligned} \Phi \xi =\frac{2({\tilde{w}}-1)}{3 b_{0}}\kappa \rho . \end{aligned}$$
(92)

Combining the above we obtain

$$\begin{aligned} (\Phi ^{2})^{2}-\frac{2 \kappa }{3 b_{0}}\rho \Phi ^{2}+\frac{2}{b_{0}}\left[ \frac{2({\tilde{w}}-1)\kappa }{3 b_{0}} \right] ^{2}\rho ^{2}=0. \end{aligned}$$
(93)

The latter can be seen as a quadratic equation either in \(\Phi ^{2}\) or in \(\rho \). We may see it as a quadratic equation for \(\Phi ^{2}\). In order to have real solutions, the condition

$$\begin{aligned} 1-\frac{8({\tilde{w}}-1)^{2}}{b_{0}}\ge 0 \end{aligned}$$
(94)

have to be satisfied. Then, it follows that

$$\begin{aligned} \Phi ^{2}=\frac{\kappa \rho }{3 b_{0}}\left( 1 \pm \sqrt{1-\frac{8({\tilde{w}}-1)^{2}}{b_{0}}} \right) . \end{aligned}$$
(95)

Incidentally, there is yet another constraint that gives us a unique solution. Indeed, from (91) we can see that there exists some time period in which the \(\Phi ^{2}\) component will be dominant over the density \(\rho \), and in that region one has

$$\begin{aligned} \xi ^{2}\approx -\frac{1}{2}b_{0}\Phi ^{2}, \end{aligned}$$
(96)

which demands \(b_{0}<0\), otherwise there would be a contradiction. With this result, we extract from (93) the unique solution

$$\begin{aligned} \Phi ^{2}=\frac{\kappa \rho }{3 b_{0}}\left( 1 - \sqrt{1-\frac{8({\tilde{w}}-1)^{2}}{b_{0}}} \right) , \end{aligned}$$
(97)

since the one with the plus sign would certainly give negative \(\Phi ^{2}\), which is clearly impossible. Setting

$$\begin{aligned} \lambda _{0} := 1 - \sqrt{1-\frac{8({\tilde{w}}-1)^{2}}{b_{0}}} <0 \end{aligned}$$
(98)

we have

$$\begin{aligned} \rho =\frac{3 b_{0}}{\kappa \lambda _{0}}\Phi ^{2}, \end{aligned}$$
(99)

which is positive as expected. Continuing, we may substitute the latter equation back into (92) to arrive at (recalling also the definition of \(\xi \) given by (89))

$$\begin{aligned} H=\lambda _{1}\Phi , \end{aligned}$$
(100)

where we have defined

$$\begin{aligned} \lambda _{1} := 2\left( 1+\frac{{\tilde{w}}-1}{\lambda _0} \right) . \end{aligned}$$
(101)

Observe that in Ref. [11] the condition \(\Phi \propto H\) was considered as a particular case, supposing a specific form for the torsion and then solving the coupled system of equations. On the other hand, let us stress that in the present case Eq. (100) is not an assumption, but an exact condition derived from the equations of the theory and by physically consistent requirements resulting in constraints on the parameters. In contrast to [11], here we have an evolution equation for \(\Phi \) driven by the presence of quadratic torsion terms which break projective invariance in the model. As we shall see, this gives \(\Phi \) specific dynamics. Then, plugging (100) along with (82) and (99) into the evolution equation (85), we find

$$\begin{aligned} {\dot{\Phi }}=-\lambda _{2}\Phi ^{2}, \end{aligned}$$
(102)

where

$$\begin{aligned} \lambda _{2} := \frac{2}{\lambda _{0}}\Big [ 3 \lambda _{0} -2 -3w +{\tilde{w}}(3 w_{c}+2) \Big ]. \end{aligned}$$
(103)

Eq. (102) can be trivially integrated to give

$$\begin{aligned} \Phi (t)=\frac{1}{\lambda _{2}t+C_{1}}, \end{aligned}$$
(104)

where \(C_{1}\) is some integration constant to be determined by the initial conditions. With this at hand, we conclude that

$$\begin{aligned} \rho (t)=\frac{3 b_{0}}{\kappa \lambda _{0}}\frac{1}{(\lambda _{2}t+C_{1})^{2}}. \end{aligned}$$
(105)

Furthermore, also (100) can be now integrated, yielding

$$\begin{aligned} a(t)=C_{2}(\lambda _{2}t+C_{1})^{\frac{\lambda _{1}}{\lambda _{2}}}, \end{aligned}$$
(106)

where \(C_{2}\) is another integration constant which can be fixed from the initial data. From the last equation we see that we have interesting power law solutions for the scale factor which depend on the parameters of the theory. Note that there is also the second Friedmann equation (81) which must be taken into account. Nevertheless, since it is a byproduct of the first Friedmann equation and the conservation laws, it is not and independent equation and its contribution is already accounted for in the analysis above. Lastly, in order to have a self-consistent theory, all equations must be satisfied and the only one we have not used so far is (83). Substituting all the above results into (83) we get the consistency relation

$$\begin{aligned} 4 {\tilde{w}}\Big [ - 2\lambda _{2}+3(1+w_{c})\lambda _{1} \Big ]=(8-b_{0})\Big ( 1+3 w + 2\lambda _{0} \Big ) \nonumber \\ \end{aligned}$$
(107)

among the parameters of the theory. Remarkably, the solutions we have provided analytically are exact ones. Some comments regarding our power law solution for the scale factor are now in order. Firstly, note that the evolution of the latter can be either slower or more rapid with respect to the one obtained for conventional forms of matter (such as dust, radiation, etc.; for a nice review of the various forms of matter in cosmology we refer the reader to [39]), depending on both the parameters of the theory and the barotropic indices. Given some data one would be able to restrict the possible values of these parameters. Secondly, restrictions on the parameters can be obtained directly from (106). Indeed, given that \(a(t)>0\), we must have \(C_{2}>0\). Furthermore, in order to have unique real solutions for any value of the ratio \(\lambda _{1} / \lambda _{2}\), it must hold that \(\lambda _{2}t+C_{1}>0\) for any t. For \(t=0\) we conclude that \(C_{1}>0\), while for late times \(\lambda _{2}t\) becomes dominant over \(C_{1}\) and the positivity is guaranteed as long as \(\lambda _{2}>0\). With these at hand, given that for some fixed time \(t=t_{0}\) the scale factor and the density acquire values \(a(t_{0})=a_{0}\) and \(\rho (t_{0})=\rho _{0}\), the integration constants are found to be

$$\begin{aligned} C_{1} =\sqrt{\frac{3 b_{0}}{\kappa \lambda _{0}\rho _{0}}} - \lambda _2 t_0, \quad C_{2}=a_{0}\left( \frac{\kappa \lambda _{0}\rho _{0}}{3 b_{0}} \right) ^{\frac{\lambda _{1}}{2\lambda _{2}}} \end{aligned}$$
(108)

and consequently the scale factor can be expressed as

$$\begin{aligned} a(t)=a_{0}\Big [ {\tilde{\lambda }}(t-t_{0})+1 \Big ]^{\frac{\lambda _{1}}{\lambda _{2}}}, \end{aligned}$$
(109)

where

$$\begin{aligned} {\tilde{\lambda }}:=\lambda _{2}\sqrt{\frac{\kappa \lambda _{0}\rho _{0}}{3 b_{0}}}>0. \end{aligned}$$
(110)

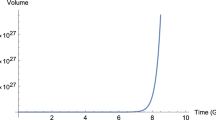
Now, at first sight it seems that there exist only power law solutions for the torsionful system. However, the expansion depends on parameters that could potentially lead to a more rapid expansion. Indeed, given the form of (103), there exists a given configuration among the barotropic indices for which \(\lambda _{2}\rightarrow {0^+}\). In this limit the scale factor goes likeFootnote 7

$$\begin{aligned} a(t) \propto e^{\lambda _{1}t}, \end{aligned}$$
(111)

which signals an exponential expansion. Although this would of course require fine tuning, it is evident that it represents a possibility. Constraints on both the torsion scalars parameters and the barotropic indices could be obtained by fitting the derived results to some given data. This could also allow one to rule out specific cases and find the allowed equations of state among the hyperfluid variables. Let us discuss here some specific characteristic cases emerging by considering different values of the ratio \(\lambda _{1} / \lambda _{2}\).

(a) Case \(\lambda _1 = 0\), \(\lambda _2 \ne 0\):

As is can be seen from (109), in this case we have a static Universe, \(a=a_{0}=\text {const}\). Note that in such a case both the Hubble parameter and its first derivative vanish (i.e. \(H=0=\dot{H}\)) in agreement with the static nature of the model. Moreover, besides fulfilling the consistency relation (107), here we find that the parameters of our theory satisfy the additional relation \(\lambda _0=1-{\tilde{w}}\).

(b) Case \(\lambda _{1}\ne 0\), \(\lambda _{2} \rightarrow 0^{+}\):

As we have already pointed out previously, in this case the scale factor experiences an exponential growth. Interestingly, in this configuration both \(\Phi \) and \(\rho \) “freeze out” and acquire the constant values

$$\begin{aligned} \Phi = \Phi _{0}, \quad \rho = \rho _{0}=\frac{3 b_{0}}{\kappa \lambda _{0}}\Phi ^{2}_{0}. \end{aligned}$$
(112)

In a sense, the freezing out of the latter two acts as an effective cosmological constant,

$$\begin{aligned} \Lambda _{\text {eff}} = \frac{12 (\lambda _{0}+{\tilde{w}}-1)^{2}}{\lambda _{0}^{2}}\Phi _{0}^{2}, \end{aligned}$$
(113)

which drives the exponential expansion. In this instance the parameters of the theory satisfy, besides Eq. (107), \(3 \lambda _{0}=2+3 w-{\tilde{w}}(2+3 w_{c})\).

(c) Case \(\lambda _{1}/ \lambda _{2}=1 \): In this limit Eq. (109) yields

$$\begin{aligned} a(t)=a_{0}\Big [ {\tilde{\lambda }}(t-t_{0})+1 \Big ]. \end{aligned}$$
(114)

In this case we notice a Milne-like expansion and in particular when \(a_{0}t_{0}=1=a_{0}{\tilde{\lambda }}\) the behaviour is identical with that of a Milne Universe [40] (i.e. \(a=t\)). The parameters also fulfill \(2 \lambda _0 = 3 w + 1 - {\tilde{w}}(1+3 w_c)\).

(d) Case \(\lambda _{1}/ \lambda _{2}=1/2 \): For such a configuration we have

$$\begin{aligned} a(t)=a_{0}\Big [ {\tilde{\lambda }}(t-t_{0})+1 \Big ]^{\frac{1}{2}}, \end{aligned}$$
(115)

indicating a radiation-like expansion. The parameters are related through \(\lambda _0 = 3 ( w - {\tilde{w}} w_c )\).

(e) Case \(\lambda _{1}/ \lambda _{2}=2/3 \): In this case we get

$$\begin{aligned} a(t)=a_{0}\Big [ {\tilde{\lambda }}(t-t_{0})+1 \Big ]^{\frac{2}{3}}, \end{aligned}$$
(116)

from which we conclude that the net effect is similar to that of dust in comparison to the solutions predicted by the Standard Cosmological Model. Here, the model parameters satisfy \(3 \lambda _0 = 1 + 6 w - {\tilde{w}} (1+6 w_c)\).

(f) Case \(\lambda _{1}/ \lambda _{2}=1/3 \): In this case we have

$$\begin{aligned} a(t)=a_{0}\Big [ {\tilde{\lambda }}(t-t_{0})+1 \Big ]^{\frac{1}{3}}. \end{aligned}$$
(117)

The above now indicates a correspondence with a stiff matter dominated Universe and the parameters obey \(3 w=1 - {\tilde{w}}(1+3w_c)\).

The above represent only some very specific correspondences with respect to standard cosmology. In particular, we should note that, depending on the parameter space, our solutions also allow for an accelerated growth when \(\lambda _{1}/\lambda _{2}>0\), in contrast to the standard picture where conventional matter always causes a slow expansion. We see therefore that torsion changes this picture dramatically and allows for interesting possibilities.

The case \({\tilde{w}}=1\):

Note that in all of the above considerations we have assumed that \({\tilde{w}}\ne 1\). In the special case for which \({\tilde{w}}=1\), the total (canonical) density does not receive contributions from the hypermomentum part, i.e. \(\rho _{c}=\rho \). Let us analyze this case further. From (92), recalling also the definition for \(\xi \) given in (89), for \({\tilde{w}}=1\) we get that either \(\Phi =0\) or \(H=2 \Phi \). The former represents a trivial solution, so we shall consider the latter possibility. Then, for \(H=2 \Phi \) Eq. (93) becomes

$$\begin{aligned} \rho =\frac{3 b_{0}}{2 \kappa }\Phi ^{2}. \end{aligned}$$
(118)

Interestingly, in this case the physical restriction \(\rho >0\) demands that \(b_{0}>0\). Substituting the above results into the conservation law (85) and using also (82) it follows that

$$\begin{aligned} {\dot{\Phi }}=-3\Big [ 2+(w_{c}-w)\Big ] \Phi ^{2}, \end{aligned}$$
(119)

or, equivalently,

$$\begin{aligned} \dot{H}=-\frac{w_{0}}{2}H^{2}, \end{aligned}$$
(120)

where \(w_{0}:=6+3(w_{c}-w)\). Again, the latter can be trivially integrated to give

$$\begin{aligned} a(t)=C_{2}\Big ( \frac{w_{0}}{2}t+C_{1}\Big )^{-\frac{2}{w_{0}}}. \end{aligned}$$
(121)

Then, classifications similar to the ones obtained in the case \({\tilde{w}}\ne 1\) follow. However, let us observe that the solution for the scale factor here is independent of the parameter \(b_{0}\) and, as a consequence, it does not depend on the coefficients of the additional quadratic torsion terms. Furthermore, in the case of a hypermomentum preserving hyperfluid [31], for which \(\rho _{c}=\rho \) and \(p_{c}=p\), we get the unique solution for the scale factor

$$\begin{aligned} {a(t)= C_2 \Big ( 3 t+ C_1 \Big )^{-\frac{1}{3}},} \end{aligned}$$
(122)

which is perfectly allowable since in our theory the torsion contributions modify the early time cosmology.

7 Conclusions

We have considered a quadratic torsionful gravity theory in n spacetime dimensions in the presence of a perfect hyperfluid and we have developed and studied its cosmology. The gravitational action we considered is an extension of the Einstein–Cartan theory including also the three allowed torsion parity even squared terms. The inclusion of the quadratic terms turns out to be most important as it solves the problem of indeterminacyFootnote 8 that one faces when only the Ricci scalar is included into the gravitational action. As for the matter part we considered the presence of a perfect hyperfluid which has been recently developed. The metric and the connection have been considered as independent variables and the equations of motion of the theory have been derived in this setup. We have studied the cosmology of the theory considering the usual FLRW background and discussed the non-Riemannian torsion driven degrees of freedom within the latter. We have then analyzed in detail the conservation laws of the perfect hyperfluid and also the torsion modified Friedman equations for our theory. Remarkably, for this seemingly complicated model, we have been able to provide exact analytic cosmological solutions, finding in particular power law solutions for the scale factor which depend on the parameters of the theory. Under certain circumstances the expansion can be very rapid, i.e. exponential-like. Under a general perspective, our solutions for the scale factor provide generalizations of the usual dust, radiation, or general barotropic perfect fluid solutions of the standard cosmology. The reason for this generalized possibility lies in the inclusion of the hypermomentum degrees of freedom, which, having a direct association with the intrinsic characteristics of the material fluid, modify the net expansion. In this sense the microstructure of the fluid alters the expansion rate in a non-trivial way and provides new interesting cosmological results.

We have also discussed some specific characteristic cases emerging by considering different values of the ratio \(\lambda _{1} / \lambda _{2}\). In particular, for \(\lambda _1/\lambda _2=0\) we have found a static Universe, while for \(\lambda _1/\lambda _2=1\) we have obtained a Milne-like expansion. In the case \(\lambda _2 \rightarrow 0^+\), corresponding to an exponential growth, we have also derived the effective cosmological constant, whereas the cases \(\lambda _1/\lambda _2 = 1/2\), \(\lambda _1/\lambda _2 = 2/3\), and \(\lambda _1/\lambda _2 = 1/3\) correspond, respectively, to a radiation-like expansion, dust effects, and stiff matter dominated Universe. For each case we have also found further bound on the parameters. Interestingly, depending on the parameter space, our torsionful solutions allow for an accelerated growth when \(\lambda _{1}/\lambda _{2}>0\), in contrast to the standard picture where conventional matter always causes a slow expansion. Finally, we have analyzed the special case \({\tilde{w}}=1\), namely the one in which the hypermomentum sector does not contribute to the total (canonical) density (\(\rho _c=\rho \)). We have derived the expression for the scale factor also in this setup, observing that for the particular case of a hypermomentum preserving hyperfluid (\(\rho _c=\rho \), \(p_c=p\)) the solution is in fact unique.

In closing, let us note that there exist many possible ways to extend our present study. For instance one could also add the quadratic curvature terms and investigate the cosmology of the Poincaré theory in the presence of the perfect hyperfluid. It would also be interesting to see which would be the effect of additional parity odd quadratic torsion terms in a more generalized setting. Finally, a probably more ambitious work would be to generalize the setup of the present study by allowing for a non-vanishing non-metricity and subsequently obtain the full cosmology of the resulting quadratic MAG theory. Some work is currently in progress on this point.