1 Introduction

Research on atomic radiative processes has always been an important research topic in some fields of physics, such as atomic and molecular physics, and optics. In 1946, Purcell discovered that the spontaneous emission rates of atoms can be enhanced when they are incorporated into a resonant cavity [1]. Henceforth, theoretical and experimental efforts of physicists were devoted to the study of the interaction between light confined in a reflective cavity and atoms. This gave rise to the birth of a new field called cavity quantum electrodynamics (CQED) [2]. These investigations have clearly indicated that the atomic radiative processes can be regulated or controlled by the environment, i.e., the boundary conditions of quantum electromagnetic field. Further, as inspired by the Unruh effect [3], some work investigated the effect of the atomic non-inertial motion on the radiative properties of atom–field coupling system [4,5,6]. A remarkable theoretical finding is that the spontaneous absorption process can occur for a uniformly accelerated atom in the ground state in vacuum, as if it is immersed in a thermal bath. In other words, the uniform acceleration is linked to the thermal bath, which is just the quintessence of the Unruh effect. In recent years, with the development of quantum theory and gravitation theory, these investigations have also been extended to the background of curved spacetimes and spacetimes with nonrivial topology [7,8,9,10].

The discovery of special relativity inevitably gives rise to the problem of constructing a relativistic thermodynamical theory. The relativistic transformation of the temperature has been controversial for a hundred years. Initially Einstein and Planck in particular argued that a uniformly moving observer in a static thermal bath with temperature \(T_{0}\) will measure a smaller temperature, \(T=T_{0}\sqrt{1-v^{2}}\). However, other scholars had different views. For instance, Ott and Arzeliès proposed a different transformation form, \(T=T_{0}/\sqrt{1-v^{2}}\), and Landsberg alleged that \(T=T_{0}\). This related work was based on the combination of classical thermodynamics and special relativity. From a completely different point of view, Costa and Matas considered a uniformly moving Unruh–DeWitt detector coupled to a thermal bath of the massless quantum scalar field in the framework of the combination of quantum thermodynamics and special relativity [11]. According to special relativity, the Minkowski vacuum is invariant for all inertial observers. As a consequence, all inertial Unruh–DeWitt detectors with different velocities in vacuum make the same response as they all measure zero temperature. However, when the moving Unruh–DeWitt detector is immersed in a thermal bath, it takes on a quite distinct characteristic. The detector’s response rate is found to be dependent on the detector’s velocity. That is to say, inertial detectors with different velocities react differently to the same static thermal bath. This implies that the temperature of the quantum scalar field is relativistic and observer-dependent. By integrating the Planckian spectrum with the directional temperature over the solid angle [12,13,14], the excitation rate of the Unruh–DeWitt detector can be exactly found without any appeal to quantum field theory. Then Landsberg and Matsas concluded to the non-existence of a relativistic temperature transformation due to the fact that an observer moving in a heat reservior cannot detect a black-body spectrum [15, 16]. However, in [17] Nakamura raised an objection and the result shows that the well-known expression with the directional temperature can be derived based on the inverse-temperature four-vector. Recently, Papadatos and Anastopoulos analyzed the thermodynamics of a quantum system in a trajectory of constant velocity that interacts with a static thermal bath of the massless quantum scalar field [18]. Their analysis of the second law of thermodynamics leads to a surprising equivalence: a moving heat bath is physically equivalent to a mixture of heat baths at rest, each with a different temperature. Although the authors claim that there is no unique rule for the Lorentz transformation of temperature, they propose that Lorentz transformations of thermodynamic states are well defined in an extended thermodynamic space that is obtained as a convex hull of the standard thermodynamic space.

In fact, the Unruh–DeWitt detector or a quantum system in interaction with a quantum scalar field is a theoretical model and has no realistic correspondence. In this paper, I consider a more realistic scenario: the interaction of a multilevel atom with the quantum electromagnetic field. It is natural to ask how the uniformly moving atom as a moving “thermometer” would respond to the thermal bath of the quantum electromagnetic field. On the one hand, I hope to find a new and simple theoretical way to control and tailor the atomic radiative processes. On the other hand, in view of the previous experience about the Unruh effect, this investigation is expected to further excavate and reveal the intrinsic structure and peculiarity of the quantum electromagnetic field. The natural units \(\hbar =c=1\) and \(k_{B}=1\) are adopted throughout the paper.

2 The general formalism

The interacting system of a multilevel atom and a quantum electromagnetic field can be described with respect to the atomic proper time \(\tau \) by the total Hamiltonian \(H(\tau )=H_{A}(\tau )+H_{F}(\tau )+H_{I}(\tau )\). \(H_{A}\) is the Hamiltonian operator that governs the evolution of the multilevel atom,

$$\begin{aligned} H_{A}(\tau )=\sum _{m}\omega _{m}\sigma _{mm}(\tau ), \end{aligned}$$
(1)

in which \(\sigma _{mm}=|m\rangle \langle m|\), \(\omega _m\) gives the energy corresponding to the stationary state \(|m\rangle \). \(H_{F}\) is the Hamiltonian operator of the electromagnetic field, given by

$$\begin{aligned} H_{F}(\tau )=\sum _{\varvec{k}\lambda } \;\omega _{\varvec{k}} a_{\varvec{k}\lambda }^{\dag }(\tau )a_{\varvec{k}\lambda }(\tau )\frac{\mathrm{d}t}{\mathrm{d}\tau }, \end{aligned}$$
(2)

where \(a_{\varvec{k\lambda }}\) (\(a_{\varvec{k\lambda }}^{\dag }\)) is the annihilation (creation) operator for a photon with the wave vector \(\varvec{k}\) and the polarization \(\lambda \), and \(\omega _{\varvec{k}}\) corresponds to the photon’s energy. \(H_{I}(\tau )\) describes the atom–field coupling and here we consider in the multipolar coupling scheme the electric dipole interaction [19]

$$\begin{aligned} H_{I}(\tau )=-e\mathbf {r}(\tau )\cdot \mathbf{E} (X_{A}(\tau )), \end{aligned}$$
(3)

where e is the electron charge, \(e\mathbf {r}\) denotes the atomic electric dipole moment operator, E(x) is the electric field operator and \(X_{A}(\tau )\) denotes the atomic spacetime trajectory. In the weak coupling regime, the evolution operator of the whole system can be expanded in the interaction representation as

$$\begin{aligned} U(\tau _{f},\tau _{i})= & {} 1-i\int _{\tau _{i}}^{\tau _{f}} \mathrm{d}\tau ^{\prime } H_{I}(\tau ^{\prime })\nonumber \\&+(-i)^{2}\int _{\tau _{i}}^{\tau _{f}} \mathrm{d}\tau ^{\prime } H_{I}(\tau ^{\prime })\int _{\tau _{i}}^{\tau ^{\prime }} \mathrm{d}\tau ^{\prime \prime } H_{I}(\tau ^{\prime \prime })+\cdot \cdot \cdot .\nonumber \\ \end{aligned}$$
(4)

So, the probability amplitude of the transition from the initial state \(| \omega _{b} \Phi _{i} \rangle \) at \(\tau _{i}\) to the final state \(| \omega _{d} \Phi _{f} \rangle \) at \(\tau _{f}\) is given in the first-order approximation by

$$\begin{aligned}&\langle \omega _{d} \Phi _{f} | U(\tau _{f},\tau _{i}) | \omega _{b} \Phi _{i} \rangle \nonumber \\&\quad =i e\int _{\tau _{i}}^{\tau _{f}} \langle \omega _{d} \Phi _{f} | \mathbf {r}(\tau ^{\prime })\cdot \mathbf{E} (X_{A}(\tau ^{\prime })) | \omega _{b} \Phi _{i} \rangle \mathrm{d}\tau ^{\prime }. \end{aligned}$$
(5)

Since we focus on the atomic transition from the initial state \(| \omega _{b} \rangle \) to the final state \(| \omega _{d} \rangle \), we should sum over all the possible final states of the field \(|\Phi _{f} \rangle \), then the atomic transition probability is found to be

$$\begin{aligned}&P(\omega _{bd},\tau _{f},\tau _{i})\nonumber \\&\quad =\sum _{i,j=1}^{3}e^{2}\langle \omega _{b}|\mathrm {r}_{i}(0) |\omega _{d}\rangle \langle \omega _{d}|\mathrm {r}_{j}(0) |\omega _{b}\rangle F_{ij}(\omega _{bd},\tau _{f},\tau _{i}),\nonumber \\ \end{aligned}$$
(6)

where we have defined the function

$$\begin{aligned}&F_{ij}(\omega _{bd},\tau _{f},\tau _{i})\nonumber \\&\quad =\int _{\tau _{i}}^{\tau _{f}}\mathrm{d}\tau ^{\prime }\int _{\tau _{i}}^{\tau _{f}}\mathrm{d}\tau ^{\prime \prime }e^{i\omega _{bd}(\tau ^{\prime }-\tau ^{\prime \prime })} \langle \Phi _{i} | \text {E}_{i}(X_{A}(\tau ^{\prime })) \text {E}_{j}(X_{A}(\tau ^{\prime \prime })) |\Phi _{i} \rangle \nonumber \\ \end{aligned}$$
(7)

and we use the notation \(\omega _{bd}=\omega _{b}-\omega _{d}\). When the interaction time between the multilevel atom with the stationary motion and the quantum electromagnetic field is sufficient, i.e., \(\tau _{f}-\tau _{i}\rightarrow \infty \), the equilibrium transition rate is found to be

$$\begin{aligned}&R_{\omega _{b}\rightarrow \omega _{d}} =\bigg (\frac{\mathrm{d}P}{\mathrm{d}\tau _{f}}\bigg )_{\tau _{f}-\tau _{i}\rightarrow \infty }\nonumber \\&\quad =\sum _{i,j=1}^{3}e^{2}\langle \omega _{b}|\mathrm {r}_{i}(0) |\omega _{d}\rangle \langle \omega _{d}|\mathrm {r}_{j}(0) |\omega _{b}\rangle \dot{F}_{ij}(\omega _{bd}), \end{aligned}$$
(8)

where

$$\begin{aligned} \dot{F}_{ij}(\omega _{bd})=\int _{-\infty }^{\infty }du \; e^{i\omega _{bd} u} G^{+}_{ij}(u), \end{aligned}$$
(9)

with the notation

$$\begin{aligned} G^{+}_{ij}(u)= \langle \Phi _{i} | \text {E}_{i}(X_{A}(\tau )) \text {E}_{j}(X_{A}(\tau ^{\prime })) |\Phi _{i} \rangle , \quad u=\tau -\tau ^{\prime }.\nonumber \\ \end{aligned}$$
(10)

It is evident that the correlation function of the electric field in the initial state \(|\Phi _{i} \rangle \) along the atomic trajectory, \(G^{+}_{ij}(u)\), is crucial to the calculation of the atomic transition rate.

Assume that initially the quantum field is in the thermodynamic equilibrium state with the temperature \(T=1/\beta \) (\(|\Phi _{i} \rangle =|\beta \rangle \)). The two-point function of the electromagnetic four-vector potential \(A_{\mu }(X)\) at finite temperature is given by [20]

$$\begin{aligned} \langle \beta |A_{\mu }(X)A_{\nu }(X^{\prime })| \beta \rangle =\frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty }\frac{\eta _{\mu \nu }}{(t-t^{\prime }+ik\beta -i\epsilon )^{2}-(x-x^{\prime })^{2}-(y-y^{\prime })^{2}-(z-z^{\prime })^{2}}, \end{aligned}$$
(11)

where \(\eta _{\mu \nu }=\text {diag}(1,-1,-1,-1)\) and \(\epsilon \rightarrow 0^{+}\). Then, due to the relation \(E_{i}(X)=\partial _{i}A_{0}(X)-\partial _{0}A_{i}(X)\), the correlation function of the electric field is expressed as

$$\begin{aligned} \langle \beta |E_{i}(X)E_{j}(X^{\prime })| \beta \rangle= & {} -\frac{1}{4\pi ^{2}}(\partial _{0}\partial _{0}^{\prime }\delta _{ij}-\partial _{i}\partial _{j}^{\prime }) \sum _{k=-\infty }^{\infty }\frac{1}{(t-t^{\prime }+ik\beta -i\epsilon )^{2}-(x-x^{\prime })^{2}-(y-y^{\prime })^{2}-(z-z^{\prime })^{2}}. \end{aligned}$$
(12)

3 Transition rate of a uniformly moving atom in a background thermal bath

Consider an atom that moves at a constant velocity along a certain direction, for example, the z direction. The atomic spacetime trajectory is denoted by

$$\begin{aligned} t_{A}(\tau )=\gamma \tau , \quad x_{A}(\tau )=x_{0}, \quad y_{A}(\tau )=y_{0}, \quad z_{A}(\tau )=z_{0}+v\gamma \tau ,\nonumber \\ \end{aligned}$$
(13)

where \(x_{0}\), \(y_{0}\) and \(z_{0}\) denote the initial coordinates of the atom and all are constant, v is the atomic velocity, and \(\gamma =1/\sqrt{1-v^{2}}\). The electromagnetic four-vector potential in the instantaneous reference frame of the atom can be obtained by the following Lorentz transformation:

$$\begin{aligned}&{\tilde{A}}_{0}({\tilde{X}})= \gamma A_{0}(X) +v \gamma A_{3}(X), \end{aligned}$$
(14)
$$\begin{aligned}&{\tilde{A}}_{1}({\tilde{X}})= A_{1} (X), \end{aligned}$$
(15)
$$\begin{aligned}&{\tilde{A}}_{2}({\tilde{X}})= A_{2}(X), \end{aligned}$$
(16)
$$\begin{aligned}&{\tilde{A}}_{3}({\tilde{X}})= \gamma A_{3}(X)+v\gamma A_{0}(X), \end{aligned}$$
(17)

where all physical quantities in the frame of the atom have been labeled by the symbol \(\tilde{}\). Due to the relation \({\tilde{E}}_{i}({\tilde{X}})={\tilde{\partial }}_{i}{\tilde{A}}_{0}({\tilde{X}})-{\tilde{\partial }}_{0}{\tilde{A}}_{i}({\tilde{X}})\), one has

$$\begin{aligned}&{\tilde{E}}_{1}({\tilde{X}})=\gamma \partial _{1}A_{0}(X)+v\gamma \partial _{1}A_{3}(X)-(\gamma \partial _{0}+v\gamma \partial _{3})A_{1}(X), \nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned}&{\tilde{E}}_{2}({\tilde{X}})=\gamma \partial _{2}A_{0}(X)+v\gamma \partial _{2}A_{3}(X)-(\gamma \partial _{0}+v\gamma \partial _{3})A_{2}(X), \nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned}&{\tilde{E}}_{3}({\tilde{X}})=\partial _{3} A_{0}(X)- \partial _{0} A_{3}(X). \end{aligned}$$
(20)

Thus the correlation functions of the electric field in the instantaneous reference frame of the atom are found to be

$$\begin{aligned}&G^{+}_{11}(X,X^{\prime })_{\beta }\nonumber \\&\quad =\frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty } \left[ -\frac{4}{A^{2}} + \frac{8\big (\frac{B}{\sqrt{1-v^{2}}}-\frac{v\Delta z}{\sqrt{1-v^{2}}}\big )^{2}- (\Delta x)^{2}}{A^{3}} \right] , \nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned}&G^{+}_{22}(X,X^{\prime })_{\beta }\nonumber \\&\quad =\frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty } \left[ -\frac{4}{A^{2}} + \frac{8\big (\frac{B}{\sqrt{1-v^{2}}}-\frac{v\Delta z}{\sqrt{1-v^{2}}}\big )^{2}- (\Delta y)^{2}}{A^{3}} \right] , \nonumber \\ \end{aligned}$$
(22)
$$\begin{aligned}&G^{+}_{33}(X,X^{\prime })_{\beta }=\frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty } \left[ -\frac{4}{A^{2}} + \frac{8\big (B^{2}- (\Delta z)^{2}\big )}{A^{3}} \right] ,\nonumber \\ \end{aligned}$$
(23)

and

$$\begin{aligned}&G^{+}_{12}(X,X^{\prime })_{\beta }=G^{+}_{21}(X,X^{\prime })_{\beta }\nonumber \\&\quad = -\frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty } \frac{8\Delta x \Delta y}{A^{3}}, \end{aligned}$$
(24)
$$\begin{aligned}&G^{+}_{13}(X,X^{\prime })_{\beta }=G^{+}_{31}(X,X^{\prime })_{\beta }\nonumber \\&\quad = \frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty } \frac{\frac{8B v\Delta x}{\sqrt{1-v^{2}}} - \frac{8\Delta x \Delta z}{\sqrt{1-v^{2}}} }{A^{3}}, \end{aligned}$$
(25)
$$\begin{aligned}&G^{+}_{23}(X,X^{\prime })_{\beta }=G^{+}_{32}(X,X^{\prime })_{\beta }\nonumber \\&\quad = \frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty } \frac{\frac{8B v\Delta y}{\sqrt{1-v^{2}}} - \frac{8\Delta y \Delta z}{\sqrt{1-v^{2}}} }{A^{3}}, \end{aligned}$$
(26)

with

$$\begin{aligned} A= & {} (t-t^{\prime }+ik\beta -i\epsilon )^{2}-(x-x^{\prime })^{2}-(y-y^{\prime })^{2}-(z-z^{\prime })^{2} , \nonumber \\ B= & {} t-t^{\prime }+ik\beta -i\epsilon . \end{aligned}$$
(27)

Substituting the atomic trajectory into the above expressions, one has

$$\begin{aligned}&G^{+}_{11}(u)_{\beta }=\frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty } \left[ -\frac{4}{A^{2}} + \frac{8\big (\frac{B}{\sqrt{1-v^{2}}}-\frac{v^{2}\gamma u}{\sqrt{1-v^{2}}}\big )^{2}}{A^{3}} \right] , \nonumber \\ \end{aligned}$$
(28)
$$\begin{aligned}&G^{+}_{22}(u)_{\beta }=\frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty } \left[ -\frac{4}{A^{2}} + \frac{8\big (\frac{B}{\sqrt{1-v^{2}}}-\frac{v^{2}\gamma u}{\sqrt{1-v^{2}}}\big )^{2}}{A^{3}} \right] , \nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned}&G^{+}_{33}(u)_{\beta }=\frac{1}{4\pi ^{2}}\sum _{k=-\infty }^{\infty } \frac{4}{A^{2}} , \end{aligned}$$
(30)

and

$$\begin{aligned} G^{+}_{ij}(u)=0 \quad \text {for} \quad i\ne j, \end{aligned}$$
(31)

where the factors A and B reduce to

$$\begin{aligned} A= & {} (\gamma u +ik\beta -i\epsilon )^{2}-(v\gamma u)^{2}, \nonumber \\ B= & {} \gamma u +ik\beta -i\epsilon . \end{aligned}$$
(32)

Treating the integration variable u as a complex number, the summand with \(k=0\) in the above expressions has one pole of order 2 at \(u=i\epsilon \), and each of the summands with \(k\ne 0\) has two poles of order 1 at \(u= \frac{-ik\beta +i\epsilon }{\gamma (1-v)}\) and \(u=\frac{-ik\beta +i\epsilon }{\gamma (1+v)}\).

Substituting Eqs. (28)–(31) into (8) and (9), by a contour integral along an infinite semicircle on the upper-half plane for \(\omega _{bd}>0\) or the lower-half plane for \(\omega _{bd}<0\) and using the residue theorem, the atomic transition rate turns out to be

$$\begin{aligned} R_{\omega _{b}\rightarrow \omega _{d}}= & {} \frac{e^{2}|\omega _{bd}|^{3}}{3\pi } |\langle \omega _{b}|\mathbf {r}(0) |\omega _{d}\rangle |^{2} \nonumber \\&\times \sum _{i=1}^{3} \alpha _{i}\Big [ \big (1+g_{i}(\omega _{bd},\beta ,v)\big )\Theta (\omega _{bd})\nonumber \\&\qquad + g_{i}(|\omega _{bd}|,\beta ,v)\Theta (-\omega _{bd}) \Big ], \end{aligned}$$
(33)

where the functions

$$\begin{aligned} g_{1}(\omega _{0},\beta ,v)= & {} -\frac{3}{2} \sum _{k=1}^{\infty } \frac{ \sqrt{1-v^{2}}}{2k^{3}\omega _{0}^{3}\beta ^{3}v^{3}} \bigg [ \Big ( 1-v^{2}+k\omega _{0}\beta v \sqrt{1-v^{2}}\nonumber \\&\qquad + k^{2}\omega _{0}^{2}\beta ^{2} v^{2} \Big ) e^{-\frac{k\omega _{0}\beta (1+v)}{\sqrt{1-v^{2}}}} \nonumber \\&- \Big ( 1-v^{2}-k\omega _{0}\beta v \sqrt{1-v^{2}} + k^{2}\omega _{0}^{2}\beta ^{2} v^{2} \Big ) e^{-\frac{k\omega _{0}\beta (1-v)}{\sqrt{1-v^{2}}}} \bigg ], \nonumber \\ \end{aligned}$$
(34)
$$\begin{aligned} g_{2}(\omega _{0},\beta ,v)= & {} g_{1}(\omega _{0},\beta ,v), \end{aligned}$$
(35)
$$\begin{aligned} g_{3}(\omega _{0},\beta ,v)= & {} \frac{3}{2} \sum _{k=1}^{\infty } \frac{ \sqrt{1-v^{2}}}{k^{3}\omega _{0}^{3}\beta ^{3}v^{3}} \bigg [ \Big ( 1-v^{2}+k\omega _{0}\beta v \sqrt{1-v^{2}} \Big ) e^{-\frac{k\omega _{0}\beta (1+v)}{\sqrt{1-v^{2}}}} \nonumber \\&- \Big ( 1-v^{2}-k\omega _{0}\beta v \sqrt{1-v^{2}} \Big ) e^{-\frac{k\omega _{0}\beta (1-v)}{\sqrt{1-v^{2}}}} \bigg ], \end{aligned}$$
(36)

with \(\Theta (\Delta \omega )\) being the standard step function; we have the notation \(\alpha _{i}=|\langle \omega _{b}|\mathrm {r}_{i}(0)| \omega _{d}\rangle |^{2}/|\langle \omega _{b}|\mathbf {r}(0)| \omega _{d}\rangle |^{2}\), \(\omega _{0}=|\omega _{bd}|\) being the energy level spacing between the states \(|\omega _{b}\rangle \) and \(|\omega _{d}\rangle \). The functions \(g_{i}(\omega _{0},\beta ,v)\) with \(i=1,2,3\) are exactly the modifying factor due to the collective effect of the thermal bath and the atomic inertial motion. Obviously, the transition rates depend on the atomic velocity, the energy level spacing, the temperature of the thermal bath, and the atomic polarizability. The results present no Planckian form of black-body radiation, \(\frac{1}{e^{\omega _{0}\beta }-1}\). This indicates that the static thermal bath as seen by the uniformly moving atom seems to be non-thermal. In other words, the temperature of the quantum electromagnetic field is relativistic and observer-dependent. This is similar to the previous findings in [11], where the interaction of a Unruh–DeWitt detector with the quantum scalar field is considered. Reversing the atom’s direction of motion, i.e., \(v\rightarrow -v\), the results remain unchanged. This can be ascribed to the spatial symmetry.

In particular, for the isotropic polarization, \(\alpha _{i}=(\frac{1}{3},\frac{1}{3},\frac{1}{3})\), the transition rate reduces to

$$\begin{aligned}&R_{\omega _{b}\rightarrow \omega _{d}}\nonumber \\&\quad = \frac{e^{2}\omega _{0}^{3}}{3\pi } |\langle \omega _{b}|\mathbf {r}(0) |\omega _{d}\rangle |^{2} \Big [ \big (1+h(\omega _{0},\beta ,v)\big ) \Theta (\omega _{bd})\nonumber \\&\qquad + h(\omega _{0},\beta ,v)\Theta (-\omega _{bd}) \Big ], \end{aligned}$$
(37)

where

$$\begin{aligned} h(\omega _{0},\beta ,v)= & {} \sum _{k=1}^{\infty } \frac{ \sqrt{1-v^{2}}}{2k\omega _{0}\beta v} \left[ e^{-\frac{k\omega _{0}\beta (1-v)}{\sqrt{1-v^{2}}}} - e^{-\frac{k\omega _{0}\beta (1+v)}{\sqrt{1-v^{2}}}} \right] \nonumber \\= & {} \frac{ \sqrt{1-v^{2}}}{2\omega _{0}\beta v} \ln \left( \frac{1-e^{-\frac{\omega _{0}\beta (1+v)}{\sqrt{1-v^{2}}}}}{1-e^{-\frac{\omega _{0}\beta (1-v)}{\sqrt{1-v^{2}}}}} \right) . \end{aligned}$$
(38)

Notably, the key factor \(h(\omega _{0},\beta ,v)\) coincides with that of the Unruh–DeWitt detector coupled with the quantum scalar field (see Eq. (3) in [11]). Although the result of a single atom coupled to the quantum electromagnetic field is quite distinct from that of the Unruh–DeWitt detector coupled to the quantum scalar field, the overall effect of an ensemble of enough atoms with arbitrary polarizabilities is similar to the case of the single Unruh–DeWitt detector.

In general, it is difficult to handle the summation in the functions \(g_{i}(\omega _{0},\beta ,v)\). So, in the following, we first examine these functions in some special cases.

When the atomic velocity is small as compared with the light velocity (\(|v|\ll 1\)), one has

$$\begin{aligned} g_{1}(\omega _{0},\beta ,v)\approx & {} \frac{1}{e^{\omega _{0}\beta }-1} \nonumber \\&+ \frac{\omega _{0}\beta e^{\omega _{0}\beta }\big [ 2\omega _{0}\beta (e^{\omega _{0}\beta }+1 )-5(e^{\omega _{0}\beta }-1) \big ]}{10(e^{\omega _{0}\beta }-1)^{3}} v^{2}, \nonumber \\ \end{aligned}$$
(39)
$$\begin{aligned} g_{3}(\omega _{0},\beta ,v)\approx & {} \frac{1}{e^{\omega _{0}\beta }-1}\nonumber \\&+ \frac{\omega _{0}\beta e^{\omega _{0}\beta }\big [ \omega _{0}\beta (e^{\omega _{0}\beta }+1 )-5(e^{\omega _{0}\beta }-1) \big ]}{10(e^{\omega _{0}\beta }-1)^{3}} v^{2}.\nonumber \\ \end{aligned}$$
(40)

The second term is exactly the modifying contribution due to the presence of the atomic inertial motion, which is proportional to \(v^{2}\) and can be positive or negative depending on \(\omega _{0}\beta \). This indicates that the atomic low velocity movement can enhance or weaken the atomic stimulated transition processes.

When the atomic velocity is close to the light velocity, \(v\rightarrow 1\), it is easy to see that \(g_{i}(\omega _{0},\beta ,v)\rightarrow 0\) with \(i=1,2,3\), and then the result unexpectedly turns into the case of a uniformly moving atom in the vacuum state. This means that ultra-relativistic atoms do not perceive the existence of the background thermal bath.

Similarly, when \(T\rightarrow 0\), \(g_{i}(\omega _{0},\beta ,v)\rightarrow 0\), then the case for an inertial atom immersed in the fluctuating vacuum is unaffectedly recovered.

Notably, in the limit of \(v\ll 1\), when the temperature of the thermal bath is high or the transition photon’s energy is small (\(T\gg \omega _{0}\)), one has

$$\begin{aligned} g_{1}(\omega _{0},\beta ,v)\approx & {} \frac{T}{\omega _{0}} \left( 1-\frac{1}{10} v^{2} \right) , \end{aligned}$$
(41)
$$\begin{aligned} g_{3}(\omega _{0},\beta ,v)\approx & {} \frac{T}{\omega _{0}} \left( 1-\frac{3}{10} v^{2} \right) . \end{aligned}$$
(42)

As compared with the corresponding case for a static atom in the thermal bath,

$$\begin{aligned} \frac{1}{e^{\omega _{0}\beta }-1} \approx \frac{T}{\omega _{0}}, \end{aligned}$$
(43)

here we can define the effective temperatures

$$\begin{aligned} T_{1}^{\text {eff}}= & {} T \left( 1-\frac{1}{10} v^{2} \right) , \end{aligned}$$
(44)
$$\begin{aligned} T_{2}^{\text {eff}}= & {} T \left( 1-\frac{3}{10} v^{2} \right) , \end{aligned}$$
(45)

as perceived by the uniformly moving atoms polarized along the x (or y) direction and the z direction, respectively. The effective temperature is also dependent on the atomic polarizability. As a result, the atom uniformly moving in the thermal bath always experiences a smaller temperature as compared with another atom at rest in the bath. It should be mentioned that the effective temperatures obtained here are different from the case of the quantum scalar field in [11], where \(T^{\text {eff}}=T(1-\frac{1}{6}v^{2})\).

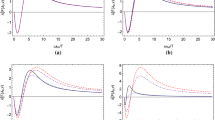
For general values of v and T, some numerical results can be given. Figure 1 shows the behavior of the stimulated absorption rate with the increase of the atomic speed. Under different values of the temperature, the atomic transition rate can present some different behaviors. This indicates that the atomic inertial motion can enhance or weaken the atomic stimulated transition processes at different degrees. Moreover, for different polarizabilities, the behavior of the transition rate can be quite distinct. In general, the transition rates for atoms polarizable perpendicular to the atomic velocity are always greater than those polarizable parallel to the atomic velocity.

Fig. 1
figure 1

Stimulated absorption rate of a uniformly moving atom in a thermal bath, as a function of the atomic velocity. The solid, dashed and dotdashed lines refer to the cases of \(\alpha _{i}=(1,0,0)\) (or \(\alpha _{i}=(0,1,0)\)), \(\alpha _{i}=(0,0,1)\), and \(\alpha _{i}=(\frac{1}{3},\frac{1}{3},\frac{1}{3})\), respectively. The atomic transition rate is depicted in the units of the spontaneous emission rate of an inertial atom in vacuum (\(\frac{e^{2}\omega _{0}^{3}|\langle \omega _{b}|\mathbf {r}(0) |\omega _{d}\rangle |^{2}}{3\pi }\)). a The case for \(\omega _{0}/T=0.1\), b the case for \(\omega _{0}/T=1\), c the case for \(\omega _{0}/T=5\), d the case for \(\omega _{0}/T=10\)

Full size image

4 Conclusions

This paper has analyzed the transition process of a multilevel atom moving at a constant velocity in interaction with a thermal bath of the quantum electromagnetic field. The calculations show that both the atomic stimulated emission rate and stimulated absorption rate are crucially dependent on the atomic velocity and the atomic polarizability. This is in sharp contrast with the case for a uniformly moving atom in the fluctuating vacuum electromagnetic field. This convincingly indicates that the temperature of quantum electromagnetic field is relativistic and observer-dependent. Notably, due to the dependence of the atomic polarizability, the temperature is directional for a single atom. However, an ensemble of sufficiently numerous atoms as a whole behaves like a single Unruh–DeWitt detector. By the collective configuration of the temperature, the atomic velocity and polarizability, theoretically the atomic stimulated transition processes can be enhanced or weakened. So, in fact, this work provides a new theoretical way to control and adjust the physical process of the atom–field coupling. In particular, when the temperature of the thermal bath is high or the transition photon is infrared (\(T\gg \omega _{0}\)), a slowly moving atom (\(v\ll 1\)) can perceive an effective temperature \(T \big ( 1-\frac{1}{10} v^{2} \big )\) for the polarizability perpendicular to the atomic velocity or \(T \big ( 1-\frac{3}{10} v^{2}\big )\) for the polarizability parallel to the atomic velocity, which is always smaller than the temperature T in the frame of the atom at rest. This is quite distinct from the case of the quantum scalar field [11]. However, for ultra-relativistic atoms, the stimulated absorption process is nearly forbidden and it seems that the atom is immersed in the vacuum (\(T=0\)). That is to say, ultra-relativistic atoms are insusceptible to the background thermal bath.

The relativity of temperature reminds one of the Unruh effect, where vacuum as seen by the inertial observers becomes like a thermal bath (black-body radiation) for the accelerated observers. In other words, an accelerating “thermometer” in empty space, removing any other contribution to its temperature, will record a non-zero temperature. Now, the temperature of quantum field is relativistic and observer-dependent, i.e., a moving “thermometer” in the static thermal bath will record a temperature different from that of the thermometer at rest. The Unruh effect is linked to the Hawking radiation and the quantum gravity. The Unruh effect and the Hawking radiation have profoundly revealed that there is a deep connection between gravity, thermodynamics and spacetime structure in the framework of quantum mechanics. So, the relativity of temperature can be treated as the analogue of the Unruh effect. I expect to see the experimental test of this theoretical work in atomic and molecular physics and optics. As compared with the controversial Unruh effect, the experimental implementation of the configuration considered in this paper should not be difficult.

Although here the result of the quantum electromagnetic field is quite distinct from that of the quantum scalar field [11], they both point to the validity of the particle number density \(n(\omega ,T,v)\mathrm{d}\omega =\frac{\omega ^{2}}{\pi ^{2}} h(\omega ,\beta ,v) \mathrm{d}\omega \) in the moving reference frame. There is still a long way to go to understanding all peculiarities of the temperature. After all, temperature is a broad concept stretching across classical physics and quantum physics. It is necessary to further consider the case of the spinor field or the massive vector field in the future.