Studying the ${\bar{D}}_1K$ molecule in the Bethe–Salpeter equation approach

Abstract

We interpret the $X_1(2900)$ as an S-wave ${\bar{D}}_1K$ molecular state in the Bethe–Salpeter equation approach with the ladder and instantaneous approximations for the kernel. By solving the Bethe–Salpeter equation numerically with the kernel containing one-particle-exchange diagrams and introducing three different form factors (monopole, dipole, and exponential form factors) in the verties, we find the bound state exists. We also study the decay width of the decay $X_1(2900)$ to $D^-K^+$.

1 Introduction

Recently, two new open flavor states were observed by LHCb collaboration in the $D^-K^+$ invariant mass distribution of $B^+\rightarrow D^+D^-K^+$, and the parameters are determined to be [1]

$$\begin{aligned} \begin{aligned} X_0(2900):M&=2.866\pm 0.007\pm 0.002 \ \mathrm {GeV},\\ \Gamma&=57\pm 12\pm 4 \ \mathrm {MeV},\\ X_1(2900):M&=2.904\pm 0.005\pm 0.001 \ \mathrm {GeV},\\ \Gamma&=110\pm 11\pm 4 \ \mathrm {MeV},\\ \end{aligned} \end{aligned}$$

respectively. Since the resonances $X_0(2900)$ and $X_1(2900)$ are observed in the $D^-K^+$ channel, they should be manifestly exotic and have minimal quark content ${\bar{c}}du{\bar{s}}$. These two states are new fully open flavor states after the discovery of X(5568) ($su{\bar{b}}{\bar{d}}$), which was reported by D0 collaboration in the $B_s\pi$ invariant mass distribution in 2016. However, since then LHCb, CMS, CDF, and ATLAS Collaborations have not found evidence for X(5568) [2,3,4,5].

In the past decades, a growing number of good candidates of exotic states have been observed, with lots of them containing $c{\bar{c}}$ or $b{\bar{b}}$ quarks [6, 7]. Thus, the discovery of $X_0(2900)$ and $X_1(2900)$ have drawn a lot of attentions. The $X_0(2900)$ can be interpreted as a $cs{\bar{u}}{\bar{d}}$ compact tetraquark both in the universal quark mass picture [8] and in the quark model [9], but not within an extended relativized quark model [10]. In Ref. [11], the authors used the two-body chromomagnetic interactions to find that the $X_0(2900)$ can be interpreted as a radial excited tetraquark and the $X_1(2900)$ can be an orbitally excited tetraquark. It was also suggested the $X_0(2900)$ can be interpreted as the S-wave $D^{*-}K^{*+}$ molecule state and the $X_1(2900)$ as the P-wave ${\bar{c}}{\bar{s}}ud$ compact tetraquark state [12]. In the chiral constituent quark model, it was shown show that no candidate of X(2900) was founded in the $IJ^P=00^+$ and $IJ^P=01^+$ $cs{\bar{q}}{\bar{q}}$ system, while there were two states in the P-wave excited $cs{\bar{q}}{\bar{q}}$ system, $D_1{\bar{K}}$ and $D_J{\bar{K}}$ , which could be candidates of X(2900) [13]. From the QCD Sum Rules, the $X_0(2900)$ and $X_1(2900)$ were studied in molecular and diquark-antidiquark tetraquark pictures, respectively, and the results for masses are in good agreement with the observed masses in the experiment [14]. Investigations bases the one-boson exchange model [15] and the phenomenological Lagrangian approach [16], showed that the $X_0(2900)$ can be a $D^{*}{\bar{K}}^{*}$ molecule, but the $X_1(2900)$ can not. In Ref. [17], the decay width for $X_0(2900)\rightarrow {\bar{D}}K$ process was found to be in agreement with the experimental data with the S-wave ${\bar{D}}^*K^*$ scenario for $X_0(2900)$ in the effective lagrangian approach. The study in Ref. [18] showed that the $X_1(2900)$ as a ${\bar{D}}_1K$ is disfavored within the meson exchange model. In Ref. [19], in the quasipotential Bethe–Salpeter (BS) equation approach, the authors supported the assignment of $X_0(2900)$ as a $D^{*}{\bar{K}}^{*}$ molecular state and $X_1(2900)$ as a $\bar{D_1}K$ virtual state.

Considering the mass of $X_1(2900)$ is about 10 MeV below the ${\bar{D}}_1K$ threshold, it is natural to explore the existence of the S-wave ${\bar{D}}_1K$ molecule. In this work, we will focus on the $X_1(2900)$ in the BS equation approach, investigating whether the $X_1(2900)$ can be an S-wave ${\bar{D}}_1K$ bound state. We will also to study the decay width of $X_1(2900) \rightarrow D^-K^+$.

In the rest of the manuscript we will proceed as follows. In Sect. 2, we will establish the BS equation for the bound state of an axial-vector meson (${\bar{D}}_1$) and a pseudoscalar meson (K). Then we will discuss the interaction kernel of the BS equation and calculate numerical results of the Lorentz scalar functions in the normalized BS wave function in Sect. 3. In Sect. 4, the decay width of the $X_1(2900)$ to $D^-K^+$ final state will be calculated. In Sect. 5, we will present a summary of our results.

2 The BS formalism for ${\bar{D}}_1K$ system

For the molecule composed of an axial-vector meson (${\bar{D}}_1$) and a pseudoscalar meson (K), its BS wave function is defined as

$$\begin{aligned} \chi ^\mu \left( x_1,x_2,P\right) = \langle 0|T{\bar{D}}_1^\mu (x_1)K(x_2)|P\rangle , \end{aligned}$$

(1)

where ${\bar{D}}_1(x_1)$ and $K(x_2)$ are the field operators of the axial-vector meson ${\bar{D}}_1$ and the pseudoscalar meson K at space coordinates $x_1$ and $x_2$, respectively, $P=Mv$ is the total momentum of bound state and v is its velocity. Let $m_{{\bar{D}}_1}$ and $m_K$ be the masses of the ${\bar{D}}_1$ and K mesons, respectively, p be the relative momentum of the two constituents, and define $\lambda _1$=$m_{{\bar{D}}_1}/(m_{{\bar{D}}_1}+m_K)$, $\lambda _2$=$m_K/(m_{{\bar{D}}_1}+m_K)$. The BS wave function in momentum space is defined as

$$\begin{aligned} \chi ^\mu _P(x_1,x_2,P) = e^{-iPX}\int \frac{d^4p}{(2\pi )^4}e^{-ipx}\chi ^\mu _P(p), \end{aligned}$$

(2)

where $X = \lambda _1x_1 + \lambda _2x_2$ is the coordinate of the center of mass and $x = x_1 - x_2$. The momentum of the ${\bar{D}}_1$ meson is $p_1=\lambda _1P+p$ and that of the K meson is $p_2=\lambda _2P-p$.

It can be shown that the BS wave function of the ${\bar{D}}_1K$ system satisfies the following BS equation:

$$\begin{aligned} \chi ^\mu _{P}(p)=S^{\mu \nu }_{{\bar{D}}_1}(p_1)\int \frac{d^4q}{(2\pi )^4}K_{\nu \lambda }(P,p,q)\chi ^\lambda _{P}(q)S_{K}(p_2), \end{aligned}$$

(3)

where $S^{\mu \nu }_{{\bar{D}}_1}(p_1)$ and $S_{K}(p_2)$ are the propagators of ${\bar{D}}_1$ and K mesons, respectively, and $K_{\nu \lambda }(P,p,q)$ is the kernel, which is defined as the sum of all the two particle irreducible diagrams with respect to $D_1$ and K mesons. For convenience, in the following we use the variables $p_l (=p\cdot v)$ and $p_t(=p- p_lv)$ as the longitudinal and transverse projections of the relative momentum (p) along the bound state momentum (P), respectively. Then, in the heavy quark limit the propagator of $D_1$ is

$$\begin{aligned} S^{\mu \nu }_{D_1}(\lambda _1P+p)=\frac{-i\left( g^{\mu \nu }-v^\mu v^\nu \right) }{2\omega _1\left( \lambda _1M+p_l-\omega _1+i\epsilon \right) }, \end{aligned}$$

(4)

and the propagator of the K meson is

$$\begin{aligned} S_K(\lambda _2P-p)=\frac{i}{\left( \lambda _2M-p_l\right) ^2-\omega _2^2+i\epsilon }, \end{aligned}$$

(5)

respectively, where $\omega _{1(2)} = \sqrt{m_{{\bar{D}}_1(K)}^2+p_t^2}$ (we have defined $p_t^2=-p_t\cdot p_t$).

In the BS equation approach, the interaction between ${\bar{D}}_1$ and K mesons arises from the light vector-meson ($\rho$ and $\omega$) exchange. Based on the heavy quark symmetry and the chiral symmetry, the relevant effective Lagrangian used in this work is shown in the following [20]:

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_{D_1D_1V}&= ig_{D_1D_1V}(D^\nu _{1b}\overleftrightarrow {\partial }_\mu D_{1a\nu }^\dag )V_{ba}^\mu \\&\quad +ig'_{D_1D_1V}(D_{1b}^\mu D_{1a}^{\nu \dag }-D_{1a}^{\mu \dag }D_{1a}^\nu )(\partial _\mu V_\nu -\partial _\nu V_\mu )_{ba}\\&\quad +ig_{{\bar{D}}_1{\bar{D}}_1V}({\bar{D}}_{1b\nu }\overleftrightarrow {\partial }_\mu {\bar{D}}_{1a}^{\nu \dag })V_{ab}^\mu \\&\quad +ig'_{{\bar{D}}_1{\bar{D}}_1V}({\bar{D}}_{1b}^\mu {\bar{D}}_{1a}^{\nu \dag }-{\bar{D}}_{1a}^{\mu \dag }{\bar{D}}_{1b}^\nu )(\partial _\mu V_\nu -\partial _\nu V_\mu )_{ab}\\ {\mathcal {L}}_{KKV}&= ig_{KKV}(K_b\overleftrightarrow {\partial }_\mu K_a^\dag )V_{ba}^\mu +ig_{{\bar{K}}{\bar{K}}V}({\bar{K}}_b\overleftrightarrow {\partial }_\mu {\bar{K}}_a^\dag )V_{ba}^\mu , \end{aligned}\nonumber \\ \end{aligned}$$

(6)

where a and b represent the light flavor quark (u and d), $V_\mu$ is a $3\times 3$ Hermitian matrix containing $\rho$, $\omega$, $K^*$, and $\phi$:

$$\begin{aligned} V= & {} \left( \begin{array}{ccc} \frac{\rho ^{0}}{\sqrt{2}}+\frac{\omega }{\sqrt{2}}&{}\rho ^{+}&{}K^{*+}\\ \rho ^{-}&{}-\frac{\rho ^{0}}{\sqrt{2}}+\frac{\omega }{\sqrt{2}}&{} K^{*0}\\ K^{*-} &{}{\bar{K}}^{*0}&{}\phi \end{array}\right) . \end{aligned}$$

(7)

The coupling constants involved in Eq. (6) are related to each other as follows [20]:

$$\begin{aligned} \begin{aligned}&g_{D_1D_1V}=-g_{{\bar{D}}_1{\bar{D}}_1V}=\frac{1}{\sqrt{2}}\beta _2 g_V,\\&\quad g'_{D_1D_1V}=-g'_{{\bar{D}}_1{\bar{D}}_1V}=\frac{5\lambda _2g_V}{3\sqrt{2}}m_{D_1},\\&\quad g_{KKV}=g_V/2, \end{aligned} \end{aligned}$$

(8)

where the parameters $\beta _2g_V$ and $\lambda _2g_V$ are given by $2g_{\rho NN}$ and $\frac{3}{10m_N}(g_{\rho NN}+f_{\rho NN})$, respectively, with $g_{\rho NN}^2/4\pi =0.84$ and $f_{\rho NN}/g_{\rho NN}=6.10$ [21]. The parameter $g_V=5.8$ is determined by the Kawarabayashi-Suzuki-Riazuddin-Fayyazuddin relations [20].

Fig. 1

One-particle exchange diagrams induced by vector mesons $\rho$ and $\omega$

Then, at the tree level, in the t-channel the kernel for the BS equation of the ${\bar{D}}_1K$ system in the lader approximation includes the following term (see Fig. 1):

$$\begin{aligned} \begin{aligned} K^{\tau \sigma }_{direct}(P,p,q;m_V)&=-(2\pi )^4\delta ^4(p'_1+p'_2-p_1-p_2)c_I \\&\quad \times \Big \{g_{D_1D_1V}g_{DDV}(p_1+q_1)_\gamma (p_2+q_2)_\rho g^{\tau \sigma }\\&\quad \times \Delta ^{\rho \gamma }(k,m_V)+g'_{D_1D_1V}g_{DDV}(p_2+q_2)_\rho \\&\quad \times \left[ k^\tau \Delta ^{\rho \sigma }(k,m_V)-k^\sigma \Delta ^{\rho \tau }(k,m_V)\right] \Big \},\\ \end{aligned}\nonumber \\ \end{aligned}$$

(9)

where $m_V$ ($V=\rho , \omega$) represents the mass of the exchanged light vector meson $\rho$ or $\omega$ , $c_I$ is the isospin coefficient: $c_0 =3, 1$ and $c_1 =-1, 1$ for $\rho$ and $\omega$, respectively, $\Delta ^{\mu \nu }$ represents the propagator for the light vector meson.

In order to describe the phenomena in the real world, we should include a form factor at each interacting vertex of hadrons to include the finite-size effects of these hadrons. For the meson-exchange case, the form factor is assumed to take the following forms:

$$\begin{aligned} \begin{aligned} F_M(k)&=\frac{\Lambda _M^2-m^2}{\Lambda _M^2-k^2}, \\ F_D(k)&=\frac{(\Lambda _D^2-m^2)^2}{(\Lambda _D^2-k^2)^2}, \\ F_E(k)&=e^{(k^2-m^2)/\Lambda _E^2}, \end{aligned} \end{aligned}$$

(10)

in the monopole (M), dipole (D), and exponential (E) models, respectively, where $\Lambda$, m and k represent the cutoff parameter, the mass of the exchanged meson and the momentum of the exchanged meson, respectively. The value of $\Lambda$ is near 1 GeV which is the typical chiral symmetry breaking scale.

In general, for an axial-vector meson ($D_1$) and a pseudoscalar meson (K) bound state, the BS wave function $\chi _P^\mu (p)$ has the following form:

$$\begin{aligned} \chi _P^\mu (p)= & {} f_0(p)p^\mu +f_1(p)P^\mu +f_2(p)\epsilon ^\mu \nonumber \\&+f_3(p)\varepsilon ^{\mu \nu \alpha \beta }p_\alpha P_\beta \epsilon _\nu , \end{aligned}$$

(11)

where $f_i(p)$ $(i = 0,1,2,3)$ are Lorentz-scalar functions and $\epsilon ^\mu$ represents the polarization vector of the bound state. After considering the constraints imposed by parity and Lorentz transformations, it is easy to prove that $\chi _P^\mu (p)$ can be simplified as

$$\begin{aligned} \chi _P^\mu (p)=f(p)\varepsilon ^{\mu \nu \alpha \beta }p_\alpha P_\beta \epsilon _\nu , \end{aligned}$$

(12)

where the scalar function f(p) contains all the dynamics.

In the following derivation of the BS equation, we will apply the instantaneous approximation, in which the energy exchanged between the constituent particles of the binding system is neglected. In our calculation we choose the absolute value of the binding energy $E_b$ of the ${\bar{D}}_1K$ system (which is defined as $E_b=M-m_{D_1}-m_K$) less than 30 MeV. In this case the exchange of energy between the constituent particles can be neglected.

Substituting Eqs. (4), (5), (9) and (10) into Eq. (3) and using the covariant instantaneous approximation in the kernel, $p_l=q_l$, one obtains the following expression:

$$\begin{aligned} \begin{aligned} f(p)&=\int \frac{d^4q}{(2\pi )^4}\frac{i}{6\omega _1(\lambda _1M+p_l-\omega _1+i\epsilon )[(\lambda _2M-p_l)^2-\omega _2^2+i\epsilon ][-(p_t-q_t)^2-m_V^2]}\\&\quad \times \Big \{g_{{\bar{D}}_1{\bar{D}}_1V}g_{KKV}\left[ 4(\lambda _1M+p_l)(\lambda _2M-p_l)\right. \\&\quad \left. +(p_t+q_t)^2+(p_t^2-q_t^2)^2/m_V^2\right] +g'_{{\bar{D}}_1{\bar{D}}_1V}g_{KKV}\omega _2(p_t\cdot q_t-q_t^2)/(\lambda _2M-\omega _2))\Big \}F^2(k_t)f(q), \end{aligned}\nonumber \\ \end{aligned}$$

(13)

where $k_t=p_t-q_t$ is the momentum of the exchanged meson in the covariant instantaneous approximation.

In Eq. (13) there are poles in the plane of $p_l$ at $-\lambda _1 M+\omega _1-i\epsilon$, $\lambda _2 M+\omega _2-i\epsilon$ and $\lambda _2 M-\omega _2+i\epsilon$. By choosing the appropriate contour, we integrate over $p_l$ on both sides of Eq. (13) in the rest frame of the bound state, then we obtain the following equation:

$$\begin{aligned} \begin{aligned} {\tilde{f}}(p_t)&=\int \frac{dq_t^3}{(2\pi )^3}\frac{1}{12\omega _1\omega _2(M-\omega _1-\omega _2)\left[ -(p_t-q_t)^2-m_V^2\right] }\\&\quad \times \Big \{3g_{{\bar{D}}_1{\bar{D}}_1V}g_{KKV}\left[ 4\omega _2(M-\omega _2)\right. \\&\quad \left. +(p_t+q_t)^2+(p_t^2-q_t^2)^2/m_V^2\right] \\&\quad +2g'_{{\bar{D}}_1{\bar{D}}_1V}g_{KKV}\omega _2(p_t\cdot q_t-q_t^2)/(\lambda _2M-\omega _2)\Big \}F^2(k_t){\tilde{f}}(q_t), \end{aligned}\nonumber \\ \end{aligned}$$

(14)

where ${\tilde{f}}(p_t)\equiv \int dp_l f(p)$.

Now, we can solve the BS equation numerically and study whether the S-wave ${\bar{D}}_1K$ bound state exists or not. It can be seen from Eq. (14) that there is only one free parameter in our model, the cutoff $\Lambda$, which enters through various phenomenological form factors in Eq. (10). It contains the information about the extended interaction due to the structures of hadrons. In fact, in a pioneering work of the molecular approach to exotic hadrons [22] the finite size effects of the exchanged mesons were clearly and simply explained and the order of magnitude of the cutoff was fixed by nuclear physics problems, in particular by that of the deuteron. In this work, we shall treat $\Lambda$ as a parameter and vary it in a wide range 0.8–4.8 GeV when the binding energy $E_b$ is in the region from $-$ 5 to $-$ 30 MeV to see if the BS equation has solutions. Concerning the necessity of the inclusion of finite size effects of the exchanged mesons, which nowadays is routinely put forward, it is worth mentioning the paper of

To find out the possible molecular bound states, one only needs to solve the homogeneous BS equation. One numerical solution of the homogeneous BS equation corresponds to a possible bound state. The integration region in each integral is discretized into n pieces, with n being sufficiently large. In this way, the integral equation is converted into an $n\times n$ nmatrix equation, and the scalar wave function will now be regarded as an n-dimensional vector. Then, the integral equation can be illustrated as ${\tilde{f}}^{(n)}(p_t)=A^{(n\times n)}(p_t,q_t){\tilde{f}}^{(n)}(q_t)$, where ${\tilde{f}}^{(n)}(p_t) ({\tilde{f}}^{(n)}(q_t))$ is an n-dimensional vector, and $A^{(n\times n)}(p_t,q_t)$ is an $n \times n$ matrix, which corresponds to the matrix labeled by $p_t$ and $q_t$ in each integral equation. Generally, $p_t$ ($q_t$) varies from 0 to $+\infty$. Here, $p_t$ ($q_t$) is transformed into a new variable t that varies from $-1$ to 1 based on the Gaussian integration method,

$$\begin{aligned} p_t=\mu +w\log \left[ 1+y\frac{1+t}{1-t}\right] , \end{aligned}$$

(15)

where $\mu$ is a parameter introduced to avoid divergence in numerical calculations, w and y are parameters used in controlling the slope of wave functions and finding the proper solutions for these functions. Then one can obtain the numerical results of the BS wave functions by requiring the eigenvalue of the eigenvalue equation to be 1.0.

In our calculation, we choose to work in the rest frame of the bound state in which $P=(M,0)$. We take the averaged masses of the mesons from the PDG [23], $m_{D_1}=2420.8$ MeV, $m_{K}=494.98$ MeV, $m_\rho =775.26$ MeV, and $m_\omega =782.65$ MeV. After searching for possible solutions in the isoscalar channel of the ${\bar{D}}_1K$ system, we find the bound state exists. We list some values of $E_b$ and the corresponding $\Lambda$ for the three different form factor models in Table 1.

Table 1 Values of $E_b$ and corresponding cutoff $\Lambda _M$, $\Lambda _D$, and $\Lambda _E$ for $I=0$ and $I=1$ ${\bar{D}}_1K$ bound states for the monopole, dipole, and exponential form factors, respectively

Fig. 2

Numerical results of the normalized Lorentz scalar function ${\tilde{f}}(p_t)$ for the $X_{1}(2900)$ in the $I=0$ (a) and $I=1$ (b) ${\bar{D}}_1K$ molecular picture with the monopole form factor

3 The normalization condition of the BS wave function

To find out whether the bound state of the ${\bar{D}}_1K$ system exists or not, one only needs to solve the homogeneous BS equation. However, when we want to calculate physical quantities such as the decay width we have to face the problem of the normalization of the BS wave function. In the following we will discuss the normalization of the BS wave function $\chi ^\mu _P(p)$.

In the heavy quark limit, the normalization of the BS wave function of the ${\bar{D}}_1K$ system can be written as [24]

$$\begin{aligned} i\int \frac{d^4pd^4q}{(2\pi )^8}{\bar{\chi }}^\mu _P(p)\frac{\partial }{\partial P_0}[I_{P\mu \nu }(p,q)]\chi ^\nu (q)=2E_P, \end{aligned}$$

(16)

where $I_{P\mu \nu }(p,q)=(2\pi )^4\delta ^4(p-q)S^{-1}_{\mu \nu }(p_1)S^{-1}(p_2)$.

In the rest frame, the normalization condition can be written in the following form:

$$\begin{aligned} \begin{aligned}&-i\int \frac{d^4p}{(2\pi )^4}\Big \{4M^2p_t^2\big [\lambda _1^2(6\lambda _2^2M^2-6\lambda _2Mp_l+p_l^2-\omega _2^2)\\&\quad +2\lambda _1\lambda _2p_l(3\lambda _2M-2p_l)+\lambda _2^2(p_l^2-\omega _1^2)\big ]f^2(q)=1. \end{aligned}\nonumber \\ \end{aligned}$$

(17)

From Eqs. (13) and (14), we obtain

$$\begin{aligned} \begin{aligned} f(p)=&\frac{i\omega _2(M-\omega _1-\omega _2)}{\pi (\lambda _1M+p_l-\omega _1+i\epsilon )(\lambda _2M-p_l+\omega _2-i\epsilon )(\lambda _2M-p_l-\omega _2+i\epsilon )}{\tilde{f}}(p_t).\\ \end{aligned} \end{aligned}$$

(18)

Then, one can recast the normalization condition for the BS wave function into the form

$$\begin{aligned} \begin{aligned}&-\int \frac{d^3p_t}{8\pi ^5}\frac{M^2p_t^2\omega _1}{\omega _2^2(M-\omega _1-\omega _2)^2}\Big \{\lambda _2^2(p_t^2-\omega _1^2)(\lambda _2M-\omega _1-3\omega _2)+\lambda _1^3(\lambda _2^2M^3-2M\omega _2^2)\\&\quad +\lambda _1\lambda _2[2\lambda _2^3M^3+\lambda _2M(p_t^2-\omega _1^2)-4\omega _2^2(\omega _1-\omega _2)-2\lambda _2^2M^2(\omega _1+3\omega _2)]\\&\quad +\lambda _1^2[3\lambda _2^3M^3-6\lambda _2M\omega _2^2+2\omega _2^2(\omega _1+\omega _2)-\lambda _2^2M^2(\omega _1+3\omega _2)]\Big \}{\tilde{f}}^2(p_t)=1. \end{aligned} \end{aligned}$$

(19)

The wave function obtained in the previous section (which is calculated numerically from Eq. (14)) can be normalized by Eq. (19).

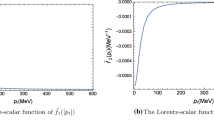
In our case, the binding energy $E_b=M_{X_{1}(2900)}-(M_{{{\bar{D}}_1}}+M_K)\simeq -12.4$ MeV, where we have used the mass of the $X_{1}(2900)$ as 2904 MeV. From our calculations, we find the $I=0$ ${\bar{D}}_1K$ system can be assigned as the $X_{1}(2900)$ state when the cutoff $\Lambda$ = 1280 MeV, 1788 MeV, and 1257 MeV for the monopole, dipole, and exponential form factors, respectively, the $I=1$ ${\bar{D}}_1K$ system can be the $X_{1}(2900)$ state when the cutoff $\Lambda$ = 1688 MeV, 2434 MeV, and 1758 MeV for the monopole, dipole, and exponential form factors, respectively. The corresponding numerical results of the normalized Lorentz scalar function, ${\tilde{f}}(p_t)$, are given in Fig. 2a and b for the $X_{1}(2900)$ states with $I=0$ and $I=1$ in the ${\bar{D}}_1K$ molecule picture for the monopole form factor. The curves for the numerical results of the normalized Lorentz scalar functions with the dipole and exponential form factors are found to be similar to those of the monopole form factor. In other words, the wave functions are not sensitive to the types of form factors.

4 The decay of $X_{1}(2900)\rightarrow D^-K^+$

Besides investigating whether the bound state of the ${\bar{D}}_1K$ system can be $X_1(2900)$ or not, we can also study the decay of the $X_1(2900)$ as the S-wave ${\bar{D}}_1K$ bound state. The $X_1(2900)$ can decay to $D^-K^+$ via the Feynman diagrams in Fig. 3. which are induced by the effective Lagrangians for the $D_1DV$ and KKV vertices (which have been given in Eq. (6)) as the following [20]:

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_{DD_1V}&= g_{DD_1V}D_{1b}^\mu V_{\mu ba}D_a^\dag +g'_{DD_1V}\\&\qquad (D_{1b}^\mu \overleftrightarrow {\partial }^\nu D_a^\dag )(\partial _\mu V_\nu -\partial _\nu V_\mu )_{ba}\\&\quad +g_{{\bar{D}}{\bar{D}}_1V}{\bar{D}}_a^\dag V_{\mu ba}{\bar{D}}_{1b}^\mu +g'_{{\bar{D}}{\bar{D}}_1V}\\&\qquad ({\bar{D}}_{1b}^\mu \overleftrightarrow {\partial }^\nu {\bar{D}}_a^\dag )(\partial _\mu V_\nu -\partial _\nu V_\mu )_{ba}+H.c.,\\ \end{aligned} \end{aligned}$$

(20)

where the coupling constants are given as $g_{DD_1V}=-g_{{\bar{D}}{\bar{D}}_1V}=-\frac{2}{\sqrt{3}}\zeta _1g_v\sqrt{m_Dm_{D_1}}$, $g'_{DD_1V}=-g'_{{\bar{D}}\bar{D_1}V}=\frac{1}{\sqrt{3}}\mu _1g_V$ [20], with the two parameters $\zeta _1$ and $\mu _1$ being involved in the coupling constants, about which the information is very scarce leading them undetermined. However, in the heavy quark limit, we can roughly assume that the coupling constants $g_{D{D_1}V}$ and $g'_{DD_1V}$ are equal to $g_{D^*D_0V}$ (=$\zeta g_V\sqrt{2m_{D^*}m_{D^0}}$) and $g'_{D^*D_0V}$ (=$1/\sqrt{2}\mu g_V$), respectively. The parameters $\mu =0.1$ $\mathrm {GeV}^{-1}$ and $\zeta =0.1$ are taken in Ref. [25].

Fig. 3

The diagrams contributing to the $X_{1}(2900)\rightarrow D^-K^+$ decay process induced by $\rho$ and $\omega$

According to the above interactions, we can write down the amplitude for the decay $X_1(2900)\rightarrow D^-K^+$ induced by light vector meson ($\rho$ and $\omega$) exchanges as shown in Fig. 3, as the following:

$$\begin{aligned} \begin{aligned} {\mathcal {M}}=&g_{KKV}\sqrt{2E}\int \frac{d^4p}{(2\pi )^4}F^2(k)\big [g_{{\bar{D}}{\bar{D}}_1V}(p_2+p'_2)^\alpha \Delta _{\alpha \mu }(k,m_V)\\&+g'_{{\bar{D}}{\bar{D}}_1V}(p_1+p'_1)^\nu (p_2+p'_2)^\alpha \\&\qquad \left( k_\mu \Delta _{\alpha \nu }(k,m_V)-k_\nu \Delta _{\alpha \mu }(k,m_V)\right) \big ]\chi _{P}^\mu (p) \end{aligned}\nonumber \\ \end{aligned}$$

(21)

In the rest frame, we define $p_1'=(E_1',-{\mathbf {p}}'_1)$ and $p_2'=(E_2',{\mathbf {p}}'_2)$ to be the momenta of D and K, respectively. According to the kinematics of the two-body decay of the initial state in the rest frame, one has

$$\begin{aligned} \begin{aligned} E_1'&=\frac{M^2-m_2^{'2}+m_1^{'2}}{2M},\quad \quad E_1'=\frac{M^2-m_1^{'2}+m_2^{'2}}{2M},\\ |{\mathbf {p}}'_1|&=|{\mathbf {p}}'_2|=\frac{\sqrt{[M^2-(m'_1+m'_2)^2][M^2-(m'_1-m'_2)^2]}}{2M}, \end{aligned}\nonumber \\ \end{aligned}$$

(22)

and

$$\begin{aligned} d\Gamma =\frac{1}{32\pi ^2}|{\mathcal {M}}|^2\frac{|{\mathbf {p}}'|}{M^2}d\Omega , \end{aligned}$$

(23)

where $|{\mathbf {p}}'_1|$ and $|{\mathbf {p}}'_2|$ are the norm of the 3-momentum of the particles in the final states in the rest frame of the initial bound state and ${\mathcal {M}}$ is the Lorentz-invariant decay amplitude of the process.

Substituting the normalized numerical solutions of the BS equation, and the cutoff $\Lambda$ are 1280 MeV, 1788 MeV, and 1257 MeV with $I=0$ and 1688 MeV, 2434 MeV, and 1758 MeV with $I=1$ for the monopole, dipole, and exponential form factors, respectively. The decay widths of the $X_1(2900)$ to $D^-K^+$ can be obtained as following:

$$\begin{aligned}&\Gamma _{X_1(2900)(I=0)\rightarrow D^-K^+}\nonumber \\&\quad =\left\{ \begin{aligned}&70.73\ \mathrm {MeV}\ \mathrm {with\ monopole\ form\ factor}, \\&98.75\ \mathrm {MeV}\ \mathrm {with\ dipole\ form\ factor}, \\&60.38\ \mathrm {MeV}\ \mathrm {with\ exponential\ form\ factor}, \end{aligned} \right. \end{aligned}$$

(24)

and

$$\begin{aligned}&\Gamma _{X_1(2900)(I=1)\rightarrow D^-K^+}\nonumber \\&\quad =\left\{ \begin{aligned}&28.14\ \mathrm {MeV}\ \mathrm {with\ monopole\ form\ factor}, \\&18.13\ \mathrm {MeV}\ \mathrm {with\ dipole\ form\ factor}, \\&12.78\ \mathrm {MeV}\ \mathrm {with\ exponential\ form\ factor}. \end{aligned} \right. \end{aligned}$$

(25)

From our calculation results, we can see that different form factors have a great influence on the decay width, and different cutoff $\Lambda$ for the same form factor also have a great influence on the decay width.

5 Summary and discussion

In this paper, we studied the $X_1(2900)$ with the hadronic molecule interpretation by regarding it as a bound state of ${\bar{D}}_1$ and K mesons in the BS equation approach. In our model, we applied the ladder and instantaneous approximations to obtain the kernel containing one-particle-exchange diagrams and introduced three different form factors (the monopole form factor, the dipole form factor, and the exponential form factor) at the interaction vertices. From the calculating results we find that there exist bound states of the ${\bar{D}}_1K$ system. The binding energy depends on the value of the cutoff $\Lambda$. For the $I=0$ ${\bar{D}}_1K$ system, we find the cutoff regions in which the solutions (with the binding energy $E_b\in$ ($-$ 5, $-$ 30) MeV) for the ground state of the BS equation can be found (in units of MeV): $\Lambda _M\sim$ (1208, 1375), $\Lambda _D\sim$ (1668, 1948), and $\Lambda _E\sim$ (1159, 1386) for the monopole form factor, the dipole form factor, and the exponential form factor, respectively. For the $I=1$ ${\bar{D}}_1K$ system, we find two the regions (in units of MeV): $\Lambda _M\sim$ (1541, 1880), $\Lambda _D\sim$ (1897, 2744), and $\Lambda _E\sim$ (1571, 2006) in which the solutions of the BS equation can be found. Thus, we can confirm that $X_1(2900)$ can be regarded as the S-wave ${\bar{D}}_1K$ molecules in our model.

On the other hand, in Ref. [18], the possibility of explaining $X_1(2900)$ as a ${\bar{D}}_1K$ molecule was excluded in the nonrelativistic limit by means of the Schr$\ddot{\mathrm {o}}$dinger equation. In the quasipotential Bethe–Salpeter equation approach [19], the ${\bar{D}}K$ bound state with $I(J^P)=0(1^-)$ only appears at a large cutoff $\Lambda$ of about 4 GeV while a virtual state with $I(J^P)=0(1^-)$ from the ${\bar{D}}K$ interaction can be found when $\Lambda$ is decreased. Therefore, more theoretical and experimental studies are needed for this state.

We applied the numerical solutions for the BS wave functions with the corresponding cutoff ($\Lambda$ = 1280 MeV, 1788 MeV, and 1257 MeV for $I=0$ and $\Lambda$ = 1688 MeV, 2434 MeV, and 1758 MeV for $I=1$ with the monopole, dipole, and exponential form factors, respectively.) to calculate the decay widths of $X_{1}(2900)\rightarrow D^-K^+$ induced by $\rho$ and $\omega$ exchanges. We predict the decay widths are 70.73, 98.75, and 60.38 MeV and 28.14, 18.13, and 12.78 MeV for $X_1(2900)$ as $I=0$ and $I=1$ ${\bar{D}}_1K$ molecules with the corresponding cutoff in the decay process, respectively. From our study, the $X_1(2900)$ is suitable as $I=0$ ${\bar{D}}_1K$ molecular state. There are two uncertain factors in the calculation of the decay width, one is that the parameters $\xi _1$ and $\mu _1$ have not been determined since the information about them is very scarce, the other is that we can not give the definite value of the cutoff $\Lambda$.