Anisotropic compact stars in higher-order curvature theory

Abstract

In this paper we shall consider spherically symmetric spacetime solutions describing the interior of stellar compact objects, in the context of higher-order curvature theory of the ${{\mathrm {f(R)}}}$ type. We shall derive the non-vacuum field equations of the higher-order curvature theory, without assuming any specific form of the ${{\mathrm {f(R)}}}$ theory, specifying the analysis for a spherically symmetric spacetime with two unknown functions. We obtain a system of highly non-linear differential equations, which consists of four differential equations with six unknown functions. To solve such a system, we assume a specific form of metric potentials, using the Krori–Barua ansatz. We successfully solve the system of differential equations, and we derive all the components of the energy–momentum tensor. Moreover, we derive the non-trivial general form of ${{\mathrm {f(R)}}}$ that may generate such solutions and calculate the dynamic Ricci scalar of the anisotropic star. Accordingly, we calculate the asymptotic form of the function ${\mathrm {f(R)}}$, which is a polynomial function. We match the derived interior solution with the exterior one, which was derived in [1], with the latter also resulting to a non-trivial form of the Ricci scalar. Notably but rather expected, the exterior solution differs from the Schwarzschild one in the context of general relativity. The matching procedure will eventually relate two constants with the mass and radius of the compact stellar object. We list the necessary conditions that any compact anisotropic star must satisfy and explain in detail that our model bypasses all of these conditions for a special compact star $\textit{Her X--1}$, which has an estimated mass and radius $(mass = 0.85 \pm 0.15M_{\circledcirc }\ and\ radius = 8.1 \pm 0.41~\text {km}$). Moreover, we study the stability of this model by using the Tolman–Oppenheimer–Volkoff equation and adiabatic index, and we show that the considered model is different and more stable compared to the corresponding models in the context of general relativity.

1 Introduction

Apart from the great successes of Newtonian gravity, it utterly failed in certain cases where strong gravitational effects were considered, such as the advances of Mercury in addition to the Michelson Morley experiment [2]. In 1915, Einstein developed the general theory of relativity (GR), which enabled the resolution of the issue with Mercury [3]. Thereafter, GR is considered as the cornerstone theory for gravitational physics. However GR has several shortcomings that indicate GR not being the most fundamental theory of gravity, such as the dark energy issues [4,5,6,7,8,9]. In addition, the GR violates the Chandrasekhar mass-limit for white dwarfs of super-Chandrasekhar, and sub-Chandrasekhar limiting mass [10,11,12,13,14,15,16,17].

Moreover, GR shows inconsistency in the regime of strong gravitational field and recent observations [4, 18,19,20]. Thus seeking for an appropriate modification of GR, is a well motivated task. The most successful modification of GR is the higher-order-curvature theory, and specifically ${\mathrm {f(R)}}$ gravity, which is successful in explaining the presence of dark matter and confronting gravitational theories with observations [21]. Moreover, the ${\mathrm {f(R)}}$ gravitational theory when quantized results to a renormalizable gravitational theory [22]. Thus, ${\mathrm {f(R)}}$ gravitational theory certainly is an appealing and well-motivated extension of GR. Modified gravity theories are divided into different categories such as those containing some four second-order curvature invariants and other that involve the invariants as a function of the Ricci scalar-like ${\mathrm {f(R)}}$ gravity model [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. The ${\mathrm {f(R)}}$ gravitational theory avoids the Ostrogradsky’s instability [40] which is a common limitation of general higher-derivative theories [41].

Numerous applications of ${\mathrm {f(R)}}$ can be found in the context of theoretical cosmology [31, 42,43,44,45,46,47,48] and in astrophysics. Spherically symmetric vacuum black hole solutions in ${\mathrm {f(R)}}$ have been derived in [1, 49,50,51,52,53,54,55,56,57,58]. In the frame of a strong gravitational background in local objects, numerous spherically symmetric black holes are derived [59,60,61,62,63,64,65,66]. Recently, the study of compact stars in amended gravitational theories has become popular. Compact stars result from the collapse of massive stars and there are several types of compact objects of interest, including white dwarfs, neutron stars, strange stars and black holes. Various models describe neutron stars in ${\mathrm {f(R)}}$ [67,68,69,70,71,72,73,74,75,76,77,78,79]. Moreover hypernuclear compact stars is studied for stellar models constructed on the basis of covariant density functional theory Hartree and Hartree-Fock Methods approximation [80]. In the present work we aim to apply the non-vacuum field equations of ${\mathrm {f(R)}}$ to a spherically symmetric spacetime without assuming any specific form of ${\mathrm {f(R)}}$, and to derive a compact anisotropic model. The resulting model shall be confronted with real compact anisotropic stars, and specifically the star $\textit{Her X--1}$.

The article is organized as follows: In Sect. 2, we give a brief summary of the ${\mathrm {f(R)}}$ gravitational theory. In Sect. 3, we apply the non-vacuum field equations of ${\mathrm {f(R)}}$ to a spherically symmetric line-element that has an unequal metric potential. We derive a system of differential equations, having six unknown functions. In order to derive an analytic solution for the differential equations in closed form, we assume a specific form of the metric potential, using the Krori–Barua ansatz. We derive the remaining unknown functions, all the components of the energy–momentum tensor, and the asymptotic form of the polynomial ${\mathrm {f(R)}}$ which generates such a solution. This solution is characterized by four constants of integration, and one of them differentiates our model from the corresponding GR description. In Sect. 4, we match the model derived in Sect. 3, with the exterior solution presented in [1], which has a spherically symmetric solution different from the Schwarzschild one, and successfully match two constants with the mass and radius of the compact stellar object. In Sect. 5, we list the necessary conditions that any realistic theoretical model must satisfy in order for it to become compatible with a realistic star. We show that our model satisfies all of these conditions that are required for any realistic compact stellar object. In Sect. 6, we study the stability using the Tolman–Oppenheimer–Volkoff (TOV) equation and adiabatic index and show that the present model satisfies these requirements implying its stability. In the final section, we present our concluding remarks.

2 Summary of the ${\mathrm {f(R)}}$ gravitational theory

In this section, we consider recall the essential features of four-dimensional higher-order curvature ${\mathrm {f(R)}}$ gravity. ${\mathrm {f(R)}}$ gravity serves as a modification GR and coincides with it when ${\mathrm {f(R)=R}}$. When ${\mathrm {f(R)}\ne {\mathrm {R}}}$, we have a theory different from Einstein’s GR. The action of ${\mathrm {f(R)}}$ gravity can take the following form (cf. [81,82,83,84,85,86,87,88]):

$$\begin{aligned} {\mathop {{\mathcal {I}}}}:=\frac{1}{2\kappa } \int d^4x \sqrt{-g} {\mathrm {f(R)}}+\frac{1}{2\kappa } \int d^4x \sqrt{-g} \mathcal{L_M}(g_{\mu \nu },\xi ), \end{aligned}$$

(1)

where $\kappa =8\pi G$, G is Newton’s gravitational constant, g is the determinant of the metric, $\mathcal{L_M}(g_{\mu \nu },\xi )$ is the action of matter fields, and $\xi$ is minimally coupled to the metric $g_{\mu \nu }$.

Upon varying the gravitational action with respect to the metric tensor $g_{\mu \nu }$, we obtain the non-vacuum field equations of ${\mathrm {f(R)}}$ gravitational theory as follows [89]:

$$\begin{aligned} {\mathop {{\mathcal {I}}}}_{\mu \nu }= R _{\mu \nu } {\mathrm {f_{R}}}-\frac{1}{2}g_{\mu \nu }{\mathrm {f( R)}}+[g_{\mu \nu }\Box -\nabla _\mu \nabla _\nu ]{\mathrm {f}}_{_{\mathrm {R}}} -\kappa T_{\mu \nu }\equiv 0, \end{aligned}$$

(2)

where $\Box$ is the d’Alembertian operator, ${\mathrm {f}}_{{\mathrm {R}}}=\frac{{\mathrm {df}}}{{\mathrm {dR}}}$ and the matter energy–momentum tensor $T_{\mu \nu }$ is defined as,

$$\begin{aligned} T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta \mathcal{L_M}}{\delta g^{\mu \nu }}. \end{aligned}$$

(3)

The trace of Eq.  (2), takes the following form,

$$\begin{aligned} {\mathop {{\mathcal {I}}}}=3\Box {{\mathrm {f}}}_{{\mathrm {R}}}+{\mathrm { R}}{f_{R}}-2{\mathrm {f}}({\mathrm {R}}) -\kappa T\equiv 0,\quad \text {where}\ T=T_\mu ^\mu . \end{aligned}$$

(4)

From Eq. (4), ${\mathrm {f(R)}}$ can be isolated to obtain the following form,

$$\begin{aligned} {\mathrm {f(R)}}=\frac{1}{2}\big [3\Box {\mathrm {f}}_{{\mathrm {R}}}+{\mathrm { R}}{f_{R}}-\kappa T\Big ].\end{aligned}$$

(5)

Using Eq. (5) in Eq. (2) we obtain the following [90],

$$\begin{aligned} {\mathop {{\mathcal {I}}}}_{\mu \nu }= & {} {\mathrm {R}}_{\mu \nu } {\mathrm {f}}_{{\mathrm {R}}}-\frac{1}{4}g_{\mu \nu }{\mathrm {R}} f _{_{\mathrm {R}}}+\frac{1}{4}g_{\mu \nu }\Box {\mathrm {f}}_{_{\mathrm { R}}} -\nabla _\mu \nabla _\nu {\mathrm {f}}_{_{\mathrm {R}}}\nonumber \\&-\kappa \left( T_{\mu \nu }-\frac{1}{4}g_{\mu \nu } T\right) . \end{aligned}$$

(6)

In this study, we shall assume that the energy–momentum tensor, $T_{\mu \nu }$, has the following specific form in order to achieve anisotropic form,

$$\begin{aligned} { T}_\mu {}^\nu {}=(p_\bot +\rho )u_\mu u^\nu +p_\bot \delta _\mu {}^\nu +(p_r-p_\bot )\zeta _\mu \zeta ^\nu , \end{aligned}$$

(7)

where $u_\mu$ is the timelike vector defined as $u^\mu =[1,0,0,0]$, and $\zeta _\mu$ is the unit spacelike vector in the radial direction defined as $\zeta ^\mu =[0,1,0,0]$ such that $u^\mu u_\mu =-1$ and $\zeta ^\mu \xi _\mu =1$. In this study, $\rho$ represents the energy-density, and $p_r$ and $p_\bot$ are the radial and tangential pressures, respectively.

In the following sections, we apply the field equations, namely, Eqs. (4) and (6) to a spherically symmetric spacetime having two unknown functions.

3 Stellar equations in the f(R) gravitational theory

To study the non-vacuum field Eqs. (4) and (6) we use the following form of a spherically symmetric spacetime having two unknown functions,

$$\begin{aligned}&ds^2=-e^{\alpha (r)}dt^2+\frac{dr^2}{e^{\beta (r)}}+r^2d\Sigma , \quad \text {where}\nonumber \\&d\Sigma =(d\theta ^2+\sin ^2d\phi ^2), \end{aligned}$$

(8)

where $\alpha (r)$ and $\beta (r)$ are unknown functions. The Ricci scalar for the metric (8) takes the following form:

$$\begin{aligned} {\textit{R}(r)}=\frac{e^{-\beta }r[r\alpha '\beta '-2r\alpha ''-r\alpha '^2-4\alpha '+4\beta '-4]+4}{2r^2}, \end{aligned}$$

(9)

where $\alpha \equiv \alpha (r)$, $\beta \equiv \beta (r)$, $\alpha '=\frac{d\alpha }{dr}$, $\alpha ''=\frac{d^2\alpha }{dr^2}$ and $\beta '=\frac{d\beta }{dr}$. For the line-element (8) the non-vanishing components of the field Eqs. (4) and (6) have the following forms:

$$\begin{aligned}&{{\mathfrak {I}}}_t{}^t=\frac{e^{-\alpha }[e^{\alpha -\beta }\{Fr^2( 2\alpha ''-\alpha '\beta '+\alpha '^2)+4rF[r\alpha '+r\beta '-1]+r^2[3\alpha 'F'-2F''+F'\beta ']-4rF'\}+4e^{\alpha }F]}{r^2}-8\pi \rho ,\nonumber \\&{{\mathfrak {I}}}_r{}^r=\frac{e^{-\beta }[Fr^2( 2\alpha ''-\alpha '\beta '+\alpha '^2)-4F[r\alpha '+r\beta '+1]-r^2[\alpha 'F'-6F''+3F'\beta ']-4rF'+4e^{\alpha }F]}{r^2}+8\pi P_r,\nonumber \\&{{\mathfrak {I}}}_\theta {}^\theta ={\mathfrak I}_\phi {}^\phi =\frac{F[4-e^{-\beta }(4-2r^2\alpha ''+r^2\alpha '\beta '-r^2\alpha '^2)]+e^{-\beta }[r^2\alpha '\beta '+2r^2F''-r^2F'\beta '-4rF']}{r^2}-8\pi P_\bot ,\nonumber \\&{{\mathfrak {I}}}= [P_r+2P_\bot -\rho ]+\frac{e^{-\beta }[r^2(6F''-2F\alpha ''-F\alpha '^2)+r[rF\beta '+3rF'-4F]\alpha '+r\beta '[4F-3rF']+12rF'-4F)+4(F-f)}{8\pi r^2}, \end{aligned}$$

(10)

where $F={\mathrm {f}}_{_{\mathrm {R}}}=\frac{{\mathrm {df}}}{{\mathrm { dR}}}=\frac{{\mathrm {df}}}{{\mathrm {dr}}}\frac{{\mathrm {dr}}}{{\mathrm { dR}}}$. The system of equations in (10) includes four nonlinear differential equations with six unknown functions, $\alpha$, $\beta$, F $\rho$, $P_r$ and $P_t$; therefore, we must impose two constraints to transform the equations in (10) into a closed system. In this study, we use the Krori–Barua ansatz that has the following form [91]:

$$\begin{aligned} \alpha =b_0r^2+b_1\quad \beta =b_2r^2, \end{aligned}$$

(11)

where $b_0$, and $b_2$ are the dimensionful parameters with the inverse unit of $r^2$, and $b_1$ is a constant. Using Eq. (11) in Eq. (10), we obtain the following:

$$\begin{aligned}&\rho =\frac{e^{-b_0r^2}[b_0c_1(b_0-b_2)r^6+[a_0{}^2+(6c_1-b_2)b_0+3c_1b_2]r^4+(2b_2-4c_1+3b_0)r^2-1]+1+c_1r^2}{16\pi r^2}, \quad F=1+c_1r^2,\nonumber \\&P_r(r)=\frac{e^{-b_2r^2}[1+(b_0+2b_2)r^2-r^4(b_0{}^2-b_0[2c_1+b_2]-5b_2c_1)+b_0c_1(b_2-b_0)r^6-e^{b_2r^2}(1+c_1r^2)]}{\pi r^2},\nonumber \\&P_\bot (r)=\frac{1+c_1r^2-e^{-b_2r^2}[1+r^2(2c_1-b_0)-r^4[b_0(b_0+2c_1-b_2)-b_2c_1]+b_0c_1r^6(b_2-b_0)]}{16\pi r^2}. \end{aligned}$$

(12)

4 Matching conditions

Given that solution (12) has a nontrivial Ricci scalar as shown in Eq. (31), we must match it with an exterior solution that has a non-constant Ricci scalar. In order to exemplify our study and confront it with a realistic physical system, we shall use the pulsar Her X–1, which has well known mass and radius, whose estimated mass and radius are $M =0.85\pm 0.15 M_\circledcirc$ and $b \thickapprox 8.1\pm 0.41$ km, respectively [92].

Fig. 1

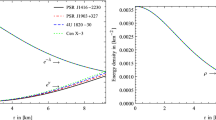
Schematic plot of the radial coordinate r in Km versus the potentials of the metric (11) using the constants constrained from RX J 1856–37 from where we put $b_0=0.0259974$ and $b_1=-3.7654625$. These values of the two constants $b_0$ and $b_1$ will be use throughout this study

Fig. 2

Plot of boundary matching of a $g_{tt}$ and b $g_{rr}$ of (12)

Thus, we match solution (11), considering $b_2=b_0$, with the uncharged one presented in [1]. The spherically symmetric uncharged solution [1] takes the following form

$$\begin{aligned} ds^2= -\Big (\frac{1}{2}-\frac{2M}{r}\Big )dt^2+\Big (\frac{1}{2}-\frac{2M}{r}\Big )^{-1}dr^2+r^2d\Omega ^2, \end{aligned}$$

(13)

where M is the total mass of the stellar compact object and $4M<r$. We have to match the interior spacetime metric (11) with the exterior spacetime given by Eq. (13) at the boundary of the star $r =b$. The continuity of the metric functions across the boundary $r =b$ yields the following conditions,

$$\begin{aligned} \alpha (r=b)=\Bigg (\frac{1}{2}-\frac{2M}{b}\Bigg ), \quad \beta (r=b)=\Bigg (\frac{1}{2}-\frac{2M}{b}\Bigg )^{-1}. \end{aligned}$$

(14)

Using the above conditions we get the constraints on the constants $b_0$, $b_1$. The functional form of these constants takes the form,

$$\begin{aligned} b_0=\frac{ln\Big (\frac{2b}{b-4M}\Big )}{b^2}, \quad b_1=ln\Big (\frac{b^2-8bM+16M^2}{4b^2}\Big ). \end{aligned}$$

(15)

In Figs. 1 and 2 we plot the metric potentials and matching metric, respectively.

5 Terms of physical viability of the solution (12)

To investigate whether the interior solution (12) is suitable to describe a physical system, several criteria must be satisfied, thus, we explore these criteria in this section.

Fig. 3

Plots of density, radial, and transverse pressures. All the plots show that the components of the energy–momentum tensors are positive as required by any real stellar

Fig. 4

Anisotropy $\Delta (r)$ and anisotropy force. Plot a shows that we have a repulsive force due to the positivity of the anisotropy

5.1 Energy–momentum tensor

For a realistic interior solution, positive values of energy-density, radial, and transverse pressures are needed. Furthermore, all these quantities have finite values at the center of the star. These energies gradually decrease toward the surface of the star, and $P_r\ge P_\bot$. Figure 3 shows the portraits of the martial energy, density, radial, and transverse pressures. The figure shows that, $\rho (r=0)_{c_1=0}=0.003104779987$, $\rho (r=0)_{c_1=-0.01}=0.003701913745$, ${\hat{p}}_r(r=0)_{c_1=0}=0.001034926662$, ${\hat{p}}_r(r=0)_{c_1=-0.01}=0.001233971248$, ${\hat{p}}_\bot (r=0)_{c_1=0}=0.001034926662$, ${\hat{p}}_\bot (r=0)_{c_1=0}=0.001233971248$. Figure 3 also displays that all the components of the energy–momentum tensor gradually decrease toward the surface of the star. From Fig. 3, values of energy-density, radial and transverse pressures at the center in the case of $c_1=0$ are smaller than those when $c_1\ne 0$. Moreover the components of the energy–momentum proceed to the surface of the star more rapidly at $c_1=-0.01$ than at $c_1=0$ and $P_r=P\bot$ at the center. However, as we approach the surface of the star ${\hat{p}}_\bot \ge P_r$. This behavior is illustrated in Fig. 4a, which also shows anisotropy behavior that is defined as $\Delta (r)={\hat{p}}_\bot -{\hat{p}}_r$. Figure 4b also reveals that the anisotropic force is positive, which means that it is a repulsive force because $P_\bot \ge P_r$.

Moreover, the gradient of the density, radial, and transverse pressures must be negative inside the stellar body, i.e., $\frac{d\rho }{dr}< 0$, $\frac{d{\hat{p}}_r}{dr}< 0$ and $\frac{d{\hat{p}}_\bot }{dr}< 0$ [93]. Using (12), we calculate the derivative of density, radial, and transverse pressures as,

$$\begin{aligned}&\rho '=\frac{d\rho }{dr}=\nonumber \\&\frac{e^{-b_0r^2}[1-b_0b_2c_1(b_0-b_2)r^8-r^6([3c_1-b_0]b_2{}^2+[8b_0c_1+b_0{}^2]b_2-2c_1b_0{}^2)-r^4(2b_2{}^2+(4b_0-7c_1)b_2-b_0{}^2-6b_0c_1)]-1}{r^3},\nonumber \\&P'_r=\frac{dP_r}{dr}=\nonumber \\&\frac{e^{-b_0r^2}[b_0b_2c_1(b_0-b_2)r^8-r^6([b_0+5c_1]b_2{}^2-[b_0b_2-2b_0c_1]b_0)-r^4(b_0{}^2-5b_2c_1+2b_2{}^2-2b_0c_1)-b_2r^2-1]+1}{r^3},\nonumber \\&P'_\bot =\frac{dP_\bot }{dr}=\nonumber \\&\frac{e^{-b_0r^2}[1-b_0b_2c_1(b_0-b_2)r^8+r^6([2c_1-b_2]b_0{}^2-[4c_1-b_2]b_2+b_2{}^2c_1)+r^4(b_0{}^2-2b_0[b_2+c_1]+b_2c_1)+b_2r^2]-1}{r^3}. \end{aligned}$$

(16)

The behavior of the gradients of density, radial, and transverse pressures are shown in Fig. 5, where it can also be seen that $\rho '$, ${\hat{p}}'_r$ and ${\hat{p}}'_\bot$ have negative values as required by a real stellar compact object.

Fig. 5

Gradients of density, radial, and transverse pressures. All figures show that the gradients of the components of the energy–momentum tensor are negative consistent with those of a real stellar

5.2 Causality

To show the behavior of sound velocities, we must calculate the gradient of energy-density, radial, and transverse pressures with the form given by Eq. (16). Using Eq. (17), we obtain the following:

$$\begin{aligned}&v_r{}^2=\frac{P'_r}{\rho '},=\nonumber \\&\frac{e^{-b_0r^2}[b_0b_2c_1(b_0-b_2)r^8-r^6([b_0+5c_1]b_2{}^2-[b_0b_2-2b_0c_1]b_0)-r^4(b_0{}^2-5b_2c_1+2b_2{}^2-2b_0c_1)-b_2r^2-1]+1}{e^{-b_0r^2}[1-b_0b_2c_1(b_0-b_2)r^8-r^6([3c_1-b_0]b_2{}^2+[8b_0c_1+b_0{}^2]b_2-2c_1b_0{}^2)-r^4(2b_2{}^2+(4b_0-7c_1)b_2-b_0{}^2-6b_0c_1)]-1},\nonumber \\&v_\bot {}^2=\frac{P'_\bot }{\rho '},=\nonumber \\&\frac{e^{-b_0r^2}[1-b_0b_2c_1(b_0-b_2)r^8+r^6([2c_1-b_2]b_0{}^2-[4c_1-b_2]b_2+b_2{}^2c_1)+r^4(b_0{}^2-2b_0[b_2+c_1]+b_2c_1)+b_2r^2]-1}{e^{-b_0r^2}[1-b_0b_2c_1(b_0-b_2)r^8-r^6([3c_1-b_0]b_2{}^2+[8b_0c_1+b_0{}^2]b_2-2c_1b_0{}^2)-r^4(2b_2{}^2+(4b_0-7c_1)b_2-b_0{}^2-6b_0c_1)]-1}.\nonumber \\ \end{aligned}$$

(17)

To ensure that the causality condition is satisfied both for radial and the transverse sound speeds, we must show that the values of $v_r{}^2$ and $v_\bot {}^2$ are less than the speed of light. To this end, we plot them in Fig. 6 to ensure that both of variables have values less than the speed of light, provided that the speed of light is unity in relativistic units.

Herrera assumed the cracking condition of a stable anisotropic compact star that results when equilibrium is disturbed could be due to local anisotropy. This condition is depend on the radial and tangential sound speeds, $v_r$ and $v_t$. Using Herrera condition [94, 95] that demonstrated that a simple requirement in order to avoid gravitational cracking is $-1\le v_t{}^2-v_r{}^2\le 0$. In Fig. 6c, we show that solution (12) is stable against cracking for $c_1=0$ and $c_1=-0.01$.

Fig. 6

Radial, transverse speed of sound, and $v_\bot {}^2-v_r{}^2$. The plots of radial and transverse speeds indicate that our model satisfies the causality condition

5.3 Energy conditions

For the non-vacuum solution, the energy conditions are considered important tools. Therefore, the dominant energy condition (DEC) implies that the speed of energy should be less than the speed of light. To fulfill the DEC, we must have $\rho -P_r >0$ and $\rho -P_\bot >0$. We show that the DEC is fulfilled in Fig. 7 moreover, we study the weak energy condition (WEC), $\rho +P_r>0$ and $\rho +P_\bot >0$, and the strong energy condition (SEC), $\rho -P_r-2P_\bot >0$, and show in Fig. 8 that both are satisfied.

Fig. 7

DEC of solution (12)

5.4 Mass–radius-relation

For a spherically symmetric spacetime the compactification factor u(r) is defined as the ratio between its mass and radius. In the compact stellar object, the compactification factor plays an important role in understanding its physical properties. Using solution (12), the gravitational mass takes the following form:

$$\begin{aligned}&M(r)=4\pi {\int _0}^r \rho \xi ^2 d\xi =\frac{1}{32b_2{}^{7/2}\,r}\Bigg \{ 2e^{-b_0r^2}b_2{}^{3/2}\nonumber \\&\quad \times \Bigg [\{4+4b_0c_1r^4+2r^2[b_0-3c_1]\}b_2{}^{2}\nonumber \\&\quad -b_0b_2r^2[2b_0c_1r^2+9c_1+2b_0]\nonumber \\&\quad -3b_0{}^{2}c_1r^2\Bigg ]+r\sqrt{\pi }b_2\,erf(\sqrt{b_2}r)[16b_2{}^3 +10b_2{}^2(b_0-c_1)\nonumber \\&\quad +b_0b_2(2b_0+9c_1)+3b_0{}^2c_1]+8b_2{}^{7/2}(c_1r^2-1)\Bigg \}, \end{aligned}$$

(18)

where erf(x) is the error function defined as follows:

$$\begin{aligned} erf(x)=\frac{2}{\sqrt{\pi }}\int _0^x e^{-t^2}dt. \end{aligned}$$

(19)

The compactification factor u(r) is defined as follows:

$$\begin{aligned}&u(r)=\frac{M(r)}{r}=\frac{1}{32b_2{}^{7/2}\,r^2}\Bigg \{ 2e^{-b_0r^2}b_2{}^{3/2}\Bigg [\{4+4b_0c_1r^4\nonumber \\&\qquad +2r^2[b_0-3c_1]\}b_2{}^{2}-b_0b_2r^2[2b_0c_1r^2+9c_1+2b_0]\nonumber \\&\qquad -3b_0{}^{2}c_1r^2\Bigg ]+r\sqrt{\pi }b_2\,erf(\sqrt{b_2}r)[16b_2{}^3 +10b_2{}^2(b_0-c_1)\nonumber \\&\qquad +b_0b_2(2b_0+9c_1)+3b_0{}^2c_1]+8b_2{}^{7/2}(c_1r^2-1)\Bigg \}. \end{aligned}$$

(20)

Figure 9 shows the behaviors of the gravitational mass and compactification factor. As it is shown in Fig. 9a the gravitational mass increases as the radial coordinate increases, contrary to Fig. 9b which reveals that the compactification factor decreases as the radial coordinate increases.

Fig. 8

WEC and SEC of solution (12). Figures 6, 7 and 8 show that the energy conditions of our model are satisfied

Fig. 9

Gravitational mass and compactification factor of solution (12)

5.5 Equation of state (EoS)

Das et al. [96] derived the EoS for a neutral compact stellar object and showed that it is almost linear; however, in this study the EoS is nonlinear. This condition can be explained by calculating the radial and transverse EoS that respectively have the following form:

$$\begin{aligned}&\omega _r=\frac{P_r}{\rho }\nonumber \\&\quad =\frac{e^{-b_2r^2}[1+b_0r^2+2r^4b_0c_1-r^4b_0{}^2-c_1r^6b_0{}^2+b_0b_2r^4 +c_1b_0b_2r^6+2b_2r^2+5b_2c_1r^4-e^{b_2r^2}(1+c_1r^2)]}{e^{-b_0r^2}[b_0c_1(b_0-b_2)r^6+[a_0{}^2+(6c_1-b_2)b_0+3c_1b_2]r^4 +(2b_2-4c_1+3b_0)r^2-1]+1+c_1r^2}, \nonumber \\&\omega _\bot \nonumber \\&\quad =\frac{P_\bot }{\rho }=\frac{1+c_1r^2-e^{-b_2r^2}[1+2r^2c_1-r^2b_0-2c_1r^4b_0+b_0b_2r^4+b_0b_2c_1r^6-b_0{}^2r^4-b_0{}^2c_1r^6+r^4c_1b_2]}{e^{-b_0r^2}[b_0c_1(b_0-b_2)r^6+[a_0{}^2+(6c_1-b_2)b_0+3c_1b_2]r^4+(2b_2-4c_1+3b_0)r^2-1]+1+c_1r^2}. \end{aligned}$$

(21)

Fig. 10

Plots of the radial and transverse EoS of solution (12)

Figure 10 illustrates the behavior of the radial and transverse EoS. Figure 10a, b show that the EoS is nonlinear. The nature of the metric potential given by Eq. (15) and perhaps indicates the reason for the nonlinearity of the EoS. This phenomena can be explained as follows, with the asymptotic forms of Eq. (21) assuming the form:

$$\begin{aligned}&\omega _r\simeq \frac{1}{3}-\frac{2b_0(4c_1-b_0)}{c_1-2b_0}r^2+O(r^4),\nonumber \\&\quad \omega _\bot \simeq \frac{1}{3}+\frac{b_0(4c_1-b_0)}{c_1-2b_0}r^2+O(r^4), \end{aligned}$$

(22)

where the constant $c_1$ has no effect on the nonlinearity of the EoS. The effect of nonlinearity originates from the contribution of the constant $b_0$.

6 Stability of solution (12)

We now discuss the most critical condition which determines how realistic is a compact stellar object, i.e., the stability condition. Here we investigate this issue from the viewpoint of the TOV equation and adiabatic index.

6.1 Equilibrium analysis through TOV equation

In this subsection, we discuss the stability of the derived model. Accordingly, we assume a hydrostatic equilibrium governed by the TOV equations. Using the TOV-equation [97,98,99], we obtain:

$$\begin{aligned} \frac{2[P_\bot -P_r]}{r}-\frac{M_g(r)[\rho (r)+P_r]e^{[\alpha (r)-\beta (r)]/2}}{r}-\frac{dP_r}{r}=0, \end{aligned}$$

(23)

where $M_g(r)$ is the gravitational mass confined in a radius r that is defined from the Tolman–Whittaker mass formula using the following equation:

$$\begin{aligned}&M_g(r)=4\pi {\int _0}^r\Big ({T_t}^t-{T_r}^r-{T_\theta }^\theta -{T_\phi }^\phi \Big )r^2e^{[\alpha (r)+\beta (r)]/2}dr\nonumber \\&\quad =\frac{r \alpha ' e^{[\beta (r)-\alpha (r)]/2}}{2}, \end{aligned}$$

(24)

Using Eq. (24) in Eq. (23), we obtain the following:

$$\begin{aligned} \frac{2(P_\bot -P_r)}{r}-\frac{dP_r}{dr}-\frac{\alpha '[\rho (r)+P_r]}{2}=F_g+F_a+F_h=0, \end{aligned}$$

(25)

where $F_g=-\frac{\alpha '[\rho (r)+P_r]}{2}$, $F_a=\frac{2(P_\bot -P_r)}{r}$ and $F_h=-\frac{dP_r}{dr}$ are the gravitational, anisotropic, and hydrostatic forces respectively. The solution of the TOV equation represented by model (12) is depicted in Fig. 11.

Fig. 11

TOV of solution (12)

The three different forces are plotted in Fig. 11, which shows that the hydrostatic and anisotropic forces are positive and dominated by the gravitational force which is negative, to maintain the hydrostatic equilibrium of the system.

Figure 11b shows that for $c_1=-0.01$, the three different forces converge more rapidly than for $c_1=0$. Thus, in the non-vanishing $c_1$ case of the higher-order curvature case, the system tends to be more stable than in the linear curvature case.

6.2 Adiabatic index

The adiabatic index $\gamma$ is defined as, follows:

$$\begin{aligned} \gamma =\frac{\rho +P}{P}\frac{dP}{d\rho }. \end{aligned}$$

(26)

This index allows us to link the structure of a spherical symmetric static object and the EoS of the interior solution, and it helps in the study of the stability of a stellar compact object [100]. In order for the interior solution to be stable, its adiabatic index must be greater than 3/4 [101] and when $\gamma =\frac{4}{3}$, the isotropic sphere will be in neutral equilibrium. According to the work of Chan et al. [102] the condition $\gamma >\Gamma$ for the stability of a relativistic anisotropic sphere should be satisfied, where $\Gamma$ is determined as follows:

$$\begin{aligned} \Gamma =\frac{4}{3}-\left\{ \frac{4(P_r-P_\bot )}{3|P'_r|}\right\} _{max}. \end{aligned}$$

(27)

Figure 12 shows that the stability condition of model (12) is verified according to the analysis of two adiabatic indexes because both have values greater than $\frac{4}{3}$. Figure 12b shows that the adiabatic index $\gamma$ at $c_1=-0.01$ has a greater value than that at $c_1=0$, which means that the case that differs from GR is more stable than the case of GR itself.

In Table 1 we present different pulsars to calculate the two constants, $b_0$ and $b_1$, that characterized our model. In Tables 2 and 3 we use the values of the constants $b_0$ and $b_1$ that are calculated in Table 1 to calculate the energy-density, radial and tangential velocities strong condition at the center and at the boundary of the pulsars presented in Table 1 for the GR and ${\mathrm {f(R)}}$.

Fig. 12

Adiabatic index of solution (12)

Table 1 Values of model parameters

Table 2 Values of physical quantities at $c_1=0$

Table 3 Values of physical quantities at $c_1=-0.01$

7 Concluding remarks

In this study, we studied compact stellar objects in ${\mathrm {f(R)}}$ gravity. We have applied the non-vacuum field equations of ${\mathrm {f(R)}}$ after rewriting them in terms of $f_R=\frac{{\mathrm {df}}({\mathrm {R}})}{{\mathrm {dR}}}$ to a spherically symmetric spacetime. We obtained a system of four nonlinear differential equations comprising six unknown functions, the three components of the energy–momentum tensor, ($\rho (r)$, $P_r$, $P_\bot$), the two components of the metric potentials, and the form $f_R=\frac{{\mathrm {df}}({\mathrm {R}})}{{\mathrm {dR}}}$. To solve such a system we have assumed the form of the metric potentials, given by Krori–Barua ansatz that contain three constants. As a result the system was rendered easy to be solved analytically. We have derived the three components of the energy–momentum and the form of ${\mathrm {f(R)}}$. We have shown that the form of the Ricci scalar associated with this compact star is not trivial and the asymptotic form of ${\mathrm {f(R)}}$ behaves as a polynomial function. This solution contains four constants of integration. One of these constants caused the deviation of our solution from the GR models, leading to the higher-order curvature terms. When this constant was set equal to zero, we recovered the GR compact star solution. In order to further simplify the system, we have assumed two constants of the metric potential to be equal and have applied the matching condition to the metric derived in [1], which has a nontrivial form of the Ricci scalar; the metric is also different from a Schwarzschild one and determines the relation between two constants and the mass and radius of a compact star, leaving the constant responsible for the deviation from GR to be arbitrary.

We have listed the necessary conditions that any non-vacuum solution must satisfy in order to become compatible with a real compact star. We have shown that the three components of the energy–momentum tensor satisfied the listed conditions for a real star. Moreover, we have studied the energy conditions, namely, the WEC, DEC and SEC and have shown that the present solution satisfied all of these conditions. In addition, we have investigated the stability of the derived solution by calculating adiabatic index and showed that it is greater than 4/3 as required [102]. It is interesting to discuss our solutions in the context of more compact objects like neutron stars, to make contact with events like the GW190814. These solutions have been studied in [103] in the context of ${\mathrm {f(R)}}$ gravity. In our case, extra caution is needed since our approach applies to inhomogeneous solutions. Nevertheless, pulsars with spin less than 3ms or even the product of the merging of two neutron stars if it is a neutron star, can initially be quite inhomogeneous, so during the ring-down, our solution could be relevant. We hope to address this issue in future work since such a study would require the implementation of a numerical recipe appropriately tailored to our solutions.

In conclusion, we have succeeded for the first time to derive a nontrivial anisotropic compact star in ${\mathrm {f(R)}}$ by assuming a specific form for the metric potential. This study can be continued by searching for a constraint other than the form of the metric potential to achieve a closed form of the system of field equations of ${\mathrm {f(R)}}$, like to assume a specific form of the EoS. We expect that the physics of the resulting model will be entirely different from that presented in this study. We hope to address this issue in the future.

Appendix A

The form of f(r)

Using the fact that $F=\frac{df(R)}{dR}=\frac{df(r)}{dr}\frac{dR(r)}{dr}$, we can get the form of f(r) by solving the following differential equation:

$$\begin{aligned}&8f-\frac{1}{8(1-(1+b_0b_2r^4+r^2[b_0-2b_2])(1+r^2[b_0-b_2])e^{-b_2r^2})^{^{^3}}} \nonumber \\&\quad \times \Bigg \{rf'\Bigg [e^{-3b_2r^2} \Bigg (4b_0{}^2b_2{}^2r^{16}[b_0-b_2]^2(b_0{}^2-4b_0b_2-3b_2{}^2)-68\nonumber \\&\quad +2b_0b_2[24b_2{}^4-21b_0b_2{}^3-70b_0{}^2b_2{}^2+47b_0{}^3b_2-4b_0{}^2]\nonumber \\&\quad \times [b_0-b_2]r^{14}+4(b_0{}^6-12b_2{}^6-24b_0{}^5b_2\nonumber \\&\quad -158b_0{}^3b_2{}^3+30b_0b_2{}^5 \nonumber \\&\quad +107b_0{}^4b_2{}^2+50b_0{}^2b_2{}^4)r^{12}+2(9b_0{}^5-28b_2{}^5\nonumber \\&\quad -95b_0{}^4b_2+286b_0b_2{}^4+364b_0{}^3b_2{}^2-564b_0{}^2b_2{}^3)r^{10}\nonumber \\&\quad -4r^8(b_0{}^4+144b_0b_2{}^3\nonumber \\&\quad -8b_0{}^3b_2-57b_2{}^4-47b_0{}^2b_2{}^2)-2r^6(351b_0b_2{}^2-234b_0{}^2b_2\nonumber \\&\quad +6b_0{}^3-37a_2{}^3)-4(109b_2{}^2-124b_0b_2+31b_0{}^2)r^4\nonumber \\&\quad -6(21b_2+b_0)r^2\Bigg )\nonumber \\&\quad +4e^{-2b_2r^2}\Bigg (33-b_0{}^2b_2{}^2(b_0-b_2)^2r^{12}\nonumber \\&\quad -b_0b_2{}^2(3b_0+5b_2)(b_0-b_2)r^{10}-4(11b_0{}^3b_2-84b_0{}^2b_2{}^2\nonumber \\&\quad -14b_2{}^4- b_0{}^4+95b_0b_2{}^3)r^8\nonumber \\&\quad +4(3b_0{}^3-109b_2{}^3-149b_0{}^2b_2+296b_0b_2{}^2)r^6\nonumber \\&\quad +4(32b_0{}^2-131b_0b_2+95b_2{}^2)r^4\nonumber \\&\quad +12(b_0+9b_2)r^2\Bigg )-1-2e^{-b_2r^2} \Bigg (30\nonumber \\&\quad -4b_0b_2(b_0-b_2)r^6-2(b_0{}^2+4b_2{}^2-7b_0b_2)r^4\nonumber \\&\quad -3(3b_2-b_2)r^2\Bigg )\Bigg ]-6r^2f''\Bigg [e^{-3b_2r^2}\nonumber \\&\quad \times \Bigg ([1+b_0b_2r^4+(2b_2-b_0)r^2] \nonumber \\&\times [1+(b_0-b_2)r^2][8+b_0b_2(b_0+3b_2)(b_0-b_2)r^8\nonumber \\&\quad -(b_0{}^3+3b_0{}^2b_2-14b_0b_2{}^2+6b_2{}^3)r^6\nonumber \\&\quad +b_2(b_0+3b_2)r^4 +(b_0+7b_2)r^2]\Bigg )\nonumber \\&\quad -e^{-2b_2r^2}\Bigg (16-2b_0b_2(b_2{}^2-b_0{}^2)r^8+(10b_0{}^2b_2-2b_0{}^3\nonumber \\&\quad -4b_2{}^2)r^6-(14b_2{}^2-8b_0{}^2+34b_0b_2)r^4+ 2(b_0+7b_2)r^2\Bigg )\nonumber \\&\quad +e^{-b_2r^2}\{8+r^2(b_0-b_2)\}\Bigg ]-6r^3f'''\Bigg [(1+b_0b_2r^4\nonumber \\&\quad +[2b_2-b_0]r^2)^2(1+[b_0-b_2]r^2)^2e^{-3b_2r^2}\nonumber \\&\quad -e^{-2b_2r^2}(2-2b_0b_2[b_2-b_0]r^6+2[b_0{}^2-4b_0b_2\nonumber \\&\quad +2b_2{}^2]r^4-2b_2r^2)+e^{-b_2r^2}\Bigg ]\Bigg \}=0. \end{aligned}$$

(28)

The above differential equation is not easy to analytically solve therefore, we are shall find some approximate asymptotic solutions. Asymptotically and by putting $b_2=b_0$ we get,

$$\begin{aligned} 3f'''+16b_0f''+8b_0f'-4b_0{}^2f=0 \end{aligned}$$

(29)

The solution of the above differential equation is lengthy and here we write its asymptotic that takes the following form,

$$\begin{aligned} f(r)=c_2+c_3\sin \left( \frac{\sqrt{24b_0}r}{3}\right) +c_4\cos \left( \frac{\sqrt{24b_0}r}{3}\right) . \end{aligned}$$

(30)

In order for the solution (30) to be compatible with the form of $F(r)=\frac{df(R)}{dR}=\frac{df(r)}{dr}\frac{dr}{dR}$ up to leading order, we must assume $c_3=0$, and $c_4=-\frac{3b_0}{4}=\frac{27c_1}{16}$ which results in $b_0=\frac{9c_1}{4}$. Equation (12) shows that when $c_1=0$ we return to the case of GR because $F=1$, which results in $f(R)=R$. Thus, the terms that contain $c_1$ make the solution (12) different from GR. Henceforth, we assume $b_2=b_0$ to make the calculations more easy to handle. Using Eq. (11) and constraints $b_2=b_0$, we obtain the Ricci scalar up at leading order, which has the following form,

$$\begin{aligned} R\approx b_0{}^2 r^2, \quad { which \ leads\ to\ } r=\pm \frac{\sqrt{R}}{b_0}. \end{aligned}$$

(31)

Using Eq. (31) in Eq. (30) we obtain the following form of ${\mathrm {f(R)}}$:

$$\begin{aligned}&{\mathrm {f(R)}}=c_2+c_4\cos \Big (\frac{\sqrt{24R}}{3\sqrt{b_0}}\Big ) \approx c_2+c_4+R -\frac{c_1}{4b_0{}^2}R^2 \nonumber \\&\quad +\frac{c_1}{45b_0{}^3}R^3 -\cdots . \end{aligned}$$

(32)

Equation (32) represents GR plus higher-order corrections so with corresponding choices of parameters such theory easily pass cosmological and astrophysical tests being realistic theory.