Anisotropic compact stars in f(R) gravity

Abstract

We derive a new interior solution for stellar compact objects in $f\mathcal {(R)}$ gravity assuming a differential relation to constrain the Ricci curvature scalar. To this aim, we consider specific forms for the radial component of the metric and the first derivative of $f\mathcal {(R)}$. After, the time component of the metric potential and the form of $f({\mathcal {R}})$ function are derived. From these results, it is possible to obtain the radial and tangential components of pressure and the density. The resulting interior solution represents a physically motivated anisotropic neutron star model. It is possible to match it with a boundary exterior solution. From this matching, the components of metric potentials can be rewritten in terms of a compactness parameter C which has to be $C=2GM/Rc^2<<0.5$ for physical consistency. Other physical conditions for real stellar objects are taken into account according to the solution. We show that the model accurately bypasses conditions like the finiteness of radial and tangential pressures, and energy density at the center of the star, the positivity of these components through the stellar structure, and the negativity of the gradients. These conditions are satisfied if the energy-conditions hold. Moreover, we study the stability of the model by showing that Tolman–Oppenheimer–Volkoff equation is at hydrostatic equilibrium. The solution is matched with observational data of millisecond pulsars with a withe dwarf companion and pulsars presenting thermonuclear bursts.

1 Introduction

Compact stars are the final stage of stellar evolution when the radial pressure, caused by the nuclear fusion in the inner core, is no longer able to oppose the gravitational forces. Gravitational compact objects involve white dwarfs, neutron stars, and black holes. The interior structure as well as the physical properties of compact stars are studied adopting the Einstein field equations of general relativity (GR). Schwarzschild presented a first solution capable of describing the interior of the compact body in hydrostatic equilibrium [1].

The stellar core was first assumed to be a fluid with equivalent radial and tangential pressures [2]. However, the chances of generating anisotropies in compact stars are considerably higher due to the existence of strong interactions between particles. In this situation, the inner regions become non-uniform as discussed in [3]. Specifically, it is the fundamental nature of particles which can generate anisotropies. As a result, anisotropic compact stars can become more compact than isotropic stars. The consequences of local variations of relative inner fields were discussed using the equation of state and some interesting results were presented in [4]. Ruderman suggested that a nuclear system with very high densities indicates that anisotropic pressure can emerge in compact stars [5]. In such a case, the radial and tangential pressures are different within the stellar core. These problems can find room in the context of modified gravity.

Due to the issue that GR is not capable to address the whole gravitational phenomenology from ultraviolet to infrared scales, modified and extended theories of gravity have been proposed as effective approaches towards quantum gravity, from one side, and towards astrophysics and cosmology from the other side. These theories are considered very useful to investigate the expansion of the universe as well as the dark energy and dark matter issues which could be explained under the standard of geometrical effects considering curvature and torsion invariants into the gravitational action [6, 6,7,8, 8,9,10,11,12,13,14,15,16]. In particular, the so-called $f\mathcal {(R)}$ gravity has gained special interest due to the fact that it is a straightforward generalization of the Hilbert–Einstein action of GR. Various models of $f\mathcal {(R)}$ gravity have been studied to investigate problems like the late cosmic acceleration [17,18,19], the ghosts of gravitational field [20,21,22], the inflationary epoch [23] and the whole expansion of the universe [24,25,26]. In $f\mathcal {(R)}$ gravity, several basic results have been achieved like the categorizations of singularities, the causal structure and the classification of energy conditions [27,28,29,30,31].

Using such modified theories, it is possible to explain the collapse and stability of astrophysical objects which escape the standard picture of GR. For example the supermassive compact object resulting from the gravitational wave event GW190814 can be framed and interpreted in the context of $f({\mathcal {R}})$ gravity (see [32] and references therein).

In this framework, the study of compact stars has recently become an interesting research topic because observations are reporting several anomalous objects which cannot be explained by GR and standard equations of state. For example, anisotropic compact stars can be analyzed considering GR with a cosmological constant [33]. The compact structure can be discussed considering various forms of the energy density and radial pressure [34]. Singularity-free solution for compact stars can be derived in [35]. The homotopy perturbations procedure can be applied to obtain stable structures [36], and perturbative models of $f\mathcal {(R)}$ gravity have been applied in [37] to study neutron stars. Neutron stars with quarks cores can also be considered, and results can be physically consistent [38]. The quadratic and cubic forms of $f\mathcal {(R)}$ were discussed using numerical methods in [39], while anisotropic compact stars in the context of $f\mathcal {(R)}$ gravity were studied in [40]. Neutron and quark stars are studied in the framework of $f\mathcal {(R)} = {\mathcal {R}}+ \alpha {\mathcal {R}}^2$ while the Brans–Dicke theory is taken into account in [41]. In [42], quark star models are derived with an equation of state in the non-perturbative form of $f\mathcal {(R)}$ gravity.

Besides these results, it is worth noticing that several modified gravities are receiving much attention to cure the shortcomings of GR like the cosmic accelerated expansion, the flat rotation curves of galaxies, possible wormhole solutions and other phenomena [43,44,45,46,47,48]. For example, a quadratic function of the Ricci scalar was studied by Starobinsky to address the inflationary behavior of early universe [49]. It was shown that higher-order $f\mathcal {(R)}$ gravity can solve issues related to supermassive neutron stars [37, 42, 50,51,52]. The easiest way to prescribe $f\mathcal {(R)}$ gravity is assuming an analytic function whose first order is the Ricci scalar. In general, the equations of motion of $f\mathcal {(R)}$ are higher-order in derivatives and supply substantial classes of solutions that are different from GR. In the framework of $f\mathcal {(R)}$ gravity, the dynamical behavior of matter and curvature fields has been studied in several works. See, for example, [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70].

In particular, spherically symmetric vacuum black hole solutions in $f\mathcal {(R)}$ have been derived in [71,72,73,74]. Furthermore, from the existence of Noether symmetries, it is possible to find out other spherically symmetric solutions [75, 76]. Using the same technique, it is possible to achieve also axially symmetric black hole solutions [77]. Non-trivial spherically symmetric black hole solutions for specific classes of $f\mathcal {(R)}$ are derived also in [78,79,80]. Due to the higher-order curvature terms in $f\mathcal {(R)}$, one can discuss strong gravitational fields in local objects. In this framework, many researches concentrate on the study of spherically symmetric black holes [81,82,83,84,85,86,87] and neutron stars [88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108].

Finally, it is worth noticing that $f\mathcal {(R)}$ gravity can be recast as scalar-tensor gravity [109] with a scalar potential of gravitational origin so the further degrees of freedom with respect to GR result as scalar field counterparts in the Einstein field equations [110,111,112,113].

The aim of the present paper is deriving a spherically symmetric inner solution assuming general forms of the Ricci scalar and the $f(R)$ function. After, we want to test the physical reliability of this solution. According to the procedure, it is possible to construct self-consistent compact stellar models capable of describing anisotropic neutron stars.

The layout of the paper is the following: In Sect. 2, a short summary of $f\mathcal {(R)}$ gravity is reported. In Sect. 3, we apply the field equations of $f(R)$ to a spherically symmetric metric with two different potentials for time and radial components. Assuming the form of radial component as well as of the first derivative of $f\mathcal {(R)}$, we are able to obtain the time component of the metric and the $f(\mathcal R)$ function. Starting from this information, we derive the density, the radial and the tangential pressures. In Sect. 4, we impose boundary conditions to match the interior with the exterior solution. We succeed in matching the constants characterizing the solution by a compactness parameter C which satisfies the constrain $C<<0.5$. In Sect. 5, we discuss the physical conditions to show that the model is consistent with a realistic compact star. In Sect. 6, the stability, adopting the Tolman–Oppenheimer–Volkoff (TOV) approach and the adiabatic index, is discussed. We show that the model satisfies both these conditions. The results are matched with observational data in Sect. 7 where we draw the conclusions.

2 A summary of f(R) gravity

In 4-dimension, the action of $f\mathcal {(R)}$ gravity is [114,115,116,117,118,119,120,121,122,123,124,125]:

$$\begin{aligned} {\mathop {{\mathcal {E}}}}:= & {} \frac{1}{2\kappa } \int d^4x \sqrt{-g} f\mathcal {(R)}\nonumber \\&+\frac{1}{2\kappa } \int d^4x \sqrt{-g} {{\mathcal {L}}_M}(g_{\mu \nu },\xi ), \end{aligned}$$

(1)

with the gravitational coupling ${\displaystyle \kappa =\frac{8\pi G}{c^4}}$, where G is the Newtonian constant, c is the speed of light and g is the determinant of the metric. Here $f({\mathcal {R}})$ is an arbitrary function of the Ricci scalar ${\mathcal {R}}$ and ${{\mathcal {L}}_M}(g_{\mu \nu },\xi )$ is the action of generic matter fields $\xi$ which are minimally coupled to the metric $g_{\mu \nu }$. Clearly, GR is recovered for $f({\mathcal R})={{\mathcal {R}}}$.

The variations of action (1) w.r.t. the metric tensor $g_{\mu \nu }$ gives the non-vacuum field equations [126]

$$\begin{aligned} {\mathop {{\mathcal {E}}}}_{\mu \nu }:= & {} {\mathcal {R}}_{\mu \nu } f_{{\mathcal {R}}}-\frac{1}{2}g_{\mu \nu }f\mathcal {( R)}\nonumber \\&+[g_{\mu \nu }\Box -\nabla _\mu \nabla _\nu ]f\mathcal { }_{_{\mathcal {R}}} -\kappa {{\mathcal {T}}}_{\mu \nu }\equiv 0, \end{aligned}$$

(2)

where $\Box$ is the d’Alembert operator and $\displaystyle f\mathcal { }_{_\mathcal { R}}=\frac{ {df}}{d{\mathcal {R}}}$. Here ${{\mathcal {T}}}_{\mu \nu }$ is the energy-momentum tensor, defined as

$$\begin{aligned} {{\mathcal {T}}}_{\mu \nu } =-\frac{2}{\sqrt{-g}}\frac{\delta \mathcal{L_M}}{\delta g^{\mu \nu }}. \end{aligned}$$

(3)

Field Eq.  (2) have the following trace:

$$\begin{aligned} {\mathop {{\mathcal {E}}}}:=3\Box f\mathcal { }_{_\mathcal { R}}+{\mathcal {R}}f\mathcal { }_{_{\mathcal {R}}}-2f\mathcal {(R)} -\kappa {{\mathcal {T}}}\equiv 0 . \end{aligned}$$

(4)

From Eq. (4), one can obtain $f\mathcal {(R)}$ in the form:

$$\begin{aligned} f\mathcal {(R)}=\frac{1}{2}\Big [3\Box {f_{{\mathcal {R}}}} +{\mathcal {R}}{f_{\mathcal {R}}}-\kappa {{\mathcal {T}}}\Big ]. \end{aligned}$$

(5)

Using Eq. (5) in Eq. (2) we get [127]

$$\begin{aligned} {\mathop {{\mathcal {E}}}}_{\mu \nu }:= & {} {\mathcal {R}}_{\mu \nu } F-\frac{1}{4}g_{\mu \nu }{\mathcal {R}}F\nonumber \\&+\frac{1}{4}g_{\mu \nu }\Box F -\nabla _\mu \nabla _\nu F-\kappa \Big ({{\mathcal {T}}}_{\mu \nu } -\frac{1}{4}g_{\mu \nu }{{\mathcal {T}}}\Big ) , \end{aligned}$$

(6)

where

$$\begin{aligned} F= & {} f_{\mathcal {R}}=\frac{ {df}}{d{\mathcal {R}}}=\frac{ {df}}{dr}\frac{dr}{d{\mathcal {R}}}. \end{aligned}$$

(7)

The energy-momentum tensor ${{\mathcal {T}}}_{\mu \nu }$ can be assumed with the following anisotropic form

$$\begin{aligned} { {\mathcal {T}}}_\mu {}^\nu {}=\Big (\frac{p_{t}}{c^2}+\epsilon \Big )u_\mu u^\nu +p_{_{_t}}\delta _\mu {}^\nu +(p-p_{_{_t}})\varepsilon _\mu \varepsilon ^\nu , \end{aligned}$$

(8)

where $u_\mu$ is a time-like vector defined as $u^\mu =[c,0,0,0]$ and $\varepsilon _\mu$ is the unit space-like vector in the radial direction. In this study $\epsilon$ is the energy-density, p and $p_t$ are the radial and the tangential pressures respectively. The energy-momentum tensor takes the diagonal form ${ {\mathcal T}}_\mu {}^\nu {}= diag(-c^2\epsilon ;\,p;\,p_{_{_t}};\, p_{_{_t}})$.

3 Compact stars in $f\mathcal {(R)}$ gravity

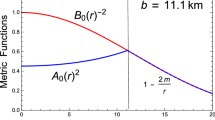
In order to consider relativistic compact stars in $f({{\mathcal {R}}})$ gravity, let us assume the following spherically symmetric space-time:

$$\begin{aligned} ds^2= & {} -e^{a(r)}dt^2+e^{-b(r)}dr^2+r^2d\Omega , \quad {\text{ with }} \quad d\Omega \nonumber \\= & {} (d\theta ^2+\sin ^2d\phi ^2), \end{aligned}$$

(9)

where a(r) and b(r) are unknown functions of the radius. The Ricci scalar of the metric (9) takes the form:

$$\begin{aligned} {\mathcal {R}(r)}=\frac{e^{-b}r[ra'b'-2ra''-ra'^2-4a'+4b'-4]+4}{2r^2},\nonumber \\ \end{aligned}$$

(10)

with $a'=\frac{da}{dr}$, $a''=\frac{d^2a}{dr^2}$ and $b'=\frac{db}{dr}$. For the line–element (9), the non-vanishing components of field Eqs. (4) and (6) have the form:

$$\begin{aligned} {\mathop {{\mathcal {E}}}}_t{}^t= & {} \frac{e^{-a}[e^{a-b}\{Fr^2( 2a''-a'b'+a'^2)+4rF[ra'+rb'-1]+r^2[3a'F'-2F''+F'b']-4rF'\} +4e^{a}F]}{r^2}-\frac{8\pi G}{c^2}\epsilon ,\nonumber \\ {\mathop {{\mathcal {E}}}}_r{}^r= & {} \frac{e^{-b}[Fr^2( 2a''-a'b'+a'^2)-4F[ra'+rb'+1]-r^2[a'F'-6F''+3F'b']-4rF'+4e^{a}F]}{r^2}+\frac{8\pi G}{c^4} p,\nonumber \\ {\mathop {{\mathcal {E}}}}_\theta {}^\theta= & {} {\mathop {{\mathcal {E}}}}_\phi {}^\phi =\frac{F[4-e^{-b}(4-2r^2a''+r^2a'b'-r^2a'^2)] +e^{-b}[r^2a'b'+2r^2F''-r^2F'b'-4rF']}{r^2}-\frac{8\pi G}{c^4} p_{_{_t}},\nonumber \\ {\mathop {{\mathcal {E}}}}= & {} \frac{8\pi G}{c^4}[p+2p_{_{_t}}-c^2\epsilon ]+\frac{1}{r^2}\Big [e^{-b}[r^2(6F''-2Fa''-Fa'^2)+r[r\,F\, b'+3rF'-4F]a'\nonumber \\&+r\beta '[4F-3rF']+12rF'-4F)+4(F-f)\Big ]. \end{aligned}$$

(11)

Moreover, we introduce the characteristic density

$$\begin{aligned} \epsilon _\star \equiv \frac{c^2}{8\pi G R_0^2}, \end{aligned}$$

(12)

where $R_0$ is a characteristic radius. It can be used to re-scale the density, the radial and the tangential pressure respectively. We get the dimensionless variables

$$\begin{aligned} {\hat{\epsilon }} = \frac{\epsilon }{\epsilon _\star }, \quad {\hat{p}} = \frac{p}{\epsilon _\star c^2}, \quad {\hat{p}}_t = \frac{p_t}{\epsilon _\star c^2}. \end{aligned}$$

(13)

Equation (11) are four non-linear differential equations in six unknown variables a, b, F $\epsilon$, p and $p_{_{_t}}$. Using ${\mathop {{\mathcal {E}}}}_r{}^r$ and ${\mathop {\mathcal { E}}}_\theta {}^\theta$, one can define the anisotropy parameter of stellar structure as:

$$\begin{aligned} \Delta (r)= & {} \frac{8\pi G}{c^4}\Big [p_{_{_t}}-p\Big ]\nonumber \\= & {} \frac{e^{-b}\Big (2Fr^2a''+4r^2F'' +r^2Fa'^2-r\,F\,a'[rb'+2]-2[rb'+2][rF'+F]\Big )+4F}{4r^2}, \end{aligned}$$

(14)

which reduces to $\Delta (r)=0$ for isotropic systems. In order to find a physical solution of the above system of differential equations, let us assume the following forms for the radial component of metric potential $g_{rr}$ and the $f({\mathcal {R}})$ derivative function F as:

$$\begin{aligned} b(y)=c_0 y^2,\quad F(y)=1+c_1y^2. \end{aligned}$$

(15)

This choice is physically motivated for the following reasons. Here y is a dimensionless variable

$$\begin{aligned} y\equiv \frac{r}{l} \in [0, 1], \end{aligned}$$

(16)

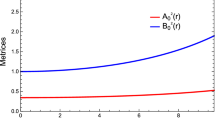
and we assume the star can extend up to the maximal radius $r =l$. The parameters $c_0$ and $c_1$ are dimensionless.They will be determined later. Equation (15) show that when $c_1=0$, we recover GR. In other words, the constant $c_1$ is responsible for the deviation from GR. Using Eqs. (15) into (14), we get the metric potential $g_{tt}$ as

$$\begin{aligned} a(y)=2ln\Big (\frac{c_0c_2+c_3e^{c_0y^2/2}}{2c_0}\Big ), \end{aligned}$$

(17)

where $c_2$ and $c_3$ are given by combinations of the parameters $c_{0}$, $c_{1}$ and l. The anisotropy parameter $\Delta (y)$ has the form

$$\begin{aligned} \Delta (y)= & {} \frac{1+y^2l^2c_1-[1+y^2l^2c_1+c_0y^2l^2+3y^2l^4c_0c_1]e^{-c_0y^2l^2}}{y^2l^2}.\nonumber \\ \end{aligned}$$

(18)

Using Eqs. (15) and (17) in Eq. (11), we get the exact form of energy, radial and tangential pressures that we report in Appendix A.

Inserting Eq. (15) in the last equation of system (11), the trace of the field Eqs. (6), we get a very lengthy differential equation in the unknown $f({\mathcal {R}})$. We report the full equation in Appendix C. Developing such a differential equation up to the first order in $\mathcal{O}\Bigg (\frac{1}{y}\Bigg )$, we get all the information we need for our purposes. It is

$$\begin{aligned} \frac{1}{2c_0{}^2ym^2}\left( 3mm_1{}^2f'''+15c_0m_1m_2f'\right) \approx 0, \end{aligned}$$

(19)

where $m=5c_0{}^2c_2{}^2+7c_0c_2c_3-c_3{}^2$, $m_1=c_3+c_0c_2$ and $m_2=173c_0{}^3c_2{}^3+138c_0{}^2c_2{}^2c_3{}+48c_0c_2c_3{}^2-8c_3{}^3$. The solution of the above differential equation takes the form

$$\begin{aligned} f(y)=c_4+c_5\sin \Bigg (\frac{\sqrt{c_0m_2}y}{\sqrt{3m\,m_0}}\Bigg )+c_6\cos \Bigg (\frac{\sqrt{c_0m_2}y}{\sqrt{3m\,m_0}}\Bigg ),\nonumber \\ \end{aligned}$$

(20)

where $c_4$, $c_5$ and $c_6$ are integration constants. For $c_{5}$, the solution (20) is compatible with F(y), given by Eq. (15), up to the leading order. Equations of density, radial and tangential pressures show that, for $c_1=0$, we return to GR. This is due to the fact that, for $F=1$, we have $f({\mathcal {R}})={\mathcal {R}}$. This means that differences with GR come from $c_1\ne 0$. See Appendix A.

Using Eqs. (15) and (17), we get the Ricci scalar, up to the leading order, in the form

$$\begin{aligned} {\mathcal {R}}\approx & {} \frac{6c_0{}^2}{m_1}-\Bigg [\frac{6c_0{}^3c_3}{m_1{}^2}+\frac{c_0{}^2[c_0c_3+5c_0{}^2-c_3{}^2]}{m_1{}^2}\Bigg ]y^2+\cdots \, ,\nonumber \\&\,\, \text{ which } \text{ leads } \text{ to } \,\, y\approx \pm \sqrt{\frac{6c_0{}^2m_1-{\mathcal R}\,m_1{}^2}{6c_0{}^3c_3+c_0{}^2[c_0c_3+5c_0{}^2-c_3{}^2]}}+\cdots .\nonumber \\ \end{aligned}$$

(21)

Using Eq. (21) into Eq. (20), we get the explicit form of $f({{\mathcal {R}}})$, that is

$$\begin{aligned} f({\mathcal R})=c_4+c_6\cos \left( \frac{\sqrt{m_2(6c_0{}^2m_1-{\mathcal R}\,m_1{}^2)}}{\sqrt{3m\,m_0({6c_0{}^2c_3{+}c_0[c_0c_3{+}5c_0{}^2{-}c_3{}^2]})}}\right) .\nonumber \\ \end{aligned}$$

(22)

Fig. 1

Density, radial and transverse pressures when $c_1=0$ and $c_1=0.5$

4 Matching conditions

The solution given in Appendix A has a non-trivial Ricci scalar as shown by Eq. (21). Let us match it with the exterior solution. To this aim, we are going to match solution given in Appendix A with the one presented in [80] that we report here:

$$\begin{aligned} ds^2= & {} -\Big (\frac{1}{2}-\frac{2MG}{c^2r}\Big )dt^2\nonumber \\&+\Big (\frac{1}{2}-\frac{2MG}{c^2r}\Big )^{-1}dr^2+r^2d\Omega ^2, \end{aligned}$$

(23)

where M is the total stellar mass and $4MG<c^2r$. We have to match the interior spacetime metric (9), using Eqs. (15) and (17), with the exterior Schwarzschild spacetime metric given by Eq. (23) at the boundary of the star, $r =l$. The continuity of the metric functions across the boundary $r =l$ gives

$$\begin{aligned} a(r=l)= & {} ln\Bigg (\frac{1}{2}-\frac{2GM}{c^2l}\Bigg ), \nonumber \\ b(r=l)= & {} ln\Bigg (\frac{1}{2}-\frac{2GM}{c^2l}\Bigg )^{-1}. \end{aligned}$$

(24)

Using the above conditions, we get the constraints on the constants $c_0$, $c_2$. These constants take the form

$$\begin{aligned} c_0= & {} -ln\Bigg (1/2-C\Bigg ), \nonumber \\ c_2= & {} \frac{c_3+2\Bigg (1/2-C\Bigg )\ln \Bigg (1/2-C\Bigg )}{\sqrt{\Bigg (1/2-C\Bigg )}\ln \Bigg (1/2-C\Bigg )}, \end{aligned}$$

(25)

where $C=\frac{2GM}{c^2l}$. Equation (25) shows that the compactness parameter must be $C<0.5$. This is also a consistency condition.

Fig. 2

Anisotropy $\Delta (y)$ and anisotropy force when $c_1=0$ and $c_1=0.5$

Fig. 3

The gradient of density, radial and transverse pressures when $c_1=0$ and $c_1=0.5$

5 The physical viability of solution

Now we are going to test if the interior solution, reported in Appendix A, can describe a realistic physical star. To this aim, we have to derive some necessary conditions which have to hold for any realistic star. They are the following.

5.1 Energy–momentum tensor

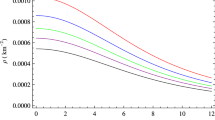
It is well-known that, for a realistic interior solution, the energy–density, the radial and transverse pressures must be positively defined. Moreover, all the components of the energy-momentum tensor should be finite at the center of the star then become decreasing in the direction of the surface of the stellar structure and the radial pressure should exceeds the tangential one.¹ The plots of the energy-momentum components, density, radial and transverse pressures are shown in Fig. 1. The values of parameters used in the figure are: ${\hat{\epsilon }}(y=0)_{c_1=0,c_3=0.5}=4.481840660$, ${\hat{\epsilon }}(y=0)_{c_1=0.5,c_3=0.5}=3.731840660$, ${\hat{p}}(y=0)_{c_1=0,c_3=0.5}={\hat{p}}_t(y=0)_{c_1=0,c_3=0.5}=1.493946887$, ${\hat{p}}(y=0)_{c_1=0.5,c_3=0.5}={\hat{p}}_t(y=0)_{c_1=0,c_3=0.5}=1.243946887$. Figure 1 shows that the density, radial and tangential pressures are decreasing towards the stellar surface. Moreover Fig. 1 shows that the values of the components of the energy momentum at the center, in case $c_1=0$, are greater than those for $c_1\ne 0$. We can also deduce, from Fig. 1, that density, radial and tangential pressures converge to the surface of the star more rapidly in case $c_1=0$ than in the case of $c_1=0.5$. Finally, it is easy to see that, when $c_1=0$, one gets ${\hat{p}}={\hat{p}}_t$ at the center however, as we reach the surface of the star, we can see that ${\hat{p}}_t\ge {\hat{p}}$.

In Fig. 2, we show the behavior of the anisotropy parameter which is defined as $\Delta (y)={\hat{p}}_t-{\hat{p}}$. Also Fig. 2 shows that the anisotropic force is positive. This means that a repulsive force, due to $p_t\ge p$, is present.

Fig. 4

Radial, transverse sound speeds and ${|}v_r{}^2-v_t{}^2{|}$ for $c_1=0$ and $c_1=0.5$

Fig. 5

DEC for $c_1=0$ and $c_1=0.5$

5.2 Causality

In order to show the behavior of sound velocities, we must calculate the gradient of energy–density, radial and transverse pressures that take the forms given in Appendix B. Let us analyze the gradient of energy-momentum tensor components reported in Appendix B. The asymptotic forms are

$$\begin{aligned}&{\hat{\epsilon }}'\approx \frac{c_0[26c_1c_3{}^2{-}11c_0c_3{}^2{+}40c_0c_1c_2c_3{-}13c_0{}^2c_2c_3{}^2{-}5c_0{}^3c_2{}^2+14c_0{}^2c_1c_2{}^2]}{2[c_1{}+c_0c_2]},\nonumber \\&{\hat{p}}'\approx \frac{c_0[14c_1c_2{}^2-5c_0c_3{}^2+24c_0c_1c_2c_3-7c_0{}^2c_2c_3-3c_0{}^3c_2{}^2+10c_0{}^2c_1c_2{}^2]}{2[c_1{}+c_0c_2]},\nonumber \\&{\hat{p}}'_t\approx \frac{c_0[6c_1c_3{}^2-3c_0c_3{}^2+8c_0c_1c_2c_3-3c_0{}^2c_2c_3-c_0{}^3c_2{}^2+2c_0{}^2c_1c_2{}^2]}{2[c_1{}+c_0c_2]},\nonumber \\ \end{aligned}$$

(26)

which give a negative gradient of the energy-momentum components provided that $c_0>c_1\ge c_2>c_3$. This condition is satisfied according to the choice in footnote 1. The behavior of density, radial and tangential pressure gradients are shown in Fig. 3. To ensure that causality conditions, either for the radial and transverse sound speeds $v_r{}^2$ and $v_\bot {}^2$, have values less than the speed of light, we use equations reported in given in Appendix B and get

$$\begin{aligned}&v_r{}^2=\frac{{\hat{p}}'}{{\hat{\epsilon }}'} \nonumber \\&\quad \approx \frac{14c_1c_3{}^2-5c_0c_3{}^2-7c_0{}^2c_2c_3+24c_0c_1c_2c_3-3c_0{}^3c_2{}^2+10c_0{}^2c_1c_2{}^2}{26c_1c_3{}^2-11c_0c_3{}^2-13c_0{}^2c_2c_3+40c_0c_1c_2c_3-5c_0{}^3c_2{}^2+14c_0{}^2c_1c_2{}^2}, \nonumber \\&v_t{}^2=\frac{{\hat{p}}'_t}{{\hat{\epsilon }}'}\nonumber \\&\quad \approx \frac{6c_1c_3{}^2-3c_0c_3{}^2-3c_0{}^2c_2c_3+8c_0c_1c_2c_3-c_0{}^3c_2{}^2+2c_0{}^2c_1c_2{}^2}{26c_1c_3{}^2-11c_0c_3{}^2-13c_0{}^2c_2c_3+40c_0c_1c_2c_3-5c_0{}^3c_2{}^2+14c_0{}^2c_1c_2{}^2}.\nonumber \\ \end{aligned}$$

(27)

Equation (27) show that both the conditions $1>v_r{}^2>0$ and $1>v_t{}^2>0$ hold using the choice in footnote 1. The behaviour of the radial and tangential sound speeds are shown in Fig. 4a, b.

The appearance of non–vanishing total radial force with different signs in different regions of the fluid is called gravitational cracking when this radial force is directed inward in the inner part of the sphere for all values of the radial coordinate r between the center and some value beyond which the force reverses its direction [128]. In Ref. [129], it is stated that a simple requirement to avoid gravitational cracking is $0< v_r{}^2-v_t{}^2<c^2$. In Fig. 4c, we show that the solution given in Appendix A is stable against cracking for $c_1=0$ and $c_1=0.5$.

5.3 Energy conditions

Energy conditions are considered an important test for non–vacuum solutions. To satisfy the dominant energy condition (DEC), we have to prove that ${\hat{\epsilon }}-{\hat{p}} >0$ and ${\hat{\epsilon }}-{\hat{p}}_t>0$. As shown in Fig. 5a, b, DEC is satisfied for suitable choices of parameter $c_1$. Furthermore, the weak energy condition (WEC), ${\hat{\epsilon }}+{\hat{p}}>0$ ${\hat{\epsilon }}+{\hat{p}}_t>0$ and the strong energy condition (SEC), ${\hat{\epsilon }}-{\hat{p}}-2{\hat{p}}_t>0$ are satisfied as shown in Fig. 6a–c.

Fig. 6

WEC and SEC of the solution given in Appendix A for $c_1=0$ and $c_1=0.5$

Fig. 7

The gravitational mass and compactification factor of solution given in Appendix A for $c_1=0$ and $c_1=0.5$

Fig. 8

The radial and transverse EoS when $c_1=0$ and $c_1=-0.01$

5.4 Mass–radius relation

The compactification factor u(r) is defined as the ratio between the mass and radius. It has a key role to understand physical properties of compact objects. Starting from the solution given in Appendix A, we can define the gravitational mass as

$$\begin{aligned} M(y)= & {} {\int _0}^y \hat{{\hat{\epsilon }}} \zeta ^2 d\zeta =\frac{1}{8yc_0{}^{5/2}c_2{}^2}\Bigg [4yc_0{}^{5/2}c_2{}^2\nonumber \\&\times \int \frac{3c_3{}^3(2y^2c_1+1)}{c_0c_2{}^2(c_3+c_0c_2e^{-c_0y^2/2})}dr\nonumber \\&-24c_0{}^{3/2}c_1c_2c_3y^2 e^{-c_0y^2/2}\nonumber \\&+6c_0c_2c_3\sqrt{2}(c_0+2c_1)\,\sqrt{\pi }\,erf(y\sqrt{c_0/2})\nonumber \\&+2c_0^{5/2}c_2{}^2e^{-c_0y^2}[1-3c_1y^2]+yc_2{}^2(8c_0-5c_1)c_0{}^2\,\nonumber \\&\times \sqrt{\pi }\,erf(y\sqrt{c_0})+4c_0{}^{3/2}\{c_0c_2{}^2(y^2c_1-1)\nonumber \\&-2c_1c_2{}^2y^4-3c_3{}^2y^2\}\Bigg ], \end{aligned}$$

(28)

where erf(x) is the error function that is defined as

$$\begin{aligned} erf(x)=\frac{2}{\sqrt{\pi }}\int _0^x e^{-t^2}dt. \end{aligned}$$

(29)

The compactification factor u(r) is then defined as

$$\begin{aligned}&u(y)=\frac{M(y)}{l}. \end{aligned}$$

(30)

Using Eq. (28) into (30), one can get the explicit form of the compactification factor. The behavior of the gravitational mass and the compactification factor are plotted in Fig. 7. Figure 7a shows that the gravitational mass increases when the radial coordinate increases while Fig. 7b shows that the compactification factor decreases for increasing radial coordinate.

5.5 Equation of state

The study of equation of state (EoS) for neutral compact stellar objects is reported in [130] . In that case, EoS is linear. In the present case, we will show that EoS cannot non-linear. To investigate this issue, we define the radial and transverse EoS as:

$$\begin{aligned} \omega _r= & {} \frac{{\hat{p}}}{{\hat{\epsilon }}}, \quad \omega _t=\frac{{\hat{p}}_t}{{\hat{\epsilon }}}, \end{aligned}$$

(31)

where $\omega _r$ and $\omega _t$ are the radial and transverse EoS. Using equations in Appendix A, one can calculate the analytical form of $\omega _r$ and $\omega _t$ whose behaviors are plotted in Fig. 8. As Fig. 8a, b show, EoS are non-linear because of the contribution of the higher–order curvature terms.

Fig. 9

The TOV of solution when $c_1=0$ and $c_1=0.5$

Fig. 10

The adiabatic index of solution given in Appendix A for $c_1=0$ and $c_1=0.5$

6 Stability of the model

In order to study the stability problem we are going to use two different procedures; the first one is the Tolman–Oppenheimer–Volkoff (TOV) equation and the second is the study of the adiabatic index.

6.1 The Tolman–Oppenheimer–Volkoff equation

To study the stability of solution in Appendix A, let us assume the hydrostatic equilibrium by using the TOV equation [131, 132] as presented in [133]. It is

$$\begin{aligned} \frac{2[{\hat{p}}_t-{\hat{p}}]}{y}- & {} \frac{M_g(y)[{\hat{\epsilon }}(y) +{\hat{p}}_t(y)]e^{[a(y)-b(y)]/2}}{y}\nonumber \\- & {} \frac{d{\hat{p}}(y)}{y}=0, \end{aligned}$$

(32)

where $M_g(y)$ is the gravitational mass calculated at the radius y. It has the following equation

$$\begin{aligned} M_g(y)= & {} 4\pi {\int _0}^y\Big ({{{\mathcal {T}}}_t}^t{-}{{{\mathcal {T}}}_r}^r{-}{{{\mathcal {T}}}_\theta }^\theta {-}{{{\mathcal {T}}}_\phi }^\phi \Big )y^2e^{[a(y)+b(y)]/2}dy\nonumber \\= & {} \frac{y a' e^{[b(y)-a(y)]/2}}{2}, \end{aligned}$$

(33)

Inserting Eq. (33) into (32), we get

$$\begin{aligned}&\frac{2({\hat{p}}_t-{\hat{p}})}{y} -\frac{d{\hat{p}}}{dy}-\frac{a'[{\hat{\epsilon }}(y)+{\hat{p}}(y)]}{2}\nonumber \\&\quad =F_g+F_a+F_h=0, \end{aligned}$$

(34)

where $F_g=-\frac{a'[{\hat{\epsilon }}+{\hat{p}}]}{2}$, $F_a=\frac{2({\hat{p}}_t-{\hat{p}})}{y}$ and $F_h=-\frac{d{\hat{p}}(y)}{dy}$ are the gravitational, the anisotropic and the hydrostatic forces respectively. The behavior of TOV equation, for the model given in Appendix A, is shown in Fig. 9. This figure shows that hydrostatic and anisotropic forces are positive and dominated on the gravitational force which is negative to keep the system in static equilibrium either when $c_1=0$ or $c_1=0.5$.

6.2 The adiabatic index

The adiabatic index $\gamma$ is defined as [134, 135]

$$\begin{aligned} \gamma =\left( \frac{{\hat{\epsilon }}+{\hat{p}}}{{\hat{p}}}\right) \frac{d{\hat{p}}}{d{\hat{\epsilon }}}. \end{aligned}$$

(35)

It allows to link the structure of a spherically symmetric static object and the EoS of the interior solution. It can be used to investigate the stability [136]. Any interior solution is stable if its adiabatic index is greater than 4/3 [137]. If $\gamma =\frac{4}{3}$, then the isotropic sphere is in neutral equilibrium. Following Chan et al. [138], the stability condition of a relativistic anisotropic sphere, $\gamma >\Gamma$, must be satisfied. Here it is

$$\begin{aligned} \Gamma= & {} \frac{4}{3}-\left\{ \frac{4({\hat{p}}-{\hat{p}}_t)}{3|{\hat{p}}'|}\right\} _{max}. \end{aligned}$$

(36)

The behaviour of the adiabatic index is shown in Fig. 10 which ensures the stability condition of our solution.

Table 1 The boundary density $\rho _l$ and slope of the radial pressure reported for various observed objects. The density and the derivative of radial pressure are derived for the values $c_1=0$ and $c_1=0.5$ at the stellar boundary l assuming a nuclear density of the order $10^{15}\,g/cm^3$

7 Discussion and conclusions

In this study, we derived an anisotropic spherically symmetric solution in the framework of $f\mathcal {(R)}$ gravity. To this aim, we used a line element containing two unknown functions and applied it to the field equations of $f\mathcal {(R)}$ deriving four non-linear differential equations: three of them are the field equations and the fourth one is the trace of the field equations. This system involves six unknown functions, two of them are the metric potentials, one is the form of $f\mathcal {(R)}$ and the other are the density, and radial and tangential pressures. We solved these differential equations assuming the forms of the radial component of the metric and of the derivative of $f\mathcal {(R)}$. Substituting these quantities in the anisotropy parameter, $\Delta ={\hat{p}}_t-{\hat{p}}_r$, we get the time component of the metric. From these results, we obtained the form of $f\mathcal {(R)}$, the density, radial, and tangential pressures. It is interesting to mention that our solution is characterized by a constant $c_1$ which parameterize the deviation with respect to GR. Specifically, for $c_1=0$, we return to GR.

Due to the fact that the obtained interior solution has a non-trivial form for the Ricci scalar, we match it with a spherically-symmetric exterior solution having also a non-trivial form of Ricci scalar. From this matching, it is possible to relate the mass and the maximal radius of the compact object with the compactness parameter, that is $C=\frac{2GM}{c^2l}$ which must be $C<<0.5$ for the physical consistency of the model. The further step is to see if this solution represents a realistic star. To this aim, we discussed the necessary conditions required by any physically consistent compact stellar object and show that our model satisfies all these conditions. In particular, we considered two cases: one for $c_1=0$ and another for $c_1=0.5$.

Finally, we checked if the model satisfies the stability conditions. To this aim, we derived the TOV equation and showed that it is in static equilibrium either when $c_1=0$ or $c_1=0.5$. We also studied the adiabatic index to complete the picture of the stability and showed that the model satisfies the adiabatic index $\gamma >4/3$.

These results can be applied to the observational data of different millisecond pulsars with white dwarf companions and pulsars presenting thermonuclear bursts as reported in Table 1.

For these objects, it is possible to calculate the density at the center and at the surface and then derive the EoS at the center and at the surface. It is interesting to see that, in the case of millisecond pulsars with a white dwarf companion, and, in the case of pulsars presenting thermonuclear bursts, our solution is compatible with observations. From the observational data in literature, as reported in the Table 1, it is possible to derive the total mass and the radius of the given pulsar.

To conclude, we derived an interior solution in the framework of $f\mathcal {(R)}$ assuming physically motivated conditions to obtain the form of $f\mathcal {(R)}$. This solution has a non-trivial form of the Ricci scalar. The internal solution can be matched with the external one considering compacteness and anisotropy parameters. In a forthcoming paper, we will consider a similar situation assuming a charged interior solution.

Appendices

Appendix A: Energy density, radial and tangential pressures.

Let us report now the quantities related to the interior solution discussed in this paper.

$$\begin{aligned} {\hat{\epsilon }}(y)= & {} \frac{1}{2y^2[c_3{}^4e^{2c_0y^2}+4c_3{}^3c_2c_0e^{3c_0y^2/2}+6c_3{}^2c_2{}^2c_0{}^2e^{c_0y^2}+4c_3c_2{}^3c_0{}^3e^{c_0y^2/2}+c_2{}^4c_0{}^4]} \nonumber \\&\times \Big [c_0c_2c_3e^{c_0y^2/2}(4c_2{}^2c_0{}^2[c_1y^2+1]+c_3{}^2c_0y^2[30c_1y^2+17]-4c_3{}^2[4c_1y^2+1])\nonumber \\&+c_0{}^3c_2{}^3c_3e^{-c_0y^2/2}[c_0y^2(11+18c_1y^2)-4-16c_1y^2]+ 4c_3{}^3c_2c_0e^{3c_0y^2/2}(c_1y^2+1)\nonumber \\&+c_0{}^4c_2{}^4e^{-c_0y^2}[y^2c_0(2+3c_1y^2)-4c_1y^2-1]+c_3{}^4e^{2c_0y^2}(c_1y^2+1)+c_3{}^2e^{c_0y^2}[6c_0{}^2c_2{}^2 (c_1y^2+1)\nonumber \\&+c_0{}^2c_3{}^2y^2(9c_1y^2+5) -c_3{}^2(4c_1y^2+1)]+c_0{}^2c_2{}^2[c_0{}^2c_2{}^2(c_1y^2+1)\nonumber \\&+3c_0c_3{}^2y^2(12c_1y^2+7)-6c_3{}^2(4c_1y^2+1)]\Big ], \nonumber \\ {\hat{p}}(y)= & {} \frac{e^{-c_0y^2}\Big \{c_3e^{c_0y^2/2}[1+c_0y^2(3+7c_1y^2)] -c_3e^{3c_0y^2/2}[1+c_1y^2]+c_0c_2[1-e^{c_0y^2}(1+c_1y^2)+c_0y^2(2+c_1y^2)]\Big \}}{2y^2[c_0c_2+c_3e^{c_0y^2/2]}}, \nonumber \\ {\hat{p}}_{_{_t}}(y)= & {} \frac{1}{2y^2[c_3{}^4e^{2c_0y^2}+4c_3{}^3c_2c_0e^{3c_0y^2/2}+6c_3{}^2c_2{}^2c_0{}^2e^{c_0y^2}+4c_3c_2{}^3c_0{}^3e^{c_0y^2/2}+c_2{}^4c_0{}^4]}\nonumber \\&\times \Big [c_0c_2c_3e^{c_0y^2/2}[4c_0{}^2c_2{}^2(1+c_1y^2) +c_0c_3{}^2y^2(3+2c_1y^2)-4c_3{}^2(1+2c_1y^2)]\nonumber \\&-c_0{}^3c_2{}^3c_3e^{-c_0y^2/2}[4(1+2c_1y^2)-c_0y^2(1-2c_1y^2)]+4c_0c_2c_3{}^3e^{3c_0y^2/2}[1+c_1y^2]\nonumber \\&-c_0{}^4c_2{}^4e^{-c_0y^2}[1+2c_1y^2+c_1c_0y^4]+c_3{}^4e^{2c_0y^2}(1+c_1y^2)\nonumber \\&+c_3{}^2e^{c_0y^2}[6c_0{}^2c_2{}^2(1+c_1y^2)+c_3{}^2c_0y^2(1+c_1y^2)- c_3{}^2(1+2c_1y^2)]\nonumber \\&+c_0{}^2c_2{}^2[c_2{}^2c_0{}^2(1+c_1y^2)+3c_0c_3{}^2y^2-6c_3{}^2(1+2c_1y^2]\Big ]. \end{aligned}$$

(A)

Appendix B: The gradients of energy–density, radial and transverse pressures.

The same as above for gradients.

$$\begin{aligned} {\hat{\epsilon }}'= & {} \frac{1}{2y^3[c_0c_2+c_3e^{c_0y^2/2}][c_0{}^2c_2{}^2+c_3{}^2e^{c_0y^2}+2c_0c_2c_3e^{c_0y^2/2}]^2}\nonumber \\&\times \Bigg [c_0{}^2c_2{}^2c_3e^{c_0r^2/2}\Big (20c_3{}^2+4c_0c_3{}^2y^2(53c_1y^2+5)\nonumber \\&-c_0{}^2\Big [10c_2{}^2+c_3{}^2y^4(114c_1y^2+67)\Big ]\Big )+2e^{3c_0y^2/2}[c_3{}^5\nonumber \\&+ c_0c_3{}^5y^2(1+13c_1y^2)-c_0{}^2c_3{}^3(c_2{}^2+c_3{}^2y^4\{5+9c_1y^2\})]\nonumber \\&+c_0{}^4c_2{}^4c_3e^{-c_0y^2/2}\Big [10-c_0{}^2y^4(23+36c_1y^2)\nonumber \\&+2c_0y^2(41c_1y^2+5)\Big ]-2c_3{}^5e^{5c_0y^2/2}+c_0c_2\Big \{2c_0{}^4c_2{}^4e^{-c_0y^2}\nonumber \\&\times (1-y^4c_0{}^2[2+3c_1y^2]+c_0y^2[1+7c_1y^2])+10c_3{}^4e^{2c_0y^2}\nonumber \\&+c_3{}^2e^{c_0y^2}[\{c_3{}^2y^4 (72c_1y^2+41)+10c_2{}^2\}c_0{}^2\nonumber \\&-2c_3{}^2y^2(5+59c_1y^2)-10c_3{}^2]+c_0{}^2c_2{}^2\Big [\Big \{5c_3{}^2y^4\Big (18c_1y^2+11\Big )\nonumber \\&+2c_2{}^2\Big \}c_0{}^2-4c_0c_3{}^2y^2(5+47c_1y^2)-20c_3{}^2\Big ]\Big \}\Bigg ],\nonumber \\ {\hat{p}}'= & {} -\frac{1}{2y^3[c_0{}^2c_2{}^2+c_3{}^2e^{c_0y^2}+2c_0c_2c_3e^{c_0y^2/2}]}\nonumber \\&\times \Bigg [e^{-c_0y^2}\Big [c_0c_2c_3e^{c_0y^2/2}\{4+c_0y^4[9+22c_1y^2]\nonumber \\&+4c_0y^2[1-6c_1y^2]\}-2c_3{}^2e^{2c_0y^2} -4c_0c_2c_3e^{3c_0y^2/2}\nonumber \\&+2e^{c_0y^2}(c_3{}^2+c_0c_3{}^2y^2[1-c_1y^2]\nonumber \\&+c_0{}^2[c_3{}^2y^4(3+7c_1y^2)-c_2{}^2])\nonumber \\&+2c_0{}^2c_2{}^2\Big \{1+c_0{}^2y^4[2+5c_1y^2]+c_0y^2[1-5c_1y^2]\Big \}\Big ]\Bigg ]\,,\nonumber \\ {\hat{p}}'_t= & {} \frac{1}{2y^3[c_0c_2+c_3e^{c_0y^2/2}][c_0{}^2c_2{}^2+c_3{}^2e^{c_0y^2}+2c_0c_2c_3e^{c_0y^2/2}]^2}\nonumber \\&\times \Bigg [c_0{}^2c_2{}^2c_3e^{c_0r^2/2}\Big (20c_3{}^2+4c_0c_3{}^2y^2(11c_1y^2+5)\nonumber \\&-c_0{}^2\Big [10c_2{}^2-c_3{}^2y^4(2c_1y^2-9)\Big ]\Big )\nonumber \\&+2e^{3c_0y^2/2}c_3{}^3[c_3{}^2+c_0c_3{}^2y^2(1+3c_1y^2)\nonumber \\&-c_0{}^2\{10c_2{}^2+c_3{}^2y^4(1+c_1y^2)\}]+c_0{}^4c_2{}^4c_3e^{-c_0y^2/2}[10\nonumber \\&+c_0{}^2y^4(8c_1y^2-1)+2c_0y^2(5+7c_1y^2)]-2c_3{}^5e^{5c_0y^2/2}\nonumber \\&+c_0c_2\Big \{2c_0{}^4c_2{}^4e^{-c_0y^2}(1+c_0y^2) (1+c_0c_1y^4)\nonumber \\&-10c_3{}^2e^{2c_0y^2}+e^{c_0y^2}[10c_3{}^4+2c_0c_3{}^4y^2(5+13c_1y^2)\nonumber \\&-c_0{}^2(20c_2{}^2c_3{}^2+c_3{}^4y^4\{7+4c_1y^2\})]\nonumber \\&+c_0{}^2c_2{}^2\Big [5c_3{}^2y^4 (2c_1y^2-1)-2c_2{}^2\nonumber \\&+4c_0c_3{}^2y^2(5+9c_1y^2)+20c_3{}^2\Big ]\Big \}\Bigg ], \end{aligned}$$

(B)

where ${\hat{\epsilon }}'=\frac{d{\hat{\epsilon }}}{dy}$,  ${\hat{p}}'=\frac{d{\hat{p}}}{dy}$   and ${\hat{p}}'_t=\frac{d{\hat{p}}_t}{dy}$.

Appendix C: Derivation of Eq. (19)

Equation (15) can be inserted in the last equation of system (11), the trace (6). We get a lengthy differential equation in y which we report here for the sake of completeness. It is

$$\begin{aligned}&f'''(y)\; \Bigg \{ {\frac{75}{2}}\,{{ c_2}}^{5}{ c_3}\, \Bigg ( \left( {y}^{8}{{ c_3}}^{4}+{\frac{58}{25}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}+1/15\,{ { c_2}}^{4} \right) {{ c_0}}^{4}\\&\quad + \left( -8/5\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2}-{\frac{77}{25}}\,{y}^{6}{{ c_3}}^{4} \right) {{ c_0}}^{3}\\&\quad + \left( -8/5\,{{ c_3}}^{2}{{ c_2}}^{2}-7/5\,{{ c_3} }^{4}{y}^{4} \right) {{ c_0}}^{2}\\&\quad +{\frac{84}{25}}\,{{ c_3}}^{4}{ c_0}\,{y}^{2}+{\frac{42}{25}}\,{{ c_3}}^{4} \Bigg ) {{ c_0}}^{ 5}{{ e}^{-1/2\,{ c_0}\,{y}^{2}}}\\&\quad -{\frac{63}{8}}\,{{ c_2}}^{3} \Bigg ( \left( {y}^{8}{{ c_3}}^{4}-{\frac{44}{3}}\,{{ c_3}}^{2}{ { c_2}}^{2}{y}^{4}-{\frac{80}{21}}\,{{ c_2}}^{4} \right) {{ c_0 }}^{4}\\&\quad + \left( {\frac{40}{21}}\,{y}^{6}{{ c_3}}^{4}+16\,{{ c_3}}^ {2}{{ c_2}}^{2}{y}^{2} \right) {{ c_0}}^{3}\\&\quad + \left( 16\,{{ c_3}} ^{2}{{ c_2}}^{2}-{\frac{40}{21}}\,{{ c_3}}^{4}{y}^{4} \right) {{ c_0}}^{2}\\&\quad -{\frac{160}{21}}\,{{ c_3}}^{4}{ c_0}\,{y}^{2}-{ \frac{80}{21}}\,{{ c_3}}^{4} \Bigg ) {{ c_3}}^{3}{{ c_0}}^{3}{ { e}^{1/2\,{ c_0}\,{y}^{2}}}\\&\quad +1/4\,{ c_2}\,{{ c_3}}^{5}{ c_0 }\, \Bigg ( \left( 252\,{{ c_2}}^{4}+60\,{{ c_3}}^{2}{{ c_2}}^{2 }{y}^{4}+{y}^{8}{{ c_3}}^{4} \right) {{ c_0}}^{4}\\&\quad + \left( -240\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2}+11\,{y}^{6}{{ c_3}}^{4} \right) {{ c_0}}^{3}\\&\quad + \left( 21\,{{ c_3}}^{4}{y}^{4}-240\,{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{2}\\&\quad +20\,{{ c_3}}^{4}{ c_0}\,{y}^{2 }+10\,{{ c_3}}^{4} \Bigg ) {{ e}^{3/2\,{ c_0}\,{y}^{2}}}\\&\quad +{ \frac{477}{8}}\,{{ c_2}}^{7}{ c_3}\, \Bigg ( \Bigg ( {\frac{74}{ 477}}\,{y}^{4}{{ c_2}}^{2}+{y}^{8}{{ c_3}}^{2} \Bigg ) {{ c_0}}^ {4}\\&\quad + \left( -{\frac{40}{477}}\,{y}^{2}{{ c_2}}^{2}-{\frac{232}{159 }}\,{y}^{6}{{ c_3}}^{2} \right) {{ c_0}}^{3}\\&\quad + \left( -{\frac{152}{159}}\,{{ c_3}}^{2}{y}^{4}-{\frac{40}{477}}\,{{ c_2}}^{2} \right) {{ c_0}}^{2} \\&\quad +{\frac{160}{159}}\,{{ c_3}}^{2}{y}^{2}{ c_0} +{\frac{80}{159}}\,{{ c_3}}^{2} \Bigg ) {{ c_0}}^{7}{{ e}^{ -3/2\,{ c_0}\,{y}^{2}}}\\&\quad +17/2\,{{ c_2}}^{9} \left( { c_0}\,{y}^{2 }-1 \right) { c_3}\, \left( { c_0}\,{y}^{2}+1/2 \right) \left( {y }^{4}{{ c_0}}^{2}\right. \\&\quad \left. -{\frac{10}{17}}\,{ c_0}\,{y}^{2}-{\frac{10}{17 }} \right) {{ c_0}}^{9}{{ e}^{-5/2\,{ c_0}\,{y}^{2}}} \end{aligned}$$

$$\begin{aligned}&\quad + \Bigg ( \left( 30\,{{ c_3}}^{7}{{ c_2}}^{3}-11/4\,{y}^{4}{{ c_3}}^{9}{ c_2} \right) {{ c_0}}^{3}-5\,{y}^{2}{{ c_3}}^{9}{ c_2}\,{{ c_0}}^{2}\\&\quad -5\,{{ c_3}}^{9}{ c_2}\,{ c_0} \Bigg ) {{ e}^{5/2 \,{ c_0}\,{y}^{2}}}+5/2\,{{ e}^{7/2\,{ c_0}\,{y}^{2}}}{{ c_3} }^{9}{ c_2}\,{ c_0}\\&\quad +{\frac{1059}{16}}\,{{ c_2}}^{6} \Bigg ( \left( {y}^{8}{{ c_3}}^{4}+{\frac{4}{1059}}\,{{ c_2}}^{4}+{ \frac{200}{353}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}\\&\quad -{\frac{672}{353}}\, \left( {\frac{5}{28}}\,{{ c_2}}^{2}+{ { c_3}}^{2}{y}^{4} \right) {{ c_3}}^{2}{y}^{2}{{ c_0}}^{3}\\&\quad + \left( -{\frac{120}{353}}\,{{ c_3}}^{2}{{ c_2}}^{2}-{\frac{392}{353}}\,{{ c_3}}^{4}{y}^{4} \right) {{ c_0}}^{2}\\&\quad +{\frac{560}{353} }\,{{ c_3}}^{4}{ c_0}\,{y}^{2}+{\frac{280}{353}}\,{{ c_3}}^{4} \Bigg ) {{ c_0}}^{6}{{ e}^{-{ c_0}\,{y}^{2}}}\\&\quad +1/4 \left( \left( {y}^{8}{{ c_3}}^{4}+210{{ c_2}}^{4}-12{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}\right. \\&\quad \left. + \left( 2{y}^{6}{{ c_3} }^{4}-90{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2} \right) {{ c_0}}^{3}\right. \\&\quad \left. + \left( -90{{ c_3}}^{2}{{ c_2}}^{2}+3{{ c_3}}^{4}{y}^{4} \right) {{ c_0}}^{2}\right. \\&\quad \left. +2{{ c_3}}^{4}{ c_0}\,{y}^{2}+{{ c_3}}^ {4} \right) {{ c_3}}^{6}{{ e}^{2{ c_0}{y}^{2}}}\\&\quad +{\frac{489 }{16}}\,{{ c_2}}^{8} \Bigg ( \left( {y}^{8}{{ c_3}}^{2}+{\frac{16 }{489}}\,{y}^{4}{{ c_2}}^{2} \right) {{ c_0}}^{4} \end{aligned}$$

$$\begin{aligned}&\quad + \left( -{\frac{8}{489}}\,{y}^{2}{{ c_2}}^{2}-{\frac{200}{163}}\,{y}^{6}{{ c_3}} ^{2} \right) {{ c_0}}^{3}\\&\quad + \left( -{\frac{8}{489}}\,{{ c_2}}^{2}- {\frac{140}{163}}\,{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2}\\&\quad +{ \frac{120}{163}}\,{{ c_3}}^{2}{y}^{2}{ c_0} +{\frac{60}{163}}\,{{ c_3}}^{2} \Bigg ) {{ c_0}}^{8}{{ e}^{-2\,{ c_0}\,{y}^{2}}}\\&\quad +{ { c_2}}^{10} \left( { c_0}\,{y}^{2}-1 \right) ^{2} \left( { c_0} \,{y}^{2}+1/2 \right) ^{2}{{ c_0}}^{10}{{ e}^{-3\,{ c_0}\,{y}^{ 2}}}\\&\quad +{\frac{51}{16}}\,{{ c_3}}^{2} \Bigg \{ -{\frac{8}{51}}\,{{ c_3}}^{6} \Bigg [ \left( {{ c_3}}^{2}{y}^{4}-{\frac{45}{2}}\,{{ c_2}}^{2} \right) {{ c_0}}^{2}+{{ c_3}}^{2}{y}^{2}{ c_0}\\&\quad +{{ c_3 }}^{2} \Bigg ] {{ e}^{3\,{ c_0}\,{y}^{2}}}+{\frac{4}{51}}\,{{ c_3}}^{8}{{ e}^{4\,{ c_0}\,{y}^{2}}}+{{ c_2}}^{2} \Bigg ( - \Bigg \{ \left( -{\frac{280}{17}}\,{{ c_2}}^{4}\right. \\&\left. -{\frac{336}{17}}\, {{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}+{y}^{8}{{ c_3}}^{4} \right) {{ c_0}}^{4}\\&\quad -{\frac{16}{17}}\,{{ c_3}}^{2}{y}^{2} \left( -35\,{{ c_2}}^{2}+{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{3}\\&\quad + \left( { \frac{560}{17}}\,{{ c_3}}^{2}{{ c_2}}^{2}-{\frac{76}{17}}\,{{ c_3}}^{4}{y}^{4} \right) {{ c_0}}^{2}\\&\quad -{\frac{120}{17}}\,{{ c_3 }}^{4}{ c_0}\,{y}^{2}-{\frac{60}{17}}\,{{ c_3}}^{4} \Bigg \} {{ c_3}}^{2}{{ e}^{{ c_0}\,{y}^{2}}}\\&\quad +{{ c_2}}^{2} \Bigg [ \left( {y}^{8}{{ c_3}}^{4}+{\frac{60}{17}}\,{{ c_2}}^{4}+{\frac{672}{17}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4} \end{aligned}$$

$$\begin{aligned}&\quad -{\frac{336}{17}}\,{{ c_3}}^{2}{y}^{2} \left( {{ c_3}}^{2}{y}^{4} +5/3\,{{ c_2}}^{2} \right) {{ c_0}}^{3}\\&\quad -{\frac{56}{17}}\,{{ c_3 }}^{2} \left( {{ c_3}}^{2}{y}^{4}+10\,{{ c_2}}^{2} \right) {{ c_0}}^{2}+{\frac{560}{17}}\,{{ c_3}}^{4}{ c_0}\,{y}^{2}\\&\quad +{\frac{ 280}{17}}\,{{ c_3}}^{4} \Bigg ] {{ c_0}}^{2} \Bigg ) {{ c_0}}^{2 } \Bigg \} \Bigg \} {y}^{3} \Bigg \{ 5/4\,{ c_2}\, \Bigg \{ -4/5\,{ c_0 }\,{y}^{2}\\&\quad +{y}^{4}{{ c_0}}^{2}-4/5 \Bigg \} { c_3}{ c_0} { e}^{-\frac{{ c_0}{y}^{2}}{2}}\\&\quad +{ c_3}{{ e}^{1/2{ c_0} {y}^{2}}}{ c_2}{ c_0}+{{ c_2}}^{2} \left( { c_0}{y}^{2}-1 \right) \left( { c_0}{y}^{2}+1/2 \right) {{ c_0}}^{2}{{ e}^ {-{ c_0}{y}^{2}}}\\&\quad +1/2{{ c_3}}^{2}{{ e}^{{ c_0}{y}^{2}}} + \left( 1/2{{ c_2}}^{2}-1/2{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2}\\&\quad -1/2\,{{ c_3}}^{2}{y}^{2}{ c_0}-1/2\,{{ c_3}}^{2} \Bigg \} ^{-3} \left( 2\,{ c_3}\,{{ e}^{1/2\,{ c_0}\,{y}^{2}}}{ c_2}\,{ c_0}\right. \\&\quad \left. +{{ c_3}}^{2}{{ e}^{{ c_0}\,{y}^{2}}}+{{ c_2 }}^{2}{{ c_0}}^{2} \right) ^{-2} -{\frac{9f''(y){y}^{2} }{8}}\;\\&\quad \times \Bigg \{ {\frac{669}{8}}\, \Bigg ( {y}^{2} \left( {\frac{394}{669}}\,{{ c_3 }}^{2}{{ c_2}}^{2}{y}^{4} -{\frac{2}{223}}\,{{ c_2}}^{4}+{{ c_3}}^{4}{y}^{8} \right) {{ c_0}}^{ 5}\\&\quad + \left( {\frac{160}{ 2007}}\,{{ c_2}}^{4}-{\frac{462}{223}}\,{{ c_3}}^{4}{y}^{8}+{\frac{240}{223}}\,{{ c_3}}^{2}{{ c_2}}^{2 }{y}^{4} \right) {{ c_0}}^{4}\\&\quad - \Bigg ( {\frac{1168}{669}}\,{{ c_3 }}^{2}{{ c_2}}^{2}{y}^{2}+{\frac{1414}{669}}\,{{ c_3}}^{4}{y}^{6} \Bigg ) {{ c_0}}^{3} \end{aligned}$$

$$\begin{aligned}&\quad + \left( -{\frac{1280}{669}}\,{{ c_3}}^{2}{{ c_2}}^{2}+{\frac{616}{669}}\,{{ c_3}}^{4}{y}^{4} \right) {{ c_0}}^{2}\\&\quad +{\frac{868}{223}}\,{{ c_3}}^{4}{ c_0}\,{y}^{2}+{\frac{ 448}{223}}\,{{ c_3}}^{4} \Bigg ) {{ c_0}}^{5}{ c_3}\,{{ c_2}}^ {5}{{ e}^{-1/2\,{ c_0}\,{y}^{2}}}\\&\quad + \Bigg \{\Bigg ({\frac{385}{4}}\,{y}^{6}{{ c_3}}^{5}{{ c_2}}^{5}-{\frac{107}{ 16}}\,{{ c_3}}^{7}{y}^{10}{{ c_2}}^{3}-7\,{y}^{2}{{ c_3}}^{3}{{ c_2}}^{7} \Bigg ) {{ c_0}}^{8}\\&\quad + \left( -{\frac{151}{4}}\,{{ c_3}}^{7}{y}^{ 8}{{ c_2}}^{3}+80\,{{ c_3}}^{3}{{ c_2}}^{7}+91\,{y}^{4}{{ c_3} }^{5}{{ c_2}}^{5} \right) {{ c_0}}^{7}\\&\quad + \left( -315\,{y}^{2}{{ c_3}}^{5}{{ c_2}}^{5}-{\frac{43}{4}}\,{{ c_3}}^{7}{y}^{6}{{ c_2} }^{3} \right) {{ c_0}}^{6}\\&\quad + \left( 94{{ c_3}}^{7}{y}^{4}{{ c_2}}^{3} -336\,{{ c_3}}^{5}{{ c_2}}^{5 } \right) {{ c_0}}^{5}+157 {{ c_0}}^{4}{{ c_3}}^{7}{y}^{2}{{ c_2}}^{3}\\&\quad +80{{ c_0}}^{3}{{ c_3}}^{7}{{ c_2}}^{3} \Bigg \} { e}^{\frac{{ c_0}{y}^{2}}{2}} - 1/2{ c_0}{{ c_3}}^{5}\\&\quad \times \Bigg \{ {y}^{2} \left( {{ c_3}}^{4}{y}^ {8}-{\frac{111}{2}}{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}+21{{ c_2 }}^{4} \right) {{ c_0}}^{5}\\&\quad + \left( 28\,{{ c_3}}^{2}{{ c_2}}^{2} {y}^{4}-336\,{{ c_2}}^{4}-11/2\,{{ c_3}}^{4}{y}^{8} \right) {{ c_0}}^{4}\\&\quad + \left( 308\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2}-{\frac{47}{ 3}}\,{{ c_3}}^{4}{y}^{6} \right) {{ c_0}}^{3}\\&\quad + \left( -27\,{{ c_3}}^{4}{y}^{4}+320\,{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{ 2}-{\frac{53}{2}}\,{{ c_3}}^{4}{ c_0}\,{y}^{2}\\&\quad -{\frac{40}{3}}{ { c_3}}^{4} \Bigg \} { c_2}{{ e}^{3/2\,{ c_0}{y}^{2}}}+{ \frac{1353}{16}}{{ c_0}}^{7}{ c_3} \\&\quad \times \Bigg \{ {y}^{6} \left( {{ c_3}}^{2}{y}^{4}+{\frac{16}{369}}{{ c_2}}^{2} \right) {{ c_0 }}^{5}\\&\quad + \left( {\frac{56}{451}}{{ c_2}}^{2}{y}^{4}-{\frac{52}{41 }}{{ c_3}}^{2}{y}^{8} \right) {{ c_0}}^{4}\\&\quad -\left( {\frac{568}{4059}}{{ c_2}}^{2}{y}^{2}+{\frac{2116}{1353}}{y}^{6}{{ c_3}} ^{2} \right) {{ c_0}}^{3}\\&\quad + \Bigg \{ -{\frac{640}{4059}}\,{{ c_2}}^{ 2}-{\frac{160}{1353}}\,{{ c_3}}^{2}{y}^{4} \Bigg \} {{ c_0}}^{2}+{ \frac{816}{451}}\,{{ c_3}}^{2}{y}^{2}{ c_0}\\&\quad +{\frac{1280}{1353}} \,{{ c_3}}^{2} \Bigg \} {{ c_2}}^{7}{{ e}^{-3/2\,{ c_0}\,{y}^{ 2}}}+{\frac{28}{3}}\, \Bigg \{{\frac{151}{112}}\,{ c_0}\,{y}^{2}\\&\quad -{ \frac{59}{56}}\,{{ c_0}}^{4}{y}^{8}+5/7-{\frac{23}{56}}\,{{ c_0} }^{2}{y}^{4} \end{aligned}$$

$$\begin{aligned}&\quad -{\frac{23}{16}}\,{{ c_0}}^{3}{y}^{6}+{{ c_0}}^{5}{y} ^{10} \Bigg \} {{ c_0}}^{9}{ c_3}\,{{ c_2}}^{9}{{ e}^{-5/2\,{ c_0}\,{y}^{2}}}\\&\quad -{\frac{11}{12}}\,{ c_0}\,{{ c_3}}^{7}{ c_2} \, \Bigg \{ \left( {\frac{36}{11}}\,{{ c_2}}^{2}{y}^{2}+{y}^{6}{{ c_3}}^{2} \right) {{ c_0}}^{3}\\&\quad + \left( -{\frac{960}{11}}\,{{ c_2}}^{2}+{\frac{82}{11}}\,{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2 }+{\frac{158}{11}}\,{{ c_3}}^{2}{y}^{2}{ c_0}\\&\quad +{\frac{160}{11}}\, {{ c_3}}^{2} \Bigg \} {{ e}^{5/2\,{ c_0}\,{y}^{2}}}-1/12\,{ c_0}\,{{ c_3}}^{9}{ c_2}\, \left( -80+{ c_0}\,{y}^{2} \right) { { e}^{7/2\,{ c_0}\,{y}^{2}}}\\&\quad +112\,{{ c_0}}^{6} \Bigg \{ {y}^{2} \left( -{\frac{1}{1344}}\,{{ c_2}}^{4}+{\frac{71}{448}}\,{{ c_3 }}^{2}{{ c_2}}^{2}{y}^{4}+{{ c_3}}^{4}{y}^{8} \right) {{ c_0}}^{ 5}\\&\quad + \left( {\frac{1}{168}} {{ c_2}}^{4}-{\frac{97}{64}}{{ c_3}}^{4}{y}^{8}+{\frac{41}{112}}{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}\\&\quad + \left( -{\frac{27}{56}}{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2}-{\frac{111}{64}}{{ c_3}}^{4}{y}^{6} \right) { { c_0}}^{3}\\&\quad + \left( -{\frac{15}{28}}{{ c_3}}^{2}{{ c_2}}^{2}+ 3/16{{ c_3}}^{4}{y}^{4} \right) {{ c_0}}^{2}\\&\quad +{\frac{77}{32}}{ { c_3}}^{4}{ c_0}{y}^{2}+5/4\,{{ c_3}}^{4} \Bigg \} {{ c_2}}^ {6}{{ e}^{-{ c_0}\,{y}^{2}}}\\&\quad +1/3\, \Bigg \{{y}^{2} \left( {{ c_3 }}^{4}{y}^{8}+{\frac{51}{4}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}-21 \,{{ c_2}}^{4} \right) {{ c_0}}^{5}\\&\quad + \left( -{\frac{105}{2}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}+420\,{{ c_2}}^{4}+2\,{{ c_3}}^{4 }{y}^{8} \right) {{ c_0}}^{4} \end{aligned}$$

$$\begin{aligned}&\quad + \left( 4{{ c_3}}^{2}{y}^{4} -{\frac{351}{2}}{{ c_2}}^{2} \right) {y}^{2}{ c_3}^ {2} { c_0}^{ 3}\\&\quad + \left( 5{{ c_3}}^{2}{y}^{4}-180{{ c_2}}^{2} \right) {{ c_3}}^{2}{{ c_0}}^{2}\\&\quad +4{{ c_3}}^{4}{ c_0}{y}^{2}+2{{ c_3 }}^{4} \Bigg \} {{ c_3}}^{6}{{ e}^{2{ c_0}{y}^{2}}}\\&\quad +{\frac{ 603{c_0}^{8}}{16}} \Bigg \{ \left( {\frac{16}{1809}}{{ c_2} }^{2}+{{ c_3}}^{2}{y}^{4} \right) {y}^{6}{{ c_0}}^{5}\\&\quad + \left( { \frac{56}{1809}}\,{{ c_2}}^{2}-{\frac{76}{67}}\,{{ c_3}}^ {2}{y}^{4} \right) {y}^{4} {{ c_0}}^{4}\\&\quad + \left( -{\frac{56}{1809}}\,{{ c_2}}^{2}-{\frac{892}{603}}\,{y}^{4}{{ c_3}}^{2} \right) {y}^{2} {{ c_0}}^{3}\\&\quad - \left( {\frac{64}{1809}}\,{{ c_2}}^{2}+{\frac{176}{ 603}}\,{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2}\\&\quad +{\frac{304}{201}} \,{{ c_3}}^{2}{y}^{2}{ c_0}+{\frac{160}{201}}\,{{ c_3}}^{2} \Bigg \}\times {{ c_2}}^{8}{{ e}^{-2\,{ c_0}\,{y}^{2}}}\\&\quad + \left( {{ c_0}}^{3}{y}^{6}-1/2\,{{ c_0}}^{2}{y}^{4}-7/6\,{ c_0}\,{y}^{2}- 4/3 \right) {{ c_0}}^{10} \\&\quad \left( { c_0}\,{y}^{2}-1 \right) \left( { c_0}\,{y}^{2}+1/2 \right) {{ c_2}}^{10}{{ e}^{-3\,{ c_0}\,{y}^{2}}}\\&\quad +{\frac{411}{16}}\,{{ c_3}}^{2} \Bigg \{ -{\frac{ 16}{1233}}\,{{ c_3}}^{6}\left( \left( 9/4\,{{ c_2}}^{2}{y}^{2}+{ y}^{6}{{ c_3}}^{2} \right) {{ c_0}}^{3}\right. \\&\quad \left. + \left( -90\,{{ c_2}}^{2 }+3\,{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2}+4\,{{ c_3}}^{2}{y} ^{2}{ c_0}+4\,{{ c_3}}^{2} \right) {{ e}^{3\,{ c_0}\,{y}^{2}} }\\&\quad +{\frac{32}{1233}}\,{{ c_3}}^{8}{{ e}^{4\,{ c_0}\,{y}^{2}}}+{ { c_0}}^{2} \Bigg [ -{\frac{34}{137}}\, \Bigg \{ {y}^{2} \Bigg [ {{ c_3}}^{4}{y}^{8} \end{aligned}$$

$$\begin{aligned}&\quad -{\frac{182}{17}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} +{\frac{28}{17}}\,{{ c_2}}^{4} \Bigg ] {{ c_0}}^{5}\\&\quad - \left( { \frac{224}{51}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}+{\frac{1120}{51 }}\,{{ c_2}}^{4}-{\frac{6}{17}}\,{{ c_3}}^{4}{y}^{8} \right) {{ c_0}}^{4}\\&\quad +{\frac{112}{51}}\,{y}^{2}{{ c_3}}^{2} \left( 19\,{{ c_2}}^{2}-{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{3}- \Bigg \{ { \frac{380}{51}}\,{{ c_3}}^{4}{y}^{4}\\&\quad -{\frac{2240}{51}}\,{{ c_3}} ^{2}{{ c_2}}^{2} \Bigg \} {{ c_0}}^{2}-{\frac{158}{17}}\,{{ c_3} }^{4}{ c_0}\,{y}^{2}-{\frac{80}{17}}\,{{ c_3}}^{4} \Bigg \} {{ c_3}}^{2}{{ e}^{{ c_0}\,{y}^{2}}}\\&\quad +{{ c_0}}^{2} \Bigg [ {y}^{2} \left( {{ c_3}}^{4}{y}^{8}+{\frac{1372}{411}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}-{\frac{16}{137}}\,{{ c_2}}^{4} \right) {{ c_0 }}^{5}\\&\quad + \Bigg \{ {\frac{1904}{411}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4 } +{\frac{160}{137}}{{ c_2}}^{4}-{\frac{588}{137}}{{ c_3}}^{4 }{y}^{8} \Bigg \}{{ c_0}}^{4}\\&\quad + \left( -{\frac{4144}{411}}\,{{ c_3 }}^{2}{{ c_2}}^{2}{y}^{2}-{\frac{476}{137}}\,{{ c_3}}^{4}{y}^{6} \right) {{ c_0}}^{3}\\&\quad +{\frac{1792}{411}}\,{{ c_3}}^{2} \left( {{ c_3}}^{2}{y}^{4}-5/2\,{{ c_2}}^{2} \right) {{ c_0}}^{2}\\&\quad +{\frac{1456}{137}}{{ c_3}}^{4}{ c_0}{y}^{2}+{\frac{2240}{411}}{{ c_3}}^{4} \Bigg ] {{ c_2}}^{2} \Bigg ] {{ c_2}}^{2} \Bigg \} \Bigg \}\\&\quad \times \Bigg [ { c_3} \,{{ e}^{1/2\,{ c_0}\,{y}^{2}}}{ c_2}\,{ c_0}+5/4\,{ c_0}\, \\&\quad \times \left( -4/5\,{ c_0}\,{y}^{2}+{{ c_0}}^{2}{y}^{4}-4/5 \right) { c_3}\,{ c_2}\,{{ e}^{-1/2\,{ c_0}\,{y}^{2}}} \end{aligned}$$

$$\begin{aligned}&\quad + \left( { c_0 }\,{y}^{2}-1 \right) {{ c_0}}^{2} \left( { c_0}\,{y}^{2}+1/2 \right) {{ c_2}}^{2}{{ e}^{-{ c_0}\,{y}^{2}}}\\&\quad +1/2\,{{ c_3}}^ {2}{{ e}^{{ c_0}\,{y}^{2}}} + \left( 1/2\,{{ c_2}}^{2}-1/2\,{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2}\\&\quad -1/2\,{{ c_3}}^{2}{y}^{2}{ c_0}-1/2\,{{ c_3}}^{2} \Bigg ]^{-3} \\&\quad \times \left( 2\,{ c_3}\,{{ e} ^{1/2\,{ c_0}\,{y}^{2}}}{ c_2}\,{ c_0}+{{ c_3}}^{2}{{ e}^{{ c_0}\,{y}^{2}}}+{{ c_2}}^{2}{{ c_0}}^{2} \right) ^{-2}\\&f'(y)y\; \Bigg \{ {\frac{1683}{8}}\,{{ c_0}}^{5}{ c_3}\, \Bigg \{ \left( -{\frac{677}{1122}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}\right. \\&\quad \left. +{\frac{74}{ 5049}}\,{{ c_2}}^{4}+{{ c_3}}^{4}{y}^{8} \right) {y}^{4}{{ c_0}} ^{6}\\&\quad -{\frac{3521}{3366}}\,{y}^{2} \left( {\frac{58}{3521}}\,{{ c_2 }}^{4}+{{ c_3}}^{4}{y}^{8}-{\frac{14804}{3521}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{5}\\&\quad + \left( -{\frac{12697}{ 3366}}\,{{ c_3}}^{4}{y}^{8}+{\frac{100}{1683}}\,{{ c_2}}^{4}-{ \frac{6176}{1683}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}\\&\quad + \left( -{\frac{217}{153}}\,{{ c_3}}^{4}{y}^{6}-{ \frac{248}{187}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2} \right) {{ c_0}}^{3}\\&\quad + \left( {\frac{12740}{1683}}\,{{ c_3}}^{4}{y}^{4}-{\frac{ 80}{51}}\,{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{2}\\&\quad +{\frac{ 602}{187}}\,{{ c_3}}^{4}{ c_0}\,{y}^{2}+{\frac{56}{33}}\,{{ c_3 }}^{4} \Bigg \} {{ c_2}}^{5}{{ e}^{-1/2\,{ c_0}\,{y}^{2}}}\\&\quad +{ \frac{501}{32}}\,{{ c_0}}^{3}{ c_3}\, \Bigg \{ \left( {{ c_3}}^{ 6}{y}^{12}+{\frac{928}{501}}\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{4}\right. \\&\quad \left. -{ \frac{7562}{501}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{8}+{\frac{80}{ 1503}}\,{{ c_2}}^{6} \right) {{ c_0}}^{6}\\&\quad -{\frac{895}{167}}\, \left( -{\frac{49028}{2685}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}+{{ c_3}}^{4}{y}^{8}+{\frac{432}{895}}\,{{ c_2}}^{4} \right) {y}^{2} {{ c_3}}^{2}{{ c_0}}^{5} \end{aligned}$$

$$\begin{aligned}&\quad -{\frac{5750}{501}}\, \left( {{ c_3}}^{ 4}{y}^{8}-{\frac{96}{115}}\,{{ c_2}}^{4}+{\frac{20048}{2875}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_3}}^{2}{{ c_0}}^{4}\\&\quad + \left( -{\frac{6384}{167}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{2}-{ \frac{200}{167}}\,{{ c_3}}^{6}{y}^{6} \right) {{ c_0}}^{3}\\&\quad + \left( {\frac{17632}{501}}\,{{ c_3}}^{6}{y}^{4}-{\frac{7392}{167} }\,{{ c_3}}^{4}{{ c_2}}^{2} \right) {{ c_0}}^{2}\\&\quad +{\frac{3472}{ 167}}\,{{ c_3}}^{6}{ c_0}\,{y}^{2}+{\frac{5440}{501}}\,{{ c_3}} ^{6} \Bigg \} {{ c_2}}^{3}{{ e}^{1/2\,{ c_0}\,{y}^{2}}}\\&\quad -{\frac{ 23}{16}}\,{ c_0}\, \Bigg \{ \left( {{ c_3}}^{6}{y}^{12}-{\frac{160 }{23}}\,{{ c_2}}^{6}\right. \\&\quad \left. -{\frac{616}{23}}\,{{ c_3}}^{2}{{ c_2}}^{4} {y}^{4} +{\frac{1233}{23}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{8} \right) {{ c_0}}^{6}\\&\quad -{\frac{158}{69}}\,{y}^{2}{{ c_3}}^{2} \left( {\frac{9822}{79}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}-{ \frac{1890}{79}}\,{{ c_2}}^{4}+{{ c_3}}^{4}{y}^{8} \right) {{ c_0}}^{5}\\&\quad + \left( {\frac{6016}{23}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{ 4}-{\frac{172}{23}}\,{{ c_3}}^{6}{y}^{8}-{\frac{5040}{23}}\,{{ c_3}}^{2}{{ c_2}}^{4} \right) {{ c_0}}^{4}\\&\quad + \left( {\frac{4656}{23 }}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{2}-{\frac{949}{69}}\,{{ c_3}}^ {6}{y}^{6} \right) {{ c_0}}^{3}+ \Bigg \{ {\frac{5280}{23}}\,{{ c_3 }}^{4}{{ c_2}}^{2}\\&\quad -{\frac{1204}{69}}\,{{ c_3}}^{6}{y}^{4} \Bigg \} {{ c_0}}^{2}-{\frac{438}{23}}\,{{ c_3}}^{6}{ c_0}\,{y} ^{2}-{\frac{680}{69}}\,{{ c_3}}^{6} \Bigg \} {{ c_3}}^{3}{ c_2} \,{{ e}^{3/2\,{ c_0}\,{y}^{2}}}\\&\quad +{\frac{4509}{32}}\,{{ c_0}}^{7 }{ c_3}\, \Bigg [ {y}^{8} \left( -{\frac{1084}{13527}}\,{{ c_2}}^{ 2}+{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{6}\\&\quad + \Bigg \{ {\frac{8354}{ 13527}}\,{{ c_2}}^{2}{y}^{6} -{\frac{145}{501}}{{ c_3}}^{2}{y}^{ 10} \Bigg \} {{ c_0}}^{5}\\&\quad + \left( -{\frac{15674}{4509}}{{ c_3}}^ {2}{y}^{8}-{\frac{7216}{13527}}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4} \end{aligned}$$

$$\begin{aligned}&\quad + \left( -{\frac{728}{4509}}{{ c_2}}^{2}{y}^{2}-{\frac{ 1928}{1503}}{y}^{6}{{ c_3}}^{2} \right) {{ c_0}}^{3}\\&\quad + \left( -{ \frac{880}{4509}}{{ c_2}}^{2}+{\frac{29536}{4509}}{{ c_3}}^{ 2}{y}^{4} \right) {{ c_0}}^{2}\\&\quad +{\frac{1136}{501}}\,{{ c_3}}^{2}{y }^{2}{ c_0}+{\frac{5440}{4509}}\,{{ c_3}}^{2} \Bigg ] {{ c_2}}^ {7}{ e}^{-\frac{3{ c_0}{y}^{2}}{2}}\\&\quad +{\frac{13{ c_0}{{ c_3}}^{5} }{48}}\Bigg \{ \left( 12\,{{ c_2}}^{2}+{{ c_3}}^{2}{y}^{4} \right) \left( {\frac{84}{13}}\,{{ c_2}}^{2}+{{ c_3}}^{2}{y}^{4 } \right) {{ c_0}}^{4}\\&\quad - \left( {\frac{1656}{13}}{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2}+{\frac{335}{13}}{{ c_3}}^{4}{y}^{6} \right) { { c_0}}^{3}\\&\quad + \left( -{\frac{440}{13}}\,{{ c_3}}^{4}{y}^{4}+{ \frac{7200}{13}}{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{2} \\&\quad -{\frac{1188}{13}}\,{{ c_3}}^{4}{ c_0}{y}^{2}-{\frac{1320}{13} }\,{{ c_3}}^{4} \Bigg \} { c_2}{{ e}^{5/2{ c_0}\,{y}^{2}}} -11\,{{ c_0}}^{9}{ c_3}\\&\quad \times \Bigg \{{\frac{731}{176}}{{ c_0}}^{ 4}{y}^{8} +{\frac{85}{66}}+{\frac{731}{528}}{{ c_0}}^{3}{y}^{6}-{ \frac{211}{88}}{ c_0}{y}^{2}\\&\quad -{\frac{151}{264}}\,{{ c_0}}^{5} {y}^{10}-{{ c_0}}^{6}{y}^{12}-{\frac{95}{12}}\,{{ c_0}}^{2}{y}^{4 } \Bigg \} {{ c_2}}^{9}{{ e}^{-5/2\,{ c_0}\,{y}^{2}}}\\&\quad -{\frac{11 }{12}}\,{ c_0}\,{{ c_3}}^{7} \left( \left( {{ c_3}}^{2}{y}^{4}- {\frac{120}{11}}\,{{ c_2}}^{2} \right) {{ c_0}}^{2}\right. \\&\quad \left. +{\frac{63}{ 22}}\,{{ c_3}}^{2}{y}^{2}{ c_0}-{\frac{150}{11}}\,{{ c_3}}^{2} \right) { c_2}\,{{ e}^{7/2\,{ c_0}\,{y}^{2}}}\\&\quad +\frac{5{ c_0}{ { c_3}}^{9}{ c_2}{ e}^{\frac{9{ c_0}{y}^{2}}{2}}}{6}\\&\quad +{\frac{7155 }{32}}{{ c_0}}^{6} \Bigg \{ \left( {\frac{32}{21465}}{{ c_2}}^{4}+{{ c_3}}^{4}{y}^{8}-{\frac{1576}{7155}}{{ c_3} }^{2}{{ c_2}}^{2}{y}^{4} \right) {y}^{4}{{ c_0}}^{6}\\&\quad -{\frac{4573}{7155}}{y }^{2} \left( {\frac{12}{4573}}{{ c_2}}^{4}+{{ c_3}}^{4}{y}^{8}- {\frac{11896}{4573}}{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{5}\\&\quad + \left( -{\frac{24796}{7155}}\,{{ c_3}}^{4}{y}^{8}+{ \frac{8}{1431}}\,{{ c_2}}^{4}-{\frac{10112}{7155}}\,{{ c_3}}^{2} {{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}\\&\quad + \left( -{\frac{9464}{ 7155}}\,{{ c_3}}^{4}{y}^{6}-{\frac{368}{795}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2} \right) {{ c_0}}^{3} \end{aligned}$$

$$\begin{aligned}&\quad + \left( {\frac{5264}{795}}\,{{ c_3}}^{4}{y}^{4}-{\frac{88}{159}}\,{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{2}\\&\quad +{\frac{5992}{2385}}\,{{ c_3}}^{4}{ c_0}\, {y}^{2}+{\frac{1904}{1431}}\,{{ c_3}}^{4} \Bigg \} {{ c_2}}^{6}{ { e}^{-{ c_0}\,{y}^{2}}}\, \\&\quad +1/2\Bigg [ \left( {{ c_3}}^{6}{y}^{ 12}+42\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{4}\right. \\&\quad \left. -{\frac{133}{4}}\,{{ c_3 }}^{4}{{ c_2}}^{2}{y}^{8}+35\,{{ c_2}}^{6} \right) {{ c_0}}^{6}\\&\quad + 7/3\,{y}^{2} \Bigg \{ {\frac{843}{14}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y} ^{4}+{{ c_3}}^{4}{y}^{8}-54\,{{ c_2}}^{4} \Bigg \} {{ c_3}}^{2}{{ c_0}}^{5}\\&\quad + \left( -{\frac{373}{2}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y }^{4}+525\,{{ c_3}}^{2}{{ c_2}}^{4}+11/2\,{{ c_3}}^{6}{y}^{8} \right) {{ c_0}}^{4}\\&\quad + \left( -{\frac{441}{2}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{2}+{\frac{43}{6}}\,{{ c_3}}^{6}{y}^{6} \right) {{ c_0}}^{3}+ \Bigg \{ 8/3\,{{ c_3}}^{6}{y}^{4}\\&\quad -{\frac{495}{2}}\,{{ c_3}}^{4}{{ c_2}}^{2} \Bigg \} {{ c_0}}^{2}+11/2\,{{ c_3}}^{6} { c_0}\,{y}^{2} +{\frac{17}{6}}\,{{ c_3}}^{6} \Bigg ] {{ c_3}}^{ 4}{{ e}^{2\,{ c_0}\,{y}^{2}}}\\&\quad +{\frac{423}{8}}\, \Bigg \{ {y}^{8} \left( -{\frac{28}{1269}}\,{{ c_2}}^{2}+{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{6}\\&\quad + \left( {\frac{218}{1269}}\,{{ c_2}}^{2}{y} ^{6}+{\frac{40}{423}}\,{{ c_3}}^{2}{y}^{10} \right) {{ c_0}}^{5}\\&\quad - \left( {\frac{190}{1269}}\,{{ c_2}}^{2}{y}^{4}+{\frac{1570}{423} }{{ c_3}}^{2}{y}^{8} \right) {{ c_0}}^{4}\\&\quad + \left( -{\frac{2}{47 }}{{ c_2}}^{2}{y}^{2}-{\frac{550}{423}}{y}^{6}{{ c_3}}^{2} \right) {{ c_0}}^{3}\\&\quad + \left( -{\frac{22}{423}}{{ c_2}}^{2}+{ \frac{2968}{423}}\,{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2}+{ \frac{106}{47}}\,{{ c_3}}^{2}{y}^{2}{ c_0}\\&\quad +{\frac{170}{141}}\,{{ c_3}}^{2} \Bigg \} {{ c_0}}^{8}{{ c_2}}^{8}{{ e}^{-2\,{ c_0 }\,{y}^{2}}}\\&\quad +{\frac{7}{12}}\, \Bigg \{ \left( {{ c_3}}^{4}{y}^{8} -{\frac{12}{7}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}+30\,{{ c_2}}^{4} \right) {{ c_0}}^{4}\\&\quad - \left( {\frac{297}{14}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2}+{\frac{41}{7}}\,{{ c_3}}^{4}{y}^{6} \right) {{ c_0}}^{3} \end{aligned}$$

$$\begin{aligned}&\quad + \left( \frac{4}{7}\,{{ c_3}}^{4}{y}^{4}+{\frac{675}{7}}\,{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{2} -{\frac{30}{7}}\,{{ c_3}}^{4}{ c_0}\,{y}^{2}\\&\quad -{\frac{33}{7}}\,{{ c_3}}^{4} \Bigg \} {{ c_3}}^{6}{{ e}^{3\,{ c_0}\,{y}^{2}}}+{{ c_0}}^{10} \left( {\frac{17}{12}}\right. \\&\quad -{\frac{19}{4}}\,{{ c_0}}^{4}{y}^{8}-{\frac{37}{24 }}\,{{ c_0}}^{3}{y}^{6}+{\frac{21}{8}}\,{ c_0}\,{y}^{2}\\&\quad \left. +\frac{7{{ c_0}}^{5}{y}^{10}}{6}+{{ c_0}}^{6}{y}^{12}+{\frac{109}{12}}\,{{ c_0}}^{2}{y}^{4} \right) {{ c_2}}^{10}{{ e}^{-3\,{ c_0}\,{y}^{2} }}\\&\quad -\frac{\,{{ c_3}}^{8}}{6} \left( \left( -{\frac{45}{2}}\,{{ c_2}}^{2} +{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2}+3/2{{ c_3}}^{2}{y}^{ 2}{ c_0}\right. \\&\quad \left. -\frac{15{{ c_3}}^{2}}{2} \right) {{ e}^{4\,{ c_0}{y}^{2} }}+\frac{{{ c_3}}^{10}{{ e}^{5{ c_0}{y}^{2}}}}{12}+{\frac{1689}{16}}\,{{ c_0}}^{2}\\&\quad \times \Bigg [ -{\frac{75}{1126}}{{ c_3}}^{2} \Bigg \{ \Bigg [ -{\frac{448}{75}}{{ c_3}}^{2}{{ c_2}}^{4}{y}^{4 }{{ c_0}}^{5}{y}^{10}\\&\quad +{\frac{5528}{225}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{8}-{\frac{8}{ 15}}\,{{ c_2}}^{6}+{{ c_3}}^{6}{y}^{12} \Bigg ] {{ c_0}}^{6}\\&\quad + \left( {\frac{17}{9}}\,{{ c_3}}^{6}{y}^{10}+{\frac{728}{75}}\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{2}-{\frac{10976}{75}}\,{{ c_3}}^{4}{ { c_2}}^{2}{y}^{6} \right) {{ c_0}}^{5}\\&\quad + \Bigg \{ {\frac{9184}{75}} \,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{4}+{\frac{484}{225}}\,{{ c_3}}^{ 6}{y}^{8} -{\frac{112}{3}}\,{{ c_3}}^{2}{{ c_2}}^{4} \Bigg \} {{ c_0}}^{4}\\&\quad + \left( {\frac{1792}{25}}\,{{ c_3}}^{4}{{ c_2}}^{2}{ y}^{2}-{\frac{1076}{225}}\,{{ c_3}}^{6}{y}^{6} \right) {{ c_0}}^{ 3}\\&\quad + \left( -{\frac{5176}{225}}\,{{ c_3}}^{6}{y}^{4}+{\frac{1232}{ 15}}\,{{ c_3}}^{4}{{ c_2}}^{2} \right) {{ c_0}}^{2}\\&\quad -{\frac{436}{25}}\,{{ c_3}}^{6}{ c_0}\,{y}^{2} -{\frac{136}{15}}\,{{ c_3}}^{ 6} \Bigg \} {{ e}^{{ c_0}\,{y}^{2}}}\\&\quad +{{ c_0}}^{2}{{ c_2}}^{2} \Bigg \{ \left( {{ c_3}}^{6}{y}^{12}+{\frac{4}{5067}}\,{{ c_2}}^{ 6}\right. \\&\quad \left. +{\frac{200}{1689}}\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{4}-{\frac{ 3394}{1689}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{8} \right) {{ c_0}}^{ 6}\\&\quad + \left( -{\frac{84}{563}}\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{2}-{ \frac{2981}{1689}}\,{{ c_3}}^{6}{y}^{10}\right. \\&\quad \left. +{\frac{7840}{563}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{6} \right) {{ c_0}}^{5} + \left( -{ \frac{6440}{563}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{4}\right. \\&\quad \left. -{\frac{8156}{ 1689}}\,{{ c_3}}^{6}{y}^{8}+{\frac{300}{563}}\,{{ c_3}}^{2}{{ c_2}}^{4} \right) {{ c_0}}^{4} \end{aligned}$$

$$\begin{aligned}&\quad -{\frac{2632}{1689}}\,{{ c_3}}^{4}{y }^{2} \left( 3\,{{ c_2}}^{2}+{{ c_3}}^{2}{y}^{4} \right) {{ c_0} }^{3}\\&\quad +{\frac{6160}{563}}\,{{ c_3}}^{4} \left( {{ c_3}}^{2}{y}^{4} -1/2\,{{ c_2}}^{2} \right) {{ c_0}}^{2}\\&\quad +{\frac{3024}{563}}\,{{ c_3}}^{6}{ c_0}\,{y}^{2}+{\frac{4760}{1689}}\,{{ c_3}}^{6} \Bigg \} \Bigg ] {{ c_2}}^{2} \Bigg \}\\&\quad \times \Bigg [ { c_3}\,{{ e}^{1/2\,{ c_0} \,{y}^{2}}}{ c_2}\,{ c_0}+5/4\,{ c_0}\, \left( -4/5\,{ c_0}\,{ y}^{2}\right. \\&\left. +{{ c_0}}^{2}{y}^{4}-4/5 \right) { c_3}\,{ c_2}\,{{ e}^ {-1/2\,{ c_0}\,{y}^{2}}} + \left( { c_0}\,{y}^{2}-1 \right) {{ c_0}}^{2}\\&\quad \times \left( { c_0}{y}^{2}+\frac{1}{2} \right) {{ c_2}}^{2}{{ e}^{ -{ c_0}{y}^{2}}}+\frac{{{ c_3}}^{2}{{ e}^{{ c_0}{y}^{2}}}}{2} + \frac{\left( {{ c_2}}^{2}-{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2}}{2}\\&\quad -1/2{{ c_3}}^{2}{y}^{2}{ c_0}-1/2{{ c_3}}^{2} \Bigg ] ^{-3} \left( 2{ c_3}{ e}^{\frac{{ c_0}{y}^{2}}{2}}{ c_2}{ c_0}\right. \\&\quad \left. +{{ c_3}}^{2}{{ e}^{{ c_0}{y}^{2}}}+{{ c_2 }}^{2}{{ c_0}}^{2} \right) ^{-2} -2 f(y)\; \Bigg \{ {\frac{9}{32}}\,{{ c_0}}^{5} \Bigg [ {y}^{4} \left( {{ c_3}}^{4}{y}^{8}\right. \\&\quad \left. +{\frac{74}{3}}\,{{ c_2}}^{4}+ 318\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{6}\\&\quad + \Bigg ( -200\,{{ c_3}}^{4}{y}^{10}-464\,{{ c_3}}^{2}{{ c_2}}^{2} {y}^{6}-{\frac{40}{3}}\,{{ c_2}}^{4}{y}^{2} \Bigg ) {{ c_0}}^{5}\\&\quad + \Bigg [ 108\,{{ c_3}}^{4}{y}^{8}-{\frac{40}{3}}\,{{ c_2}}^{4} \end{aligned}$$

$$\begin{aligned}&\quad -304 \,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \Bigg ] {{ c_0}}^{4} + \left( 504\,{{ c_3}}^{4}{y}^{6}+320\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2} \right) {{ c_0}}^{3}\\&\quad + \left( -28\,{{ c_3}}^{4}{y}^{4}+160\,{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{2}\\&\quad -336\,{{ c_3}}^{4}{ c_0}\,{y}^{2}-112\,{{ c_3}}^{4} \Bigg ] { c_3}\,{{ c_2}}^{5}{ { e}^{-1/2\,{ c_0}\,{y}^{2}}}\\&\quad -{\frac{195}{64}}\,{{ c_0}}^{3}{ c_3}\, \Bigg \{ \left( -{\frac{16}{39}}\,{{ c_2}}^{6}+{{ c_3}}^ {6}{y}^{12}\right. \\&\quad \left. -{\frac{240}{13}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{8}-{ \frac{1392}{65}}\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{4} \right) {{ c_0}}^{6}\\&\quad -{\frac{252}{65}}\, \left( {{ c_3}}^{4}{y}^{8}-{\frac{80}{ 21}}\,{{ c_2}}^{4}-{\frac{44}{3}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^ {4} \right) {y}^{2}{{ c_3}}^{2}{{ c_0}}^{5}\\&\quad -{\frac{492}{65}}\, \left( {{ c_3}}^{4}{y}^{8}-{\frac{80}{41}}\,{{ c_2}}^{4}-{\frac{140}{41}}\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_3}}^{2} {{ c_0}}^{4}\\&\quad + \left( -{\frac{4032}{65}}\,{{ c_3}}^{4}{{ c_2}}^{ 2}{y}^{2}-{\frac{32}{13}}\,{{ c_3}}^{6}{y}^{6} \right) {{ c_0}}^{ 3}\\&\quad + \left( -{\frac{2016}{65}}\,{{ c_3}}^{4}{{ c_2}}^{2}+{\frac{ 144}{13}}\,{{ c_3}}^{6}{y}^{4} \right) {{ c_0}}^{2}\\&\quad +{\frac{192}{ 13}}\,{{ c_3}}^{6}{ c_0}\,{y}^{2}+{\frac{64}{13}}\,{{ c_3}}^{6} \Bigg \} {{ c_2}}^{3}{{ e}^{1/2\,{ c_0}\,{y}^{2}}}+{\frac{7}{ 16}}\,{ c_0}\\&\quad \times \Bigg \{ \left( {\frac{240}{7}}\,{{ c_2}}^{6}+{{ c_3}}^{6}{y}^{12}-27\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{8}+198\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{4} \right) {{ c_0}}^{6}\\&\quad -6/7\,{y}^{2}{ { c_3}}^{2} \Bigg \{ 252\,{{ c_2}}^{4}+{{ c_3}}^{4}{y}^{8}+60{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \Bigg \} {{ c_0}}^{5}\\&\quad + \left( -{ \frac{39{{ c_3}}^{6}{y}^{8}}{7}}-216\,{{ c_3}}^{2}{{ c_2}}^{4 }+{\frac{360}{7}}{{ c_3}}^{4}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4} \end{aligned}$$

$$\begin{aligned}&\quad + \left( {\frac{1440{{ c_3}}^{4}{{ c_2}}^{2}{y}^{2 }}{7}}-{\frac{86{{ c_3}}^{6}{y}^{6}}{7}} \right) {{ c_0}}^{3}\\&\quad + \Bigg \{ {\frac{720{{ c_3}}^{4}{{ c_2}}^{2}}{7}} -{\frac{93}{7}} {{ c_3}}^{6}{y}^{4} \Bigg \} {{ c_0}}^{2}-{\frac{60}{7}}{{ c_3}}^{6}{ c_0}{y}^{2}\\&\quad -{\frac{20{{ c_3}}^{6} }{7}}\Bigg \} {{ c_3}}^{3}{ c_2}{ e}^{\frac{3{ c_0}{y}^{2}}{2}}+{\frac{2397{{ c_0}}^{7}{ c_3}{{ c_2}}^{7}}{64}}\\&\quad \times \Bigg \{ {y}^{8} \left( { \frac{16{{ c_2}}^{2}}{47}}+{{ c_3}}^{2}{y}^{4} \right) {{ c_0 }}^{6}\\&\quad - \left( {\frac{296{{ c_2}}^{2}{y}^{6}}{799}}+{\frac{1908 {{ c_3}}^{2}{y}^{10}}{799}} \right) {{ c_0}}^{5}\\&\quad - \left( \frac{216{{ c_2}}^{2}{y}^{4}}{799}+{\frac{516{{ c_3} }^{2}{y}^{8} }{799}}\right) {{ c_0}}^{4}\\&\quad + \left( {\frac{2464{y}^{6}{{ c_3}}^{2}}{799}}+{\frac{160{{ c_2}}^{2}{y}^{2} }{799}}\right) {{ c_0}}^{3}\\&\quad + \left( {\frac{432{{ c_3}}^{2}{y}^{4}}{799}}+{\frac{80{{ c_2}}^{2} }{799}}\right) {{ c_0}}^{2}\\&\quad -{\frac{960{{ c_3}}^{2}{y}^{2}{ c_0}}{799}} -{\frac{320{{ c_3}}^{2}}{799}} \Bigg \}{ e}^{-\frac{3{ c_0}{y}^{2}}{2}}\\&\quad +3/8\,{ c_0}\, \Bigg \{ \left( 84\,{{ c_2}}^{4}+{{ c_3}}^{4}{y}^{8}+30\,{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}\\&\quad + \left( -120\,{{ c_3}}^{2 }{{ c_2}}^{2}{y}^{2}+11\,{{ c_3}}^{4}{y}^{6} \right) {{ c_0}}^{3 } \end{aligned}$$

$$\begin{aligned}&\quad + \left( 21\,{{ c_3}}^{4}{y}^{4}-120\,{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{2}+20\,{{ c_3}}^{4}{ c_0}\,{y}^{2}\\&\quad +10\,{{ c_3}}^{4} \Bigg \} {{ c_3}}^{5}{ c_2}\,{{ e}^{5/2\,{ c_0}\,{y}^ {2}}}-{\frac{31}{4}}\,{{ c_0}}^{9} \left( { c_0}\,{y}^{2}-1 \right) ^{2}\\&\quad \times \left( { c_0}\,{y}^{2}+1/2 \right) ^{2} \left( { \frac{20}{31}}+{\frac{20}{31}}\,{ c_0}\,{y}^{2}-{{ c_0}}^{2}{y}^ {4} \right) { c_3}\,{{ c_2}}^{9}{{ e}^{-5/2\,{ c_0}\,{y}^{2}} }\\&\quad +{\frac{33}{16}}\,{ c_0}\,{{ c_3}}^{7} \Bigg \{ \Bigg [ {\frac{ 80}{11}}\,{{ c_2}}^{2}-{{ c_3}}^{2}{y}^{4} \Bigg ] {{ c_0}}^{2}- {\frac{20}{11}}\,{{ c_3}}^{2}{y}^{2}{ c_0}\\&\quad -{\frac{20}{11}}\,{{ c_3}}^{2} \Bigg \} { c_2}\,{{ e}^{7/2\,{ c_0}\,{y}^{2}}}+5/4 \,{ c_0}\,{{ c_3}}^{9}{ c_2}\,{{ e}^{9/2\,{ c_0}\,{y}^{2}}} \\&\quad +{\frac{843}{32}}\,{{ c_0}}^{6} \Bigg \{ \left( {{ c_3}}^{4}{y}^{8 }+{\frac{8}{281}}\,{{ c_2}}^{4}+{\frac{489}{281}}\,{{ c_3}}^{2}{ { c_2}}^{2}{y}^{4} \right) {y}^{4}{{ c_0}}^{6}\\&\quad - \left( {\frac{ 1059{{ c_3}}^{4}{y}^{10}}{281}}+{\frac{600{{ c_3}}^{2} {{ c_2}}^{2}{y}^{6}}{281}}+{\frac{4{{ c_2}}^{4}{y}^{2} }{281}}\right) {c_0}^{5}\\&\quad - \left( {\frac{51{{ c_3}}^{4}{y}^{8}}{281}}+{ \frac{4{{ c_2}}^{4}}{281}}+{\frac{420{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4}}{281}} \right) {{ c_0}}^{4}\\&\quad + \left( {\frac{1736{{ c_3}}^{4}{y}^{6}}{281}} +{\frac{360{{ c_3}}^{2}{{ c_2}}^{ 2}{y}^{2}}{281}} \right) {{ c_0}}^{3}\\&\quad + \left( {\frac{168}{281}}\,{{ c_3} }^{4}{y}^{4}+{\frac{180}{281}}\,{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{2} -{\frac{840}{281}}\,{{ c_3}}^{4}{ c_0}\,{y}^{2}\\&\quad -{ \frac{280}{281}}\,{{ c_3}}^{4} \Bigg \} {{ c_2}}^{6}{{ e}^{-{ c_0}\,{y}^{2}}}-1/8\,{{ c_3}}^{4} \Bigg \{ \Bigg [ -210\,{{ c_2}} ^{6}\\&\quad +{{ c_3}}^{6}{y}^{12}+{\frac{153}{4}}\,{{ c_3}}^{4}{{ c_2}} ^{2}{y}^{8} -378\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{4} \Bigg ] {{ c_0} }^{6} \end{aligned}$$

$$\begin{aligned}&\quad + \left( 3\,{{ c_3}}^{6}{y}^{10}-36\,{{ c_3}}^{4}{{ c_2}}^{ 2}{y}^{6}+630\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{2} \right) {{ c_0}}^ {5}\\&\quad + \left( 6\,{{ c_3}}^{6}{y}^{8}+630\,{{ c_3}}^{2}{{ c_2}}^{4} -171\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}+ \Bigg \{ 7\,{{ c_3}}^{6}{y}^{6}\\&\quad -270\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^ {2} \Bigg \} {{ c_0}}^{3}+ \left( -135\,{{ c_3}}^{4}{{ c_2}}^{2}+ 6\,{{ c_3}}^{6}{y}^{4} \right) {{ c_0}}^{2}\\&\quad +3\,{{ c_3}}^{6}{ c_0}\,{y}^{2}+{{ c_3}}^{6} \Bigg \} {{ e}^{2\,{ c_0}\,{y}^{2}}}\\&\quad +{ \frac{387}{16}}\, \left( { c_0}\,{y}^{2}-1 \right) \Bigg \{ \left( {{ c_3}}^{2}{y}^{8}+{\frac{8}{129}}\,{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}\\&\quad + \left( -{\frac{4}{129}}\,{{ c_2}}^{2}{y}^{2}-{ \frac{60}{43}}\,{y}^{6}{{ c_3}}^{2} \right) {{ c_0}}^{3}\\&\quad + \left( -{\frac{40}{43}}\,{{ c_3}}^{2}{y}^{4}-{\frac{4}{129}}\,{{ c_2}}^ {2} \right) {{ c_0}}^{2}\\&\quad +{\frac{40}{43}}\,{{ c_3}}^{2}{y}^{2}{ c_0}+{\frac{20}{43}}\,{{ c_3}}^{2} \Bigg \} \left( { c_0}\,{y} ^{2}+1/2 \right) {{ c_0}}^{8}{{ c_2}}^{8}{{ e}^{-2\,{ c_0}\,{ y}^{2}}}\\&\quad +3/8\, \left( \left( 70{{ c_2}}^{4}+{{ c_3}}^{4}{y}^{8} -6{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}\right. \\&\quad \left. + \left( -45{{ c_3}}^{2}{{ c_2}}^{2}{y}^{2}+2{{ c_3}}^{4}{y}^ {6} \right) {{ c_0}}^{3}\right. \\&\quad \left. + \left( 3{{ c_3}}^{4}{y}^{4}-45{{ c_3}}^{2}{{ c_2}}^{2} \right) {{ c_0}}^{2}+2{{ c_3}}^{4}{ c_0 }{y}^{2}+{{ c_3}}^{4} \right) {{ c_3}}^{6}{{ e}^{3{ c_0} {y}^{2}}}\\&\quad +{{ c_0}}^{10} \left( { c_0}\,{y}^{2}-1 \right) ^{3} \left( { c_0}\,{y}^{2}+1/2 \right) ^{3}{{ c_2}}^{10}{{ e}^{-3 \,{ c_0}\,{y}^{2}}}\\&\quad -3/8\,{{ c_3}}^{8} \left( \left( {{ c_3}}^{2 }{y}^{4}-15\,{{ c_2}}^{2} \right) {{ c_0}}^{2}+{{ c_3}}^{2}{y}^{ 2}{ c_0}+{{ c_3}}^{2} \right) {{ e}^{4\,{ c_0}\,{y}^{2}}}\\&\quad +1/8 \,{{ c_3}}^{10}{{ e}^{5\,{ c_0}\,{y}^{2}}} -{\frac{159}{16}}\,{ { c_0}}^{2} \Bigg [ -{\frac{15}{106}}\,{{ c_3}}^{2} \Bigg \{ \left( 4\,{{ c_2}}^{6}+{{ c_3}}^{6}{y}^{12}\right. \end{aligned}$$

$$\begin{aligned}&\quad \left. +{\frac{17}{5}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{8}+{\frac{336}{5}}\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{4} \right) {{ c_0}}^{6}\\&\quad + \left( {\frac{17}{5}}\,{{ c_3}}^{6}{y}^{10}-{\frac{336}{5}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y} ^{6}-56\,{{ c_3}}^{2}{{ c_2}}^{4}{y}^{2} \right) {{ c_0}}^{5}\\&\quad + \left( 9/5\,{{ c_3}}^{6}{y}^{8}-56\,{{ c_3}}^{2}{{ c_2}}^{4}-{ \frac{56}{5}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}} ^{4}\\&\quad + \left( 112\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{2}-{\frac{36}{5}} \,{{ c_3}}^{6}{y}^{6} \right) {{ c_0}}^{3}\\&\quad + \left( 56\,{{ c_3}}^ {4}{{ c_2}}^{2}-{\frac{68}{5}}\,{{ c_3}}^{6}{y}^{4} \right) {{ c_0}}^{2}-12\,{{ c_3}}^{6}{ c_0}\,{y}^{2}\\&\quad -4{{ c_3}}^{6} \Bigg \} {{ e}^{{ c_0}{y}^{2}}}-{{ c_0}}^{2} \Bigg \{ \left( {\frac{2}{159}}{{ c_2}}^{6}-{{ c_3}}^{6}{y}^{12}\right. \\&\quad \left. +{\frac{1059}{ 106}}{{ c_3}}^{4}{{ c_2}}^{2}{y}^{8}+{\frac{150}{53}}{{ c_3 }}^{2}{{ c_2}}^{4}{y}^{4} \right) {{ c_0}}^{6}\\&\quad +{\frac{51}{106}} \left( {{ c_3}}^{4}{y}^{8}+{\frac{60}{17}}{{ c_2}}^{4}+{\frac{672}{17}}{{ c_3}}^{2}{{ c_2}}^{2}{y}^{4} \right) {y}^{2}{{ c_3}}^{2}{{ c_0}}^{5}\\&\quad + \left( -{\frac{453}{106}}\,{{ c_3}}^{6}{y}^ {8}+{\frac{90}{53}}\,{{ c_3}}^{2}{{ c_2}}^{4}+{\frac{588}{53}}\, {{ c_3}}^{4}{{ c_2}}^{2}{y}^{4} \right) {{ c_0}}^{4}\\&\quad + \left( -{ \frac{840}{53}}\,{{ c_3}}^{4}{{ c_2}}^{2}{y}^{2}-{\frac{364}{53} }\,{{ c_3}}^{6}{y}^{6} \right) {{ c_0}}^{3} \end{aligned}$$

$$\begin{aligned}&\quad + \left( -{\frac{420}{ 53}}\,{{ c_3}}^{4}{{ c_2}}^{2}+{\frac{168}{53}}\,{{ c_3}}^{6}{y }^{4} \right) {{ c_0}}^{2}\\&\quad +{\frac{420}{53}}\,{{ c_3}}^{6}{ c_0} \,{y}^{2}+{\frac{140}{53}}\,{{ c_3}}^{6} \Bigg \} {{ c_2}}^{2} \Bigg ] {{ c_2}}^{2} \Bigg \} \\&\quad \times \Bigg [ { c_3}\,{{ e}^{1/2\,{ c_0}\,{y}^{2}}}{ c_2}\,{ c_0}+5/4\,{ c_0}\, \left( -4/5\,{ c_0} \,{y}^{2}+{{ c_0}}^{2}{y}^{4}-4/5 \right) \\&\quad \times { c_3}\,{ c_2}\,{ { e}^{-1/2\,{ c_0}\,{y}^{2}}} + \left( { c_0}\,{y}^{2}-1 \right) {{ c_0}}^{2}\\&\quad \times \left( { c_0}\,{y}^{2}+1/2 \right) {{ c_2} }^{2}{{ e}^{-{ c_0}\,{y}^{2}}}+1/2\,{{ c_3}}^{2}{{ e}^{{ c_0}\,{y}^{2}}} \\&\quad + \left( 1/2\,{{ c_2}}^{2}-1/2\,{{ c_3}}^{2}{y}^{4} \right) {{ c_0}}^{2}-1/2\,{{ c_3}}^{2}{y}^{2}{ c_0}-1/2\,{{ c_3}}^{2} \Bigg ] ^{-3} \\&\quad \times \Bigg [ 2\,{ c_3}\,{{ e}^{1/2\,{ c_0}\,{y }^{2}}}{ c_2}\,{ c_0}+{{ c_3}}^{2}{{ e}^{{ c_0}\,{y}^{2}}} + {{ c_2}}^{2}{{ c_0}}^{2} \Bigg ] ^{-2}=0. \end{aligned}$$

The above lengthy differential equation can be rewritten in a compact form as

$$\begin{aligned} f'''(y)N(y)+f''(y)N_1(y)+f'(y)N_2(y)+f(y)N_3(y)=0, \end{aligned}$$

where $N(y),\, N_1(y),\,N_2(y),\, N_3(y)$ are complicated functions of y obtained by summing up the coefficients of the same derivatives. The asymptotic form of this differential equation, up to $O\left( \frac{1}{y}\right)$, gives Eq. (19).