1 Introduction

Since the remarkable advance in astrophysical observation in the last decade, the study of strong gravitational field regime in alternative theories was becoming more interesting [1,2,3,4]. Neutron Stars (NSs) are one of the most compact objects for testing different theoretical models of gravity. In fact, the theory of General Relativity (GR) explains very well the observations at the weak gravitational background [5], but one can imagine that the theory of GR is a subject of modification around a NSs. The deviation from GR can be explored via Gravitational Waves (GWs) signal, from the collision between binary neutron stars (NSs), binary black holes (BHs) or binary BH-NS, which carry information about the properties of NSs [6, 7].

The golden era of gravitational-wave astronomy was launched by the first observation of GWs signal coming from a binary black hole merger [8, 9], at LIGO and Virgo observatories. After two years, the detection of gravitational waves from a binary neutron star merge GW170817 [10] together with gamma-ray burst GRB 170817A [11,12,13] has considerably advanced our understanding in alternative theory of gravity [14,15,16,17,18]. On August 14, 2019, the LIGO/Virgo Collaboration (LVC) announced the detection of GWs sourced by the collision of a black hole with mass \(M\approx 23.2^{+1.1}_{-1.0}M_{Sun}\) and a compact object with mass \(M\approx 2.59^{+0.08}_{-0.09}M_{Sun}\) GW19081 [19], where \(M_{Sun}\) is solar mass. It is difficult to identify the nature of this object, whether it is the most massive NS or the least massive BH, because neither electromagnetic counterpart nor measurable tidal deformation signature was imprinted in GW19081-event.

According to mass–radius relation in general relativity, where the nuclear matter is described by the realistic Equation of States (EoSs) SLy, FPS [20], Brussels–Montreal–Skyrme (BSk) [21], the Arnowitt–Deser–Misner (ADM) mass is lower than the value \(M_{Max}=2.5M_{Sun}\) [3]. However, the Limit of the maximum mass can be broken if we describe the gravity by a model that belong generalized Proca theories instead of GR which is due to the nonminimal coupling \(\beta A_\mu A^\mu R+\beta ( (\nabla _\mu A^\mu )^2-\nabla _\mu A_\nu \nabla ^\nu A^\mu )\), where \(\beta \) is a real constant, \(A_\mu \) is the vector field and R is Ricci scalar [22]. The mass–radius relation for NSs in alternative theory of gravity, such as: f(R)-gravity where the Ricci scalar is replaced by an arbitrary function of R in the Hilbert–Einstien (HE) action, have been extensively studied in the literature [23,24,25,26,27,28]. In Ref. [28], many models of f(R)-gravity have been adopted to discuss the mass–radius diagram for static neutron star by solving modified Tolman–Oppenheimer–Volkoff (TOV) equations numerically. For each special function chosen by the authors, specifics constraint on the model’s parameter must be imposed to hold the positivity of energy-matter tensor trace \(T^{(m)}=\rho -3 P\), where \(\rho \) and P are the energy density and the pressure of the matter inside the NS, respectively.

In our present paper, we propose to study a spherical NSs in scalar-torsion theories of gravity [29,30,31] in which we consider an arbitrary function F[T, X, Y] (the details on the quantities T, X and Y will be illustrated in the next section). These theories are based on the formalism of Teleparallel equivalent to general relativity (TEGR) [32] and they are a generalization to modified Teleparallel gravity (F(T)-gravity) [33,34,35,36], scalar-torsion gravity without derivative coupling [37] or conformally coupled scalar-torsion gravity [38]. The main reason to deal with F[T, X, Y] theories, instead of F(R) theories, is that the field equations of gravity are second order differential equations. This will allow us to avoid Ostrogradsky instability [39] which is related to presence of extra scalar degree of freedom [40]. Moreover, modified Teleparallel gravity did not only explain the late accelerate universe [41, 42] but it may also provide an alternative to inflation [43, 44]. In addition, compact stars was investigated in the context of the Teleparallel equivalent of general relativity, for many models of modified Teleparallel gravity [45,46,47,48], to understand the structure and properties of the observed (or not observed) NSs. However, the conservation equation of relativistic stars in f(T)-modified gravity coincides with its general relativistic counterpart only for a tetrad field in the diagonal gauge and a constant torsion scalar solution, but for a diagonal-off tetrad field the conservation equation is always the same to that in GR [49]. Therefore, it is interesting to investigate the properties of NSs in F[T, X, Y]-theories, by integrating TOV equations in these theories numerically using different EoSs, and to observe the deviation from GR for a specific model.

Another important quantity we will take into consideration is the moment of inertia which can be obtained from the perturbed equations of a slowly rotating star. A slowly rotating neutron star can be studied by using the perturbative approach introduced by Hartle in 1967 [50] and the tetrads, that correspond to axially symmetric spacetime, obtained in [51]. The estimation of moment of inertia and the mass of NS will allow us to constraint the equation of state of NSs to calculate the radius using the mass and moment of inertia of binary NSs [52]. Since, the modification of gravity effects the mass and radius of NS, one can expect that alternative theories of gravity will also effect the moment of inertia as it was show in Refs. [53,54,55,56,57]. Inspiring from these works, we will extend our investigation on NS in the frame of F[T, X, Y]-theory to a slowly rotating star.

This paper is constructed as follow: First, we briefly introduce the fundamental concepts of teleparallel gravity and the general gravitational equations of F[T, X, Y]-theory in Sect. 2. Second, in Sect. 3, we derive the generalized TOV equations of the model and we study the behaviour of the metric, energy density, pressure and the scalar field at the center of the star and at large value of the radial coordinate. In Sect. 4, we calculate the equation of a slowly rotating star in F[T, X, Y]-theory, using a particular tetrad, as well as we define the moment of inertia. Then, we present and discuss the numerical solutions, mass–radius and mass–moment of inertia relations of all equations in Sect. 5. Final, we conclude our we by a conclusion in Sect. 6.

2 Brief review of scalar-torsion theories

In this section we briefly review the fundamental formalism of Teleparallel gravity, the general form of the action functional and the general dynamical equations field in F[T, X, Y]-theories. In teleparallel gravity, the basic variables are the tetrad \(e^a_\mu \) and the spin connection \(\omega ^a_{\;\;b\mu }\) as well as we can add a scalar field \(\varphi \) to the theory. Note that in our work we will use the Latin letters \(a,b,c\ldots =\{0,1,2,3\}\) for Lorentz indices, where we define Minkowski metric \(\eta _{ab}\) with the signature \((-,+,+,+)\), and the Greek indices \(\mu ,\nu \ldots =\{0,1,2,3\}\) for spacetime indices. The Minkowski is related to the metric \(g_{\mu ,\nu }\), usually used in GR, by

$$\begin{aligned} g_{\mu \nu }=\eta _{ab}e^a_\mu e^b_\nu ,\qquad \eta _{ab}=g_{\mu \nu }e_a^\mu e_b^\nu , \end{aligned}$$
(1)

where

$$\begin{aligned} e_a^\mu e^a_\nu =\delta ^\mu _\nu ,\qquad e_a^\mu e^b_\nu = \delta ^b_a . \end{aligned}$$
(2)

In addition, the Lorentz transformation of the tetrad and the spin connection is given by

$$\begin{aligned}&e^a_\mu \rightarrow \Lambda ^a_b e^b_\mu \end{aligned}$$
(3)
$$\begin{aligned}&\omega ^a_{\;\;b\mu } \rightarrow \Lambda ^a_{\;\;c}\Lambda ^b_{\;\;d} \omega ^c_{\;\;d\mu }-\Lambda ^b_{\;\;c} \partial _\mu \Lambda ^c_a \end{aligned}$$
(4)

We will use the classical formulation of teleparallel gravity in which the spin connection vanishes (Weitzenb\(\ddot{o}\)ck gauge). Therefore, the theory that we will study depend only on the scalar field, the tetrad and the matter field. So, the torsion tensor reads

$$\begin{aligned} T^a_{\;\;\mu \nu }=\partial _{\mu } e_\nu ^a -\partial _{\nu } e_\mu ^a. \end{aligned}$$
(5)

In order to construct the teleparallel theory, we need to define the scalar torsion

$$\begin{aligned} T=S_{\lambda }^{\;\;\mu \nu }T^{\lambda }_{\;\;\mu \nu }, \end{aligned}$$
(6)

where \(S_{\lambda }^{\;\;\mu \nu }\) is called the supper penitential [34]

$$\begin{aligned} 2S_{\lambda }^{\;\;\mu \nu }=K_{\lambda }^{\;\;\mu \nu }+\delta _\lambda ^\nu T_{\mu }-\delta _\lambda ^\mu T_{\nu }, \end{aligned}$$
(7)

with

$$\begin{aligned} 2K_{\mu \;\;\;\;\nu }^{\;\;\lambda }=T_{\mu \;\;\;\;\nu }^{\;\;\lambda }+T_{\lambda }^{\;\;\mu \nu }-T_{\nu \mu }^{\;\;\;\;\lambda }, \end{aligned}$$
(8)

In this context, the Ricci scalar coincide with the following expression

$$\begin{aligned} R=-T+\frac{2}{e}\partial _\mu (e T^{\lambda }_{\;\;\lambda \nu }). \end{aligned}$$
(9)

where \(e=det(e^a_\mu )\) is the determinant of the tetrad field. Because of the second therm in the left side of this expression, the resulting field’s equations of a torsion Lagrangian will be identical to those in GR (This why we call this theory Teleparallel gravity equivalent to General relativity).

Now, we consider a modified theory of teleparallel gravity with the following shift symmetric action, i.e., when the functions in the Lagrangian are invariant under the transformation \(\varphi \rightarrow \varphi +const\):

$$\begin{aligned} S= \int d^4 x\, e \, \left( F[T,X,Y]+L_m \right) \end{aligned}$$
(10)

where \(L_m\) is Lagrangian of matter, \(X=-1/2\partial _\mu \varphi \partial ^\mu \varphi \) is the kinetic term and \(Y=g^{\mu \nu }T^{\lambda }_{\;\;\lambda \nu }\partial _\mu \varphi \) is the derivative coupling term [30]. The action (10) is a sub-set of the Lagrangian studied in Refs. [33, 34] in which they show the most scalar-torsion theory with second order derivatives that give field equations of second order. In addition, the gravitational waves propagation speed in this action is constrained to the speed of light and thus the measurements of the GWs’s speed by Ligo/Virgo from GW170817 and GRB 170817A events are satisfied [33].

In order to derive the general equations, we vary the Eq. (10) with respect to scalar and tetrad fields. By doing so, we get

$$\begin{aligned} \delta S= & {} \int d^4x\; e \left( \left( T_a^{\mu }+T_a^{\mu (m)}\right) \delta e^a_\mu + \frac{\delta F[T,X,Y]}{\delta \varphi } \delta \varphi \right) ,\nonumber \\ \end{aligned}$$
(11)

where

$$\begin{aligned}&T_a^{\mu }=\frac{1}{e}\frac{\delta \left[ e F[T,X,Y]\right] }{\delta e^a_\mu }, \end{aligned}$$
(12)
$$\begin{aligned}&T_a^{\mu (m)}=\frac{1}{e}\frac{\delta \left[ e L_m\right] }{\delta e^a_\mu }. \end{aligned}$$
(13)

In the Eq. (11), we distinct two equations, which should be vanished, where the first equation is the term proportional to \(\delta e^a_\mu \) while the second one is the term proportional to \(\delta \varphi \). The equations corresponding to tetrads field is the first term equal to zero and it given by [30]

$$\begin{aligned} T_a^{\mu }= & {} 4\partial _\lambda (F_T)S_a^{\;\;\lambda \mu }\nonumber \\&+4e^{-1}\partial _\lambda (e S_a^{\;\;\lambda \mu })F_T\nonumber \\&-4F_T T^\sigma _{\;\;\lambda a}S_\sigma ^{\;\;\mu \lambda }-\partial _a\varphi \left( F_X\partial ^\mu \varphi - F_Y T^\mu \right) \nonumber \\&+F_Y T^b \left( T^\mu _{\;\; a b}+T_a e_b^\mu \right) \nonumber \\&+e^{-1}\partial _\nu \left( e F_Y T^b\left( e_b^\mu e_a^\nu - e_a^\mu e_b^\nu \right) \right) \nonumber \\= & {} T_a^{\mu (m)}, \end{aligned}$$
(14)

where \(F_T\equiv \partial F[T,X,Y]/\partial T\), \(F_X\equiv \partial F[T,X,Y]/\partial X\) and \(F_X\equiv \partial F[T,X,Y]/\partial X\). In addition, by imposing the symmetry conditions on the energy-momentum of the matter \(T^{[\mu \nu ](m)}=0\), where this tensor is obtained by using the relation \(T^{\mu \nu (m)}=\eta ^{ab} e_b^{\nu }T_a^{\mu (m)}\), we writ the antisymmetric equation as

$$\begin{aligned} \eta ^{ab}e_b^{[\nu }T_a^{\mu ]}=0. \end{aligned}$$
(15)

Similarly, the equation for the scalar field reads:

$$\begin{aligned} \nabla _\mu J^\mu =0, \end{aligned}$$
(16)

where

$$\begin{aligned} J^\mu =F_Y T^\mu -G_X \partial ^\mu \varphi . \end{aligned}$$
(17)

Finally, the general equation that determine the spacetime evolution of fluid is the matter conservation equation:

$$\begin{aligned} \nabla _\mu T^{\mu \nu (m)}=0, \end{aligned}$$
(18)

where

$$\begin{aligned} T^{\mu \nu (m)}=\left( P+\rho \right) u^\mu u^\nu + g^{\mu \nu } P. \end{aligned}$$
(19)

The four-vector \(u^\mu \), \(\rho \) and P correspond to velocity vector, energy density and pressure of the matter present in the background, respectively. Note that these equations are very important to study the behaviour of many astrophysical object like: BHs, NSs, Boson stars...ex and the nature of dark energy which might be the main reason of the late-time accelerated expansion of the our universe. But in our work we will focus only on NSs.

3 Generalized TOV equations

To study a non-rotating neutron star described by spherically symmetric and static background, we consider the following metric:

$$\begin{aligned} ds^2=-f(r)dt^2+h(r)dr^2+r^2(d\theta ^2+ \sin ^2 \theta d\phi ^2), \end{aligned}$$
(20)

where functions f and h depend only on the radial coordinate r. We consider also the energy-momentum tensor \(T^{\mu (m)}_\nu =diag(-\rho (r),P(r),P(r),P(r))\) and we suppose that the scalar field \(\varphi (r)\) depend also only on r. By using these definitions and substituting the metric (20) in the matter conservation equation (18), we get

$$\begin{aligned} P'+\frac{f'}{f}\left( \rho + P \right) =0, \end{aligned}$$
(21)

where the prime denotation correspond to the first derivative with respect to r. Due to the new extra degree of freedom that appear in the tetrad fields, we can have many possibles combinations to reproduce the metric (20). In this paper, we will use the following non-diagonal tetrad [49]

$$\begin{aligned} {\overline{e}}^a_\mu = \left( \begin{array}{llll} \sqrt{f(r)} &{} \quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \sqrt{h(r)} \;\sin \theta \;\cos \phi &{}\quad r \;\cos \theta \;\cos \phi &{}\quad -r \;\sin \theta \; \sin \phi \\ 0 &{}\quad \sqrt{h(r)}\; \sin \theta \; \sin \phi &{}\quad r \;\cos \theta \; \sin \phi &{} \quad r \;\sin \theta \; \cos \phi \\ 0 &{}\quad \sqrt{h(r)} \;\cos \theta &{}\quad -r \;\sin \theta &{} \quad 0 \end{array}\right) .\nonumber \\ \end{aligned}$$
(22)

Note that the off-diagonal tetrad form is obtained from the product of a diagonal tetrad \(e_a^\mu = diag(f(r),h(r),r^2,r^2\sin ^2\theta )\) and a local Lorentz transformation matrix \(\mathbf{H} \) which is given by

$$\begin{aligned} \mathbf{H} = \left( \begin{array}{llll} 1 &{}\quad 0 &{} \quad 0 &{}\quad 0\\ 0 &{} \quad \sin \theta \;\cos \phi &{} \quad \cos \theta \; \cos \phi &{} \quad - \sin \theta \sin \phi \\ 0 &{}\quad \sin \theta \;\sin \phi &{}\quad \cos \theta \; \sin \phi &{}\quad \sin \theta \cos \phi \\ 0 &{}\quad \cos \theta &{}\quad -\sin \theta &{}\quad 0 \end{array}\right) . \end{aligned}$$
(23)

Next, the scalar torsion and it derivative is obtained by inserting the tetrad (22) in it expression (6). Doing so, it follows that

$$\begin{aligned} T= & {} \frac{2 \left( \sqrt{h}-1\right) }{h r}\frac{f'}{f}-\frac{2 \left( \sqrt{h}-1\right) ^2}{h r^2}, \end{aligned}$$
(24)
$$\begin{aligned} T'= & {} h' \frac{\left( 2-\sqrt{h}\right) f'}{f h^2 r}+2 \frac{\sqrt{h}-1}{hr}\left( \frac{1}{h r}+\frac{ f'}{f r}+\frac{f'^2}{f^2}+\frac{f''}{f }\right) \nonumber \\&+\frac{4 \left( \sqrt{h}-1\right) ^2}{h r^3}. \end{aligned}$$
(25)

We notice that the Minkowski limit is found when the functions h and f tend to 1, since the scalar torsion vanished at that limit. Using the tetrad (22), the Eq. (14) are reduced to

$$\begin{aligned} -\rho= & {} \frac{r \left( r \left( F h+\varphi ' F_{Y}'\right) -4 \left( \sqrt{h}-1\right) F_{T}'+2 F_{Y} \varphi '\right) -4 \left( \sqrt{h}-1\right) F_{T}}{h r^2}+\frac{F_{Y} \varphi ''}{h}\nonumber \\&+\frac{f' \left( r F_{Y} \varphi '-4 \left( \sqrt{h}-1\right) F_{T}\right) }{2 f h r}-\frac{h' \left( r F_{Y} \varphi '+4 F_{T}\right) }{2 h^2 r}, \end{aligned}$$
(26)
$$\begin{aligned} P= & {} -\frac{4 \left( \sqrt{h}-1\right) F_{T}-r \left( \varphi ' \left( r F_{X} \varphi '-2 \left( \sqrt{h}-2\right) F_{Y}\right) +F h r\right) }{h r^2}+ \frac{f' \left( r F_{Y} \varphi '-2 \left( \sqrt{h}-2\right) F_{T}\right) }{f h r}, \end{aligned}$$
(27)
$$\begin{aligned} P= & {} \frac{r \left( \varphi ' \left( r F_{Y}'-\left( \sqrt{h}-2\right) F_{Y}\right) +F h r-2 \left( \sqrt{h}-1\right) F_{T}'\right) +2 \left( \sqrt{h}-1\right) ^2 F_{T}}{h r^2}+\frac{F_{Y} \varphi ''}{h}-\frac{\left( f'\right) ^2 F_{T}}{2 f^2 h}\nonumber \\&+\frac{f' \left( -4 \sqrt{h} F_{T}+2 r F_{T}'+r F_{Y} \varphi '+6 F_{T}\right) }{2 f h r}+\frac{f'' F_{T}}{f h}-h' \left( \frac{f' F_{T}}{2 f h^2}+\frac{r F_{Y} \varphi '+2 F_{T}}{2 h^2 r}\right) . \end{aligned}$$
(28)

We would like to mention that the three equations are not independent where the third equation can be obtained by using the Eqs. (26), (27) and (21). Therefore, we need two equations from these equations and thus we will consider only the Eqs. (26) and (27), in the following. In addition, since the vector \(J_\mu =(0,-\frac{f' F_{Y}}{2 f}-\frac{-2 \sqrt{h} F_{Y}+r F_{X} \varphi '+2 F_{Y}}{r},0,0)\), the equation of scalar field is given by

$$\begin{aligned}&\frac{r^2 \left( f'\right) ^2 F_{Y}}{4 f^2}-\frac{r^2 f'' F_{Y}}{2 f}\nonumber \\&\quad +\frac{r h' \left( r F_{X} \varphi '+2 F_{Y}\right) }{2 h}\nonumber \\&\quad -r \left( -2 \left( \sqrt{h}-1\right) F_{Y}'+r \varphi ' F_{X}'+2 F_{X} \varphi '\right) \nonumber \\&\quad +2 \left( \sqrt{h}-1\right) F_{Y}'\nonumber \\&\quad +\frac{f'}{2f} \left( \frac{r^2 F_{Y} h'}{2 h}-r^2 \left( F_{Y}'+ F_{X} \varphi '\right) +2 r \left( \sqrt{h}-2\right) F_{Y}\right) \nonumber \\&\quad -r^2 F_{X} \varphi ''=0. \end{aligned}$$
(29)

We have four nonlinear deferential equations to determine the variation of four functions with respect to the radial coordinate r. In order to determine the numerical solutions, we need the expression of the function F, the explicit form of the equation of state \(P(\rho )\) as well as initial conditions on the functions f, h, \(\rho \) and \(\varphi \). In this paper, we will use the analytic expressions of EoS for a realistic NSs, which has been derived in Refs. [20, 21]. In this Refs, they introduce the variables \(\xi =log_{10}(\rho /g\;\mathrm{cm}^{-3})\) and \(\zeta =log_{10}(P/g\;\mathrm{cm}^{-3})\) to express the parametrization of \(P(\rho )\) and it is given by

$$\begin{aligned} \zeta= & {} \frac{\text {a}_1+\text {a}_2 \xi +\text {a}_3 \xi ^3}{(\text {a}_4 \xi +1)}d\left( \text {a}_5 (\xi -\text {a}_6)\right) \nonumber \\&+(\text {a}_7+\text {a}_8 \xi )d\left( \text {a}_9 (\text {a}_{10}-\xi )\right) +(\text {a}_{11}+\text {a}_{12} \xi )d\left( \text {a}_{13} (\text {a}_{14}-\xi )\right) \nonumber \\&+(\text {a}_{15}+\text {a}_{16} \xi )d\left( \text {a}_{17} (\text {a}_{18}-\xi )\right) \nonumber \\&+\frac{\text {a}_{19}}{\text {a}^2_{20} (\text {a}_{21}-\xi )^2+1}+\frac{\text {a}_{22}}{\text {a}^2_{23} (\text {a}_{24}-\xi )^2+1}, \end{aligned}$$
(30)

where

$$\begin{aligned} d(x)=\frac{1}{e^x+1}. \end{aligned}$$
(31)

The parameters \(\text {a}_i\) can be found in Ref. [20] for the SLy and FPS and in [21] for the BSk19, BSk20 and BSk21. However, the coefficients of our EoS’s parametrization is a bit different from those in these literature like: for SLy and FPS, we have \(\text {a}_{19\ldots 24}=0\) and for BSk19, BSk20 and BSk21 the notations in [21] are found by performing the transformations \(\text {a}_{10}\rightarrow \text {a}_6\) and \(\text {a}_{11\ldots 24}\rightarrow \text {a}_{10\ldots 23}\) [22]. In order to be able to solve the equations and study the asymptotical behaviour at the center of the star and at infinity, we consider a particular function of F. The simplest model in the F(T, X, Y)-theories is to consider a linear function as:

$$\begin{aligned} F=\frac{\kappa }{2} T+\gamma Y+ \alpha X, \end{aligned}$$
(32)

where \(\kappa =c^4/(8\pi G)\) (G is Newton constant and c is the speed of light), \(\gamma \) and \(\alpha \) are real constant. In this case, the fields equations read

$$\begin{aligned} \rho= & {} \frac{\alpha r^2 \left( \varphi '\right) ^2+2 (h-1) \kappa -4 \gamma \sqrt{h} r \varphi '}{2 h r^2}\nonumber \\&+\frac{h' \left( 2 \kappa +\gamma r \varphi '\right) }{2 h^2 r}-\frac{\gamma \varphi ''}{h}, \end{aligned}$$
(33)
$$\begin{aligned} P= & {} \frac{\alpha r^2 \left( \varphi '\right) ^2-2 h \kappa +2 \kappa +4 \gamma r \varphi '}{2 h r^2}\nonumber \\&+\frac{f' \left( 2 \kappa +\gamma r \varphi '\right) }{2 f h r}, \end{aligned}$$
(34)
$$\begin{aligned} 0= & {} \alpha \varphi ''+\frac{\gamma f''}{2 f}+\frac{2 \gamma }{r^2}-\frac{2 \gamma \sqrt{h}}{r^2}-\frac{\gamma \left( f'\right) ^2}{4 f^2}\nonumber \\&+\frac{2 \alpha \varphi '}{r}+f' \left( \frac{\alpha \varphi '}{2 f}-\frac{\gamma \sqrt{h}}{f r}+\frac{2 \gamma }{f r}\right) \nonumber \\&+h'\left( -\frac{\alpha \varphi '}{2 h}-\frac{\gamma f'}{4 f h}-\frac{\gamma }{h r}\right) . \end{aligned}$$
(35)

To simplify these equations, we first solve the Eq. (34) for \(f'\) to obtain

$$\begin{aligned} \frac{f'}{f}= & {} \frac{-\alpha r^2 \left( \varphi '\right) ^2+2 h \kappa +2 h P r^2-2 \kappa -4 \gamma r \varphi '}{r \left( 2 \kappa +\gamma r \varphi '\right) }. \end{aligned}$$
(36)

Second we replace the obtained \(f'\) and its derivative in the Eqs. (33) and (34) and then by solving the resulting equations for \(h'\) and \(\varphi ''\), we found

$$\begin{aligned} \frac{h'}{h}= & {} \frac{1}{\kappa r \left( 2 \alpha \kappa -3 \gamma ^2\right) \left( 2 \kappa +\gamma r \varphi '\right) }\left( 2 \gamma ^4 \sqrt{h} r^2 \left( \varphi '\right) ^2 \right. \nonumber \\&\left. +2 \gamma ^3 r \varphi ' \left( 4 \sqrt{h} \kappa +h \left( -\kappa +P r^2+\rho r^2\right) -3 \kappa \right) \right. \nonumber \\&\left. +\gamma ^2 \kappa \left( 6\kappa -4 h^{3/2} \left( \kappa +P r^2\right) -4 \sqrt{h} \kappa \right. \right. \nonumber \\&\left. \left. +2 h \left( \kappa +5 P r^2+2 \rho r^2\right) -\alpha \left( 2 \sqrt{h}+3\right) r^2 \left( \varphi '\right) ^2 \right) \right. \nonumber \\&\left. +2 \gamma \kappa \alpha r \varphi ' \left( 2\kappa -4 \sqrt{h} \kappa +h \left( 2 \kappa +P r^2-\rho r^2\right) \right) \right. \nonumber \\&\left. +2 \alpha \kappa ^2 \left( \alpha r^2 \left( \varphi '\right) ^2-2 \left( -h \kappa +h \rho r^2+\kappa \right) \right) \right) , \end{aligned}$$
(37)
$$\begin{aligned} \varphi ''= & {} \frac{1}{\kappa r^2\left( 3\gamma ^2 -2 \alpha \kappa \right) }\left( \gamma ^3 \sqrt{h} r^2 \left( \varphi '\right) ^2-\gamma ^2 r \varphi ' \left( 2 \sqrt{h} \kappa \right. \right. \nonumber \\&\left. \left. +h \left( \kappa -P r^2-\rho r^2\right) +3 \kappa \right) \right. \nonumber \\&\left. + \gamma \sqrt{h} \kappa \left( \sqrt{h} \left( 4 \kappa +5 P r^2-\rho r^2\right) \right. \right. \nonumber \\&\left. \left. -2 h \left( \kappa +P r^2\right) -2 \kappa -\alpha r^2\left( \varphi '\right) ^2\right) \right. \nonumber \\&\left. +\alpha \kappa r \varphi ' \left( h \left( 2 \kappa +P r^2-\rho r^2\right) +2 \kappa \right) \right) . \end{aligned}$$
(38)

However, since in the case \(\gamma =\sqrt{2\alpha \kappa /3}\) the coefficients of \(h'\) and \(\varphi '\) in Eq. (33) correspond to those in Eq. (34), we can not obtain these equations which means that there is no solution for this system of equations. An other important equation which is derived by using the Eq. (36) to eliminate \(f'\) from Eq. (21). Doing so, it follow that

$$\begin{aligned} P'= & {} \frac{2 h P r^2-\alpha r^2 \left( \varphi '\right) ^2-4 \gamma r \varphi '+2 h \kappa -2 \kappa }{2r \left( 2 \kappa +\gamma r \varphi '\right) }\left( P+\rho \right) .\nonumber \\ \end{aligned}$$
(39)

As we can see the equation is different from that in GR due to the coupling constants of the model. Therefore, we can say that the pressure of the stellar structure is modified by the scalar field and the torsion and thus one can expect that the mass and the radius will be different from those in GR. Now, in order to avoid the irregularity at the center (\(r=0\)) of NSs, we must impose the boundary conditions \(P'(0)=\rho '(0)=f'(0)=h'(0)=\varphi '(0)=0\). In this case, we can express the solutions around \(r=0\), as

$$\begin{aligned} P(r)= & {} P_c+\sum ^\infty _{i=2} P_i r^i, \qquad \rho (r)=\rho _c+\sum ^\infty _{i=2} \rho _i r^i,\nonumber \\ h(r)= & {} 1+\sum ^\infty _{i=2} h_i r^i,\nonumber \\ f(r)= & {} f_c+\sum ^\infty _{i=2} f_i r^i, \qquad \varphi (r)=\varphi _c + \sum ^\infty _{i=2} \varphi _i r^i, \end{aligned}$$
(40)

where \(P_c\), \(\rho _c\), \(f_c\), \(\varphi _c\), \(P_i\), \(\rho _i\), \(f_i\), \(h_i\) and \(\varphi _i\) are constants and the subscript c means the value of each function at the center of the Neutron star. In this development, we have chosen the condition \(h(0)=1\) to have regular solutions at the center of the star as well as \(\varphi _c\) can be replaced by zero since the model we chose is shift symmetric about the scalar field (either \(\varphi _c\) is vanished or not the behaviour of the metric, \(\varphi '\), \(\rho \) and P stand the same). And the constant \(\rho _c\), which is the central density of NSs, is related to the pressure \(P_c\) through the equation of state \(P_c(\rho _c)\). If we insert the series (40) in the Eqs. (36), (37), (38) and (18), it follows that

$$\begin{aligned} f(r)= & {} f_c\left( 1+\frac{\left( \rho _c \left( \alpha \kappa -2 \gamma ^2\right) -3 P_c \left( \gamma ^2-\alpha \kappa \right) \right) }{3 \kappa \left( 2 \alpha \kappa -3 \gamma ^2\right) }r^2\right) +O(r^3),\nonumber \\ \end{aligned}$$
(41)
$$\begin{aligned} h(r)= & {} 1+\frac{2 \gamma ^2 \rho _c-2 \alpha \kappa \rho _c+3 \gamma ^2 P_c}{9 \gamma ^2 \kappa -6 \alpha \kappa ^2}r^2+O(r^3), \end{aligned}$$
(42)
$$\begin{aligned} \varphi '(r)= & {} \frac{2\gamma \left( \rho _c-3 P_c\right) }{6 \alpha \kappa -9 \gamma ^2}r+O(r^3), \end{aligned}$$
(43)
$$\begin{aligned} P(r)= & {} P_c+\frac{\left( P_c+\rho _c\right) \left( \rho _c \left( 2 \gamma ^2-\alpha \kappa \right) +3 P_c \left( \gamma ^2-\alpha \kappa \right) \right) }{6 \kappa \left( 2 \alpha \kappa -3 \gamma ^2\right) }r^2+O(r^3).\nonumber \\ \end{aligned}$$
(44)

We observe the constants \(\gamma \) effects the behavior of these function at center of the stars and thus our model deviates from GR for non vanishing value of \(\gamma \). In fact, when \(\gamma =0\) or \(\alpha =0\) the behaviour of GR at the center of star is recovered but the deviation from GR is due to \(\gamma \) since the coupling constant \(\alpha \) can be absorbed by rescaling the scalar field as we will see in Sect. 5. According to Ref. [58], for a physically acceptable stellar solution it is important to take into account the condition \(P''(r)<0\), which leads us to the conditions:

3.1 For \(\varphi '<0\)

$$\begin{aligned}&\text {If}\ 0<\rho _c<3 P_c,\;\text {then} \frac{\gamma }{\sqrt{\alpha \;\kappa }}<-\sqrt{\frac{3 P_c+\rho _c}{3 P_c+2 \rho _c}}<0\quad \text {or}\nonumber \\&\quad 0<\frac{\gamma }{\sqrt{\alpha \;\kappa }}<\sqrt{\frac{2}{3}}, \end{aligned}$$
(45)
$$\begin{aligned}&\text {If}\ 0<3 P_c< \rho _c,\;\text {then} -\sqrt{\frac{3 P_c+\rho _c}{3 P_c+2 \rho _c}}<\frac{\gamma }{\sqrt{\alpha \;\kappa }}<0\quad \text {or}\nonumber \\&\quad \frac{\gamma }{\sqrt{\alpha \;\kappa }}>\sqrt{\frac{2}{3}}. \end{aligned}$$
(46)

3.1.1 For \(\varphi '>0\)

$$\begin{aligned}&\text {If}\ 0<\rho _c<3 P_c,\;\text {then} -\sqrt{\frac{2}{3}}<\frac{\gamma }{\sqrt{\alpha \;\kappa }} <0 \quad \text {or} \nonumber \\&\quad \frac{\gamma }{\sqrt{\alpha \;\kappa }}>\sqrt{\frac{3 P_c+\rho _c}{3 P_c+2 \rho _c}} \end{aligned}$$
(47)
$$\begin{aligned}&\text {If}\ 0<3 P_c< \rho _c,\;\text {then} \frac{\gamma }{\sqrt{\alpha \;\kappa }}<-\sqrt{\frac{2}{3}} \quad \text {or}\nonumber \\&\quad 0<\frac{\gamma }{\sqrt{\alpha \;\kappa }}<\sqrt{\frac{3 P_c+\rho _c}{3 P_c+2 \rho _c}}. \end{aligned}$$
(48)

Where in the both cases we assumed that \(\gamma /\sqrt{\alpha \;\kappa }\ne 0\).

Furthermore, outside the stars (P(r) and \(\rho (r)\) are vanished) and at spatial infinity \(r\rightarrow \infty \), we demand asymptotically flat solution and \(\varphi \simeq 0\), where the gravitational field is weak. By using the Eqs. (26), (27) and (28) and by expanding the functions h and \(\varphi \) as: \(h(r)=1+\delta _h(r)\) and \(\varphi '(r)=\delta _\varphi (r)\) (\(\delta _h(r)<<1\) and (\(\delta _\varphi (r)<<1\)), we get the asymptotic behavior

$$\begin{aligned} h(r)= 1- \frac{2M}{r},\quad \varphi '(r)=\frac{\varphi '_\infty }{r^2},\quad f(r)=f_\infty e^{\frac{2(A\gamma + M\kappa )}{r\kappa }},\nonumber \\ \end{aligned}$$
(49)

where M, A and \(f_\infty \) are constants of integration. Indeed, the constant M is the physical mass of the NS measured by an observer at infinity and it is called the Arnowitt–Deser–Misner (ADM) mass. Note that: the constant \(f_\infty \) can be used to rescale the time coordinate as \(t\rightarrow f_\infty t\), the constant A must be vanish in order to recover the Newtonian limit and \(\varphi '_\infty \) can have the particular value \(-\gamma M/(\gamma ^2+\alpha \kappa )\), if we impose that \(J^r=0\).

4 Slowly rotating neutron star

To see more deviations from GR, we will study the equations of the approximate metric of a slowly rotating star for the particular model presented in the last section. In this section, we propose a generalization to the metric (20) by considering further stationary and axisymmetric spacetimes as well as we assume that the perturbed scalar field is vanished. The standard form of such metric is given by [53]

$$\begin{aligned} ds^2= & {} -f(r)dt^2+h(r)dr^2+r^2(d\theta ^2+ \sin ^2 \theta d\phi ^2)\nonumber \\&+2 \omega (r,\theta )r^2 \sin ^2\theta d\phi dt+O\left( \Omega ^2\right) , \end{aligned}$$
(50)

where \(\omega (r,\theta )\) is the angular velocity resulting from a free falling of a particle from infinity to the point \((r,\theta )\) and it can be called the rate of rotational of the inertial frame at \((r,\theta )\) [50]. In addition, this angular velocity is at the same order of the angular velocity of the fluid present in the star \(\Omega =u_\phi /u_t\) which is small enough to not effect the variation of the metric, the pressure and the energy density e.i., the condition on \(\Omega \) can be described as \(\Omega r_s\ll c\) (\(r_s\) is the star’s radius). The velocity \(\Omega \) is defined such that \(u^\mu u_\mu =-1\) is verified and thus the components of the vector \(u^\mu \) is given by

$$\begin{aligned} u^\mu= & {} \frac{1 }{\sqrt{f(t)+2 \Omega \omega (r,\theta )r^2 \sin ^2\theta +\Omega ^2 r^2 \sin ^2\theta }}\left( 1,0,0,\Omega \right) \nonumber \\ \end{aligned}$$
(51)
$$\begin{aligned}\approx & {} \frac{1}{\sqrt{f(t)}}\left( 1-\Omega \omega (r,\theta )r^2 \sin ^2\theta ,0,0,\Omega \right) +O(\Omega ^2).\nonumber \\ \end{aligned}$$
(52)

Since we are working in teleparallel gravity frame, one must define a tetrad field that give us the metric (50). To do so, we use the tetrad which is obtained by solving the equations that enforce the relations \(\eta ^{ab}e^\mu _a e^\nu _b=0\) for \(\mu \ne \nu \) and \(\{\mu ,\nu \}\ne \{0,3\}\). We will also use the antisymmetric equations resulting from the violation of Lorentz symmetry, after extracting the perturbed equations. Let’s start by performing a perturbation as: \(e_\mu ^a={\overline{e}}_\mu ^a+\delta e_\mu ^a\), where \({\overline{e}}_\mu ^a\) correspond to (22) and \(\delta e_\mu ^a\) is chosen as

$$\begin{aligned} \delta e_\mu ^a= & {} \left( \begin{array}{llll} 0&{}0&{}0&{}\frac{r^2 \sin ^2(\theta ) \sigma (r,\theta )}{\sqrt{f(r)}}\\ -r \sin (\theta ) \sin (\phi ) (\sigma (r,\theta )+\omega (r,\theta ))&{}0&{}0&{}0\\ r \sin (\theta ) \cos (\phi ) (\sigma (r,\theta )+\omega (r,\theta ))&{}0&{}0&{}0\\ 0&{}0&{}0&{}0 \end{array}\right) \nonumber \\&+O(\Omega ^2), \end{aligned}$$
(53)

where \(\sigma (r,\theta )\) is a arbitrary function of r and \(\theta \). Like in the last section, where the non-perturbed tetrad can be derived by using the matrix \(\mathbf{H} \) and the diagonal tetrad, \(\delta e_\mu ^a\) can also be found as follow

$$\begin{aligned} \delta e_\mu ^a = \mathbf{H} .\left( \begin{array}{llll} 0&{}0&{}0&{}\frac{r^2 \sin ^2(\theta ) \sigma (r,\theta )}{\sqrt{f(r)}}\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ r (\sigma (r,\theta )+\omega (r,\theta ))&{}0&{}0&{}0 \end{array}\right) +O(\Omega ^2).\nonumber \\ \end{aligned}$$
(54)

The equations of a slowly rotating stars is derived by inserting the metric (50) and its corresponding tetrad in the Eq. (14). At the first order perturbation, the only non-vanishing components are

$$\begin{aligned}&\frac{f^{1/2}}{F_T h^{1/2} r^4}\partial _r \left[ \frac{r^4 F_T \partial _r\omega }{f^{1/2}h^{1/2}}\right] \nonumber \\&\quad +\frac{1}{r^2\sin ^3\theta }\partial _\theta \left[ \sin ^3\theta (\partial _\theta \omega )\right] \nonumber \\&\quad -\frac{ (\Omega +\omega ) (P+\rho )}{\kappa }-\frac{ h^{-1/2} (F_{Y} \varphi '-2 F_{T}')\omega }{\kappa r}=0, \end{aligned}$$
(55)
$$\begin{aligned}&\quad \frac{f^{1/2}}{F_T h^{1/2} r^4}\partial _r \left[ \frac{r^4 F_T \partial _r\omega }{f^{1/2}h^{1/2}}\right] \nonumber \\&\qquad +\frac{1}{r^2\sin ^3\theta }\partial _\theta \left[ \sin ^3\theta (\partial _\theta \omega )\right] \nonumber \\&\qquad -\frac{(\Omega +\omega ) (P+\rho )}{\kappa }+\frac{ h^{-1/2} (F_{Y} \varphi '-2 F_{T}') \sigma }{\kappa r}=0.\nonumber \\ \end{aligned}$$
(56)

These two equations are equivalent when \(F_{Y} \varphi '-2 F_{T}'=0\) or when \(\omega =-\sigma \) and, in both cases, we can deal only with Eq. (55). The first case has similar to those in GR and the Lagrangian is also equivalent to R since the solution to \(F_{Y} \varphi '-2 F_{T}'=0\) for any function F is \(F=T+H(X)\equiv R+H(X)\), where H is an arbitrary function. In the second case, the resulting tetrad is equivalent to that in Ref. [51] where the authors considered it as a good tetrad that solves the antisymmetric field. Note that even we use the diagonal and the perturbed tetrad with a non-vanishing spin connection, we will have the same equations as it reported in Ref. [51].

Now, to study the star’s angular momentum J, we will work with the special function of model studied in the last section. We can also simplify this equation by defining the function \(\overline{\omega }=1+(\omega /\Omega )\) expanding \(\overline{\omega }\) as [50]

$$\begin{aligned} \overline{\omega } =- \sum ^{\infty }_{l=1} \overline{\omega }_l \left( \frac{1}{\sin \theta }\frac{dP_l}{d\theta }\right) , \end{aligned}$$
(57)

where \(P_l\) are Legendre polynomials and l is integer number. Substituting the expressions (32) and (57) in (55), we obtain:

$$\begin{aligned}&\frac{f^{1/2}}{h^{1/2} r^4}\partial _r \left[ \frac{r^4\partial _r \overline{\omega }_l}{f^{1/2}h^{1/2}}\right] \nonumber \\&\quad +\frac{(l(l+1)-2)}{r^2}\overline{\omega }_l-\frac{2\overline{\omega }_l \left( P+\rho \right) }{\kappa }\nonumber \\&\quad -\frac{\gamma h^{-1/2} \varphi '}{\kappa r}(\overline{\omega }_l-1)=0. \end{aligned}$$
(58)

In order to have the asymptotic behavior \(\overline{\omega }_l=1+2 I/r^3\) (where \(I=J/\Omega \) is the inertial momentum), when \(r\rightarrow \infty \), we impose that \(l=1\) which means that \(\overline{\omega }\) depend only on the radial coordinate r. By doing so and by using the asymptotic behaviors (49), the analytical solution of Eqs. (58), at large value of r, reads

$$\begin{aligned} \overline{\omega }= & {} 1-C \;6 \left( \frac{\varphi _{\infty }\gamma }{\kappa }\right) ^{3/2} B_{3}\left[ 2\left( \frac{\varphi _{\infty }\gamma }{\kappa }\right) ^{3/2}\right] , \end{aligned}$$
(59)
$$\begin{aligned}\approx & {} 1- C\;\left( \frac{\varphi _{\infty }\gamma }{\kappa \;r}\right) ^{3}, \end{aligned}$$
(60)

where C is a constant of integration and \(B_{n}\) (n is an integer) is the modified Bessel function of the first kind. Thus, in this case \(2\,I=C\;(\varphi _{\infty }\gamma /\kappa )^{3}\) since the inertial momentum is the term propositional to \(2/r^3\). At the center of neutron star, the regularity of the function \(\overline{\omega }\) should be satisfied e.i., \(\overline{\omega }'=0\) for \(r=0\), and \(\overline{\omega }_c=\overline{\omega }(0)\) is determined numerically to ensure \(\overline{\omega }(r\rightarrow \infty )=1\). Therefore, using this initial conditions and the asymptotic from of \(\overline{\omega }\), it follows that

$$\begin{aligned} I=\frac{1}{3\kappa }\int ^{r_s}_{0}\frac{h^{1/2}}{f^{1/2}}(P+\rho )r^4 \overline{\omega } dr+\frac{\gamma }{6\kappa }\int ^{\infty }_{0}\frac{r^3}{f^{1/2}}\varphi '(\overline{\omega }-1) dr.\nonumber \\ \end{aligned}$$
(61)

where the inertial momentum of the star can be studied independently from its angular velocity. We can also extract the approximate behavior of \(\overline{\omega }\) at the center, where it is calculated by

Fig. 1
figure 1

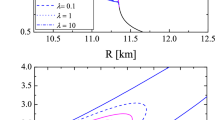
Left graph: For FPS EoS and different value of \(\overline{\gamma }\), we plot the variation of energy density \(\rho /\rho _0\) (with solid curves), \(P/\rho _0\) (with dashed curves) and \(\varphi _s\) (with dotted curves) as function of s. The vertical lines in the small graph represent the radius of NSs for \(\gamma =0\; (GR)\) (solid line), \(\gamma =0.4\) (dashed line) and \(\gamma =0.5\) (dotted line). Right graph: For the same EoS, we plot also the metrics h (with solid lines), f (with dashed curves) and \(\omega /\Omega \) (with dotted curves) as function of s in the right graph

Full size image
Fig. 2
figure 2

The mass–radius (left graph) and mass–central (right graph) density relations of NS using the EoSs: FPS, SLy, BSk19, BSk20 and BSk21 for: \(\overline{\gamma }=0\) (solid lines), \(\overline{\gamma }=0.4\) (Dashed lines), \(\overline{\gamma }=0.5\) (dotdashed lines)

Full size image
Fig. 3
figure 3

The variation of the moment of inertia as function of the NS mass for \(\overline{\gamma }=\{0\; \text {(solid lines)},0.4\; \text {(dashed lines)},0.5\; \text {(dotdashed lines)}\}\) using the EoSs: FPS, SLy, BSk19, BSk20 and BSk21

Full size image
$$\begin{aligned} \overline{\omega }=\overline{\omega }_c+\frac{\rho (0) \left( \gamma ^2+\overline{\omega }_c \left( 6 \alpha \kappa -8 \gamma ^2\right) \right) -3 P(0) \left( \gamma ^2+\overline{\omega }_c \left( 4 \gamma ^2-2 \alpha \kappa \right) \right) }{9 \kappa \left( 2 \alpha \kappa -3 \gamma ^2\right) }r^2.\nonumber \\ \end{aligned}$$
(62)

We observe that the constant \(\gamma \) affect the variation of angular velocity at the center, so a deviation from GR is expected to happen where GR is recovered by setting \(\gamma =0\). We will use the approximation (62), as initial conditions at \(r=0\), to avoid numerical instability. In fact, we integrate the Eq. (58) from the center of the star, using the Eq. (62) with an arbitrary value of \(\overline{\omega }_c\), to the surface of the star \(r=r_s\), then, at Large value of r, we solve the Eq. (58) by imposing the condition \(\overline{\omega }(r\gg r_s)\approx 1-2I/r\). Next, we look for the values \(\overline{\omega }_c\) and I in which \(\overline{\omega }\) and its radial derivative are continues at the surface. To do so, we define the quantities [57]

$$\begin{aligned} u(r)= & {} \frac{ r^4}{\sqrt{f(r)} \sqrt{h(r)}}\omega '(r), \end{aligned}$$
(63)
$$\begin{aligned} \chi (r)= & {} \frac{ 1}{\sqrt{f(r)} \sqrt{h(r)}}\omega (r). \end{aligned}$$
(64)

These definitions will allow us to rewrite the Eq. (62) to two first order equations as

$$\begin{aligned} \chi '(r)= & {} \frac{u(r)}{r^4}-\frac{1}{2} \chi (r) \left( \frac{f'(r)}{f(r)}+\frac{h'(r)}{h(r)}\right) , \end{aligned}$$
(65)
$$\begin{aligned} u'(r)= & {} \frac{2 r^4 h(r) \chi (r) (P(r)+\rho (r))}{\kappa }\nonumber \\&-\varphi '(r) \left( \frac{2 \gamma r^3}{\kappa \sqrt{f(r)}}-\frac{2 \gamma r^3 \sqrt{h(r)} \chi (r)}{\kappa }\right) . \end{aligned}$$
(66)

In GR, the solution to the function u is a constant at the exterior of the star where this constant correspond to the moment of inertia, but for non vanishing scalar field u become constant when \(r\rightarrow \infty \).

5 Numerical results

In this section, we will present our numerical results obtained by solving the Eqs. (33), (34), (35), (63) and (64). Our numerical integration is performed by considering that \(\kappa =c^4/(8\pi G)\) and by following the method used in Ref. [3], where they defined the dimensionless quantities:

$$\begin{aligned} y=\frac{\rho }{\rho _0},\qquad z=\frac{P}{\rho _0 c^2},\qquad s=Ln\frac{r}{r_0}, \end{aligned}$$
(67)

where

$$\begin{aligned}&\rho _0 = m_n n_0=1.6749\times 10^{14}\; \mathrm{g}\,\mathrm{cm}^{-3},\nonumber \\&\qquad r_0=\frac{c}{\sqrt{G \rho _0}}=89.664 \; km. \end{aligned}$$
(68)

Here \(m_n=1.6749\times 10^{-24}g\) and \(n_0=0.1 fm^{-1}\) are the neutron mass and he typical number density of NSs, respectively. We also define the rescaled scalar field and the constant \(\gamma \) as:

$$\begin{aligned} \overline{\varphi }=\sqrt{\frac{\kappa }{\alpha }}\varphi ,\qquad \overline{\gamma }=\frac{\gamma }{\sqrt{\alpha \kappa }}. \end{aligned}$$
(69)
Fig. 4
figure 4

The normalized moment of inertia, \(I/(Mr_s^2)\) (left graph) and \(I/M^3\) (right graph), as a function of the stellar compactness C for the same EoS and parameters used in Fig. 4. We plot also the best fit of the normalized moment of inertia-compactness relations for: \(\overline{\gamma }=\{0\; \text {(solid lines)},0.4\; \text {(Dashed lines)},0.5\; \text {(dotdashed lines)}\}\). We plot also deviations of the polynomial fits and the data \(Abs( 1-I/I_{fit})\) in the bottom of the two graphs

Full size image
Table 1 The fitting coefficients that appear in Eqs. (70) and (71) for GR and our model
Full size table

Now, we suppose two solutions which are the inside and outside of the star. If we integrate the equations of motion with respect to s, instead of the radial coordinate r, from \(s=-10\) to the surface of the stars, we obtain the internal solution and if we integrate from the surface to large value of s, where we assume that outside the star \(P=0\) and \(\rho =0\), we get the external solution. Moreover, in our model the radius is determined numerically by the condition \(P(r_s)\approx 10^{-11}\rho _0\) as well as we impose \(f_{in}(r_s)=f_{out}(r_s)\), \(h_{in}(r_s)=h_{out}(r_s)\) and \(\varphi _{in}'(r_s)=\varphi _{out}'(r_s)\) to insure the continuity of the metric and scalar field. The initial conditions are chosen to satisfy the regularity at the center (\(\rho (r=0)=\rho _c\), \(h(r=0)=1\) and \(\varphi '(r=0)=0)\)), continuity the metric, scalar field and its derivatives at the surface as well as the flatness at infinity (\(f(r=\infty )=1\), \(h(r=\infty )=1\) and \(\varphi '(r=0)=0)\)). To insure these, we use the asymptotic behaviors of each function as initial conditions. Therefor, we are left with only two free parameters which are \(\overline{\gamma }\) and \(\rho _c\). Next, we solve the system of Eqs. (63) and (64), as it is explained in the last section, with help of the numerical result of the nonperturbed metric and the scalar field. As an example, we show, in Fig. 1, the variation of the perturbed and non-perturbed metric as well as the energy density \(\rho \) with respect to s for a neutron star with \(M=1.5 M_{Sun}\) and FPS EoS using three different values \(\overline{\gamma }\). We can see the functions \(\omega /\Omega \), P, \(\rho \) and f deviate significantly from those of GR at the center of the star, become slightly different from GR’s function that when r (or s) is close to the surface and they become identical when \(s\rightarrow \infty \). The function h has the same characteristic at the surface and at \(s\rightarrow \infty \) but \(h\rightarrow 1\) when \(r\rightarrow 0\) (e.i.\(s\rightarrow -\infty \)) for all values of \(\overline{\gamma }\). We observe also that the central density decrease and the radius increase when \(\overline{\gamma }\) goes from 0 to 0.5. Finally, \(\omega /\Omega \) tend to 0 faster than the \(f-1\) and \(h-1\) do, since we have showed that asymptotical behavior are: \(\omega /\Omega \thicksim 1/r^3\) but \(h-1\thicksim f-1 \thicksim 1/r\) when \(r\rightarrow \infty \). Finally, we note scalar field gradient increase from the zero, at the center, until it arrive to a maximum (depending on \(\overline{\gamma }\)) when r is close to the radius of the star. Then, radial derivative of the scalar field starts to decease to zero as we expected in Sect. 4.

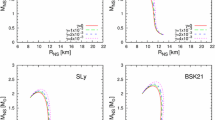
In order to compare our model with GR, which can be defined by \(\gamma =0\) and \(c=0\), we plot mass–radius relation in Fig. 2 for different realistic equation of state and for the value \(\overline{\gamma }=\{0,0.4,0.5\}\), by varying \(\rho _c\) from \(2\rho _0\) to \(25\rho _0\). We observe that the maximum mass increases when \(\overline{\gamma }\) increases for the five equations of state where the value of the maximum mass depend on the EoS and \(\gamma \). We observe also that the maximum of the mass can exceed the value \(2M_{Sun}\), where \(M_{Sun}\) is the mass of the sun, for the FPS and BSk19 EoSs in the case of \(\overline{\gamma }=\{0.4,0.5\}\) which may explain the observation the pulsar PSR J1614-2230 [59]. Furthermore, the NS mass can also exceed the value \(2.5 M_{Sun}\), which is the mass of the compact object calculated from the GW190814 event, for SLy, BSk20 and BSk21. In Fig. 2, we plot also the variation of NS mass with respect the central density for the same values of \(\overline{\gamma }\) and the same EoSs used in Fig. 2. We notice that the deviation from GR become important for high central density. These differences are important to get a deviation from GR at the perturbed level since the Eq. (62) depend on the nonperturbed metric and the scalar field.

We show in Fig. 3 the variation of the moment of inertia I with respect the mass of NS by following the same steps outlined for the mass–radius relation. Note that the quantity I is multiplied by \(c^2/G\) in order to obtain the dimension of moment of inertia which is \(\mathrm{g}\,\mathrm{cm}^2\). We observe the effect of the coupling constant \(\overline{\gamma }\), for different equation of state, is important when central density is higher. In other words, the deviation from GR becomes important when the central density is higher like we highlighted in our discussion of the mass-radius relation. We observe also a maximum of moment of inertia for each case, where the lower \(\overline{\gamma }\) gives bigger maximum but it is the opposite for FPS EoS.

There are two universality relations of normalizations of inertia-momentum as function of the compactness \(C=(G/c^2) M/r_s\). The first relation is suggested for the first time in [60], and extensively studied by Breu and Rezzolla [61]. These latter suggest a fourth polynomial with vanishing second and third order terms relation between the normalized moment of inertia \(I/(Mr_s^2)\) and compactness and it is written as:

$$\begin{aligned} \frac{I}{M r_s^2}=A_1+A_2 C+A_4 C^4, \end{aligned}$$
(70)

where the coefficients \(A_1\), \(A_2\) and \(A_4\) are constant determined by fitting this form with our results. The second one is a fourth polynomial relation between \(I/M^3\) the inverse of the completeness, so the relation can be written as [61]

$$\begin{aligned} \frac{I}{M^3}=B_1C^{-1}+B_2 C^{-2}+B_3 C^{-3}+B_4 C^{-4}. \end{aligned}$$
(71)

The numerical values for the fitting coefficients \(A_1\ldots B_4\) are given in Table 1, where the coefficient are different from those we found in the Literature [54, 56] because we did not use the same EoS. In Fig. 4, we show the variation of \(I/M^3\) (right graph) and \(I/(Mr_s^2)\) (left graph) as function of C with equal number of points for the same values of the parameters and equations of state in Fig. 3. When \(\overline{\gamma }=\{0.4,0.5\}\) the normalized moment of inertia is lower than GR for the same compactness value due to the significant deviation of I, M and \(r_s\) in our model from GR. In addition, we observe that the blue points, which correspond to the FPS EoS, are above the best fit curve when \(\overline{\gamma }=\{0.4,0.5\}\) and \(C > rsim 0.1\). We plot also the best fit of I for different value of \(\overline{\gamma }\) as well as we show the relative deviation \(Abs( 1-I/I_{fit})\) of the data points from the fitting curve. We notice that the deviation is always under \(10\%\) and it is under \(5\%\) when \(0.08 > rsim C > rsim 0.3\) and therefore the representations (70) and (71) can be good functions to describe the behavior of the moment of inertia as function of the compactness for GR and our model.

6 Conclusion

This paper is devoted to studying a slowly rotating neutron star in the frame of scalar torsion theory for different realistic equations of state. We derived the general equations of motion that describe a spherical symmetric and static neutron star where the gravity is described by the Lagrangian (10). The non diagonal tetrad, which corresponds to the spherical symmetric metric, was used to extract the general equations. By following the same steps we extend our study to a slowly rotating neutron star with an arbitrary angular velocity \(\Omega \) using the tetrad (53). However, we showed that the second order differential equation of the function \(\omega \) is independent from \(\Omega \) and thus moment of inertia of NS can be found without its velocity. In order to see the behaviour of mass, radius and moment of inertia, we suppose a particular case \(F=(\kappa /2)T+\gamma Y+ c X\) where the GR is found by setting \(c=0\) and \(\gamma =0\) or by considering a vanishing scalar field.

In addition, a particular case of scalar torsion theory has been studied in details at the center of the star where we showed the effect of the parameters \(\gamma \) and c on the perturbed and non-perturbed metric, the scalar field, the energy density as well as the pressure but these parameters has no effect on them when \(r\rightarrow \infty \). Therefore, according to TOV equations, the deviation of the particular model from GR happens when \(\gamma \) is different from zero at the center of the star and they become identical to GR at infinity. To confirm this, we numerically integrate all the equations from \(r=0\) to \(r=\infty \) for \(\overline{\gamma }=\{0,0.4,0.5\}\) and for the EoSs FPS, SLy, BSk19, BSk20, BSk21. Then, we show the mass-radius and moment of inertia-compactness relations where we found that the deviation from GR become important at high density. We found also the moment of inertia and mass has a maximum which depend on the parameter \(\overline{\gamma }\) and the equation of stat. We have also showed that our model is well fitted with universal relations (70) and (71) in which the relative deviation is lower than \(10\%\) for the value of \(\overline{\gamma }\) that we chose.

Finally, scalar-torsion theory might be an alternative theory that can describe strong gravity with NS as a source. Therefore, it would be interesting to investigate more properties of NS Like: studying the ghost and Laplacian stability, calculating the axial and polar quasi-normal modes or moment of inertia for a rapidly rotating neutron star, in scalar-torsion theories. But we leave these issues for future works and publications.