Ergodic sampling of the topological charge using the density of states

Abstract

In lattice calculations, the approach to the continuum limit is hindered by the severe freezing of the topological charge, which prevents ergodic sampling in configuration space. In order to significantly reduce the autocorrelation time of the topological charge, we develop a density of states approach with a smooth constraint and use it to study SU(3) pure Yang Mills gauge theory near the continuum limit. Our algorithm relies on simulated tempering across a range of couplings, which guarantees the decorrelation of the topological charge and ergodic sampling of topological sectors. Particular emphasis is placed on testing the accuracy, efficiency and scaling properties of the method. In their most conservative interpretation, our results provide firm evidence of a sizeable reduction of the exponent z related to the growth of the autocorrelation time as a function of the inverse lattice spacing.

1 Introduction

In four spacetime Euclidean dimensions, gauge field configurations can be classified according to their topological charge Q, defined as

$$\begin{aligned} Q = \frac{1}{32 \pi ^2} \int d^4 x \, \epsilon _{\mu \nu \rho \sigma } \mathrm {Tr} \left( G_{\mu \nu } G_{\rho \sigma } \right) \ , \end{aligned}$$

(1)

where $G_{\mu \nu }(x)$ is the field tensor. This integral can be rephrased as a mapping from a three-sphere to a SU(2) group, exposing the fact that Q is related to the homotopy group $\pi _3: S^3 \mapsto SU(2)$. With the normalisation in Eq. (1), Q is integer-valued.

$\chi$, the susceptibility of Q per unit of volume, is related to the mass of the $\eta ^{\prime }$ particle by the Witten-Veneziano formula [1, 2]. Therefore, the topological charge Q and the topological susceptibility $\chi$ play a phenomenologically relevant role in the theory of the strong interactions and in any theoretically convenient generalisation of the latter such as the large-N limit of SU(N) gauge theories [3]. It is hardly surprising then that precise measurements of Q and $\chi$ have been one of the most active areas of activity of Lattice Gauge Theory since its earliest days (see e.g. [4, 5] for recent reviews). In addition, more recent investigations have used lattice determinations of topological quantities to estimate the mass of axions from first principles in order to determine a bound for their density in the Universe [6,7,8].

On a finite lattice with periodic boundary conditions in all directions, gauge configurations split into topological sectors labelled by the value of Q and separated by free energy barriers [9]. Monte Carlo simulations have shown a sharp growth of the height of these barriers as $a \rightarrow 0$, with a consequent freezeout of the topological sector in numerical calculations [10]. The phenomenon becomes even more pronounced as the number of colours N increases [11, 12]. This dramatic slowing down of Q and the resulting very large autocorrelation times pose serious problems of ergodicity in simulations and cause a very slow convergence of physical observables such as hadron masses to their thermodynamic limit values [13, 14]. Since the toroidal topology of the domain plays a crucial role in the freezeout, other setups have been proposed based for example on open boundary conditions in time [15] (used at large N in [16, 17]) or on non-orientable manifolds [18]. While these setups are very promising, their properties and potential drawbacks such as the loss of translational invariance with open boundary conditions in time, need further study.

In this work, we take an alternative approach to the problem of topological freezing without abandoning the use of periodic boundary conditions in all directions. For the theory formulated on a torus, we build a sequence of couplings that interpolate from a relatively strong value to a weak coupling value and we perform numerical simulations using an algorithm in which the coupling is also a dynamical variable taking values in the prebuilt set. More specifically, we use the density of states approach [19, 20] formulated with a Gaussian constraint [21] and tempering [22, 23]. The idea behind this approach is that the strong coupling values will act as an ergodic reservoir of topological sectors, while the tempering guarantees thermal equilibrium of the latter in the Monte Carlo at weaker coupling. Preliminary results of our investigation have appeared in [24].

The rest of the work is organised as follows. In Sect. 2, we recall some key properties of the density of states approach. Section 3 develops the formalism for a Gaussian constraint and discusses a simplifying approximation. The lattice gauge theory model, the simulations and results are described in Sect. 4. This is a long section as it covers our discussion of the topological charge and demonstrates that the density of states approach leads it to couple more weakly to the long timescale modes of the system. Techniques to analyse the autocorrelation time in this situation are developed. We work on three lattice sizes and present our results concerning scaling in Sect. 5, before summarising our findings in Sect. 6. Two appendices provide more technical details: “Appendix A” compares a multi-histogram calculation using our reference simulations with the density of states approach; “Appendix B” contains tables recording details of the simulations performed in this study.

2 Density of states method

The density of states technique has been shown to be useful in a variety of models with continuous variables. For example: U(1) [20], complex action [25], Bose gas [26]. Other versions of the technique have also been used to study SU(3) gauge theory [27, 28]. In this paper we further develop the technique and use it to make a detailed study of SU(3) lattice gauge theory that extends the results of [24].

The density of states approach developed in [19] reconstructs canonical expectation values from a sufficiently large and closely spaced set of functional integrals each constrained to have central action $S_i$. These constrained functional integrals provide an approximate way to define observables on the micro-canonical ensemble at $S_i$ and while the original development of the subject employed a sharp constraint, in this paper we use a Gaussian constraint of width $\delta$. The choice of an analytic Gaussian constraint allows simulations to use the global HMC algorithm which commonly underlies simulations of lattice gauge theory. The constrained functional integrals are defined using double bracket notation as,

$$\begin{aligned} \langle \langle B[\phi ]\rangle \rangle _i = {1\over \mathcal{N}_i} \int \mathcal{D}\phi \, B[\phi ] e^{-a_i S[\phi ]} e^{-(S[\phi ] - S_i)^2/2\delta ^2} \ . \end{aligned}$$

(2)

Where B and $\phi$ denote generic operators and fields respectively. The need for the term $e^{-a_i S[\phi ]}$ is explained below.

$\mathcal{N}_i$ is a normalisation factor written as a constrained functional integral without the operator B,

$$\begin{aligned} \mathcal{N}_i = \int \mathcal{D}\phi \, e^{-a_i S[\phi ]} e^{-(S[\phi ] - S_i)^2/2\delta ^2} \ . \end{aligned}$$

(3)

Noting the definition of the density of states,

$$\begin{aligned} \rho (S) = \int \mathcal{D}\phi \, \delta (S[\phi ]-S) \ . \end{aligned}$$

(4)

We see that since the expression for $\mathcal{N}_i$ involves only the action, the functional integral defining it can be replaced by an ordinary integral over the density of states,

$$\begin{aligned} \mathcal{N}_i = \int dS\, \rho (S) e^{-a_i S } e^{-(S - S_i)^2/2\delta ^2} \ . \end{aligned}$$

(5)

So the $\mathcal{N}_i$ are closely related to the density of states evaluated at $S_i$. This is most apparent in the limit $\delta \rightarrow 0$, when the Gaussian constraints become delta functions and the double bracket expressions truly represent the evaluation of an observable on the micro-canonical ensemble. In this formal limit there would be no need for the $a_i$’s. However, at finite $\delta$, the constraint is wide enough to require the term $e^{-a_i S[\phi ]}$ to compensate the growth of the density of states in the measure and to ensure that the mean constrained action $\langle \langle S\rangle \rangle$ really is at $S_i$. The value of $a_i$ needed to accomplish this is determined by an iterative procedure described below. The simulations which underly the method provide estimates of these double bracketed expectations (2) for a set of closely spaced $S_i$ labelled by the index $i = 1\dots N_{TEMPER}$, which we refer to as “tempers” (we reserve the term “replica” to refer to repeats of the whole simulation procedure with identical parameters, but different random number sequences). Having chosen an appropriate set of central action $S_i$ to characterise the tempers, the method consists of two phases.

Robbins Monro (RM) Phase to determine $a_i$ through a procedure of minimising $\langle \langle S - S_i\rangle \rangle _i$ for an iterative sequence of $a_i$’s. This quantity converges to zero when $a_i$ becomes the derivative of the (log) density of states at $S_i$. Knowledge of the final $a_i$’s is sufficient to construct a piecewise approximation to the density of states that can immediately be used to estimate canonical expectation values of operators that depend only on the action, such as moments of the plaquette.

Measurement Phase (MP) at fixed $a_i$ as determined by the RM phase. This is necessary to compute canonical expectation values of generic operators through a reweighting procedure. For example, the topological charge requires more information than is contained in the density of states alone. Moreover, the measurement phase provides dynamic information about the efficiency of the method through the autocorrelation.

We are particularly concerned about the accuracy, the relationship between expectation values computed using RM phase and those based on the measurement phase (MP), the autocorrelation time and the efficiency of the tempering method. To achieve these aims we have repeated the whole simulation procedure consisting of both phases, $N_{REPLICA}$ times, as this provides a way of estimating the errors inherent in the method.

While the density of states method is applicable to any model, and indeed has been used to study phase transitions [20], the Yang Mills theory we study here is far from any phase transition and all results are smooth functions of parameters. The conclusions that rely on working in this context are not restricted to lattice gauge theory but are expected to hold for other models in which there is a single coupling multiplying the action as this most closely mimics simple statistical mechanics systems.

3 Formalism

According to the density of states approach, $\log \rho (S)$ is approximated as piecewise linear with coefficients given by the $a_i$ appearing in (2),

$$\begin{aligned} \rho (S) = \rho _{i} e^{a_{i} (S-S_{i})} ,\ {(S_{i-1} + S_{i})\over 2}< S < {(S_{i} + S_{i+1})\over 2} \ . \end{aligned}$$

(6)

Where $\rho _i$ is shorthand for $\rho (S_{i})$. By convention we take $S_i$ to grow with i. Piecewise continuity leads to,

$$\begin{aligned} \rho _{i+1} = \rho _i e^{(a_i + a_{i+1}) (S_{i+1}-S_i)/2} \ . \end{aligned}$$

(7)

This relation along with the $(S_i, a_i)$ is sufficient to compute the piecewise approximation to the density of states in terms of the value $\rho _{i_c}$ at some base index $i_c$. As $\rho$ varies over many orders of magnitude, the base index is chosen depending on the particular problem. When reweighting to coupling $\beta$ it is chosen so as to minimise $|a_{i_c} - \beta |$.

To avoid unduly long formulae, the expressions given here assume fixed spacing $S_{i+1} - S_{i} = \delta _S$ and also fixed Gaussian width $\delta _i = \delta$. However, motivated by the desire to ensure effective mixing across the range of tempers, variable spacing is used in simulations.

Besides $\delta$ and $\delta _S$ another parameter provides a useful scale to the problem. This parameter is model dependent and we define $\sigma$ to be the standard deviation of action fluctuations in the unconstrained system. The strength of the Gaussian constraint is determined by the dimensionless ratio $\delta /\sigma$. Although $\sigma$ depends on the coupling, for this study it does not change very much over the narrow range of tempers and thus provides a useful scale. For the pure gauge SU(3) studied here, $a_i$ turns out to be approximately linear: $a_i \approx a_{i_c} - (i-i_c)\delta _S/\sigma ^2$ for indices close to the base index $i_c$ where $\sigma$ can be regarded as constant. Consequently for small k, $\rho _{i_c+k} \approx \rho _{i_c}e^{k a_{i_c} \delta _S} e^{-k^2 \delta _S^2/2 \sigma ^2}$. However, we emphasise that this observation relies on the smoothness of the model and limited range of tempers and should not be regarded as any kind of modified version of the density of states method.

3.1 Canonical expectation values of the action and its variance: LLR

The parameters $a_i$ obtained from the RM phase for each $S_i$ provide the piecewise estimate of the log of the density of states, so without any measurement phase we have access to the full probability density of the action for a range of couplings $\beta$. Estimates can be made of canonical expectation values of functions of the action, the most common being $\langle S\rangle$ and $\langle (S-\langle S\rangle )^2\rangle$ which in the lattice gauge theory studied here are directly related to moments of the plaquette. We shall call this approach “LLR” as a shorthand to distinguish it from the “reweighting” approach discussed in the next section.

Direct application of the piecewise approximation (6),(7) leads to the following expression for the partition function.

$$\begin{aligned} \mathcal{Z}_{LLR}= & {} \int dS \, \rho (S) e^{-\beta S} \end{aligned}$$

(8)

$$\begin{aligned}= & {} \sum _i {\rho _i e^{-\beta S_i} \over a_i-\beta } \left[ e^{(a_i-\beta )\delta _S/2}-e^{-(a_i-\beta )\delta _S/2} \right] \nonumber \\\approx & {} \mathcal{Z}_{LLR'} = {\delta _S} \sum _i \rho _i e^{-\beta S_i} \ . \end{aligned}$$

(9)

And similar formulae for the expectation values $\langle S\rangle$ and $\langle (S-\langle S\rangle )^2\rangle$. These results, because of their reliance on the piecewise approximation, should be taken to be accurate to order $\delta _S^2/\sigma ^2$.

The further approximation on the third line can be seen as an expansion for $(a_i-\beta )\delta _S \ll 1$ or can be regarded as a trapezium evaluation of the integral. In numerical work we always use the full expression but the approximate one, which we denote as “$\mathrm LLR'$” approach is simpler yet remarkably accurate. Because of its advantages in exposition we develop some formalism for this $\mathrm LLR'$ approximation and define weights $v_i$:

$$\begin{aligned} v_i = \rho _i e^{- \beta S_i} \end{aligned}$$

(10)

then

$$\begin{aligned} \langle f(S) \rangle _{LLR'} = { \sum _i v_i f(S_i) \over \sum _i v_i } \ . \end{aligned}$$

(11)

These weights can be normalised to $\sum _i v_i = 1$, but for numerical reasons in the course of intermediate computations, it is convenient to choose the weight at the central index $v_{i_c}$ to be unity by defining $\rho _{i_c} = \rho (S_{i_c})=e^{\beta {S_{i_c}}}$.

The full LLR formulae are straightforward to derive from (8), but ugly in comparison with (10) and (11).

3.2 Canonical expectation values of arbitrary operators:reweighting

Observables that are not simply functions of the action can not be computed using the density of states alone and a measurement phase is needed The measurements are performed on a set of constrained tempering runs with parameters ($S_i,a_i$) and reweighting is then used to obtain the canonical expectation value:

$$\begin{aligned} \langle B[\phi ] \rangle = {1\over \mathcal{Z}} \int \mathcal{D}\phi \, B[\phi ] e^{-\beta S[\phi ]} \ . \end{aligned}$$

(12)

To relate this to the constrained functional integrals we consider sums of spaced Gaussians. We intend to use the functional integral equivalent of the approximate identity presented below,

$$\begin{aligned} K(x)= & {} {1\over \sqrt{2\pi }}{\delta _x\over \delta } \sum _i e^{-(x-i\delta _x)^2/2\delta ^2}\nonumber \\= & {} 1 + 2 \sum _{i>0} e^{-2 \left( \frac{i \pi \delta }{\delta _x}\right) ^2} \cos \left( \frac{2 i \pi x }{\delta _x}\right) \nonumber \\= & {} 1 + 2 e^{-2 \left( \frac{ \pi \delta }{\delta _x}\right) ^2} \cos \left( \frac{2 \pi x }{\delta _x}\right) +\cdots \nonumber \\\approx & {} 1 \end{aligned}$$

(13)

where the omitted terms are exponentially suppressed in $1/\delta _x$. This identity should be more properly understood in its integral form,

$$\begin{aligned} \int _\varGamma dx\, f(x)K(x) \approx \int _\varGamma dx\, f(x) \end{aligned}$$

(14)

where f(x) are smooth test functions of width exceeding $\delta$ or $\delta _x$ defined over the domain $\varGamma$.

This approximation is extremely accurate and can be checked in this one-dimensional context either analytically for Gaussian test functions, or numerically to understand the errors introduced by a finite set of Gaussians, and by the choice of the ratio $\delta /\delta _x$. In the limit $\delta \rightarrow 0$ the sum of Gaussians becomes a comb of delta functions, the right hand side of (14) becomes a trapezium approximation and the accuracy of the approximation in this limit is order $\delta _x^2$.

Returning to (12) we introduce the functional integral generalisation of the sum (13) into the expression to obtain:

$$\begin{aligned} \langle B[\phi ] \rangle\approx & {} {1\over \mathcal{Z}} {\delta _S\over \sqrt{2 \pi } \delta } \sum _i \int \mathcal{D}\phi \, B[\phi ] e^{-\beta S[\phi ]} e^{-(S[\phi ] - S_i)^2/2\delta ^2}.\nonumber \\ \end{aligned}$$

(15)

In the light of the discussion above, the accuracy of the approximation is rather better than anticipated from the delta function limit, but nonetheless still contains an order $\delta _S^2/\sigma ^2$ term when there are only a finite set of Gaussians.

Notice that from the definition of the double bracket quantities it is possible to reweight in the usual sense, that is, to include part of the exponential term as a measured operator rather than use for importance sampling in the Monte Carlo simulation.

$$\begin{aligned} \langle \langle B[\phi ] e^{(a_i-\beta )S}\rangle \rangle _i= {1\over \mathcal{N}_i} \int \mathcal{D}\phi \, B[\phi ] e^{-\beta S[\phi ]} e^{-(S[\phi ] - S_i)^2/2\delta ^2} \ , \end{aligned}$$

(16)

this resembles the terms in the sum (15), so the canonical expectation value can be written in terms of the double bracket quantities as:

$$\begin{aligned} \langle B[\phi ] \rangle \approx {1\over \mathcal{Z}} {\delta _S\over \sqrt{2 \pi } \delta } \sum _i \mathcal{N}_i \langle \langle B[\phi ]e^{(a_i-\beta )S}\rangle \rangle _i \ . \end{aligned}$$

(17)

With,

$$\begin{aligned} \mathcal{Z} = {\delta _S\over \sqrt{2 \pi } \delta } \sum _i \mathcal{N}_i \langle \langle e^{(a_i-\beta )S}\rangle \rangle _i \ . \end{aligned}$$

(18)

The normalisation factors, $\mathcal{N}_i$, only involve the action (5), so they can be evaluated using the piecewise approximation. This introduces an additional approximation of order $\delta _S^2/\sigma ^2$.

$$\begin{aligned} \mathcal{N}_i \approx \sum _j \rho _j \int _{(S_{j-1} + S_j)/2}^{(S_{j+1} + S_j)/2}dS \, e^{a_j(S - S_j)}\times e^{-a_i S } e^{-(S - S_i)^2/2\delta ^2} .\quad \end{aligned}$$

(19)

So the $\mathcal{N}_i$ can be analytically evaluated in terms of truncated Gaussian integrals or error functions. Using this expression in (17) and (18), we obtain the reweighting formula for fixed separation between Gaussians:

$$\begin{aligned} \langle B[\phi ] \rangle \approx { \sum _i \mathcal{N}_i \langle \langle B[\phi ]e^{(a_i-\beta )S}\rangle \rangle _i \over \sum _i \mathcal{N}_i \langle \langle e^{(a_i-\beta )S}\rangle \rangle _i } \ . \end{aligned}$$

(20)

We define the following weights

$$\begin{aligned} w_i = {\delta _S \over \delta } { \mathcal{N}_i \over \sqrt{2\pi } \delta } e^{(a_i - \beta )S_i} \end{aligned}$$

(21)

where the prefactors are motivated by the simple relation between $w_i$ and the $\mathrm LLR'$ weights, $v_i$ (10), in various limits explored in section (3.2.2) below.

The reweighting formula takes its final form, which overall is accurate to order $\delta _S^2/\sigma ^2$.

$$\begin{aligned} \langle B[\phi ] \rangle \approx { \sum _i w_i \langle \langle B[\phi ]e^{(a_i-\beta )(S-S_i)}\rangle \rangle _i \over \sum _i w_i \langle \langle e^{(a_i-\beta )(S-S_i)}\rangle \rangle _i } \ . \end{aligned}$$

(22)

This expectation value is defined in terms of the ratio of sums and it is important to avoid bias in estimating the ratio. Bootstrap techniques are used as explained later.

3.2.1 Quenched approximation

If the fluctuations of the action are ignored and we approximate (22) by neglecting the exponential factors in the double brackets, we obtain a simpler formula

$$\begin{aligned} \langle B[\phi ] \rangle \approx { \sum _i w_i \langle \langle B[\phi ]\rangle \rangle _i \over \sum _i w_i } \ . \end{aligned}$$

(23)

At the risk of confusion in the lattice gauge theory community, we term this approximation “quenched”, following the more general usage in the theory of disordered systems.

In an attempt to justify this approximation we first consider the term $(a_i-\beta )$. Provided that the range of reweighting is sufficiently narrow to allow the approximate linear relation $a_i = a_{i_c} - (i-i_c)\delta _S/\sigma ^2$, and noting that $(a_{i_c}-\beta ) < \delta _S/\sigma ^2$, we have:

$$\begin{aligned} a_i-\beta \approx -(i-i_c)\delta _S/\sigma ^2 \ . \end{aligned}$$

(24)

The double bracket expectation of the second term in the exponent vanishes, $\langle \langle S - S_i \rangle \rangle _i = 0$, according to the tuning of $a_i$ during the RM phase. Of course, because this second term appears in the exponent, fluctuations of the action cause higher moments to contribute. However, the role of the Gaussian constraint is precisely to limit the size of these fluctuations and we expect even moments to scale as:

$$\begin{aligned} \langle \langle (S - S_i )^{2n}\rangle \rangle _i \sim \delta ^{2n} \ . \end{aligned}$$

(25)

Therefore, provided the exponential can be expanded, we may anticipate the overall result:

$$\begin{aligned} \langle \langle e^{(a_i-\beta )(S-S_i)}\rangle \rangle _i \sim 1 + \mathcal{O}(\delta \delta _S/\sigma ^2) \ . \end{aligned}$$

(26)

If, by ignoring possible correlations between S and $B[\phi ]$, we make a similar assumption for the numerator of (22), we may expect that the quenched approximation differs from the full formula by terms of order $\delta \delta _S/\sigma ^2$. Since, in practical work, we set $\delta /\delta _S$ to be a value of order 1, the quenched approximation is plausibly accurate to the same order $\delta _S^2/\sigma ^2$ as was the full reweighting formula (22). However, it will become clear in the numerical work that while the quenched approximation is often good, it can lead to very different predictions in some circumstances.

The quenched approximation has a much simpler structure than the full expression and it can be interpreted as a reweighting at each time step or configuration of the Monte Carlo simulation in the measurement phase. This allows for a straightforward understanding of the quenched autocorrelation as that of the evolution of the reweighted quantity. Indeed, this is the basis for the autocorrelation time reported in [24].

In the full expression, (22), the expectation value is defined in terms of the ratio of sums. The signal to evaluate the autocorrelation time will be dominated by the larger of the autocorrelators of the numerator and denominator, in practice always the numerator. It is then important to avoid bias in estimating the ratio and bootstrap techniques are used as explained later.

3.2.2 Limits

Further intuition about the reweighting formula comes from considering various limits. Firstly, consider the limit $\delta /\sigma \rightarrow 0$ holding other quantities, including $\delta _S$, fixed. The weights simplify, $w_i = v_i$, and moreover in this limit fluctuations of the action are suppressed, so the reweighting formula becomes the quenched version (23) resembling the density of states result in the $\mathrm LLR'$ approximation (11) extended to operators that do not solely depend on the action.

For fixed spacing $\delta _S$, without taking any limit, the weights can be written as:

$$\begin{aligned} w_i= & {} {1\over \sqrt{2\pi }} {\delta _S\over \delta } v_i \sum _j {\rho _j\over \rho _i} e^{a_j(S_i-S_j)} \nonumber \\&\times {1\over \sqrt{2\pi }\delta } \int _{S_j-S_i-\delta _S/2}^{S_j-S_i+\delta _S/2} dS e^{(a_j-a_i)S}e^{-S^2/2\delta ^2} \ . \end{aligned}$$

(27)

When the range of reweighting is sufficiently narrow to allow the the approximate linear behaviour $a_i = a_{i_c} - (i-i_c)\delta _S/\sigma ^2$, the term ${(\rho _j/ \rho _i)} e^{a_j(S_i-S_j)} = 1$, and the integral becomes a function of $j-i$, so the sum is independent of i and the weights $w_i$ are proportional to the $LLR'$ weights $v_i$.

Numerically, because the ranges over which we reweight are small, the $a_i$ are linear and the weights obey $w_i \propto v_i$ rather accurately. When the sum of weights is normalised to unity, $w_i$ and $v_i$ differ by at most $4\times 10^{-3}$.

The limit $\delta \rightarrow \infty$, corresponding to no constraint, resembles the situation usually treated with the multi-histogram approach (see “Appendix A” for a general comparison). Relying on the approximate linearity of the $a_i$, the expression (27) can be simplified by expanding in $\sigma ^2/\delta ^2$. However, fluctuations are not suppressed in this limit and the reweighting formula (22) does not reduce to the multi-histogram formula.

A more interesting limit is to take $\delta /\sigma \rightarrow 0$, $\delta _S/\sigma \rightarrow 0$ holding the ratio $\delta _S/\delta$ fixed. Again we assume a narrow range and rely on linearity of the $a_i$ to obtain,

$$\begin{aligned} w_i = {\delta _S\over \delta } v_i {\sigma \over \sqrt{\delta ^2 + \sigma ^2}} \rightarrow {\delta _S\over \delta } v_i \ . \end{aligned}$$

(28)

Since fluctuations are suppressed in this limit the reweighting formula again becomes the quenched version (23).

4 Lattice gauge theory

Pure Yang Mills lattice gauge theory has been used as a testing ground for the density of states method since [19] studied SU(2) with a sharp “top hat” constraint and either Metropolis or Heat Bath algorithm. The smooth Gaussian constraint allows the HMC method to be used as described for SU(2) in [21]. The tempering method was introduced for SU(3) in [24].

We work with SU(3) in four dimensions and employ a standard Wilson action, on $16^4, 20^4$ and $24^4$ lattices. The HMC algorithm was used with the same trajectory length and integrator as [24] and these parameters allow us to validate our simulations in comparison with results in [10].

Fig. 1

Reference simulations using an unconstrained approach illustrating the range of parameters under consideration over the lattice sizes $16^4$, $20^4$, $24^4$. Top: Plaquette expectation. Bottom: Plaquette variance, including a volume factor for scaling

Preliminary simulations generated for the purposes of comparison used the canonical unconstrained approach rather than the density of states method. These simulations consider several size lattices and a range of couplings among which many trajectories at constant boxsize can be identified to define a continuum limit. Figure 1 illustrates the range of parameters considered and these are given in Table 1. At larger values of $\beta$ the dynamics of the topological charge becomes extremely slow. All simulations, both these unconstrained comparison runs and later constrained runs, use the HiRep code¹ [29, 30] and are initialised by thermalising a random configuration.

As can be seen in Fig. 1, the $\beta$ values for each lattice size all overlap in the approximate range $6.0< \beta < 6.2$. A comparison of the predictions for plaquette observables from simulations in this range confirms the absence of finite size effects for this observable to the accuracy of these results. This conclusion matches the claim in [10] that finite size effects are small for the parameters we consider both for these local observables and later on for the more extended ones.

A table of parameter values for the constrained runs is given in “Appendix B”, but some rough observations are given here as a prelude to a discussion of the method of selecting them. The action is of order $1.5\times 10^5$ at $16^4$, $3.6\times 10^5$ at $20^4$ and $7.3\times 10^5$ at $24^4$. The standard deviation of the action in the unconstrained case is about $\sigma =196$ at $16^4$, $\sigma =286$ at $20^4$ and $\sigma =391$ at $24^4$ in the centre of the reweighting range. This parameter provides the scale for the spacing $\delta _S$ of order 210 at $16^4$, 310 at $20^4$ and 420 at $24^4$. The width of the Gaussian constraints were set to be about 1.2 times the spacing in each case, $\delta /\delta _S = 1.2$.

4.1 Tempering method

Constrained functional integrals are estimated from HMC simulations with action $H(a_i,\phi ,S_i)$ which incorporates the Gaussian constraint (see Eq. (2)).

$$\begin{aligned} H(a_i,\phi ,S_i) = a_i S[\phi ] + (S[\phi ] - S_i)^2/2\delta ^2 \ . \end{aligned}$$

(29)

Table 1 Parameters of canonical reference simulations. For each lattice size, the range of $\beta$ was spanned by 24 simulations

Because the constraint might allow energy barriers to block the simulation dynamics there is concern that density of states simulations will be slower than unconstrained simulations. For pure gauge theory even the unconstrained simulations are notorious for the slow dynamics apparent in topological modes. In an attempt to overcome this problem we use tempering [22] (this was called the replica exchange method in [23, 24]). Tempering is a technique that considers an ensemble of simulations over a range of $\beta$, or in our case $S_i$, and allows configurations to migrate over this range. Configurations suffering from slow dynamics at large $\beta$ can diffuse to small $\beta$ where they evolve more quickly before returning to small $\beta$. We chose a set of $N_{TEMPER}=24$ tempers each with a fixed central action $S_i$. The central energies are listed in Table 12 in “Appendix B” and correspond to a range of coupling given in Table 2. These ranges are much narrower than the ranges of the unconstrained reference simulations.

Table 2 Parameters of measurement phase of density of states simulations. There were 24 tempers, or simulations at specific values of $S_i$. To aid comparison, the range of central action is given in terms of a coupling range below

At regular intervals (every 15 HMC steps in the measurement phase), the tempering method swaps configurations between pairs of tempers with the following probability

$$\begin{aligned}&\mathrm{min}(1,exp\lbrace H(a_1,\phi _1,S_1) + H(a_2,\phi _2,S_2) \nonumber \\&\quad - H(a_1,\phi _2,S_1) - H(a_2,\phi _1,S_2) \rbrace ) \ . \end{aligned}$$

(30)

This preserves detailed balance of the entire system of multiple tempers and aids ergodicity.

Fig. 2

Average swap probabilities during the course of the measurement phase. Averaged over all replicas. Errors are a combination of statistical and from the variation between replicas. The overlapping symbols indicate that the probabilities for $16^4$, $20^4$ and $24^4$ are indistinguishable

In order to ensure that swap probabilities remain constant across the range of tempers, the values of the set of central energies $S_i$ and the width of the Gaussians $\delta _i$ were chosen so that the overlap of probability distributions remain fixed. This amounts to a requirement on the ratio of the spacing $\delta _S$ and the standard deviation of the constrained action (given by $\delta _i/\sqrt{1 + \delta _i^2/\sigma ^2}$). The absolute values of $\delta _i/\sigma$ and $\delta _S/\sigma$ determine the potential accuracy of the method. The effect of this tuning was monitored through the swap probabilities as shown in Fig. 2 where the aim was for a swap probability of 0.5. Effects from the edge of the temper range are apparent, but do not extend far into the main range.

Fig. 3

Evolution of configurations showing how swaps between adjacent tempers lead to global mixing. Example for $24^4$ over a short part of the run for one replica near the middle of the measurement phase. The bold line shows the history of a certain configuration

Figure 3 shows the swap history over a short part of the measurement phase of the simulation illustrating how the pair swaps enable mixing though the whole space. For all lattice sizes, more than half the configurations appear at some point in every temper. In other words, they appear at every possible central energy. Moreover, every configuration always appears in at least half the tempers.

4.2 Observables

Besides the plaquette expectation value which is an action dependent quantity and hence can be computed using either of the techniques outlined in Sect. 2, it turned out that the variation of the plaquette provides a sensitive test of the accuracy of the method.

Other observables were defined after configurations had been evolved according to the Wilson flow [31]. The simplest such observables were the action density E and its clover version $E_{sym}$ which have been studied before in the context of Wilson flow [31].

At $16^4$ the flow time was set to $t=2$ and this was scaled for the simulations at $20^4$ to $t=3.125$ and at $24^4$ to $t=4.5$ so as to preserve the extent of the smoothing radius as the same fraction of the lattice in each case, keeping the physical length fixed. These choices correspond to a requirement on the dimensional parameter t:

$$\begin{aligned} \sqrt{2\, d\, t} = L/4 \ . \end{aligned}$$

(31)

Where d is the dimension ($d=4$) and L is the linear size of the box in lattice units. Fixing the extent of the smoothing to 1/4 of the lattice will allow us to study scaling in Sect. 5.

Topological charge was the observable of most interest as it provides a test of the efficiency of the tempering method in improving autocorrelation times. The charge was computed after Wilson flow of the operator to a value of t that was scaled according to the size of the lattice as described above. The charge was defined in terms of plaquette-like quantities on the smoothed configuration [31, 32] that amount to the continuum expression given in the introduction (1).

4.3 RM phase

With a single coupling constant and far from any phase transition, the value of $a_i$ for a given central energy $S_i$ will be close to the value of the coupling $\beta$ at which $\langle S-S_i\rangle = 0$. The preliminary simulations allow a fit to the dependence of $\langle S \rangle$ on $\beta$ which provides a value that is used as a seed for the RM phase. Since the seed is known so accurately, the role of the RM phase is simply to improve rather than to search for the solution in a complex landscape. The literature [33] indicates that the efficiency of the Robbins Monro technique can depend sensitively on the relaxation parameters. This may be true for high dimension problems common in AI but is not the case for this improvement of a one dimensional problem. Indeed, a simple Gaussian model for the RM process allows the effect of different RM schedules to be explored for much longer convergence times than are possible for the real system. The model consists of sampling $\langle \langle S-S_i\rangle \rangle$ from a Gaussian of width $\delta /\sqrt{1+\delta ^2/\sigma ^2}$ and mean $-(a_i - a_i^{*})\delta ^2/({1+\delta ^2/\sigma ^2})$ where $a_i^{*}$ is the assumed solution. It was found that there was little advantage in more elaborate tuning than the choice of parameters $n_0$ and c in the RM iteration:

$$\begin{aligned} a_i(n) = a_i(n-1) - {c\over n_0 + n} \langle \langle S- S_i\rangle \rangle _i \ . \end{aligned}$$

(32)

In the RM phase, $\langle \langle S- S_i\rangle \rangle _i$ was computed from 50 measurements on consecutive HMC configurations with fixed $a_i$. Test runs which made an update according to (32) every measurement had the same behaviour and were barely any faster. These simulations were performed without any replica swaps during the evaluation of $\langle \langle S- S_i\rangle \rangle _i$ because, while these do not usually affect final convergence, they do prevent it at the very edges of the temper range. Moreover they lead to larger early fluctuations which would require a different tuning regime. Swaps were allowed between evaluations of $\langle \langle S- S_i\rangle \rangle _i$.

The value of c was chosen to be rather smaller than the supposed optimal one as larger values tended to drive the system too far from the accurate seed value. This choice does not compromise the convergence properties of the algorithm. The starting iteration $n_0$ was set to 20 as a compromise between excess change over the first few iterations and speed of convergence later (the value was slightly raised to $n_0=25$ for $24^4$).

In contrast to the details of the RM schedule, starting and following independent RM simulations was useful both to test the convergence and to provide a bootstrap mechanism for computing errors arising from inaccuracy in this phase. The whole simulation procedure is repeated for a set of $N_{REPLICA}$ replicas. During the RM phase, each replica or RM iterate starts from a different random configuration separately thermalised with a different sequence of random numbers, but with the same seed value $a_i(0)$. We distinguish the replicas with an upper index $a = 1\dots N_{REPLICA}$ and in this work there are $N_{REPLICA}=8$ different replicas. The mean over replicas at each RM phase iteration step n, is denoted with an overbar as,

$$\begin{aligned} {\bar{a}_i(n)} = {1\over N_{REPLICA}} \sum _{a=1}^{N_{REPLICA}} a_i^a(n) \ . \end{aligned}$$

(33)

According to the theory of the Robbins Monro technique [33], different iterates will asymptotically converge to a Gaussian distribution of width proportional to $1/\sqrt{n}$. The variance in replica space is therefore a convenient convergence parameter,

$$\begin{aligned} C_i(n) = {1\over N_{REPLICA}} \sum _{a=1}^{N_{REPLICA}} (a_i^a(n)-{\bar{a}_i(n)} )^2 \ . \end{aligned}$$

(34)

Fig. 4

Convergence during the RM phase at $20^4$ for the temper with central action 363310. Top: history of $a_i(n)$ showing 8 independent replicas all starting from the seed 6.28980. The mean is also shown as the thick line. Bottom: history of convergence parameter $C_i(n)$ defined in the text

4.3.1 Convergence

Examples of typical convergence are shown in Fig. 4. Ideal behaviour is for the convergence parameter to decrease as 1/n.

During the RM phase the behaviour of the convergence parameter is characterised by a noisy initial phase after which the scaling regime is reached. The shape of these curves varies considerably between replicas and tempers but all eventually display the asymptotic behaviour.

The primary convergence criterion is to ensure that convergence parameter has reached the asymptotic regime, but this still leaves some flexibility in exactly when to stop. In the present work we first ensure that the convergence has reached the asymptotic phase and terminate after a fixed number of iterations $n_{max}$. $n_{max}=442$ iterations for $16^4$ and 500 in the case of $20^4$ and $24^4$.

The error in the final value of $a_i$ may be estimated from the standard deviation, $\sqrt{C_i({n_{max}})/N_{REPLICA}}$, at the end of the RM phase. When averaged over tempers, this was $2.7\times 10^{-5}$, $1.7\times 10^{-5}$, $1.3\times 10^{-5}$ for $16^4$, $20^4$ and $24^4$ respectively. Note that these values are similar to the difference between the final mean value ${\bar{a}_i}(n_{max})$ and the initial seed value. As is clear from the behaviour of the convergence parameter of the RM phase convergence shown in Fig. 4 it takes considerable effort to improve the accuracy of the $a_i$.

Fig. 5

Predictions for the mean plaquette and its variance. Rows show $16^4$, $20^4$ and $24^4$. The first column shows the mean plaquette with errors that are too small to be visible and this appears the same whether computed using information from the RM phase (LLR) or reweighting results from the measurement phase. The second and third columns show the plaquette variance computed using LLR and reweighting respectively. Errors are shown with shaded regions. All plots also show data points obtained using traditional unconstrained methods

4.3.2 Predictions from RM phase

The LLR procedure of Sect. 3.1 was followed to compute the plaquette and its variation based solely on the $S_i$ and the $a_i$ determined by the RM phase. This was done separately for each of the 8 replicas and at the final stage errors are evaluated using bootstrap. Note that the scales are different for each size shown in Fig. 5. For the values of $\beta$ shown in these plots, the original runs using traditional HMC were supplemented by additional unconstrained runs at $20^4$ and $24^4$ intended to improve statistics.

The range of $\beta$ considered for these measurements was limited because deviations from a smooth plot appear near the edges of the temper range. The full LLR version of the weights (10) changes abruptly from an approximately linear dependence on $\beta$ and it is straightforward to choose a cutoff that amounts to discarding three tempers at each boundary. The resulting ranges are given in Table 3.

Although the plaquette can easily be measured using traditional techniques, it is reassuring that we obtain the same results, with high accuracy, using the density of states method. The mean plaquette shown in the first column of Fig. 5 appears the same whether computed using density of states information from the RM phase or reweighting results from the measurement phase. The plaquette variance shown in the second column of Fig. 5 provides a more sensitive test. Indeed, an early $20^4$ run with shorter RM phase and values of $a_i$ only known to accuracy of around $1\times 10^{-4}$ (compared to $3 \times 10^{-5}$ for the data shown in Fig. 5), led to errors in the variance about five times bigger then in the data presented here. The third column of Fig. 5 is discussed in the next section.

4.4 Measurement phase

The measurement phase has a duration of $2 \times 10^4$ HMC steps with potential swaps every 15 steps and was repeated for each of the 8 RM replicas and also for all three lattice sizes. There are two distinct contributions to the error: from uncertainly in the $a_i$ arising from the RM phase and from statistical fluctuation in the measurement phase due to limited length runs. We refer to these as the RM error and MP error respectively.

The set of $\beta$ at which to compute canonical expectation values by the reweighting procedure of Sect. 3.2 as adapted for simulations below, are chosen sufficiently close to give a good approximation to a continuous curve in the plots. We choose a $\beta$ spacing of 0.002 irrespective of lattice size.

4.4.1 Reweighting

In order to relate the formalism developed in Sect. 3 to the output of simulations it is helpful to explicitly recognise that in the measurement phase of the constrained Monte Carlo, the double bracket quantities appearing in (22) are identified as averages over HMC configurations or time-steps t for a particular temper i. The usual estimator is:

$$\begin{aligned} \langle \langle B[\phi ]e^{(a_i-\beta )(S-S_i)}\rangle \rangle _i = {1\over T} \sum _t e^{(a_i-\beta )(S_i[t]-S_i)} B_i [t] \ . \end{aligned}$$

(35)

Table 3 Ranges of $\beta$ for LLR predictions based on the RM phase

Fig. 6

The average normalised weight for $\beta$ near the centre of the temper range. Shown for $16^4$, $\beta =6.118$; other sizes and $\beta$ are very similar. The time dependent weight (39) is averaged over all measurements and all RM replicas. Errors are too small to be visible

Where $S_i[t]$ and $B_i [t]$ are the measurements of the respective observables at that configuration or time-step.

For each HMC configuration and separately for each RM replica labelled by index a, we perform the following temper sums appearing in the numerator and denominator of equation (22). Usually, the variance of the operator is also a quantity of interest so computations involving $B_i^2[t]$ are made at the same time.

$$\begin{aligned} B^a[t]= & {} \sum _i w^a_i e^{(a^a_i - \beta )(S^a_i[t]-S_i)} B^a_i[t] \end{aligned}$$

(36)

$$\begin{aligned}= & {} \sum _i w^a_i[t] B^a_i[t] \end{aligned}$$

(37)

$$\begin{aligned} w^a[t]= & {} \sum _i w^a_i e^{(a^a_i - \beta )(S^a_i[t]-S_i)} = \sum _i w^a_i[t] \ . \end{aligned}$$

(38)

Where we have defined the time dependent weights,

$$\begin{aligned} w^a_i[t] = w^a_i e^{(a^a_i - \beta )(S^a_i[t]-S_i)} \ . \end{aligned}$$

(39)

Which in the quenched approximation reduce to the ordinary static weights $w^a_i$ (21).

Using these definitions the reweighting expression (22) for a particular RM replica, a, becomes

$$\begin{aligned} \langle B[\phi ]\rangle = {\sum _t B^a[t] \over \sum _t w^a[t] } \ . \end{aligned}$$

(40)

The integrated autocorrelation time is defined as the maximum of the autocorrelation time in numerator and denominator and is computed according to the prescription in [34]. In order to estimate the ratio that appears in the reweighting formula (40) without bias, a bootstrap technique is used over the $2\times 10^4$ measurements divided by the autocorrelation time. The same bootstrap selection is employed for both numerator and denominator. This procedure also yields an estimate of the error of the ratio due to the fluctuations in the measurements. We call this statistical error the “measurement phase (MP) error”.

The procedure above is repeated for the $N_{REPLICA}$ different RM replicas. A separate analysis over these reweighted measurements gives the error associated with imprecision in knowledge of the value of the $a_i$’s that were derived in the RM phase. Depending on the observable, the relative sizes of the errors arising from each source, RM or measurement, is different and in plots the two different contributions to the error are represented by distinct shaded regions.

The static weights, named $w_i$ and defined by equation (21) in the formalism above, are computed in such a way as to avoid danger of numerical overflow, based on the parameters $(S_i, a_i)$ and the desired $\beta$ for reweighting using generalisations of the formulae (21) adapted for variable action spacing. When the reweighting parameter $\beta$ happens to be similar to a value of $a_i$ in the middle of the temper range, the static weights are largest for tempers that are near that central part of the range. For time varying weights (39) there are fluctuations and the weights of more distant tempers contribute. Although these weights vary for each step of the measurement simulation, their average is very stable. Figure 6 shows how the average normalised time dependent weight varies across the temper index for $\beta$ chosen near the centre of the temper range. Plots for other size lattices or other values of $\beta$ near the centre of the tempering range look very similar indicating that the range of tempers that contribute appreciable weight is fairly constant at about seven tempers for our parameters.

As $\beta$ approaches an edge of the temper range, reweighting becomes less accurate since tempers not simulated could have significant weights. The reweighting range is determined by requiring that the average normalised weight for edge tempers be less than 1%. A different criterion based on the limiting the fraction of weights that are greater than 0.01 for example, leads to the same range. The resulting ranges are apparent from the plots, but are explicitly given in Table 4. There appears to be a slight decrease in the useful fraction of the temper range as the lattice size increases.

Table 4 Ranges of $\beta$ for reweighting predictions based on the measurement phase according to criteria in the text

Table 5 Plaquette observables for $16^4$ at $\beta = 6.118$. Entries are computed using LLR, $\mathrm LLR'$ or reweighted measurements with quenched (QRewt) or varying weights (Rewt). Multi-histogram results based on unconstrained simulations are given for comparison (see “Appendix B”)

Table 6 Plaquette observables for $20^4$ at $\beta = 6.290$

Table 7 Plaquette observables for $24^4$ at $\beta = 6.438$

4.4.2 Plaquette predictions

The expectation of the mean plaquette and variance can be computed via either of the techniques, LLR based on the RM phase or reweighting measurements, and it is interesting to compare the results. A plot of the mean is indistinguishable from the left column of Fig. 5 though as is apparent from Tables 5, 6, 7, the LLR approach leads to greater accuracy. The plaquette variance according to the reweighting method is shown in the right column of Fig. 5. The RM errors for each approach are similar but the reweighting approach is also subject to MP errors which for the run length chosen, are a few times larger that the RM errors.

In order to provide more detail about the relative size of the RM errors from uncertainly in the $a_i$ from the RM and the MP errors due to limited length runs, Tables 5, 6, 7 show data for a representative value of $\beta$ chosen in the centre of the range for each lattice size. Overall, because it is only subject to RM and not MP errors, the LLR approach that only uses the density of states is more accurate than reweighting. In this case it is possible to see that the difference between measurements using the full formulae based on (9) and those using the approximation denoted $\mathrm LLR'$ are always smaller than the error due to uncertainty in $a_i$. The tables also show results from unconstrained simulations reweighted to the reference $\beta$ using multi-histogram [35] (see “Appendix B”). Note that the error from this approach reflects both the intrinsic statistical error of the unconstrained simulations and also how close the reference $\beta$ happens to be to one of the widely spaced set of $\beta$ used in those simulations, so the way it changes with lattice size is not significant.

The tables also allow us to compare the use of quenched and fluctuating weights for reweighted measurements. Both lead to very similar results for the mean plaquette and its errors. However there is a clear difference in the result for the plaquette variance and comparison with either density of states or traditional simulations favours the approach derived in (22), that is, the one with fluctuating weights. This result clearly indicates that the quenched approach is incorrect, we will continue to study it to illuminate the autocorrelation of the topological charge, but in all further plots of expectation values we use the fluctuating weights. For both the plaquette mean and variance, the MP error for the chosen run length is a few times larger than the RM error.

Fig. 7

The symmetric cloverleaf energy density after Wilson flow using reweighted measurements. Rows for $16^4$, $20^4$, $24^4$. Also shown for comparison are results from traditional simulations supplemented by additional runs. Left: the mean value. Right: the variance (with a volume factor). Errors from the measurement and the RM phase are similar but small and are shown as the shaded region barely visible in the case of the mean

The autocorrelation times displayed in the tables are the integrated version computed using the Wolff criterion as described in Sect. 4.6 and are order 1 HMC step remaining fairly constant as $\beta$ varies. The consequences of the use of fluctuating weights are most apparent in the integrated autocorrelation time which becomes half the value obtained in a quenched analysis. The equivalent value for the traditional simulation dropped to a plateau of about 3 HMC steps for $\beta > 6$. For varying weights, the MP and RM errors are of similar size while for quenched weights the MP error is larger.

Fig. 8

The topological charge based on reweighted measurements. Also shown for comparison are results from unconstrained simulations with additional runs. Left: the charge itself which must be zero. Right: the variance of the charge. From top to bottom: $16^4$, $20^4$, $24^4$. Errors from the measurement and the RM phase are shown as shaded regions. The Q data point for $24^4$ at $\beta =6.43$ is off plot

Table 8 Topological charge observables for $16^4$ at $\beta = 6.118$. All tables are computed using reweighted measurements with quenched weights (QRewt) or fluctuating weights (Rewt). Entries for reference simulations reweighted according to multi-histogram (see “Appendix B”) are given for comparison

Table 9 Topological charge observables for $20^4$ at $\beta = 6.290$

Table 10 Topological charge observables for $24^4$ at $\beta = 6.438$

4.4.3 Observables defined after Wilson flow

Wilson flow corresponds to an operation that cannot be treated without using reweighting. Expectation values for the symmetric cloverleaf energy density, $E_{sym}$, after Wilson flow are shown in Fig. 7 and the equivalent results for the energy density after Wilson flow are very similar. For the values of $\beta$ shown, the traditional unconstrained simulations have been supplemented with additional runs to improve statistics. As we have come to expect for the plaquette, the mean value of $E_{sym}$ has small error and agrees closely with the reference simulations for all sizes. The variance is much better behaved than it was for the original plaquette variance without Wilson flow and has closer agreement with the unconstrained simulations. Errors arising from RM and measurement are of similar size and both less than 0.1% for the mean and less than 2% for the variance.

A discussion of the autocorrelation time for these observables is postponed until after we discuss the computation of autocorrelation in the case of the topological charge.

4.5 Topological charge

We devote a whole section to this topic because a strong motivation for studying alternative approaches such as density of states is the freezing of the topological charge in the continuum limit of traditional simulations.

The expectation of the topological charge must of course vanish and the left column of Fig. 8 shows that the reweighted measurements always contain zero within the error range, while the rather longer traditional simulations have not yet met this requirement. Vanishing charge is often regarded as a check that simulations are sufficiently long and the widely varying sizes of the error bars for the variance of the traditional simulations at larger sizes, even with the help of supplemental runs, indicates that these simulations are not yet ergodic. Even the configurations of the measurement phase simulations rarely change charge at large size, but the swaps lead to much more rapid change of fixed central energy trajectories. These qualitative considerations are more formally studied with the autocorrelator below.

The effect of Wilson flow on the topological charge is well known [31] and for measurements on either traditional unconstrained or constrained simulations the flowed charge bunches close to integer values. Several tempers that can have different (each almost integer) values of the charge contribute to the reweighted charge which is no longer expected to be close to an integer.

The variance or topological susceptibility is shown in the right column of Fig. 8. Note that the scale varies and that the size of the errors of the reweighted results actually decreases as the lattice size increases.

Tables 8, 9 and 10, show detailed results for a single value of $\beta$ from the centre of the range at each lattice size to illustrate the relative size of the RM and MP error and to expose the relation between reweighting with quenched or fluctuating weights. The values predicted for mean or variance of the topological charge by either type of reweighting is close. The unconstrained results reweighted according to multi-histogram always have large errors and become poorer at larger lattice size. Note that, as described in the next section, $\tau _{int}$ is computed using a different criterion for fluctuating weight than for quenched weights. Both RM and MP errors for each quantity are fairly similar for quenched and unquenched. MP errors are in all cases larger than RM errors.

The autocorrelation time and the dramatic difference between the its value for quenched and fluctuating weights is the subject of the next section.

Fig. 9

Quenched and fluctuating autocorrelation functions for the topological charge for a representative example at $\beta = 6.290$ for $20^4$. Both functions are normalised. Top: over short times where for the fluctuating weight autocorrelator the first few points show the rapid decay component. Bottom: over long times showing typical fluctuations

4.6 Autocorrelation

The autocorrelation time determines the size of errors and so is used as a way of evaluating the efficiency of competing algorithms. The particular autocorrelation time relevant to computing errors is the integrated form, $\tau _{int}$ as distinct from $\tau _{exp}$ which characterises the long time decay of the correlation function. This distinction is emphasised by Madras and Sokal [36], but a connection appeared in more recent work by Wolff [34] (also see [10]) as an estimate for $\tau _{exp}$ helps determine an optimal value for the upper limit of the sum defining $\tau _{int}$. It turns out that the present work illuminates the different definitions as it allows us to give an estimate for $\tau _{exp}$ in a case where $\tau _{int}$ and $\tau _{exp}$ are very different.

Fig. 10

Autocorrelation times obtained from the autocorrelation function for topological charge based on reweighting measurements with fixed weights. Showing the integrated $\tau _{int}$ and the fitted $\tau _{fit}(A=1)$ as described in the text for, from top to bottom, $16^4$, $20^4$ and $24^4$. Also shown for comparison are results from unconstrained simulations. For each $\tau$ the largest source of error is shown with a shaded region. The RM errors of each $\tau$ are of similar size but the MP error for $\tau _{int}$ is larger

First observe that the autocorrelation functions for the quenched and fluctuating weight approaches have distinct character. Typical autocorrelation functions, $\varGamma (t)$, are shown in Fig. 9. Each autocorrelation function is normalised to $\varGamma (0)=1$ and it is clear that while the quenched approach leads to the usual decay, the fluctuating weight approach suffers from a rapid decay over a few HMC steps followed by a component with a long timescale. The techniques used to analyse these cases are different.

4.6.1 Quenched autocorrelation

The top curve of the upper plot of Fig. 9, shows that the quenched autocorrelation function for the topological charge has the usual long timescale decay. We first review the standard technique for computing $\tau _{int}$ by analysing this usual case.

The expression for the integrated autocorrelation time is:

$$\begin{aligned} \tau _{int}(W) = {1\over 2} + \sum _{t=1}^{W} {\varGamma (t)\over \varGamma (0)} \ . \end{aligned}$$

(41)

We follow the prescription of Wolff [34] to determine the window, W, by minimising the combination of truncation and statistical errors, estimated as:

$$\begin{aligned} e^{-W/\tau _{exp}} + 2\sqrt{W\over T} \ . \end{aligned}$$

(42)

Where T is the duration of the measurement simulations, 20000 steps. For smooth autocorrelation functions without timescales much longer than $\tau _{int}$, the exponential autocorrelation time, $\tau _{exp}$ appearing in this expression, is estimated as $S\, \tau _{int}$ with the parameter S in the range $1\sim 2$. All quenched reweighted autocorrelation functions behave like the example shown in Fig. 9 without any indication of timescales longer that $\tau _{int}$ which is of the order of 100’s of HMC steps. So we take the conventional value $S = 1.5$.

As a rough justification for this approach and the one we will follow for fluctuating weights, we consider a direct fit of the normalised autocorrelation function to a single exponential decay:

$$\begin{aligned} A e^{-t/\tau _{fit}} \ . \end{aligned}$$

(43)

We first make a fit in which we set $A=1$, thus guaranteeing the normalisation and the short time behaviour that appears in $\tau _{int}$. Fits are made over the range 1 to a few 1000’s and we have checked that the value of the right hand cut has negligible effect on the fit parameters. The resulting averaged values for $\tau _{fit}$ are shown, in Fig. 10. The similarity between $\tau _{fit}(A=1)$ and $\tau _{int}$ is striking.

An alternative fit in which A is also a fitting parameter leads to a rather longer $\tau _{fit}(A)$ which resembles $\tau _{exp}$ according to the hypothesis $\tau _{exp} = S\,\tau _{int}$ and provides reassurance that the choice $S=1.5$ is reasonable. We do not attempt to tune S using this fitting information as this would have little effect on the resulting value of W or $\tau _{int}(W)$.

Figure 10 also shows error estimates for $\tau _{int}$ and $\tau _{fit}(A=1)$. For a single replica, the error of the integrated autocorrelation time is:

$$\begin{aligned} \varDelta \tau _{int} = 2\sqrt{W\over T}\tau _{int} \ . \end{aligned}$$

(44)

We regard this as the MP error and observe that it is far larger than the error for the fitted version, $\varDelta \tau _{fit}$, which arises from uncertainty in the fitting procedure. The RM errors are similar for each. It is unsatisfactory that the measurement phase statistical errors of two ways of computing the autocorrelation time are so different. The fitting error of $\tau _{fit}$ appears to be underestimated. Indeed, when the measurement phase is repeated for a replica with identical RM parameters but a different sequence of random numbers, there is a significant difference in the results of the fit which are well beyond the error estimate $\varDelta \tau _{fit}$.

Fig. 11

Autocorrelation times obtained from the autocorrelation function for topological charge based on reweighting measurements with fluctuating weights. Showing the integrated $\tau _{int}$, the fitted $\tau _{fitL}$ and the combination $A\,\tau _{fitL}$ as described in the text for, from top to bottom, $16^4$, $20^4$ and $24^4$. Also shown for comparison are results from traditional simulations. For each $\tau$ the RM error and the MP error are shown with shaded regions. The MP error for $\tau _{int}$ is dominant, the RM errors of each $\tau$ are of similar size and the statistical fitting error of $\tau _{fitL}$ is smallest and omitted from the plot

4.6.2 Fluctuating weight autocorrelation

The action or plaquette observable has a short autocorrelation time never more than a few HMC steps irrespective of exactly which $\tau$ is computed. This short timescale appears in the varying weights (39) and pollutes any long timescale that may be present in any observable computed by reweighting with these weights.

In the case of the topological charge the fluctuations of the weights do not entirely hide the long timescale component. Figure 9 shows an example of the fluctuating weight autocorrelation function for the topological charge over both short and long times. This autocorrelation function suffers a rapid decay over a few HMC steps, but clearly leaves a well distinguished long timescale component. This feature is observed for all RM replicas and all lattice sizes, though with differing amplitude for the long component. Over the longer timescales shown in the lower plot of Fig. 9, the varying weight autocorrelation function continues to have short time fluctuations that manifest as the greater thickness of the line compared with the quenched version. It is also apparent from this plot that long timescale fluctuations persist for both autocorrelation functions but with larger amplitude for the quenched than the fluctuating weight case.

The Wolff procedure described in the previous section for computing the integrated autocorrelation time for fixed weights is not appropriate for the fluctuating weight results with mixed decay times. Indeed, reference [34] suggests that the choice of parameter S must be reexamined in this situation. We have considered many alternative approaches with the aim of finding a robust prescription. Our final approach is to directly fit the following normalised double exponential decay according to the two stages described below.

$$\begin{aligned} (1-A) e^{-t/\tau _{fitS}} + A e^{-t/\tau _{fitL}} \ . \end{aligned}$$

(45)

Fitting multiple exponentials has a reputation of being fraught with problems, but in this case the two $\tau$ parameters take such different values, $\tau _{fitL}/\tau _{fitS} > 100$, that the technique is robust for the variety of autocorrelation functions arising from different RM replicas, $\beta$ and lattice sizes. Nonetheless, the procedure for the fit is in two stages.

Firstly, all three parameters of the function are fitted over a short range, up to a cut at about 300 steps. Secondly, with short timescale parameters A and $\tau _{fitS}$ frozen, the single parameter $\tau _{fitL}$ is fitted over a much longer time range of more than 1000 steps. We find that the dependence of $\tau _{fitL}$ on the short range cut is smaller than the statistical errors, and that there is negligible dependence on the long range cut when it is taken to be sufficiently large. The same cuts are used for all RM replicas but they take different values according to lattice size ($16^4: 1500, 20^4: 3000, 24^4: 4000$).

The integrated autocorrelation time for a double exponential decay with such widely separated timescales will, for sufficiently large window, be dominated by the long timescale and we expect,

$$\begin{aligned} \tau _{int} \approx A\, \tau _{fitL}\ . \end{aligned}$$

(46)

A more accurate equation involving logs along the lines of the one discussed in [10, 34] can be derived, but since our approach relies on widely separated scales, the simpler equation (46) is adequate.

In view of Eq. (46), we set the value of S used to estimate $\tau _{exp}$ appearing in (42) to $S=1/A$ and follow the Wolff procedure. Figure 11 shows $\tau _{int}$ computed according to this technique along with $A \tau _{fitL}$ from the fit. The MP error for $\tau _{int}$ is computed using (44) and as for the quenched case, it is large, making the agreement all the more remarkable. This value of $\tau _{int}$ is used to estimate errors in the topological charge measurements and these appear in Tables 8, 9, 10, and Fig. 8.

The proportionality factor A introduced in (45) can be interpreted as the coupling to the long timescale. Its value of around $0.2\pm 0.05$ does not appear to be very sensitive to the value of the reweighting coupling $\beta$ or even to the size of the lattice. We expect it to depend on the parameters of the density of states method, in particular the ratio $\delta / \sigma$.

4.6.3 Comments

While the shape of the autocorrelation function is very different for the quenched and the fluctuating weights, it is interesting to see if the long time behaviour matches. In other words, is $\tau _{exp}$ the same? Our best estimates of this quantity are based on fits: $\tau _{fit}(A)$ in the quenched case and $\tau _{fitL}$ for fluctuating weights. A comparison of these quantities is not shown, but although there are large fluctuations, they are compatible within the errors.

To summarise this discussion of the autocorrelation time of the topological charge: we have used information from the fit of a double exponential to the fluctuating weight autocorrelation function in order to tune the parameter S, and obtain a better value for the Wolff window leading to a more accurate prediction for $\tau _{int}$. We find relations between the integrated and fitted autocorrelation times. For the quenched case: $\tau _{int} \approx \tau _{fit}(A=1)$, and for varying weights: $\tau _{int} \approx A \tau _{fitL}$. Finally, we observe that our estimates for the long time $\tau _{exp}$ behaviour of either quenched or fluctuating weights is similar.

We conclude this section by clarifying how these insights carry over to the computation of $\tau _{int}$ for other observables. The quenched case is straightforward and the standard Wolff procedure outlined at the start of Sect. 4.6.1 for the topological charge is used for all observables. For the fluctuating weight case, even for quantities such as $E_{sym}$ after Wilson flow that have $\tau _{int} \approx 50\sim 60$ for unconstrained simulations, there is no clear long timescale remaining that would allow any improved estimate of $\tau _{exp}$. Hence S can take the conventional value, $S=1.5$ and we follow the ordinary Wolff procedure outlined at the start of Sect. 4.6.1.

5 Scaling

The analysis reported so far has involved figures presenting densities against $\beta$ and with the exception of Fig. 1, have been for a single lattice size. In this section, scaling properties are discussed and the density of states method is used to illustrate the approach to the continuum at fixed box size.

As was discussed in Sect. 4.2, Wilson flow introduces a new scale into the system; the parameter t specifying the endpoint of the flow is dimensional and equation (31) shows how it represents the scale over which the configuration is smoothed. Our simulations, both constrained and unconstrained choose t in such a way that that the scale of smoothing is a fixed fraction of the size of the lattice. Then, by comparing results for couplings, $\beta$, corresponding to the same physical box size, the Wilson flow scale is physically identical and quantities on different lattice sizes can be compared.

Fig. 12

Scaling plot of the symmetric clover link energy based on reweighted measurements and also showing traditional results. Three lines correspond to data from the three lattice sizes. The shaded areas represent the MP errors which are slightly larger than the RM errors (not shown)

Fig. 13

Scaling plot of the Topological charge susceptibility based on reweighted measurements and also showing traditional results. Three lines correspond to data from the three lattice sizes. The shaded areas represent the MP errors which are considerably larger than the RM errors (not shown)

Figures 12 and 13 plot global quantities for the box, versus the boxsize and display this for different lattice resolutions. Namely, the figures show the global observables $V E_{sym}$, $V^2 \mathrm{Var}(E_{sym})$ and $Q^2$.

The scaling of the symmetric clover link energy at the top of Fig. 12 is almost linear and all data from different size lattices and from both traditional and density of states simulations coincide. The variance of this quantity displayed in the lower part of Fig. 12 shows noisier data and the lines of reweighted data from different size lattices do not quite coincide.

Figure 13 shows the topological charge variance scaling. As was the case in Fig. 8, the data points from the traditional simulations are noisy and especially for larger lattices, indicate worse ergodicity than the density of states data.

Fig. 14

Overall plot of autocorrelation times for topological charge both for unconstrained simulations and density of states. The band of data points shows $\tau _{int}$ for traditional simulations for each lattice size. The shaded regions display $\tau _{int}$ computed using reweighting and indicate the statistical error which dominates the RM error

6 Conclusions

We have presented a comprehensive and detailed study of the use of the density of states method for SU(3) Yang Mills theory. To do this we derived the reweighting formalism appropriate for a smooth Gaussian constraint and emphasised that the expression for a canonical expectation value is a ratio of weighted sums and that the weights fluctuate because they contain a term that depends on the action. We explored the quenched approximation in which this variation is neglected and found that when the weights vary there is a dramatic effect on autocorrelation times which is absent for the quenched approximation. However we want to emphasise that as there is no theoretical basis for the quenched approximation and even though it appears to be reasonably accurate for the expectation values of most observables, there is a notable exception, the plaquette variance, identifying the approximation as uncontrollable.

We compared predictions for the plaquette and its variance (which are both simple functions of the action) from the LLR approach based solely on reconstructing the density of states obtained from RM phase, and the reweighting approach based on information from the measurement phase. We found that these were always compatible, though reweighting led to greater uncertainty associated with the finite duration of the measurement phase. We noted that the plaquette variance is a delicate test of the accuracy of the technique and indeed it is also a good check for multi-histogram reweighting of traditional unconstrained simulations.

For quantities that are defined after Wilson Flow, and for which only the reweighting approach is possible, our method allows families of continuum limit trajectories to be defined. These are characterised by the boxsize associated with the value of the coupling constant for which we are performing the reweighting. Scaling of the topological charge susceptibility at finite temperature is an interesting area of investigation [6] and we have demonstrated the possibility of going to reasonably small lattice spacing with only modest size lattices and fairly short runs.

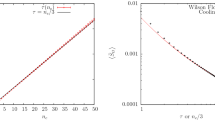
The main conclusion of the preliminary work [24] concerned the reduction in autocorrelation time for the topological charge. The conclusions presented here are more nuanced. Figure 14 shows the growth of the autocorrelation time for traditional simulations along with $\tau _{int}$ for reweighted results in each of the regions where we have computed it. The rate of growth of $\tau _{int}$ for traditional unconstrained simulations is compatible with that reported in the high statistics study [10]; namely $z\sim 5$ for the model $\tau _{int}\propto a^{-z}$. The density of states method yields a much smaller value for $\tau _{int}$ and more importantly, the rate of growth appears to be much less. The size of the errors evident in the reweighting data shown in Fig. 14 prohibit anything better than a crude estimate. Using three values corresponding to the same box size gives $z\sim 1\pm 2.5$. While the uncertainty in this estimate makes it almost meaningless, it is clearly smaller than the exponent for unconstrained simulations. This is an exciting result as it offers the potential to compute accurate values of the topological charge with less effort. However, the small value of $\tau _{int}$ is mainly the consequence of the reduction in the coupling of the topological charge to the long timescale modes of the problem. These modes have not gone away, and indeed long timescale modes themselves are often the primary subject of interest in studies of the relative performance of different algorithms rather than the topological charge which is frequently used simply as a proxy for studying these modes. In the text we discussed our estimate of $\tau _{exp}$ which is a better measure of the long timescales of the problem (though, as always, there may be even longer timescales beyond the duration of the simulations). This does show a decrease from the equivalent parameter of standard HMC simulations We highlight that the changes to the HMC algorithm necessary for the density of states approach, namely the Gaussian constraint and tempering swap, do not affect the scaling behaviour of the timing of our implementation with the number of lattice points.

A notable aspect of this study is that we explored the errors of the method by tracking eight replicas for each lattice size. We noticed that there was considerable variation in the convergence during the RM phase. Our study chose a simple common time duration for this phase, but a more sophisticated temper dependent criterion for terminating the RM phase that could put more effort into controlling the scaling convergence of the RM process, might provide better overall accuracy.

We distinguished two sources of error: the RM errors and the MP errors. For all results using reweighting the relative contribution of RM and MP errors depend on the particular observable under study. The RM errors can be reduced by increasing the number of replicas in the RM phase and the MP errors can be reduced with a longer measurement phase. For our choice of $N_{REPLICA}$ and duration of the measurement phase the largest contribution to the error for most observables was from measurement.

This work has kept $\delta /\delta _S$ fixed at 1.2 and scaled $\delta$ for different size lattices according to a fixed fraction of the standard deviation of the constrained action. These parameters affect the accuracy and efficiency of the method and a more detailed study would be welcome. For example, it would be interesting to investigate the dependence of the topological charge susceptibility on $\delta /\sigma$ while preserving the ratio $\delta /\delta _S$ (along the lines of figure 6 of reference [20] which studies the dependence of $C_V$ in a U(1) theory), and the coupling of the topological charge to the long timescale modes. The number of tempers used in the tempering method was 24 for all lattice sizes. A wider range of tempers would be expected to allow better mixing of regimes with faster and slower Monte Carlo dynamics and thus improve the autocorrelation time. As the lattice size increases, the spacing $\delta _S$ is expected to grow as $\sqrt{V}$ in order to preserve the same level of accuracy. The corresponding spacing in $\beta$ will therefore decrease in the same way. If the efficiency of the tempering depends on the span of $\beta$, then more tempers will be needed (with $N_{TEMPER} \sim \sqrt{V}$). This scaling prediction and the effects of the length of the RM and measurement phases and the number of replicas on the accuracy require further study.

7 Note added

While this manuscript was in preparation, two studies appeared that report on investigations of the topological charge. Ref. [37] performs a study in SU(6) with a novel algorithm where a tempering procedure is used to move across systems with boundary conditions interpolating between partially open and periodic; this algorithm is proved to be successful at reducing the correlation time of the topological charge. Ref. [38] studies topological properties at finite temperature using a density of states method that allows it to sample rare events. The relative merits of our algorithm and those new proposals would need to be assessed by dedicated studies.

Appendices

Appendix A: Multi-histogram

The density of states method reconstructs canonical expectation values from a set of constrained expectation values at fixed central action. It is natural to contrast this approach with traditional multi-histogram reweighting [35] which reconstructs canonical expectation values at intermediate couplings from a set of unconstrained expectation values at fixed coupling. The multi-histogram approach does not benefit from the tempering update step and hence a timing comparison would be meaningless.

Rather than make a detailed comparison, requiring additional unconstrained runs at values of the coupling commensurate with the set of central actions discussed in the main paper, this appendix studies multi-histogram based on the unconstrained reference simulations. To recap, these simulations were at 24 widely spaced $\beta$ values for each lattice size, covering the ranges listed in Table 1. In the following, so as to directly compare with the density of states results, we only consider the narrower ranges that appear in the figures; so only 7, 6, 4 (for $16^4$, $20^4$ and $24^4$) of the 24 runs were necessary. Errors are obtained using a bootstrap approach of resampling the original data taking into account the autocorrelation time for the observable in question. These errors are reported in the column “RM-err” of Tables 5, 6, 7, 8, 9 and 10.

Fig. 15

Free energy difference between Multihistogram and density of states approaches. Only shown for $16^4$. The gap is related to normalisation as discussed in the text. Errors are shown as shaded regions

Multihistogram provides access to the partition function or the free energy of the system and allows a direct comparison with the density of states approach via Eq. (9). A plot of $F= -\ln (\mathcal{Z})/\beta$ appears linear over the ranges in question and no useful graphical comparison is possible. Figure 15 shows the difference between F computed with multihistogram and with LLR. Averages are taken over the bootstrap samples in the case of multihistogram, and over RM replicas for LLR, and the results are normalised by setting $F(\beta =6.118) =0$. This difference between very different approaches is compatible with zero at two sigmas.

Fig. 16

Plaquette variance from Multihistogram. Also shown for comparison are results from unconstrained simulations with additional runs. From top to bottom: $16^4$, $20^4$. The plot for $24^4$ is not shown as plagued by huge fluctuations. Errors are shown as shaded regions

Despite the accuracy suggested by Fig. 15, the free energy does not encode much more information than the first moments of the plaquette expectation values. The plaquette variance shown in Fig. 16 should be compared with the LLR predictions in the middle column of Fig. 5 (though note a small shift of scale at $20^4$). The LLR prediction has smaller error and is smoother. While the quality of the LLR prediction does decrease for larger lattice sizes, the multihistogram results deteriorate much more markedly and indeed are useless at $24^4$. As already emphasised, the reason for poor performance of the multi-histogram results is not the method itself, but our choice of data to illustrate it.

Multihistogram can also be used for quantities such as the symmetric cloverleaf or topological charge, both after Wilson flow. These behave better than the plaquette variance, but again the excessive spacing of the coupling in the reference simulations leads to declining quality for the larger lattice sizes.

Appendix B: Run details

This appendix records details of the main simulations.

Table 11 Parameter ranges for the canonical reference simulations

Table 12 Parameters $S_i$ and $\delta _i$ used for density of states runs

Table 13 Results of RM phase: mean value of $a_i$ for each temper

Table 11 shows the couplings used for the reference simulations. The last column uses the fitting function from Gattringer and Lang [39] to compute the box size. The duration of these reference simulations was between $6\times 10^4$ and $12\times 10^4$ steps at $16^4$, between $5\times 10^4$ and $11\times 10^4$ at $20^4$ and fixed at $9.6\times 10^4$ at $24^4$. Extended simulations to improve data points over a restricted range at $20^4$ and $24^4$ were mentioned in the text. These simulations were for four $\beta$ values and two replicas at $20^4$ and for two $\beta$ values and four replicas at $24^4$. For all extended simulations the duration was $10^5$ steps with Wilson Flow measurements only every 10 steps.

The list of central action for the density of states runs is given in Table 12. Spacing, $\delta _S$, is variable and can be read off from the differences in $S_i$. The width of the Gaussian constraint $\delta _i$ is also shown and the ratio $\delta _i/\delta _S$ is kept fixed at 1.2. The equivalent ranges in terms of the coupling $\beta$ are given in Table 2.

Table 13 is the result of the RM phase and lists the mean $a_i$ across replicas. The RM error of this quantity varies slightly between tempers and lattice size, but it is bounded by $4 \times 10^{-5}$ in all cases. Averaged over tempers, the error is $2.7\times 10^{-5}$, $1.7\times 10^{-5}$, $1.3\times 10^{-5}$ for $16^4$, $20^4$ and $24^4$ respectively.