Abstract
Aria is a plant hosting a \({350}\,\hbox {m}\) cryogenic isotopic distillation column, the tallest ever built, which is being installed in a mine shaft at Carbosulcis S.p.A., Nuraxi-Figus (SU), Italy. Aria is one of the pillars of the argon dark-matter search experimental program, lead by the Global Argon Dark Matter Collaboration. It was designed to reduce the isotopic abundance of \({^{39}\hbox {Ar}}\) in argon extracted from underground sources, called Underground Argon (UAr), which is used for dark-matter searches. Indeed, \({^{39}\hbox {Ar}}\) is a \(\beta \)-emitter of cosmogenic origin, whose activity poses background and pile-up concerns in the detectors. In this paper, we discuss the requirements, design, construction, tests, and projected performance of the plant for the isotopic cryogenic distillation of argon. We also present the successful results of the isotopic cryogenic distillation of nitrogen with a prototype plant.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Large liquid argon detectors offer one of the best avenues for detecting galactic weakly interacting massive particles (WIMPs) via their scattering on atomic nuclei. However, Atmospheric Argon (AAr) has a naturally occurring radioactive isotope, \({^{39}\hbox {Ar}}\), of isotopic abundance of \({8\times 10^{-16}}\) in mass, which is a \(\beta \)-emitter of cosmogenic origin, and whose activity of about \({1}\,{\hbox {Bq}\,\hbox {kg}}^{-1}\) raises background and pile-up concerns. Indeed, the liquid argon target allows for powerful discrimination between nuclear and electron recoil scintillation signals via pulse-shape discrimination [1,2,3], provided the background rate is not too high. However, this discrimination method cannot be applied in experiments that look at the ionization signal only [4, 5]. Argon extracted from underground wells, called Underground Argon (UAr), has a greatly reduced \({^{39}\hbox {Ar}}\) content and is therefore pivotal to the physics potential of dark-matter search experiments.
The DarkSide-50 experiment, a liquid argon time projection chamber (LAr TPC) at Laboratori Nazionali del Gran Sasso (LNGS), used a \({150}\,{\hbox {kg}}\) active mass of UAr extracted from \({\hbox {CO}_2}\) wells in Cortez, CO, USA, and measured the \({^{39}\hbox {Ar}}\) depletion factor (DF) with respect to AAr to be \(1400\pm 200\) [2]. A new production chain was recently set up to significantly increase the production of UAr. This new production needs to meet the target requirements of the Global Argon Dark Matter Collaboration (GADMC), a worldwide effort that unifies the DarkSide, DEAP-3600, MiniCLEAN, and ArDM experimental groups, for the construction of new experiments for argon dark-matter searches. In order of increasing size, these new experiments are a potential DarkSide-LowMass, with an approximately \({1}\,{\hbox {t}}\) target, optimized for the detection of low-mass dark matter, aiming at improving the world-leading results of the DarkSide-50 experiment [4, 5]; the \({51.1}\,{\hbox {t}}\) target mass DarkSide-20k detector [6], under construction at LNGS, Italy; and the prospective Argo experiment, consisting of a \({400}\,{\hbox {t}}\) target mass, that will push the experimental sensitivity down to the so-called neutrino floor. The argon procurement for this new production chain starts from the Urania plant, now under construction in Cortez, CO, USA, that will extract and purify UAr at a maximum production rate of about \({330}\,{\hbox {kg}\,\hbox {day}}^{-1}\). The \({^{39}\hbox {Ar}}\) activity of UAr, though remarkably lower than that of AAr, is neither low enough for the needs of the DarkSide-LowMass experiment, where it would be the limiting background to the dark-matter sensitivity, nor for the Argo experiment, where it would cause a significant pile-up rate if the detector is built as a dual-phase TPC.
The cryogenic isotopic distillation plant Aria, which is currently in the installation phase in a mine shaft at CarboSulcis S.p.A., in Nuraxi-Figus (SU), Italy, was designed to further reduce the \({^{39}\hbox {Ar}}\) isotopic fraction of UAr by another factor of 10 per pass, with a production rate of several \({\hbox {kg}}\, \mathrm{d}^{-1}\). While the \({350}\,\hbox {m}\) tall, \({31.8}\,{\hbox {cm}}\) inner diameter, distillation column under construction fits the needs of DarkSide-LowMass in terms of production rate, a new, wider column would be needed for the larger Argo detector.
Cryogenic isotopic distillation with rectifying columns is a well-established technique [7] and has received significant attention in the context of stable isotope separation for the main biogenic elements such as carbon and oxygen. Some industrial-scale plants have already been built. However, for argon isotopic distillation, this is the first time that such a plant is being proposed and constructed. In addition to cryogenic distillation, a few other techniques are currently available for the separation of argon isotopes. These techniques are based on the difference in molecular mass, such as centrifugal separation and diffusion separation, the latter based on the different average speed, at thermal equilibrium, among isotopes of the same energy. However, their application is limited by the low yield and the high cost per unit mass of separated isotopes. The cryogenic isotopic distillation plant Aria appears as a very promising new avenue for the depletion from \({^{39}\hbox {Ar}}\) of such large quantities of argon, at reasonable cost and time. It is interesting to note that target purification via distillation, though not isotopic, with cryogenic columns in the context of dark-matter search detectors was also pursued by other collaborations using xenon [8,9,10,11].
The technological capability to achieve efficient isotopic separation with cryogenic distillation allows the wide application of the Aria project to other fields, where the production of stable isotopes is required, such as in medical applications. However, in this paper, we will focus on the application of the Aria plant to the isotopic distillation of argon.
A very important achievement for this project was a nitrogen distillation run of the prototype plant, a short version of the Aria column using only the reboiler, the condenser, and one central module, together with all the auxiliary equipment of the full column, installed in a surface building. The successful outcome of this run paved the way to the continuation of the project and the construction of the full plant.
2 Design requirements
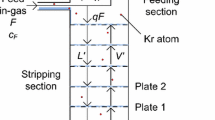
Isotopic separation by cryogenic distillation exploits the relative volatility of different isotopes. For ideal mixtures, the relative volatility is given by the ratio of the isotopes’s vapor pressures at a given temperature. Continuous distillation with a large number of distillation stages, where the liquid and vapor phases undergo a countercurrent exchange at thermodynamic equilibrium, is used to optimize the separation of isotopes that have relative volatility close to unity. As shown in Fig. 1, heat is constantly provided from a bottom heat exchanger, called reboiler, that vaporizes the liquid, and extracted from a top heat exchanger, called a condenser, that condenses the vapor. To perform the isotopic separation, the column temperature varies between the boiling point of \({^{40}\hbox {Ar}}\) (bottom) and of \({^{39}\hbox {Ar}}\) (top) at the operating pressure, between 1.1 and 1.5 bar. The pre-cooled UAr feed enters the column at a given height and flow. The vapor rises in the column and re-condenses, while the liquid sinks by gravity and then reboils. In the rectifying section (above the feed point), the mass fraction of \({^{39}\hbox {Ar}}\) is larger than in the feed argon, while in the stripping section (below the feed point) it is smaller than in the feed argon. Liquid argon depleted of \({^{39}\hbox {Ar}}\) is then collected continuously from the bottom of the column, while argon enriched of \({^{39}\hbox {Ar}}\) is collected from the top. The ratio between the liquid flow in the column and the distillate flow is called the reflux ratio, \(R=L/D\), and is often much larger than 1. When the column is filled and performs distillation without extracting any product from the top or the bottom, the column is said to be operated at total reflux or \(R=\infty \). Since the \({^{39}\hbox {Ar}}\) has a very low isotopic fraction even in atmospheric argon, its volatility relative to the other argon isotopes has never been measured. Therefore, for the following calculations, , the relative volatility of \({^{39}\hbox {Ar}}\) to \({^{40}\hbox {Ar}}\), \(\mathrm {\alpha _{39{-}40}}\), or its more commonly used natural logarithm, \(\mathrm {ln\alpha _{39{-}40}}\), was derived from the measured relative volatility of \(^{36}\hbox {Ar}\) to \({^{40}\hbox {Ar}}\), \(\mathrm {\alpha _{36{-}40}}\). Our calculation, discussed in Appendix A, yields \(\mathrm {ln\alpha _{39{-}40}}\) = \((1.333 \pm 0.036)\times 10^{-3}\), at the mean operating temperature of the column of \({89.5}\,{\hbox {K}}\). To optimize the distillation process, the Aria column makes use of a high-performance packing material. The two related quantities that characterize the separation capability of distillation columns are the number of equivalent theoretical stages, N, and the Height Equivalent to a Theoretical Plate, HETP [12], with
where \(L_\mathrm{a}\) is the total column active height.
For the \({^{39}\hbox {Ar}}\) vs. \({^{40}\hbox {Ar}}\) distillation, the minimum number of theoretical stages needed to achieve a given separation, \(S^0_{39{-}40}\), is obtained when the column operates at total reflux and is given by the Fenske equation [13]:
with
where \(x_D\) is the mass fraction of \({^{39}\hbox {Ar}}\) in the top, \(x_B\) the mass fraction of \({^{39}\hbox {Ar}}\) in the bottom, and \(x_D,x_B \ll 1\).
Requiring, for instance, a separation of 10, from Eq. (2) it follows that \(N_\mathrm{min}\)=1727. Moreover, when the column operates at finite reflux, the number of required stages is larger than \(N_\mathrm{min}\). To include such a large number of stages, the column needs to be very tall and be filled with high-performance packing, i.e. with a small HETP. Moreover, for efficient use of the packing, there is a limitation on the liquid flow per unit area, usually specified by the vendor. Therefore, both the height and the diameter of the column are important for distilling large volumes.
A cheap and convenient way to support such a tall column is to install it in an underground vertical mineshaft dug in the 1940s in Carbosulcis, with a \({5}\,{\hbox {m}}\) diameter and a \({350}\,\hbox {m}\) depth. This facility was made available to Aria at the end of 2018, after the end of its coal extraction cycle.
The first phase of the Aria project, which is the subject of this paper, consists of a column with an internal diameter of d = \({31.8}\,{\hbox {cm}}\) and a wall thickness of \({3}\,{\hbox {mm}}\). The column is enclosed in a vacuum cold box with a \({71.1}\,{\hbox {cm}}\) diameter and a total height approximately equal to the mineshaft depth. The support structure of the column in the shaft is designed in a way to allow for the installation at later times of a wider column with a maximum cold box diameter of \({2.0}\,{\hbox {m}}\).
The rest of the paper is organized as follows. In Sect. 3 we discuss the plant design, followed by a description of the column in Sect. 4. In Sect. 5 we present the column vacuum leak tests. In Sect. 6 we discuss the prototype tests and the validation of some characteristics of the plant with measurements and in Sect. 7 the projected performance of Aria for argon isotopic distillation.
3 Plant design
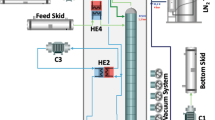
Simplified diagram of the Aria plant. The full description can be found in the text. The color-coding of the heat exchangers is such that the red section provides heat to the fluid while the blue section removes heat from it. The diagram also reports the values of operating pressure and temperature for \({^{39}\hbox {Ar}}\)–\({^{40}\hbox {Ar}}\) distillation, as obtained from a plant engineering simulation (Aspen-HYSYS)
The Aria plant simplified scheme is displayed in Fig. 2. The column, cryogenic tanks, and heat exchangers are enclosed in a cold box (grayed area) which is vacuum-tight and designed to reduce thermal losses. The cryogenic circuit of the plant is designed with two independent loops: the argon loop (dark green lines for the liquid and light green lines for the vapor/gas) and the refrigeration loop, with nitrogen gas (cyan lines) and liquid (dark blue lines) that are used to evaporate and to condense the argon. The Aria plant was designed in a way that minimizes nitrogen consumption and optimizes energy efficiency by using a closed-loop refrigeration circuit and appropriate use of heat exchangers.
UAr will be transported from the Urania plant being constructed in Cortez, Colorado, USA, to Aria in Sardinia, Italy, and then from Aria to LNGS, Italy, inside gas skids. The argon gas from the Feed Skid is fed into the distillation column through a flow controller and pressure-regulated to about \({1}\,{\hbox {bar}}\). A heat exchanger (HE4) with the output distillate stream is used to cool the argon before it enters the column. Argon vapor is condensed in the heat exchanger (HE1) in the top module of the column, while liquid argon is vaporized in the reboiler (HE3) in the bottom module. The bottom stream comes out of the column as a liquid, gets heated as it passes through an air heater (H1), compressed (C1), and then is delivered to the bottom skid. This is the argon, depleted of \({^{39}\hbox {Ar}}\), that will be used in the experiments. At the top of the column, the distillate stream, enriched in \({^{39}\hbox {Ar}}\), is delivered to the Distillate storage after passing through HE4 and a compressor (C2).
Liquid nitrogen is used as the cooling fluid in the heat exchanger (HE1) of the column condenser. The nitrogen vapor from the output of HE1 is heated through the heat exchanger HE2 and then compressed by a screw-rotary compressor (C3) to a pressure value between 2 bar and 4 bar. After cooling in HE2, the compressed gas is used as heating fluid in the heat exchanger (HE3) of the reboiler. The liquefied nitrogen is passed through a nitrogen phase separator tank (BT) and then pumped by a modular reciprocating pump (P1) with a delivery pressure up to \({100}\,{\hbox {bar}}\), all the way up to the top of the column, and fed back to HE1. Liquid nitrogen is stored and fed into the circuit from an external \({50}\,{\hbox {m}^3}\) tank. The excess nitrogen gas from the system is fed back to the tank after being liquefied by four \({4}\,{\hbox {kW}}\) cryogenerators (Stirling Cryogenics), inherited from the ICARUS experiment at LNGS.
Brazed plate heat exchangers are used for the reboiler (HE3), the condenser (HE1), and HE2. These heat exchangers are characterized by high heat transfer efficiency and limited size and are the ideal solution for this application. Coil heat exchangers (H1 and HE4) are used for the inlet and outlet argon flows.
Figure 2 reports also the values of operating pressure and temperature, for \({^{39}\hbox {Ar}}\)–\({^{40}\hbox {Ar}}\) distillation, obtained with a plant engineering simulation using the Aspen HYSYS package. It can be seen that the column operating temperature varies from the top to the bottom between \({87.8}\,{\hbox {K}}\) and \({90.9}\,{\hbox {K}}\).
4 Column and cold box structure
For construction and transportation, both the column and the surrounding cold box have a modular structure. The 30 modules were assembled at the production site. The 28 central modules are identical cylindrical elements about \({12}\,{\hbox {m}}\) tall, with a \({71.1}\,{\hbox {cm}}\) diameter and an approximate weight of \({3}\,{\hbox {t}}\). The top module, about \({9.5}\,{\hbox {m}}\) tall and \({1.2}\,{\hbox {m}}\) diameter, hosts the top of the distillation column, about \({1}\,{\hbox {m}}\) high; the condenser (HE1); a liquid nitrogen buffer tank; not shown in the simplified diagram of Fig. 2; and two heat recovery exchangers (HE4 and HE2). The bottom module, about \({4}\,{\hbox {m}}\) tall and \({1.5}\,{\hbox {m}}\) diameter, hosts the bottom of the distillation column, about \({1}\,{\hbox {m}}\) high, the reboiler (HE3), and a nitrogen phase separator tank (BT). Figure 3 shows some of the central modules stored at the Carbosulcis site, ready for installation in the shaft. Figure 4 displays the top module while Fig. 5 shows the bottom module.
The structure of the cold box, the internal equipment, and the piping are fully welded to reduce the risk of leaks. All welds were performed at the manufacturing company where the modules were assembled, except for the orbital welds between modules, which will be performed in the mineshaft.
To account for the thermal contraction of the structure, the modules are connected through axial bellows. At cold temperatures, the bellows expand by about 3 cm. Due to the presence of bellows, the support of each module is independent of the others. The load is distributed laterally to the shaft walls. Every module is supplied with anchor points, whose sizing takes into consideration both the static weight and the stresses due to the cold box operating pressure. The anchor points are bolted to a structure, discussed in Sect. 4.3, which is fixed to the lateral wall of the shaft.
4.1 Internal structure
The 28 central modules are filled with a structured stainless steel packing (Sulzer CY gauze). To stay below the flooding limit and therefore guarantee an efficient distillation and minimize the pressure drop along the column, the packing vendor suggests, based on measurements performed with chlorobenzene/ethylbenzene mixtures, to limit the specific liquid volume flow rate or load, \({\hat{V}}_{L}\), to \({5}\,{\hbox {m}^3\,\hbox {h}^{-1}\hbox {m}^{-2}}\) for argon. Given the column inner diameter of \({31.8}\,{\hbox {cm}}\), this corresponds to a liquid volume flow rate, \(V_{L}\), of \({0.4}\,{\hbox {m}^3\,\hbox {h}^{-1}}\), which is equivalent to a mass flow rate of \({550}\,{\hbox {kg}\,\hbox {h}}^{-1}\) (see Table 2 for argon parameters). The quantities N, HETP, and the pressure drop per unit length along the column, \(\varDelta p_C/\varDelta z\), do not have a fixed value in a packed distillation column but depend on both the \(F_G\) sizing parameter [14] and the operating pressure, \(p_C\). The parameter \(F_G\), also called F-factor or vapor load, is defined as \({\hat{V}}_{G}\cdot \sqrt{\rho _G}\), with \({\hat{V}}_{G}\) the specific vapor volume flow rate and \(\rho _G\) the vapor argon density at equilibrium. Fig. 6 shows the dependence of both HETP and \(\varDelta p_C/\varDelta z\) on both \(F_G\) and \(p_C\) for the packing which is used for Aria, as measured by the vendor with chlorobenzene/ethylbenzene mixtures. With the liquid load of \({5}\,{\hbox {m}^3\,\hbox {h}^{-1}\hbox {m}^{-2}}\) and at \(p_C = {1.3} \hbox { bar}\), \({\hat{V}}_{G}\) is \({972}\,{\hbox {m}^3\,\hbox {h}^{-1}\hbox {m}^{-2}}\) and \(F_G\) is \({0.73}\,{\sqrt{\hbox {Pa}}}\). For the distillation of argon with the Aria plant, the following calculations use values from the curves of Fig. 6 at \(p_C={960}{\hbox { mbar}}\), i.e. an HETP of \({10}\,{\hbox {cm}}\) and a \(\varDelta p_C/\varDelta z\) of \({0.7}\,{\hbox {mbar}~\mathrm{m}^{-1}}\), under the assumption that these curves are universal, i.e. independent of the distilled substance. To verify this assumption, it is essential to measure these parameters in a cryogenic environment. Such measurements with argon and nitrogen are the main focus of the tests described in Sect. 6.
Equivalent number of theoretical stages, HETP, and pressure drop per unit length, \(\varDelta p_C/\varDelta z\) vs. sizing parameter \(F_G\). Blue (cyan) line: measurements with chlorobenzene/ethylbenzene mixtures at \(p_C={0.96}{\hbox { bar}}\) (0.40 bar), Sulzer CY Gauze Packing, partial data-set extracted from the Structured Packing brochure of Sulzer Ltd. website. The black stars correspond to the values assumed for the calculations of Aria distillation with argon in this paper, at \(p_C={1.3}{\hbox { bar}}\). The full green dots (squares) correspond to the values measured during the nitrogen distillation Run A (Run B), at \(p_C={2.7} {\hbox { bar}}\) (2.3 bar), with the prototype column, discussed in Sect. 6, and are meant to be average values over the respective runs
To avoid the channeling of the fluid in the packing and to optimize the uniformity across the column section, each module is divided into four sub-sections of packing, with an active height of \({2.56}\,{\hbox {m}}\) each, interleaved with a liquid distributor, shown in Fig. 7. The liquid formed on the distributor plate is streamed, through 0.3 cm holes located at 3 cm, 4 cm, and 5 cm height in perforated pipes uniformly distributed along the plate surface, to the packing section below. The vapor rises towards the packing section above through \({12.5}\,{\hbox {cm}}\) high chimneys. The total active height of the column is about \({287}\,{\hbox {m}}\), which corresponds to a number of theoretical stages, N = 2870, while the pressure drop along the column is about 0.7 bar, with 0.5 bar due to the distributors, at \(F_G\) = \({0.73}\,{\sqrt{\hbox {Pa}}}\).
In order for the column to efficiently distill argon, it must be filled with approximately \({2.5}\,{\hbox {t}}\) of argon. The total mass is largely dominated by the liquid phase, with the vapor phase contributing only to \({5}\,{\%}\) of the total. The two major contributions come from the distributors, of \({0.3}\,{\hbox {m}^3}\), and from the packing wetting, called the holdup, of \({1.1}\,{\hbox {m}^3}\). The packing wettability was assumed to be \({5}\,{\%}\) for this calculation, as specified by the packing vendor. This value was given for an organic mixture and, therefore, will need to be verified for cryogenic temperatures with argon.
The thermal load of the column was calculated assuming the maximum liquid flow specified by the packing producer, as discussed in Sect. 4. The required thermal duty for the cryogenic system is about \({25}\,{\hbox {kW}}\), broadly given by the maximum liquid flow times the heat of vaporization. The total electric power needed for the plant operation is about \({500}\,{\hbox {kW}}\), including the load from the cryocooler, compressors, fluid, and vacuum system pumps.
4.2 Thermal insulation
To minimize heat transfer through conduction and radiation from the environment to the cryogenic distillation column, a \({10^{-5}}\,{\hbox {mbar}}\) vacuum is made in the cold box. To maintain the desired vacuum level, several pump stations of total pumping speed \({10^4}\,{\hbox {L~s}^{-1}}\) are installed along the column. Additionally, 20 layers of multi-layer insulation (MLI) are wrapped around the column, and 10 are wrapped around all the other lines and reservoirs within the cold box. With this insulation, the residual thermal radiation input power to the column is about \({1}\,{\hbox {Wm}^{-2}}\), a few percent of the thermal duty cycle of the column. Insulation is also provided on the equipment and piping outside of the cold box, to minimize heat losses and for personal protection against the risk of injuries by accidental contact. For cold points, the insulation is based on synthetic rubber covered with aluminum sheets. Vacuum jacketed pipes are used for long-distance connections.
4.3 Support structure in the shaft
The support structure of the column is made of austenitic steel and is assembled by bolted connections. It is made of discrete planar structures supporting the column every fourth meter. A horizontal cross-sectional drawing of one of these supports is shown in Fig. 8. To keep a safety margin, three of these supporting structures per central module are foreseen, each one able, in principle, to bear the module weight independently. The support structures are anchored to the mine-shaft wall with bars penetrating the rock up to an average depth of about \({120}\,{\hbox {cm}}\) for the central support, and up to \({80}\,{\hbox {cm}}\) for the other two. For filling the 300 mm wall openings created to host the anchoring bars, a cement-based thixotropic mortar is used, with high mechanical strength and compensated shrinkage. Figure 9 shows the installation of the first support structure in the well. Load tests were performed applying a \({3}\,{\hbox {t}}\) load and no significant deflection was observed.
5 Vacuum leak tests of individual modules
Leak detection is a critical step in the construction of Aria since its functioning depends on a high cold box insulating vacuum and the distillation process should not be contaminated by air. For that reason, the pressure of the process column and related lines is kept above the atmospheric pressure. The leak-check procedure has to be quite strict, in particular for those lines that will undergo thermal stresses. Indeed, the column and the service lines will be temperature -cycled to liquid argon/nitrogen temperatures several times during their lifetime.
An upper limit of \({10^{-9}}\,{\hbox {mbar\,L~s}^{-1}}\) was set on the leak rate for each leak check performed on single modules during testing, mainly on welds. Each column segment was tested twice. The first phase of tests took place at the manufacturing company site (Polaris s.r.l.), where the column and the service lines were fully tested, before wrapping them around with MLI. The second phase of the leak checks, carried out at CERN, Switzerland, included also a full check of the cold box and bellows. For the tests, each module was closed temporarily with end-caps, the space between the cold box and the distillation column was evacuated with a turbopump system, and the column and the service lines were filled with a mixture of 90% air and 10% helium. In this way, the potential leak can be found by the leak detector associated with the turbopump system. All the modules were validated in a two-step approach to confirm a leak rate smaller than \({10^{-9}}\,{\hbox {mbar\,L~s}^{-1}}\) on each module. Since there are 30 column segments in total, the total leak rate is expected to be smaller than \({3\times 10^{-7}}\,{\hbox {mbar\,L~s}^{-1}}\) at room temperature. An additional one-off leak test was performed at CERN to validate module tightness after a thermal cycle down to \({87}\,{\hbox {K}}\). The reboiler unit was chosen for this test, due to its complex internal weld configuration, and tightness below \({10^{-9}}\,{\hbox {mbar\,L~s}^{-1}}\) was again confirmed.
6 Performance test at total reflux with a prototype column
To verify the theoretical calculations of the distillation performance and test the mechanical and cryogenic infrastructure prior to column installation in the mineshaft, a prototype plant was built in a surface building.
6.1 Prototype construction
The prototype plant is a short version of the Aria column using only the reboiler, the condenser and one central module, for a total height of \({26}\,{\hbox {m}}\), together with the auxiliary equipment, which is the same as that of the full column. It is located in the Laveria building of the Carbosulcis mine, Nuraxi-Figus site, as shown in Figs. 10 and 11. The mechanical support, made of galvanized and cold-painted carbon steel, consists of a square base structure with four feet of concrete and a modular iron pillar structure equipped on each side with two diagonal support beams. The structure includes seven-level platforms, to allow the presence of operators along the height of the column. Though self-supporting, the support is fixed to the building structure at two different heights for additional safety.
After welding together the three modules, the column and the four service lines were leak-checked with a calibrated leak detector. An external calibration leak was used to estimate the helium diffusion time along all the lines. The diffusion time was measured to be between four and twenty seconds, depending on the line. It was therefore decided to wait at least two minutes between every leak check to make sure that a possible signal could be associated with the precisely tested weld. The standard technique of filling sealed bags with helium around the welds was used for the procedure. The helium bags, once filled with helium, were not removed until the last leak check. Using this method, an upper limit of \({10^{-9}}\,{\hbox {mbar\,L~s}^{-1}}\) was set on all the welds between the modules.
Leak detection will become increasingly difficult during the assembly of the modules in the shaft. With the aforementioned procedure, the increased size of the column, as the modules are assembled together, will cause a much longer response time for the leak detection system and reduce its sensitivity. To overcome this difficulty, the use of some new tools is foreseen. Devices called clamshells, developed at CERN, will surround the welds and create a small sealed space that can be quickly evacuated. Helium will flow inside the tube/column, and the potential leak in the weld can be detected with a very fast response time.
6.2 Prototype operation
For the commissioning of the prototype plant, nitrogen was used both in the auxiliary circuit for cooling and in the processing circuit for the distillation inside the column. The operating parameters of the auxiliary system were similar to those discussed in Sect. 3.
A dedicated slow-control system monitors and controls the distillation process and all equipment in real-time. This system uses LabVIEW (NI) as a system-design platform and development environment, and it is organized with a distributed layered architecture. The control cabinets are interconnected by a private WLAN network, inside the CarboSulcis network, with a Real-Time Controller (NI cRIO 9039) reading out the data of the different expansion chassis (NI 9049) distributed over the network. Also, PROFIBUS, a standard for Fieldbus communication in automation technology, is integrated into the system to control third-party equipment such as compressors, vacuum gauges, and vacuum pumps. The slow control also features advanced controls such as Proportional Integral Derivative control, cascade control, threshold logic, interlocks over valves, inverters, and temperature controllers. Historical data are stored in a relational database (PostgreSQL).
Plant operation started by feeding the cooling liquid nitrogen to the auxiliary circuit from the external storage tank and nitrogen of purity grade 5 into the column. Eight hours were needed to reach the target temperature. The total amount of nitrogen filling the column was estimated by taking into account that it was stored in 16 gas bottles of \({50}\,{\hbox {L}}\) each, with an initial pressure of \({200}\,{\hbox {bar}}\) and a final pressure of \({80}\,{\hbox {bar}}\). Using the Peng-Robinson equation of state, the total mass was determined to be \({110}\,{\hbox {kg}}\).
The measurements reported in this paper refer to two distillation runs of the plant, Run A of 70 h duration and Run B of 88 h duration, with two different screw-rotary C3 compressor settings, with the column operated at total reflux. The two runs started and stopped with switching on and off the compressor and, with some delay, the pumps.
Measured vapor mass flow in the auxiliary system downstream of the compressor vs time, for \({^{29}\hbox {N}_2}\)–\({^{28}\hbox {N}_2}\) distillation in the prototype plant. The vertical cyan band represents the time during which the rotary pump compressor was switched off. The horizontal blue lines represent the average values over Run A and Run B, taken only for time periods after the distillation transients of both runs are over, as observed in Fig. 16. They correspond to \({412}\,{\hbox {kg}\,\hbox {h}}^{-1}\) and \({247}\,{\hbox {kg}\,\hbox {h}}^{-1}\), respectively
Figures 12 and 13 show the measured pressure vs. time and mass flow vs. time in the auxiliary system, downstream of the compressor. For these first two runs, the automated feedback system regulating the flow downstream of the compressor, foreseen in the plant design, was not used. The auxiliary system gas pressure and flow stability were guaranteed only by regulating, by hand, a bypass valve between the compressor and the gas flow meter. Better stability was reached during Run B, where fluctuations were limited to \(\pm {0.3}\,{\hbox {bar}}\) and \(\pm {20}\,{\hbox {m}^3\,\hbox {h}}^{-1}\). The pressure inside the column, \(p_{C}\), was measured by digital pressure transmitters with diaphragm seal measuring cell, located, respectively, below the first distributor from the top and right above the reboiler. Figure 14 shows the measured pressure inside the column, \(p_{C}\), in the top vs. time. The different pressure in the column compared to what is expected for argon, as discussed in Sect. 3, comes from the different thermodynamic properties of the nitrogen and the operating temperature gradients of the heat exchangers of the reboiler and of the condenser of about \({5}\,{\hbox {K}}\). Since nitrogen was used both for cooling and as distillation fluid, the mass flow rate in the cooling circuit was the same as that inside the column. The measured pressure drop between condenser and reboiler in the column, \(\varDelta p_C\) vs. time is shown in Fig. 15. As discussed in Sect. 4.1, half of the pressure drop comes from the distributors. The pressure drop per unit length only relative to the packing, \(\varDelta p_C/\varDelta z\), given an active height of the prototype column, \(L^P_{a}\), of \({10.24}\,{\hbox {m}}\), is reported in Table 1. Since \(\varDelta p_C \ll p_C\), in the following, we will assume that both pressure and temperature are constant along the column. The nitrogen temperature inside the column was derived from the pressure measurement using the Antoine equation [15]. From the data of Fig. 14 it follows that, during Run B, the temperature ranged from 83 to \({87}\,{\hbox {K}}\). The measured vacuum level in the cold box during the two runs was stable around \({3\times 10^{-6}}\,{\hbox {mbar}}\).
Measured pressure inside the column, \(p_{C}\), in the top vs time, for \({^{29}\hbox {N}_2}\)–\({^{28}\hbox {N}_2}\) distillation in the prototype plant. The red horizontal lines indicate the average pressure values in Run A and Run B of \({2.7}\,{\hbox {bar}}\) and \({2.3}\,{\hbox {bar}}\), respectively. The averages are taken only for time periods after the distillation transients of both runs are over, as observed in Fig. 16
Measured pressure drop between condenser and reboiler in the column, \(\varDelta p_C\), vs time, for \({^{29}\hbox {N}_2}\)–\({^{28}\hbox {N}_2}\) distillation in the prototype plant. The red horizontal lines indicate the average pressure drop values in Run A and Run B of \({12.9 \pm 5.4}\,{\hbox {mbar}}\) and \({6.9 \pm 2.7}\,{\hbox {mbar}}\), respectively. The averages are taken only for time periods after the distillation transients of both runs are over, as observed in Fig. 16
6.3 Expected values for nitrogen distillation
The nitrogen molecule, \({\hbox {N}_2}\), is mainly formed by two stable isotopes, \(^{14}\hbox {N}\) and \(^{15}\hbox {N}\), leading to an isotopic fraction of \({0.7}\,{\%}\) for the \({^{29}\hbox {N}_2}\) and \({99.3}\,{\%}\) for the \({^{28}\hbox {N}_2}\), and therefore, to an isotopic ratio, \(R_{{\mathrm{N}_2}}\), between the two molecules, of \({7.4 \times 10^{-3}}\). The relative volatility between \({^{28}\hbox {N}_2}\) and \({^{29}\hbox {N}_2}\), \(\alpha _{28{-}29}\), and its temperature dependence are discussed in Appendix A. Our fit gives an average value for \(\mathrm {ln\alpha _{28{-}29}}\) of \({2.828 \times 10^{-3}}\), at the mean column operating temperature of \({85}\,{\hbox {K}}\). This value of the relative volatility is large enough to give a sizeable separation, at total reflux, even with the prototype column. Indeed, by scaling the number of theoretical stages assumed for Aria by the ratio of active heights, we obtain for the prototype column 100 theoretical stages and, therefore, \(S^0_{28-29}\)=1.33.
6.4 Distillation measurements
A quadrupole mass spectrometer (Extrel MAX-300) measured the fluid composition, sampling in the reboiler, in the condenser, and in the feed line at the output of the gas bottles, using up to \({18}\,{\hbox {m}}\) long and \({0.18}\,{\hbox {mm}}\) diameter copper capillaries. With this mass spectrometer, the peaks corresponding to \({^{28}\hbox {N}_2}\) and \({^{29}\hbox {N}_2}\) are well separated, and, therefore, isotopic ratio measurements were directly taken from the peak height ratio. Figure 16 shows the measured isotopic ratios \(R_{{\mathrm{N}_2}}\) vs. time from the reboiler and condenser after offline spectrometer calibration. The calibration was performed using the isotopic ratio measured in the feed line to correct both the top and bottom isotopic ratios. Indeed, a small offset in the measured isotope ratio to the natural isotopic composition of nitrogen at the start of the run, on the order of \({1\times 10^{-3}}\), was observed, together with a linear decrease in time of \({1.6\times 10^{-6}}\,{\hbox { h}^{-1}}\). We attribute the latter effect to a signal drift of the mass spectrometer (an effect which can partly be explained by the instrument sensitivity to atmospheric conditions, which is also observed in other quadrupole mass spectrometers; see for instance [16]). For this calibration, since we did not fully understand the origin of the signal drift, we used two correction methods, one based on the ratio and one on the difference between the natural and the measured isotopic ratio values. The difference between the results obtained with the two methods was conservatively taken as a systematic uncertainty and is shown as a band in the final plot. The figure shows that when the plant started operation, the two measured isotopic ratios were the same. Over time, they started to diverge as the distillation took place, eventually reaching a plateau value. It should be noted that at the end of Run A, the isotopic ratio in the reboiler dropped almost to the feed value, while that of the condensers increased only after about 10 h. This is because when the compressor and the pumps are switched off, i.e. the distillation process is stopped, the liquid present in the columns sinks quickly to the reboiler under gravity, and mixes with the liquid already present there, whereas this is not the case for the vapor. The separation, \(S^0_{28-29}\), defined in Eq. (4), is given by \(R_{{\mathrm{N}_2}}\)(reboiler)/\(R_{{\mathrm{N}_2}}\)(condenser) and is shown vs. time in Fig. 17. The observed transient time needed to reach plateau operation is approximately \({16}\,{\hbox {h}}\). It is important to point out that the time to reach the steady-state is strongly dependent on the fluid to be distilled, the duty at the reboiler, and the number of theoretical stages. Further investigation is therefore required before extrapolating this value to the Aria column’s performance with argon.
6.5 Measurement interpretation
From the measured separation \(S^0_{28-29}\) and the calculated dependence of \(\alpha _{28-29}\) on temperature, discussed in Appendix A, it is possible to derive the number of theoretical stages as
Since the measurement is performed at total reflux, \(N^{P}=N^{P}_{\mathrm {min}}\). Moreover, we expect that, once the transients of Run A and Run B are over, \(N^{P}\) becomes independent of the temperature. Given \(N^{P}\) and the active height of the prototype column, \(L^P_{a}\), of \({10.24}\,{\hbox {m}}\), Eq. (1) can be used to derive the HETP. Figure 18 shows HETP vs. time after the transient times of Run A and Run B have elapsed. The green band represents the combined systematic uncertainty from the spectrometer calibration (largely dominated by the difference between the two calibrations) and the relative volatility, as discussed in Appendix A. The comparison between our measurements and packing vendor data is shown in Fig. 6. Our measured HETP values are larger by about 50%, whereas the \(\varDelta p_C/\varDelta z\) ones are found to be in good agreement with the extrapolated curves from packing vendor data. These curves also show that, at these \(F_G\) values, HETP increases with \(p_C\), whereas \(\varDelta p_C/\varDelta z\) is independent of \(p_C\); our measurements at larger pressures are also consistent with this trend. In conclusion, we consider that our measurements represent a validation of the concept of cryogenic distillation with the Aria plant. Of course, a measurement of the HETP in a prototype run with argon is going to be important to define with precision the Aria performance and operating parameters.
HETP vs. time for \({^{29}\hbox {N}_2}\)–\({^{28}\hbox {N}_2}\) distillation in the prototype plant. The green band represents the combined systematic uncertainty from the spectrometer calibration (largely dominant) and the relative volatility. The lower range corresponds to the additive correction while the upper range corresponds to the multiplicative one. The horizontal lines indicates the HETP values in Run A and Run B of \({12.6 \pm 1.4}\,{\hbox {cm}}\) and \({11.6 \pm 1.2}\,\hbox {cm}\), respectively, calculated averaging the values obtained with the two calibrations. The statistical uncertainty is added in quadrature to the mean half-difference of the HETP obtained from the two calibrations
7 Projected performance of Aria with argon, at finite reflux
The McCabe–Thiele method [17] is used in the following to calculate the performance of Aria for argon distillation at finite reflux. It is a graphical method for calculating the performance of binary distillation columns and relies on some simplifying assumptions, such as constant pressure along the column. This method has previously been used to calculate the performance of cryogenic distillation columns by collaborations using xenon as an active target for dark-matter search [8, 10, 11], but it has never been validated with argon. The input parameters of the calculation are summarized in Table 2. For these calculations, the feed was assumed to be a saturated vapor. The relative volatility, \(\alpha _{39{-}40}\), is assumed to be constant along the column and equal to the value corresponding to its mean operating temperature. The McCabe–Thiele calculation was performed for different values of B/F, where B and F are the mass flow rates in the bottom and feed streams, respectively. Figure 19, which displays B vs. B/F , shows that the choice of the column working point is based on a compromise between output flow rate and efficient use of the input UAr, a valuable material. For the following discussion, we take as benchmark working point the B/F value of \({50}\,{\%}\). The actual working point will be defined in due time depending on UAr availability. The McCabe–Thiele diagram corresponding to this benchmark working point is shown in Fig. 20. The output parameters of the calculation are shown in Table 3. The calculation also yields the location of the feed point in the column, which turns out to be at about \({20}\,{\%}\) height from the top of the column. The feed connections are located at this point. The obtained value of \(S_{39{-}40}\), the separation of Eq. (4) calculated at finite reflux, can be compared with that obtained at total reflux, \(S^0_{39{-}40} = 46\). If \(x_B\) were required to be \({3\times 10^{-20}}\), then B would become \({1.1}\,{\hbox {kg}\,\hbox {day}}^{-1}\), with the same feed point.
\({^{39}\hbox {Ar}}\)–\({^{40}\hbox {Ar}}\) distillation with the McCabe–Thiele method, with the input parameters of Table 2: B mass flow vs. B/F. The error bar at \(B/F = 0.5\) represents the systematic uncertainty from \(\mathrm {ln\alpha _{39{-}40}}\). Other systematic uncertainties on this curve are discussed in the text and in Table 4
McCabe–Thiele diagram for the \({^{39}\hbox {Ar}}\)–\({^{40}\hbox {Ar}}\) distillation with the input parameters of Table 2, for B/F= \({50}\,{\%}\). The insert is a blow-up of the region indicated by the shaded lines. The graphical construction starts from the equilibrium curve between \({^{39}\hbox {Ar}}\) and \({^{40}\hbox {Ar}}\), displayed in green, in the diagram of the mass fraction of \({^{39}\hbox {Ar}}\) in the liquid phase, \(y({^{39}\hbox {Ar}})\), vs. the mass fraction of \({^{39}\hbox {Ar}}\) in the vapor phase, \(x({^{39}\hbox {Ar}})\). The number of theoretical stages is calculated by constructing vertical and horizontal segments between the equilibrium curve (green) and the stripping (red) and rectifying (blue) lines, which start at the (\(x_B\),\(x_B\)) and (\(x_D\),\(x_D\)) points, respectively, and cross at the intercept with the so-called q-line (pink). Indeed, the q-line , which starts at the (\(x_F\),\(x_F\)) point, is horizontal in this diagram, since the feed is a saturated vapor
The dominant systematic uncertainties in this calculation come from the uncertainties on the relative volatility \(\alpha _{39{-}40}\) value and on the number of theoretical stages, N. The uncertainty coming from the knowledge of \(\alpha _{39{-}40}\), whose experimental precision is estimated in Appendix A, turns out to be 5%. The uncertainty on the number of theoretical stages has a stronger effect on B. Indeed, a 10% variation on N leads to a 30% change in B. At present, the HETP value for argon at the \(F_G\) and \(p_C\) operating values of Aria is not known from a direct measurement, and, therefore, it is difficult to quantify this uncertainty. However, if the measurements of HETP reported in Sect. 6 are confirmed in a run with argon, the value of B may decrease by 30–50% relative to its value in Table 3. The effect of varying \(\alpha _{39{-}40}\) along the column according to the temperature profile was estimated by modifying the standard McCabe–Thiele calculation, with the equilibrium curve between \({^{39}\hbox {Ar}}\) and \({^{40}\hbox {Ar}}\) assumed to be varying stage by stage. A marginal difference in the final result was obtained. Eventually, all the output flow-rates are proportional to \({V}_L\), i.e. halving this value leads to halving B. Since we can control this flow rate by modifying the pressure in the auxiliary system through the screw-rotary compressor settings, we do not consider this factor to be a systematic uncertainty. Table 4 summarizes the various contributions to the systematic uncertainty on B.
A major assumption in the above calculation is the binary distillation hypothesis that isotopes present in the gas other than \({^{39}\hbox {Ar}}\) and \({^{40}\hbox {Ar}}\) do not influence the calculation. It is well known that \(^{36}\hbox {Ar}\) and \(^{38}\hbox {Ar}\) have significant isotopic fractions in AAr, of 0.33% and 0.06%, respectively, though it has been reported that their isotopic fraction is about forty times lower in UAr [18]. However, the assumption of a binary mixture is considered to be reasonable, for two main reasons. On the one hand, the two additional isotopes are mostly recovered in the distillate stream, because their relative volatility to \({^{40}\hbox {Ar}}\) is larger than 1, and therefore we expect no significant difference in the composition of the bottom stream. On the other hand, the isotopic fraction of both the distillate and the bottom flow of \(^{36}\hbox {Ar}\) and \(^{38}\hbox {Ar}\) are only expected to change by a small factor since for each isotope i
or
Therefore, the thermodynamic properties of the isotope mixture and the value of \(\alpha _{39{-}40}\) are marginally changed during the distillation process.
The presence of a significant isotopic abundance of \(^{36}\hbox {Ar}\) can be very useful for measuring the HETP for argon with the prototype column and for reducing the uncertainty on the calculation of the expected B mass flow rate for the Aria column run, reported in Table 4. The presence of \(^{36}\hbox {Ar}\) will also be useful for the Aria commissioning run using atmospheric argon. At total reflux, the separation factor \(S_{36{-}40}\) is 1.78 for the prototype column and \({14.8\times 10^{6}}\) for the full column. At finite reflux, a calculation with the McCabe–Thiele method with the same parameters of Table 2, requiring a reduction factor of 1000, gives the results shown in Table 5 for the full column,
To obtain \({1}\,{\hbox {t}}\) of argon with a reduced isotopic fraction of 10 and with a B/F of 50%, a \({148}\,{\hbox {day}}\) long run is needed. To accomplish such a distillation run, \({4.5}\,{\hbox {t}}\) of UAr is needed to operate the column.
Another factor that has to be taken into account, when calculating the plant’s performance in terms of \({^{39}\hbox {Ar}}\) suppression, is the cosmogenic activation of the argon [18]. Cosmogenic activation occurs at the extraction site in Colorado, during transportation, and at the Aria site, and during the operation of the plant, since the argon to be processed and after processing is stored on the surface. Preliminary studies indicate that the dominant mechanism for cosmogenically activating \({^{39}\hbox {Ar}}\) comes from cosmic ray neutron interactions. These interactions, mostly occurring while the UAr is in storage at the Aria site, are estimated to contribute to approximately of the total \(^{39}\)Ar activity remaining after the UAr has been distilled.
The \({^{39}\hbox {Ar}}\) isotopic fraction is so low that it cannot be detected with a mass spectrometer. Therefore, to verify the performance of Aria in terms of isotopic distillation, a new experiment, DArT in ArDM [19], based on a radioactivity measurement, was recently designed and approved at the Canfranc Underground Laboratory (LSC), Spain. The experiment is expected to set an upper limit on the DF, at 90% C.L., of \({6\times 10^{-4}}\). Therefore, it is expected to measure the residual \({^{39}\hbox {Ar}}\) content after distillation in the commissioning phase of the Aria plant with atmospheric argon with good precision.
Other species like \({\hbox {O}_2}\) or \({\hbox {N}_2}\) may act as contaminants that can hinder the performance of a dual-phase TPC with argon. However, the volatility ratio of argon with these species is much larger than among argon isotopes. For instance, argon has relative volatility to oxygen, \(\alpha _{Ar-O_2}\), of about 1.1 at \({90}\hbox {K}\) [20]. Therefore, in a distillation run, all such substances that are more volatile than argon will go to the top stream, whereas less volatile species will go to the bottom stream. From mass conservation, it follows that the mass fractions of less volatile components, such as, for instance, oxygen, in the bottom stream, \((x_B)^{LV}\), relative to the less volatile mass fractions in the feed, \((x_F)^{LV}\) are such that
For UAr these mass fractions are expected to be very small, between \({1}\, \hbox {ppm}\) and \({100} \,\hbox {ppm}\).
8 Conclusion and outlook
The design, construction, prototype tests, and performance simulations of the Aria cryogenic distillation column that is currently in the installation phase at Carbosulcis S.p.A., in Gonnesa (SU), Italy were discussed in detail. The measurements performed with the prototype showed broad agreement between measured HETP and the expected value and validated the concept of performing cryogenic distillation with this plant. The successful run of the Aria plant is expected to have a tremendous impact in the field of isotopic separation, with applications ranging from nuclear physics to medicine and beyond.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The datasets generated during and/sor analysed during the current study are available from the corresponding author on reasonable request.]
References
P. Agnes, T. Alexander, A.K. Alton, K. Arisaka, H.O. Back, B. Baldin, K. Biery, G. Bonfini, M. Bossa, A. Brigatti et al. (DarkSide-50 Collaboration), Phys. Lett. B 743, 456 (2015)
P. Agnes, L. Agostino, I.F.M. Albuquerque, T. Alexander, A.K. Alton, K. Arisaka, H.O. Back, B. Baldin, K. Biery, G. Bonfini et al. (DarkSide-50 Collaboration), Phys. Rev. D 93, 081101 (2016)
P.A. Amaudruz, M. Baldwin, M. Batygov, B. Beltran, C.E. Bina, D. Bishop, J. Bonatt, G. Boorman, M.G. Boulay, B. Broerman et al. (DEAP-3600 Collaboration), Phys. Rev. Lett. 121, 071801 (2018)
P. Agnes, I.F.M. Albuquerque, T. Alexander, A.K. Alton, G.R. Araujo, D.M. Asner, M. Ave, H.O. Back, B. Baldin, G. Batignani et al. (DarkSide-50 Collaboration), Phys. Rev. Lett. 121, 081307 (2018)
P. Agnes, I.F.M. Albuquerque, T. Alexander, A.K. Alton, G.R. Araujo, D.M. Asner, M. Ave, H.O. Back, B. Baldin, G. Batignani et al. (DarkSide-50 Collaboration), Phys. Rev. Lett. 121, 111303 (2018)
C.E. Aalseth, F. Acerbi, P. Agnes, I.F.M. Albuquerque, T. Alexander, A. Alici, A.K. Alton, P. Antonioli, S. Arcelli, R. Ardito et al. (DarkSide-20k Collaboration), Eur. Phys. J. Plus 133, 131 (2018)
B. Andreev, E. Magomedbekov, A. Raitman, M. Pozenkevich, Y. Sakharovsky, A. Khoroshilov, in Separation of Isotopes of Biogenic Elements in Two-phase Systems, ed. by B. Andreev, E. Magomedbekov, A. Raitman, M. Pozenkevich, Y. Sakharovsky, A. Khoroshilov (Elsevier, Amsterdam, 2007)
Z. Wang, L. Bao, X.H. Hao, Y.L. Ju, K. Pushkin, M. He, J. Instrum. 9, P11024 (2014)
Z. Wang, L. Bao, X. Hao, Y. Ju, Rev. Sci. Instrum. 85, 015116 (2014)
K. Abe, J. Hosaka, T. Iida, M. Ikeda, K. Kobayashi, Y. Koshio, A. Minamino, M. Miura, S. Moriyama, M. Nakahata et al. (XMASS Collaboration), Astropart. Phys. 31, 290 (2009)
E. Aprile et al. (XENON Collaboration), Eur. Phys. J. C 77, 275 (2017)
T.H. Chilton, A.P. Colburn, Ind. Eng. Chem. 27, 255 (1935)
M.R. Fenske, Ind. Eng. Chem. 24, 482 (1932)
H.Z. Kister, Distillation Design (McGraw-Hill, New York, 1992)
M.P. Edejer, G. Thodos, J. Chem. Eng. Data 12, 206 (1967)
W. D’Autry, K. Wolfs, S. Yarramraju, A. Van Schepdael, J. Hoogmartens, E. Adams, Anal. Chem. 82, 6840 (2010)
W.L. McCabe, E.W. Thiele, Ind. Eng. Chem. 17, 605 (1925)
R. Saldanha, H. Back, R. Tsang, T. Alexander, S. Elliott, S. Ferrara, E. Mace, C. Overman, M. Zalavadia, Phys. Rev. C 100, 024608 (2019)
C.E. Aalseth, F. Acerbi, P. Agnes, I.F.M. Albuquerque, T. Alexander, A. Alici, A.K. Alton, P. Antonioli, S. Arcelli, R. Ardito et al. (DarkSide-20k Collaboration), J. Instrum. 15, P02024 (2020)
A.M. Clark, F. Din, J. Robb, Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 221, 517 (1954)
G. Boato, G. Casanova, G. Scoles, M.E. Vallauri, Nuovo Cim. 20, 1315 (1961)
M.W. Lee, S. Fuks, J. Bigeleisen, J. Chem. Phys. 53, 4066 (1970)
G. Boato, G. Casanova, A. Levi, J. Chem. Phys. 37, 201 (1962)
J.N.Canongia Lopes, A.A.H. Pádua, L.P.N. Rebelo, J. Bigeleisen, J. Chem. Phys. 118, 5028 (2003)
E. Ancona, G. Boato, G. Casanova, Nuovo Cim. 24, 1315 (1962)
Acknowledgements
The second phase of the leak checks, carried out at CERN, was performed under service agreement KN3155/TE. We acknowledge the professional contribution of the Mine and Electrical Maintenance staff of Carbosulcis S.p.A. Part of the project funding comes from Intervento finanziato con risorse FSC 2014-2020 – Patto per lo Sviluppo della Regione Sardegna. This paper is based upon work supported by the U. S. National Science Foundation (NSF) (Grants No. PHY-0919363, No. PHY-1004054, No. PHY-1004072, No. PHY-1242585, No. PHY-1314483, No. PHY- 1314507, associated collaborative grants, No. PHY-1211308, No. PHY-1314501, No. PHY-1455351 and No. PHY-1606912, as well as Major Research Instrumentation Grant No. MRI-1429544), the Italian Istituto Nazionale di Fisica Nucleare (Grants from Italian Ministero dell’Istruzione, Università, e Ricerca ARIA e la Ricerca della Materia Oscura – Fondo Integrativo Speciale per la Ricerca (FISR) and Progetto Premiale 2013 and Commissione Scientifica Nazionale II). We acknowledge the financial support by LabEx UnivEarthS (ANR-10-LABX-0023 and ANR-18-IDEX-0001), the Natural Sciences and Engineering Research Council of Canada, SNOLAB, Arthur B. McDonald Canadian Astroparticle Physics Research Institute, and the São Paulo Research Foundation (Grant No. FAPESP – 2017/26238-4). The authors were also supported by the Unidad de Excelencia María de Maeztu: CIEMAT – Física de partículas (Grant No. MDM 2015-0509), the Polish National Science Centre (Grant No. UMO-2019/33/B/ST2/02884), the Foundation for Polish Science (Grant No. TEAM/2016 - 2/17), the International Research Agenda Program AstroCeNT (Grant No. MAB/2018/7) funded by the Foundation for Polish Science from the European Regional Development Fund, the European Union’s Horizon 2020 research and innovation program under grant agreement No 962480, the Science and Technology Facilities Council, part of the United Kingdom Research and Innovation, and The Royal Society (United Kingdom). I.F.M.A is supported in part by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq). We also wish to acknowledge the support from Pacific Northwest National Laboratory, which is operated by Battelle for the U.S. Department of Energy under Contract No. DE-AC05-76RL01830.
Author information
Authors and Affiliations
Consortia
Appendix A: Fits to relative volatility data
Appendix A: Fits to relative volatility data
Dependence of \(\mathrm {ln\alpha _{36-40}}\) on temperature. The data points are taken from [21] (blue squares) and [22] (red dots). Fits with the function \(y= A\cdot 1/T^2 + B \) are overlaid. The continuous lines correspond to the mean values and the dashed lines to the 1\(\sigma _{{\mathrm {ln}}{\hat{\alpha }}}\) deviations. The errors on the single measurement were set all equal in the fit and determined in retrospect requiring the reduced \(\chi ^2\) to be 1
In Fig. 21 we report the measured dependence of \(\mathrm {ln\alpha _{36-40}}\) on temperature. The data points are taken from [21] and from [22] in the temperature range around the mean operating temperature of the column. Fits with the function \(\mathrm {ln{\alpha }_{36{-}40}} = A\cdot 1/T^2 + B \) are overlaid. The choice of this parametrization follows the theoretical arguments of [23]. The errors on the single measurement were set all equal in the fit and determined in retrospect requiring the reduced \(\chi ^2\) to be 1. Applying error propagation for the estimate of \({\mathrm{ln}{{\hat{\alpha }}}_{36{-}40}} = {\hat{A}}\cdot 1/T^2 + {\hat{B}} \) and of the uncertainty \(\sigma _{\mathrm{ln}{{\hat{\alpha }}}}\) as
with \(V_{ij}\) being the elements of the covariance matrix, one obtains, for the points of [21], the mean fit curve and error band shown in Fig. 21. Indeed, at the mean operating temperature of the column of \({89.5}\,{\hbox {K}}\), \(\mathrm {ln\alpha _{36{-}40}}\)= \({5.925\times 10^{-3}}\) with a statistical error of \({0.0369\times 10^{-3}}\). A different parametrization was also tried with 1/T dependence, as suggested in some textbooks [7]. Summing the change in \(\mathrm {ln\alpha _{36{-}40}}\) due to this effect in quadrature with the statistical error, we obtain \({(5.925 \pm 0.038) \times 10^{-3}}\). The same procedure applied to the data from [22] gives \({(5.625 \pm 0.021)\times 10^{-3}}\). The two values are inconsistent. Since we do not know which one is right, we take as best estimate the mean of the two and as uncertainty the half-difference summed in quadrature with the uncertainty of the two measurements, obtaining \(\mathrm {ln\alpha _{36{-}40}}\) = \({(5.77 \pm 0.015)\times 10^{-3}}\). According to the model of [24], the dependence of \(\mathrm {ln\alpha _{A-40}}\) on the isotopic mass A is \(\mathrm {ln\alpha _{A-40}}\) \(\propto (40-A)/A\). Therefore, \(\mathrm {ln\alpha _{39{-}40}}\) can be derived from \(\mathrm {ln\alpha _{36{-}40}}\) by multiplying it by 0.2308, with an uncertainty difficult to estimate and that we assume to be negligible for now. Therefore, at the mean operating temperature of the column of \({89.5}\,{\hbox {K}}\), \(\mathrm {ln\alpha _{39{-}40}}\) = \((1.333 \pm 0.036)\times 10^{-3}\).
Dependence of \(\mathrm {ln\alpha _{28{-}29}}\) on temperature. The data points are taken from [25]. A fit with the function \(y= A\cdot 1/T^2 + B \) is overlaid. The continuous line corresponds to the mean value and the dashed lines to the 1\(\sigma _{{\mathrm {ln}}{\hat{\alpha }}}\) deviation. The errors on the single measurement were set all equal in the fit and determined in retrospect requiring the reduced \(\chi ^2\) to be 1
In Fig. 22 we report the dependence of \(\mathrm {ln\alpha _{28{-}29}}\) on temperature. The data points are taken from [25]. A fit with the function \(\mathrm {ln\alpha _{28-29}} = A\cdot 1/T^2 + B \) is overlaid. Again, the errors on the single measurement were set all equal in the fit and determined in retrospect requiring the reduced \(\chi ^2\) to be 1. Repeating the same procedure used for argon, at the mean operating temperature of the prototype column of \({85}\,{\hbox {K}}\), we obtain \(\mathrm {ln\alpha _{28-29}}\) = \({(2.828 \pm 0.020)\times 10^{-3}}\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Agnes, P., Albergo, S., Albuquerque, I.F.M. et al. Separating \({^{39}\hbox {Ar}}\) from \({^{40}\hbox {Ar}}\) by cryogenic distillation with Aria for dark-matter searches. Eur. Phys. J. C 81, 359 (2021). https://doi.org/10.1140/epjc/s10052-021-09121-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09121-9