The chirality-flow formalism for the standard model

Abstract

In a recent paper we introduced the chirality-flow formalism, a method for simple and transparent calculations of Feynman diagrams based on the left- and right-chiral $\mathfrak {sl}(2,\mathbb {C})$ nature of spacetime. While our previous work focused on massless QED and QCD at tree-level, we here extend the chirality-flow formalism to the full (tree-level) Standard Model, including massive particles and electroweak interactions – for which the W-interaction simplifies elegantly due to its chiral nature. We illustrate how values of Feynman diagrams can be immediately written down with some representative examples.

1 Introduction

In a recent paper [1] we introduced the chirality-flow formalism – a flow-like method for treating the Lorentz structure of scattering amplitudes – together with its tree-level Feynman rules in massless QED and QCD. This method builds on the spinor-helicity formalism [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] and is inspired by the color-flow decomposition of the color structure of gluons into fundamental and anti-fundamental representations [18,19,20]. It similarly decomposes the Lorentz structure of spin-one bosons into the dotted and undotted left- and right-chiral fields of the Weyl-van-der-Waerden formalism [21,22,23,24,25,26,27,28,29], denoted by dotted and undotted lines respectively, and corresponding to the two $\mathfrak {sl}(2,\mathbb {C})$ copies of spacetime. This allows for recasting Feynman diagrams into simple and intuitive chirality-flow diagrams, the values of which can be immediately written down in terms of Lorentz-invariant spinor inner products.

In the present paper we extend the chirality-flow method to the case of massive particles, focusing on the Standard Model at tree-level. This entails dealing with massive spinors, fourvectors, and polarization vectors by decomposing them into combinations of massless spinors [11, 28, 30]. More specifically, we write the Dirac spinor as a linear combination of left- and right-chiral Weyl spinors, and massive momenta as a linear combination of massless momenta, which are also used to describe the massive polarization vectors. Using the chirality-flow concepts and notation introduced in [1], the extension to the full Standard Model then turns out to be straightforward, and the left-chiral weak part of the Standard Model simplifies elegantly. In principle, this extension is to be anticipated, since the “chirality flows” represent the only Lorentz-invariant quantities at hand, the antisymmetric contraction of two left- or right-chiral spinors, i.e., the spinor inner products.

This paper is organized as follows: After reviewing some key features of the massless chirality-flow formalism in Sect. 2, we introduce massive fourvectors, spinors and polarization vectors in Sect. 3. The Feynman rules and their consistent application are described in Sect. 4, and values of representative Feynman diagrams are written down in Sect. 5. Finally, we conclude in Sect. 6.

2 Massless chirality-flow

In this section we go through the basic concepts introduced for massless chirality-flow in [1]. The new structures encountered in the massive case can be expressed in terms of these massless objects. Introductions to the spinor-helicity method itself can be found in for example [28, 29, 31,32,33,34,35,36,37,38].

2.1 Weyl spinors

We begin by recapitulating our notation for massless Weyl spinors. After crossing such that fermions and anti-fermions are outgoing (i.e. fourmomenta point away from the blobs that represent the internal process), the four possible types of Weyl spinors are,

(2.1)

Here, the right-chiral Weyl spinors $\langle i|=\langle p_i|$ and $|j\rangle =|p_j\rangle$ describe massless fermions and anti-fermions of negative helicity and momentum $p_i$ and $p_j$ respectively, while the left-chiral Weyl spinors $[i|=[p_i|$ and $|j]=|p_j]$ describe positive-helicity fermions and anti-fermions.¹

In Eq. (2.1) the left graphical rules correspond to the conventional Feynman rules (showing the fermion-flow arrows, momentum labels and helicity labels), whereas the right graphical rules correspond to the chirality-flow rules (showing the chirality-flow arrows, and using dotted lines for left-chiral particles with dotted indices and solid lines for right-chiral particles with undotted indices).

We recall that spinor indices can be raised and lowered using the Levi–Civita tensor

$$\begin{aligned} \lambda _{i,\alpha }&= \epsilon _{\alpha \beta }\lambda _i^{\beta }, \quad \tilde{\lambda }_{i,\dot{\alpha }} = \epsilon _{\dot{\alpha }\dot{\beta }}\tilde{\lambda }_i^{\dot{\beta }}, \nonumber \\ \lambda _i^{\alpha }&= \epsilon ^{\alpha \beta }\lambda _{i,\beta }, \quad \tilde{\lambda }_i^{\dot{\alpha }} = \epsilon ^{\dot{\alpha }\dot{\beta }}\tilde{\lambda }_{i,\dot{\beta }}, \nonumber \\ \epsilon ^{12}&= -\epsilon ^{21} = \epsilon _{21} = -\epsilon _{12} = 1~. \end{aligned}$$

(2.2)

Considering that $\epsilon$ is the only SL(2,$\mathbb {C}$) invariant object, the definitions for the (antisymmetric, Lorentz-invariant) spinor inner products follow as²

(2.3)

where $\langle i j\rangle ^*=[j i]$ for physical momenta (i.e. when $p_i^0,p_j^0>0$). From this, the chirality-flow representations of a Kronecker delta follow

(2.4)

We note that the indices in the spinor inner products Eq. (2.3), as well as in Eq. (2.4) are always intuitively read along the chirality-flow arrows, leading to the chirality-flow arrows opposing the fermion-flow arrow directions in Eq. (2.1).

For later comparison, we also write our two-component Weyl spinors of momentum $p_i$, $p_j$ and helicity ± in four-component notation

(2.5)

2.2 Massless fourvectors

We recall that a fourvector p can be mapped to Hermitian $2\!\times \!2$-matrices, or bispinors,

(2.6)

where we use a slash notation for the bispinors, not to be confused with the Feynman slash (see Appendices A and B for a summary of our notation and conventions and see [1] for further details). The index structures of momentum-bispinors are translated to the chirality-flow picture as

(2.7)

using the momentum-dot notation introduced in [1]. The spinor indices are then contracted with the rest of the amplitude.

If the fourmomentum p is lightlike, its bispinor decomposes into an outer product of massless Weyl spinors

(2.8)

or in the chirality-flow picture,

(2.9)

where p in the right graphical rules denotes that the line ends correspond to massless Weyl spinors of momentum p (cf. (2.1)).

In Feynman diagrams, we often encounter internal fermions for which the momentum p is a linear combination of lightlike external momenta $p_i$ (in the massless case), allowing us to write

(2.10)

or in the chirality-flow picture,

(2.11)

Also, factors of momentum $p^\mu$ which are not contracted with $\tau /\bar{\tau }$-matrices may be encountered. However, as is argued in section 4.4 of [1], it is always possible to make this contraction within a given Feynman diagram (see also section 4.3). Therefore, we are free to write

(2.12)

or in chirality-flow notation

(2.13)

Finally, a massless momentum $p^\mu$ can be written in terms of a $\tau /\bar{\tau }$ matrix and spinors of momentum p,

$$\begin{aligned} p^\mu = \frac{1}{\sqrt{2}}\langle p | \bar{\tau }^\mu | p] = \frac{1}{\sqrt{2}} [ p | \tau ^\mu | p\rangle . \end{aligned}$$

(2.14)

2.3 Polarization vectors

A key ingredient of the massless chirality-flow formalism is the polarization vector. It is well-known [10, 15] how to express a massless polarization vector in terms of its momentum p and an arbitrary reference momentum r satisfying $r^2 = 0$ and $r\cdot p \ne 0$ (different choices of r amount to different choices of gauge, and r may be chosen to simplify a given calculation). We denote an outgoing polarization vector of helicity $h \in \{+,-\}$ by $\big (\epsilon ^\mu _{h}(p,r)\big )^*$, while an incoming polarization vector is given by $\epsilon ^\mu _{h}(p,r)=\big (\epsilon ^\mu _{-h}(p,r)\big )^*$. For this reason, we only consider outgoing polarization vectors and drop the $*$ for convenience.

The outgoing polarization vectors are

$$\begin{aligned} \epsilon _+^\mu (p,r)&= \frac{\lambda _r^{\alpha }\bar{\tau }^\mu _{\alpha \dot{\beta }}\tilde{\lambda }_p^{\dot{\beta }}}{\lambda _r^{\gamma } \lambda _{p,\gamma }}= \frac{\tilde{\lambda }_{p,\dot{\alpha }}\tau ^{\mu ,\dot{\alpha }\beta }\lambda _{r,\beta }}{\lambda _r^{\gamma } \lambda _{p,\gamma }} \nonumber \\&\leftrightarrow \frac{\langle r|\bar{\tau }^\mu |p]}{\langle rp\rangle } = \frac{[p|\tau ^\mu |r\rangle }{\langle rp\rangle }, \nonumber \\ \epsilon _-^\mu (p,r)&= \frac{\lambda _p^{\alpha }\bar{\tau }^\mu _{\alpha \dot{\beta }}\tilde{\lambda }_r^{\dot{\beta }}}{\tilde{\lambda }_{p,\dot{\gamma }} \tilde{\lambda }_{r}^{\dot{\gamma }}} = \frac{\tilde{\lambda }_{r,\dot{\alpha }}\tau ^{\mu ,\dot{\alpha }\beta }\lambda _{p,\beta }}{\tilde{\lambda }_{p,\dot{\gamma }} \tilde{\lambda }_{r}^{\dot{\gamma }}} \nonumber \\&\leftrightarrow \frac{\langle p|\bar{\tau }^\mu |r]}{[pr]} = \frac{[r|\tau ^\mu |p\rangle }{[pr]}, \end{aligned}$$

(2.15)

which, as for any fourvector, may be converted into bispinors by contracting with $\tau _\mu$ or $\bar{\tau }_\mu$ (cf. Eq. (2.6))

$$\begin{aligned} \epsilon _{+}^{\dot{\beta }\alpha }(p,r)&= \frac{\tilde{\lambda }_p^{\dot{\beta }}\lambda _r^{\alpha }}{\lambda _r^{\gamma } \lambda _{p,\gamma }} \leftrightarrow \frac{|p]\langle r|}{\langle rp\rangle }, \nonumber \\ \bar{\epsilon }_{+,\beta \dot{\alpha }}(p,r)&= \frac{\lambda _{r,\beta }\tilde{\lambda }_{p,\dot{\alpha }}}{\lambda _r^{\gamma } \lambda _{p,\gamma }} \leftrightarrow \frac{|r\rangle [p|}{\langle rp\rangle }, \nonumber \\ \epsilon _{-}^{\dot{\beta }\alpha }(p,r)&= \frac{\tilde{\lambda }_r^{\dot{\beta }}\lambda _p^{\alpha }}{\tilde{\lambda }_{p,\dot{\gamma }} \tilde{\lambda }_{r}^{\dot{\gamma }}} \leftrightarrow \frac{|r]\langle p|}{[pr]}, \nonumber \\ \bar{\epsilon }_{-,\beta \dot{\alpha }}(p,r)&= \frac{\lambda _{p,\beta }\tilde{\lambda }_{r,\dot{\alpha }}}{\tilde{\lambda }_{p,\dot{\gamma }} \tilde{\lambda }_{r}^{\dot{\gamma }}} \leftrightarrow \frac{|p\rangle [r|}{[pr]}, \end{aligned}$$

(2.16)

from which (using Eq. (2.1)) the chirality-flow expressions follow [1]

(2.17)

Note that we have two alternative chirality-flow replacements of $\epsilon ^\mu _{\pm }(p,r)$. In a full chirality-flow diagram we must choose the version which gives a continuous flow, i.e. which ensures that no arrows point toward or away from each other along any line in the chirality-flow diagram. The systematic treatment of how to achieve this is given in Sect. 4.4.

2.4 Linking objects

The missing ingredients for the massless chirality-flow formalism are the additional objects which occur in vertices and propagators, the metric and the $\tau /\bar{\tau }$-matrices (from $\gamma$-matrices).

The metric, which always appears contracting two Lorentz indices, can be translated to a double line, i.e. parallel dotted and undotted lines with arrows opposing [1]

(2.18)

where in a given diagram the arrow directions which give a continuous flow are chosen. A $\tau /\bar{\tau }$-matrix is given by

(2.19)

where the double line to the right in each diagram corresponds to the $\mu$-index. At this point, no external spinors are connected to the line ends.

In both cases, the motivation for these replacements lies in the fact that for a full amplitude, the indices are always contracted. For the $\tau /\bar{\tau }$-matrices the proof also involves charge conjugation [1].

3 The chirality-flow formalism with massive particles

In this section we will set the stage for the massive chirality-flow formalism, in essence by treating massive spinors and fourvectors as combinations of their massless equivalents, and by carefully considering the spin properties of spin-1/2 and spin-1 particles.

3.1 Spin and helicity

It is well established that massive and massless particles have rather different properties under Poincaré transformations, having different little groups [39,40,41]. Considering only Poincaré symmetry, a massless particle can be fully described by its momentum $p^\mu$ and its helicity $h=\pm J$, where J is the total spin of the particle. In contrast, a massive particle is described by its momentum $p^\mu$, total spin J, and its spin ${J_s}$ projected onto some axis $s^\mu$, where the fourvector $s^\mu$ must satisfy $s\cdot p= 0$ and $s^2=-1$, and is often referred to as the polarization vector since $s^\mu = \epsilon ^\mu _0$ is the longitudinal polarization vector for spin-1 particles (see e.g. [28, 34, 42]). If the spatial part of $s^\mu$ points in the direction $\hat{\mathbf{p }}=\mathbf{p} /|\mathbf{p} |$, then ${J_s}= h$ is the helicity of the particle.

Analogous to helicity amplitudes for massless particles, it is possible to define spin amplitudes involving massive particles, in which each external particle is given a definite spin ${J_s}$. However, massive spin amplitudes depend on the directions $s^\mu$ along which we measure ${J_s}$ for each particle, making the choice of $s^\mu$ physical. Only the sum of squared spin amplitudes involving a massive particle are independent of the choice of axis.

In the following sections, we will describe how to separate a massive momentum into a sum of two massless ones, and in this process we will also define the spin axis $s^\mu$. We will then describe the massive spinors and polarization vectors required to calculate massive spin amplitudes in terms of Weyl spinors of these massless momenta.

We note that this decomposition is not the only way to treat massive particles. A few years ago an alternate set of massive spinor-helicity variables was introduced which made the little group structure explicit [43]. Such variables contain all spin projections of a particle, and (among other things) have inspired a series of recursion relations [44,45,46,47], each with applications to different types of processes. While such an approach is related to this work (see [44] for how to relate the two approaches), we here choose to build on the older spinor helicity variables, and use Feynman diagrams to be as general as possible. Nonetheless, adapting the chirality-flow method to the new spinor-helicity variables is a potentially interesting future research direction.

3.2 Massive fourvectors

A massive fourvector p can be described using two lightlike fourvectors $p^\flat$ and q satisfying $p^\flat \cdot q\ne 0$. After choosing q arbitrarily, we express the massive fourvector p as [11, 28,29,30]

$$\begin{aligned} p = p^\flat + \alpha q, \ \ \mathrm {where} \ \ \alpha =\frac{p^2}{2p\cdot q}=\frac{p^2}{2p^\flat \cdot q} \;\xrightarrow {\;\;p^2\rightarrow 0\;\;}\; 0 . \end{aligned}$$

(3.1)

Using Eq. (2.10), we have with the above

(3.2)

or in graphical notation,

(3.3)

which trivially reduce to Eq. (2.9) in the limit $p^2\rightarrow 0\Rightarrow \alpha \rightarrow 0$. For fermion propagators in massive Feynman diagrams, we may use this to extend Eq. (2.11) to the case where some of the momenta $p_i$ are not lightlike, but instead refer to massive on-shell momenta with $p_i^2=m_i^2$.

Using the decomposition into lightlike vectors in Eq. (3.1), we define the axis $s^\mu$ along which the spin of a fermion (see Sect. 3.3) or vector boson (see Sect. 3.4) is measured via [11, 28]

$$\begin{aligned} s^\mu = \frac{1}{m}\left( p^{\flat \mu } - \alpha q^\mu \right) = \frac{1}{m}\left( p^{\mu } - 2\alpha q^\mu \right) . \end{aligned}$$

(3.4)

From Eq. (3.1), $s^\mu$ is easily shown to satisfy the required relations $s^2=-1$ and $s\cdot p= 0$ (see Appendix A.2 for more details). Therefore, the arbitrary choice of each q is physical, and different choices of q lead to different spin directions, implying different spin amplitudes.

3.2.1 Helicity and the eigenvalue decomposition

A special case of the decomposition in Eq. (3.1) is the eigenvalue decomposition for which the spatial part of $s^\mu$ points along the direction of motion, $\hat{\mathbf{p }}=\mathbf{p} /|\mathbf{p} |$. Therefore, in this decomposition the particles are helicity eigenstates.

It is easily shown that both and have the (“forward” and “backward”) eigenvalues $\lambda _{f/b}= p^0 \pm |\mathbf{p} |$, such that the determinant of is $\lambda _{f}\lambda _{b}= m^2$. Further, the eigenvectors $|p_{f/b}], |p_{f/b}\rangle$ of and are massless spinors satisfying

(3.5)

where $\varphi \equiv \varphi _{p_fp_b}$ is a relative phase (see Appendix B.2) and $\hat{p}^{\perp } = \hat{p}^1 +i\hat{p}^2$. (If $\hat{p}^{\perp } = 0$, $\varphi$ can be set to 0.)

These spinors can be translated to momenta using Eq. (2.14),

$$\begin{aligned} p_{f/b}^\mu = \frac{1}{\sqrt{2}} \langle p_{f/b}|\bar{\tau }^\mu |p_{f/b}] = \frac{1}{\sqrt{2}} [p_{f/b}|\tau ^\mu |p_{f/b}\rangle , \end{aligned}$$

(3.6)

with $\mathbf{p} _{f}$ pointing in the same direction as $\hat{\mathbf{p }}$ and $\mathbf{p} _{b}$ pointing in the opposite direction, giving

$$\begin{aligned} p_{f}^\mu = \frac{\lambda _{f}}{2} \big (1,\hat{\mathbf{p }}\big ), \quad p_{b}^\mu = \frac{\lambda _{b}}{2} \big (1,-\hat{\mathbf{p }}\big ). \end{aligned}$$

(3.7)

It is easy to check that a special case of Eq. (3.1) is $p^\mu =p_f^\mu +p_b^\mu$, corresponding to the choice $\alpha = 1$, $q^\mu =p_{b}^\mu$, and $p^{\flat ,\mu }=p_{f}^\mu$. With this choice, Eq. (3.2) becomes

(3.8)

and the spin fourvector $s^\mu$ in Eq. (3.4) is

$$\begin{aligned} s^\mu = \frac{1}{m}\left( p_{f}^\mu - p_{b}^\mu \right) = \frac{1}{m}\left( |\mathbf{p} | , p^0 \hat{\mathbf{p }}\right) , \end{aligned}$$

(3.9)

i.e. it is pointing along the direction of motion. Therefore, with this decomposition ${J_s}=h$ measures the helicity.

3.3 Dirac spinors from massless Weyl spinors

Similar to describing massive momenta in terms of momenta $p^\flat$ and q, we describe massive Dirac spinors in terms of massless Weyl spinors of momenta $p^\flat$ and q [17, 28, 29, 33, 48,49,50]. The arbitrary reference fourvector q can be chosen to simplify calculations, but carries physical meaning as it defines the spin axis $s^\mu$ in Eq. (3.4), along which the spin is measured.

We let $u^{J_s}(p)$, $\bar{u}^{{J_s}}(p)$, $v^{J_s}(p)$, and $\bar{v}^{J_s}(p)$ denote the momentum space Dirac spinors of momentum p and spin ${J_s}=(+,-)\leftrightarrow (\frac{1}{2},-\frac{1}{2})$ along the $s^\mu$-axis, and calculate the spin using the operator

$$\begin{aligned} \mathcal {O}_s= -\frac{s^\mu \Sigma _\mu }{2} = \frac{\gamma ^5s^\mu \gamma _\mu }{2}, \end{aligned}$$

(3.10)

where $\Sigma ^\mu /2$ is the Lorentz-covariant spin operator for Dirac spinors and $\Sigma \cdot p = 0$ (see Appendix A.2 for details).

We may write the Dirac spinors for outgoing fermions $\bar{u}^{J_s}(p)$ and anti-fermions $v^{J_s}(p)$ in the chirality-flow picture as 

(3.11)

where in the massless limit $p^\flat =p$ and $\alpha = 0$, such that we recover Eq. (2.5). The factors

$$\begin{aligned} e^{i\varphi }\sqrt{\alpha }=\frac{m}{\langle p^\flat q \rangle }, \quad e^{\!-i\varphi }\sqrt{\alpha }=\frac{m}{[ q p^\flat ]}, \end{aligned}$$

(3.12)

are required such that the spinors satisfy the Dirac equation, and the phase is given by

$$\begin{aligned}{}[ q p^\flat ] =e^{i\varphi }\sqrt{2p^\flat \!\cdot q}, \quad \langle p^\flat q \rangle = e^{-i\varphi }\sqrt{2p^\flat \!\cdot q}, \end{aligned}$$

(3.13)

as in Eq. (3.5). Explicit forms of the Weyl spinors are given in Eq. (B.1) (fixing the phase $\varphi$).

Similarly, for incoming anti-fermions $\bar{v}^{J_s}(p)$ and fermions $u^{J_s}(p)$ we write

(3.14)

In Eqs. 3.11 and 3.14 the leftmost graphical rules correspond to the conventional Feynman rules (showing the fermion-flow arrows, momentum labels and spin labels; the thicker lines imply massive particles), and the rightmost graphical rules correspond to the chirality-flow rules (showing the chirality-flow arrow, cf. (2.1)).

3.3.1 Helicity eigenstates

For our spinors to be helicity eigenstates we use the eigenvalue decomposition detailed in Sect. 3.2.1, equivalent to choosing $\alpha =1$, $q^\mu =p_{b}^\mu$ and $p^{\flat ,\mu }=p_{f}^\mu$, in Eq. (3.1). Outgoing (anti-)fermions of helicity ± are then given by

(3.15)

while incoming spinors are given by

(3.16)

where we use Eq. (3.5) to define both the Weyl spinors (for which explicit forms are given in Eq. (B.6)) and the phase $\varphi$,

$$\begin{aligned} e^{i\varphi }=\frac{m}{\langle p_fp_b \rangle }, \quad e^{\!-i\varphi }=\frac{m}{[ p_bp_f]}. \end{aligned}$$

(3.17)

3.4 Polarization vectors

It is also well known how to use Eq. (3.1) to describe massive polarization vectors [15, 17, 28, 29, 33, 48,49,50]. Let $\big (\epsilon ^\mu _{s}(p)\big )^*$ denote the polarization vectors of outgoing vector bosons with momentum p and spin (polarization) label ${J_s}\in \{+,0,-\}$ along the spin axis $s^\mu$. Since incoming polarization vectors are described by $\epsilon ^\mu _{s}(p)=\big (\epsilon ^\mu _{-s}(p)\big )^*$, we will again only consider outgoing polarization vectors, and drop the $*$ for convenience.

The positive and negative polarization vectors may be written in a form analogous to the massless case, Eq. (2.16),

$$\begin{aligned} \epsilon _{+}^{\dot{\beta }\alpha }(p^\flat ,q)&= \frac{\tilde{\lambda }_{p^\flat }^{\dot{\beta }}\lambda _q^{\alpha }}{\lambda _q^{\gamma } \lambda _{p^\flat ,\gamma }} \leftrightarrow \frac{|p^\flat ]\langle q|}{\langle qp^\flat \rangle }, \nonumber \\ \bar{\epsilon }_{+,\beta \dot{\alpha }}(p^\flat ,q)&= \frac{\lambda _{q,\beta }\tilde{\lambda }_{p^\flat ,\dot{\alpha }}}{\lambda _q^{\gamma } \lambda _{p^\flat ,\gamma }} \leftrightarrow \frac{|q\rangle [p^\flat |}{\langle q p^\flat \rangle }, \nonumber \\ \epsilon _{-}^{\dot{\beta }\alpha }(p^\flat ,q)&= \frac{\tilde{\lambda }_q^{\dot{\beta }}\lambda _{p^\flat }^{\alpha }}{\tilde{\lambda }_{p^\flat ,\dot{\gamma }} \tilde{\lambda }_{q}^{\dot{\gamma }}} \leftrightarrow \frac{|q]\langle p^\flat |}{[p^\flat q]}, \nonumber \\ \bar{\epsilon }_{-,\beta \dot{\alpha }}(p^\flat ,q)&= \frac{\lambda _{p^\flat ,\beta }\tilde{\lambda }_{q,\dot{\alpha }}}{\tilde{\lambda }_{p^\flat ,\dot{\gamma }} \tilde{\lambda }_{q}^{\dot{\gamma }}} \leftrightarrow \frac{|p^\flat \rangle [q|}{[p^\flat q]}, \end{aligned}$$

(3.18)

where, unlike the reference spinor r in Eq. (2.16), the arbitrary reference spinor q carries physical meaning as it defines the spin axis $s^\mu$. These expressions can be straightforwardly translated to the graphical representation

(3.19)

where we use thicker wavy lines to imply that the vector bosons are massive, and the arrow directions which give a continuous flow in a given diagram are chosen.

The additional, longitudinal, polarization vector equals the spin vector

$$\begin{aligned}&\epsilon ^\mu _{0}(p^\flat ,q) = s^\mu = \frac{1}{m}\left( p^{\flat \mu } - \alpha q^\mu \right) \nonumber \\&\leftrightarrow \! \frac{1}{m\sqrt{2}} \Big (\!|p^\flat ]\langle p^\flat | - \alpha |q]\langle q|\!\Big ) \ \mathrm { or } \ \frac{1}{m\sqrt{2}} \Big (\!|p^\flat \rangle [p^\flat |-\alpha |q\rangle [q|\!\Big ) , \end{aligned}$$

(3.20)

and using the momentum-dot notation, we can translate this into

(3.21)

where in this case there is no massless equivalent. These graphical representations come from using the first form of $\epsilon ^\mu _{0}$ in Eq. (3.20). Alternatively, we could have rewritten $\epsilon ^\mu _{0}$ as a linear combination of two spinors as in Eq. (3.19) using one of the last two expressions instead.

3.4.1 Helicity eigenstates

To describe external vector bosons as helicity eigenstates we choose $\alpha =1$, $q^\mu =p_{b}^\mu$ and $p^{\flat ,\mu }=p_{f}^\mu$, such that $p=p_f+ p_b$, as in Sect. 3.2.1. The chirality-flow representations for these states are then

(3.22)

where in the massless case the longitudinal polarization disappears, $p_f\rightarrow p$ and the reference momentum $q = p_b$ becomes an unphysical gauge choice (see [1] for more details).

4 Chirality-flow Feynman rules with massive particles

In this section, we describe the (tree-level) electroweak vertices and propagators. For convenience, all tree-level Standard Model rules are also collected in Appendix C, while a derivation of the QCD chirality-flow rules can be found in [1].

We treat the momenta of all particles as outgoing, and use ’t Hooft-Feynman gauge. Further details about the electroweak sector can be found³ in [51]. We also remark that – while we focus on tree-level – similar chirality-flow structures of vertices and propagators are also expected to be applicable for loop methods which rely on four-dimensional tree objects. For physics beyond the Standard Model, we note that it is possible to use chirality-flow to describe any theory for which the Lorentz structure can be written down in terms of momenta, the (Minkowski) metric, Dirac (Pauli) matrices, massless Weyl spinors, and polarization vectors. For this reason, the extension to for example $R_\xi$ or axial gauges should also be straightforward.

4.1 Vertices

4.1.1 Triple vertices

The Lorentz structure of the fermion-vector vertices is in principle unchanged compared to the massless case, and separates nicely into two chiral parts. Using Eq. (2.19) to describe the $\tau /\bar{\tau }$ matrices, we have

(4.1)

with, in general, different couplings to the left and right chiral parts, $C_{L/R}$. In particular, $C_R=0$ for W-interactions, corresponding to the fact that W-bosons only couple to particles in the left chiral gauge group.⁴ For the weak SU$(2)_L$ sector, Feynman rules are thus further simplified in the chirality-flow formalism.

Assuming a diagonal flavor matrix, $C_L=1/(\sqrt{2}\sin \theta _W)$ for left chiral leptons coupling to W, whereas the coupling to the Z-boson is given by $-Q_f \sin \theta _W/\cos \theta _W$ for right chiral fermions, and by $(T_3^f-Q_f \sin ^2 \theta _W)/(\cos \theta _W \sin \theta _W)$ for left chiral fermions, where $T_3^f$ is the eigenvalue of the third weak isospin generator and $\theta _W$ is the Weinberg angle. The coupling to the photon is given by $C_L=C_R=Q_F$.

Fermions may also couple to scalars, giving a fermion-scalar vertex of the form

(4.2)

where we used Eq. (2.4) to describe the Kronecker deltas, and where, for a general scalar coupling, the constants $C_L$ and $C_R$ may be different. In the Standard Model the only known scalar, the Higgs, couples with $C_L=C_R=-m_f/(2 \sin \theta _W m_W)$ in terms of the fermion mass $m_f$ and the W mass $m_W$.

Here we note that the appearance of a single dotted or undotted line in Eq. (4.2) may give rise to an odd number of chirality-flow lines in a graph, meaning that the sign flips from reversing chirality-flow arrows have to be accounted for (as described below in Sect. 4.3). We also remark that although it may appear in the graphical representation to the right as if the scalar has no effect at all, its momentum enters via momentum conservation.

A Lorentz scalar may also couple to two vector bosons in a vertex of the form

(4.3)

where for brevity we write the metric without arrows, to indicate that either choice in Eq. (2.18) may be required (recall that flow arrows must never oppose or point away from each other). Here, again, the presence of the scalar manifests itself only via momentum conservation. In the tree-level Standard Model, this Lorentz structure is applicable to the Higgs coupling to W and Z, for which $C_{WWh} = m_W/\sin (\theta _W)$ and $C_{ZZh} = m_Z/(\sin \theta _W\cos \theta _W) = m_W/(\sin \theta _W\cos ^2\theta _W)$.

There is also a pure scalar vertex,

(4.4)

with completely trivial Lorentz structure, and $C_{hhh}=-3 m_h^2/(2 \sin \theta _W m_W)$. For the non-Abelian vertex with three spin-1 bosons, the Lorentz structure is as for QCD,

(4.5)

where Eq. (2.13) has been used for the momenta $p_1-p_2$ etc., and where $C_{\gamma W^+W^-}=-1$ and $C_{ZW^+W^-}=-\cos (\theta _W)/\sin (\theta _W)$.

To complete the list of trivalent vertices, we give the Lorentz structure of two scalars coupling to a spin-1 particle

(4.6)

This vertex enters in the Standard Model only at loop level, but we include it here to complete the list of Standard Model Lorentz structures (note that the ghost-ghost-vector vertex has the same chirality-flow structure but a different momentum-dot argument).

4.1.2 Four-boson vertices

We start with the vertex with four vector bosons, which has a Lorentz structure similar to the color-flow version of the four-gluon vertex (see section 5.1 in [1]),

(4.7)

Here, the value of $C_{V_1 V_2 V_3 V_4}$ depends on the involved electroweak bosons. Specifically, we have $C_{W^+ W^- W^+ W^-}=1/\sin ^2\theta _W$, $C_{W^+ Z W^- Z }=-\cos ^2\theta _W/\sin ^2\theta _W$, $C_{W^+ Z W^- \gamma }=-\cos \theta _W/\sin \theta _W$ and $C_{W^+ \gamma W^- \gamma }=-1$.

We can also have a vertex with two scalars and two vectors, connected with the chirality flow

(4.8)

where in the Standard Model $C_{WWhh}=1/(2 \sin ^2\theta _W$) and $C_{ZZhh}=1/(2 \sin ^2\theta _W \cos ^2\theta _W)$.

Finally, we have the quartic scalar vertex, with trivial Lorentz structure

(4.9)

In the tree-level Standard Model, this vertex is applicable to the quartic Higgs coupling with $C_{hhhh}=-3m_h^2/(4 \sin ^2 \theta _W m_W^2)$.

4.2 Propagators

Adding masses to the chirality-flow picture gives rise to increasing complexity for the Fermion propagator,

(4.10)

which can be drawn in terms of a combination of four different chirality flows, coupling the left- and right-chiral components,

(4.11)

Like the fermion-fermion-scalar vertex (Eq. (4.2)), the appearance of a single dotted or undotted line may imply a sign flip when reversing chirality-flow arrow directions (see below in Sect. 4.3).

Next, we consider the vector propagator for a massive particle which – aside from the trivial addition of a term $-m^2$ in the denominator – is unchanged

(4.12)

Note that, as in the massless case, the arrow direction consistent with the rest of the chirality-flow diagram must be chosen. To complete the Standard Model list of propagators, we also need to treat the scalar propagator,

(4.13)

for which there is no flow of chirality, and hence no graphical representation in the chirality-flow picture.

4.3 Chirality-flow arrows and signs

Now that we have the chirality-flow Feynman rules, we describe how to apply them consistently. For chirality-flow to work a continuous flow is required, i.e., we cannot connect chirality-flow lines with arrows opposing or pointing away from each other. However, aligned arrows are not always immediately obtained. When we connect two fermion lines in the chirality-flow formalism, we often find situations where the chirality-flow arrows as stated in Sect. 3.3 point towards or away from each other, with (assuming massless, outgoing particles)

(4.14)

as the simplest example. In such situations, it is necessary to flip the chirality-flow arrows for one of the involved fermion lines, above either to the left or to the right of the $\times$-sign.

In massless QED and QCD, each fermion line contains an odd number of $\tau /\bar{\tau }$-matrices (one for each vertex and propagator). Therefore, we can flip the chirality-flow arrow directions of a fermion line with n gauge bosons attached via the relation

$$\begin{aligned} \langle i | \bar{\tau }^{\mu _1} \tau ^{\mu _2} \cdots \bar{\tau }^{\mu _{2n-1}} | j ] = [j | \tau ^{\mu _{2n-1}} \cdots \bar{\tau }^{\mu _2} \tau ^{\mu _{1}} | i \rangle , \end{aligned}$$

(4.15)

where every even-numbered $\tau /\bar{\tau }$-matrix will be contracted with a momentum from the propagator (via Eq. (2.6)), and every odd-numbered $\tau /\bar{\tau }$-matrix corresponds to a fermion-fermion-vector vertex (see Eq. (4.1)). Assuming that the fermion arrow points to the left, and that the attached bosons have outgoing momenta, this gives the graphical representation

(4.16)

i.e., a swap of chirality-flow arrows (see sections 4.1 and 4.2 in [1]). Note that the labels of the momentum dots are unchanged by the arrow flip, and that we have an even number of chirality-flow lines (consistent with not obtaining an overall minus sign when changing all arrow directions).

We then connect different fermion lines using the chirality-flow structure of the vector propagator

(4.17)

choosing the arrow directions which give a continuous flow. For the simple example in Eq. (4.14) above, we may for example flip the arrow directions on the left half and connect the flow lines to obtain

(4.18)

The remaining two structures in massless QED and QCD, external momenta (Eq. (2.14)) and external gauge bosons (Eq. (2.15)), both have the form of Eq. (4.15) with $n=1$. We conclude that Feynman diagrams in these theories only contain contractions of Eq. (4.15) [1]. Therefore, for each disconnected piece⁵ in a massless QED or QCD chirality-flow diagram, we only need to choose the chirality-flow arrow of one external particle in order to assign chirality-flow arrows. Every other chirality-flow arrow connected to that particle by chirality-flow lines is then fixed by the vertex and propagator rules (arrows flow through a vertex and fermion propagator, and point in opposite directions in a boson double-line).

In contrast to massless QED and QCD, the full (tree-level) Standard Model also gives rise to fermions containing an even number of $\tau /\bar{\tau }$ matrices. This is either due to the scalar-fermion-fermion vertex, Eq. (4.2), or due to the mass term of the fermion propagator, Eq. (4.11), each of which does not contain a $\tau /\bar{\tau }$. To swap the chirality-flow arrow in such cases we use either of

$$\begin{aligned} \langle i | \bar{\tau }^{\mu _1} \cdots \tau ^{\mu _{2n}} | j\rangle&= - \langle j | \bar{\tau }^{\mu _{2n}} \cdots \tau ^{\mu _{1}} | i\rangle , \nonumber \\ [i | \tau ^{\mu _1} \cdots \bar{\tau }^{\mu _{2n}} | j ]&= -[j | \tau ^{\mu _{2n}} \cdots \bar{\tau }^{\mu _{1}} |i ] , \end{aligned}$$

(4.19)

each containing a minus sign. This implies that signs now need to be tracked when swapping chirality-flow arrows. We also remark that in the equation analogous to Eq. (4.16), we would now have an odd number of chirality-flow lines.

4.4 Application

With the above in mind, we use the following method to calculate a Feynman diagram:

• (i) Collect all common non-chirality-flow factors in front. Such factors can come from vertices, propagators, and denominators of external gauge bosons.

• (iia) If there are no fermion lines involved:

  • Without drawing the arrows, draw and connect all chirality-flow lines according to the Feynman rules.

  • Since we have an even number of flow lines, we can choose an arbitrary chirality-flow arrow direction for one flow line. Follow this arrow direction through the diagram, remembering that all double-lines should have opposing arrows, and vertices and momentum dots should have a continuous flow.

  • Repeat for all disconnected chirality-flow pieces (see footnote 5 for the definition of disconnected).

• (iib) If there is at least one fermion line:

  • For each fermion line and any bosons connected to it, draw the chirality-flow lines without arrows. Do not yet connect flow lines from different fermion lines.

  • Use Eq. (2.1) to set the chirality-flow arrows of external fermions. Then, for the rest of each fermion line draw the chirality-flow arrow directions in the only way possible.

  • Use Eq. (4.15) or (4.19) to swap the chirality-flow arrows of each line, such that they can be connected with Eq. (4.17). Remember that we obtain a minus sign when swapping arrows on an odd number of flow lines.

  • For any remaining disconnected pieces, choose a chirality-flow direction for one particle and follow it through the diagram as described in step (iia).

5 Examples

In this section we illustrate some new features of the massive and electroweak vertices, propagators and external particles. More extensive examples of the massless formalism are given in section 6 in [1]. We remind the reader that thicker lines in Feynman diagrams imply that the particle is massive, that we use ’t Hooft–Feynman gauge, and that the Feynman rules are conveniently collected in Appendix C.

5.1 $e^+e^- \rightarrow \gamma \gamma$

First we explore the effect of a massive fermion by considering the Feynman diagram

(5.1)

corresponding to $e^-_{1+} e^+_{2-}\rightarrow \gamma _{3+} \gamma _{4-}$ where each particle is a helicity eigenstate. In this example the effect of the mass enters at two levels, in the external particle wave functions and in the fermion propagator.

For the external spinors, we recall that (unlike in the massless case) a helicity eigenstate is a linear combination of two different chirality eigenstates, as given in Sect. 3.3.1. Recalling Eq. (3.16) we have

(5.2)

where $p^\mu _{i,f/b}=\frac{p_i^0 \pm |\mathbf{p} _i|}{2}(1,\pm \hat{\mathbf{p }}_\mathbf{i })$ from Sect. 3.2.1. Explicit spinors can be found in Eq. (B.6), and the phases are given by Eq. (3.17) or (3.5).

Collecting overall factors from the vertices ($-ie\sqrt{2}$), fermion propagator ($\frac{i}{(p_3-p_2)^2-m_e^2}$), and two polarization vectors ($\frac{1}{\langle r_3 3 \rangle [ 4 r_4]}$, see Eq. (2.17)), then connecting the matching line types as given by the Fermion propagator Eq. (4.11), we arrive at the expression

(5.3)

While the line contractions themselves, via Eq. (2.3), give the diagram expressed in terms of spinor inner products, we have written out the contractions in terms of brackets as a service to the reader.

We note that when the mass goes to zero, both Weyl spinors $|1_b]$ and $\langle 2_b|$ also go to zero as they are proportional to $\sqrt{\lambda _{i,b}} = \sqrt{p_i^0 - \vert \mathbf{p} _i\vert }$. This implies that the only surviving chirality-flow diagram in the massless case is the first diagram above, (cf. Eq. (6.19) in [1]). We further note that in the massless limit this Feynman diagram can be removed by an unphysical gauge choice, using $r_4=p_3$ and $r_3=p_2= p_{2f}$ (implying that the diagram with the photons exchanged cannot be removed by this gauge choice).

We also remark that for this diagram, we did not need to adjust any chirality-flow arrows since we only have one fermion line, and the arrows from the external photon polarization vectors can be aligned accordingly, without additional minus signs.

5.2 $e^+e^- \rightarrow Zh$

Next we consider a diagram relevant for associated Higgs production, $e^-_{1+}e^+_{2-}\rightarrow h_3 Z_{4,0}$,

(5.4)

Aside from a massive fermion, this diagram involves both an internal and an external massive vector boson, the vector-vector-scalar vertex from Eq. (4.3), and a Z-fermion-fermion vertex with different couplings to left- and right-chiral particles. For the Z-boson, the superscript 0 in $4^0$ refers to the longitudinal polarization, with chirality-flow representation given in Eq. (3.21). We will use the general spin basis, such that the spins are measured relative to spin axes $s^\mu _i$, not relative to the particles’ directions of motion.

Collecting overall factors from the Zff- and ZZh-vertices (Eqs. (4.1) and (4.3)), from the massive spin-1 propagator (Eq. (4.12)), as well as from the normalization of the polarization vector (Eq. (3.21)), and treating the massive external fermions using the general spin decomposition Eq. (3.14)

(5.5)

where the lightlike vectors $p^\flat$ and q are given by Eq. (3.1), we get two chirality-flow diagrams

(5.6)

Explicit Weyl spinors can be found in Eq. (B.1) and the phases $\varphi _{1,2}$ are given by Eq. (3.12).

In the Standard Model, the couplings $C_L,C_R$ assume the values given below Eq. (4.1), however, here they can be adjusted to match the theory at hand. As in the previous example, we draw the chirality-flow arrows as dictated by the external fermions, but note that flipping all of the arrows does not introduce any additional signs.

We see that only the second chirality-flow diagram contributes when the fermions are massless since $\alpha _{1,2}\rightarrow 0$. Further, we can simplify this calculation with a clever choice of $q_{1,2,4}$. For instance, we can remove all but one of the four terms with the choice $q_1 = p_4^\flat$, $q_2 = q_4 = p_1^\flat$, which fixes the axes $s^\mu _i$ along which the spin of each particle is measured for all Feynman diagrams contributing to this process.

5.3 $q\bar{q} \rightarrow q\bar{q}h$

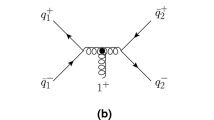
As a final example we consider $q_{1-}\bar{q}_{2-} \rightarrow q_{3+} \bar{q}_{4+} h_5$, and calculate

(5.7)

which nicely displays the chiral nature of the W-boson, and demonstrates the treatment of chirality-flow arrow signs when multiple fermion lines are present. Note that if we use massless spinors (but keep the mass in the coupling), then the corresponding helicity amplitude will vanish since the incoming particles have the same helicity.

We again begin by collecting overall factors from the vertices (Eqs. (4.1) and (4.2)) and the two propagators (Eqs. (4.12) and (4.11)). We also include Kronecker deltas in color for the quarks, $\delta _{{q_2}{q_1}}\delta _{{q_3}{q_4}}$. The massive fermions are treated using the general spin decomposition (Eqs. (3.11) and (3.14)), but we do not immediately join them together with the vector propagator,

(5.8)

Here, the internal, unlabeled ends of chirality-flow lines are not yet connected to external spinors, and the couplings are assumed to take their Standard Model values given below Eq. (4.1), but can be changed to suit the theory at hand.

On the solid (dotted) lines, to be joined in the middle, the chirality-flow arrows are pointing towards (away from) each other. To join the flow lines, we must either flip the flow arrows on the first term (containing $q_2,p_1^\flat$) or on the second (in square brackets). If we flip them on the first term we use

(5.9)

a special case of Eq. (4.16). Note that this arrow swap is not possible at the vertex level itself (i.e. $\tau \ne \bar{\tau }$), but requires each external flow line to be contracted with a Weyl spinor.

The Feynman diagram is then immediately written down in terms of inner products

(5.10)

which vanishes in the massless limit ($\alpha _i \rightarrow 0$) as it should. We can also make this diagram disappear by choosing $q_2=q_3$, allowing to simplify the amplitude calculation.

Note that we could alternatively have flipped the arrows on the chirality-flow factors in the square bracket of Eq. (5.8). In this case we must be more careful, since the term proportional to $\sqrt{\alpha _4}$ comes with a minus sign under arrow reversal,

(5.11)

a special case of Eq. (4.19). The chirality-flow graphs in Eq. (5.10) would then be written down with the arrow direction reversed, giving a factor $(-1)^3$ in the first graph to compensate the minus sign in Eq. (5.11). Thus, in accordance with Sect. 4.3, we obtain the same result regardless of which fermion line had its chirality-flow arrows flipped.

6 Conclusion and outlook

In a recent paper we showed that it is possible to define a chirality-flow description of the Lorentz structure of Feynman rules and diagrams for massless QED and QCD. Using this method, along with its graphical interpretation, the values of amplitudes from Feynman diagrams can be immediately written down in a transparent and intuitive manner, offering superior simplicity for helicity-assigned diagrams.

Here we prove that the flow idea can be extended to the full standard model, in essence by treating massive fermions and spin-1 bosons as combinations of their massless analogs. In principle, this extension is to be anticipated, since the “flows” describing the Lorentz structure are nothing but the only Lorentz-invariant quantities at hand, the antisymmetric contraction of two left- or right-chiral spinors, i.e., the spinor inner products. For the same reason, we expect the formulation of Feynman rules beyond leading order, or for physics beyond the Standard Model to be straightforward.

The addition of mass implies a modest complication, resulting in twice as many terms for external fermions, as well as for internal Fermion propagators, and another polarization vector to keep track of for external vector bosons. On the other hand, the chirality-flow diagrams are simplified for weak interactions involving W-bosons, where – due to the left chiral nature – only one term in the vector-fermion vertex is present.

Aside from offering an intuitive and transparent way of thinking about and calculating Feynman diagrams, we expect our method to be computationally beneficial (at least) for programs that base their calculations on helicity-assigned Feynman diagrams, due to the complete avoidance of Dirac matrices.

Appendices

Appendix A: Dirac spinors

1.1 A.1 Conventions and the chiral representation

Here we summarize our conventions for spinors and gamma matrices in the chiral basis. For a more complete set of our conventions, as well as some useful algebraic relations see [1]. For general reviews on chiral spinors and the spinor-helicity formalism we refer to [28, 29, 31,32,33,34,35,36,37,38].

We use the Dirac matrices in the chiral, or Weyl basis,

$$\begin{aligned} \gamma ^{\mu }&= \begin{pmatrix} 0 &{} \sigma ^{\mu } \\ \bar{\sigma }^{\mu } &{} 0 \end{pmatrix} = \begin{pmatrix} 0 &{} \sqrt{2}\tau ^{\mu } \\ \sqrt{2}\bar{\tau }^{\mu } &{} 0 \end{pmatrix}, \nonumber \\ \gamma ^5&= i \gamma ^0 \gamma ^1 \gamma ^2\gamma ^3 = \begin{pmatrix} -1 &{} 0 \\ 0 &{} 1 \end{pmatrix}, \end{aligned}$$

(A.1)

where the $\sigma$-matrices are the Pauli matrices,

$$\begin{aligned} \sigma ^\mu&= (\sigma ^0,\varvec{\sigma }) = (\sigma ^0,\sigma ^1,\sigma ^2,\sigma ^3) \nonumber \\&= \left( \begin{pmatrix} 1 &{} 0\\ 0 &{} 1 \end{pmatrix}, \begin{pmatrix} 0 &{} 1\\ 1 &{} 0 \end{pmatrix}, \begin{pmatrix} 0 &{} -i\\ i &{} 0 \end{pmatrix}, \begin{pmatrix} 1 &{} 0\\ 0 &{} -1 \end{pmatrix}\right) , \nonumber \\ \bar{\sigma }^\mu&= (\sigma ^0,-\varvec{\sigma }), \end{aligned}$$

(A.2)

and the $\tau$-matrices (Infeld-van-der-Waerden matrices) are $\tau ^\mu =\frac{1}{\sqrt{2}}\sigma ^\mu$ and $\bar{\tau }^\mu =\frac{1}{\sqrt{2}}\bar{\sigma }^\mu$. The normalization of the $\tau$-matrices is chosen such that no unnecessary powers of 2 are carried around in the algebraic relations,

$$\begin{aligned}&\mathrm {Tr}\big (\tau ^{\mu }\bar{\tau }^\nu \big ) =g^{\mu \nu }\, \ \Leftrightarrow \ \mathrm {Tr}\big (\bar{\tau }^\mu \bar{\tau }^\nu \big ) = \mathrm {Tr}\big (\tau ^\mu \tau ^\nu \big ) = \delta ^{\mu \nu }, \end{aligned}$$

(A.3)

$$\begin{aligned}&\tau ^{\mu ,\dot{\alpha }\beta }\tau _{\mu }^{\dot{\gamma }\eta } =\epsilon ^{\dot{\alpha }\dot{\gamma }}\epsilon ^{\beta \eta }, \quad \bar{\tau }^\mu _{\alpha \dot{\beta }}\bar{\tau }_{\mu ,\gamma \dot{\eta }} =\epsilon _{\alpha \gamma }\epsilon _{\dot{\beta }\dot{\eta }}, \nonumber \\&\tau _\mu ^{\dot{\alpha }\beta }\bar{\tau }^\mu _{\gamma \dot{\eta }} =\delta _{\gamma }^{\ \beta }\delta _{\ \dot{\eta }}^{\dot{\alpha }}, \end{aligned}$$

(A.4)

where $g^{\mu \nu }=\mathrm {diag}(1,-1,-1,-1)$ denotes the Minkowski metric and $\epsilon$ the Levi–Civita tensor defined in Eq. (2.2). Note that $\bar{\tau }^\mu$ has lower indices, with the first index undotted, while $\tau ^\mu$ has upper indices with the first index dotted.

Since we use the chiral basis, the momentum-space Dirac spinors divide into their left- and right-chiral parts which can be projected out using the projection operator $P_{R/L} = \frac{1}{2}(1\pm \gamma ^5)$

$$\begin{aligned} u^{{J_s}} = \begin{pmatrix} |u^{{J_s}}_L] \\ |u^{{J_s}}_R\rangle \end{pmatrix} \quad \text {and}\quad v^{{J_s}} = \begin{pmatrix} |v^{{J_s}}_L] \\ |v^{{J_s}}_R\rangle \end{pmatrix} \;.\quad \end{aligned}$$

(A.5)

Here, ${J_s}$ is the spin along axis $s^\mu$ (see Appendix A.2), and the L/R labels refer to particles which transform under the left- and right-chiral representations of the (restricted) Lorentz group. (Compared to Sect. 3.3 we have absorbed a factor $\sim \sqrt{\alpha } e^{\pm i \varphi }$ into the kets as required.)

1.2 A.2 Relativistic spin operator for massive spinors

The threevector spin operator $\Sigma ^i/2$ can be promoted to a fourvector operator $\Sigma ^\mu /2$ (see e.g. [42]) defined as⁶

$$\begin{aligned} \frac{1}{2}\Sigma ^\mu = -\frac{1}{4m}\epsilon ^{\mu \nu \lambda \omega }P_\nu \sigma _{\lambda \omega }, \end{aligned}$$

(A.6)

where $P_{\nu }$ is the momentum operator ($P_{\nu } = i\partial /\partial x^{\nu }$), $\epsilon ^{\mu \nu \lambda \omega }$ ($\epsilon ^{0123}\equiv 1 \Rightarrow \epsilon _{0123}= -1$) is the four-dimensional Levi-Civita tensor, and $\sigma ^{\mu \nu }$ is defined as

$$\begin{aligned} \sigma ^{\mu \nu } = \frac{i}{2}\left[ \gamma ^\mu ,\gamma ^\nu \right] . \end{aligned}$$

(A.7)

In the rest frame of the particle ($p^\mu \overset{\text {rest}}{=}(m,\mathbf{0} )$), Eq. (A.6) takes the form of the familiar spin operator

$$\begin{aligned} \frac{1}{2}\Sigma ^i&\overset{\text {rest}}{=}\frac{i}{4}\epsilon ^{ijk}\gamma ^j\gamma ^k = \frac{1}{2}\gamma ^5\gamma ^0\gamma ^i = \frac{1}{2} \begin{pmatrix} \sigma ^i &{} 0 \\ 0 &{} \sigma ^i \end{pmatrix}, \nonumber \\ \frac{1}{2}\Sigma ^0&\overset{\text {rest}}{=}0, \end{aligned}$$

(A.8)

which also shows that $\Sigma ^\mu p_\mu = 0$.

For massive particles, we measure the total spin J and its spin ${J_s}$ projected onto some axis $s^\mu$ which must equal (see e.g. [34, 42])

$$\begin{aligned} s^\mu \overset{\text {rest}}{=}(0,\hat{\mathbf{s }}), \end{aligned}$$

(A.9)

in the rest frame. From this frame, we also find the relations

$$\begin{aligned} \qquad s^2= -1, \quad s\cdot p= 0, \end{aligned}$$

(A.10)

and that for Dirac spinors, the spin projected onto $s^\mu$ is given by the operator

$$\begin{aligned} \mathcal {O}_s=-\frac{\Sigma ^\mu s_\mu }{2} = \frac{1}{4m}\epsilon ^{\mu \nu \lambda \omega }s_\mu P_\nu \sigma _{\lambda \omega }. \end{aligned}$$

(A.11)

To obtain the last form of $\mathcal {O}_s$ in Eq. (3.10) we use the identity

$$\begin{aligned} \frac{1}{2}\epsilon ^{\mu \nu \lambda \omega }\sigma _{\lambda \omega } = -i\gamma ^5\sigma ^{\mu \nu } = \gamma ^5 (\gamma ^\mu \gamma ^\nu - g^{\mu \nu }), \end{aligned}$$

(A.12)

to find

(A.13)

where we used that $s\cdot p= 0$. We act $P_\mu \equiv i\partial _\mu$ on the u and v spinors, then make use of the Dirac equation to replace the operator with m for any on-shell spinor.

Making this substitution in Eq. (A.13) gives Eq. (3.10), namely

$$\begin{aligned} \mathcal {O}_s= -\frac{\Sigma ^\mu s_\mu }{2} = \frac{1}{2}\gamma ^5s^\mu \gamma _\mu ~. \end{aligned}$$

(A.14)

Appendix B: Weyl spinors

Here we give some useful properties and explicit values of the Weyl spinors and their inner products.

1.1 B.1 Explicit representations of spinors and their inner products

A generic massless Weyl spinor of (real) momentum p can be expressed in terms of light-cone coordinates $p^{\pm } = p^0\pm p^3$, $p^{\perp } = p^1+ip^2$ and $p^{\perp ^*}=p^1-ip^2$ (see appendix A.2 of [1] for more details)

$$\begin{aligned} |p\rangle&= \frac{e^{-i\theta /2}}{\sqrt{|p^+|}} \begin{pmatrix} p^+\\ p^{\perp } \end{pmatrix}, \nonumber \\ |p]&=\mathrm {sgn}(p^0) \frac{e^{i\theta /2}}{\sqrt{|p^+|}} \begin{pmatrix} p^{\perp ^*}\\ -p^+\end{pmatrix}, \nonumber \\ \langle p|&= \frac{e^{-i\theta /2}}{\sqrt{|p^+|}} \Big (\,p^{\perp }\,,\,-p^+\,\Big ), \nonumber \\ [p|&=\mathrm {sgn}(p^0) \frac{e^{i\theta /2}}{\sqrt{|p^+|}} \Big (\,p^+\,,\,p^{\perp ^*}\,\Big ), \end{aligned}$$

(B.1)

where the phase $\theta$ is a little group phase which we set to 0 throughout the rest of the paper, and the $\mathrm {sgn}(p^0)$ term is required⁷ to consistently take $p \rightarrow -p$ in Eq. (2.8)

(B.2)

In the special frame $p^+ = p^\perp = 0$ a valid representation of the Weyl spinor is

$$\begin{aligned} |p\rangle&= \begin{pmatrix}0 \\ \sqrt{|p^-|}\end{pmatrix}, \quad&|p] =\mathrm {sgn}(p^0) \begin{pmatrix} \sqrt{|p^-|} \\ 0 \end{pmatrix}, \nonumber \\ \langle p|&= \Big (\,\sqrt{|p^-|}\,,\,0\,\Big ), \quad&[p| =\mathrm {sgn}(p^0) \Big (\,0\,,\,\sqrt{|p^-|}\,\Big ) , \end{aligned}$$

(B.3)

which affects Eqs. B.4 and B.9 below.

From Eq. (B.1) (with $\theta =0$) we obtain the explicit forms of the inner products

$$\begin{aligned} \langle i j \rangle&= \frac{1}{\sqrt{|p_i^+||p_j^+|}}\big (p_i^\perp p_j^+ - p_j^\perp p_i^+\big ), \nonumber \\ [i j]&= \frac{\mathrm {sgn}(p_i^0p_j^0)}{\sqrt{|p_i^+||p_j^+|}}\big (p_i^+ p_j^{\perp ^*} - p_j^+p_i^{\perp ^*}\big ), \end{aligned}$$

(B.4)

as well as the Hermitian conjugation relations

$$\begin{aligned} |p\rangle ^\dagger = \mathrm {sgn}(p^0)[p|, \quad |p]^\dagger = \mathrm {sgn}(p^0)\langle p|. \end{aligned}$$

(B.5)

Since Eq. (B.1) holds for any massless spinor, we can use it to represent both the spinors of momenta $p^\flat$ and q introduced in Sect. 3.2, or the forward and backward moving spinors of momenta $p_{f/b}$ introduced in Sect. 3.2.1 (for which the spinor wave functions are helicity eigenstates). For convenience, we will also give the $p_{f/b}$ spinors with $p^0>0$ from Eq. (3.5) in terms of $\hat{\mathbf{p }}= \mathbf{p} /|\mathbf{p} |$

$$\begin{aligned} |p_{f}\rangle&= \sqrt{\frac{\lambda _{f}}{2(1+\hat{p}^3)}} \begin{pmatrix}1+\hat{p}^3 \\ \hat{p}^{\perp }\end{pmatrix}, \nonumber \\ | p_{f}]&= \sqrt{\frac{\lambda _{f}}{2(1+\hat{p}^3)}} \begin{pmatrix}\hat{p}^{\perp ^*}{} 1+\hat{p}^3)\end{pmatrix}, \nonumber \\ |p_{b}\rangle&= \sqrt{\frac{\lambda _{b}}{2(1-\hat{p}^3)}} \begin{pmatrix}1-\hat{p}^3 \\ -\hat{p}^{\perp }\end{pmatrix}, \nonumber \\ |p_{b}]&= \sqrt{\frac{\lambda _{b}}{2(1-\hat{p}^3)}} \begin{pmatrix}-\hat{p}^{\perp ^*}{} 1-\hat{p}^3)\end{pmatrix}, \nonumber \\ \langle p_{f}|&= \sqrt{\frac{\lambda _{f}}{2(1+\hat{p}^3)}} \Big (\,\hat{p}^{\perp },\,-(1+\hat{p}^3)\,\Big ), \nonumber \\ [ p_{f}|&= \sqrt{\frac{\lambda _{f}}{2(1+\hat{p}^3)}} \Big (\,1+\hat{p}^3,\,\hat{p}^{\perp ^*}\,\Big ) \;, \nonumber \\ \langle p_{b}|&= \sqrt{\frac{\lambda _{b}}{2(1-\hat{p}^3)}} \Big (-\hat{p}^{\perp },\,-(1-\hat{p}^3)\,\Big ) , \nonumber \\ [p_{b}|&= \sqrt{\frac{\lambda _{b}}{2(1-\hat{p}^3)}} \Big (\,1-\hat{p}^3,\,-\hat{p}^{\perp ^*}\,\Big ). \end{aligned}$$

(B.6)

1.2 B.2 Useful identities

In addition to momentum conservation and judicious multiplication by 1 it is often useful to use the Schouten identity,⁸ which has a nice flow representation

(B.7)

and the relation for $s_{ij}$

(B.8)

to simplify the results of Feynman diagrams.

Since $\langle ij \rangle = \mathrm {sgn}(p_i^0p_j^0)[ ji]^*$, we can also express the inner product in terms of the invariant mass and a phase

$$\begin{aligned} \langle ij \rangle\equiv & {} e^{-i\varphi _{ij}} \sqrt{|s_{ij}|}, \quad [ ji] = \mathrm {sgn}(p_i^0p_j^0) e^{i\varphi _{ij}} \sqrt{|s_{ij}|},\nonumber \\ e^{-i\varphi _{ij}}= & {} \frac{p_i^\perp p_j^+ - p_j^\perp p_i^+}{\sqrt{|s_{ij}p_i^+p_j^+|}}, \end{aligned}$$

(B.9)

which we used in Eqs. (3.5), (3.13) and (3.17).

Appendix C: Tables with conventions and Feynman rules

We collect here the chirality-flow Feynman rules for the full (tree-level) Standard Model, and compare them to other spinor-helicity notations (Tables 1–5).

Table 1 “Rosetta stone” showing massive fixed-spin-axis fermions in several common notations. To translate the Dirac spinors to the helicity basis, replace $p^\flat \rightarrow p_f$, $q\rightarrow p_b$, and remove $\sqrt{\alpha }$. The phase $\varphi$ is defined in Eq. (3.12) in the general spin basis (see Sect. 3.3) or in Eq. (3.17) in the helicity basis (see Sect. 3.3.1). Massless spinors are found by setting $\alpha =0$ and replacing $p^\flat \rightarrow p$

Table 2 The QCD “Rosetta Stone” translating the chirality-flow notation to widely-used spinor-helicity notations. Here Z(2, 3, 4) denotes the set of cyclic permutations and S(2, 3, 4) the set of all permutations of the integers 2, 3, 4, and $V_3^{\mu _1\mu _2\mu _3} = (p_1-p_2)^{\mu _3}g^{\mu _1\mu _2} + (p_2-p_3)^{\mu _1}g^{\mu _2\mu _3} + (p_3-p_1)^{\mu _2}g^{\mu _3\mu _1}$. The external spinors and polarization vectors are trivially extended from Tables 1 and 3 respectively. For more information on the various forms of the four-gluon vertex, see Sect. 5.1 in [1]. The color factors are normalized such that $\mathrm {Tr}\big (t^at^b\big ) =\delta ^{ab}$ and $if^{abc}= \mathrm {Tr}\big (t^a[t^b,t^c]\big )$ (see Sect. 2 in [1] for details)

Table 3 Part one of the electroweak “Rosetta Stone” translating the chirality-flow notation to widely-used spinor-helicity notations. To translate the polarization vectors to the helicity basis, replace $p^\flat \rightarrow p_f$ and $q\rightarrow p_b$. Incoming polarization vectors of spin ${J_s}$ are equal to outgoing ones of spin $-{J_s}$. Massless polarization vectors are given by replacing $p^\flat \rightarrow p$, and $q \rightarrow r$ where r is an unphysical reference momentum. Due to lack of space, only the index and bra-ket forms of $\epsilon _0^\mu (p)$ corresponding to the left chirality-flow diagram are given. The external spinors are given in Table 1. Details about the polarization vectors, vertices, and propagators are given in Sects. 3.4, 4.1, and 4.2 respectively

Table 4 Part two of the electroweak “Rosetta Stone”, translating boson vertices from the chirality-flow notation to the standard notation. The coupling constants for every Standard Model process are found in Table 5. The external spinors and polarization vectors are given in Tables 1 and 3 respectively

Table 5 All coupling factors for electroweak interaction vertices. $T_f^3$ is the eigenvalue of the third isospin operator, $Q_f$ is the electric charge and $\theta _W$ is the Weinberg angle