Abstract
For magnetic fields larger than the characteristic scale linked to axion-electrodynamics, quantum vacuum fluctuations due to axion-like fields can dominate over those associated with the electron-positron fields. This conjecture is explored by investigating both the axion-modified photon capture by a strong magnetic field and the Coulomb potential of a static pointlike charge. We show that in magnetic fields characteristic of neutron stars \(\sim 10^{13}\)–\(10^{15}\;\mathrm{G}\), the capture of gamma photons prior to the production of a pair can prevent the existence of an electron-positron plasma, essential for explaining the pulsar radiation mechanism. This incompatibility is used to limit the axion parameter space. Our bounds improve existing outcomes in the region of mass \(m\sim 10^{-10}\)–\(10^{-5}\;{\mathrm{eV}}\). The effect of capture, known in QED as relating to gamma-quanta, is extended in axion electrodynamics to include X-ray photons with the result that a specially polarized part of the heat radiation from the surface is canalized along the magnetic field. Besides, we find that in the regime in which the dominance takes place, the running QED coupling depends on the field strength and the modified Coulomb potential is of Yukawa-type in the direction perpendicular to the magnetic field at distances much smaller than the axion Compton wavelength, while along the field it follows approximately the Coulomb law at any length scale. Despite the Coulomb singularity manifested in the latter case, we argue that the ground-state energy of a non-relativistic hydrogen atom placed in a strong magnetic field turns out to be bounded due to the nonrenormalizable feature of axion-electrodynamics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Upon quantization, the axial chiral \({\mathrm {U(1)_{A}}}\)-invariance is exonerated of representing a quantum symmetry in the theory of the strong interactions, namely Quantum Chromodynamics (QCD). The occurrence of an anomalous contribution in the QCD Lagrangian – linked to a nontrivial topological structure of the QCD vacuum – prevents the conservation of the axial current by dispossessing the theory from the Charge-Parity (CP)-symmetry. However – with astonishing experimental accuracy – QCD manifests itself as a CP-preserving framework and the anomalous “\(\theta -\)term” seems to be fully irrelevant. This famous controversy – known as the strong CP-problem – is reconciled through the Peccei-Quinn mechanism [1], where a global \({\mathrm {U(1)_{PQ}}}\)-symmetry is promoted to compensate the CP-violating term once it is broken spontaneously. While the described solution is perhaps the most appealing among other possible ideas, it did not come free of a new challenge for the contemporary physics. This is because the associated Nambu-Goldstone boson, i.e. the QCD axion, emerged as a plausible particle candidate [2, 3]. Although soon after its introduction this hypothetical degree of freedom was ruled out [4, 5], it certainly paved the way for more general class of axions embedded in the DFSZ and KSVZ axion models [6,7,8,9], this way opening a new front linked to their detection. Experimental endeavours toward this task are nowadays being carried out worldwide, based – predominantly – on the axion-diphoton coupling that is present in many effective Lagrangian densities such as axion-electrodynamics (AED) [10]; a framework whose phenomenology is subject to an intense scrutiny owing to its relevance, not just in particle physics, but also in research branches sharing its main features [11,12,13].
At lab scales, direct searches of Axion-Like Particles (ALPs) rely on plausible traces of axion-photon oscillations mediated by a constant magnetic field. Descriptions of the most popular detection methods can be found in Refs. [14,15,16,17,18,19]. The realization of this process could be relevant, indeed, in polarimetric arrangements [20,21,22,23,24]Footnote 1 and in Light-Shining-through-a-Wall setups [31,32,33,34,35,36,37,38]. Although the outcomes of these ongoing experiments have not verified the existence of the QCD axion yet, valuable bounds in its parameter space have been inferred instead, as well as in ALPs that are predicted in string theory [39,40,41,42] and in various Standard Model extensions which attempt to incorporate the dark matter of our Universe [43,44,45,46,47,48,49]. Constraints on axions – or, more general, ALPs – are also deduced from their potential astro-cosmological consequences which are not reflected accordingly by the current observational data of our universe [50,51,52]. A basic assumption underlying this line of argument is that the interplay between the axionic degrees of freedom and the well established Standard Model sector – i.e., photons in first place – is extremely feeble. As a consequence, ALPs produced copiously in the core of stars via the Primakoff effect might escape from there almost freely, constituting a leak of energy that accelerates the cooling of the star and, thus, shortens its lifetime. Therefore, the number of red giants in the helium-burning phase in globular clusters should diminish considerably. That this fact does not take place – at least not significantly – constraints the axion-diphoton coupling g to lie below \(g\lesssim 10^{-10}\ {\mathrm {GeV^{-1}}}\) for ALP masses m below the \({\mathrm {keV}}\) scale [53,54,55].
Precisely on the surface of stellar objects identified as neutron stars [56,57,58,59] and magnetars, magnetic fields as large as \(B\sim {\mathcal {O}}(10^{13}\)–\(10^{15})\ {\mathrm {G}}\) are predicted to exist. As these strengths are bigger than the characteristic scale \(B_{0}=4.42\times 10^{13}\, {\mathrm {G}}\) of Quantum Electrodynamics (QED) [60, 62,63,64], such astrophysical scenarios are propitious for the realization of a variety of yet unobserved quantum processes, which are central in our current understanding on the nature and origin of the pulsar radiation. Notable among them are, the photon capture effect by the magnetic field owing to the resonant behavior [65] of the vacuum polarization in QED [66,67,68]Footnote 2, the one-photon production of electron-positron pairs and the photon splitting effect [72,73,74]. Clearly, the strong-field environments provided by these compact objects can also be favorable for an ALPs phenomenology – as they are in QED – contrary to what is predicted relying on the weak coupling treatment. This occurs, because the aforementioned field strengths could compensate for the weakness of the coupling and significantly stimulate quantum vacuum fluctuations of axion-like fields. This paper is devoted to analyzing this possibility in the ALPs phenomenology. Theoretically, the problems linked to field strengths overpassing the corresponding characteristic scale of AED have not yet attracted adequate attention, save Refs. [75, 76], where the virtual-fermion-induced correction to the ALP mass in an external magnetic field of arbitrary strength was determined via the corresponding self-energy operator. This, however, involves a coupling constant which differs from the one mediating the interaction between an ALP and two photons.
In this paper we provide a further step toward the understanding of this subject by studying the characteristic magnetic field regime resulting from AED for which the polarization operator is responsible. We shall demonstrate that for sufficiently large magnetic fields, the axion-like fields lead to both stronger refraction and screening effects as compared with the predictions of QED [at least when we are kinematically far from the vacuum polarization resonance]. Hence, in the first part of the paper we reveal how virtual ALPs might be responsible for the capture of \(\gamma \)-quanta by the magnetic field lines in the magnetosphere of neutron stars and magnetars before the analogous effect starts acting in QED. We argue that such a phenomenon can prevent the photo-production of an electron-positron pair, and thus, the main channel responsible for the generation of this type of plasma. The suppresion of this production mechanism is incompatible with the existence of the plasma itself, which is understood nowadays as an essential part in the formation of the pulsar radiation. As a consequence of this inconsistency, new bounds on the parameter space of ALPs are inferred by taking as reference the magnetic field associated with two pulsars: \({\mathrm{SGR}}\) 1806-20 [57, 58, 77,78,79] and \({\mathrm{RX}}\) J1856.5-3754 [80,81,82,83,84,85,86]. We shall mention at this point that considerable attention is currently paid to the possibility of probing ALPs via observational effects induced by them in neutron star magnetospheres [87,88,89,90].
The second part of our investigation is oriented to study the screening that virtual ALPs induce on the running QED coupling and so on the Coulomb potential of a static pointlike charge, when placed in a strong magnetic field. Contrary to studies developed within QED [91,92,93,94], our investigation reveals that along the field direction, and within the regime where the associated ALPs phenomenology could dominate over the corresponding QED effects, the screening due to ALPs is very weak, no matter how strong the field strength is (within the limits imposed on it by the unitarity). Hence, the modified potential we obtain follows the Coulomb law approximately. As a consequence, the existence of certain ALPs at extremely large magnetic fields might lead to a reestablishment of the formula for the unscreened ground-state energy of a nonrelativistic electron in the hydrogen atom [95]. The longstanding problem linked to this formula, i.e. the fact that the energy spectrum is unbounded from below when the magnetic field grows unlimitedly, was solved when the screening induced by the vacuum polarization of QED was incorporated and the virtuality of ALPs was ignored [91, 92, 96,97,98,99]. We will see that in AED, by requiring the unitarity of the scattering matrix, a limitation arises for the largest treatable magnetic field, which may cause dramatic changes in judgements about the limiting ground-state energy. Also we show that, in a vicinity of the point-like charge perpendicular to the magnetic field, the Coulomb potential is of Yukawa type. This feature allows for certain energy regimes in which the electromagnetic interaction becomes very weak.
The investigation carried out here relies on a quantized approach of AED developed previously in Ref. [111]. In Sect. 2.1 the leading order contributions to the polarization tensor in the presence of an external electromagnetic field and a homogeneous axion background are established. Later on, in Sect. 2.2 the analisis is restricted to the case in which the latter is absent and the electromagnetic background is a constant magnetic field. Parallely, an approximation-independent eigenmode expansion of the polarization tensor is given in terms of its eigenvectors and eigenvalues, valid in a magnetic field both in QED and AED. We determine the polarization tensor with an accuracy of the second order in the axion-diphoton coupling with the magnetic field. Although the neutral nature of quantum vacuum fluctuations due to axion-like fields contrasts with those associated with the charged Dirac ones, the outcomes resulting from the axion-photon theory pretty much resemble those obtained in QED. This similarity is stressed in Sect. 2.2, where various asymptotes of the eigenvalues of the polarization tensor are established in parallel. Also in that section the plausible regions of parameters of undiscarded ALPs, where the contribution of the latter could dominate over the QED effects, are established.
In Sect. 3.1 we define the mass shell by solving the dispersion equation for a photon of the extraordinary polarization mode interacting with an ALP in the presence of a magnetic field to find two branches of the spectrum: the massless one and the massive one for the axion-like particle. Parallely, we find that the flattening of the massless branch near small values of the transverse momentum results in vanishing of the group velocity component across the magnetic field. This phenomenon forms a basis for the photon capture considered in the subsequent sections 3.2 and 3.3. In the former we recall the effect of \(\gamma \)-quantum capture in QED and argue that in AED the same effect might destroy the accepted mechanism of electron-positron plasma production in pulsars and hence of their radio-emission, if it was not eliminated by the already existing restrictions on the ALP mass and coupling constant. In Sect. 3.3 we deal with the capture of soft photons that occurs in AED. We consider the refraction of radiation, when it leaves the region of strong field, and assure ourselves that the heat radiation from the pulsar surface belonging to the extraordinary mode is canalized parallel to the magnetic field, and it may leave it, whereas the radiation polarized in the orthogonal direction is not canalized and is subject to the angular distribution determined by the refraction law. We believe that the effect that the radiation of a certain polarization condenses close to the magnetic field direction, while the orthogonally polarized radiation is distributed over the angle, might become a valuable criterion for probing ALPs among the plausible signatures induced in the thermal spectra of neutron stars [86, 100].
Finally, in Sect. 4.1 we determine the photon propagator in order to use it subsequently in Sect. 4.2 in the establishment of the running QED coupling. We show that, in the regime where AED dominates over QED, the screening caused by the magnetized vacuum can screen a point-like charge to zero when the magnetic field grows unlimitely at a fixed momentum. Properties of the electromagnetic interaction in this axion-dominating scenario are further inferred via the axion-modified Coulomb potential. Its anisotropization, short-ranging and dimensional reduction are revealed manifestly through numerical evaluations. We show, in particular, that for field strengths larger than the characteristic scale associated with this effective theory, the modified potential is short-ranged in the direction perpendicular to the magnetic field while it follows approximately the behavior of Coulomb’s law along \(\pmb {B}\). Section 4.3 is devoted to support analytically these results. There, asymptotic expressions for the modified Coulomb potential in the limits of strong magnetic fields are determined. In addition, the imprints that virtual ALPs leave within the ground state energy of a nonrelativistic electron in a hydrogen atom are evaluated. Our conclusions are exposed finally in Sect. 5, whereas some important details of our calculations are presented in Appendices A and B.
2 Axion-electrodynamics
2.1 General considerations in a constant magnetic field and a homogeneous axion background
To leading order in the axion-diphoton coupling g, the Lagrangian density describing AED combines the standard Maxwell Lagrangian with the free Lagrangian density of the pseudoscalar field \(\phi (x)\) and with the scalar interaction Lagrangian density involving the dual of the electromagnetic field tensor \(\tilde{f}^{\mu \nu }=\frac{1}{2}\epsilon ^{\mu \nu \alpha \beta }f_{\alpha \beta }\) where \(f_{\mu \nu }=\partial _{\mu }a_{\nu }-\partial _{\nu } a_{\mu }\) and \(\epsilon ^{0123}=1\). Explicitly,

Hereafter, we use a metric with signature  , and Heaviside−Lorentz units with the speed of light and the Planck constant set to unity \(c=\hbar =1\). To abbreviate, the following notations have also been used: \(f^{2}\equiv f_{\mu \nu }f^{\mu \nu }\), \(\tilde{f}f\equiv \tilde{f}_{\mu \nu }f^{\mu \nu }\), \((\partial \phi )^{2}\equiv (\partial _{\mu }\phi )(\partial ^{\mu }\phi )\). Here m refers to the ALP mass, whereas g denotes its coupling strength to two photons. As the interacting term has a mass dimension \(-5\), this framework belongs to the class of perturbatively nonrenormalizable theories. In this connection,
, and Heaviside−Lorentz units with the speed of light and the Planck constant set to unity \(c=\hbar =1\). To abbreviate, the following notations have also been used: \(f^{2}\equiv f_{\mu \nu }f^{\mu \nu }\), \(\tilde{f}f\equiv \tilde{f}_{\mu \nu }f^{\mu \nu }\), \((\partial \phi )^{2}\equiv (\partial _{\mu }\phi )(\partial ^{\mu }\phi )\). Here m refers to the ALP mass, whereas g denotes its coupling strength to two photons. As the interacting term has a mass dimension \(-5\), this framework belongs to the class of perturbatively nonrenormalizable theories. In this connection,  can be regarded as a Wilsonian effective Lagrangian parametrizing the leading order contribution of its ultraviolet completion, i.e. a renormalizable theory linked to physics beyond the Standard Model which might contain new heavy particles at the energy scale \(\varLambda _{{\mathrm {UV}}}\sim \frac{1}{g}\). If this hypothetical theory satisfies fundamental principles such as Lorentz and gauge invariance, and preserves – in addition – the unitarity, quantum processes due to fluctuations of modes of the fields in
can be regarded as a Wilsonian effective Lagrangian parametrizing the leading order contribution of its ultraviolet completion, i.e. a renormalizable theory linked to physics beyond the Standard Model which might contain new heavy particles at the energy scale \(\varLambda _{{\mathrm {UV}}}\sim \frac{1}{g}\). If this hypothetical theory satisfies fundamental principles such as Lorentz and gauge invariance, and preserves – in addition – the unitarity, quantum processes due to fluctuations of modes of the fields in  , taking place at energies substantially below \(\varLambda _{{\mathrm {UV}}}\), should also be described in a unitary way.
, taking place at energies substantially below \(\varLambda _{{\mathrm {UV}}}\), should also be described in a unitary way.
Diagrammatic representations of three contributions to the vacuum polarization tensor in the presence of both an external electromagnetic background (vertical wavy lines in the upper graph) and a cold dark axion background (vertical dashed line in the intermediate graph). In contrast to the latter, the former is mediated by quantum fluctuations of pseudoscalar fields. Here, the horizontal dashed line represents the ALP propagator \(\varDelta _{{\mathrm {F}}}(x,\tilde{x})\), whereas the horizontal wavy lines must be understood as amputated photon legs. The lowest diagram is the contribution resulting from the original axion-diphoton vertex
In the following we evaluate consequences of the vacuum polarization tensor in AED under the influence of a constant external field \(\mathscr {F}_{\mu \nu }=\partial _{\mu }\mathscr {A}_{\nu }(x)-\partial _{\nu }\mathscr {A}_{\mu }(x)\), the Lorentz invariants of which satisfy the conditions \(\mathfrak {F}=\frac{1}{4}\mathscr {F}_{\mu \nu }\mathscr {F}^{\mu \nu }>0\) and \(\mathfrak {G}=\frac{1}{4}\mathscr {F}_{\mu \nu }\tilde{\mathscr {F}}^{\mu \nu }=0\) simultaneously. This kind of field configuration is called magnetic-like, because an inertial reference frame exists, where it is purely magnetic, with no admixture of electric field. Hence, we replace \(f_{\mu \nu }\) in Eq. (1) by \(f_{\mu \nu }+\mathscr {F}_{\mu \nu }\), and due to this operation, the Lagrangian density  acquires an additional interaction
acquires an additional interaction  , which is responsible for the appearance of the upper Feynman diagram shown in Fig. 1. Since cold relic axions – resulting from vacuum misalignment in the early universe [45,46,47, 55] – are a viable candidate for dark matter, quantum fluctuations of the axion-like field \(\phi (x)\) might occur not on an empty vacuum but rather over a background field which is supposed to fit the problem of the missing mass of the universe. This coherent classical field is identified as a solution of the equation of motion in the presence of the magnetic field. Ignoring the effect due to the local virial dark matter velocity \(v\sim 10^{-3}\), it can be approximated by a homogeneous sinusoidally time-varying field:Footnote 3
, which is responsible for the appearance of the upper Feynman diagram shown in Fig. 1. Since cold relic axions – resulting from vacuum misalignment in the early universe [45,46,47, 55] – are a viable candidate for dark matter, quantum fluctuations of the axion-like field \(\phi (x)\) might occur not on an empty vacuum but rather over a background field which is supposed to fit the problem of the missing mass of the universe. This coherent classical field is identified as a solution of the equation of motion in the presence of the magnetic field. Ignoring the effect due to the local virial dark matter velocity \(v\sim 10^{-3}\), it can be approximated by a homogeneous sinusoidally time-varying field:Footnote 3
with \(\varrho _{{\mathrm {DM}}}\approx 0.3\;{\mathrm{GeV/cm}}^3\) referring to the local dark matter density [102, 103], \(\varOmega \equiv \sqrt{1+g^2B^2/m^2}\) and \(\tau \equiv m t\). However, the existence of Eq. (2) comes accompanied with a time-dependent electric field parallel to \(\pmb {B}\)
As a consequence, the propagation of photons actually takes place on an electromagnetic field background whose invariant \(\mathfrak {G}(t)=\pmb {E}\cdot \pmb {B}=\frac{gB^2\sqrt{2\varrho _{{\mathrm {DM}}}}}{m\varOmega }\cos (\varOmega \tau )\) does not vanish in general [104]. Clearly, the inclusion of \(\varPhi (t)\) in  is carried out via the replacement \(\phi \rightarrow \phi +\varPhi (t)\). This operation leads to the emergence of an interaction vertex which is exhibited in the lower panel of Fig. 1. At this point we find convenient to remark that the inclusion of the axion background is only meaningful if a certain ALP is identified as the main constituent of the dark matter. ALPs which are not related to the latter scenario are by themselves well motivated particle candidates and, indeed, most of the so-called direct searches are oriented to look for ALPs belonging to this last group. For details we refer the reader to Refs. [14,15,16,17,18].
is carried out via the replacement \(\phi \rightarrow \phi +\varPhi (t)\). This operation leads to the emergence of an interaction vertex which is exhibited in the lower panel of Fig. 1. At this point we find convenient to remark that the inclusion of the axion background is only meaningful if a certain ALP is identified as the main constituent of the dark matter. ALPs which are not related to the latter scenario are by themselves well motivated particle candidates and, indeed, most of the so-called direct searches are oriented to look for ALPs belonging to this last group. For details we refer the reader to Refs. [14,15,16,17,18].
As the graphs mentioned so far drive the dispersive and electrostatic effects in AED, it turns out to be convenient to have a theoretical formulation in which its analytical expression appears explicitly. To this end, we rewrite the effective action of the theory  in the following form:
in the following form:

Notice that the last term in the second line of this expression is responsible for the vertex involved in the one-loop diagram [lowest graph depicted in Fig. 1]. The calculation of this Feynman diagram was developed in Ref. [111], and unless necessary, its contribution will be ignored from now on. To bring the theory into a tractable form, the pseudoscalar ALP field \(\phi (x)\) is integrated out from the generating functional of the photon Green’s functions
where \(j\equiv j^\mu (x)\) is the external source and the term proportional to \(\zeta ^{-1}\) guarantees a covariant quantization. The effective action that results from this functional integration is

Here \(\varDelta _{{\mathrm {F}}}(x,\tilde{x})=\int \frac{d^4p}{(2\pi )^4}\frac{i e^{-ip(x-\tilde{x})}}{p^2-m^2+i0}\) stands for the ALP propagator with the \(i0-\)prescription allowing to elude the pole at \(p^2=m^2\). The source term contained within \(\varGamma [a]\), i.e.  , depends upon the strong magnetic field and the homogeneous time-dependent axion dark matter background
, depends upon the strong magnetic field and the homogeneous time-dependent axion dark matter background
The time dependence of this four-pseudovector field leads to a violation of the Lotentz-invariance, in addition to the one induced by the background magnetic field. Besides, the bilinear term in the expression above defines the inverse photon Green function,

where \(\square =\partial ^{2}/\partial t^{2}-\nabla ^{2}\) is the d’Alembert operator and the leading-order term of the polarization tensor \(\varPi _{\mu \nu }(x,\tilde{x})\) combines the two contributions represented in Fig. 1:
While the first line in the expression above is a symmetric nonlocal tensor depending quadratically on the external electromagnetic field, the term contained in the second line is antisymmetric translation-non-invariant and local, depending linearly on \(\eta _{\mu }(t)\). The presence of this contribution within the polarization tensor resembles the Chern-Simons term found in the context of the standard model plasma [105], with the particularity that \(\eta _\alpha \) plays the role of the axial vector responsible for the generation of long-range magnetic fields in the ground state. Its occurrence induces properties on the quantum vacuum akin to a medium in which – in addition to the breaking of the Lorentz and time-translational symmetries – the parity invariance is no longer preserved. It is worth pointing out that the propagation of electromagnetic waves in parity violating scenarios has been studied previously [see for instance Refs. [106,107,108,109]].
In contrast to Eq. (7), the strongest nonlocal interacting term – second line in Eq. (6) – depends linearly on the external background and quadratically on small-amplitude electromagnetic waves. This feature guarantees that, for very strong magnetic fields, a controlled perturbative expansion in the coupling \(g^2\) can be carried out. Consequently, corrections to \(\varPi _{\mu \nu }(x,\tilde{x})\) will always remain smaller as compared to the expression above, independently of how strong the external field is [for details see Appendix A]. Hence, Eq. (8) should be understood as the starting point of further considerations. Observe that the treatment followed so far provides the following equations of motion for the small-amplitude electromagnetic wave [\(\partial a =0\)]:

We anticipate that this dispersion equation is essential to establish the capture effect in AED (see Sect. 3).
At this point it is worth mentioning that when both \(\eta _\alpha (t)\) and \(E_\parallel (t)\) vary slowly, the problem under consideration absorbs some features linked to QED embedded into a combination of constant magnetic \(\mathbf {B}\) and electric \(\mathbf {E}\) fields studied earlier in the works published under the participation of one of us [see [113,114,115]]. However, in order to facilitate the understanding the effect of photon capture, we shall refer hereafter to the case in which ALPs and dark matter are unrelated quantities. An analysis including both the effect of the cold axion background and the external magnetic field is beyond the scope of this manuscript. Nevertheless, the reader interested in this subject may find attractive the predictions reported in Ref. [110], where – contrary to our case – the magnetic field has been taken \(B\ll m/g\).
2.2 Polarization tensor, eigenvalues and dominance over QED counterpart
When the external field is a constant magnetic-like background characterized by \(\mathscr {A}^{\mu }(x)=-\frac{1}{2}\mathscr {F}_{\ \,\,\nu }^{\mu }x^{\nu }\) and the invariants \(\mathfrak {F}=\frac{1}{2}\pmb {B}^{2}\), \(\mathfrak {G}=0\), i.e. for ALPs which do not represent the main constituent of dark matter, the Fourier transform of the polarization tensor can be written in the following form  . Because of the Dirac delta \(\delta ^{4}(q_{1}-q_{2})\), the tensorial portion
. Because of the Dirac delta \(\delta ^{4}(q_{1}-q_{2})\), the tensorial portion  does not depend on which choice \(q=q_1\) or \(q=q_2\) is taken. Besides, it turns out to be symmetric
does not depend on which choice \(q=q_1\) or \(q=q_2\) is taken. Besides, it turns out to be symmetric  , transverse
, transverse  and can be diagonalized in a similar way as it occurs with the vacuum polarization tensor established for QED with magnetic field [114,115,116]:Footnote 4
and can be diagonalized in a similar way as it occurs with the vacuum polarization tensor established for QED with magnetic field [114,115,116]:Footnote 4

The scalar eigenvalues \(\varkappa _{j}\) in the approximation considered are
where the form factor linked to the one-loop correction satisfies \(\pi (q^2) \ll 1\) provided \(q^{2}\) is not exponentially large. where \(\pi (q^2)\sim g^2 m^2\ll 1\) is the form factor linked to the one-loop correction [lowest graph in Fig. 1]. As we are interested in the strong field regime \(B\gg m/g\), the contribution due to the latter can be safely ignored. Note that the external field and hence the anisotropy is introduced through the interaction with an ALP. In the special Lorentz frame, where the external field is purely magnetic and directed along the axis denoted as \(\parallel \), the Lorentz scalar \(q\tilde{\mathscr {F}}^{2}q/(2\mathfrak {F})\) becomes \(q_{0}^{2}-q_{\parallel }^{2}\) where the photon energy is \(q_{0}\) and the momentum component along the magnetic field is \(\pmb {q}_{\parallel }\). There is also an extra Lorentz scalar \(q\mathscr {F}^{2}q/(2\mathfrak {F})=q_{\perp }^{2}\), with \(\pmb {q}_{\perp }\) denoting the projection of the momentum \(\pmb {q}\) onto the plane perpendicular to \(\pmb {B}\), so that \(2\mathfrak {F}q^{2}=q\tilde{\mathscr {F}}^{2}q-q\mathscr {F}^{2}q\). At this point it is worth remarking that the set of eigenvectors \(\flat _{j}^{\mu }\) with \(j=1,2,3\) is built from first principles, independently of any approximation used in the calculations [114, 115]. Explicitly,
The eigenvectors contained in this decomposition are mutually orthogonal \(\flat _{j\mu }\flat _{\ell }^{\mu }=-\delta _{j\ell }\flat ^2_\ell \) and transverse \(q_{\mu }\flat _{j}^{\mu }=0\) with \(j=1,2,3\). Besides, they satisfy the completeness relation  .
.
When AED is embedded in the QED action, the eigenvalues of the polarization tensor [see Eq. (11)] add to the corresponding eigenvalues of the QED polarization tensor. In this subsection we exploit this property to establish regions of ALPs parameters for which a dominance over the QED effects could take place. This seems to be particularly accessible because the nontrivial eigenvalue of the vacuum polarization tensor, i.e. \(\varkappa _2\) [see Eq. (11)] exhibits a quadratic growth in the external field while the corresponding eigenvalue in QED grows linearly [118,119,120,121] instead [\(b\gg 1\)]:
Here \(\alpha =1/137\) denotes the fine structure constant, \(b=B/B_0\) and \(B_0=m_e^2/e\approx 4.42\times 10^{13}\, {\mathrm{G}}\) the characteristic QED scale. In this context, \(m_e\) and e refer to the electron mass and the absolute value of its charge. It is worth mentioning that the application of these asymptotes requires \(q_\perp ^2\ll m_e^2 b\).
In order to establish undiscarded ALPs parameters which might lead to strong refraction as well as to a more pronounced screening property than the one predicted from QED, we first consider the situation in which \(q_0^{2}-q_\parallel ^2\ll {{\mathrm {min}}}\{m^{2},m_e^2\}\) and \(q_\perp ^{2}\ll {{\mathrm {min}}}\{m^{2},m_e^2b\}\). In this case the nontrivial eigenvalue of the polarization tensor [see Eq. (11)] is real:
and a direct comparison with the infrared behavior of \(\varkappa _2^{\mathrm{QED}}\) [first line in Eq. (13)] can be established. Here, we have introduced the parameter \(\mathfrak {b}=B/B_c\) with \(B_c=m/g\) denoting the characteristic field scale associated with AED. We will see very shortly that this scale plays in AED the role that \(B_0\) does in QED, in the sense that for magnetic field strengths larger than it [\(B\gg B_c\)], the effects induced by the vacuum polarization mediated by ALPs are expected to become much more pronounced than in the contrary situation [\(B\ll B_c\)].
Now, as the asymptotic expression given in Eq. (14) has the same momentum dependence as its QED counterpart [first line in Eq. (13)], one can establish a region of dominance of AED over QED directly on the parameter space of ALPs. Indeed, by demanding that Eq. (14) exceeds the corresponding QED expression we find \(\mathfrak {b}^2> \alpha b/(3\pi )\). This condition leads to the relation
To evaluate the consequences of this inequality we shall refer to various existing estimates of the ALP parameters g and m. Let us star with considering the best laboratory limit obtained by the OSCAR collaboration: \(g<4\times 10^{-8}\, {\mathrm{GeV}}^{-1}\) for \(m\lesssim {\mathrm{100}}\, \upmu \)eV [38]. For the boundary values in this range, the characteristic magnetic field \(B_c\approx 1.2\times 10^{14}\ {\mathrm{G}}\) is a little above the value of characteristic magnetic field in QED, \(B_{0}=4.4\times 10^{13}\;{\mathrm{G}}\). The latter is comparable with the magnetic fields that might exist in the magnetosphere of neutron stars and magnetars. For a magnetic field exceeding this characteristic scale by two orders of magnitude – which could be realized at the surface of cosmological gamma-ray bursters if they are rotation-powered neutron stars [126,127,128] – we obtain that \(\mathfrak {b}^2\sim 10^4\) is four orders of magnitude larger than \(\alpha b/(3\pi )\sim 1\). Under such a circumstance the vacuum polarization linked to virtual ALPs would prevail over the one associated with virtual electron-positron pairs. We remark that much more stringent bounds – resulting from the nonobservation of astro-cosmological consequence linked to ALPs – are available [see Fig. 3]. For instance, the modified solar sound-speed profile can be monitored by helioseismology, providing a conservative upper limit: \(g<5\times 10^{-10}\;{\mathrm {GeV}}^{-1}\) for \(m\sim (10^{-5}\)–\(10^{-3})\; {{\mathrm {eV}}}\) [55]. With these estimates the characteristic value \(B_{c}\sim (10^{15}\)–\(10^{17})\;{{\mathrm {G}}}\) remains within the limits admitted in the core of neutron stars \(\lesssim 10^{18}\; {{\mathrm {G}}}\),Footnote 5 and the dominance of AED over QED could also take place. To gain a more extended idea, we have inserted in Fig. 3 a dashed black line which results when Eq. (15) is evaluated at \(B=10^{13}\; {\mathrm{G}}\). This line divides the depicted parameter space of ALPs into two zones. Dominance of AED over QED might occur for those parameter combinations lying to the left of the line. For the chosen field strength, there is not region left in which the dominance could occur. However, we remark that the light-red region crossed by the dashed curve is a results of the present investigation [see details in Sect. 3.2].
Next, let us consider in Eq. (11) the situation in which \({{\mathrm {max}}}\{m^{2},m_e^2\} \ll q_0^{2}-q_\parallel ^2\ll m_e^2 b\) and \(q_\perp ^{2}\ll {{\mathrm {min}}}\{m^{2},m_e^2b\}\). Under such restrictions the nontrivial eigenvalue [see Eq. (11)] is also real:
and can be compared with the corresponding QED expression given in the second line in Eq. (13). Hence, the vacuum polarization of AED would dominate over the QED contribution if \(m\mathfrak {b}\gg (2\alpha b/\pi )^{1/2} m_e\) corresponding to \(g\gg m_e [2\alpha /(B B_0)]^{1/2}\). Observe that, if the largest magnetic field admitted in neutron stars and magnetars is \(\lesssim 10^{18}\; {{\mathrm {G}}}\), the previous condition translates into \(g\gg 0.47\;{\mathrm{GeV}}^{-1}\). We find opportune to emphasize that this value is out of the region exhibited in Fig. 3, and so discarded for any ALP mass m embedded within the interval \((10^{-8}\)–\(10^{9})\;{\mathrm{eV}}\). Therefore, in the energy regime analyzed above no dominance of AED over QED occurs for \(B\lesssim 10^{18}\; {{\mathrm {G}}}\). However, for a magnetic field \(B\sim 10^{22}\, {\mathrm{G}}\) the dominance could take place if \(g\gg 10^{-3}\, {\mathrm{GeV}}^{-1}\). For ALPs masses \(m< 10 \, {\mathrm{MeV}}\), values of g overpassing the previous limitation have been ruled out [see Fig. 3]. A small window \(10^{-2}\ {{\mathrm {GeV}}}<m<1\, {\mathrm{GeV}}\) with \(g<10^{-2} \, {\mathrm{GeV}}^{-1}\) remains for which \( B_c\sim (10^{19}\)–\(10^{21})\; {{\mathrm {G}}}\). While fields of this order of magnitude are not within the reach of neutron stars and magnetars, it is likely that they have existed right after the electroweak phase transition [122, 123].
We want to conclude this section indicating that the regions of dominance found here have to be considered as exploratory. This is because, in an axion-dominating regime the fine- structure constant used so far could undergo a substantial screening. Indeed, a more elaborate procedure will require to replace \(\alpha \) by the value of the running QED coupling \(\alpha _{{{\mathrm {scr}}}}(\pmb {q})\) which depends upon the magnetic field strength and the typical momentum transfer of the physical scenario. This problem is further investigated in Sect. 4.2.
3 Anisotropy in refraction and capture of photons in a superstrong magnetic field
3.1 Dispersion laws and group velocities
Although resulting from different nature, the singularity exhibited in the second eigenvalue at \(q^2 = m^2\) [see Eq. (13)] somewhat resembles the known situation in QED, where there appears an inverse square root singularity in \(\varkappa ^{{\mathrm {QED}}}_{2}\) at the border to the continuum of free electron and positron states produced by a single photon: the cyclotronic resonance of the vacuum [65, 116], or the pole where the electron and positron are bound to form a positronium atom [69,70,71]. The genuine dispersion relations associated with the mode-2 are neither \(q_{0}=\vert \pmb {q}\vert \) nor \(q_{0}=\sqrt{\pmb {q}^{2}+m^{2}}\) but rather
Observe that the dispersion law labeled with a negative sign describes a massless particle as \(q_{0-}\) vanishes when both components \(q_{\perp }\) and \(q_\parallel \) vanish. Conversely, the dispersion relation \(q_{0+}\) corresponds to a massive branch because \(\lim _{q_{\parallel ,\perp }\rightarrow 0}q_{0+}^{2}=m_{*}^{2}\) with \(m_{*}=m\sqrt{1+\mathfrak {b}^{2}}\) the effective mass, which reduces to the ALP mass m only when the external field is zero. Therefore, a small-amplitude electromagnetic wave characterized by the second propagation mode is actually a state in which massive and massless particles coexist. Both branches of the dispersion law [see Eq. (17)] are depicted in Fig. 2 for various values of the \(\mathfrak {b}\) parameter. As \(\mathfrak {b}\) grows, the massless dispersion curves tend to stick to the horizontal axis. This behavior can be understood from Eq. (17) when the case \(q_\perp \ll m_*\) is considered. To obtain the corresponding asymptotic formula one has to take into account that, for any value of \(\mathfrak {b}\), the factor \(4\mathfrak {b}^2/(1+\mathfrak {b}^2)\leqslant 4\). Hence, if \(q_\perp \ll m_*/2\), the second term within the squared root is very small. Consequently,
This result describes the trend that \(q_{0-}\) exhibits in Fig. 2 when the magnetic field grows gradually and applies whenever \(m_*\gg q_\perp \). Hence, the pattern in this figure obtained is to be interpreted in such a way that an ALP and mode-2 photon interact in the magnetic field to produce the spectrum of two disconnected branches: one massless and one massive. The massless branch may be referred to as belonging to a photon modified by its interaction with an ALP, while the massive branch corresponds to an axion-like particle modified by its interaction with the mode-2 photon. No mixed state between the axion-like branch and the photon is formed. Here we encounter a vast difference with QED in this type of background, where the free photon dispersion curve quasi-intersects with the dispersion curve of an electron-positron pair – mutually free or bound into a positronium atom – before the interaction between the photon and the pair is taken into account. This quasi-intersection results in forming the photon-pair mixed state, the polariton, after this interaction comes into play [66,67,68,69,70,71]. In such a context, photon-positronium oscillations occur [130, 131].
Dipersion relations linked to the second propagation mode of the vacuum polarization tensor in quantum AED [see Eq. (17)]. While the dashed line represents the light cone law, the horizontal dotted one shows the situation for which \(q_0^2-q_\parallel ^2=m^2\). The four curves below the light cone line are associated with the massless branch. Conversely, above this one, four massive dispersion laws are depicted. These curves were determined by choosing various magnetic field parameters \(\mathfrak {b}_i\) with \(i=1,2,3,4,5,6 \) so that \(\mathfrak {b}_1=1,\ \mathfrak {b}_2=2,\ \mathfrak {b}_3=3,\ \mathfrak {b}_4=4,\ \mathfrak {b}_5=10,\ \mathfrak {b}_6=100\)
When calculating the components of the group velocity  linked to Eq. (18), we find
linked to Eq. (18), we find

As a consequence, the angle \(\theta \) between the direction of propagation of the electromagnetic energy and the external magnetic field [\(\mathfrak {b}\gg 1\)]

does not coincide with the one [\(\tan \vartheta =q_{\perp }/ q_{\parallel }\)] between the photon momentum \( \pmb {q}\) and \(\pmb {B}\), [\(\tan \theta <\tan \vartheta \)]. Furthermore, we observe that it tends to vanish when \(q_{\perp }\ll m_*\approx m\mathfrak {b}\) the faster, the stronger the field is, since one has [see Eq. (19)]:

This implies that the group velocity of massless excitations tends to be parallel to the magnetic field for hard, as well as for soft photons with \(q_\perp \ll m_*\).
The described situation resembles the main feature on which the capture effect of photons with energy much lower than the first pair creation threshold relies in QED [68]. Following our discussion below Eq. (14), we expect that this phenomenon could also be realized via a certain class of virtual ALPs rather than by virtual electron-positron pairs, provided \(\mathfrak {b}\gg 1\). We will see very shortly that, in addition to \(\gamma -\)quanta [66, 67], and as a direct consequence of Eq. (19), X-rays, optical light [68], infrared radiation and electromagnetic microwaves could undergo the capture due to the magnetized vacuum of AED near the surface of neutron stars.
Let us investigate the refractive properties linked to the massive branch [lower sign in Eq. (17)]. When \(\mathfrak {b}\gg 1\) and \( q_\perp \ll m_*\approx m\mathfrak {b}\) the associated dispersion relation approaches \(q_{0+}^{2}\approx 2q_{\perp }^{2}+q_{\parallel }^{2}+m_{*}^{2}\). In this case the components of the group velocity  are
are

As a result, the cosine of the angle \(\eta \) between the group velocity vector  and the momentum is
and the momentum is

In terms of the angle \(\vartheta \) between the photon momentum and the magnetic field [see below Eq. (19)], this expression reads
Within the range \(0<\vartheta <\pi /2\) the angle \(\eta \) remains very small and achieves its maximum value of \(\eta \approx \arccos [0.943]=0.339\, {\mathrm{rad}}\) at \(\vartheta \approx 36^\circ \). This is the deflection that the direction of propagation of the wave undergoes from its momentum vector due to the anisotropy of the medium.
3.2 Implications of plausible captures of \(\pmb \gamma \) quanta mediated by virtual axion-like particles
Let us now consider the photon capture effect in different terms. In understanding that the group velocity specifies the direction of propagation of the wave envelope, the suppression of its perpendicular component implies the effect of capture of the mode-2 photon by the strong magnetic field, as described previously in QED. We will see, however, that this phenomenon has quite different features in the present context. Observe that Eqs. (19) and (22) apply for \(q_{\perp }\ll m_*\) with \(\mathfrak {b}\gg 1\). Beyond this limit, i.e. for \(q_\perp \gg m_*\), the components of the group velocity approach

and the angle  between the direction of propagation of the electromagnetic energy and \(\pmb {B}\) does not deviate substantially from the one formed by the momentum of the small-amplitude wave and the external field [\(\theta \approx \vartheta =\arctan (q_\perp /q_\parallel )\)].
between the direction of propagation of the electromagnetic energy and \(\pmb {B}\) does not deviate substantially from the one formed by the momentum of the small-amplitude wave and the external field [\(\theta \approx \vartheta =\arctan (q_\perp /q_\parallel )\)].
Suppose that we have a magnetic field with its lines of force curved as it is adopted in models describing the magnetosphere of pulsars and neutron stars. Whenever the curvature radius of the field is much larger than the photon wavelength and the Compton wavelength of ALPs, the analysis developed so far will also apply. When propagating in such a field a photon changes its momentum components \(q_{\perp }\) and \(q_{\parallel }\), while its energy \(q_{0}\) is kept constant, because the external field does not depend on time. Thereby the photon evolves along its dispersion curve. Let primarily the so-called curvature \(\gamma \)-quantum with \(q_{0}>2m_{e}\) be injected in the direction parallel to the magnetic field, as it is the case within the widely accepted scenario of the events that take place in the pulsar magnetosphere. The curvature gamma-quantum is emitted by an electron propagating along a curved magnetic line of force. As the photon propagates inside the dipole-shaped magnetic field it gains a crucial pitch angle with the direction of this field, kinematically sufficient for the photon to create an electron-positron pair. This takes place when \(q_{0}^{2}-q_{\parallel }^{2}=4m_{e}^2\). A “classical” on-shell photon is characterized by the vacuum dispersion law \(q_{0}^2-q_{\parallel }^2=q_{\perp }^2\) [dashed line in Fig. 2] unless the magnetic field exceeds too much the characteristic scale \(B_\star =0.1\; m_{e}^2/e\approx 4.42\times 10^{12}\, {\mathrm{G}}\), in which case the resonant phenomena [66] must be taken into account.Footnote 6 Therefore, before reaching the necessary pitch angle – which happens for mode-2 photons at \(q_{\perp }=2m_{e}\) – the photon propagates straightforwardly in the coordinate space and then it produces the pair. This is the mechanism of the formation of the electron-positron plasma by mode-2 photons responsible for the further directed electromagnetic emission of the pulsar.
Now, in accordance with Eq. (21) the admission of the axion-photon interaction makes the curvature photon of mode-2 be captured by the magnetic line of force practically immediately after the photon is emitted, provided \(q_{\perp }\ll m_*\). This condition might lead to the capture of massless mode-2 photons with energy larger than the characteristic energy scale associated with the electron mass, i.e. for \(q_0> m_{e}\). However, if this was the case, a single sufficiently hard – belonging to the \(\gamma \)-range – photon in the magnetic field has no chance to produce a pair for long, such that the established mechanism of the pulsar radiation would be destroyed, provided \(B_{\mathrm{c}}\ll B_{0}\).Footnote 7 Indeed, following our preceding discussion, in the magnetic field the production of an electron-positron pair by a \(\gamma \)-photon is possible if \(q_{0-}^{2}-q_{\parallel }^{2}\geqslant 4m_{e}^{2}\).Footnote 8 Substituting \(q_{0-}^{2}-q_{\parallel }^{2}=4m_{e}^{2}\) into Eq. (17) we obtain the equation
for the threshold value of \(q_{\perp }^{2}\) that borders this process. Its solution is
The accepted mechanism of plasma generation in neutron stars is destroyed if it may take place at the values \(\left( q_{\perp }^{2}\right) _{\text {thr}}\) exceeding substantially the threshold value of \(\left( q_{\perp }^{2}\right) _{\text {thr}}=4m_{e}^{2}\) characteristic of QED in a magnetic field. This occurs if the three conditions
are met simultaneously, along with \(B_c \ll B_0\). In such a case the photon is captured by the magnetic line of force, and it cannot create a pair before it has propagated far enough along the line to leave the region of the strong dipole field of the pulsar where, however, the one-photon pair creation is strongly suppressed. Clearly, the occurrence of this phenomenon would suppress the main channel responsible for supplying an electron-positron plasma in the neutron star magnetospheres. This suppression would forbid the existence of the plasma itself, and therefore, the so far accepted source of pulsar radiation. Other recognized radiation emission mechanisms such as the splitting of photons turn out to be suppressed as well because – in the regime under consideration – QED undergoes a sort of quantum triviality [read discussion below Eq. (38)]. The incompatibility between both models demands, either to look for alternative mechanisms that would explain the pulsar emissions in the presence of virtual ALPs, or to exclude the (\(g,\;m\)) region dictated by Eq. (27) provided the field strength is known from observations. While the determination of the magnetic fields linked to neutron stars are made indirectly and turn out to be model-dependent, it is natural to investigate the upper bounds that result from the latter possibility.
Limit of dominance of AED over QED (dashed black curve). The dominance takes place for those combinations of ALP parameters lying above this limiting line. The light-red and light-blue curves demarcate regions discarded by the noncapture of a \(\gamma -\)quanta mediated by ALPs, prior to the creation of an electron-positron pair. The occurrence of this phenomenon would prevent the plasma generation near the surface of neutron stars, responsible for the pulsars emission. The figure includes a compilation of exclusion areas adapted from Refs. [14,15,16,17,18]. The colored sectors in gray and orange show the exclusion regions corresponding to OSCAR and PVLAS collaborations, respectively. While the excluded area in cyan has been established from beam dump experiments, the dark blue zone in the right upper corner has been excluded by investigations of electron-positron collider (LEP). The picture includes a yellow band linked to the predictions of the hadronic axion model, for which \(m\approx 6\; \mu {\mathrm {eV}} \times 10^{12}\;{\mathrm {GeV}}/f\) with f referring to the scale at which Peccei-Quinn symmetry is broken. The corresponding couplings of the axion to the Standard Model particles depend on this scale \(g=(E/N-1.92)\alpha /(2\pi f)\) and on the model-depending parameter \(E/N\in (5/3,44/3)\) [133, 134]. Colored in green and light red appear the regions ruled out by particle decay experiments. Furthermore, the portion discarded by investigating the energy loss in horizontal branch (HB) stars are shown in dark red, whereas the excluded area resulting from the solar monitoring of a plausible ALP flux (CAST+SUMICO) has been added in olive [124, 125]). In light brown the portion discarded by measuring the duration of the neutrino signal of the supernova SN1987A is depicted. The light blue area results from cosmological investigations
Let us consider the scenario provided by \({\mathrm{RX}}\) J1856.5-3754 – a representative pulsar belonging to the seven nearby X-ray thermal isolated neutron stars known as “Magnificent Seven”– to which considerable observational resources have been devoted [80,81,82,83,84,85,86]. In the surface of \({\mathrm{RX}}\) J1856.5-3754 the magnetic field is \(B\approx 1.5\times 10^{13}\;{\mathrm{G}}\) [83]. The area excluded by the existence of an electron-positron plasma in the surface of this neutron star is colored in light-blue [see Fig. 3]. Our result is expected to be reliable whenever the ALP mass m exceeds substantially the energy scale linked to the curvature radius \(\sim \mathcal {R}_{\mathrm{curv}}^{-1}\), a restriction introduced by the adiabatic approximation. Hence, if we identify the curvature radius \(\mathcal {R}_{\mathrm{curv}}\) with the star radius  , the previous condition will allow us to probe ALPs with masses \(m\gg 10^{-11}\;{\mathrm{eV}}\).
, the previous condition will allow us to probe ALPs with masses \(m\gg 10^{-11}\;{\mathrm{eV}}\).
More stringent constraints can be established from neutron stars holding a more intense magnetic field. At the time of writing, the strongest magnetic field belong to the soft \(\gamma -\)repeater \({\mathrm{SGR}}\) 1806-20 [57, 58]. Although a field as strong as \(B\approx 7 \times 10^{15}\;{\mathrm{G}}\) has been inferred for this magnetar [77], in our numerical assessment we used a more conservative value \(B\approx 2.4\times 10^{15}\; {\mathrm{G}}\) [78, 79]. It is worth mentioning that, for this field strength, the effect of the QED vacuum polarization [see Eq. (13)] still can be treated as a perturbation. The respective region ruled out by the noncapture of a \(\gamma -\)quanta mediated by ALPs, prior to the creation of an electron-positron pair is exhibited in Fig. 3 [light red colored]. Noteworthy, the area discarded in this way turns out to be much wider than the one linked to \({\mathrm{RX}}\) J1856.5-3754, and improves existing bounds in the region \(m\sim 10^{-10}\)–\(10^{-5}\;{\mathrm{eV}}\).
3.3 Magnetically-induced canalization of linearly polarized radiation as a signature of axion-like particles
The direct thermal radiation emitted by the hot surface of neutron stars is directly observable in the X-ray range [see, e.g., Ref. [132]]. In this subsection we inspect the consequence associated with the capture of their mode-2 part by the strong magnetic field due to the presence of ALPs, as pointed out below Eq. (21). In this connection, we will start demanding that \(q_\parallel ^2 <m_e^2\) and \(q_\perp ^2\ll m_*^2<m_e^2\), so that the photon energy \(q_0\ll m_e\). Observe that the previous conditions guarantee the applicability of Eq. (18), and therefore, the capture of heat radiation due to a plausible dominance of AED over QED.
Let us consider the refraction law of electromagnetic waves – with energy belonging to the thermal range – when they leave the region of strong magnetic field and enter the space free of it. This consideration will be independent of what mechanisms are responsible for formation of the vacuum polarization and dispersion laws, in other words of whether there are ALPs or we just face the usual QED with magnetic field. Suppose that an electromagnetic wave is created at the surface of a neutron star inside a strong magnetic field, which gradually disappears. Conventionally, the field \(\pmb {B}\) changes only along its own direction, but it is transversely homogeneous. We assume that both the photon wave length \(\lambda \) and the Compton wave length of the ALP are much smaller than the length scale \(\ell \) over which the magnetic field varies substantially. Under such a restriction, the adiabatic approximation is valid, wherein the dielectric properties of the medium may be considered as depending on the coordinate. Then the photon energy \(q_{0}\) and the photon momentum component \(q_{\perp }\) across the magnetic field do not change, when the wave leaves the region occupied by the magnetic field, due to the corresponding space-time translational invariance. On the contrary, the momentum component along the magnetic field \(q_{\parallel }\) does change, because the magnetic field varies in this direction. We shall supply this component with the subscript “\(\infty \)”, when it relates to the region in which the magnetic field is not present.
There are two different dispersion laws:
The last relation is a consequence of relativistic covariance, the function \(f(q_{\perp }^{2})\) is model-dependent and it is different for each propagating mode. According to Eq. (18) one has
provided the conditions \(q_{\perp }\ll m_*\) and \(\mathfrak {b}\gg 1\) are fulfilled.Footnote 9 The refraction index at infinity is \(n_\infty =\vert \pmb {q}_\infty \vert /q_{0}=1\), whereas at the magnetic cap of the star
The adiabatic approximation allows us to divide the region between the star surface and the observatory into a set of equally thin portions with length \(\ell \) so that – within the boundaries of each of them – the corresponding refraction index can be assumed constant [see Fig. 4], and the Snell’s law can be applied to each interface:
where \(\vartheta _{\infty }\) (\(\vartheta \)) is the angle between the outgoing [incoming] momentum \(\pmb {q}_{\infty }\) (\(\pmb {q}\)) and the magnetic field direction. With the use of the relation \(\sin \vartheta _{\infty }=q_{\perp }/\vert \pmb {q}_{\infty }\vert =q_{\perp }/q_{0}\) and the substitution of Eq. (30) into the expression above we find
This can also be written as
provided that \(q_{0}\sin \vartheta _{\infty }\ll m_*\) and \(\mathfrak {b}\gg 1\). The critical angle \(\vartheta _{\mathrm{cr}}\) for total internal reflection is achieved when \(\vartheta _{\infty }=\pi /2\). It depends on the energy:
Only approximately one half of the isotropic long-wave radiation has a chance to leave the magnetic field.
The capture effect further modifies the situation. We have found [see Eq. (19)] that on the massless photon branch, for \(q_{\perp }^{2}\) as small as \(q_{\perp }^{2}=q_{0}^{2}\sin ^{2}\vartheta _{\infty }\ll m^2_*\) all photons are canalized towards the direction of the magnetic field. The fulfillment of this inequality is guaranteed for all incident angles provided that the photon energy \(q_0\ll m_*<m_e\). As the previous condition is stronger than the one required at the beginning of this subsection, one is forced to limit \(q_\parallel ^2\ll m_*^2< m_e^2 \). On the other hand, the dispersion curve passes through the point \(\vartheta _{\infty }=\vartheta =0\), which means that the wave parallel to the magnetic field is not deflected, when it goes out of it. Therefore the whole mode-2 part of the radiation would gather in a beam going out of the magnetic field parallel to it. Another possibility is that \(q_0\gg m_*\). Under this condition the canalization of the second propagation mode takes place with the particularization that the refractive effect becomes very weak: \(0<\sin \vartheta _{\infty }\ll m_*/q_{0-}\ll 1\). In this case, the propagation of the gathered radiation would not deviate considerably from the magnetic field direction and the condition of dominance [see Eq. (18)] still holds.
As the mode-2, in the ALP-dominating regime, is canalized parallelly to the background magnetic field, most of its energy is concentrated at momenta \(\vert q_{\perp }\vert \ll m_*\). Following the analysis developed in Appendix B [see Eq. (B.3)], mode-2 is a transverse wave with its electric field lying in the plane spanned by the vectors \(\pmb {B}\) and \(\pmb {q}\). In accord with the analysis above [see Eq. (33)], it leaves the background field with the refraction angle close to the incident angle, when both are small. On the other hand, the mode-3 component of the heat radiation, whose electric field is normal to the plane formed by the background magnetic field and the direction of propagation, is not canalized. (Recall, that it is not influenced by the presence of ALPs and remains as calculated via QED [see Ref. [68]]). Its original angular distribution is only modulated by the refraction law Eq. (33), and it is not concentrated along any direction. Therefore, if ALPs exist and the vacuum polarization induced by them dominates over the one of QED, the heat photons with energies \(q_{0}\ll m_*<m_e\) polarized in the plane to which the vectors \(\pmb {B}\) and \(\pmb {q}\) belong, peak along the direction of the magnetic field against the smooth background of photons polarized orthogonal to this plane. Hence, if the direction of the observed photon flux deviates from being parallel to the magnetic field we would face the smooth background of photons polarized orthogonal to this plane– that are not subject to the capture. The registered radiation would be scant of photons polarized in the said plane.
The peaking (or not peaking) of photons in the parallel direction constitutes a suitable way to make sure that ALPs exist (or do not). In the latter case, constraints on the parameter space of ALPs could also be inferred directly from the observed photon flux. Clearly, this procedure would require to derive an expression for the flux of canalized photons to be detected by including both the capture and the refraction effect. While the establishment of such a formula is beyond the scope of this investigation, we plan to treat this problem in a forthcoming publication.
It is also worth mentioning at this point that there exists already significant progress in high-purity polarimetric techniques for X-ray probes [135, 136] which are expected to be exploited in the envisaged experiment at HIBEF collaboration [137, 138]. These techniques are planned to be used in polarimeters designed to investigate the soft X-ray emission in the strong magnetic fields of neutron stars and white dwarfs [139,140,141,142].Footnote 10 Eventually, these polarimetric measurements could allow us as well to probe the dominance of AED over QED, and provide new constraints on the ALP parameter space [143]. Indeed, if the proposed effect could be extinguished from the future observations one will be able to ban the values of the ALP coupling \(g>q_{0}/B\), where the pulsar value is taken for the magnetic field B and the x-ray value for the photon energy \(q_{0}\).
4 The modified Coulomb potential in axion-electrodynamics
In this section we study how the screening caused by a plausible dominance of AED over QED modifies the running QED coupling and so the Coulomb potential.
4.1 Photon propagator
Aside from influencing the propagation of photons, the polarization tensor [see Eq. (11)] also induces modifications of Coulomb’s law. This distortion is determined here through the temporal component of the electromagnetic four-potential

where  is the four-current density of a point-like static charge
is the four-current density of a point-like static charge  placed at the origin \(\tilde{\pmb {x}}=\pmb {0}\) of our reference frame. In this expression
placed at the origin \(\tilde{\pmb {x}}=\pmb {0}\) of our reference frame. In this expression  denotes the effective photon propagator, i.e. the result of summing up the infinite series that determines the renormalized photon propagator when diagrams of all orders are included [144]. Consequently, the problem of determining how the quantum vacuum fluctuation of a pseudoscalar axion field \(\phi (x)\) modifies the Coulomb potential
denotes the effective photon propagator, i.e. the result of summing up the infinite series that determines the renormalized photon propagator when diagrams of all orders are included [144]. Consequently, the problem of determining how the quantum vacuum fluctuation of a pseudoscalar axion field \(\phi (x)\) modifies the Coulomb potential  reduces, to a large extent, to finding the explicit expression for
reduces, to a large extent, to finding the explicit expression for  . Here this is accomplished by using the identity
. Here this is accomplished by using the identity

where  is given in Eq. (8) which corresponds to summing up the geometric series of one-photon-reducible diagrams. However, the close analogy between our problem and the one previously analyzed in QED allows us to apply the model- and approximation-independent expression for
is given in Eq. (8) which corresponds to summing up the geometric series of one-photon-reducible diagrams. However, the close analogy between our problem and the one previously analyzed in QED allows us to apply the model- and approximation-independent expression for  found in Ref. [91] directly. This general formula links the previous object with the corresponding eigenvalues and eigenvectors of the polarization tensor in QED. It only remains to carry out an appropriate replacement of these eigenvalues by those resulting from the photon-ALP oscillations. Hence, up to an inessential longitudinal contribution, the photon propagator reads
found in Ref. [91] directly. This general formula links the previous object with the corresponding eigenvalues and eigenvectors of the polarization tensor in QED. It only remains to carry out an appropriate replacement of these eigenvalues by those resulting from the photon-ALP oscillations. Hence, up to an inessential longitudinal contribution, the photon propagator reads

where the shorthand notation  has been used. We insert this formula into Eq. (35) bearing in mind the details explained below. As a consequence, the axion-modified Coulomb potential is given by
has been used. We insert this formula into Eq. (35) bearing in mind the details explained below. As a consequence, the axion-modified Coulomb potential is given by

When establishing this expression we used the fact that \(\flat _{1}^0=\flat _{3}^0=0\), i.e. that the first and third eigenmodes do not contribute to the electrostatic interaction. This feature could be anticipated because, in the stationary limit \(q_0=0\), “virtual” photons associated with \(\flat _{1,3}^\mu \) carry magnetic fields only, while off-shell photons of mode-2 are purely electric.
4.2 Running QED coupling and Coulomb potential
Let us start this subsection by analyzing general features linked to the running QED coupling \(\alpha _{{\mathrm {scr}}}(\pmb {q})\) when the dominance of AED over QED polarization tensor takes place. To this end, we shall refer ourselves to the electrostatic energy  between two electrons. The insertion of Eq. (37) into this formula with
between two electrons. The insertion of Eq. (37) into this formula with  defines the running QED coupling. Indeed, by expressing
defines the running QED coupling. Indeed, by expressing  , we find [\(\mathfrak {b}\gg 1\)]
, we find [\(\mathfrak {b}\gg 1\)]
with \(\alpha =e^2/(4\pi )\) defined when the magnetic field background vanishes, i.e. at \(\mathfrak {b}\rightarrow 0\) and \(\vert \pmb {q}\vert \rightarrow 0\) [60, 61]. Notably, if the dominance of AED over QED takes place, \(\alpha _{{\mathrm {scr}}}(\pmb {q})\) is free of the characteristic Landau pole arising in QED that rises the coupling constant to an infinite value for large enough momentum.Footnote 11 Furthermore, its dependence on the magnetic field leads to an anisotropic behavior along and transverse to \(\pmb {B}\). This dependence decreases the value of the running QED coupling as the magnetic field B grows while keeping the momentum fixed. Indeed, for \(q_\perp ^2\ll q_{\parallel }^2\ll m^2\), one finds that \(\alpha _{{\mathrm {scr}}}(\pmb {q})\sim \alpha \mathfrak {b}^{-2}\ll 1\) tends to be screened to zero. This phenomenon makes QED an almost “trivial” theory in the aforementioned regime, meaning that the corresponding matter sector and the small-amplitude electromagnetic waves turn out to be very weakly interacting between each other.
The described situation becomes particularly dramatic if the axion mass turns out to be larger than the first pair creation threshold, i.e. \(m> 2m_e\) because – in line with the discussion of Sect. 3.2 – this would imply a complete suppression of radiation emission mechanisms such as the recombination of pairs and the photon splitting effect as well as the main production channels in highly-magnetized pulsars. This quantum triviality [146,147,148] persists if, for instance, both \(q_{\parallel }^2\ll q_\perp ^2\ll m^2\) and \(1\ll q_\perp ^2/q_\parallel ^2\ll \mathfrak {b}^2\). Indeed, in this case the running QED coupling also becomes extremely small \(\alpha _{{\mathrm {scr}}}(\pmb {q})\sim \alpha q_\parallel ^2/(q_\perp ^2\mathfrak {b}^2)\ll 1\). Also, electrons and positrons with energy larger than \(m>2m_e\), i.e. with \(q_{\perp }^2\ll m^2 \ll q_\parallel ^2\) and \(q_\parallel ^2/m^2 \ll \mathfrak {b}^2\) might undergo the quantum triviality since \(\alpha _{{\mathrm {scr}}}(\pmb {q})\sim \alpha q_\parallel ^2/m_*^2\ll 1\). Conversely, for \(q_{\perp }^2/m^2\ll 1\ll \mathfrak {b}^2 \ll q_\parallel ^2/m^2\) or \(1\ll \mathfrak {b}^2\ll q_\perp ^2/q_\parallel ^2\ll m^2/q_\parallel ^2\) the screening effects are negligibly small and the running QED coupling approximates to it standard value \(\alpha _{{\mathrm {scr}}}(\pmb {q})\sim \alpha \).
Now we proceed to investigate how the running QED coupling modifies the Coulomb potential. To this end, we write Eq. (37) in an equivalent form

where the original integration variables have been changed to cylindrical ones, and the integral representation of the Bessel function of order zero

has been used [149]. Here \(\varphi \) (\(\tilde{\varphi }\)) is the polar angle associated with \(\pmb {q}_\perp \) (\(\pmb {x}_\perp \)) and the square of the momentum \(\pmb {q}\) must be understood as \(\pmb {q}^2=q_\perp ^2+q_\parallel ^2\).
Electrostatic energy of an electron  due to the anisotropic Coulomb potential \(a_0(\pmb {x})\) [see Eq. (41)] of a pointlike static charge induced by quantum vacuum fluctuations due to an axion-like field over a constant magnetic-like background. Here the energy is shown in units of the electron energy at the Compton wavelength of an ALP
due to the anisotropic Coulomb potential \(a_0(\pmb {x})\) [see Eq. (41)] of a pointlike static charge induced by quantum vacuum fluctuations due to an axion-like field over a constant magnetic-like background. Here the energy is shown in units of the electron energy at the Compton wavelength of an ALP  . The left [right] panel depicts the behavior along the axis \(\pmb {x}_\perp \) [\(\pmb {x}_\parallel \)] passing through the charge
. The left [right] panel depicts the behavior along the axis \(\pmb {x}_\perp \) [\(\pmb {x}_\parallel \)] passing through the charge  perpendicular [parallel] to the magnetic field, \(\vert \pmb {x}_\parallel \vert =0\) [\(\vert \pmb {x}_\perp \vert =0\)]. In both panels, the dashed curve is the Coulomb potential, whereas solid curves were determined from the following values \(\mathfrak {b}=100\) (in gray), \(\mathfrak {b}=10\) (in olive), and \(\mathfrak {b}=1\) (in cyan). The red dotted curve in each panel must be understood as the limiting case when \(\mathfrak {b}\rightarrow \mathfrak {b}_{{\mathrm {max}}}\)
perpendicular [parallel] to the magnetic field, \(\vert \pmb {x}_\parallel \vert =0\) [\(\vert \pmb {x}_\perp \vert =0\)]. In both panels, the dashed curve is the Coulomb potential, whereas solid curves were determined from the following values \(\mathfrak {b}=100\) (in gray), \(\mathfrak {b}=10\) (in olive), and \(\mathfrak {b}=1\) (in cyan). The red dotted curve in each panel must be understood as the limiting case when \(\mathfrak {b}\rightarrow \mathfrak {b}_{{\mathrm {max}}}\)
The integration over \(q_\parallel \) can be performed by using the residues theorem. For this, we point out that the integrand in Eq. (39) has four poles on the imaginary axis:
with the positive roots taken for \(x_\parallel <0\) and the negative ones for \(x_\parallel >0\). As before, \(m_*=m\sqrt{1+\mathfrak {b}^2}\) with \(\mathfrak {b}=gB/m\) is the ALP mass dressed by the external field [see below Eq. (17)]. With these details in mind, and after developing the change of variable \(u=2\mathfrak {b}q_\perp /(m_*\sqrt{1+\mathfrak {b}^2})\), it turns out that
In this formula,  is the Coulomb potential evaluated at the effective wavelength \(\lambda _*=m_*^{-1}\) of an ALP. Depending on whether the magnetic field strength is smaller or larger than the characteristic scale of the theory \(B_c=m/g\), this quantity will reduce either to the Compton wavelength of the axion \(\lambda =m^{-1}\) or to a sort of “Larmour” length [\(\lambda _*\xrightarrow {\mathfrak {b}\gg 1} (gB)^{-1}\)], respectively. As the framework under consideration allows for exploring distances larger than the natural length scale of the theory \(g\sim \varLambda _{{\mathrm {UV}}}^{-1}\) [111], the effective wavelengths of interest are those for which the condition \(\lambda _*\gg g\) is fullfilled. Observe that, in the strong field limit [\(\mathfrak {b}\gg 1\)], the latter translates into an upper bound for the largest magnetic field that can be considered in the theory \(B_{{\mathrm {max}}}=g^{-2}\sim \varLambda _{{\mathrm {UV}}}^2\), corresponding to a parameter \(\mathfrak {b}_{{\mathrm {max}}}=(mg)^{-1}\) with \(1\gg mg\).
is the Coulomb potential evaluated at the effective wavelength \(\lambda _*=m_*^{-1}\) of an ALP. Depending on whether the magnetic field strength is smaller or larger than the characteristic scale of the theory \(B_c=m/g\), this quantity will reduce either to the Compton wavelength of the axion \(\lambda =m^{-1}\) or to a sort of “Larmour” length [\(\lambda _*\xrightarrow {\mathfrak {b}\gg 1} (gB)^{-1}\)], respectively. As the framework under consideration allows for exploring distances larger than the natural length scale of the theory \(g\sim \varLambda _{{\mathrm {UV}}}^{-1}\) [111], the effective wavelengths of interest are those for which the condition \(\lambda _*\gg g\) is fullfilled. Observe that, in the strong field limit [\(\mathfrak {b}\gg 1\)], the latter translates into an upper bound for the largest magnetic field that can be considered in the theory \(B_{{\mathrm {max}}}=g^{-2}\sim \varLambda _{{\mathrm {UV}}}^2\), corresponding to a parameter \(\mathfrak {b}_{{\mathrm {max}}}=(mg)^{-1}\) with \(1\gg mg\).
Equation (41) has been written in terms of the dimensionless coordinates \(\tilde{x}_{\perp ,\parallel }=\frac{\vert \pmb {x}_{\perp ,\parallel }\vert }{2\lambda _{*}}\sqrt{1+\frac{1}{\mathfrak {b}^{2}}}\) and functions which grow monotonically with the increasing of u:
For large values of their argument [\(u\gg 1\)], they behave as
whereas for small values of \(u\ll 1\) they approach
The formula found above [Eq. (41) with (42) included] is our starting point for further considerations. Its consequences on the electrostatic energy of an electron  is depicted in Fig. 5 for various values of the parameter \(\mathfrak {b}\). The curves in the left [right] panel have been determined by setting \(\vert \pmb {x}_\parallel \vert =0\) [\(\vert \pmb {x}_\perp \vert =0\)]. For a common value of \(\mathfrak {b}\geqslant 1\), the corresponding curves in the left and right panels display different shapes and each panel reveals a different trend of the curves with the growing of \(\mathfrak {b}\). These features constitute clear manifestations of the anisotropy that the running-QED coupling presents due to its dependence on the external field. In the left panel [\(\vert \pmb {x}_\parallel \vert =0\)], the curves tend to stick closer to each other, falling down rather sharply as the magnetic field grows gradually and the distance from the particle location is much smaller than the Compton wavelength of an ALP [\(\vert \pmb {x}_\perp \vert \ll \lambda \)]. Observe that the red dotted curve exhibits a region in which the Coulomb interaction vanishes practically. This flattening is a manifestation of QED triviality due to the dominance of AED at asymptotically large B [read also the discussion below Eq. (38)]. Conversely, when \(\vert \pmb {x}_\perp \vert =0\), the growing of the external field makes the curves slightly deviate from the standard Coulomb potential, and for \(\mathfrak {b}\rightarrow \mathfrak {b}_{{\mathrm {max}}}\) the curves converge rather fast to a certain asymptotic function [red dotted curve]. This trend is consistent with the momentum regime [\(1\ll \mathfrak {b}^2\ll q_\perp ^2/q_\parallel ^2\ll m^2/q_\parallel ^2\)] discussed last below Eq. (38), in which the screening effect due to virtual ALPs turns out to be insignificant.
is depicted in Fig. 5 for various values of the parameter \(\mathfrak {b}\). The curves in the left [right] panel have been determined by setting \(\vert \pmb {x}_\parallel \vert =0\) [\(\vert \pmb {x}_\perp \vert =0\)]. For a common value of \(\mathfrak {b}\geqslant 1\), the corresponding curves in the left and right panels display different shapes and each panel reveals a different trend of the curves with the growing of \(\mathfrak {b}\). These features constitute clear manifestations of the anisotropy that the running-QED coupling presents due to its dependence on the external field. In the left panel [\(\vert \pmb {x}_\parallel \vert =0\)], the curves tend to stick closer to each other, falling down rather sharply as the magnetic field grows gradually and the distance from the particle location is much smaller than the Compton wavelength of an ALP [\(\vert \pmb {x}_\perp \vert \ll \lambda \)]. Observe that the red dotted curve exhibits a region in which the Coulomb interaction vanishes practically. This flattening is a manifestation of QED triviality due to the dominance of AED at asymptotically large B [read also the discussion below Eq. (38)]. Conversely, when \(\vert \pmb {x}_\perp \vert =0\), the growing of the external field makes the curves slightly deviate from the standard Coulomb potential, and for \(\mathfrak {b}\rightarrow \mathfrak {b}_{{\mathrm {max}}}\) the curves converge rather fast to a certain asymptotic function [red dotted curve]. This trend is consistent with the momentum regime [\(1\ll \mathfrak {b}^2\ll q_\perp ^2/q_\parallel ^2\ll m^2/q_\parallel ^2\)] discussed last below Eq. (38), in which the screening effect due to virtual ALPs turns out to be insignificant.
4.3 Leading behavior for small and large distances relative to \(\lambda _*(1+1/\mathfrak {b}^2)^{-1/2}\)
Let us investigate the behavior of \(a_0(\pmb {x})\) [see Eq. (41)] on the axis \(\pmb {x}_\parallel =\pmb {0}\). In such a situation, the integrand that remains combines \(J_0(\tilde{x}_\perp u)\) with a function that tends asymptotically to 1 with the growing of u, whatever be the value of \(\mathfrak {b}\). Hence, the whole integrand reaches the maximum value as the argument of the Bessel function \(J_0(\tilde{x}_\perp u)\) satifies the condition \(\tilde{x}_\perp u\ll 1\). Following this analysis we infer that, when \(\vert \pmb {x}_\perp \vert \) is small on the scale of \(\lambda _*/(1+1/\mathfrak {b}^2)^{1/2}\), the main contribution to the integral in Eq. (41) results from the region in which \(1\ll u\ll \tilde{x}_\perp ^{-1}\), provided \(\mathfrak {b}\gg \vert \pmb {x}_\perp \vert /\lambda \). As a consequence, one can exploit Eq. (43) and integrate over u by using formula (6.616.1) of Ref. [150].Footnote 12 With these details in mind, the modified potential approaches

This formula looks like a pure Yukawa potential in which the scale \(\sim \lambda _*(1+1/\mathfrak {b}^2)^{-1/2}\) characterizes the short-range behavior. This kind of dependence is somewhat expected, since the second propagation mode coexists with a massive branch determined by the ALP sector.
For \(B\gg B_c\) [\(\mathfrak {b}\gg 1\)], \(\lambda _*\approx (m\mathfrak {b})^{-1}=1/(gB)\) is independent of the ALP mass and \(\sqrt{1+1/\mathfrak {b}^2}\sim 1\). The resulting expression can be read off directly from Eq. (45), and tends to be tiny as \(\mathfrak {b}\) grows progressively for any nonzero distance \(\vert \pmb {x}_\perp \vert \ll \lambda _*\). The sharp trend exhibited by the curves in the left panel of Fig. 5, nearby the particle location [\(\vert \pmb {x}_\perp \vert =0\)], can be understood qualitatively by considering the generalized limit of Eq. (45) when \(\mathfrak {b}\rightarrow \infty \):
Here, \({\mathrm {Ei}}(z)=-\int _{-z}^\infty dt\; t^{-1}e^{-t}\) is the exponential integral function [149]. With this result at hand, Eq. (45) becomes a magnetic field independent delta potential

Although this result explains why the curves tend to collapse toward the vertical axis with the growing of \(\mathfrak {b}\) [see Fig. 5], and so the trivial interplay for \(\vert x_\perp \vert \ne 0\), it has to be considered with caution. This is because the \(\mathfrak {b}\) parameter is actually limited from above by \(\mathfrak {b}_{{\mathrm {max}}}\) and \(x_\perp \) must be larger than g [see discussion below Eq. (41)]. It is worth pointing out that, in the limit of \(\mathfrak {b}\rightarrow \mathfrak {b}_{{\mathrm {max}}}\) and \(\vert \pmb {x}_\perp \vert \rightarrow g\) the axion-Coulomb potential is regular and reads

When \(\pmb {x}_\perp =\pmb {0}\), the Bessel function \(J_0(\tilde{x}_\perp u)=1\), and the exponentials which remain in Eq. (41) decrease very fast for large values of \(\tilde{x}_\parallel u\). Hence, for distances \(\vert \pmb {x}_\parallel \vert \ll \lambda _*(1+1/\mathfrak {b}^2)^{-1/2}\), the main contribution to the integral in Eq. (41) results from the region in which \(1\ll u\ll \tilde{x}_\parallel ^{-1}\). Once again, we exploit Eq. (43) and keep the factor \(u/\sqrt{1+u^2}\) as it stands. These steps reduce the integral to one in which (6.616.1) of Ref. [150] can be used. Consequently,

The outcome above applies whenever \(\mathfrak {b}\gg \vert \pmb {x} _\parallel \vert /\lambda \). In the limit of \(\mathfrak {b}\gg 1\), this expression approaches

We note that, as the exponent involved in this formula is much smaller than unity [\(m_*\vert \pmb {x}_\parallel \vert \ll 1\)], the screening induced by the vacuum polarization does not deviate Eq. (49) from the Coulomb potential  substantially. This fact agrees with the behavior shown in the right panel of Fig. 5, which exhibits that – for distances smaller than the ALP wavelength – the behavior of the curves is very similar to the one associated with Coulomb’s law. The limit of \(\vert \pmb {x}_\parallel \vert \rightarrow g\) is readable from Eq. (49) and gives
substantially. This fact agrees with the behavior shown in the right panel of Fig. 5, which exhibits that – for distances smaller than the ALP wavelength – the behavior of the curves is very similar to the one associated with Coulomb’s law. The limit of \(\vert \pmb {x}_\parallel \vert \rightarrow g\) is readable from Eq. (49) and gives  .
.
Although Eq. (49) has been derived under the restriction \(x_\parallel /\lambda \ll \mathfrak {b}^{-1}\) with \(\mathfrak {b}\gg 1\), it can be used to explore regions of \(\vert \pmb {x}_\parallel \vert \) for which the condition \(\vert \pmb {x}_\parallel \vert \sim \lambda \) holds. Indeed, at \(\vert \pmb {x}_\parallel \vert =\lambda \) and \(\mathfrak {b}=10^2\), this expression differs from the exact formula [see Eq. (41)] by \(2.6\%\) only. The accuracy increases even further as \(\mathfrak {b}\) grows, reaching values down to \(0.4\%\) if \(\mathfrak {b}\geqslant 10^3\). Noteworthy, when both \(\vert \pmb {x}_\parallel \vert \sim \lambda \) and \(\mathfrak {b}\gg 1\) are met, the second term in Eq. (49) drops and

Observe that this formula differs from the standard Coulomb law by a factor 1/2. Thus, the behavior of the axion-modified Coulomb potential in the longitudinal direction saturates in the sense that – unlike the direction perpendicular to \(\pmb {B}\) [see Eq. (45)] – it reaches a universal shape, independent of the external field strength. This fact helps to understand why the curves in the right panel of Fig. 5 converge to the red one, the behavior of which differs from the case \(\pmb {x}_\parallel =0\) [left panel] as \(\mathfrak {b}\gg 1\).
The procedure for obtaining Eq. (48) can be extended easily to the case in which \(\vert \pmb {x}_\perp \vert \ll \lambda _*/(1+1/\mathfrak {b}^2)^{1/2}\). This gives rise to the following short-range anisotropic potential [\(\mathfrak {b}\gg 1\)]

where \(\vert \pmb {x}\vert =(\vert \pmb {x}_\perp \vert ^2+\vert \pmb {x}_\parallel ^2)^{1/2}\) and \(m_*\approx m\mathfrak {b}\). In the limit of \(\pmb {x}_\parallel \rightarrow 0\), Eq. (51) reproduces the result given in Eq. (45) with the particularization \(\mathfrak {b}\gg 1\). Conversely, if \(\pmb {x}_\perp \rightarrow 0\), the former reduces to Eq. (49) with the condition \(\mathfrak {b}\gg 1\) taken into account.
Let us now consider the case \(\vert \pmb {x}_\parallel \vert \gg \lambda _*(1+1/\mathfrak {b}^2)^{-1/2}\) while \(\vert \pmb {x}_\perp \vert \) is arbitrary. Since the functions \(\varLambda _\pm (u)\) increase monotonically with the growing of u, the main countribution to the integral in Eq. (41) results from the region in which \(u\ll 1\). It is then justified to Taylor expand all instances in the integrand depending only on this variable [see Eq. (44)]. After applying once again the integral (6.616.1) of Ref. [150] the modified Coulomb potential reads

This formula is an anisotropic Coulomb’s law which tends to vanish as the external field grows unless \(\vert \pmb {x}_\perp \vert =0\). It resembles closely the longe-range behavior found within a pure QED context, when the external magnetic field exceeds the characteristic scale associated with this framework \(B_0=m_e^2/e\approx 4.42\times 10^{13}\ {\mathrm{G}}\) [91, 92, 94]. However, in QED, \(\mathfrak {b}^2\) is replaced by the factor \(\alpha b/(3\pi )\) [see first line in Eq. (13)]. Observe that, at \(\vert \pmb {x}_\perp \vert =0\), Eq. (52) reduces to a pure Coulomb form  .
.
Now, if \(\vert \pmb {x}_\parallel \vert =0\), and \(\tilde{x}_\perp \gg 1\), the integral in Eq. (41) is dominated by the region where \(u\ll \tilde{x}_\perp ^{-1}\ll 1\). In such a case, the part of the integrand which does not include the Bessel function can be Taylor expanded in u. As a consequence, the long-range behavior of the axion-Coulomb potential, perpendicular to the direction of the field, reads [\(\mathfrak {b}\gg 1\)]

The axion-modified Coulomb law should affect, first of all, the field of an atomic nucleus, placed in a magnetic field. We now show that, although the potential along the magnetic field [\(\mathfrak {b}\gg 1\)] resembles the \(\sim 1/\vert \pmb {x}_\parallel \vert \) law approximately, the ground-state energy of a nonrelativistic electron of a hydrogen atom:Footnote 13
remains bounded from below. Observe that, the singularity is here cut off by the Larmor length \(L_B=(m_e\sqrt{b})^{-1}\), whereas \(a_B=(m_e\alpha )^{-1}\) is the Bohr radius. Both length scales depend on \(\alpha \) which is not affected substantially in the considered regime. As a consequence of integrating out \(x_\parallel \), we end up with the expression of Elliott and Loudon [95] [ ]:
]:
Prior to the inclusion of the QED screening due to the vacuum polarization tensor [91, 92], it was commonly accepted that Eq. (54) is unbounded from below when the magnetic field grows unlimitedly. With its reappearance one could think that a possible dominance of AED over QED restores this problem. However, as long as AED is combined with QED, the resulting framework is nonrenormalizable. This means that the above expression would provide reliable predictions whenever the Larmor length exceeds the characteristic scale of AED [\(L_B\gg g\)]. This bounds the field parameter \(b=B/B_0\ll (m_e g)^{-2}\) and simultaneously limits the ground state energy
ruling out the reinstatement of the aforementioned problem.
5 Conclusion
We have considered the interaction between axion-like particles and photons inside the background of a superstrong constant magnetic field. Only the extraordinary photon mode – mode-2 – whose electric field lies in the plane spanned by the external magnetic field and the photon momentum interacts with the ALP , while the ordinary mode – mode-3 – remains the same as it was in strong-magnetic-field QED. We have obtained that the axion contribution to the polarization operator grows quadratically with the magnetic field, while the QED part of the polarization operator of the extraordinary mode is known [118,119,120,121] to grow only linearly (while the ordinary-mode part grows much more slowly). In this ALP-dominating regime we established the common ALP-extraordinary-photon dispersion law determining their mass shell. It consists of two nonintersecting branches, with no mixed state forming – in contrast to QED, where the photon mixes with the electron-positron state to form a polariton. One branch is massless in the sense that the frequency as a function of spatial momentum turns to zero when all components of the latter are zero. This implies that the mass defined as the rest energy is zero. This branch is associated with the photon modified by its interaction with an ALP. The other branch is massive and it is attributed to an ALP, modified by its interaction with the photon.
The massless branch exhibits the important feature of flattening for components perpendicular to the \(\pmb {B}\) direction which are smaller than the ALP mass. This feature leads to strong birefringence, because the dispersion curve of the mode-3 photon, which remains the same as in QED, does not show such feature. The flattening results in bending the direction of the wave envelope propagation (the group velocity) towards the external field and in the capture of mode-2 photons by curved lines of force of the magnetic field of pulsars. Contrary to the analogous effect known in QED, in the present scenario not only \(\gamma \)-quanta of curvature radiation undergo the capture, but also heat photons in the X-ray range. Under certain circumstances the capture of gamma-quanta is more efficient in AED and its potential consequence might be the destruction of the well established mechanism of formation of pulsar radiation. We have used this incompatibility to exclude a certain region in the axion parameter space. Furthermore, when applied to the softer thermal radiation of the pulsar surface the capture causes that the mode-2 X-ray quanta all gather together to peak near the direction of the magnetic field, while beyond this direction all photons are those of mode 3, i.e. they are polarized orthogonal to the plane spanned by the magnetic field and the observation direction. Their angular distribution is determined by the refraction at the border of the strong magnetic field area, studied in the paper, and by the mechanisms of formation of the soft radiation (see their review in Ref. [132]).
Despite the charge-neutrality of quantum vacuum fluctuations of axion like fields, we have seen that the presence of a magnetic field whose strength overpasses the characteristic scale of AED could induce a strong screening of static electric charges. This screening depends on the field strength, and for certain energy regimes the running coupling could be screened almost to zero, making the QED building blocks very weakly interacting between each other. Moreover, the dependence on the magnetic background promotes an anisotropic behavior in the Coulomb potential. Indeed, at distances from the source much smaller than the Compton wavelength of the ALP, and for magnetic field strengths larger than m/g, the Coulomb potential of a point-like charge is replaced by a Yukawa-type potential in the direction perpendicular to the magnetic field, while along the field the Coulomb law is preserved in a modified form at any length scale. We find that at unlimitedly large magnetic fields the longstanding problem – overcome in QED – that the ground-state energy of a hydrogen atom is unbounded from below, seems to be reinstated in AED. However, the nonrenormalizable feature of this theory rules out this possibility.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The calculations in this study have been carried out by analytical means; the data shown in the figures can be reproduced from the formulas given in the corresponding sections.]
Change history
15 December 2021
An Erratum to this paper has been published: https://doi.org/10.1140/epjc/s10052-021-09897-w
Notes
Optical effects due to a plausible spatial dependence of the cold axion background have been investigated [101].
In case that the antisymmetric part of the polarization tensor is included [see Eq. (7)] and \(\eta _{\alpha }(t)\) is approximated as a constant four-vector, a similar diagonalization for the whole
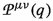 holds. However, the involved eigenvectors are complex and the eigenwaves are elliptically polarized, producing a sort of Faraday effect. An example of this scenario is given by a charged-nonsymmetric magnetized plasma of electrons and positrons [117].
holds. However, the involved eigenvectors are complex and the eigenwaves are elliptically polarized, producing a sort of Faraday effect. An example of this scenario is given by a charged-nonsymmetric magnetized plasma of electrons and positrons [117].Studies relying on the Virial theorem corroborate this upper limit. For details, we refer the reader to Ref. [112].
When taking into account the resonant phenomena owing to the singularity of the polarization tensor in momentum space in the point, where the photon creates a free or bound pair (the positronium atom), it was shown that the capture effect is present in QED. Its role in QED was reduced to a certain increase of the interval where he photon freely propagates before it turns into the pair. We shall not take this correction into account in the consideration that follows.
As for mode-3 photons being not affected by the presence of ALPs these could contribute to the plasma creation only if their energy is larger than \(m_{e}\left[ 1+\left( 1+b\right) ^{1/2}\right] >2m_{e}\). For sufficiently large magnetic field they cannot save the necessary plasma creation mechanism resting on the less energetic mode-2 photons, once the latter ones are excluded from the game by the presence of ALPs, as described above.
Kinematically, the process of pair creation by a “photon” belonging to the massive branch is allowed provided \(q_{0}^{2}-q_{\parallel }^{2}\geqslant 4m_e^2\). However, the curvature \(\gamma \)-quantum, i.e. the one emitted in the pulsar magnetosphere by an electron moving along a curved magnetic line of force, is presumably the standard zero-mass photon. The option of creating excitations belonging to the masive branch is not seen. Thereby, the plasma creation by the massive-branch “photon” is left beyond discussion.
Note that in mode-3 the function \(f(q_\perp ^2)\) is proportional to \(q^2_\perp \) at small \(q_\perp \). Therefore, this region of momentum is an arena for utmost manifestation of birefringence.
In the optical regime, polarization measurements are within reach. They currently provide evidences for vacuum birefringence in radiation coming from isolated neutron stars [86].
Traditionally, the appearance of the Landau pole is a result of developing a perturbative calculation of the polarization tensor when the magnetic field is not present. However, there are theoretical evidences relying on nonperturbative procedures which show that a point-like charge can be screened fully to zero for asymptotically large momentum [145, 146].
The integral tabulated in Ref. [150] reads
$$\begin{aligned} \int _0^\infty dx\; e^{-\alpha x } J_0(\beta \sqrt{x^2+2\gamma x})=e^{\alpha \gamma }\frac{e^{-\gamma \sqrt{\alpha ^2+\beta ^2}}}{\sqrt{\alpha ^2+\beta ^2}}. \end{aligned}$$Changing the variable to \(t=(x^2+2\gamma x)^{1/2}\), it becomes
$$\begin{aligned} \int _0^\infty \frac{dt\; t}{\sqrt{t^2+\gamma ^2}}J_0(\beta t)e^{-\alpha \sqrt{t^2+\gamma ^2}}=\frac{e^{-\gamma \sqrt{\alpha ^2+\beta ^2}}}{\sqrt{\alpha ^2+\beta ^2}} \end{aligned}$$which is the desired representation for our calculations.
Valid in a shallow well potential
References
R.D. Peccei, H.R. Quinn, CP conservation in the presence of pseudoparticles. Phys. Rev. Lett. 38, 1440 (1977)
F. Wilczek, Problem of strong P and T invariance in the presence of instantons. Phys. Rev. Lett. 40, 279 (1978)
S. Weinberg, A new light boson? Phys. Rev. Lett. 40, 223 (1978)
T.W. Donnelly, S.J. Freedman, R.S. Lytel, R.D. Peccei, M. Schwartz, Do axions exist? Phys. Rev. D 18, 1607 (1978)
A. Zehnder, S.J. Freedman, R.S. Lytel, R.D. Peccei, M. Schwartz, Axion search in a monochromatic transition: a new lower limit for the axion mass. Phys. Lett. B 104, 494 (1981)
M. Dine, W. Fischler, M. Srednicki, A simple solution to the strong CP problem with a harmless axion. Phys. Lett. B 104, 199 (1981)
A.R. Zhitnitskii, On possible suppression of the axion–hadron interactions. Yad. Fiz. 31, 497 (1980) [Sov. J. Nucl. Phys. 31, 260 (1980) (translation)]
J.E. Kim, Weak-interaction singlet and strong CP invariance. Phys. Rev. Lett. 43, 103 (1979)
M.A. Shifman, A.I. Vainshtein, V.I. Zakharov, Can confinement ensure natural CP invariance of strong interactions? Nucl. Phys. B 166, 493 (1980)
F. Wilczek, Two applications of axion electrodynamics. Phys. Rev. Lett. 58, 1799 (1987)
F.W. Hehl, Y.N. Obukhov, J.P. Rivera, H. Schmid, Relativistic nature of a magnetoelectric modulus of \({{\rm Cr}}_2{{\rm O}}_3\) crystals: a four-dimensional pseudoscalar and its measurement. Phys. Rev. A 77, 022106 (2008)
R. Li, J. Wang, X.L. Qi, S.C. Zhang, Dynamical axion field in topological magnetic insulators. Nat. Phys. 6, 284 (2010)
H. Ooguri, M. Oshikawa, Instability in magnetic materials with a dynamical axion field. Phys. Rev. Lett. 108, 161803 (2012)
J. Jaeckel, A. Ringwald, The low-energy frontier of particle physics. Annu. Rev. Nucl. Part. Sci. 60, 405 (2010)
A. Ringwald, Exploring the role of axions and other WISPs in the dark universe. Phys. Dark Univ. 1, 116 (2012)
J.L. Hewett et al., The Proceedings of the 2011 workshop on Fundamental Physics at the Intensity Frontier, Argone National Laboratory (2012). arXiv:1205.2671 [hep-ex]
R. Essig et al., Working Group Report: New Light Weakly Coupled Particles. arXiv:1311.0029 [hep-ph]
S. Alekhin et al., A facility to search for hidden particles at the CERN SPS: the SHiP physics case. Rep. Prog. Phys. 79, 124201 (2016)
E. Aprile et al. [XENON Collaboration], Excess electronic recoil events in XENON1T. Phys. Rev. D 102, 072004 (2020)
R. Cameron et al. [BFRT Collaboration], Search for nearly massless, weakly coupled particles by optical techniques. Phys. Rev. D 47, 3707 (1993)
A. Cadène et al., Vacuum magnetic linear birefringence using pulsed fields: status of the BMV experiment. Eur. Phys. J. D 68, 16 (2014)
S.J. Chen et al. [Q&A Collaboration], Q & A experiment to search for vacuum dichroism, pseudoscalar-photon interaction and millicharged fermions. Mod. Phys. Lett. A 22, 2815 (2007)
H.H. Mei et al. [Q&A Collaboration], Axion search with Q & A experiment. Mod. Phys. Lett. A 25, 983 (2010)
F. Della Valle et al. [PVLAS Collaboration], First results from the new PVLAS apparatus: a new limit on vacuum magnetic birefringence. Phys. Rev. D 90, 092003 (2014)
J.T. Mendonça, Axion excitation by intense laser fields. Eurphys. Lett. 79, 21001 (2007)
H. Gies, Strong laser fields as a probe for fundamental physics. Eur. Phys. J. D 55, 311 (2009)
B. Döbrich, H. Gies, Axion-like-particle search with high-intensity lasers. JHEP 1010, 022 (2010)
S. Villalba-Chávez, A. Di Piazza, Axion-induced birefringence effects in laser driven nonlinear vacuum interaction. JHEP 1311, 136 (2013)
S. Villalba-Chávez, Laser-driven search of axion-like particles including vacuum polarization effects. Nucl. Phys. B 881, 1 (2014)
S. Villalba-Chávez, T. Podszus, C. Müller, Polarization-operator approach to optical signatures of axion-like particles in strong laser pulses. Phys. Lett. B 769, 233 (2017)
A.S. Chou et al. [GammeV (T-969) Collaboration], Search for axion-like particles using a variable baseline photon regeneration technique. Phys. Rev. Lett. 100, 080402 (2008)
J.H. Steffen, A. Upadhye, The GammeV suite of experimental searches for axion-like particles. Mod. Phys. Lett. A 24, 2053 (2009)
A. Afanasev et al., New experimental limit on optical photon coupling to light neutral scalar bosons. Phys. Rev. Lett. 101, 120401 (2008)
P. Pugnat [OSQAR Collaboration], Results from the OSQAR photon regeneration experiment: No light shining through a wall. Phys. Rev. D 78, 092003 (2008)
C. Robilliard et al., No light shining through a wall: Results from a photoregeneration experiment. Phys. Rev. Lett. 99, 190403 (2007)
M. Fouche et al., Search for photon oscillations into massive particles. Phys. Rev. D. 78, 032013 (2008)
K. Ehret et al. [ALPS collaboration], New ALPS results on hidden-sector lightweights. Phys. Lett. B 689, 149 (2010)
R. Balou et al. [OSCAR collaboration], New exclusion limits on scalar and pseudoscalar axionlike particles from light shining through a wall. Phys. Rev. D. 92, 092002 (2015)
E. Witten, Some properties of O(32) superstrings. Phys. Lett. B 149, 351 (1984)
P. Svrcek, E. Witten, Axions in string theory. JHEP 06, 051 (2006)
O. Lebedev, S. Ramos Sanchez, The NMSSM and string theory. Phys. Lett. B 684, 48 (2010)
M. Cicoli, M. Goodsell, A. Ringwald, The type IIB string axiverse and its low-energy phenomenology. JHEP 1210, 146 (2012)
L. Covi, J.E. Kim, L. Roszkowski, Axinos as cold dark matter. Phys. Rev. Lett. 82, 4180 (1999)
G.G. Raffelt, Axions-motivation, limits and searches. J. Phys. A 40, 6607 (2007)
L.F. Abbott, P. Sikivie, A cosmological bound on the invisible axion. Phys. Lett. B 120, 133 (1983)
J. Preskill, M.B. Wise, F. Wilczek, Cosmology of the invisible axion. Phys. Lett. B 120, 127 (1983)
L.D. Duffy, K. van Bibber, Axions as dark matter particles. New J. Phys. 11, 105008 (2009)
P. Sikivie, Dark matter axions. Int. J. Mod. Phys. A 25, 554 (2010)
H. Baer, A.D. Box, H. Summy, Neutralino versus axion/axino cold dark matter in the 19 parameter SUGRA model. JHEP 1010, 023 (2010)
A. Melchiorri, A.D. Palosa, A. Strumia, New bounds on millicharged particles from cosmology. Phys. Lett. B 650, 416 (2007)
G. Galanti, M. Roncadelli, Astrophysical axion bounds diminished by screening effects. J. High Energy Astrophys. 20, 1 (2018)
I.G. Irastorza, J. Redondo, New experimental approaches in the search for axion-like particles. Prog. Part. Nucl. Phys. 102, 89 (2018)
G.G. Raffelt, Astrophysical axion bounds diminished by screening effects. Phys. Rev. D 33, 897 (1986)
G.G. Raffelt, Particle physics from stars. Annu. Rev. Nucl. Part. Sci. 49, 163 (1999)
G.G. Raffelt, Astrophysical axion bounds. Lect. Notes Phys. 741, 51 (2008)
R.M. Manchester, G.B. Hobbs, A. Teoh, M. Hobbs, The Australia Telescope National Facility Pulsar Catalogue. Astron. J. 129, 1993 (2005)
C. Kouveliotou et al., An X-ray pulsar with a superstrong magnetic field in the soft gamma-ray. Nature 393, 235 (1998)
A.I. Ibrahim, J.H. Swank, W. Parke, New evidence for proton cyclotron resonance in a magnetar strength field from SGR 1806-20. Astrophys. J. Lett. 584, L17 (2003)
J.S. Bloom, S.R. Kulkarni, F.A. Harrison, T. Prince, E.S. Phinney, D.A. Frail, Expected characteristics of the subclass of supernova gamma-ray bursts (S-GRBs). Astrophys. J. 506, L105 (1998)
V.B. Berestetsky, E.M. Lifshits, L.P. Pitayevsky, Quantum Electrodynamics (Pergamon Press, Moscow, 1989)
M.D. Schwartz, Quantum Field Theory and the Standard Model (Cambridge University Press, Cambridge, 2014)
A. Shabad, Polarization of the Vacuum and Quantum Relativistic Gas in an External Field (Nova Science Publs, New York, 1991)
Trudy Fiz, Inst. Akad. Nauk SSSR 192, 5 (1988)
W. Dittrich, H. Gies, Probing the Quantum Vacuum. Perturbative Effective Action Approach in Quantum Electrodynamics and its Application, Tracts Mod. Phys., vol. 166. Springer, New York (2000)
A.E. Shabad, Cyclotronic resonance in the vacuum polarization. Lett. Nuovo Cimento 3, 457 (1972)
A.E. Shabad, V.V. Usov, Gamma-quanta capture by magnetic field and pair creation suppression in pulsars. Nature (London) 295, 215 (1982)
A.E. Shabad, V.V. Usov, Propagation of \(\gamma \)-radiation in strong magnetic fields of pulsars. Astrophys. Space Sci. 102, 327 (1984)
A.E. Shabad, Photon propagation in a supercritical magnetic field. Sov. Phys. JETP 98, 186 (2004)
H. Herold, H. Ruder, G. Wunner, Can \(\gamma \) quanta really be captured by pulsar magnetic fields? Phys. Rev. Lett. 54, 1452 (1985)
A.E. Shabad, V.V. Usov, Gamma-quanta conversion into positronium atoms in a strong magnetic field. Astrophys. Space Sci. 117, 309 (1985)
A.E. Shabad, V.V. Usov, Photon dispersion in a strong magnetic field with positronium formation: theory. Astrophys. Space Sci. 128, 377 (1986)
S.L. Adler, J.N. Bahcall, C.G. Callan, M.N. Rosenbluth, Photon splitting in a strong magnetic field. Phys. Rev. Lett. 25, 1061 (1970)
S.L. Adler, Photon splitting and photon dispersion in a strong magnetic field. Ann. Phys. 67, 599 (1971)
S.L. Adler, C. Schubert, Photon splitting in a strong magnetic field: recalculation and comparison with previous calculations. Phys. Rev. Lett. 77, 1695 (1996)
L.A. Vassilevskaya, N.V. Mikheev, A.Ya. Parkhomenko, Axion self-energy in a magnetic field. Phys. Atom. Nucl. 64, 294 (2001)
N.V. Mikheev, D.A. Rumyantsev, YuE Shkol’nikova, On the resonant production of axions in a magnetars magnetosphere. JETP Lett. 90, 604 (2009)
Y.N. Gnedin et al., Radio emission of the magnetar SGR 1806-20: evolution of the magnetic field in the region of the radio afterglow. Astron. Rep. 51, 863 (2007)
Y.N. Gnedin et al., Magnetar giant flare oscillations and the nuclear symmetry energy. Phys. Rev. C 90, 025802 (2014)
McGill SGR/AXP Online Catalog. http://www.physics.mcgill.ca/~pulsar/magnetar/main.html
F.M. Walter, S.J. Wolk, R. Neuhäuser, Discovery of nearby isolated neutron star. Nature 379, 233 (1996)
V. Burtwitz, V.E. Zavlin, R. Neuhäuser, P. Predehl, J. Trümper, A.C. Brinkman, The Chandra LETGS high resolution X-ray spectrum of isolated neutron star RX J1856.5-3754. A & A 379, L35 (2001)
V. Burtwitz, F. Haberl, R. Neuhäuser, P. Predehl, J. Trümper, V.E. Zavlin, The thermal radiation of the isolated neutron star RX J1856.5-3754 observed with Chandra and XMM-Newton. A & A 399, 1109 (2003)
M.H. van Kerkwijk, D.L. Kaplan, Timing the nearby isolated neutron star RX J1856.5-3754. Astrophys. J. 673, 163 (2008)
F.M. Walter, T. Eisenbeiss, J.M. Lattimer, B. Kim, V. Hambaryan, R. Neuhäuser, Revisiting the parallax of the isolated neutron star RX J1856.5-3754 using HST/ACS imaging. Astrophys. J. 724, 669 (2010)
N. Sartore, A. Tiengo, S. Mereghetti, A. De Luca, R. Turolla, F. Harberl, Spectral monitoring of RX J1856.5-3754 with XMM-Newton. A & A 541, 66 (2012)
R.P. Mignani, V. Testa, D.G. Caniulef, R. Taverna, R. Turolla, S. Zane, K. Wu, Evidence for vacuum birefringence from the first optical-polarimetry measurement of the isolated neutron star RX J1856.5-3754. Mon. Not. R. Astron. Soc. 465, 492 (2017)
A. Hook, Y. Kahn, B. Safdi, Z. Sun, Radio signal from axion dark matter conversion in neutron star magnetospheres. Phys. Rev. Lett. 121, 241102 (2018)
B. Safdi, Z. Sun, Y. Chen, Detecting axion dark matter with radio lines from neutron star populations. Phys. Rev. D 99, 123021 (2019)
M. Buschmann, R.T. Co, C. Dessert, B.R. Safdi, Axion emission can explain a new hard x-ray excess from nearby isolated neutron stars. Phys. Rev. Lett. 126, 021102 (2021)
J.W. Foster, et. al, Green bank and Effelsberg Radio Telescope searches for axion dark matter conversion in neutron star magnetospheres. Phys. Rev. Lett. 125, 171301 (2020)
A.E. Shabad, V.V. Usov, Modified Coulomb Law in a strongly magnetized vacuum. Phys, Rev. Lett. 98, 180403 (2007)
A.E. Shabad, V.V. Usov, Electric field of a point-like charge in a strong magnetic field and ground state of a hydrogen-like atom. Phys. Rev. D 77, 025001 (2008)
N. Sadooghi, A. Sodeiri Jalili, New look at the modified Coulomb potential in a strong magnetic field. Phys. Rev. D. 76, 065013 (2007)
T.C. Adorno, D.M. Gitman, A.E. Shabad, Coulomb field in a constant electromagnetic background. Phys. Rev. D 93, 125031 (2016)
R.J. Elliott, R. Loudon, Theory of the absorption edge in semiconductors in a high magnetic field. J. Phys. Chem. Solids 15, 196 (1960)
M.I. Vysotsky, Atomic levels in superstrong magnetic fields and D = 2 QED of massive electrons: Screening. JETP Lett. 92, 15 (2010)
B. Machet, M.I. Vysotsky, Modification of Coulomb law and energy levels of the hydrogen atom in a superstrong magnetic field. Phys. Rev. D. 83, 025022 (2011)
V.S. Popov, B.M. Karnakov, On the spectrum of the hydrogen atom in an ultrastrong magnetic field. JETP 114, 1 (2012)
V.S. Popov, B.M. Karnakov, Zh. Eksp. Teor. Fiz. 141, 5 (2012)
R. Perna, W.C.G. Ho, L. Verde, M. van Adelsberg, R. Jimenez, Signatures of photon-axion conversion in the thermal spectra and polarization of neutron stars. Astrophys. J. 748, 116 (2012)
J.I. McDonal, L.B. Ventura, Optical properties of dynamical axion backgrounds. Phys. Rev. D 101, 123503 (2020)
J.I. Read, The local dark matter density. J. Phys. G 41, 063101 (2014)
P.F. de Salas et al., On the estimation of the local dark matter density using the rotation curve of the Milky Way. JCAP 10, 037 (2019)
E. Masaki, A. Aoki, J. Soda, Stability of axion dark matter-photon conversion. Phys. Rev. D 101, 043505 (2020)
A. Boyarsky, O. Ruchayskiy, M. Shaposhnikov, Long-range magnetic field in the ground state of the standard model plasma. Phys. Rev. Lett. 109, 111602 (2012)
S.M. Carroll, G.B. Field, R. Jackiw, Limits on a Lorentz- and parity-violating modification of electrodynamics. Phys. Rev. D 41, 1231 (1990)
J.F. Nieves, P.B. Pal, Third electromagnetic constant of an isotropic medium. Am. J. Phys. 62, 207 (1994)
A. Adrianov, D. Espriu, The axion shield. Phys. Lett. B 684, 101 (2010)
S. Karki, B. Altschul, Problems with Lorentz violation originating from a cosmologically varying pseudoscalar field. Phys. Rev. D 102, 035009 (2020)
D. Espriu, A. Renau, Photon propagation in a cold axion background with and without magnetic field. Phys. Rev. D 85, 025010 (2012)
S. Villalba-Chávez, A. Golub, C. Müller, Axion-modified photon propagator, Coulomb potential and Lamb-shift. Phys. Rev. D 98, 115008 (2018)
R. Mallick, S. Schramm, V. Dexheimer, A. Bhattacharyya, Magnetic field and neutron stars: a comprehensive study. Proc. Sci. ICPAQGP2015, 066 (2017)
A.E. Shabad, V.V. Usov, Real and virtual photons in an external constant electromagnetic field of most general form. Phys. Rev. D. 81, 125008 (2010)
I.A. Batalin, A.E. Shabad, Kratkie Soobshchenia po Fizike 60, 894 (1971)
I.A. Batalin, A.E. Shabad, Green’s function of a photon in a constant homogeneous electromagnetic field of general form. Sov. Phys. JETP 33, 483 (1971)
A.E. Shabad, Photon dispersion in a strong magnetic field. Ann. Phys. 90, 166 (1975)
H. Pérez-Rojas, A.E. Shabad, Polarization of relativistic electron and positron gas in a strong magnetic field. Propagation of electromagnetic waves. Ann. Phys. 121, 432 (1979)
V.V. Skobelev, Izv. Vyssh. Uchebn. Zaved. Fiz. No. 10, 142 (1975)
A.E. Shabad, Kratkie Soobshcheniapo Fizike (Sov. Phys. Lebedev Inst. Reps.) 3, 13 (1976)
D.B. Melrose, R.J. Stoneham, Vacuum polarization and photon propagation in a magnetic field. Nuovo Cimento A 32, 435 (1976)
J.S. Heyl, L. Hernquist, Birefringence and dichroism of the QED vacuum. J. Phys. A 30, 6485 (1997)
T. Vachaspati, Magnetic fields from cosmological phase transitions. Phys. Lett. B 265, 258 (1991)
K. Enqvist, P. Olesen, V. Semikoz, Galactic dynamo and nucleosynthesis limit on the Dirac neutrino masses. Phys. Rev. Lett. 69, 2157 (1992)
M. Arik et al., Search for sub-eV mass solar axions by the CERN axion solar telescope with 3He buffer gas. Phys. Rev. Lett. 107, 261302 (2011)
V. Anastassopoulos et al., New CAST limit on the axion–photon interaction. Nat. Phys. 13, 584 (2017)
V.V. Usov, Millisecond pulsars with extremely strong magnetic fields as a cosmological source of \(\gamma \)-ray bursts. Nature 357, 472 (1992)
J.I. Katz, Yet another model of gamma-ray bursts. Astrophys. J 490, 633 (1997)
M.A. Ruderman, L. Tao, W. Kluzniak, A central engine for cosmic gamma-ray burst sources. Astrophys. J 542, 243 (2000)
J. Jaeckel, M. Spannowsky, Probing MeV to 90 GeV axion-like particles with LEP and LHC. Phys. Lett. B 753, 482 (2016)
L.B. Leinson, V.N. Oraevskii, Positronium-photon and photon-positronium quantum transitions in strong magnetic fields. Sov. J. Nucl. Phys. 42, 245 (1985)
L.B. Leinson, V.N. Oraevskii, Gamma-positronium in strong magnetic fields. Phys. Lett. B 165, 422 (1985)
A.Y. Potekhin, Atmospheres and radiating surfaces of neutron stars. Phys. Usp. 57(8), 735 (2014)
L. Di Luzio, F. Mescia, E. Nardi, Redefining the axion window. Phys. Rev. Lett. 118, 031801 (2017)
L. Di Luzio, F. Mescia, E. Nardi, Window for preferred axion models. Phys. Rev. D 96, 075003 (2017)
B. Marx et al., Determination of high-purity polarization state of X-rays. Opt. Commun. 284, 915 (2011)
B. Marx et al., High-precision X-ray polarimetry. Phys. Rev. Lett. 110, 254801 (2013)
H.P. Schlenvoigt, T. Heinzl, U. Schramm, T.E. Cowan, R. Sauerbrey, Detecting vacuum birefringence with x-ray free electron lasers and high-power optical lasers: a feasibility study. Phys. Scr. 91, 023010 (2016)
P. Soffita et al., XIPE: the X-ray imaging polarimetry explorer. Exp. Astron. 36, 523 (2013)
D. Bernard [HARPO Collaboration], Polarimetry of cosmic gamma-ray sources above \(e^+e^-\) pair creation threshold. Nucl. Instrum. Methods A 729, 765 (2013)
W.B. Iwakiri et al., Performance of the PRAXyS X-ray polarimeter. Nucl. Instrum. Methods A 838, 89 (2016)
I. Caiazzo, J. Heyl, Vacuum birefringence and the X-ray polarization from black-hole accretion disks. Phys. Rev. D 97, 083001 (2018)
C. Wang, D. Lai, Polarization evolution in a strongly magnetized vacuum: QED effect and polarized X-ray emission from magnetized neutron stars. Mon. Not. R. Astron. Soc. 398, 515 (2009)
E. Gabrielli, K. Huitu, S. Roy, Photon propagation in magnetic and electric fields with scalar/pseudoscalar couplings: a new look. Phys. Rev. D. 74, 073002 (2006)
M. Göckeler, R. Horsley, V. Linke, P. Rakow, H. Stüben, Is there a Landau pole problem in QED? Phys. Rev. Lett. 80, 4119 (1998)
H. Gies, J. Jaeckel, Renormalization flow of QED. Phys. Rev. Lett. 93, 110405 (2004)
L.D. Landau, A.A. Abrikosov, I.M. Khalatnikov, Dokl. Akad. Nauk SSSR 95, 497 (1954)
E.J. Ferrer, A. Sanchez, Magnetic field effect in the fine-structure constant and electron dynamical mass. Phys. Rev. D 100, 096006 (2019)
F.W.J. Olver, D.W. Lozier, R.F. Boisvert, C.W. Clark, NIST Handbook of Mathematical Functions (Cambridge University Press, Cambridge, 2010)
I.S. Gradshteyn, I.M. Ryzhik, Table of Integrals, Series and Products, 7th edn. (Elsevier, San Diego, 2007)
Acknowledgements
S.V.-C. and C.M. thank A. Golub for useful discussions. Both authors gratefully acknowledge the funding by the German Research Foundation (DFG) under Grants No. 258838303 (MU 3149/2-1) and No. 388720772 (MU 3149/5-1). A. Shabad is thankful to the University of Düsseldorf for the kind hospitality extended to him during his research visit in 2016. He acknowledges the support of the Russian Foundation for Basic Research under the project No. 20-02-00193.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original online version of this article was revised: The affiliation ’P.N. Lebedev Phys. Inst. Russian Academy of Sciences, Leninsky prospect 53, Moscow 119991, Russia’ for author A. E. Shabad was missing. .
Appendices
Appendix A: Higher order contributions in strong fields [\(\mathfrak {b}\gg 1\)]
This appendix is devoted to precise that, in the strong field regime [\(B\gg B_c\)], the polarization tensor of AED [ ] is not affected substantially by higher-order corrections to the diagram depicted in Fig. 1. To this end, we will refer to the nonlocal theory described by \(\varGamma [a]\) in Eq. (6). Bearing in mind that only one-particle-irreducible diagrams may contribute to the inverse two-point Green’s function of photons, we find the two next-to-leading order diagrams depicted in Fig. 6. The precise structure of the involved vertices is not necessary to understand the following arguments. The only important property of them to keep track of is that the three-point nonlocal vertex is proportional to \(\mathfrak {b}\), while the one connecting four points does not depend on the external field. Another important feature of this framework is that the photon propagator involved in each of these diagrams is the one modified by the leading order contribution of the polarization tensor in Eq. (7). This axion-modified photon propagator has been determined explicitly in Eqs. (36), and behaves as
] is not affected substantially by higher-order corrections to the diagram depicted in Fig. 1. To this end, we will refer to the nonlocal theory described by \(\varGamma [a]\) in Eq. (6). Bearing in mind that only one-particle-irreducible diagrams may contribute to the inverse two-point Green’s function of photons, we find the two next-to-leading order diagrams depicted in Fig. 6. The precise structure of the involved vertices is not necessary to understand the following arguments. The only important property of them to keep track of is that the three-point nonlocal vertex is proportional to \(\mathfrak {b}\), while the one connecting four points does not depend on the external field. Another important feature of this framework is that the photon propagator involved in each of these diagrams is the one modified by the leading order contribution of the polarization tensor in Eq. (7). This axion-modified photon propagator has been determined explicitly in Eqs. (36), and behaves as  when \(\mathfrak {b}\rightarrow \infty \). Hence, at very strong field strengths [\(\mathfrak {b}\gg 1\)], the two one-loop pieces in Fig. 6 turn out to be suppressed by a factor \(\propto \mathfrak {b}^{-2}\) as compared with
when \(\mathfrak {b}\rightarrow \infty \). Hence, at very strong field strengths [\(\mathfrak {b}\gg 1\)], the two one-loop pieces in Fig. 6 turn out to be suppressed by a factor \(\propto \mathfrak {b}^{-2}\) as compared with  [see Eqs. (10), (11) and (14)].
[see Eqs. (10), (11) and (14)].
Next-to-leading order irreducible diagrams which contribute to the respective two-point Green’s function. Here the internal wavy lines have to be understood as the photon propagator including the leading order term of the vacuum polarization. The filled blobs represent the nonlocal interactions vertices linked to \(\varGamma [a]\) [see Eq. (6)]
Irreducible-two-loop contributions of the inverse axion-modified photon propagator. The same notation as in Fig. 6 should be understood
We note that the insertion of the nonlocal three point vertex comes accompanied with an axion-modified photon propagator at least. This feature prevents the growing of higher order contributions with the field strength, and so, protects the perturbative character of each contribution in the expansion. For instance, at two-loop level, there are eight Feynman diagrams which contribute to the irreducible two-point function of photons [see Fig. 7]. With the exception of the last graph – which is \(\propto \mathfrak {b}^{-8}\) – the remaining six contributions are suppressed by a factor \(\propto \mathfrak {b}^{-6}\) when \(\mathfrak {b}\gg 1\). Clearly, this pattern also manifests in irreducible vertices involving more than two points, a fact that has been exploited implicitly in our two-loop analysis since the establishment of some of these diagrams relies already on the one-loop correction of the three-point nonlocal vertex, for instances. This consideration justifies the applicability of the pursued approach within pure AED up to the unitarity limit of \(B_{\text {max}}=\varLambda _{\text {UV}}^{2}\sim g^{-2},\) or \(\mathfrak {b}_{\text {max}}=(mg)^{-1}\), imposed by the nonrenornalizability.
Appendix B: Degrees of freedom in AED
In QED, there are two photon degrees of freedom that propagate in the magnetized vacuum with different dispersion laws [116]. This property of birefringence is a clear manifestation of the anisotropy induced by the external field via the polarization tensor. Let us investigate a similar issue within the framework of AED. Primarily, this theory contains three degrees of freedom: two (massless) photon degrees and one (massive) axion-like degree of freedom. The interaction cannot change the overall number of degrees of freedom. The homogeneous free-wave equation (9) for vector-potentials of mode-2 in momentum representation is satisfied separately by each of the two terms in the expansion
Hence the two arbitrary coefficients here \(\mathcal {A}_{2}^{(\pm )}(q)\) are independent of each other, i.e. there is no way to correlate the amplitudes of excited photon and axion-like waves on the basis of the field equation alone. We write a (positive frequency) solution of the free-wave equation (9) for each eigenmode as
where \(q_{0}^{\left( 2\right) }=q_{0-}\) [see Eq.(20)]. The other two values are independent of the ALPs presence and are determined by the dispersion laws of mode-1, which in the loop approximation of QED coincides with the vacuum dispersion law \(q_{0}^{\left( 1\right) }=\vert \pmb {q}\vert \), and of mode-3 whose dispersion law is of the general form \(q_{0}^{\left( 3\right) }=[q_{\parallel }^{2}+f(q_{\perp }^{2})]^{\frac{1}{2}}\), the same as \(q_{0-}\) [see Eq. (20)]. The eigenvectors \(\overline{\flat }_{j}^{\mu }\) are chosen to differ – in the rest frame of the magnetic field – from the vectors (12) by a factor: \(\overline{\flat }_{j}^{\mu }=\flat _{j}^{\mu }/(q_{\perp }B^{2})\). The division by \(q_{\perp }\) is crucial, as we shall see, to exclude mode-1 and to gather conveniently the two massless degrees of freedom in modes-2 and -3. Note that the set of eigenvectors \(\bar{\flat }_j\) remains an orthogonal basis also when the background field is absent. Therefore, these formulae may be used, too.
Then the electric \(\pmb {e}_{j}\sim q_{0}\;\bar{\pmb {\flat }}_{j}-\pmb {q}\;\bar{\flat }_{j}^{0}\) and magnetic \(\pmb {h}_{j}\sim \pmb {q}\times \bar{\pmb {\flat }}_{j}\) fields of each mode behave as:
Here \(\pmb {n}_{\perp ,\parallel }=\pmb {q}_{\perp }/\vert \pmb {q}_{\perp }\vert \) is a unit vector along the perpendicular direction of \(\pmb {B}\). It may seem that \(\pmb {e}_{\parallel }^{(2)}\) in Eq. (B.3) is singular in \(q_{\perp }=0\). This is not the case, however, because if \(q_{\perp }=0\) also \(q_{\parallel }^{2}-q_{0}^{2}=0\) for a massless branch [see Eq. (18)].
Now, in the vacuum with no background magnetic field there are two polarizational degrees of freedom, and these are modes 3 and 2. The mode-3 is identically transverse, \(\pmb {e}_3\cdot \pmb {q}=\pmb {h}_3\cdot \pmb {q}=\pmb {e}_3\cdot \pmb {h}_3=0\), whereas the mode-2 becomes transverse under the vacuum dispersion law: \(\pmb {e}_2\cdot \pmb {q}=q_{\parallel }^2\left( \pmb {q}^{2}-q_{0}^{2}\right) /q_\perp =0\) if \(q_{0}^{2}=q_{\parallel }^{2}+q_{\perp }^{2}\). In this case, the relations \(\pmb {h}_2\cdot \pmb {q}=\pmb {e}_2\cdot \pmb {h}_2=0\) are fulfilled identically. As for mode-1, it is seen from Eq. (B.3) that it nullifies in the vacuum as long as the dispersion law is \(q^{2}=0\).
In the magnetic field, mode-2 is the so-called extraordinary wave, whose longitudinal electric component is generally nonzero, \(\pmb {e}_2\cdot \pmb {q}\ne 0\), since now the dispersion law implies \(q^{2}\ne 0\). The exclusion is provided in the background magnetic field by the momentum parallel to the latter: \(\pmb {q}_{\perp }=\pmb {0}\). In this case the longitudinal component of mode-2, \(\pmb {e}_2\cdot \pmb {q}=q_{\parallel }^2(q_{\parallel }^{2}-q_{0}^{2})/q_\perp \rightarrow 0\) due to the dispersion law \(q_{0}^{2}-q_{\parallel }^{2}=f(q_{\perp }^{2})\) [see Eq. (28)], since for the massless branch the function \(f(q_{\perp }^{2})\) turns to zero as fast as \(q_{\perp }^{2}\) in QED or faster than \(q_{\perp }^{2}\) in the ALPs theory according to Eq. (21). The identically transverse mode-3 continues to represent the second degree of freedom in the magnetic field, too. As for mode-1, in the background magnetic field, at least as long as the one-loop approximation of QED is used, its dispersion law remains \(q^{2}=0\) [116]. Therefore the electric and magnetic fields in mode-1 vanish according to Eq. (B.3), leaving again only two polarizational degrees of freedom on the mass-shell \(q^2=\varkappa _j\). The vanishing of mode-1 may more directly be seen already from the expression for \(\flat _{1}^{\mu }\) in Eq. (12). The four-gradient term \(\sim q^{\mu }\) in it gives no contribution to the field strength, whereas the \(q^{2}\)-term nullifies thanks to the dispersion law \(q^{2}=0\). Therefore, with the choice of the amplitude of the free waves fixed as in Eq. (B.2), mode-1 remains unphysical for every direction of propagation. Because of this reason, this mode is not considered throughout the paper.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Villalba-Chávez, S., Shabad, A.E. & Müller, C. Magnetic dominance of axion electrodynamics: photon capture effect and anisotropy of Coulomb potential. Eur. Phys. J. C 81, 331 (2021). https://doi.org/10.1140/epjc/s10052-021-09046-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09046-3








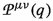 holds. However, the involved eigenvectors are complex and the eigenwaves are elliptically polarized, producing a sort of Faraday effect. An example of this scenario is given by a charged-nonsymmetric magnetized plasma of electrons and positrons [
holds. However, the involved eigenvectors are complex and the eigenwaves are elliptically polarized, producing a sort of Faraday effect. An example of this scenario is given by a charged-nonsymmetric magnetized plasma of electrons and positrons [
