1 Introduction

The properties of matter at ultra-high densities \(\left( \ge 10^{15} \text{ g }/\text{cm}^3 \right) \), in the interior of compact objects, have been a subject of study for decades in nuclear physics and astrophysics. Many equations of state (EoS) have been considered in the literature, based on different theoretical models and astronomical observations (see [1,2,3,4,5,6,7] and references therein).

The equation of state for supranuclear matter in compact stars plays a fundamental role in the mechanisms triggering supernova explosions and limiting the mass in the formation of black holes and neutron stars. The formulation of an EoS, from a microscopic and experimental point of view, is often postulated from the calculations of two-body potentials and from the nucleon-nucleon dispersion data at densities that go beyond the nuclear saturation density [8,9,10]. Regardless of the theory for determining an EoS model, it will always result in a connection between internal pressure and mass-energy density. In the case of non-rotating stars and a certain type of EoS, the structure and hydrostatic equilibrium of these objects will be determined by the constitutive equations, that is, the Tolman–Oppenheimer–Volkoff (TOV) equation and the equation that determines the mass profile within the matter configuration.

In Physics, barotropic EoS relate pressure and density straightforwardly and elegantly. A fluid which is not barotropic is baroclinic, i.e., pressure is not the only function of density, and the most paradigmatic example of a baroclinic EoS is the ideal gas equation: \(P=NRT/V\). There are other examples of baroclinic fluids: the non-local EoS,

$$\begin{aligned} P(r)=\rho (r)-\frac{2}{r^{3}}\int _{0}^{r}{\bar{r}}^{2}\rho ({\bar{r}})\ \mathrm {d}{\bar{r}} . \end{aligned}$$

In this type of non-local (or quasi-local) equation of state a collective behaviour on the physical variables \(\rho (r)\) and P(r) is present. The radial pressure P(r) is not only a function of the energy density \(\rho (r)\) at that point, but a functional throughout the rest of the configuration. Any change in the radial pressure takes into account the effects of the variations of the energy density within the entire volume (see [11,12,13,14], and references therein).

The polytropic equation of state, \(P = \kappa {\hat{\rho }}^{1 + \frac{1}{n}}\), is one of the most venerable barotropic EoS used in the context of Newtonian and relativistic theory, to deal straightforwardly and elegantly with a variety of astrophysical scenarios (see [4, 15,16,17,18] and references therein). The pioneering works of Chandrasekhar, Tooper and Kovetz [15, 16, 19] opened the way for the study of relativistic polytropes solving the constitutive equations numerically and determining the physical variables. As discussed in Ref. [20], in General Relativity, there are two possible relativistic polytropic equations of state leading to the same Newtonian limit. The difference between them is due to the role played by the baryonic mass density \({\hat{\rho }}\), or by the total energy density \(\rho \).

Most compact object models are considered spherically symmetrical, but the assumption of pressure isotropy can prove to be a somewhat simplifying premise to the matter description. The existence of an anisotropy factor in the local pressures, that is, the possibility that there are two distinct components for the pressure, one radial and the other tangential, induces a more realistic description of the internal structure of a star. On the subject of pressure anisotropy in compact object configuration the literature is numerous: see for example [21,22,23,24,25,26,27] and references therein. It is particularly stimulating a recent paper discussing the permanence in the time of the isotropic pressure assumption [28].

It is worth mentioning that there are several heuristic strategies in introducing anisotropy in relativistic fluids: the earliest one [22]; quasilocally [29]; covariantly [30]; the most recent double polytrope [31] and finally, providing a metric function or a density profile [12, 13, 32,33,34]. All these strategies have their advantages and disadvantages but have proven to lead to viable models [27]. This physical viability is important because stability and physically acceptability are essential when considering astrophysical scenarios involving self-gravitating matter configurations. In addition to solving the structure equations for a particular set of equations of state, the emerging physical variables have to comply with the several acceptability conditions stated in [35, 36].

In this work, we consider the later approaches mentioned above to introduce anisotropy in relativistic bounded matter configuration, i.e., providing a barotropic EoS and an ansatz on the energy density profile. We assumed a polytrope for the barotropic EoS and found that anisotropic polytropes could have a singular tangential sound velocity at the matter distribution surface when the polytropic index is \(n > 1\). Thus, we implemented a generalisation of the polytropic equation of state, consisting of a polytrope plus a linear and an independent density terms. Along this line, we developed an algorithm to generate exact anisotropic polytropic solutions, beginning with an ansatz on the density profiles. Thus, with this scheme, we avoided cumbersome and counter-intuitive change of variables. Following this approach, we discuss an independent generalisation the present polytropic EoS which appears during the evaluation of the work [37].

This paper is organized as follows. Section 2 describes the general equation framework of General Relativity. In Sect. 3 we list the set of acceptable conditions adhered by our models; next Sect. 4 describes the algorithm to obtain any polytrope, starting from an energy density profile. In Sect. 5 we implement the generalization of a polytropic EoS and show that both relativistic versions have the same Newtonian limit. In Sect. 6, we model two matter distributions starting from two physical interesting density profiles. Next, in Sect. 7, we discuss the acceptability conditions and finally in Sect. 8 we wrap-up our final remarks.

2 The field equations

Let us consider the interior of a dense star described by a spherically symmetric space-time line element written as

$$\begin{aligned} \mathrm {d}s^2 = \mathrm{e}^{2\nu (r)}\,\mathrm {d}t^2-\mathrm{e}^{2\lambda (r)}\,\mathrm {d}r^2- r^2 (\mathrm {d}\theta ^2+\sin ^2(\theta )\mathrm {d}\phi ^2 ), \end{aligned}$$
(1)

with regularity conditions at \(r=r_c=0\), i.e. \(\mathrm{e}^{2\nu _c}=\) constant, \(\mathrm{e}^{-2\lambda _c}= 1\), and \(\nu ^{\prime }_c=\lambda ^{\prime }_c=0\).

Additionally, the interior metric should match continuously the Schwarzschild exterior solution at the surface of the sphere, \(r=r_b\). This implies that \(\mathrm{e}^{2\nu _b}=\mathrm{e}^{-2\lambda _b}=1-\mu = 1 -2M/r_b\), where M is the total mass and \(\mu =2M/r_b\) the compactness of the configuration. From now on, subscripts b and c indicate the evaluation of a particular variable at the boundary and at the center of the matter distribution, respectively.

We shall consider a distribution of matter consisting of a non-Pascalian fluid represented by an energy-momentum tensor:

$$\begin{aligned} T_\mu ^\nu = \text{ diag }\left[ \rho (r),-P(r),-P_\perp (r),-P_\perp (r) \right] , \end{aligned}$$
(2)

where \(\rho (r)\) is energy density, with P(r) and \(P_\perp (r)\) the radial and tangential pressure, respectively.

From the Einstein field equations we obtain these physical variables in terms of the metric functions as

$$\begin{aligned} \rho (r)= & {} \frac{ \mathrm{e}^{-2\lambda } (2 r \lambda ^{\prime }-1 )+1 }{8\pi r^{2}} , \end{aligned}$$
(3)
$$\begin{aligned} P(r)= & {} \frac{{\mathrm{e}^{-2\,\lambda }} (2r \,\nu ^{\prime } +1 ) -1}{8 \pi \,{r}^{2}}\, \quad \text {and} \end{aligned}$$
(4)
$$\begin{aligned} P_\perp (r)= & {} -\frac{\mathrm{e}^{-2\lambda }}{8\pi }\left[ \frac{\lambda ^{\prime }-\nu ^{\prime }}{r}-\nu ^{\prime \prime }+\nu ^{\prime }\lambda ^{\prime }-\left( \nu ^{\prime }\right) ^2\right] , \end{aligned}$$
(5)

where primes denote differentiation with respect to r.

Now assuming

$$\begin{aligned} m(r)=\frac{r}{2} (1- \mathrm{e}^{-2\lambda } ) , \end{aligned}$$
(6)

the Tolman–Oppenheimer–Volkoff equation – i.e. \(T^{\mu }_{r \; ; \mu }~=~0\), the hydrostatic equilibrium equation – for this anisotropic fluid can be written as

$$\begin{aligned} \frac{\mathrm {d} P}{\mathrm {d} r} +(\rho +P)\frac{m + 4 \pi r^{3}P}{r(r-2m)} -\frac{2}{r}\left( P_\perp -P \right) =0 , \end{aligned}$$
(7)

and together with

$$\begin{aligned} \frac{\mathrm {d} m}{\mathrm {d} r}=4\pi r^2 \rho , \end{aligned}$$
(8)

constitute the relativistic stellar structure equations.

Clearly, it is equivalent to solve the Einstein system (3)–(5) or to integrate the structure equations (7), (8). In the first case we obtain the physical variables \(\rho (r)\), P(r) and \(P_\perp (r)\) provided the metric functions \(\lambda (r)\) and \(\nu (r)\), while in the second approach we integrate the structure equations (7), (8) giving two barotropic equations of state, \(P=P(\rho )\) and \(P_{\perp }=P_{\perp }(P(\rho ),\rho ) \equiv P_{\perp }(\rho )\).

These two EoS involving the radial and tangential pressures, together with the matching conditions – initial conditions for the system of first-order differential equations –, \(P(r_b)=P_{b}=0\) and \(m(r_b)=m_{b}=M\), lead to a system of differential equations for \(\rho (r)\) which can be solved to obtain the inner structure of a self-gravitating relativistic compact object.

As is well known, stellar compact objects have been modelled for decades as Pascalian fluids, that is, with an isotropic pressure distribution. However, a considerable number of studies have shown that the pressures within compact objects could be anisotropic, i.e. non-Pascalian fluids with unequal radial and tangential pressures, \(\Delta \equiv P_\perp -P\ne 0\) [22, 23, 27, 38], and it can influence the stability of the compact object – inducing cracking or overturning –, its mass-radius ratio, or/and its maximum mass (see [39,40,41,42] and references therein, particularly, Ref. [23]).

3 Physical acceptability conditions

Stability is a crucial concept when considering self-gravitating stellar models: only objects in stable equilibrium are of astrophysical interest. Thus, in addition to solving the structure equations (7) and (8) for a particular set of equations of state (i.e. \(P=P(\rho )\) and \(P_{\perp }=P_{\perp }(\rho )\)), the emerging physical variables have to comply with the several acceptability conditions [35]. As Ivanov [36] recently showed, there are several independent acceptability conditions to be fulfilled by any general relativistic anisotropic model of a compact object.

In this work, “physically acepted” models are those which comply with the following nine conditions:

C1:

\(2m/r < 1\); this implies

(a):

that the metric potentials \(\text {e}^{\lambda }\) and \(\text {e}^{\nu }\) are positive, finite and free from singularities within the matter distribution, satisfying \(\text {e}^{\lambda _{c}} = 1\) and \(\text {e}^{\nu _{c}}=\) constant at the center of the configuration;

(b):

the inner metric functions match to the exterior Schwarzschild solution at the boundary surface;

(c):

the interior redshift should decrease with the increase of r [43, 44];

C2:

Positive density and pressures, finite at the center of the configuration with \(P_c=P_{\perp c}\) [44];

C3:

\(\rho ^{\prime } < 0\), \(P^{\prime } < 0\) \(P_{\perp }^{\prime } < 0\) with density and pressures having maximums at the center, thus \(\rho ^{\prime }_{c}=P^{\prime }_{c} = P^{\prime }_{\perp c}=0\), with \(P_{\perp } \ge P\);

C4:

The strong energy condition for imperfect fluids: \(\rho - P - 2P_{\perp } \ge 0\) [45, 46];

C5:

The dynamic perturbation analysis restricts the adiabatic index [23, 47,48,49]

$$\begin{aligned} \Gamma = \frac{\rho + P}{P} v_s^{2} \ge \frac{4}{3} . \end{aligned}$$
C6:

Causality conditions on sound speeds: \(0 < v_{s}^2 \le 1\) and \(0 < v_{s \perp }^2 \le 1\);

C7:

The Harrison–Zeldovich–Novikov stability condition: \(\mathrm {d}M(\rho _c)/\mathrm {d}\rho _c > 0\) [50, 51];

C8:

Cracking instability against local density perturbations, \(\delta \rho = \delta \rho (r)\), briefly described in the next section and in Refs. [42, 52, 53];

C9:

The adiabatic convective stability condition \(\rho ^{\prime \prime } \le 0\), which is more restrictive than the outward decreasing density and pressure profiles [53].

Notice that the standard \(2m/r < 1\) condition is different from the stronger \((m/r)^{\prime } > 0\), as required by Ivanov in [36]. Clearly, if \((m/r)^{\prime } > 0\) we obtain well behaved metric functions but, there are cases with \((m/r)^{\prime } < 0\) having physically reasonable metric coefficients [54]. Thus, \((m/r)^{\prime } > 0\) should be considered as a sufficient but not a necessary condition to obtain “well behaved” metric potentials.

The restriction \(0 \ge P_{\perp }^{\prime } \ge P^{\prime }\) also presented in [36], implies the most simple cracking condition, i.e. \(-1 \le v^{2}_{s_\perp } -v_s^2 \le 0\) [39, 41]. But our models include a more elaborate cracking criterion with variable local density perturbations, \(\delta \rho ~=~\delta \rho (r)\) described in Refs. [42, 52, 53] (see Appendix A-2 for a discussion).

Ivanov, also, correctly requires that \(P_{\perp } \ge P\) and we shall show that, at least for the polytropic EoS, this condition leads to more stable matter configurations.

In the next sections we shall discuss the impact of barotropic and baroclinic fluids to model anisotropic compact objects.

4 All barotropic equations of state

In general, barotropic fluids are those where the pressure is the only function of density, i.e., \(P=P(\rho )\), and vice-versa. Although they may be considered unrealistic, their simplicity motivates a pedagogical value in illustrating the several approaches used to solve different systems and “physically” interesting scenarios.

In this work we shall consider the “pedagogical” barotropic EoS for radial pressure, \(P~=~P(\rho )\) and from this assumption formally integrate \(\nu ^{\prime }\) from Eq. (4) as,

$$\begin{aligned} \nu (r) = \frac{1}{2} \int \frac{1}{r} \{{\mathrm{e}}^{2\lambda } [8\pi {{r}}^2P(\rho ) +1 ] -1 \} {\mathrm{d}}r + \mathcal {\mathbf{C }} , \end{aligned}$$
(9)

where \(\mathcal {{\mathbf {C}}}\) is an integration constant that can be obtained from the condition: \({\nu (r_b)}={-\lambda (r_b)}\). A similar equation is reported in [31], but in our case we shall implement this formal integration by considering any barotropic EoS, \(P=P(\rho )\), as an input. Given any barotropic EoS and a \(\lambda \) function – so it is possible to integrate Eq. (9) –, we can determine the baroclinic EoS for the tangential pressure via Eq. (5), (or equivalently, from the TOV equation (7)) as

$$\begin{aligned} P_\perp= & {} P(\rho ) +\frac{{\mathrm{e}^{2\lambda }} }{4}{ { \left( \rho +P(\rho )\right) ( 8\,\pi \,{r}^{2}{ P(\rho )} -{\mathrm{e}^{-2\lambda }} +1 ) }}\nonumber \\&+\frac{r}{2} v_s^2 \rho ^{\prime } , \end{aligned}$$
(10)

where \(v_s^2\) is the radial sound velocity. The tangential sound velocity can be expressed through a more complex relation, as

$$\begin{aligned} v_{s_\perp }^2= & {} \frac{\mathrm{d}P_\perp }{{\mathrm{d}} \rho } = \frac{1}{2}\left[ 3 +r\frac{\rho ^{\prime \prime }}{\rho ^{\prime }} \right] v_s^2\nonumber \\&+ \frac{1}{\rho ^{\prime }}\left[ \frac{{{\mathrm{e}}^{2\lambda }} }{4}{ { \left( \rho +P(\rho )\right) ( 8\,\pi \,{r}^{2}{ P(\rho )} -{{\mathrm{e}}^{-2\lambda }}+1 ) }} \right] ^{\prime }\nonumber \\&+ \frac{r}{2} (v_s^2)^{\prime } . \end{aligned}$$
(11)

The input barotropic EoS can be either an analytic relation between the pressure and the density, \(P \leftrightarrow \rho \), or a more realistic “numeric” relation. In the next section we work out several cases with analytic EoS, implementing an exact integration of Eq. (9) (with \(P(\rho ,r)\) depending on r, \(\lambda \) and \(\lambda ^{\prime }\)). We carry out the analytic barotropic example by using a generalization of the polytropic EoS of the form \(P = \kappa {\rho }^\gamma +\alpha \rho -\beta \) with \(\kappa \), \(\alpha \) and \(\beta \) parameters to be determined. This generalization avoids some pathologies that, we will prove exist in all “standard” polytropic non-Pascalian fluids. Those models having \(\alpha ~=~\beta ~=~0\), with \(1~<~\gamma ~<~2\), unavoidably present a singularity in the tangential sound velocity (11) at the boundary of the matter distribution.

5 A generalized polytropic equation of state

The polytropic EoS deals with a variety of physically attractive astrophysical scenarios [20]. As we have mentioned, we “need” a barotropic EoS and a particular density profile, i.e. a specific \(\lambda (r)\).

In this section, we shall discuss the barotropic polytropic EoS as one of the examples considered to integrate the Eq. (9). We consider an equation that includes polytropes and what we will call the “master” equation of state:

$$\begin{aligned} P = \kappa {\hat{\rho }}^{\gamma }+\alpha {\hat{\rho }}-\beta , \end{aligned}$$
(12)

where P, \({\hat{\rho }} ={\mathcal {N}}m_{0}\) , \(\kappa \) and \(\gamma =1+1/n\) are: the isotropic pressure, the (baryonic) mass density, the polytropic constant and n the polytropic index, respectively. Notice that the number of particles is \({\mathcal {N}}\), while \(m_{0}\) represents the baryonic particle mass. Observe that \(\kappa , \alpha \) and \(\beta \) are non-independent parameters related at the boundary surface as:

$$\begin{aligned} \beta =\kappa \hat{\rho _b}^{\gamma }+\alpha {\hat{\rho }}_b . \end{aligned}$$
(13)

In Sect. 6 we use two distinct “seeds” \(\lambda (r)\)-function: a Tolman VII-like seed-metric [35, 55] and a generalization of Buchdahl’s one-parameter solution [35, 43]. In this case \(\nu \) – Eq. (9) – can be obtained analytically.

5.1 One Newtonian and two relativistic polytropes

Following [20], we briefly present both cases for our “master” polytropic EoS (12):

  1. 1.

    In the first case we are considering the baryonic particle density, \({\mathcal {N}} ={\hat{\rho }} / m_0\) with \(m_0\) the baryonic mass. The equation of state (12) is combined with the adiabatic first law of thermodynamics, resulting in:

    $$\begin{aligned}&\mathrm {d}\left( \frac{\rho }{{\mathcal {N}}} \right) + P\mathrm {d}\left( \frac{1}{{\mathcal {N}}} \right) = 0 \Rightarrow \frac{\mathrm {d}}{\mathrm {d}{{{\hat{\rho }}}}} \left( \frac{\rho }{\hat{\rho }}\right) = \frac{P}{ {{{\hat{\rho }}}}^{2}}\nonumber \\&\quad \Rightarrow \frac{1}{{{{\hat{\rho }}}}}\frac{\mathrm {d} \rho }{\mathrm {d}{\hat{\rho }}}-\frac{\rho }{{{{\hat{\rho }}}}^2}= \frac{P}{ {{{\hat{\rho }}}}^{2}} , \end{aligned}$$
    (14)

    thus

    $$\begin{aligned} \frac{\mathrm {d} \rho }{\mathrm {d}{{{\hat{\rho }}}}}-\frac{\rho }{{\hat{\rho }}} = \kappa {{{\hat{\rho }}}}^{\gamma -1}+{\alpha }-\frac{\beta }{{\hat{\rho }}} , \end{aligned}$$
    (15)

    where \(\gamma =1 + \frac{1}{n}\) is the polytropic exponent. Then Eq. (15) can be integrated and, by using (12), we obtain two possible solutions

    $$\begin{aligned} \left\{ \begin{array}{lllll} \gamma \ne 1 \Rightarrow \rho = \dfrac{\kappa {{{\hat{\rho }}}}^\gamma }{\gamma -1}+\left[ \alpha \ln ({{{\hat{\rho }}}})+ C_{1} \right] {{{\hat{\rho }}}} +\beta &{} \\ \\ \gamma = 1 \Rightarrow \rho = \left[ (\alpha +\kappa ) \ln ({{{\hat{\rho }}}})+C_{1}\right] {{{\hat{\rho }}}} +\beta \end{array} \right. \end{aligned}$$
    (16)

    where \(C_{1}\) is a constant of integration.

  2. 2.

    The second approach takes into account the energy density \(\rho \) and starts with

    $$\begin{aligned} P = \kappa \rho ^{\gamma }+\alpha \rho -\beta , \end{aligned}$$
    (17)

    so that Eq. (14) leads to

    $$\begin{aligned} \frac{\mathrm {d} \rho }{\mathrm {d}{{{\hat{\rho }}}}}-\frac{1}{{\hat{\rho }}}\left[ (1+\alpha )\rho -\beta \right] = \frac{\kappa }{{\hat{\rho }}}\ {\rho }^{\gamma } , \end{aligned}$$
    (18)

    and formally we get

    $$\begin{aligned} \int \frac{\mathrm {d} \rho }{\kappa { \rho }^{\gamma }+(1+\alpha )\rho -{\beta }}=\ln {\left[ \frac{{\hat{\rho }}}{C}\right] } \quad \text {with} \quad \gamma \ne 1 . \end{aligned}$$
    (19)

    Note that when \(\alpha =\beta =0\) we obtain

    $$\begin{aligned} \rho = \frac{{{{\hat{\rho }}}}}{{ C}} \left[ 1-\kappa \left( \frac{{\hat{\rho }}}{ C}\right) ^{\frac{1}{n}} \right] ^{-n} = \frac{{\hat{\rho }}}{\left[ C^{\frac{1}{n}} -\kappa {{{\hat{\rho }}}}^{\frac{1}{n}}\right] ^n} , \end{aligned}$$
    (20)

    as in [20], and if \(\gamma = 1\), the result is

    $$\begin{aligned} \rho = C{{{\hat{\rho }}}}^{1+\alpha + \kappa } + \frac{\beta }{1+\alpha +\kappa } , \end{aligned}$$
    (21)

    where C is the constant of integration.

5.2 The relativistic “master” polytropic equation of state

Following the second approach for relativistic polytropes – using the energy density \(\rho \) and not the baryonic mass density \({\hat{\rho }}\) –, we rewrite (17) in the form of

$$\begin{aligned} P= & {} \kappa {\rho }^{1 + \frac{1}{n}}+\alpha \rho -\beta = \kappa \left[ \frac{ e^{-2\lambda }\left( 2 r \lambda ^{\prime }-1\right) +1 }{8\pi r^{2}} \right] ^{1 +\frac{1}{n}}\nonumber \\&+ \alpha \left[ {\frac{ e^{-2\lambda }\left( 2 r \lambda ^{\prime }-1\right) +1 }{8\pi r^{2}}}\right] -\beta . \end{aligned}$$
(22)

From Eq. (22), and the fact that on the surface the radial pressure vanishes, we have

$$\begin{aligned} \beta =\kappa {\rho _b}^{1 + \frac{1}{n}}+\alpha \rho _b , \end{aligned}$$
(23)

with

$$\begin{aligned} \kappa = \frac{\sigma - \alpha \left[ 1 - \varkappa \right] }{ {\rho _c}^{\frac{1}{n}}\left[ 1 - \varkappa ^{1 + \frac{1}{n}}\right] } , \end{aligned}$$
(24)

where

$$\begin{aligned} \sigma = \frac{P_c}{\rho _c} \quad \text{ and } \quad \varkappa =\frac{ \rho _b}{\rho _c} . \end{aligned}$$
(25)

It is clear from the matching conditions \(\kappa \) depends on the significant physical parameters: \(\sigma \), \(\varkappa \) and \(\alpha \).

By using Eq. (22) in the expression of the radial and the tangential sound velocities we obtain

$$\begin{aligned} v_s^2= & {} \kappa \left[ 1+\frac{1}{n} \right] \rho ^{\frac{1}{n}} +\alpha \quad \text {and} \end{aligned}$$
(26)
$$\begin{aligned} v_{s_\perp }^2= & {} \frac{1}{2}\left[ 3+r\frac{\rho ^{\prime \prime }}{\rho ^{\prime }} \right] v_s^2+\frac{1}{\rho ^{\prime }}\left[ \frac{{\mathrm{e}^{2\lambda }} }{4} \left( \rho +P\right) \right. \nonumber \\&\left. ( 8\,\pi \,{r}^{2}{ P} -{\mathrm{e}^{-2\lambda }}+1 ) \right] ^{\prime } + \frac{\kappa r(n+1)\rho ^{\frac{1}{n}}}{2n^2\rho }{\rho ^{\prime }} , \end{aligned}$$
(27)

respectively.

Observe that the parameters in Eq. (22) are physically meaningful. Some are simple relations, like \(\sigma = P_c/\rho _c\), describing how rigid is the centre of the matter distribution. Others, like \(\varkappa = \rho _b/\rho _c\), sketches the density drop from the centre to the surface of the compact object, and from Eq. (26) it is clear that \(\alpha \) is related to the causality of the radial sound velocity \(0~<~v_s^2~<~1\). There are more complex relation like \(\kappa \) given by Eq. (24) or \(\beta \) by equation (23).

At this point, it is evident from expression (27) that, if the density vanishes at the surface of the distribution, the tangential sound velocity becomes singular at the boundary of the distribution for any polytropic index \(n > 1\). This is a general result when “standard” polytropic EoS are implemented together with the strategy to provide an educated guess on the metric functions and was the rationale for introducing a “master” polytropic EoS (22).

Note that if \(n\rightarrow \infty \) the master equation becomes a linear EoS: \(P=(\kappa +\alpha )\rho -\beta \), the equation (24) results in \(\sigma =\kappa (1-\varkappa )\), the sound velocity tends to \(v_s^2=\kappa +\alpha \) and the last term of (27) vanishes.

Clearly, we can see then that the “master” barotropic equation (22) includes the following particular cases:

  1. 1.

    For \(\alpha =\beta =0\), we get back the standard polytropic EoS:

    $$\begin{aligned} P = \kappa {\rho }^{1 + \frac{1}{n}} , \end{aligned}$$
    (28)

    where both \(\kappa = \sigma /\rho _{c}^{\frac{1}{n}} \) and n are positive parameters. The vanishing \(\beta \) implies

    $$\begin{aligned} \rho (r_b)=P(r_b)=P_\perp (r_b)=0 , \end{aligned}$$
    (29)

    at the boundary of the distribution.

    As we have pointed out above, observe from Eqs. (27) and (29), that the tangential sound velocity – for a “standard” polytropic non Pascalian fluid – clearly diverges. At the boundary surface, \(r = r_b\), the last term in equation (27) becomes infinite for \(n > 1\). The tangential sound velocity defined as (27) will be singular at the boundary surface of the distribution and this is frequently overlooked in the literature (see, for example, Refs. [31, 56,57,58,59,60,61]). This is the main motivation for introducing a more general polytropic anisotropic equation of state.

  2. 2.

    When \(n = 1\), Eq. (22) corresponds to a quadratic equation of state, i.e.

    $$\begin{aligned} P = \kappa \rho ^2 +\alpha \rho -\beta , \end{aligned}$$
    (30)

    with, the radial sound velocity

    $$\begin{aligned} v_s^2=2\kappa \rho + \alpha , \end{aligned}$$
    (31)

    and the polytropic parameter depending on

    $$\begin{aligned} \kappa = \frac{\sigma - \alpha \left[ 1 - \varkappa \right] }{ {\rho _c} [1 - \varkappa ^{2} ] } . \end{aligned}$$
    (32)

    This case was considered by Feroze and Siddiqui [62] when, using the Durgapal–Bannerji scheme [63], they generalized a previous work by Maharaj [64, 65]. In these two papers the authors show that their anisotropic solutions could describe a possible compact object.

  3. 3.

    If \(\beta =0\), this EoS is known as the generalized equation of state [66]:

    $$\begin{aligned} P = \kappa {\rho }^{1 + \frac{1}{n}} + \alpha \rho . \end{aligned}$$
    (33)

    A simple inspection shows that \(P = 0\) on the surface implies that

    $$\begin{aligned} {\alpha }=-\kappa {\rho _b}^{\frac{1}{n}} , \end{aligned}$$
    (34)

    and the radial sound velocity can be written as

    $$\begin{aligned} v_s^2 =\kappa \left[ \frac{ (n+1)}{n} \rho ^{\frac{1}{n}} -{\rho _b}^{\frac{1}{n}}\right] . \end{aligned}$$
    (35)

    Thus, the parameters \(\kappa \) and \(\sigma \) are related as follows

    $$\begin{aligned} \kappa = \frac{\sigma }{{\rho _c}^{\frac{1}{n}}\left[ 1-{\varkappa }^{\frac{1}{n}}\right] } . \end{aligned}$$
    (36)

    Equation (33) has been used for cosmological purposes, with values \(n~>~0\). In the early universe, when the energy density was high, the polytropic part dominates over the linear component [66]. Later, in a series of works [67,68,69] this EoS was implemented to model charged and neutral anisotropic polytropes.

  4. 4.

    Obviously, in the case of \(\kappa =0\), our master equation (22) corresponds to a linear state equation:

    $$\begin{aligned} P = \alpha \rho -\beta , \end{aligned}$$
    (37)

    where \(\beta =\alpha \rho _b\), now the radial sound speed is constant: \(v_s^2=\alpha \) and we have

    $$\begin{aligned} \alpha = \frac{\sigma }{1 - \varkappa } . \end{aligned}$$
    (38)

    Nilsson and Uggla [70] worked out a detailed study for an static, perfect fluid spherical distribution of matter described by: \((\eta -1)P=\rho -\rho _0\), where the constants \(\rho _0\) and \(\eta \) satisfy \(\rho _0 \ge 0\) and \(\eta \ge 1\). Later on, P.H. Chavanis [71] analyses the structure and stability of compact objects with linear EoS. In Ref. [72] the authors, considering the framework of the bag model, describe cold quark matter by using a linear EoS of the type of \(P=k(\rho -\rho _b)\), with two free parameters k and \(\rho _b\).

  5. 5.

    Recently, K.N. Singh and collaborators [73], based on some dubious motivations, discussed several viable polytropic anisotropic models with \(\alpha = 0\).

6 Analytical anisotropic polytropic solutions

As discussed previously, to integrate (9) we need to provide both, the equation of state \(P(\rho )\) and the “mass function” \(\text {e}^{2\lambda (r)}\) – or the density profile. Also observe that, by using Eq. (22), we can split the integral (9) in two parts

$$\begin{aligned} \nu= & {} \int \left[ 4\pi \, r \left( \alpha \,\rho -\beta \right) {\mathrm{e}^{2\,\lambda }} -\frac{1-{\mathrm{e}^{2\,\lambda }}}{2r}\right] \mathrm{d}r\nonumber \\&+ 4\pi \kappa \int r{\mathrm{e}^{2\,\lambda }} \rho ^{1+\frac{1}{n}}\,\mathrm{d}r+ \mathcal {{\mathbf {C}}} , \end{aligned}$$
(39)

this last expression can be very useful when considering particular cases of the equation of state, such as those shown in the previous section.

In the present work we have selected two well known \(\lambda (r)\)-seed-functions generating a pair of reasonable density profiles:

$$\begin{aligned} \text{ Seed } \text{1: }&\mathrm{e}^{2\lambda }= \left[ 1+Ar^2 + Br^4\right] ^{-1} \Rightarrow \rho = -\dfrac{3A + 5B{r}^2 }{8\pi }\, \end{aligned}$$
(40)
$$\begin{aligned} \text {and,}&\nonumber \\ \text{ Seed } \text{2: }&\mathrm{e}^{2\lambda }=\dfrac{K(1+A{r}^{2})}{K+B{r}^{2}} \Rightarrow \rho =\frac{ \left( K A-B \right) \left( 3+A{r}^{2} \right) }{8\pi K \left( 1+A{r}^{2}\right) ^{2}} . \nonumber \\ \end{aligned}$$
(41)

Here A, B and K are parameters determined from the matching conditions, \(P(r_b)=0\) and \(m(r_b)=M\).

The \(\lambda (r)\)-seed-function 1 corresponds to a two-parameters Tolman VII-like metric element [35, 55]. This family of solutions is one of the most frequent parabolic density profiles considered in stable models of neutron stars (see [74,75,76,77]). From the \(\lambda \)-function (40) we obtain the condition

$$\begin{aligned} r\frac{\rho ^{\prime \prime }}{\rho ^{\prime }}=1 \, \end{aligned}$$
(42)

in Eq. (27), which is consistent with criteria C2 and C9.

The second \(\lambda \)-function (41) is a generalization of Buchdahl’s one-parameter solution [35, 43], obtained when \(B =-A\) and \(K=2\). Now, the constraint for the derivative of the density profile turns to be

$$\begin{aligned} r\frac{\rho ^{\prime \prime }}{\rho ^{\prime }}= {\frac{5 - (22+3{A}{r}^{2} )A{r}^{2}}{ (5+ A{r}^{2} ) (1+ A{r}^{2} ) }} . \end{aligned}$$
(43)

The two parameters A and B can be determined as

$$\begin{aligned} \lambda {=}\lambda (A,B,r) \Rightarrow \rho (A,B,r) \Rightarrow \left\{ \begin{array}{l} P(A,B,r_b){=}0 \Rightarrow A \\ \quad m(B,r_b){=}\mu \, r_b/2 \Rightarrow B . \end{array} \right. \end{aligned}$$

Notice that instead of the total mass M we have used the compactness parameter \(\mu =2M/r_b\) and that in the case of the standard (\(\alpha =0\)) polytropic equation (26), we have \(P_b~=~\rho _b~=~P_{\perp b}~=~0\).

Some exact solutions of Einstein’s equations may contain only one free parameter in the metric functions which emerges from the boundary conditions, as

$$\begin{aligned} \lambda =\lambda (C,r) \Rightarrow \rho (C,r) \Rightarrow C \Leftarrow P(C,r_b)=0 , \end{aligned}$$

then \(\mu \) should have a unique precise value for any polytropic index n. The requirement to have an exact value for compactness \(\mu \) of any polytropic index n is sometimes overlooked. In Ref. [56], the authors incorrectly employed \(\mu = 0.96\) instead of the right \(\mu \) considered in [33].

In the next sections, we shall use Eq. (22) – and two \(\lambda \)-seed-functions, (40) and (41) – to model spherically symmetric and anisotropic compact objects. This scheme starts by providing a particular density profile and not a cumbersome and superfluous changes of variables to solve the field equations analytically.

Fig. 1
figure 1

Physical variables and metric functions for a matter configuration with EoS-1. The various plates illustrate different values of n having \(\sigma = 0.12\). The normalised distributions of density, radial/tangential pressures, mass and components of the metric tensor are given in terms of the dimensionless radius \(\xi =r/r_b\). All the physical and geometrical variables are well behaved and comply with acceptability criteria C1, C2, and C3

Full size image

6.1 Modeling the anisotropic, polytropic EoS-1

To build the first model, we integrate Eq. (39) by using Eq. (40), and obtain

$$\begin{aligned} \nu= & {} \frac{\lambda \left( 1+ 5\alpha \right) }{4} + \frac{A(1+\alpha )+16\pi \beta }{4\sqrt{{A}^{2}-4\,B}} \mathrm{arctanh}\left[ {\frac{A+2B {r}^{2}}{\sqrt{{A}^{2}-4B}}}\right] \nonumber \\&+ 4\pi \kappa \int r{\mathrm{e}^{2\,\lambda }} \rho ^{1+\frac{1}{n}}\,\mathrm{d}r +\mathcal {{\mathbf {C}}} . \end{aligned}$$
(44)

In the Appendix we have sketched the integration strategy for \(n = 0.5\), 1.0, 1.5 and 2.0.

Next, from the matching conditions \(P(r_b)=0\) and \(m(r_b)=M\) we solve two of the five unknown parameters:

$$\begin{aligned} \beta =k\rho _b^{1+\frac{1}{n}}+\alpha \rho _b \quad \text {and} \quad A=-\frac{\mu + B r_b^{4}}{ r_b^{2}} . \end{aligned}$$

Now, from Eq. (40), the density profile is

$$\begin{aligned} \rho = \frac{3\mu - (5Br^2-3Br_b^2 )r_b^2}{8\pi r_b^{2}} , \end{aligned}$$
(45)

and it is easy to see that:

$$\begin{aligned} \rho _c=\frac{3 (\mu +Br_b^{4} )}{ 8 \pi r_b^{2}}\quad \text{ and }\quad \rho _b= \dfrac{5\mu }{8\pi r_b^2} - \dfrac{2}{3}\rho _c , \end{aligned}$$
(46)

with the mass function expressed as

$$\begin{aligned} m= \frac{\mu }{2} \frac{{r}^{5}}{r_b^{4} } +\frac{4\pi \rho _c}{3} \left( 1-\frac{{r}^{2}}{r_b^{2}} \right) r^3 . \end{aligned}$$
(47)

Finally, the constant B (Eq. (46)) is related to the quantity \(\varkappa \), by

$$\begin{aligned} B= \frac{3\mu }{r_b^4}\frac{1-\varkappa }{3\varkappa +2} . \end{aligned}$$
(48)
Fig. 2
figure 2

Physical variables and metric functions for a matter configuration with EoS-2. The different plates illustrate various values of n having \(\sigma = 0.12\). The normalised distributions of density, radial/tangential pressures, mass and the components of the metric tensor are given in terms of the dimensionless radius \(\xi =r/r_b\). All the physical and geometrical variables are well behaved and comply with acceptability criteria C1, C2, and C3

Full size image

Figure 1 displays the profiles of the metric function and the physical variables for this EoS. The various plates illustrate different values of the polytropic index for a fixed stiffness parameter \(\sigma ~=~0.12\).

6.2 Modeling the anisotropic, polytropic EoS-2

The second \(\lambda \)-seed-function (41) drives to an integral (39) of the form

$$\begin{aligned} \nu= & {} -\left[ \frac{1+3\alpha }{4} + \frac{ A\left( 1+\alpha \right) }{2B} -\frac{8\pi \beta }{B}\left[ \frac{1}{2} - \frac{A}{B}\right] \right] \nonumber \\&\times \ln \left[ 2+ B{r}^{2}\right] -\frac{4\pi A\beta \,{r}^{2}}{B}+ \frac{\alpha \ln \left[ 1+A{r}^{2} \right] }{2} \nonumber \\&+ 4\pi \kappa \int r \mathrm{e}^{2\,\lambda }\, \rho ^{1+\frac{1}{n}} \,\mathrm{d}r +\mathcal {{\mathbf {C}}} . \end{aligned}$$
(49)

Again, the integration approach is in the appendix for \(n = 0.5, 1.0, 1.5\) and 2.0, and the conditions \(P(r_b)=0\) and \(m(r_b)=M\) lead to

$$\begin{aligned} \beta =k\rho _b^{1+\frac{1}{n}}+\alpha \rho _b , \quad A=\frac{2\mu +B r_b^2}{2 \left( 1- \mu \right) r_b^2 } . \end{aligned}$$

Now, the density can be written as

$$\begin{aligned} \rho = \frac{ \left[ 2+B r_b^2 \right] \left[ \left( 6[1-\mu ]+B r^2 \right) r_b^2 +2\mu {r}^{2} \right] \mu }{8\pi \left[ \left( 2[1 -\mu ]+B r^2\right) r_b^2 +2\mu {r}^{2} \right] ^{2}} , \end{aligned}$$
(50)

while at the surface boundary we have

$$\begin{aligned} \rho _c= \dfrac{3\mu }{16\pi } \dfrac{2+B r_b^2 }{(1 -\mu ) r_b^2} \quad \text{ and } \quad \rho _b=\frac{\mu }{32\pi ^2}\frac{ 3\mu +4\pi r_b^{2}\rho _c}{r_b^{4}\, \rho _c} . \end{aligned}$$
(51)

For this model, the mass is

$$\begin{aligned} m=\frac{4\pi \mu \rho _c \, {r}^{3}}{ 8 \pi \rho _c r^2 +3 \mu \left( 1 - \dfrac{r^2}{r_b^2} \right) } , \end{aligned}$$
(52)

and the constant B (Eq. (51)) is given by

$$\begin{aligned} B = \frac{(1-\mu ) \sqrt{ 24\varkappa +1}-\mu -6\varkappa +1 }{3\varkappa r_b^{2}} . \end{aligned}$$
(53)

Now, in Fig. 2 we plot the profiles for the metric function and the physical variables for this EoS2. Again, the various plates illustrate different polytropic indexes for a fixed stiffness parameter \(\sigma ~=~0.12\).

7 Acceptability conditions for EoS-1 and EoS-2 models

In this section we shall show that, for various values of \(n = 0.5, 1.0, 1.5\) and 2.0, there are some plausible EoS-1 and EoS-2 models, satisfying the acceptability conditions discussed in Sect. 3. The physical parameters are: \(\mu \), \(\varkappa \), \(\alpha \) and \(\sigma \), and Table 1 displays the values of the chosen parameters to model physically significant anisotropic compact objects.

Table 1 Physical parameters for analytic polytropic solutions for EoS-1 and EoS-2, which fulfil the acceptability conditions. For EoS-1 the other \(\alpha \) values correspond to: \(-\,0.10\) (\(n=1.0\)), \(-\,0.15\) (\(n=1.5\)) and \(-\,0.25\) (\(n=2.0\)). The parameter \(\sigma \) can take values between 0.10 and 0.18 approximately. The model EoS-1 could describe the mass of the millisecond pulsar in SR J1738+0333. The mass for the EoS-2 compact object is close to the lowest-mass-pulsar J0453+1559 companion (\(1.174 \pm 0.004~M_\odot \))
Full size table

The anisotropic EoS-1 could resemble the mass millisecond pulsar in SR J1738+0333. This binary system of a pulsar and a pulsating white dwarf has recently become a gravitational laboratory [78,79,80]. Now, regarding the EoS-2 model, it is also interesting to point out that those parameters could describe a low-mass pulsar. The mass for the EoS-2 compact object (\(1.15~M_\odot \)) is close to the lowest-mass-pulsar J0453+1559 companion (\(1.174 \pm 0.004~M_\odot \)), the smallest precisely measured mass for any Neutron Star.

Fig. 3
figure 3

The radial pressure, P, as a function of energy density, \(\rho \), for different values of the polytropic index n corresponding to an object of radius \(r_b=10\) Km and \(\sigma =0.12\). The displayed profiles utilize the parameters listed in Table 1, and the dotted line represents the EoS stiff limit, \(P=\rho \). The resulting models for EoS-2 are stiffer than those emerging from EoS-1, and the higher the polytropic index is, the stiffer the model becomes

Full size image
Fig. 4
figure 4

The adiabatic index \(\Gamma \) as a function of the dimensionless radius \(\xi =r/r_b\) for the EoS-1 (left) and EoS-2 (right), for different values of the index n and \(\sigma = 0.12\). The C5 condition is completely satisfied by both models

Full size image
Fig. 5
figure 5

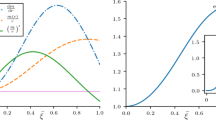
Velocity of sound vs the dimensionless radius \(\xi =r/r_b\) for a matter configuration with master anisotropic polytropic: EoS-1 (left) and EoS-2 (right). The upper plates show the radial speed of sound while the lower ones the tangential for different values of n having \(\sigma = 0.12\). In both cases, the radial sound velocity is a monotonically decreasing function. Condition C6 is satisfied by not exceeding the velocity of light and the tangential velocity of sound has a finite value on the surface of the star

Full size image
Fig. 6
figure 6

The plate on the left shows the total mass function vs central density for the EoS-2 model and in the inset the EoS-1 case. The plate on the right shows the \(\rho ''\) vs the dimensionless radius \(\xi =r/r_b\) for the EoS-2 model, on the other hand, \(\rho ''=-\,0.054\) cm\(^{-4}\) is constant for the EoS-1 model

Full size image
Fig. 7
figure 7

The function \(\delta {\mathcal {R}}/\delta \rho \) vs the dimensionless radius \(\xi =r/r_b\) for a matter configuration with master anisotropic polytropic: EoS-1 (left) and EoS-2 (right) for different values of n and \(\sigma = 0.12\). The same function is shown in the small insets but with the pressure gradient zero, i.e. \(\delta {\mathcal {R}}_p = 0\)

Full size image

Figure 3 plots the radial pressure vs energy density, with densities corresponding to an object of radius \(r_b=10\) Km and \(\sigma =0.12\) with \(0.1< \sigma < 0.18\), for both matter configuration. The models resulting from EoS-2 are stiffer than those from EoS-1.

The physical variables and the metric function distribution for the interior structures of “master polytropic spheres” are shown in Fig. 1 (EoS-1) and Fig. 2 (EoS-2). As stated in C1, \(g_{rr}~=~\mathrm{e}^{2\lambda } \ge 1\) having a maximum at the sphere boundary, while the \(g_{tt}=\mathrm{e}^{2\nu }\) component is always less than one and has a minimum at \(\xi =0\). There are unstable polytropes in Ref. [16], exhibiting a maximum for \(g_{rr}\) at some point, \(\xi \), within the sphere.

In our case, for \(\sigma = 0.12\), the density, the radial/tangential pressure distributions decrease rapidly as a function of the radius but always maintaining the conditions \(\rho > P\) and \(\rho > P_\perp \). This guarantees the fulfilment of C2, C3, and C4. For both equations of state, the tangential pressure at the boundary become larger as n increases, which suggests that for higher n values, i.e. \(n> 2\), the strong energy condition, C4, may not be satisfied.

As Fig. 4 shows, the condition for the adiabatic index (C5) is satisfied for both equations of state; while in Fig. 5 we display condition C6. That is, the minimum and maximum levels so that both the radial and tangential sound velocity do not exceed the velocity of light.

Conditions C7 and C9 have to do exclusively with the intrinsic properties of seed functions. In the case of C7 we can observe from Eqs. (47) and (52) that they are the corresponding mass functions for the equations of state EoS-1 and EoS-2. By inspection, from equation (47) it is easy to see that M is a linear function of the central density \(\rho _c\), while Eq. (52) has an asymptotic behaviour towards a value of \(\approx 1.31\) \(M_\odot \) (see the left plate of Fig. 6).

On the other hand, for condition C9 (\(\rho ''<0\)) it is easy to appreciate that for EoS-1:

$$\begin{aligned} \rho ''(r)= -\frac{5B}{4\pi }= \text{ constant } <0 , \end{aligned}$$

since \(B>0\). With the values of the parameters in Table 1, \(\rho ''=-\,0.054\) cm\(^{-4}\), while for EoS-2 we have:

$$\begin{aligned} \rho ''(r)= \frac{ A\left( 2A-B\right) (3A^2r^4+22Ar^2-5 ) }{8\pi (1+Ar^2)^4} , \end{aligned}$$

whose profile is ploted on the right side of Fig. 6. Clearly, EoS-1 fulfils the adiabatic convection criterion C9 but EoS-2 is only stable in a region near the nucleus.

Concerning the cracking instability, condition C8, we plot \(\delta {\mathcal {R}}/\delta \rho \) in Fig. 7. The small plate displays the same function with a vanishing pressure gradient, i.e, \(\delta {\mathcal {R}}_p = 0\). It is clear that when density perturbations do not affect the pressure gradient, the \(\delta {\mathcal {R}}\)-sign can change and potential cracking instabilities may appear. However, if the gradient reacts to the perturbation, \({\mathcal {R}}_p\ne 0\) then \({\mathcal {R}}\) does not change sign and the matter configuration becomes stable against cracking [42]. In our modeling EoS-1 is stable to local density perturbations, while EoS-2 is not.

8 Conclusions and final remarks

We checked most of the models for polytropic anisotropic relativistic spheres encountered in the literature and found several misunderstanding. We have noticed that some anisotropic polytropic models may have singular tangential sound velocity for polytropic indexes greater than one and this is overlooked in several papers (see, for example, Refs. [31, 56,57,58,59,60,61]). It is a general result when employing the “standard” polytropic EoS together with an ansatz on the metric functions. This pathology is not present in polytropes when other strategies are implemented obtaining the anisotropic pressure [20, 29,30,31].

We achieved a generalization to the polytropic equation of state in terms of physically meaningful parameters:

  • \(\sigma = P_c/\rho _c\), describing the stiffness at the centre of the matter distribution;

  • \(\varkappa = \rho _b/\rho _c\), sketching the density drop from the centre to the surface of the compact object,

  • and \(\alpha \), related to the causality of the radial sound velocity.

Matching conditions define the dependence of \(\kappa \) on our significant physical parameters (\(\sigma \), \(\varkappa \) and \(\alpha \)) and this dependence is not apparent in the calculations presented Table 1 of Ref. [37].

We found two new analytical anisotropic solutions for the “master” EoS starting from intuitive ansatz for the density profiles, avoiding cumbersome and redundant auxiliary variables. Both solutions were obtained by taking one of the metric functions as a seed function to integrate Eq. (9) via a barotropic equation of state, i.e. equation (22). We evaluated the relativistic master polytropic equation for different values of index n: 0.5, 1.0, 1.5 and 2.0.

We sketched an algorithm to generate exact anisotropic solutions starting from a barotropic EoS and by choosing a particular guess on the form of one of the metric functions to close the system of Einstein’s equations. Any barotropic EoS, together with a density profile, could feed equation 9 to obtain the other metric function. It is not necessary to introduce any changes of variables to expedite a possible analytical integration, and most of these substitutions (also employed in Refs. [59, 62, 64, 73]) appears to be redundant. The models discussed this work do not lack physical meaning, and we list several candidates that can be described within this anisotropic-polytropic framework. We have also checked the acceptability conditions for these two new solutions and found that the EoS-1 is stable for the whole set of nine criteria.