Abstract
We extend the already existing two-loop calculation of the effective bottom-Yukawa coupling in the MSSM. In addition to the resummation of the dominant corrections for large values of tg\(\beta \), we include the subleading terms related to the trilinear Higgs coupling \(A_b\) and contributions induced by the electroweak gauge couplings. This calculation has been extended to the NNLO corrections to the MSSM strange-Yukawa coupling. Our analysis leads to residual theoretical uncertainties of the effective Yukawa couplings at the per-cent level.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The discovery of a Standard-Model-like Higgs boson at the LHC [1, 2] completed the theory of electroweak and strong interactions. The existence of an elementary Higgs boson [3,4,5,6,7,8] is a necessary ingredient of a weakly interacting renormalizable theory with spontaneous symmetry breaking [9, 10]. The measured Higgs mass of (\(125.09 \pm 0.24\)) GeV [11] ranges at the order of the weak scale. However, if embedded in a Grand Unified Theory (GUT), radiative corrections tend to push the Higgs mass towards the GUT scale, if the Higgs couples to particles at this large scale. This problem is known as the hierarchy problem [12,13,14,15]. A solution to this problem might be offered by supersymmetry (SUSY) at the TeV scale [16,17,18,19,20,21,22].
The minimal supersymmetric extension of the Standard Model (MSSM) contains two Higgs doublets yielding five elementary Higgs bosons after electroweak symmetry breaking, two neutral CP-even (scalar) bosons h, H, one neutral CP-odd (pseudoscalar) boson A and two charged bosons \(H^\pm \). The MSSM Higgs sector is described by two input parameters at leading order, which are generally chosen as \(\mathrm{tg}\beta =v_2/v_1\), the ratio of the two vacuum expectation values \(v_{1,2}\), and the pseudoscalar Higgs mass \(M_A\), if all SUSY parameters are real. Including the one-loop and leading two-loop corrections, the upper bound on the light scalar Higgs mass is lifted to \(M_h\lesssim 130\) GeV if stop masses are constrained to less than 10 TeV [23,24,25,26,27,28]. The more recent three-loop results modify this upper bound by less than 1 GeV [29,30,31]. The Higgs couplings to gauge bosons and fermions involve mixing angles \(\alpha \) and \(\beta \), which are defined by diagonalizing the neutral and charged Higgs mass matrices. They are listed in Table 1 relative to the SM Higgs couplings.
For large \(\mathrm{tg}\beta \) values the down-type Yukawa couplings are enhanced and the up-type Yukawa couplings suppressed, if the light (heavy) scalar Higgs mass does not range at its upper (lower) bound, where the couplings become Standard-Model-like (up to a sign for the heavy scalar Higgs boson)Footnote 1. At present and future colliders this property leads to the dominance of bottom-Yukawa-coupling induced heavy-Higgs processes for large \(\mathrm{tg}\beta \) values as heavy Higgs decays into bottom quarks and heavy Higgs bremsstrahlung off bottom quarks at hadron and \(e^+e^-\) colliders. In addition, Higgs-boson production via gluon fusion \(gg\rightarrow H,A\) is dominantly induced by the bottom-loop contributions for large \(\mathrm{tg}\beta \). The strongly enhanced strange-Yukawa coupling on the other hand plays a role for the subleading charged Higgs decay mode \(H^+\rightarrow c{{\bar{s}}}\) that can reach branching ratios at the per-cent level or the reverse charged Higgs production process \(c{{\bar{s}}}\rightarrow H^+\) [33].
The soft SUSY-breaking terms in the MSSM induce mixing of the current sfermion eigenstates \({\tilde{f}}_L\) and \({\tilde{f}}_R\). The sfermion mass matrix in the current eigenstate basis is given byFootnote 2
with the factors \(r_d=1/r_u=\mathrm{tg}\beta \) for down- and up-type sfermions. The parameter \(\mu \) denotes the higgsino mass parameter of the superpotential and \(A_f\) the soft SUSY-breaking trilinear couplings. The sfermion mass eigenstates \({{\tilde{f}}}_{1,2}\) emerge from the current eigenstates \({{\tilde{f}}}_{L,R}\) through rotations by mixing angles \(\theta _f\),
which scale with the masses \(m_f\) of the SM fermions. Mixing effects are only relevant for the third-generation sfermions \({{\tilde{t}}}, {{\tilde{b}}}, {\tilde{\tau }}\) and will thus be neglected for the strange squarks in this work. The mixing angles are determined by
while the masses of the squark mass eigenstates read as
The topic of this work is the extension of the next-to-next-to-leading-order (NNLO) SUSY–QCD and top-induced SUSY–electroweak corrections of the effective bottom-Yukawa couplings [34, 35] to the terms induced by the soft SUSY-breaking trilinear coupling \(A_b\), the electroweak couplings \(\alpha _1={g'}^2/(4\pi )\), \(\alpha _2=g^2/(4\pi )\) [\(g,g'\) being the isospin and hypercharge gauge couplings, respectively] and to the SUSY–QCD corrections of the strange-Yukawa couplings. The results will play a role in all processes to which the bottom- and strange-Yukawa couplings contribute. In particular the neutral and charged Higgs decay widths and Higgs radiation off bottom quarks at hadron colliders, which constitutes the dominant heavy Higgs boson production channel for large \(\mathrm{tg}\beta \) at the LHC [36,37,38], are affected.
2 Effective bottom- and strange-Yukawa couplings
The dominant parts of the SUSY–QCD (and SUSY–electroweak) corrections to processes mediated by the bottom- and strange-Yukawa couplings can be described in terms of effective bottom- and strange-Yukawa couplings. These corrections arise in the limit of heavy supersymmetric particles relative to the energy scale of the particular process. The reliability of this large mass approximation has been analyzed for neutral MSSM Higgs decays into bottom quarks \(h/H/A\rightarrow b{{\bar{b}}}\) [39], charged Higgs decays to top and bottom quarks \(H^\pm \rightarrow tb\) [40] and Higgs radiation off bottom quarks at \(e^+e^-\) colliders [41, 42] and hadron colliders [43,44,45,46,47] by comparing to the full next-to-leading-order (NLO) results. For large values of \(\mathrm{tg}\beta \) the approximation agrees with the NLO results at the sub-per-cent level for SUSY masses in the TeV range.
2.1 Effective Lagrangian
The dominant contributions to the MSSM bottom- and strange-Yukawa couplings can be obtained from the effective Lagrangian [39, 40]
with the individual leading one-loop terms for the bottom Yukawa couplings (\(C_F= 4/3\)) [48,49,50]

and for the strange-Yukawa couplingsFootnote 3
where \(s_q = \sin \theta _q\), \(c_q = \cos \theta _q\) (\(q=t,b,c,s\)) are related to the squark mixing angles \(\theta _q\) of Eq. (3). The final contribution in the mass-eigenstate-basis can be derived as
where the \(\Delta _{q,1}\) terms have been shown to be properly resummed in this way [39]Footnote 4. The auxiliary function I is given by
The field amplitudes \(\phi _1^0\) and \(\phi _2^0\) of the neutral components of the Higgs doublets that couple to down- and up-type quarks, respectively, are transformed to the mass eigenstates h, H, A by the mixing angles \(\alpha ,\beta \)
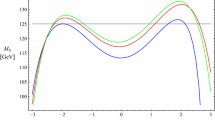
The two vacuum expectation values are connected to the Fermi constant \(G_F\) by \(v^2={v_1^2+v_2^2} = 1/({\sqrt{2}G_F})\). The would-be Goldstone field \(G^0\) is ’eaten’ by the Z boson and builds up its longitudinal component. The top-Yukawa coupling \(\lambda _t\) determines the top mass by \(m_t = \lambda _t v_2/\sqrt{2}\) at leading order. The soft SUSY-breaking trilinear couplings of the top, bottom and strange squarks are denoted by \(A_t, A_b\) and \(A_s\), the higgsino mass parameter by \(\mu \) and the strong coupling constant by \(\alpha _s\). The renormalization scale is depicted as \(\mu _R\). The corrections \(\Delta _{b,s}\) modify the relation between the bottom (strange) quark mass \(m_b~(m_s)\) and the bottom (strange) Yukawa coupling \(\lambda _b~(\lambda _s)\),
The effective Lagrangian of Eq. (5) can be expressed as (omitting the mass and Goldstone terms)
with the effective (resummed) couplings
Even though the SUSY corrections \(\Delta _q\) are loop-suppressed, they are significant for large values of \(\mathrm{tg}\beta \). In these regions they dominate the supersymmetric corrections to the bottom- and strange-Yukawa couplings. The effective Lagrangian in Eq. (5) has been derived by integrating out the heavy SUSY particles so that it is not only valid for large values of \(\mathrm{tg}\beta \). By using power counting it has been shown that the Lagrangian of Eq. (5) resums all terms of \(\mathcal{O}\left[ (\alpha _s\,\mu \,\mathrm{tg}\beta )^n\right] \) and \(\mathcal{O}\left[ (\alpha _s\,A_{b,s})^n\right] \). For the bottom-Yukawa coupling a resummation of the \({{{\mathcal {O}}}}\left[ (\lambda ^2_t\,A_t\,\mathrm{tg}\beta )^n\right] \) terms is achieved in addition [39, 40] (including mixed contributions).
2.2 Low energy theorems
The derivation of higher-order corrections to the effective Yukawa couplings would need the calculation of the related three-point functions in the low-energy limit. This, however, can be reduced to the determination of self-energy diagrams by means of low energy theorems [51,52,53,54,55]. These are based on the feature that in the limit of vanishing Higgs momentum, matrix elements with an external Higgs boson can be generated from the corresponding matrix elements without the external Higgs particle by the shifts \(v_1\rightarrow \sqrt{2}\phi _1^0\) and \(v_2\rightarrow \sqrt{2}\phi _2^{0*}\). Thus, only the calculation of the related parts of the bottom and strange quark self-energies is required. The dominant parts \(\Delta _{q,1/2}~(q=b,s)\) originate from the scalar part \(\Sigma _S(m_q^2)\) of the self-energyFootnote 5. This affects the relation between the bottom- (strange-) Yukawa coupling \(\lambda _b~(\lambda _s)\) and the mass \(m_q\) of the bottom (strange) quark,
with the dominant terms of the self-energy \(\Sigma _S(m_q^2)\) for heavy SUSY particles
The NLO–QCD parts of \(\Delta _b\) and \(\Delta _s\) in Eq. (5) can be obtained from off-diagonal mass insertions of the type \(\lambda _q (A_q v_1 - \mu v_2)\) (up to a factor \(1/\sqrt{2}\)) in the squark propagators, as shown in Fig. 1 at one-loop order.
One-loop diagrams of the SUSY–QCD contributions to a the bottom and b the strange self-energies with the off-diagonal mass insertions related to the \(\Delta _q~(q=b,s)\) corrections of the bottom- and strange-Yukawa couplings. The contributing particles involve bottom and strange quarks b, s and squarks \({\tilde{b}},{\tilde{s}}\) as well as gluinos \({\widetilde{g}}\)
This results in the finite expressions of Eqs. (6, 7) (supplemented by the SUSY–electroweak corrections originating from higgsino, wino and bino exchange to the bottom-Yukawa couplings) after transforming the fields from current-eigenstates to the mass eigenstates. These contributions are not renormalized at NLO due to the absence of tree-level bottom and strange couplings involving \(A_q\) or \(\mu \).
3 NNLO corrections
The NNLO analysis of the effective bottom- and strange-Yukawa couplings necessitates the calculation of the leading NNLO corrections to the bottom and strange self-energies. The NNLO expressions of the bottom-Yukawa couplings have been obtained in Refs. [34, 35, 56,57,58]. We will extend these results to the non-\(\mathrm{tg}\beta \)-enhanced \(A_b\) terms and to the strange Yukawa couplings. In this work we will neglect intergenerational mixing so that issues related to the flavour sector [59,60,61,62,63,64,65] can be disregarded.
3.1 Bottom-Yukawa couplings
3.1.1 SUSY–QCD corrections to \(\Delta _{b,1}\)
Since the effective insertions according to Fig. 1 are always proportional to \(A_b - \mu \,\mathrm{tg}\beta \), the contributions of all two-loop diagrams for the bottom-Yukawa coupling are the same for the \(A_b\) and the \(\mu \,\mathrm{tg}\beta \) contributions (up to the relative overall sign). The renormalization proceeds along the lines of Ref. [34, 35] so that the SUSY–QCD corrections to the \(\Delta _{b,1}\) terms are the same as for the \(\Delta _{b,2}\) contributions after renormalization (including the SUSY-restoring counter terms [66]). Denoting the (renormalized) NNLO-corrected SUSY–QCD part \(\Delta _{b,2}^{QCD}\) of Refs. [34, 35] as
with the NNLO correction \(\delta _b\) and
the effective correction to the bottom-Yukawa couplings of Eq. (8) acquires the form
where \(A_b^0\) denotes the bare trilinear coupling that is renormalized in SUSY–QCD and \(\delta _t\) the SUSY–QCD corrections to \(\Delta _{b,2}^{elw,t}\) [34, 35]. The NNLO SUSY–QCD corrections \(\delta _1\) (\(\delta _2\)) to \(\Delta _{b,2}^{elw,1}\) (\(\Delta _{b,2}^{elw,2}\)) will be derived and discussed in the next subsection. The renormalization of \(A_b\) emerges from a non-leading order contribution in our context: for the \(\overline{\mathrm{MS}}\)-renormalized trilinear coupling within dimensional regularization in \(n=4-2\epsilon \) dimensions we obtain
so that \(A_b\) is not renormalized at \({{{\mathcal {O}}}}(\alpha _s\,A_b)\). We have explicitly checked that the divergence corresponding to the counterterm of \(A_b\) is generated by the diagram of Fig. 2 with an insertion \(\lambda _b\,v_1\) (up to a factor \(1/\sqrt{2}\)) at the virtual bottom-quark line. Thus the final expression including the \({{{\mathcal {O}}}}(A_b)\) terms is given by Eq. (18) with \(A_b^0\) replaced by the renormalized \(A_b(\mu _R^2)\) coupling,
with \(\Delta _{b,1}, \Delta _{b,2}^{QCD}, \Delta _{b,2}^{elw,t}, \Delta _{b,2}^{elw,1}\) and \(\Delta _{b,2}^{elw,2}\) defined in Eq. (6).
In this work we adopt the renormalization program of Ref. [67], i.e. the counterterm for the top-Yukawa-induced electroweak contributions \(\Delta _{b,2}^{elw,t}\) is modified for the trilinear coupling \(A_t\) that is defined in the \(\overline{\mathrm{MS}}\) scheme. This leads to a vanishing counterterm for \(A_t\) at the order we are calculating.
3.1.2 SUSY–QCD corrections to \(\Delta ^{elw,1/2}_{b,2}\)
For the calculation of the SUSY–QCD corrections to the terms \(\Delta _{b,2}^{elw,1}\) and \(\Delta _{b,2}^{elw,1}\) we will reduce the associated higgsino propagators to the contributions relevant for the \(\mathrm{tg}\beta \)-enhanced corrections. For the neutralinos in the basis \((\tilde{B}, {{\tilde{W}}}^3, {{\tilde{H}}}_1^0, {{\tilde{H}}}_2^0)\), the full inverse propagator matrix is given by

where the part \({{{\mathcal {D}}}}\) is subleading in the limit of heavy SUSY particles that we are working in. Keeping only linear terms in \(\mathcal{D}\), the propagator matrix is then given by

Inserting the corresponding diagonal and off-diagonal propagators into the self-energies of Fig. 3 and keeping only the \(\mathrm{tg}\beta \)-enhanced terms in the numerators of the off-diagonal propagators contained in \({{{\mathcal {A}}}}\), we arrive at the proper expressions for \(\Delta _{b,2}^{elw,1}\) of Eq. (6) where the identities
have been used. Including only the \(\mathrm{tg}\beta \)-enhanced contributions ensures that terms proportional to \(v_2\) are kept thanks to the relation \(v\,c_\beta \mathrm{tg}\beta = v_2\) that are then shifted by the full Higgs field \(v_2 \rightarrow \sqrt{2}\phi _2^{0*}\) according to the discussion of Sect. 2.2.
One-loop diagrams of sbottom-self-energy insertions contributing to the SUSY–QCD corrections \(\Delta _{b,2}^{elw,1}\) of the bottom-quark self-energy involving bottom quarks b, bottom squarks \({\tilde{b}}\), binos \({{\tilde{B}}}\) and higgsinos \({{\tilde{H}}}_1^0\). The crossed lines indicate off-diagonal propagator contributions
For the calculation of \(\Delta _{b,2}^{elw,2}\) we have to use the off-diagonal propagators of Eq. (22) proportional to the isospin gauge coupling g, but have to include chargino propagators for the diagrams involving top squarks in addition. In the basis \((\tilde{W}^+, {{\tilde{H}}}_1^+, {{\tilde{H}}}_2^+)\), the full inverse chargino propagator matrix is given by

where the term \({{{\mathcal {D}}}}\) is subleading in the heavy-SUSY-particle limit. The propagator matrix is then obtained as

where the normalization factor reads
Inserting the corresponding \(\mathrm{tg}\beta \)-enhanced terms of the off-diagonal propagators into the self-energies of Fig. 4, we obtain the proper expressions for \(\Delta _{b,2}^{elw,2}\) of Eq. (6).
One-loop diagrams of sbottom-self-energy insertions contributing to the SUSY–QCD corrections \(\Delta _{b,2}^{elw,2}\) of the bottom-quark self-energy involving bottom quarks b, sbottoms \({\tilde{b}}\), stops \({\tilde{t}}\), winos \({{\tilde{W}}}^{3,\pm }\) and higgsinos \({{\tilde{H}}}_1^{0,\pm }\). The crossed lines indicate the \(\mathrm{tg}\beta \)-enhanced off-diagonal wino-higgsino propagator contributions
The leading \(\mathrm{tg}\beta \)-enhanced terms of the off-diagonal chargino- and neutralino-propagator-matrix entries have been used for the calculation of the two-loop SUSY–QCD corrections of corrections \(\Delta _{b,2}^{elw,1/2}\) to the bottom Yukawa couplings in Eq. (6). The relevant two-loop diagrams of the bottom self-energy are depicted in Fig. 5. The technical method of our calculation follows the analysis of Refs. [34, 35]. The diagrams of Fig. 5 are evaluated with single crosses in each sbottom/stop or gaugino/higgsino line individually. However, for the additional contributions going with \(s_b^2, c_b^2, s_t^2, c_t^2\) in Eq. (6) diagrams with three crosses have to be taken into account, too, as exemplified for one diagram involving top quarks and stops in Fig. 6. This means that there are contributions with three off-diagonal propagators inserted in the two-loop diagrams. These diagrams complete the corrections to the terms proportional to \(s_b^2, c_b^2, s_t^2, c_t^2\) in Eq. (6) by means of the relations of Eq. (23) and
For the contributions to \(\Delta _{b,2}^{elw,2}\), crosses involving the off-diagonal entry of the top-quark propagator matrix

in the \((t_L, t_R)\) basis induced by the large top mass have to be considered, too. It should be noted that the symmetry factors between the self-energies and the effective coupling of the Lagrangian have to be taken into account properly for the shift \(v_2\rightarrow \sqrt{2}\phi _2^{0*}\).
For the finite result of the two-loop corrections to \(\Delta _{b,2}^{elw,1/2}\) we have to renormalize the sbottom and stop masses as well as the sbottom and stop mixing angles. The counterterm of the \(\Delta _{b,2}^{elw,1}\) term can be derived as
where \(\Delta _{b,2}^{elw,1}\) is the NLO expression of Eq. (6). The renormalization constants are given by
where we neglected kinematical \({{{\mathcal {O}}}}(m_b)\) terms consistently but kept the full mixing-angle dependence. The scalar integrals are defined as
where \({\bar{\mu }}\) deotes the ’t Hooft mass.
For the \(\Delta _{b,2}^{elw,2}\) term we have to renormalize the stop contributions in addition so that the full counterterm is given by
with the NLO contribution \(\Delta _{b,2}^{elw,2}\) of Eq. (6), the renormalization constants \(\delta m_{\tilde{b}_i}^2, \delta \theta _b\) of Eq. (30) and
for the stop renormalization constants, where we kept all terms proportional to the top mass \(m_t\). The final results have been explicitly checked to be ultraviolet finite after renormalization. The whole calculation has been performed twice independently with different methods and implementations.
Due to the mismatch between the \((n-2)\) gluonic d.o.f. and the 2 d.o.f. of the gluinos in dimensional regularization, anomalous counterterms have to be added to restore supersymmetry [66]. This affects the SUSY-counterparts \({\hat{g}}, {\hat{g}}'\) of the electroweak gauge couplings at the \({{\tilde{B}}} q{\tilde{q}}\) and \({{\tilde{W}}} q{\tilde{q}}\) vertices (\(q = t,b\) and \({\tilde{q}}= {\tilde{b}}, {\tilde{t}}\)),
as well as the SUSY-counterparts of the Higgs Yukawa couplingsFootnote 6,
This results in anomalous counterterms of the contributions \(\Delta _{b,2}^{elw,1/2}\),
where \(\Delta _{b,2}^{elw,1/2}\) denote the one-loop expressions of Eq. (6).
3.2 Strange Yukawa couplings
The translation of the results for the bottom-Yukawa couplings to the Higgs boson couplings to strange quarks requires a careful investigation of the corresponding quark-mass contributions. Since in the calculation of the bottom-Yukawa coupling the bottom quark is treated strictly massless and the external momentum dependence is omitted, there is no difference for the individual two-loop diagrams, if the bottom parameters are replaced by their corresponding strange parameters. Care must be taken for the proper summation over all quark/squark flavours for the diagrams with gluino-self-energy insertions since the strange-squark mass coincides with the left- and right-handed squark masses of the second generation and the sbottom and stop masses of the third generation are independent. Another difference to the bottom-quark case is the absence of sizeable charm-Yukawa-induced SUSY–electroweak contributions to the strange-Yukawa coupling, since we are neglecting the charm-Yukawa coupling \(\lambda _c\). The final result can be cast into the form
where \(\delta _s\) (\(\delta _{1/2}\)) denotes the NNLO SUSY–QCD corrections to the QCD (electroweak) part of the strange Yukawa couplings and \(\Delta ^{QCD}_{s,1/2}, \Delta ^{elw, 1/2}_{s,2}\) are defined in Eq. (7). The expression above for \(\Delta _s\) is then inserted into the effective Lagrangian of Eq. (5) and into the resummed couplings of Eq. (13), respectively, resumming in this way all terms of \({{{\mathcal {O}}}}\left[ (\Delta _s)^n\right] \).
4 Results
The final results of this paper have been implemented in the program Hdecay [68,69,70]. This code computes the MSSM Higgs couplings and masses based on the RG-improved expressions of Ref. [71]. Moreover, the partial decay widths and branching ratios of the MSSM Higgs bosons are calculated including higher-order corrections [36,37,38]. For large \(\mathrm{tg}\beta \) values the dominant neutral Higgs boson decays are into \(b{{\bar{b}}}\) and \(\tau ^+\tau ^-\). In Ref. [39] their branching ratios have been analyzed including the correction \(\Delta _b\) of Eq. (6) at the one-loop level.
4.1 Higgs decays into bottom and strange quarks
The QCD and SUSY–QCD corrected partial decay widths of the neutral Higgs bosons \(\Phi =h,H,A\) into bottom quarks can be expressed as [39]
with \({\overline{m}}_b(M_\Phi )\) denoting the \(\overline{\mathrm{MS}}\) bottom mass at the scale of the Higgs mass \(M_\Phi \) and quark mass effects beyond \({{{\mathcal {O}}}}(m_b^2)\) are neglected. The QCD corrections \(\delta _\mathrm{QCD}\) and the top quark induced contributions \(\delta _t^\Phi \) are known [72,73,74,75,76,77,78,79,80,81,82,83,84,85,86] and can be found in Refs. [36,37,38] in compact form. The QCD corrections \(\delta _{\mathrm{QCD}}\) are taken into account up to \(\hbox {N}^4\)LO and the corrections \(\delta _t^\Phi \) at the NNLO level in Hdecay.
The leading contributions of the SUSY–QCD corrections [87, 88] have been absorbed in the resummed bottom-Yukawa couplings \(\tilde{g}_b^\phi \) as given in Eq. (13). The remainder \(\delta _{SQCD}^{rem}\) is small, i.e. at the sub-per-cent level, in phenomenologically relevant scenarios for large \(\mathrm{tg}\beta \) values [39]. This observation at NLO implies the expectation that at higher orders the remainders after factorizing the corrections involved in the effective Lagrangian of Eq. (12) are even smaller and thus negligible in general. This underlines that the results of our work constitute the major part of the corrections beyond NLO with tiny remainders at higher loop-levels. It should be noted that our two-loop corrections to the \(A_b,A_s\)-induced terms are formally of three-loop order of the related physical observables involving the corresponding effective Yukawa couplings, but they modify the relations between the Yukawa couplings and quark masses at NNLO. In our analysis we include the full (two-loop corrected) \(\Delta _b\) (\(\Delta _s\)) contributions including the QCD and electroweak parts in the couplings \(\tilde{g}_b^\phi \) (\({{\tilde{g}}}_s^\phi \)).
The strange Yukawa coupling plays a phenomenological role for charged Higgs decays into charm and strange quarks \(H^+\rightarrow c{{\bar{s}}}\). Neglecting regular quark mass effectsFootnote 7 this partial decay width can be expressed as [89,90,91]Footnote 8
with the same QCD-correction-factor \(\delta _{QCD}\) as in Eq. (38). The small remainder of the genuine SUSY–QCD corrections after absorbing the dominant part in the effective strange-Yukawa coupling \({{\tilde{g}}}_s^{A}\) is neglected.
4.2 Numerical results
We perform our numerical analysis of the MSSM Higgs boson decays into bottom and strange quarks for the MSSM benchmark scenario \(M_h^{125}\) [32] as a representative caseFootnote 9:
For the Higgs masses and couplings we use the RG-improved two-loop expressions of Ref. [71], so that the leading corrections at the one- and two-loop level to the Higgs masses and the effective mixing angle \(\alpha \) are taken into account. The bottom \(\overline{\mathrm{MS}}\)-mass has been chosen as \(\overline{m_b}(\overline{m_b})=4.18\) GeV, which corresponds to a pole mass \(m_b=4.84\) GeV according to the implementation in Hdecay that determines the bottom-quark pole mass from the \(\overline{\mathrm{MS}}\)-mass at the scale of the pole mass. The strange \(\overline{\mathrm{MS}}\)-mass has been initialized as \(\overline{m_s}(2~\mathrm{GeV})=95\) MeV and the strong coupling constant as \(\alpha _s(M_Z)=0.118\). The top pole mass has been taken to be \(m_t=172.5\) GeV. In the mass matrices of the stop and sbottom states effective top and bottom masses are implemented as discussed in Ref. [67]. With this set-up we obtain the following squark masses e.g. for \(\mathrm{tg}\beta =40\),
We will present the impact of the new results on the bottom- and strange-Yukawa couplings as well as related observables. Figure 7 displays the scale dependence of the SUSY–QCD parts of \(\Delta _b\) and \(\Delta _s\),
with and without the \(A_b,A_s\) contributions \(\Delta _{b,1}, \Delta _{s,1}\) for the \(M_h^{125}\) scenario. For \(\mathrm{tg}\beta =40\) the \(\Delta _b\) and \(\Delta _s\) corrections range at the level of 30%. The scale dependence is reduced significantly from one- to two-loop order to a few per cent at NNLO, while the additional contributions of the \(A_b, A_s\) terms are small, i.e. at the per-cent level, as can be inferred from the differences between the red and blue curves. The comparison between the blue and red curves shows that the additional scale dependence induced by \(A_b\) and \(A_s\) is numerically small in line with neglecting terms that are not of \({{{\mathcal {O}}}}(\mu \mathrm{tg}\beta )\) or \({{{\mathcal {O}}}}(A_{b,s})\). The effects of the contributions induced by \(A_b, A_s\) are significantly larger than the NLO remainder so that this can naturally be expected for the remainders at NNLO and beyond, too. However, in general the sizes and directions of the total \(\Delta _b\) and \(\Delta _s\) corrections depend on the MSSM scenario, in particular on the sign and size of \(\mu \) and the value of \(\mathrm{tg}\beta \). The central scales have been chosen equal to the average of the corresponding SUSY masses, i.e. \(\mu _0=(m_{{\tilde{q}}_1} + m_{{\tilde{q}}_2} + m_{{\tilde{g}}})/3\) for \(\Delta _{b,1/2}^{QCD}\), \(\Delta _{s,1/2}^{QCD}\). For the electroweak parts we have adopted \(\mu _0=(m_{{\tilde{t}}_1} + m_{{\tilde{t}}_2} + \mu )/3\) for \(\Delta _{b,2}^{elw,t}\) and the average of the involved SUSY particles for the strong-coupling scale involved in the individual contributions to \(\Delta _{q,2}^{elw,1/2}\) \((q=b,s)\) at NNLO. These choices are suitable as the appropriate natural central scales.
In Fig. 8 we present the individual and total contributions to \(\Delta _b\) and \(\Delta _s\) as a function of \(\mathrm{tg}\beta \) for the \(M_h^{125}\) scenario.Footnote 10 While the SUSY-QCD parts \(\Delta _{b/s,2}^{QCD}\) dominate the contributions, the electroweak contributions \(\Delta _{b/s,2}^{elw,t/1/2}\) amount to \({{{\mathcal {O}}}}(10\%)\) reaching up to about 20% for large \(\mathrm{tg}\beta \)-values. Especially the terms \(\Delta _{b/s,2}^{elw,t/2}\) cannot be neglected if a prediction with an accuracy at the per-cent level should be achieved. The two-loop corrections to the electroweak terms range accidentially at the per-cent level in this benchmark scenarioFootnote 11. They can be larger in other scenarios reaching a level of 10–15% in general.
Dependence of the full SUSY–QCD + SUSY–electroweak corrections \(\Delta _b\) (upper plot) and \(\Delta _s\) (lower plot) on \(\mathrm{tg}\beta \) at one-loop and two-loop order with and without the \(A_b,A_s\) contributions in the \(M_h^{125}\) scenario, and the individual contributions to \(\Delta _b\) and \(\Delta _s\)
To exemplify this, we show the size of the two-loop corrections to the terms \(\Delta _{b,s}^{elw,1/2}\) in Fig. 9 as a function of the gaugino masses \(M=M_1=M_2\) with all other MSSM parameters kept fixed at their values of the \(M_h^{125}\) scenario. For small gaugino masses the corrections can amount to more than 20%.
Partial decay widths of the heavy scalar H and the pseudoscalar A Higgs bosons to \(b{{\bar{b}}}\) (upper two plots) and charged Higgs decays to \(c{{\bar{s}}}\) (lower plot) in the \(M_h^{125}\) scenario. The dashed blue bands display the scale dependence at the one-loop level and the full red bands at the two-loop level by varying the renormalization scales of \(\Delta _b\) and \(\Delta _s\) between 1/3 and 3 times the central scale fixed by the average of the involved SUSY-particle masses
As a particular application we analyze the partial decay widths of the heavy neutral MSSM Higgs bosons into \(b{{\bar{b}}}\) pairs and of the charged Higgs boson into \(c{{\bar{s}}}\) in Fig. 10 for the \(M_h^{125}\) scenario, respectively. The two-loop parts of \(\Delta _b\) (\(\Delta _s\)) reduce the partial decay widths to \(b{{\bar{b}}}\) (\(c{{\bar{s}}}\)) pairs for the central scale choices by \({{{\mathcal {O}}}}(10\%)\). The NLO bands (dashed blue curves) and the NNLO bands (full red curves) are generated by varying the renormalization scales of \(\Delta _b\) and \(\Delta _s\) between 1/3 and 3 times the corresponding central scales \(\mu _0\).Footnote 12 A significant reduction of the dashed one-loop bands of \({{{\mathcal {O}}}}(10\%)\) to the full two-loop bands at the per-cent level can be inferred from these results which is expected based on the previously known two-loop corrections [34, 35]. All NNLO results are positioned at the lower ends of the NLO error bands.
5 Conclusions
We have calculated the NNLO corrections to the effective bottom- and strange-quark-Yukawa couplings within the MSSM, extending previous analyses to non-leading terms that are mediated by the soft SUSY-breaking trilinear couplings \(A_b,A_s\) and the weak couplings \(\alpha _1, \alpha _2\) for large values of \(\mathrm{tg}\beta \). The dominant contributions of the SUSY–QCD corrections arise from virtual two-loop squark and gluino exchange, that factorize and can be absorbed in effective Yukawa couplings. We have derived the two-loop SUSY–QCD corrections to the effective bottom- and strange-Yukawa couplings beyond the leading contributions obtained previously.
In summary, the significant scale dependence of \({{{\mathcal {O}}}}\left( 10\%\right) \) of the NLO predictions for processes involving the bottom- and strange-quark-Yukawa couplings of MSSM Higgs bosons necessitate the inclusion of NNLO corrections. For the NNLO-corrected Yukawa couplings, we observe a reduction of the scale dependence to the per-cent level. These results were previously known for the leading terms of the bottom-Yukawa couplings. In this work they have been established for the non-leading \(A_b\) and electroweak terms and the strange-Yukawa couplings. The improved NNLO results for the bottom- and strange-Yukawa couplings provide a quantitative basis for experimental analyses at the LHC and future \(e^+e^-\) colliders as the ILC.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited [Authors’ comment: Since it describes an analytical calculation and there is no external data in the manuscript.]
Notes
Scenarios with a SM-like heavy scalar Higgs boson are disfavoured by the present searches [32].
For convenience, the D-terms have been absorbed in the soft SUSY-breaking sfermion mass parameters \(M_{{{\tilde{f}}}_{L/R}}^2\).
Due to the tiny charm-Yukawa coupling \(\lambda _c\) we neglect electroweak corrections induced by \(\lambda _c\). Moreover, for the strange and charm squarks we neglect mixing effects, i.e. work with \(c_{s/c}^2 = 1\) and \(s_{s/c}^2 = 0\).
The \(A_{b,s}\) terms in the resummed expression of Eq. (8) are formally of three-loop order and thus subleading compared to the \(\Delta _{q,2}\) contributions. Electroweak contributions to \(\Delta _{q,1}\) have therefore been neglected, since these are expected to be phenomenologically irrelevant.
The fermionic self-energy can be split into a scalar, vectorial and axial-vectorial part as
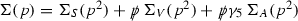 .
.The same anomalous counterterms arise for the charged higgsino coupling \(\lambda _{H^\pm {\tilde{t}}b}\), too.
Hdecay includes the full quark-mass dependence up to NLO.
\(V_{cs}\) denotes the corresponding CKM-matrix element.
The values for \(A_b, A_\tau , A_t\) have been obtained from \(X_t = A_t - \mu /\mathrm{tg}\beta = 2.8\) TeV. The trilinear coupling \(A_s\) has been chosen as \(A_s=A_b\). The soft SUSY-breaking squark mass parameter \(M_{{{\tilde{Q}}}}\) is defined in the on-shell scheme. We have determined the corresponding \(\overline{\mathrm{MS}}\) parameters by appropriate iterations. The \(\overline{\mathrm{MS}}\) squark-mass parameters of the second generation have been identified with the corresponding ones of the third generation.
The values of \(A_t=A_b=A_\tau \) have been derived from \(X_t=2.8\) TeV for each value of \(\mathrm{tg}\beta \) accordingly.
For the \(\Delta _{b,2}^{elw,t}\) terms they amount to about 1.7%, for \(\Delta _{b,2}^{elw,1}\) to about 0.4% and for \(\Delta _{b,2}^{elw,2}\) to about -0.7%.
We have extended the usual range to a factor of three, because for a factor of two, the bands do not overlap so that the more restricted range is not appropriate.
References
G. Aad et al., [ATLAS Collaboration]. Phys. Lett. B 716, 1 (2012)
S. Chatrchyan et al., [CMS Collaboration]. Phys. Lett. B 716, 30 (2012)
P.W. Higgs, Phys. Lett. 12, 132 (1964)
P.W. Higgs, Phys. Rev. Lett. 13, 508 (1964)
P.W. Higgs, Phys. Rev. 145, 1156 (1966)
F. Englert, R. Brout, Phys. Rev. Lett. 13, 321 (1964)
G.S. Guralnik, C.R. Hagen, T.W. Kibble, Phys. Rev. Lett. 13, 585 (1964)
T.W.B. Kibble, Phys. Rev. 155, 1554 (1967)
G’t Hooft, Nucl. Phys. B 35, 167 (1971)
G’t Hooft, M.J.G. Veltman, Nucl. Phys. B 44, 189 (1972)
G. Aad et al., [ATLAS and CMS Collaborations]. JHEP 1608, 045 (2016)
E. Gildener, S. Weinberg, Phys. Rev. D 13, 3333 (1976)
S. Weinberg, Phys. Rev. D 13, 974 (1976)
S. Weinberg, Phys. Rev. D 19, 1277 (1979)
L. Susskind, Phys. Rev. D 20, 2619 (1979)
Y.A. Golfand, E.P. Likhtman, JETP Lett. 13, 323 (1971), [Pisma Zh. Eksp. Teor. Fiz. 13 (1971) 452]
D.V. Volkov, V.P. Akulov, Phys. Lett. 46B, 109 (1973)
J. Wess, B. Zumino, Nucl. Phys. B 70, 39 (1974)
P. Fayet, S. Ferrara, Phys. Rep. 32, 249 (1977)
H.P. Nilles, Phys. Rept. 110, 1 (1984)
R. Barbieri, Riv. Nuovo Cim. 11N4, 1 (1988)
H.E. Haber, G.L. Kane, Phys. Rep. 117, 75 (1985)
P. Draper, G. Lee, C.E.M. Wagner, Phys. Rev. D 89(5), 055023 (2014)
E. Bagnaschi, G.F. Giudice, P. Slavich, A. Strumia, JHEP 1409, 092 (2014)
K. Cheung, R. Huo, J.S. Lee, Y.L. Sming Tsai, JHEP 1504, 151 (2015)
J. Pardo Vega, G. Villadoro, JHEP 1507, 159 (2015)
H. Bahl, W. Hollik, Eur. Phys. J. C 769, 499 (2016)
P. Slavich et al., arXiv:2012.15629 [hep-ph]
S.P. Martin, Phys. Rev. D 75, 055005 (2007)
R.V. Harlander, P. Kant, L. Mihaila, M. Steinhauser, Phys. Rev. Lett. 100, 191602, (2008) [Erratum ibid. 101, 039901 (2008)]
R.V. Harlander, J. Klappert, A. Voigt, Eur. Phys. J. C 77(12), 814 (2017)
E. Bagnaschi et al., Eur. Phys. J. C 79(7), 617 (2019)
G. Aad et al., [ATLAS Collaboration]. JHEP 1603, 127 (2016)
D. Noth, M. Spira, Phys. Rev. Lett. 101, 181801 (2008)
D. Noth, M. Spira, JHEP 1106, 084 (2011)
M. Spira, Fortsch. Phys. 46, 203 (1998)
M. Spira, Prog. Part. Nucl. Phys. 95, 98 (2017)
A. Djouadi, Phys. Rep. 459, 1 (2008)
J. Guasch, P. Häfliger, M. Spira, Phys. Rev. D 68, 115001 (2003)
M. Carena, D. Garcia, U. Nierste, C.E. Wagner, Nucl. Phys. B 577, 88 (2000)
P. Häfliger, M. Spira, Nucl. Phys. B 719, 35 (2005)
P. Häfliger, M. Spira, PoS HEP2005, 351 (2006)
S. Dittmaier, M. Krämer, A. Mück, T. Schlüter, JHEP 0703, 114 (2007)
S. Dawson, C.B. Jackson, P. Jaiswal, Phys. Rev. D 83, 115007 (2011)
S. Dittmaier, P. Häfliger, M. Krämer, M. Spira, M. Walser, Phys. Rev. D 90(3), 035010 (2014)
P. Häfliger, PhD thesis, ETH (Zürich) DISS-ETH-16970, (2006)
M. Walser, PhD thesis, ETH (Zürich) DISS-ETH-17592, (2008)
L.J. Hall, R. Rattazzi, U. Sarid, Phys. Rev. D 50, 7048 (1994)
R. Hempfling, Phys. Rev. D 49, 6168 (1994)
M. Carena, M. Olechowski, S. Pokorski, C.E. Wagner, Nucl. Phys. B 426, 269 (1994)
J.R. Ellis, M.K. Gaillard, D.V. Nanopoulos, Nucl. Phys. B 106, 292 (1976)
M.A. Shifman, A.I. Vainshtein, M.B. Voloshin, V.I. Zakharov, Sov. J. Nucl. Phys. 30, 711 (1979), [Yad. Fiz. 30, 1368 (1979)]
M. Spira, A. Djouadi, D. Graudenz, P.M. Zerwas, Nucl. Phys. B 453, 17 (1995)
B.A. Kniehl, M. Spira, Z. Phys. C 69, 77 (1995)
W. Kilian, Z. Phys. C 69, 89 (1995)
L. Mihaila, C. Reisser, JHEP 1008, 021 (2011)
A. Crivellin, C. Greub, Phys. Rev. D 87, 015013, (2013) Erratum: [Phys. Rev. D87(2013), 079901]
L. Mihaila, N. Zerf, JHEP 1705, 019 (2017)
C. Hamzaoui, M. Pospelov, M. Toharia, Phys. Rev. D 59, 095005 (1999)
K.S. Babu, C.F. Kolda, Phys. Rev. Lett. 84, 228 (2000)
A.J. Buras, P.H. Chankowski, J. Rosiek, L. Slawianowska, Nucl. Phys. B 619, 434 (2001)
A.J. Buras, P.H. Chankowski, J. Rosiek, L. Slawianowska, Nucl. Phys. B 659, 3 (2003)
G. Isidori, A. Retico, JHEP 0111, 001 (2001)
L. Hofer, U. Nierste, D. Scherer, JHEP 0910, 081 (2009)
M. Gorbahn, S. Jäger, U. Nierste, S. Trine, Phys. Rev. D 84, 034030 (2011)
S.P. Martin, M.T. Vaughn, Phys. Lett. B 318, 331 (1993)
E. Accomando, G. Chachamis, F. Fugel, M. Spira, M. Walser, Phys. Rev. D 85, 015004 (2012)
A. Djouadi, J. Kalinowski, M. Spira, Comput. Phys. Commun. 108, 56 (1998)
A. Djouadi, M.M. Mühlleitner, M. Spira, Acta Phys. Polon. B 38, 635 (2007)
A. Djouadi, J. Kalinowski, M. Mühlleitner, M. Spira, Comput. Phys. Commun. 238, 214 (2019)
M. Carena, H.E. Haber, S. Heinemeyer, W. Hollik, C.E. Wagner, G. Weiglein, Nucl. Phys. B 580, 29 (2000)
E. Braaten, J.P. Leveille, Phys. Rev. D 22, 715 (1980)
N. Sakai, Phys. Rev. D 22, 2220 (1980)
T. Inami, T. Kubota, Nucl. Phys. B 179, 171 (1981)
S.G. Gorishnii, A.L. Kataev, S.A. Larin, Sov. J. Nucl. Phys. 40, 329 (1984), [Yad. Fiz. 40 (1984) 517]
M. Drees and K.I. Hikasa, Phys. Rev. D41 (1990) 1547
M. Drees and K.I. Hikasa, Phys. Lett. B240 (1990) 455 [Erratum-ibid. B262 (1991) 497]
S.G. Gorishnii, A.L. Kataev, S.A. Larin, L.R. Surguladze, Mod. Phys. Lett. A 5, 2703 (1990)
S.G. Gorishnii, A.L. Kataev, S.A. Larin, L.R. Surguladze, Phys. Rev. D 43, 1633 (1991)
A.L. Kataev, V.T. Kim, Mod. Phys. Lett. A 9, 1309 (1994)
L.R. Surguladze, Phys. Lett. B 341, 60 (1994)
K.G. Chetyrkin, J.H. Kühn, A.K. Kwiatkowski, Proceedings of the Workshop “QCD at LEP”, Aachen, (1994), arXiv:hep-ph/9407271
K.G. Chetyrkin, Phys. Lett. B 390, 309 (1997)
K.G. Chetyrkin, A. Kwiatkowski, Nucl. Phys. B 461, 3 (1996)
K. Melnikov, Phys. Rev. D 53, 5020 (1996)
S.A. Larin, T. van Ritbergen, J.A.M. Vermaseren, Phys. Lett. B 362, 134 (1995)
J.A. Coarasa, R.A. Jimenez, J. Solà, Phys. Lett. B 389, 312 (1996)
H. Eberl, K. Hidaka, S. Kraml, W. Majerotto, Y. Yamada, Phys. Rev. D 62, 055006 (2000)
C.S. Li, R.J. Oakes, Phys. Rev. D 43, 855 (1991)
A. Mendez, A. Pomarol, Phys. Lett. B 252, 461 (1990)
A. Djouadi, P. Gambino, Phys. Rev. D 51, 218 (1995). Erratum: [Phys. Rev. D53 (1996) 4111]
Acknowledgements
The authors are indebted to M. Mühlleitner for carefully reading the manuscript and very useful comments. This work is supported in part by the Swiss National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Ghezzi, M., Glaus, S., Müller, D. et al. Refinements of the bottom and strange MSSM Higgs Yukawa couplings at NNLO. Eur. Phys. J. C 81, 259 (2021). https://doi.org/10.1140/epjc/s10052-021-09035-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09035-6














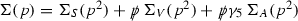 .
.