1 Introduction

One has actually registered a renewed and increasing interest in the study of the physics of wormholes, from the recent discovery of the deep connection that exists between such objects and quantum entanglement [1,2,3]. But that concept is much older, and was introduced some decades ago by Flamm [4] and Weyl [5, 6] who are considered the first authors to suggest possible solutions of the Einstein’s equations which could represent a tunnel interconnecting two apparently disjoint regions of the Universe or even different universes [7]. The first solutions effectively found (Einstein and Rosen [8], Wheeler [9] and Kerr [10,11,12]) resulted in the so-called non-traversable wormholes. Some decades after these works, Michael Morris and Kip Thorne, taking into account static, spherically symmetrical and non-rotating space-times, found the first wormhole traversable solution [13].

By means of an immersion diagram, one shows that the Schwarzschild’s solution can resemble a wormhole, but it would not be traversable, since the radius of its throat overlap with the black hole event horizon. Despite this, we can get other solutions with specific redshift functions without horizons [13, 14]. An interesting generalization in this sense was carried out in [15] by taking a linear shape function, the so-called zero tilde Schwarzschild-like wormhole, which is static and traversable. Another wormhole based on Schwarzschild black hole solution was obtained by Damour and Solodukhin [16], upon modifying the time coefficient of the metric adding to it a very tiny positive constant. Although this deviation from the original black hole may seem very small, the new redshift function changes completely the nature of the object. It is worth to point out that features of the stationary counterparts of these objects were studied in [17,18,19,20].

In general, for the existence and stability of a macroscopic wormhole it is necessary that there is a kind of exotic matter around the object, as dark energy (quintessence, phantom), but in some cases such a restriction is unnecessary [21,22,23]. The presence of negative electromagnetic energy permeating these objects already was pointed out regarding the Einstein–Rosen bridge [7], and vacuum fluctuations of quantum fields, which generally also present a negative energy density, can play a relevant role in determining certain intriguing features of the wormholes, such as the existence of closed timelike curves associated to them [24].

The more popular macroscopic physical manifestation of the vacuum fluctuations of quantum fields, the Casimir [25] effect, has been studied in several contexts [26,27,28,29,30]. It was originally related to the force that arises between two neutral, parallel, metallic and planar conductors placed in an ideal Minkowsky’s vacuum. This force arises due to changes in the zero point oscillations of the quantum electrodynamics caused by the presence of material boundaries. The Casimir effect also occurs in cavities situated in more general space-times, or can be associated to the geometry and topology itself, in a gravitational analogue of the phenomenon [31]. In this sense, diverse works in the literature seek to describe such an effect in space-times of wormholes [32,33,34,35]. In particular, Sorge [36] recently investigated the phenomenon in the parallel plates configuration orbiting an Ellis wormhole [37]. In these context, the Casimir effect is influenced by the geometry of the spacetime as well as by the inertial effects coming from the rotation of the apparatus around the wormhole.

In this article, we will seek to study changes caused by gravito-inertial and frame-dragging effects in the quantum vacuum energy density of a massless scalar field confined within a Casimir apparatus orbiting rotating wormholes, namely, the Damour-Solodukhin and Teo ones, both considered in [17, 19], neglecting tidal effects inside the cavity. Then, we will compare the Casimir energy densities obtained for these different scenarios, and also with the one calculated for the Kerr black hole, according to [38]. Thus, we advocate that by means of the Casimir force measurement one may indirectly distinguish among the several astrophysical objects, as rotating wormholes and black holes, eventually orbited by a device of the type considered here. We will also study the thermal Casimir effect around the rotating D–S wormhole, comparing it with the one that occurs in the Kerr black hole spacetime and already studied in the literature. Even being unlikely that in the near future we will be able to verify such predictions experimentally with real wormholes, analogues of these objects in condensed matter [39] can turn this work feasible, as already occurs in the black hole studies.

The work is divided as follows: In Sect. 2, we will find the Casimir energy density of the massless scalar field inside a cavity orbiting the rotating Damour–Solodukhin wormhole, then comparing it with the one regarding the Kerr black hole. In this section we still compare it with the obtained in the Ellis wormhole spacetime upon turning off the rotation parameter of the former. In Sect. 3 we will calculate the Casimir energy density in the same configuration related to the Teo wormhole. In Sect. 4 we will investigate the thermal Casimir effect on the plates orbiting the rotating D–S wormhole once more and in Sect. 4, finally, we will conclude and close the paper.

2 Casimir effect around the rotating Damour–Solodukhin wormhole

We begin by reviewing the properties of the D–S wormhole spacetime, which is obtained from the deformation of the Schwarzschild’s metric, given by (\(c=G=1\))

$$\begin{aligned} ds^2=f(r)dt^2-\frac{dr^2}{f(r)}-r^2(d\theta ^2+\sin ^2{\theta }d\phi ^2), \end{aligned}$$
(1)

with \(f(r)=1-\frac{2M}{r}\). The wormhole structure corresponding to Eq. (1) is obtained by embedding the space-like slice with \(t=const.\) and \(\theta =\pi /2\) into a manifold described by cylindrical coordinates, with spatial line element \(d\sigma \) given by

$$\begin{aligned} d\sigma ^2=d\rho ^2+\rho ^2 d\phi ^2+dz^2=\frac{dr^2}{f(r)}+r^2d\phi ^2, \end{aligned}$$
(2)

implying \(r=\rho \) and

$$\begin{aligned} \frac{dz}{dr}=\pm \sqrt{\frac{1}{f(r)}-1}. \end{aligned}$$
(3)

The expression above can be integrated and results in the curve z(r) that, when is rotated around z axis, yields both the mouth and the throat of the wormhole. However, the wormhole throat coincides with the event horizon of the black hole and, therefore, it is not traversable.

In order to overcome this trouble, Damour and Solodukhin [16] proposed to deform the Schwarzschild black hole adding a constant and positive term \(\lambda ^2\ll 1\) to the metric coefficient \(g_{00}\) so that

$$\begin{aligned} ds^2=(f(r)+\lambda ^2)dt^2-\frac{dr^2}{f(r)}-r^2(d\theta ^2+\sin ^2{\theta }d\phi ^2).\nonumber \\ \end{aligned}$$
(4)

Then, even the parameter \(\lambda \) being a very small amount, the geometry and topology of the object change drastically. Such an object does not present an event horizon and now is, in principle, a traversable wormhole. We can change the metric by the identifications \(t\rightarrow t/(1+\lambda ^2)\) and \(M\rightarrow M(1+\lambda ^2)\) in order to recuperate the usual time when \(r\rightarrow \infty \). Thus, we find

$$\begin{aligned} ds^2= & {} \left( 1-\frac{2M}{r}\right) dt^2-\frac{dr^2}{1-\frac{2M(1+\lambda ^2)}{r}}-r^2d\Omega ^2\nonumber \\= & {} \left[ 1-\frac{b_0}{(1+\lambda ^2)r}\right] dt^2-\frac{dr^2}{1-\frac{b_0}{r}}-r^2d\Omega ^2. \end{aligned}$$
(5)

where \(b_0=2 M(1+\lambda ^2)\) is the wormhole throat radius.

We will now investigate the influence of a rotating D–S wormhole on the Casimir energy density between the parallel plates, at zero temperature. As in the case examined by Sorge for a Kerr black hole [38], the Casimir apparatus orbits, with angular velocity \(\Omega \) at the equatorial plane, a wormhole represented by the rotational parameter a and throat radius, \(b_0\).

The corresponding spacetime is described by the line element [19]

$$\begin{aligned} ds^2= & {} \left[ 1-\frac{b_0 r}{(1+\lambda ^2)\Sigma }\right] \!dt^2+\frac{2b_0ar}{(1+\lambda ^2)\Sigma }dtd\phi \nonumber \\&-\frac{\Sigma }{{\widetilde{\Delta }}} dr^2-\Sigma d\theta ^2-\frac{{\widetilde{A}}}{\Sigma }\sin ^2{\theta } d\phi ^2, \end{aligned}$$
(6)

where

$$\begin{aligned} \Sigma= & {} r^2+a^2\cos ^2\!\theta , \nonumber \\ {\widetilde{\Delta }}= & {} r^2+a^2-b_0r, \nonumber \\ {\widetilde{A}}= & {} (r^2+a^2)^2-a^2{\widetilde{\Delta }}\sin ^2{\theta }, \end{aligned}$$
(7)

We can also define the quantity \({\widetilde{\omega }}_{d}\), which is the angular velocity of the “dragging” of the spacetime around the wormhole, namely

$$\begin{aligned} {\widetilde{\omega }}_{d}=-\frac{ {\hat{g}}_{t\phi }}{ {\hat{g}}_{\phi \phi }}=\frac{ab_0r}{(1+\lambda ^2){\widetilde{A}}}, \end{aligned}$$
(8)

which is lower than the one computed in the Kerr black hole spacetime, for the same parameters, due to factor \(1+\lambda ^2\). Such expressions are written in the Boyer-Linquidist coordinates and in terms of the D–S wormhole throat radius, \(b_{0}\), previously defined. For \(\lambda =0\) Eq. (6) reduces to the Kerr black hole, and \(a=0\) yields the usual Schwarzschild solution. The rotating wormhole throat radius, \(b_r\), obtained by imposing that \({\widetilde{\Delta }}=0\), is now given by

$$\begin{aligned} b_r=\frac{b_0}{2}+\sqrt{\frac{b_0^2}{4}-a^2}. \end{aligned}$$
(9)

For convenience, and without loss of generality, we consider the metric approximately constant between the plates, since the separation distance between them, L, is assumed to be much smaller than the radius of the orbit, (\(L \ll r\)). The cavity is in a locally co-moving referential system which has Cartesian coordinates (x, y, z) defined on one of the plates, so that the axis z is tangential to the path of the circular orbit. Thus, the relationships between the spherical coordinates of the rotating system and the Cartesian ones inside the cavity are \(dy = dr\), \(dz = rd\phi '\) and \(dx = -rd\theta \), where \(\phi '=\phi -\Omega t\), with \(\Omega \) being the angular velocity of the plates around the rotating wormhole. Substituting these relations into Eq. (6), particularizing for \(\theta =\pi /2\) (i.e., the orbit is at the equatorial plane, in which \(\Sigma = r^2\)), and collecting the terms, the metric becomes

$$\begin{aligned} ds^2= & {} {\widetilde{C}}^{-2}\left( \Omega \right) \!dt^2+2\frac{{\widetilde{A}}}{r^3}\left( {\widetilde{\omega }}_{d}-\Omega \right) dtdz\nonumber \\&-\frac{r^2}{{\widetilde{\Delta }}} dy^2- dx^2-\frac{{\widetilde{A}}}{r^{4}}dz^2, \end{aligned}$$
(10)

Besides this, we get

$$\begin{aligned} {\widetilde{C}}^{-2}\left( \Omega \right) =\frac{r^2 {\widetilde{\Delta }}}{{\widetilde{A}}}\left[ 1-\frac{{\widetilde{A}}^{2}}{{\widetilde{\Delta }}r^4}\left( \Omega -{\widetilde{\omega }}_d\right) ^2\right] , \end{aligned}$$
(11)

where the parameter \(\lambda ^2\) that characterizes the wormhole is implicit in the dragging angular velocity \(\tilde{\omega _d}\). With these equations, we can calculate the normal modes and the Casimir energy, as well.

2.1 Normal modes

The massless scalar field confined in the cavity situated in the previously described spacetime obeys the covariant Klein-Gordon equation, given by

$$\begin{aligned} \left[ \frac{1}{\sqrt{-{\hat{g}}}}\partial _{\mu }\left( \sqrt{-{\hat{g}}}{\hat{g}}^{\mu \nu }\partial _{\nu }\right) +\xi R\right] \phi \left( t, \mathbf{x } \right) =0, \end{aligned}$$
(12)

where we will consider \(\xi = 0\) (minimal coupling). As said before, we also consider the metric (10) approximately constant between the plates, since the separation distance between them is much smaller than the radius of the orbit, and thus we neglect tidal effects inside the Casimir apparatus. Then, Eq. (12) takes the form,

$$\begin{aligned} {\hat{g}}^{\mu \nu }\partial _{\mu }\partial _{\nu }\!\phi \left( t,{\mathbf {r}}\right) =0, \end{aligned}$$
(13)

where \({\hat{g}}^{\mu \nu }\) is the inverse of the metric tensor built from Eq. (10).

Proposing a solution to Eq. (13) in the form \(\phi \left( t,{\mathbf {r}}\right) \propto e^{i\left( k_{x}x+k_{y}y-\omega t\right) }Z\left( z\right) \) we get the following equation for Z(z)

$$\begin{aligned}&{\hat{g}}^{zz}\frac{d^{2}}{dz^{2}}Z\!\left( z\right) -2i\omega {\hat{g}}^{tz}\frac{d}{dz}Z\!\left( z\right) \nonumber \\&\quad -\left( k_{x}^{2}{\hat{g}}^{xx}+k_{y}^{2}{\hat{g}}^{yy}+\omega ^{2}{\hat{g}}^{tt}\right) \!\!Z\!\left( z\right) =0. \end{aligned}$$
(14)

Let us suppose a solution of the type \(Z\!\left( z\right) =e^{i \alpha z}\), and then we arrive at

$$\begin{aligned} {\hat{g}}^{zz}\alpha ^{2}-2\omega {\hat{g}}^{tz}\alpha +\left( k_{x}^{2}{\hat{g}}^{xx}+k_{y}^{2}{\hat{g}}^{yy}+\omega ^{2}{\hat{g}}^{tt}\right) =0. \end{aligned}$$
(15)

Thus, the solutions of Eq. (15) for \(\alpha \) are given by

$$\begin{aligned} \alpha =\frac{\omega {\widetilde{A}} \left( \Omega -{\widetilde{\omega }}_{d}\right) {\widetilde{C}}^{2}_{\Omega }}{r^3}\pm \frac{\sqrt{{\widetilde{\Delta }}}}{{\widetilde{C}}^{2}_{\Omega }{r}}\sqrt{\omega ^{2}-{\widetilde{C}}^{-2}_{\Omega }\left( k_{x}^{2}+\frac{{\widetilde{\Delta }}}{r^{2}}k_{y}^{2}\right) }, \nonumber \\ \end{aligned}$$
(16)

where we have substituted the expressions for \({\hat{g}}^{\mu \nu }\). The solution for \(Z\!\left( z\right) \) can be written as

$$\begin{aligned} Z\left( z\right)= & {} \exp {\left[ i\frac{\omega {\widetilde{A}} \left( \Omega -{\widetilde{\omega }}_{d}\right) {\widetilde{C}}^{2}_{\Omega }}{r^3}z\right] }\nonumber \\&\times \sin {\left[ z\frac{\sqrt{{\widetilde{\Delta }}} {\widetilde{C}}^{2}_{\Omega }}{r}\sqrt{\omega ^{2}-{\widetilde{C}}^{-2}_{\Omega }\left( k_{x}^{2}+\frac{{\widetilde{\Delta }}}{r^{2}}k_{y}^{2}\right) }\right] }. \end{aligned}$$
(17)

The solutions of Eq. (13) must satisfy the Dirichlet boundary conditions on the plates. Considering one of them at \(z=0\) and the other at \(z=L\), thus \(\phi \left( t,x,y,0\right) =\phi \left( t,x,y,L\right) =0\), for which the eigenfrequencies are given by

$$\begin{aligned} \omega _{n}=\frac{r}{\sqrt{{\widetilde{\Delta }}}{\widetilde{C}}^{2}_{\Omega }}\left[ \left( \frac{n\pi }{L}\right) ^{2}+\frac{{\widetilde{\Delta }} {\widetilde{C}}^{2}_{\Omega }}{r^2}\left( k_{x}^{2}+\frac{{\widetilde{\Delta }}}{r^{2}}k_{y}^{2}\right) \right] ^{\frac{1}{2}}. \end{aligned}$$
(18)

Writing the eigenfunctions for the scalar field, \(\phi _n\), we have

$$\begin{aligned} \phi _{n}\left( t,x,y,z\right) =N_{n}e^{i\left( k_{x,n}x+k_{y,n}y-\omega _n t\right) }e^{i\beta _{n}z}\sin {\!\left( \frac{n \pi }{L}z\right) }, \end{aligned}$$
(19)

where \(\beta _{n}=\frac{{\widetilde{A}}\left( \Omega -{\widetilde{\omega }}_{d}\right) {\widetilde{C}}^{2}_{\Omega }}{r^3}\omega _n\) and \(N_{n}\) is the normalization constant, which can be obtained from the internal product given by

$$\begin{aligned} \langle \phi _{n},\phi _{m}\rangle =i\int _{S}\left[ \left( \partial _{\mu }\phi _{n}\right) \phi _{m}^{*}-\phi _{m}\left( \partial _{\mu }\phi _{n}^{*}\right) \right] \sqrt{-{\hat{g}}_{S}}n^{\mu }dS,\nonumber \\ \end{aligned}$$
(20)

in which S symbolizes the space-like hyper-surface throughout which the integration is performed and \(n^{\mu }\) is a time-like vector, which is given by

$$\begin{aligned} \left( n^{\mu }\right) =r\sqrt{\frac{{\widetilde{\Delta }}}{{\widetilde{A}}}}\left[ \frac{{\widetilde{A}}}{r^{2}{\widetilde{\Delta }}},0,0,-\frac{{\widetilde{A}}}{r{\widetilde{\Delta }}}\left( \Omega -{\widetilde{\omega }}_{d}\right) \right] , \end{aligned}$$
(21)

so that it is a unitary vector, i.e., \({\hat{g}}_{tt}(n^t)^2+{\hat{g}}_{zz}(n^z)^2=1\). Considering that \({\hat{g}}_{S}=\frac{{\hat{g}}}{{\hat{g}}_{tt}}=-{\widetilde{C}}^{2}_{\Omega }\) and \(dS=dxdydz\), from the orthonormality requirement

$$\begin{aligned} \langle \phi _{n},\phi _{m}\rangle =\delta ^{(2)}(\mathbf{k}_n-\mathbf{k}_m)\delta _{nm}, \end{aligned}$$
(22)

with

$$\begin{aligned}&\delta ^{(2)}(\mathbf{k}_n- \mathbf{k}_m)\nonumber \\&=\frac{1}{(2\pi )^2}\int \int dxdy e^{i [x(k_{x,n}-k_{x,m})+y(k_{y,n}-k_{y,m})]}, \end{aligned}$$
(23)

where \(\mathbf{k}_n=(k_{x,n},k_{y,n})\) is the momenta of the propagation modes parallel to the plates, and by taking into account the solutions (19), we arrive at the following expression for \(N_n\)

$$\begin{aligned} N_{n}^{2}=\frac{{\widetilde{C}}^{-3}_{\Omega }}{\left( 2\pi \right) ^{2}L\omega _{n}r}\sqrt{\frac{{\widetilde{A}}}{{\widetilde{\Delta }}}}. \end{aligned}$$
(24)

2.2 Casimir energy

Now, we can use the completely defined normal modes and calculate the Casimir energy. The operator energy density for the massless scalar field is

$$\begin{aligned} T_{tt}=\partial _{t}\phi \partial _{t}\phi ^{*}-\frac{1}{2}{\hat{g}}_{tt}\left( {\hat{g}}^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi ^{*}\right) . \end{aligned}$$
(25)

With the aid of Eq. (19), Eq. (25) turns into

$$\begin{aligned} T_{tt}= & {} \frac{N_n^2}{2} \left\{ \!\left[ \omega _n^2\!+\!{\widetilde{C}}^{-2}_{\Omega }\left( k_x^2\!+\!\frac{{\widetilde{\Delta }}}{r^{2}}k_y^2\right) \!\right] \!\sin ^2\!\left( \frac{n\pi }{L}z\right) \right. \nonumber \\&\left. +\frac{r^{2}}{{\widetilde{\Delta }} }\!\left( \frac{n\pi }{L}\right) ^2\!{\widetilde{C}}^{-4}_{\Omega }\!\cos ^2\!\left( \frac{n\pi }{L}z\right) \!\right\} . \end{aligned}$$
(26)

whose expected value is given by

$$\begin{aligned} \left\langle 0|T_{tt}|0\right\rangle =\sum _{n}\int \int T_{tt}dk_xdk_y. \end{aligned}$$
(27)

Adopting the same procedures used in [36], we obtain the following result

$$\begin{aligned} \langle \epsilon _{vac}\rangle \!=\frac{r}{L}\sqrt{\frac{{\widetilde{A}}}{{\widetilde{\Delta }}^2\Sigma }}{\widetilde{C}}^{-2}_{\Omega }\!\sum _{n}\!\int \frac{1}{2}\frac{d^{2}k}{\left( 2\pi \right) ^{2}}\left[ \left( \frac{n\pi }{s}\right) ^{2}+k^{2}\right] ^{\frac{1}{2}}, \nonumber \\ \end{aligned}$$
(28)

where \(s^2=\frac{{\widetilde{\Delta }}{\widetilde{C}}^{2}_{\Omega }L^2}{r^2}\). The integral can be solved by the Schwinger proper-time method and the sum can be calculated via Riemann zeta function regularization procedure, which result in

$$\begin{aligned} \langle \epsilon _{vac}\rangle \!=-\frac{\pi ^2}{1440L^4}\sqrt{\frac{{\widetilde{A}}}{{\widetilde{\Delta }}^5}}\frac{r^3}{ {\widetilde{C}}^{5}_{\Omega }}. \end{aligned}$$
(29)

Finally, knowing that the proper length of the cavity is \(L_p={\widetilde{C}}_{\Omega }\frac{\sqrt{{\widetilde{\Delta }}}}{r}L\), the Casimir energy in the cavity orbiting a rotating D–S wormhole is

$$\begin{aligned} \langle \epsilon _{vac}\rangle \!=-\frac{\pi ^2}{1440L_{p}^{4}}\left[ 1-\frac{{\widetilde{A}}^{2}}{{\widetilde{\Delta }} r^4}\left( \Omega -{\widetilde{\omega }}_d\right) ^2\right] ^{\frac{1}{2}}. \end{aligned}$$
(30)

We can see that this local regularized vacuum energy depends on the rotational parameters, \(\Omega \) of the plates around the wormhole and a associated to this latter, on its throat radius, \(b_r\), and on the specific parameter that characterizes the D–S wormhole, \(\lambda \).

Fig. 1
figure 1

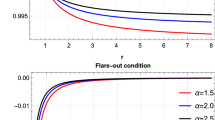
a At the left panel it is shown the ratio between the Casimir energy density inside the cavity in the considered spacetimes and in the Minkowsky one, which orbit both the rotating D–S wormhole and Kerr black hole (in this latter, \(\lambda =0, b_0=2M\)), as a function of the radial coordinate, \(r>b_r\). b At the right panel the same ratio is shown for a higher value of the rotational parameter, a

Full size image

Notice that, in the situation for which the angular velocity of the plates matches the spacetime dragging one, \(\Omega ={\tilde{\omega }}_d\) (i.e., in the reference frame of a ZAMO - Zero Angular Momentum Observer), we obtain the usual Minkowskian Casimir energy density. Notice also that \({\tilde{\omega }}_d-r^2\tilde{A}^{-1}\sqrt{{\tilde{\Delta }}}<\Omega <{\tilde{\omega }}_d+r^2\tilde{A}^{-1}\sqrt{{\tilde{\Delta }}}\) so that the Casimir energy is real and the system exhibits stability.

Nearby the wormhole throat, the Casimir energy density can be approximated to

$$\begin{aligned} \langle \epsilon _{vac}\rangle \!\approx -\frac{\pi ^2}{1440L_{p}^{4}} \frac{\left( a^2+b_r^2\right) |\left( 1+\lambda ^2\right) \left( a^2+b_r^2\right) \Omega -2 a|}{\left( 1+\lambda ^2\right) \sqrt{b_r^3 \left( a^2-b_r^2\right) (r-b_r)}},\nonumber \\ \end{aligned}$$
(31)

for \(a > b_r\) and \(r>b_r\), where we explicitly written \({\widetilde{\Delta }}\) and \({\widetilde{\omega }}_d\) in terms of \(b_r\), given in Eq. (9), which now is one of the free parameters of the model, so that

$$\begin{aligned} {\widetilde{\Delta }}=r^2+a^2-\left( \frac{a^2+b_r^2}{b_r}\right) r, \end{aligned}$$
(32)

and

$$\begin{aligned} {\widetilde{\omega }}_d=\frac{2 a(a^2+b_r^2)r}{b_r(1+\lambda ^2){\widetilde{A}}}. \end{aligned}$$
(33)

2.3 Rotating D–S wormhole versus Kerr black-hole

It is interesting to compare the Casimir energy density which we obtained with that one generated in the Kerr spacetime, according to the Sorge’s paper [38]. For such a purpose, we must still write Eq. (30) in terms of the rotating wormhole throat, \(b_r\). In Fig. 1 we depict the ratio between the Casimir energy in the considered curved space and the modulus of the Minkowsky one, \(R=\frac{1440L_{p}^{4}}{\pi ^2}\langle \epsilon _{vac}\rangle \!\), for both the D–S wormhole and Kerr black hole, as a function of the radial coordinate, r, at the exterior of the wormhole throat. The angular velocity of the orbiting plates, \(\Omega \), was chosen in order to satisfy the constraint \(\Omega _{-}<\Omega <\Omega _{+}\) for any r, with \(\Omega _{\pm }=\widetilde{\omega _d}\pm {\widetilde{A}}^{-1}r^{2}{\widetilde{\Delta }}^{1/2}\), which allows equatorial circular orbits.

We can still notice in the Fig. 1 that the value of the Casimir energy density of the plates around the rotating D–S wormhole tends to be greater than in the Kerr spacetime, beyond being numerically smaller than the Casimir energy in the Minkowsky one, for the same configuration, when we take \(a<b_r\). For \(a>b_r\), the curve profile presents a behaviour quite different, and the numerical value for the Casimir energy density is greater than in the Minkowsky spacetime. This energy around the D–S wormhole is still higher than the calculated one in the Kerr spacetime. The traversable rotating D–S wormhole drains the vacuum energy and needs a greater quantity of this latter in order to maintain the same configuration of the Casimir apparatus orbiting around the object.

2.4 Static D–S wormhole versus Ellis wormhole

We can also compare the Casimir energy density in the static D–S wormhole spacetime with that one recently found by Sorge [38] upon considering the static Ellis wormhole, expressing the latter in the Schwarzschild coordinates. The comparison can be made by turning off the rotation of the former (\(a=0\), in Eq. (30)), yielding

$$\begin{aligned} \langle \epsilon _{vac}\rangle ^{DS}= -\frac{\pi ^2}{1440L_{p}^{4}} \sqrt{\frac{1 - \frac{b_0}{(1+\lambda )r}-r^2\Omega ^2}{1 - \frac{b_0}{r}}}, \end{aligned}$$
(34)

with the restriction \(r\Omega <\sqrt{1-\frac{b_0}{(1+\lambda )r}}\), for \(r>b_0\). Notice that upon making \(\lambda =0\) we obtain the result found in [38] for \(b_0=2M\) (Schwarzschild black hole). On the other hand, the Casimir energy in the Ellis wormhole spacetime is given by [36]

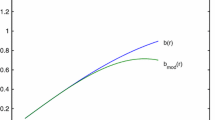
$$\begin{aligned} \langle \epsilon _{vac}\rangle ^{E}= -\frac{\pi ^2}{1440L_{p}^{4}} \sqrt{\frac{1 - r^2\Omega ^2}{1-\frac{b_0^2}{r^2}}}, \end{aligned}$$
(35)

where now \(r\Omega <1\) for \(r>b_0\). It is worth to notice that the Casimir energy density associated to both the wormholes converge for a same value at asymptotic regions (or for \(b_0\rightarrow 0\)).

In Fig. 2, we depict the ratio between the Casimir energy densities around both the D–S and Ellis wormholes and the same quantity in the Minkowsky spacetime, as a function of the coordinate r. The absolute values of these quantities are greater than the unit at \(r<\left[ \frac{\lambda b_0}{\Omega ^2(1+\lambda )}\right] ^{1/3}\), in D–S wormhole spacetime, and \(r<\sqrt{\frac{b_0}{\Omega }}\), for the Ellis wormhole spacetime.

Fig. 2
figure 2

Ratio between the Casimir energy densities around both D–S and Ellis wormholes and the Minkowsky one, as a function of the radial coordinate, \(r>b_r\)

Full size image

3 The Casimir effect around the rotating Teo wormhole

In this section, we will discuss some features of the Teo’s solution in the context of the Casimir effect. The corresponding metric is given by [17, 18]

$$\begin{aligned} ds^2= & {} \left( 1-\frac{4a^2}{r^4}\right) dt^2-\frac{dr^2}{1-\frac{b_0}{r}}\nonumber \\&-r^2d\theta ^2-r^2d\phi ^2+\frac{4a}{r}d\phi dt, \end{aligned}$$
(36)

which we have particularized to \(\theta =\pi /2\). Here, the parameter a is for the angular momentum of the wormhole. We also notice that the metric reduces to the one that describes a static Schwarzschild-like wormhole when \(a=0\) [15]. Thus, if we adopt the transformations indicated just above Eq. (10) into 36, it becomes

$$\begin{aligned} ds^2=C_{\Omega }^{-2}dt^2{+}2r(\omega _d-\Omega )dtdz-dx^2-\frac{dy^2}{1-\frac{b_r}{r}}-dz^2,\nonumber \\ \end{aligned}$$
(37)

where the time coefficient is now

$$\begin{aligned} C_{\Omega }^{-2} =\left[ 1-r^2\Omega ^2-\frac{4a^2}{r^4}+\frac{12a\Omega }{r}\right] , \end{aligned}$$
(38)

with \(\omega _d=\frac{4a}{r^3}\).

The Casimir energy density between the orbiting plates can be obtained through the same procedure used in Sect. 3, which yields

$$\begin{aligned} \langle \epsilon _{vac}\rangle ^{T}=-\frac{\pi ^2}{1440L_p^4}\sqrt{\frac{1-r^2\Omega ^2-\frac{4a^2}{r^4}+\frac{12a\Omega }{r}}{1-\frac{b_r}{r}}} \end{aligned}$$
(39)
Fig. 3
figure 3

Ratio between the calculated Casimir energy densities and the Minkowsky one in both Teo and rotating D–S wormhole spacetimes, as well as in the Kerr black hole, as a function of the radial coordinate, \(r>b_r\)

Full size image

In Fig. 3 we depict the Casimir energy densities in the rotating wormhole spacetimes, as well as in the Kerr black hole. We notice that the Teo wormhole presents the smallest value and D–S, the greatest one. The absolute value of the Casimir energy density in Teo wormhole spacetime will be greater than in the Minkowsky one when the plates orbit at

$$\begin{aligned} r<\left( \frac{12a}{\Omega }+\frac{b_r}{\Omega ^2}+\frac{\sqrt{b_r^2+24a\Omega b_r+128a^2\Omega ^2}}{\Omega ^2}\right) ^{1/3}. \end{aligned}$$
(40)

Nearby the wormhole throat, the Casimir energy density between the plates is approximately given by

$$\begin{aligned} \langle \epsilon _{vac}\rangle ^{T}\approx -\frac{\pi ^2}{1440L_p^4}\sqrt{\frac{1}{r-b_r}\left( 12a\Omega -\frac{4a^2}{b_r^3}+b_r-\Omega ^2b_r^3\right) }. \end{aligned}$$
(41)

We can also compare the Casimir energy associated to the static counterpart of Teo’s wormhole (making \(a=0\) in Eq. (39)) with Ellis’s one (given in Eq. (35)). We notice that \(\langle \epsilon _{vac}\rangle ^{E}> \langle \epsilon _{vac}\rangle ^{T}_{Stat}\), for plates orbiting out of the wormhole throats of same radii, \(r>b_0\), and same angular velocity, \(\Omega \).

4 Thermal Casimir effect

The Helmholtz free energy of the plates orbiting the DS wormhole, immersed in a thermal bath at a (coordinate) temperature T, is given by

$$\begin{aligned} \Delta _T{\mathcal {F}}_0=\beta ^{-1}\sum _n\ln \big (1-e^{-\beta \omega _n}\big ), \end{aligned}$$
(42)

where \(\beta = 1/k_BT\), with \(k_B\) being the Boltzmann constant. From the above expression and following Zhang [40], we arrive at the following renormalized expression for the free energy

$$\begin{aligned} \Delta _T{\mathcal {F}}^{ren}= & {} -\frac{S_p}{32\pi L^{3}_p}\sum ^{\infty }_{m=1}\left[ \frac{\coth (\pi m{\hat{\beta }})}{(m{\hat{\beta }})^{3}}\right. \nonumber \\&\left. +\frac{\pi }{(m{\hat{\beta }})^{2}\sinh ^{2}(\pi m{\hat{\beta }})}\right] +V_p\frac{\pi ^{2}(k_BT)^{4}{\widetilde{C}}^{4}_{\Omega }}{90}, \end{aligned}$$
(43)

where \(S_p\) and \(V_p\) are the proper area of the plates and proper volume of the cavity, respectively, and \({\hat{\beta }}=1/\big (2L_Pk_BT{\widetilde{C}}_{\Omega }\big )\). The last term in Eq. (43) comes from the leading term of the free energy expansion for high temperatures, and gives the usual black body free energy density that must be subtracted from (42) as a renormalization procedure.

The proper temperature is given by \(T_p= \widetilde{C_{\Omega }} T\), and this means that for a co-moving observer all the Casimir thermal quantities are the same as obtained in the Minkowsky spacetime, in both Kerr black hole and D–S wormhole spacetimes, as well as in Teo wormhole. However, we can verify that, for a same coordinate temperature T, one gets \(T^{DS}_p>T^{K}_p\) provided \(\widetilde{C^{DS}_{\Omega }}>\widetilde{C^{K}_{\Omega }}\) for any r and provided that the parameters are the same. Thus, for instance, the leading term of the expansion for high temperatures of the renormalized (Casimir) thermal internal energy

$$\begin{aligned} U^{ren}(T)=-T^{2}_p\frac{\partial }{\partial T_p}\bigg (\frac{\Delta _T{\mathcal {F}}^{ren}}{T_p}\bigg ), \end{aligned}$$
(44)

is given by

$$\begin{aligned} U^{ren}(T)\approx V_p\frac{\pi ^{2}(k_BT_p)^{4}}{30}, \end{aligned}$$
(45)

and the Casimir pressure is trivially obtained from \(P^{ren}(T)=\frac{\partial {U^{ren}(T)}}{\partial {V_p}}\), yielding a repulsive force between the plates. In this regime, for a same coordinate temperature, \(U_{DS}^{ren}(T)>U_{K}^{ren}(T)\) and \(|P_{DS}^{ren}(T)|>|P_{K}^{ren}(T)|\).

At low temperatures, the leading correction to Eq. (44) is given by

$$\begin{aligned} U^{ren}(T)\approx \frac{\pi S_p(k_BT_p)}{2L^{2}_p}e^{-\pi /(L_pk_BT_p)}, \end{aligned}$$
(46)

and the decreasing exponential character of this term now continues ensuring us that \(U_{DS}^{ren}(T)>U_{K}^{ren}(T)\), in this temperature regime. Since \(V_p=S_pL_p\), the Casimir pressure now is given by

$$\begin{aligned} P^{ren}(T)\approx \left( \frac{\pi S_p^3k_BT_p}{V_p^{3}}-\frac{\pi ^2S_p^4}{2V_p^4}\right) e^{-\pi /(L_pk_BT_p)}. \end{aligned}$$
(47)

From here on, we can calculate a critical proper temperature, \(T_p^{(c)}\), below which the corresponding thermal Casimir force changes from repulsive from attractive, reinforcing the Casimir force near zero temperature. Such a temperature is given by

$$\begin{aligned} T_p^{(c)}=\frac{\pi S_p}{2k_BV_p}, \end{aligned}$$
(48)

and it is higher for the DS wormhole case.

The Casimir entropy \(S^{ren}=-\frac{\partial \Delta _T\mathcal { F}^{ren}}{\partial T_p}\), at high temperatures is

$$\begin{aligned} S^{ren}\approx \frac{V_p\pi ^2k_B^4T_p^3}{90} , \end{aligned}$$
(49)

with \(S^{ren}_{DS}>S_{K}^{ren}\) for a same coordinate temperature. On the other hand, in the regime of very low temperatures, we get the decreasing exponentially correction to the Casimir entropy

$$\begin{aligned} S^{ren} \approx \frac{\pi k_B S_p }{2 L_p^{2}}e^{-\pi /(L_pk_BT_p)}, \end{aligned}$$
(50)

and hence we conclude that also \(S_{DS}^{ren}>S_{K}^{ren}\).

It is worth to notice that, for a ZAMO, the values of the Casimir thermodynamic quantities, in both D–S and Kerr spacetimes, reach maximum values, since \(\tilde{C}_{\Omega }\) is a maximum, and so is the proper temperature, when \(\Omega ={\tilde{\omega }}_d\), for a given coordinate temperature and same parameters.

With respect to the Teo’s wormhole, the relationship between the proper temperature and the coordinate one continues to be valid, namely \(T_p=\tilde{C}_{\Omega }T\), with \(\tilde{C}_{\Omega }\) given by Eq. (38). Thus, it is interesting to mention that \(T_p<T\) in the interval \(\root 3 \of {\frac{6 a}{\Omega }-\frac{4 \sqrt{2} a}{\Omega }}< r<\root 3 \of {\frac{6 a}{\Omega }+\frac{4 \sqrt{2} a}{\Omega }}\). In other words, a comoving observer will measure a temperature lesser than another distant, given the same parameters, as well as for all the Casimir thermodynamic quantities.

5 Final remarks

In this paper, we have investigated the Casimir effect on material boundaries corresponding to parallel plates orbiting rotating wormholes along an equatorial circular trajectory, through the explicit calculation of the renormalized quantum vacuum energy density of a massless scalar field obeying Dirichlet boundary conditions on the plates, at both zero and finite temperatures. The only approximation used was that the length of the plates is much less than its radial coordinate, \(L\ll r\), i.e., in a zero tidal approximation inside the cavity.

We found that, at zero temperature, the referred energy densities depend on the geometric parameters of the Casimir apparatus as its proper length, \(L_p\), on the parameters of the wormhole space-times themselves such as the rotational one, a, its spinning throat radius, \(b_r\), and the parameter that characterizes the D–S wormhole, as well as on the angular velocity of the plates, \(\Omega \).

We have firstly calculated the Casimir energy density for a D–S wormhole spacetime, and graphically compared our findings with those ones valid in the Kerr black hole spacetime, given in [36]. We obtained that the Casimir energy regarding the analyzed case is greater than the one referring to the Kerr black hole. We also have shown that the profiles of the obtained curves as a function of the radial coordinate changes drastically when we assumed different regimes of the spacetime rotation, in such a way that from a minimum with low rotations (lower values of a), it has a maximum, for higher values of a. In the latter, both the Casimir energies (e.g., in the DS wormhole and Kerr black hole spacetimes) are greater than the one calculated in the flat spacetime, and in the former, lower.

We also have compared the Casimir energy density in a static D–S wormhole (by taking \(a=0\)) with that one calculated for an Ellis wormhole, given in [38], and we obtained that the absolute value of the computed energy density is lower than the one regarding this latter. We have also calculated the region of the spacetime in which the absolute value of these quantities are greater than in the Minkowsky spacetime.

In the sequence, we obtained the Casimir energy density for the same configuration in the Teo wormhole, comparing graphically it with the result found for the D–S wormhole and in Kerr black hole. We have noticed that it is the lowest of these computed quantities, for the same values in the parameter space.

Finally, we have calculated the Casimir thermodynamic quantities, namely, internal energy, pressure and entropy, from the renormalized Helmholtz free energy, following the reference [40], in the D–S wormhole spacetime. As well as in the Teo wormhole and Kerr black hole cases, the dependence of those quantities on the proper temperature \(T_p\) (i.e., as measured by a co-moving observer) is the same of the one obtained in the flat spacetime. Due to the fact that the proper temperature for the rotating D–S wormhole is greater than that one measured in the Kerr spacetime, for a given coordinate temperature T, all its computed thermodynamic quantities are greater than the ones calculated in this latter, at least in the regimes of high and low temperatures.

We conclude thus that gravito-inertial and frame-dragging effects on vacuum fluctuations of quantum fields allow indirectly detecting both the geometry and topology of the spacetime, enabling us to distinct among the possible different types of rotating wormholes and black holes.