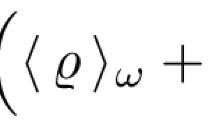1 Introduction

The studies within the cosmological perturbation theory up to second order yield that the influence of inhomogeneities on cosmological parameters inferred from a Hubble diagram can reach at most one percent level [1,2,3,4,5,6,7]. Similar results are reached by ray tracing into Newtonian N-body numerical simulations [8,9,10], relativistic N-body numerical simulations [11,12,13,14] or relativistic hydrodynamical numerical simulations of an inhomogeneous dust model [15,16,17,18,19,20]. It is suggested that inhomogeneities manifest on the Hubble diagram through the emergence of spatial curvature during structure formation [21,22,23,24,25].

The negligible impact of inhomogeneities on the global evolution and observational parameters of cosmological models is supported by general considerations concerning the backreaction effect [26,27,28,29,30,31] and perturbative analysis of weak gravitational lensing [32]. However, these approaches are often criticized as incomplete or inconclusive because of restrictive assumptions made [33,34,35,36]. There are also works which do not confirm the irrelevance of inhomogeneities despite similar methods and techniques used in studies [37,38,39]. Moreover, it is argued that the phenomena of virialization of clusters and volume dominance of voids significantly affect the Hubble diagram and may even explain dark energy [40,41,42,43,44].

Investigations to light propagation in inhomogeneous cosmologies have brought the development of various constructions for the models. They include a Swiss-cheese arrangement of the Lemaître–Tolman or the Szekeres holes into the Robertson–Walker background space-time [45,46,47,48,49,50] or a regular lattice of the Schwarzschild spheres approximately glued by the Lindquist–Wheeler technique [51,52,53,54,55,56,57,58]. With the help of numerical simulations, it is also possible to study evolving configurations consisting of interacting black holes [59,60,61,62,63,64,65,66,67,68]. An exceptional example of model with point masses periodically distributed on a cubic lattice, presented in [69, 70], can be built as a perturbative solution to the Einstein equations for a dust. The post-Newtonian formalism is another framework utilizing a perturbative approach in which a model is hierarchically constructed from autonomous cells whose matching conditions determine an overall dynamics [71,72,73,74,75,76].

Above, we described general context of inhomogeneous cosmology. Now, let us explain our motivation behind the present work. The linear perturbation theory gives some approximate solution to the Einstein equations, for which all the terms \(\mathcal {O}(\lambda ^2)\) are neglected. Here, \(\lambda \) is the perturbative parameter. For example, the energy–momentum tensor chosen in the matter-dominated era is \(T_{\mu \,\!\nu }=\rho \,U_\mu \,U_\nu +\delta T_{\mu \,\!\nu }\), where deviations \(\delta T_{\mu \,\!\nu }\) are of the order of \(\lambda ^2\). We will call this energy–momentum tensor dust-like if only these additional terms \(\delta T_{\mu \,\!\nu }\) are small enough. We should emphasize that the terms \(\delta T_{\mu \,\!\nu }\) have physical meaning since a variety of phenomena contribute to all the energy–momentum tensor elements. These phenomena are for example proper motions of galaxies or the pressure of the intra-cluster gas. Therefore, the observations of the velocity dispersion of galaxy cluster members and the properties of the intra-cluster medium constrain the smallness of \(\delta T_{\mu \,\!\nu }\). To satisfy these empiric conditions within the linear perturbation theory, the value of the parameter \(\lambda \) and the resulting amplitude of the inhomogeneities should be small.

The principal goal of this paper is to find a cosmological model which remains dust-like within the observational constraints, but at the same time allows much higher amplitude of the inhomogeneities than the linear perturbation theory. We studied decaying mode of the linear perturbation theory in [77] and expanded it to the third-order perturbations in [78]. In the recent paper, we consider the growing mode of the perturbation theory up to the fourth order. To control the fifth and higher-order contributions to \(\delta T_{\mu \,\!\nu }\), we calculate the exact Einstein tensor corresponding to the resulting metric. Compared to our previous works, this improves the analysis of convergence of the presented perturbative scheme.

We organize this paper as follows. In Sect. 2 we present the model construction scheme, while in Sect. 3 we analyze the properties of this model for a given exemplary density distribution.

2 The model construction

Consider the following space-time metric in Cartesian-like coordinates (t, x, y, z):

$$\begin{aligned} g_{\mu \,\!\nu }=\begin{pmatrix} -1 &{} 0 &{} 0 &{} 0 \\ 0 &{} c_{11} &{} c_{12} &{} c_{13} \\ 0 &{} c_{12} &{} c_{22} &{} c_{23} \\ 0 &{} c_{13} &{} c_{23} &{} c_{33} \end{pmatrix}\,, \end{aligned}$$
(1)

where six metric functions \(c_{ij}=c_{ij}(\lambda ,t,x,y,z)\) depend on space-time coordinates and some auxiliary parameter \(\lambda \). We adopt geometrized units for which \(c=1\) and \(G=1\). Since Christoffel symbols \(\varGamma ^\mu _{0\,\!0}=0\) vanish for all \(\mu \), the vector \(U^\mu =(1,0,0,0)\) is always tangent to some time-like geodesic. Worldlines of dust particles are geodesics. Therefore for the universe filled with dust, the coordinates we use are comoving.

The task we want to address in this article is the following. Suppose that the Einstein equations are satisfied exactly. How to find the metric functions \(c_{ij}\) so that the energy–momentum tensor \(T_{\mu \,\!\nu }=G_{\mu \,\!\nu }/(8\pi )\) is dust-like and the density distribution has inhomogeneities with the amplitude growing during the time evolution?

For the dust-like energy–momentum tensor, every element except the density \(\rho =T_{0\,\!0}\) is negligible compared to \(\rho \). A variety of exact solutions to the Einstein equations, which tend to describe the Universe in the matter-dominated era, assume the dust energy–momentum tensor for simplicity. In that case, all the \(T_{\mu \,\!\nu }\) elements other than the density are exactly zero. However, many physical processes could contribute to these energy–momentum tensor elements. For example, proper motions of galaxies act as a pressure, while this contribution is very small. This justifies the dust-like assumption for \(T_{\mu \,\!\nu }\) in the matter-dominated era if only the smallness of its elements other than the density is properly controlled.

The task of finding metric functions \(c_{ij}\) for which the energy–momentum tensor has the properties described above is quite complicated in general. To handle it in the specific case, we consider two simplifying model restrictions:

  1. (i)

    Metric functions \(c_{ij}\) are invariant over every permutation of spatial variables (x, y, z).

  2. (ii)

    Metric functions \(c_{ij}\) are analytic in \(\lambda \), and the parameter \(\lambda \) is proportional to the amplitude of inhomogeneities. Additionally, we assume that for \(\lambda =0\) we recover the Einstein–de Sitter (EdS) space-time, which is the spatially flat universe homogeneously filled with dust. This means that metric functions in this limit read: \(c_{ij}(0,t,x,y,z)=a(t)^2\) for \(i=j\) and zero otherwise. The scale factor in this case is \(a(t)=\mathcal {C}\,t^{2/3}\), where \(\mathcal {C}\) is a constant.

The assumption (ii) enables us to consider the usual perturbation theory around the EdS background. We may take Taylor expansion of the metric and the resulting energy–momentum tensor around \(\lambda =0\):

$$\begin{aligned} g_{i\,\!j}=\sum \limits _{k=0}^{\infty } \lambda ^k\,g^{(k)}_{i\,\!j}\,, \quad T_{\mu \,\!\nu }=\sum \limits _{k=0}^{\infty } \lambda ^k\,T^{(k)}_{\mu \,\!\nu }\,, \end{aligned}$$
(2)

and analyze k-order metric elements \(g^{(k)}_{i\,\!j}\) and k-order energy–momentum tensor \(T^{(k)}_{\mu \,\!\nu }\) order by order. The form of the metric (1) implies that perturbations are performed in the synchronous comoving gauge in each order. The scalar perturbations in the linear order admit two modes: the decaying and the growing one. In our previous paper [78], we analyze the decaying mode consistent with the assumption (i) in the orders higher than the linear order. In the current paper, we concentrate on the growing mode. We begin with the linear perturbations, and then we correct the solution in consecutive orders. At the end of this procedure, we insert the approximate fourth-order metric into exact Einstein equations to account for the higher-order contributions.

2.1 Perturbation theory in the linear order

We assume the following ansatz for the spatial part of the metric in the k-order, which is consistent with the symmetry restriction (i):

$$\begin{aligned} g^{(k)}_{i\,\!j}= & {} a(t)^2\,\Bigg ( \left( t^{\alpha _k} A_k(x^i)+t^{\beta _k} \sum \limits _{l=1}^3 B_k(x^l) \right) \delta _{ij}+ \nonumber \\&+t^{\phi _k} F_k(x^i,x^j) (1-\delta _{ij}) \Bigg )\,. \end{aligned}$$
(3)

In each order, we introduce three functions \(A_k\), \(B_k\), \(F_k\) and three coefficients \(\alpha _k\), \(\beta _k\) and \(\phi _k\), which should be specified in the process of the model construction. Function \(F_k\) should be symmetric. The condition (i) implicates that the energy–momentum tensor in each order \(k\ge 1\) has four types of components: \(T^{(k)\,\!0}\,{}_0\), \(T^{(k)\,\!0}\,{}_i\), \(T^{(k)\,\!i}\,{}_j\) for \(i=j\) and \(T^{(k)\,\!i}\,{}_j\) for \(i\ne j\). The structural form of components within each type is invariant over every permutation of spatial variables.

Let us start with the linear order perturbations. If we specify the powers:

$$\begin{aligned} \alpha _1=2/3\,, \quad \beta _1=0\,,\quad \phi _1=0\,, \end{aligned}$$
(4)

then the elements \(T^{(1)\,\!0}\,{}_i\) and \(T^{(1)\,\!i}\,{}_j|_{i\ne j}\) are equal to zero, and all the terms of \(T^{(1)\,\!0}\,{}_0\) together with all the terms of \(T^{(1)\,\!i}\,{}_j|_{i=j}\) have a simple power-law dependence on time. For simplicity, we put the function \(F_1=0\). Then, we may eliminate pressure-like terms \(T^{(1)\,\!i}\,{}_j|_{i=j}=0\) by demanding that the function \(B_1\) satisfies the differential equation:

$$\begin{aligned} \frac{\mathrm {d}^2}{\mathrm {d} w^2}B_1(w)=\frac{10}{9}\,\mathcal {C}^2\,A_1(w)\,,\quad w=x,y,z\,. \end{aligned}$$
(5)

After that, the first order density \(\rho ^{(1)}\equiv -T^{(1)\,\!0}\,{}_0\) is:

$$\begin{aligned} \rho ^{(1)}=\frac{-1}{12\pi t^{4/3}}\,\left( A_1(x)+A_1(y)+A_1(z) \right) \,. \end{aligned}$$
(6)

This way, we obtain exact dust solution to the cosmological perturbation theory in the linear order, in which the density distribution in space is given by the arbitrary function \(A_1\). Let us analyze in details the model for one exemplary function \(A_1\) given below.

In the beginning, we comment on the dimensions of the physical quantities important for model construction. We are working in the geometrized units \(c=1\) and \(G=1\). In this system of units, all of the physical quantities are dimensionless or their dimension can be expressed as some power of the unit of length. We choose the megaparsec as basic unit of length. Then, the age of the EdS universe \({t_0^{\scriptscriptstyle {(EdS)}}}=9.32\,\mathrm {Gyr}\), compatible with the Hubble constant value \(H_0=70\,\mathrm {km/s/Mpc}\), reads \({t_0^{\scriptscriptstyle {(EdS)}}}=2855.57\,\mathrm {Mpc}\). There is a natural convention of normalizing the scale factor to unity at the age of the universe \(a({t_0^{\scriptscriptstyle {(EdS)}}})=1\). From that follows the value of the constant \(\mathcal {C}=4.97\times 10^{-3}\). The density of the EdS model \(\rho ^{(0)}=1/(6\pi t^2)\) evaluated at the universe age defines the critical density \(\rho _{cr}=\rho ^{(0)}({t_0^{\scriptscriptstyle {(EdS)}}})\), which value is \(\rho _{cr}=6.51\times 10^{-9}\,\mathrm {Mpc}^{-2}\). The critical density introduces a natural density scale. We define the quantity \(\varOmega :=\rho /\rho _{cr}\) as a density measured in the critical density units.

Now, we choose the function \(A_1\) as:

$$\begin{aligned} A_1(w)=-s_0\,\sin (\mathcal {B}_0\,w)-s_1\,\sin (\mathcal {B}_1\,w)\,, \end{aligned}$$
(7)

where \(s_0=1\), \(s_1=0.5\), \(\mathcal {B}_0=\pi /25\) and \(\mathcal {B}_1=\pi /5\). If we fix the lambda parameter value as \(\lambda =4.42\times 10^{-4}\), then the maximal density at \({t_0^{\scriptscriptstyle {(EdS)}}}\) is \(\varOmega =1.2\). Density distribution illustrated in Fig. 1 forms periodic, cubic lattice. We choose the function \(A_1\) in Eq. (7) as the simplest periodic function with two modes, which provide interesting density distribution.

Fig. 1
figure 1

Top: The model isodensity surfaces at \({t_0^{\scriptscriptstyle {(EdS)}}}\), which form an infinite, periodic lattice. Bottom: The density distribution within the elementary cell

Full size image

The linear size of the elementary cell at \({t_0^{\scriptscriptstyle {(EdS)}}}\) is around \(50\,\mathrm {Mpc}\). Because the metric is nontrivial, the length of a segment depends on its orientation and position in space. The linear size of the elementary cell measured near to the overdense region gives the value slightly lower than \(50\,\mathrm {Mpc}\), while the result of the same measurement performed close to the underdense region could be slightly higher than \(50\,\mathrm {Mpc}\). For scales much larger than the size of the elementary cell the model universe becomes homogeneous and isotropic in common sense, and FLRW space-time arises as a natural candidate for an effective average model. Although the density distribution profile is restricted by the model symmetry, quite complicated distributions are allowed. In the given example, one can identify large overdensity and underdensity regions of a size comparable to the typical size of superclusters of galaxies and smaller substructures with a size around a few megaparsecs.

2.2 Perturbation theory in the second order

The function \(B_1\) which is the solution of the Eq. (5) for the above proposition of the arbitrary function \(A_1\) is:

$$\begin{aligned} B_1(w)=\frac{10\,\mathcal {C}^2}{9}\left( \frac{s_0}{\mathcal {B}_0^2}\sin (\mathcal {B}_0\,w)+\frac{s_1}{\mathcal {B}_1^2}\sin (\mathcal {B}_1\,w) \right) \,. \end{aligned}$$
(8)

In the above formula there appear two small constants: \((\mathcal {C}/\mathcal {B}_0)^2=1.56\times 10^{-3}\) and \((\mathcal {C}/\mathcal {B}_1)^2=6.25\times 10^{-5}\), where \(\mathcal {C}^2=2.47\times {10}^{-5}\). The metric function \(B_1\) is then much smaller than the metric function \(A_1\). However, in the second-order energy–momentum tensor elements appear some terms containing derivatives of the function \(B_1\) divided by \(\mathcal {C}^2\). These terms are the same order of magnitude as the terms with the function \(A_1\) alone. For that reason, one cannot neglect the metric function \(B_1\) in the first-order metric \(g^{(1)}\), if the second-order energy–momentum tensor is considered. Nevertheless, the existence of these small constants enables one to identify the leading terms in the second-order energy–momentum tensor and to neglect the terms which are much smaller compared to the leading terms.

From now on, we denote by the symbol \(\approx \) the approximation of some expression, in which all the terms proportional to \(\mathcal {C}^2\) are neglected. Because some subexpressions could have a different time dependence, the validity of this approximation should be checked in each epoch of time. Let us write the leading terms of \(T^{(2)\,\!x}\,{}_x\).

$$\begin{aligned}&T^{(2)\,\!x}\,{}_x \approx \frac{1}{72\pi t^{2/3}}\bigg [6 A_1(y)^2-A_1(y)\,A_1(z)+6 A_1(z)^2 \nonumber \\&\quad -\frac{9}{4\mathcal {C}^2}\bigg (\frac{\mathrm {d}}{\mathrm {d} y}A_1(y)\frac{\mathrm {d}}{\mathrm {d} y}B_1(y)+ \frac{\mathrm {d}}{\mathrm {d} z}A_1(z)\frac{\mathrm {d}}{\mathrm {d} z}B_1(z)\bigg ) \nonumber \\&\quad +\frac{9}{2\mathcal {C}^2}\bigg (\frac{\mathrm {d}^2}{\mathrm {d} y^2}B_2(y)+\frac{\mathrm {d}^2}{\mathrm {d} z^2}B_2(z)-A_1(y)\frac{\mathrm {d}^2}{\mathrm {d} y^2}B_1(y) \nonumber \\&\quad -A_1(z)\frac{\mathrm {d}^2}{\mathrm {d} z^2}B_1(z)-A_1(z)\frac{\mathrm {d}^2}{\mathrm {d} y^2}B_1(y)-A_1(y)\nonumber \\&\quad \frac{\mathrm {d}^2}{\mathrm {d} z^2}B_1(z)\bigg ) \nonumber \\&\quad -\frac{9}{\mathcal {C}^2}\frac{\partial ^{2}}{\partial y\partial z}F_2(y,z) -14(A_2(y)+A_2(z)) \bigg ]. \end{aligned}$$
(9)

In the beginning, time dependence of different terms was not the same. However, it can be simplified to a single power-law \(t^{-2/3}\), when we fix the following values of the powers:

$$\begin{aligned} \alpha _2=4/3, \qquad \beta _2=2/3, \qquad \phi _2=2/3\,. \end{aligned}$$
(10)

If we wish that the terms containing the second-order metric functions \(B_2\) and \(F_2\) are the same order of magnitude as the terms containing functions \(A_k\), then functions \(B_2\) and \(F_2\) should be proportional to \(\mathcal {C}^2\). We will verify this assumption at the end of the presented procedure. In that case, \(T^{(2)\,\!0}\,{}_i\approx 0\) and \(T^{(2)\,\!i}\,{}_j\approx 0\) for \(i\ne j\). The corresponding elements \(T^{(2)\,\!y}\,{}_y\) and \(T^{(2)\,\!z}\,{}_z\) one would obtain by performing permutation of the spatial variables in the formula Eq. (9).

On the right-hand side of Eq. (9) it is possible to separate terms depending on two variables. These terms are equal to zero when the following differential equation is satisfied:

$$\begin{aligned} \frac{\partial ^{2}}{\partial v\partial w}F_2\left( v, w\right)= & {} -\frac{1}{9} \, {\mathcal {C}}^{2} A_1\left( v\right) A_1\left( w\right) \nonumber \\&- \frac{1}{2} \, A_1\left( w\right) \frac{\mathrm {d}^{2}}{\mathrm {d} v^{2}}B_1\left( v\right) \nonumber \\&- \frac{1}{2} \, A_1\left( v\right) \frac{\mathrm {d}^{2}}{\mathrm {d} w^{2}}B_1\left( w\right) \, . \end{aligned}$$
(11)

The variables \(v,w \in \{x,y,z\}\) and \(v\ne w\). The remaining terms depending on one variable can be eliminated by the following condition:

$$\begin{aligned} \frac{\mathrm {d}^{2}}{\mathrm {d} w^{2}}B_2\left( w\right)= & {} - \frac{4}{9}{\mathcal {C}}^{2} \, {\left( 3 \, A_1\left( w\right) ^{2} - 7 \, A_2\left( w\right) \right) } \nonumber \\&+ \frac{1}{2} \, \frac{\mathrm {d}}{\mathrm {d} y}A_1\left( w\right) \frac{\mathrm {d}}{\mathrm {d} w}B_1\left( w\right) \nonumber \\&+ A_1\left( w\right) \frac{\mathrm {d}^{2}}{\mathrm {d} w^{2}}B_1\left( w\right) \,. \end{aligned}$$
(12)

If the above differential equations are satisfied, then all of the elements \(T^{(2)\,\!i}\,{}_j\approx 0\) for \(i=j\). This is guaranteed by the symmetry condition imposed on the metric.

The conditions Eqs. (11) and (12) enable to simplify the form of the second-order density \(\rho ^{(2)}=-T^{(2)\,\!0}\,{}_0\). As the result, one gets:

$$\begin{aligned} \rho ^{(2)}= & {} \frac{1}{18\pi t^{2/3}}\Big (2A_1(x)^2+2A_1(y)^2+2A_1(z)^2 \nonumber \\&-5A_2(x)-5A_2(y)-5A_2(z)\,\Big ). \end{aligned}$$
(13)

Specification of the arbitrary function \(A_2\) determines the second-order density. In our example, we choose this function such that perturbed density at the second order has the same spatial distribution as the first-order density perturbation:

$$\begin{aligned} \rho ^{(2)}=-\frac{\mathcal {K}}{t^{2/3}}\,\left( A_1(x)+A_1(y)+A_1(z) \right) \,. \end{aligned}$$
(14)

We introduced the parameter \(\mathcal {K}\), which controls the growth rate of the density contrast. In this case, the function \(A_2\) takes the form:

$$\begin{aligned} A_2(w)=\frac{18}{5}\,\pi \,\mathcal {K}\,A_1(w)+\frac{2}{5}\,A_1(w)^2\,. \end{aligned}$$
(15)

The right-hand sides of Eqs. (11) and (12) depend only on the first-order metric functions and the arbitrary function \(A_2\). In the case of our example, these functions are composed of the trigonometric functions and it is very simple to find solutions to Eqs. (11) and (12). Taking the constants of integration equal to zero for simplicity we obtained:

$$\begin{aligned} F_2\left( v, w\right)= & {} -\frac{11\,\mathcal {C}^2}{9}\,\left( \frac{{s}_{0}^{2} \cos \left( {\mathcal {B}}_{0} v\right) \cos \left( {\mathcal {B}}_{0} w\right) }{ {\mathcal {B}}_{0}^{2}} \right. \nonumber \\&+\frac{ {s}_{0} {s}_{1} \cos \left( {\mathcal {B}}_{1} v\right) \cos \left( {\mathcal {B}}_{0} w\right) }{ {\mathcal {B}}_{0} {\mathcal {B}}_{1}} \nonumber \\&+ \frac{ {s}_{0} {s}_{1} \cos \left( {\mathcal {B}}_{0} v\right) \cos \left( {\mathcal {B}}_{1} w\right) }{ {\mathcal {B}}_{0} {\mathcal {B}}_{1}} \nonumber \\&\left. + \frac{ {s}_{1}^{2} \cos \left( {\mathcal {B}}_{1} v\right) \cos \left( {\mathcal {B}}_{1} w\right) }{ {\mathcal {B}}_{1}^{2}} \right) \end{aligned}$$
(16)

and

$$\begin{aligned}&B_2\left( w\right) = \frac{7}{60} \, {\mathcal {C}}^{2} ({s}_{0}^{2}+{s}_{1}^{2}) w^{2} \nonumber \\&\quad + \frac{{\mathcal {C}}^{2} {s}_{0} {s}_{1}\,\cos \left( {\mathcal {B}}_{0} w + {\mathcal {B}}_{1} w\right) }{ {\left( {\mathcal {B}}_{0}^{2} + 2 \, {\mathcal {B}}_{0} {\mathcal {B}}_{1} + {\mathcal {B}}_{1}^{2}\right) }} \left( \frac{46}{45}+\frac{5\,\mathcal {B}_0}{18\,\mathcal {B}_1}+\frac{5\,\mathcal {B}_1}{18\,\mathcal {B}_0} \right) \nonumber \\&\quad + \frac{{\mathcal {C}}^{2} {s}_{0} {s}_{1}\,\cos \left( {\mathcal {B}}_{0} w - {\mathcal {B}}_{1} w\right) }{ {\left( {\mathcal {B}}_{0}^{2} - 2 \, {\mathcal {B}}_{0} {\mathcal {B}}_{1} + {\mathcal {B}}_{1}^{2}\right) }} \left( -\frac{46}{45}+\frac{5\,\mathcal {B}_0}{18\,\mathcal {B}_1}+\frac{5\,\mathcal {B}_1}{18\,\mathcal {B}_0} \right) \nonumber \\&\quad + \frac{56\,\pi \,\mathcal {C}^2\,\mathcal {K}}{5}\,\left( \frac{s_0\,\sin (\mathcal {B}_0\,w)}{\mathcal {B}_0^2}+\frac{s_1\,\sin (\mathcal {B}_1\,w)}{\mathcal {B}_1^2} \right) \nonumber \\&\quad + \frac{71\,\mathcal {C}^2}{360}\,\left( \frac{s_0^2\,\cos (2\mathcal {B}_0\,w)}{\mathcal {B}_0^2}+\frac{s_1^2\,\cos (2\mathcal {B}_1\,w)}{\mathcal {B}_1^2} \right) \,. \end{aligned}$$
(17)

As it was expected, the functions \(F_2\) and \(B_2\) are proportional to \(\mathcal {C}^2\), so the method of construction of the metric functions is self-consistent. This way we end up with a dust-like solution up to the second order of the perturbation theory.

2.3 The third and the fourth-order perturbations

It is possible to apply the procedure given in the previous subsection in the consecutive orders of the perturbation theory. First, we fix the values of the powers:

$$\begin{aligned} \alpha _k=(2\,k)/3, \qquad \beta _k=(2\,k-1)/3, \qquad \phi _k=(2\,k-1)/3\,, \end{aligned}$$
(18)

which appear in the time evolution part of the metric functions. This way, we simplify the time dependence of the energy–momentum tensor subexpressions to a single power law. Next, we assume that metric functions \(B_k\) and \(F_k\) are proportional to \(\mathcal {C}^2\) and neglect the terms of the energy–momentum tensor which are small compared to the leading-order terms. Since \(T^{(k)\,\!0}\,{}_i\) and \(T^{(k)\,\!i}\,{}_j|_{i\ne j}\) contain only the functions \(B_k\) and \(F_k\) and the constant \(\mathcal {C}^2\) is small, we may expect that \(T^{(k)\,\!0}\,{}_i\approx 0\) and \(T^{(k)\,\!i}\,{}_j\approx 0\) for \(i\ne j\).

In the remaining elements \(T^{(k)\,\!i}\,{}_j|_{i=j}\) one can identify terms depending on two variables, which can be eliminated when the function \(F_k\) satisfies an appropriate differential equation similar to Eq. (11). Then, in the formula for \(T^{(k)\,\!i}\,{}_j|_{i=j}\) remain some terms depending on the one variable only. They can be set to zero by demanding that the function \(B_k\) satisfies some differential equation similar to Eq. (12).

The differential equations for the metric functions \(F_k\) and \(B_k\) enable one to simplify the formula for the k-order density \(\rho ^{(k)}\). In effect, \(\rho ^{(k)}\) depends only on the metric functions \(A_l\), for \(l\le k\). This way, specification of the arbitrary metric function \(A_k\) determines the spatial profile of the k-order density. In our example, we analyze the case for which the spatial distribution of the density in each order is the same. This means that:

$$\begin{aligned} \rho ^{(k)}=-\mathcal {K}\,t^{(2k-6)/3}\,\left( A_1(x)+A_1(y)+A_1(z) \right) \,, \end{aligned}$$
(19)

for \(k\ge 2\). The time dependence \(t^{(2k-6)/3}\) of the k-order density is a consequence of the specific values of the powers Eq. (18).

The right-hand sides of the differential equations for \(F_k\) and \(B_k\) depend on the metric functions \(F_l\) and \(B_l\) known from the previous orders \(l<k\) and the metric functions \(A_m\), for \(m\le k\). After the arbitrary function \(A_k\) is fixed, one can solve these differential equations and obtain the resulting \(F_k\) and \(B_k\). It is easy to verify that these functions are proportional to \(\mathcal {C}^2\), so the method is self-consistent.

We apply the presented method up to fourth order of the perturbation theory. The resulting metric functions are made of simple trigonometric and monomial functions, but the expressions become quite large, and we decided not to display them here. We attach to this article the supplementary material containing all the necessary formulas beyond the second order. It includes the Sagemath script [79], which implements the method described in this section up to the fourth-order perturbations.

2.4 Exact solution

By the method presented in the previous subsections, we construct a dust-like solution to the fourth-order perturbation theory. Now, we want to consider contributions from higher orders. For this purpose, we take the space-time metric as a fourth-order polynomial in the parameter \(\lambda \):

$$\begin{aligned} g_{i\,\!j}=\sum \limits _{k=0}^{4} \lambda ^k\,g^{(k)}_{i\,\!j}\,, \end{aligned}$$
(20)

where the metric functions in each order \(g^{(k)}\) were constructed by the method described in Sects. 2.1–2.3. Then, we calculate the exact Einstein tensor corresponding to this metric \(G_{\mu \,\!\nu }\). The resulting energy–momentum tensor \(T_{\mu \,\!\nu }=G_{\mu \,\!\nu }/(8\pi )\) could differ slightly from its fourth-order counterpart, however, we will show in the subsequent section that this difference is small, and \(T_{\mu \,\!\nu }\) remains close to the energy–momentum tensor of the dust. For this paper, we call such energy–momentum tensor dust-like. The crucial thing is how small could be an acceptable departure of the dust-like energy–momentum tensor elements from the pure dust. We will show in Sect. 3.2 that for a large amplitude of the inhomogeneities considered, the third-order perturbations do not satisfy the observational constraints of the pressure value in the matter-dominated era, while the fourth-order model does. This way, we investigate the convergence of our perturbative framework, which is an improvement compared to our previous papers [77, 78].

3 Model properties

3.1 Density distribution

Let us begin with the analysis of the distribution of the model density \(\rho =-T^{0}\,{}_0\). In the model construction method presented in the previous section, in each order \(k\ge 1\) one can specify the shape of the k-order density distribution \(\rho ^{(k)}\) through arbitrary function \(A_k\). We fix the \(A_1\) function as in the definition Eq. (7). The functions \(A_k\) for \(1<k\le 4\) have been specified so that the density \(\rho ^{(k)}\) has the same spatial distribution as \(\rho ^{(1)}\). The formula for \(\rho ^{(k)}\) is given by the Eq. (19). The density in each order \(\rho ^{(k)}\) has a different power in a time dependence. To some extent, we can control the growth rate of the inhomogeneities by manipulating the contribution of each order \(\rho ^{(k)}\) to the total density. In our example, the parameter \(\mathcal {K}\) describes the contribution of the high-order densities \(\rho ^{(k)}|_{1<k\le 4}\) in comparison to the linear order contribution \(\rho ^{(1)}\), given by the Eq. (6).

From now on, we fix the parameter \(\lambda =4.42\times 10^{-4}\). For this value of \(\lambda \), the maximal density at the EdS universe age \({t_0^{\scriptscriptstyle {(EdS)}}}\) up to the first order is \(\varOmega ^{(0)}+\varOmega ^{(1)}=1.2\), where \(\varOmega ^{(k)}=\rho ^{(k)}/\rho _{cr}\). For \(\mathcal {K}=0\) we expect that the first-order density gives a dominant contribution to the total density. Indeed, the total density expressed in the units of the critical density \(\varOmega =\rho /\rho _{cr}\) evaluated at the maximum of the overdensity region \(\mathbf {x}_{O}=(12.5,12.5,12.5)\) and at the \({t_0^{\scriptscriptstyle {(EdS)}}}\) is \(\varOmega =1.1999\). The shape of the isodensity surfaces remains practically unchanged in comparison to the isodensity surfaces of the perturbation theory up to the first order. Therefore, the density of the full model \(\rho \) is approximated very well by the density of the perturbation theory up to the first-order perturbations. Also, one can think about Fig. 1 as it describes the density distribution in space of the density of the full model \(\rho \). We examined also two specific values \(\mathcal {K}=0.1\) and \(\mathcal {K}=-0.1\), for which the density of the full model is very close to the density of the fourth-order perturbation theory.

The density has a spatial distribution, which forms an infinite, cubic lattice. For scales much larger than the elementary cell the model becomes homogeneous and isotropic in common sense. It is then reasonable to approximate our inhomogeneous universe by the FLRW solution with some average density distribution \(\langle \rho \rangle \) if only scales much larger than the elementary cell are considered. We will use a natural definition of the average of some physical quantity f over the elementary cell \(\mathcal {D}\), at the hypersurface of the constant time t:

$$\begin{aligned} \langle f \rangle _{\mathcal {D}}(t)=\frac{\int _{\mathcal {D}}\mathrm {d}^3 x\,f(t,\mathbf {x})\,\sqrt{\mathrm {det}g_{i\,\!j}}}{\int _{\mathcal {D}}\mathrm {d}^3 x\,\sqrt{\mathrm {det}g_{i\,\!j}}}\,. \end{aligned}$$
(21)

It should be pointed out that the volume element is not trivial and depends on the position in space. The isosurfaces of the square root of the spatial part of the metric determinant are shown in Fig. 2. Comparison of this figure with Fig. 1 shows that underdensity regions have larger values of the volume element than overdensities.

Fig. 2
figure 2

The isosurfaces of the geometrical factor \(\sqrt{\mathrm {det}g_{i\,\!j}}\) appearing in the volume element \(\sqrt{\mathrm {det}g_{i\,\!j}}\,\mathrm {d}^3x\). The domain is the elementary cell

Full size image

In Fig. 3 we present by the solid blue curve the model average density over the elementary cell \(\langle \varOmega \rangle _{\mathcal {D}}(t)\) as a function of time, calculated for the case \(\mathcal {K}=0\). For two other values of \(\mathcal {K}=0.1\) and \(\mathcal {K}=-0.1\) we obtain the same result. For comparison, by a red dashed curve we plot on the same figure the density of the Einstein–de Sitter model, which was used as a background space-time \(g^{(0)}\) for the model construction.

Fig. 3
figure 3

Blue – the model average density expressed in the critical density units as a function of time. Red dashed curve corresponds to the time dependence of the density of the Einstein–de Sitter model

Full size image

It is evident that both curves overlap, so the density of the EdS model is indeed an averaged density of the full inhomogeneous model considered here.

The notion of the average density enables one to define the density contrast as:

$$\begin{aligned} \delta =\max \limits _{x^\mu \in \mathcal {D}}\frac{|\rho -\langle \rho \rangle _{\mathcal {D}}|}{\langle \rho \rangle _{\mathcal {D}}}\,. \end{aligned}$$
(22)

In Fig. 4 we present the density contrast as a function of time for three values of \(\mathcal {K}\). For \(\mathcal {K}=0\) density contrast grows with time exactly as the growing mode of the first-order perturbation theory, where \(\delta \propto t^{2/3}\). For the parameter \(\mathcal {K}=0.1\) density contrast grows faster than \(t^{2/3}\), while for the value \(\mathcal {K}=-0.1\) it grows slower. It is interesting to notice, that the density contrast of the exact solution to the Einstein equations could differ from the prediction of the first-order perturbation theory. Important difference appears when second and higher-order terms contribute significantly to the total density.

3.2 Is the energy–momentum tensor dust-like?

We developed our model within the framework of the perturbation theory up to the fourth order. Then, we treated the resulting fourth-order polynomial in \(\lambda \) parameter (Eq. (20)) as a metric of the full model, for which the Einstein equations are satisfied exactly. In effect, we have to deal with the contributions to the energy–momentum tensor coming from fifth and higher orders, which we do not control. We have to check whether the resulting energy–momentum tensor of the full model \(T_{\mu \,\!\nu }=G_{\mu \,\!\nu }/(8\pi )\) resembles the properties of the energy–momentum tensor from the fourth-order perturbation theory.

Fig. 4
figure 4

The dependence of the density contrast in time. Blue curve corresponds to \(\mathcal {K}=0\), orange refers to \(\mathcal {K}=0.1\) and light green to \(\mathcal {K}=-0.1 \)

Full size image

In the previous subsection, we have checked that the density of the full model practically does not change in comparison with the EdS model density perturbed up to the fourth order. Now, we analyze the values of the other elements of the energy–momentum tensor. Because of the symmetry condition imposed on the metric, there are four types of the \(T^{\mu }{}_{\nu }\) components.

Fig. 5
figure 5

The elements of the energy–momentum tensor relative to the energy density, evaluated at the center of the overdensity region. The blue curves represent pressure-like terms \(T^{i}{}_{j}|_{i=j}\), the orange ones correspond to the elements \(T^0{}_i\), while the green curves refer to \(T^{i}{}_{j}|_{i\ne j}\). The second-order quantities are plotted by the dotted lines, the third-order by the dashed-dotted lines, while the fourth-order by the dashed lines. Solid lines correspond to the exact energy–momentum tensor described in Sect. 2.4

Full size image

In Fig. 5 we present the absolute value of the remaining three types of the energy–momentum elements relative to the density. The energy–momentum tensor elements plotted on this figure are evaluated at the position of the maximal density \(\mathbf {x}_{O}=(12.5,12.5,12.5)\) and shown as functions of time. To show the convergence of the perturbative expansion for each type of the energy–momentum tensor elements, we plot the second-order, the third-order, and the fourth-order quantities by the dotted, the dashed-dotted, and the dashed curves respectively. As we explained in Sect. 2.4, after we finished the perturbative construction, we have calculated the exact Einstein tensor to account for the higher-order terms. We show the corresponding exact energy–momentum tensor elements by the solid lines in Fig. 5. One can see that the difference between these solid lines and the fourth-order prediction is visible but small. In each order perturbations, the pressure-like terms are one order of magnitude smaller than the pressure-like terms in the previous order. At the same time, the remaining elements practically do not change. Because there is a logarithmic scale in Fig. 5, some curves overlap.

The blue curves correspond to the elements \(T^{i}{}_{j}|_{i=j}\) representing the pressure measured by the observer which is at rest in the comoving reference frame (t, x, y, z). To verify whether the values of these elements are small enough we have to consider some interpretation of the source of this pressure.

If the model energy–momentum tensor describes galaxies which are members of rich galaxy clusters and have their proper motions, then the energy–momentum tensor could be interpreted in the framework of the Jeans’ theory of a collisionless system of particles. Within this model framework, the stress-energy tensor (the spatial part of the energy–momentum tensor) is directly related to the velocity dispersion tensor of these particles \(\sigma _{i\,\!j}\):

$$\begin{aligned} T^i{}_j=\rho \,\sigma ^2_{i\,\!j}\,. \end{aligned}$$
(23)

Since the density is positive, the elements of \(T^i{}_j\) should be positive also. Unfortunately, the resulting pressure \(T^{i}{}_{j}|_{i=j}\) is negative in some regions. However, this problem can be solved in the following way. We increase a bit the pressure by adding the small positive term \(\mathcal {P}\,t^{-2/3}\) to the right-hand side of the second-order formula Eq. (9), where \(\mathcal {P}=1.006\times 10^{-4}\). Then, after recalculation of the metric functions, one can check that in the case \(\mathcal {K}=0\) the order of magnitude of the energy–momentum tensor elements remain unchanged in comparison to the case \(\mathcal {P}=0\), but the pressure \(T^{i}{}_{j}|_{i=j}\) is always positive within the elementary cell. For other values of \(\mathcal {K}\) the corresponding \(\mathcal {P}\) should be different.

The positiveness of the pressure enables us to interpret it in terms of the velocity dispersion. The values of the pressure of order \(10^{-6}\) in the geometrized units correspond to the velocity dispersion of order of \(1000\,\mathrm {km/s}\). This value of the velocity dispersion is consistent with observations of galaxy clusters. Therefore, for the high amplitude of the inhomogeneities considered here, the pressure-like terms of the fourth-order energy–momentum tensor are consistent with the observational constraints. The values of the pressure-like terms of the third-order solution are one order of magnitude higher, so the respective velocity dispersion is too high. We see that the fourth-order perturbations are needed to achieve the acceptable difference between the resulting energy–momentum tensor and the energy–momentum tensor of the dust. If this difference is acceptably small, we call the resulting energy–momentum tensor dust-like.

In Fig. 6 we present one of the elements of the velocity dispersion tensor \(\sigma _{x\,\!x}\), which is related to the model energy–momentum tensor element \(T^{x}{}_{x}\) by the formula Eq. (23), for the case \(\mathcal {K}=0\) and at the time \({t_0^{\scriptscriptstyle {(EdS)}}}\). We calculate \(T^{x}{}_{x}\) from the exact Einstein tensor described in Sect. 2.4.

Fig. 6
figure 6

The velocity dispersion element \(\sigma _{x\,\!x}\). Top panel: isosurfaces of constant \(\sigma _{x\,\!x}\) within the elementary cell. Bottom: The cross-section of the \(\sigma _{x\,\!x}\) profile. The colors encode the scale of the velocity dispersion in the same way as in the top panel

Full size image

The nondiagonal elements \(T^{i}{}_{j}|_{i\ne j}\) are very close to zero. The order of magnitude of these elements is \(10^{-10}\). This suggests that the distribution of the velocities should be isotropic. As can be seen in Fig. 6, this is not the case of the resulting \(\sigma _{i\,\!j}\). However, the order of magnitude of the spatial part of the resulting energy–momentum tensor \(T^{i}{}_{j}\) is consistent with the values of the velocity dispersion found in the galaxy clusters.

The energy flux terms \(T^{0}{}_i\) are one order of magnitude lower than the pressure-like terms \(T^{i}{}_{j}|_{i=j}\), therefore we conclude, that the resulting energy–momentum tensor of the full inhomogeneous solution considered here is really dust-like.

3.3 Curvature of space

The EdS model is the background space-time for the perturbative construction scheme presented in Sect. 2. The EdS universe is spatially flat. In this subsection, we will analyze the behavior of the spatial curvature of the full model.

In the Einstein–de Sitter model understood as a special case of the Friedmann–Lemaître cosmological model, additionally, there vanish the curvature scalar of hypersurfaces orthogonal to the fluid flow \(\mathcal {R}\) and the isotropic pressure p. By the Stewart–Walker lemma [80], in the perturbed Einstein–de Sitter model at the first order, these two scalar fields are gauge-invariant. In contrast, the perturbation of the matter energy density \(\rho \) is not gauge-invariant but one can consider its spatial gradient \(X{_\nu }=P{_\nu }{^\alpha }\nabla {_\alpha }\rho \) as a suitable perturbative quantity. Geometric, kinematic and dynamic gauge-invariant quantities which characterize properties of the perturbed space-time, energy–momentum field and its flow are mutually related by the Ellis–Bruni equations [81]. In special cases, when this set of equations becomes closed, it provides analytic solution for the behavior of inhomogeneities. When we restrict our considerations only to perturbations of the scalar type then the fluid flow is necessarily irrotational and the magnetic part of the Weyl tensor vanishes [82]. If we further assume that the perturbed flow is geodesic and the fluid is nonconductive and inviscid then we arrive at the following set of equations for perturbative quantities

$$\begin{aligned}&U{^\alpha }\nabla {_\alpha }\mathcal {R}+\frac{2}{3}\theta \mathcal {R}=0, \end{aligned}$$
(24)
$$\begin{aligned}&U{^\alpha }\nabla {_\alpha }(8\pi X{_\nu })+\frac{11}{6}\theta 8\pi X{_\nu }-\frac{1}{4}\theta P{_\nu }{^\alpha }\nabla {_\alpha }\mathcal {R}=0, \end{aligned}$$
(25)
$$\begin{aligned}&p=0, \end{aligned}$$
(26)

where \(P{_\mu }{_\nu }=U{_\mu }U{_\nu }+g{_\mu }{_\nu }\) is the projection tensor and \(\theta \) is the expansion scalar in the background. It appears that the imposed assumptions do not allow for nonzero pressure perturbations. Furthermore, they confine only the temporal evolution of perturbations leaving their spatial variability free. Curvature perturbations decrease with the expansion of the model but solving for density perturbations reveals two separate modes, one decaying and one growing. These modes differ in their physical nature, since the growing mode is govern entirely by the curvature perturbations of hypersurfaces. In particular, imposing zero curvature perturbations on hypersurfaces eliminates the growing mode of density perturbations.

After these general considerations, let us go back to the specific exact solution presented in Sect. 2.4. The scalar curvature of the hypersurface of a constant time \(\mathcal {R}\) is conventionally related to the quantity:

$$\begin{aligned} \varOmega _k=-\mathcal {R}/(6\,H(t)^2)\,, \end{aligned}$$
(27)

where H(t) is the Hubble parameter. We used the Hubble parameter H(t) of the background EdS universe. In Fig. 7 we show a dependence of the \(\varOmega _k\) on the position within the elementary cell, at the time \({t_0^{\scriptscriptstyle {(EdS)}}}\). The overdense regions have negative values of \(\varOmega _k\), so the scalar curvature is positive in these regions. Within the underdense regions the situation is opposite. The \(\varOmega _k\) parameter is positive and the scalar curvature \(\mathcal {R}\) is negative there.

Fig. 7
figure 7

The isosurfaces of constant \(\varOmega _k\) parameter evaluated at the age of the EdS universe \({t_0^{\scriptscriptstyle {(EdS)}}}\). The domain is the elementary cell

Full size image

Let us analyze the dependence of the scalar curvature \(\mathcal {R}\) on time. In Figure 8 we plot \(\mathcal {R}\) evaluated at the position \(\mathbf {x}_{O}=(12.5,12.5,12.5)\) of the maximal density.

Fig. 8
figure 8

The scalar curvature of the hypersurface of a constant time \(\mathcal {R}\) as a function of time. We plot three cases with a different \(\mathcal {K}\) parameter. Blue curve for \(\mathcal {K}=0\), orange curve corresponding to \(\mathcal {K}=0.1\) and light-green for the value \(\mathcal {K}=-0.1 \)

Full size image

It is seen that the scalar curvature decreases with time and space tends to flatten during the time evolution. The orange curve corresponds to the model with the value \(\mathcal {K}=0.1\), while the light-green curve refers to \(\mathcal {K}=-0.1\). We note that for the case \(\mathcal {K}=0.1\), for which the growth rate of the inhomogeneities is higher than for the case \(\mathcal {K}=-0.1\), the scalar curvature \(\mathcal {R}\) decreases more slowly than for the case with \(\mathcal {K}=-0.1\). This shows that the growth rate of the inhomogeneities is related to the scalar curvature \(\mathcal {R}\) behavior.

Finally, we calculate the average over the elementary cell of the parameter \(\varOmega _k\). The results for three different values of \(\mathcal {K}\) and for different instants of time are plotted on Fig. 9.

Fig. 9
figure 9

Average \(\varOmega _k\) parameter as a function of time. As on the previous plots, the blue points correspond to \(\mathcal {K}=0\), the orange ones to \(\mathcal {K}=0.1\) and light-green points reffer to \(\mathcal {K}=-0.1 \)

Full size image

In the paper [23], the authors based on their silent universe model suggest that the scalar curvature of space could emerge with time. In our case, we observe that the average \(\varOmega _k\) parameter grows slightly with time, however, values of \(\langle \varOmega _k\rangle _{\mathcal {D}}\) are very small. The growth rate of \(\langle \varOmega _k\rangle _{\mathcal {D}}\) depends on the \(\mathcal {K}\) parameter, but in each case, the values of the \(\langle \varOmega _k\rangle _{\mathcal {D}}\) are smaller than \(10^{-2}\). This means that on average the space is almost flat.

3.4 Local measurments of the Hubble constant

At the end of this paragraph let us analyze expansion of our inhomogeneous universe. In Fig. 10 we plot the expansion scalar \(\theta =-K^{i}{}_i\) as a function of time, where \(K^{i}{}_j\) is the extrinsic curvature tensor of the hypersurface of a constant time t. The blue curve represents the expansion scalar at the position of the maximum density \(\mathbf {x}_{O}=(12.5,12.5,12.5)\), while the light-blue curve correspond to \(\theta \) evaluated at the position of the minimum density \(\mathbf {x}_{U}=(37.5,37.5,37.5)\). The red dashed curve shows the expansion scalar of the EdS universe.

Fig. 10
figure 10

Expansion scalar \(\theta \) as a function of time. The quantity \(\theta \) is evaluated at the overdensity – blue curve or at the underdensity – light-blue curve. For comparison, the expansion scalar of the EdS universe is plotted by red dashed curve

Full size image

On the basis of this figure we deduce that underdense regions expand faster than overdense regions, although on average the model universe expand exactly as the Einstein–de Sitter homegeneous case. Therefore, local measurments of the Hubble constant could differ from the EdS Hubble parameter H(t) evaluated at the universe age \({t_0^{\scriptscriptstyle {(EdS)}}}\), while the measurements of the Hubble constant on basis of some obervables related to scales much larger than the elementary cell should be consistent with the EdS prediction.

To simulate how observer living in our inhomogeneous universe would perform local measurement of the Hubble constant, we made the following numerical experiment. For a given observer position \(\mathbf {x}_0=(x_0,y_0,z_0)\) we generate ten random directions \((\theta ,\phi )\) with probability distribution uniform on the unit sphere. For each direction we generate randomly ten points belonging to the line \(\gamma (l)=({t_0^{\scriptscriptstyle {(EdS)}}},x_0+l\,\sin \theta \cos \phi , y_0+l\,\sin \theta \sin \phi , z_0+l\,\cos \theta )\). This way we simulate one hundred sources distributed randomly in the close neighborhood of the observer. To generate the Hubble diagram we have to calculate for each source the physical distance to the observer d and its time derivative \(\dot{d}\). The physical distance we obtain by numerical integration:

$$\begin{aligned} d(\widetilde{l})=\int \limits _{0}^{\widetilde{l}}\sqrt{\gamma '(l)^i\,\gamma '(l)^j\,g_{i\,\! j}}\,\mathrm {d}l\,. \end{aligned}$$
(28)

Since the metric elements depend explicitly on time, to get the respective \(\dot{d}\) we need to take the time derivative of the integration kernel and perform numerical integration again.

Fig. 11
figure 11

The Hubble diagram generated for the observer located at the overdensity – blue points and for the observer at the underdensity – light-blue points. The red and orange lines are the respective linear fits to the generated points

Full size image

The resulting Hubble diagram generated for two different observer’s positions is plotted in Fig. 11. The blue points correspond to the observer located at the maximum density \(\mathbf {x}_{O}\), whereas the light-blue points are generated for the observer located at the minimum density \(\mathbf {x}_{U}\). For the points in the range of distances \(d\in (5,20)\,\mathrm {Mpc}\) we perform the linear fit to get the resulting local Hubble constant. For the observer located at the overdensity \(\mathbf {x}_{O}\) we obtain \(H_0=69.12\,\mathrm {km/s/Mpc}\), while the observer located at the underdensity measures \(H_0=71.11\,\mathrm {km/s/Mpc}\). It is clear that in both cases the resulting value differs significantly from the EdS Hubble constant \(H_0=70\,\mathrm {km/s/Mpc}\), which was fixed at the beggining of the perturbative approach described in Sect. 2. The difference we obtained here is slightly lower than the current observational difference between the Hubble constant estimation from CMB \(H_0=67.37 \pm 0.54\,\mathrm {km/s/Mpc}\) [83] and from the local measurements \(H_0=74.03 \pm 1.42 \,\mathrm {km/s/Mpc}\) [84]. However, the order of magnitude of the difference we get here is comparable to the current observational difference. It is then reasonable to expect that inhomogeneities could play an important role concerning local Hubble constant measurements.

In our previous paper [78] we haven’t noticed a dependence of the local measurement of \(H_0\) on the position within the elementary cell. However, in the previous model we considered smaller scale of the inhomogeneities, of the order of \(3\,\mathrm {Mpc}\). Currently, the scale of the inhomogeneous region is close to \(25\,\mathrm {Mpc}\) with the additional substructures of the scale around \(3\,\mathrm {Mpc}\). It is quite clear that the local measurements of the Hubble constant should depend on the scale of the inhomogeneities under consideration.

4 Conlusions

In the current paper, we constructed an example of the dust-like solution to the Einstein equations representing an inhomogeneous cosmological model with growing amplitude of the inhomogeneities. By the term dust-like we mean that an observer which is at rest in the comoving reference frame measures nonzero energy–momentum tensor elements \(T^{\mu }{}_{\nu }\) other than the energy density \(-T^{0}{}_{0}\), but which are negligible in comparison to \(-T^{0}{}_{0}\).

The model construction method is based on the perturbation theory around the Einstein–de Sitter background. By using the additional simplifying symmetry condition and identifying leading terms of the energy–momentum tensor elements, we can get the solution to the perturbation theory up to the fourth-order perturbations. Then, we consider the resulting fourth-order metric as the polynomial in the perturbative parameter and calculate the exact Einstein tensor. This way, we analyze the higher-order contributions, what is the main improvement compared to our previous papers [77, 78]. We interpret the pressure-like terms of the energy–momentum tensor in the framework of the Jeans’ theory of the collisionless system of particles. We show that the pressure-like terms of the energy–momentum tensor satisfying exact Einstein equations, containing higher-order contributions unconstrained by the fourth-order perturbation theory, correspond to the particles velocity dispersion around \(1000\,\mathrm {km/s}\). This is a reasonable value for the velocity dispersion of the galaxy cluster members. Therefore, we conclude that this solution remains dust-like in the presented sense and we analyze its basic properties.

Many of the current discussions concerning the possible influence of the inhomogeneities on the cosmological observations focus on the problem of backreaction. In these approaches, one asks whether the existence of the inhomogeneities affects properties of the average space-time. Recently, most researchers conclude that the effect of backreaction is possible but it is rather negligible. In the presented model there is no backreaction effect at all. If we consider Eq. (20) as a definition of the Green-Wald family of metrics \(g_{\mu \,\!\nu }(\lambda )\) [85], then the effective energy–momentum tensor \(t_{\mu \,\!\nu }\) is zero since our model is based on the ordinary perturbation theory. Moreover, the average over the whole space of the density \(\langle \rho \rangle _{\mathcal {D}}(t)\), the average curvature parameter \(\langle \varOmega _k\rangle _{\mathcal {D}}\) and the average expansion \(\langle \theta \rangle _{\mathcal {D}}\) overlap with the respective quantities of the background EdS model. At the same time, local physical quantities could differ significantly from the EdS background. We note nonnegligible differences considering the local volume element \(\sqrt{\mathrm {det}g_{i\,\!j}}\,d^3 x\), local curvature of space and local expansion parameter \(\theta \). In effect, we show that some local measurements could differ from the expectations of the EdS background model. As an example, we verify that the local measurements of the Hubble constant could differ from the EdS value. Such an effect could possibly explain the current Hubble tension problem.

We want to stress, that our model is not a complete description of the real Universe. It is rather a step toward understanding the role of the large-scale inhomogeneities in the interpretation of the cosmological observables. The present paper is a large improvement of our previous work [77, 78], but many issues could be done better in the future. First of all, there is a much more challenging task of considering perturbations around the nonflat background with nonzero cosmological constant. One can also look for more complicated density distributions beyond our symmetry restrictions. We point also, that in the present model the density, the scalar curvature of space and the expansion parameter are decreasing functions of time in all spatial positions. Therefore, the presented model could be interpreted as a description for a large scale inhomogeneous regions behavior but does not provide the framework for the formation of the individual structures for which we expect some kind of collapse and very high values of the density contrast. Nevertheless, the model gives an explicit example of an important influence of the inhomogeneities on the local observations of the Hubble constant, while at the same time the observables related to the scales much larger than the elementary cell overlap with the prediction of the background homogeneous model.