Cosmology of cubic galileon in modified teleparallel gravity

Abstract

In this present paper, we study the cosmological evolution of the cubic galileon along with modified teleparallel gravity at perturbed and non-perturbed levels. We show the dynamical equations of motion and investigate the evolution of different cosmological parameters by using the dynamical variables analysis. In addition, a detailed analysis of different cosmological evolution in the matter, radiation and de Sitter eras is presented by solving the dynamical equations numerically. In our analysis, we find that the equations of motion in the Friedmann–Robertson–Walker (FRW) background metric is characterized by a stable de Sitter era and a tracker solution in which $H{\dot{\varphi }}$ is always constant. We find also that the equation of state of dark energy associated to the proposed model in this work can deviate from − 2 at the matter era. Moreover, the conditions of avoiding ghost and Laplacian instabilities in our model are derived; then we show that the model is free of these instabilities. Furthermore we place an observational constraint on the parameters of the model through Monte Carlo numerical method using growth rate and observational Hubble data. Finally, using the best-fit values of parameters in the model we compare our growth rate of matter perturbation with the prediction of $\varLambda$CDM model and the latest measurement.

1 Introduction

In the last two decades, comprehending the evolution of dark energy and dark matter in the context of modified gravity has received much attention [1, 2]. In fact, the modifications added to General Relativity (GR) are interpreted as a dark energy that can be responsible for the accelerate expansion of the universe. The simplest way to describe dark energy is by supposing a constant $\varLambda$ energy density with an equation of state (EoS) $w_{DE}=-\,1$, but it causes several problems, such as the fine-tuning and coincidence problems [3]. Thus, a large family of modified gravity theories have been proposed to find the origin of dark energy [4] in which dark energy’s EoS deviates from the value − 1 at late time. One can classify these theories in two classes: the first class introduces a matter field source as dark energy, like quintessence [5, 6], Brans and Dicke [7], k-essence [8] and Degenrat–Higher-Order-Scalar–Tensor (DHOST) theories [9]. And the second one replace the Ricci scalar R by a general function like f(R)-gravity [10, 11] and f(R, T) [12] where T is the torsion scalar.

Horndeski gravity, proposed in 1974 [13], is the most general scalar–tensor theory with a single scalar that leads to second-order equations which allows us to avoid the Ostrogradsky instabilities [14]. Depending on the model belonging to Horndeski modified gravity Lagrangian, like the covariant galileon [15] and Dvali–Gabadzde [16] models, one can have a deviation of the effective gravitational coupling from the Newtonian gravitational constant. Therefore, the growth matter rate will also deviate from that in the $\varLambda$CDM model which might be a solution to the $\sigma _8$-tension. However, in order to satisfy the propagation speed of gravitational waves (GWs), detected by GW170817 [17] from a binary neutron star merged together with gamma-ray burst GRB 170817A [18], Horndeski theories need to be reduced to the form $L_H=G_4(\varphi ) R+G_2(\varphi ,X)+G_3(\varphi ,X)\square \varphi$ [19]. The cubic galileon [20,21,22], which is included in the Lagrangian $L_H$, contains self-acceleration de Sitter attractors responsible for the accelerated universe, but it is in tension with the joint observation data of SN Ia [23, 24], CMB [25, 26], BAO [27], large-scale structure, and weak lensing. This is due to the bad behavior of the EoS corresponding to dark energy where one found that $w_{DE}=-\,2$ at the matter era for the tracker solution [28].

An alternative formulation of gravity, called teleparallel gravity (TG) [29], is proposed by Pellegrini and Plebanski [30] based on Moller’s work [31, 32]. In this theory, we use the tetrads fields $e_\mu ^a$ rather than the metric field $g_{\mu \nu }$ where the gravity is considered as a gauge theory unlike, in GR,where the gravitational interaction is geometrized. In fact, TG can be unified with the fundamental forces of the Standard Model [33] because it is a gauge theory of translation.

The equations of teleparallel gravity are equivalent to those in General Relativity (GR) because of the divergence term that appears in the relation between scalar torsion T and Ricci scalar R: $R=T+\partial _\mu (e T_\mu )$, where e is the determinant of the tetrads and $T_\mu$ is the torsion vector. However, the field equations of these two theories will not remain the same if we consider nonlinear terms of T, which have been studied in the literature [34,35,36]. The theories described by the Lagrangian f(T)-functions [37, 38] as well as a scalar field term can be considered to lead to $f(T,\varphi )$ [39,40,41,42,43,44]. It is well known that $f(T,\varphi )$-gravity is a second-order theory whereas the background equations of $f(R,\varphi )$-gravity contain fourth- and third-order derivatives of the metric. Moreover, in modified teleparallel gravity the Lorentz invariance is violated and thus introducing new extra degrees of freedom is necessary [45, 46]. Indeed, unlike in GR, these new variables are involved at the perturbation level which means that the effect on the large structure in the universe is significant.

In Ref. [47], the Horndeski theory in a teleparallel gravity frame work was explored keeping the second-order equations of motion. One shows that the theory has a much richer phenomenology and there are new terms in the Lagrangian which can explain dark energy without the cosmological constant. Afterward, the theory was generalized to get $c_T=1$ without dropping the terms $G_5(\varphi ,X)$ and $G_4(\varphi ,X)$ in Ref. [47]. Inspired by these two papers, we study the cosmological evolution of the cubic galileon in modified teleparallel gravity at the late time of the universe. We propose to study different cosmological parameters, the conditions of ghosts and Laplacian instability, and we constrain the model with the growth rate factor (GRF) and observational Hubble data (OHD).

The present paper is organized as follows. In Sect. 2, we present a general model of cubic galileon in Teleparallel gravity frame work (CGTG) and show the equations of the model in a homogeneous and isotropic universe. In Sect. 4, we calculate the perturbation equations corresponding to the perturbed background, scalar field and matter density. In Sect. 5, we address phase-space dynamical equations and we study the analytic and numerical evolution of dynamical systems. In Sect. 6, a numerical analysis got from Monte Carlo Markov chain is presented to derive the best-fit value of each cosmological parameter. We compare the growth rate evolution prediction for our model with that in the $\varLambda$CDM model. Finally, we conclude with the obtained results in Sect. 7.

2 The model

Let us assume a theory of modified gravity in which we consider the cubic galileon field and modified teleparallel gravity in the following action:

$$\begin{aligned} S=\int \mathrm{d}^4 x e \left( \frac{1}{16\pi G} (f(T)+L_\varphi )+L_m+L_r\right) , \end{aligned}$$

(1)

with

$$\begin{aligned} L_\varphi =-c_1 X-c_2 X \nabla ^\mu \nabla _\mu \varphi , \end{aligned}$$

(2)

where G is the gravitational coupling and $X= -\frac{1}{2}\nabla ^\mu \varphi \nabla _\mu \varphi$ is the kinetic therm of the scalar field $\varphi$, $e=\sqrt{-g}$ is the determinant of the tetrad field $e^{a}_{\mu }$ and T is the torsion scalar (for more details see Appendix A). $L_m$ and $L_r$ are the Lagrangian of matter and radiation, respectively. Our proposed model is invariant under the shift transformation $\varphi \longrightarrow \varphi +\mathrm{const}$. In addition, the gravitation wave propagation speed, in our model, is constrained to the speed of light, which is proved in Ref. [48]. In other words, the model satisfies the constraint observed by the detection of gravitational waves (GW) GW170817 [17] from a binary neutron start merger together with the gamma-ray burst GRB170817A [18]. The general equations of motion corresponding to our model are obtained by varying the action (1) with respect to tetrads and scalar field. Thus, it follows that

$$\begin{aligned} \delta S= & {} \int \mathrm{d}^4 x \left( \frac{1}{16\pi G}\left( \frac{\delta (e f(T))}{\delta e^{a}_{\mu }}+\frac{\delta (e L_\varphi )}{\delta g^{\alpha \beta }}\frac{\delta g^{\alpha \beta }}{\delta e^{a}_{\mu }}\right) \nonumber \right. \\&\left. +\frac{\delta (e L_m)}{\delta g^{\alpha \beta }}\frac{\delta g^{\alpha \beta }}{\delta e^{a}_{\mu }}+\frac{\delta (e L_r)}{\delta g^{\alpha \beta }}\frac{\delta g^{\alpha \beta }}{\delta e^{a}_{\mu }}\right) \delta e^{a}_{\mu }\nonumber \\&+\frac{1}{16\pi G}\int \mathrm{d}^4 x e \frac{\delta L_\varphi }{\delta \varphi } \delta \varphi , \end{aligned}$$

(3)

where

$$\begin{aligned} \delta g^{\alpha \beta }= \eta ^{ab}(\delta e^{\alpha }_{a} e^{\beta }_{b}+ e^{\alpha }_{a} \delta e^{\beta }_{b}). \end{aligned}$$

(4)

The first term in the action (3) corresponds to the motion’s equations of the tetrad field and the second corresponds to the equation of the scalar field. These equations can be written as

$$\begin{aligned} T_{a(T)}^{\mu } e^{a}_{\nu } =T_{\mu (\varphi )}^{\nu }+4\pi G (T_{\mu (m)}^{\nu }+T_{\mu (r)}^{\nu } ), \end{aligned}$$

(5)

where

$$\begin{aligned} T_{a(T)}^{\mu }= & {} \frac{1}{4} f e^{\mu }_{a}+f_{T} (\nabla _{\nu } (e^{\rho }_{a} S_{\rho }^{\nu \mu })\nonumber \\&-\,e^{\lambda }_{a} T^{\rho }_{\nu \lambda }S_{\rho }^{\nu \mu })+e^{\rho }_{a} \partial _{\nu } f_{T} S_{\rho }^{\mu \nu }, \end{aligned}$$

(6)

$$\begin{aligned} T_{(\varphi )}^{\mu \nu }= & {} c_1 (\partial ^{\mu }\varphi \partial ^{\nu }\varphi -g^{\mu \nu }X)+c_2 (\partial ^{\mu } \varphi \partial ^{\nu } \varphi \nabla ^\lambda \nabla _\lambda \varphi \nonumber \\&-\,\partial _{\lambda }\varphi (\partial ^{\mu }\varphi \nabla ^\lambda \nabla ^\nu \varphi + \partial ^{\nu }\varphi \nabla ^\lambda \nabla ^\mu \varphi ), \end{aligned}$$

(7)

$$\begin{aligned} T_{(i)}^{\mu \nu }= & {} (\rho _{i}+P_{i})u^{\mu }u^{\nu }+\rho _{i}g_{\mu \nu }, \end{aligned}$$

(8)

where $i=\{m,r\}$ and $\rho _{i}$, $P_{i}$ and $u^{\mu }$ are energy density, pressure and the four velocity vector, of the radiation and matter present in the universe, respectively. Note that the tensor of energy–momentum of the matter fluid is conserved. The equation of conservation is given by

$$\begin{aligned} \nabla _{\mu }T_{(i)}^{\mu \nu }=0, \end{aligned}$$

(9)

Since the energy–momentum tensor is symmetric and invariant under local Lorentz transformation, the antisymmetric part in the tensor (7) must vanish. Thus, it leads us to the constraint

$$\begin{aligned} (S_{\lambda }^{\sigma \nu }g^{\lambda \mu }-S_{\lambda }^{\sigma \mu }g^{\lambda \nu })\partial _\sigma f_T=0. \end{aligned}$$

(10)

The general equation of scalar field of our model is calculated by

$$\begin{aligned} \nabla _{\mu }(c_1 \nabla ^\mu \varphi -c_2 (\nabla ^\mu \varphi \nabla _\nu \nabla ^\nu \varphi +\nabla ^\mu X))=0. \end{aligned}$$

(11)

This equation is the identical to the scalar field’s equation of the cubic galileon model addressed in Ref. [20]. In our model, we have the same equation of the scalar field but it not for the background.

3 Cosmological equations

Now, we consider a flat, homogeneous and isotropic spacetime where the metric is written as

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+a(t)^2\delta _{ij} \mathrm{d}x^i \mathrm{d}x^j, \end{aligned}$$

(12)

where a(t) is the scale factor. This metric can be expressed by the following tetrad:

$$\begin{aligned} e^{a}_{\mu }=\mathrm{diag}(1,a(t),a(t),a(t)). \end{aligned}$$

(13)

Note that, since we are working in the framework of the teleparallel equivalent to general relativity (TEGR), we can define the torsion tensor in (126) by a vanishing spin connection ($\omega ^a_{b\mu }=0$). In addition, as is shown in Ref. [38], even with an arbitrary tetrad in an arbitrary coordinate system along with the corresponding spin connection, the field equations in covariant f(T) gravity are always the same. In our paper, we will use the diagonal tetrad form to study the cosmological evolution of our model. In this case, the scalar torsion is obtained by $T=6({\dot{a}}/{a})^2$ and the background equation of motion in FRLW spacetime is obtained by replacing the metric (12) in (5) and assuming that the scalar field depends only on the cosmic time t. In this case, Eqs. (5) and (11) are reduced to

$$\begin{aligned}&\frac{f}{2}-6 H^2 f_T+\frac{1}{2} c_1 {\dot{\varphi }}^2-3 c_2 H {\dot{\varphi }}^3+8\pi G(\rho _m+\rho _r) =0, \end{aligned}$$

(14)

$$\begin{aligned}&\frac{f}{2}-6 H^2 f_T-2 {\dot{H}} f_T-24 {\dot{H}} H^2 f_{TT}\nonumber \\&\quad -\frac{1}{2} c_1 {\dot{\varphi }}^2-c_2 {\dot{\varphi }}^2 \ddot{\varphi }= 8\pi G(P_m+P_r), \end{aligned}$$

(15)

$$\begin{aligned}&c_1 (\ddot{\varphi }+3 H {\dot{\varphi }})-3 c_2 (2 H {\dot{\varphi }} \ddot{\varphi }+3 H^2 {\dot{\varphi }}^2+ {\dot{H}} {\dot{\varphi }}^2 )=0, \end{aligned}$$

(16)

where $H=\frac{{\dot{a}}}{a}$ is the Hubble parameter and the dot represents a derivative with respect to t. Equations (14) and (15) can be written in terms of dark energy densities and pressure as follows:

$$\begin{aligned}&3H^2=8\pi G(\rho _{DE}+\rho _m+\rho _r), \end{aligned}$$

(17)

$$\begin{aligned}&-(3H^2+2{\dot{H}}^2)=8\pi G(P_{DE}+P_{m}+P_{r}), \end{aligned}$$

(18)

where the density $\rho _{DE}$ and the pressure $P_{DE}$ are given, respectively, by

$$\begin{aligned} 8\pi G\;\rho _{DE}= & {} 3H^2+\frac{f}{2}-6 H^2 f_T+\frac{1}{2} c_1 {\dot{\varphi }}^2-3 c_2 H {\dot{\varphi }}^3, \end{aligned}$$

(19)

$$\begin{aligned} 8\pi G\; P_{DE}= & {} 3H^2+2{\dot{H}}^2+\frac{f}{2}-6 H^2 f_T-2 {\dot{H}} f_T \nonumber \\&-24 {\dot{H}} H^2 f_{TT}-\frac{1}{2} c_1 {\dot{\varphi }}^2-c_2 {\dot{\varphi }}^2 \ddot{\varphi }. \end{aligned}$$

(20)

Moreover, the equation of state of dark energy can be defined as

$$\begin{aligned} w_{DE}=\frac{P_{DE}}{\rho _{DE}}. \end{aligned}$$

(21)

Finally, substituting the metric (12) in (11), we get

$$\begin{aligned} {\dot{\rho }}_i+3H(\rho _i+P_i)=0, \end{aligned}$$

(22)

where $P_m=0$ ( for matter) and $P_r=\frac{1}{3}\rho _r$ (for radiation).

4 Perturbed equations

In this section, we present the perturbation equations of motion for the model we proposed in Sect. 2. However, we start by deriving the equations of scalar perturbation by considering the scalar part in the scalar–vector–tensor (SVT) decomposition of $\delta e^{a}_\mu$ which is given by

$$\begin{aligned} \delta e^{0}_\mu= & {} \delta ^{0}_{\mu } (1+\varPhi )+a(t)\delta ^{i}_{\mu } \partial _i(F+\alpha ),\nonumber \\ \delta e^{a}_\mu= & {} a(t)\delta ^{a}_{\mu } (1+\varPsi )+\delta ^{0}_{\mu } \partial ^a \alpha +a(t)\delta ^{i}_{\mu }\partial _i\partial ^a B, \end{aligned}$$

(23)

where $\varPhi$, $\varPsi$, F, B and $\alpha$ are scalar quantities and depend on the spacetime. We observe the appearance of new extra degrees of freedom in the scalar teleparallel quantities, which is not familiar for the GR metric. In fact, the components B and $\alpha$ play a crucial role in the cosmological perturbation theory, since the Lorentz symmetry is violated in F(T)-gravity. In addition, we chose this particular form in order to introduce the Newton gauge and flat gauge in the following. The metric corresponding to the tetrad (23) is given by

$$\begin{aligned} ds^2= & {} -(1+2\varPhi )dt^2+a(t)\partial _i F dtdx^i \nonumber \\&+\,a(t)^2(\delta _{ij}(1+2\varPsi )+\partial _i\partial _j B)dx^idx^j. \end{aligned}$$

(24)

In order to simplify the equations of the perturbation, we fix the gauge by setting $B=0\text { and }F=0$ (Newtonian gauge). In addition, the scalar field, the matter density and four velocity of matter are decomposed into homogeneous and perturbed parts: $\varphi \longmapsto \varphi (t)+\delta \varphi (t,x,y,z)\text {, } \rho _m\longmapsto \rho _m(t)+\delta \rho _m(t,x,y,z)\text { and } u^{\mu }\longmapsto \delta u^{\mu }(t,x,y,z)$, respectively. Substituting the expressions of tetrads (23) in the Eq. (5), the components of the perturbed equations are obtained as follows.

The energy density (0, 0):

$$\begin{aligned}&f_T \left( \frac{2 \varDelta \varPsi }{a^2}-6 H^2 \varPhi -6 H {\dot{\varPsi }}\right) \nonumber \\&\quad -c_2 {\dot{\varphi }}^2\left( \frac{\varDelta \delta \varphi }{a^2}-9 H \delta {\dot{\varphi }}+3 {\dot{\varphi }} (4 H \varPhi +{\dot{\varPsi }}\right) )+c_1 {\dot{\varphi }} ({\dot{\varphi }} \varPhi -\delta {\dot{\varphi }} ) \nonumber \\&\quad -24 H^3 f_{TT} \left( 3 H \varPhi +3 {\dot{\varPsi }}+\frac{\varDelta \alpha }{a} \right) =8 \pi G\; \delta \rho _m. \end{aligned}$$

(25)

The energy flux and momentum density (0, i):

$$\begin{aligned}&c_1 \delta \varphi {\dot{\varphi }}+c_2 {\dot{\varphi }}^2 (\dot{\delta \varphi }-3 \delta \varphi H-{\dot{\varphi }} \varPhi )\nonumber \\&-2 f_T (H \varPhi +{\dot{\varPsi }} )-24 H {\dot{H}} \varPsi f_{TT}=8 \pi G\; \rho _m v. \end{aligned}$$

(26)

The momentum flux ($i=j$):

$$\begin{aligned}&f_T\left( \frac{\varDelta \varPhi }{a^2}+\frac{\varDelta \varPsi }{a^2}\right) -\frac{12 H^2 \varDelta {\dot{\alpha }} f_{\text {TT}}}{a}\nonumber \\&\quad -\frac{12 \varDelta \alpha (2 H^3 (6 {\dot{H}} f_{\text {TTT}}+f_{\text {TT}})+3 {\dot{H}} H f_{\text {TT}})}{a}\nonumber \\&\quad -3 \overset{\text {..}}{\varPsi } (12 H^2 f_{\text {TT}}+f_T) \nonumber \\&\quad +\frac{3}{2} c_2 {\dot{\varphi }}^2 \delta \ddot{\varphi }-\frac{3}{2} {\dot{\varPhi }} (c_2 {\dot{\varphi }}^3+24 H^3 f_{\text {TT}}+2 H f_T)\nonumber \\&\quad -9 H {\dot{\varPsi }} (12 (H^2 (4 {\dot{H}} f_{\text {TTT}}+f_{\text {TT}})+{\dot{H}} f_{\text {TT}})+f_T)+\frac{3}{2} \delta {\dot{\varphi }} \nonumber \\&\quad \times {\dot{\varphi }} (c_1+ 2 c_2 \overset{\text {..}}{\varphi })-\frac{3}{2} \varPhi ({\dot{\varphi }}^2 (4 c_2 \overset{\text {..}}{\varphi }+c_1)\nonumber \\&\quad +72 H^4 (4 {\dot{H}} f_{\text {TTT}}+f_{\text {TT}})+6 H^2 (20 {\dot{H}} f_{\text {TT}}+f_T)+4 {\dot{H}} f_T) =0.\nonumber \\ \end{aligned}$$

(27)

The anisotropic parts ($i \ne j$):

$$\begin{aligned} \varPhi - \varPsi =12 a \alpha H {\dot{H}} \frac{f_{TT}}{f_T}. \end{aligned}$$

(28)

This equation shows that the extra degree $\alpha$ implies $\varPhi \ne \varPsi$ in the case of $f_{TT}\ne 0$. Using Eq. (11), we also derive the first order of the scalar field equation:

$$\begin{aligned}&\frac{\varDelta \delta \varphi }{a^2} (2 c_2 (\ddot{\varphi }+2 H {\dot{\varphi }} )-c_1 ) +c_2 \frac{\varDelta \varPhi }{a^2} {\dot{\varphi }}^2+3 c_2 {\dot{\varphi }}^2 \ddot{\varPsi }\nonumber \\&\quad +\,\delta \ddot{\varphi } (c_1-6 c_2 H {\dot{\varphi }} )-3 {\dot{\varphi }}{\dot{\varPsi }} (c_1-2 c_2 (\ddot{\varphi }+3 H {\dot{\varphi }} ))+3 \dot{\delta \varphi } (c_1 H \nonumber \\&\quad -\,2 c_2 (H \ddot{\varphi }+ (3 H^2+{\dot{H}} ) {\dot{\varphi }} ) )-\dot{\varPhi }{\dot{\varphi }} (c_1-9 c_2 H {\dot{\varphi }} )\nonumber \\&\quad -\,\varPhi (6 H {\dot{\varphi }} (c_1-4 c_2 \ddot{\varphi } )+2 c_1 \ddot{\varphi }\nonumber \\&\quad -\,12 c_2 (3 H^2+{\dot{H}} ) \dot{\varphi }^2 ) =0. \end{aligned}$$

(29)

Note that this equation is the same equation as derived for the cubic galileon [20]. In teleparallel gravity, the constraint (10) is satisfied at background level but in the linear perturbation becomes

$$\begin{aligned} \varPsi =-\frac{H}{\dot{f_T}}\delta f_T, \end{aligned}$$

(30)

where $\delta f_T=f_{TT}(12({\dot{\varPsi }}+H\varPhi )+4H\frac{\varDelta \alpha }{a})$. Finally, the equations of conservation corresponding to matter at linear perturbation is written as

$$\begin{aligned}&\delta {\dot{\rho }}_m+3H \delta \rho _m+3\rho _m{\dot{\varPsi }}-\rho _m\frac{\varDelta v}{a^2}=0, \end{aligned}$$

(31)

$$\begin{aligned}&{\dot{v}}=\varPhi . \end{aligned}$$

(32)

4.1 Sub-horizon approximation

In order to show the evolution of the growth rate and confront our model with the observations of large-scale structures, one must derive the expression of the effective gravitational coupling. To do so, we study the cosmological perturbation of our model on sub-horizon scale $k\gg a H$ and we define the gauge-invariant contrast as

$$\begin{aligned} \delta _m=\frac{\delta \rho _m}{\rho _m}-3 H v, \end{aligned}$$

(33)

where in deep Hubble radius $\delta _m\approx \frac{\delta \rho _m}{\rho _m}$. Thus, taking the derivative of Eq. (31) and using Eqs. (32) and (33), one gets in Fourier space

$$\begin{aligned} \ddot{\delta }_m+2H\delta _m-\frac{k^2}{a^2}\varPhi =0, \end{aligned}$$

(34)

where k is a comoving wavenumber. On a sub-Hubble approximation scale, Eqs. (25) and (29) are reduced to

$$\begin{aligned} 2f_T \frac{k^2}{a^2}\varPsi -c_2 {\dot{\varphi }}^2\frac{k^2}{a^2}\delta \varphi -24 H^3 f_{TT} \frac{k^2}{a} \alpha= & {} 8\pi G\;\delta \rho _m, \end{aligned}$$

(35)

$$\begin{aligned} (2 c_2 (\ddot{\varphi }+2 H \dot{\varphi } )-c_1 )\frac{k^2}{a^2} \delta \varphi +c_2 \dot{\varphi }^2\frac{k^2}{a^2}\varPhi= & {} 0. \end{aligned}$$

(36)

Solving Eqs. (28), (30), (35) and (36) with respect to $\varPhi$, $\varPsi$, $\delta \varphi$ and $\alpha$, we take the limit $k\longmapsto \infty$, we get

$$\begin{aligned}&-\frac{k^2}{4\pi G a^2}\varPhi \simeq \left( \frac{ (c_1-2 c_2 (\overset{\text {..}}{\varphi }+2 H \dot{\varphi } ) )}{f_T (c_1-2 c_2 \ddot{\varphi }-4 c_2 H {\dot{\varphi }} )-c_2^2 {\dot{\varphi }}^4/2}\nonumber \right. \\&\qquad \left. -\frac{144 a^2{\dot{H}} (H^2+{\dot{H}} ) (c_1-2 c_2 (\ddot{\varphi }+2 H {\dot{\varphi }} ) ){}^2}{k^2 (8 c_2 H {\dot{\varphi }} f_T+c_2^2 {\dot{\varphi }}^4-2 f_T (c_1-2 c_2 \ddot{\varphi } ) )^2}f_{TT}^2\right) \rho _m\delta _m, \end{aligned}$$

(37)

$$\begin{aligned}&-\frac{k^2}{4\pi G a^2}\delta \varphi \simeq \left( \frac{ (c_2 {\dot{\varphi }}^2 )}{f_T (c_1-2 c_2 \ddot{\varphi }-4 c_2 H {\dot{\varphi }} )-c_2^2 {\dot{\varphi }}^4/2}\nonumber \right. \\&\qquad \left. -\frac{144 a^2{\dot{H}} (H^2+{\dot{H}} ) (c_1-2 c_2 (\ddot{\varphi }+2 H {\dot{\varphi }} ) ){}^2}{k^2 (8 c_2 H {\dot{\varphi }} f_T+c_2^2 {\dot{\varphi }}^4-2 f_T (c_1-2 c_2 \ddot{\varphi } ) )^2}f_{TT}^2\right) \rho _m\delta _m, \end{aligned}$$

(38)

$$\begin{aligned}&-\frac{4\pi G k^2}{a^2}\alpha \simeq \frac{6 {\dot{H}} (c_1-2 c_2 (\ddot{\varphi }+2 H \dot{\varphi } ) )}{ H k^2 (8 c_2 H {\dot{\varphi }} f_T+c_2^2 {\dot{\varphi }}^4-2 f_T (c_1-2 c_2 \ddot{\varphi } ) )}af_{TT} \rho _m\delta _m,\nonumber \\ \end{aligned}$$

(39)

and the effective gravitational potential, $\varPsi _{\text {eff}}=\varPhi -\varPsi$, is calculated by

$$\begin{aligned} \begin{aligned}&-\frac{k^2}{a^2}\varPsi _{\text {eff}}\\&\quad \simeq 4\pi G\; \frac{a^2 72 {\dot{H}}^2 (c_1-2 c_2 (\ddot{\varphi }+2 H \dot{\varphi } ) )}{k^2 f_T (8 c_2 H {\dot{\varphi }} f_T+c_2^2 {\dot{\varphi }}^4-2 f_T (c_1-2 c_2 \ddot{\varphi } ) )}f_{TT}^2 \rho _m\delta _m. \end{aligned} \end{aligned}$$

(40)

By taking into account only the first-order approximation of the Eq. (37), we can define the effective gravitational coupling as

$$\begin{aligned} \frac{G_{\text {eff}}}{G}= \frac{ (c_1-2 c_2 (\overset{\text {..}}{\varphi }+2 H \dot{\varphi } ) )}{f_T (c_1-2 c_2 \ddot{\varphi } )-4 c_2 H {\dot{\varphi }} f_T-c_2^2 {\dot{\varphi }}^4/2}. \end{aligned}$$

(41)

In the case $c_2=0$ and $f_T=1$, we recover General Relativity ($G_{\text {eff}}=1$) which is also the case of quintessence and k-essence models [8]. However, if we consider $c_2=0$, the effective gravitational coupling takes the form

$$\begin{aligned} \frac{G_{\text {eff}}}{G}=\frac{1}{f_T }. \end{aligned}$$

(42)

This result agrees with $G_{\text {eff}}$ found in Ref. [44]. Finally, if we set $f_T=1$, we obtain

$$\begin{aligned} \frac{G_{\text {eff}}}{G}=\frac{2 (c_2 {\dot{\varphi }}^2 )}{2 (c_1-2 c_2 \ddot{\varphi } )-8 c_2 H {\dot{\varphi }}-c_2^2 {\dot{\varphi }}^4}. \end{aligned}$$

(43)

The latter result corresponds to the gravitational coupling of the cubic galileon studied extensively in Ref. [22].

4.2 Ghost and Laplacian instability

Now, we derive the condition for the absence of ghost and Laplacian instability in the small-scale limit by taking the flat gauge in consideration where we set $B=0$ and $\varPsi =0$. So, after expanding the action (1) up to second order and integrating by parts, the action is written as

$$\begin{aligned} \begin{aligned} \delta ^2S =&\frac{1}{16\pi \; G}\int \mathrm{d}^4x a^3 \Bigg (A_1 \delta {\dot{\varphi }}^2+A_2 \frac{(\nabla \delta \varphi )^2}{a^2} \\&+\left( A_3\delta {\dot{\varphi }}+A_4\frac{\varDelta \delta \varphi }{a^2}+24H^3f_{TT}\frac{\varDelta \alpha }{a}\right) \varPhi + (A_4 \delta {\dot{\varphi }}+A_5 \delta \varphi \\&+A_6 \varPhi )\frac{\varDelta F}{a^2}+\varSigma \varPhi ^2+4H^2f_{TT}\frac{\varDelta \alpha ^2}{a^2}\Bigg )+\delta ^2S_m+\delta ^2S_r, \end{aligned}\nonumber \\ \end{aligned}$$

(44)

where the explicit form of $A_{1,...,5}$ and $\varSigma$ is given by

$$\begin{aligned}&A_1=-\frac{c_1}{2}+3c_2 H{\dot{\varphi }}, \quad \nonumber \\&A_2=\frac{c_1-2c_2(2H {\dot{\varphi }}-\ddot{\varphi })}{2},\quad \nonumber \\&A_3={\dot{\varphi }}(c_1-9c_2H {\dot{\varphi }}), \quad A_4=c_2 {\dot{\varphi }}^2,\nonumber \\&A_5={\dot{\varphi }}(c_1-3c_2H {\dot{\varphi }}),\quad \nonumber \\&A_6=(2 H f_T + c2 {\dot{\varphi }}^3), \nonumber \\&\varSigma =\frac{1}{2}(6H^2f_T+72 H^4f_{TT}-c_1{\dot{\varphi }}^2+12 c_2H {\dot{\varphi }}^3). \end{aligned}$$

(45)

For the matter part, we used the Schutz–Sorkin action [49], which has been studied in detail by expanding up to second order as [50]

$$\begin{aligned} \delta ^2S_i=&\int d^4x a^3\Bigg (({\dot{v}}_i-3H c_{i}^2-\alpha )\delta \rho _i-\frac{c_{i}^2}{2(\rho _i+P_i)} \delta \rho _{i}^2\nonumber \\&-\frac{(\rho _i+P_i)}{2a^2}((\nabla v_i)^2+2\nabla v_i\nabla F)+\frac{\rho _i}{2}\varPhi ^2\Bigg ), \end{aligned}$$

(46)

where $c_{i}^2$ is the sound speed of the matter fluid. Varying the action (44) with respect to $\varPhi$, F and $\alpha$, we obtain the constraints

$$\begin{aligned}&2\varSigma \varPhi +A_3\delta {\dot{\varphi }}+A_4\frac{\varDelta \delta \varphi }{a^2}+24H^3f_{TT}\frac{\varDelta \alpha }{a}+A_6 \frac{\varDelta F}{a^2} = 0, \end{aligned}$$

(47)

$$\begin{aligned}&(A_4 \delta {\dot{\varphi }}+A_5 \delta \varphi +A_6 \varPhi ) = 8\pi G\rho _m v_m, \end{aligned}$$

(48)

$$\begin{aligned}&3H^3f_{TT}\varPhi +H^2f_{TT}\frac{\varDelta \alpha }{a} = 0. \end{aligned}$$

(49)

Note we assumed that $c_{m}^2=0$. And the equation of perturbed matter and radiation in flat gauge are obtained by varying the action (44) with respect to v and $\delta \rho _m$. Thus, the equations are written as follows:

$$\begin{aligned}&({\dot{v}}_i-3H c_{i}^2-\alpha )-\frac{c_{i}^2}{(\rho _i+P_i)}\delta \rho _{i} = 0, \end{aligned}$$

(50)

$$\begin{aligned}&\delta {\dot{\rho }}_i+3H(1+c_{i}^2)\delta \rho _i-(\rho _i+P_i)\varDelta (v_i+F) = 0. \end{aligned}$$

(51)

By solving Eqs. (48–51) for the quantities $\alpha$, $\varPhi$, F and v, then plugging the results in the action (44), we can write the order action in Fourier space as

$$\begin{aligned} \begin{aligned} \delta ^2S_i=\int d^4x a^3\left( \overrightarrow{{\dot{\chi }}}^t K \overrightarrow{{\dot{\chi }}}-\frac{k^2}{a^2}\overrightarrow{\chi }^t N \overrightarrow{\chi }-\overrightarrow{\chi }^tM\overrightarrow{\chi }-\overrightarrow{\chi }^tB\overrightarrow{{\dot{\chi }}}\right) , \end{aligned}\nonumber \\ \end{aligned}$$

(52)

where K, N, M and B are $3\times 3$ matrices and

$$\begin{aligned} \begin{aligned} \overrightarrow{\chi }^t=\left( H\frac{\delta \varphi }{{\dot{\varphi }}},\delta \rho _m /k,\delta \rho _r /k\right) . \end{aligned} \end{aligned}$$

(53)

After integrating the terms containing the $k^2/a^2$ in B and having absorbed them into N, we get the non-vanishing matrix components, in the small-scale limit ($k\longmapsto \infty$),

$$\begin{aligned} \begin{aligned}&Q_S=\left( \frac{{\dot{\varphi }}}{H}\right) ^2 \\&K_{11}=A_1+\frac{A_4(A_3A_6+A_4(\varSigma +\rho _m+\rho _r-36 H^4f_{TT}))}{A_{6}^2}, \\&K_{22}=\frac{a^2 }{2\rho _m}, \quad K_{33}=\frac{a^2}{2(\rho _r+P_r)},\\&\left( \frac{{\dot{\varphi }}}{H}\right) ^2 N_{11}=-A_2+\frac{3(\rho _m+\rho _r+P_r)A_{4}^2-2A_4A_5A_6}{2A_{6}^2}\\&\qquad +\frac{1}{2a}\frac{d}{dt}\left[ \frac{A_{4}^2}{A_6}\right] , \quad N_{22}=0, \quad N_{33}=\frac{a^2 c_{r}^2}{2(\rho _r+P_r)}. \end{aligned} \end{aligned}$$

(54)

Providing that there no off-diagonal components in the matrix K and N the matter and the scalar field are decoupled. To avoid the scalar ghosts, the matrix K must be definite positive. Proving that $K_{22}$ and $K_{33}$ are positive, one requires that $K_{11}>0$. The dispersion relation corresponding to the action (52) takes the form

$$\begin{aligned} \begin{aligned} \mathrm{det}(c_{s}^2K-N)=0. \end{aligned} \end{aligned}$$

(55)

The solutions of this equation correspond to the matter speed squared $c_{m}^2$ and $c_{r}^2$ and the speed squared of the perturbed scalar field $\delta \varphi$ defined by $c_{S}^2=N_{11}/K_{11}$. Since $c_{m}^2>0$ and $c_{r}^2>0$, the Laplacian instability is absent only if $c_{S}^2$ is positive.

4.3 Tensor perturbation

The derivation of the speed of gravitational waves requires one to use the perturbed tensor $h_{ij}$ as component of the tetrads, which obey the traceless and divergence conditions ($h_{ii}=0$ and $\partial _i h_{ij}=0$) and it given by

$$\begin{aligned} \begin{aligned} \delta e_{\mu }^a=a(t)\delta _{\mu }^i\delta _{ai}h_{ij}. \end{aligned} \end{aligned}$$

(56)

Hence, the perturbative components of the metric become

$$\begin{aligned} \begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+a(t)^2(\delta ^{ij}+h_{ij})\mathrm{d}x^i\mathrm{d}x^j. \end{aligned} \end{aligned}$$

(57)

Expanding the action (5) up to second order and after integrating by part, we obtain

$$\begin{aligned} \begin{aligned} \delta ^2S=\frac{1}{16\pi \; G}\int \mathrm{d}^4x a^3 f_T\left( \frac{(\nabla h_{ij})^2}{a^2}-({\dot{h}}_{ij})^2\right) . \end{aligned} \end{aligned}$$

(58)

The variation of this equation with respect to $h_{ij}=0$ yields the following equation:

$$\begin{aligned} \begin{aligned} \ddot{h}_{ij}+3H(1+\beta _T){\dot{h}}_{ij}+\frac{k^2}{a^2}{h}_{ij}=0, \end{aligned} \end{aligned}$$

(59)

where the dimensionless parameter is defined as

$$\begin{aligned} \begin{aligned} \beta _T=\frac{{\dot{f}}_T}{H f_T}. \end{aligned} \end{aligned}$$

(60)

We can see that the speed of GWs is equal to the speed of light. Thus, we showed that the model is not disfavored by the experimental observation constraint of GW170817. However, unlike the GR theory the parameter $\beta _T$ deviates from zero and grows in time when the scalar and Hubble factor evolves. The parameter $\beta _T$ will affect the amplitude of the GR waveform given by [51]

$$\begin{aligned} h_{gw}\sim h_{GR} e^{\int \beta _T da}, \end{aligned}$$

(61)

where $h_{GR}$ is the amplitude of gravitational waves emitted by a binary system of masses orbiting one another.

5 Dynamical analysis and numerical solution

In this section, we will give the form of the function f(T); then we use the expressions derived in the last sections. In addition, we will solve the equations of motion numerically in terms of the dynamical variable. Thus, we will see the cosmological effect of the terms in our model.

5.1 Dynamical equations

Now, we present the dynamical analysis of our model by choosing a particular function $f=T+\kappa T^m$, where $\kappa$ and m are real constants. Thus, the equations of motion (14) and (17) are reduced to

$$\begin{aligned}&3 H^2 = \frac{1}{2} c_1 {\dot{\varphi }}^2-3 c_2 H \dot{\varphi }^3 \nonumber \\&\quad -\kappa 6^m \left( m-\frac{1}{2}\right) (H^2 )^m+8\pi \; G(\rho _m+\rho _r), \end{aligned}$$

(62)

$$\begin{aligned}&-(3 H^2+2 {\dot{H}}) = \frac{1}{2} c_1 {\dot{\varphi }}^2+c_2 {\dot{\varphi }}^2 \ddot{\varphi } \nonumber \\&\quad +\kappa 6^m \left( H^2 \left( m-\frac{1}{2}\right) + m\frac{(2 m-1)}{3} {\dot{H}}\right) (H^2)^{m-1}\nonumber \\&\quad +8\pi \; G\frac{\rho _r}{3}. \end{aligned}$$

(63)

If we consider that the first order of the Hubble parameter and scalar field are constant at the de Sitter epoch, we can derive the constant $c_2$ and $\kappa$. By imposing $\ddot{\varphi }=0$ and ${\dot{H}}=0$ at the de Sitter era and by solving Eqs. (62) and (63) for $c_2$ and $\kappa$ we find

$$\begin{aligned} \begin{aligned} c_1=3 H_{ds} {\dot{\varphi }}_{ds} c_2,\quad \kappa =6^{1-m} (H_{ds}^2){}^{1-m}\frac{ (\dot{\varphi }_{ds}^3/H_{ds})c_2 +1}{2(2 m-1)}, \end{aligned}\nonumber \\ \end{aligned}$$

(64)

where the de Sitter point is represented by the “ds” subscript. It is convenient to study the FRLW equation in the framework of dynamical variables defined as follows:

$$\begin{aligned}&x_1=\frac{1}{H {\dot{\varphi }}},\quad x_2=-\frac{c_2 \dot{\varphi }^3}{H},\quad x_3=\kappa 6^m \left( m-\frac{1}{2}\right) (H^2 )^{m-1},\quad \nonumber \\&\varOmega _m=8\pi \; G\frac{\rho _m}{3 H^2},\qquad \varOmega _r=8\pi \; G\frac{\rho _r}{3 H^2}. \end{aligned}$$

(65)

By using the variables (65), we can rewrite Eq. (62) as

$$\begin{aligned} \varOmega _{DE}+\varOmega _m+\varOmega _r=1, \end{aligned}$$

(66)

where

$$\begin{aligned} \varOmega _{DE}=x_2\left( 1-\frac{x_1}{2}\right) -\frac{x_3}{6}. \end{aligned}$$

(67)

Equations (64) and (16) can also be written as

$$\begin{aligned}&3+2 \epsilon _H+\frac{1}{3} m x_3 \epsilon _H-x_2 \epsilon _{\varphi }-\frac{3 x_1 x_2}{2}+\frac{x_3}{2}+\varOmega _r =0, \end{aligned}$$

(68)

$$\begin{aligned}&x_2 \epsilon _H-x_1 x_2 \epsilon _{\varphi }+2 x_2 \epsilon _{\varphi }-3 x_1 x_2+3 x_2 =0. \end{aligned}$$

(69)

By solving these two equations for $\epsilon _H$ and $\epsilon _{\varphi }$, we obtain

$$\begin{aligned} \epsilon _H= & {} \frac{3 ((4-2 x_1) \varOmega _r+3 x_2 x_1^2-12 x_2 x_1-x_3 x_1-6 x_1+6 x_2+2 x_3+12 )}{2 (m x_3 x_1-2 m x_3+6 x_1-3 x_2-12 )}, \end{aligned}$$

(70)

$$\begin{aligned} \epsilon _{\varphi }= & {} \frac{3 (3 x_2 x_1-2 m x_3 x_1+2 m x_3-2 \varOmega _r-12 x_1-x_3+6 )}{2 (m x_3 x_1-2 m x_3+6 x_1-3 x_2-12 )}. \end{aligned}$$

(71)

In terms of dynamical variables and by using Eqs. (70) and (71), the expressions of $w_{DE}$, $G_{\text {eff}}$, $c_{S}^2$ and $\beta _T$ read

$$\begin{aligned} w_{DE}= & {} \frac{6 x_2 \left( \varOmega _r-3 \left( x_1-4\right) x_1-3\right) -2 \left( x_1-2\right) x_3 \left( m \varOmega _r+3 m-3\right) }{\left( 3 \left( x_1-2\right) x_2+x_3\right) \left( 2 m x_3-x_1 \left( m x_3+6\right) +3 x_2+12\right) },\nonumber \\ \end{aligned}$$

(72)

$$\begin{aligned} G_{\text {eff}}= & {} 6 (2 m-1) \left( 3 x_1^2 \left( m x_3+6\right) -2 x_1 \left( 2 m x_3+9 x_2+12\right) \nonumber \right. \\&\left. +(2 m+3) x_3+6 \left( \varOmega _r+5\right) +12 x_2\right) /\varDelta _1, \end{aligned}$$

(73)

$$\begin{aligned} c_{S}^2= & {} (9 (2 m-1) x_2^2 ((m (72 m-55)+3) x_3\nonumber \\&-6 (2 m-1) (\varOmega _r-20))\nonumber \\&-6 x_2 (6 (2 m-1) x_3(m (2 m-1) \varOmega _r\nonumber \\&+m (32 m-1)-3)+36 (1-2 m)^2 (\varOmega _r+14)\nonumber \\&+m (m (38 m-27)+3) x_3^2)+(m x_3+12 m-6)^2 ((2 m\nonumber \\&+3) x_3+6 (\varOmega _r+5))+x_1 (3 x_2 (6 (2 m-1) x_3 (m (2 m-1) \varOmega _r\nonumber \\&+m (80 m-9)-3)+36 (1-2 m)^2 (\varOmega _r\nonumber \\&+34)+m (m (86 m-55)+3) x_3^2)-405 (1-2 m)^2 x_2^3\nonumber \\&-108 (2 m-1) x_2^2 ((8 m-5) m x_3+36 m-18)\nonumber \\&-4 (m x_3+6) (m x_3+12 m-6){}^2)+486 (1-2 m)^2 x_2^3\nonumber \\&+3 x_1^2 (m x_3+6) (45 (1-2 m)^2 x_2^2-12 (2 m\nonumber \\&-1) x_2 (m x_3+12 m-6)+(m x_3+12 m-6){}^2))/\varDelta _2, \end{aligned}$$

(74)

$$\begin{aligned} \beta _T= & {} \frac{3 (m-1) m x_3 \left( 2 \left( 2 \varOmega _r+3 x_2+x_3+6\right) +x_1 \left( -2 \left( \varOmega _r+3\right) +3 \left( x_1-4\right) x_2-x_3\right) \right) }{\left( m x_3+12 m-6\right) \left( m \left( x_1-2\right) x_3+6 x_1-3 \left( x_2+4\right) \right) }, \end{aligned}$$

(75)

$$\begin{aligned} Q_S= & {} \frac{3 x_2 \left( 2 m^2 \left( x_1-2\right) x_3^2+9 (1-2 m)^2 \left( x_1 \left( x_2^2+8\right) -2 \left( x_2^2+x_2+8\right) \right) -3 (2 m-1) x_3 \left( x_2-8 m \left( x_1-2\right) \right) \right) }{2 \left( m x_3-3 (2 m-1) \left( x_2-2\right) \right) {}^2} , \end{aligned}$$

(76)

where

$$\begin{aligned} \varDelta _1= & {} \left( m x_3+12 m-6\right) \left( (2 m+3) x_3+6 \left( \varOmega _r(t)+5\right) \right) \nonumber \\&+3 x_1^2 \left( m x_3+6\right) \left( m x_3+12 m-6\right) \nonumber \\&+x_1 \left( 3 x_2 \left( (2 m-7) m x_3-60 m+30\right) \nonumber \right. \\&\left. -4 \left( m x_3+6\right) \left( m x_3+12 m-6\right) \right) +(9-18 m) x_2^2\nonumber \\&+6 x_2 \left( (3-2 m) m x_3+12 m-6\right) , \end{aligned}$$

(77)

$$\begin{aligned} \varDelta _2= & {} 3 (m (x_1-2) x_3+6 x_1-3 (x_2+4)) (2 m^2 (x_1-2) x_3^2\nonumber \\&+9 (1-2 m)^2 (x_1 (x_2^2+8)-2 (x_2^2\nonumber \\&+x_2+8))+3 (2 m-1) x_3 (8 m (x_1-2)-x_2)). \end{aligned}$$

(78)

By solving Eqs. (68) and (69) for $\epsilon _{H}$ and $\epsilon _{\varphi }$ and substituting the results in the derivatives of $x_1$, $x_2$, $x_3$ and $\varOmega _r$ with respect to E-floding time $N=ln(a(t))$, we find

$$\begin{aligned} x_1'= & {} \frac{3 \left( 1-x_1\right) x_1 \left( 3 \left( x_1-2\right) x_2-(2 m+1) x_3-2 \left( \varOmega _r+9\right) \right) }{2 m \left( x_1-2\right) x_3-6 \left( x_2-2 x_1+4\right) }, \end{aligned}$$

(79)

$$\begin{aligned} x_2'= & {} \frac{3 x_2 \left( x_1 \left( 2 \varOmega _r-6 m x_3-3 \left( x_1-7\right) x_2+x_3-30\right) +(6 m-5) x_3-10 \varOmega _r-6 x_2+6\right) }{2 m \left( x_1-2\right) x_3-6 \left( x_2-2 x_1+4\right) }, \end{aligned}$$

(80)

$$\begin{aligned} x_3'= & {} \frac{3 (m-1) x_3 \left( 2 \left( 2 \varOmega _r+3 x_2+x_3+6\right) +x_1 \left( 6-2 \varOmega _r+ \left( x_1-4\right) x_2-x_3\right) \right) }{m \left( x_1-2\right) x_3+6 x_1-3 \left( x_2+4\right) }, \end{aligned}$$

(81)

$$\begin{aligned} \varOmega _r'= & {} \frac{\varOmega _r \left( 2 \left( (3-4 m) x_3+6 \left( \varOmega _r-1\right) +3 x_2\right) +x_1 \left( (4 m-3) x_3-6 \varOmega _r+9 \left( x_1-4\right) x_2+6\right) \right) }{2 m x_3-x_1 \left( m x_3+6\right) +3 x_2+12}, \end{aligned}$$

(82)

where the prime represents the derivative with respect to N. Note that we used the constraint $\varOmega _{DE}+\varOmega _m+\varOmega _r=1$ to eliminate $\varOmega _m$. In order to avoid divergences during the cosmological evolution, we require that

$$\begin{aligned} 2 m x_3-x_1 \left( m x_3+6\right) +3 x_2+12\ne 0. \end{aligned}$$

(83)

The critical points of the system are derived by solving the equations $x_1'=0$, $x_2'=0$, $x_3'=0$ and $\varOmega _r'=0$ [52, 53] and we summarized their values and the stability properties in Table 1. In order to study the stability of this point we perturb the dynamical equations of $x_1$, $x_2$, $x_3$ and $\varOmega _r$ around each fixed point obtained: $x_1=x^c_1+\delta x_1$, $x_2=x^c_2+\delta x_2$, $x_3=x^c_2+\delta x_3$, $\varOmega _r=\varOmega _r^c+\delta \varOmega _r$. Thus, we get the following linear differential system of equations:

$$\begin{aligned} \delta \overrightarrow{\mathbf{x }}'=\mathbf{H }\delta \overrightarrow{\mathbf{x }}, \end{aligned}$$

(84)

where $\mathbf{H }$ is Hessian matrix and $\overrightarrow{\mathbf{x }}$ is given by

$$\begin{aligned} \delta \overrightarrow{\mathbf{x }}^t=(\delta x_1,\delta x_2,\delta x_3,\delta \varOmega _r). \end{aligned}$$

(85)

We see there is a stable and an unstable fixed point, corresponding to the de Sitter solution. We see also there are two critical saddle points ($O_2$ and $O_6$), with $w_{\text {eff}}=0$, which correspond to the matter era solution. Moreover, the points $O_7$ and $O_4$, with $w_{\text {eff}}=1/3$ (radiation domination), are saddle but this is not the case for $O_4$ when $m\geqslant 1$. In order to understand the role of the fixed points we will estimate the evolution of the cosmological parameters analytically in the three eras. Then we solve the differential equations of (79)–(82) numerically, in the next section. However, since the point $O_5$ has the strange value $w_{\text {eff}}=1/5$ and the point $O_3$ is saddle, they will not be taken into consideration.

Table 1 The critical points with the eigenvalues found by using the Hessian matrix. In the last column we give the value of $w_{\text {eff}}$ for each critical point

5.2 Tracker solution

It is obvious that Eq. (79) is characterized by the solution $x_1=1$, which is called a tracker solution [20]. In fact, along the cosmological evolution of this quantity ${\dot{\varphi }}H$ remains constant. In this case the dynamical equations are reduced to

$$\begin{aligned} x_2'= & {} \frac{6 x_2 \left( 2 \varOmega _r-3 x_2+x_3+6\right) }{m x_3+3 x_2+6}, \end{aligned}$$

(86)

$$\begin{aligned} x_3'= & {} -\frac{3 (m-1) x_3 \left( 2 \varOmega _r-3 x_2+x_3+6\right) }{m x_3+3 x_2+6}, \end{aligned}$$

(87)

$$\begin{aligned} \varOmega _r'= & {} -\frac{\varOmega _r \left( (4 m-3) x_3-6 \varOmega _r+21 x_2+6\right) }{m x_3+3 x_2+6}. \end{aligned}$$

(88)

From Eqs. (87) and (88), we can deduce the relation

$$\begin{aligned} \frac{x_3'}{x_3}=\frac{(1-m)}{2}\frac{x_2'}{x_2}. \end{aligned}$$

(89)

And from (87) and (88), we can also deduce

$$\begin{aligned} \frac{\varOmega _r'}{\varOmega _r}-\frac{x_2'}{2x_2}=-4. \end{aligned}$$

(90)

Integrating these last two equations with respect to N leads to

$$\begin{aligned} x_2= & {} \frac{x_2(N=0)}{\varOmega _r(N=0)^2} a^8 \varOmega _r^2, \end{aligned}$$

(91)

$$\begin{aligned} x_3= & {} x_3(N=0)\left( \frac{x_2}{x_2(N=0)}\right) ^{\frac{(1-m)}{2}}. \end{aligned}$$

(92)

Since $\varOmega _r(N=0)H_0^2/H^2=a^4\varOmega _r$, it follows that $x_2=x_2(N=0)(H/H_0)^{-4}$ and $x_3=x_3(N=0)(H/H_0)^{2(m-1)}$, where $H_0$ is the value of H at $N=0$ and $x_2(N=0)=2+x_3(N=0)/3-\varOmega _r(N=0)-\varOmega _m(N=0)$. So, if we want to keep the dark energy density sub-dominated at the radiation epoch, we must impose the condition $m<1$. Furthermore, it is easy to have an equation corresponding to Hubble parameters by substituting the expression of $\varOmega _r$, $\varOmega _m$, $x_2$ and $x_3$ in the constraint (66). Thus, we obtain

$$\begin{aligned} \left( \frac{H}{H_0}\right) ^2= & {} \left( 1+\frac{x_3^{(0)}}{6}-\varOmega _{r_0}-\varOmega _{m_0}\right) \left( \frac{H}{H_0}\right) ^{-4}\nonumber \\&-\frac{x_3^{(0)}}{6}\left( \frac{H}{H_0}\right) ^{2(m-1)}+\frac{H_0^2\varOmega _{m_0}}{H^2 a^3}+\frac{H_0^2\varOmega _{r_0}}{H^2 a^4}.\nonumber \\ \end{aligned}$$

(93)

Along the tracker the equation of state of dark energy and the effective total equation of state, defined by $w_{\text {eff}}=-1-\frac{2}{3}\epsilon _H$, evolve as

$$\begin{aligned} w_{\text {eff}}= & {} \frac{-(m-1) x_3+2 \varOmega _r-6 x_2}{m x_3+3 x_2+6}, \nonumber \\ w_{DE}= & {} -\frac{2 \left( x_3 \left( m \varOmega _r+3 m-3\right) +3 x_2 \left( \varOmega _r+6\right) \right) }{\left( 3 x_2-x_3\right) \left( m x_3+3 x_2+6\right) }. \end{aligned}$$

(94)

In the matter and radiation epoch the effective total equation of state ($\mid x_2 \mid \ll 0$ and $\mid x_3 \mid \ll 0$) is reduced to $w_{\text {eff}}=\varOmega _r/3$. As regards the critical point, this can be seen as a transition from the point $O_6$ to the point $O_7$. However, the evolution of EoS of dark energy, at the early epoch, can take two regimes: The first regime is characterized by $\mid x_3\mid \ll \mid x_2 \mid \ll 0$ in which we have

$$\begin{aligned} w_{DE}=-2-\varOmega _r/3. \end{aligned}$$

(95)

This behavior is identical to that of the the cubic galileon and is not favored by the experimental observations [21]. But in the second regime, where we the condition $\mid x_2\mid \ll \mid x_3 \mid \ll 0$ is satisfied in the matter and radiation epochs, we have

$$\begin{aligned} w_{DE}=m-1+\frac{1}{3} m \varOmega _r. \end{aligned}$$

(96)

Here, since the EoS takes the value $m-1$ and $-1+(4m)/3$ at the matter and radiation areas, respectively, one can have $w_{DE}>-2$ in the matter area for $m<-1$. The quantities associated to $c_S^2$, $Q_S$ and $\beta _T$ for the tracker solution are given by

$$\begin{aligned} c_S^2= & {} (9 (2 m-1) x_2^2 ((2 m (3 m-5)+3)\nonumber \\&x_3-6 (2 m-1) (\varOmega _r+1))\nonumber \\&-3 x_2 (6 (2 m-1) x_3 (m (2 m-1) \varOmega _r \nonumber \\&+m (8 m+7)-3)+36 (1-2 m)^2 (\varOmega _r+6)\nonumber \\&+m (m (14 m-11)+3) x_3^2)+(m x_3+12 m-6)^2 ((m\nonumber \\&+3) x_3+6 (\varOmega _r+4))+81 (1-2 m)^2 x_2^3)/\varDelta _2, \end{aligned}$$

(97)

$$\begin{aligned} Q_S= & {} \frac{3 x_2 \left( \!-\!2 m^2 x_3^2\!-\!9 (1\!-\!2 m)^2 \left( x_2 \left( x_2\!+\!2\right) \!+\!8\right) \!-\!3 (2 m\!-\!1) x_3 \left( 8 m\!+\!x_2\right) \right) }{2 \left( m x_3-3 (2 m-1) \left( x_2-2\right) \right) ^2},\nonumber \\ \end{aligned}$$

(98)

$$\begin{aligned} \beta _T= & {} -\frac{3 (m-1) m x_3 \left( 2 \varOmega _r-3 x_2+x_3+6\right) }{\left( m x_3+12 m-6\right) \left( m x_3+3 x_2+6\right) }, \end{aligned}$$

(99)

with

$$\begin{aligned} \varDelta _2= & {} 3 (m (x_1-2) x_3+6 x_1-3 (x_2+4))(2 m^2 (x_1-2) x_3^2\nonumber \\&+9 (1-2 m)^2 (x_1(x_2^2+8)-2 (x_2^2+x_2+8))\nonumber \\&+3 (2 m-1) x_3(8 m (x_1-2)-x_2)). \end{aligned}$$

(100)

During the cosmological evolution of the universe in the matter and radiation eras ($\mid x_2 \mid \ll 0$ and $\mid x_3 \mid \ll 0$), the quantities $c_S^2$, $Q_S$ and $\beta _T$ evolve as $c_S^2=(\varOmega _r+4)/6$, $Q_S=3x_2$ and $\beta _T\simeq 0$, respectively. Hence, for $x_2>0$, the ghost and the Laplacian instability are automatically avoided in the matter and radiation epochs. Finally, expanding the effective gravitational coupling about $x_2=0$ and $x_3=0$ gives

$$\begin{aligned} \begin{aligned} G_{\text {eff}}=1+\left( \frac{m x_3}{6-12 m}+\frac{x_2}{2 \varOmega _r+8}\right) . \end{aligned}. \end{aligned}$$

(101)

For $x_2 \ll x_3$, we observe that $G_{\text {eff}}$ depends on m where $G_{\text {eff}}$ can be smaller than 1 but this is not the case when $x_3 \ll x_2$.

5.3 Small regime

We can study this regime by considering a linear perturbation of $x_1$, $x_2$ and $x_3$ around zero. Thus, it follows that

$$\begin{aligned} x_1'= & {} \frac{1}{4} \left( \varOmega _r+9\right) x_1, \end{aligned}$$

(102)

$$\begin{aligned} x_2'= & {} \frac{1}{4} x_2 \left( 5 \varOmega _r-3\right) , \end{aligned}$$

(103)

$$\begin{aligned} x_3'= & {} (1-m) \left( \varOmega _r+3\right) x_3, \end{aligned}$$

(104)

$$\begin{aligned} \varOmega _r'= & {} \left( \varOmega _r-1\right) \varOmega _r. \end{aligned}$$

(105)

We see that the points $O_4$ and $O_2$ correspond to critical points of Eqs. (102)–(105) and thus a transition $O_4$ to $O_2$ may occur. By integrating these equations, we obtain the analytical solution as follows:

$$\begin{aligned} \begin{aligned}&x_1= C_2 a^{5/2}\root -4 \of {\varOmega _r}, \quad x_2=C_3 \sqrt{a} \varOmega _r^{\frac{5}{4}},\\&\quad x_3=C_4 a^{4-4 m} \varOmega _r^{m-1}, \end{aligned} \end{aligned}$$

(106)

with

$$\begin{aligned} \varOmega _r=\frac{1}{ C_1 a+1}, \end{aligned}$$

(107)

where $C_1$, $C_2$, $C_3$ and $C_4$ are constants of integration. From Eq. (107), we can characterize the radiation era by $a\ll 1/C_1$ and the matter era by $a\gg 1/C_1$. Thus, the dynamical variables $x_1$ and $x_2$ increase in the two eras but the evolution of $x_3$ depends on the parameter m. The dynamical variable $x_3$ increases if $m<1$, remains constant for $m=1$, and decreases in the case $m>1$. In this regime, the EoS of dark energy given by Eq. (72) becomes

$$\begin{aligned} \begin{aligned} w_{DE}=-\frac{2 x_3 \left( m \varOmega _r+3 m-3\right) +3 x_2 \left( \varOmega _r-3\right) }{36 x_2-6 x_3}. \end{aligned} \end{aligned}$$

(108)

For the case $\mid x_3\mid \ll \mid x_2\mid$, we have $w_{DE}=\left( 3-\varOmega _r\right) /12$ which is the same in the cubic galileon’s EoS in the small regime [20]. In addition, if $\mid x_2\mid \ll \mid x_3\mid$, the equation of state is reduced to $w_{DE}=\left( m \varOmega _r+3 m-3\right) /3$. In fact, the EoS evolves as 1/6 (radiation area) $\longmapsto$ 1/4 (matter area) in the first case, whether it is evolves as $-1+(4m)/3$ (radiation area) $\longmapsto$ $(m-1)$ (matter area) in the second one like we found in the tracker. By taking the limit $x_1\longrightarrow 0$, $x_2\longrightarrow 0$ and $x_3\longrightarrow 0$, the propagation speed of scalar field perturbations and the parameter $\beta _T$ are given by

$$\begin{aligned} c_S^2= & {} \frac{1}{24} \left( \varOmega _r+5\right) , \end{aligned}$$

(109)

$$\begin{aligned} Q_S= & {} 6 x_2, \end{aligned}$$

(110)

$$\begin{aligned} \beta _T= & {} \frac{m(m-1)\left( \varOmega _r+3\right) }{6-12 m}x_3. \end{aligned}$$

(111)

When $x_2>0$, we observe that the ghost and Laplacian instability are absent where $c_S^2=1/4$ and $c_S^2=5/24$ at the matter and the radiations epochs, respectively. In addition, in these epochs the sign of the parameter $\beta _T$ depends on the value of m and the sign of $x_3$. In the small regime, $G_{\text {eff}}$ is expanding to

$$\begin{aligned} \begin{aligned} G_{\text {eff}}=1+\left( \frac{m x_3}{6-12 m}+\frac{x_2}{\varOmega _r+5}\right) . \end{aligned} \end{aligned}$$

(112)

We have the same result as found in (101) for $\mid x_2\mid \ll \mid x_3\mid$ but we have a small change in the case $\mid x_3\mid \ll \mid x_2\mid$.

5.4 de Sitter solution

This point corresponds to $O_1$ and it can be found by considering $\epsilon _H=0$, $\epsilon _{\varphi }=0$ and $\varOmega _r=0$; then we solve Eqs. (68) and (69) for $x_1$ and $x_3$. The stable de Sitter fixed point is calculated by

$$\begin{aligned} \begin{aligned} P_{ds}=(x_1,x_2,x_3,\varOmega _r)=(1,x_2,3 (x_2-2),0). \end{aligned} \end{aligned}$$

(113)

Substituting this point in (72)–(75), we obtain

$$\begin{aligned}&w_{DE}=-1,\quad w_{\text {eff}}=-1,\quad \beta _T=0,\nonumber \\&c_S^2 =-\frac{(m-1) \left( x_2-2\right) }{6 \left( (3 m-1) x_2+2 (m-1)\right) },\nonumber \\&Q_S=\frac{3 x_2 \left( m x_2+2 m-2\right) \left( (3 m-1) x_2+2 (m-1)\right) }{(m-1)^2 \left( x_2-2\right) ^2},\nonumber \\&G_{\text {eff}}=\frac{2-4 m}{(m-1) \left( x_2-2\right) }. \end{aligned}$$

(114)

At this point, the universe is dominated by dark energy, where the conditions for avoidance of the Laplacian instability are satisfied for the cases: $\left( m<\frac{7}{19}\wedge \frac{10-10 m}{19 m-7}<x_2<2\right)$, $\left( \frac{7}{19}<m\le \frac{1}{2}\wedge \left( x_2<2\vee x_2>\frac{10-10 m}{19 m-7}\right) \right)$, $\left( \frac{1}{2}<m<1\wedge \right. \left. \left( x_2<\frac{10-10 m}{19 m-7}\vee x_2>2\right) \right)$ and $\left( m>1\wedge \frac{10-10 m}{19 m-7}<x_2<2\right)$, where $\wedge \equiv$ and $\vee \equiv$ or. In addition, $G_{\text {eff}}$ is bigger than one, if $0<m<\frac{1}{2}$ and $0<x_2<-\frac{2 m}{m-1}$. And we have $0<G_{\text {eff}}<1$ when $\left( m\le 0\wedge 0<x_2<2\right) \vee \left( 0<m<\frac{1}{2}\right)$ and $-\frac{2 m}{m-1}<x_2<2$.

5.5 Numerical analysis

In order to show the cosmological evolution of the dynamical variables in more detail, we solve the system of equations (79)–(82) numerically for different values of m. The initial conditions are chosen to get the values $\varOmega _{m_0}=0.31$ and $\varOmega _{r_0}=9.3 \times 10^{-5}$ at the present time, $N=0$; the condition of stability and the Laplacian stability for the de Sitter fixed point are taken into account. In fact, by using the definition $\varOmega _{de_0}=1-\varOmega _{m_0}-\varOmega _{r_0}$, it follows that

$$\begin{aligned} x_2^{(0)}=2\frac{\varOmega _{m_0}+ \varOmega _{r_0}-x_3^{(0)}-1}{x_1^{(0)}-2}. \end{aligned}$$

(115)

Hence, the cosmological evolution of the dynamical variables depends on the numerical values of $x_3^{(0)}$, $x_1^{(0)}$ and m. If we assume that $x_1^{(0)}=1$, we get the tracker solution discussed above because the variable $x_1$ is equal to one along the three cosmological areas in this condition. Furthermore, as depicted in the right of Fig. 1, the value of $x_2$ at the de Sitter epoch depends on the initial conditions. We note that the dashed line represents the points where the denominator vanishes.

In Fig. 1, the evolution of $\varOmega _{DE}$, $\varOmega _{m}$, $\varOmega _{r}$ and $w_{\text {eff}}$ are plotted versus N for $m=0.25$ with the initial conditions $x_1^{(0)}=1$ and $x_3^{(0)}=-2.5$, where after radiation domination a long finite time of dark matter era is attained before a transition to dark energy domination occurs. In Fig. 2, we plot the evolution of the EoS corresponding to the tracker solution versus the e-folding time $N=-log(1+z)$, where $z=1/a-1$ is the redshift, for different values of m and $x_3^{(0)}$. When $m=-1$, the equation of state of dark energy takes the path $-7/3\mapsto -2\mapsto -1$ during the matter, radiation and de Sitter epochs, respectively. This behavior is in tension with the joint data based on SN Ia, CMB and BAOs [21] because $w_{DE}$ takes the value -2 at the matter era. Therefore, all solutions with $m\le -1$ are excluded due to the large deviation of the EoS from -1. We observe, in Fig. 2, when $-1<m<0$, $-2<w_{DE}<-1$ at the matter era and $w_{DE}>-1$, if $m>0$. This confirms our analytical estimation in Sect. 5.2, where we obtained $w_{DE}^{(m)}=m-1$. Moreover, when we set $m=0.25$ and decrease the initial condition on $x_3$, $w_{DE}$ crosses the line -1 and starts to approach the value -2 in the matter epoch.

Fig. 1

Left graph: the evolution of $\varOmega _{DE}$ (orange line), $\varOmega _{m}$ (green line), $\varOmega _{r}$ (blue line) and $w_{\text {eff}}$ (red line) versus N for $m=0.25$, $x_3^{(0)}=-2.5$, $x_1^{(0)}=1$, $\varOmega _{m_0}=0.31$ and $\varOmega _{r_0}=9.3\times 10^{-5}$. Right graph: phase-space trajectories on the $x_2$–$x_3$ plane for $m=0.25$ and $x_1=1$. The solid line and the dashed line are described by the equations $x_3=3(x_2-2)$ and $x_3=-3(x_2+2)/m$, respectively

Fig. 2

Variation of $w_{DE}$ as a function of N for $x_1^{(0)}=1$, $\varOmega _{m_0}=0.31$ and $\varOmega _{r_0}=9.3\times 10^{-5}$ with different value of m and $x_3^{(0)}$. Left graph: $x_3^{(0)}=-3.5$ with $m=$ $0.5\, \text {(purple color)}$, $\, 0.25 \, \text {(red color)}$, $\, -\,0.25 \, \text {(green color)}$, $\, -\,0.5\, \text {(orange color)}$ and $\, -1 \, \text {(blue color)}$. Right graph: $m=0.25$ with $x_3^{(0)}=$ $-4.5 \, \text {(purple color)}$, $\, -3.5 \, \text {(red color)}$, $\, -2.5\, \text {(green color)}$, $\, -\,0.2 \, \text {(orange color)}$ and $\, -10^{-4}\, \text {(blue color)}$

Fig. 3

Variation of $w_{DE}$ as a function of N for $m=0.25$, $\varOmega _{m_0}=0.31$ and $\varOmega _{r_0}=9.3\times 10^{-5}$ with different value of $x_1^{(0)}$ and $x_3^{(0)}$. Left graph: $x_3^{(0)}=5\times 10^{-6}$ with $x_1^{(0)}=$ $\, 0.9 \, \text {(green color)}$, $\, 0.99\, \text {(orange color)}$ and $\, 0.999999 \, \text {(blue color)}$. Right graph: $x_1^{(0)}=0.999$ with $x_3^{(0)}=$ $\, -\,0.1\, \text {(green color)}$, $\, -1 \, \text {(orange color)}$ and $\, -3\, \text {(blue color)}$

Fig. 4

The variation of $Q_S$ (left graph), $Q_S$ (middle graph) and $\beta _T$ (right graph) with respect to N for $m=0.25$ and different initial conditions. a ($x_1^{(0)}=0.999$, $x_3^{(0)}=-1$), b ($x_1^{(0)}=0.99$, $x_3^{(0)}=-\,0.5\times 10^{-6}$) and c ($x_1^{(0)}=1$, $x_3^{(0)}=-2.5$)

In Fig. 3, we plot also the evolution of $w_{DE}$ as a function of N by varying the initial conditions $x_1^{(0)}$ and $x_3^{(0)}$ in the left and right graphs, respectively, for $m=0.25$. According to our numerical estimation in the right plot, the EoS of dark energy deviates from -2 at matter era when we increase $x_3^{(0)}$ like in the tracker solution. However, in the left plot, a similar behavior of $w_{DE}$ to the cubic galileon (in the small regime) is recovered, for a small value of $x_3^{(0)}$.

In Fig. 4, we show the evolution of $c_S^2$ for our model with $m=0.25$ and the initial conditions like those given in Figs. 2 and 3. The numerical estimation confirm the analytical analysis above where we have $c_S^2=5/6$, $c_S^2=2/3$ and $c_S^2=0.08$ during the radiation, the matter and the de Sitter eras, respectively. However, for a small value of $x_3^{(0)}$ the numerical estimation gives $c_S^2= 1/4$ (radiation epoch), $c_S^2= 5/24$ (matter epoch) and $c_S^2= 1.1972\times 10^{-7}$ (de Sitter epoch). Since in the two cases $0<c_S^2<1$ along the cosmic evolution, the Laplacian instability of the scalar perturbation is absent. However, a small Laplacian instability appears in the small regime, which is due to the initial conditions we chose. This does not seem to be catastrophic because the duration is short and one can arrange to avoid this instability by changing the values the parameters in the model. We also showed the evolution of $\beta _T$ as a function of N for three values of $x_3^{(0)}$. We observe that in three cases $\beta _T$ vanishes in all epochs but it deviates from zero in the late universe by changing the value of $x_3^{(0)}$. This means that if our model describes the evolution of our universe, the amplitudes of the gravitational waves have changed in the past.

6 Observation constraint

In order to better see the deviation of our model from General Relativity and confront with the measurement of observational data, we study the density perturbation of the matter by introducing the growth rate of the matter density

$$\begin{aligned} f \sigma _8 (a)=\sigma _8(a)\frac{dln\delta _m}{dlna}, \end{aligned}$$

(116)

where $\sigma _8 (a)=\sigma _8 \delta _m(a)/\delta _m(1)$ is the rms fluctuation of the linear density field inside a radius of $8 h^{-1} Mpc$, and $\sigma _8$ represent its present value. The equation of the contrast $\delta _m$, in the sub-horizon regime, is given by

$$\begin{aligned} \delta _m''+(2+\epsilon _H)\delta _m'-\frac{3}{2}G_{\text {eff}}\varOmega _m \delta _m= 0, \end{aligned}$$

(117)

where $\varOmega _m=1-\varOmega _r-\varOmega _{DE}$. In the following, we will only focus on the tracker solution. In order to place an observational constraint on the cosmological parameters of the model, we perform a Markov chain Monte Carlo integration implemented with the Metropolis algorithm [54] by using the growth rate factor (GRF) and observational Hubble data (OHD) listed in Table 3. So, the combined likelihood function of the data reads

$$\begin{aligned} {\mathcal {L}}_{\text {tot}}=e^{-(\chi _{\text {GRF}}^2+\chi _{\text {OHD}}^2)/2}, \end{aligned}$$

(118)

where $\chi _{\text {GRF}}^2$ and $\chi _{\text {OHD}}^2$ are defined as follows:

$$\begin{aligned} \chi _{\text {GRF}}^2= & {} \sum \left( \frac{f\sigma _{8;obs}(z_i)-f\sigma _{8;th}(z_i,\varOmega _{m_0},m,x_3^{(0)})}{\sigma _i}\right) ^2, \end{aligned}$$

(119)

$$\begin{aligned} \chi _{\text {OHD}}^2= & {} \sum \left( \frac{H_{obs}(z_i)-H_0 E(z_i,\varOmega _{m_0},m,x_3^{(0)})}{\sigma _i}\right) ^2, \end{aligned}$$

(120)

where $E=(x_2^{(0)}/x_2)^{1/4}$. Expanding $\chi _{\text {OHD}}^2$ yields

$$\begin{aligned} \chi _{\text {OHD}}^2=A H_0^2-2 B H_0+C, \end{aligned}$$

(121)

where

$$\begin{aligned}&A=\sum \left( \frac{E(z_i,\varOmega _{m_0},m,x_3^{(0)})}{\sigma _i}\right) ^2, \nonumber \\&B=\sum \frac{H_{obs}(z_i) E(z_i,\varOmega _{m_0},m,x_3^{(0)})}{\sigma _i^2}, \nonumber \\&C=\sum \left( \frac{H_{obs}(z_i)}{\sigma _i}\right) ^2. \end{aligned}$$

(122)

It is obvious that $\chi _{\text {OHD}}^2$ defined by Eqs. (121) is minimized when $H_0=-B/A$. In this case, we write

$$\begin{aligned} \chi _{\text {OHD}}^2=-\frac{B^2}{A}+C. \end{aligned}$$

(123)

Note that in the following we will use this result to constrain our model instead of that in Eqs.(121). Since our analysis is independent from $H_0$, the numerical integration is done over the parameters $\varOmega _{m_0}$, $x_3^{(0)}$, m and $\sigma _8$. In Table 2, we show the best-fit parameters with their 1$\sigma$ confident level for our model and $\varLambda$CDM model as well as the Bayes factor. The minimum value for $\chi ^2$ of the model studied in this paper is slightly smaller than that in the $\varLambda$CDM model where the difference in two models is $\delta \chi =0.9352$, which is consistent within $1\sigma$ level. However, since the Bayes factor is $1.1<ln(B_{12})<3$, the evidence against our model is not strong.

Fig. 5

The $1\sigma$–$2\sigma$ confident levels contours in the planes ($\varOmega _{m_0}$, m), (m, $\sigma _8$), ($x_3^{(0)}$, $\varOmega _{m_0}$), ($x_3^{(0)}$, $\sigma _8$) and ($\varOmega _{m_0}$, $\sigma _8$) resulting from the MCMC analysis on our model. In the right graph the contours with no shading correspond to $1\sigma$–$2\sigma$ confident levels of $\varLambda$CDM

Table 2 The $1\sigma$ confident level results from the MCMC analysis on our model and $\varLambda$CDM model

In Fig. 5 we plot the 1$\sigma$ and 2$\sigma$ confidence contours in the planes ($\varOmega _{m_0}$, m), (m, $\sigma _8$), ($x_3^{(0)}$, $\varOmega _{m_0}$), ($x_3^{(0)}$, $\sigma _8$) and ($\varOmega _{m_0}$, $\sigma _8$) for the models presented in Table 2. We notice that our best-fit values of $\sigma _8$ and $\varOmega _{m_0}$ are close to the results obtained in the $\varLambda$CDM model.

Fig. 6

The evolution of $G_{\text {eff}}$ and $w_{DE}$ versus N for the best-fit values addressed in Table 2

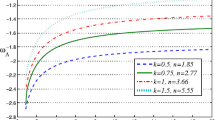
The variation of $G_{\text {eff}}$ and $w_{DE}$ is plotted in Fig. 6 for the best-fit values. We observe that effective gravitational coupling starts to evolve at late universe; then it becomes constant in the future. Indeed, $G_{\text {eff}}$ starts to decrease at low redshift until it reaches the value 0.74 at $N=-\,0.30$ before going to the value 1.251 in the future of the universe. Moreover, the actual value of $G_{\text {eff}}$ and its first derivative appears to be consistent with the constraint obtained from the Solar System [55] and nucleosynthesis constraint [56] observations, which are given by

$$\begin{aligned} |G_{\text {eff}}(N=0)/G-1 |\le 0.2,\quad |{\dot{G}}_{\text {eff}}(N=0)|/G |\le 10^{-5}H_0^{-1}. \end{aligned}$$

(124)

Finally, we compare the growth rate of the two models using the best value presented above with the experiment data of the Table 3, in Fig. 7. A difference appears between the models during the cosmological evolution where the growth rate in the $\varLambda$CDM model is slightly lower than ours from the redshift $z=0.5$ to $z=0$.

Fig. 7

The evolution of growth rate of matter fluctuation for our model (Black curve) and $\varLambda$CDM model (dashed curve) using the best-fit values addressed in Table 2. We plot also the RSD observations data taken from Table 3

7 Conclusion

In the present work, we have investigated the cubic galileon in modified teleparalellel gravity frameworks where the Lagrangian is constituted by a general function f(T), a kinetic therm X and a cubic galileon term $X\nabla _\mu \nabla ^\mu \varphi$. Then we calculated the equations of motion in FRW-metric and then the equations corresponding to scalar and tensor perturbations. We found that the expression of the effective gravitational coupling $G_{\text {eff}}$ in our model can be a generalization to the cubic galileon and teleparallel gravity. We found also that the gravitation wave speed is equal to the propagation speed of light but the amplitude can evolve in time. The scalar propagation speed sound has been derived for the model proposed in Sect. 2.

In this model, the dynamical analysis showed the existence of a stable point (de Sitter solution) characterized by ${\dot{\varphi }}=\mathrm{const}$ and $H=\mathrm{const}$. In addition, two interesting behaviors have been found, where the first is as a tracker in which the value of $H{\dot{\varphi }}$ stays constant with the variation of the cosmic time and the second one is characterized by the conditions $x_1\ll 1$, $x_3\ll 1$ and $x_2\ll 1$ during the matter and radiation dominance. In the tracker solution, the equation of state of dark energy evolves as $-1+(4m)/3$ (radiation domination) $\mapsto$ $m-1$ (matter domination) $\mapsto$ $-1$ (dark energy domination), for $x_2\ll x_3\ll 1$ and $-7/2$ (radiation domination) $\mapsto$ $-2$ (matter domination) $\mapsto$ $-1$ (dark energy domination), for $x_3\ll x_2\ll 1$ where the one mentioned last is disfavored by the observational data. However, in the small regime ($x_1\ll 1$, $x_3\ll 1$ and $x_2\ll 1$), the EoS of dark energy behaves like $w_{DE}$ found in the tracker solution for $x_2\ll x_3\ll 1$ but we got the same evolution as found in the small regime of the cubic galileon for $x_3\ll x_2\ll 1$. In these two regimes, the derived expression of the effective gravitational coupling deviates smoothly from GR in the radiation and matter epochs; then it becomes constant at the de Sitter epoch.

The numerical integration of dynamic equations allowed us to check the evolution of different quantities as a function of N for different initial conditions and values of m. In fact, we showed that the EoS can avoid the value $-2$ at the matter era when $m>1$ and $x_3^{(0)}>0$. Furthermore, in our numerical estimation, it is not only the ghost and Laplacian instability that is absent for the values chosen in Fig. 4, but a variation of the amplitude of GW occurs at late universe.

In Sect. 6, we studied the growth of a matter perturbation by solving the equation corresponding to the contrast $\delta _m$ numerically in sub-horizon scale. Afterward, we implemented a MCMC numerical integration using the Metropolis algorithm to get the best-fit values of $\varOmega _{m_0}$, $x_3^{(0)}$, m and $\sigma _8$. The best-fit values $\varOmega _{m_0}$ and $\sigma _8$ obtained are consistent with values of $\varOmega _{m_0}$ and $\sigma _8$ in the $\varLambda$CDM model. We also compared the growth rate with experimental data and the prediction of the growth rate associated to the $\varLambda$CDM model. We noticed that our model and the $\varLambda$CDM model show a smooth difference from each other but the $\varLambda$CDM model is not preferred over our model because of the lack of experiment data. Therefore, a combined data analysis of SNIa, CMB, and BAO on our model would be interesting but we leave this to future work.

Appendices

Appendix A: Teleparallel gravity

In teleparallel gravity, we use the tetrad fields $e_\mu ^a$ rather than the metric $g_{\mu ,\nu }$ constantly used in GR. The relationships between the two field reads

$$\begin{aligned} g_{\mu ,\nu }=e_\mu ^a e_\nu ^b \eta _{ab} \end{aligned}$$

(125)

where $\eta _{ab}$ is the Minkowski metric with the signature $(-,+,+,+)$. In this theory, one works with a torsion tensor defined as follows:

$$\begin{aligned} T^a_{\;\;\mu \nu }=\partial _{\mu } e_\nu ^a -\partial _{\nu } e_\mu ^a. \end{aligned}$$

(126)

In terms of spacetime indices we write

$$\begin{aligned} T^{\lambda }_{\;\;\mu \nu }=e_a^\lambda T^a_{\;\;\mu \nu }, \end{aligned}$$

(127)

where $e_a^\nu$ is the inverse of $e_\nu ^a$. One can also define the torsion vector as

$$\begin{aligned} T_{\mu }=T^\lambda _{\;\;\lambda \mu }. \end{aligned}$$

(128)

The Ricci scalar in terms of the torsion can be calculated as

$$\begin{aligned} R=-T+\frac{2}{e}\partial _\mu (eT_{\mu }), \end{aligned}$$

(129)

where

$$\begin{aligned} T= & {} S_{\lambda }^{\;\;\mu \nu }T^{\lambda }_{\;\;\mu \nu }, \end{aligned}$$

(130)

$$\begin{aligned} 2S_{\lambda }^{\;\;\mu \nu }= & {} K_{\lambda }^{\;\;\mu \nu }+\delta _\lambda ^\nu T_{\mu }-\delta _\lambda ^\mu T_{\nu }, \end{aligned}$$

(131)

$$\begin{aligned} 2K_{\mu \;\;\;\;\nu }^{\;\;\lambda }= & {} T_{\mu \;\;\;\;\nu }^{\;\;\lambda }+T_{\lambda }^{\;\;\mu \nu }-T_{\nu \mu }^{\;\;\;\;\lambda }. \end{aligned}$$

(132)

Appendix B: Experimental data

The observational data are listed in the tables below

Table 3 RSD (left table) and Hubble (right table) observational data