Distinguishing magnetically and electrically charged Reissner–Nordström black holes by magnetized particle motion

Abstract

In the present paper, we investigate the dynamics of magnetized particles around magnetically and electrically Reissner–Nordström (RN) black hole. The main idea of the work is to distinguish the effects of electric and magnetic charges of the RN black hole and spin of the rotating Kerr black hole through the dynamics of the magnetized particles. In this study, we have treated a magnetized neutron star as a magnetized test particle, in particular, the magnetar SGR (PSR) J1745-2900 orbiting around the supermassive black hole Sagittarius A* (SMBH SgrA*) with the magnetic interaction parameter $b=0.716$ and the parameter $\beta =10.2$. The comparison of the effects of the magnetic and electric charges, and magnetic interaction parameters on the dynamics of the magnetar modeled as a magnetized particle near the SMBH Sgr A* has shown that the magnetic charge of the RN black hole can mimic the spin parameter of a rotating Kerr black hole up to $a/M \simeq 0.82$. The external magnetic field can mimic the magnetic charge of the RN black hole up to $Q_m/M=0.4465$. We have shown that the electric charge of the RN black hole can mimic the black hole magnetic charge up to $Q_m/M=0.5482$ and the magnetic field interaction with the magnetized particle acts against the increase of the mimicking value of the black hole spin parameter. The studies may be helpful to explain the observability of radio pulsars around the SMBH SgrA* system and taking it as a real astrophysical laboratory to get more precise constraints on the central black hole and dominated parameters of the alternate gravity. Finally, we have investigated the effects of magnetic and electric charge of the RN black hole in the center-of-mass energy of head-on collisions of magnetized particles with neutral, electrically charged, and magnetized particles. Both electric and magnetic charges of the RN black hole would lead to an increase in the center of the mass–energy of the collisions.

1 Introduction

Studies of dynamics of particle motion around a compact gravitational object are one of the interesting and highly motivated special subjects in relativistic astrophysics. They may be helpful in developing new approaches to describing the gravitational and electromagnetic interaction in both the strong-field and the weak-field regimes. Particularly, black holes as a simple astrophysical object can simply be described with the black hole’s total mass M, the spin parameter a, and electric/magnetic charge Q. For the first time the static spherically-symmetric electrically and magnetically charged black hole solution have been obtained by Reissner and Nordström independently and this case is called the Reissner–Nordström black hole (RN BH) solution [1, 2].

Due to the recent direct detection of gravitational waves from the close binary black holes [3,4,5] and neutron stars mergers by the LIGO-VIRGO Collaboration, observations of the SMBH M87 image by Event Horizon Telescope (EHT) consortium [6, 7], the gravitational redshift in strong gravity regime in observations of S2 star dynamics in SgrA* close environment by GRAVITY Collaboration [8, 9] and other relevant recent astrophysical observations of black holes and neutron stars motivate the great interest to probe the black hole and alternate gravity properties. For astrophysical stellar-mass black holes, the particle dynamics at the inner edge and X-ray spectra analysis of the accretion disks [10] provide important information on the black hole spin and the constraints on the parameters of alternate theories of gravity.

To study the spacetime structure around RN black hole one may consider the test particle motion [11,12,13,14,15,16,17,18,19,20,21,22]. The properties of the RN solution and impact of the electromagnetic field on spacetime structure around compact objects have been explored in Refs. [23,24,25,26].

The role of the external electromagnetic field surrounding black holes or proper magnetic field of neutron stars on the astronomical observation of compact objects through electromagnetic radiation or its influence on astrophysical processes around it plays a very important role. Since the external test electromagnetic field with the magnitude $<10^{19}\mathrm G$ does not change the spacetime structure, the role of the external electromagnetic field on the energetic processes and dynamics of charged and magnetized particles around the gravitational compact objects is essential. The no-hair theorem implies that no black hole can have its own intrinsic magnetic field [27] and this shows one way to explore the external magnetic field surrounding black holes. In particular, the studies of external electric and magnetic field structure around rotating and static black holes immersed in an external asymptotically uniform magnetic field have been performed in the pioneering work of Wald in Ref. [28]. In past years, different properties of the electromagnetic fields in the vicinity of black holes immersed in external asymptotically uniform magnetic fields and proper magnetic field of rotating magnetized neutron stars with the dipolar structure were widely studied by several authors in different models of gravity [29,30,31,32,33,34,35,36,37,38,39]. This electromagnetic field will change the dynamics of charged particle in a close black hole environment [40,41,42,43,44,45,46,47]. Together with charged particles one may study the influence of an electromagnetic field near the black hole on the magnetized particle’s motion. The dynamics of particles with the intrinsic non-zero dipolar magnetic field around non-rotating and rotating black holes immersed in an external magnetic field have been studied in [48, 49]. Our recent work was devoted to a study of the magnetized particle motion around an RN black hole in a magnetic field in different gravity models and theories [50,51,52,53,54,55,56,57,58,59,60,61]. The electromagnetic field properties and its influence on particle dynamics have been explored in Refs. [29,30,31, 62,63,64,65,66,67,68,69,70,71,72,73,74,75,76].

Numerous astronomical observations in the whole electromagnetic spectrum show the brightness of the galactic center where a supermassive black hole is situated; it being much more luminous than any other place of the galaxy. From the astrophysical point of view, in order to explain the enormous luminosity of active galactic nuclei including jet phenomena, the investigations of energy release processes from the vicinity of black holes through different possible mechanisms are always interesting. It is a topic of focus in relativistic astrophysics. The energy extraction mechanism in the so-called ergosphere region of rotating black holes has first been suggested by Penrose and is called the classical Penrose effect [77]. It was developed in Refs. [78, 79] in the presence of an external magnetic field; then we speak of a magnetic Penrose process (MPP). Astrophysical applications of such processes have been widely studied in Refs. [80,81,82]. More recently, Banados et al. [18] have shown that for an extremely rotating black hole head-on collisions can produce particles of extremely high center-of-mass energy (the so-called Banados–Silk–West, BSW process). Energy release and particle collisions in the vicinity of a rotating black hole in Hořava–Lifshitz gravity have been investigated in detail in our paper in Ref. [83]. Here we will explore the effects of magnetic and electric charge of the RN black hole in the center-of-mass energy of collisions of the magnetized particles.

The RN BH is the exact analytical solution of the nonlinear Einstein–Maxwell system. We consider in our study two types of the RN black holes: (i) electrically charged, (ii) magnetically charged ones. For a magnetically charged RN BH there is an intrinsic magnetic field created by the BH, which interacts with the magnetic dipole moment of the magnetized test particle. In the case of a nonlinear RN BH which is electrically charged, since it is static, there is no magnetic field created by the BH. Due to this, we assume that a test linear electromagnetic field is created by the current of charged particles in the accretion disk and interacts with the magnetic moment of magnetized test particles.

In this paper, we study the dynamics of the magnetized particle motion around the RN black hole. We explore the influence of the electromagnetic field of the charged black hole on the magnetized particle orbits and compare the results with the particle dynamics around the Kerr black hole. Furthermore, we study magnetized particles collisions around both magnetically and electrically charged RN black holes. The paper is organized as follows: In Sect. 2 we study the dynamics of the magnetized particles around the electrically RN black hole in the external magnetic field. In Sect. 3 magnetized particle motion in the vicinity of magnetically charged RN black hole is explored. We consider possible astrophysical applications of the obtained results in Sects. 4 and 5, studying collisions of the magnetized particles in the vicinity of electrically and magnetically charged RN black hole. Finally, we summarize our results in Sect. 6.

We use the space-time signature $(-,+,+,+)$ and the geometrized units system $G_\mathrm{N}= c = 1$. Latin indices run from 1 to 3 and Greek ones from 0 to 3.

2 Magnetized particle motion around electrically charged RN black hole in magnetic field

The spacetime exterior to electrically charged RN black hole with total mass M and electric charge Q can be described by the metric:

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{1}{f(r)}dr^2+r^2d\theta ^2+r^2\sin ^2\theta d\phi ^2 , \end{aligned}$$

(1)

where the radial metric function is

$$\begin{aligned} f(r)=1-\frac{2M}{r}+\frac{Q^2}{r^2} . \end{aligned}$$

(2)

Since there is no electromagnetic interaction between magnetized particles and electric charged RN black hole we assume that the black hole is immersed in an external asymptotically uniform magnetic field and finally, the electromagnetic four-potentials can be expressed using the Wald method [28] in the following form:

$$\begin{aligned} A_{\phi }= & {} \frac{1}{2}B_0r^2\sin ^2\theta ,\end{aligned}$$

(3)

$$\begin{aligned} A_t= & {} - \frac{Q}{r} , \end{aligned}$$

(4)

where $B_0$ is the asymptotic value of the external magnetic field. One may immediately find the non-zero components of the electromagnetic tensor using the definition $F_{\mu \nu }=A_{\nu ,\mu }-A_{\mu ,\nu }$ in the following form:

$$\begin{aligned} F_{r \phi }= & {} B_0r\sin ^2\theta , \end{aligned}$$

(5)

$$\begin{aligned} F_{\theta \phi }= & {} B_0r^2\sin \theta \cos \theta . \end{aligned}$$

(6)

The orthonormal components of the magnetic field around the electrically charged RN black hole measured by a proper observer are

$$\begin{aligned} B^{\alpha }= & {} \frac{1}{2} \eta ^{\alpha \beta \sigma \mu } F_{\beta \sigma } w_{\mu } , \end{aligned}$$

(7)

where $w_{\mu }$ is four-velocity of the proper observer, $\eta _{\alpha \beta \sigma \gamma }$ is the pseudo-tensorial form of the Levi-Civita symbol $\epsilon _{\alpha \beta \sigma \gamma }$ with the relations

$$\begin{aligned} \eta _{\alpha \beta \sigma \gamma }=\sqrt{-g}\epsilon _{\alpha \beta \sigma \gamma } , \quad \eta ^{\alpha \beta \sigma \gamma }=-\frac{1}{\sqrt{-g}}\epsilon ^{\alpha \beta \sigma \gamma } , \end{aligned}$$

(8)

and with $g=\mathrm{det|g_{\mu \nu }|}=-r^4\sin ^2\theta$ for the spacetime metric (1) we have

$$\begin{aligned} B^{\hat{r}}=B_0 \cos \theta , \quad B^{\hat{\theta }}=\sqrt{f(r)}B_0\sin \theta . \end{aligned}$$

(9)

According to Ref. [48] the equation of motion of magnetized particles in the spacetime of a black hole immersed in the external magnetic field can be described by the Hamilton–Jacobi equation:

$$\begin{aligned} g^{\mu \nu }\frac{\partial \mathcal{S}}{\partial x^{\mu }} \frac{\partial \mathcal{S}}{\partial x^{\nu }}=-m^2\Bigg (1-\frac{D^{\mu \nu }F_{\mu \nu }}{2m} \Bigg )^2 , \end{aligned}$$

(10)

where m is mass of the particle, $\mathcal{S}$ is the action for magnetized particles in the spacetime of the black hole, the scalar term came from the product of polarization and electromagnetic field tensors $D^{\mu \nu }F_{\mu \nu }$ being responsible for the interaction between the external magnetic field and dipole moment of magnetized particles. The polarization tensor $D^{\mu \nu }$ corresponding to the magnetic dipole moment of the magnetized particles is described by the relation [48]

$$\begin{aligned} D^{\alpha \beta }=\eta ^{\alpha \beta \sigma \nu }u_{\sigma }\mu _{\nu } , \quad D^{\alpha \beta }u_{\beta }=0 , \end{aligned}$$

(11)

where $\mu ^{\nu }$ and $u^{\nu }$ are the four-vector of magnetic dipole moment and four-velocity of the magnetized particles as observed by the proper observer. The electromagnetic field tensor can be decomposed through $F_{\alpha \beta }$ by the electric $E_{\alpha }$ and the magnetic $B^{\alpha }$ field components as

$$\begin{aligned} F_{\alpha \beta }=u_{[\alpha }E_{\beta ]}-\eta _{\alpha \beta \sigma \gamma }u^{\sigma }B^{\gamma }. \end{aligned}$$

(12)

One can find the product of polarization and electromagnetic tensors taking into account the condition given in Eq. (11) in the following form:

$$\begin{aligned} D^{\mu \nu }F_{\mu \nu }=2\mu ^{\hat{\alpha }}B_{\hat{\alpha }} =2\mu B_0 \sqrt{f(r)} , \end{aligned}$$

(13)

where $\mu =\sqrt{| \mu _{\hat{i}}\mu ^{\hat{i}}|}$ is the norm of the dipole magnetic moment of the magnetized particles. Here we have assumed that the direction of the magnetic dipole moment of the particles is perpendicular to the equatorial plane being parallel to the external magnetic field and the magnetic dipole moment $\mu ^{\alpha }=(0,\mu ^{\theta },0)$.

Here we investigate the dynamics of the magnetized particles in circular orbits around the electrically charged RN black hole. The action for magnetized particles in the equatorial plane (where $\theta =\pi /2$ and $\dot{\theta }=0$) can be described by

$$\begin{aligned} \mathcal{S}=-Et+L\phi +\mathcal{S}_r , \end{aligned}$$

(14)

which allows one to separate the variables in the Hamilton–Jacobi equation. The equation of radial motion of the magnetized particles can be found to be

$$\begin{aligned} \dot{r}^2=\mathcal{{E}}^2-V_\mathrm{eff}(r,Q,l,b) , \end{aligned}$$

(15)

where the effective potential of radial motion of the magnetized particles has the following form:

$$\begin{aligned} V_\mathrm{eff}=f(r)\left[ \left( 1-b\sqrt{f(r)}\right) ^2+\frac{l^2}{r^2}\right] \end{aligned}$$

(16)

where $l=L/m$ is specific angular momentum of the particle and $b = 2\mu B_0/m$ is the magnetic coupling parameter responsible for the interaction between dipole moment of the magnetized particle and the external magnetic field. In real astrophysical scenarios one may treat a neutron star with the magnetic dipole moment $\mu =(1/2)B_\mathrm{NS}R_\mathrm{NS}^3$ like a magnetized particle, orbiting a supermassive black hole (SMBH) immersed in an external magnetic field with different configurations. In such a case the magnetic coupling parameter b can easily be estimated through the observational parameters of the neutron star and we have an approximate value of the external magnetic field around the SMBH in the following form:

$$\begin{aligned} b =\frac{B_\mathrm{NS}R_\mathrm{NS}^3B_\mathrm{ext}}{m_\mathrm{NS}}\simeq & {} \frac{\pi }{10^3}\left( \frac{B_\mathrm{NS}}{10^{12}\mathrm G}\right) \left( \frac{B_\mathrm{ext}}{10\mathrm G}\right) \nonumber \\&\times \left( \frac{R_\mathrm{NS}}{10^6\mathrm cm}\right) ^3\left( \frac{m_\mathrm{NS}}{1.4 M_{\odot }}\right) ^{-1} . \end{aligned}$$

(17)

One may apply the calculation to estimating the value of the magnetic coupling parameter for a realistic case of the magnetar SGR (PSR) J1745-2900 orbiting around Sagittarius A* (Sgr A*). In the estimation of the coupling parameter we have considered a magnetic field around SgrA* that is of the order of 10 G, the magnetic dipole moment of the magnetar $\mu \approx 1.6 \times 10^{32} \mathrm G\cdot cm^3$ and its mass $m \approx 1.4 M_{\odot }$ ([84]);

$$\begin{aligned} b_\mathrm{PSR J1745-2900}\simeq 0.716 \left( \frac{B_\mathrm{ext}}{10\mathrm G}\right) . \end{aligned}$$

(18)

Fig. 1

The radial profiles of the effective potential for radial motion of magnetized particles with the specific angular momentum $\mathcal{L}/M=4$, around the electrically charged RN black hole for the different values of the electric charge of the black hole and the magnetic coupling parameter b

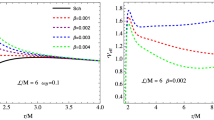
Figure 1 illustrates the radial dependence of the effective potential for radial motion of the magnetized particles around electrically charged RN black hole immersed in the external magnetic field for the fixed values of the specific angular momentum $\mathcal{L}/M=4$ and the different values of the black hole charge and the magnetic coupling parameters proving the comparison with the Schwarzschild case. One can see that the maximum value of the effective potential decreases with the increase of the magnetic coupling parameter, and it implies that magnetized particle can be at circular orbits with a lower energy in the existence of external magnetic field. However, the electric charge of the black hole causes an increase of the maximum value and the point where it is maximum comes close to the central black hole.

Generally, the circular motion of a particle around an axially symmetric black hole is described by the following standard condition:

$$\begin{aligned} \dot{r}=0 , \quad \frac{\partial V_\mathrm{eff}(r;Q,l,b)}{\partial r}=0 . \end{aligned}$$

(19)

One can find specific angular momentum of the particle for circular motion through the solution of Eq. (19) with respect to l in the following form:

$$\begin{aligned} l^2(r;Q,b)=\frac{ r^2\left[ 1-b \sqrt{f(r)}\right] \left[ 1-2 b \sqrt{f(r)}\right] }{ [r (r-3 M)+2 Q^2 ] (M r-Q^2 )^{-1}} , \end{aligned}$$

(20)

and the specific energy of the particle for circular orbits can be found by inserting Eq. (20) into the effective potential given by Eq. (16) in the following form:

$$\begin{aligned} \mathcal{E}^2(r;Q,b)= & {} f(r)\left( 1-b \sqrt{f(r)}\right) \Bigg \{1-b \sqrt{f(r)}\nonumber \\&+\frac{\left( 1-2 b\sqrt{f(r)}\right) \left( M r-Q^2\right) }{r (r-3 M)+2 Q^2}\Bigg \}. \end{aligned}$$

(21)

Fig. 2

The radial dependence of the specific energy (top panel) and angular momentum (bottom) corresponding to circular orbits for magnetized particles around the electrically charged RN black hole for the different values of the electric charge of the black hole and the magnetic coupling parameter b.

Radial profiles of specific energy and angular momentum corresponding to the circular motion of the magnetized particles around the electrically charged RN black hole immersed in the external magnetic field is demonstrated in Fig. 2 with a comparison of the Schwarzschild case. It is seen that the increase of the magnetic coupling parameter and the black hole charge causes decreasing of both energy and angular momentum. It does mean that a particle with a magnetic dipole moment can be in a circular orbit with less energy/angular momentum in the presence of the external magnetic field than in the absence due to the feature of magnetic interaction. The distance where the energy and angular momentum is minimum shifts towards the central black hole. The effects of the black hole charge are strong at the close environment of the black hole and at the circular orbits, the particle feels more magnetic interaction due to a decrease of the gravitational effect of the black hole charge. Moreover, the minimal radius of circular orbits also shifts towards the central object due to the increase of the RN black hole charge.

Now we will investigate when the orbits of the magnetized particles are circular, or more specifically the innermost stable circular ones. We use the following standard condition:

$$\begin{aligned} V_\mathrm{eff}''(r)=0 . \end{aligned}$$

(22)

Due to the complicated form of the relation between electric charge and ISCO radius of the magnetized particles, we will provide an analysis of the effects of the black hole charge and magnetic coupling parameter on the ISCO radius by plotting the condition given by Eq. (22).

Fig. 3

Dependence of the ISCO radius of a magnetized particle around magnetically charged RN black holes from the magnetic charge (top panel) and the parameter $\beta$ (bottom)

The effects of the electric charge of the RN black hole on the ISCO radius of magnetized particles for different values of the magnetic coupling parameter is shown in Fig. 3. One can see that the ISCO radius decreases under the effect of the black hole charge and positive (negative) values of the magnetic coupling parameter cause an increase (a decrease) of the ISCO radius.

3 Magnetized particles motion around the magnetically charged RN black hole

In this section, we perform the studies of the dynamics of magnetized particles around the magnetically charged RN black holes described by the lapse function

$$\begin{aligned} f(r)=1-\frac{2M}{r}+\frac{Q_{m}^2}{r^2} . \end{aligned}$$

(23)

The electromagnetic four-potential is

$$\begin{aligned} A_{\phi }= & {} Q_{m}\cos \theta . \end{aligned}$$

(24)

Using the potential given in Eq. (24) one may immediately obtain the non-zero component of the electromagnetic field tensor,

$$\begin{aligned} F_{\theta \phi }=-Q_m \sin \theta . \end{aligned}$$

(25)

The orthonormal radial component of the magnetic field generated by the magnetic charge of the RN black hole

$$\begin{aligned} B^{\hat{r}}=\frac{Q_m}{r^2} . \end{aligned}$$

(26)

Equation (26) implies that the radial component of the magnetic field around the magnetically charged black holes is not affected by the spacetime curvature and looks like the standard Newtonian expression.

In the analysis of the dynamics of the magnetized particle around the magnetically charged RN black hole, we assume the direction of the magnetic dipole moment of the magnetized particle to be parallel to the equatorial plane and to the magnetic field of the generic black hole. The components then are $\mu ^{i}=(\mu ^{r},0,0)$, the other configurations of magnetic dipole moment components cannot provide the magnetized particle with a stable equilibrium. In fact, in the equilibrium of the minimum energy of the magnetic interactions the direction of magnetic field lines and magnetic dipole moment of the magnetized particle have to be the same. Moreover, the second part of the condition (11) allows one to study the particle motion in the proper frame and the choice of the observer velocity may help to avoid a relative motion problem. The magnitude of the magnetic moment is constant and maintained during the motion. One may rewrite the interaction using Eqs. (13) and (5) in the following form:

$$\begin{aligned} \mathcal{D}^{\alpha \beta }F_{\alpha \beta } = \frac{2\mu Q_m}{r^2} . \end{aligned}$$

(27)

Since the axial symmetric configuration of the proper magnetic field of the RN black hole does not break the spacetime symmetries, there are still two conserved quantities, the energy $p_t = -E$ and the angular momentum $p_{\phi }= l$. The radial motion of a magnetized particle around the magnetically charged RN black hole in the equatorial plane, where $\theta =\pi /2$, with $p_{\theta }=0$, using Eqs. (13), (10) and the action given in Eq. (14), is described by the following form:

$$\begin{aligned} \dot{r}^2=\mathcal{{E}}^2-V_\mathrm{eff}(r;l,\mathcal{B}) . \end{aligned}$$

(28)

The effective potential has the form

$$\begin{aligned} V_\mathrm{eff}(r;l,\mathcal{B},Q_m)= & {} \left( 1-\frac{2M}{r}+\frac{Q_{m}^2}{r^2}\right) \nonumber \\&\times \left[ \left( 1-\frac{\mathcal{B}}{r^2}\right) ^2+\frac{l^2}{r^2}\right] , \end{aligned}$$

(29)

where the relation

$$\mathcal{B} =\frac{\mu }{m}Q_m$$

is a new introduced parameter which is responsible for the interaction between dipole moment of the magnetized particles and the proper magnetic field of magnetically charged RN black hole and $\beta =\mu /(m M)$ is a parameter which characterizes the parameters of the magnetized particle and the central black hole being always positive for the system when the magnetized neutron star is treated as a magnetized test particle orbiting around a SMBH,

$$\begin{aligned} \beta= & {} \frac{B_\mathrm{NS}R_\mathrm{NS}^3}{2m_\mathrm{NS}M_\mathrm{SMBH}}\nonumber \\\simeq & {} 0.18 \left( \frac{B_\mathrm{NS}}{10^{12}\mathrm G}\right) \left( \frac{R_\mathrm{NS}}{10^6 \mathrm cm}\right) \left( \frac{m_\mathrm{NS}}{M_{\odot }}\right) ^{-1}\left( \frac{M_\mathrm{SMBH}}{10^6M_{\odot }}\right) ^{-1}.\nonumber \\ \end{aligned}$$

(30)

For the system of the magnetar SGR (PSR) J1745-2900 with magnetic dipole moment $\mu \simeq 1.6\times 10^{32} \mathrm G\cdot cm^3$ and mass $m \approx 1.5 M_{\odot }$ orbiting around the supermassive black hole Sgr A* ($M \simeq 3.8 \times 10^6M_{\odot }$) [84], the value of the parameter $\beta$ can be easily estimated based on the observational data,

$$\begin{aligned} \beta =\frac{\mu _\mathrm{PSR\, J1745-2900}}{m_\mathrm{PSR\, J1745-2900} M_\mathrm{SgrA *}}\approx 10.2 . \end{aligned}$$

(31)

The circular stable orbits of the magnetized particle around the central object can be defined by the standard conditions,

$$\begin{aligned} V_\mathrm{eff}'=0 , \quad V_\mathrm{eff}'' \ge 0 . \end{aligned}$$

(32)

The specific angular momentum and energy of the magnetized particle along the circular orbits can be described by the following expressions:

$$\begin{aligned} l^2= & {} \frac{r^2-\beta M Q_m}{2 Q_m^2+r (r-3 M)}\nonumber \\&\times \left\{ \beta M Q_m \left( 2\!-\!\frac{5 M}{r}\!+\!\frac{3 Q_m^2}{r^2}\right) \!+\!M r\!-\!Q_m^2\right\} ,\qquad \end{aligned}$$

(33)

$$\begin{aligned} \mathcal{E}^2= & {} \frac{ [Q_m^2+r (r-2 M) ]^2 (r^4-\beta ^2 M^2 Q_m^2 )}{r^6 [2 Q_m^2+r (r-3 M)]} . \end{aligned}$$

(34)

Fig. 4

The radial dependence of the specific angular momentum (top panel) and energy (bottom) for circular orbits of magnetized particles around the magnetically charged RN black hole for different values of the magnetic charge of the black hole and the parameter $\beta$. The magnetic charge reads $Q_m \rightarrow Q_m/M$

Figure 4 demonstrates radial profiles of the specific angular momentum and energy of the magnetized particles for circular motion around the magnetically charged RN black hole with the comparison to the Schwarzschild spacetime in the top and bottom panels, respectively. One can see from the figure that the increase of both the magnetic charge of the RN black hole and the parameter $\beta$ causes decreasing in the minimum value of the specific angular momentum and energy for the circular motion of the magnetized particles.

One can easily obtain the equation for the ISCO taking into account the conditions (32) for the effective potential (29) in the following form:

$$\begin{aligned}&2 r^4 (9 M Q_m^2 r+M r^2 (r-6 M)-4 Q_m^4 ) \nonumber \\&\quad +2M^2Q_m^2\beta ^2 [Q_m^2 r (12 r-37 M)+12 Q_m^4\nonumber \\&\quad + r^2 (30 M^2-21 M r+4 r^2 ) ] \ge 0 . \end{aligned}$$

(35)

It is seen from Eq. (35) that when the magnetic charge of RN black hole vanishes, $Q_m=0$, it gives ISCO radii with $r_\mathrm{ISCO}=6M$. Since it is difficult to solve analytically Eq. (35) with respect to the radial coordinate we can only analyze the ISCO profiles, presenting them in plot form.

Fig. 5

Dependence of the ISCO radius of a magnetized particle around the magnetically charged RN black holes from the magnetic charge (top panel) and the parameter $\beta$ (bottom)

The dependence of the ISCO radius from the magnetic charge of the RN black hole is presented in Fig. 5 for different values of the parameter $\beta$. One can see from the figure that the increase of the magnetic charge ISCO radius of the magnetized particles decreases and the decreasing rate increases with the increase of the values of the parameter $\beta$. Moreover, there is an upper limit for the values of the magnetic charge of the black hole for each non-zero value of the parameter $\beta$ due to the increase of the interaction. It means that no stable orbits can exist when $\beta Q_m < (\beta Q_m)_\mathrm{upper}$.

4 Astrophysical applications

The importance of the detailed analysis of test particle dynamics around black holes in various theories of gravity is in deep understanding of the effects of the black hole parameters on the circular orbits of the particles. It may be helpful in the explanations of the physical properties of spacetime around a black hole in the observations of real astrophysical events/phenomena. In observations of star motion around astrophysical black holes, one may describe the black hole by its total mass, which one can measure in the Newtonian framework. Spin and (electric and magnetic) charge parameters of the black hole play the role of effects of the general relativistic framework. However, for now, measurements of the parameters in direct astrophysical observations are impossible. One way to obtain constraints to the values of black hole parameters is by using data from indirect observations such as the photon sphere and ISCO radius. On the other hand, it is impossible to see which gravity parameter effects are dominant for the motion of particles around a black hole when the two different gravity parameters effects are similar. In fact, as the spin of the rotating Kerr black hole and charge of the RN black hole similarly affect the ISCO radius of test particles and the photon sphere, an increase of both of them causes decreasing of it. The other most interesting and actual problem is how to distinguish the effects of spin and charge parameters based on the observational data as regards the ISCO radius, for example, at the accretion disks. Fortunately, one way to estimate the range of possible values for the parameters is to compare their effects on ISCO radius and photon sphere in detail. Moreover, even in the charged static black hole model, distinguishing the type of charge—magnetic or electric—is also one of the more crucial important issues in relativistic astrophysics. Since we are studying magnetized particle motion, in this section, we will focus on the scenarios when the parameter effect plays a dominant role in the studies of the magnetized particle motion.

In our comparison of the behavior of the ISCO radius of magnetized particles around a magnetically and electrically charged RN black hole with the ISCO radius of the particle rotating around a Kerr black holes we use the following well-known expression for ISCO radius of test particles (note that a magnetized particle feels like a test particle in the absence of magnetic fields) corresponding to retrograde and prograde orbits [85]:

$$\begin{aligned} r_\mathrm{isco}= 3 + Z_2 \pm \sqrt{(3- Z_1)(3+ Z_1 +2 Z_2 )} , \end{aligned}$$

(36)

where

$$\begin{aligned} Z_1= & {} 1+\left( \root 3 \of {1+a}+ \root 3 \of {1-a} \right) \root 3 \of {1-a^2} , \nonumber \\ Z_2^2= & {} 3 a^2 + Z_1^2 . \end{aligned}$$

At the next step, we show how to distinguish the effects of different parameters on the ISCO radius considering test particle dynamics around black holes. They are (i) the Kerr black hole case, (ii) the electrically and magnetically charged RN black hole case, and (iii) the case of a Schwarzschild black hole immersed in an external asymptotically uniform magnetic field. Then we compare the obtained results.

4.1 Magnetically charged RN black hole versus Kerr black hole

In this subsection, we will focus on the study of a magnetized particle motion around a magnetically charged RN. Then we compare it with the particle dynamics in Kerr black hole spacetime showing a degeneracy between the magnetic charge of the RN black hole and the spin of the rotating Kerr black hole, these providing the same values of the ISCO radius.

Fig. 6

Relation between degeneracy values of spin parameter of the rotating Kerr black hole and magnetic charge of RN black hole which provides the same values of the ISCO radius for the fixed values of the parameter $\beta =5,10,15$

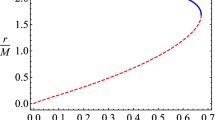
Figure 6 illustrates the relation between degeneracy values of the spin parameter of a rotating Kerr black hole and the magnetic charge of the RN black hole providing the same values of the ISCO radius to magnetized particles. One can see from the figure that the upper mimicker values of the magnetic charge of the RN black hole decrease with the increase of the parameter $\beta$ due to increasing interaction between the magnetically charged RN black hole and the magnetized particle’s dipole moment. When $a/M=Q_\mathrm{m}/M=0$ the magnetized particle feels the gravitation field of the Schwarzschild black hole without external magnetic field orbiting in the ISCO radius; then we have 6M. Moreover, numerical calculations show that magnetic charge of the RN black hole can mimic the spin of Kerr black hole up to $a/M \simeq 0.82$ in the range of its values $Q_m/M \in (0,\ 0.6475)$ for the magnetar SGR (PSR) J1745-2900 with the parameter $\beta =10.2$. It implies that the spin effects of SMBH Sgr A* ($a/M=0.44$) can reflect a magnetic charge of the SMBH RN Sgr A* with a magnetic charge $Q_m/M \simeq 0.5268$.

4.2 Magnetically charged RN black hole vs Schwarzschild black hole in external magnetic field

In this subsection, we will compare the effects of the external magnetic field around a Schwarzschild black hole and magnetic charge of the RN black hole by the motion of the magnetized particles. Here, we will focus on how the magnetic charge parameter can mimic the magnetic interaction of the external magnetic field around the Schwarzschild black hole for the same ISCO radius for magnetized particles. For the first time, the dynamics of the magnetized particles around a Schwarzschild black hole in the external magnetic field has been formulated and studied in detail by de Felice in [48]. Here we have extended this study to the different modified and alternate theories of gravity.

The important result has been shown that magnetized particle orbits cannot be stable at $b\ge 1$ [55, 57], which helps to estimate the upper value of the external magnetic field for a magnetized particle. Simple numerical calculations show that for the magnetar SGR (PSR) J1745-29 orbiting around Sgr A* $B_\mathrm{ext}\le 14 \mathrm G$. The value of magnetic field near the SMBH Sgr A* is around $100 \mathrm G$ and there the magnetic interaction parameter for the magnetar (SGR) PSR J1745-2900 is $b \simeq 7.16$. One may predict that the magnetar’s orbit in the SMBH Sgr A* environment cannot be stable and the stability analysis shows that the possible value for the surface magnetic field of the pulsar which may orbit around the Sgr A* environment is less than $10^{12}$ G.

Fig. 7

Relation between magnetic interaction parameter b and magnetic charge of the RN black hole $Q_m$ giving the same value of ISCO radius of the magnetized particles for the fixed values of the parameter $\beta =0, 15$

Figure 7 demonstrates the relation between magnetic interaction parameter and magnetic charge of the RN black hole. One can see that the magnetic interaction parameter with the value $b<1$ can mimic magnetic charge of the RN black hole in the range $Q_m/M \in (0.3289 \div 0.8273)$ when the parameter $\beta \in (0 \div 15)$. Using applications of the obtained results we have found that the mimic value of the magnetic charge of the supermassive RN black hole SgrA* when the magnetar (SGR) PSR J1745-2900 is treated as a magnetized particle is $Q_m/M=0.4465$.

4.3 Electrically charged RN black hole in the external magnetic field versus Kerr one

In this subsection, we will compare the effects of the spin of the rotating Kerr black hole and the electric charge of the RN black hole (immersed in the external magnetic field) on the ISCO radius of magnetized particles.

Fig. 8

Relation between degeneracy values of spin parameter of the rotating Kerr black hole and magnetic charge of RN black hole which provides the same values of the ISCO radius for the fixed values of the parameter $\beta =5,10,15$.

Figure 8 demonstrates relations between the spin of the Kerr black hole and the electric charge of the RN black hole, which provides the same value for ISCO radius of the magnetized particles with different values of the magnetic coupling parameter with a comparison of the test particle’s ISCO. One can see that in the absence of an external magnetic field the black hole charge can mimic the spin parameter up to $a/M \simeq 0.4759$. Moreover, the black hole charge can mimic the spin parameter for the particle with magnetic coupling parameter $b=0.2$ and $b=-\,0.2$ up to $a/M\simeq 0.3569$ and $a/M \in (0.0334,\ 0.5347)$, respectively.

4.4 Magnetically charged RN black hole vs electrically charged RN in external magnetic field

Finally, we will focus on possible ways to distinguish the effects of magnetic and electric charges of the RN black hole on the dynamics of the magnetized particles. In this subsection, we assume that the magnetized particle is the magnetar (SGR) PSR J1745-2900 orbiting around SgrA* with the parameters $\beta =10.2$ and $b=0.716$ where the external magnetic field is about 10 G.

Fig. 9

Relation between magnetic charge and electric charge of the RN black hole providing the same value of the ISCO radius of the magnetized particle for the fixed values of the parameter $\beta =10.2$ and $b=0.716$.

Fig. 10

The dependence of the center-of-mass energy of collision of two magnetized particles with the same value of initial energy $\mathcal{E}_1=\mathcal{E}_2=1$ and the parameter $\beta =10.2$ from the radial coordinate, around the magnetically charged RN black hole for different values of the magnetic charge parameter of the black hole. The top panel corresponds to the collision of two magnetized particles with the same direction of magnetic dipole moment, and the bottom one corresponds to collisions of the magnetized particles with the opposite direction of magnetic dipole moment

Figure 9 illustrates the relation between magnetic and electric charges of the RN black hole providing the same value for the ISCO radius of the magnetar (SGR) PSR J1745-2900. One can see from the figure that the relation is linear and represents the case that electric charge can mimic the black hole magnetic charge up to $Q_{m}/M=0.548232$. It implies that the effect of magnetic interaction between the magnetar and magnetically charged RN is almost twice stronger than the effect of the electric charge of the RN black hole on the spacetime around the black hole where the magnetar orbits are stable.

5 Magnetized particles acceleration near RN black holes

One of the actual issues in relativistic astrophysics is energy release processes from rotating black holes by different scenarios. The active galactic nuclei with luminosity $\sim 10^{45}\, \mathrm{erg}\cdot \mathrm{s}^{-1}$ are powered by central black holes. The first model for energy extraction from rotating Kerr black holes was suggested by Penrose [86] and developed by several authors during the last 50 years. The model implies that in a large ergosphere the acceleration processes become more efficient. When the ergoregion disappears the energy release from the rotation of the Kerr black hole does not occur. The process has been extended to a magnetic Penrose process (MPP) by Wagh et al. [78] and developed by Tursunov et al. [79].

For the first time acceleration of particles by the collision falling to Kerr black hole is studied in Ref. [18] in the case of the extreme rotating black hole where the center-of-mass energy of the colliding particles may diverge. The effects of the external magnetic field on acceleration processes of charged particles around black holes have been studied by the authors (see for example to Ref. [66]). It was shown that the efficiency of the energy extraction process is more effective in head-on collision cases. Here we will investigate the collisions in two different cases.

5.1 Magnetized particles acceleration near magnetically charged RN black holes

Here we will explore the acceleration of the magnetized particles near a magnetically charged RN black hole using the following standard expression for the center-of-mass energy of two colliding particles with the same mass:

$$\begin{aligned} \mathcal{E}_\mathrm{cm}^2=\frac{E^2_\mathrm{cm}}{4m^2 c^4}=1-g_{\alpha \beta }u_1^{\alpha }u_2^{\beta } , \end{aligned}$$

(37)

where $u_{1,2}^{\alpha }$ are the four-velocities of the colliding particles. Now we plan to investigate several scenarios of collisions of the magnetized particles in the equatorial plane (where $\theta =\pi /2$) with magnetized, electrically (magnetically) charged, and neutral particles in the frame of the proper observer.

5.1.1 Two magnetized particle collisions

The four-velocity of the magnetized particle in the equatorial plane ($\theta =\pi /2; \dot{\theta }=0$) has the following components:

$$\begin{aligned} \dot{t}= & {} \frac{\mathcal{E}}{f(r)} , \nonumber \\ \dot{r}^2= & {} \mathcal{E}^2-f(r)\left[ \left( 1-\beta \frac{MQ_m}{r^2}\right) ^2+\frac{l^2}{r^2}\right] \ , \nonumber \\ \dot{\phi }= & {} \frac{l}{r^2} . \end{aligned}$$

(38)

Consequently, the expression for the center-of-mass energy of the two magnetized particles given in Eq. (37) after inserting Eq. (38) takes the following form:

$$\begin{aligned} \mathcal{E}_\mathrm{cm}^2= & {} 1+\frac{\mathcal{E}_1\mathcal{E}_2}{f(r)}-\frac{l_1l_2}{r^2} \nonumber \\&-\frac{1}{f(r)} \sqrt{ \mathcal{E}_1^2-f(r)\left[ \left( 1-\beta _1 \frac{MQ_m}{r^2}\right) ^2+\frac{l^2_1}{r^2}\right] } \nonumber \\&\times \sqrt{ \mathcal{E}_2^2-f(r)\left[ \left( 1-\beta _2 \frac{MQ_m}{r^2}\right) ^2+\frac{l^2_2}{r^2}\right] } , \end{aligned}$$

(39)

where r stands for the radius of the collision point.

Fig. 11

Dependence of center-of-mass energy of collision of charged and magnetized particles with the same initial energy $\mathcal{E}_1=\mathcal{E}_2=1$, around the magnetically charged RN black hole for the different values of the magnetic charge $Q_m$ of the black hole. Top (bottom) panel corresponds to the cases of collisions between magnetized particles with the parameter $\beta =10.2$ and negatively (positively) charged particles

Figure 10 illustrates the radial dependence of the center-of-mass energy of two colliding particles with the same (opposite) direction of magnetic dipole moment (in the top (bottom) panel) around the magnetically charged RN black hole with the comparison of a Schwarzschild black hole. Here we consider head-on collisions of two magnetized particles with the specific angular momentum $l_1=2M$ and $l_2=-2M$ but with the same initial energies, $\mathcal{E}_1=\mathcal{E}_2=1$ using the parameter of the magnetar PSR J1745-2900 orbiting SgrA* to evaluate magnetized particles with the value of the parameter $\beta =10.2$. One can see from the top panel of the figure that the center-of-mass energy of the colliding magnetized particles with the same direction of magnetic dipoles increases with the increase of the magnetic charge parameter of the RN black hole. However, in the cases when the particles collide in the opposite direction to their magnetic dipoles, the center of mass energy decreases, with increasing magnetic charge of the black hole. Meanwhile the minimal distance where the magnetized particles can collide grows large as the magnetic charge growth due to the repulsive behavior of the magnetic interaction. Moreover, even in the Schwarzschild case, when the charge dipole’s direction goes to the opposite, the center-of-mass energy slightly decreases, and the particles cannot collide at a small distance to the event horizon due to dominant effects of the dipole interaction of the magnetized particles.

5.1.2 Magnetized and charged particles collisions

Now, we will study the center-of-mass energy of the collisions of the magnetized and (negatively and positively) charged particles. Generally, the four-velocity of a charged particle can be found using the following Lagrangian:

$$\begin{aligned} \mathcal{L}=\frac{1}{2}mg_{\mu \nu }u^{\mu } u^{\nu }+e u^{\mu }A_{\mu } , \end{aligned}$$

(40)

here e is the electric charge of the particle. The conserved quantities of energy and angular momentum have the form

$$\begin{aligned} E= & {} mg_{tt}\dot{t}, \end{aligned}$$

(41)

$$\begin{aligned} L= & {} mg_{\phi \phi }\dot{\phi }+eA_{\phi }, \end{aligned}$$

(42)

and one can immediately find the expressions for the four-velocity of the charged particle in the equatorial plane in the following form:

$$\begin{aligned} \dot{t}= & {} \frac{\mathcal{E}}{f(r)} , \nonumber \\ \dot{r}^2= & {} \mathcal{E}^2-f(r)\Bigg [1+\frac{l}{r^2}\left( l-\mathcal{Q} \right) \Bigg ] , \nonumber \\ \dot{\phi }= & {} \frac{l-\mathcal{Q}}{r^2} , \end{aligned}$$

(43)

where $\mathcal {Q}=(e/m)Q_m$ is a parameter corresponding to the interaction of the magnetic field generated by the magnetic charge of the magnetically charged RN black hole and the electrically charged particle.

We may now find the expression for the center-of-mass energy of collisions of magnetized and charged particles inserting Eqs. (43) and (38) into (37) in the following form:

$$\begin{aligned} \mathcal{E}_\mathrm{cm}^2= & {} 1+\frac{\mathcal{E}_1\mathcal{E}_2}{f(r)}-\frac{l_1-\mathcal{Q}}{r^2}l_2\nonumber \\&-\frac{1}{f(r)}\sqrt{\mathcal{E}_1^2-f(r)\Bigg [1+\frac{l_1}{r^2}\left( l_1-\mathcal{Q} \right) \Bigg ]} \nonumber \\&\times \sqrt{\mathcal{E}_2^2-f(r)\left[ \left( 1-\beta \frac{MQ_m}{r^2}\right) ^2+\frac{l^2_2}{r^2}\right] } . \end{aligned}$$

(44)

The radial dependence of center-of-mass energy of collisions of magnetized and electrically charged particles with different signs around the magnetically charged RN black hole for different values of the magnetic charge of the RN black hole is shown in Fig. 11. In this figure, the left panel corresponds to negatively charged particles and the right one to positively charged particles. Here, we have chosen for the value of the parameter $\beta$ for magnetized particles the parameter of the magnetar PSR J1745-2900 orbiting around SgrA* as $\beta =10.2$ and considered head-on collision with the specific angular momentum $l_1=-l_2=2M$ and the same initial energies $\mathcal{E}_1=\mathcal{E}_2=1$. One may see that the center-of-mass energy of collisions of negatively charged and magnetized particles is slightly bigger than the energy of the collisions of positively charged and magnetized particles. One may explain the result through the feature of electromagnetic interaction between the magnetically charged black hole and electrically charged particles being different.

5.1.3 Magnetized and neutral particles collisions

Finally, in the last subsection, we will study the center of mass energy of collisions of magnetized and neutral particles around a magnetically charged RN black hole. One may find the equations of motion for neutral particles around the black hole in the following form:

$$\begin{aligned} \dot{t}= & {} \frac{\mathcal{E}}{f(r)} , \nonumber \\ \dot{r}^2= & {} \mathcal{E}^2-f(r)\Bigg (1+\frac{l^2}{r^2}\Bigg ) , \nonumber \\ \dot{\phi }= & {} \frac{l}{r^2} . \end{aligned}$$

(45)

The expression for the center-of-mass energy of collisions of magnetized and neutral particles can be obtained by inserting Eqs. (38) and (45) into Eq. (37) in the following form:

$$\begin{aligned}&\mathcal{E}_\mathrm{cm}^2=1 + \frac{\mathcal{E}_1\mathcal{E}_2}{f(r)}-\frac{l_1l_2}{r^2} -\frac{1}{f(r)}\sqrt{\mathcal{E}_1^2-f(r)\left( 1+\frac{l_1^2}{r^2}\right) } \nonumber \\&\quad \times \sqrt{\mathcal{E}_2^2-f(r)\left[ \left( 1-\beta \frac{MQ_m}{r^2}\right) ^2+\frac{l_2^2}{r^2}\right] }\ . \end{aligned}$$

(46)

Fig. 12

Dependence of center-of-mass energy of collision of neutral and magnetized particles with the same initial energies $\mathcal{E}_1=\mathcal{E}_2=1$, around the magnetically charged RN black hole for the different values of the magnetic charge parameter for the fixed value of the parameter $\beta =10.2$ for the magnetized particle.

The radial dependence of the center-of-mass energy for the colliding magnetized and neutral particle’s system is given in Fig. 12. Here we have also considered the head-on collision of the particles with the angular momentum $l_1=-l_2=2M$ having for the same value of initial energy $\mathcal{E}_1=\mathcal{E}_2=1$. One may see from the figure that, similarly to the above-considered cases, we have center-of-mass energy growth with the increase of the value of the magnetic charge of magnetically charged RN black hole near the horizon due to amplification of the magnetic interaction between the black hole and magnetized particles. However, in all cases of the collisions in the Schwarzschild black hole case, the center-of-mass energy is bigger than in the RN black hole case as the collisions take place at higher distances from the horizon of the black hole.

5.2 Magnetized particles acceleration near electrically charged RN black hole

Now, we will study the collisions of the magnetized particles with (i) magnetized, (ii) electrically charged and (ii) neutral particles around an electrically charged RN black hole immersed in external asymptotically uniform magnetic fields in the proper frame of references considering the external magnetic field as a test field.

5.2.1 The collisions of two magnetized particles

One may find the four-velocity of the magnetized particle in the equatorial plane ($\dot{\theta }=0$) using the Hamilton–Jacobi equation given in Eq. (10) in the weak magnetic interaction limit when $(D_{\mu \nu }F^{\mu \nu } )^2=0$ in the following form:

$$\begin{aligned} \dot{t}= & {} \frac{\mathcal{E}}{f(r)} , \nonumber \\ \dot{r}^2= & {} \mathcal{E}^2-f(r)\left( 1+\frac{l^2}{r^2}-b \sqrt{f(r)} \right) , \nonumber \\ \dot{\phi }= & {} \frac{l}{r^2} . \end{aligned}$$

(47)

Consequently, we have the expression for the center-of-mass energy of collisions of two magnetized particles after substituting Eq. (47) in to Eq. (37) in the following form:

$$\begin{aligned} \mathcal{E}_\mathrm{cm}^2= & {} 1+\frac{\mathcal{E}_1\mathcal{E}_2}{f(r)}-\frac{l_1l_2}{r^2} \nonumber \\&-\frac{1}{f(r)}\sqrt{\mathcal{E}_1^2-f(r)\left[ 1+\frac{l_1^2}{r^2}-b_1\sqrt{f(r)} \right] } \nonumber \\&\times \sqrt{\mathcal{E}_2^2-f(r)\left[ 1+\frac{l_2^2}{r^2}-b_2\sqrt{f(r)}\right] } . \end{aligned}$$

(48)

Fig. 13

Dependence of center-of-mass energy of collisions of two magnetized particles with the same initial energy $\mathcal{E}_1=\mathcal{E}_2=1$ from the radial coordinate, around electrically charged RN black hole for the different values of the black hole charge for the fixed values of the magnetic coupling parameter of the colliding magnetized particles.

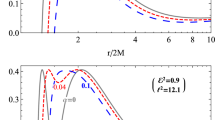
Figure 13 illustrates the dependence of the center-of-mass energy of collisions of two magnetized particles with the same (top and bottom panels) and opposite (the middle panel) direction of magnetic dipole moment around electrically charged RN black hole immersed in an external asymptotically uniform magnetic field from radial coordinates for the different values of the black hole charge and the fixed absolute value of the magnetic coupling parameter. One can see from the top and bottom panels that increase of the black hole charge causes increasing in the center-of-mass energy in the case of the collisions of the two magnetized particles with the same direction for their magnetic dipole moments. However, in the case when their dipole directions are opposite the energy does not change with increasing the electric charge of the central black hole. As we have a larger distance, the particles cannot collide due to the dominance of the repulsive feature of the magnetic interaction between the colliding magnetized particles; then the center-of-mass energy does not appear anymore.

5.2.2 Collision of two magnetized and charged particles

In this subsection, we will consider the collisions of magnetized and electrically charged particles with the electric charge e. The four-velocity of a charged particle is found using the following standard Lagrangian for charged particles in the electromagnetic field:

$$\begin{aligned} \mathcal{L}=\frac{1}{2}mg_{\mu \nu }u^{\mu } u^{\nu }+e u^{\mu }A_{\mu } . \end{aligned}$$

(49)

One can immediately find the expressions for the four-velocity of the electrically charged particles in the equatorial plane using the well-known Euler–Lagrange equation in the following form:

$$\begin{aligned} \dot{t}= & {} \frac{\mathcal{E}}{f(r)} ,\nonumber \\ \dot{r}^2= & {} \left( \mathcal{E}-\frac{e}{m}\frac{Q}{r}\right) ^2-f(r)\Bigg [1+\Bigg (\frac{l}{r}-\omega _\mathrm{B} r\Bigg )^2\Bigg ] ,\nonumber \\ \dot{\phi }= & {} \frac{l}{r^2}-\omega _\mathrm{B} , \end{aligned}$$

(50)

where $\omega _\mathrm{B}=eB/(2mc)$ is the interaction parameter between the external magnetic field and electrically charged particle that is so-called cyclotron frequency.

The expression for the center-of-mass energy of collisions of magnetized and charged particles after substituting Eqs. (50) and (47) into Eq. (37) takes the following form:

$$\begin{aligned} \mathcal{E}_\mathrm{cm}^2= & {} 1+\frac{\mathcal{E}_1\mathcal{E}_2}{f(r)}-\left( \frac{l_1}{r^2}-\omega _\mathrm{B}\right) l_2\nonumber \\&-\sqrt{\left( \mathcal{E}_1-\frac{e}{m}\frac{Q}{r}\right) ^2-f(r)\left[ 1+\Big (\frac{l_1}{r}-\omega _\mathrm{B} r\Big )^2\right] } \nonumber \\&\times \frac{1}{f(r)} \sqrt{\mathcal{E}_2^2-f(r)\left[ 1+\frac{l_2^2}{r^2}-b \sqrt{f(r)}\right] } . \end{aligned}$$

(51)

Fig. 14

Dependence of center-of-mass energy of collisions of positively (on the top panel) and negatively (on the bottom panel) charged particles and magnetized particles with the same value of initial energy $\mathcal{E}_1=\mathcal{E}_2=1$ and magnetic coupling parameters, around electrically charged RN black hole for the different values of the black hole charge

Figure 14 presents the dependence of the center-of-mass energy of collisions of electrically charged and magnetized particles around an electrically charged black hole from radial coordinates for the different values of the black hole charge in two cases: magnetized particles with the coupling parameter colliding with negatively (on the top panel) and positively (in the bottom panel) charged particles with the absolute value of magnetic interaction parameter $|\omega _\mathrm{B}|=0.1$. Here, we have chosen the value of the specific charge of the charged particles as the unit. One may see from the figure that the increase of the black hole charge causes an increase in the center-of-mass energy in both cases. However, from the top panel, in the case of head-on collisions of the magnetized particles with negatively charged particles, one may say that at the extreme value of the black hole charge the center-of-mass energy reaches its minimum at a lower value than in the Schwarzschild case. One may note that far from the black hole the center-of-mass energy vanishes due to the repulsive interaction of charged and magnetized particles.

5.2.3 Collision of magnetized and neutral particles

Finally, here we will study the collisions of magnetized and neutral particles. One may find the expression for the center-of-mass energy of collisions of neutral and magnetized particles after substituting Eqs. (47) and (45) into (37) in the following form:

$$\begin{aligned}&\mathcal{E}_\mathrm{cm}^2=1 + \frac{\mathcal{E}_1\mathcal{E}_2}{f(r)}-\frac{l_1l_2}{r^2} -\frac{1}{f(r)}\sqrt{\mathcal{E}_2^2-f(r)\left( 1+\frac{l_2^2}{r^2}\right) } \nonumber \\&\quad \times \sqrt{\mathcal{E}_1^2-f(r)\left( 1+\frac{l_1^2}{r^2}-b \sqrt{f(r)} \right) } . \end{aligned}$$

(52)

Fig. 15

Dependence of center-of-mass energy of collisions of the magnetized particles, with the parameter $b=0.1$, and a neutral particle having the same initial energy $\mathcal{E}_1=\mathcal{E}_2=1$, in the vicinity of the electrically charged RN black hole for the different values of the black hole charge.

Figure 15 shows the radial dependence of the center-of-mass energy of collisions of neutral particles and magnetized particles with the magnetic coupling parameter $b=0.1$ around a magnetically charged RN black hole for different values of the black hole charge. Here we have considered a head-on collision with the specific angular momentum $l_1=-l_2=2M$ and the same value for the initial energy of the particles. One may see from the figure that the center-of-mass energy increases with the increase of the electric charge of the black hole.

6 Conclusion

In the present paper, we have explored the dynamics of magnetized particles in the vicinity of both a magnetically and electrically charged RN black hole. The main purpose of the exploration is to formulate the basic principles for distinguishing the effects of magnetic and electric charge of the RN black hole from the ones of the spin of the rotating Kerr black hole together with the question of how to distinguish the effects of the magnetic charge from the electric one.

In the case of an electrically charged RN black hole due to the absence of interaction between the electric charge of the black hole and the dipole moment of the magnetized particles, we have assumed that the black hole is immersed in an external asymptotically uniform magnetic field. We have shown that the specific energy and angular momentum of the magnetized particles for circular orbits decreases in the presence of the black hole charge and an external magnetic field. Moreover, the ISCO radius of the magnetized particles decreases with the increase of the electric charge of the RN black hole, while a positive magnetic coupling parameter causes an increase of the ISCO radius.

Magnetized particle motion around the magnetically charged RN black hole has formulated. It is shown that the ISCO radius decreases with the increase of both the magnetic charge and the parameter $\beta$ up to the upper limit for their interaction, which has achieved in magnetic field interaction, due to dominant Lorentz forces which cause the magnetized particle to escape from the circular orbits.

We have concentrated on distinguishing the effects of electric and magnetic charges of the RN black hole and the spin of Kerr black holes on the dynamics of the magnetized particles. Here we have treated the magnetar SGR (PSR) J1745-2900 orbiting around the SMBH Sgr A* as a magnetized test particle with the magnetic interaction parameter $b=0.716$ and the parameter $\beta =10.2$. A comparison of the effect of the three parameters on the dynamics of the magnetar around the Sgr A* environment has shown that the magnetic charge of the RN black hole can mimic the spin parameter of the rotating Kerr black hole up to $a/M\simeq 0.82$. The external magnetic field can mimic the magnetic charge of the RN black hole up to $Q_m/M=0.4465$. Moreover, we have shown that the electric charge of the RN black hole can mimic the magnetic charge of the black hole up to $Q_m/M=0.5482$. The effect of the electric charge of the black hole on the magnetized particle dynamics comes from spacetime only, and the effect of the magnetic charge come from both spacetime and electromagnetic interaction. However, in the case of a neutral particle motion, the effects of magnetic and electric charges of the RN black hole are completely equivalent. One may conclude that the magnetic field interaction with the magnetic dipole moment of magnetized particle acts against the increase of the mimicked value of the black hole spin parameter and radio pulsars to be observed in a close environment of SgrA* can be used to get better constraints on the black hole and alternate gravity parameters.

Finally, we have also explored collisions of magnetized particles with magnetized, electrically charged, and neutral particles around magnetically and electrically charged RN black hole in the presence of the external asymptotically uniform magnetic field. We have shown that the center-of-mass energy of the collisions of magnetized particles increases with the increase of both electric and magnetic charges of the RN black hole. Moreover, it is found that when the magnetic dipole moments of the two colliding magnetized particles are oppositely directed, the center-of-mass energy decreases as we go far outwards from the central black hole, and at a critical distance the energy disappears. It implies that the collision of the magnetized particles does not occur over the critical distance due to the dominant effects of the magnetic repulsive interaction between the two oppositely directed magnetic dipoles.