Study of quasi-two-body $B_{(s)}\rightarrow \phi (f_0(980)/f_2(1270)\rightarrow )\pi \pi$ decays in perturbative QCD approach

Abstract

In 2017, LHCb collaboration reported their first observation of the rare decays $B_s \rightarrow \phi (f_0(980)$ $/f_2(1270) \rightarrow ) \pi ^+\pi ^-$ and the evidence of $B^0 \rightarrow \phi (f_0(980)/f_2(1270)\rightarrow )\pi ^+\pi ^-$. Motivated by this, we study these quasi-two-body decays in the perturbative QCD approach. The branching fractions, CP asymmetries and the polarization fractions are calculated. We find that within the appropriate two-meson wave functions, the calculated branching fractions are in agreement with the measurements of LHCb. Based on the narrow-width approximation, We also calculate the branching fractions of the quasi-two-body $B_{d,s}\rightarrow \phi (f_0(980)/f_2(1270)\rightarrow ) \pi ^0\pi ^0$ and $B_{d,s}\rightarrow \phi (f_2(1270)\rightarrow ) K^+K^-$, and hope the predictions to be tested in the ongoing LHCb and Belle II experiments. Moreover, the processes $B_{d,s}\rightarrow \phi f_2(1270)$ are also analyzed under the approximation. We note that the CP asymmetries of these decays are very small, because these decays are either penguin dominant or pure penguin processes.

1 Introduction

Similar to two-body decays, three-body non-leptonic B mesons decays could provide us opportunities to test the factorization hypothesis adopted in studying two-body hadronic decays, to test the standard model (SM) by measuring the Cabibbo–Kobayashi–Maskawa (CKM) matrix parameters such as the phases $\alpha$ and $\gamma$, and to understand the mechanism of the CP violation especially the sources of the strong phases. In the experimental side, lots of three-body B meson decays have been analyzed extensively by the BaBar [1,2,3,4,5,6,7,8,9], Belle [10,11,12,13,14,15,16], CLEO [17], and LHCb [18,19,20,21,22,23,24,25] collaborations. Such abundant experimental analyses promote the theoretical studies. Unlike the two-body B decays where the kinematics are fixed, in three-body decays the momentum of each final state is variable. In addition, both resonant and non-resonant contributions are involved, therefore how to distinguish the resonant and non-resonant contributions reliably is very important in studying the three-body decays. As an effective approach, Dalitz plot is particularly adopted to analyze the three-body decays, where the phase space can be divided into different regions with special kinematical configurations. The centre of the Dalitz plot indicates that all three final particles have a large energy ($E\sim m_B/3$) in the B meson rest frame and none of them flies collinearly to any others. The edges of the Dalitz plot correspond to the kinematical configuration where the two mesons fly collinearly, generating an invariant mass recoiling against the third bachelor meson. The three corners represent the kinematical configurations where one of the final mesons is soft or even rest, and the other two particles move back-to-back with large energy ($E \sim m_B/2$). In the naive factorization, the contribution at the centre of the Dalitz plot is viewed to be both power-suppressed and $\alpha _s$ suppressed with respect to that at the edge. However, recent studies based on QCD factorization showed that the power corrections are large, which means that the centre region maybe as important as the regions at the edge [26, 27]. In this work, we only focus on the physics at the edge of the Dalitz plot, where the two collinear mesons move almost in the same direction and can be viewed as a cluster, where two moving particles might form many resonances with different angular momenta. These decays are the so-called quasi-two-body decays beyond the narrow-width approximation [26].

In order to analyze the amplitude in experiments, many popular methods have been adopted, such as the isobar model [28, 29], the K-matrix formalism [30], and the quasi-model-independent analysis [25]. Among them, the isobar model is particularly adopted by BaBar, Belle and LHCb experiments. Within this model, the decay amplitude can be modeled as a coherent combination of all individual decay channels and can be expressed as

$$\begin{aligned} {\mathcal {A}}=\sum _{i=1}^{N}C_i{\mathcal {A}}_i, \end{aligned}$$

(1)

${\mathcal {A}}_i$ being the decay amplitude of each individual decay channel. The complex coefficients $C_i$ describes the relative magnitude and the phase of each decay channel. On the theoretical side, the three-body B decays have been studied extensively in various methods, such as the approaches based on the symmetry principles [31,32,33,34,35], QCD factorization (QCDF) approach [27, 36,37,38,39,40,41,42,43], perturbative QCD approach (PQCD) [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59], and other theoretical methods [60,61,62].

In 2017, LHCb Collaboration reported the measurement of the decay $B_s^0\rightarrow \phi \pi ^+\pi ^-$ and the evidence of $B^0\rightarrow \phi \pi ^+\pi ^-$ [22]. Based on the combined analysis of the $\pi ^+\pi ^-$ mass spectrum and the angles among the final states, the corresponding branching fractions of the quasi-two-body decays are given as¹

$$\begin{aligned}&{\mathcal {B}}(B_s^0\rightarrow \phi (f_0(980)\rightarrow )\pi ^+\pi ^-)\nonumber \\&\quad =(1.12\pm 0.16^{+0.09}_{-0.08}\pm 0.11)\times 10^{-6}, \end{aligned}$$

(2)

$$\begin{aligned}&{\mathcal {B}}(B_s^0\rightarrow \phi (f_2(1270)\rightarrow )\pi ^+\pi ^-)\nonumber \\&\quad =(0.61\pm 0.13^{+0.12}_{-0.05}\pm 0.06)\times 10^{-6}. \end{aligned}$$

(3)

Motivated by above results, we shall investigate above two quasi-two-body decays in the PQCD approach. As aforementioned, the $\pi \pi$ pair and the bachelor $\phi$ meson move fast and back-to-back in the B meson rest frame, which indicates that the interaction between the $\pi \pi$ pair and the bachelor $\phi$ meson is highly suppressed. On the other hand, the interactions between the two pions can be described by a two-meson wave function, where both resonant and nonresonant contributions are involved. It is obvious that these quasi-two-body decays are very similar to the two-body decays, by substituting one particle by a system involving two fast moving particles, the factorization formalism would be applicable.

In the PQCD approach, the physics with the scale above the W boson mass $m_W$ is weak interaction, which can be calculated perturbatively. Using the obtained Wilson coefficients at the scale $m_W$ and the renormalization group equation we can evaluate the Wilson coefficients including the physics from the $M_W$ to the $m_b$, the b quark mass. In the picture of PQCD, the physics between the scale $m_b$ and the factorization scale $\Lambda _h$ is dominated by the hard gluon exchange, and can be calculated perturbatively, which is the so-called hard kernel $\mathcal {H}$. The soft dynamics below the factorization scale is nonperturbative, which can be parameterized into the universal hadronic wave functions of the initial and final states. Thus, the decay amplitude of the quasi-two-body $B_{(s)}^0 \rightarrow \phi (f_0 /f_2\rightarrow ) \pi ^+\pi ^-$ decays can be written as the convolution

$$\begin{aligned}&{\mathcal {A}}=C(t)\otimes \mathcal {H}(x_i,b_i,t)\otimes \Phi _B(x_1,b_1)\otimes \Phi _{\phi }(x_2,b_2)\nonumber \\&\quad \otimes \Phi _{\pi \pi }(x_3,b_3)\otimes \exp ^{-S(t)}, \end{aligned}$$

(4)

where the $x_i$ are the momentum fraction of the quarks, $b_i$ are the conjugate variables of the quarks’ transverse momenta $k_{iT}$, and t is the largest scale appearing in the hard kernel $\mathcal {H}(x_i,b_i,t)$. $\Phi _B$ and $\Phi _{\phi }$ are the wave functions of the B meson and $\phi$ meson, and the $\Phi _{\pi \pi }$ is the $\pi \pi$ pair wave function. Recent developments on wave function of B meson are referred to Refs. [63, 64]. The Sudakov form factor $\exp ^{-S(t)}$ caused by the intrinsic transverse momenta of the quarks could suppress the soft dynamics effectively [65,66,67].

The paper is organized as follows: In Sect. 2, we introduce the wave functions used in the PQCD calculations, and the theoretical decay amplitudes are also presented in this section. The numerical results and the discussions are given in Sect. 3. Finally, we summarize this work in Sect. 4.

2 Decay formalism

In SM, the effective Hamiltonian $\mathcal {H}_{eff}$ for the quark-level transition $b\rightarrow s q{\bar{q}}$ governing the considered quasi-two-body decays is given as [68]

$$\begin{aligned}&\mathcal {H}_{eff}=\frac{G_F}{\sqrt{2}}\nonumber \\&\quad \times \left\{ V_{ub}V^*_{us}(C_1O_1+C_2O_2)-V_{tb}V^*_{ts}\sum _{i=3}^{10}C_i O_i\right\} , \end{aligned}$$

(5)

where $V_{IJ}$ are the CKM matrix elements and $G_F$ is the Fermi constant. The explicit expressions for the local four-quark operators $O_i$ ($i = 1,\ldots , 10$) and their corresponding Wilson coefficients $C_i$ can be found in Ref. [68].

In PQCD, the most important inputs are the wave functions of the initial and final states, including the B meson, the $\phi$ meson and the $\pi \pi$ pair. The wave functions of the B meson and the $\phi$ meson have been well determined by the two-body B decays [69,70,71,72,73,74,75,76,77,78,79,80,81], and the wave functions of $\pi \pi$ pair corresponding to the different spins have been also discussed in Refs. [49,50,51, 82,83,84,85,86,87]. In this work we will discuss the contributions of S-wave and T-wave $\pi \pi$ pair wave functions, which are related to the intermediate resonances $f_0$ and $f_2$, respectively. For the S-wave two-pion wave function, it is given as [86, 88]

$$\begin{aligned} \Phi _{\pi \pi }^S= & {} \frac{1}{\sqrt{2N_c}}\left[ P/\phi _S(z,\xi ,\omega )\nonumber \right. \\&\left. +\omega \phi _S^s(z,\xi ,\omega )+\omega (n/v/-1) \phi _S^t(z,\xi ,\omega )\right] , \end{aligned}$$

(6)

where z represents the momentum fraction of the light quark in the $\pi \pi$ pair, and $\xi$ is the momentum fraction of one pion in the $\pi \pi$ pair. The P is the momentum of the $\pi \pi$ pair, satisfying the condition $P^2=\omega ^2$ with the invariant mass of $\pi \pi$ pair. The n and v are the light-like vectors. The $\phi _S$ and $\phi _S^{s,t}$ are the twist-2 and twist-3 light-cone distribution amplitudes, which are given explicitly as [89, 90]

$$\begin{aligned} \phi _S(z,\xi ,\omega )= & {} \frac{F_S(\omega )}{\sqrt{6}}9 a_sz(1-z)(2z-1), \end{aligned}$$

(7)

$$\begin{aligned} \phi _S^s(z,\xi ,\omega )= & {} \frac{F_S(\omega )}{2\sqrt{6}}, \end{aligned}$$

(8)

$$\begin{aligned} \phi _S^t(z,\xi ,\omega )= & {} \frac{F_S(\omega )}{2\sqrt{6}}(1-2z), \end{aligned}$$

(9)

with $F_S(\omega )$ being the time-like form factor. For a narrow intermediate resonance, $F_S(\omega )$ is particularly described by the Breit–Wigner line-shape. However, for the resonance $f_0(980)$, because the abnormal enhancement from the KK system is found around $980~ \mathrm{MeV}$ in the $\pi \pi$ scattering, the Breit–Wigner line-shape of $f_0(980)$ is modified to be Flatt$\acute{e}$ model [91]. In our calculations, we here adopt the formulae updated by LHCb collaboration in Ref. [92],

$$\begin{aligned} F_S(\omega )=\frac{m_{f_0}^2}{m^2_{f_0}-\omega ^2-i m_{f_0}(g_{\pi \pi }\rho _{\pi \pi }+g_{KK}\rho _{KK}F^2_{KK})},\nonumber \\ \end{aligned}$$

(10)

where

$$\begin{aligned} \rho _{\pi \pi }=\sqrt{1-\frac{4m^2_{\pi }}{\omega ^2}},\quad \rho _{KK}=\sqrt{1-\frac{4m_K^2}{\omega ^2}}. \end{aligned}$$

(11)

In above functions, $g_{\pi \pi }$ and $g_{KK}$ are the coupling constants extracted from $f_0(980)\rightarrow \pi \pi$ and $f_0(980)\rightarrow KK$ decays, respectively, whose values are taken as $g_{\pi \pi }=(0.165\pm 0.018)~\mathrm{GeV}^2$ and $g_{KK}/g_{\pi \pi }=4.21\pm 0.33$ [93]. The factor $F_{KK}= e^{-\alpha q^2}$ with $\alpha =-2.0$ could suppress the contribution from KK scattering [94]. In this work we shall use the Gegenbauer moment $a_s=0.3\pm 0.2$, which is in agreement with that determined in Ref. [86].

Fig. 1

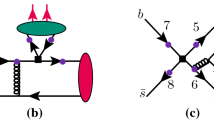
Typical Feynman diagrams for the quasi-two-body decay $B_{(s)}\rightarrow \phi \pi \pi$ in PQCD, where the black squares stand for the weak vertices, and large (purple) spots on the quark lines denote possible attachments of hard gluons. The green ellipse represent $\pi \pi$-pair and the red one is the light bachelor $\phi$ meson

Now, we turn to discuss the D-wave $\pi \pi$ pair wave function. Because of the conservation of angular momentum, the $\pm 2$ polarization components of tensor structure cannot contribute to the concerned decay amplitudes. So, the behavior of the tensor structure in B meson decays is very similar to the vector one. To describe the contribution of tensor structure conveniently, we therefore define a new polarization vector $\epsilon ^{\prime }$ associated with the polarization tensor $\epsilon _{\mu \nu }$ of tensor state. Within the same treatments used in Refs. [71, 73, 95,96,97,98,99,100], the new defined vector is proportional to the polarization vector of the vector meson with the coefficients $\sqrt{\frac{2}{3}}$ and $\sqrt{\frac{1}{2}}$ for the longitudinal and transverse polarizations, respectively. Thus, for the D-wave two-pion system, the longitudinal and transverse wave functions are expressed as [49]

$$\begin{aligned}&\Phi _D^L(\pi \pi )=\frac{1}{\sqrt{2N_c}}\left[ P/\phi _D(z,\xi ,\omega )\right. \nonumber \\&\qquad +\omega \phi _D^s(z,\xi ,\omega )+\frac{P/_1 P/_2-P/_2P/_1}{\nonumber }\\&\qquad \times \left. {\omega (2\xi -1)}\phi _D^t(z,\xi ,\omega )\right] , \end{aligned}$$

(12)

$$\begin{aligned}&\quad \Phi _D^T(\pi \pi )=\frac{1}{\sqrt{2N_c}}\left[ \gamma _5 \epsilon ^{\prime }_T/\; P/\phi _D^T(z,\xi ,\omega )\right. \nonumber \\&\qquad +\omega \gamma _5\epsilon ^{\prime }_T/\;\phi _D^a(z,\xi ,\omega )\nonumber \\&\qquad \left. +i\omega \frac{\epsilon ^{\mu \nu \rho \sigma }\gamma _{\mu }\epsilon ^{\prime }_{T\nu }P_{\rho }v_{\sigma }}{P\cdot v}\phi _D^v(z,\xi ,\omega )\right] , \end{aligned}$$

(13)

where $\phi _D(z,\zeta ,\omega )$ and $\phi _D^{T}(z,\zeta ,\omega )$ are the twist-2 light-cone distribution amplitudes associating to the longitudinal and transverse polarization components respectively, and the rest $\phi _D^{s,t}(z,\zeta ,\omega )$ and $\phi _D^{a,v}(z,\zeta ,\omega )$ are the twist-3 light-cone distribution amplitudes. The explicit expressions of the twist-2 distribution amplitudes are the same as those of KK pair [57, 101]

$$\begin{aligned} \phi _D(z,\xi ,\omega )= & {} \sqrt{\frac{2}{3}} \frac{9F_D^{\parallel }(\omega )}{\sqrt{2N_c}}a_D z(1-z)(2z-1)\zeta (\xi ), \end{aligned}$$

(14)

$$\begin{aligned} \phi _D^T(z,\xi ,\omega )= & {} \sqrt{\frac{1}{2}} \frac{9F_D^{\perp }(\omega )}{\sqrt{2N_c}}a_D^Tz(1-z)(2z-1)\tau (\xi ), \end{aligned}$$

(15)

with the factors $\zeta (\xi )$ and $\tau (\xi )$ describing the phase space of two-pion pair

$$\begin{aligned} \zeta (\xi )=1-6\xi +6\xi ^2,\quad \tau (\xi )=(2\xi -1)\sqrt{\xi (1-\xi )}. \end{aligned}$$

(16)

$F_D^{\parallel ,\perp }$ are the D-wave two-pion time-like form factors, which can be well modeled by the Breit–Wigner line shape [102]:

$$\begin{aligned} F_D^{\parallel }(\omega )=\frac{m_R^2}{m_R^2-\omega ^2-im_R\Gamma (\omega )}, \end{aligned}$$

(17)

with the nominal mass $m_R$ being the mass of the parent resonance. The dependence of the decay width of the resonance on invariant mass $\omega$ is given by

$$\begin{aligned} \Gamma (\omega )=\Gamma _0\left( \frac{|q|}{|q_0|}\right) ^5\frac{m_R}{\omega }X^2(\kappa ), \end{aligned}$$

(18)

with the nominal decay width of resonance $\Gamma _0$. Moreover, $|q_0|$ is the value of daughter $\pi$’s momentum |q| when $\omega =m_R$. The factor $X(\kappa )$ is the Blatt–Weisskopf angular momentum barrier factor [103], whose expression can be given as

$$\begin{aligned} X(\kappa )=\sqrt{\frac{9+3\kappa _0^2+\kappa _0^4}{9+3\kappa ^2+\kappa ^4}},\quad \kappa =r|q|. \end{aligned}$$

(19)

The effective radius r of the intermediate resonance cannot affect the numerical results remarkably, and it is chosen to be $r=4.0\,\mathrm{GeV}^{-1}$, following the experimental analysis [9]. $\kappa _0$ is the value of the $\kappa$ when $\omega =m_R$. As for the transverse time-like form factor $F_D^{\perp }$, it can be determined by the approximate relation [45]

$$\begin{aligned} \frac{F_D^{\perp }}{F_D^{\parallel }}\simeq \frac{f_R^{T}}{f_R}, \end{aligned}$$

(20)

with $f_R^{(T)}$ being the (transverse) decay constant of the tensor resonance. For the rest twist-3 light-cone distribution amplitudes, the expressions are given by

$$\begin{aligned} \phi _D^s(z,\xi ,\omega )= & {} \sqrt{\frac{2}{3}} \frac{-9F_D^{\perp }(\omega )}{4\sqrt{2N_c}}a_D(1-6z+6z^2)\zeta (\xi ),\nonumber \\ \phi _D^t(z,\xi ,\omega )= & {} \sqrt{\frac{2}{3}} \frac{9F_D^{\perp }(\omega )}{4\sqrt{2N_c}}(2z-1)(1-6z+6z^2)\zeta (\xi ),\nonumber \\ \phi _D^a(z,\xi ,\omega )= & {} \sqrt{\frac{1}{2}} \frac{3F_D^{\parallel }}{2\sqrt{2N_c}}a_D^T(2z-1)^3\tau (\xi ),\nonumber \\ \phi _D^v(z,\xi ,\omega )= & {} \sqrt{\frac{1}{2}} \frac{-3F_D^{\parallel }}{2\sqrt{2N_c}}a_D^T(1-6z+6z^2)\tau (\xi ). \end{aligned}$$

(21)

In Ref. [49], the authors discussed the processes $B_{(s)}\rightarrow P(f_2\rightarrow ) \pi \pi$ decays in detail, and obtained the longitudinal Gegenbauer moment $a_D=0.4\pm 0.1$. In addition, $a_D^T=0.8\pm 0.2$ had also been fixed from experimental results of $B\rightarrow K\pi \pi$ decays [10].

Based on the effective Hamiltonian and the wave functions, we can perform the theoretical calculation in PQCD approach. In the leading order, the diagrams contributing to the decay amplitude are plotted in Fig. 1. The first two diagrams are the emission type diagrams, where diagram (a) is the $\pi \pi$ emission and the $\phi$ meson is emitted in diagram (b). The last two diagrams are the annihilation diagrams, where the produced antiquark flows into the $\phi$ meson in diagram (c) and flows into $\pi \pi$-pair in diagram (d).

We take $B_{s,d}\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-$ decays as examples for illustration. At first, we discuss the contributions of the emission diagrams, as shown in Fig. 1a, b. If the hard gluons are from the spots “1” and “2”, the $\pi \pi$ pair or $\phi$ can be factorized out, and we call them factorizable diagrams. When inserting the $(V-A)(V-A)$ and $(V-A)(V+A)$ current, due to the charge conjugation invariance, the S-wave two-pion pair cannot be emitted, namely

$$\begin{aligned} F_{\pi \pi }^{LL}=F_{\pi \pi }^{LR}=0 , \end{aligned}$$

(22)

where the subscript $\pi \pi$ means two-pion pair is emitted, and the superscripts LL and LR indicate the inserted $(V-A)(V-A)$ and $(V-A)(V+A)$ currents, respectively. When the $\phi$ meson is emitted, the amplitude is given by

$$\begin{aligned} F_{\phi }^{LL,LR}= & {} 8\pi C_F f_V m_B^4 \int _{0}^{1}dx_1dz\nonumber \\&\times \int _0^{\infty }b_1db_1b_zdb_z \phi _B(x_1,b_1)\nonumber \\&\frac{1}{\sqrt{1-\eta ^2}}\Big \{\Big [(\eta ^2-1)(z+1)\phi _S(z,\xi ,\omega )\nonumber \\&+\eta (2z-1)(\phi _S^s(z,\xi ,\omega ) +\phi _S^t(z,\xi ,\omega ))\Big ]\nonumber \\&\left. \times E_{ef}(t_a)h_{ef}(x_1,z(1-r_V^2),b_1,b_z)\right. \nonumber \\&+\eta \Big [\phi _S(z,\xi ,\omega )-2\phi _S^s(z,\xi ,\omega )\Big ]\nonumber \\&\times E_{ef}(t_b)h_{ef}(z,x_1(1-r_V^2),b_z,b_1)\Big \}. \end{aligned}$$

(23)

with $r_V=m_{\phi }/m_B$ and $\eta =\omega /m_B$. In the above formula, $C_F=\frac{4}{3}$ is the color factor and $f_V$ is the decay constant of the $\phi$ meson. The functions $E_{ef}$, $h_{ef}$ and the typical scales $t_{a,b}$ are referred to Ref. [104]. If we insert the $(S-P)(S+P)$ current arising from the Fierz transformation of the $(V-A)(V+A)$ one, the contribution from diagram with two-pion pair emission is given by

$$\begin{aligned} F_{\pi \pi }^{SP}= & {} -16\pi C_F F_S \eta m_B^4\int _0^1dx_1dx_3\nonumber \\&\times \int _0^{\infty }b_1db_1b_3db_3\phi _B(x_1,b_1)\Big \{\Big [\phi _V^s(x_3)r_V(x_3+2)\nonumber \\&\left. +\sqrt{1-\eta ^2}(\phi _V(x_3)\nonumber \right. \\&\left. -\phi _V^t(x_3)r_Vx_3)\Big ]E_{ef}(t_a)h_{ef}(x_1,x_3(1-\eta ^2),b_1,b_3)\right. \nonumber \\&\left. +2r_V\eta \phi _V^s(x_3)E_{ef}^{t_b}h_{ef}(x_3,x_1(1-\eta ^2),b_3,b_1)\right\} ,\nonumber \\ \end{aligned}$$

(24)

with the S-wave time-like form factor $F_S$ of the $\pi \pi$ pair. For the diagrams with the emitted vector $\phi$ meson, the decay amplitude vanishes due to the fact that the vector meson can not be produced through the $(S\pm P)$ currents [105], i.e.

$$\begin{aligned} F_{\phi }^{SP}=0. \end{aligned}$$

(25)

If the hard gluons come from spots “3” and “4”, all three wave functions are involved, and we call them the nonfactorizable emission diagrams. Their amplitudes with different currents can be written as

$$\begin{aligned} M_{\pi \pi }^{LL}= & {} 16\sqrt{\frac{2}{3}}\pi C_F m_B^4\int _0^1dx_1dx_3dz\nonumber \\&\times \int _0^{\infty }b_1db_1b_3db_3b_zdb_z\phi _B(x_1,b_1)\phi _S(z,\xi ,\omega )\nonumber \\&\times \Big \{\Big [\sqrt{1-\eta ^2}(\phi _V(x_3)(\eta ^2+1)(z-1)\nonumber \\&-\phi _V^t(x_3)r_Vx_3)+\phi _V^s(x_3)r_Vx_3\Big ] E_{enf}(t_c)h_{enf}(\alpha ,\beta _1,b_1,b_z)\nonumber \\&+\Big [\sqrt{1-\eta ^2}((z+x_3)\phi _V(x_3) -r_Vx_3\phi _V^t(x_3))-r_Vx_3\phi _V^s(x_3)\Big ]\nonumber \\&\times E_{enf}(t_d)h_{enf}(\alpha ,\beta _2,b_1,b_z)\Big \}, \end{aligned}$$

(26)

$$\begin{aligned} M_{\phi }^{LL}= & {} -16\sqrt{\frac{2}{3}}\pi C_F m_B^4 \int _0^1dx_1dzdx_3\nonumber \\&\times \int _0^{\infty }b_1db_1b_3db_3\phi _B(x_1,b_1)\phi _V(x_3)\sqrt{1-\eta ^2}\nonumber \\&\times \Big \{\Big [\phi (z,\xi ,\omega )(1-x_3) +z\eta (\phi _S^t(z,\xi ,\omega )-\phi _S^s(z,\xi ,\omega ))\Big ]\nonumber \\&\times E_{enf}(t_c)h_{enf}(\alpha ,\beta _1,b_1,b_3) \nonumber \\&+\Big [z\eta (\phi _S^s(z,\xi ,\omega )\nonumber \\&+\phi _S^t(z,\xi ,\omega ))-\phi _S(z,\xi ,\omega )(z+x_3)\Big ]\nonumber \\&\times E_{enf}(t_d)h_{enf}(\alpha ,\beta _2,b_1,b_3)\Big \}, \end{aligned}$$

(27)

$$\begin{aligned} M_{\pi \pi }^{LR}= & {} 16\sqrt{\frac{2}{3}}\pi C_F \eta m_B^4\nonumber \\&\times \int _0^1dx_1dzdx_3\int _0^{\infty }b_1db_1b_zdb_z\phi _B(x_1,b_1)\nonumber \\&\times \left\{ \left[ \phi _S^s(z,\xi ,\omega )(\sqrt{1-\eta ^2}(\phi _V(x_3)(1-z)\right. \right. \nonumber \\&+\phi _V^t(x_3)r_V(x_3+z-1)) +\phi _V^s(x_3)r_V(x_3-z+1))\nonumber \\&-\phi _S^t(z,\xi ,\omega )(\sqrt{1-\eta ^2}(\phi _V(x_3)(z-1)\nonumber \\&\left. \left. +\phi _V^t(x_3)r_V(x_3-z+1))\right] \right. +\phi _V^s(x_3)r_v(x_3+z-1))\nonumber \\&\left. \times E_{enf}(t_c)h_{enf}(\alpha ,\beta _1,b_1,b_z)\right. \nonumber \\&\left. -\left[ \phi _S^s(z,\xi ,\omega )(\sqrt{1-\eta ^2}(\phi _V(x_3)z \right. \right. \nonumber \\&\left. \left. +r_V\phi _V^t(x_3)(x_3-z))+r_V\phi _V^s(x_3)(x_3+z))\right. \right. \nonumber \\&\left. \left. +\phi _S^t(z,\xi ,\omega )(\sqrt{1-\eta ^2}(r_V\phi _V^t(x_3)(x_3+z)-z\phi _V(x_3))\right. \right. \nonumber \\&\left. \left. +r_V\phi _V^s(x_3)(x_3-z))\right] \right. E_{enf}(t_d)h_{enf}(\alpha ,\beta _2,b_1,b_z)\Big \}, \end{aligned}$$

(28)

$$\begin{aligned} M_{\phi }^{LR}= & {} 16\sqrt{\frac{2}{3}}\pi C_F r_V M_B^4\nonumber \\&\times \int _0^1dx_1dx_3dz\int _0^{\infty }b_1db1b_3db3\phi _B(x_1,b_1)\nonumber \\&\times \left\{ \left[ \phi _S(z,\xi ,\omega )(\phi _V^s(x_3)+\phi _V^t(x_3)\sqrt{1-\eta ^2})(1-x_3)\right. \right. \nonumber \\&\left. \left. +\eta \left( \phi _S^s(z,\xi ,\omega )(\phi _V^s(x_3)(z-x_3+1)\right. \right. \right. \nonumber \\&\left. \left. \left. -\phi _V^t(x_3)\sqrt{1-\eta ^2}(z+x_3-1))\right. \right. \right. \nonumber \\&\left. \left. \left. +\phi _S^t(z,\xi ,\omega )(\phi _V^s(x_3)(z+x_3-1)\right. \right. \right. \nonumber \\&\left. \left. \left. +\phi _V^t(x_3)\sqrt{1-\eta ^2}(x_3-z-1))\right) \right] \right. \nonumber \\&\left. \times E_{enf}(t_c)h_{enf}(\alpha ,\beta _1,b_1,b_3)\right. \nonumber \\&\left. -\left[ \phi _S(z,\xi ,\omega )(\phi _V^s(x_3)x_3-x_3\sqrt{1-\eta ^2}\phi _V^t(x_3))\right. \right. \nonumber \\&\left. \left. +\eta \left( \phi _S^s(z,\xi ,\omega )(\phi _V^s(x_3)(z+x_3)\right. \right. \right. \nonumber \\&\left. \left. \left. +\phi _V^t(x_3)\sqrt{1-\eta ^2}(z-x_3))\right. \right. \right. \left. \left. \left. +\phi _S^t(z,\xi ,\omega )(\phi _V^s(x_3)(z-x_3)\right. \right. \right. \nonumber \\&\left. \left. \left. +\phi _V^t(x_3)\sqrt{1-\eta ^2}(z+x_3))\right) \right] \right. \nonumber \\&\times E_{enf}(t_d)h_{enf}(\alpha ,\beta _2,b_1,b_3)\Big \}, \end{aligned}$$

(29)

$$\begin{aligned} M_{\pi \pi }^{SP}= & {} 16\sqrt{\frac{2}{3}}\pi C_F m_B^4\int _0^1dx_1dzdx_3\nonumber \\&\times \int _0^{\infty }b_1db_1b_zdb_z\phi _B(x_1,b_1)\phi _S(z\xi ,\omega ) \nonumber \\&\times \Big \{\Big [r_Vx_3\phi _V^s(x_3)+\sqrt{1-\eta ^2}(r_Vx_3\phi _V^t(x_3)\nonumber \\&-\phi _V(x_3)((1-\eta ^2)x_3+1-z+\eta ^2)\Big ]\nonumber \\&\left. \times E_{enf}(t_c)h_{enf}(\alpha ,\beta _1,b_1,b_z)\right. \nonumber \\&\left. -\left[ r_Vx_3\phi _V^s(x_3)-\sqrt{1-\eta ^2}(r_Vx_3\phi _V^t(x_3)+\phi _V(x_3)(1-\eta ^2)z)\right] \right. \nonumber \\&\times E_{enf}(t_d)h_{enf}(\alpha ,\beta _2,b_1,b_z)\Big \}, \end{aligned}$$

(30)

$$\begin{aligned} M_{\phi }^{SP}= & {} 16\sqrt{\frac{2}{3}}\pi C_F m_B^4\sqrt{1-\eta ^2}\nonumber \\&\times \int _0^1dx_1dx_3dz\int _0^{\infty }b_1db_1b_3db_3\phi _B(x_1b_1)\phi _V(x_3)\nonumber \\&\times \Big \{\Big [\phi _S(z,\xi ,\omega )(z-(1-\eta ^2)(x_3-1))\nonumber \\&-z\eta (\phi _S^s(z,\xi ,\omega )+\phi _S^t(z,\xi ,\omega ))\Big ] \times E_{enf}(t_c)h_{enf}(\alpha ,\beta _1,b_1,b_3)\nonumber \\&-\Big [\phi _S(z,\xi ,\omega )(x_3+\eta ^2(z-x_3)) +z\eta (\phi _S^s(z,\xi ,\omega )+\phi _S^t(z,\xi ,\omega ))\Big ]\nonumber \\&\times E_{enf}(t_d)h_{enf}(\alpha ,\beta _2,b_1,b_3)\Big \}. \end{aligned}$$

(31)

All functions $E_{enf}$, $h_{enf}$, $\alpha$ and $\beta _{1,2}$ can also be found in Ref. [104].

Now, let us calculate the contributions of the annihilation diagrams. Although there still exist some controversies, the annihilation diagrams can be calculated in PQCD without endpoint singularity by keeping the intrinsic transverse momentum of each quark. Similarly, the annihilation diagrams can also be divided into two kinds, factorizable and nonfactorizable. If the gluons come from the spots “5” and “6”, the wave function of B meson can be factorized out, and the corresponding diagrams are called factorizable annihilation diagrams. If the gluons are emitted from the spots “7” and “8”, their contributions are nonfactorizable. For the factorizable annihilation diagrams, the amplitudes associated with the $(V-A)(V-A)$,$(V-A)(V+A)$ and $(S-P)(S+P)$ currents are

$$\begin{aligned} A_{\pi \pi }^{LL}= & {} 8\pi C_Ff_Bm_B^4\int _0^1dzdx_3\nonumber \\&\times \int _0^{\infty }b_zdb_zb_3db_3\Big \{\Big [\phi _S(z,\xi ,\omega )\phi _V(x_3)\sqrt{1-\eta ^2}\nonumber \\&\times (1+x_3(\eta ^2-1)) +2\phi _S^s(z,\xi ,\omega )r_V\eta (\phi _V^s(x_3)(x_2-2)\nonumber \\&-\phi _V^t(x_3)x_3\sqrt{1-\eta ^2})\Big ]\ E_{af}(t_e)h_{af}(\alpha _1,\beta ,b_z,b_3)\nonumber \\&-\Big [\phi _S(z,\xi ,\omega )z\sqrt{1-\eta ^2}-2\phi _V^s(x_3)r_V\eta \nonumber \\&\times (\phi _S^s(z,\xi ,\omega )(z+1) +\phi _S^t(z,\xi ,\omega )(z-1))\Big ]\nonumber \\&\times E_{af}(t_f)h_{af}(\alpha _2,\beta ,b_3,b_z)\Big \}, \end{aligned}$$

(32)

$$\begin{aligned} A_{\phi }^{LL}= & {} 8\pi C_Ff_Bm_B^4\int _0^1dx_3dz\nonumber \\&\times \int _0^{\infty }b_3db_3b_zdb_z\Big \{\Big [\phi _S(z,\xi ,\omega )\phi _V(x_3)(1-z)\sqrt{1-\eta ^2}\Big ]\nonumber \\&+2r_V\eta \phi _V^s(x_3)(\phi _S^s(z,\xi ,\omega )(z-2)\nonumber \\&-\phi _S^t(z,\xi ,\omega )z)\Big ] E_{af}(t_e)h_{af}(\alpha _1,\beta ,b_3,b_z)\nonumber \\&-\Big [\phi _S(z,\xi ,\omega )\phi _V(x_3)x_3-2r_V\eta \phi _S^s(z,\xi ,\omega )\nonumber \\&\times (\phi _V^s(x_3)(1+x_3)+\phi _V^t(x_3)(x_3-1))\Big ]\nonumber \\&\times E_{af}(t_f)h_{af}(\alpha _2,\beta ,b_z,b_3)\Big \}, \end{aligned}$$

(33)

$$\begin{aligned} A_{\pi \pi }^{LR}= & {} A_{\pi \pi }^{LL}, \end{aligned}$$

(34)

$$\begin{aligned} A_{\phi }^{LR}= & {} A_{\phi }^{LL}, \end{aligned}$$

(35)

$$\begin{aligned} A_{\pi \pi }^{SP}= & {} 16\pi C_Ff_Bm_B^4\int _0^1dzdx_3 \int _0^{\infty }b_zdb_zb_3db_3\nonumber \\&\times \Big \{\Big [2\phi _S^s(z,\xi ,\omega )\phi _V(x_3)\eta -r_V\phi _S(z,\xi ,\omega )(\phi _V^s(x_3)\nonumber \\&+\phi _V^t(x_3))(1-x_3)\Big ] E_{af}(t_e)h_{af}(\alpha _1,\beta ,b_z,b_3) \nonumber \\&-\Big [2\phi _S(z,\xi ,\omega )\phi _V^s(x_3)r_V +\phi _V(x_3)\eta z(\phi _S^t(z,\xi ,\omega )\nonumber \\&-\phi _S^s(z,\xi ,\omega ))\Big ] E_{af}(t_f)h_{af}(\alpha _2,\beta ,b_3,b_z)\Big \},\nonumber \\ \end{aligned}$$

(36)

$$\begin{aligned} A_{\phi }^{SP}= & {} 16\pi C_Ff_Bm_B^4 \int _0^1dx_3dz\int _0^{\infty }b_3db_3b_zdb_z\nonumber \\&\times \Big \{\Big [2r_V\phi _S(z,\xi ,\omega )\phi _V^s(x_3) -(1-z)\eta \phi _V(x_3)(\phi _S^s(z,\xi ,\omega )\nonumber \\&+\phi _S^t(z,\xi ,\omega ))\Big ] \times E_{af}(t_e)h_{af}(\alpha _1,\beta ,b_3,b_z)\nonumber \\&-\Big [2\eta \phi _V(x_3)\phi _S^s(z,\xi ,\omega )\nonumber \\&-r_Vx_3\phi _S(z,\xi ,\omega )(\phi _V^s(x_3)+\phi _V^t(x_3))\Big ]\nonumber \\&\times E_{af}(t_f)h_{af}(\alpha _2,\beta ,b_z,b_3)\Big \}. \end{aligned}$$

(37)

Within the same way, we obtain the expressions of the amplitudes of the nonfactorizable annihilation diagrams as

$$\begin{aligned} W_{\pi \pi }^{LL}= & {} 16\sqrt{\frac{2}{3}} \pi C_Fm_B^4\int _0^1dx_1dzdx_3\nonumber \\&\times \int _0^{\infty }b_1db_1b_zdb_z\phi _B(x_1,b_1)\nonumber \\&\times \Big \{\Big [z\phi _S(z,\xi ,\omega )\phi _V(x_3)\sqrt{1-\eta ^2}\nonumber \\&+r_V\eta \Big (\phi _S^s(z,\xi ,\omega )(\phi _V^s(x_3)(x_3-z-3) +\phi _V^t(x_3)(x_3+z-1)) \nonumber \\&-\phi _S^t(z,\xi ,\omega )(\phi _V^s(x_3)(x_3+z-1) +\phi _V^t(x_3)(x_3-z+1))\Big )\nonumber \\&\times E_{anf}(t_g)h_{anf}(\alpha ,\beta _1,b_1,b_z) -\Big [\phi _S(z,\xi ,\omega )\phi _V(x_3)(1-x_3)\nonumber \\&+r_V\eta \Big (\phi _S^s(x_3)(\phi _V^s(x_3)(x_3-z-1) -\phi _V^t(x_3)(x_3+z-1))\nonumber \\&+\phi _S^t(z,\xi ,\omega )(\phi _V^s(x_3)(x_3+z-1)\nonumber \\&+\phi _V^t(x_3)(1-x_3+z))\Big )\Big ]E_{anf}(t_h)h_{anf}(\alpha ,\beta _2,b_1,b_z)\Big \},\nonumber \\ \end{aligned}$$

(38)

$$\begin{aligned} W_{\phi }^{LL}= & {} 16\sqrt{\frac{2}{3}}\pi C_Fm_B^4\int _0^1dx_1dx_3dz\nonumber \\&\times \int _0^{\infty }b_1db_1b_3db_3\phi _B(x_1,b_1)\nonumber \\&\times \Big \{\Big [x_3\phi _S(z,\xi ,\omega )\phi _V(x_3)\sqrt{1-\eta ^2}\nonumber \\&+r_V\eta \Big (\phi _S^s(z,\xi ,\omega )(\phi _V^s(x_3)(z-x_3-3) -\phi _V^t(x_3)(z+x_3-1))\nonumber \\&+\phi _S^t(z,\xi ,\omega )(\phi _V^s(x_3)(z+x_3-1)\nonumber \\&+\phi _V^t(x_3)(x_3-z-1))\Big ) E_{anf}(t_g)h_{anf}(\alpha ,\beta _1,b_1,b_3)\nonumber \\&-\Big [\phi _S(z,\xi ,\omega )\phi _V(x_3)\sqrt{1-\eta ^2}(1-z)\nonumber \\&+r_V\eta \Big (\phi _S^s(z,\xi ,\omega )(\phi _V^s(x_3)(z-x_3-1) +\phi _V^t(x_3)(z+x_3-1))\nonumber \\&+\phi _S^t(z,\xi ,\omega )(\phi _V^t(x_3)(1-z+x_3) -\phi _V^s(x_3)(z+x_3-1))\Big )\Big ]\nonumber \\&\times E_{anf}(t_h)h_{anf}(\alpha ,\beta _2,b_1,b_3)\Big \}, \end{aligned}$$

(39)

$$\begin{aligned} W_{\pi \pi }^{LR}= & {} 16\sqrt{\frac{2}{3}}\pi C_Fm_B^4\nonumber \\&\times \int _0^1dx_1dzdx_3\int _0^{\infty }b_1db_1b_zdb_z\phi _B(x_1,b_1)\nonumber \\&\times \Big \{\Big [r_V\phi _S(z,\xi ,\omega )(\phi _V^s(x_3)\nonumber \\&-\phi _V^t(x_3))(1+x_3) +\phi _V(x_3)\eta (2-z)(\phi _S^s(z,\xi ,\omega )\nonumber \\&+\phi _S^t(z,\xi ,\omega ))\Big ] \times E_{anf}(t_g)h_{anf}(\alpha ,\beta _1,b_1,b_z)\nonumber \\&+\Big [r_V\phi _S(z,\xi ,\omega )(\phi _V^t(x_3)-\phi _V^s(x_3))(x_3-1)\nonumber \\&+\phi _V(x_3)\eta z(\phi _S^s(z,\xi ,\omega ) +\phi _S^t(z,\xi ,\omega ))\Big ]\nonumber \\&\times E_{anf}(t_h)h_{anf}(\alpha ,\beta _2,b_1,b_z)\Big \}, \end{aligned}$$

(40)

$$\begin{aligned} W_{\phi }^{LR}= & {} 16\sqrt{\frac{2}{3}}\pi C_Fm_B^4\int _0^1dx_1dx_3dz\nonumber \\&\times \int _0^{\infty }b_1db_1b_3db_3\phi _B(x_1,b_1)\nonumber \\&\times \Big \{\Big [r_V\phi _S(z,\xi ,\omega )(\phi _V^s(x_3)+\phi _V^t(x_3))(2-x_3)\nonumber \\&+\eta (1+z)\phi _V(x_3)(\phi _S^s(z,\xi ,\omega ) +\phi _S^t(z,\xi ,\omega ))\Big ]\nonumber \\&\times E_{anf}(t_g)h_{anf}(\alpha ,\beta _1,b_1,b_3) +\Big [r_Vx_3\phi _S(z,\xi ,\omega )(\phi _V^t(x_3)\nonumber \\&+\phi _V^s(x_3)) +\eta (1-z)\phi _V(x_3)(\phi _S^s(z,\xi ,\omega ) -\phi _S^t(z,\xi ,\omega ))\Big ]\nonumber \\&\times E_{anf}(t_h)h_{anf}(\alpha ,\beta _2,b_1,b_3)\Big \}, \end{aligned}$$

(41)

$$\begin{aligned} W_{\pi \pi }^{SP}= & {} 16\sqrt{\frac{2}{3}} \pi C_F m_B^4\int _0^1dx_1dzdx_3\nonumber \\&\times \int _0^{\infty }b_1db_1b_zdb_z\phi _B(x_1,b_1)\nonumber \\&\times \Big \{\Big [\phi _S(z,\xi ,\omega )\phi _V(x_3)\sqrt{1-\eta ^2}(1-x_3)\nonumber \\&+r_V\eta \Big (\phi _S^s(z,\xi ,\omega )(\phi _V^s(x_3)(x_3-z-3)\nonumber \\&-\phi _V^t(x_3)(x_3+z-1)\nonumber \\&+\phi _S^t(z,\xi ,\omega )(\phi _V^s(x_3)(x_3+z-1)\nonumber \\&+\phi _V^t(x_3)(z-x_3-1))\Big )\Big ]\nonumber \\&\times E_{anf}(t_g)h_{anf}(\alpha ,\beta _1,b_1,b_z)\nonumber \\&-\Big [\phi _S(z,\xi ,\omega )\phi _V(x_3)\sqrt{1-\eta ^2}z\nonumber \\&+r_V\eta \Big (\phi _S^s(z,\xi ,\omega )(\phi _V^s(x_3)(x_3-z-1)\nonumber \\&+\phi _V^t(x_3)(x_3+z-1))+\phi _S^t(z,\xi ,\omega )(\phi _V^t(x_3)(1-x_3+z)\nonumber \\&-\phi _V^s(x_3)(x_3+z-1))\Big )\Big ]\nonumber \\&\times E_{anf}(t_h)h_{anf}(\alpha ,\beta _2,b_1,b_z)\Big \}, \end{aligned}$$

(42)

$$\begin{aligned} W_{\phi }^{SP}= & {} 16\sqrt{\frac{2}{3}} \pi C_F m_B^4\int _0^1dx_1dx_3dz\nonumber \\&\times \int _0^{\infty }b_1db_1b_3db_3\phi _B(x_1,b_1)\nonumber \\&\times \Big \{\Big [\phi _S(z,\xi ,\omega )\phi _V(x_3)\sqrt{1-\eta ^2}(1-z)\nonumber \\&+r_V\eta \Big (\phi _S^s(z,\xi ,\omega )(\phi _V^s(x_3)(z-x_3-3)\nonumber \\&+\phi _V^t(x_3)(z+x_3-1))\nonumber \\&-\phi _S^t(z,\xi ,\omega )(\phi _V^s(x_3)(z+x_3-1)\nonumber \\&+\phi _V^t(x_3)(z-x_3+1))\Big )\Big ]\nonumber \\&\times E_{anf}(t_g)h_{anf}(\alpha ,\beta _1,b_1,b_3)\nonumber \\&-\Big [\phi _S(z,\xi ,\omega )\phi _V(x_3)\sqrt{1-\eta ^2}x_3\nonumber \\&+r_V\eta \Big (\phi _S^s(z,\xi ,\omega )(\phi _V^s(x_3)(z-x_3-1) -\phi _V^t(x_3)(z+x_3-1))\nonumber \\&+\phi _S^t(z,\xi ,\omega )(\phi _V^s(x_3)(z+x_3-1) +\phi _V^t(x_3)(1-z+x_3))\Big )\Big ]\nonumber \\&\times E_{anf}(t_h)h_{anf}(\alpha ,\beta _2,b_1,b_3)\Big \}, \end{aligned}$$

(43)

where all related functions can also be found in Ref. [104].

With the above amplitudes with respect to the various currents, we then calculate the total decay amplitudes of the considered $B_{d,s}\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-$ decays. It should be emphasized that for the quark structure of $f_0$ we adopt the two-quark picture with the mixing between the $q\bar{q} = \frac{1}{\sqrt{2}} (u\bar{u}+d\bar{d})$ and $s\bar{s}$, though the four-quark picture is also supported by some experimental results [106]. As a result, the total decay amplitudes of the $B_{d,s}\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-$ decays can be obtained as

$$\begin{aligned}&{\mathcal {A}}(B_{d}\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-) ={\mathcal {A}}_{B_d}(q\bar{q})\sin \theta +{\mathcal {A}}_{B_d}(s\bar{s})\cos \theta ,\nonumber \\ \end{aligned}$$

(44)

$$\begin{aligned}&{\mathcal {A}}(B_{s}\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-) ={\mathcal {A}}_{B_s}(q\bar{q})\sin \theta +{\mathcal {A}}_{B_s}(s\bar{s})\cos \theta ,\nonumber \\ \end{aligned}$$

(45)

where ${\mathcal {A}}_{B_{d,s}}(q\bar{q})$ and ${\mathcal {A}}_{B_{d,s}}(s\bar{s})$ are the amplitudes from the $q\bar{q}$ and $s\bar{s}$ components respectively with the explicit expressions:

$$\begin{aligned} {\mathcal {A}}_{B}(q\bar{q})= & {} -\frac{G_F}{2}V_{td}V_{tb}^*\left\{ \left( a_3-a_5+\frac{1}{2}(a_7-a_9)\right) F_{\phi }^{LL}\right. \nonumber \\&\left. \left. +(C_4-\frac{1}{2}C_{10}\right) M_{\phi }^{LL} +\left( C_6-\frac{1}{2}C_8\right) M_{\phi }^{SP}\right\} , \end{aligned}$$

(46)

$$\begin{aligned} {\mathcal {A}}_B(s\bar{s})= & {} -\frac{G_F}{\sqrt{2}}V_{td}V_{tb}^*\left\{ \left( a_3+a_5 \right. \right. \nonumber \\&\left. \left. -\frac{1}{2}(a_7-a_9)\right) (A_{\phi }^{LL} +A_{\pi \pi }^{LL})\right. \nonumber \\&+\left. (C_4-\frac{1}{2}C_{10}\right) (M_{\phi }^{LL}+M_{\pi \pi }^{LL})\nonumber \\&+\left. (C_6-\frac{1}{2}C_8\right) (M_{\phi }^{SP}+M_{\pi \pi }^{SP})\Big \}, \end{aligned}$$

(47)

$$\begin{aligned} {\mathcal {A}}_{B_s}(q\bar{q})= & {} \frac{G_F}{2}\left\{ V_{ub}^*V_{us}C_2M_{\pi \pi }^{LL}-V_{tb}^*V_{ts} \left[ \left( 2C_4+\frac{1}{2}C_{10}\right) M_{\pi \pi }^{LL}\right. \right. \nonumber \\&\left. \left. +\left( 2C_6+\frac{1}{2}C_8\right) M_{\pi \pi }^{SP}\right] \right\} , \end{aligned}$$

(48)

$$\begin{aligned} {\mathcal {A}}_{B_s}(s\bar{s})= & {} -\frac{G_F}{\sqrt{2}}V_{tb}^*V_{ts} \left\{ \left( a_3+a_4+a_5-\frac{1}{2}(a_7-a_9-a_{10})\right) F_{\phi }^{LL}\right. \nonumber \\&+\left( C_3+C_4-\frac{1}{2}(C_9+C_{10})\right) (M_{\phi }^{LL} +M_{\pi \pi }^{LL})\nonumber \\&+\left( C_5-\frac{1}{2}C_7\right) (M_{\phi }^{LL}+M_{\pi \pi }^{LR}) \nonumber \\&+\left( C_6-\frac{1}{2}C_8\right) (M_{\phi }^{SP}+M_{\pi \pi }^{SP})\nonumber \\&+\left( a_3+a_4+a_5-\frac{1}{2}(a_7+a_9+a_{10})\right) \nonumber \\&\times (A_{\phi }^{LL}+A_{\pi \pi }^{LL}) +\left( a_6-\frac{1}{2}a_8\right) (A_{\phi }^{SP}+A_{\pi \pi }^{SP})\nonumber \\&+\left( C_3+C_4-\frac{1}{2}(C_9+C_{10})\right) \nonumber \\&\times (M_{\phi }^{LL}+M_{\pi \pi }^{LL}) \left. +\left( C_5-\frac{1}{2}C_7\right) (M_{\phi }^{LR}\right. \nonumber \\&\left. +M_{\pi \pi }^{LR})+\left( C_6-\frac{1}{2}C_8\right) (M_{\phi }^{SP}+M_{\pi \pi }^{SP})\right\} . \end{aligned}$$

(49)

These $a_i(i=3,4,5,6,7,8,9,10)$ are the combined Wilson coefficients defined as

$$\begin{aligned} a_i= & {} C_i+\frac{1}{3}C_{i+1},\quad i=3,5,7,9 \end{aligned}$$

(50)

$$\begin{aligned} a_i= & {} C_i+\frac{1}{3}C_{i-1},\quad i=4,6,8,10, \end{aligned}$$

(51)

with $C_i$ are the Wilson coefficients. In this same way, we can also calculate the amplitudes of $B_{d,s}\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-$, however we do not present them here due to the limited space.

Finally, we can obtain the differential branching fraction

$$\begin{aligned} \frac{d^2{\mathcal {B}}}{d \zeta d\omega } =\frac{\tau \omega |\vec {p}_1||\vec {p}_3|}{32\pi ^3 m_{B}^3}|{\mathcal {A}}|^2. \end{aligned}$$

(52)

The magnitudes of three-momenta of one pion and the bachelor particle $\phi$ in the rest frame of the $\pi \pi$-pair are given by

$$\begin{aligned} |\vec {p}_1|= & {} \frac{\sqrt{\lambda (\omega ^2,m_\pi ^2,m_{\pi }^2)}}{2\omega }, \nonumber \\ |\vec {p}_3|= & {} \frac{\sqrt{\lambda (m_{B}^2,m_\phi ^2,\omega ^2)}}{2\omega }, \end{aligned}$$

(53)

with the standard K$\ddot{a}$ll$\acute{e}$n function $\lambda (a,b,c)= a^2+b^2+c^2-2(ab+ac+bc)$.

3 Numerical results and discussions

We start this section with listing the parameters used in the numerical calculations, such as the mass of the mesons, the decay constants and the lifetimes of the B mesons, the width of the intermediate resonances, the CKM matrix elements, and the QCD scale [102],

$$\begin{aligned}&m_{B}/m_{B_s}=5.279/5.366 ~\mathrm{GeV}, \nonumber \\&\quad m_{f_0}=(0.99\pm 0.02)~\mathrm{GeV},\quad m_{f_2}=1.275~\mathrm{GeV},\nonumber \\&\quad V_{tb}=1.0,\quad V_{td}=0.00854^{+0.00023}_{-0.00016},\nonumber \\&\quad V_{ub}=0.00361^{+0.00011}_{-0.00009},\nonumber \\&\quad V_{us}=0.22650\pm 0.00048,\quad V_{ts} =0.03978^{+0.00082}_{-0.00060},\nonumber \\&\quad \Lambda _{QCD}^{f=4} =(0.25\pm 0.05)~\mathrm{GeV},\nonumber \\&\quad f_B=0.19\pm 0.02~\mathrm{GeV},\quad f_{B_s} =0.23\pm 0.02~\mathrm{GeV}\nonumber \\&\quad \Gamma _{f_2}=186 ~\mathrm{MeV},\quad \tau _{B_d}/\tau _{B_s}=1.519/1.515~\mathrm{ps}. \end{aligned}$$

(54)

Based on the obtained decay amplitudes in previous section and the input parameters above, we can calculate the CP-averaged branching fractions, the CP asymmetries, and the polarization fractions of final states for these considered $B_{d,s}\rightarrow \phi (f_{0,2}\rightarrow ) \pi ^+\pi ^-$ decays. In Table 1, we present our results of the branching fractions, together with the currently available experimental measurements from the LHCb Collaboration [22]. We acknowledge that there are many uncertainties in our calculations. In this work we mainly take three kinds of errors into accounts, as shown in tables. The first errors are caused by parameters in the distribution amplitudes of the B mesons, $\phi$ meson and the $\pi \pi$ pair, such as the shape parameter of $B_{(s)}$ meson $\omega /\omega _s=0.4\pm 0.04/0.5\pm 0.05$ GeV, the Gegenbauer moments of the $\phi$ meson distribution amplitudes, and the Gegenbauer moments $a_S$, $a_D^{(T)}$ corresponding to the S-wave and D-wave two-pion distribution amplitudes, respectively. The second kinds of errors arise from the higher order and higher power corrections, which are represented by varying the $\Lambda _{QCD}=(0.25\pm 0.05)$ GeV and the factorization scale t from 0.8t to 1.2t. The last ones are from the uncertainties of the CKM matrix elements. From the table, it can be seen that the major uncertainties are the first ones, so we hope the future developments of the nonperturbative approaches such as the QCD sum rules and the Lattice QCD approach, can reduce this kind of uncertainties.

From the Table 1, we find that for the decays $B_s\rightarrow \phi \pi ^+\pi ^-$, our results could accommodate the current experimental results with large uncertainties, although for the $B_s$ the theoretical cental value is twice of the experimental data. We also note that the branching fraction of $B_s\rightarrow \phi (f_{0}\rightarrow )\pi ^+\pi ^-$ decay is much larger than that of $B_d\rightarrow \phi (f_{0}\rightarrow )\pi ^+\pi ^-$ decay by three orders, and three reasons lead to this large difference. Firstly, $B_d\rightarrow \phi (f_{0}\rightarrow )\pi ^+\pi ^-$ is suppressed by the CKM matrix elements $|{V_{td}}/{V_{ts}}|^2$. Secondly, for the $B_s\rightarrow \phi (f_{0}\rightarrow )\pi ^+\pi ^-$ that is induced by $b\rightarrow s q{\bar{q}}$ transition, the contributions from tree operators are sizable, as shown in Eq. (48). Lastly, for decay $B_s\rightarrow \phi (f_0\rightarrow )\pi ^+ \pi ^-$, the spectator quark ${\bar{s}}$ flows into both $\phi$ and $\pi \pi$-pair, while the spectator quark ${\bar{d}}$ in decay $B_d\rightarrow \phi (f_0\rightarrow )\pi ^+ \pi ^-$ only enters into $\pi \pi$-pair. The branching fraction of $B_d\rightarrow \phi \pi ^+\pi ^-$ is at the order of ${{\mathcal {O}}}(10^{-9})$, which can be tested in the ongoing LHCb and Belle II experiments.

Table 1 CP averaged branching ratios (in $10^{-6}$) of $B_{d,s}\rightarrow \phi (f_0/f_2 \rightarrow ) \pi ^+\pi ^-$ decays in PQCD approach together with experimental data from Refs. [22, 102]

Table 2 The direct CP asymmetries parameters and the fractions of longitudinal polarization of final states (in $\%$) of $B_{d,s}\rightarrow \phi (f_0/f_2 \rightarrow ) \pi ^+\pi ^-$ decays in PQCD approach

As aforementioned, although the narrow-width approximation cannot be used in studying the quasi-two-body decays with the subprocess $f_0\rightarrow KK$, it is still reliable in the decays with the subprocess $f_0\rightarrow \pi \pi$, i.e.,

$$\begin{aligned} {\mathcal {B}}(B\rightarrow M(R\rightarrow )P_1P_2)\simeq {\mathcal {B}}(B\rightarrow MR)\times {\mathcal {B}}(R\rightarrow P_1P_2).\nonumber \\ \end{aligned}$$

(55)

Using the this approximation and isospin relations, we could estimate the quasi-two-body decays $B\rightarrow \phi (f_0\rightarrow ) \pi ^0\pi ^0$ within the experimental branching fractions of $B\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-$. To achieve this goal, we first define the ratio $\mathcal {R}_1$ as

$$\begin{aligned} \mathcal {R}_1= & {} \frac{{\mathcal {B}}(B\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-)}{{\mathcal {B}}(B\rightarrow \phi (f_0\rightarrow )\pi ^0\pi ^0)}\nonumber \\\simeq & {} \frac{{\mathcal {B}}(B\rightarrow \phi f_0) \times {\mathcal {B}}(f_0\rightarrow \pi ^+\pi ^-)}{{\mathcal {B}}(B\rightarrow \phi f_0) \times {\mathcal {B}}(f_0\rightarrow \pi ^0\pi ^0)}\nonumber \\= & {} \frac{{\mathcal {B}}(f_0\rightarrow \pi ^+\pi ^-)}{{\mathcal {B}}(f_0\rightarrow \pi ^0\pi ^0)}=2, \end{aligned}$$

(56)

Thereby, the branching fractions of $B_{d,s}\rightarrow \phi (f_0\rightarrow )\pi ^0\pi ^0$ can be obtained as

$$\begin{aligned} {\mathcal {B}}(B_{d}\rightarrow \phi (f_0\rightarrow )\pi ^0\pi ^0)\simeq & {} \frac{{\mathcal {B}}(B_{d}\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-)}{2}\nonumber \\= & {} (1.49_{-1.22}^{+1.86})\times 10^{-9}, \end{aligned}$$

(57)

$$\begin{aligned} {\mathcal {B}}(B_{s}\rightarrow \phi (f_0\rightarrow )\pi ^0\pi ^0)\simeq & {} \frac{{\mathcal {B}}(B_{s}\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-)}{2}\nonumber \\= & {} (1.17_{-0.56}^{+2.03})\times 10^{-6}. \end{aligned}$$

(58)

Similarly, the branching fractions of the quasi-two-body $B_{d,s}\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-$ decays are predicted to be

$$\begin{aligned} {\mathcal {B}}(B_{s}\rightarrow \phi (f_2\rightarrow )\pi ^0\pi ^0)\simeq & {} \frac{{\mathcal {B}}(B_{s}\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-)}{2}\nonumber \\= & {} (3.75_{-1.92}^{+2.24})\times 10^{-7}, \end{aligned}$$

(59)

$$\begin{aligned} {\mathcal {B}}(B_{d}\rightarrow \phi (f_2\rightarrow )\pi ^0\pi ^0)\simeq & {} \frac{{\mathcal {B}}(B_{d}\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-)}{2}\nonumber \\= & {} (1.23_{-0.47}^{+0.86})\times 10^{-9}. \end{aligned}$$

(60)

Since the branching fraction of $f_0\rightarrow \pi \pi$ decay is still unknown, so we cannot extract the branching fractions of the corresponding two-body $B_{d,s}\rightarrow \phi f_0$ decays under the narrow-width approximation with the measured quasi-two-body decays. However, we could theoretically evaluate the ratio $\mathcal {R}_{2}$ between the $B_{s}\rightarrow \phi f_0$ and the $B_{d}\rightarrow \phi f_0$ decays using the narrow-width approximation

$$\begin{aligned} \mathcal {R}_2= & {} \frac{{\mathcal {B}}(B_{s}\rightarrow \phi f_0)}{{\mathcal {B}}(B_{d}\rightarrow \phi f_0)}\nonumber \\= & {} \frac{{\mathcal {B}}(B_{s}\rightarrow \phi f_0)\times {\mathcal {B}}(f_0\rightarrow \pi ^+\pi ^-)}{{\mathcal {B}}(B_{d}\rightarrow \phi f_0) \times {\mathcal {B}}(f_0\rightarrow \pi ^+\pi ^-)}\nonumber \\\simeq & {} \frac{{\mathcal {B}}(B_{s}\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-)}{{\mathcal {B}}(B_{d} \rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-)}\approx 8\times 10^2. \end{aligned}$$

(61)

Once one of the $B_{s}\rightarrow \phi f_0$ and $B_{d}\rightarrow \phi f_0$ decays were measured in the future experiments, we could estimate the branching fraction of another decay. For the decays $B\rightarrow \phi f_2$, the branching fraction of $f_2\rightarrow \pi \pi$ decay has been measured to be $(84.2^{+2.9}_{-0.9})\%$ [102]. Therefore, under the narrow width approximation, the branching fractions of $B_{d,s}\rightarrow \phi f_2$ decays are estimated to be

$$\begin{aligned} {\mathcal {B}}(B_d \rightarrow \phi f_2)\simeq & {} \frac{{\mathcal {B}}(B_d\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-)}{\frac{2}{3}\times {\mathcal {B}}(f_2\rightarrow \pi \pi )}\nonumber \\= & {} (4.38_{-1.69}^{+3.18})\times 10^{-9}, \end{aligned}$$

(62)

$$\begin{aligned} {\mathcal {B}}(B_s \rightarrow \phi f_2)\simeq & {} \frac{{\mathcal {B}}(B_s\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-)}{\frac{2}{3}\times {\mathcal {B}}(f_2\rightarrow \pi \pi )}\nonumber \\= & {} (1.33_{-0.66}^{+0.80})\times 10^{-6}. \end{aligned}$$

(63)

In 2013, one of authors (Zou) has studied the branching fractions of the decays $B_{d}\rightarrow \phi f_2$ and $B_s \rightarrow \phi f_2$ [95] in PQCD approach, where $f_2$ was regarded as pure $q\bar{q}$ state. Compared current results and ones in Ref. [95], these branching fractions are in agreement with each other with large uncertainties. The acceptable differences origin from the mixing angle between $q{\bar{q}}$ and $s{\bar{s}}$.

The branching fraction of $f_2\rightarrow K\overline{K}$ decay has been measured to be $(4.6^{+0.5}_{-0.4})\%$ [102]. Using the narrow width approximation again, we can evaluate the branching fractions of corresponding quasi-two-body $B \rightarrow \phi (f_2\rightarrow )K^+K^-$ decays. At first, we define the ratio $\mathcal {R}_{3}$ and calculate it as

$$\begin{aligned} \mathcal {R}_3= & {} \frac{{\mathcal {B}}(B\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-)}{{\mathcal {B}}(B\rightarrow \phi (f_2\rightarrow )K^+K^-)}\nonumber \\\simeq & {} \frac{{\mathcal {B}}(B\rightarrow \phi f_2)\times {\mathcal {B}}(f_2\rightarrow \pi ^+\pi ^-)}{{\mathcal {B}}(B\rightarrow \phi f_2) \times {\mathcal {B}}(f_2\rightarrow K^+K^-)}\nonumber \\= & {} \frac{{\mathcal {B}}(f_2\rightarrow \pi ^+\pi ^-)}{{\mathcal {B}}(f_2\rightarrow K^+K^-)}\approx 24.4. \end{aligned}$$

(64)

So the branching fractions of $B_{d,s}\rightarrow \phi (f_2\rightarrow )K^+K^-$ decays can be obtained as

$$\begin{aligned} {\mathcal {B}}(B_d\rightarrow \phi (f_2\rightarrow )K^+K^-)= & {} {\mathcal {B}}(B_d\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-)\frac{1}{\mathcal {R}_3}\nonumber \\\approx & {} 1.0\times 10^{-10}, \end{aligned}$$

(65)

$$\begin{aligned} {\mathcal {B}}(B_s\rightarrow \phi (f_2\rightarrow )K^+K^-)= & {} {\mathcal {B}}(B_s\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-)\frac{1}{\mathcal {R}_3}\nonumber \\\approx & {} (3.07_{-1.56}^{+1.84})\times 10^{-8}. \end{aligned}$$

(66)

We note that the branching fractions of $B_{d,s}\rightarrow \phi (f_0\rightarrow )K^+K^-$ cannot be obtained through the corresponding $B_{d,s}\rightarrow \phi (f_0\rightarrow )\pi ^+\pi ^-$ decays, because the narrow-width approximation cannot work in describing the line-shape of $f_0$, as discussed in previous section.

At last, we turn to discuss the calculated CP asymmetries and the fractions of longitudinal polarizations, which are given in Table 2. It is known to us the direct CP asymmetry is proportional to the interference between contributions from the tree and penguin operators. Because the transitions $b\rightarrow s s {\bar{s}}$ and $b\rightarrow s d {\bar{d}}$ are pure penguin processes, and $b\rightarrow s u {\bar{u}}$ is penguin dominated, so the CP asymmetries of these decays are very small or even zero. Specifically, for the $B_d \rightarrow \phi (f_0/f_2\rightarrow ) \pi ^+ \pi ^-$ decays that are pure penguin processes, the direct asymmetries are zero. For the $B_s \rightarrow \phi (f_0/f_2\rightarrow )\pi ^+\pi ^-$ decays, the tree contributions are suppressed heavily by the CKM matrix elements, so the interference between the tree contribution and the penguin one is very small, leading to small direct CP asymmetries. From the Table 2, we find that the $B_{d,s}\rightarrow \phi (f_2\rightarrow )\pi ^+\pi ^-$ decays are dominated by the longitudinal polarization contributions, which obeys the naive factorization assumption. The reason is that the contributions from transverse polarizations are power suppressed compared with these of longitudinal ones.

4 Summary

In this work we investigated the $B_{d,s}\rightarrow \phi \pi ^+\pi ^-$ decays with the $f_0(980)$ and $f_2(1270)$ as the intermediate resonant states, motivated by the recent measurements of LHCb collaboration. Within the S wave and D wave two-pion wave functions, we calculated the branching fractions, the CP asymmetries, and the fractions of the longitudinal polarizations. The obtained theoretical branching fractions of $B_s\rightarrow \phi (f_0(980)/f_2(1270)\rightarrow )\pi ^+\pi ^-$ decays are in agreement with the LHCb measurements within the uncertainties. Furthermore, we also studied the $B_d \rightarrow \phi (f_0(980)/f_2(1270)\rightarrow )\pi ^+\pi ^-$ decays, and the predictions can be tested in the ongoing LHCb and Belle II experiments. The CP asymmetries are small and even zero, because these concerned decays are either dominant by the penguin contribution or even pure penguin processes. For the D-wave decay channels, the fractions of the longitudinal polarizations are close to unity, which are consistent with the power counting of the naive factorization. Within the narrow width approximation, we also estimated the branching fractions of the $B_{d,s}\rightarrow \phi (f_2(1270)\rightarrow )\pi ^0\pi ^0$ and $B_{d,s}\rightarrow \phi (f_2(1270)\rightarrow )K^+K^-$ decays and the branching fractions of two-body decays $B_{d,s}\rightarrow \phi f_2(1270)$, which could be measured in the experiments in future.