Hybrid nature of the abnormal solutions of the Bethe–Salpeter equation in the Wick–Cutkosky model

Abstract

In the Wick–Cutkosky model, where two scalar massive constituents interact by means of the exchange of a scalar massless particle, the Bethe–Salpeter equation has solutions of two types, called “normal” and “abnormal”. In the non-relativistic limit, the normal solutions correspond to the usual Coulomb spectrum, whereas the abnormal ones do not have non-relativistic counterparts – they are absent in the Schrödinger equation framework. We have studied, in the formalism of the light-front dynamics, the Fock-space content of the abnormal solutions. It turns out that, in contrast to the normal ones, the abnormal states are dominated by the massless exchange particles (by 90 % or more), what provides a natural explanation of their decoupling from the two-body Schrödinger equation. Assuming that one of the massive constituents is charged, we have calculated the electromagnetic elastic form factors of the normal and abnormal states, as well as the transition form factors. The results on form factors confirm the many-body nature of the abnormal states, as found from the Fock-space analysis. The abnormal solutions have thus properties similar to those of hybrid states, made here essentially of two massive constituents and several or many massless exchange particles. They could also be interpreted as the Abelian scalar analogs of the QCD hybrid states. The question of the validity of the ladder approximation of the model is also examined.

1 Introduction

In their pioneering papers [1, 2], Wick and Cutkosky (W-C) have found the solutions of the Bethe–Salpeter (BS) equation [3] for two scalar particles interacting by the exchange of a massless scalar particle. In addition to the states which, in the non-relativistic limit, reproduce the spectrum of the Schrödinger equation with the Coulomb potential, there was found another set of solutions which do not have any non-relativistic counterparts. These solutions were called “abnormal”. Their discovery triggered the discussion as to whether they do indicate a mathematical inconsistency of the W-C model or of the BS equation, or whether they represent new physical systems, whose existence does not contradict any physical principles, although they are not covered by the Schrödinger equation. In the latter case, they might provide examples of relativistic systems which could exist in nature, but which would not be described by continuous extensions of non-relativistic quantum mechanics. A thorough discussion of this issue can be found in Ref. [4] (Sects. 6 and 8).

One would hope that a complementary lighting to the above questioning might come from experimental data. Unfortunately the conditions of the emergence of abnormal states are not easy to realize. Considering the W-C model as a simplified model of QED, abnormal states would appear as highly excited states for values of the fine structure constant $\alpha$ above $0.5\div 1$. Such values might be reached with the aid of heavy ions and dedicated electron-ion scattering experiments might be envisaged. However, to have a clear experimental distinction of abnormal bound states from the ionization threshold, one actually would need to increase the values of $\alpha$ up to $4\div 5$, which then further reduce the probability of an experimental success. Another possibility is an analogy of the model with hadron dynamics, where hadrons mutually interact by means of the exchange of light particles, like the pions, and where the coupling constants might lie in the range of values needed for the existence of abnormal states. However, here, the exchanged particles being massive, drastic changes occur with respect to the massless case: the interaction forces become of short-range and one realizes that abnormal states are produced only with very small mass values of the exchanged particle, much smaller than the pion mass. The framework of Quantum Chromodynamics, where quarks mutually interact by means of exchange of massless gauge particles, the gluons, with sufficiently strong forces, might provide another domain to search for possible evidences of abnormal solutions.

In the absence of any direct experimental indication about the existence or nonexistence of abnormal states, one is entitled to explore all possible theoretical paths that might provide complementary information about their properties. From this point of view, we have found that an analysis of the Fock-space content of the abnormal, as well as normal, states would be of great help. The BS amplitude allows one to extract the wave function related to the two-body sector of the Fock space [5]. Its norm, which is positive and bounded by 1, is then interpreted as the weight of that sector in the whole Fock space.

Complementary information to the above analysis comes from the knowledge of the electromagnetic form factors, assuming that one of the massive constituents of the bound state is charged. Their asymptotic behavior qualitatively probes the compositeness of the states: a rapid decrease would be the signature of a many-body structure [6,7,8].

Our calculations, as well as the results of Ref. [9], show that, in the window of allowed coupling constants, the normal solutions are essentially dominated by the two-body sector of the Fock space. We will show in the present work that, on the contrary, the abnormal solutions have a two-body contribution that vanishes in the limit of zero binding energies and remains small (less than 10%) in all its domain of existence. They are therefore dominated by the many-body sectors, composed of the two massive constituents and of several massless exchange particles. This feature explains why the abnormal solutions disappear from the spectrum in the non-relativistic limit, the latter being formulated in the two-body sector alone, while the other sectors, containing massless particles, are by essence relativistic.

The asymptotic behaviors of the form factors also corroborate the above conclusions. The form factors of the abnormal solutions asymptotically decrease, for spacelike momenta, faster, by factors of the order of $10^{3}$, than those of the normal solutions. Also, the transition form factors between normal and abnormal solutions display global suppressions, by factors of $5\div 10$, with respect to the normal-normal or abnormal-abnormal transition form factors, signalling a different nature of the normal and abnormal solutions.

These results suggest that the abnormal solutions might correspond to states called “hybrids” in the literature. In the present model, they are dominated by Fock space sectors containing two massive constituents and several or many massless constituents, corresponding to the exchanged-particle fields. They could be considered as the Abelian scalar analogs of the QCD hybrids, which, in the mesonic sector, are dominated by their coupling to the set of fields made of a quark, an antiquark and one or several gluon fields.

Finally, the question of the validity of the ladder approximation of the model, because of the necessity of having large values of the coupling constant to create abnormal states, still remains an open issue.

The plan of the paper is the following. Sec. 2 is devoted to an introductory definition of the BS amplitude and of the Fock-space sectors. In Sec. 3, the properties of the solutions of the W-C model are displayed and some solutions are found numerically. In Sec. 4 the elastic and transition electromagnetic form factors are expressed through the BS amplitudes and are calculated numerically, with special emphasis put on their asymptotic behavior. Concluding remarks follow in Sec. 5. Three appendices give technical details about some of the formulas used in the main text. Preliminary results of the present study were presented in Ref. [10].

2 Fock space sectors

The BS amplitude, satisfying the BS equation, is defined as

$$\begin{aligned} \varPhi (x_1,x_2;p)\equiv \langle 0 |T[\phi _1(x_1)\phi _2(x_2)]|p\rangle , \end{aligned}$$

(1)

where $\phi _a(x)$ ($a=1,2)$ are Heisenberg field operators, T means time ordering, $|p\rangle$ is the state vector of the bound system and $\langle 0 |$ is the vacuum state vector. Since the amplitude $\varPhi (x_1,x_2;p)$ depends on two 4D variables, $x_1$ and $x_2$, it is usually called “two-body” BS amplitude, though this terminology, to some extent, is misleading. Asking the questions “what is the content of a system?” or “is it two-body or many-body?” requires that we analyze the state vector $|p\rangle$ of this system, entering in the matrix element (1), by decomposing it onto the states $| n\rangle$ with definite numbers n of particles (the Fock sector decomposition), schematically:

$$\begin{aligned} |p\rangle =\sum _{n=2}^{\infty }\psi _n^{}|n\rangle , \end{aligned}$$

(2)

and studying the contributions of the two-body component $\psi _2$, the three-body component $\psi _3$, etc., in the full normalization integral. The answer to the above questions depends on which component (or sum of components) is dominant. It should be mentioned that the state vector $|p\rangle$ is usually defined on a t-constant plane in the 4D space. There are however some advantadges to choose the so called light-front plane $t+z=0$ (or light-front plane of general orientation, see [5]). In this case, the corresponding Fock components $\psi _n$ are called the light-front wave functions. The two-body light-front wave function $\psi _2$ is related to the BS amplitude (1) by Eq. (A.2) from Appendix A.

In the W-C model, in the ladder approximation, the Fock decomposition can contain two constituent (massive) particles and any number of exchange (massless) particles. The state $|2\rangle$ (two-body sector) contains two constituents only, the state $|3\rangle$ (three-body sector) contains two constituents and one exchange particle, the state $|n\rangle$ (n-body sector) contains two constituents and $(n-2)$ exchange particles, etc. Assuming that the state vectors $|n\rangle$ ($n=2,3,\ldots$) are normalized to unity, the state vector $|p\rangle$ is then normalized as

$$\begin{aligned} \langle p|p\rangle =\sum _{n=2}^{\infty }N_n=1, \end{aligned}$$

(3)

where, schematically, $N_n=\int |\psi _n|^2\ldots$ is the contribution of the n-body Fock sector (see eq. (A.1) for the exact definition of $N_2$). In practice, knowing the BS amplitude $\varPhi (x_1,x_2;p)$ we are able to find $N_2$ only. The calculation of $N_2$ from the BS amplitude is presented in Appendix A. If it is dominant, this would mean that the contribution of the other sectors, containing exchange particles, is small. The limiting case, when it is enough to keep the two-body state only (the case corresponding to $N_2=1$), whereas the states containing exchange particles can all be omitted, is realized in non-relativistic systems. On the contrary, when the two-body contribution $N_2$ is small, the system is dominated by two constituents with an indefinite number of exchange massless particles, whose contribution $\sum _{n=3}^{\infty }N_n$ is close to 1.

For the normal solutions of the W-C model (in the equal-mass case), the above analysis has been made in Ref. [9]. It was found that for small binding energies the two-body (constituent) sector dominates, as expected. When the binding energy increases (i.e., the total mass M decreases), the two-body contribution $N_2$ decreases in parallel. However, it still dominates and as $M\rightarrow 0$, it tends, in this model, to 64%. That is, the sectors $|n\rangle$ with $n\ge 3$ contribute in total to 36% of the total normalization of the normal state vector. In the present paper, we will carry out the same analysis for the abnormal states.

3 Wick–Cutkosky solutions

The BS equation [3] for the amplitude (1) containing two spinless fields, restricted to the equal-mass case $m_1=m_2=m$, reads, in momentum space,

$$\begin{aligned} \varPhi (k,p)= & {} \frac{i^2}{\left[ (\frac{p}{2}+k)^2-m^2 +i\epsilon \right] \left[ (\frac{p}{2}-k)^2-m^2+i\epsilon \right] } \nonumber \\&\quad \times \int \frac{d^4k'}{(2\pi )^4}iK(k,k',p)\varPhi (k',p), \end{aligned}$$

(4)

where p and k are the total and relative four-momenta, respectively, and K is the interaction kernel. The bound state mass squared is $M^2=p^2$. For nonconfining interactions, the mass M is smaller than 2m, allowing the introduction of the binding energy B (defined positive) through the relation $M^2=(2m-B)^2$. In the ladder approximation of the kernel, represented by the exchange of a scalar particle with mass $\mu$, the kernel has the form

$$\begin{aligned} iK(k,k',p)=\frac{i(-ig)^2}{(k-k')^2-\mu ^2+i\epsilon }, \end{aligned}$$

(5)

leading to an attractive interaction and the possible emergence of bound states.

3.1 General properties of the solutions

The W-C model corresponds to the case $\mu =0$ in Eq. (5). In the non-relativistic limit, this model leads to the well-known Coulomb bound state spectrum. Cutkosky showed that in the relativistic case, the BS amplitude, henceforth limited to S-wave states, characterized by a principal quantum number $n=1,2,\ldots$, can be represented in terms of n functions $\left\{ g_n^{\nu } \right\} _{{\nu }=0,1\ldots n-1}$, depending on a single scalar argument $z\in [-1,+1]$, as

$$\begin{aligned}&\varPhi _n(k,p)=- {i \over \sqrt{N_{tot}}} \sum _{{\nu }=0}^{n-1}\int _{-1}^1g_{n}^{\nu }(z)dz \nonumber \\&\quad \times \frac{m^{2(n-{\nu })+1}}{[m^2-\frac{1}{4}M^2 -k^2-p\text{[ }0.08cm]{\cdot }k\,z-\imath \epsilon ]^{2+n-{\nu }}}, \ n=1,2,\ldots . \nonumber \\ \end{aligned}$$

(6)

$N_{tot}$ is a dimensionless normalization factor, determined in Appendix C, ensuring the condition $F_{el}(0)=1$ for the elastic form factor. The factor $m^{2(n-{\nu })+1}$ in the numerator is introduced to deal with dimensionless $g_{n}^{\nu }(z)$ functions.

By inserting (6) in the BS equation (4), Cutkosky obtained [Eq. (14) of Ref. [2]] a system of homogeneous coupled integral equations for the functions $g_n^{\nu }$. For S-waves, it reads¹:

$$\begin{aligned}&g_n^{\nu }(z)= {\lambda \over 2} \sum _{{\nu }'=0}^{\nu } \frac{ (n-{\nu }+1)(n-{\nu })}{ (n-{\nu }'+1) (n-{\nu }')} \int _{-1}^1dt \int _0^1 dx\nonumber \\&\quad \times x(1-x)^{n-{\nu }-1} \int _{-1}^{+1}dz' \frac{\delta [ z -xt-(1-x)z'] }{ [1-\eta ^2(1-z^2) ]^{{\nu }-{\nu }'+1}} g_n^{{\nu }'}(z'),\nonumber \\ \end{aligned}$$

(7)

where $\lambda$ is related to the coupling constant $g^2$ of the interaction kernel (5) by $\lambda = {g^2\over 16 \pi ^2m^2},$ and the total mass square $M^2$, eigenvalue of the system (7), appears through the parameter

$$\begin{aligned} \eta ^2={M^2\over 4m^2}. \end{aligned}$$

Integrating Eq. (7), first with respect to t through the $\delta$ function, taking into account the bounds to be satisfied by t and x, and distinguishing the two cases, $z>z'$ and $z'>z$, one obtains the set of equations

$$\begin{aligned} g_n^{\nu }(z)= & {} {\lambda \over 2} \sum _{{\nu }'=0}^{{\nu }} c_n^{{\nu }{\nu }'} \; \int _{-1}^{+1} dz' \; {[R(z,z')]^{n-{\nu }} \over [Q(z')]^{{\nu }-{\nu }'+1}} \; g_n^{{\nu }'} (z'), \nonumber \\&n=1,2,\ldots , \; \; {\nu }=0,1,...n-1, \end{aligned}$$

(8)

where we have introduced

$$\begin{aligned} c_n^{{\nu }{\nu }'}= & {} \frac{ (n-{\nu }+1)}{ (n-{\nu }'+1) (n-{\nu }')},\nonumber \\ Q(z)= & {} 1-\eta ^2(1-z^2), \end{aligned}$$

(9)

and

$$\begin{aligned} R(z,z')=\left\{ \begin{array}{ll} \frac{1-z}{1-z'},&{} \text{ for } z'<z, \\ \frac{1+z}{1+z'},&{} \text{ for } z'>z. \end{array} \right. \end{aligned}$$

(10)

By expanding Eq. (8), one is left with a $n\times n$ triangular system of one-dimensional integral equations of the form

$$\begin{aligned} g_n^0(z)= & {} {\lambda \over 2} \left[ c_n^{00} \int _{-1}^{+1} dz' \; { [R(z,z')]^n \over Q(z')} \; g_n^0 (z') \right] , \nonumber \\ g_n^1(z)= & {} {\lambda \over 2} \left[ c_n^{10} \int _{-1}^{+1} dz' \; {[R(z,z')]^{n-1} \over [Q(z')]^2} \; g_n^0 (z') \right. \nonumber \\&\quad + \left. c_n^{11} \int _{-1}^{+1} dz' \; { [R(z,z')]^{n-1} \over Q(z') } \; g_n^1 (z') \right] , \nonumber \\ g_n^2(z)= & {} {\lambda \over 2} \left[ c_n^{20} \int _{-1}^{+1} dz' \; {[R(z,z')]^{n-2} \over [Q(z')]^3} \; g_n^0 (z') \right. \nonumber \\&\quad + \left. c_n^{21} \int _{-1}^{+1} dz' \; {[R(z,z')]^{n-2} \over [Q(z')]^2 } \; g_n^1 (z')\right. \nonumber \\&\quad +\left. c_n^{22} \int _{-1}^{+1} dz' \; { [R(z,z')]^{n-2} \over Q(z') } \; g_n^2 (z')\right] , \nonumber \\&\ldots \ \ \ \ \ \ \ \ldots \ \ \ \; \ldots \ \ \ \ldots \; \ \ \ \ldots \ , \nonumber \\ g_n^{n-1}(z)= & {} {\lambda \over 2} \left[ c_n^{n-1,0} \int _{-1}^{+1} dz' \; { R(z,z') \over [Q(z')]^n} \; g_n^0 (z') + \ldots \right. \nonumber \\&\quad + \left. c_n^{n-1,n-1} \; \int _{-1}^{+1} dz' \; { R(z,z') \over Q(z')} \; g_n^{n-1}(z') \right] .\nonumber \\ \end{aligned}$$

(11)

Remarkably, the function $g_n^0$, which allows the calculation of the energy spectrum via the $M^2$-dependence of Q [Eq. (9)], is totally decoupled from the rest of the system. It fulfills the single equation (11), that we will hereafter write in terms of the fine structure coupling constant $\alpha$, usual in the Coulomb problems:

$$\begin{aligned} g_n^0(z)= & {} \frac{\alpha }{2\pi n} \int _{-1}^1 {[R(z,z')]^n \over Q(z')} \; g_n^0 (z'),\nonumber \\ \alpha= & {} \pi \lambda = {g^2\over 16\pi m^2}. \end{aligned}$$

(12)

The remaining equations allow the determination of $g_n^{v>0}$ – and so of the BS amplitude (6) – by solving an inhomogeneous problem with an inhomogeneous term given by $g_n^0$. Notice that it is a quite unusual situation in Quantum Mechanics that a part of the total system wave function, which, as we will see in what follows is far from being dominant, determines the full spectrum of the system.

Although the results presented here are limited to S-wave only, it is worth noticing that for $l\ne 0$ the corresponding spherical function $Y_{lm}$ would appear as a prefactor in Eq. (6). The angular momentum l would enter in the system of equations (8) and (11), but it turns out to be absent in the first equation (11) determining the spectrum. As a consequence, the BS amplitude would depend on l, while the spectrum would remain l- degenerate.

In view of its numerical solution, it is interesting to write Eq. (12) in a differential form:

$$\begin{aligned}&g_n^{0\,\prime \prime }(z)+2(n-1)z(1-z^2)^{-1}g_n^{0\,\prime }(z) \nonumber \\&\quad -n(n-1)(1-z^2)^{-1}g_n^0(z)\nonumber \\&\quad +\frac{\alpha }{\pi }\frac{1}{(1-z^2)Q(z)}g_n^0(z)=0, \end{aligned}$$

(13)

with the boundary conditions $g_n^0(\pm 1)=0$.

For a fixed n, Eq. (13) has an infinite number of solutions, labeled by an additional quantum number $\kappa =0,1,2,\ldots$, which also labels the corresponding discrete spectrum of mass squared eigenvalues $M_{n\kappa }^{2}$. We will use the notation $g^{\nu }_{n\kappa }$ to identify a particular solution. The function $g_{n\kappa }^0$ has $\kappa$ nodes within the interval $]-1,+1[$ and a well-defined parity given by $\kappa$ [2]:

$$\begin{aligned} g^0_{n\kappa } (-z)= (-1)^{\kappa } g^0_{n\kappa }(z) \end{aligned}$$

The parity is also preserved inside the ensemble $\{ g_{n\kappa }^{\nu } \}$ when varying $\nu =0,1,\ldots$ and this entails, through Eq. (6), that for even (odd) values of $\kappa$, the BS amplitude $\varPhi (k,p)$ is an even (odd) function of the relative energy $k_0^{}$ in the c.m. frame.

The mass squared $M^2$ of the ground state $g_{10}^0$ as function of the coupling constant $\alpha$ is shown in Fig. 1. Its value vanishes for $\alpha =2\pi$. In the range $\alpha \in [0,2\pi ]$, $M^2\ge 0$, the total mass of the system M is well defined as well as its binding energy $B=2m-M>0$. This determines the domain where this model is physically consistent with a well-defined ground state. It is worth mentioning, however, that the solutions of the BS equation, as well as its spectral parameter $M^2$, can be analytically continued for $\alpha >2\pi$ without encountering any kind of singularity. This is illustrated with the dashed line in the lower right corner of the figure. All excited states lie above the $M^2(\alpha )$ curve and thus can have a well-defined M even in the unphysical region.

Fig. 1

Dependence of the squared mass of the ground state ($n=1, \kappa =0)$ on the coupling constant $\alpha$. Beyond the critical value $\alpha =2\pi$, the solutions are smootly continued without any singularity but having negative values of $M^2$. The physical region, where the system has well-defined ground state mass and binding energy, is thus limited to $\alpha \in [0,2\pi ]$

Among the infinity of solutions existing for a given n, the one with $\kappa =0$ coincides, in the limit of small binding energies $B/m\ll 1$, with the solution of the non-relativistic Coulomb problem with main quantum number n. This solution is called, following the original works of Wick and Cutkosky [1, 2], “normal”. Indeed, these authors, analyzing in this limit the system of equations for the functions $g_n^v(z)$ determining the BS amplitude (6), reproduced, for $\kappa =0$, the Coulomb spectrum, i.e. the Balmer series

$$\begin{aligned} B_n=\frac{m\alpha ^2}{4n^2}. \end{aligned}$$

(14)

This result corresponds to the Schrödinger equation with the potential $V(r)=-\frac{\alpha }{r}$. The relativistic perturbative correction to the binding energy (14) was found in [11]; the binding energy, incorporating it, reads

$$\begin{aligned} B_n=\frac{m\alpha ^2}{4n^2}\left[ 1 - {4\alpha \over \pi } \ln \left( {1\over \alpha }\right) + {\mathcal O}(\alpha ) \right] . \end{aligned}$$

(15)

On the contrary, the solutions corresponding to non-zero values of $\kappa$ ($\kappa =1,2,\ldots$), have a spectrum totally decoupled from the non relativistic one. They are genuinely of relativistic nature, without non-relativistic counterparts, and were named “abnormal” by Wick.

These different behaviours are illustrated in Fig. 2 where we have displayed the dependence of the coupling constant $\lambda ={\alpha \over \pi }$ on the binding energy B for the lowest solutions of the W-C model. Upper panel contains only the n=1 states with $\kappa =0,1,2,3,4$. The curve corresponding to $\kappa =0$ (black solid line) is tangent to the non-relativistic (NR) one (black dashed line) from which it departures logarithmically, as it is visible, starting at $B\approx 0.001$. The perturbative results, provided by Eq. (15), are indistinguishable from the exact ones in the considered energy range. Those corresponding to $\kappa >0$ (colored solid lines) do not have any non-relativistic counterparts. Lower panel represents the spectrum for $n\ge 1$ states and different values of $\kappa =0,1,2,3$. The horizontal line $\lambda =2$ ($\alpha =2\pi$) indicates the maximal value of the coupling constant ensuring a well-defined ground state.

Fig. 2

Spectrum of the W-C model as a function of the coupling constant $\lambda (B)$ in the low energy limit. Upper panel corresponds to n=1 states with different values of $\kappa =0,1,..$ . The case $\kappa =0$ is compared to the non relativistic solution. Horizontal lines correspond respectively to the maximal values of the coupling constant for a well-defined ground state ($\lambda =2$) and to the minimal value for which the abnormal solutions exist ($\lambda =1/4$). Lower panel contains the full spectrum for $n\le 6$ and $\kappa \le 3$ to make explicit the different crossings. Notice that the unphysical solutions with odd $\kappa$ (giving no contribution to the S-matrix) are naturally inserted in the spectrum

The normal and abnormal solutions have also different domains of existence with respect to the coupling constant $\alpha$. As a mathematical solution of the BS equation (4), the normal solutions exist for any (positive) values of $\alpha$, although, as we have already discussed, they have a clear physical meaning only in the range $\alpha \in [0,2\pi ]$, where $M^2\ge 0$. However, the very existence of the abnormal solutions (all of them) requires a coupling constant greater than some critical value, $\alpha \ge {\pi \over 4}$ ($\lambda \ge 1/4$). This can be clearly seen from the results of Fig. 2, where all the abnormal states (color line) were found above the horizontal $\lambda =1/4$ line.

Wick and Cutkosky [1, 2] found the following approximate analytic expression for the abnormal spectrum near the continuum threshold ($B\rightarrow 0$):

$$\begin{aligned} M_{n\kappa }^2\simeq 4m^2\left( 1 - e^{ -{(\kappa -1)\pi / \sqrt{{\alpha \over \pi }-{1\over 4}}}}\right) ,\;\kappa =2,3,\ldots \ , \end{aligned}$$

(16)

where the condition $\alpha >\pi /4$ is explicitly obtained. At $B/m\ll 1$ this spectrum vs. $\kappa$ does not depend on n. It also indicates that to be able to distinguish abnormal states from the continuum threshold on experimental grounds, the coupling constant should be increased at least up to values of $\alpha \approx 4\div 5$; otherwise, for values of $\alpha$ very close to $\pi /4$, the exponential in Eq. (16) is nearly zero and the discrete spectrum becomes hardly distinguishable from the continuum.

It is worth noting that the existence of a lower bound of the coupling constant for the abnormal solutions is reminiscent of the massive-exchange case, i.e. $\mu \ne 0$ in the kernel (5), which was considered with some detail in [12] both in the BS and the Light-Front Dynamics frameworks. The $B_{\mu }(\alpha )$ dependences (Figs. 5 and 7 of [12]) are similar to those displayed in Fig. 2), what suggest the possibility to associate a mass with the abnormal states. However, essential differences in the number of bound states for a given $\mu$ remain: infinite in the W-C model and (at most) finite in the massive case.

In summary, the range of the coupling constants to be considered in this model is $0<\alpha <2\pi$ ($0<\lambda <2$) for the normal states, i.e. $\kappa =0$, and ${\pi \over 4}<\alpha <2\pi$ ($1/4<\lambda <2$) for the abnormal ones ($\kappa >0$). On another hand, according to Refs. [13, 14], the abnormal solutions with odd values of $\kappa$ do not contribute to the S-matrix and therefore only those with even $\kappa$ can have a physical meaning. In the subsequent part of this work, we will concentrate on the latter case. Furthermore we will restrict ourselves, to the $l=0$ states with $n=1$ and $n=2$.

For $n=1$ states, the sum (6) is reduced to a single term involving only the function $g_1^0$ satisfying the homogeneous integral equation

$$\begin{aligned} g_1^0(z)=\frac{\alpha }{2\pi }\int _{-1}^1 \frac{R(z,z')}{Q(z')} \, g_1^{0}(z')dz', \end{aligned}$$

(17)

or, equivalently, in its differential form

$$\begin{aligned} {g''}_1^0(z)+\frac{\alpha }{\pi }\frac{1}{(1-z^2)Q(z)}g_1^0(z)=0, \end{aligned}$$

(18)

with the boundary conditions $g_1^0(\pm 1)=0$. The corresponding BS amplitude is expressed in terms of $g_1^0$ as

$$\begin{aligned} \varPhi _1(k,p)=\int _{-1}^1\frac{-im^3 \,g_{1}^0(z)dz}{[m^2-\frac{1}{4}M^2 -k^2-p\text{[ }0.08cm]{\cdot }k\,z-\imath \epsilon ]^{3}}. \end{aligned}$$

(19)

For $n=2$ states, the sum (6) involves two functions $g_2^0$ and $g_2^1$. The function $g_2^0$ satisfies the homogeneous integral equation:

$$\begin{aligned} g_2^0(z)=\frac{\alpha }{4\pi }\int _{-1}^1 \frac{R^2(z,z')}{Q(z')} \, g_2^{0}(z')dz', \end{aligned}$$

(20)

and in differential form

$$\begin{aligned}&{g''_2}^0(z)+\frac{2z}{(1-z^2)}{g'}_2^0(z)-\frac{2}{(1-z^2)}g_2^0(z) \nonumber \\&\quad +\frac{\alpha }{\pi }\frac{1}{(1-z^2)Q(z)}g_2^0(z)=0, \end{aligned}$$

(21)

with the boundary conditions $g_2^0(\pm 1)=0$, while $g_2^1$ is determined from $g_2^0$ through the integral equation

$$\begin{aligned} g_2^1(z)= & {} \frac{\alpha }{6\pi }\int _{-1}^1\frac{R(z,z') }{[Q(z')]^2} \,g_2^{0}(z')dz' \nonumber \\&\quad + \frac{\alpha }{2\pi }\int _{-1}^1\frac{R(z,z')}{Q(z')} \, g_2^{1}(z')dz', \end{aligned}$$

(22)

which can also be rewritten in the form of an inhomogeneous differential equation:

$$\begin{aligned}&{g''}_2^1(z)+\frac{\alpha }{\pi }\frac{1}{(1-z^2)Q(z)}g_2^1(z) \nonumber \\&\quad = - \frac{\alpha }{3\pi }\frac{1}{(1-z^2)[Q(z)]^2}g_2^0(z). \end{aligned}$$

(23)

The BS amplitude (6) is now expressed in terms of two functions $g_2^1$ and $g_2^0$:

$$\begin{aligned} \varPhi _2(k,p)= & {} \int _{-1}^1\frac{-im^3 \,g_{2}^1(z)dz}{[m^2-\frac{1}{4}M^2 -k^2-p\text{[ }0.08cm]{\cdot }k\,z-\imath \epsilon ]^{3}} \nonumber \\&\quad +\int _{-1}^1\frac{-i m^5\,g_{2}^0(z)dz}{[m^2-\frac{1}{4}M^2 -k^2-p\text{[ }0.08cm]{\cdot }k\,z-\imath \epsilon ]^{4}}.\nonumber \\ \end{aligned}$$

(24)

3.2 Numerical solutions for some selected states $g_{n\kappa }^v$

We present, in this subsection, the numerical results concerning the first states of the W-C spectrum. We fix hereafter $m=1$ and the coupling constant to the value $\alpha =5$. We will consider along the work an ensemble of states with $n=1,2$ and $\kappa =0,2,4$ that, for the sake of simplicity in notation, will be numbered with No. 1-6 in the Tables 1 and 2.

Table 1 Binding energy B and two-body norm ($N_2$) of the low-lying normal ($\kappa =0$) and abnormal ($\kappa =2$) states, for the coupling constant value $\alpha =5$

The binding energies for the lowest $n=1,2$ normal ($\kappa =0$) and abnormal ($\kappa =2$) states $g_{n\kappa }^{\nu }$ are presented in Table 1. All $\nu =0$ components are arbitrarily normalized to $g_{n\kappa }^0(0)=1$. The corresponding solutions for the $n=1$ states – $g_{10}^0$ and $g_{12}^0$ – are displayed in Figs. 3 and 4. They have comparable sizes and their nodal structure is determined by $\kappa$ only.

Fig. 3

$g_{10}^0$ for the normal state No. 1 of Table 1

Fig. 4

$g_{12}^0$ for the abnormal state No. 3 of Table 1

The two components $g_{2\kappa }^0$ and $g_{2\kappa }^1$ of the $n=2$ states are plotted in Fig. 5 (state No. 2 with $\kappa =0$) and Fig. 6 (state No. 4 with $\kappa =0$). The component $\nu =1$ is dominant in both cases, but for the state No. 4 it is $\sim 1000$ times larger (see the scaling factor in Fig. 6). This enhancement is due to the $Q^2$ factor in the denominator of the right-hand-side of Eq. (23), which, in the limit $B\rightarrow 0$ and around $z=0$, behaves as $Q^2\approx B^2$. Thus, for $n>1$ states with small binding energies, the component $g_{n\kappa }^0$ that determines $M^2$ is negligibly small with respect to the other components. We will see, however, in the following section that they all play equivalent roles in the construction of the BS amplitude itself and in the form factors.

Fig. 5

Components $g_{20}^0$ and $g_{20}^1$ of the normal state No. 2 from Table 1

Fig. 6

$g_{22}^0$ and $g_{22}^1$ (scaled by a factor $10^3$) of the abnormal state No. 4 (Table 1)

In the rightest column of Table 1 we have also included the norm $N_2$ of the two-body contributions in the Fock space, as it is defined in Appendix A. For the states with $n=1$, $N_2$ is given by Eq. of Appendix A and for $n=2$, by Eqs. (A.7). We remark therein that the two-body norm $N_2$ for the abnormal ($\kappa =2$) states is much smaller than for the normal ($\kappa =0$) ones. This comparison concerns however states covering the two extreme cases in the spectrum: deeply bound states (Nos. 1 and 2) and nearthreshold ones (Nos. 3 and 4). To better understand this difference, we have studied the dependence of $N_2$ on the binding energy for the first normal and abnormal states. Results are displayed in Fig. 7.

Fig. 7

$N_2$-dependence on the binding energy for the $n=1$ and $n=2$ states: normal (upper panel) and abnormal (lower panel)

The upper panel concerns the normal states. The behaviours of the the $n=1$ (black solid line) and $n=2$ (red solid line) states are quite similar: $N_2$ decreases monotonically from $N_2\approx 1$ when $B\approx 0$ down to an asymptotic value when $B\rightarrow 2m$. We found numerically $N_2(2m)\approx 0.64$ for n=1 and $N_2(2m)\approx 0.59$ for n=2. For the ground state n=1, these limiting values were found analytically in [9], as well as the perturbative expansion in their vicinity. Thus, the limit $B\rightarrow 0$ is described by Eq. (A.13), i.e.,

$$\begin{aligned} N_2(B)= 1+{1\over \pi }\sqrt{{4B\over m}}\ln \left( {4B\over m}\right) . \end{aligned}$$

At $B/m=10^{-5}$, this perturbative expansion gives $N_2=0.980$ in close agreement with the black curve of Fig. 7. We conclude from this study that the normal states are dominated by two-body norms. This is particularly true in the limit $B\rightarrow 0$, where $N_2\rightarrow 1$, but remains also true in all the energy domain, although decreasing with increasing B.

A very different behaviour is observed with the abnormal states, represented in the lower panel of Fig. 7. As one can see, the two body norm $N_2$ of these states not only remains comparatively very small, but also vanishes in the non-relativistic limit, making them, in this region, genuine many-body states. The one order of magnitude observed in Table 1 for the binding energies hides in fact a deeper and striking difference between normal and abnormal BS states, independent of their comparison with the non-relativistic spectrum. It is provided by their two-body content: abnormal states do not have in the limit $B\rightarrow 0$ any two-body contribution and have, thus, genuine many-body structures. Beyond this limit the norm of the two-body sector remains extremely small. This is the reason why they are absent in the non-relativistic limit reduced to the two-body Schrödinger equation.

The results presented in Table 1 are completed in Table 2 by studying the $\kappa =4$ excitations of $n=1,2$ states. The same conclusion holds, even in a more dramatic way. Their two body norms are one order of magnitude smaller than for the $\kappa =2$ states of Table 1. This can be expected due to their smaller binding energies and in view of the behaviour described in the lower panel of Fig. 7.

Table 2 Same as in Table 1, for the abnormal states with $\kappa =4$

The abnormal solution $g_{14}^0$ for $n=1, \kappa =4$ state (No. 5 in Table 2), is shown in Fig.  8, displaying its more involved nodal structure (4 zeros in $]-1,+1[$). The functions $g_{24}^{\nu }$ of the abnormal state $n=2, \kappa =4$ (No. 6 in Table 2), are plotted in Fig. 9. The extreme smallness of the binding energy of this state generates a huge enhancement factors in the inhomogeneous equation (23) (through the factor Q) which results in a huge dominance of the $\nu =1$ component in the full BS amplitude. Notice that $g_{24}^1$ has been reduced by a factor $10^5$ to become comparable with $g_{24}^0$.

Fig. 8

$g_{14}^0$ from state No. 5 in Table 2

Fig. 9

$g_{24}^{\nu }$ from state No. 6 in Table 2

4 Electromagnetic form factors

We suppose that one of the two constituent particles is charged. The electromagnetic form factor of the system can be expressed in terms of its BS amplitude. It is enough to consider inelastic transitions from an initial $| i\rangle$ to a final $| f\rangle$ state. The elastic form factors are obtained from them as a particular case, with $f=i$.

Fig. 10

Feynman diagram for the electromagnetic form factor

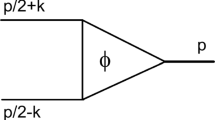
The electromagnetic vertex $J_{\mu }$, corresponding to a transition $| i\rangle \rightarrow | f\rangle$ is shown graphically in Fig. 10. The corresponding vertex amplitude reads (we use Itzykson and Zuber [15] conventions for the Feynman rules):

$$\begin{aligned} iJ_{\mu }= & {} \int \frac{d^4k}{(2\pi )^4}\, \frac{i[-i(p+p'-2k)_{\mu }]}{(k^2-m^2+i\epsilon )} \nonumber \\&\quad \times \frac{i\left[ -i\overline{\varGamma } \left( \frac{1}{2}p' -k,p'\right) \right] }{[(p'-k)^2-m^2+i\epsilon ]} \frac{i\left[ i\varGamma \left( \frac{1}{2}p-k,p\right) \right] }{[(p-k)^2-m^2+i\epsilon ]},\nonumber \\ \end{aligned}$$

(25)

where $\varGamma (k,p)$ is the vertex function, related to the BS amplitude by the equation

$$\begin{aligned}&\varPhi (k,p)=\frac{\varGamma (k,p)}{\left[ (\frac{p}{2}+k)^2-m^2+i\epsilon \right] \left[ (\frac{p}{2}-k)^2-m^2+i\epsilon \right] }.\nonumber \\ \end{aligned}$$

(26)

$\overline{\varGamma }$ is the conjugate of $\varGamma$, obtained from the latter by complex conjugation and use of the antichronological product. A similar definition also holds for the BS amplitude $\overline{\varPhi }$ [4].

The electromagnetic vertex for the transition $i\rightarrow f$ is expressed in terms of the BS amplitude as (see e.g. Eq. (7.1) in [5]):

$$\begin{aligned} J_{\mu }= & {} i\int \frac{d^4k}{(2\pi )^4}(p+p'-2k)_\mu \; (k^2-m^2) \nonumber \\&\quad \times \overline{\varPhi }_f\left( \frac{1}{2}p'-k,p'\right) \varPhi _i \left( \frac{1}{2}p-k,p\right) . \end{aligned}$$

(27)

It has the following general decomposition in terms of two scalar functions (see² [16]): $F(Q^2)$ and $G(Q^2)$

$$\begin{aligned} J_{\mu }= & {} \left[ (p_{\mu }+{p'}_{\mu })+ ({p'}_{\mu }-p_{\mu })\frac{Q_c^2}{Q^2}\right] F(Q^2) \nonumber \\&\quad - ({p'}_{\mu }-p_{\mu })\frac{Q_c^2}{Q^2}G(Q^2). \end{aligned}$$

(28)

Here, $q=p'-p$, $Q^2=-q^2=-(p'-p)^2$ and

$$\begin{aligned} Q_c^2={M_f}^2-M_i^2, \end{aligned}$$

(29)

$M_i$ and $M_f$ being the masses of the initial and final states, respectively.

Since $q\text{[ }0.08cm]{\cdot }J=Q_c^2 G(Q^2)$, the above decomposition does not suppose, in general, current conservation $q\text{[ }0.08cm]{\cdot }J=0$, which implies

$$\begin{aligned} G(Q^2) \equiv 0. \end{aligned}$$

(30)

A direct proof of this result from the BS equation is presented in Appendix B. The current conservation becomes a stringent self-consistency criterion of our results: the calculated form factor $G(Q^2)$ should be identically zero, or very small within the numerical uncertainties.

We also note that since $J_{\mu }$ [Eq. (28)] is not singular at $Q^2=0$, the following relation should hold:

$$\begin{aligned} F(0)=G(0). \end{aligned}$$

(31)

Equation (30) then implies that $F(0)=0$ for the transition form factors (for which $Q_c^2\ne 0$).

From Eq. (28), the form factors are expressed through $J_{\mu }$ as

$$\begin{aligned} F(Q^2)= & {} \frac{ (p+p')\text{[ }0.08cm]{\cdot }J\,Q^2 + q\text{[ }0.08cm]{\cdot }J \, Q_c^2}{[(M_f-M_i)^2 +Q^2][(M_f+M_i)^2+Q^2]},\nonumber \\ G(Q^2)= & {} \frac{q\text{[ }0.08cm]{\cdot }J}{Q_c^2}. \end{aligned}$$

(32)

Considering these formulas at $Q^2=0$ (which does not imply $q=0$), one gets the relation $F(0)=\left. \frac{q\text{[ }0.08cm]{\cdot }J}{Q_c^2}\right| _{Q^2=0}=G(0)$, which reproduces Eq. (31).

The expressions for the form factors are obtained by substituting in Eqs. (32) the current J [Eq. (27)], then substituting the BS amplitudes (6), using the Feynman parametrization and integrating over k. In this way, we find the form factors in the form of integrals over products of functions $g_n^{\nu }(z)$ and $g_{n'}^{\nu '}(z')$. (Details of similar calculations can be found in Ref. [17].) The result for the transition form factor $F(Q^2)$ can be written in the form:

$$\begin{aligned} F(Q^2)=\sum _{\nu =0}^{n-1}\sum _{\nu '=0}^{n'-1}F_{nn'}^{\nu \nu '}, \end{aligned}$$

(33)

and similarly for $G(Q^2)$. The expressions of the functions of the right-hand-side of this equation for the cases $n=1,2$ and $n'=1,2$ are given in Appendix C.

In the following subsections, we examine the numerical results for the elastic and transition form factors for some states from Tables 1 and 2, corresponding to the coupling constant $\alpha =5$.

4.1 Elastic form factors $F_e(Q^2)$

There are two regions of interest in studying the elastic form factors ($F_e$): the region near the origin, giving insight into the size of the system, and the asymptotic region $Q^2\gg m^2$, related to the many-body structure of the wave function [6,7,8].

With the elastic form factor of a bound state, normalized to $F_e(Q^2=0)=1$, the squared radius is given by

$$\begin{aligned} <r^2>= -6 \left( dF_e\over dQ^2\right) _{Q^2=0} \end{aligned}$$

(34)

and the root mean squared (r.m.s.) radius by $R=\sqrt{<r^2>}$. In the non-relativistic theory, the size of a bound state scales, as a function of its binding energy, as $R\approx {1\over \sqrt{mB}}$.

On the other hand, as mentioned in the Introduction, the asymptotics of $F_e$ should qualitatively probe the compositeness of the state. According to [6,7,8], the elastic form factors of a n-body system should decrease as $1/(Q^2)^{n-1}$, where n is the number of the constituents of the state. It is, however, worth emphasizing here some essential differences of the W-C model with the theoretical framework in which the above asymptotic behaviors have been obtained. The latter have been derived in theories characterized by dimensionless coupling constants, like QCD and the parton model. In the W-C model, bosonic fields interact by the exchange of a scalar particle; the coupling constant g is then dimensionful, having the dimension of mass. This has an immediate consequence on the behavior of the BS amplitude at large momenta. In the W-C model, as can be checked from Eqs. (4) and (5), the BS amplitude behaves at large momenta as $1/(k^2)^3$. In QCD, in the ladder approximation, where quarks interact by means of an exchange of a gluon field, the scalar part of the BS amplitude behaves at large momenta as $1/(k^2)^2$, up to logarithms. Extending the comparison to bosonic $\phi ^4$-like theories, where the coupling constant is also dimensionless, the interaction between two bosonic constituents is realized either by contact terms, or by the exchange of a two-particle loop; in both cases the large-momentum behavior of the BS amplitude is again $\frac{1}{(k^2)^2}$, up to logarithms. The faster decrease of the BS amplitude in the W-C model affects the behaviors of the form factors: one thus expects in this model behaviors of the type $1/(Q^2)^n$, up to logarithms, instead of $1/(Q^2)^{n-1}$.

In QCD, the number n represents the number of valence quarks (including, eventually, the number of valence gluons, in the case of hybrids). The Fock sectors of the state which contain the sea quarks, therefore with higher n’s, are expected to decrease asymptotically faster and thus to display rapidly the asymptotic dominance of the valence quark sector, a phenomenon well observed on experimental grounds. In the W-C model, for the normal solutions, one indeed expects the dominance of the two-body sector, as was concluded in Sec. 3. However, for the abnormal solutions, the two-body sector is weakly contributing to the composition of the corresponding states, which are dominated by higher sectors of the Fock space. One therefore expects here a competition between the contributions of the higher sectors of the Fock space, which asymptotically decrease more rapidly, but have large coefficients, and the contribution of the two-body sector, which dominates in the asymptotic region, but with a small coefficient.

For abnormal solutions, or hybrid states, of the W-C model, a refined analysis necessitates the distinction between three regimes in the $Q^2$ evolution of the form factors, rather than two: the very small $Q^2$ regime, determined by the binding energy (and equivalently by the rms radius), the intermediate $Q^2$ region where the decrease is determined by the many-body components (and therefore is fast) and the asymptotic region, where the many-body contribution is exhausted, and only the two-body contribution survives. Since in the W-C model the content of any state is a two-body component plus an indefinite number of exchange particles, the asymptotic behavior of all the elastic form factors is finally determined by its two-body contribution. Therefore, the asymptotic $Q^2$-dependence should be the same, though with different coefficients, for all elastic form factors. In particular, we predict that the ratios of all elastic form factors should tend to constants at $Q^2\rightarrow \infty$.

We first examine the $n=1$ states. They are defined by a single component $g_{1\kappa }^0$, the same that determines the binding energy. We have plotted, in Fig. 11, in solid lines, the elastic form factors for the two $n=1$ states of Table 1: on top, the normal state No. 1 ($\kappa =0$ , $B=0.999$), and at bottom, the abnormal state No. 3 ($\kappa =2$, $B=0.00359$).

Fig. 11

Elastic form factors of $n=1$ states of Table 1 (solid lines): No. 1 (normal) on top and No. 3 (abnormal) at bottom; the dashed line corresponds to the state with $\kappa =0$ with the same binding energy (and rms radius) as the state No. 3 with $\kappa =2$

The corresponding rms radii are $R_1=1.16$ fm and $R_3=15.7$ fm, respectively, which roughly scale as $\sim {1\over \sqrt{mB}}$. Both states have only one component $g_{n\kappa }^0$, which in turn determines the energy. It is then natural that they have a similar behaviour, close to that of the non-relativistic one. At this level, one cannot see any drastic difference between a normal and an abnormal state. The behaviours of their form factors are quite similar, however with a much faster decrease for the state No. 3, as expected from its smaller binding energy and its many-body structure. At $Q^2=1$, the value of $F_e$ for the state No. 3 is three orders of magnitude smaller than that of the state No. 1. In order to disentangle the contributions of the binding energy and of the asymptotic behaviour, we have adjusted, at a second step, $\alpha$ of the state No. 1 to have the same binding energy as the state No. 3. The result is displayed in dashed line on the lower panel: both curves are tangent to each other at the origin, implying that the rms radii are the same, but one notices that the abnormal state form factor still decreases much faster than that of the normal one, by a factor 10 at $Q^2=1$.

One can show that the elastic form factors behave, when $Q^2/m^2\rightarrow \infty$ as

$$\begin{aligned} F_e(Q^2)= & {} \Big ({m^2\over Q^2}\Big )^2 \left[ c_2 \ln \left( {Q^2\over m^2}\right) + c_0 \right] \nonumber \\&\quad + {\mathcal O}\left( \Big ({m^2\over Q^2}\Big )^3\ln \left( {Q^2\over m^2}\right) , \Big ({m^2\over Q^2}\Big )^3\right) . \end{aligned}$$

(35)

For the states $n=1$, the coefficient $c_2$ has a simple expression in terms of the BS amplitude:

$$\begin{aligned} c_2(n=1)=\frac{1}{4\pi ^2}\frac{[g_{1\kappa }^{0\,\prime }(-1)]^2}{N_{tot}}, \end{aligned}$$

(36)

where $g'(-1)$ is the derivative of g with respect to z at $z=-1$ and $N_{tot}$ is the normalization factor that ensures the condition $F_e(0)=1$ when g is arbitrarily normalized (its expression is given in Eq. (C.3)). The expression of $c_0$ is more complicated and depends on the bound state mass M, as well as on the function g over the whole region of z in the interval $[-1,+1]$.

For the normal state $n=1,\kappa =0$, $c_0$ is negative in general, but changes sign and becomes positive for small binding energies. The expression of g takes a simple form in the two extreme cases of non-relativistic limit and maximal binding energy ($M=0$). Normalizing g so that $g(0)=1$, one has in the first case $g(z)=(1-|z|)$, with $N_{tot}=1/(32\pi \alpha ^5)$, and in the second case $g(z)=(1-z^2)$, with $N_{tot}=1/(270\pi ^2)$ [1, 2]. One obtains, in these two extreme cases, the asymptotic behaviors [9]

$$\begin{aligned} F_e(Q^2)\simeq & {} \frac{8\alpha ^5}{\pi }\Big ({m^2\over Q^2}\Big )^2 \left[ \ln \left( {Q^2\over m^2}\right) + \frac{2\pi }{\alpha } \right] \nonumber \\&(\mathrm {non-relativistic\ limit}\; M\rightarrow 2m), \end{aligned}$$

(37)

$$\begin{aligned} F_e(Q^2)\simeq & {} 270 \Big ({m^2\over Q^2}\Big )^2 \left[ \ln \left( {Q^2\over m^2}\right) - 4\right] \nonumber \\&(\mathrm {ultra-relativistic\ case}\; M=0). \end{aligned}$$

(38)

Notice that in Eq. (37), we have neglected $\alpha$-independent constant factors in front of the additive term $2\pi /\alpha$. The fact that $c_0$ is generally negative, except for small binding energies, where it can, however, take a large value (proportional to $1/\alpha$), has as a main consequence the screening of the logarithmic tail, requiring, for a numerical analysis of the asymptotic behaviors, very large values of $Q^2$ ($Q^2\gg 100\div 1000\ m^2$).

In order to put in evidence the asymtptotic behavior (35) and to determine its leading terms we have computed the “reduced form factor” $\bar{F}_e(Q^2)$, defined as

$$\begin{aligned} \bar{F}_e(Q^2)\equiv & {} {1 \over \ln \left( {Q^2\over m^2}\right) } \; \Big (\frac{Q^2}{m^2}\Big )^2 \; F_e(Q^2) \nonumber \\&\quad _{{\mathop {Q^2\rightarrow \infty }\limits ^{{\displaystyle =}}}} c_2 + {c_0 \over \ln \left( {Q^2\over m^2}\right) }, \end{aligned}$$

(39)

which should tend, when $Q^2\rightarrow \infty$, to a constant (up to logarithmic corrections). The asymptotic coefficients $c_i$ can be extracted from $\bar{F}_e(Q^2)$ and its derivative at a given $Q^2$ with the relations

$$\begin{aligned} c_0= - \; { d\bar{F}(Q^2)\over dQ^2} \; Q^2 \ln ^2\left( {Q^2\over m^2}\right) \end{aligned}$$

(40)

and

$$\begin{aligned} c_2= \bar{F}(Q^2) - {c_0 \over \ln \left( {Q^2\over m^2}\right) } \end{aligned}$$

(41)

Fig. 12

Asymptotic behaviours of the elastic form factor of the $n=1$ state No. 1 of Table 1. Upper panel: the elastic form factor $F_e$ multiplied by $Q^{\sigma }$ with $\sigma =2$ (red), $\sigma =4$ (blue), and $\sigma =4$ divided by $\ln (Q^2)$. Lower panel: the asymptotic coefficients $c_0$ and $c_2$ defined in Eq. (39)

The results for the $n=1$ state No. 1 from Table 1 are displayed in Fig. 12. The upper panel represents the elastic form factor multiplied by $Q^{\sigma }$ with $\sigma =2$ (red line), $\sigma =4$ (blue line) and $\sigma =4$ divided by the logarithmic term, as in Eq. (39), to exhibit the asymptotic behaviour derived in Eq. (35) and the important contribution that the logarithmic term can have in the domain ${Q^2}\in [0,1000]$, even at $Q^2 \sim 1000$. The latter is seen in the difference between the blue and black lines, which exactly correspond to $\bar{F}_e$. In the lower panel we have plotted the coefficients $c_0$ and $c_2$ in the “asymptotic” domain ${Q^2}\in [100,1000]$, together with the full reduced form factor $\bar{F}_e$. They already show a nice convergence at ${Q^2}=1000$, but the difference between $\bar{F}_e$ and its asymptotic value $c_2$ remains sizeable, due to the large contribution of $c_0$, which decreases very slowly. We have also checked the stability of our results with respect to the number of grid points ($n_{grid}=400,800,1600$) used in computing the form factors: the sensitivity is not visible by eyes and is not significant in our analysis.

Fig. 13

Same as in Fig. 12, but for the $n=1$ abnormal state No. 3 from Table 1

Figure 13 contains the same results for the $n=1$ abnormal state No. 3. Due to the faster decrease of the corresponding elastic form factor, (see the lower panel of Fig. 11) the asymptotic regime is reached at $Q^2\approx 50$, with the asymptotic constant $c_2\approx 0.0004$, which is seven orders of magnitude smaller than for the normal state No. 1.

Figures 14 and 15 contain the elastic form factors of the two $n=2$ states. The result for the normal state No. 2 ($\kappa =0, B=0.2084$) is represented in the upper panel of Fig. 14. One first observes a much faster decrease than for the $n=1$ state No. 1 (upper panel of Fig. 11), having comparable binding energies: one order of magnitude at $Q^2 =1$. One also remarks the appearance of two zeroes in the form factor, which becomes negatives in the range $Q^2\in [1.5,3.0]$. This is a consequence of the complex structure of the state. Indeed, the different contributions $F^{\nu \nu '}$ depending on $g_{20}^\nu g_{20}^{\nu '}$ are indicated in the lower panel. As one can see, the physical $F_e$ results from strong cancellations of terms which have opposite signs and are one order of magnitude larger than the physical value they build. Although these components are of the same order, the contribution due to $g^0_{20}$ – which determines the binding energy of the state – is far from being dominant.

Fig. 14

Upper panel: elastic form factor of the normal state No. 2 of Table 1 ($n=2$, $\kappa =0$). The different contributions $F^{\nu \nu '}$ depending on $g_{20}^\nu g_{20}^{\nu '}$ are indicated in the lower panel

The elastic form factor of the abnormal state No. 4 ($\kappa =2, B=0.00112$) is displayed in Fig. 15. The same remark concerning the faster decrease than the n=1 state No. 3 with comparable binding energy holds. Notice also the non trivial structure – similar to a diffraction pattern – seen at $Q^2\approx 0.01$ and detailed in the lower panel. Such a structure, as well as the zeroes in upper panel of Fig 14, is totally unusual in a two-scalar system interacting by the simple kernel (5) and indicates the complexity of the wave function for any state solution with $n>1$, be it normal or abnormal. The decomposition of $F_e$ in terms of the different components $F^{\nu \nu '}$ is similar than for the state No. 2, i.e., strong cancellations occur among opposite sign larger terms.

Fig. 15

Elastic form factor of the abnormal state No. 4 of Table 1 ($n=2$, $\kappa =2$). The non-trivial structure at $Q^2\approx 0.01$ is detailed in the lower panel

The corresponding rms radii, extracted using Eq. (34), are $R_2=3.8$ fm (state No. 2) and $R_4=49.0$ fm (state No.4). Just on the basis of their binding energies one should expect twice smaller values. The reason is again the complex structure of the BS amplitude of $n>1$ states, with a $\nu >0$ dominating component (by a factor of $10^3$ in state No. 4) that plays no role in determining the binding energy – and so for the spatial extension – of the system.

Fig. 16

Asymptotic behaviour of the elastic form factors of $n=2$ states of Table 1 (solid lines): No. 2 (normal) on top and No. 4 (abnormal) at bottom

As it was the case for the $n=1$ states, the comparison of the elastic form factors of the $n=2$ normal and abnormal states (upper panels of Figs. 14 and 15) shows that the abnormal state form factors decrease faster than the normal ones as functions of $Q^2$. At $Q^2=1$ the ratio normal/abnormal is three orders of magnitude. Even after adjusting the coupling constant of state No. 2, to have the same binding energy than the state No. 4, the conclusion remains unchanged.

It is also interesting to examine the asymptotic behaviour, which is supposed to have the same form (39) than for $n=1$ states. This is done in the two panels of Fig. 16. They show again the importance of logarithmic corrections and the different orders of magnitudes of the asymptotic constant $c_2$ between normal and abnormal sates. Notice the scaling factor introduced in some of the plots to include the comparison in the same frame.

The ratios of form factors for the normal states Nos. 1 and 2 and for the abnormal ones 3 and 4 are shown in Fig. 17 (upper panel). They indeed tend to constants. The value of this constant is $\sim 7$. The ratio of form factors for the abnormal states No. 3 and the normal one No. 1 is shown in the lower panel of the same figure. It also tends to a constant. The value of this constant is $\sim 10^{-5}$. Note that the ratio of form factors of different nature (abnormal/normal) is much smaller than normal/normal and abnormal/abnormal, as expected. Surprisingly, the ratios normal/normal and abnormal/abnormal are the same. These asymptotic behaviors of the elastic form factors bring additional arguments in favor of the interpretation of the abnormal states of the W-C model as hybrids.

Fig. 17

Upper panel: Dotted curve is the ratio of the form factors $F(Q^2)$ for the normal ground state No. 1 and for the normal excited state No. 2. Solid curve is the same for the abnormal states No. 3 and No. 4. Lower panel: The ratio of the form factors $F(Q^2)$ for the abnormal state No. 3 from Table 1 and the normal one No. 1

4.2 Transition form factors $F_{if}(Q^2)$

For the sake of completness in the study of abnormal solutions of the W-C model we present here the results for the transition form factors. There are four states in Table 1 and, hence, six possible transitions between them. The corresponding transition form factors F are shown in Figs. 18 and 19. The comparison reveals a hierarchy of the transition form factors. In Fig. 18 we can see that the form factor for the transition between two normal states, No. 1 ($n=1,\kappa =0$) $\rightarrow$ No. 2 ($n=2,\kappa =0)$ (upper panel), dominates, by a factor $\sim 100$, over the maximal values of the normal $\rightarrow$ abnormal transitions (central and lower panels).

The transition form factor $F(Q^2)$ between two abnormal states, No. 3 ($n=1,\kappa =2$) $\rightarrow$ No. 4 ($n=2,\kappa =2$), is displayed in Fig. 19 (upper panel). Its maximal value has the same order of magnitude as the normal-normal one, though it decreases much faster. At last, the form factors for the transitions between the normal and abnormal states (Figs. 18 and 19, both central and bottom panels) are approximately 100 times smaller than the abnormal$\leftrightarrow$abnormal form factor. This hierarchy is apparently related to the need of rebuilding the state structure for the normal$\leftrightarrow$abnormal transitions.

At first glance, this dominance can be simply due to the very different binding energies: two such states will have a small overlap, without invocating any abnormal character. Indeed, one can hardly separate unambiguously the effect of different structures from the different binding energies (the latter result in different wave functions). That is why we have carried out the complex analysis based on the behavior of the form factor (elastic and inelastic) and on the content of the Fock sectors.

Fig. 18

Transition form factors from normal state No. 1 ($n=1,\kappa =0$) to other states listed in Table 1. $1\rightarrow 2$: No.2 ($n=2, \kappa =0$, normal) (upper panel); $1\rightarrow 3$: No. 3 ($n=1, \kappa =2$, abnormal) (central panel) and $1\rightarrow 4$: No.4 ($n=2,\kappa =2$, abnormal) (lower panel)

Fig. 19

Same as in Fig. 18 between $3\rightarrow 4$: No. 3($n=1,\kappa =2$, abnormal) and No. 4 ($n=2,\kappa =2$, abnormal) (upper panel); $2\rightarrow 3$: the state No. 2 ($n=2,\kappa =0$, normal) and the No. 3 ($n=1,\kappa =2$, abnormal) (central panel) and $2\rightarrow 4$: the state No. 2 ($n=2, \kappa =0$, normal) and No. 4 ($n=2,\kappa =2$, abnormal) (lower panel)

For all the transitions that were considered in this section we have calculated simultaneously the transition form factor $G(Q^2)$. The contraction of the electromagnetic current J with the momentum transfer q results in $q\text{[ }0.08cm]{\cdot }J=Q_c^2G(Q^2)$ [Eq. (32)]. Therefore, the current conservation implies $G(Q^2)\equiv 0$ for any $Q^2$ (Eq. 30). A formal proof of this equality, using the BS equation, is given in Appendix B. Computing a quantity that we know from the first principles (current conservation) that should be identically zero could be in principle considered, at most, as being superfluous. However, as is seen from the derivation given in Appendix B, this property is directly related to the fact that g is indeed a solution of the BS equation and the form factors, mainly the 3D integrals (C.4) and (C.8), have been accurately computed. It thus constitutes a test for our numerical solutions. Similar tests were successfully carried out in Ref. [16] for the form factors corresponding to the electro-desintegration of a bound system (the transition discrete $\rightarrow$ continuous spectrum).

The kind of results obtained in computing $G(Q^2)$ is illustrated in Fig. 20, in a single example corresponding to the transition between No. 2 $(n=2,\kappa =0)$ $\rightarrow$ No. 3 $(n=1,\kappa =2)$ states. As in the elastic case, the form factor $G(Q^2)$ results from the sum of two terms: $G^{10}(Q^2)$ (proportional to $g_2^1g_1^0$ ) and $G^{00}(Q^2)$ (proportional to $g_2^0g_1^0$). They are indicated respectively at upper panel in dashed ($G^{10}(Q^2)$) and in dotted ($G^{00}(Q^2)$) lines. The sum of them, i.e., the full form factor $G(Q^2)$, is indicated by a thick solid line and is indistinguishable from zero at the scale of the figure. It is in fact $\approx 10^{-6}$.

Note however that the sensitivity of $G(Q^2)$ to the accuracy in solving the BS equation, that is, in computing the functions g(z) and in calculating the 3D integrals (C.8), is very high. The result $G(Q^2)\equiv 0$ is due to delicate cancellations between terms which are several orders of magnitude greater. A small error in these calculations results in non-zero $G(Q^2)$. This is demonstrated in the lower panel of Fig. 20. Thus, an error in computing the binding energy, e.g., setting $B_i= 3.512 \cdot 10^{-3}$ instead of $B_i= 3.51169 \cdot 10^{-3}$ and $B_f=0.2084$ instead of $B_f = 0.2084099$, provides $G(Q^2) \approx -0.005$. This value is comparable with the maximum value of the corresponding form factor $F(Q^2)$ (in central panel of Fig. 19). An apparent violation of current conservation would hide in fact a lack of accuracy in the computational procedure.

Fig. 20

Contributions to the $2\rightarrow 3$ transition form factor $G(Q^2)$: the dashed line is $G^{10}(Q^2)$ and the dotted line $G^{00}(Q^2)$. The sum of them (solid line) is the full form factor $G(Q^2)$ (upper panel): it is of the order of $10^{-6}$ and results from contributions of several orders of magnitude greater. A small error in computing the binding energy, e.g., $B_i= 3.512 \cdot 10^{-3}$ instead of $B_i= 3.51169 \cdot 10^{-3}$ and $B_f=0.2084$ instead of $B_f = 0.2084099$, would provide $G(Q^2) \approx -0.005$ (lower panel), a size comparable with $F(Q^2)$ in Fig. 19

To summarize this section, the comparison of the elastic form factors presented in Figs. 11, 14, 15, of the normal states with the abnormal ones, shows that the elastic form factors of the abnormal states vs. $Q^2$ decrease much faster than for the normal ones. At $Q^2\sim 1$, the abnormal form factors are about $10^3$ times smaller than the normal ones, whereas the behaviors of the elastic form factors of the normal states with $n=1$ and $n=2$ remain very close to each other. These observations confirm that the abnormal states are dominated by the many-body Fock states [6,7,8].

The transitions between the normal and abnormal states, in comparison to the normal-normal and abnormal-abnormal transitions, are also suppressed. This suppression indicates that the normal and abnormal states have different structures and the transitions between them require the rebuilding of the states.

The quality of our numerical calculation is quite sufficient to justify the above conclusions. This is demonstrated in Fig. 20 for the transition form factor $G(Q^2)$. As is explained in Sec. 4 and proved in Appendix B, the electromagnetic current conservation requires $G(Q^2)=0$. This is indeed observed in Fig. 20, top, (solid line) as a result of rather delicate cancellations of several contributions. Numerical changes of B and g(z), which seem insignificant, may noticeably change the value of $G(Q^2)$ (Fig. 20, bottom).

The calculations of the form factors for the transitions to the states given in the Table 2, with the precision used so far, are unstable and require much higher precision. We do not present them here.

5 Concluding remarks

Our present analysis shows that the abnormal solutions of the W-C model have a different internal structure than the normal ones, which can be traced back to their decomposition properties into Fock space sectors on light-front planes. This constitutes a genuine property of these states and we propose it as an alternative characteristic to the traditional explanation in terms of temporal degrees of freedom excitations. Whereas the normal solutions are dominated by the two-body Fock sector made of the two massive constituents, the abnormal ones are dominated by the Fock sectors made of the two massive constituents and several or many massless exchange particles. This feature is also manifested through the fast decrease of the electromagnetic form factors of the abnormal states, signalling their many-body compositeness. Therefore, the abnormal states do not appear as pathological solutions of the BS equation, but rather as solutions having specifically a relativistic origin, through the dominance, in their internal structure, of the massless exchange particles.

Another particular feature of the abnormal solutions is the relatively large value of the coupling constant needed for their existence ($\alpha >\pi /4$). While the stability condition of the W-C model also requires that $\alpha$ be bounded by the upper value $2\pi$, the corresponding window of permissible values does not belong to the domain of perturbation theory and the question of the validity of the ladder approximation can be raised. This question has been examined in Ref. [18] in the light of the incorporation into the model of the renormalization effects. It turns out that the above domain of values of the coupling constant is incompatible with a consistent treatment of such effects. The renormalization constants violate the inequalities which follow from the positivity conditions coming from the spectral functions of the renormalized fields.

The latter result brings us to questioning the effect of the higher-order multiparticle exchange diagrams. This problem has been dealt with in Ref. [19] in a model of QED, where the two massive constituents are static and tied at fixed positions in three-dimensional space. The abnormal solutions corresponding essentially to excitations of degrees of freedom described by the relative time variable (or equivalently, of the relative energy variable), this model should rather preserve their possible existence. It turns out that in this configuration, the two-particle Green’s function is exactly calculable: it does not display any abnormal type of bound state in its structure; only the normal ground-state is present in the spectrum. On the other hand, the BS equation, in the ladder approximation, still continues exhibiting abnormal solutions. A similar conclusion is also obtained from a different approach, based on a three-dimensional reduction of the BS equation with the inclusion of multiparticle exchange diagrams [20].

The above considerations support, as mentioned, another interpretation of the abnormal solutions of the W-C model. It is possible that excitations of the degrees of freedom described by the relative time variable correspond, from the point of view of the Fock decomposition, to filling of the higher Fock sectors. These two interpretations may not contradict each other, but rather be compatible.

In the W-C model, the even-relative-energy abnormal solutions appear as theoretically acceptable states, and are a constitutive part of the corresponding S-matrix. The fact that they are dominated in Fock space by the many-body massless exchange particles may suggest that they are a kind of “hybrid” states. They might represent the Abelian scalar analogs of the hybrids that are searched for in QCD, which are coupled essentially to a pair of quark-antiquark and one or several gluon fields. Here, however, the non-Abelian property of the gauge group, as well as the existence of gluon self-interactions, make the latter states better adapted for experimental, as well as theoretical, investigations. On the other hand, the possible relevance of the multiparticle exchange diagrams in the kernel of the BS equation remains a key ingredient for the ultimate conclusion as to whether the W-C model may have any experimental impact. Note, however, that it is natural to expect that since the multiparticle exchanges add extra exchange particles in the intermediate states, they do not reduce but rather increase the higher Fock components.

In any event, in spite of the fact that the W-C model is an oversimplified model, it nevertheless contains the phenomenon of the particle creation and gives an interesting example of natural generation of hybrid states. Therefore, the hybrid systems can naturally exist in more sophisticated field theories and be detected in appropriate experiments.

The question of a possible existence of abnormal states in the case of massive-particle exchanges is currently under investigation by the present authors.

Appendices

Two-body contribution $N_2$ to the full norm

According to Eq. (3), the full normalization is the sum of contributions of all the Fock sectors. If the two-body wave function ($\psi _2$ in Eq. (2)) is known, then the contribution of the two-body sector in the full norm reads:

$$\begin{aligned} N_2=\frac{1}{(2\pi )^3}\int |\psi |^2(\mathbf {k}_{\perp },x) \frac{d^2k_{\perp }dx}{2x(1-x)}. \end{aligned}$$

(A.1)

We recall that we follow the definition of the wave function of light-front dynamics, where the state vector $|p\rangle$ is defined on a light-front plane. More precisely, we use the explicitly covariant version of light-front dynamics [5], in which the light-front plane is defined by the equation $\omega \text{[ }0.08cm]{\cdot }x=0$, where $\omega$ is a four-vector with the property $\omega ^2=0$.

The light-front wave function, which is the coefficient of the two-body contribution $|2\rangle$ in the Fock decomposition (2), can be extracted from the BS amplitude by projecting it on the light-front plane (see Eq. (3.57) of Ref. [5]):

$$\begin{aligned} \psi (\mathbf {k}_{\perp },x)=\frac{x(1-x)}{\pi \sqrt{N_{tot}}} \int _{-\infty }^{\infty }\varPhi \left( k+\frac{\beta \omega }{\omega \text{[ }0.08cm]{\cdot }p},p\right) d\beta , \end{aligned}$$

(A.2)

where $N_{tot}$ is the full normalization factor (the same as in Eqs. (C.4) and (C.8) below) providing the normalization of the elastic form factor $F(0)=1$.

Substituting here the BS amplitude (24) and making the transformations resulting in Eq. (3.67) of Ref. [5], we obtain, for $n=2$, an expression similar³ to Eq. (3.67):

$$\begin{aligned} \psi (\mathbf {k}_{\perp },x)= & {} -\frac{ix(1-x)}{\pi \sqrt{N_{tot}}} \int _{-\infty }^{\infty }d\beta \int _{-1}^1 dz \nonumber \\&\times \frac{m^3g_2^1(z)}{[(\mathbf {k}\,^2+\kappa _0^2)(1-zz_0)+\beta (z_0-z)-\imath \epsilon )]^3} \nonumber \\&-\frac{ix(1-x)}{\pi \sqrt{N_{tot}}}\int _{-\infty }^{\infty } d\beta \int _{-1}^1 dz \nonumber \\&\times \frac{m^5g_2^0(z)}{[(\mathbf {k}\,^2+\kappa _0^2)(1-zz_0) +\beta (z_0-z)-\imath \epsilon )]^4},\nonumber \\ \end{aligned}$$

(A.3)

where

$$\begin{aligned} z_0= & {} 1-2x,\quad \kappa _0^2=m^2-\frac{1}{4}M^2, \nonumber \\ \mathbf {k}^2= & {} \frac{\mathbf {k}\,^2_{\perp }+m^2}{4x(1-x)}-m^2. \end{aligned}$$

(A.4)

To calculate these integrals, we use the formulas:

$$\begin{aligned}&\int _{-\infty }^{\infty }\frac{d\beta }{(\beta u+v-\imath \epsilon )^3} =\frac{i\pi }{v^2}\delta (u), \nonumber \\&\quad \int _{-\infty }^{\infty }\frac{d\beta }{(\beta u+v-\imath \epsilon )^4}=\frac{2i\pi }{3v^3}\delta (u). \end{aligned}$$

(A.5)

In our case, $v=(\mathbf {k}\,^2+\kappa _0^2)(1-zz_0),\quad u=z-z_0$. In this way, we find

$$\begin{aligned} \psi (\mathbf {k}_{\perp },x)= & {} \frac{m^3x(1-x)g_2^1(1-2x)}{\sqrt{N_{tot}}[\mathbf {k}_{\perp }^2+m^2-x(1-x)M^2]^2} \nonumber \\&\quad +\frac{2m^5x(1-x)g_2^0(1-2x)}{3\sqrt{N_{tot}} [\mathbf {k}_{\perp }^2+m^2-x(1-x)M^2]^3}.\nonumber \\ \end{aligned}$$

(A.6)

Substituting $\psi (\mathbf {k}_{\perp },x)$ into the two-body normalization integral (A.1) and integrating, one finds for $n=2$

$$\begin{aligned} N_2= & {} \frac{1}{3\cdot 2^7\pi ^2 N_{tot}}\int _{-1}^1dz\,(1-z^2) \left\{ \frac{[g_2^1(z)]^2}{[Q(z)]^3}\right. \nonumber \\&\quad +\left. \frac{g_2^1(z)g_2^0(z)}{[Q(z)]^4} +\frac{4}{15}\frac{[g_2^0(z)]^2}{[Q(z)]^5}\right\} , \end{aligned}$$

(A.7)

with Q(z) defined in Eq. (9).

The case $n=1$, is obtained by keeping in the wave function (A.6) the first term only and replacing in it $g_2^1$ by $g_1^0$. This gives:

$$\begin{aligned} N_2=\frac{1}{384 \pi ^2 N_{tot}}\int _{-1}^1\frac{(1-z^2)[g_1^0(z)]^2dz}{[Q(z)]^3}. \end{aligned}$$

(A.8)

It is interesting to investigate analytically the behavior of $N_2$ in the non-relativistic limit when the binding energy $B=2m-M$ tends to zero. One can show that in this limit at leading order $N_2(B\rightarrow 0)=1$ and then find the law of approaching of $N_2(B)-1$ to 0. We will demonstrate this in the case $n=1$ [Eq. (A.8)]. Q(z) [Eq. (9)] can be represented as $Q(z)\approx z^2+\frac{B}{m}$. Then

$$\begin{aligned} \frac{1}{[Q(z)]^3}\approx \frac{1}{\left( z^2+\varepsilon \right) ^3}\approx \frac{3\pi }{8\varepsilon ^{5/2}}\delta (z),\quad \varepsilon =\frac{B}{m}. \end{aligned}$$

We substitute this formula in (A.8) and find the leading term when $B\rightarrow 0$:

$$\begin{aligned} N_2(B\rightarrow 0)=\frac{[g_1^0(0)]^2m^{5/2}}{2^{10}\pi N_{tot}B^{5/2}}. \end{aligned}$$

(A.9)

We then calculate $N_{tot}$ when $B\rightarrow 0$. For $n=1$, the sum (33) is reduced to one term only, determined by Eq. (C.2) of Appendix C. $N_{tot}$ is given by Eq. (C.3). Replacing in (C.3) the variable $\xi _+=\frac{1}{2}(1+y)$ and keeping the leading term only, we transform the integrand as

$$\begin{aligned} \frac{m^2 (5-6\xi _+) -2M^2\xi _+(1-\xi _+)}{[m^2-\xi _+(1-\xi _+)M^2]^4}\approx & {} \frac{2}{m^6(y^2+\varepsilon )^3} \\\approx & {} \frac{3\pi }{4\varepsilon ^{5/2}}\delta (y). \end{aligned}$$

We omitted the derivative of the delta-function $\delta '(y)$ which enters with a coefficient of the same order as $\delta (y)$, however, it does not contribute for symmetric g(z). Therefore, we get

$$\begin{aligned} N_{tot}= & {} \frac{m^{5/2}}{2^7\pi B^{5/2}}\int _{-1}^1g(z)dz \int _{-1}^1g(z')dz'\int _0^1du \nonumber \\&\quad \times u^2(1-u)^2 \delta \Bigl ((1+z)u+(1+z')(1-u)-1\Bigr ).\nonumber \\ \end{aligned}$$

(A.10)

From the delta-function we find $u=-z'/(z-z')$. This expression is in the limits $0 \le u \le 1$, if $-1\le z\le 0$, $0\le z'\le 1$ and $0\le z\le 1$, $-1\le z'\le 0$. For symmetric g(z) these two domains give equal contributions. Therefore, integrating over u by means of the delta-function, we find for symmetric g(z):

$$\begin{aligned} N_{tot}(B\rightarrow 0)= & {} \frac{3m^{5/2}}{2^6\pi B^{5/2} } \nonumber \\&\quad \times \int _{0}^1\int _{0}^1 \frac{z^2 {z'}^2 g(z) g(z')}{(z+z')^5} dz dz'. \end{aligned}$$

(A.11)

When $B\rightarrow 0$, the limiting expression of g(z) is [1, 2]: $g(z)\approx 1-|z|$. Calculating the integral in (A.11):

$$\begin{aligned} \int _{0}^1\int _{0}^1 \frac{z^2 {z'}^2g(z) g(z')}{(z+z')^5} dz dz'= \frac{1}{48}, \end{aligned}$$

we get

$$\begin{aligned} N_{tot}(B\rightarrow 0)=\frac{m^{5/2}}{2^{10}\pi \, B^{5/2}}. \end{aligned}$$

Substituting it in (A.9), we obtain $N_2(B\rightarrow 0)=1$, as should be for the normal state in the non-relativistic case.

The next order correction was found in Ref. [9], Eq. (24). It reads:

$$\begin{aligned} N_2-1=\frac{2\alpha }{\pi }\ln (\alpha ). \end{aligned}$$

(A.12)

In the given order, we can use the Balmer formula: $B=\frac{1}{4}m\alpha ^2$, that is $\alpha =\sqrt{\frac{4B}{m}}$. Substituting this $\alpha$ in (A.12), we find for $B\ll m$:

$$\begin{aligned} N_2-1=\frac{1}{\pi }\sqrt{\frac{4B}{m}}\ln \left( \frac{4B}{m}\right) . \end{aligned}$$

(A.13)

Proof that $G(Q^2)\equiv 0$

The vanishing of the form factor G for the transition between different states is realized if the initial and final states are associated with the solutions of the BS equation. Let us rewrite the BS equation (4) so that it would contain the functions $\varPhi _i(\frac{1}{2}p - k,p)$ and $\varPhi _f(\frac{1}{2}p' - k,p')$ entering in the expression (27) for the current. The corresponding equations, obtained from Eq. (4) by the variable shift $k\rightarrow \frac{1}{2}p-k$, are (assuming time-reversal and CP invariances)

$$\begin{aligned}&\left[ (p - k)^2 - m^2\right] (k^2 - m^2)\varPhi _i \left( \frac{1}{2}p - k,p\right) \nonumber \\&\quad =16i\alpha \pi m^2 \int \frac{d^4k'}{(2\pi )^4}\frac{\varPhi _i\left( \frac{1}{2}p - k',p\right) }{(k-k')^2+\imath \epsilon } \equiv K*\varPhi _i, \nonumber \\ \end{aligned}$$

(B.1)

$$\begin{aligned}&\quad \overline{\varPhi }_f\left( \frac{1}{2}p' - k,p'\right) \left[ (p' - k)^2 - m^2\right] (k^2 - m^2) \nonumber \\&\quad =16i\alpha \pi m^2 \int \frac{d^4k'}{(2\pi )^4} \frac{\overline{\varPhi }_f\left( \frac{1}{2}p' - k',p'\right) }{(k-k')^2+\imath \epsilon } \equiv \overline{\varPhi }_f*K,\nonumber \\ \end{aligned}$$

(B.2)

where the argument $\frac{1}{2}p - k$ is the relative momentum of the particles having the momenta $p-k$, k and similarly for $\frac{1}{2}p' - k$. Also notice that the kernel K is the same in both equations.

According to Eq. (32):

$$\begin{aligned} G(Q^2)=q\text{[ }0.08cm]{\cdot }J/Q_c^2, \end{aligned}$$

with $q=p'-p$ and J determined by Eq. (27). The integrand of $q\text{[ }0.08cm]{\cdot }J$ [cf. Eq. (27)] contains the scalar product

$$\begin{aligned} q\text{[ }0.08cm]{\cdot }(p+p'-2k)= \Bigl ({p'}^2-p^2-2(p'-p)\text{[ }0.08cm]{\cdot }k\Bigr ). \end{aligned}$$

On the other hand:

$$\begin{aligned}&\Bigl ({p'}^2-p^2-2(p'-p)\text{[ }0.08cm]{\cdot }k\Bigr )(k^2-m^2)\\&\quad =\Bigl ((p'-k)^2-m^2\Bigr )(k^2-m^2)\\&\qquad -\Bigl ((p-k)^2-m^2\Bigr )(k^2-m^2)\\&\quad =\left[ \Bigl ((p'-k)^2-m^2\Bigr )(k^2-m^2)-*K\right] \\&\qquad -\left[ \Bigl ((p-k)^2-m^2\Bigr )(k^2-m^2)-K*\right] . \end{aligned}$$

After substitution in $q\text{[ }0.08cm]{\cdot }J$, the first operator acts on $\overline{\varPhi }_f$ and gives zero, and similarly with the second operator acting on $\varPhi _i$. Hence

$$\begin{aligned} q\text{[ }0.08cm]{\cdot }J=0 \qquad \Rightarrow \qquad G(Q^2)=0. \end{aligned}$$

We emphasize that this result is obtained provided $\varPhi _{i,f}$ satisfy the BS equation with a given kernel. Numerical uncertainties in $\varPhi _{i,f}$ result in deviations of $G(Q^2)$ from zero. This is observed in Fig. 20 (bottom).

Expressions of the form factors

In general, the elastic and transition form factors are obtained as a sum of $n\times n'$ terms $F^{\nu \nu '}$, involving the different components of the BS amplitude in the initial (n) and final ($n'$) states. They have the general form given in Eq. (33):

$$\begin{aligned} F(Q^2)= \sum _{\nu =0}^{n-1}\sum _{\nu '=0}^{n'-1} F^{\nu \nu '}(Q^2). \end{aligned}$$

(C.1)

We present here explicit expressions for calculating the elastic form factors in the cases $n=1,2$ and the transition form factors between $n=1,2$ and $n'=1,2$ states.

The elastic form factor, $F_e$, for $n=1$ states, determined by a single component $g\equiv g_1^0$, is given by

$$\begin{aligned} F_e(Q^2)= & {} {m^6\over 32\pi ^2N_{tot}} \; \int _{-1}^1 dz \; g(z) \; \int _{-1}^1 dz' g(z') \nonumber \\&\quad \times \int _0^1 du\; u^2(1-u)^2 \; {N \over D^4}, \end{aligned}$$

(C.2)

with the integrands given by

$$\begin{aligned} N(z,z',u,Q^2)= & {} A(z,z',u)+B(z,z',u)\; Q^2, \\D(z,z',u,Q^2)= & {} m^2 - M^2\xi _+(1-\xi _+) -B(z,z',u)\; Q^2, \end{aligned}$$

in terms of functions A and B:

$$\begin{aligned} \xi _{\pm }(z,z',u)= & {} {1\over 2} \left[ (1+z)u \pm (1+z')(1-u) \right] , \\A(z,z',u)= & {} m^2(5-6\xi _+) -2M^2\xi _+(1-\xi _+), \\B(z,z',u)= & {} -{1\over 4} (1+z)(1+z') u(1-u)\nonumber \\= & {} -{1\over 4} (\xi _+^2-\xi _-^2). \end{aligned}$$

The total norm $N_{tot}$, defined to fulfill $F(0)=1$, is obtained by

$$\begin{aligned} N_{tot}= & {} {m^6\over 32\pi ^2} \ \int _{-1}^1 dz \ g(z) \ \int _{-1}^1 dz' g(z') \int _0^1 du\; u^2(1-u)^2 \nonumber \\&\quad \times \frac{m^2 (5-6\xi _+) -2M^2\xi _+(1-\xi _+)}{[m^2-\xi _+(1-\xi _+)M^2]^4}. \end{aligned}$$

(C.3)

For $n=2$ states, the BS amplitude is determined by two components $g_2^0,g^1_2$ (index $\kappa$ is here irrelevant and omitted). The expressions of the different form factors $F_e^{\nu \nu '}$ can be written in close analogy with (C.2) and read

$$\begin{aligned} F_e^{\nu \nu '}(Q^2)= & {} \frac{m^6}{32\pi ^2N_{tot} } \int _{-1}^{+1} dz \; g_2^\nu (z) \int _{-1}^{+1} dz' \; g_2^{\nu '}(z') \nonumber \\&\quad \times \int _0^1 du\; u^{3-\nu } (1-u)^{3-\nu '} \left( {m^2\over D}\right) ^{2-\nu -\nu '} {N^{\nu \nu '} \over D^4 }, \end{aligned}$$

(C.4)

with the integrands expressed in terms of functions $A_{\nu \nu '}$ and $B_{\nu \nu '}$ as

$$\begin{aligned} N^{\nu \nu '} = A_{\nu \nu '} \;+\; B_{\nu \nu '}\; Q^2, \end{aligned}$$

(C.5)

with $A_{11}\equiv A$, $B_{11}\equiv B$ and the remaining ones given by

$$\begin{aligned} A_{10}= & {} {1\over 4} \left[ 4m^2 (6-7\xi _+) -4M_i^2\xi _+(2-\xi _+-\xi _+^2) \right] , \nonumber \\ A_{00}= & {} {1\over 3} \left[ 4m^2 (7-8\xi _+) -8M_i^2\xi _+(1-\xi _+^2) \right] , \nonumber \\ B_{10}= & {} - {1\over 4} \left[ (2-\xi _+) (\xi _+^2-\xi _-^2) \right] , \nonumber \\ B_{00}= & {} - {1\over 3} \left[ (3-2\xi _+) (\xi _+^2-\xi _-^2) \right] , \end{aligned}$$

(C.6)

and the symmetry relation $F^{10}=F^{01}$. The total norm is given by

$$\begin{aligned}&N_{tot}= {m^6\over 32\pi ^2} \sum _{\nu ,\nu '=0}^1 \int _{-1}^{+1} dz \; g_2^\nu (z) \; \int _{-1}^{+1} dz' \; g_2^{\nu '}(z') \nonumber \\&\quad \times \int _0^1 du\; u^{3-\nu } (1-u)^{3-\nu '} \left. \left( {m^2\over D}\right) ^{2-\nu -\nu '} {N^{\nu \nu '} \over D^{4} }\right| _{Q^2=0}. \end{aligned}$$

(C.7)

Notice that since $A_{11}\equiv A$, $B_{11}\equiv B$, $F_e^{11}(Q^2)$ from Eq. (C.4) provides the case n=1.

The transition form factor between $n=1,2$ and $n'=1,2$ states offers several possibilities: $1\rightarrow 1$, $1\rightarrow 2$, $2\rightarrow 1$ and $2\rightarrow 2$. We give below the expressions of the components $F_{if}^{vv'}$ of the transition form factors between an initial state $n=2$ and a final state $n=2$, determined, respectively, by the components ($g_2^{0,i},g_2^{1,i}$) ($g_2^{0,f},g_2^{1,f}$) and the total norms of the corresponding elastic form factors $N_{tot}^i$, $N_{tot}^f$:

$$\begin{aligned} F^{\nu \nu '}_{if}= & {} {m^6\over 32\pi ^2\sqrt{N_{tot}^{i} N_{tot}^{f} } } \int _{-1}^{+1} dz g_2^{\nu ,i}(z) \int _{-1}^{+1} dz' g_2^{\nu ',f}(z') \nonumber \\&\quad \times \int _0^1 du\;u^{3-\nu } (1-u)^{3-\nu '} \left( {m^2\over D}\right) ^{2-\nu -\nu '}{N^{\nu \nu '}_{if} \over D_{if}^{4}}.\nonumber \\ \end{aligned}$$

(C.8)

The integrand $N^{\nu \nu '}_{if}$ and D can be written in the form

$$\begin{aligned} N^{\nu \nu '}_{if}(z,z',u)= & {} A^{\nu \nu '} + B^{\nu \nu '} \; Q^2 + C^{\nu \nu '} \; Q_c^2, \end{aligned}$$

(C.9)

$$\begin{aligned} D_{if}(z,z',u)= & {} m^2-\xi _+ (1-\xi _+)M_i^2 \nonumber \\&\quad - B^{11} \; Q^2 + {1\over 2} C^{11} \;Q_c^2, \end{aligned}$$

(C.10)

involving now $Q_c^2={M_f}^2-M_i^2$ and new functions $C^{\nu \nu '}$. The functions A and B are the same as for the elastic case with $M^2\equiv M_i^2$ and the functions $C^{\nu \nu '}$ are defined as

$$\begin{aligned} C^{11}= & {} - (\xi _+-\xi _-)(1-\xi _+), \\C^{10}= & {} -2 {1\over 4} (\xi _+-\xi _-)(2-\xi _+-\xi _+^2), \\C^{00}= & {} - 4 {1\over 3} (\xi _+-\xi _-)(1-\xi _+^2). \end{aligned}$$

(C.11)

The transition form factor $G(Q^2)$ is obtained by an expansion similar to (C.1). The corresponding components $G^{\nu \nu '}_{if}$ are given by (C.8), where the integrands $N_{if}^{\nu \nu '}$ are replaced by

$$\begin{aligned} \bar{N}_{if}^{\nu \nu '}(z,z',u)= & {} A^{\nu \nu '} \;+\; \bar{B}^{\nu \nu '}\; Q^2 \;+\; C^{\nu \nu '}\; Q_c^2 \nonumber \\&\quad +{D}^{\nu \nu '} \; \left( {Q^2\over Q_c^2}\right) . \end{aligned}$$

(C.12)

Their form is similar to that of (C.9), with the same $A^{\nu \nu '}$ and $C^{\nu \nu '}$, but with two new coefficients $\bar{B}^{\nu \nu '}$ (instead of $B^{\nu \nu '}$) and $D^{\nu \nu '}$ given by:

$$\begin{aligned} \bar{B}^{11}= & {} - {1\over 4}(5\xi _-^2-6\xi _+\xi _-+\xi _-^2), \\\bar{B}^{10}= & {} {1\over 4} (\xi _+ - \xi _-) [\xi _-(4+3\xi _+)- \xi _+(2-\xi _+)], \\\bar{B}^{00}= & {} {1\over 3} (\xi _+ - \xi _-) [ \xi _+(2\xi _+-3) + \xi _-(3+6\xi _+) ], \\{D}^{11}= & {} + 3\xi _-( M_i^2\xi _+-2m^2), \\{D}^{10}= & {} - {\xi _-\over 4} \left[ 28m^2-4M_i^2 \xi _+(3+\xi _+) - (\xi _+^2-\xi _-^2)Q^2 \right] , \\{D}^{00}= & {} + 2 {\xi _-\over 3} [ -16m^2 + 2M_i^2 \xi _+(3+2\xi _+) \nonumber \\&+ (\xi _+^2-\xi _-^2)Q^2]. \end{aligned}$$

(C.13)

A few remarks concerning the results of this section are in order:

• The equality (31) follows from the equality of (C.5) and (C.12) at $Q^2=0$.

• The elastic form factor (C.4) is obtained from the transition form factor (C.8) setting $i=f$, and hence $N^i_{tot}=N^f_{tot}=N_{tot}, M_i=M_f=M$ and $Q_c=0$.

• The normalization factors $N_{tot}^{i,f}$ which enter in Eqs. (C.8) are those of the corresponding elastic form factors. The functions $g_n^0$ can be normalized arbitrarily since any multiplicative factor included in the definition of g is cancelled by a redefinition of $N_{tot}$. The function $g_2^1$ is, according to Eq. (23), determined by the choice for $g_2^0$. We have used, for convenience, the normalization $g_n^0(0)=1$.

• The transitions $n=2 \;\rightarrow \;n'=1$ are obtained by keeping only the terms $F^{00}$ and $F^{10}$ in (C.8), as well as in the corresponding expression $N_{tot}$.

• The transitions $n=1 \;\rightarrow \;n'=2$ are similarly obtained by keeping the terms $F^{00}$ and $F^{01}$.

• The transition $n=1 \;\rightarrow \;n'=1$ is given by the single term $F^{00}$.