Gluon dynamics from an ordinary differential equation

Abstract

We present a novel method for computing the nonperturbative kinetic term of the gluon propagator from an ordinary differential equation, whose derivation hinges on the central hypothesis that the regular part of the three-gluon vertex and the aforementioned kinetic term are related by a partial Slavnov–Taylor identity. The main ingredients entering in the solution are projection of the three-gluon vertex and a particular derivative of the ghost-gluon kernel, whose approximate form is derived from a Schwinger–Dyson equation. Crucially, the requirement of a pole-free answer determines the initial condition, whose value is calculated from an integral containing the same ingredients as the solution itself. This feature fixes uniquely, at least in principle, the form of the kinetic term, once the ingredients have been accurately evaluated. In practice, however, due to substantial uncertainties in the computation of the necessary inputs, certain crucial components need be adjusted by hand, in order to obtain self-consistent results. Furthermore, if the gluon propagator has been independently accessed from the lattice, the solution for the kinetic term facilitates the extraction of the momentum-dependent effective gluon mass. The practical implementation of this method is carried out in detail, and the required approximations and theoretical assumptions are duly highlighted.

1 Introduction

The exceptional property of infrared saturation displayed by gluon propagators simulated on large-volume lattices in the Landau gauge [1,2,3,4,5,6,7], away from it [8,9,10,11], and even in the presence of dynamical quarks [11,12,13,14], has been the focal point of intense study during over a decade, through a variety of continuum approaches  [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40, 64, 67, 68, 84, 107, 115, 122, 125]. In fact, this special nonperturbative feature has often been associated with the emergence of a mass gap, whose origin, dynamics, and phenomenological implications are fundamental for our understanding of the gauge sector of QCD  [41,42,43,44,45,46,47,48,49,50,51,52].

Fig. 1

Diagrammatic representations of the three-gluon vertex, $\Gamma ^{abc}_{\alpha \mu \nu }(q,r,p)$, and the ghost-gluon kernel, $H^{abc}_{\alpha \mu }(q,p,r)$,with the corresponding momentum conventions

A significant part of the recent research on this subject has been carried out within the formalism that arises from the synthesis of the pinch-technique (PT) [41, 53,54,55] with the background-field method (BFM) [56], known as the “PT-BFM scheme” [49, 57]. In this framework, it is natural to express $\Delta (q^2)$ (in Euclidean space) as the sum of two distinct pieces [58],

$$\begin{aligned} \Delta ^{-1}(q^2) = q^2J(q^2) + m^2(q^2)\,, \end{aligned}$$

(1.1)

where $J(q^2)$ corresponds to the so-called “kinetic term”, while $m^2(q^2)$ represents a momentum-dependent gluon mass scale. The actual generation of $m^2(q^2)$ hinges crucially on the nonperturbative structure of the fully dressed three-gluon vertex, [28, 29, 59,60,61,62,63,64,65,66,67,68,69], entering in the Schwinger–Dyson equation (SDE) for $\Delta (q^2)$. In particular, must be decomposed as

(1.2)

where $V_{\alpha \mu \nu }$ is comprised by longitudinally coupled massless poles [70,71,72,73,74], and $\Gamma _{\alpha \mu \nu }$ denotes the remainder of the three-gluon vertex, which does not contain poles. This treatment leads finally to a system of coupled integral equations, one governing $J(q^2)$ and the other $m^2(q^2)$, which furnishes, in principle, the individual evolution of both quantities. In practice, however, the theoretical complexity associated with these equations can be handled only approximately; consequently, even though considerable progress has been achieved  [58, 75, 76], a complete solution of the problem still eludes us.

In the present work, we develop a novel approach for determining $J(q^2)$ and $m^2(q^2)$, which affords an entirely different vantage point on this problem. In particular, the decompositions given in Eqs. (1.1) and (1.2), in conjunction with the dynamical details described in  [24, 58, 77], prompt a corresponding splitting of the central Slavnov–Taylor identity (STI)

(1.3)

where $F(p^2)$ denotes the ghost dressing function, $H_{\sigma \nu }(q,p,r)$ is the ghost-gluon kernel whose diagrammatic representations is given in Fig. 1, and $\mathrm{P}_{\sigma \alpha }(q) = g_{\sigma \alpha } - q_\sigma q_\alpha /q^2$ is the standard transverse projector.

Specifically, out of Eq. (1.3) one obtains two “partial” STIs, by matching appropriately the terms appearing on both sides: one STI arises when the terms containing $m^2(q^2)$ are exclusively associated with $V_{\alpha \mu \nu }$, while the other emerges after $\Gamma _{\alpha \mu \nu }$ has been paired with $J(q^2)$ [24, 58, 77,78,79,80,81]. As was explained in detail in [69], the standard Ball–Chiu (BC) construction [82], may be applied directly at the level of the latter STI, furnishing exact relations (“BC solutions”), which involve the longitudinal form factors of $\Gamma _{\alpha \mu \nu }$, $J(q^2)$, $F(q^2)$, and three of the form factors comprising $H_{\nu \mu }$.

It is important to emphasize at this point that the STI splitting described above, plausible as it may seem, constitutes an Ansatz rather than a formal field-theoretic result. In that sense, it should be interpreted as our central working hypothesis, given that the entire procedure developed in the present work depends decisively on this particular assumption.

As has been recently pointed out [83], for certain special kinematic configurations involving a single momentum scale, the BC solutions constitute ordinary differential equations (ODEs) for $J(q^2)$. In the simplest such case, corresponding to the so-called “asymmetric” configuration, the closed form of the solution for $J(q^2)$ involves (a) the value of the ghost dressing function at the origin, F(0); (b) a special projection of $\Gamma _{\alpha \mu \nu }(q,r,p)$, to be denoted by $L^\mathrm {asym}(q^2)$ [see Eqs. (2.12) and (2.13)]; (c) a finite renormalization constant, ${{\widetilde{Z}}}_1$, and a special form factor, ${{\mathcal {W}}}(q^2)$, which are both related with the ghost-gluon kernel.

Of the above ingredients, both (a) and (b) have been computed on the lattice. Specifically, $F(q^2)$ is particularly well established from the analysis of [1,2,3,4,5], and its value at the origin is accurately determined (for continuum studies, see [17,18,19, 68, 84,85,86,87]). Similarly, from the lattice simulations of [88, 89], $L^\mathrm {asym}(q^2)$ is known over a wide range of momenta. As for (c), in the absence of lattice simulations for the ghost-gluon kernel, the function ${{\mathcal {W}}}(q^2)$ is approximately determined within the one-loop dressed approximation of the corresponding SDE, while ${{\widetilde{Z}}}_1$ has been estimated through a one-loop calculation [83].

There is an additional feature of the ODE under study, which is of paramount importance for the self-consistency of this entire approach. Given that the ODE is of first order, its solution is fully determined once a single initial (boundary) condition has been chosen. Now, it turns out that the general solution of the ODE displays a simple pole at the origin, which must be eventually eliminated, given that the physical $J(q^2)$ is known to diverge only logarithmically in the deep infrared [63]. The removal of the pole is accomplished by choosing the initial condition at the renormalization point $\mu$ in a rather special and unique way. In particular, $J(\mu ^2)$ is given by a specific integral, whose kernel is comprised by the exact same ingredients that enter in the solution of the ODE; evidently, the actual numerical value that $J(\mu ^2)$ will finally acquire depends on the particular details of these inputs.

The main conclusion drawn from the above considerations is that, under the STI splitting Ansatz of Eq. (1.3), and for a given set of ingredients [(a)-(c) above], the $J(q^2)$ is uniquely determined from the ODE and its initial value at $\mu ^2$. This property, in turn, makes the decomposition given in Eq. (1.1) unambiguous: indeed, for a fixed $\Delta ^{-1}(q^2)$, the unique $J(q^2)$ obtained from the ODE implies directly the corresponding uniqueness of $m^2(q^2)$. In fact, the latter may be obtained from $m^2(q^2) = \Delta ^{-1}(q^2) - q^2J(q^2)$, by substituting for $J(q^2)$ the solution of the ODE, and employing for $\Delta ^{-1}(q^2)$ the lattice data of [3].

Note, however, that, as will become clear in the main body of this work, the above claims are subject to certain important caveats. Specifically, while in principle the value of $J(\mu ^2)$ is self-consistently determined, in practice it is fixed by hand, due to uncertainties in the computation of the main ingredients, and most notably of the function ${{\mathcal {W}}}(q^2)$. In fact, if the approximate computation of ${{\mathcal {W}}}(q^2)$ presented in Sect. 6 were to be taken at face value, the resulting $J(\mu ^2)$ would lead to a tachyonic gluon mass (see related discussion in Sects. 3 and 7). The implementation of technical improvements that would help us overcome these practical limitations is already underway.

The article is organized as follows. In Sect. 2, a concise derivation of the ODE for $J(q^2)$ is presented, based on the non-Abelian Ward identity satisfied by $\Gamma _{\alpha \mu \nu }(q,r,p)$. In Sect. 3 we discuss the solution of the ODE, placing particular emphasis on the role played by the initial condition. Then, in Sect. 4 we elaborate on the uniqueness of the propagator decomposition given in Eq. (1.1). In Sect. 5 we take a deeper look into the field-theoretic nature of the quantity ${{\mathcal {W}}}(q^2)$, and demonstrate how it may be obtained, at least in principle, from a lattice simulation. The SDE-based approximation (one-loop dressed) of this quantity is derived and discussed in Sect. 6. In Sect. 7 we evaluate the ODE solutions for $J(q^2)$, and determine the corresponding $m^2(q^2)$, using as guidance the lattice data of [3]. Finally, in Sect. 8 we summarize our results and present our conclusions.

2 ODE from non-Abelian Ward identity

In this section we present a novel derivation of the ODE that governs $J(q^2)$, by resorting to a procedure that, even though closely related to that of [83], exploits a distinct aspect of the fundamental STI.

As in [83], the starting point of our considerations is the typical quantity considered in lattice simulations of the (transversely projected) three-gluon vertex  [11, 90,91,92,93,94,95,96,97,98,99], namely

$$\begin{aligned}&L(q,r,p)\nonumber \\&= \frac{W^{\alpha '\mu '\nu '}(q,r,p)\mathrm{P}_{\alpha '\alpha }(q)\mathrm{P}_{\mu '\mu }(r)\mathrm{P}_{\nu '\nu }(p)\Gamma ^{\alpha \mu \nu }(q,r,p)}{W^{\alpha \mu \nu }(q,r,p)W_{\alpha \mu \nu }(q,r,p)}\,. \end{aligned}$$

(2.1)

Note that, in its primary form, L(q, r, p) involves the full vertex , given by Eq. (1.2); however, by virtue of the basic property $\mathrm{P}_{\alpha '\alpha }(q)\mathrm{P}_{\mu '\mu }(r)\mathrm{P}_{\nu '\nu }(p)V^{\alpha \mu \nu }(q,r,p) =0$ [58], one ends up with the expression of Eq. (2.1). The action of the tensors $W^{\alpha '\mu '\nu '}(q,r,p)$ consists in projecting out particular components of the $\Gamma ^{\alpha \mu \nu }(q,r,p)$, evaluated in certain simple kinematic limits [11, 88], involving a single kinematic variable. More specifically, the special configuration $p \rightarrow 0\,, r = - q \,$, denominated as the asymmetric limit and denoted by $L^\mathrm {asym}(q^2)$, can be projected by setting into Eq. (2.1) $W_{\alpha \mu \nu }(q,r,p) \rightarrow \lambda _{\alpha \mu \nu } (q)$, where $L(q,r,p)\rightarrow L^\mathrm {asym}(q^2)$.

The standard treatment of this quantity involves the tensorial decomposition of $\Gamma _{\alpha \mu \nu }(q,r,p)$ in the BC basis, expressing the answer in terms of the form factors that survive in the kinematics considered, and then replacing the longitudinal ones by the corresponding BC solutions for them. However, in the case of the asymmetric limit, a more direct procedure may be adopted, which capitalizes on the non-Abelian Ward-identity satisfied by $\Gamma _{\alpha \mu \nu }(q,r,p)$.

To fix the ideas with the aid of a textbook example, consider the Takahashi identity, $p^{\mu }\Gamma _{\mu }(p,k,k+p) = S^{-1}(k+p) - S^{-1}(k)$, relating the photon–electron vertex, $\Gamma _{\mu }(p,k,k+p)$, with the electron propagator, S(k). In the limit $p\rightarrow 0$, a straightforward Taylor expansion of both sides, followed by an appropriate matching of terms, yields the standard Ward identity, $\Gamma _{\mu }(0,k,k) = \partial S^{-1}(k)/\partial k^{\mu }$. We emphasize that a crucial assumption in this derivation, frequently implicit in the standard expositions, is that the form factors comprising $\Gamma _{\mu }(p,k,k+p)$ do not contain poles as $p\rightarrow 0$.

A completely analogous procedure may be followed in order to obtain $\Gamma _{\alpha \mu \nu }(q,-q,0)$ from the STI that $\Gamma _{\alpha \mu \nu }(q,r,p)$ satisfies when contracted by $p_{\nu }$, and subsequently substitute the answer into Eq. (2.1). Note that the aforementioned assumption of absence of poles is fulfilled, precisely because all such structures have been included into the term $V_{\alpha \mu \nu }(q,r,p)$, which has dropped out.

For the purposes of this section, it is convenient to cast the relevant STI in the form [24, 58, 77,78,79,80,81]

$$\begin{aligned} p^\nu \Gamma _{\alpha \mu \nu }(q,r,p) = F(p^2) \,{{\mathcal {C}}}_{\alpha \mu }(r,p,q) \,, \end{aligned}$$

(2.2)

with

$$\begin{aligned}&{{\mathcal {C}}}_{\alpha \mu }(r,p,q) := {{\mathcal {T}}}_{\mu \alpha }(r,p,q) - {{\mathcal {T}}}_{\alpha \mu }(q,p,r)\,, \qquad \nonumber \\&\quad {{\mathcal {T}}}_{\mu \alpha }(r,p,q) := r^2 J(r^2) \mathrm{P}_\mu ^\sigma (r) H_{\sigma \alpha }(r,p,q)\,. \end{aligned}$$

(2.3)

The diagrammatic representations of the three-gluon vertex, $\Gamma _{\alpha \mu \nu }(q,r,p)$, and the ghost-gluon kernel, $H_{\alpha \mu }(q,p,r)$, are given in Fig. 1, where all momenta are incoming, $q + p + r = 0$.

Note that, as explained in the Introduction, Eq. (2.2) is obtained from the fundamental STI of Eq. (1.3) by substituting on its l.h.s., and $\Delta ^{-1}(q^2) \rightarrow q^2J(q^2)$ on its r.h.s.

Then, in complete analogy with the QED Ward identity described above, we have that

$$\begin{aligned} \Gamma _{\alpha \mu \nu }(q,-q,0)= & {} \left[ \frac{\partial }{\partial p^\nu }F(p^2)\, {{\mathcal {C}}}_{\alpha \mu }(r,p,q) \right] _{p=0} \nonumber \\= & {} F(0) \left[ \frac{\partial \,{{\mathcal {C}}}_{\alpha \mu }(r,p,q)}{\partial p^\nu } \right] _{p=0} \,, \end{aligned}$$

(2.4)

where we have used that ${{\mathcal {C}}}_{\alpha \mu }(-q,0,q) =0$. In evaluating the partial derivatives contained in Eq. (2.4), we will consider q as an independent variable, while $r=-p-q$.

The key observation that facilitates the ensuing derivation is that, in the Landau gauge, the ghost-gluon kernels appearing in ${{\mathcal {T}}}_{\mu \alpha }(r,p,q)$ and ${{\mathcal {T}}}_{\alpha \mu }(q,p,r)$ may be written as [81, 83]

$$\begin{aligned}&H_{\sigma \alpha }(r,p,q) = Z_1 g_{\sigma \alpha } + p^\rho K_{\sigma \alpha \rho }(r,p,q) \,, \qquad \nonumber \\&H_{\sigma \mu }(q,p,r) = Z_1 g_{\sigma \mu } + p^\rho K_{\sigma \mu \rho }(q,p,r)\,, \end{aligned}$$

(2.5)

where the kernels K do not contain poles as $p\rightarrow 0$. $Z_1$ is the finite constant renormalizing $H_{\sigma \alpha }(r,p,q)$; in particular, in the so-called Taylor scheme [100, 101], $Z_1 =1$. However, as explained in [83], in the “asymmetric” momentum subtraction (MOM) scheme, adopted in the lattice simulation of [11, 88], the corresponding renormalization constant, to be denoted by ${{\widetilde{Z}}}_1$, departs from unity, by an approximate amount given in Eq. (6.18).

Then, from Eq. (2.5) follows that, at lowest order in p,

$$\begin{aligned}&\left[ \frac{\partial H_{\sigma \alpha }(r,p,q)}{\partial p^\nu } \right] _{p=0} \!\!\!\!\!\!= K_{\sigma \alpha \nu }(-q,0,q)\,, \qquad \nonumber \\&\left[ \frac{\partial H_{\sigma \mu }(q,p,r)}{\partial p^\nu } \right] _{p=0} \!\!\!\!\!\!= K_{\sigma \mu \nu }(q,0,-q)\,. \end{aligned}$$

(2.6)

Next, we employ the tensor decomposition of $K_{\sigma \mu \nu }(q,0,-q)$ introduced in [83]

$$\begin{aligned} K_{\sigma \mu \nu }(q,0,-q) = - \frac{{{\mathcal {W}}}(q^2)}{q^2} g_{\sigma \mu }q_\nu + \cdots \,, \end{aligned}$$

(2.7)

where the ellipses denote terms proportional to $g_{\mu \nu }q_\sigma$, $g_{\sigma \nu }q_\mu$, and $q_\sigma q_\mu q_\nu$, which get annihilated by the various projectors in Eq. (2.1); evidently, $K_{\sigma \mu \nu }(q,0,-q) = - K_{\sigma \mu \nu }(-q,0,q)$.

Finally, note that the projector $\mathrm{P}_{\alpha \mu }(r)$ in ${{\mathcal {T}}}_{\mu \alpha }(r,p,q)$ effectively commutes with the derivative, because

$$\begin{aligned} \left[ \frac{\partial \mathrm{P}_{\alpha \mu }(r) }{\partial p^\nu }\right] _{p=0} \!\!\!\!\!\!= \frac{2 q_\alpha q_\mu q_\nu }{q^4} - \frac{q_\alpha g_{\mu \nu } + q_\mu g_{\alpha \nu } }{q^2} \,, \end{aligned}$$

(2.8)

and all terms vanish when contracted by the corresponding projectors.

Armed with these relations, it is elementary to show that

$$\begin{aligned}&\left[ \mathrm{P}^{\alpha }_{\alpha '}(q)\mathrm{P}^{\mu }_{\mu '}(r)\frac{\partial {{\mathcal {T}}}_{\mu \alpha }(r,p,q)}{\partial p^{\nu } } \right] _{p=0} \!\!\!\!\!\!\nonumber \\&\quad = \left\{ {{\widetilde{Z}}}_1 [J(q^2) + q^2 J^{\prime }(q^2)] + \frac{1}{2} J(q^2) {{\mathcal {W}}}(q^2) \right\} \lambda _{\alpha ' \mu ' \nu } (q) \,, \nonumber \\&\left[ \mathrm{P}^{\alpha }_{\alpha '}(q)\mathrm{P}^{\mu }_{\mu '}(r)\frac{\partial {{\mathcal {T}}}_{\alpha \mu }(q,p,r)}{\partial p^{\nu } } \right] _{p=0}\nonumber \\&\quad = -\frac{1}{2} J(q^2) {{\mathcal {W}}}(q^2) \lambda _{\alpha ' \mu ' \nu } (q) \,, \end{aligned}$$

(2.9)

where [88]

$$\begin{aligned} \lambda _{\alpha \mu \nu } (q):= 2 q_\nu \mathrm{P}_{\alpha \mu }(q)\,. \end{aligned}$$

(2.10)

Then, substituting the results of Eq. (2.9) into Eq. (2.4), we find that

$$\begin{aligned}&\mathrm{P}^{\alpha }_{\alpha '}(q)\mathrm{P}^{\mu }_{\mu '}(-q)\Gamma _{\alpha \mu \nu }(q,-q,0) = F(0) \left\{ [ {{\widetilde{Z}}}_1 \nonumber \right. \\&\left. \quad + {{\mathcal {W}}}(q^2) ]J(q^2) + q^2 J^\prime (q^2) {{\widetilde{Z}}}_1 \right\} \lambda _{\alpha ' \mu ' \nu } (q) \,. \end{aligned}$$

(2.11)

Returning to the r.h.s. of Eq. (2.1), we substitute for $\mathrm{P}^{\alpha }_{\alpha '}(q)\mathrm{P}^{\mu }_{\mu '}(-q)\Gamma _{\alpha \mu \nu }(q,-q,0)$ the r.h.s. of Eq. (2.11), and set $W_{\alpha \mu \nu }(q,r,p) \rightarrow \lambda _{\alpha \mu \nu } (q)$, while its l.h.s becomes $L(q,r,p)\rightarrow L^\mathrm {asym}(q^2)$, the quantity measured on the lattice. Thus, finally we obtain

$$\begin{aligned} L^\mathrm {asym}(q^2) = F(0) \left\{ [ {{\widetilde{Z}}}_1 + {{\mathcal {W}}}(q^2) ]J(q^2) + q^2 J^\prime (q^2) {{\widetilde{Z}}}_1 \right\} \,, \nonumber \\ \end{aligned}$$

(2.12)

which is the central relation employed in [83], as well as in the present work. Evidently, from Eqs. (2.11) and (2.12), we obtain the additional simple relation

$$\begin{aligned} \mathrm{P}_{\alpha '}^{\alpha }(q)\mathrm{P}_{\mu '}^{\mu }(-q)\Gamma _{\alpha \mu \nu }(q,-q,0) = L^\mathrm {asym}(q^2) \lambda _{\alpha '\mu '\nu } (q) \,. \nonumber \\ \end{aligned}$$

(2.13)

3 Physical solution and special initial condition

The linear first-order ODE for $J(q^2)$ is obtained from a simple rearrangement of the expression given in Eq. (2.12). Specifically, setting $x = q^2$, and denoting by “prime” the differentiation with respect to x, we have

$$\begin{aligned} x J'(x) + f_1(x) J(x) = f_2(x) \,, \end{aligned}$$

(3.1)

where

$$\begin{aligned} f_1(x) := 1 + \frac{{{\mathcal {W}}}( x )}{ {{\widetilde{Z}}}_1 } \,, \qquad f_2(x) := \frac{L^\mathrm {asym}(x)}{F(0) {{\widetilde{Z}}}_1 } \,. \end{aligned}$$

(3.2)

The solution of Eq. (3.1) is given by [83],

$$\begin{aligned} J(x) = \frac{1}{ x \, {\sigma }(x) }\left[ \mu ^2 {\sigma }(\mu ^2)\,J(\mu ^2) + \int _{\mu ^2}^x \!\!dt \, {\sigma }( t ) \, {f_2}(t) \right] \,, \nonumber \\ \end{aligned}$$

(3.3)

with

$$\begin{aligned} \sigma (x) := \exp \left[ \int \! \frac{dx}{x}\,(f_1(x)-1) \right] = \exp \left[ \int \! dx\, \frac{{{\mathcal {W}}}(x)}{x\,{{\widetilde{Z}}}_1}\right] \,.\nonumber \\ \end{aligned}$$

(3.4)

Of course, the central assumption when using the STI given in Eqs. (2.2) and (2.3) is that the physical J(x) contains no pole at the origin, such that, as $x\rightarrow 0$, we have $x J(x) \rightarrow 0$. As has been explained in detail in [83], this crucial property may be reconciled with the form of Eq. (3.3) provided that the sum rule

$$\begin{aligned} \int _0^{\mu ^2}\!\!\! dt \, {\sigma }( t ) \, {f_2}(t) = \mu ^2 {\sigma }(\mu ^2) J(\mu ^2) \,, \end{aligned}$$

(3.5)

is satisfied.

The way to interpret the above “no-pole condition” is the following: for a given $f_1(x)$ and $f_2(x)$, and in order to eliminate the pole, the value of the initial (boundary) condition for the solution, namely $J(\mu ^2)$, cannot be chosen freely, but must be rather determined from Eq. (3.5), as

$$\begin{aligned} J(\mu ^2) = \frac{1}{\mu ^2 {\sigma }(\mu ^2)} \int _0^{\mu ^2}\!\!\! dt \, {\sigma }( t ) \, {f_2}(t) \,. \end{aligned}$$

(3.6)

It is important to emphasize at this point that the value of $J(\mu ^2)$ is not restricted to acquire a prescribed value, dictated by the renormalization condition, as is normally the case with genuine Green’s functions. For instance, within the MOM scheme, one must impose $\Delta ^{-1}(\mu ^2) = \mu ^2$, while $J(\mu ^2)$ must simply satisfy $\mu ^2 = \mu ^2J(\mu ^2) + m^2(\mu ^2)$. Clearly, the deviation of $J(\mu ^2)$ from unity, say $J(\mu ^2) = 1 -b$, determines the value of the gluon mass at the renormalization point, namely $m^2(\mu ^2) = b \mu ^2$. Therefore, in order for the gluon mass not to become “tachyonic”, we must have $b>0$. This last condition, in turn, allows, at least in principle, the falsification of the entire mechanism: in the ideal situation where the ingredients entering in the integral of Eq. (3.6) have been determined with high accuracy, a negative b would decisively discard such a dynamical scenario.

The above discussion holds, in principle, for any value of the renormalization point $\mu$. If $\mu$ is chosen to be relatively deep in the ultraviolet, such as $\mu = 4.3$ GeV, it is reasonable to expect that $m^2(\mu ^2) \approx 0^{+}$, and that $J(\mu ^2)\approx 1^{-}$. In that limit, Eq. (3.5) may be viewed as an integral constraint that the quantities comprising $\sigma (t)$ and $f_2(t)$ must satisfy; this point of view has been pursued in detail in [83].

Once the condition Eq. (3.6) has been implemented at the level of Eq. (3.3), it is elementary to show that the solution may be cast in the manifestly pole-free form

$$\begin{aligned} J(x) = \frac{1}{x \,\sigma (x)} \int _0^x dt \, \sigma (t) f_2(t) \,; \end{aligned}$$

(3.7)

indeed, as one may verify by the simple change of variables $t\rightarrow x\,y$, the above solution is finite at the origin, and it automatically reproduces the initial condition given by Eq. (3.6).

Then, after an integration by parts, Eq. (3.7) becomes

$$\begin{aligned} J(x) = f_2(x) - \frac{1}{x\sigma (x)}\int _0^x dt \, t \, [ \sigma ( t ) f_2( t ) ]^\prime \,, \end{aligned}$$

(3.8)

where the “prime” now denotes the derivative with respect to t. This last expression makes manifest the fact that the behavior of J(x) near the origin, $x=0$, is dominated by the logarithmic divergence associated with $L^\mathrm {asym}(x)$. In fact, the implementation of the aforementioned change of variables allows one to write

$$\begin{aligned} J(x) = f_2(x) - \frac{x}{ \sigma (x)}\int _0^1 dy \, y \, \frac{ d [ \sigma ( x\, y ) f_2(x\, y) ] }{d(xy)} \,, \end{aligned}$$

(3.9)

illustrating clearly that the contribution from the integral vanishes as $x\rightarrow 0$. It turns out that this last form of the solution is advantageous for the numerical treatment, and will be employed in the corresponding sections.

Given the important implications of the analysis presented above (see next section), it would be instructive to inspect its main points, and in particular the role of Eq. (3.6), in the context of a simple toy model.

To that end, let us set

$$\begin{aligned} f_1(x) = 1\,, \qquad f_2(x) = 1 + b \,\ln \left( \frac{x}{\mu ^2}\right) \,, \qquad b>0\,. \nonumber \\ \end{aligned}$$

(3.10)

It is clear that, for this particular choice of $f_1(x)$, Eq. (3.4) yields $\sigma (x) =1$. Then, substituting the $f_2(x)$ into Eq. (3.8) we find that the pole is eliminated provided that

$$\begin{aligned} J(\mu ^2) = 1-b \,. \end{aligned}$$

(3.11)

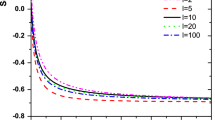
Evidently, as b varies, the form of $f_2(x)$ changes, and so does the boundary condition for $J(\mu ^2)$, as shown in Fig. 2. The corresponding solution is obtained from Eq. (3.7),

$$\begin{aligned} J(x) = 1-b + b \,\ln \left( \frac{x}{\mu ^2}\right) \,. \end{aligned}$$

(3.12)

This elementary construction demonstrates clearly that if one insists on a pole-free solution, the initial condition is determined dynamically from the various ingredients entering in the ODE.

Fig. 2

The $f_2(x)$ (left panel) and J(x) (right panel) given by Eqs. (3.10) and (3.12), for different values of b. Notice that, for each value of b, a different $J(\mu ^2)$ is obtained

Within this simplified context, it is interesting to see how the choice of a boundary condition that violates Eq. (3.11) leads to the appearance of a pole. To that end, let us impose what appears to be a “natural” choice, namely $J(\mu ^2)=1$. Then, it is straightforward to establish from Eq. (3.3) that the solution becomes

$$\begin{aligned} J(x) = \frac{b\,\mu ^2}{x} + 1-b + b \,\ln \left( \frac{x}{\mu ^2}\right) \,. \end{aligned}$$

(3.13)

Finally, there is an equivalent way of treating this toy model, which does not make explicit use of the equations employed until now, but leads to identical conclusions. In particular, since $f_1(x) = 1$, the original ODE in Eq. (3.1) simplifies to

$$\begin{aligned} {[}x J(x)]^{\prime }= f_2(x) \,, \end{aligned}$$

(3.14)

whose solution is

$$\begin{aligned} x J(x) = c + x \left[ 1-b + b \,\ln \left( \frac{x}{\mu ^2}\right) \right] \,, \end{aligned}$$

(3.15)

where c is the constant of integration. At this point, the only way to avoid the pole in J(x) is to set $c=0$; once this choice has been made, the solution is completely fixed, and becomes precisely that of Eq. (3.12).

4 Uniqueness of the gluon propagator decomposition

It is well-known (see, e.g., [102]), that the inverse quark propagator, $S^{-1}(p)$, can be expressed in the form

$$\begin{aligned} S^{-1}(p) = A(p)p/+ B(p) \mathbb {1} \,, \end{aligned}$$

(4.1)

where A(p) and B(p) are scalar functions whose ratio defines the dynamical quark mass function ${\mathcal {M}}(p)= B(p)/A(p)$. Due to the distinct Dirac structures associated with these functions, the decomposition in Eq. (4.1) is mathematically unique, in the sense that

$$\begin{aligned} A(p) = \frac{1}{p^2}\mathrm{Tr}[p/S^{-1}(p)]\,,\qquad B(p) = \frac{1}{4} \mathrm{Tr}[S^{-1}(p)]\,, \end{aligned}$$

(4.2)

with no freedom of assigning a piece of A(p) to B(p), or vice versa.

Evidently, the above arguments do not apply at the level of the decomposition in Eq. (1.1), as no analogue to the relations of Eq. (4.2) exists for $J(q^2)$ and $m^2(q^2)$. Thus, unlike A(p) and B(p), these latter functions may not be determined from $\Delta ^{-1}(q^2)$ through the direct application of some simple mathematical operations. This basic fact is usually expressed in the literature [77] by stating that one may redefine $J(q^2)$ and $m^2(q^2)$, provided that one does not change $\Delta ^{-1}(q^2)$. Thus, introducing a function $h(q^2) = q^2 j(q^2)$, one may define ${{\widetilde{J}}}(q^2) := J(q^2) + j(q^2)$ and ${{\widetilde{m}}}^2(q^2) := m^2(q^2) - h(q^2)$, such that $\Delta ^{-1}(q^2) = q^2{{\widetilde{J}}}(q^2) + {{\widetilde{m}}}^2(q^2)$. At this level, $j(q^2)$ is only mildly constrained: since we require $m^2(0) = {{\widetilde{m}}}^2(0) = \Delta ^{-1}(0)$, we must have $h(0)=0$, and $j(q^2)$ may not diverge as a pole (or stronger) at the origin. However, as we will show in what follows, the above operation is excluded on the grounds of the dynamics that the physical $J(q^2)$ must obey; in particular, the validity of the ODE Eq. (3.1), coupled to the fact that its boundary condition is fixed, makes the decomposition in Eq. (1.1) unique, in the sense that $j(q^2)=0$.

The basic argument is very simple: if we assume the validity of Eqs. (2.2) and (2.3), the $J(q^2)$ must satisfy the first-order linear equation of Eq. (3.1), which originates from this partial STI. The exact solution of Eq. (3.1), given by Eq. (3.3), has its initial condition at the point $\mu$ completely determined from the no-pole condition Eq. (3.5), or, equivalently, Eq. (3.6). Therefore, the solution for $J(q^2)$ is unique. Thus, once $J(q^2)$ has been obtained from its own ODE, $m^2(q^2)$ is directly determined, at least in principle, from Eq. (1.1), namely $m^2(q^2) = \Delta ^{-1}(q^2) - q^2 J(q^2)$, assuming, of course, that $\Delta ^{-1}(q^2)$ itself is known, e.g., from the lattice.

Note that the implicit assumption when employing the above argument is that the ingredients entering in Eqs. (3.3) and (3.6), namely $L^\mathrm {asym}(q^2)$, F(0), ${{\widetilde{Z}}}_1$, and ${{\mathcal {W}}}(q^2)$, together with the $\Delta ^{-1}(q^2)$ used in the last step, have an unambiguous field theoretic meaning, which is independent of how exactly one might choose to implement the decomposition of Eq. (1.1).

For the case of $L^\mathrm {asym}(q^2)$, F(0), and $\Delta ^{-1}(q^2)$ the validity of this assumption is evident, since all these quantities are defined in terms of the fundamental fields entering in the Yang-Mills Lagrangian, and have been simulated on the lattice. In particular, F(0) and $\Delta (q^2)$ are defined as the Fourier transforms of¹$\langle {\bar{c}}^a(x) c^{b}(y)\rangle$ and $\langle A_{\mu }^{a}(x) A_{\mu }^{b}(y) \rangle$, respectively, while $L^\mathrm {asym}(q^2)$ is obtained from an appropriate projection of the quantity $\langle A_{\alpha }^{a}(x) A_{\mu }^{b}(y) A_{\nu }^{c}(z) \rangle$. As for ${{\widetilde{Z}}}_1$, it may be computed from the renormalization constants for $L^\mathrm {asym}(q^2)$, $F(q^2)$, and $\Delta ^{-1}(q^2)$, denoted by $\widetilde{Z}_3$, $\widetilde{Z}_c$, and $\widetilde{Z}_A$; in particular, from the STI of Eq. (2.2) follows that $\widetilde{Z}_1 = \widetilde{Z}_3 \widetilde{Z}_c \widetilde{Z}_A^{-1}$. It is understood that all relevant quantities ought to be evaluated within a common renormalization scheme, such as the “asymmetric” MOM scheme used in [11, 88].

The quantity ${{\mathcal {W}}}(q^2)$ is less familiar, having been only recently introduced in [83]; nonetheless, as we will show in the next section, ${{\mathcal {W}}}(q^2)$ is also unique, in the same sense as all other ingredients considered above.

We end this section by emphasizing that the arguments presented become possible once the validity of the partial STI in Eqs. (2.2) and (2.3) has been assumed. Moreover, the uniqueness demonstration put forth is rather abstract, in the sense that it works only within the ideal scenario where all ingredients required for computing the solution and its boundary condition are known with high precision. As we will see in Sect. 7, with the present precision, the practical implementation of such a “unique” decomposition is clearly not possible.

5 “Theoretical” determination of ${{\mathcal {W}}}(q^2)$ from the lattice

In this section we describe the theoretical possibility of determining the function ${{\mathcal {W}}}(q^2)$ from lattice simulations of the ghost-gluon kernel. In particular, we show how to obtain ${{\mathcal {W}}}(q^2)$ through a series of operations on a particular projection of the quantity $\langle A_{\nu }^{e}(x) c^{m}(x) {\bar{c}}^b(y) A_{\mu }^{c}(z) \rangle$, which, in principle, may be evaluated on the lattice by means of the standard functional “averaging” over the SU(3) field space. Evidently, this way of computing ${{\mathcal {W}}}(q^2)$ is completely independent of any particular modeling of the underlying dynamics, such as the decomposition put forth in Eq. (1.1). We hasten to emphasize that the aim of this consideration is not to devise a practical procedure for extracting ${{\mathcal {W}}}(q^2)$, but rather to establish its field theoretic uniqueness, which, in view of the discussion in the previous section, would determine unambiguously the $J(q^2)$ and $m^2(q^2)$ components.

The starting point of our analysis is the tensorial decomposition of Eq. (2.7), from which the function ${{\mathcal {W}}}(q^2)$ may be projected out, according to [83]

$$\begin{aligned}&{{\mathcal {W}}}(q^2) = - \frac{1}{3} q^\sigma \mathrm{P}^{\mu \nu }(q) K_{\nu \mu \sigma }(q,0,-q) \,. \end{aligned}$$

(5.1)

Then, the use of Eq. (2.6) yields immediately

$$\begin{aligned}&{{\mathcal {W}}}(q^2) = - \frac{1}{3} q^\sigma \mathrm{P}^{\mu \nu }(q) \left[ \frac{\partial H_{\nu \mu }(q,p,r)}{\partial p^\sigma } \right] _{p = 0} \,. \end{aligned}$$

(5.2)

The tensorial decomposition of the ghost-gluon kernel is given by [82, 87, 103]

$$\begin{aligned}&H_{\nu \mu }(q,p,r) = g_{\nu \mu } A_1 + q_\mu q_\nu A_2 \nonumber \\&\quad + r_\mu r_\nu A_3 + q_\mu r_\nu A_4 + r_\mu q_\nu A_5 \,, \end{aligned}$$

(5.3)

where $A_i \equiv A_i(q,p,r)$. Then, from Eq. (5.1) we have that

$$\begin{aligned} {{\mathcal {W}}}(q^2) = - q^\sigma \left[ \frac{\partial A_1(q,p,r)}{\partial p^\sigma } \right] _{p = 0} \,. \end{aligned}$$

(5.4)

Therefore, the lattice extraction of ${{\mathcal {W}}}(q^2)$ may proceed through the corresponding determination of the form factor $A_1(q,p,r)$, for an extended set of momenta values (q, p, r).

To explore this point further, we consider the connected correlation function [104]

$$\begin{aligned}&f^{abc}\mathcal {H}^{{\scriptscriptstyle \mathrm{con}}}_{\nu \mu }(q,p,r) = f^{aem} \int d^4 x \, d^4 y \, d^4 z \, e^{-iq\cdot x - i p\cdot y - i r\cdot z}\langle \nonumber \\&\quad A_{\nu }^{e}(x) c^{m}(x) {\bar{c}}^b(y) A_{\mu }^{c}(z) \rangle \,, \end{aligned}$$

(5.5)

where A, c and ${\bar{c}}$ are gluon, ghost and anti-ghost fields, respectively. Our basic assumption will be that the $\mathcal {H}^{{\scriptscriptstyle \mathrm{con}}}_{\nu \mu }(q,p,r)$ defined in Eq. (5.5) may be simulated on the lattice, following standard theoretical procedures. Next, we introduce its amputated counterpart, $\mathcal {H}^{{\scriptscriptstyle \mathrm{amp}}}_{\nu \mu }(q,p,r)$, obtained from $\mathcal {H}^{{\scriptscriptstyle \mathrm{con}}}(q,p,r)$ through multiplication by $\Delta ^{-1}(r^2)$ and $D^{-1}(p^2)$, which are also accessible on the lattice. As can be seen in Fig. 3, $\mathcal {H}^{{\scriptscriptstyle amp}}_{\nu \mu }(q,p,r)$ consists of two pieces, the desired quantity $H_{\nu \mu }(q,p,r)$, and the “one-particle reducible” contribution, denoted by $H^{{\scriptscriptstyle \mathrm{opr}}}_{\nu \mu }(q,p,r)$, i.e.,

$$\begin{aligned} \mathcal {H}^{{\scriptscriptstyle amp}}_{\nu \mu }(q,p,r)= & {} H_{\nu \mu }(q,p,r) + H^{{\scriptscriptstyle \mathrm{opr}}}_{\nu \mu }(q,p,r) \,. \end{aligned}$$

(5.6)

$H^{{\scriptscriptstyle \mathrm{opr}}}_{\nu \mu }(q,p,r)$, in turn, may be expressed as

$$\begin{aligned} H^{{\scriptscriptstyle \mathrm{opr}}}_{\nu \mu }(q,p,r)= \Sigma _\nu (q) D(q^2)\Gamma _\mu (q,p,r)\,, \end{aligned}$$

(5.7)

where $\Gamma _\mu (q,p,r)$ is the fully-dressed ghost-gluon vertex, and $\Sigma _\nu (q)$ is shown diagrammatically in Fig. 3 [see green dashed box]; note that [104]

$$\begin{aligned}&\Sigma ^{ab}_\nu (q) D^{bc}(q^2) = g f^{anm} \int d^4 x \, e^{-i p\cdot x} \nonumber \\&\quad \langle A_{\nu }^{m}(x) c^{n}(x) {\bar{c}}^c(0) \rangle \,. \end{aligned}$$

(5.8)

Fig. 3

Diagrammatic representation of Eqs. (5.6) and (5.7). The amputated $\mathcal {H}^{{\scriptscriptstyle \mathrm{amp}}}_{\nu \mu }(q,p,r)$ expressed as the sum of the $H_{\nu \mu }(q,p,r)$, and the “one-particle reducible” contribution, $H^{{\scriptscriptstyle \mathrm{opr}}}_{\nu \mu }(q,p,r)$

The basic observation that allows the completion of this procedure is that the tensorial decomposition of $H^{{\scriptscriptstyle \mathrm{opr}}}_{\nu \mu }(q,p,r)$ does not contain a $g_{\nu \mu }$ component, simply because $\Sigma _\nu (q) = q_\nu \Sigma (q^2)$ and $\Gamma _\rho (q,p,r) = q_\rho \,B_1(q,p,r) + r_\rho \, B_2(q,p,r)$. Consequently, the co-factor of $g_{\nu \mu }$ in the tensorial decomposition of $\mathcal {H}^{{\scriptscriptstyle amp}}_{\nu \mu }(q,p,r)$ is precisely the $A_1(q,p,r)$ appearing in Eq. (5.3). Therefore, $A_1(q,p,r)$ may be finally obtained from $\mathcal {H}^{{\scriptscriptstyle amp}}_{\nu \mu }(q,p,r)$ through the action of the projector $\mathcal {R}^{\mu \nu }(q,r)$, namely [87]

$$\begin{aligned} A_1(q,p,r)= \mathcal {R}^{\mu \nu }(q,r) \mathcal {H}^{{\scriptscriptstyle amp}}_{\nu \mu }(q,p,r)\,, \end{aligned}$$

(5.9)

with

$$\begin{aligned}&\mathcal {R}^{\mu \nu }(q,r)\nonumber \\&=\frac{[q^2r^2 - (q\cdot r)^2]g^{\mu \nu } + (q\cdot r)\left( q^\mu r^\nu +q^\nu r^{\mu }\right) -r^2q^{\mu }q^{\nu } - q^2r^{\mu }r^{\nu }}{2[q^2r^2 - (q\cdot r)^2]}\,. \end{aligned}$$

(5.10)

It is clear that, in order to obtain ${{\mathcal {W}}}(q^2)$ from Eq. (5.4), the form factor $A_1(q,p,r)$ must be evaluated for various kinematic set-ups. Now, out of the three momenta q, p and r, we can treat q and p as independent. Using the standard (Euclidean space) parametrization $q = \sqrt{q^2}\,(1,0,0,0)$, $p = \sqrt{p^2}\,(\cos \theta ,\sin \theta ,0,0)$ and $r = - q - p$, the form factor $A_1(q,p,r)$ can be regarded as a function of $q^2$, $p^2$ and $\theta$, i.e., $A_1(q,p,r)\rightarrow A_1(q^2,p^2,\theta )$. Then, applying the chain rule of differentiation at the level of Eq. (5.4), it is elementary to show that

$$\begin{aligned} {{\mathcal {W}}}(q^2) = \lim _{p^2 \rightarrow 0} {{\mathcal {W}}}(q^2,p^2,\theta ) \,, \end{aligned}$$

(5.11)

where we defined a generalized function ${{\mathcal {W}}}(q^2,p^2,\theta )$ as

$$\begin{aligned} {{\mathcal {W}}}(q^2,p^2,\theta ):= & {} - 2 \sqrt{ q^2 p^2} \cos \theta \frac{\partial A_1(q^2,p^2,\theta )}{\partial p^2 } \nonumber \\&+ \sqrt{ \frac{ q^2 }{ p^2 } } \sin \theta \frac{\partial A_1(q^2,p^2,\theta )}{\partial \theta } \,. \end{aligned}$$

(5.12)

Note that the form of ${{\mathcal {W}}}(q^2,p^2,\theta )$ simplifies considerably for the choices $\theta = 0, \pi /2, \pi$.

In the absence of lattice data, we may gain a concrete insight on how the ${{\mathcal {W}}}(q^2)$ may be obtained from Eq. (5.12) by employing the results for $A_1(q^2,r^2,\theta )$ computed from the corresponding one-loop dressed SDE, given by Eq. (6.16). The derivative is taken numerically, by interpolating the grid of points for $A_1(q^2,r^2,\theta )$ with a tensor product of B-splines [105], and differentiating the interpolant.

In Fig. 4 we show the results for ${{\mathcal {W}}}(q^2,p^2,\theta )$ for $\theta = 0$, $\theta = \pi /2$ and $\theta = \pi$. Note that although the surfaces are different for each $\theta$, they all reduce to the same curve (marked in red) for $p \rightarrow 0$, which is none other than the $\widetilde{{\mathcal {W}}}(q^2)$ computed by means of Eq. (6.16), shown in Fig. 7.

Fig. 4

Generalized ${{\mathcal {W}}}(q^2,p^2,\theta )$ (colored surfaces) for $\theta = 0$ (left), $\theta = \pi /2$ (center) and $\theta = \pi$ (right). The red dashed lines are the $p \rightarrow 0$ limits, which, using Eq. (5.11), yield $\widetilde{{\mathcal {W}}}(q^2)$

6 SDE approximation of ${{\mathcal {W}}}(q^2)$

Fig. 5

The SDE governing the ghost-gluon scattering kernel

In this section we resort to the one-loop dressed SDE that governs the ghost-gluon scattering kernel $H_{\nu \mu }(q,p,r)$, in order to obtain an approximate expression for ${{\mathcal {W}}}(q^2)$.

We hasten to mention that the function $\sigma (q^2)$ obtained from this particular ${{\mathcal {W}}}(q^2)$ yields a value for $J(\mu ^2)$ that exceeds unity, and, according to the discussion following Eq. (3.6), furnishes a negative $m^2(\mu ^2)$. As we will see in the following section, this drawback will be ameliorated by adjusting appropriately (“by hand”) the form of $\sigma (q^2)$. Therefore, the computation presented here is to be understood as an initial “ballpark” estimate of the overall shape of $\sigma (q^2)$, which requires further refinement (see discussion in Sect. 8).

The starting point of the analysis are the diagrams $(d^{\nu \mu }_1)$ and $(d^{\nu \mu }_2)$ of Fig. 5, which, in the Landau gauge, may be easily cast in the form [see also Eq. (2.5)]

$$\begin{aligned} (d^{\nu \mu }_i) = p_\rho K_{i}^{\nu \mu \rho }(r,p,q)\,, \qquad i=1,2 \,. \end{aligned}$$

(6.1)

In order to make contact with Eq.  (2.6), the two $K_{i}^{\nu \mu \rho }(r,p,q)$ must be subsequently evaluated in the asymmetric limit, $p=0$.

The ghost-gluon vertex, $\Gamma _\mu (q,p,r)$, appearing in both diagrams, reads

$$\begin{aligned} \Gamma _\mu (q,p,r) = q_\mu B_1(q,p,r) + r_\mu B_2(q,p,r)\,, \end{aligned}$$

(6.2)

where, in the Landau gauge, only the first component survives.

Setting $t :=q-\ell$, the three-gluon vertex $\Gamma ^{\mu \alpha \beta }(-q,t,\ell )$ of diagram $(d^{\nu \mu }_2)$ is conveniently decomposed into “longitudinal” and “transverse” contributions [82],

$$\begin{aligned} \Gamma ^{\mu \alpha \beta }(-q,t,\ell ) = {\Gamma }_{\!\!{{\scriptscriptstyle \mathbf {L}}}}^{\mu \alpha \beta }(-q,t,\ell ) + {\Gamma }_{\!\!{{\scriptscriptstyle \mathbf {T}}}}^{\mu \alpha \beta }(-q,t,\ell ) \,, \end{aligned}$$

(6.3)

with [69, 82, 103, 106],

$$\begin{aligned}&{\Gamma }_{\!\!{{\scriptscriptstyle \mathbf {L}}}}^{\mu \alpha \beta }(-q,t,\ell ) = \sum _{i = 1}^{10} X_i(-q,t,\ell ) \ell ^{\mu \alpha \beta }_i \,,\qquad \nonumber \\&\quad {\Gamma }_{\!\!{{\scriptscriptstyle \mathbf {T}}}}^{\mu \alpha \beta }(-q,t,\ell ) = \sum _{i = 1}^{4} Y_i(-q,t,\ell ) t^{\mu \alpha \beta }_i \,, \end{aligned}$$

(6.4)

where the explicit form of the basis tensors $\ell _i$ and $t_i$ is given in Eqs. (3.4) and (3.5) of [69].

The multiplicative renormalization of the SDE of Fig. 5 proceeds by substitution of the unrenormalized quantities by their renormalized counterparts, denoted by a subscript R, through the relations

$$\begin{aligned} \Delta _{{\scriptscriptstyle R}}(q^2)= & {} {Z}_A^{-1} \Delta (q^2) \,, \nonumber \\ F_{{\scriptscriptstyle R}}(q^2)= & {} {Z}_c^{-1} F(q^2) \,, \nonumber \\ \Gamma ^\mu _{{\scriptscriptstyle R}}(q,p,r)= & {} \widetilde{Z}_1 \Gamma ^\mu (q,p,r) \,, \nonumber \\ \Gamma ^{\alpha \mu \nu }_{{\scriptscriptstyle R}}(q,p,r)= & {} \widetilde{Z}_3 \Gamma ^{\alpha \mu \nu }(q,p,r) \,, \nonumber \\ g_{{\scriptscriptstyle R}} = Z_g^{-1} g= & {} \widetilde{Z}_1^{-1}{Z}_A^{1/2}{Z}_c \, g = \widetilde{Z}_3^{-1}{Z}_A^{3/2}g \,, \end{aligned}$$

(6.5)

where g is the coupling constant. Then, using the identity $q^\nu H_{\nu \mu }(q,p,r) = \Gamma _\mu (q,p,r)$ [87] and Eq. (2.5) it is straightforward to see that the $K_i^{\nu \mu \rho }$ should renormalize as $\Gamma _\mu (q,p,r)$, i.e.,

$$\begin{aligned} K_{i,\, {{\scriptscriptstyle R}}}^{\nu \mu \rho }(q,p,r) = \widetilde{Z}_1 K_{i}^{\nu \mu \rho }(q,p,r) \,. \end{aligned}$$

(6.6)

After implementing the above replacements into the unrenormalized SDE it is easy to check that the only renormalization constant remaining in the expressions for the $K_{i,\, {{\scriptscriptstyle R}}}^{\nu \mu \rho }$ is the finite $\widetilde{Z}_1$.

$\widetilde{Z}_1$ can be determined by imposing the “asymmetric” MOM scheme conditions,

$$\begin{aligned} \Delta _{{\scriptscriptstyle R}}^{-1}(\mu ^2) = \mu ^{2} \,; \qquad \quad F_{{\scriptscriptstyle R}}(\mu ^2) = 1\,; \quad \quad L^\mathrm {asym}_{{\scriptscriptstyle R}}(\mu ^2) = 1\,, \nonumber \\ \end{aligned}$$

(6.7)

chosen because it was implemented on the lattice data of [88, 89]. Then, using the STI for the renormalization constants, $\widetilde{Z}_1 = \widetilde{Z}_3 {Z}_c {Z}_A^{-1}$, one finds, in terms of the unrenormalized propagators and three-gluon vertex,

$$\begin{aligned} \widetilde{Z}_1 = \frac{F(\mu ^2)}{\mu ^2\Delta (\mu ^2)L^\mathrm {asym}(\mu ^2)} \,. \end{aligned}$$

(6.8)

In practice, since $\widetilde{Z}_1$ is finite and $\mu$ rather large (4.3 GeV), we will approximate Eq. (6.8) by means of a perturbation expression [see Eq. (6.18)].

From now on, the subscript “R” will be suppressed, being understood that all quantities are renormalized as described above.

Then, Eq. (5.1) is employed to project out ${{\mathcal {W}}}(q^2)$, and the results obtained are passed to Euclidean space, following standard conventions (see, e.g., Eq. (5.1) of [87]), and spherical coordinates are used. To that end, we introduce the kinematic variables $x := q^2$, $y:= \ell ^2$, and $u := y+x - 2 \sqrt{y x }c_{\phi }$, with $s_{\phi } := \sin \phi$, $c_{\phi } := \cos \phi$, where $\phi$ denotes the angle between the virtual momentum $\ell$ and the physical momentum q. Furthermore, the vertex form factors are expressed as functions of the squares of their incoming momenta, e.g., $B_i(q - \ell ,\ell ,- q) \rightarrow B_i(u,y,x)$. Then, the complete one-loop dressed expression for ${{\mathcal {W}}}(x)$, renormalized within the “asymmetric” MOM scheme, is given by

$$\begin{aligned} {{\mathcal {W}}}(x) ={{\mathcal {W}}}_{1}(x) + {{\mathcal {W}}}_{2}(x) \,, \end{aligned}$$

(6.9)

with

$$\begin{aligned} {{\mathcal {W}}}_{1}(x)= & {} \lambda \int _0^\infty \!\!\!\! dy \sqrt{xy} \Delta (y) F(y) \int _0^\pi \!\!\! d\phi \, s^4_{\phi } c_{\phi } \,\nonumber \\&\times \frac{F(u)}{u} B_1( y, 0, y )B_1(u,y,x) \,, \nonumber \\ {{\mathcal {W}}}_{2}(x)= & {} - 2 \lambda \int _0^\infty \!\!\!\! dy y \sqrt{xy} \Delta (y) \!\nonumber \\&\times \int _0^\pi \!\!\!\! d\phi \, s^4_{\phi } \Delta (u) B_1(u,0,u) \, \frac{F(u)}{u^2} \,{{\mathcal {K}}}(x,y,u)\,,\nonumber \\ \end{aligned}$$

(6.10)

where the kernel appearing in the second equation is defined as

$$\begin{aligned} {{\mathcal {K}}}(x,y,u):= & {} (x - c_\phi \sqrt{x\,y})c_\phi X_1\nonumber \\&+( y - c_\phi \sqrt{x\,y} )c_\phi X_4\nonumber \\&- \sqrt{x\,y}( s_\phi ^2 - 3 ) X_7 - c_\phi x \,u X_3 \nonumber \\&- c_\phi y \, u X_6 - 3c_\phi x \, y X_9 \nonumber \\&+ \frac{1}{2}{c_\phi x \, y \, u}( Y_1 + Y_2 + 3Y_3 ) - u \sqrt{x \,y}\, Y_4 \,, \nonumber \\ \end{aligned}$$

(6.11)

and

$$\begin{aligned} \lambda := C_\mathrm {A} \alpha _s {{\widetilde{Z}}}_1/12\pi ^2, \end{aligned}$$

(6.12)

In addition, we suppress the functional dependence of $X_i \equiv X_i( x, u, y )$ and $Y_j \equiv Y_j( x, u, y )$ for compactness. Note that the three-gluon vertex form factors $X_i$ with $i = 2, \,5, \,8$ and 10 do not contribute to ${{\mathcal {W}}}(x)$ in the Landau gauge.

Past this point, we will introduce a number of approximations for the various form factors entering in Eqs. (6.10) and (6.11), in order to simplify the numerical treatment. In particular, we retain only the longitudinal form factors $X_i$ of $\Gamma ^{\mu \alpha \beta }(-q,t,\ell )$. Also, since several studies found rather weak dependence of the full three-gluon vertex on the specific kinematics [64, 69, 88, 107], we further approximate the $X_i$ by restricting them to the “totally symmetric configuration” $y = u = x$, i.e.,

$$\begin{aligned} X_i( x, u, y ) \rightarrow X_i^s(y)\,. \end{aligned}$$

(6.13)

For the form factors $B_1$, we first apply the symmetrization procedure expressed by Eq. (3.6) of Ref. [87], to preserve the Landau gauge ghost-anti-ghost symmetry of the ghost-gluon vertex² [86, 87, 108]. This operation entails the substitution

$$\begin{aligned}&B_1 (y,0,y) \rightarrow \frac{1}{2}[B_1(y,0,y) + B_1(x,u,y)] \,, \,\, \nonumber \\&\quad B_1 (u,0,u) \rightarrow \frac{1}{2}[B_1(u,0,u) + B_1(x,u,y)] \,, \end{aligned}$$

(6.14)

in Eq. (6.10). Then, in analogy to Eq. (6.13), the $B_1$ are also considered to depend on a single kinematic variable, namely the momentum of the gluon entering into each ghost-gluon vertex, which corresponds to the third argument of each $B_1$. The final outcome of these approximations is to substitute in Eq. (6.10)

$$\begin{aligned}&B_1(u,y,x) \rightarrow B_1(x)\,,\,\, B_1(y,0,y) \rightarrow B_1(y)\,,\,\, \nonumber \\&\quad B_1 (u,0,u) \rightarrow {{\overline{B}}}_1(u,y)\,, \end{aligned}$$

(6.15)

where ${{\overline{B}}}_1(u,y) := \frac{1}{2}[ B_1(u) + B_1(y)]$. Lastly, the one-variable $B_1$ is taken to correspond to the so-called “soft-ghost” configuration, $p = 0$, of the general kinematics form factor. This configuration is the most natural choice, since it is exact for $B_1(y,0,y)$ and $B_1(u,0,u)$.

Fig. 6

$X_1^{s}(q^2)$, $q^2X_3^{s}(q^2)$ in the symmetric configuration, and $B_1(q^2)$ in the “soft-ghost” limit

Denoting by $\widetilde{{\mathcal {W}}}_{1}(x)$ and $\widetilde{{\mathcal {W}}}_{2}(x)$ the quantities obtained from Eq. (6.10) after the implementation of the above approximations, and by $\widetilde{{\mathcal {W}}}(x)$ their sum, as indicated by Eq. (6.9), we have

$$\begin{aligned} \widetilde{{\mathcal {W}}}_{1}(x)= & {} \lambda B_1(x)\int _0^\infty \!\!\!\! dy \sqrt{xy} \Delta (y) F(y) B_1(y)\nonumber \\&\times \int _0^\pi \!\!\! d\phi \, s^4_{\phi } c_{\phi } \,\frac{F(u)}{u} \,, \nonumber \\ \widetilde{{\mathcal {W}}}_{2}(x)= & {} - 2\lambda \int _0^\infty \!\!\!\! dy y \sqrt{xy} \Delta (y) \!\int _0^\pi \!\!\!\! d\phi \, \nonumber \\&\times s^4_{\phi } \Delta (u) {{\overline{B}}}_1(u,y) \, \frac{F(u)}{u^2} \,\widetilde{{\mathcal {K}}}(x,y,u) \,, \end{aligned}$$

(6.16)

with

$$\begin{aligned} \widetilde{{\mathcal {K}}}(x,y,u):= & {} (u c_\phi - \sqrt{y x } s_\phi ^2 \nonumber \\&+ 3 \, \sqrt{y x })X_1^{s}(y) - c_\phi [ ( x + y )u + 3xy ]X_3^{s}(y).\nonumber \\ \end{aligned}$$

(6.17)

The numerical evaluation of the above formulas proceeds by substituting into Eq. (6.16) known results for the various functions entering in it.

Specifically, for $\Delta (q^2)$ and $F(q^2)$ we use the standard fits given in Eqs. (4.1) and (6.1) of [87], respectively, which are in excellent agreement with the quenched SU(3) lattice data of [3]. In particular, from Eq. (6.1) of [87], one has $F(0) = 2.82$. Notice that both quantities are renormalized at $\mu = 4.3$ GeV, and we employ $\alpha _s = 0.27$, as determined by the lattice simulation of [89].

In addition, for $X_1^{s}(y)$ and $X_3^{s}(y)$ we use the results of [69] [ see left and central panels of Fig. 6], while $B_1(y)$ [see right panel of Fig. 6] is obtained from [87].

Finally, for the “asymmetric” MOM scheme $\widetilde{Z}_1$ we use value

$$\begin{aligned} {{\widetilde{Z}}}_1 \approx 1 - \frac{37 C_\mathrm {A} \alpha _s}{96\pi } \approx 0.9 \,, \end{aligned}$$

(6.18)

whose determination is based on the one-loop analysis presented in Appendix A of [83].

Fig. 7

The individual contributions $\widetilde{{{\mathcal {W}}}}_{1}(q^2)$ and $\widetilde{{{\mathcal {W}}}}_{2}(q^2)$ given by Eq. (6.16), and their respective sum $\widetilde{{{\mathcal {W}}}}(q^2)$ (left panel). The corresponding ${\widetilde{\sigma }}(q^2)$ determined using the Eq. (3.4)

The resulting $\widetilde{{\mathcal {W}}}(q^2)$, and the corresponding ${{\widetilde{\sigma }}}(q^2)$ obtained from Eq. (3.4), are shown in Fig. 7; as can be seen in the inset, $\widetilde{{\mathcal {W}}}_{2}(x)$ captures the main bulk of the total contribution to $\widetilde{{\mathcal {W}}}(x)$. As is clear from Eq. (6.16), we find that $\widetilde{{\mathcal {W}}}(0)=0$, which, due to Eq. (3.4), implies that ${{\widetilde{\sigma }}}(0)=1$.

It turns out that ${{\widetilde{\sigma }}}(q^2)$ can be accurately fitted [see Fig. 7] by the functional form

$$\begin{aligned} {{\widetilde{\sigma }}}(q^2) = \exp \left[ - \frac{s_{\scriptscriptstyle \mathrm {1}} (q^2/s_{\scriptscriptstyle \mathrm {2}})^{s_{\scriptscriptstyle \mathrm {3}}} }{1 + ( q^2/s_{\scriptscriptstyle \mathrm {2}} )^{s_{\scriptscriptstyle \mathrm {4}}} }\right] \,, \end{aligned}$$

(6.19)

where the adjustable parameters are $s_{\scriptscriptstyle \mathrm {1}} = 2.91$, $s_{\scriptscriptstyle \mathrm {2}} = 1.57$ $\hbox {GeV}^2$, $s_{\scriptscriptstyle \mathrm {3}} = 1.22$, and $s_{\scriptscriptstyle \mathrm {4}} = 1.07$.

From Eq. (3.4), it is straightforward to see that

$$\begin{aligned} {\mathcal {W}}(q^2) = {{\widetilde{Z}}}_1 q^2 \frac{d\ln [ {\sigma }(q^2) ]}{dq^2} \,. \end{aligned}$$

(6.20)

Then, combining Eqs. (6.19) and (6.20), one obtains an excellent fit for $\widetilde{{\mathcal {W}}}(q^2)$, given by

$$\begin{aligned} \widetilde{\mathcal {W}}(q^2) = - \frac{ {{\widetilde{Z}}}_1 s_{\scriptscriptstyle \mathrm {1}} (q^2/s_{\scriptscriptstyle \mathrm {2}})^{s_{\scriptscriptstyle \mathrm {3}} + s_{\scriptscriptstyle \mathrm {4}} }\left[ s_{\scriptscriptstyle \mathrm {3}} - s_{\scriptscriptstyle \mathrm {4}} + s_{\scriptscriptstyle \mathrm {3}}(q^2/s_{\scriptscriptstyle \mathrm {2}})^{-s_{\scriptscriptstyle \mathrm {4}}} \right] }{\left[ 1 + ( q^2/s_{\scriptscriptstyle \mathrm {2}} )^{s_{\scriptscriptstyle \mathrm {4}}} \right] ^2} \,. \nonumber \\ \end{aligned}$$

(6.21)

Note that variations of the fit given in Eq. (6.19) will be used extensively in the numerical analysis presented in the following section.

7 Determining $J(q^2)$ and $m^2(q^2)$

We next turn to the numerical treatment of the ODE solution given in Eq. (3.9), followed by the indirect determination of $m^2(q^2)$ from the lattice data for the gluon propagator reported in [3].

7.1 General considerations

The two key equations for our analysis are the ODE solution and its initial condition, given by Eqs. (3.9) and (3.6), respectively. As already mentioned in Sect. 3, the numerical value that arises from the computation of the integral on the r.h.s. of Eq. (3.6) is not a-priori known, and must be adjusted by resorting to certain general physical considerations. In particular, due to the MOM condition $\Delta ^{-1}(\mu ^2)=\mu ^2$, $J(\mu ^2)$ and $m^2(\mu ^2)$ are related by

$$\begin{aligned} J(\mu ^2) = 1- \frac{m^2(\mu ^2)}{\mu ^2}\,; \end{aligned}$$

(7.1)

therefore, any theoretical input on the behavior of $m^2(q^2)$ in the vicinity of $\mu$ will automatically reflect on the value of $J(\mu ^2)$.

At this stage, there are three theoretical requirements imposed on $m^2(q^2)$ : (a) it remains positive-definite for all momenta (no “tachyonic” solutions), (b) it displays a power-law running as $q^2\rightarrow \infty$, modulated by renormalization-group logarithms, and (c) is a monotonically decreasing function, i.e., $dm^2(q^2)/dq^2 < 0$, within the entire range of space-like (Euclidean) momenta.

While the motivation behind condition (a) is easy to appreciate, the remaining two requirements need some additional clarifications. Regarding (b), as has been argued in a series of articles [109,110,111,112,113], the operator-product expansion of the gluon propagator indicates that $m^2(q^2)$ must behave as $m^2(q^2)\sim q^{-2} \sum _i c_i \,{{\mathcal {O}}}_i^{(d=4)}$, where ${{\mathcal {O}}}_i^{(d=4)}$ denote all relevant dimension 4 condensates, (e.g., gluon condensate, $\langle 0\vert \!\!: \!G^a_{\mu \nu }G^{\mu \nu }_a\!\!:\!\vert 0\rangle$), and $c_i$ are (gauge-dependent) constants. As for (c), the Bethe-Salpeter amplitude that controls the formation of the massless bound state excitations is proportional to $dm^2(q^2)/dq^2$ [24]; and the analysis of the corresponding dynamical equation reveals that the resulting amplitude has a fixed sign for all momenta [24, 79, 81].

Evidently, from condition (a) follows that $J(\mu ^2) < 1$. From condition (c), it is clear that the value of the gluon propagator at the origin furnishes an upper bound on $m^2(\mu ^2)$, because monotonicity implies that $m^2(\mu ^2) < m^2(0) = \Delta ^{-1}(0)$. Since, in addition, from Eq. (7.1), $m^2(\mu ^2) = \mu ^2[1-J(\mu ^2)]$, one arrives at the inequality $\mu ^2[1-J(\mu ^2)] < m^2(0)$. Then, combining the two constraints from (a) and (c), we obtain the allowed range for $J(\mu ^2)$, valid for any $\mu$, namely

$$\begin{aligned} 1 - \frac{m^2(0)}{\mu ^2}< J(\mu ^2) < 1, \quad \forall \, \mu \,. \end{aligned}$$

(7.2)

For the particular choice $\mu = 4.3$ GeV, which corresponds to the largest available momentum in the lattice data of [89], we have that $\Delta ^{-1}(0) \approx 0.15 \,\mathrm{GeV}^2$, and Eq. (7.2) yields

$$\begin{aligned} 0.992< J(\mu ^2)< 1, \quad \mu = 4.3 \, \mathrm{GeV}. \end{aligned}$$

(7.3)

Finally, when condition (b) is invoked, the allowed interval for $J(\mu ^2)$ becomes even narrower than the one quoted in Eq. (7.2); indeed, if the power-law behavior has set in at energies comparable to the renormalization point, $m^2(\mu ^2)$ is expected to be considerably smaller than $m^2(0)$, forcing $J(\mu ^2)$ to deviate from unity only by a slight amount.

It turns out that the initial estimate of $\sigma (q^2)$, namely the ${{\widetilde{\sigma }}}(q^2)$ obtained in the previous section, when substituted into Eq. (3.6), yields the value $J(\mu ^2) = 1.14$, which clearly violates the bound given in Eq. (7.2). Therefore, the ${{\widetilde{\sigma }}}(q^2)$ will be duly deformed, by appropriately adjusting the parameters entering in the fit of Eq. (6.19). In particular, a set of $m^2(\mu ^2)$ is chosen that is generally compatible with the trend described in (b) and (c), the corresponding values for $J(\mu ^2)$ are computed from Eq. (7.1), and $\sigma (q^2)$ is engineered such that, when inserted into the r.h.s. of Eq. (3.6), the prescribed value for $J(\mu ^2)$ emerges.

It must be clear from these comments that, due to the uncertainties related with the computation of the ${{\mathcal {W}}}(q^2)$ and $\sigma (q^2)$, the solutions obtained from this treatment are expected to display a considerable spread. As may be seen on the left panel of Fig. 13, this effect is particularly pronounced in the case of the running masses $m^2(q)$. Evidently, in practice, the mathematical uniqueness advocated in the previous sections is compromised due to inherent computational limitations.

Fig. 8

The lattice data for $L^\mathrm {asym}(q^2)$ (circles) from [88, 89], and the fit given by Eq. (7.4) (black continuous curve), and the green shaded band defining the spread

Fig. 9

Left panel: the $\sigma (q^2)$ that, when inserted into Eq. (3.6), give rise to the values of $J(\mu ^2)$ associated with the $m^2(\mu ^2)$ reported in the legend. The three central curves are obtained by adjusting the fitting parameters of Eq. (6.19) as quoted in Table 1.  Right panel: the corresponding curves ${{\mathcal {W}}}(q^2)$, given by (6.20). The reference curves ${\widetilde{\sigma }}(q^2)$ and $\widetilde{{\mathcal {W}}}(q^2)$, given by Eqs. (6.19) and (6.21), are also shown for comparison

7.2 Input for $L^\mathrm {asym}(q^2)$

The necessary input for $L^\mathrm {asym}(q^2)$, required for the determination of $f_2(q^2)$ through Eq. (3.2), is obtained from the lattice data of [88, 89], shown in Fig. 8. Specifically, we use a fit to the data, whose functional form is given by

$$\begin{aligned} L^\mathrm {asym}(q^2)= & {} F(q^2)T(q^2) + \nu _{\scriptscriptstyle \mathrm {1}} \nonumber \\&\times \left( \frac{1}{ 1 + ( q^2 /\nu _{\scriptscriptstyle \mathrm {2}} )^2 } - \frac{1}{ 1 + ( \mu ^2 /\nu _{\scriptscriptstyle \mathrm {2}} )^2 } \right) \,, \end{aligned}$$

(7.4)

with

$$\begin{aligned} T(q^2)= & {} 1 + \frac{ 3 \lambda _s }{ 4 \pi }\left( 1 + \frac{ \tau _{\scriptscriptstyle \mathrm {1}} }{ q^2 + \tau _{\scriptscriptstyle \mathrm {2}} } \right) \nonumber \\&\times \left[ 2 \ln \left( \frac{q^2 + \eta ^2(q^2)}{\mu ^2 + \eta ^2(\mu ^2)} \right) + \frac{1}{6}\ln \left( \frac{q^2}{\mu ^2}\right) \right] \,, \end{aligned}$$

(7.5)

where $F(q^2)$ is again given by Eq. (6.1) of [87], and

$$\begin{aligned} \eta ^2(q^2) = \frac{\eta _{\scriptscriptstyle \mathrm {1}} }{q^2 + \eta _{\scriptscriptstyle \mathrm {2}} } \,. \end{aligned}$$

(7.6)

The values of the parameters are $\lambda _s=0.276$, $\tau _{\scriptscriptstyle \mathrm {1}} = 4.05$ $\hbox {GeV}^2$, $\tau _{\scriptscriptstyle \mathrm {2}} = 0.16$ $\hbox {GeV}^2$ , $\nu _{\scriptscriptstyle \mathrm {1}} = 0.52$, $\nu _{\scriptscriptstyle \mathrm {2}} = 0.012$ $\hbox {GeV}^2$, and $\eta _{\scriptscriptstyle \mathrm {2}} = 0.41$ $\hbox {GeV}^2$, and $\eta _{\scriptscriptstyle \mathrm {1}} =10.2$ $\hbox {GeV}^4$. This fit has a $\chi ^2/\mathrm{d.o.f} = 0.024$, and satisfies, by construction the “asymmetric” MOM renormalization condition, i.e., $L^{\mathrm {asym}}(\mu ^2)=1$, employed in Eq. (3.1).

The sizable errors displayed by the lattice points, especially for low momenta, motivate the use of a band rather than a single curve for $L^\mathrm {asym}(q^2)$. In particular, the green-shaded band surrounding the central curve encompasses partially the spread of the data in the infrared region. The curves delimiting this band are obtained by varying the parameter $\eta _{{\scriptscriptstyle 1}}$ by $\pm 2\%$, keeping all other fitting parameters fixed. This variation produces a spread in $L^\mathrm {asym}(q^2)$, which ranges from $\pm \, 40\%$ to $\pm \,20\%$ as one moves from 100 to 300 MeV.

7.3 Results

(i) The starting point of the numerical analysis is the choice of the interval where the values of $m^2(\mu ^2)$ are expected to lie. In the absence of a strict theoretical argument, we resort to previous SDE-based results [58, 75, 76], and, for $\mu = 4.3$ GeV, we consider the following three values: $m^2(\mu ^2)=(35 \, \mathrm{{MeV}})^2$, $m^2(\mu ^2)=(50 \, \mathrm{{MeV}})^2$, and $m^2(\mu ^2)=(100 \, \mathrm{{MeV}})^2$. Then, from Eq. (7.1) we have that $J(\mu ^2)=0.9999$, $J(\mu ^2)=0.9998$, and $J(\mu ^2) = 0.9994$, respectively.

Table 1 Values of the fitting parameters of $\sigma (q^2)$ given by Eq. (6.19)

(ii) Next, we generate new versions of $\sigma (q^2)$, by adjusting the fitting parameters of Eq. (6.19), such that the values of $J(\mu ^2)$ corresponding to the selected $m^2(\mu ^2)$ are accurately reproduced through Eq. (3.6). Since, as mentioned above, there is a band associated with $L^\mathrm {asym}(q^2)$, the estimated $\sigma (q^2)$ for each $J(\mu ^2)$ forms also a band rather than a single curve. As can be seen on the left panel of Fig. 9, the $\sigma (q^2)$ form three distinct “clusters”, whose bands are barely discernible; the specific values of the fitting parameters giving rise to the three central curves are quoted in Table 1. Observe that, as $m^2(\mu ^2)$ decreases, $\sigma (q^2)$ drops faster in the region of momenta ($0-1$) GeV.

The corresponding set of ${{\mathcal {W}}}(q^2)$, obtained by means of (6.20), are displayed on the right panel of Fig. 9; in this case, the bands associated with them are clearly visible.

(iii) We are now in position to determine $J(q^2)$, by substituting into Eq. (3.9) the $L^\mathrm {asym}(q^2)$ and $\sigma (q^2)$ introduced above. The results, for the three choices of $J(\mu ^2)$ mentioned in (i), are shown in Fig. 10. Evidently, the bands associated with the inputs induce corresponding bands to the solutions for $J(q^2)$, which can be clearly seen in the corresponding plots. The three sets of $J(q^2)$ are practically indistinguishable; plainly, the implementation of different boundary conditions, which differ at the fourth decimal place, is imperceptible at the level of $J(q^2)$. However, as we will see below, these minute differences have sizable impact on the behavior of $m^2(q^2)$.

Fig. 10

The kinetic term $J(q^2)$ obtained from Eq. (3.9) for the boundary conditions: (i) $J(\mu ^2)=0.9999$ or equivalently $m^2(\mu ^2)=(35\,\mathrm{{MeV}})^2$ (left panel); (ii) $J(\mu ^2)=0.9998$ or equivalently $m^2(\mu ^2)=(50\,\mathrm{{MeV}})^2$ (central panel); (iii) $J(\mu ^2)=0.9994$ or equivalently $m^2(\mu ^2)=(100\,\mathrm{{MeV}})^2$ (right panel)

All $J(q^2)$ may be accurately fitted within the interval $q^2\in [10^{-3}, 50]\,\text { GeV}^2$ by means of minimal variations in the adjustable parameters of the function

$$\begin{aligned} J(q^2)= & {} 1 + \frac{ 3 \lambda _{{\scriptscriptstyle \mathrm {\omega }}} }{ 4 \pi }\left( 1 + \frac{ \omega _{\scriptscriptstyle \mathrm {1}} }{ q^2 + \omega _{\scriptscriptstyle \mathrm {2}} } \right) \nonumber \\&\times \left[ 2 \ln \left( \frac{q^2 + \eta ^2(q^2)}{\mu ^2 + \omega _{\scriptscriptstyle \mathrm {3}}} \right) + \frac{1}{6}\ln \left( \frac{q^2}{\mu ^2}\right) \right] \,, \end{aligned}$$

(7.7)

with $\eta ^2(q^2)$ given by Eq. (7.6). For the $J(q^2)$ corresponding to $m^2(\mu ^2) = (50\,\text {MeV})^2$ (middle panel of Fig. 10), the values of the fitting parameters are $\lambda _{{\scriptscriptstyle \mathrm {\omega }}}=0.379$, $\omega _{\scriptscriptstyle \mathrm {1}}=1.53$ $\hbox {GeV}^2$, $\omega _{\scriptscriptstyle \mathrm {2}}=0.084$ $\hbox {GeV}^2$, $\omega _{\scriptscriptstyle \mathrm {3}}=0.291$ $\hbox {GeV}^2$, $\eta _{\scriptscriptstyle \mathrm {1}}=5.24$ $\hbox {GeV}^4$, and $\eta _{\scriptscriptstyle \mathrm {2}}=0.226$ $\hbox {GeV}^4$.

Note that, in the deep infrared, $q^2 < 10^{-3}\text { GeV}^2$, this particular fit departs by $10\%$ from the correct rate of logarithmic divergence³ displayed by the solution.

As can be seen on the left panel of Fig. 11, the tiny differences between the various $J(q^2)$ may be better appreciated by forming the quantity $q^2 J(q^2)$, which is the natural combination entering in the gluon propagator. In the right panel of the same figure we zoom into the vicinity of $\mu ^2$, where the difference in the initial conditions becomes fairly distinguishable.

Fig. 11

Left panel: the product $q^2J(q^2)$ and corresponding bands. Right panel: a magnification in the renormalization region. Notice that, exactly at $\mu ^2$, the band associated to each curve disappears, because the boundary condition is also fulfilled by the limiting curves

(iv) Finally, we combine the $J(q^2)$ determined above with the lattice data for the gluon propagator reported in [3], in order to deduce the form of the mass function $m^2(q^2)$.

In principle, a simple subtraction of $q^2J(q^2)$ from $\Delta ^{-1}(q^2)$ should suffice for recovering the desired quantity, namely $m^2(q^2) = \Delta ^{-1}(q^2) - q^2J(q^2)$. In fact, in the ideal case of vanishing error bars, this operation would furnish a unique result, as already explained in Sect. 4. In practice, however, for momenta larger than 1 GeV, this particular approach is prone to numerical instabilities,⁴ and must be replaced by a more robust method.

Specifically, we first introduce certain functional forms for $m^2(q^2)$, which accommodate the three requirements, (a)-(c), postulated in Sect. 7.1, and, in addition, contain adjustable parameters that control the size and shape of $m^2(q^2)$ in the intermediate range of momenta. These functional forms are then combined with the $q^2J(q^2)$ obtained in the previous step, in order to construct the gluon propagator $\Delta (q^2)$, and its dressing function $q^2 \Delta (q^2)$. The parameters controlling the shape of $m^2(q^2)$ are then adjusted such that the resulting $\Delta (q^2)$ and $q^2 \Delta (q^2)$ match as accurately as possible the lattice data of [3].

The three functional forms for $m^2(q^2)$ that we will employ are given by

$$\begin{aligned} m^2(q^2)= & {} \frac{m_{\scriptscriptstyle \mathrm {0}}^2 }{1 +(q^2/{\kappa _{\scriptscriptstyle \mathrm {A}}^2})\ln [ (q^2 + \kappa _{\scriptscriptstyle \mathrm {B}}^2 )/\kappa _{\scriptscriptstyle \mathrm {B}}^2 ] } \,, \end{aligned}$$

(7.8)

$$\begin{aligned} m^2(q^2)= & {} \frac{m_{\scriptscriptstyle \mathrm {0}}^2\left[ 1 + (\kappa _{\scriptscriptstyle \mathrm {C}}^2/\kappa _{\scriptscriptstyle \mathrm {D}}^2)^{1 + \gamma } \right] }{1 + [ (q^2 + \kappa _{\scriptscriptstyle \mathrm {C}}^2)/\kappa _{\scriptscriptstyle \mathrm {D}}^2 ]^{1 + \gamma } }\,, \end{aligned}$$

(7.9)

$$\begin{aligned} m^2(q^2)= & {} \frac{m_{\scriptscriptstyle \mathrm {0}}^2}{1 + b_1q^2 + b_2 q^4 } \,. \end{aligned}$$

(7.10)

The results obtained using the form of Eq. (7.8) and implementing a standard $\chi ^2$ minimization procedure are shown in Figs. 12,  13, and in Table 2.

Fig. 12

The gluon propagator, ${\Delta }(q^2)$ (first column), the gluon dressing function, $q^2\Delta (q^2)$ (second column), and the dynamical gluon mass, $m^2(q^2)$ (third column), obtained by fixing the values $m^2(\mu ^2)=(35\,\mathrm{{MeV}})^2$ (blue curves), $m^2(\mu ^2)=(50\,\mathrm{{MeV}})^2$ (purple curves), and $m^2(\mu ^2)=(100\,\mathrm{{MeV}})^2$ (green curves)

Fig. 13

Left panel: direct comparison of the solid curves for $m^2(q^2)$ shown on the panels of the third column of Fig. 12. Right panel: the central $m^2(q^2)$ for $m^2(\mu ^2)=(50\,\mathrm{{MeV}})^2$, evaluated using the three functional forms introduced in Eqs. (7.8), (7.9) and (7.10)

Focusing on Fig. 12, it is interesting to notice that, as the value of $m^2(\mu ^2)$ increases, the bands for $\Delta (q^2)$ and $q^2 \Delta (q^2)$ become narrower, while the corresponding bands for $m^2(q^2)$ get wider. This trend may be understood by recognizing that the fitting procedure employed is constrained, in the sense that the requirements of monotonicity and positivity for $m^2(q^2)$ take precedence over minimizing the value of $\chi ^2$ when matching $\Delta (q^2)$ with the lattice data. Clearly, as $m^2(\mu ^2)$ approaches zero, the requirement of positivity imposed on the $m^2(q^2)$ becomes increasingly harder to fulfill: evidently, if $m(q^2)$ is close to zero at $\mu =4.3\, {GeV}$, it is more likely to turn negative as $q^2$ increases further. Therefore, the fitting parameters in Eqs. (7.8), (7.9), and (7.10) must be tightly interlocked in order to prevent this, thus reducing the available parameter space, and leaving little room for improving the shape of $\Delta (q^2)$. As a result, the functional space for $m^2(q^2)$ gets limited (narrow bands), while the error in matching the lattice $\Delta (q^2)$ increases (wide bands). As $m^2(\mu ^2)$ increases, the fitting becomes more “comfortable”, thus extending the available parameter space; this gives rise to smaller $\chi ^2$ for $\Delta (q^2)$ (narrower bands), while increasing the range of acceptable $m^2(q^2)$ (wider bands).

The use of the other two functional forms for $m^2(q^2)$, namely Eqs. (7.9) and (7.10), produces results that are practically indistinguishable at the level of $\Delta (q^2)$ and $q^2 \Delta (q^2)$; the difference in the corresponding $m^2(q^2)$ is also negligible, as may be clearly seen from the right panel of Fig. 13. This observation suggests that, once the main theoretical features [(a)–(c) mentioned above], have been incorporated into the fitting functions, the results are essentially insensitive to the particular details of the functional forms used.

Table 2 Values of the fitting parameters entering in the fit expressions for $m^2(q^2)$ given by Eqs. (7.8), (7.9), and (7.10). These values reproduce the curves shown in Fig. 13

8 Discussion and conclusions

In this article we have developed a novel approach for the accurate determination of the kinetic and mass terms of the gluon propagator, $J(q^2)$ and $m^2(q^2)$, respectively, based on a first-order linear ODE, satisfied by the former quantity. The validity of the ODE is a direct consequence of a special hypothesis, according to which, the regular part of the three-gluon vertex and the $J(q^2)$ are related by a variant of the fundamental STI. This STI is evaluated in the limit of one vanishing gluon momentum (“asymmetric configuration”), where all kinematic dependence is reduced to that of a single momentum scale, $q^2$. The main ingredients entering in the ODE originate from the three-point sector of the theory: a particular projection, $L^\mathrm {asym}(q^2)$, of the three-gluon vertex, a special derivative, ${{\mathcal {W}}}(q^2)$, of the ghost-gluon kernel, and the function $\sigma (q^2)$ constructed from it.

A crucial aspect of the analysis presented is related with the initial condition, used to fully determine the physical solution, and to guarantee the absence of spurious poles from $J(q^2)$. Specifically, the initial condition, imposed at the renormalization point $\mu ^2$, is completely fixed by an integral expression, whose integrand is comprised exclusively of ingredients entering in the ODE. As a result, for a given set of $L^\mathrm {asym}(q^2)$ and ${{\mathcal {W}}}(q^2)$, the kinetic term $J(q^2)$ is uniquely determined from the ODE. This fact, in turn, makes the decomposition given in Eq. (1.1) unambiguous, in the sense that, for a fixed gluon propagator (e.g., obtained from the lattice), no further freedom exists in reshuffling pieces between $J(q^2)$ and $m^2(q^2)$.

As we have emphasized in the main text, the practical implementation of this new method relies crucially on the use of lattice inputs for certain key quantities. In particular, the determination of $J(q^2)$ from the ODE exploits the lattice results of [88, 89] for $L^\mathrm {asym}(q^2)$, while the extraction of $m^2(q^2)$ makes extensive use of the data for $\Delta (q^2)$ reported in [3]. The results for $m^2(q^2)$ obtained from the numerical analysis of Sect. 7 are in good quantitative agreement with those found in earlier studies [58, 75, 76], suggesting an overall self-consistency of concepts and approximations.

As can be appreciated from Fig. 8, the lattice data of [88, 89] are afflicted by sizable errors, yielding a fairly wide band for the $L^\mathrm {asym}(q^2)$ used in our analysis. It would be clearly useful to reduce the error by increasing the number of field configurations used in the corresponding simulations, because this would lead, by means of the ODE, to a more accurate determination of the dynamical gluon mass.

It is clear that the quantity ${{\mathcal {W}}}(q^2)$, defined in Eqs. (2.7) and (5.4), is of central importance for the successful implementation of the proposed approach, because its exponentiation determines the key function $\sigma (q^2)$ through Eq. (3.4). For the purposes of the initial analysis reported here, an approximate version of the one-loop dressed SDE governing ${{\mathcal {W}}}(q^2)$ has been employed, where the input for the $X_i$ was evaluated in the symmetric configuration, and the $Y_i$ have been set to zero. However, the result of this computation turns out to be physically not acceptable, because it eventually yields, through Eq. (3.6), $J(\mu ^2) > 1$, and, consequently, a tachyonic gluon mass. To ameliorate this shortcoming, the function $\sigma (q^2)$ obtained from this approximation has been then appropriately modified (by hand) by varying its fitting parameters, in order to achieve acceptable values for $J(\mu ^2)$ and a reasonable ultraviolet behavior for $m^2(q^2)$.

Evidently, the behavior of ${{\mathcal {W}}}(q^2)$ deserves further detailed scrutiny, which may proceed in three complementary fronts. First, instead of substituting into Eq. (6.16) expressions for the $X_i$ evaluated in the symmetric configuration, the full angular dependence, known rather accurately from the work of [69], must be used. Second, the transverse form factors $Y_i$ appearing in Eq. (6.4) must be worked out from the corresponding SDE equation for the three-gluon vertex, at least in some typical kinematic limits, in order to estimate the impact they have on the shape of ${{\mathcal {W}}}(q^2)$. Third, the omitted diagram $(d^{\sigma \mu }_3)$ in Fig. 5 may be evaluated, using an appropriate truncation for the 1PI four-particle correlation function $\Gamma _{\mu \sigma } \sim \langle A_{\mu }^{a}(x) A_{\sigma }^{b}(y) {\bar{c}}^m(x) c^{n}(z)\rangle$ entering in it. This particular function has been studied in [107, 115], and its effect on the ghost-gluon vertex has been found to be of the order of 2$\%$; it remains to be seen how its inclusion might affect the determination of a quantity as delicate as $m^2(q^2)$.

It is clear from our analysis that the value of the $m(\mu ^2)$ is controlled by the corresponding value of $J(\mu ^2)$; the latter must be fixed with high precision (fourth decimal place) in order to distinguish between $m(\mu ^2)$ in the range of $(35-100)$ MeV. Given that $J(\mu ^2)$ is determined by the integral in Eq. (3.6), whose central ingredients are $L^\mathrm {asym}(q^2)$ and ${{\mathcal {W}}}(q^2)$, it would seem that an analogous precision may be required at the level of these two quantities. A detailed study of the response of this integral under variations of $L^\mathrm {asym}(q^2)$ and ${{\mathcal {W}}}(q^2)$ is required, in order to shed light on this important point.

It should be emphasized that the proposed method is applicable only to dynamics associated with the gluon propagator, and is meant to be exploited in close synergy with the broader functional methods. For example, it would be most interesting if the precision required in the determination of $J(\mu ^2)$ would make indispensable the use of the aforementioned correlation function $\Gamma _{\mu \sigma }$, signaling perhaps a new era of precision calculations in the field of SDEs.

It is important to stress that the present treatment takes explicit advantage of certain crucial properties of the Green’s functions involved that are specific to the Landau gauge, such as the decomposition of $H_{\nu \mu }$ in Eq. (2.5), and the ensuing finiteness of the ghost-gluon vertex renormalization constant, $\widetilde{Z}_1$. Consequently, the ODE of Eq. (3.1) and its solution given by Eq. (3.9), as they now stand, are restricted to the Landau gauge. Nevertheless, since the STI of Eq. (1.3) is valid for all linear $R_{\xi }$ covariant gauges, it is natural to expect that an analogous ODE could be derived for general $R_{\xi }$ gauges. In this respect, the appearance of F(0) in our expressions, through the function $f_2(x)$ of Eq. (3.2), is puzzling, given that for $R_{\xi }$ gauges other than Landau the ghost dressing function has been found to vanish at the origin [75, 116, 117], which would seem to leave $f_2(x)$ undefined. It must be noted, however, that the ingredients originating from the ghost-gluon scattering kernel in the STI could behave very differently away from the Landau gauge, possibly introducing divergences that would compensate the vanishing F(0), yielding finally a well-defined ODE. In particular, Eq. (2.5) would no longer be valid, which implies that the $\widetilde{Z}_1$ would be divergent, and the ODE of Eq. (3.1) would have contributions originating from derivatives of $H_{\nu \mu }$ other than the term ${{\mathcal {W}}}(q^2)$. It would be interesting to investigate how the ODE is realized for general $R_{\xi }$ in the future.

Since throughout the analysis presented we have assumed the absence of dynamical quarks, the conclusions drawn pertain to pure Yang-Mills SU(3) rather than QCD. In principle, the transition to QCD may be implemented by using the available unquenched lattice results for the quantities $L^\mathrm {asym}(q^2)$, $\Delta (q^2)$, and F(0) [11, 14, 118,119,120,121], as well as appropriately modified results for the $X_i$, $B_1$, and $\alpha _s$. The results of such a study may be contrasted with those obtained from the SDE-based approach presented in [37, 67, 122,123,124,125], and could further corroborate a variety of underlying concepts and techniques. We hope to report progress in this direction in the near future.