Radiative three-body D-meson decays in and beyond the standard model

Abstract

We study radiative charm decays $D \rightarrow P_1 P_2 \gamma$, $P_{1,2}=\pi ,K$ in QCD factorization at leading order and within heavy hadron chiral perturbation theory. Branching ratios including resonance contributions are around $\sim 10^{-3}$ for the Cabibbo-favored modes into $K \pi \gamma$ and $\sim 10^{-5}$ for the singly Cabibbo-suppressed modes into $\pi ^+ \pi ^- \gamma , K^+ K^- \gamma$, and thus in reach of the flavor factories BES III and Belle II. Dalitz plots and forward–backward asymmetries reveal significant differences between the two QCD frameworks; such observables are therefore ideally suited for a data-driven identification of relevant decay mechanisms in the standard-model dominated $D \rightarrow K \pi \gamma$ decays. This increases the potential to probe new physics with the $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$ decays, which are sensitive to enhanced dipole operators. CP asymmetries are useful to test the SM and look for new physics in neutral $|\Delta C|=1$ transitions. Cuts in the Dalitz plot enhance the sensitivity to new physics due to the presence of both s- and t, u-channel intermediate resonances.

1 Introduction

Decays of charmed hadrons provide unique avenues for studying flavor in the up-quark sector, complementary to K and B physics, and with great opportunities for experimental study at the LHCb [1], Belle II [2], and BES III [3] experiments. We discuss the three-body Cabibbo-favored standard-model (SM) dominated modes $D \rightarrow K \pi \gamma$ as well as the Cabibbo-supressed modes $D \rightarrow \pi \pi \gamma$ and $D \rightarrow K K \gamma$. The latter receive $|\Delta C|=1$ flavor changing neutral current (FCNC) contributions and are sensitive to new physics (NP). Our goal is to study QCD and flavor dynamics in and beyond the standard model (BSM) in the charm sector. Multi-body decays supply off-resonant contributions to $D_{(s)} \rightarrow V \gamma$, $V=\rho , {\bar{K}}, \phi$ [4] and, due to their richer final states, provide opportunities for SM tests through angular observables, such as polarization studies in $D \rightarrow K_1 (\rightarrow K \pi \pi ) \gamma$ decays [5]. Due to the poor convergence of the expansion in inverse powers of the charm-quark mass, $1/m_c$, strategies to probe for NP in D decays are based on null tests, exploiting approximate symmetries of the SM, such as CP and flavor symmetries, or flavor universality [6].

We perform a comprehensive study of available theory tools for radiative charm decay amplitudes. A new result is the analysis of $D \rightarrow P_1 P_2 \gamma$ at leading order QCD factorization (QCDF), with the $P_1 P_2$-form factor as a main ingredient. The framework is formally applicable for light and energetic $(P_1 - P_2)$ systems. At the other end of the kinematic spectrum, for large $(P_1 - P_2)$ invariant masses, we employ the soft-photon approximation. We also re-derive the heavy-hadron chiral perturbation theory (HH$\chi$PT) amplitudes for $D \rightarrow K \pi \gamma$ decays put forward in Refs. [7, 8], and provide results for the FCNC modes $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$. We find differences between our results and those in [7] which we detail in Appendix B2.

We compare the predictions of the QCD methods, with the goal to validate and improve the theoretical description via the study of the SM dominated decays. Then, we work out the NP sensitivities of the FCNC modes $D \rightarrow \pi \pi \gamma$ and $D \rightarrow K K \gamma$ in several distributions and observables.

The methods we employ, such as QCDF, are well-known and established methods in B physics. In charm physics the expansion parameters are numerically larger, and the systematic computation of amplitudes from first principles becomes a challenging task – hence the importance of null tests. On the other hand, while B physics has entered the precision era, very few radiative or semileptonic rare charm decays have been observed so far. Notably, there are no data on $D \rightarrow PP \gamma$ decay rates or its distributions. Therefore, while QCDF and HH$\chi$PT are not expected to perform as well as in B physics, we take their qualitative agreement within their ranges of validity as indicative of providing the correct order of magnitude in charm physics. This is sufficient to make progress given the experimental situation and leaves room for theory improvements, which can come also in a data-driven way, as we very concretely propose to do using decay distributions.

The paper is organized as follows: in Sect. 2 we introduce kinematics and distributions, and use QCD factorization methods (Sect. 2.2) and Low’s theorem (Sect. 2.3) for predictions for small and large PP-invariant masses, respectively. In Sect. 2.4 we work out the HH$\chi$PT amplitudes and Dalitz plots. We provide SM predictions for branching ratios and the forward–backward asymmetries in all three approaches and compare them in Sect. 3. In Sect. 4 we analyze the maximal impact of BSM contributions on the differential branching ratios and the forward–backward asymmetries. New-physics signals in CP asymmetries are worked out in Sect. 5. We conclude in Sect. 6. Auxiliary information on parametric input parameters and form factors is provided in two appendices.

2 Radiative three-body decays in QCD frameworks

We review the kinematics of the radiative three-body decays $D \rightarrow P_1 P_2 \gamma$ in Sect. 2.1. We then work out the SM predictions using QCD factorization methods in Sect. 2.2, Low’s theorem in Sect. 2.3, and HH$\chi$PT in Sect. 2.4.

2.1 Kinematics

The general Lorentz decomposition of the $D(P) \rightarrow P_1(p_1) P_2(p_2) \gamma (k, \epsilon ^*)$ amplitude reads

$$\begin{aligned} \mathcal {A}(D \rightarrow P_1 P_2 \gamma ) =&A_-(s,t) \left[ (p_1 \cdot k)(p_2 \cdot \epsilon ^{*})\right. \nonumber \\&\left. - (p_2 \cdot k)(p_1 \cdot \epsilon ^{*})\right] + A_+(s,t) \epsilon ^{\mu \alpha \beta \gamma } \epsilon ^{*}_\mu p_{1\alpha } p_{2\beta } k_\gamma \,, \end{aligned}$$

(1)

with parity-even $(A_+)$ and parity-odd $(A_-)$ contributions. The four-momenta of the D, $P_1$, $P_2$ and photon are denoted by $P, p_1,p_2$ and k, respectively; the photon’s polarization vector is $\epsilon ^*$. Above, $s=(p_1 + p_2)^2$ and $t=(p_2 + k)^2$ refer to the squared invariant masses of the $P_1$–$P_2$ and $P_2$–$\gamma$ systems, respectively. We denote the negatively charged meson or the $\overline{K}^0$ by $P_2$. Moreover, $\epsilon ^{\mu \alpha \beta \gamma }$ is the totally antisymmetric Levi-Civita tensor; we use the convention $\epsilon ^{0123}=+1$. The double differential decay rate is then given by

$$\begin{aligned} \frac{d{}^2\Gamma (D \rightarrow P_1 P_2 \gamma )}{d{}s d{}t} = \frac{1}{32(2\pi )^3 m_D^3} \left( |\mathcal {A}_L|^2 + |\mathcal {A}_R|^2\right) \, , \end{aligned}$$

(2)

where $m_D$ is the D-meson mass. We obtain

$$\begin{aligned} \frac{d{}^2\Gamma }{d{}s d{}t}&= \frac{ |A_-|^2 + |A_+|^2}{128 (2\pi )^3 m_D^3}\nonumber \\&\quad \times \big [m_1^2(t-m_2^2)(s-m_D^2)-m_2^4m_D^2 - st(s+t-m_D^2) \nonumber \\&\quad + m_2^2(st+(s+t)m_D^2 - m_D^4)\big ]\,. \end{aligned}$$

(3)

The subscript L(R) refers to the left- (right-)handed polarization state of the photon, and

$$\begin{aligned} \mathcal {A}_L&= \frac{1}{\sqrt{2}}(A_- + \mathrm {i}A_+) x \, , \quad \quad \mathcal {A}_R = \frac{1}{\sqrt{2}}(A_- - \mathrm {i}A_+) x \, , \end{aligned}$$

(4)

$$\begin{aligned} x&= \sqrt{m_1^2(t-m_2^2)(s-m_D^2)-m_2^4m_D^2 - st(s+t-m_D^2) + m_2^2(st+(s+t)m_D^2 - m_D^4)}/2 \, , \end{aligned}$$

(5)

where $m_1 (m_2)$ denotes the mass of the $P_1 (P_2)$ meson. The single differential distribution in the squared invariant di-meson mass is then given by

$$\begin{aligned} \begin{aligned} \frac{d{}\Gamma }{d{}s}&= \int _{t_\mathrm{min}}^{t_\mathrm{max}} dt \frac{d{}^2\Gamma }{d{}s d{}t} \, , \\ t_\mathrm{min}&= \frac{(m_D^2 - m_{1}^2 + m_{2}^2)^2}{4s} \\&- \left( \sqrt{\frac{(s - m_{1}^2 + m_{2}^2)^2}{4s} - m_2^2} + \frac{m_D^2 - s}{2\sqrt{s}}\right) ^2\, ,\\ t_\mathrm{max}&= \frac{(m_D^2 - m_{1}^2 + m_{2}^2)^2}{4s} \\&- \left( \sqrt{\frac{(s - m_{1}^2 + m_{2}^2)^2}{4s} - m_2^2} - \frac{m_D^2 - s}{2\sqrt{s}}\right) ^2 \, , \end{aligned} \end{aligned}$$

(6)

and $(m_{1}+m_{2})^2 \le s \le m_D^2$.

2.2 QCD Factorization

Rare $c \rightarrow u \gamma$ processes can be described by the effective four-flavor Lagrangian [4]

$$\begin{aligned} \mathcal {L}_{\text {eff}} =&\frac{4G_F}{\sqrt{2}}\left( \sum _{q, q'\in \{d, s\}}V_{cq}^* V_{uq'}\sum _{i=1}^2 C_i O_i^{(q, q')} \right. \nonumber \\&\left. +\sum _{i=3}^6 C_i O_i + \sum _{i=7}^8 \left( C_i O_i + C_i^\prime O_i^\prime \right) \right) \, . \end{aligned}$$

(7)

Here, $G_F$ is Fermi’s constant and $V_{ij}$ are elements of the Cabibbo–Kobayashi–Maskawa (CKM) matrix. The operators relevant to this work are given by

$$\begin{aligned} \begin{aligned}&O_1^{(q, q')} = \left( \overline{u}_L \gamma _\mu T^a q_L'\right) \left( \overline{q}_L \gamma ^\mu T^a c_L\right) \, , \\&O_2^{(q, q')} = \left( \overline{u}_L \gamma _\mu q_L'\right) \left( \overline{q}_L \gamma ^\mu c_L\right) \, ,\\&O_7 = \frac{e m_c}{16\pi ^2} \left( \overline{u}_L \sigma ^{\mu \nu } c_R\right) F_{\mu \nu }\, , \\&O_7^\prime = \frac{e m_c}{16\pi ^2} \left( \overline{u}_R \sigma ^{\mu \nu } c_L\right) F_{\mu \nu }\, , \end{aligned} \end{aligned}$$

(8)

where the subscripts L(R) denote left-(right-)handed quark fields, $F_{\mu \nu }$ is the photon field strength tensor, and $T^a$ are generators of SU(3) normalized to $\text {Tr}\{T^aT^b\} = \delta ^{ab}/2$, respectively. Because of an efficient cancellation due to the Glashow–Iliopoulos–Maiani mechanism, only the four-quark operators $O_{1,2}^{(q, q')}$ are induced at the W-scale $\mu _W$ and receive order-one coefficients at the scale $\mu _c \sim m_c$ of the order of the charm-quark mass. At leading order in the strong coupling $\alpha _s$, the coefficients are given for $\mu _c \in \left[ m_c/\sqrt{2}, \sqrt{2}m_c\right]$ by [4]

$$\begin{aligned}&C_1 \in \left[ -1.28, -0.83\right] , \qquad C_2 \in \left[ 1.14, 1.06\right] \, , \nonumber \\&{\tilde{C}}\equiv \frac{4}{9}C_1 + \frac{1}{3}C_2 \in \left[ -0.189, -0.018\right] \, . \end{aligned}$$

(9)

The peculiar combination of Wilson coefficients ${\tilde{C}}$ arises in the weak annihilation amplitude (see below); note that an accidental numerical cancellation occurs in this combination, leading to a large scale uncertainty (see Table 1). This effect is partially mitigated by higher-order QCD corrections which we do not take into account in this work; see, e.g., Ref. [4]. The tiny SM contributions to $C_{3-8}$ are a result of renormalization group running and finite threshold corrections at the bottom-mass scale, and can be neglected for the purpose of this work. For instance, the SM contribution of the electromagnetic dipole operator $O_7$ is strongly suppressed, $|C_7^\text {eff}| \simeq \mathcal {O}(0.001)$ at $\mu _c=m_c$ at next-to-next-to-leading order [6].

In this section we use QCDF methods [9,10,11] to calculate the leading weak annihilation (WA) contribution shown in Fig. 1.

Fig. 1

The weak annihilation diagram for $D \rightarrow P_1 P_2 \gamma$. The blue cross indicates the dominant photon emission from the light quark of the D meson. Photon emission from the other quark lines is suppressed by powers of $\lambda _\text {QCD}/m_c$ or $\alpha _s$

We obtain

$$\begin{aligned} \begin{aligned}&\mathcal {A}^{\text {WA}}_- = i \frac{G_F e}{\sqrt{2}} {\tilde{C}} \frac{f_D Q_u}{\lambda _D (v\cdot k)} \sum _{q, q'\in \{d, s\}} V_{cq}^* V_{uq'} f^{P_1 P_2}_{(q, q')}(s) \, ,\\&\mathcal {A}^{\text {WA}}_+ = \frac{G_F e}{\sqrt{2}} {\tilde{C}} \frac{f_D Q_u}{\lambda _D (v\cdot k)} \sum _{q, q'\in \{d, s\}} V_{cq}^* V_{uq'} f^{P_1 P_2}_{(q, q')}(s) \, , \end{aligned} \end{aligned}$$

(10)

where $Q_u=2/3$ denotes the electric charge of the up-type quarks, and we decomposed $P=v\,m_D$. The nonperturbative parameter $\lambda _D \sim \Lambda _{\text {QCD}}$ is poorly known and thus source of large theoretical uncertainties. In the following we use $\lambda _D = 0.1\, \mathrm{GeV}$ [4]. For the final states $\pi ^+ \pi ^- \gamma$ and $K^+ K^- \gamma$, the remaining form factors $f^{P_1 P_2}_{(q, q')}(s)$ can be expressed in terms of the electromagnetic pion and kaon form factors [12]. For the final states $\pi ^+ K^-\gamma$ and $\pi ^0 \overline{K} \gamma$, we use the form factors extracted from $\tau ^- \rightarrow \nu _\tau K_s \pi ^0$ decays [13] in combination with isospin relations. We obtain for the non-vanishing form factors

$$\begin{aligned} \begin{aligned}&f^{\pi ^+ \pi ^-}_{(d,d)} = - F^{\text {em}}(s)\, ,\\&f^{K^+K^-}_{(d,d)} = 3F^{(I=0)}_{K^+}(s) - F^{(I=1)}_{K^+}(s)\, ,\\&f^{K^+ K^-}_{(s,s)} = -3F^s_{K^+}(s)\, ,\\&f^{\pi ^+K^-}_{(s,d)} =- f^{\overline{K}\pi ^-}_+\, , \\&f^{\pi ^0\overline{K}^0}_{(s,d)} = \frac{1}{\sqrt{2}}f^{\overline{K}\pi ^-}_+ \, . \end{aligned} \end{aligned}$$

(11)

More details about the form factors are given in Appendix  B1. We recall that QCDF holds for light and energetic $P_1$–$P_2$ systems. This limits the validity of the results to $s \lesssim 1.5\, \mathrm{GeV}^2$, corresponding to an approximate upper limit on a light hadron’s or hadronic system’s invariant mass squared, including the $\phi$. The WA decay amplitudes are independent of t.

2.3 Soft photon approximation

Complementary to QCDF, we use Low’s theorem [14] to estimate the decay amplitudes in the limit of soft photons. This approach holds for photon energies below $m_P^2/E_P$ [15], which results in $s\gtrsim 2.3 \, \mathrm{GeV}^2$ for $D \rightarrow K^+ K^- \gamma$ and $s\gtrsim 3.4 \, \mathrm{GeV}^2$ for decays with a final-state pion. The amplitude is then given by [16]

$$\begin{aligned} \mathcal {A}_-^\mathrm{Low}=-\frac{e\mathcal {A}(D \rightarrow P_1 P_2)}{(p_1\cdot k)(p_2\cdot k)}\, , \end{aligned}$$

(12)

while $\mathcal {A}_+^\mathrm{Low}=0$. There is no such contribution to $D \rightarrow \pi ^0 {\bar{K}}^0 \gamma$, since only neutral mesons are involved. The modulus of the $D \rightarrow P_1 P_2$ amplitudes can be extracted from branching ratio data using

$$\begin{aligned}&\mathcal {B}(D \rightarrow P_1 P_2) \nonumber \\&\quad = \frac{|\mathcal {A}(D \rightarrow P_1 P_2)|^2}{16\pi m_D \Gamma _D}\sqrt{\left( 1-\frac{(m_1 + m_2)^2}{m_D^2}\right) \left( 1-\frac{(m_1 - m_2)^2}{m_D^2}\right) }\, , \end{aligned}$$

(13)

where $\Gamma _D$ is the total width of the D meson. Using the parameters given in Appendix A, we obtain

$$\begin{aligned} \begin{aligned}&\left| \mathcal {A}(D \rightarrow \pi ^+ \pi ^-)\right| = (4.62 \pm 0.04) \cdot 10^{-7}\, \text {GeV}, \\&\left| \mathcal {A}(D \rightarrow \pi ^+ K^-)\right| = (2.519 \pm 0.014) \cdot 10^{-6}\, \text {GeV}, \\&\left| \mathcal {A}(D \rightarrow K^+ K^-)\right| = (8.38 \pm 0.09) \cdot 10^{-7}\, \text {GeV}. \end{aligned} \end{aligned}$$

(14)

Low’s theorem predicts that the differential decay rate behaves as [17]

$$\begin{aligned} \frac{d{}\Gamma }{d{}s} \sim \frac{1}{m_D^2-s}\, . \end{aligned}$$

(15)

Consequently, there is a singularity at the boundary of the phase space. This corresponds to a vanishing photon energy in the D meson’s rest frame. The tail of the singularity dominates the decay rate for small photon energies. We remove these events for integrated rates by cuts in the photon energy, as they are of known SM origin and hamper access to flavor and BSM dynamics.

2.4 HH$\chi$PT

As a third theory description we use the framework of heavy hadron chiral perturbation theory (HH$\chi$PT), which contains both the heavy quark and the $SU(3)_L \times SU(3)_R$ chiral symmetry. The effective Lagrangian was introduced in [18,19,20] and extended by light vector resonances by Casalbuoni et al. [21, 22]. We follow the approach of Fajfer et al., who studied radiative two-body decays $D\rightarrow V \gamma$ [23, 24] and Cabibbo allowed three-body decays $D\rightarrow K^- \pi ^+ \gamma$ [7] and $D \rightarrow \overline{K}^0 \pi ^0 \gamma$ [8] in this way.

The light mesons are described by $3\times 3$ matrices

$$\begin{aligned}&u = \exp \left( \frac{\mathrm {i} \Pi }{f}\right) \, , \qquad \Pi = \left( \begin{array}{ccc} \frac{\pi ^0}{\sqrt{2}} + \frac{\eta _8}{\sqrt{6}} &{} \pi ^+ &{} K^+ \\ \pi ^- &{} -\frac{\pi ^0}{\sqrt{2}} + \frac{\eta _8}{\sqrt{6}} &{} K^0 \\ K^- &{} \overline{K}^0 &{} -\frac{2\eta _8}{\sqrt{6}} \\ \end{array}\right) \, , \nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned}&{\hat{\rho }}_\mu = \mathrm {i} \frac{g_v}{\sqrt{2}}\rho _\mu \, , \qquad \rho _\mu = \left( \begin{array}{ccc} \frac{\rho _\mu ^0 + \omega _\mu }{\sqrt{2}} &{} \rho _\mu ^+ &{} K^{\star +}_\mu \\ \rho _\mu ^- &{} \frac{-\rho _\mu ^0 + \omega _\mu }{\sqrt{2}} &{} K^{\star 0}_\mu \\ K^{\star -}_\mu &{} \overline{K} ^{\star 0}_\mu &{} \Phi _\mu \\ \end{array}\right) \, ,\nonumber \\ \end{aligned}$$

(17)

where $f\simeq f_\pi$ is the pion decay constant and $g_v = 5.9$ [25,26,27]. To write down the photon interaction with the light mesons in a simple way, we define two currents

$$\begin{aligned} \begin{aligned} \mathcal {V}_\mu&= \frac{1}{2}\left( u^\dagger D_\mu u + u D_\mu u^\dagger \right) , \\ \mathcal {A}_\mu&= \frac{1}{2}\left( u^\dagger D_\mu u - u D_\mu u^\dagger \right) \, . \end{aligned} \end{aligned}$$

(18)

Here, the covariant derivative acting on u and $u^\dagger$ is given by $D_\mu u^{(\dagger )} = \partial _\mu u^{(\dagger )} + \mathrm {i}e B_\mu Q u^{(\dagger )}$, with the photon field $B_\mu$ and the diagonal charge matrix $Q=\text {diag}(2/3, -1/3, -1/3)$. The even-parity strong Lagrangian for light mesons is then given by [25,26,27]

$$\begin{aligned} \mathcal {L}_{\text {light}}= & {} -\frac{f^2}{2} \left[ {{\,\mathrm{Tr}\,}}_F\left( \mathcal {A}_\mu \mathcal {A}^\mu \right) + a {{\,\mathrm{Tr}\,}}_F \left( \left( \mathcal {V}_\mu - {\hat{\rho }}_\mu \right) ^2 \right) \right] \nonumber \\&+ \frac{1}{2g_v^2}{{\,\mathrm{Tr}\,}}_F \left( F_{\mu \nu }({\hat{\rho }}) F^{\mu \nu }({\hat{\rho }})\right) \, , \end{aligned}$$

(19)

where $F_{\mu \nu }({\hat{\rho }}) = \partial _\mu {\hat{\rho }}_\nu - \partial _\nu {\hat{\rho }}_\mu + \left[ {\hat{\rho }}_\mu , {\hat{\rho }}_\nu \right]$ denotes the field strength tensor of the vector resonances. In general, a is a free parameter, which satisfies $a=2$ in case of exact vector meson dominance (VMD). In VMD there is no direct vertex that connects two pseudoscalars and a photon. In this case, the photon couples to pseudoscalars via a virtual vector meson. Analogously, the matrix element ${\langle }{P_1 P_2| \overline{q}\gamma ^\mu (1-\gamma _5)q^\prime |0}{\rangle }$ also vanishes. However, we do not use the case of VMD and exact flavor symmetry, but allow for SU(3) breaking effects. Therefore, we choose to set $a=1$ and replace the model coupling $g_v$, decay constant f, and vector meson mass $m_V=\sqrt{a/2}g_v f$ in $\mathcal {L}_\text {light}$ with the respective measured masses, decay constants and couplings $g_v = \sqrt{2}m_V^2/g_V$. They are defined by

$$\begin{aligned} {\langle }{V(q, \eta )|j_V^\mu |0}{\rangle } = \eta ^{*\mu }(q) g_V(q^2)\, , \end{aligned}$$

(20)

where $j_{K^\star , \overline{K}^\star , K^{\star \pm }, \Phi }^\mu = \overline{q}\gamma ^\mu q^\prime$ and $j_{\omega , \rho }^\mu =\frac{1}{\sqrt{2}}(\overline{u}\gamma ^\mu u \pm \overline{d}\gamma ^\mu d)$. Here, q and $\eta$ denote the vector meson’s momentum and polarization vector, respectively. For our numerical evaluation we use $g_V(0) \simeq g_V(m_V^2)=m_Vf_V$, where $f_V$ is the vector meson decay constant with mass dimension one. With these couplings the following $V\gamma$ interactions arise [24]

$$\begin{aligned} \mathcal {L}_{V_0\gamma } = -\frac{e}{\sqrt{2}} B_\mu \left( g_\rho \rho ^{0\mu } + \frac{1}{3} g_\omega \omega ^\mu - \frac{\sqrt{2}}{3} g_\Phi \Phi ^\mu \right) . \end{aligned}$$

(21)

Instead of the VVP interactions generated by the odd-parity Lagrangian [28], we use effective VP$\gamma$ interactions

$$\begin{aligned} \mathcal {L}_{VP\gamma } = - \frac{1}{2}e g_{VP\gamma } \epsilon _{\mu \nu \rho \sigma } F^{\mu \nu }(B) \partial ^\rho V^\sigma P^\dagger + \text {h.c.} \end{aligned}$$

(22)

and determine the effective coefficients $g_{VP\gamma }$ from experimental data [7, 29]

$$\begin{aligned} \Gamma (V\rightarrow P\gamma ) = \frac{\alpha _{\text {em}} m_V^3}{24} |g_{VP\gamma }|^2 \left( 1-\frac{m_P^2}{m_V^2}\right) ^3\, . \end{aligned}$$

(23)

Fig. 2

SM Dalitz plots for the decays $D \rightarrow \overline{K}^0 \pi ^0 \gamma$ (upper left), $D \rightarrow K^- \pi ^+ \gamma$ (upper right), $D \rightarrow \pi ^+ \pi ^- \gamma$ (lower left) and $D \rightarrow K^+ K^- \gamma$ (lower right) based on HH$\chi$PT at $\mu _c = m_c$

The heavy pseudoscalar and vector mesons are represented by $4\times 4$ matrices

(24)

where $P^{\star (\dagger )}_{a\mu }$, $P^{(\dagger )}_a$ annihilate (create) a heavy spin-one and spin-zero meson $h_a$ with quark flavor content $c{\overline{q}_a}$ and velocity v, respectively. The annihilation operators are normalized as

$$\begin{aligned} \begin{aligned}&{\langle }{0 | P_a | h_a(v)}{\rangle } = 1\, , \\&{\langle }{0 | P_a^{\star \mu } | h_a^\star (v, \eta )}{\rangle } = \eta ^\mu \, . \end{aligned} \end{aligned}$$

(25)

The heavy-meson Lagrangian reads

$$\begin{aligned} \mathcal {L}_{\text {heavy}}&= \mathrm {i}{{\,\mathrm{Tr}\,}}_D\left( H_a v_\mu \left( D^\mu \right) _{ab} \overline{H}_b\right) \nonumber \\&\quad + \mathrm {i}g {{\,\mathrm{Tr}\,}}_D \left( H_a \gamma _\mu \gamma _5 (\mathcal {A}^\mu )_{ab} \overline{H}_b \right) \nonumber \\&\quad + \mathrm {i}{\tilde{\beta }} {{\,\mathrm{Tr}\,}}_D \left( H_a v_\mu \left( \mathcal {V}^\mu - {\hat{\rho }}^\mu \right) _{ab} \overline{H}_b \right) \, , \end{aligned}$$

(26)

where the covariant derivative is defined as $\left( D^\mu \right) _{ab} \overline{H}_b = \partial ^\mu \overline{H}_a + \left( \mathcal {V}^\mu \right) _{ab} \overline{H}_b - \mathrm {i}e Q_c B^\mu \overline{H}_a$, with the electric charge of the charm quark $Q_c=2/3$. The parameter $g=0.59$ was determined by experimental data of strong $D^\star \rightarrow D \pi$ decays [30, 31]. The coupling ${\tilde{\beta }}$ seems to be very small and will be neglected [32]. The odd-parity Lagrangian for the heavy mesons is given by

$$\begin{aligned} \mathcal {L}= & {} \mathrm {i}\lambda {{\,\mathrm{Tr}\,}}\left( H_a \sigma _{\mu \nu } F^{\mu \nu }({\hat{\rho }})_{ab} \overline{H}_b\right) \nonumber \\&-\lambda ^\prime e {{\,\mathrm{Tr}\,}}\left( H_a \sigma _{\mu \nu } F^{\mu \nu }(B) \overline{H}_a \right) \, , \end{aligned}$$

(27)

with $\sigma _{\mu \nu } = \frac{\mathrm {i}}{2}\left[ \gamma _\mu , \gamma _\nu \right]$. The couplings $\lambda$ and $\lambda ^\prime$ can be extracted from rations $R_\gamma ^{0/+}= \Gamma (D^{\star 0/+}\rightarrow D^{0/+}\gamma )/\Gamma (D^{\star 0/+}\rightarrow D^{0/+}\pi )$. $\lambda =-0.49\, \mathrm{GeV}^{-1}$ and $\lambda ^\prime =-0.102\, \mathrm{GeV}^{-1}$ are in good agreement with data [7]. The partonic weak currents can be expressed in terms of chiral currents as [23, 33]

$$\begin{aligned} \begin{aligned} (\overline{q}_a Q)^\mu _{\text {V-A}} \simeq J_{Q\overline{q}_a}^\mu&= \frac{1}{2}\mathrm {i}\alpha {{\,\mathrm{Tr}\,}}\left( \gamma ^\mu (1-\gamma _5) H_b u_{ba}^\dagger \right) \\&\quad + \alpha _1 {{\,\mathrm{Tr}\,}}\left( \gamma _5 H_b \left( {\hat{\rho }}^\mu - \mathcal {V}^\mu \right) _{bc} u_{ca}^\dagger \right) \\&\quad + \alpha _2 {{\,\mathrm{Tr}\,}}\left( \gamma ^\mu \gamma _5 H_b v_\alpha ({\hat{\rho }}^\alpha - \mathcal {V}^\alpha )_{bc} u_{ca}^\dagger \right) \\&\quad + \ldots \, ,\\ (\overline{q}_j q_i)_{\text {V-A}}^\mu \simeq J_{ij}^\mu&= \mathrm {i}f^2 \left\{ u \left[ \mathcal {A}^\mu + a \left( \mathcal {V}^\mu - {\hat{\rho }}^\mu \right) \right] u^\dagger \right\} _{ij}\, , \end{aligned} \end{aligned}$$

(28)

where the ellipsis denotes higher-order terms in the chiral and heavy-quark expansions. The definition of the heavy-meson decay constants implies $\alpha =f_h \sqrt{m_h}$. The parameters $\alpha _1$ and $\alpha _2$ can be extracted from $D\rightarrow V$ transition form factors [7]

$$\begin{aligned} \begin{aligned} A_1(q^2_{\text {max}})&= 2 \frac{\sqrt{m_D}}{m_D + m_V} \frac{m_V^2}{g_V}\alpha _1\, ,\\ A_2(q^2_{\text {max}})&= 2 \frac{m_D + m_V}{m_D^{{3}/{2}}} \frac{m_V^2}{g_V}\alpha _2\, . \end{aligned} \end{aligned}$$

(29)

Using the $D \rightarrow K^\star$ form factors [34] we obtain $\alpha _1 = 0.188\, \mathrm{GeV}^{\frac{1}{2}}$ and $\alpha _2 = 0.086\, \mathrm{GeV}^{\frac{1}{2}}$. The signs in (29) are due to the conventions in [34]. The weak tensor current is given by [35]

$$\begin{aligned} \begin{aligned}&\overline{q}\sigma ^{\mu \nu }(1+\gamma _5)Q \simeq J_{Q\overline{q}_a}^{\mu \nu } \\&\quad = \frac{1}{2}\mathrm {i}\alpha {{\,\mathrm{Tr}\,}}\left( \sigma ^{\mu \nu } (1+\gamma _5) H_b u_{ba}^\dagger \right) \\&\qquad + \mathrm {i}\alpha _1 \left( g^{\mu \alpha }g^{\nu \beta } - \frac{1}{2}i \epsilon ^{\mu \nu \alpha \beta }\right) {{\,\mathrm{Tr}\,}}\left( \gamma _5 H_b \left[ \gamma _\alpha \left( {\hat{\rho }}_\beta - \mathcal {V}_\beta \right) _{bc}\right. \right. \\&\left. \left. \qquad - \gamma _\beta \left( {\hat{\rho }}_\alpha - \mathcal {V}_\alpha \right) _{bc}\right] u_{ca}^\dagger \right) \\&\qquad - \alpha _2 {{\,\mathrm{Tr}\,}}\left( \sigma ^{\mu \nu } \gamma _5 H_b v_\alpha \left( {\hat{\rho }}^\alpha - \mathcal {V}^\alpha \right) _{bc} u^\dagger _{ca}\right) + \ldots \, , \end{aligned} \end{aligned}$$

(30)

where, again, the ellipsis denotes higher-order terms in the chiral and heavy-quark expansions.

The parity-even and parity-odd amplitudes are given in terms of four form factors

$$\begin{aligned} A_-^\mathrm{HH\chi PT}&= \frac{G_F e}{\sqrt{2}} \sum _{q, q'\in \{d, s\}}V_{cq}^*V_{uq'} \left[ \left( C_2 - \frac{1}{6}C_1\right) \sum _{i} A_i^{(q, q')}\right. \nonumber \\&\left. \quad + \frac{1}{2}C_1 \sum _{i} E_i^{(q, q')}\right] \, ,\nonumber \\ A_+^\mathrm{HH\chi PT}&= \frac{G_F e}{\sqrt{2}} \sum _{q, q'\in \{d, s\}}V_{cq}^*V_{uq'} \left[ \left( C_2 - \frac{1}{6}C_1\right) \sum _{i} B_i^{(q, q')}\right. \nonumber \\&\left. \quad + \frac{1}{2}C_1 \sum _{i} D_i^{(q, q')}\right] \, . \end{aligned}$$

(31)

Fig. 3

The SM predictions for the differential branching ratios of the decays $D \rightarrow \overline{K}^0 \pi ^0 \gamma$ (upper left), $D \rightarrow K^- \pi ^+ \gamma$ (upper right), $D \rightarrow \pi ^+ \pi ^- \gamma$ (lower left) and $D \rightarrow K^+ K^- \gamma$ (lower right). Blue bands correspond to QCDF, green bands to HH$\chi$PT and the red dashed lines to the soft photon approximation. The lighter shaded areas and lines illustrate extrapolations beyond the model’s region of applicability. QCDF branching ratios are obtained for $\lambda _D=0.1\, \mathrm{GeV}$ and are $\propto (0.1\, \mathrm{GeV}/\lambda _D)^2$

Table 1 SM and BSM branching ratios for $D \rightarrow \pi ^0 \overline{K}^0 \gamma$ , $D \rightarrow \pi ^+ K^- \gamma$, $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$. QCDF is applicable for $s \lesssim 1.5\, \mathrm{GeV}^2$; to enable sensible comparison we also provide HH$\chi$PT branching ratios with this cut. Also given are HH$\chi$PT predictions for $E_\gamma \ge 0.1\, \mathrm{GeV}$, see text for details. The QCDF branching ratios are obtained for $\lambda _D=0.1\, \mathrm{GeV}$. The SM predictions are $\propto (0.1\, \mathrm{GeV}/\lambda _D)^2$

Fig. 4

The forward–backward asymmetry $A_\mathrm{FB}(s)$ (32) as a function of s. The red bands contain only non-resonant contributions. The green, orange and light blue bands contain additional contributions of a specific resonance channel. The dark blue bands are the complete forward–backward asymmetries according to HH$\chi$PT. To leading order QCDF $A_\mathrm{FB}(s)=0$

Fig. 5

The dominant diagrams to $D\rightarrow VP(\rightarrow P P \gamma )$ in the $\lambda _\text {QCD}/m_c$ and $\alpha _s$ expansion. At order $\alpha _s^0$ QCDF reproduces the naive factorization [9]. The diagrams are shown for charged final state mesons. For the final state with uncharged mesons the u and q quark have to be exchanged

Fig. 6

The SM predictions for the differential branching ratios of the decays $D \rightarrow \pi ^+ \pi ^- \gamma$ (left) and $D \rightarrow K^+ K^- \gamma$ (right) from a direct QCDF computation (blue bands in upper plots), HH$\chi$PT computations (green bands in lower plots) and from the $D \rightarrow K^- \pi ^+ \gamma$ distribution multiplied by $|V_{cd}/V_{cs}|^2$ and $|V_{us}/V_{ud}|^2$, respectively (red bands). The prediction for the SM-like mode $D \rightarrow K^- \pi ^+ \gamma$ in this figure is from the respective models but could be taken from data

Fig. 7

Comparison of QCDF-based SM predictions of differential branching ratios for $D \rightarrow \pi ^+ \pi ^- \gamma$ (upper plots) and $D \rightarrow K^+ K^- \gamma$ (lower plots) within different BSM scenarios. One BSM coefficient is set to zero while the other one exhausts the limit (37) with CP-phase $0, \pm \pi /2, \pi$

Fig. 8

As in Fig. 7 but for HH$\chi$PT

Fig. 9

The forward–backward asymmetry in the SM (blue band) and beyond for the decays $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$ as a function of s, based on the HH$\chi$PT form factors

Fig. 10

As in Fig. 9 but within QCDF (40)

Fig. 11

Predictions for the CP asymmetries in $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$ as a function of s, within the SM and beyond (using (40)), based on QCDF. For the BSM scenarios, we have set one coefficient $C_7^{(\prime )}$ to 0 and the other one to 0.05, 0.2. The weak phase of $C_7^{(\prime )}$ is $\phi _w=\pm \pi /2$. We performed a cut $s \le 1.5\, \mathrm{GeV}^2$ to remain within the region where QCDF applies

Fig. 12

As in Fig. 11 but for HH$\chi$PT and with cut $s \le 2\, \mathrm{GeV}^2$ to avoid large bremsstrahlung contributions in the normalization

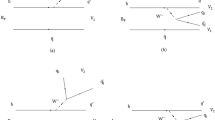
Here, A and B belong to the charged current operator $(\overline{u}q^\prime )_{\mu V-A}(\overline{q}c)^\mu _{V-A} \equiv 4 O_2^{(q',q)}$ and D and E to the neutral current operator $(\overline{q}q^\prime )_{\mu V-A}(\overline{u}c)^\mu _{V-A} \equiv 8 O_1^{(q',q)} + 4 O_2^{(q',q)} /3$. The corresponding diagrams are shown in Figs. 18 and 19. The non-zero contributions are listed in Appendix B2, where we also provide a list with differences between our results and those in Ref. [7]. We neglect the masses of the light mesons in the form factors, but consider them in the phase space. To enforce Low’s theorem, we remove the bremsstrahlung contributions $A_{1,2}$ in (31) and add (12) to $A_-^\mathrm{HH\chi PT}$. For the strong phase we have taken the value predicted by HH$\chi$PT. In Fig. 2 we show Dalitz plots based on the SM HH$\chi$PT predictions. Besides the dominant bremsstrahlung effects for large s, the intermediate $\rho$, $\omega$, $K^\star$ and $\Phi$ resonances are clearly visible as bands in s, t and the third Mandelstam variable, $u=(p_1+k)^2=m_D^2+m_1^2 +m_2^2-s-t$.

3 Comparison of QCD frameworks

In this section, we compare the predictions obtained using the different QCD methods in Sect. 2. We anticipate quantitative and qualitative differences between QCDF to leading order and HH$\chi$PT. First, we study differential and integrated branching ratios in Sect. 3.1. In Sect. 3.2 we propose to utilze a forward–backward asymmetry, defined below in Eq. (32), to help disentangling the resonance contributions to the branching ratios. This subsequently improves the NP sensitivity of the $D \rightarrow P^+ P^- \gamma$ decays. We consider the U-spin link, exploited already for polarization-asymmetries in radiative charm decays [36], in Sect. 3.3.

3.1 Branching ratios

The branching ratios for the various decay modes, obtained from QCDF (blue bands), HH$\chi$PT (green bands) and Low’s theorem (red dashed lines), are shown in Fig. 3. The width of the bands represents the theoretical uncertainty due to the $\mu _c$ dependence of the Wilson coefficients.

The shape of the QCDF results is mainly given by the $P_1-P_2$ form factors and their resonance structure. For the $D \rightarrow P_1^+ P_2^- \gamma$ decays, the high-s regions of the HH$\chi$PT predictions are dominated by bremsstrahlung effects. Since we have replaced the model’s own bremsstrahlung contributions by those of Low’s theorem, the results approach each other asymptotically towards the large-s endpoint. Without this substitution, the differential branching ratios from HH$\chi$PT in this region would be about one order of magnitude larger. For lower s, the impact of the resonances becomes visible.

In the soft photon approximation the photon couples directly to the mesons. Therefore, there is no such contribution for the $D \rightarrow \pi ^0 \overline{K}^0 \gamma$ decay. Its distribution is dominated by the $\omega$ resonance which has a significant branching ratio to $\pi ^0 \gamma$; this is manifest in the Dalitz plot in Fig. 2.

Apart from the $K^*, \rho$, and $\phi$ peaks, the shapes of the differential branching ratios differ significantly between QCDF and HH$\chi$PT, due to the t and u-channel resonance contributions in the latter. This is shown in the Dalitz plot in Fig. 2.

In Table 1 we give the SM branching ratios for the four decay modes. We employ phase space cuts $s \le 1.5\, \mathrm{GeV}^2$, the region of applicability of QCDF, or $E_\gamma \ge 0.1 \, \mathrm{GeV}$, corresponding to $s \le 3.1 \, \mathrm{GeV}^2$, to avoid the soft photon pole. Here, $E_\gamma =(m_D^2-s)/(2 m_D)$ is the photon energy in the D meson’s rest frame. Applying the same cuts in both cases, the HH$\chi$PT branching ratios are generally larger than the QCDF ones, except for the $D \rightarrow K^+ K^- \gamma$ mode, where they are of comparable size.

We recall that SM branching ratios within leading order QCDF are proportional to $(1/\lambda _D)^2$. Since $\lambda _D$ is of the order of $\Lambda _\mathrm{QCD}$ and we employ a rather low value $\lambda _D = 0.1\, \mathrm{GeV}$ [4], the values in Table 1 should be regarded as maximal branching ratios. The large uncertainty of these values arises from the residual scale dependence of the Wilson coefficient $\bar{C}$ (9). A measurement of the branching ratios of the SM-like modes $D \rightarrow K \pi \gamma$ thus provides an experimentally extracted value of ${\bar{C}}/\lambda _D$. Color-allowed modes feature Wilson coefficients with significantly smaller scale uncertainty, and allow for a cleaner, direct probe of $\lambda _D$ [4]. While $\lambda _D$ is poorly known, it effectively drives the annihilation with initial state radiation and experimental constraints are informative even in the presence of sizable systematic uncertainties inherent to QCDF in charm.

3.2 Forward–backward asymmetry

Angular observables are also suitable for testing QCD models. We define the forward–backward asymmetry

$$\begin{aligned} \begin{aligned} A_\mathrm{FB}(s)&= \frac{\int _{t_\mathrm{min}}^{t_\mathrm{0}} dt \frac{d{}^2\Gamma }{d{}s d{}t} -\int _{t_\mathrm{0}}^{t_\mathrm{max}} dt \frac{d{}^2\Gamma }{d{}s d{}t}}{\int _{t_\mathrm{min}}^{t_\mathrm{0}} dt \frac{d{}^2\Gamma }{d{}s d{}t} + \int _{t_\mathrm{0}}^{t_\mathrm{max}} dt \frac{d{}^2\Gamma }{d{}s d{}t}} \, ,\\ t_\mathrm{0}&= \frac{1}{2s}\left( -s^2 + s(m_D^2 + m_1^2 + m_2^2) + m_D^2(m_2^2 - m_1^2)\right) \, , \end{aligned} \end{aligned}$$

(32)

where the first (second) term in the numerator corresponds to $0 \le \cos (\theta _{2\gamma }) \le 1$ $(-1 \le \cos (\theta _{2\gamma }) \le 0)$. Here, $\theta _{2\gamma }$ is the angle between $P_2$ and the photon in the $P_1 - P_2$ center-of-mass frame. In Fig. 4 we show the SM forward–backward asymmetry based on HH$\chi$PT. In all decay modes $A_\mathrm{FB}(s)$ is dominated by intermediate vector resonances. To illustrate this, the forward–backward asymmetries are also shown without or only with individual resonance contributions. The $(P_1P_2)_\text {res}$ resonances contribute to $A_\mathrm{FB}$ only via interference terms, since the corresponding form factors depend only on s. For $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$ the diagrams of the neutral current operator, which contain $(P_1\gamma )_\text {res}$ and $(P_2\gamma )_\text {res}$ resonances, give the same contribution to the amplitude in the forward and backward region of the phase space. For $P_1 \ne \overline{P}_2$ this symmetry does not exist. In case of the charged current operator, these resonances contribute in different ways to the forward and backward region due to the asymmetric factorization of the diagrams $B_3$ (B20), (B23), (B26). This effect is primarily responsible for the shape of $A_\mathrm{FB}$ in $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$ decays. $A_\mathrm{FB}(D \rightarrow \pi ^0 \overline{K}^0 \gamma )$ is, like the differential branching ratio shown in Fig. 2, dominated by the $\omega$ resonance.

Since the WA form factors are only dependent on s, the SM forward–backward asymmetry vanishes to leading order QCDF. Therefore, we add contributions from t and u-channel resonances using a phenomenological approach. To this end, we combine $D \rightarrow VP$ amplitudes with the effective $VP\gamma$ coupling from Eq.  (22).

We obtain

$$\begin{aligned} \mathcal {A}^\text {pheno}_+&= \frac{G_F e}{\sqrt{2}}V_{cq}^* V_{uq'} \left( C_2 - \frac{1}{6}C_1\right) \nonumber \\&\quad \times \left( \frac{2m_V f_P g_{VP\gamma }A_0^{DV}(m_1^2)}{(p_2+k)^2 - m_V^2 + \mathrm {i}m_V \Gamma _V}\right. \nonumber \\&\left. \quad + \frac{2m_V f_V g_{VP\gamma }F_1^{DP}((p_1+k)^2)}{(p_1+k)^2 - m_V^2 + \mathrm {i}m_V \Gamma _V}\right) \, , \end{aligned}$$

(33)

where the first (second) term in (33) corresponds to the left (right) diagram in Fig. 5. The amplitude for the final state $\pi ^0 \overline{K}^0 \gamma$ can be obtained from Eq. (33) by substituting $C_2-1/6C_1 \rightarrow C_2/2$, $m_1 \rightarrow m_2$, and $p_1 \leftrightarrow p_2$, and multiplying by the factor $-1/\sqrt{2}$. The $D\rightarrow P$ and $D\rightarrow V$ transition form factors are taken from Ref. [34]. As expected, resulting distributions based on (33) exhibit the same main resonance features as the ones in HHchiPT, and are therefore not shown.

3.3 The U-spin link

We further investigate the U-spin link between the SM-dominated mode $D \rightarrow K^- \pi ^+ \gamma$ and the BSM-probes $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$. In practice, a measurement of $\mathcal{{ B}}(D \rightarrow K^- \pi ^+ \gamma )$ can provide a data-driven SM prediction for the branching ratios of the FCNC decays. The method is phenomenological and serves, in the case of branching ratios, as an order-of-magnitude estimate. The U-spin approximation is expected to yield better results in ratios of observables (which arise already at lowest order in the U-spin limit), such that overall systematics drops out. Useful applications have been made for polarization asymmetries in $D \rightarrow V \gamma$ decays [36]. However, three-body radiative decays are considerably more complicated due to the intermediate resonances, and we do not pursue the U-spin link for the forward–backward or CP asymmetries.

A comparison between $|V_{us}|^2/|V_{ud}|^2 d{{\mathcal {B}}} (D \rightarrow K^- \pi ^+ \gamma )/ds$ with $d{{\mathcal {B}}} (D \rightarrow K^+ K^- \gamma )/ds$ and $|V_{cd}|^2/|V_{cs}|^2 d{{\mathcal {B}}}(D \rightarrow K^- \pi ^+ \gamma )/ds$ with $d{{\mathcal {B}}} (D \rightarrow \pi ^+ \pi ^- \gamma )/ds$ is shown in Fig. 6. For $s\gtrsim 1.5~\mathrm{GeV}$ the predictions of the direct calculations and the U-spin relations are in good agreement. This holds for both the extrapolations of QCDF and the HH$\chi$PT predictions. In the second case this is due to the dominance of the bremsstrahlung contributions and the U-spin relations of the $D\rightarrow P_1 P_2$ amplitudes. For $s \lesssim 1.5~\mathrm{GeV}$, there are large deviations due to the differences in phase space boundaries and the different intermediate resonances.

At the level of integrated SM branching ratios we find

$$\begin{aligned}&\frac{ {{\mathcal {B}}} - {{\mathcal {B}}}(\text {U-spin link})}{{{\mathcal {B}}}} \big \vert ^\text {QCDF}_{s \le 1.5~\mathrm{GeV}^2} \sim -0.33 \, (0.3) \, , \end{aligned}$$

(34)

$$\begin{aligned}&\frac{ {{\mathcal {B}}} - {{\mathcal {B}}}(\text {U-spin link})}{{{\mathcal {B}}}} \big \vert ^{\text {HH}\chi \text {PT}}_{s \le 1.5~\mathrm{GeV}^2} \sim 0.35 \, (-2.3) \, , \end{aligned}$$

(35)

$$\begin{aligned}&\frac{ {{\mathcal {B}}} - {{\mathcal {B}}}(\text {U-spin link})}{{{\mathcal {B}}}} \big \vert ^{\text {HH}\chi \text {PT}}_{E_\gamma \ge 0.1~\mathrm{GeV}} \sim 0.07 \, (-0.11) \, , \end{aligned}$$

(36)

for the $D \rightarrow \pi ^+ \pi ^- (K^+ K^-)\gamma$ modes. Equations (34)–(36) underline the main features of Fig. 6: as a result of the dominance of bremsstrahlung photons from Low’s theorem the corrections (36) are small; the proximity of the $\phi$ to the phase space boundary in $D \rightarrow KK \gamma$ makes the U-spin limit in (35) poor. In the other cases the U-spin symmetry performs as expected, within $\sim 30$%.

4 BSM analysis

BSM physics can significantly increase the Wilson coefficients contributing to $c \rightarrow u \gamma$ transitions. Examples are supersymmetric models with flavor mixing and chirally enhanced gluino loops, or leptoquarks, see Ref. [4] for details. In the following we work out BSM spectra and phenomenology in a model-independent way. Experimental data obtained from $D \rightarrow \rho ^0 \gamma$ decays provide model-independent constraints [6, 37]

$$\begin{aligned} |C_7|, |C_7^\prime | \lesssim 0.3\, . \end{aligned}$$

(37)

These values are in agreement with recent studies of $D \rightarrow \pi l l$ decays [38]. In Sect. 5.1 we discuss the implications of CP asymmetries in hadronic charm decays that can lead to constraints on the imaginary parts of the dipole operators.

The $D \rightarrow P_1 P_2$ matrix elements of the tensor currents can be parameterized as

$$\begin{aligned}&{\langle }{P_1(p_1)P_2(p_2)| \overline{u}\sigma ^{\mu \nu } k_\mu (1\pm \gamma _5) c| D(P)}{\rangle } \nonumber \\&\quad = m_D \left[ a^\prime p_1^\nu + b^\prime p_2^\nu + c^\prime P^\mu {\mp } 2 i h^\prime \epsilon ^{\nu \alpha \beta \gamma } p_{1\alpha } p_{2\beta } k_\gamma \right] \, . \end{aligned}$$

(38)

with the form factors $a^\prime , b^\prime , c^\prime , h^\prime$ given in App.B 2. The form factors depend on s and t and satisfy

$$\begin{aligned} a' p_1 \cdot k + b' p_2 \cdot k + c' P \cdot k=0 \, . \end{aligned}$$

(39)

The BSM amplitudes are then obtained as

$$\begin{aligned} \begin{aligned}&\mathcal {A}_-^\mathrm{BSM} = i \frac{G_F e}{\sqrt{2}} \frac{m_c }{4\pi ^2 }(C_7 + C_7^\prime )\frac{(b^\prime - a^\prime )}{v\cdot k} \, ,\\&\mathcal {A}_+^\mathrm{BSM} = \frac{G_F e}{\sqrt{2}} \frac{m_c m_D}{2\pi ^2 } (C_7 - C_7^\prime ) h^\prime \, . \end{aligned} \end{aligned}$$

(40)

In Figs. 7 and 8 we show differential branching ratios for the FCNC modes based on QCDF and HH$\chi$PT, respectively, both in the SM (blue) and in different BSM scenarios. One of the BSM coefficients, $C_7$ or $C_7^\prime$, is set to zero while the other one is taken to saturate the limit (37) with CP-phases $0, \pm \pi /2, \pi$. The same conclusions are drawn for both QCD approaches: the $D\rightarrow K^+ K^- \gamma$ branching ratio is insensitive to NP in the dipole operators. In particular, the benchmarks for $O_7^\prime$ and the SM prediction are almost identical. For $O_7$ small deviations occur directly beyond the $\phi$ peak. On the other hand, BSM contributions can increase the differential branching ratio of $D \rightarrow \pi ^+ \pi ^- \gamma$ by up to one order of magnitude around the $\rho$ peak. However, due to the intrinsic uncertainties from the Breit–Wigner contributions around the resonance peaks it is difficult to actually claim sensitivity to NP. This is frequently the case in D physics for simple observables such as branching ratios. The NP sensitivity is higher in observables involving ratios, such as CP asymmetries, discussed in the next section.

The NP impact on $A_\mathrm{FB}$ is sizable, see Fig. 9 for the HH$\chi$PT predictions.

However, due to the complicated interplay of s-, t- and u-channel resonances further study in SM-like $D \rightarrow K \pi \gamma$ decays is suggested to understand the decay dynamics before drawing firm conclusions within NP. Since the form factors depend on s and t, the pure BSM contributions (40) induce a forward–backward asymmetry within QCDF, whereas it vanishes in the SM (see Fig. 10).

Fig. 13

Dalitz plot of $A_\mathrm{CP}(s,t)$ for $D \rightarrow \pi ^+ \pi ^- \gamma$ (upper plots) and $D \rightarrow K^+ K^- \gamma$ decays (lower plots) based on HH$\chi$PT. We have set one BSM coefficient, $C_7$ or $C_7^{\prime }$, to 0 and the other one to 0.1, with weak phase $\phi _w= \pi /2$. We employed a cut $s \le 2\, \mathrm{GeV}^2$ to avoid large bremsstrahlung contributions in the normalization

5 CP Violation

Another observable that offers the possibility to test for BSM physics is the single- or double-differential CP asymmetry. It is defined, respectively, by

$$\begin{aligned} A_\mathrm{CP}(s) =\int d{} t A_\mathrm{CP}(s,t) \, , ~~~ A_\mathrm{CP}(s,t) =\frac{1}{\Gamma + \overline{\Gamma }}\left( \frac{d{}^2\Gamma }{d{}sd{}t} - \frac{d{}^2\overline{\Gamma }}{d{}sd{}t}\right) \, . \end{aligned}$$

(41)

Here, $\overline{\Gamma }$ refers to the decay rate of the CP-conjugated mode. Within the SM, $D \rightarrow K^+ K^- \gamma$ is the only decay that contains contributions with different weak phases and thus the only decay mode with a nonvanishing CP asymmetry. A maximum of $A^{\text {SM}}_\mathrm{CP}(s) \lesssim 1.4 \cdot 10^{-4}$ located around the $\phi$ peak is predicted by QCDF. Since the $\phi$ is a narrow resonance, the CP asymmetry decreases rapidly with increasing s. BSM contributions can contain further strong and weak phases and thus significantly increase the CP asymmetry. In Fig. 11 we show the predictions for the CP asymmetries within the SM and for several different BSM scenarios, based on QCDF. We assign a non-zero value to one of the BSM coefficients and set the weak phase to $\phi _w=\pm \pi /2$. The BSM CP asymmetries $A_\mathrm{CP}(s)$ can, in principle, reach $\mathcal {O}(1)$ values. Constraints can arise from data on CP asymmetries in hadronic decays; these are further discussed in Sect. 5.1. We emphasize that $A_\mathrm{CP}$ depends on cuts used in the normalization $\Gamma + {{\bar{\Gamma }}}$. In Fig. 11 we include the contributions up to $s=1.5~\mathrm{GeV}^2$.

HH$\chi$PT predicts a SM CP asymmetry $A_\mathrm{CP}^\text {SM}(s) \lesssim 0.7\cdot 10^{-4}$ for the $D \rightarrow K^+ K^- \gamma$ decay. In Fig. 12 we show the same BSM benchmarks as before, employing HH$\chi$PT. We performed a cut $s\le 2\, \mathrm{GeV}$ to avoid large bremsstrahlung effects in the normalization, which would artificially suppress $A_\mathrm{CP}$. Still, the CP asymmetries obtained using HH$\chi$PT are smaller than those using QCDF, since a larger part of the phase space is included in the normalization.

For $D \rightarrow \pi ^+ \pi ^- \gamma$, the contributions of $\mathcal {A}_-$ and $\mathcal {A}_+$ to the CP asymmetries are of roughly the same size. Therefore, the relative signs of the dipole Wilson coefficients in (40) results in a constructive increase (for $C_7^\prime$) and a cancellation (for $C_7$), respectively, of the CP asymmetry. For the $D \rightarrow K^+ K^- \gamma$ mode, the $\phi$ resonance contributes only to $A_+$. Therefore, in this case the CP asymmetry is dominated by the parity-even amplitude.

In order to get additional strong phases and thus an increase of the CP asymmetry, one could consider further heavy vector resonances such as the $\phi (1680)$. Intermediate scalar particles like $f_0(1710)$ [39] would also add additional strong phases. We remark that $A_\mathrm{CP}$ can change its sign in dependence of s; therefore, binning is required to avoid cancellations. $A_\mathrm{CP}$ is very small beyond the $(P_1P_2)_\text {res}$ peak due to the cancellation of the $(P_1 \gamma )_\text {res}$ and $(P_2 \gamma )_\text {res}$ contributions upon integration over t. To avoid this cancellation one could use the s- and t-dependent CP asymmetry $A_\mathrm{CP}(s,t)$ as shown in Fig. 13. Note that part of the resonance contribution to the asymmetry is removed by the bremsstrahlung cut.

Fig. 14

Dalitz plot of $A_\mathrm{CP}^\mathrm{SM}(s,t)$ for $D \rightarrow K^+ K^- \gamma$ decays based on HH$\chi$PT for $s \le 2\, \mathrm{GeV}^2$

5.1 CP phases and $\Delta A_\mathrm{CP}$

We briefly discuss the impact of the chromomagnetic dipole operators $O_8^{(\prime )}$ on radiative charm decays, where

$$\begin{aligned} O_8= & {} \frac{g_s m_c}{16\pi ^2} \left( \overline{u}_L \sigma ^{\mu \nu } G_{\mu \nu } c_R\right) \,,\nonumber \\ O_8^\prime= & {} \frac{g_s m_c}{16\pi ^2} \left( \overline{u}_R \sigma ^{\mu \nu } G_{\mu \nu } c_L\right) \, , \end{aligned}$$

(42)

and $G_{\mu \nu }$ denotes the chromomagnetic field strength tensor. We do not consider contributions from $O_8^{(\prime )}$ to the matrix element of $D \rightarrow PP \gamma$ decays, which is beyond the scope of this work. The corresponding contributions for the $D \rightarrow V \gamma$ decays have been worked out in Ref. [4].

The QCD renormalization-group evolution connects the electromagnetic and the chromomagnetic dipole operators at different scales. To leading order we find the following relation [4],

$$\begin{aligned}&C_7^{(\prime )}(m_c) \simeq 0.4 \big ( C_7^{(\prime )}(\Lambda ) - C_8^{(\prime )}(\Lambda ) \big ) \,, \nonumber \\&C_8^{(\prime )}(m_c) \simeq 0.4 C_8^{(\prime )}(\Lambda ) \,, \end{aligned}$$

(43)

which is valid to roughly 20% if $\Lambda$, the scale of NP, lies within 1–10 TeV. It follows that CP asymmetries for radiative decays are related to hadronic decays, a connection discussed in [40, 41] in the context of $\Delta A_\mathrm{CP}=A_\mathrm{CP}(D\rightarrow K^+ K^-)-A_\mathrm{CP}(D \rightarrow \pi ^+\pi ^-)$. The latter is measured by LHCb, $\Delta A_\mathrm{CP}=-(15.4 \pm 2.9) \cdot 10^{-4}$ [42], and implies $\Delta A_\mathrm{CP}^\mathrm{NP} \sim \mathrm{Im }(C_8-C_8^\prime ) \sin \delta \lesssim 2 \cdot 10^{-3}$ for NP from dipole operators, with a strong phase difference $\delta$ and Wilson coefficients evaluated at $\mu =m_c$. For $\sin \delta \sim O(1)$, and $C_8$ only (or $C_8^\prime$ only), strong constraints on the electromagnetic dipole operators follow from (43), unless $C_7(\Lambda ) \gg C_8(\Lambda )$, as $\mathrm{Im} \, C_7 \simeq \mathrm{Im } \, C_8 \lesssim 2 \cdot 10^{-3}$. We study the corresponding CP asymmetries for $D \rightarrow PP \gamma$ in the Dalitz region as this avoids large cancellations from t- or u-channel resonances. Note that the latter have not been included in Ref. [40]. We find values of $A_\mathrm{CP}(s,t)$ up to $\sim (3-4) \times 10^{-3}$ which is more than one order of magnitude above the SM with maximal values of $\sim 2 \times 10^{-4}$, shown in Fig. 14 for $D \rightarrow K^+ K^- \gamma$. (As already discussed, the corresponding SM asymmetry for $D \rightarrow \pi ^+ \pi ^-\gamma$ vanishes at this order.) The largest values for $A_\mathrm{CP}(s,t)$ arise around the resonances, notably the $K^* \rightarrow K \gamma$ contributions to $D \rightarrow K K \gamma$.

The BSM CP asymmetries scale linearly with $\mathrm{Im} \, C_7^{(\prime )}$. We checked explicitly that the CP asymmetries for $\mathrm{Im} \, C_7^{(\prime )} \simeq 2 \cdot 10^{-3}$ agree, up to an overall suppression factor of 50, with those shown in Fig. 13 which are based on $\mathrm{Im} \, C_7^{(\prime )} \simeq 0.1$, and are therefore not shown.

Note that the $\Delta A_\mathrm{CP}$ constraint can be eased with a strong phase suppression. In general, it can be escaped in the presence of different sources of BSM CP violation in the hadronic amplitudes. Yet, our analysis has shown that even with small CP violation in the dipole couplings sizable NP enhancements can occur.

6 Conclusions

We worked out predictions for $D \rightarrow PP \gamma$ decay rates and asymmetries in QCDF and in HH$\chi$PT. The $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$ decays are sensitive to BSM physics, while $D \rightarrow K \pi \gamma$ decays are SM-like and serve as “standard candles”. Therefore, a future measurement of the $D \rightarrow K \pi \gamma$ decay spectra can diagnose the performance of the QCD tools. The forward–backward asymmetry (32) is particularly useful as it vanishes for amplitudes without t- or u-channel dependence; this happens, for instance, in leading-order QCDF. On the other hand, t- or u-channel resonances are included within HH$\chi$PT, and give rise to finite interference patterns, shown in Fig. 4. Within QCDF, the value of ${{\tilde{C}}}/\lambda _D$ can be extracted from the branching ratio.

While branching ratios of $D \rightarrow \pi ^+ \pi ^- \gamma$ can be affected by NP, these effects will be difficult to discern due to the large uncertainties. On the other hand, the SM can be cleanly probed with CP asymmetries in the $D \rightarrow \pi ^+ \pi ^- \gamma$ and $D \rightarrow K^+ K^- \gamma$ decays, which can be sizable, see Figs. 11 and 12. We stress that the sensitivity of the CP asymmetries is maximized by performing a Dalitz analysis or applying suitable cuts in t (see Fig. 13), as otherwise large cancellations occur. Values of the CP asymmetries depend strongly on the cut in s employed to remove the bremsstrahlung contribution. The latter is SM-like and dominates the branching ratios for small photon energies. The forward–backward asymmetries also offer SM tests, see Fig. 9, but requires prior consolidation of resonance effects.

Radiative charm decays are well-suited for investigation at the $e^+ e^-$ flavor facilities Belle II [2], BES III [3], and future $e^+ e^-$-colliders running at the Z-pole [43]. Branching ratios for $D^0 \rightarrow \pi ^+ \pi ^- \gamma$ and $D^0 \rightarrow K^+ K^- \gamma$ decays are of the order $10^{-5}$, see Table 1. With fragmentation fraction $f(c \rightarrow D^0) \simeq 0.59$ and $c{\bar{c}}$ production rates of $550 \cdot 10^9$ (Fcc-ee) and $65 \cdot 10^9$ (Belle II with $50 \mathrm{ab}^{-1}$) [43] this gives $6 \cdot 10^{11}$ and $8 \cdot 10^{10}$ neutral D-mesons and sizeable (unreconstructed) event rates of $6 \cdot 10^6$ and $8 \cdot 10^5$, respectively. Rates for the “standard candles” $D^0 \rightarrow \pi ^+ K^-\gamma$ are one order of magnitude larger. We look forward to future investigations.

Appendices

Appendix A: Parameters

The couplings, masses, branching ratios, total decay widths and the mean life time are taken from the PDG [44]. The mass of the $\eta _8$ results from the Gell–Mann–Okubo (GMO) mass formula [45, 46]

$$\begin{aligned} m_{\eta _8} = \sqrt{\frac{4m_K^2 - m_\pi ^2}{3}} = 0.56929\, \mathrm{GeV}. \end{aligned}$$

The CKM matrix elements are taken from the UTfit collaboration [47]

$$\begin{aligned} V_{ud}&= 0.97431 \pm 0.00012, \quad \quad V_{us} = 0.22514 \pm 0.00055, \\ V_{cd}&= (-0.22500 \pm 0.00054) \exp \left[ \mathrm {i}(0.0351 \pm 0.0010)^{\circ } \right] , \\ V_{cs}&= (0.97344 \pm 0.00012) \exp \left[ \mathrm {i}(-0.001880 \pm 0.000055)^{\circ } \right] . \end{aligned}$$

The decay constant of the D-meson is given by the FLAG working group [48]

$$\begin{aligned}&f_D = (0.21215 \pm 0.00145)\, \mathrm{GeV},\\&f_{D_s} = (0.24883 \pm 0.00127)\, \mathrm{GeV},\\&f_K = (0.1556 \pm 0.0004)\, \mathrm{GeV}, \\&f_\pi = (0.1302 \pm 0.0014)\, \mathrm{GeV}. \end{aligned}$$

The $q\overline{q}-s\overline{s}$ mixing scheme [49] and $\chi$PT [50] provide decay constants for $\eta _8$ and $\eta _0$

$$\begin{aligned} f_{\eta _8} = \sqrt{\frac{4}{3}f_K^2 - \frac{1}{3}f_\pi ^2} = (0.1632 \pm 0.0006)\, \mathrm{GeV}, \\ f_{\eta _0} = \sqrt{\frac{2}{3}f_K^2 + \frac{1}{3}f_\pi ^2} = (0.1476 \pm 0.0005)\, \mathrm{GeV}. \end{aligned}$$

These values are in agreement with values extracted from $\eta ^{(\prime )} \rightarrow \gamma \gamma$ decays [49]

$$\begin{aligned} f_{\eta _8} = (0.164 \pm 0.006)\, \mathrm{GeV}, f_{\eta _0} = (0.152 \pm 0.004)\, \mathrm{GeV}. \end{aligned}$$

The decay constants of the vector mesons are given by [51, 52] (and references therein)

$$\begin{aligned}&f_{\rho } = (0.213 \pm 0.005)\, \mathrm{GeV}&f_{\omega } = (0.197 \pm 0.008) \, \mathrm{GeV}, \\&f_{\Phi } = (0.233 \pm 0.004)\, \mathrm{GeV},&f_{K^*} = (0.204 \pm 0.007) \, \mathrm{GeV}. \end{aligned}$$

Appendix B: Form factors

1.1 1. Vacuum $\rightarrow PP$ transition form factors

The electromagnetic pion form factor $F_{\pi }^{\text {em}}$ is defined as

$$\begin{aligned} {\langle }{\pi ^+(p_1) \pi ^-(p_2)|j^{\text {em}}_{\mu }|0}{\rangle } = (p_1 - p_2)_{\mu } F_{\pi }^{\text {em}}(s) \, , \end{aligned}$$

(B1)

with the electromagnetic current

$$\begin{aligned} j_{\mu }^{\text {em}}&= \frac{2}{3} \overline{u} \gamma _{\mu } u - \frac{1}{3} \overline{d} \gamma _{\mu } d - \frac{1}{3} \overline{s} \gamma _{\mu } s\nonumber \\&= \frac{1}{2} (\overline{u} \gamma _{\mu } u - \overline{d} \gamma _{\mu } d) + \frac{1}{6} (\overline{u} \gamma _{\mu } u + \overline{d} \gamma _{\mu } d) - \frac{1}{3} \overline{s} \gamma _{\mu } s\nonumber \\&= \frac{1}{\sqrt{2}}j_{\mu }^{(I=1)} + \frac{1}{3\sqrt{2}}j_{\mu }^{(I=0)} - \frac{1}{3} j_{\mu }^s \nonumber \\&= J_{\mu }^{(I=1)} + J_{\mu }^{(I=0)} + J_{\mu }^s \, . \end{aligned}$$

(B2)

In the isospin symmetry limit, only the $I=1$ current contributes to $F_{\pi }^{\text {em}}$, which reads [12]

$$\begin{aligned} F_{\pi }^{\text {em}}(s)&= \left[ \sum _{n=0}^{3} c_n BW_n^{KS}(s)\right] _{fit} \nonumber \\&\quad + \left[ \sum _{n=4}^{\infty } c_n BW_n^{KS}(s)\right] _{dual-QCD_{N_C=\infty }}, \end{aligned}$$

(B3)

where the coefficients $c_n$ are given by

$$\begin{aligned} \begin{aligned} c_0&= 1.171\pm 0.007, \quad c_1 = -0.119\pm 0.011, \\ c_2&= 0.0115 \pm 0.0064, \quad c_3 = -0.0438\pm 0.02,\\ c_n&= \frac{2(-1)^n \Gamma (1.8)m_{\rho }^2}{\sqrt{\pi } m_n^2 \Gamma (n+1)\Gamma (1.3-n)} \qquad n\ge 4, \\ m_n^2&= m_{\rho }^2(1+2n) \end{aligned} \end{aligned}$$

(B4)

and the functions $BW_n^{KS}(s)$ read

$$\begin{aligned}&BW_n^{KS}(s) = \frac{m_n^2}{m_n^2 - s - \mathrm {i}\sqrt{s} \Gamma _n(s)}, \nonumber \\&\Gamma _n(s)= \frac{0.2m_n^3}{s} \left( \frac{p(s)}{p(m_n^2)} \right) ^3, \nonumber \\&p(s) = 0.5 \sqrt{s-4m_{\pi }^2}. \end{aligned}$$

(B5)

The masses and widths of the $\rho$ meson and its first resonance are fitted as well

$$\begin{aligned} \begin{aligned}&m_{\rho } = (0.7739\pm 0.0006)\, \mathrm{GeV}, \quad m_{\rho '} = (1.357 \pm 0.018)\, \mathrm{GeV},\\&\Gamma _{\rho }= (0.1149 \pm 0.0010)\, \mathrm{GeV}, \quad \Gamma _{\rho '}=(0.437\pm 0.060)\, \mathrm{GeV}. \end{aligned} \end{aligned}$$

(B6)

$F_{\pi }^{\text {em}}$ is shown in Fig. 15.

Fig. 15

The real and imaginary part of the electromagnetic form factor $F_{\pi }^{\text {em}}$ (B3) (left) as well as the absolute value (right) as a function of the invariant mass squared s

The electromagnetic kaon form factor $F_{K^+}^{\text {em}}$, defined as

$$\begin{aligned} {\langle }{K^+(p_1) K^-(p_2)|j^{\text {em}}_{\mu }|0}{\rangle } = (p_1 - p_2)_{\mu } F_{K^+}^{\text {em}}(s) \, , \end{aligned}$$

(B7)

is taken from [12] and shown in Fig. 16. It can be decomposed into an isospin-one component $F_{K^+}^{(I=1)}$ and two isospin-zero components $F_{K^+}^{(I=0)}$, $F_{K^+}^s$, with $\omega$ and $\phi$ contributions, respectively,

$$\begin{aligned} \begin{aligned}&F_{K^+}^{\text {em}}(s) = F_{K^+}^{(I=1)}(s) + F_{K^+}^{(I=0)}(s) + F_{K^+}^s(s),\\&F_{K^+}^{(I=1)}(s) = \frac{1}{2} (c_{\rho }^K BW_{\rho }(s) + c_{\rho '}^K BW_{\rho '}(s) + c_{\rho ''}^K BW_{\rho ''}(s)), \\&F_{K^+}^{(I=0)}(s) = \frac{1}{6} (c_{\omega }^K BW_{\omega }(s) + c_{\omega '}^K BW_{\omega '}(s) + c_{\omega ''}^K BW_{\omega ''}(s)) , \\&F_{K^+}^s(s) = \frac{1}{3} (c_{\phi } BW_{\phi }(s) + c_{\phi '} BW_{\phi '}(s)). \end{aligned} \end{aligned}$$

(B8)

The requisite parameters are given by

$$\begin{aligned} \begin{aligned}&m_{\phi } = 1.019372 \, \mathrm{GeV}, \quad m_{\phi } = 1.68\, \mathrm{GeV},\\&m_{\rho '} = 1.465\, \mathrm{GeV},\\&m_{\rho ''} = 1.720\, \mathrm{GeV}, \quad m_{\omega '} = 1.425\, \mathrm{GeV},\\&m_{\omega ''} = 1.67\, \mathrm{GeV},\\&\Gamma _{\phi } = 0.00436\, \mathrm{GeV}, \quad \Gamma _{\phi '} = 0.150\, \mathrm{GeV},\\&\Gamma _{\rho } = 0.150\, \mathrm{GeV}, \quad \Gamma _{\rho '} = 0.400\, \mathrm{GeV},\\&\Gamma _{\rho ''} = 0.250\, \mathrm{GeV}, \quad \Gamma _{\omega } = 0.0084\, \mathrm{GeV}, \\&\Gamma _{\omega '} = 0.215\, \mathrm{GeV}, \quad \Gamma _{\omega ''} = 0.315\, \mathrm{GeV},\\&c_{\phi } = (1.018\pm 0.006), \quad c_{\phi '} = (-0.018\pm 0.006), \\&c^K_{\rho } = (1.195\pm 0.009), \quad c^K_{\rho '} = (-0.112\pm 0.010), \\&c^K_{\rho ''} = (-0.083\pm 0.019), \\&c^K_{\omega } = (1.195\pm 0.009), \quad c^K_{\omega '} = (-0.112\pm 0.010), \\&c^K_{\omega ''} = (-0.083\pm 0.019). \end{aligned} \end{aligned}$$

(B9)

Fig. 16

The real and imaginary parts of the electromagnetic kaon form factors (B8) (left) as well as their absolute values (right) as a function of s. The upper (lower) plots show $F_{K^+}^{(I=1,0)}$ ($F_{K^+}^s$)

The $\overline{K} \pi ^-$ form factors are defined as

$$\begin{aligned}&{\langle }{\pi ^-(p_1) \overline{K}(p_2)| \overline{s}\gamma _\mu u| 0}{\rangle } \nonumber \\&\quad = f_+^{\overline{K}\pi ^-}(s) \left( p_2 - p_1\right) _\mu + f_-^{\overline{K}\pi ^-}(s) \left( p_2 + p_1\right) _\mu \nonumber \\&\quad = -\frac{\Delta _{K \pi }}{s} f_0^{\overline{K}\pi ^-}(s) \left( p_2 + p_1\right) _\mu \nonumber \\&\qquad + \left[ \left( p_2 - p_1\right) _\mu + \frac{\Delta _{K \pi }}{s} \left( p_2 + p_1\right) _\mu \right] f_+^{\overline{K}\pi ^-}(s), \end{aligned}$$

(B10)

with $\Delta _{K\pi } = m_K^2-m_\pi ^2$. The vector form factor $f_+^{\overline{K}\pi ^-}$, shown in Fig. 17, can be parametrized with a dispersion relation with three subtractions at $s=0$ [13]

$$\begin{aligned} f_+^{\overline{K} \pi ^-}(s)&= f_+^{\overline{K} \pi ^-}(0) \cdot \exp \left[ \lambda _+' \frac{s}{m_\pi ^2} + \frac{1}{2} \left( \lambda _+'' - \lambda _+'^2\right) \frac{s}{m_\pi ^4}\right. \nonumber \\&\left. \quad + \frac{s^3}{\pi } \int _{s_{K\pi }}^{s_{cut}} d{}s' \frac{\delta _1^{K\pi }(s')}{(s')^3(s'-s-\mathrm {i}\epsilon )}\right] \, , \end{aligned}$$

(B11)

with $s_{K\pi }=(m_K + m_\pi )^2$. The phase $\delta _1^{K\pi }(s)$ is extracted from a two resonance model [13]

$$\begin{aligned} {\tilde{f}}_+^{\overline{K}\pi ^-}(s) = \frac{f_+^{\overline{K}\pi ^-}(s)}{f_+^{\overline{K}\pi ^-}(0)} = \frac{m^2_{K^\star } - \kappa _{K^\star } {\tilde{H}}_{K\pi }(0) + \beta s}{D(K^\star )} - \frac{\beta s}{D(K^{\star \prime })}\, , \end{aligned}$$

(B12)

where

Fig. 17

The real and imaginary part (left) of the $f_+^{\overline{K}\pi ^-}$ form factor (B10) as well as the absolute value (right) versus s in the two resonance models as well as in the dispersive description. The form factor is extracted from $\tau ^- \rightarrow \nu _\tau K_s \pi ^-$ decays [13]. For ${\bar{K}}^0 \pi ^0$ and $K^+ \pi ^-$, we use isospin relations (11)

$$\begin{aligned} \begin{aligned}&D(n) = m_n^2 - s - \kappa _n \text {Re}\left( {\tilde{H}}_{K\pi }(s)\right) - \mathrm {i}m_n \gamma _n(s)\, , \\&\gamma _n(s) = \gamma _n \frac{s}{m_n^2} \frac{\sigma _{K\pi }^3(s)}{\sigma _{K\pi }^3(m_n^2)}, \qquad \gamma _n = \gamma _n(m_n^2)\, ,\\&\sigma _{K\pi }(s) = \frac{2q_{K\pi }(s)}{\sqrt{s}} = \frac{1}{s} \sqrt{\left( s - (m_K + m_\pi )^2\right) \left( s - (m_K - m_\pi )^2\right) }\, ,\\&\kappa _n = \frac{192\pi f_K f_\pi }{\sigma ^3_{K\pi }(m_n^2)}\frac{\gamma _n}{m_n}\, . \end{aligned} \end{aligned}$$

(B13)

The function ${\tilde{H}}_{K\pi }$ is a $\chi$PT loop integral function [53]

$$\begin{aligned} {\tilde{H}}_{K\pi }(s)= & {} H_{K\pi }(s) - \frac{2}{3 f_\pi ^2}L_{K\pi }^r s\nonumber \\= & {} \frac{1}{f_\pi ^2}\left[ s M_{K\pi }^r(s) - L_{K\pi }(s)\right] \, ; \end{aligned}$$

(B14)

explicit expressions for $M^r(s)$ and L(s) can be found in chapter 8 of Ref. [54]:

$$\begin{aligned} M_{K\pi }^r(s)&= \frac{1}{12s}(s-2\Sigma )\overline{J}_{K\pi }(s) + \frac{\Delta ^2}{3s^2}\overline{\overline{J}}_{K\pi }(s) \nonumber \\&\quad - \frac{1}{6}k_{K\pi }(\mu ) + \frac{1}{288\pi ^2}\, , \nonumber \\ L_{K\pi }(s)&= \frac{\Delta ^2}{4s}\overline{J}_{K\pi }(s)\, , \nonumber \\ k_{K\pi }(\mu )&= \frac{1}{32\pi ^2} \frac{1}{\Delta } \left( m_K^2 \ln \left( \frac{m_K^2}{\mu ^2}\right) - m_\pi ^2 \ln \left( \frac{m_\pi ^2}{\mu ^2}\right) \right) \, , \nonumber \\ \overline{\overline{J}}_{K\pi }(s)&= \overline{J}_{K\pi }(s) - s \overline{J}_{K\pi }^\prime (0)\, , \nonumber \\ \overline{J}_{K\pi }(s)&= J_{K\pi }(s) - J_{K\pi }(0) \nonumber \\&= \frac{1}{32\pi ^2} \left( 2 + \left[ \frac{\Delta }{s} - \frac{\Sigma }{\Delta }\right] \ln \left( \frac{m_\pi ^2}{m_K^2}\right) \right. \nonumber \\&\left. \quad - \frac{v}{s}\ln \left( \frac{(s+v)^2 - \Delta ^2}{(s-v)^2 - \Delta ^2}\right) \right) , \nonumber \\ \overline{J}_{K\pi }^\prime (0)&= \frac{1}{32\pi ^2} \left( \frac{\Sigma }{\Delta ^2} + 2\frac{m_K^2 m_\pi ^2}{\Delta ^3}\ln \left( \frac{m_\pi ^2}{m_K^2}\right) \right) , \nonumber \\ v(s)&= s\sigma _{K\pi }(s), \nonumber \\ \Sigma&= m_K^2 + m_\pi ^2, \nonumber \\ \Delta&= m_K^2 - m_\pi ^2. \end{aligned}$$

(B15)

The renormalization scale $\mu$ is set to the physical resonance mass $\mu = m_{K^\star }$ [13]. The resonance masses and width parameters are unphysical fitting parameters. They are obtained as [13]

$$\begin{aligned}&m_{K^\star }^{\text {fit}} = (0.94341 \pm 0.00058) \, \mathrm{GeV}, \nonumber \\&\gamma _{K^\star }^{\text {fit}} = (0.06672 \pm 0.00086) \, \mathrm{GeV}, \nonumber \\&m_{K^{\star \prime }}^{\text {fit}} = (1.374 \pm 0.030) \, \mathrm{GeV}, \nonumber \\&\gamma _{K^{\star \prime }}^{\text {fit}} = (0.24 \pm 0.10) \, \mathrm{GeV}, \nonumber \\&s_{cut} = 4\, \mathrm{GeV}^2\, , \qquad \mu = m^{\text {phy}}_{K\star } = 0.892 \, \mathrm{GeV}, \nonumber \\&\beta =(-3.9\pm 1.5)\cdot 10^{-2}, \nonumber \\&\lambda _+^\prime =(24.66\pm 0.69)\cdot 10^{-3}, \nonumber \\&\lambda _+^{\prime \prime } =(11.99\pm 0.19)\cdot 10^{-4}, \nonumber \\&|V_{us}|f_+^{\overline{K}\pi ^-}(0) = 0.21664 \pm 0.00048. \end{aligned}$$

(B16)

1.2 2. HH$\chi$PT form factors

1.2.1 a. Vector form factors

The Feynman diagrams are shown in Figs. 18 and 19.

Fig. 18

Feynman diagrams for the $D\rightarrow \pi ^+ K^- \gamma$ decay, which contribute to the parity-even form factors A and E. The diagrams for the decays $D\rightarrow \pi ^+ \pi ^- \gamma$ and $D\rightarrow K^+ K^- \gamma$ are obtained by adjusting the flavors. We have added the diagrams $E_{1,2}$ and $E_{2,2}$ (see [7]) to make the amplitude E gauge invariant for any choice of a. Additionally, for each of the diagrams $A_{1,1}$, $A_{1,2}$, $A_{1,3}$, $A_{2,2}$, $A_{2,3}$, $A_{2,4}$, $E_{1,1}$, $E_{1,2}$, $E_{1,3}$, $E_{2,1}$ and $E_{2,3}$ there is another one where the photon is coupled via a vector meson

Fig. 19

Feynman diagrams for the $D\rightarrow \pi ^+ K^- \gamma$ decay, which contribute to the parity-odd form factors B and D. The diagrams for the decays $D\rightarrow \pi ^+ \pi ^- \gamma$ and $D\rightarrow K^+ K^- \gamma$ are obtained by adjusting the flavors

$\underline{D \rightarrow \pi ^0 \overline{K} \gamma }$

$$\begin{aligned} E_1^{(d,s)}&= \mathrm {i}g \frac{f_D f_K}{f_\pi } \frac{v\cdot k}{v\cdot k + v\cdot p_1 + \Delta }\nonumber \\&\quad \times \left( \frac{1}{v\cdot k + \Delta } - \frac{1}{v\cdot p_1 + \Delta }\right) \nonumber \\&\quad \times \left( \sqrt{2}\lambda ^\prime + \frac{1}{2} \lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \right) \end{aligned}$$

(B17)

$$\begin{aligned} D_1^{(d,s)}&= -\sqrt{2} \frac{f_D f_K}{f_\pi }\lambda ^\prime \left( \frac{1}{v\cdot k + \Delta } + g \frac{v\cdot p_2}{v\cdot p_1 + v\cdot k}\right. \nonumber \\&\left. \quad \left[ \frac{1}{v\cdot k + \Delta }+\frac{1}{v\cdot p_1 + \Delta }\right] \right) \nonumber \\ D_2^{(d,s)}&= -\frac{1}{2}\frac{f_D f_K}{f_\pi } \lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \left( \frac{1}{v\cdot k + \Delta } \right. \nonumber \\&\left. \quad +g \frac{v\cdot p_2}{v\cdot p_1 + v\cdot k}\left[ \frac{1}{v\cdot k + \Delta }+\frac{1}{v\cdot p_1 + \Delta }\right] \right) \nonumber \\ D_3^{(d,s)}&= -\sqrt{\frac{2}{m_D}} f_K (\alpha _1 m_D - \alpha _2 v\cdot p_2) \nonumber \\&\quad \times \left( \frac{m_\rho ^2g_{\rho \pi \gamma }}{g_\rho } BW_\rho (p_1+k) + \frac{m_\omega ^2g_{\omega \pi \gamma }}{g_\omega } BW_\omega (p_1+k)\right) \nonumber \\&\quad + \frac{1}{\sqrt{2}}g_{\overline{K}^\star } g_{\overline{K}^\star \overline{K} \gamma } \frac{f_D}{f_\pi } \left( 1+ g\frac{m_D-v\cdot p_1}{v\cdot p_1 + \Delta }\right) \nonumber \\&\quad \times BW_{\overline{K}^\star }(p_2+k) \nonumber \\ D_4^{(d,s)}&=-f_D \frac{1}{v\cdot k + \Delta } \left( 1 - m_{K^\star }^2 BW_{\overline{K}^\star }(p_1 + p_2)\right) \nonumber \\&\quad \times \left( \sqrt{2}\lambda ^\prime + \frac{1}{2} \lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \right) \nonumber \\ D_5^{(d,s)}&=\frac{1}{\sqrt{2}}\frac{f_D}{f_K} (g_\rho g_{\rho \pi \gamma } BW_\rho (p_1+k) \nonumber \\&\quad - g_\omega g_{\omega \pi \gamma } BW_\omega (p_1+k)) \nonumber \\ D_6^{(d,s)}&= \frac{1}{\sqrt{2}}f_D f_K \frac{m_D^2}{m_D^2 - m_{K^0}^2} \left( \frac{m_\rho ^2}{g_\rho }g_{\rho \pi \gamma } BW_\rho (p_1+k)\right. \nonumber \\&\left. \quad - \frac{m_\omega ^2}{g_\omega }g_{\omega \pi \gamma } BW_\omega (p_1+k)\right) \end{aligned}$$

(B18)

$\underline{D \rightarrow \pi ^+ K^- \gamma }$

$$\begin{aligned} A_1^{(d,s)}&= \mathrm {i}\frac{f_D f_\pi }{f_K}\frac{p_1\cdot k - m_D(v\cdot k + v\cdot p_1)}{(p_1\cdot k)(p_2\cdot k)} \nonumber \\ A_2^{(d,s)}&= -\mathrm {i}\sqrt{m_Dm_{D_s}} \frac{f_{D_s}f_\pi }{f_K} \frac{g}{(p_1\cdot k)(p_2\cdot k)} \nonumber \\&\quad \times \left( \frac{p_2\cdot k(m_D - v\cdot p_2)}{m_D(v\cdot p_2 +\Delta )} \right. \nonumber \\&\left. \quad + \frac{p_2\cdot k \left[ p_1\cdot p_2 - (v\cdot p_1)(v\cdot p_2)\right] }{m_D(v\cdot p_2+\Delta )(v\cdot p_2 + v\cdot k + \Delta )} \right. \nonumber \\&\left. \quad + \frac{(m_D-v\cdot p_1)p_1\cdot k + m_Dp_1\cdot p_2 + m_D(v\cdot p_1)(v\cdot p_2)}{m_D(v\cdot p_2 + v\cdot k + \Delta )}\right) \nonumber \\ A_3^{(d,s)}&= \mathrm {i}\sqrt{\frac{m_{D_s}}{m_D}} \frac{f_{D_s}f_\pi }{f_K} g \frac{v\cdot k}{v\cdot k + v\cdot p_2 + \Delta } \nonumber \\&\quad \times \left( \frac{2\lambda ^\prime - \frac{\sqrt{2}}{3}\lambda g_v \frac{g_\Phi }{m_\Phi ^2}}{v\cdot p_2 + \Delta } - \frac{2\lambda ^\prime + \frac{1}{\sqrt{2}}\lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) }{v\cdot k + \Delta }\right) \end{aligned}$$

(B19)

$$\begin{aligned} B_1^{(d,s)}&= 2 \frac{f_D f_\pi }{f_K}\lambda ^\prime \left( \frac{1}{v\cdot k + \Delta } + g \frac{f_{D_s}}{f_D }\right. \nonumber \\&\left. \quad \sqrt{\frac{m_{D_s}}{m_D}}\frac{v\cdot p_1}{(v\cdot p_2 + v\cdot k)}\left[ \frac{1}{v\cdot k + \Delta }+\frac{1}{v\cdot p_2 + \Delta }\right] \right) \nonumber \\ B_2^{(d,s)}&= \frac{1}{\sqrt{2}}\frac{f_\pi }{f_K} \lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \frac{1}{v\cdot k + \Delta } \nonumber \\&\quad \times \left( f_D + g \sqrt{\frac{m_{D_s}}{m_D}}f_{D_s} \frac{v\cdot p_1}{(v\cdot p_2 + v\cdot k)}\right) \nonumber \\&\quad - g \lambda g_v \sqrt{\frac{m_{D_s}}{m_D}}\frac{f_{D_s} f_\pi }{f_K} \frac{\sqrt{2}g_\Phi }{3m_\Phi ^2}\frac{v\cdot p_1}{(v\cdot p_2 + v\cdot k)(v\cdot p_2 + \Delta )} \nonumber \\ B_3^{(d,s)}&= \frac{2}{\sqrt{m_D}} f_\pi \frac{m^2_{K^{\star }}g_{K^{\star \pm } K^\pm \gamma }}{g_{K^{\star }}} \nonumber \\&\quad \times (\alpha _1 m_D - \alpha _2 v\cdot p_1)BW_{K^{\star -}}(p_2+k) \nonumber \\&\quad - g_{\rho } g_{\rho ^\pm \pi ^\pm \gamma } \frac{f_D}{f_K} \left( 1+ g\sqrt{\frac{m_{D_s}}{m_D}}\frac{f_{D_s}}{f_D}\frac{m_D-v\cdot p_2}{v\cdot p_2 + \Delta }\right) \nonumber \\&\quad \times BW_{\rho ^+}(p_1+k) \end{aligned}$$

(B20)

$$\begin{aligned} D_1^{(d,s)}&= \frac{f_D}{v\cdot k + \Delta } \left( 1 - m_{K^\star }^2 BW_{\overline{K}^\star }(p_1 + p_2)\right) \nonumber \\&\quad \times \left( 2\lambda ^\prime + \frac{1}{\sqrt{2}} \lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \right) \nonumber \\ D_2^{(d,s)}&=-\frac{f_D}{f_\pi } g_{K^\star } g_{K^{\star \pm } K^\pm \gamma } BW_{K^{\star -}}(p_2+k) \nonumber \\&\quad - \frac{f_D}{f_K} g_\rho g_{\rho ^\pm \pi ^\pm \gamma } BW_{\rho ^+}(p_1+k) \nonumber \\ D_3^{(d,s)}&= {f_D f_K} \frac{m_D^2}{m_D^2 - m_{K^0}^2} \nonumber \\&\quad \times \left( \frac{m_\rho ^2}{g_\rho }g_{\rho ^\pm \pi ^\pm \gamma } BW_{\rho ^+}(p_1+k) \right. \nonumber \\&\left. \quad +\frac{m_{K^\star }^2}{g_{K^\star }}g_{K^{\star \pm } K^\pm \gamma } BW_{K^{\star -}}(p_2+k)\right) \end{aligned}$$

(B21)

$\underline{D \rightarrow \pi ^+ \pi ^- \gamma }$

$$\begin{aligned} A_1^{(d,d)}&= \mathrm {i}f_D\frac{p_1\cdot k - m_D(v\cdot k + v\cdot p_1)}{(p_1\cdot k)(p_2\cdot k)} \nonumber \\ A_2^{(d,d)}&= -\mathrm {i}m_D f_{D} \frac{g}{(p_1\cdot k)(p_2\cdot k)} \nonumber \\&\quad \times \left( \frac{p_2\cdot k(m_D - v\cdot p_2)}{m_D(v\cdot p_2 +\Delta )}\right. \nonumber \\&\left. \quad + \frac{p_2\cdot k \left[ p_1\cdot p_2 - (v\cdot p_1)(v\cdot p_2)\right] }{m_D(v\cdot p_2+\Delta )(v\cdot p_2 + v\cdot k + \Delta )} \right. \nonumber \\&\left. \quad + \frac{(m_D-v\cdot p_1)p_1\cdot k + m_Dp_1\cdot p_2 + m_D(v\cdot p_1)(v\cdot p_2)}{m_D(v\cdot p_2 + v\cdot k + \Delta )}\right) \nonumber \\ A_3^{(d,d)}&= \mathrm {i}f_D g \frac{v\cdot k}{v\cdot k + v\cdot p_2 + \Delta } \nonumber \\&\quad \times \left( \frac{2\lambda ^\prime + \frac{1}{\sqrt{2}}\lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} - \frac{g_\rho }{m_\rho ^2}\right) }{v\cdot p_2 + \Delta }\right. \nonumber \\&\left. \quad - \frac{2\lambda ^\prime + \frac{1}{\sqrt{2}}\lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) }{v\cdot k + \Delta }\right) \end{aligned}$$

(B22)

$$\begin{aligned} B_1^{(d,d)}&= 2 f_D\lambda ^\prime \left( \frac{1}{v\cdot k + \Delta } + g \frac{v\cdot p_1}{(v\cdot p_2 + v\cdot k)}\right. \nonumber \\&\left. \quad \left[ \frac{1}{v\cdot k + \Delta }+\frac{1}{v\cdot p_2 + \Delta }\right] \right) \nonumber \\ B_2^{(d,d)}&= \frac{1}{\sqrt{2}} \lambda g_v f_D \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \nonumber \\&\quad \times \frac{1}{v\cdot k + \Delta }\left( 1 + g \frac{v\cdot p_1}{(v\cdot p_2 + v\cdot k)}\right) \nonumber \\&\quad + \frac{1}{\sqrt{2}}g \lambda g_v f_D \left( \frac{g_\omega }{3m_\omega ^2} - \frac{g_\rho }{m_\rho ^2}\right) \nonumber \\&\quad \times \frac{v\cdot p_1}{(v\cdot p_2 + v\cdot k)(v\cdot p_2 + \Delta )} \nonumber \\ B_3^{(d,d)}&= \frac{2}{\sqrt{m_D}} f_\pi \frac{m_\rho ^2}{g_\rho }g_{\rho ^{\pm } \pi ^\pm \gamma } \nonumber \\&\quad \times (\alpha _1 m_D - \alpha _2 v\cdot p_1)BW_{\rho ^-}(p_2+k) \nonumber \\&\quad - g_{\rho } g_{\rho ^\pm \pi ^\pm \gamma } \frac{f_D}{f_\pi } \left( 1+ g\frac{m_D-v\cdot p_2}{v\cdot p_2 + \Delta }\right) \nonumber \\&\quad \times BW_{\rho ^+}(p_1+k) \end{aligned}$$

(B23)

$$\begin{aligned} D_1^{(d,d)}&=f_D \frac{1}{v\cdot k + \Delta } \left( 1 - m_\rho ^2 BW_{\rho }(p_1 + p_2)\right) \nonumber \\&\quad \times \left( 2\lambda ^\prime + \frac{1}{\sqrt{2}} \lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \right) \nonumber \\ D_2^{(d,d)}&= -\frac{f_D}{f_\pi } g_{\rho } g_{\rho ^{\star \pm } \pi ^\pm \gamma } \nonumber \\&\quad \times (BW_{\rho ^-}(p_2+k) + BW_{\rho ^+}(p_1+k)) \nonumber \\ D_3^{(d,d)}&= {f_D f_\pi } \frac{m_D^2}{m_D^2 - m_{\pi ^0}^2} \frac{m_\rho ^2}{g_\rho }g_{\rho ^\pm \pi ^\pm \gamma } \nonumber \\&\quad \times \left( BW_{\rho ^+}(p_1+k) + BW_{\rho ^-}(p_2+k)\right) \end{aligned}$$

(B24)

$\underline{D \rightarrow K^+ K^- \gamma }$

$$\begin{aligned} A_1^{(s,s)}&= \mathrm {i}f_D\frac{p_1\cdot k - m_D(v\cdot k + v\cdot p_1)}{(p_1\cdot k)(p_2\cdot k)} \nonumber \\ A_2^{(s,s)}&= -\mathrm {i}\sqrt{m_Dm_{D_s}} f_{D_s} \frac{g}{(p_1\cdot k)(p_2\cdot k)} \nonumber \\&\quad \times \left( \frac{p_2\cdot k(m_D - v\cdot p_2)}{m_D(v\cdot p_2 +\Delta )}\right. \nonumber \\&\left. \quad + \frac{p_2\cdot k \left[ p_1\cdot p_2 - (v\cdot p_1)(v\cdot p_2)\right] }{m_D(v\cdot p_2+\Delta )(v\cdot p_2 + v\cdot k + \Delta )} \right. \nonumber \\&\left. \quad + \frac{(m_D-v\cdot p_1)p_1\cdot k + m_Dp_1\cdot p_2 + m_D(v\cdot p_1)(v\cdot p_2)}{m_D(v\cdot p_2 + v\cdot k + \Delta )}\right) \nonumber \\ A_3^{(s,s)}&= \mathrm {i}\sqrt{\frac{m_{D_s}}{m_D}} f_{D_s} g \frac{v\cdot k}{v\cdot k + v\cdot p_2 + \Delta }\nonumber \\&\quad \times \left( \frac{2\lambda ^\prime - \frac{\sqrt{2}}{3}\lambda g_v \frac{g_\Phi }{m_\Phi ^2}}{v\cdot p_2 + \Delta } - \frac{2\lambda ^\prime + \frac{1}{\sqrt{2}}\lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) }{v\cdot k + \Delta }\right) \end{aligned}$$

(B25)

$$\begin{aligned} B_1^{(s,s)}&= 2 f_D\lambda ^\prime \left( \frac{1}{v\cdot k + \Delta } + g \frac{f_{D_s}}{f_D }\right. \nonumber \\&\left. \quad \sqrt{\frac{m_{D_s}}{m_D}}\frac{v\cdot p_1}{(v\cdot p_2 + v\cdot k)}\left[ \frac{1}{v\cdot k + \Delta }+\frac{1}{v\cdot p_2 + \Delta }\right] \right) \nonumber \\ B_2^{(s,s)}&= \frac{1}{\sqrt{2}}\lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \frac{1}{v\cdot k + \Delta }\nonumber \\&\quad \times \left( f_D + g f_{D_s}\sqrt{\frac{m_{D_s}}{m_D}} \frac{v\cdot p_1}{(v\cdot p_2 + v\cdot k)}\right) \nonumber \\&\quad - g \lambda g_v \sqrt{\frac{m_{D_s}}{m_D}}f_{D_s} \frac{\sqrt{2}g_\Phi }{3m_\Phi ^2}\frac{v\cdot p_1}{(v\cdot p_2 + v\cdot k)(v\cdot p_2 + \Delta )}\nonumber \\ B_3^{(s,s)}&= \frac{2}{\sqrt{m_D}} f_K \frac{m^2_{K^{\star }}}{g_{K^{\star }}} g_{K^{\star \pm } K^\pm \gamma } \nonumber \\&\quad \times (\alpha _1 m_D - \alpha _2 v\cdot p_1)BW_{K^{\star -}}(p_2+k)\nonumber \\&\quad - g_{K^\star } g_{K^{\star \pm } K^\pm \gamma } \frac{f_D}{f_K} \left( 1+\right. \nonumber \\&\left. \quad g\sqrt{\frac{m_{D_s}}{m_D}}\frac{f_{D_s}}{f_D}\frac{m_D-v\cdot p_2}{v\cdot p_2 + \Delta }\right) BW_{K^{\star +}}(p_1+k) \end{aligned}$$

(B26)

$$\begin{aligned} D_1^{(s,s)}&=f_D \frac{1}{v\cdot k + \Delta } \left( 1 - m_\Phi ^2 BW_{\Phi }(p_1 + p_2)\right) \nonumber \\&\quad \times \left( 2\lambda ^\prime + \frac{1}{\sqrt{2}} \lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \right) \nonumber \\ D_1^{(d,d)}&= f_D \frac{1}{v\cdot k + \Delta }\left( m_\omega ^2 BW_\omega (p_1+p_2)\right. \nonumber \\&\left. \quad -m_\rho ^2 BW_\rho (p_1+p_2) \right) \left( \lambda ^\prime + \frac{1}{2\sqrt{2}} \lambda g_v \left( \frac{g_\omega }{3m_\omega ^2} + \frac{g_\rho }{m_\rho ^2}\right) \right) \nonumber \\ D_2^{(s,s)}&=-\frac{f_D}{f_K} g_{K^\star } g_{K^{\star \pm } K^\pm \gamma } \left( BW_{K^{\star +}}(p_1+k)\right. \nonumber \\&\left. \quad + BW_{K^{\star -}}(p_2+k)\right) \nonumber \\ D_3^{(s,s)}&= -\frac{f_D f_{\eta _8}}{2} \frac{m_D^2}{m_D^2 - m_{\eta _8}^2} \frac{m_{K^\star }^2}{g_{K^\star }} g_{K^{\star \pm } K^\pm \gamma }\nonumber \\&\quad \times \left( BW_{K^{\star +}}(p_1+k) + BW_{K^{\star -}}(p_2+k)\right) \nonumber \\ D_3^{(d,d)}&= -\frac{f_D}{2} m_D^2 \left( \frac{f_{\eta _8}}{m_D^2 - m_{\eta _8}^2} + \frac{f_{\pi }}{m_D^2 - m_{\pi }^2}\right) \nonumber \\&\quad \times \frac{m_{K^\star }^2}{g_{K^\star }} g_{K^{\star \pm } K^\pm \gamma }\left( BW_{K^{\star +}}(p_1+k) + BW_{K^{\star -}}(p_2+k)\right) \end{aligned}$$

(B27)

$$\begin{aligned} BW_n(x)&= \frac{1}{x^2 - m_n^2 + \mathrm {i}m_n \Gamma _n}\, ,\nonumber \\ \Delta&= m_{D^\star }-m_D \end{aligned}$$

(B28)

1.2.2 b. Tensor form factors

See Fig. 20.

Fig. 20

Feynman diagrams contributing to the tensor current form factors $a^\prime$, $b^\prime$, $c^\prime$ and $h^\prime$

$\underline{D \rightarrow \pi ^+ \pi ^-}$

$$\begin{aligned} a^\prime&= -\frac{g^2f_D\left( p_2\cdot k -(v\cdot k)(v\cdot p_2)\right) }{f_\pi ^2 (v\cdot p_2 + \Delta )(v\cdot p_1 + v\cdot p_2 + \Delta )}\nonumber \\&\quad + \frac{\alpha _1(v\cdot k)}{f_\pi ^2 \sqrt{m_D}}\left[ 1 + \frac{f_\pi ^2 m_\rho ^4}{g_\rho ^2} BW_\rho (p_1+p_2) \right] \nonumber \\&\quad - \frac{\sqrt{2}\lambda f_D g_v }{(v\cdot p_1+v\cdot p_2+\Delta )}\frac{m_\rho ^2}{g_\rho }\nonumber \\&\quad \times \left( p_2\cdot k -(v\cdot k)(v\cdot p_2)\right) BW_\rho (p_1+p_2) \end{aligned}$$

(B29)

$$\begin{aligned} b^\prime&= \frac{gf_D}{f_\pi ^2 (v\cdot p_2 + \Delta )} \left[ v\cdot k +\frac{g\left( p_1 \cdot k -(v\cdot k)(v\cdot p_1)\right) }{(v\cdot p_1+v\cdot p_2+\Delta )}\right] \nonumber \\&\quad - {\frac{\alpha _1(v\cdot k)}{f_\pi ^2 \sqrt{m_D}}}\left[ {1} + {\frac{f_\pi ^2 m_\rho ^4}{g_\rho ^2} BW_\rho (p_1+p_2)}\right] \nonumber \\&\quad + \frac{\sqrt{2}\lambda f_D g_v}{(v\cdot p_1+v\cdot p_2+\Delta )}\frac{m_\rho ^2}{g_\rho }\nonumber \\&\quad \times \left( p_1\cdot k - (v\cdot k)(v\cdot p_1)\right) BW_\rho (p_1+p_2) \end{aligned}$$

(B30)

$$\begin{aligned} c^\prime&= \frac{gf_D}{f_\pi ^2 m_D (v\cdot p_2 + \Delta )}\nonumber \\&\quad \times \left[ -p_2\cdot k + \frac{g\left( (p_2\cdot k)(v\cdot p_1)-(p_1\cdot k)(v\cdot p_2)\right) }{(v\cdot p_1+v\cdot p_2+\Delta )}\right] \nonumber \\&\quad + {\frac{\alpha _1}{f_\pi ^2 m_D^{\frac{3}{2}}}(p_2\cdot k-p_1\cdot k)}\left[ {1} + {\frac{f_\pi ^2 m_\rho ^4}{g_\rho ^2} BW_\rho (p_1+p_2)}\right] \nonumber \\&\quad - \frac{\sqrt{2}\lambda f_D g_v}{m_D(v\cdot p_1+v\cdot p_2+\Delta )}\frac{m_\rho ^2}{g_\rho }\left( (p_1\cdot k)(v\cdot p_2)\right. \nonumber \\&\left. \quad - (p_2\cdot k)(v\cdot p_1)\right) BW_\rho (p_1+p_2) \end{aligned}$$

(B31)

$$\begin{aligned} h^\prime&= \frac{gf_D}{2f_\pi ^2 m_D (v\cdot p_2 + \Delta )} \left[ 1 + \frac{g v\cdot k}{(v\cdot p_1+v\cdot p_2+\Delta )}\right] \nonumber \\&\quad + {\frac{\alpha _1}{f_\pi ^2 m_D^{\frac{3}{2}}}}\left[ {1} + {\frac{f_\pi ^2 m_\rho ^4}{g_\rho ^2} BW_\rho (p_1+p_2)}\right] \nonumber \\&\quad + {\frac{\lambda f_D g_v\left( v\cdot k\right) }{\sqrt{2}m_D(v\cdot p_1+v\cdot p_2+\Delta )}\frac{m_\rho ^2}{g_\rho }BW_\rho (p_1+p_2)} \end{aligned}$$

(B32)

$\underline{D \rightarrow K^+ K^-}$

$$\begin{aligned} a^\prime&= -\frac{g^2f_D\left( p_2\cdot k -(v\cdot k)(v\cdot p_2)\right) }{f_K^2 (v\cdot p_2 + \Delta )(v\cdot p_1 + v\cdot p_2 + \Delta )} \nonumber \\&\quad + {\frac{\alpha _1(v\cdot k)}{f_K^2 \sqrt{m_D}}}\left[ {1} + \frac{f_K^2}{2} \left( \frac{m_\rho ^4}{g_\rho ^2}BW_\rho (p_1+p_2) \right. \right. \nonumber \\&\left. \left. \quad + \frac{m_\omega ^4}{g_\omega ^2}BW_\omega (p_1+p_2)\right) \right] \nonumber \\&\quad - \frac{\lambda f_D g_v\left( p_2\cdot k -(v\cdot k)(v\cdot p_2)\right) }{\sqrt{2}(v\cdot p_1+v\cdot p_2+\Delta )}\nonumber \\&\quad \times \left( \frac{m_\rho ^2}{g_\rho }BW_\rho (p_1+p_2) + \frac{m_\omega ^2}{g_\omega }BW_\omega (p_1+p_2)\right) \end{aligned}$$

(B33)

$$\begin{aligned} b^\prime&= \frac{gf_D}{f_K^2 (v\cdot p_2 + \Delta )} \left[ \frac{f_{D_s} \sqrt{m_{D_s}}}{f_D \sqrt{m_D}}v\cdot k \right. \nonumber \\&\left. \quad +\frac{g\left( p_1 \cdot k -(v\cdot k)(v\cdot p_1)\right) }{(v\cdot p_1+v\cdot p_2+\Delta )}\right] \nonumber \\&\quad - {\frac{\alpha _1(v\cdot k)}{f_K^2 \sqrt{m_D}}}\left[ {1} + \frac{f_K^2}{2} \right. \nonumber \\&\left. \quad \times \left( \frac{m_\rho ^4}{g_\rho ^2}BW_\rho (p_1+p_2) + \frac{m_\omega ^4}{g_\omega ^2}BW_\omega (p_1+p_2)\right) \right] \nonumber \\&\quad + \frac{\lambda f_D g_v\left( p_1\cdot k - (v\cdot k)(v\cdot p_1)\right) }{\sqrt{2}(v\cdot p_1+v\cdot p_2+\Delta )}\nonumber \\&\quad \times \left( \frac{m_\rho ^2}{g_\rho }BW_\rho (p_1+p_2) + \frac{m_\omega ^2}{g_\omega }BW_\omega (p_1+p_2)\right) \end{aligned}$$

(B34)

$$\begin{aligned} c^\prime&= \frac{gf_D}{f_K^2 m_D (v\cdot p_2 + \Delta )} \left[ -\frac{f_{D_s} \sqrt{m_{D_s}}}{f_D \sqrt{m_D}}p_2\cdot k \right. \nonumber \\&\left. \quad + \frac{g\left( (p_2\cdot k)(v\cdot p_1)-(p_1\cdot k)(v\cdot p_2)\right) }{(v\cdot p_1+v\cdot p_2+\Delta )}\right] \nonumber \\&\quad + {\frac{\alpha _1}{f_K^2 m_D^{\frac{3}{2}}}(p_2\cdot k-p_1\cdot k)}\nonumber \\&\quad \times \left[ {1} + \frac{f_K^2}{2} \left( \frac{m_\rho ^4}{g_\rho ^2}BW_\rho (p_1+p_2)\right. \right. \nonumber \\&\left. \left. \quad + \frac{m_\omega ^4}{g_\omega ^2}BW_\omega (p_1+p_2)\right) \right] \nonumber \\&\quad - \frac{\lambda f_D g_v\left( (p_1\cdot k)(v\cdot p_2) - (p_2\cdot k)(v\cdot p_1)\right) }{\sqrt{2}m_D(v\cdot p_1+v\cdot p_2+\Delta )}\nonumber \\&\quad \times \left( \frac{m_\rho ^2}{g_\rho }BW_\rho (p_1+p_2) + \frac{m_\omega ^2}{g_\omega }BW_\omega (p_1+p_2)\right) \end{aligned}$$

(B35)

$$\begin{aligned} h^\prime&= \frac{gf_D}{2f_K^2 m_D (v\cdot p_2 + \Delta )} \nonumber \\&\quad \times \left[ \frac{f_{D_s} \sqrt{m_{D_s}}}{f_D \sqrt{m_D}} + \frac{g v\cdot k}{(v\cdot p_1+v\cdot p_2+\Delta )}\right] \nonumber \\&\quad + {\frac{\alpha _1}{f_K^2 m_D^{\frac{3}{2}}}}\left[ {1} + \frac{f_K^2}{2} \left( \frac{m_\rho ^4}{g_\rho ^2}BW_\rho (p_1+p_2) \right. \right. \nonumber \\&\left. \left. \quad + \frac{m_\omega ^4}{g_\omega ^2}BW_\omega (p_1+p_2)\right) \right] \nonumber \\&+ \frac{\lambda f_D g_v\left( v\cdot k\right) }{2\sqrt{2}m_D(v\cdot p_1+v\cdot p_2+\Delta )}\nonumber \\&\quad \times \left( \frac{m_\rho ^2}{g_\rho }BW_\rho (p_1+p_2) + \frac{m_\omega ^2}{g_\omega }BW_\omega (p_1+p_2)\right) \end{aligned}$$

(B36)

1.2.3 c. Differences with respect to [7]

In the following, we list some differences between our results and those obtained in Ref. [7]. Equation numbers refer to Ref. [7].

• 1. Eq. (9): the factor i should be absent

• 2. Eq. (15): the electromagnetic coupling e is missing

• 3. Eq. (18): the factor i in front of the $A_2$ term is missing

• 4. Eq. (21): the sign in front of a should be a $+$ (as written in [23])

• 5. The Wilson coefficients $a_1$ and $a_2$ are missing in the amplitudes in Eqs. (24) and (25).

• 6. The contributions of the diagrams $A_{4,1}^+$, $C_{4,1}^+$ and $A_{4,1}^0$ vanish in our calculation.

• 7. We believe that there are diagrams that have not been shown in Ref. [7]: For each of the diagrams $A_{1,1}^0$, $A_{1,2}^0$, $A_{1,3}^0$, $A_{2,2}^0$, $A_{2,3}^0$, $A_{2,4}^0$, $C_{1,1}^0$, $C_{1,2}^0$, $C_{1,3}^0$ and $C_{1,4}^0$ there is another one in which the photon couples via a vector meson. Moreover, we find two additional diagrams for $C^0$. The first one is the same diagram as $A_{2,2}^0$, but with a different factorization. The second is another diagram with a $V \rightarrow P P \gamma$ vertex. Only with these two additional diagrams we obtain an expression that is gauge invariant for any value of a. However, we obtain $C^0=0$, as in Ref. [7].

• 8. We reproduce $A_1^+$, but for $A_1^0$ we get an expression $\sim (q\cdot k)-M(v \cdot k + v \cdot q)$.

• 9. We have an extra factor of 2 in $D_3^0$.

• 10. We obtain a relative minus sign for each vector meson in a diagram; however, we get the same relative signs for $R_\gamma ^{0/+}$ as given in Eqs. (24) and (25) [23].