Non-parametric reconstruction of the cosmological jerk parameter

Abstract

The cosmological jerk parameter j is reconstructed in a non-parametric way from observational data independent of a fiducial cosmological model. The Cosmic Chronometer data as well as the Supernovae data (the Pantheon compilation) are used for the purpose. The reconstructed values are found to be consistent with the standard $\Lambda$CDM model within the $2\sigma$ confidence level. The model dependent sets like Baryon Acoustic Oscillation and the CMB Shift data are also included thereafter, which does not significantly help in improving or de-proving the confidence level in favour of $\Lambda$CDM. The deceleration parameter q is also reconstructed from the same data sets. This is used to find the effective equation of state parameter for the model independent datasets only. $\Lambda$CDM model is excluded for some part of the evolution in $1\sigma$, but is definitely included in $2\sigma$ in the domain ($0 \le z \le 2.36$) of all the reconstructions.

1 Introduction

Even after more than a couple of decades of its discovery [1, 2], the accelerated expansion of the universe is yet to be attributed to a universally accepted form of dark energy, responsible for the alleged acceleration. Therefore, the quest for dark energy has been alive along all possible ways. A “reverse engineering”, where one makes an attempt to find the characteristics of the matter responsible for a particular evolution history, is amongst the prominent ways for quite a long time. Normally this “reconstruction” is related to figure out a physical characteristics of the matter component, such as the equation of state parameter of the dark energy $w_{DE}$, or even the potential $V(\phi )$ if the dark energy is taken as a scalar field.

Another direction of reconstruction is through the kinematical parameters, such as the deceleration parameter $q = - \frac{1}{aH^2} \frac{d^2 a}{dt^2}$ where a is the scale factor, and $H=\frac{1}{a}\frac{da}{dt}$, the fractional rate of increase in the linear size of the universe called the Hubble parameter. For a long time, H had been the only cosmological parameter which could be estimated from observational data. As H was found to be evolving, the next higher order derivative of a, namely q was the quantity of interest, Now that q can be measured and is found to be evolving, the third order derivative of a finds a natural importance. Expressed in a dimensionless way, this quantity called the “jerk” is defined as

$$\begin{aligned} j = \frac{1}{aH^3} \frac{d^3 a}{dt^3}. \end{aligned}$$

(1)

There has already been some work in the reconstruction of a cosmological model through these kinematical parameters. Reconstruction of the deceleration parameter q can be found in the work of Gong and Wang [3, 4], Lobo et al. [5], Mamon and Das [6], Cardenas and Motta [7], Gómez-Valent [8] and references therein. Very recently Yang and Gong [9] reconstructed the cosmic acceleration and estimated the redshift at which the transition from a decelerated to an accelerated expansion took place using Gaussian Process. Reconstruction through the jerk parameter has been carried out by Luongo [10], Rapetti et al. [11], Zhai et al. [12], Mukherjee and Banerjee [13, 14], Mamon and Bamba [15], Mukherjee et al. [16]. Density perturbations also have been investigated for models reconstructed through the jerk parameter [17]. Very recently a $\Lambda$CDM model has been recovered from a reconstruction of cosmographic parameters like q and j [18]. Although the possible importance of the jerk parameter in the game of reconstruction was pointed out long back [19], not much work has been done to utilize its full potential. Also, the work already done is an estimation of parameters with a functional form of j being used as an ansatz. This is necessarily restrictive, as the functional form for j is already chosen.

A more unbiased way is to attempt a non-parametric reconstruction, where the evolution of the relevant quantity is determined directly from observational data without any ansatz a priori. Such attempts normally involve the reconstruction of $w_{DE}$ [20,21,22,23,24,25,26,27]. There are some efforts towards a non-parametric reconstruction of q. Some recent examples can be found in works of Nunes et al. [28], Arjona and Nesseris [29], Velten et al. [30] and Haridasu et al. [31]. However, there is hardly any attempt to model the dark energy through a reconstruction of the jerk parameter in a non-parametric way. Although there is no convincing reason that a reconstruction of kinematic parameters like q or j is more useful than that of a physical quantity like the dark energy equation of state parameter, this indeed provides an alternative route towards the understanding of dark energy in the absence of a convincing physical theory.

In the present work, the jerk parameter j is reconstructed for the first time from the observational data in a non-parametric way. We have utilized various combinations of the Supernova distance modulus data, the Cosmic Chronometer (CC) measurements of the Hubble parameter, the Baryon Acoustic Oscillation (BAO) data and also the Cosmic Microwave Background (CMB) Shift parameter data to examine their effect on the reconstruction.

The reconstruction yields the result that for any combination, the $\Lambda$CDM model is well allowed within a $2\sigma$ confidence level, and for lower z values, within a $1\sigma$ confidence level.

Indeed there are apprehensions that the CMB Shift parameter data depends crucially on a fiducial cosmological model [32] and so does the BAO data [33]. However, we do not ignore them. Our reconstruction is based on the combinations both including and excluding the CMB Shift and the BAO datasets. The final result, when we extract the physical information, that of the effective equation of state parameter $w_{eff}$, looks qualitatively very much similar for various combinations of the datasets.

In Sect. 2, the methodology is discussed in brief. The details of the observational data used is discussed in Sect. 3. Section 4 contains the actual reconstruction. The last section includes a discussion of the results obtained.

2 The methodology

At the outset, we do not assume any fiducial model for the universe except that it is given by a spatially flat, isotropic and homogeneous metric given by

$$\begin{aligned} ds^2 = -c^2 dt^2 + a^2(t) (dr^2 + r^2 d\theta ^2 + r^2 \sin ^2\theta d\phi ^2 ). \end{aligned}$$

(2)

We pretend that we do not even know the Einstein equations and pick up only the kinematical quantities. We define the reduced Hubble parameter as, $h(z)=\frac{H(z)}{H_0}$. A subscript 0 indicates the value of the quantity at the present epoch and z is the redshift given as $1+z = \frac{a_0}{a}$. The luminosity distance of any object (such as a Supernova), can be obtained as

$$\begin{aligned} d_L(z)= \frac{c(1+z)}{H_0} \int _{0}^{z} \frac{dz'}{h(z')}, \end{aligned}$$

(3)

For convenience, we define a dimensionless comoving distance,

$$\begin{aligned} D(z) \equiv (1+z)^{-1} \frac{H_0}{c} d_L(z). \end{aligned}$$

(4)

Combining Eqs. (3) and (4) and taking derivative with respect to z, we obtain the relation between Hubble parameter and the comoving distance as,

$$\begin{aligned} H(z)= & {} \frac{H_0}{D'}, \end{aligned}$$

(5)

$$\begin{aligned} h(z)= & {} \frac{1}{D'}, \end{aligned}$$

(6)

where a prime denotes the derivative with respect to z. In terms of the dimensionless quantities h, D and their derivatives, the cosmological deceleration parameter and the jerk parameter can be written as

$$\begin{aligned} q(z)= & {} -1 + (1+z)\frac{h'}{h} , \nonumber \\= & {} -1 - (1+z) \frac{D''}{D'} . \end{aligned}$$

(7)

$$\begin{aligned} j(z)= & {} 1 - 2(1+z)\frac{h'}{h} + (1+z)^2 \frac{\left( h'^2 + hh''\right) }{h^2} ,\nonumber \\= & {} 1 + 2 (1+z) \frac{D''}{D'} + (1+z)^2 \frac{\left( 3 D''^2 - D' D'''\right) }{D'^2}. \end{aligned}$$

(8)

The uncertainty in q(z), $\sigma _q$ is estimated by the standard technique of error propagation from Eq. (7),

$$\begin{aligned} \left( \frac{\sigma _q}{1+q}\right) ^2 = \left( \frac{\sigma _h'}{h'}\right) ^2 + \left( \frac{\sigma _h}{h}\right) ^2 - \frac{2\sigma _{hh'}}{hh'} . \end{aligned}$$

(9)

Similarly, the uncertainty associated with j(z), $\sigma _j$ is obtained from Eq. (8) as

$$\begin{aligned}&\left( \frac{\sigma _j}{j-1}\right) ^2 = \left\{ \frac{ (1+z)\left[ 2h'\sigma _{h'} + h\sigma _{h''} + h''\sigma _{h}\right] - 2\left( h\sigma _{h'} + h'\sigma _{h}\right) }{(1+z)(h'^2 + hh'')-2hh'}\right\} ^2 \nonumber \\&\quad + \left( \frac{2\sigma _{h}}{h}\right) ^2- \frac{2 (1+z) \left[ 2h'\sigma _{h'h} + h\sigma _{h''h} + h''\sigma _{h}^2\right] - 4\left( h\sigma _{h'h} + h'\sigma _{h}^2\right) }{(1+z)(h h'^2 + hh'')-2h^2h'}.\nonumber \\ \end{aligned}$$

(10)

As $D'(z)$ is connected to h(z) through Eq. (6), the uncertainty $\sigma _{D'}$ is related to $\sigma _{h}$ by

$$\begin{aligned} \vert \sigma _{D'} \vert = \frac{1}{h^2} \vert \sigma _{h} \vert . \end{aligned}$$

(11)

In order to implement the reconstruction, the widely used Gaussian processes (GP) [34,35,36], which is a powerful model-independent technique, is adopted. This is a distribution over functions which generalizes the idea of a Gaussian distribution for a finite number of quantities to the continuum. Given a set of data points one can use Gaussian processes to reconstruct the most probable underlying continuous function describing the data, and also obtain the associated confidence levels, without assuming a concrete parametrization of the aforesaid function. It requires only a probability on the target function f(z). For a detailed overview one can refer to the Gaussian Process website.¹

In cosmology, GP has attracted a wide application in reconstructing or testing models without an a priori fiducial model [9, 24, 37,38,39,40,41,42,43,44,45,46,47]. For a pedagogical introduction to GP, one can refer to Seikel et al. [37]. The publicly available GaPP² (Gaussian Processes in Python) code has been used in this work.

Assuming that the observational data, such as the distance data D, or Hubble data H, obeys a Gaussian distribution with a mean and variance, the posterior distribution of reconstructed function f(z) can be expressed as a joint Gaussian distribution of different data-sets involving D or H. In this process, the key ingredient is the covariance function $k(z, \tilde{z})$ which correlates the values of different D(z) and H(z) at redshift points z and $\tilde{z}$. The covariance function $k(z, \tilde{z})$ depends on a set of hyperparameters (e.g. the characteristic length scale l and the signal variance $\sigma _f$). This approach also provides a robust way to estimate derivatives of the function in a stable manner. The hyperparameter l corresponds roughly to the distance one needs to move in the input space before the function value changes significantly, while $\sigma _f$ describes the typical change in the function value.

The choice of covariance function, given in (12) affects the reconstruction to some extent. Here we have used the Matérn ($\nu = \frac{9}{2}$, $p=4$) covariance [34] between two redshift points separated by $\vert z-\tilde{z} \vert$ distance units, as in equation (13). This leads to the most reliable and stable results amongst the other significant choices [48].

$$\begin{aligned}&k_{\nu =p+\frac{1}{2}}(z,\tilde{z}) = \sigma _f^2 \exp \left( \frac{-\sqrt{2p+1}}{l} \vert z - \tilde{z} \vert \right) \frac{p!}{(2p)!}\nonumber \\&\quad \times \sum _{i=0}^{p} \frac{(p+i)!}{i!(p-i)!} \left( \frac{2\sqrt{2p+1}}{l} \vert z - \tilde{z} \vert \right) ^{p-i} , \end{aligned}$$

(12)

$$\begin{aligned}&k_{\frac{9}{2}}(z,\tilde{z}) = \sigma _f^2 \exp \left( \frac{-3 \vert z - \tilde{z} \vert }{l} \right) \left[ 1 + \frac{3 \vert z - \tilde{z} \vert }{l}\right. \nonumber \\&\quad \left. + \frac{27 ( z - \tilde{z})^2}{7l^2} + \frac{18 \vert z - \tilde{z} \vert ^3}{7l^3} + \frac{27 \left( z - \tilde{z} \right) ^4}{35l^4}\right] . \end{aligned}$$

(13)

Table 1 The Cosmic Chronometer Hubble parameter H(z) measurements (in units of km s$^{-1}$ Mpc$^{-1}$) and their errors $\sigma _H$ at redshift z obtained from the differential age method (CC)

Table 2 The Baryon Acoustic Oscillation Hubble parameter measurements H(z) (in units of km s$^{-1}$ Mpc$^{-1}$) and their errors $\sigma _H$ at redshift z obtained from the radial BAO method (BAO)

3 Observational datasets

Supernova distance modulus data, Cosmic Chronometer data, radial Baryon Acoustic Oscillation data and CMB Shift Parameter data have been utilized in this work.

3.1 Cosmic chronometer data

Cosmic Chronometer (CC) H(z) data points are measured by calculating the differential ages of galaxies [49,50,51,52,53,54], as a function of the redshift z and is given by

$$\begin{aligned} H(z) = -\frac{1}{1+z} \frac{dz}{dt}. \end{aligned}$$

(14)

A complete compilation of the CC data used in this work is enlisted in Table 1.

Fig. 1

Plots for H(z) reconstructed from CC data (left), BAO data (middle), and combined CC + BAO data (right). The solid black line is the “best fit” and the associated 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions are shown in lighter shades

3.2 BAO data

An alternative compilation of the H(z) data can be deduced from the radial BAO peaks in the galaxy power spectrum, or from the BAO peak using the Ly-$\alpha$ forest of QSOs, which are based on the clustering of galaxies or quasars [55,56,57,58,59,60,61,62,63,64,65,66,67]. Table 2 includes almost all data reported in various surveys so far. One may find that some of the H(z) data points from clustering measurements are correlated since they either belong to the same analysis or there is an overlap between the galaxy samples. Here in this paper, we mainly consider the central value and standard deviation of the data into consideration. Therefore, we assume that they are independent measurements as in [68].

3.3 Reconstructed $H_0$

After the preparation of CC or/and BAO data, we utilize the GP method to reconstruct the Hubble parameter H(z) and the results are shown Fig. 1. The value of the Hubble constant $H_0$ obtained from this model independent reconstruction is shown in Tables 3 and 4.

Further, we normalize the datasets to obtain the dimensionless or reduced Hubble parameter $h(z) = H(z)/H_0$. Considering the error of Hubble constant, we calculate the uncertainty in h(z) as,

$$\begin{aligned} {\sigma _{h}}^2 = \frac{{\sigma _H}^2}{ {H_0}^2} + \frac{H^2}{{H_0}^4}{\sigma _{H_0}}^2, \end{aligned}$$

(15)

where $\sigma _{H_0}$ is the error associated with $H_0$.

3.4 SN-Ia data

For the supernova data, we use the recent Pantheon compilation [69] consisting of 1048 SNIa, which is the largest spectroscopically confirmed SN-Ia sample by now. It consists of different supernovae surveys, including SDSS, SNLS, various low-z and also some high-z samples from HST. We include the covariance matrix along with systematic errors in our calculation. The numerical data of the full Pantheon SNIa catalogue and a detailed description is publicly available.³$^,$⁴ The distance modulus of each supernova can be estimated as

$$\begin{aligned} \mu (z) = 5 \log _{10} \frac{d_L(z)}{\text{ Mpc }} + 25, \end{aligned}$$

(16)

where $d_L$ is the luminosity distance as in Eq. (3).

The distance modulus of SN-Ia can be derived from the observation of light curves through the empirical relation (Tripp formula [70])

$$\begin{aligned} \mu = m^*_B + \alpha X_1 - \beta C - M_B + \Delta _M + \Delta _B, \end{aligned}$$

(17)

where $X_1$ and C are the stretch and colour correction parameters, $m^*_B$ is the observed apparent magnitude and $M_B$ is the absolute magnitude in the B-band for SN-Ia while $\alpha$ and $\beta$ are two nuisance parameters characterizing the luminosity-stretch, and luminosity-colour relations respectively. $\Delta _M$ is a distance correction based on the host-galaxy mass of the SN-Ia and $\Delta _B$ is a distance correction based on predicted biases from simulations. Usually, the nuisance parameters $\alpha$ and $\beta$ are optimized simultaneously with the cosmological model parameters or are marginalized over. However, this method is model dependent.

We shall adopt the following strategy. Based on the new approach called BEAMS with Bias Corrections (BBC) [71] the nuisance parameters in the Tripp formula [70] were retrieved and the observed distance modulus is reduced to the difference between the corrected apparent magnitude $m_B$ and the absolute magnitude $M_B$ i.e., $\mu = m_B - M_B$. In the Pantheon sample by Scolnic et al. [69], the corrected apparent magnitude $m_B = m^{*}_B + \alpha X_1 - \beta C$ along with $\Delta _M$ and $\Delta _B$ corrections are reported. We shall avoid marginalizing the over nuisance parameters $\alpha$, $\beta$ but marginalize over the Pantheon data for $M_B$ in combination with the H(z) data, for the reconstructed value $H_0$. The values of $\alpha$ and $\beta$ thus become irrelevant for the present method of estimation.

Table 3 Table showing the reconstructed value of $H_0$ and best fit values of $M_B$ for the Pantheon supernova data corresponding to the different H(z) datasets used in reconstruction

Table 4 Table showing the effect of local (R19) and global (P18) measurements of Hubble parameter on reconstructed value of $H_0$, and the corresponding marginalized constraints on the absolute magnitude $M_B$ of SN-Ia

With the smooth function H(z) reconstructed from the Hubble data, we use a simple trapezoidal rule [72] for the calculation of the comoving distance,

$$\begin{aligned} d_c(z)= & {} c \int _{0}^{z} \frac{dz'}{H(z')} , \nonumber \\\simeq & {} \frac{c}{2} \sum _{i=0}^{n} (z_{i+1} - z_i) \left[ \frac{1}{H(z_{i+1})}+\frac{1}{H(z_{i})}\right] . \end{aligned}$$

(18)

The uncertainty in $d_c$ is obtained by error propagation formula,

$$\begin{aligned} \sigma ^2_{d_{c}} = \sum _{i=0}^{n} s_i^2 , \end{aligned}$$

(19)

where,

$$\begin{aligned} s_i = \frac{c}{2} (z_{i+1} - z_i) \left[ \frac{\sigma ^2_{H_{i+1}}}{H^4_{i+1}}+\frac{\sigma ^2_{H_{i}}}{H^4_{i}}\right] ^\frac{1}{2}. \end{aligned}$$

(20)

Thus, we obtain the smooth function of the comoving distance $d_c (z)$ and its error $\sigma _{d_c}(z)$ from the Hubble data. This $d_c(z)$ can be rewritten in a dimensionless form by scaling with $\frac{H_0}{c}$, such that

$$\begin{aligned} D_{\mathrm{GP}}= & {} \frac{H_0}{c}d_c(z) ,\end{aligned}$$

(21)

$$\begin{aligned} \sigma _{D_{\mathrm{GP}}}= & {} D_{\mathrm{GP}} \sqrt{\left( \frac{\sigma _{H_0}}{H_0}\right) ^2 + \left( \frac{\sigma _{d_c}}{d_c}\right) ^2}. \end{aligned}$$

(22)

The subscript GP indicates Gaussian Process. Further, we convert the distance modulus of SN-Ia to the normalized comoving distance through the relation (4)

$$\begin{aligned} D(z) = \frac{1}{1+z} \frac{H_0}{c} 10^{\frac{\mu - 25}{5}} = \frac{H_0}{c(1+z)} 10^{\frac{m_B - M_B - 25}{5}}. \end{aligned}$$

(23)

For this we perform another Gaussian Process on the apparent magnitudes $m_B$ of the SN-Ia data and reconstruct them at the same redshift z as that of the Hubble data.

The total uncertainty or error propagation ${\varvec{\Sigma }}_\mu$ and ${\varvec{\Sigma }}_D$ in $\mu$ and D respectively are estimated following the standard practice. The total uncertainty matrix of distance modulus is given by,

$$\begin{aligned} {\varvec{\Sigma }}_\mu = \mathbf {C}_{stat} + \mathbf {C}_{sys} \end{aligned}$$

(24)

where $\mathbf {C}_{stat}$ and $\mathbf {C}_{sys}$ are the statistical and systematic uncertainties respectively.

The uncertainty of D(z) is propagated from that of $\mu$ and $H_0$ using the standard error propagation formula,

$$\begin{aligned} {\varvec{\Sigma }}_D = \mathbf {D}_1 {\varvec{\Sigma }}_\mu {\mathbf {D}_1}^T + \sigma _{H_{0}}^2 \mathbf {D}_2 \mathbf {D}_2^{T} \end{aligned}$$

(25)

where $\sigma _{H_0}$ is the uncertainty of Hubble constant, the superscript ‘T’ denotes the transpose of any matrix, $\mathbf {D}_1$ and $\mathbf {D}_2$ are the Jacobian matrices,

$$\begin{aligned} \mathbf {D}_1= & {} \text{ diag }\left( \frac{\ln 10}{5} \mathbf {D}\right) \end{aligned}$$

(26)

$$\begin{aligned} \mathbf {D}_2= & {} \text{ diag }\left( \frac{1}{H_0} \mathbf {D}\right) \end{aligned}$$

(27)

where $\mathbf {D}$ is a vector whose components are the normalized comoving distances of all the SN-Ia.

The absolute magnitude of SN-Ia is degenerate with the Hubble parameter $H_0$. We get the constraints on $M_B$ by minimizing the $\chi ^2$ function, considering a uniform prior $M_B$ $\in [-35,-5]$. The $\chi ^2$ function is given by,

$$\begin{aligned} \chi ^2 = \Delta D^T \cdot \Sigma ^{-1} \cdot \Delta D, \end{aligned}$$

(28)

where $\Delta D = (D - D_{\mathrm{GP}})$ and $\Sigma = \Sigma _D + \sigma _{D_{\mathrm{GP}}}^2$ respectively. The Markov Chain Monte Carlo (MCMC) analysis is performed for maximizing the likelihood function. We adopt a python implementation of the ensemble sampler for MCMC, the emcee,⁵ introduced by Foreman-Mackey et al. [73]. The results are plotted using the GetDist⁶ module of python, developed by Lewis [74]. Plots for the marginalized $M_B$ constraints are shown in the first three columns ([a], [b], [c]) of Fig. 2. The best fit results are given in Table 3.

Fig. 2

Plots for marginalized likelihood of absolute magnitude $M_B$ for the Pantheon SN-Ia data using reconstructed H(z) from CC data ([a]), BAO data ([b]), and combined CC + BAO data ([c]). Plot for the marginalized matter density parameter $\Omega _{m0}$ ([d]) from the CMB Shift parameter data considering a fiducial $\Lambda$CDM model

3.5 CMB shift parameter data

The so-called shift parameter is related to the position of the first acoustic peak in the power spectrum anisotropies of the cosmic microwave background (CMB). However the shift parameter R is not directly measurable from the cosmic microwave background, and its value is usually derived from data assuming a spatially flat cosmology with dark matter and cosmological constant,

$$\begin{aligned} R = \sqrt{\Omega _{m0}}\int _{0}^{z_c}\frac{dz'}{h(z')}. \end{aligned}$$

(29)

where $z_c$ = 1089 is the redshift of recombination. We use the CMB shift parameter $R = 1.7488 \pm 0.0074$ [75] and matter density parameter is marginalized assuming a fiducial $\Lambda$CDM model. The $\chi ^2$ for CMB Shift parameter data is given by $\left( \frac{1.7488 - R(\Omega _{m0},~ 1089)}{0.0074}\right) ^2$. Plots for the marginalized $\Omega _{m0}$ is shown in the last column [d] of Fig. 2. The best fit result is given by $\Omega _{m0} \simeq 0.299 \pm 0.013.$

3.6 $H_0$ data

In view of the known tussle between the value of $H_0$ as given by the Planck data [76], and that from HST observations of 70 long-period Cepheids in the Large Magellanic Clouds by the SH0ES team [77], reconstruction using both of them have been carried out separately. The recent global and local measurements of $H_0 = 67.27 \pm 0.60$ km s$^{-1}$ Mpc$^{-1}$ for TT+TE+EE+lowE (P18) [76] and $H_0 = 74.03 \pm 1.42$ km s$^{-1}$ Mpc$^{-1}$ (R19) [77] with a $4.4 \sigma$ tension between them, are considered for the purpose.

Fig. 3

Plots for the reconstructed dimensionless Hubble parameter h(z), it’s derivatives $h'(z)$ and $h''(z)$ using CC data. The black solid line is the best fit curve and the associated 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions are shown in lighter shades. The specific points (in the left figure) with error bars represent the observational data. The black dashed line is for the $\Lambda$CDM model with $\Omega _{m0} = 0.3$

Fig. 4

Plots for the reconstructed dimensionless Hubble parameter h(z), it’s derivatives $h'(z)$ and $h''(z)$ using CC + BAO data. The black solid line is the best fit curve and the associated 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions are shown in lighter shades. The specific points (in the left figure) with error bars represent the observational data. The black dashed line is for the $\Lambda$CDM model with $\Omega _{m0} = 0.3$

Fig. 5

Plots for the reconstructed dimensionless co-moving luminosity distance D(z), it’s derivatives $D'(z)$, $D''(z)$ and $D'''(z)$ using the Pantheon data. The black solid line is the best fit curve. The associated 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions are shown in lighter shades. The specific points (in the top two figures) with error bars represent the observational data. The black dashed line is for the $\Lambda$CDM model: $\Omega _{m0} =0.3$

Fig. 6

Plots for the reconstructed dimensionless co-moving luminosity distance D(z), it’s derivatives $D'(z)$, $D''(z)$ and $D'''(z)$ using combined Pantheon + BAO data. The black solid line is the best fit curve. The associated 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions are shown in lighter shades. The specific points (in the top two figures) with error bars represent the observational data. The black dashed line is for the $\Lambda$CDM model: $\Omega _{m0} =0.3$

Fig. 7

Plots for the reconstructed dimensionless co-moving luminosity distance D(z), it’s derivatives $D'(z)$, $D''(z)$ and $D'''(z)$ using combined Pantheon + CC data. The black solid line is the best fit curve. The associated 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions are shown in grey. The specific points (in the top two figures) with error bars represent the observational data. The black dashed line is for the $\Lambda$CDM model: $\Omega _{m0} =0.3$

Fig. 8

Plots for the reconstructed dimensionless co-moving luminosity distance D(z), it’s derivatives $D'(z)$, $D''(z)$ and $D'''(z)$ using combined Pantheon + CC + BAO + CMB data. The black solid line is the best fit curve. The associated 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions are shown in lighter shades. The specific points (in the top two figures) with error bars represent the observational data. The black dashed line is for the $\Lambda$CDM model: $\Omega _{m0} =0.3$

4 The reconstruction

The reconstructed functions h(z), D(z), and their respective derivatives are plotted against z for different sets of the data, and shown in Figs. 3, 4, 5, 6, 7 and 8. The black solid line is the best fit curve, and the black dashed line represents the $\Lambda$CDM model with $\Omega _{m0}=0.3$. The shaded regions correspond to the 68, 95 and $99.7\%$ confidence levels (CL). The specific points marked with error bars represent the observational data used in reconstruction. For the Pantheon data, Eqs. (23) and (25) are used to estimate the D data points and the uncertainty ${\varvec{\Sigma }}_D$ from the observed $\mu$ and ${\varvec{\Sigma }}_{\mu }$ respectively. For the CC and BAO data, we consider Eq. (15) and convert the H–$\sigma _H$ data to h–$\sigma _{h}$ data set. From (6) we can clearly see $D'(z)$ is related to h(z). So, we can take into account the h data points, the uncertainty associated $\sigma _{h}$ , and represent it using Eqs. (6) and (11). Thus, given a set of observational data points we have used the Gaussian Process to construct the most probable underlying continuous function h(z) or D(z) describing the data, along with their derivatives, and have also obtained the associated confidence levels.

Fig. 9

Plots for q(z) reconstructed from CC data (top left), Pantheon data (top middle), CC + Pantheon data (top right), CC + BAO data (bottom left), Pantheon + BAO + CMB data (bottom middle), and CC + Pantheon + BAO + CMB data (bottom right). The solid black line is the “best fit” and the black dashed line represents the $\Lambda$CDM model with $\Omega _{m0}=0.3$

Fig. 10

Plots for j(z) reconstructed from CC data (top left), Pantheon data (top middle), CC + Pantheon data (top right), CC + BAO data (bottom left), Pantheon + BAO + CMB data (bottom middle), and CC + Pantheon + BAO + CMB data (bottom right). The solid black line is the “best fit”. The black dashed line represents the $\Lambda$CDM model with $\Omega _{m0}=0.3$ where $j=1$

4.1 Reconstruction of q

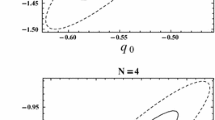
Using the reconstructed values of h(z), D(z) and their derivatives in Eq. (7), the deceleration parameter q is now reconstructed. As already mentioned, the Gaussian Process is employed for this. The plots are shown in Fig. 9 for various combination of the datasets. The shaded regions correspond to the 68, 95 and $99.7\%$ confidence levels (CL). The black solid lines show the “best fit” values of the reconstructed function, and the black dashed lines corresponds to the $\Lambda$CDM model with $\Omega _{m0}=0.3$. For a comparison, one can note that the expected value of $q_{\Lambda CDM}$ at $z=0$ is ${q_0}_{\Lambda CDM} = \frac{3}{2}\Omega _{m0} - 1 = -0.55$. Although the best fit curve appears to deviate from the a monotonic behaviour, the deceleration parameter as given by the $\Lambda$CDM is included generally in $1\sigma$, and at most in the $2\sigma$ confidence level.

4.2 Reconstruction of j

We now reconstruct the cosmological jerk parameter j using the Gaussian Process from the reconstructed function h(z), D(z) and their higher order derivatives using Eq. (8). If one use the standard Einstein equations with a cold dark matter and a Cosmological constant, j is a constant whose value is unity. Results for the reconstructed jerk is given in Fig. 10. The shaded regions correspond to the 68, 95 and $99.7\%$ confidence levels (CL). The black solid lines show the “best fit” values of the reconstructed function, and the black dashed lines corresponds to the $\Lambda$CDM model with $\Omega _{m0}=0.3$ and $j=1$. The plot shows that the $\Lambda$CDM model, is allowed within a $2\sigma$ error bar. Plots for the “best fit value” of the jerk parameter clearly indicate that j has an evolution, and also, this evolution may well be non-monotonic. The reconstructed best fit $q_0$ and $j_0$ at the present epoch is shown in Table 5.

Table 5 Table showing the reconstructed value along with the 1$\sigma$ uncertainty of $q_0$ and $j_0$ corresponding to the different datasets used

In Fig. 10, we used the value of $H_0$, generated by the reconstruction, as described in Sect. 3.3. We further examine if the two different strategies for determining value of $H_0$ affect our reconstruction differently. We proceed with the analysis similar to that above except we add the P18 or R19 data to the H(z) data tables. For comparison one can refer to Tables 3 and 4 to get an insight as to how including the $H_0$ measurement affects our reconstruction. Plots for the reconstructed j(z) along with a comparison for the model independent CC + Pantheon data is shown in Fig. 11.

Fig. 11

Plots for the reconstructed jerk j, using the P18 + CC + Pantheon data (left) and from R19 + CC + Pantheon data (middle). The black dashed line corresponds to the $\Lambda$CDM model, with $\Omega _{m0} = 0.3$ where $j=1$. A comparison among the three cases is shown in the right column

Fig. 12

Plots for the effective equation of state parameter, from the reconstructed deceleration q, for combined CC + Pantheon data (left), CC + Pantheon + P18 data (second from left) and CC + Pantheon + R19 data (third from left). The black dashed line represents the effective EoS for $\Lambda$CDM model, considering $\Omega _{m0} = 0.3$. A comparison among the three results is given in the extreme right

4.3 Reconstructing the effective EOS

We now relax our pretension of not knowing Einstein equations. We use the definition of deceleration parameter

$$\begin{aligned} \frac{\dot{H}}{H^2} = -(1+q), \end{aligned}$$

(30)

in Einstein equations,

$$\begin{aligned} 3H^2= & {} 8\pi G \rho , \end{aligned}$$

(31)

$$\begin{aligned} 2\dot{H} + 3H^2= & {} -8\pi G p , \end{aligned}$$

(32)

where $\rho$ and p are the total energy density and pressure contribution from all components constituting the Universe. Therefore, the effective equation of state parameter is

$$\begin{aligned} w_{\mathrm{eff}} = \frac{p}{\rho } = -\frac{2\dot{H} + 3H^2 }{3H^2 } = \frac{-1 + 2q}{3}. \end{aligned}$$

(33)

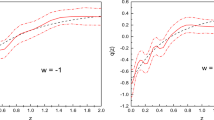
Using the reconstructed q(z) for the different data combinations, we arrive at the effective EoS parameter $w_{\mathrm{eff}}$ non-parametrically. The evolution of $w_{\mathrm{eff}}$ is shown in Fig. 12. The black solid line represent the best fit curve. The shaded regions show the uncertainty associated with $w_{\mathrm{eff}}$ corresponding to the 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence level. The reconstructed values of $w_{\mathrm{eff}}$ at $z=0$ is shown in Table 6.

Table 6 Table showing the reconstructed value along with the 1$\sigma$, 2$\sigma$ and 3$\sigma$ uncertainty of $w_{\mathrm{eff}}(0)$ corresponding to the different datasets used

For the $\Lambda$CDM model, the dark matter contributes only to the energy density while the cosmological constant $\Lambda$ contributes to both the energy density and pressure. The effective EOS (33) thus takes the following form.

$$\begin{aligned} w_{{\mathrm{eff}},\Lambda } = \frac{p_\Lambda }{\rho _\Lambda + \rho _m} = -\frac{1}{1 + \frac{\Omega _{m0}}{1-\Omega _{m0}}(1+z)^3}. \end{aligned}$$

(34)

Considering the value of $\Omega _{m0} = 0.299 \pm 0.013$ from the CMB Shift parameter marginalization we can calculate the value of the effective EOS for the $\Lambda$CDM model to be $-0.701$ with $\pm 0.013$ uncertainty at $z=0$ using the standard error propagation method. For higher redshift ($z>1.5$), the reconstructed $w_{\mathrm{eff}}$ in the present work indicates a non-monotonic behaviour. However, the corresponding $w_{{\mathrm{eff}}}$ for the $\Lambda$CDM model is included definitely in the $2\sigma$ confidence level.

Fig. 13

Plots showing a comparison between the reconstructed jerk j(z) and the estimated $j_{\mathrm{fit}}(z)$ using the combined CC + Pantheon data (left), CC + Pantheon + P18 data (middle) and the CC + Pantheon + R19 data (right). The black solid line is the best fit curve from GP reconstruction. The 1$\sigma$ and 2$\sigma$ CL are shown in dashed and dotted lines respectively. The bold dot-dashed line represents the best fit function from $\chi ^2$-minimization. The associated 1$\sigma$ uncertainty is shown by the shaded region

4.4 Fitting function for j(z)

In this section we attempt to write an approximate fitting function for the reconstructed jerk parameter in the low redshift range $0< z < 1$ for the model independent CC+Pantheon, CC+Pantheon+R19 and CC+Pantheon+P18 combination. We consider a polynomial function for j(z) with respect to redshift z as,

$$\begin{aligned} j_{\mathrm{fit}} (z) = \sum _{i=0}^{n} j_i z^i. \end{aligned}$$

(35)

This polynomial is non-linear in z, but it is linear in $j_i$’s. Thus estimating the above equation by the method of least squares or $\chi ^2$ minimization holds.

We define the $\chi ^2$ function as

$$\begin{aligned} \chi ^2 =\sum \dfrac{\left[ j(z)- j_{\mathrm{fit}}(z)\right] ^2}{\sigma ^2}. \end{aligned}$$

Here in this work we perform the fitting using a trial and error estimation for different orders of i in Eq. (35). To check the goodness of the fit we calculate the minimized $\chi ^2$ for every ith order fitting. The value of the reduced $\chi ^2_\nu = \frac{\chi ^2}{\nu }$, where $\nu$ signifies the degrees of freedom, is estimated. This procedure entails to go from order to order in the polynomial and getting the best-fitting $\chi ^2$, and truncating once the reduced $\chi ^2$ falls below one. We start with $i = 1$ followed by $i=2$ and so on and check for which order i the value of $\chi ^2_\nu < 1$. The measure of $\chi ^2_\nu$ obtained for the three cases studied are mentioned below. Again, the estimated $j_i$’s along with their $1\sigma$ uncertainties are given. A comparison between the reconstructed j(z) and estimated $j_{\mathrm{fit}}$ are shown in Fig. 13. We also plot the correlations between the parameters $j_i$’s in Fig. 14. We note that the process fails for $z>1$, but we can do a reasonable estimate for $z<1$. So we show the plots only in the domain $0 \le z \le 1$.

For CC + Pantheon data,

$$\begin{aligned} j_{\mathrm{fit}}(z) = 0.901 + 0.611~ z + 0.987~ z^2. \end{aligned}$$

(36)

The final set of parameters $j_i$’s and their 1$\sigma$ uncertainty are,

$$\begin{aligned}&j_0 = 0.901^{+0.032}_{-0.032},\quad j_1 = 0.611^{+0.231}_{-0.230}\quad \text {and}\\&\quad j_2 = 0.987^{+0.314}_{-0.314}.\quad \chi ^2_\nu = 0.670. \end{aligned}$$

Similarly, for the CC + Pantheon + P18 data,

$$\begin{aligned} j_{\mathrm{fit}}(z) = 0.917 + 0.788~ z + 0.899~ z^2. \end{aligned}$$

(37)

The final set of parameters $j_i$’s and their 1$\sigma$ uncertainty are,

$$\begin{aligned}&j_0 = 0.917^{+0.045}_{-0.045},\quad j_1 = 0.788^{+0.291}_{-0.291} \quad \text {and}\\&\quad j_2 = 0.899^{+0.366}_{-0.367}.\quad \chi ^2_\nu = 0.868. \end{aligned}$$

And finally for the CC+Pantheon+R19 data,

$$\begin{aligned} j_{\mathrm{fit}}(z) = 0.956 + 1.376~ z - 0.188~ z^2. \end{aligned}$$

(38)

The final set of parameters $j_i$’s and their 1$\sigma$ uncertainty are,

$j_0 = 0.956^{+0.044}_{-0.044}$, $j_1 = 1.376^{+0.311}_{-0.311}$  and  $j_2 = -0.188^{+0.403}_{-0.403}$.  $\chi ^2_\nu = 0.817$.

In all the three cases, the coefficients in the polynomial are estimated by the $\chi ^2$ minimization technique, and the polynomial is truncated once the reduced $\chi ^2$ falls below one to prevent over-fitting. If we proceed on fitting with any higher order polynomial, the $1\sigma$ uncertainty for the fitted function will not be contained within the $1\sigma$ error margin of j(z) reconstructed by GP.

Fig. 14

Plots showing the correlations between the fit parameters, $j_i$’s. The shaded regions show the confidence contours on the parameter space of $j_0$, $j_1$ and $j_2$ respectively for CC + Pantheon (left), CC + Pantheon + P18 (middle) and CC + Pantheon + R19 (right) datasets

5 Discussion

The major aim of the present work is a reconstruction of the cosmological jerk parameter j from the observational datasets. The reconstruction is non-parametric, so j is unbiased to any particular functional form to start with. Also, it does not depend on the theory of gravity, only except the assumption that the universe is described by a 4 dimensional spacetime geometry and it is spatially flat, homogeneous and isotropic. It deserves mention that although a non-parametric reconstruction is there in the literature for quite some time now for reconstructing physical quantities like the equation of state parameter or the quintessence potential and the cosmographic quantity like the deceleration parameter q, it has hardly been used to reconstruct the jerk parameter. We have reconstructed q from the datasets, in order to self-consistently reconstruct the j-parameter and the effective equation of state.

Kinematical quantities, that can be defined with the metric (namely the scale factor a) alone, form the starting quantities of interest in the present case. As the deceleration parameter q is now an observed quantity and is found to evolve, the next higher order derivative, the jerk parameter is the focus of attention. Surely the parameters made out of even higher derivatives like snap (4th order derivative of a), crack (5th order derivative) etc. could well be evolving [78]. But we focus on j which is the evolution of q, the highest order derivative that is an observationally measured quantity. For a parametric reconstruction of j, one can still start from the higher order derivatives [79, 80] and integrate back to j, and estimate the parameters, coming in as constants of integration, with the help of data. But this does not form the content of the present work as already mentioned. Instead we have directly reconstructed q and j non-parametrically from the datasets, without assuming any kind of parametrizations to start with.

It is found that for various combinations of datasets, the jerk parameter corresponding to the $\Lambda$CDM model is included in the $2\sigma$ confidence level.

The effective equation of state parameter $w_{\mathrm{eff}}$ is linear in q, so the plots for both of them will look similar. We use the reconstruction of q to plot $w_{\mathrm{eff}}$ against the redshift z in Fig. 12. The plots indicates that $w_{\mathrm{eff}}$ has an evolution which is not necessarily monotonic. The plots also indicate that the universe might have another stint of accelerated expansion in the recent past before entering into a decelerated phase and finally giving way to the present accelerated expansion. For the reconstruction of $w_{\mathrm{eff}}$, the model dependent data sets like BAO and CMB data are not included.

For the reconstructed j, this non-monotonicity is not apparent when only CC or Supernova (Pantheon) data are individually employed, and j decreases slowly for the former and increases rapidly for the latter (Fig. 10). When these two data sets are combined, the non-monotonicity appears and this nature is preserved even when the model dependent datasets like CMB Shift and BAO data are included. It should also be noted that the exclusion of the CMB Shift and BAO does not (i.e., when CC and Pantheon data are used) seriously affect the agreement with $\Lambda$CDM within the $2\sigma$ error bar.

It may be noted that we obtained the marginalized constraints on $H_0$, $M_B$ and $\Omega _{m0}$, by keeping the nuisance parameters $\alpha$ and $\beta$ fixed using the BBC framework. As there may be correlations between these parameters keeping them fixed may adversely affect the model independent nature of the reconstruction to an extent. However, we have employed the BEAMS with Bias Corrections (BBC) [71] so that the model dependence could be minimized.

There is a very recent work by Bengaly [81] which shows, in a model independent way, that the accelerated expansion of the universe is correct even in $7\sigma$! So the observational constraints on the kinematic parameters find even more importance. The present work is an attempt to reconstruct the jerk parameter in a non-parametric way. Some of the recent parametric reconstructions of j show that the present value of j indicates that the $\Lambda$CDM model is not included in the $1\sigma$ level [15, 16]. The present work also shows that the evolution of j may exclude the corresponding value in the $\Lambda$CDM for a part of the evolution in $1\sigma$, but at a $2\sigma$ level $j=1$ is indeed included. It deserves mention that a recent model independent study [82] shows that if the GRB (Gamma Ray Burst) data are included, the current value of j is quite different from the standard $\Lambda$CDM value of $j=1$.

It deserves mention that a very recent work by Steinhardt, Sneppen and Sen [83] points out some errors in the quoted values of the redshift z in the Pantheon dataset. We have worked out the reconstruction of j with the corrected values of z given in [83]. There is hardly any qualitative difference in the plots. The only noticeable difference found is in the lower middle panel of Fig. 10 for the best fit curve where Pantheon + BAO + CMB data are combined. However, even in $1\sigma$, there is no change in the conclusion. The result that $\Lambda$CDM is always included in $2\sigma$ always remains valid.