Phenomenology of NNLO jet production at the LHC and its impact on parton distributions

Abstract

We present a systematic investigation of jet production at hadron colliders from a phenomenological point of view, with the dual aim of providing a validation of theoretical calculations and guidance to future determinations of parton distributions (PDFs). We account for all available inclusive jet and dijet production measurements from ATLAS and CMS at 7 and 8 TeV by including them in a global PDF determination, and comparing to theoretical predictions at NNLO QCD supplemented by electroweak (EW) corrections. We assess the compatibility of the PDFs, specifically the gluon, obtained before and after inclusion of the jet data. We compare the single-inclusive jet and dijet observables in terms of perturbative behaviour upon inclusion of QCD and EW corrections, impact on the PDFs, and global fit quality. In the single-inclusive case, we also investigate the role played by different scale choices and the stability of the results upon changes in modelling of the correlated experimental systematics.

1 Introduction

The inclusive jet cross-section is the simplest hadron collider observable with a purely strongly interacting final state. The computation of next-to-next-to-leading order (NNLO) QCD corrections to it was completed recently [1,2,3] (see also Ref. [4]), and opens up the possibility of doing precision phenomenology with jet observables. Whereas single-inclusive jets have been used for the determination of the parton distributions (PDFs) of the proton [5] for over 30 years [6], there is a number of unsettled theoretical issues related to the definition of the observable which is most promising and appropriate for precision QCD studies, such as the determination of the PDFs and of the strong coupling constant $\alpha _s$.

The simplest inclusive observable, the single-inclusive jet cross-section [7, 8], has the undesirable feature of being non-unitary: each event is counted more than once, so the integral of the differential cross-section is not equal to the total cross-section. The dijet cross-section is free of this issue and it appears to be especially well-suited for PDF determination [9]. However, for this observable several scale choices are possible, because the more complex nature of the final state offers a wide choice of dimensionful kinematic variables; consequently, the significant scale dependence of NLO results has so far effectively prevented the use of this observable for PDF determination.

The availability of NNLO calculations has opened up the possibility of settling these issues, though their full understanding has posed a theoretical challenge, with the single-inclusive jet and dijet observables presenting different features. On the one hand, the issue of scale choice for the dijet observable has been essentially settled by the NNLO computation, with the scale dependence being under control at NNLO and the dijet invariant mass $m_{jj}$ emerging as the preferred choice. On the other hand, the single-inclusive jet cross-section has shown a dependence on the choice of scale which is not significantly reduced from NLO to NNLO [10], so that the understanding of the perturbative behavior, the scale dependence [11], and even the appropriate definition [12] of this observable are non-trivial. A careful analysis reveals that the apparent lack of improvement of scale stability from NLO to NNLO is due to an accidental NLO scale cancellation which occurs for particular values of the jet radius [12, 13]. The persistence of a dependence on the central scale choice at NNLO can in turn be understood as a consequence of infrared sensitivity, which is aggravated by particular scale choices [11]. It then appears that the non-unitary definition of the observable is in fact necessary for perturbative stability, with dijets offering essentially the only viable unitary stable alternative [12]. From these studies the partonic transverse energy $\widehat{H}_T$ emerges as the optimal scale choice [11] for the calculation of single-inclusive jet cross-sections.

In this work, we address these issues from a phenomenological point of view, specifically within the context of a global PDF determination: we study the effect of adding jet cross-sections to a global dataset, with various choices of the observable (single-inclusive jet, or dijet) and of the scale. In each case, we assess the fit quality and the impact of the jet data on the PDFs, at various perturbative orders. This allows us to achieve two main goals. First, we can test phenomenologically the conclusions of past theoretical studies [1,2,3, 10,11,12], by checking which observable and which scale choice leads to better perturbative stability, better PDF compatibility with other data and better fit quality, and more stringent constraints on the PDFs. Secondly, these results make it possible to optimize the choice of jet observables in view of their inclusion in future global PDF fits, and assess their impact as a means of PDF determination.

We will consider the complete inclusive jet [14,15,16,17] and dijet [16, 18, 19] dataset from ATLAS and CMS at $\sqrt{s}=7$ and 8 TeV. Whereas most recent global determinations of the proton PDFs [20,21,22] include some of these jet datasets (for instance, NNPDF3.1 included the ATLAS and CMS single-inclusive data with $\sqrt{s}=2.76$ and 7 TeV), and other studies have assessed the impact of some jet measurements on smaller datasets [19, 23], this is the first time that the full LHC-Run I jet dataset is being considered, and specifically the first time dijet data are included in a modern global PDF determination.

Thanks to the availability of such a wide dataset, we will be able to pursue the two main goals discussed above, by including these jet data in the NNPDF3.1 dataset, while keeping the rest of the global dataset and adopting the same general PDF fitting methodology. In addition, we will look into two further secondary issues. First, we will study the impact of the inclusion of electroweak (EW) corrections to jet predictions. Second, we will assess the sensitivity of results to the treatment of experimental correlated systematic uncertainties, thus addressing the issue, recently raised e.g. in Ref. [24], of the sensitivity of some LHC jet datasets to variations in the experimental correlation model, which may lead to substantial differences in fit quality.

The outline of this paper is as follows. In Sect. 2 we discuss the experimental data for single-inclusive jet and inclusive dijet production. In Sect. 3 we present the theory, and in particular discuss NNLO QCD and EW corrections and scale choices. Our results for the global PDF analyses that we performed are presented in Sect. 4, where we also discuss their implications and summarize our findings. Future implications and avenues for further research are briefly addressed in Sect. 5.

2 Experimental data

We now discuss the single-inclusive jet and dijet data. We first summarize available inclusive jet production data from the LHC. We then review the jet cross-sections included in the NNPDF3.1 PDF determination and their treatment. We finally provide details on the treatment and kinematic coverage of the single-inclusive jet and dijet datasets that we will use in this paper.

2.1 Jet production at the LHC

The ATLAS and CMS collaborations have performed a number of measurements of the single-inclusive and dijet cross-sections at different center of mass energies, ranging from $\sqrt{s}=2.76$ to 13 TeV. In this work, we will focus on the 7 and 8 TeV data, for which single-inclusive and dijet data corresponding to the same underlying dataset and integrated luminosity can be compared.

The $\sqrt{s}=7$ and 8 TeV data are summarized in Table 1, where for each dataset we indicate the experiment, the measured quantity, the center of mass energy $\sqrt{s}$, the integrated luminosity $\mathcal {L}$, the number of datapoints $n_\mathrm{dat}$, and the published reference. All measurements are performed using the anti-$k_t$ algorithm [25] in the four-momentum recombination scheme, which leads to jets with non-vanishing invariant mass.

The relevant kinematic variables are defined as follows.

For single-inclusive jets, $p_T$ and y are the jet transverse momentum and rapidity.

For dijets, $m_{jj}$ is the dijet invariant mass, $y^*=|y_1-y_2|/2$ and $|y_\mathrm{max}|=\max (|y_1|,|y_2|)$ are respectively the absolute rapidity difference and maximum absolute rapidity of the two leading jets of the event.

Finally, for dijet triple-differential distributions, $p_{T,\mathrm avg}=(p_{T,1}+p_{T,2})/2$ is the average transverse momentum of the two leading jets, and $y_b=|y_1+y_2|/2$ is the boost of the dijet system.

Table 1 The LHC single-inclusive jet and dijet cross-section data that will be used in this study. For each dataset we indicate the experiment, the measurement, the center of mass energy $\sqrt{s}$, the luminosity $\mathcal {L}$, the jet radius R, the measured distribution, the number of datapoints $n_\mathrm{dat}$ and the reference

In addition to the data listed in Table 1, ATLAS and CMS have also performed measurements at $\sqrt{s}=13$ TeV, though so far with smaller integrated luminosities than for their Run I counterparts: at Run II, the single-inclusive jet measurements from ATLAS [26] and CMS [27] have $\mathcal {L}=3.2$ fb$^{-1}$ and $\mathcal {L}=71$ pb$^{-1}$ respectively, while the dijet measurements from ATLAS [26] and CMS [28] have $\mathcal {L}=3.2$ fb$^{-1}$ and $\mathcal {L}=2.3$ fb$^{-1}$. For this reason, we do not include these datasets. Very recently, CMS has presented a single-inclusive jet measurement at $\sqrt{s}=13$ TeV, based on a luminosity of $\mathcal {L}=35.9$ fb$^{-1}$ [29].

We will also not include single-inclusive jet data at $\sqrt{s}=2.76$ TeV [30, 31] and 5.02 TeV [32]. The main motivation for these measurements was to provide a baseline for proton-lead and lead-lead data taken at the same center of mass energy. A possible exception could be the 5.02 TeV CMS double-differential cross-section data, based on an integrated luminosity of $\mathcal {L}=27.4$ pb$^{-1}$: indeed, a recent study [33] claims that they might also impact the proton PDFs. We will investigate this dataset in a follow-up study based on an update of the nNNPDF1.0 analysis [34] of nuclear parton distribution functions.

In addition, ATLAS and CMS have also presented several measurements of multijet ($\ge 3$ jets) production. For example, ATLAS has provided measurements of three jet cross-sections at 7 TeV [35], differential in three-jet mass $m_{jjj}$ and the sum of the absolute rapidity separations between the three leading jets, $|y_*|$; and of four-jet cross-sections at 8 TeV [36], differential in the $p_T$ of the four leading jets in the event.

CMS also has a measurement of the 3-jet production cross-section at 7 TeV [37] differential in the invariant mass of the three jets $m_{jjj}$. Because theoretical predictions are currently only available up to NLO for these observables, they will not be considered here, though they are important for other applications such as the validation of Monte Carlo event generators and searches for physics beyond the Standard Model.

2.2 Jet data in NNPDF3.1

The present study will be based on the PDF fitting framework adopted for the NNPDF3.1 global PDF determination [20]. As already mentioned, the NNPDF3.1 dataset includes several single-inclusive jet data. Specifically, for ATLAS the $\sqrt{s}=7$ TeV data from 2010 [38] and 2011 [14] and the $\sqrt{s}=2.76$ TeV [30] data (including cross-correlations between the 2.76 TeV and the 7 TeV data). For the 2011 7 TeV data only the central rapidity bin ($y_\mathrm{jet}\le 0.5$) was included, due to the difficulty in achieving a satisfactory description of the complete set of rapidity bins using the default experimental covariance matrix. From the CMS experiment, NNPDF3.1 included the measurements at $\sqrt{s}=7$ TeV [16] and 2.76 TeV [31], with their cross-correlations. Finally the CDF Run II data with the $k_T$ algorithm [39] was also included. Note that the value of the jet radius R is different for each of these measurements: $R=0.4$ for the ATLAS 7 TeV 2010 and the 2.76 TeV measurements; $R=0.6$ for the ATLAS 7 TeV 2011 measurement; and $R=0.7$ for the CDF and CMS measurements.

In the default NNPDF3.1 PDF determination, theory predictions for all these data were obtained by combining NLO coefficient functions with NNLO perturbative evolution, because full NNLO results were not available then. In order to account for the missing NNLO corrections, a missing higher order uncertainty, estimated from scale variations, was added to jet data, as a fully correlated systematics. A variant PDF set was also produced by only including the two datasets for which the NNLO corrections were available at the time, namely the ATLAS and CMS 7 TeV 2011 data, with all the remaining jet data removed, and now using full NNLO theory. This reduced, but fully NNLO, dataset was also used for the determination of the strong coupling in Ref. [40], for the PDFs with QED corrections [41] and the PDFs with small-x resummation [42], and for the recent studies of theoretical uncertainties on PDFs [43, 44]. In all these previous studies, the renormalization and factorization scales were set equal to the jet transverse momentum, $\mu _{F}=\mu _{R}=p_{T,\mathrm jet}$.

2.3 Jet data in this analysis

The single-inclusive jet data from ATLAS and CMS used in this work are the double-differential (y, $p_T$) distributions listed in Table 1. The ATLAS 7 TeV data cover the range 100 GeV $\le p_T\le$ 1.992 TeV and $0\le |y|\le 3$, while the ATLAS 8 TeV data cover the same rapidity range, but with an extended range of transverse momenta, namely 70 GeV $\le p_T\le$ 2.5 TeV. In our default fit we include only the central rapidity bin ($y_\mathrm{jet}\le 0.5$) of the ATLAS 7 TeV, for ease of comparison with NNPDF3.1. This is not expected to affect results, as in Ref. [20] it was shown that PDFs fitted to the central rapidity bin provide an equally good fit to all other rapidity bins, and in Ref. [45] it was checked explicitly that PDFs determined including each rapidity bin from this data in turn are indistinguishable. We will revisit this issue in Sect. 4.2.4, where we will discuss variant fits in which all rapidity bins are included, and we will consider alternative correlation models both for these data and for their 8 TeV counterpart, as suggested in Refs. [15, 24].

The CMS 7 TeV data cover the range 100 GeV $\le p_T\le$ 2.0 TeV and $0\le |y|\le 2.5$, and the CMS 8 TeV data the extended range 74 GeV $\le p_T\le$ 2.5 TeV and $0\le |y|\le 3.0$. We note that in the case of the CMS 8 TeV single-inclusive jets, measurements for $p_T < 74$ GeV are also available, but these are excluded from the fit because non-perturbative and resummation corrections, not accounted for by fixed-order computations, are large at small $p_T$. We therefore retain only 185 points out of a total of 239.

For the dijet cross-sections we consider three Run I measurements from ATLAS and CMS, specifically the ATLAS and CMS 7 TeV [16, 18] double-differential distributions and the CMS 8 TeV triple-differential distributions [19]. Note that currently ATLAS dijet measurements are only available at 7 and 13 TeV, but not at 8 TeV. The ATLAS data are double-differential in $m_{jj}$ and $|y^{*}|$. The corresponding ranges are 260 GeV $\le m_{jj}\le$ 4.27 TeV and $0\le y^*\le 3.0$. The CMS 7 TeV data [16] are instead double-differential in $m_{jj}$ and $|y_\mathrm{max}|$. The ranges are $200~\mathrm{GeV} \le m_{jj} \le 5$ TeV and $0 \le |y|_\mathrm{max} \le 2.5$.

The CMS 8 TeV [19] data are triple differential in $p_{T,\mathrm avg}$, $y_b$, and $|y^{*}|$. The ranges are 133 GeV $\le p_{T,\mathrm avg}\le$ 1.78 TeV and $0 \le y_b, y^* \le 3$.

For all these measurements, we will use the complete set of systematic uncertainties and correlations available from HepData. Various correlation models, whereby specific systematic uncertainties are decorrelated to a different extent, have been proposed, depending on the dataset. As a representative example, we will study some of these models in the case of the ATLAS 7 TeV and 8 TeV single-inclusive jet cross-sections.

3 Theoretical calculations and implementation

In this section we present the main aspects of the theoretical computations on which our phenomenological studies are based. First we address QCD corrections, discuss the scale choice, and assess the size of NNLO corrections. Then we discuss EW corrections, assess their size, and explain how they are combined with QCD corrections for the purpose of PDF determination.

3.1 QCD corrections

Single-inclusive and dijet observables display a somewhat different perturbative behavior. We discuss the two observables in turn: for each of them, we present the dependence of results on the central scale, its optimal choice, and the NNLO corrections.

The single-inclusive jet cross-section is in general rather sensitive to the choice of central scale, even at NNLO. A detailed study of the scale dependence of the NNLO QCD predictions for single-inclusive jet production was carried out in [11], where three different scales (and their multiples) were discussed in detail: the individual jet transverse momentum $p_T$, the leading jet transverse momentum $p_{T,1}$, and the scalar sum of the transverse momenta of all partons in the event

$$\begin{aligned} \widehat{H}_T = \sum _{i\in \mathrm{partons}} p_{T,i} \, . \end{aligned}$$

(3.1)

Note that $p_{T,1}$ and $\widehat{H}_T$ are event-based choices, i.e. all jets in the event have the same scale, while $p_T$ is a jet-based choice, i.e. it is a property of the individual jet within a given event.

The commonly used scale choices $\mu =p_T$ or $\mu =p_{T,1}$ lead to predictions which even at NNLO may differ by an amount which is comparable to, or larger than, their scale dependence [10], a behavior which was traced in Ref. [11] to the infrared sensitivity of the second-jet contribution, and which is aggravated by the choice $\mu =p_{T,1}$. In Ref. [11] scale choices were thus compared according to a number of criteria: perturbative convergence; scale uncertainty as error estimate; perturbative convergence of the individual jet spectra; and stability of the second jet distribution. The event-based scale $\mu =\widehat{H}_T$ and the jet-based scale $\mu =2p_T$ were singled out as optimal choices. Here we will adopt $\mu =\widehat{H}_T$ as central scale choice; results obtained with this scale choice will be compared in Sect. 4 to those found using $\mu =p_T$, which was the baseline choice adopted in previous NNPDF determinations, specifically NNPDF3.1.

NNLO QCD corrections computed with NNLOJET [46] will be included by supplementing theoretical predictions accurate to NLO QCD with K-factors defined as

$$\begin{aligned} K_\mathrm{NNLO}^\mathrm{QCD} \equiv \frac{\sum _{ij}\widetilde{\sigma }^\mathrm{NNLO}_{ij} \otimes \mathcal {L}^\mathrm{NNLO}_{ij}}{\sum _{ij} \widetilde{\sigma }^\mathrm{NLO}_{ij}\otimes \mathcal {L}^\mathrm{NNLO}_{ij}} \, , \end{aligned}$$

(3.2)

where the sum runs over partonic subchannels, $\widetilde{\sigma }_{ij}$ are partonic cross-sections, and $\mathcal {L}_{ij}$ the corresponding parton luminosities, computed both in the numerator and the denominator using NNPDF3.1 NNLO as a fixed input PDF set.

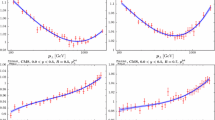
In Fig. 1 we show the NNLO QCD K-factors, Eq. (3.2), corresponding to the ATLAS 7 TeV and CMS 8 TeV single-inclusive jet cross-sections evaluated with the NNPDF3.1 NNLO PDF set and $\mu =\widehat{H}_T$ as central scale. Results are shown as a function of the jet $p_T$ in different jet rapidity bins, with the central (forward) bins in the left (right) plot. At central rapidities, the NNLO K-factor increases monotonically with $p_T$ from about 5% to about 20–25%. This growth with $p_T$ becomes less marked as the jet rapidity increases: in fact at 8 TeV for $|y|\ge 1.5$ the K-factor depends only mildly on the jet $p_T$. The K-factors display moderate point-to-point fluctuations, especially in the forward rapidity bins.

Fig. 1

The NNLO QCD K-factors, Eq. (3.2), for the ATLAS 7 TeV (top) and CMS 8 TeV (bottom) single-inclusive jet cross-sections evaluated using NNPDF3.1 PDFs and scale $\mu =\widehat{H}_T$. Results are shown as a function of the jet $p_T$ in different jet rapidity bins, with the central (forward) bins shown in the left (right) plot

We now turn to dijets. A variety of scale choices is possible: two popular choices are the dijet invariant mass $m_{jj}$ and the average transverse momentum $p_{T,\mathrm avg}$ of the two leading jets. Theoretical predictions computed with either of these scale choices differ significantly at NLO. This difference is substantially reduced at NNLO, with $\mu =m_{jj}$ emerging as a preferred choice, based on the criteria of perturbative convergence, and residual scale dependence of the NNLO prediction [47, 48]. This is the scale choice which we will adopt in the sequel.

In Fig. 2 we display the NNLO QCD K-factors, Eq. (3.2), computed with this scale choice and the NNDPF3.1 NNLO PDF set, for the ATLAS 7 TeV and CMS 8 TeV dijet cross-sections. For ATLAS, the K-factors at small rapidity separations are somewhat below unity for low invariant masses, then grow monotonically with $m_{jj}$ up to about $K\sim 1.15$ at the highest $m_{jj}\sim 4$ TeV. For larger rapidity separations, $1.5 \le |y^*| \le 3.0$, the K-factors are less sensitive to $m_{jj}$, and their value corresponds to corrections between 10 and 20%. For CMS, as previously mentioned, the measurement is presented as a triple-differential distribution in $p_{T,\mathrm avg}$, $y^*$, and $y_b$. As seen in Fig. 2, the qualitative behavior of the K-factors is similar in all rapidity bins, and shows a monotonic growth with $p_{T,\mathrm avg}$. However, the value depends strongly on the rapidity difference, with the K-factor larger at larger $y^*$. For example, in the $0 \le y_b,y^* \le 1$ bin the K-factor ranges from a few percent at low $p_{T,\mathrm avg}$ to up to 15%, while in the $0 \le y_b \le 1$ and $2 \le y^* \le 3$ bin it goes up to 25%. These K-factors display sizable point-to-point fluctuations.

Fig. 2

The NNLO QCD K-factors, Eq. (3.2), corresponding to the ATLAS 7 TeV (top) and CMS 8 TeV (bottom) dijet cross-sections evaluated with NNPDF3.1 PDF and scale $\mu =m_{jj}$. Results are shown as function of the jet $p_T$ in different jet rapidity bins, with the most central (forward) bins in the left (right) plot

3.2 Electroweak corrections

We have determined EW corrections for all of the single-inclusive jet and dijet datasets considered in this work by using the calculation of Ref. [49], suitably extended to the case of single-inclusive jets. The EW corrections computed in Ref. [49] include $O(\alpha \alpha _s)$ and $O(\alpha ^2)$ tree level contributions (where $\alpha$ and $\alpha _s$ are the electromagnetic and strong couplings, respectively), and the weak radiative corrections of $O(\alpha \alpha _s^2)$. In particular, they include the virtual exchange of weak bosons that give rise to the dominant EW Sudakov logarithms, suitably combined with the respective hard QCD emissions to cancel infrared singularities. This is what will be referred to as EW corrections in the remainder of this paper.

We include EW corrections through a K-factor defined as

$$\begin{aligned} K^\mathrm{EW} \equiv \frac{\sum _{ij}\widetilde{\sigma }^\mathrm{LO\> QCD+EW}_{ij}\otimes \mathcal {L}^\mathrm{NNLO}_{ij}}{ \sum _{ij}\widetilde{\sigma }^\mathrm{LO,QCD}_{ij}\otimes \mathcal {L}^\mathrm{NNLO}_{ij}} \, , \end{aligned}$$

(3.3)

where the partonic cross-sections in the numerator are obtained by combining the contributions computed in Ref. [49] with the LO QCD computation. The K-factor defined in Eq. (3.3) has been computed using a proprietary code [49]. Electroweak K-factors have been evaluated using consistently the NNPDF3.1 NNLO PDF set, and the same scale choice as that of the corresponding NNLO QCD predictions. Note that because of cancellations between (negative) Sudakov logarithms and (positive) subleading Born contributions, the K-factors are quite sensitive to the underlying parton decomposition, and it is consequently important to make a consistent choice of PDFs in the computation of QCD and EW K-factors.

The K-factors thus computed are shown in Fig. 3 for the ATLAS 7 TeV and CMS 8 TeV single-inclusive jet cross-sections and for the ATLAS and CMS 7 TeV dijet cross-sections. Results are shown as a function of $p_T$ for single-inclusive jets and as a function of $m_{jj}$ for dijets, in bins of rapidity y (single-inclusive), absolute rapidity difference $y^*$ (ATLAS dijets) or maximum absolute rapidity $y_\mathrm{max}$ (CMS dijets). In all cases the qualitative behavior is similar: the K-factor is close to unity for small values of $p_T$ or $m_{jj}$; it is flat (in fact slightly decreasing) for large values of the rapidity variable; and it grows with respectively $p_T$ or $m_{jj}$ at central rapidity, the growth being stronger at smaller rapidity. The largest EW correction can reach 20% or more for transverse momenta or invariant masses in the TeV range and smaller rapidity.

Fig. 3

The EW K-factors, Eq. (3.3), for the ATLAS and CMS single-inclusive (top) and dijet (bottom) measurements. For single-inclusive jets the K-factors are shown as a function of jet $p_T$ in six different rapidity bins. For dijets they are shown as a function of the dijet invariant mass $m_{jj}$ for different $y^*$ bins for ATLAS (left) or $y_\mathrm{max}$ bins for CMS (right)

3.3 Implementation

For each dataset, we produce fast interpolation grids, accurate to NLO in QCD, whereby partonic matrix elements are precomputed in such a way that the numerical convolution with generic input PDFs can be efficiently approximated by means of interpolation techniques. To this purpose, we use NLOJET++ [50] interfaced to FastNLO [51]. The computation is performed with the scale choices discussed in Sect. 3.1, and it is benchmarked against the NNLOJET computation. These fast interpolation grids are then combined with PDF evolution kernels, in a format compliant with the NNPDF framework, using APFELgrid [52]. Such a combination is required to speed up the computation of hadronic observables when the fit is performed.

Fast interpolation grids accurate to NNLO, for instance in the APPLfast format, are not yet publicly available: indeed, the NNLOJET+APPLfast fast interpolation tables with NNLO QCD corrections are so far only available for jet production in deep-inelastic scattering [53]. We therefore implement NNLO and EW corrections by supplementing our NLO grids with the QCD and EW K-factors defined above, which we combine through the multiplicative prescription

$$\begin{aligned}&\frac{d^2\sigma }{dp_T dy}\Bigg |_\mathrm{NNLO_{QCD}+EW} = \frac{d^2\sigma }{dp_T dy} \Bigg |_\mathrm{NLO_{QCD}}\nonumber \\&\quad \times K_\mathrm{NNLO}^\mathrm{QCD}(p_T,y,\sqrt{s}) \times K^\mathrm{EW}(p_T,y,\sqrt{s}) \, . \end{aligned}$$

(3.4)

The first term on the right-hand side of the equation is the output of the NLO computation, while the second and third terms are the bin-by-bin QCD and EW K-factors defined in Eqs. (3.2) and (3.3), respectively. If the EW K-factor is not included, Eq. (3.4) exactly reproduces the NNLO results obtained with NNLOJET.

As observed in Sects. 3.1–3.2, QCD K-factors are affected by point-to-point fluctuations which reveal an underlying numerical uncertainty. For illustration purposes, this uncertainty is displayed in Fig. 4 for the central rapidity bins of the ATLAS 7 TeV single-inclusive jet and of the CMS 8 TeV dijet distributions. We have estimated this uncertainty through the procedure for the suppression of outliers as described in Ref. [54]. When performing PDF fits, this numerical uncertainty is added in quadrature to the experimental uncertainty, fully uncorrelated datapoint by datapoint. An alternative possibility would be to perform a smooth interpolation of the K-factor, see Ref. [55].

Fig. 4

The NNLO QCD K-factors for the central rapidity bins of the ATLAS 7 TeV single-inclusive jets (left) and CMS 8 TeV dijets (right), with the Monte Carlo numerical uncertainties shown as filled bands around the central result

Finally, we note that the theoretical computations of single-inclusive and dijet observables are subject to non-perturbative corrections and to missing higher order uncertainties (MHOU). The former arise from the underlying event and multiple parton interactions, and are estimated by the experimental collaborations by comparing predictions obtained from different Monte Carlo parton shower generators. In the case of all of the CMS measurements, they are provided in terms of point-by-point rescaling factors, which we apply to the data together with an additional, fully correlated, systematic uncertainty, which we estimate as the difference between the value at each datapoint before and after rescaling. The estimate of MHOUs requires some care, especially for single-inclusive jets. This is due to the fact that there are accidental cancellations which occur for values of the jet radius $R\sim 0.5$ which are close to the values adopted by ATLAS and CMS, where the NLO scale dependence evaluated in a standard way is artificially small [12, 13], and thus is not a good estimator of the MHOU. A more reliable estimate of the MHOU requires performing uncorrelated scale variation [13, 56]. The inclusion of MHOU in PDF fits, though in principle possible using the formalism of Refs. [43, 44], goes beyond the scope of this paper, and we will not consider it further.

4 Results

We now present our main results. They consist of a set of global PDF determinations, in which the NNPDF3.1 global dataset is supplemented by the single-inclusive jet and inclusive dijet data presented in Sect. 2.3: by comparing fit results, we study the impact of varying the jet observable, the data, and the theory settings. Specifically, we have performed fits including either single-inclusive or dijet data, in each case using either the full data set, or 7 TeV data or 8 TeV data only, and with theory at pure NLO QCD, pure NNLO QCD, or NNLO QCD supplemented by EW corrections as discussed in Sect. 3.2. For the single-inclusive 7 TeV data we have also performed fits with alternative choices of central scale. Finally, for the ATLAS 7 TeV and 8 TeV single-inclusive jet data we have studied the effect of the treatment of correlated systematics . We will first present in Sect. 4.2 all PDF sets based on single-inclusive data, including variations of scale choice and decorrelation model, then in Sect. 4.3 PDF sets based on inclusive dijet data, and finally in Sect. 4.4 draw general comparative conclusions on the behavior of different observables at different perturbative orders.

4.1 PDF sets

Fig. 5

Correlation coefficients between the data of Table 1 and the gluon PDF g(x). Each curve corresponds to a different datapoint, with the value of $p_T$ corresponding to the color code on the right of the plot, and only curves for the points in the largest and smallest rapidity bins are shown. The shaded bands denote regions in which the maximum correlation is greater than 90% of the maximum correlation in the whole plot

The inclusion of jet data in a global NNPDF3.1-like PDF determination essentially impacts only the gluon PDF, as was shown in Ref. [20], while leaving other PDFs essentially unchanged. The impact of the jet data on the gluon PDF can be assessed by computing the correlation coefficient (as defined in Ref. [57], see also Ref. [58]) between each datapoint and the gluon. The correlations for the largest and smallest rapidity bins of the datasets of Table 1 are shown in Fig. 5, computed using the default baseline NNLO PDF set (before inclusion of the jet data, #bn, see Table 2 below). Correlations are seen to be large or very large (up to almost one) for all $x\gtrsim 10^{-2}$. Interestingly, the choice of the rapidity variable $y_\mathrm{max}$ appears to maximize the range in which a large correlation with the gluon is observed.

The full list of PDF determinations that we will discuss is given in Table 2, together with an ID that will be used to identify them. In this and all subsequent tables and plots “jets” is short for single-inclusive jets. Each row corresponds to a different choice of dataset or methodological settings, while columns correspond to the theory adopted: QCD at NLO or NNLO, without or with EW corrections included. By NLO or NNLO we mean that jets have been consistently added with NLO or NNLO theory to the respective NLO or NNLO global fit; note that EW corrections instead are only included for the jet observable, with all other observables in the global fit computed using pure QCD theory.

Table 2 The PDF determinations discussed in this study and their IDs. Each row corresponds to a different choice of input jet dataset or fit settings (listed in the first column), and each column corresponds to a different theory accuracy (listed in the first row). The ID encodes the process used (j for single-inclusive jets and d for dijets); the data used (a for all, 7 or 8 for the 7 TeV or 8 TeV datasets); the perturbative accuracy (n for QCD NNLO, w if EW corrections included); and the choice of scale (pt when $\mu =p_T^\mathrm{jet}$); special treatment of the ATLAS 7 TeV data (cor for all bins included, correlated; dec, decorrelated; pcor, partially correlated); and special treatment of the ATLAS 8 TeV data (dec for all bins included, decorrelated; pcor, partially correlated). In this and subsequent tables and plots “jets” is short for single-inclusive jets

The jet data of Table 1 are added to a baseline dataset, which essentially coincides with the NNPDF3.1 dataset. This dataset includes: fixed-target neutral-current (NC) DIS structure function data from NMC [59, 60], SLAC [61] and BCDMS [62]; charged-current (CC) DIS structure function data from CHORUS [63] and NuTeV [64, 65]; HERA data from their combined measurements [66], including charm-production cross sections [67] and b-tagged structure functions [68, 69]; fixed-target Drell–Yan data from E866 [70,71,72] and E605 [73]; collider Drell–Yan data from CDF [74] and D0 [75,76,77]; and Drell–Yan, inclusive gauge boson, and top-pair production data from ATLAS [78,79,80,81,82,83,84,85], CMS [86,87,88,89,90,91,92,93] and LHCb [94,95,96,97]. In total this baseline dataset contains $n_\mathrm{dat}=3813$ datapoints, see Ref. [20] for more details. The number of datapoints corresponding to the jet data included in the various fits of Table 2 is given in Tables 3 and 4 below.

In all of these fits, experimental systematic uncertainties are fully correlated across bins of different kinematic variables, while statistical uncertainties coming from the unfolding are correlated only across bins of transverse momentum (for jets) or invariant mass (for dijets), but not across rapidity bins. The possibility of removing some or all of these correlations will be discussed in Sect. 4.2.4 below. Multiplicative uncertainties are treated with the $t_0$-method [98], and all fits in Table 2 are iterated once to ensure convergence of the $t_0$ method and preprocessing (see Ref. [20] for more details).

For jet or dijet data, non-perturbative corrections are included by default, as are Monte Carlo uncertainties due to finite numerical precision of NNLO QCD K-factor computations (see Sect. 3 for details). The factorization and renormalization scales are by default taken to be $\mu =\widehat{H}_T$ for single-inclusive jets, and $\mu =m_{jj}$ for dijets (see the discussion in Sect. 3). An alternative choice of scale for single-inclusive jets will be considered in Sect. 4.2.3 below.

All the fits listed in Table 2 otherwise closely follow the NNPDF3.1 analysis [20]. Specifically, the same settings and codes are used for the computation of physical observables in the baseline dataset, and the same choice of kinematic cuts, of values of physical parameters, and of fitting methodology are adopted. All PDF sets include $N_\mathrm{rep}$ = 100 Monte Carlo replicas. The ReportEngine software [99] is used in the sequel to analyze each fit and compute various fit metrics. Specifically, we consider the $\chi ^2$ of the theory prediction for each dataset or combinations of datasets, defined according to Eqs. (7)–(8) of Ref. [100], and the distance d between pairs of fits (see e.g. Eq. (48) of Ref. [101] for its definition).

The values of the $\chi ^2$ per datapoint for all fits with default settings at NLO and NNLO with or without EW corrections and single-inclusive jet or dijet data are collected in Tables 3 and 4, respectively; $\chi ^2$ values are shown for all data in the global dataset, grouped by process type (DIS NC, DIS CC, Drell–Yan, Z $p_T$, top pair) and for all jet data, both those which are and those which are not included in each fit. The values of $\chi ^2$ per datapoint for all jet data (included or not included) for all fits performed with alternative choices of central scale or alternative decorrelation models are collected in Table 5. In these tables, $\chi ^2$ values corresponding to data not included in each fit are enclosed in square brackets.

Table 3 The $\chi ^2$ per datapoint for all fits of Table 2 including single-inclusive jet data, with default settings. Results are shown for all datasets, aggregated by process type. For jets data, results are shown both for the sets included in each fit, and also for those not included, enclosed in square brackets. Combined results are also shown for all single-inclusive jet and for all dijet data, both for the full set, and for those included in each fit. The number of datapoints in each dataset is also shown

Table 4 Same as Table 3, but now for dijets. The baseline is repeated for ease of reference

4.2 Single-inclusive jets

We first present PDF sets obtained by including single-inclusive jet data. We discuss in turn the impact and consistency of individual datasets; perturbative QCD stability and the impact of EW corrections; the choice of central scale; and alternative data treatment and decorrelation models for the ATLAS 7 TeV data.

4.2.1 Impact and consistency of datasets

We provide a general comparative assessment of the impact of single-inclusive jet data on PDFs by comparing fits performed with the default theory settings of Sect. 3 and the highest theory accuracy, i.e. NNLO QCD theory for jet data and the rest of the global fit, and EW corrections included in the jet predictions only. According to the data included, these correspond to the fits #bn, #janw, #j7nw, and #j8nw of Table 2.

First, we compare fit #janw, that contains all of the single-inclusive jet data, to the baseline #bn, which does not include any jet data. Note that, as discussed in Sect. 2.3, in our default global dataset only the central rapidity bin of the ATLAS 7 TeV data is included. Fits in which the full 7 TeV ATLAS dataset is included will be discussed in Sect. 4.2.4 below. In Fig. 6 we display the distance between the PDF central values for the two fits, and the gluon PDF in both fits, normalized to the baseline, both at $Q=100$ GeV. Recall that the distance d is the difference in units of the standard deviation $\sigma$ of the mean, so for a sample of 100 replicas $d\sim 1$ corresponds to statistically identical PDFs (replicas extracted from the same underlying distribution) and $d\sim 10$ corresponds to PDFs that differ by one sigma. From Table 3, we note that individual jet datasets are well described (with $\chi ^2$ per datapoint of order one), except the 8 TeV ATLAS data ($\chi ^2=3.22$), to be investigated in greater detail below. In comparison to the baseline fit, the inclusion of the single-inclusive jet data leads to a slight deterioration in the description of the ATLAS top pair rapidity distributions, whose $\chi ^2$ per datapoint increases from 1.22 to 2.01. On the other hand, it leads to an improvement in the description of the dijet data, especially the 8 TeV CMS data, which are not included in any of these fits. This suggests that the inclusion of single-inclusive and dijet data have a similar impact on PDFs, as we shall also see in Sect. 4.3.1 and discuss in greater detail in Sect. 4.4 below.

As mentioned above, and as it is clear from the distance plot in Fig. 6, single-inclusive jet data only have an impact on the gluon. The regions which are most affected are $x\simeq 0.05$, $0.1\lesssim x \lesssim 0.2$, and $0.3\lesssim x\lesssim 0.5$, consistently with the correlation plots of Fig. 5: in these regions the gluon PDF changes by up to slightly more than half sigma. In comparison to the baseline, the central gluon PDF is suppressed by about 2% in the small x region and enhanced by about 4% in the large x regions, though it always remains within the uncertainty band of the baseline.

Fig. 6

Comparison between the baseline fit with no jet data (#bn) and the fit with all single-inclusive jet data included (#janw), both with default settings and the most accurate theory (NNLO QCD, including EW corrections for jets). The distance (see text) between all PDFs (left) and the ratio of the gluon PDF to the baseline (right) are shown at the scale $Q=100$ GeV. The shaded band is the 68% confidence interval, while the dashed lines are the edge of one sigma interval

Fig. 7

Comparison between the baseline fit with no jet data (#bn), and the fits with only 7 TeV (#j7nw) or only 8 TeV (#j8nw) jet data included. The relative uncertainty on the gluon PDF (left) and the ratio of the gluon PDF to the baseline (right) are shown at $Q=100$ GeV. All results are shown as ratios to the baseline

We next assess the relative impact of different jet datasets, by adding to the comparison of the baseline (#bn) and the fit with all single-inclusive jet data (#janw) also fits in which only 7 TeV (#j7nw) or 8 TeV (#j8nw) jet data are included, all with the same settings (NNLO QCD+EW). The comparison is shown in Fig. 7, where we compare the gluon and its relative uncertainty. Here and henceforth, when comparing relative uncertainties, the uncertainties shown are computed as a ratio to a common baseline, i.e. the plot displays all uncertainties as a percentage of the same reference fit. From Table 3, we note that the unsatisfactory description of the ATLAS 8 TeV data persists even when the 7 TeV data are not included in the fit, and the deterioration in fit quality for the ATLAS top data in the global fit is also similar. On the other hand, the fit in which only 7 TeV jets are included shows excellent fit quality both for the jet data and the global dataset. A significant difference between these two datasets is that for the 7 TeV data only the central rapidity bin is included, while for the 8 TeV data all rapidity bins are included: this suggests that the 8 TeV data may also be affected by similar issues in the treatment of correlations between rapidity bins. We will see in Sect. 4.2.4 that this is indeed the case.

The relative pull of the jet datasets at 7 TeV and 8 TeV can be inferred from Fig. 7. They both lead to a comparable suppression of the gluon PDF of about 1% in the region $0.3\lesssim x\lesssim 0.5$, while they respectively enhance it by 4% and 2% in the region $0.1\lesssim x \lesssim 0.2$. However, the decrease in gluon uncertainty is rather more marked upon inclusion of the 8 TeV data, and in fact, results obtained including all jet data, or only 8 TeV are almost identical. Specifically, in comparison to the baseline, inclusion of the 8 TeV data results in a reduction of the relative gluon uncertainty at $x\simeq 0.2$ from 4 to 1.5%, to be compared to the reduction 4 to 3% when the 7 TeV data are included. A similar behavior was observed in the recent CT18 global PDF determination [22], which includes the ATLAS and CMS jet datasets at 7 TeV and the CMS jet dataset at 8 TeV.

4.2.2 Impact of higher-order QCD and EW corrections

Fig. 8

Same as Fig. 7, but now comparing fits with NLO, NNLO and NNLO+EW theory for 7 TeV (top: fits #j7, #j7n, #j7nw respectively) and 8 TeV (bottom: fits #j8, #j8n, #j8nw). All results are now shown as ratios to the NNLO fit

Having assessed the impact of various single-inclusive jet data on PDFs with optimal theory settings, we now turn to the assessment of the perturbative stability of results. To this purpose, we compare fits at NLO, NNLO and with EW corrections (included for jet data only). The comparison is performed separately for the 7 TeV and 8 TeV data (fits #j7, #j7n, #j7nw; and #j8, #j8n, #j8nw respectively) both in oder to check consistency and to get a more detailed picture of the impact of different datasets. The gluon PDFs at $Q=100$ GeV and their uncertainty for these fits are compared in Fig. 8.

It is clear from the figure that, both for 7 TeV and 8 TeV data, at NLO the gluon undergoes a significant distortion in the region $0.1\lesssim x \lesssim 0.5$ in comparison to the NNLO results shown in Fig. 7. Specifically, at the peak, $x\sim 0.3$ the NLO gluon turns out to be by 30–40% larger than the baseline. This effect is driven by the jet data: we have verified that in the baseline (without jet data) the NLO gluon does show some distortion in comparison to the NNLO baseline, but by a much smaller amount, with the largest enhancement of order 5%. This is thus evidence for large missing NNLO corrections to the single-inclusive jet cross section in the NLO fit. The effect is more pronounced for the 8 TeV data, which can be understood as a consequence of their greater precision.

The effect of EW corrections is rather more moderate, with the shift of the central value always within the NNLO uncertainty band. Also, EW corrections seem to have an opposite effect when added to the fit to the 7 TeV or the 8 TeV data, leading to a slight enhancement of the gluon in the former case and a significant suppression for $x\gtrsim 0.2$ in the latter case. For both datasets, the uncertainty on the gluon for $x\gtrsim 0.1$, where the jet data have an impact, is reduced by a non-negligible amount by the inclusion of NNLO corrections. On the other hand the impact of the EW corrections is less clear. All this suggests that NNLO corrections have a significant impact, by affecting the best-fit large-x gluon shape and improving its precision, while the impact of EW corrections is minor, and not clear-cut.

The effect of the inclusion of the NNLO and EW corrections on fit quality is less clear. Indeed, from Table 3, we observe that generally the fit quality to jet data deteriorates somewhat upon inclusion of NNLO corrections, and a little more upon inclusion of EW corrections. On the other hand, the global fit quality, as measured by the total $\chi ^2$, is unchanged for the 7 TeV data, and it improves significantly, from 1.39 to 1.27, for the more precise 8 TeV data, with the improvement mostly driven by the top and Z $p_T$ data which are most sensitive to the gluon. However, as already noted in Sect. 4.2.1, the $\chi ^2$ of the top data deteriorates when adding the jet data to the baseline, and the fit quality to the ATLAS 8 TeV data remains unchanged. This suggests that, for the more precise 8 TeV data, the NNLO corrections reduce a tension between top and jets (especially ATLAS).

In summary, we conclude that, consistently with previous theoretical investigations [11, 12] NNLO corrections have a sizable impact on single-inclusive jets, and in particular their inclusion leads to a reduction of the uncertainty on the large-x gluon PDF and an improved consistency of the jet data with the rest of the global dataset, demonstrated by a reduction of the shift of the gluon central value upon inclusion of jets, and as an improvement of the global $\chi ^2$ (for the more precise 8 TeV jet data), when going from NLO to NNLO. Electroweak corrections do not appear to lead to improvements either in terms of fit quality or PDF uncertainty.

Table 5 Same as Table 3 for fits performed with alternative choices of central scale or alternative decorrelation models. Now only $\chi ^2$ values for jet data are shown. Results for the fits with default settings #j7, #j7n and #janw, already shown in Table 3 are included for ease of reference. Note that for the fits with alternative decorrelation models for the ATLAS 7 TeV data (#janw-7cor, #janw-7dec and #janw-7pcor) the number of ATLAS 7 TeV data is $n_\mathrm{dat}=140$ instead of $n_\mathrm{dat}=30$ as for all other fits

Fig. 9

Same as Fig. 6, but now comparing fits to the 7 TeV data with the choices of central renormalization and factorization scale scale $\mu =\widehat{H}_T$ (as shown in Fig. 8, top) and $\mu =p_T^\mathrm{jet}$ at NLO (fits #j7 and #j7-pt) and NNLO (fits #j7n and #j7n-pt). The gluon is shown as ratio to the fits with $\mu =\widehat{H}_T$

4.2.3 Impact of the choice of scale

We now turn to an assessment of the impact of the choice of central scale: specifically, we compare results obtained by fitting with our default scale choice $\mu =\widehat{H}_T$, chosen as optimal based on the studies of Ref. [11], and with the scale choice $\mu =p_T^\mathrm{jet}$ used in NNPDF3.1 [20] and previous NNPDF studies. For ease of comparison to Ref. [20], the comparison is performed for fits to the 7 TeV data (fits #j7 and #j7-pt at NLO, and #j7n and #j7n-pt at NNLO). In Fig. 9 we show the distance between PDF central values of the two pairs of fits, at NLO and NNLO, and compare the corresponding gluon PDFs.

Inspection of Table 5 shows that at NLO the scale choice $\mu =\widehat{H}_T$ leads to a better description of the jet data, both included and not included in the fits, with respect to $\mu =p_T^\mathrm{jet}$. However, the effect of the scale choice on the PDFs is very mild (see Fig. 9), with a localized modification of the gluon below the half sigma level for $x\simeq 0.2$ and no effect on the other PDFs. On the other hand, at NNLO the two scale choices lead to almost indistinguishable results, both in terms of fit quality and PDF shape, with the scale choice $\mu =\widehat{H}_T$ leading to a slightly better description of data not included in the fit, and a difference in gluon central values barely above statistical indistinguishability.

We conclude that the scale choice $\mu =\widehat{H}_T$ is perturbatively more stable, in that it leads to a better NLO fit, but that at NNLO the choice of central scale is not an issue. Both conclusions are in agreement with the findings of Ref. [11].

4.2.4 Impact of the choice of correlation models

We finally discuss the impact of different correlation models on the ATLAS single-inclusive jet data. As repeatedly mentioned, only the central rapidity bin of the ATLAS 7 TeV data was included in NNPDF3.1 and thus in our default fit because it was not possible to obtain a good fit when all rapidity bins were included, yet PDFs fitted to each rapidity bin turned out to be very close to each other [20, 45]: this suggests issues in the covariance matrix for these data, as extensively discussed in Ref. [24]. Further, as shown in Sect. 4.2.1, the corresponding ATLAS 8 TeV data appear to be fully consistent with the 7 TeV data, yet lead to a poor $\chi ^2$ when included in the global fit, which suggests that they may suffer from a similar problem.

Here we will first check that indeed the inclusion of all rapidity bins from the 7 TeV ATLAS data does not change the results for the PDFs, as argued in Refs. [20, 45], but now by fitting all rapidity bins simultaneously, rather than one at a time as in Ref. [45], and with the new scale choice and jet dataset adopted here. We will then address the issue of the impact of the choice of correlation model, in particular by decorrelating different rapidity bins as suggested in Ref. [24] for the 7 TeV data and in Ref. [15] for the 8 TeV data.

To this purpose, we have performed five variant fits of our most accurate fit with default settings (#janw) in which alternative treatments of the 7 TeV or 8 TeV ATLAS data are considered in turn (see Table 5). Concerning the 7 TeV data, in a first fit (#janw-7cor) all ATLAS rapidity bins are included: so in this fit the 7 TeV and 8 TeV are treated on an equal footing, with all bins included and correlated systematics treated using the published covariance matrix. The correlation pattern is then modified: in fit #janw-7uncor systematics are assumed to be uncorrelated across rapidity bins, and in fit #janw-7pcor systematics are partially decorrelated, following the prescription suggested in Ref. [24]. Concerning the 8 TeV data, we start with the default fit (#janw), and we obtain from it two variants by modifying, as suggested in Ref. [15], the treatment of three (out of 659) correlated systematic uncertainties, related to the jet energy scale, specifically to the flavour response, the fragmentation and the pile-up. In fit #janw-8dec these three uncertainties are completely decorrelated; in fit #janw-8pcor they are partly decorrelated by splitting each uncertainty into three components and decorrelating one of them (see Table 6 or Ref. [15]).

The fit with only the central rapidity bin of the ATLAS 7 TeV data (#janw), and the fit in which all ATLAS data are included, with fully correlated systematics (#janw-cor), are compared in Fig. 10, where we show distances between the two sets of PDFs, and we compare directly the gluon PDFs, shown as a ratio to the default optimal fit. It is clear that all PDFs including the gluon are essentially unchanged. On the other hand, the $\chi ^2$ now increases very substantially. However, the $\chi ^2$ to all other jet and dijet data (both fitted and not fitted) is essentially unchanged, consistently with the fact that the gluon is very stable. In short, we confirm the previous conclusion [20, 45] that including all rapidity bins of the ATLAS 7 TeV data has almost no impact on the PDFs, despite the considerable deterioration of the $\chi ^2$ for this data (Fig. 11).

Fig. 10

Same as Fig. 6, but now comparing the default most accurate fit to single-inclusive jet data (all datasets, NNLO QCD+EW, fit #janw), in which only the central rapidity bin of the ATLAS 7 TeV data is included, to a fit in which all rapidity bins are included (#janw-7cor). The gluon is shown as ratio to the former fit

Fig. 11

Same as Fig. 6, but now comparing the fits to single-inclusive jet data (all datasets, NNLO QCD+EW), in which all rapidity bins of the ATLAS 7 TeV data are included, either with (fit #janw-7cor) or without (fit #janw-7dec) experimental correlations on selected systematic uncertainties. The gluon is shown as ratio to the former fit

Fig. 12

Same as Fig. 6, but now comparing the default most accurate fit to single-inclusive jet data (all datasets, NNLO QCD+EW, fit #janw), to a fit in which selected systematic uncertainties are decorrelated in the ATLAS 8 TeV data (fit #janw-8dec). The gluon is shown as ratio to the former fit

Inspection of the $\chi ^2$ values from Table 5 further reveals that as soon as systematics are decorrelated the $\chi ^2$ value improves considerably. However, once again the $\chi ^2$ to all other jet and dijet data changes very little. Hence once again we conclude that the PDFs are stable upon decorrelation. In fact, all $\chi ^2$ values remain essentially the same regardless of whether correlations are completely removed, or only partially removed following the suggestion of Ref. [24], thereby validating the conclusion that these correlations are the problematic ones. The stability of PDFs in general and the gluon in particular upon decorrelation is confirmed by a direct comparison, shown in Fig. 10. Distances between all PDFs before and after decorrelation is seen to be compatible with statistical fluctuations.

Turning now to the 8 TeV data, a similar pattern is found. Namely, upon decorrelation the $\chi ^2$ for the ATLAS data improves considerably, but $\chi ^2$ values for all other datasets are almost unaffected, with very similar results obtained when fully or partially decorrelating the relevant sources of systematics following Ref. [15], thus validating the prescription of this reference. Also in this case, the stability of the PDFs is confirmed by direct comparison in Fig. 12.

In summary, firstly, we confirm the conclusion of Refs. [20, 45] that inclusion of all of the ATLAS 7 TeV jet data with full correlations has a significant impact on the fit quality but not on the PDFs. Furthermore, we confirm that the correlation model suggested in Ref. [24] leads to a good description of this data, without any significant change in the PDFs when the decorrelation is performed. And finally, we find that the ATLAS 8 TeV data behave in a very similar way, and in particular that the correlation model suggested in Ref. [15] leads to good fit quality without significant change in PDFs.

4.3 PDF fits with dijet data

We now turn to PDF fits in which dijet data rather that single-inclusive jet data are included. Also in this case, we first discuss the impact and compatibility of these data, and then the perturbative stability of results.

4.3.1 Impact and consistency of datasets

We assess the impact of dijet data on PDFs by comparing fits with optimal settings, i.e. with NNLO QCD theory, and EW corrections included (for jets only), and either the full dataset (#danw), or the 7 TeV (#d7nw) or 8 TeV (#d8nw) data included in turn.

We start by comparing to the baseline #bn, with no jet data, fit #danw in which all dijet data are included; PDFs are compared in Fig. 13. From Table 4, we see that individual dijet datasets are overall fairly well described (the $\chi ^2$ per datapoint is around 1.5 for each of them). Inclusion of the dijet datasets in the baseline leads to an improved description of single-inclusive jet data, just like (see Sect. 4.2) inclusion of single-inclusive jet data leads to an improved description of dijets. This confirms consistency of the single-inclusive and dijet data. Unlike in the case of single-inclusive jet data, no tension is observed between dijet data and the rest of the global dataset (specifically top rapidity distributions), whose $\chi ^2$ is left almost unchanged.

As in the case of single-inclusive jets, only the gluon PDF is affected by the inclusion of dijet data, with the strongest impact observed in the regions $x\simeq 0.01$ and $0.06\lesssim x \lesssim 0.4$ (see Fig. 13). In the former region the gluon is suppressed by about 2%, corresponding to a shift in central value by about one sigma; in the latter it is enhanced by up to 10% around $x\sim 0.3$ , corresponding to a shift by about one and a half sigma, hence outside the error band of the baseline. These shifts are qualitatively similar to those observed upon inclusion of the single-inclusive jet data, but somewhat more pronounced and in a somewhat wider kinematic region.

Fig. 13

Same as Fig. 6, but now for dijets

Fig. 14

Same as Fig. 7, but now for dijets

We then turn to the assessment of the relative impact of different datasets, by comparing to the baseline (#bn) the fits in which only 7 TeV (#d7nw) or only 8 TeV (#d8nw) dijet data are included, see Fig. 14. From Table 4, we see that the fit quality is equally good for 7 TeV or 8 TeV data, however the fit to the 8 TeV dijet data is closer to the fit in which all dijet data are included, in that it leads to a similar description of all of the jet and dijet data, including those that are not included in either fit. Such a description is better in both fits than in the fit to the 7 TeV dijet datasets only, and is accompanied by a similar change in the description of the ATLAS top pair differential rapidity distributions. This suggests that among the dijet data, the 8 TeV data provide the dominant contribution.

The relative impact of the 7 TeV and 8 TeV data on the gluon central values and uncertainty can be directly inferred from Fig. 14. The impact of the two datasets on the gluon central value is qualitatively the same, and thus also the same as that of the full dijet dataset, but with the 8 TeV data having a stronger impact, almost equivalent to the impact of the full dataset. The reduction in uncertainty in comparison to the baseline due to either dataset is almost the same, with a slightly stronger reduction observed for the 7 TeV data, by about 3–4% to 3% at $x\simeq 0.2$. Consequently, the gluon PDF determined when including all of the dijet data is very close to that found when including only the 8 TeV data, thus confirming that the 8 TeV data have a dominant impact on the gluon central value.

Fig. 15

Same as Fig. 8, but now for dijets

4.3.2 Impact of higher order QCD and EW corrections

As for single-inclusive jets, we assess the perturbative stability of fits with dijet data by comparing fits at NLO, NNLO and with EW corrections, separately for the 7 TeV and 8 TeV data, i.e., respectively, fits #d7, #d7n, #d7nw; and #d8, #d8n, #d8nw. The gluon PDFs for these fits are compared in Fig. 15.

The figure shows that the perturbative behavior of the gluon upon inclusion of the dijet data is very similar to what observed when including single-inclusive jets. Namely, at NLO the gluon is distorted in the region $0.1\lesssim x \lesssim 0.5$ in comparison to the NNLO results already shown in Fig. 14, with the effect more pronounced for the dominant and more precise 8 TeV data, again providing evidence for large missing NNLO corrections. The effect of the EW corrections is even less marked than in the case of single-inclusive jets: in fact, their inclusion leaves the gluon PDF almost unchanged. For both datasets, inclusion of the NNLO corrections leads to a reduction in uncertainty, more marked for 8 TeV data, while inclusion of the EW corrections has no clear effect; in fact, for the 8 TeV data it leads to a slight increase of the uncertainty. As in the case of single-inclusive jets, we conclude that NNLO corrections have a strong impact by modifying the gluon shape and reducing its uncertainty, while EW corrections have essentially no impact.

Unlike in the case of single-inclusive jets, where the inclusion of NNLO corrections did not have a clear impact on fit quality, for dijets at NNLO there is a clear improvement in $\chi ^2$ values (see Table 4). Specifically, when all dijet data are included at NLO, the $\chi ^2$ of the global fit deteriorates significantly in comparison to the baseline, with the largest effect seen in data which are most sensitive to the gluon, such as the Z $p_T$ distribution and the top rapidity distribution. This deterioration goes away upon inclusion of NNLO corrections. Indeed, when NNLO corrections are included, the quality of the global fit including dijets improves considerably, corresponding now to a fit quality which is essentially the same for the fits with or without the dijet data. Accordingly, the fit quality to the dijet data is significantly better at NNLO than at NLO. The effect is driven by the more precise 8 TeV data. Indeed, the same pattern is observed when only 8 TeV data are included, while with 7 TeV data only fit quality to the dijet data at NLO and NNLO is essentially the same, and so is the fit quality with or without dijet data.

This means that inclusion of NNLO corrections is crucial in order to ensure compatibility of the dijet data with the rest of the global dataset. Interestingly, when fitting dijet data no clear improvement in the fit quality of single-inclusive jet data (not fitted) is seen when going from NLO to NNLO. Inclusion of EW corrections has no significant effect on fit quality.

We conclude that for dijets NNLO corrections have a significant impact on both fit quality, the central value of the gluon PDF and its uncertainty, with a clear pattern of improvement when going from NLO to NNLO.

4.4 Single-inclusive jets vs. dijets: a comparative assessment

Having assessed the impact on PDFs of jet and dijet datasets separately, we now assess them comparatively, in terms of perturbative stability, fit quality, and impact on PDFs. Specifically, we compare directly PDFs obtained in fits to all single-inclusive (#janw) and dijet (#danw) datasets with the most accurate NNLO+EW theory and default settings in Figs. 16 and 17, where the baseline fit (with no jet data) and, in the latter case, the CT18 PDF fit [22] are also shown for reference. Also, in Figs. 18 and 19 we compare to a representative set of datapoints from each of the single-inclusive jet and dijet datasets predictions obtained using PDFs from the baseline fit, the fit with single-inclusive jets, and the fit with dijets. Predictions are shown as a ratio to the experimental data, which are shown either with full uncertainties, or with uncorrelated uncertainties only, with the correlated uncertainties kept into account as a shift of the datapoint (see e.g. Eqs. (85–86) of Ref. [5]).

Fig. 16

Same as Fig. 6, but now comparing the fits with all single-inclusive jet data (#janw), and that with all dijet data (#danw) and highest theory accuracy (NNLO QCD+ EW) and default settings. In the gluon comparison (right) results are displayed as a ratio to the baseline with no jet data included (also shown for reference)

Fig. 17

Same as Fig. 7, but now comparing the baseline (#bn) to the fits with all single-inclusive jet (#janw) and dijet data (#danw) of Fig. 16. All results are shown as a ratio to the CT18 fit (also shown for reference)

Based on the $\chi ^2$ values from Tables 3 and 4 and the PDF comparisons in Figs. 16, 17, 18, 19, our conclusions are the following.

• 1. Concerning the relative impact on PDFs of single-inclusive jets and dijets:

  • (a) The effect on PDFs of the inclusion of jet and dijet data in the NNPDF3.1 global dataset is qualitatively the same. Namely, they only affect the gluon, by leading to an enhancement of its central value in the region $0.1\lesssim x \lesssim 0.4$, accompanied by a suppression in the region $0.01\lesssim x \lesssim 0.1$. The suppression is by about 1%, while the enhancement at the peak, localized at $x\simeq 0.3$ is by about 2.5% for single-inclusive jets, but stronger, by about 7.5% for dijets. An enhanced gluon is also present in the CT18 PDF determination, which, as mentioned, includes the 8 TeV CMS single-inclusive jet data, and whose gluon PDF is consistent with our result within its rather larger uncertainty.

  • (b) The inclusion of either single-inclusive or dijets leads to a reduction in the gluon uncertainty, with a somewhat stronger reduction observed for single-inclusive jets. It should be noted in this respect that for the most accurate 8 TeV dijet dataset, which as shown in Sects. 4.2.1–4.3.1 is mostly responsible for the shift in central value (though not on the uncertainty), only CMS data are currently available. The constraining power of the dijet dataset is consequently at present more limited than that of the single-inclusive jet dataset.

  • (c) The inclusion of single-inclusive jet or dijet data does not lead to a deterioration in the description of the rest of the data in comparison to the baseline fit: almost all $\chi ^2$ values for other datasets are unchanged. This shows that the single-inclusive and dijet data are not only consistent with each other, but also with the rest of the global dataset, and their impact on the gluon central value, accompanied by a reduction in uncertainty, corresponds to a genuine addition of new information in the fit. Indeed, a comparative assessment of the impact of jet, Z $p_T$ and top production data on the gluon distribution in Ref. [45] showed good consistency, specifically wih the top data also leading to an enhancement of the gluon in the $x\gtrsim 0.1$ region. An exception is the ATLAS top rapidity distributions, which seem to be in tension with the ATLAS 8 TeV single-inclusive jet data, as discussed in Sect. 4.2.1. The quality of the fit to this data also deteriorates, though by a smaller amount, when dijet data are fitted; note however that in this case the quality of the fit to CMS top rapidity data improves.

• 2. Concerning relative fit quality:

  • (a) The quality of the fit to single-inclusive jet data and dijet data when each of them is fitted is comparable, though somewhat better for dijets ($\chi ^2=1.65$ vs. $\chi ^2=1.88$). The quality of the fit to dijets when single inclusive jets are fitted and conversely are almost identical ($\chi ^2=2.10$ for dijets when fitting single-inclusive jets vs. $\chi ^2=2.06$ for single-inclusive jets when fitting dijets), and only marginally worse than the quality of the fit to each dataset when it is fitted. This confirms the full consistency of the two datasets, with a marginal preference for dijets.

  • (b) The fit including dijet data is also somewhat more internally consistent than the fit including single-inclusive jet data. Indeed, the $\chi ^2$ per datapoint of the global fit is closer to one (1.22 vs 1.28), and also, the $\chi ^2$ for individual datasets is generally better. In particular, this happens for top production data, also sensitive to the large-x gluon. It is unclear whether this is due to a greater theoretical accuracy of the NNLO dijet observable, or to better quality of the dijet data (specifically a better control of correlated systematics). However, the issue is phenomenologically immaterial, given that the shape and size of the data to theory ratio are qualitatively comparable for all of the jet and dijet data (including for the rapidity bins not displayed in Figs. 18 and 19), regardless of which dataset is actually fitted.

• 3. Concerning relative perturbative stability:

  • (a) When fitting the dijet data, fit quality to the fitted data improves significantly from NLO to NNLO ($\chi ^2=2.44$ at NLO vs. 1.65 at NNLO), but the fit quality to the single-inclusive jet data actually deteriorates from NLO to NNLO (from $\chi ^2=1.54$ to 2.06). When fitting the single-inclusive jet data, the fit quality to the fitted data does not improve and actually deteriorates from NLO to NNLO (from $\chi ^2=1.25$ to $\chi ^2=1.88$) but, perhaps surprisingly, the fit quality to the dijet data, not fitted, does improve (from $\chi ^2=3.29$ at NLO to the NNLO $\chi ^2=2.10$). Whereas this shows a good theoretical consistency of the dijet data, it is unclear whether the lack of improvement of the single-inclusive jet data is due to a less stable perturbative behavior of the jet observable, or to issues with data.

  • (b) As already noted in Sect. 4.3.2, the fit quality to all other data included in the global datasets deteriorates at NLO when including jet data, with a greater deterioration seen in the case of dijets, and more moderate for single-inclusive jets: the total $\chi ^2$ per datapoint for the global fit goes from $\chi ^2=1.20$ of the baseline to 1.28 in the former case and 1.33 in the latter. At NNLO, when dijets are fitted the global fit quality significantly improves and becomes almost the same as that of the baseline ($\chi ^2=1.22$, in comparison to $\chi ^2=1.18$ of the baseline) while for the fit to single-inclusive jets it does not improve. The greater deterioration of fit quality at NLO for dijets can be understood as a consequence of the fact, observed in point 1.a above, that dijets have a greater pull on the gluon: hence missing NNLO corrections lead to a stronger loss of accuracy. The lack of improvement in the description of single-inclusive jets shows again that this observable seems to be somewhat less well-behaved, either for theoretical or experimental reasons.

We generally conclude that single-inclusive jets and dijets are mutually consistent and at NNLO consistent with the global dataset and have a similar impact on the gluon. The dijet observable has a better behaved perturbative behavior and a stronger pull on the gluon PDF and it appears to be marginally preferable, though it leads to a less pronounced decrease of the gluon uncertainty, possibly because ATLAS dijet measurements are not yet available at 8 TeV, while single-inclusive jet measurements are available both from ATLAS and CMS.

Fig. 18

The theory to data ratio for a representative set of points from each single-inclusive jet dataset introduced in Sect. 2. Specifically, we show the central rapidity bins for all the ATLAS and CMS jet datasets at 7 and 8 TeV. Theoretical predictions are computed from fits #bn, #janw and #danw with corresponding theoretical accuracy, and shown as a ratio to the experimental data. For the data, either the full uncertainty is shown (left) or only the uncorrelated uncertainty, with the correlated uncertainty kept into account as a shift of the datapoint (right)

Fig. 19

Same as Fig. 18, but for dijets. For the ATLAS data only the unshifted data are shown because the breakdown of the statistical covariance matrix into fully uncorrelated components is not available

5 Summary and outlook

We have presented an extensive phenomenological investigation of inclusive jet production at the LHC, exploiting recent theory calculations, in particular of NNLO QCD corrections, and studying for the first time in a systematic and comparative way the inclusive dijet observable, along with the single-inclusive jet observable which is routinely used for PDF determination.

We have found full consistency between the constraints imposed on parton distributions, specifically the gluon, by single-inclusive jets and dijets, thus conclusively establishing the viability of the dijet observable for precision QCD phenomenology and PDF determination, as originally suggested 25 years ago [9]. We have also validated the conclusions of previous theoretical studies [1,2,3, 10,11,12]. Specifically we have shown that NNLO corrections are crucial in order to ensure compatibility of the jet observables with the rest of the global dataset, and also that while at NLO the choice of central scale makes a significant impact (with the scale choice $\widehat{H}_T$ for single-inclusive jets better behaved at NLO), at NNLO perturbative stability appears to be achieved.

In a comparative assessment of single-inclusive jets vs. dijets, we have found that the dijet observable has a more marked impact on the gluon central value. Also, phenomenologically it displays a better-behaved perturbative behavior, with a clear improvement of data-theory agreement as the perturbative order of the theory prediction increases. However, the single-inclusive jet observable leads to a more significant reduction of the gluon uncertainty. Either, or both, of the latter observations could be due to theoretical reasons but also to the nature of the current data. Specifically, there are indications that some of the single-inclusive datasets are in tension with the rest of the global datasets, which could explain the less clear perturbative behavior of fits including this observable. Also, the current dijet dataset is more limited than the single-inclusive dataset, thus possibly explaining the more limited effect of dijets on the gluon uncertainty.

One of our main results is that the more recent 8 TeV data generally have a rather more significant impact than previous 7 TeV data; interestingly, the dijet 8 TeV CMS data are triple-differential, and this may enhance their impact on PDF determination. We accordingly expect that the availability of more precise data, possibly also for a greater variety of kinematic observables, including more differential measurements, from LHC Run-II 13 TeV data, and then from data coming from future LHC Run-III and HL-LHC [102] runs will settle these issues and lead to a clear and consistent theoretical picture. Eventually, the availability of correlations between single-inclusive jet and dijets data will allow for their simultaneous inclusion in a PDF determination, thereby allowing for maximal use of the available information. Indeed, we expect this to be a first step towards a widening of the set of jet observables used in precision PDF studies, which include not only multi-differential jet cross-sections [46], but also jet substructure observables, whose study has undergone rapid progress recently [103]. The inclusion of dijet data in the forthcoming NNPDF4.0 global PDF analysis will be a first step in this direction.