Abstract
We study the quantum gravitational system coupled to a charged scalar, Dirac fermions, and electromagnetic fields. We use the “exact” or “functional” renormalization group equation to derive the effective action \(\Gamma _0\) by integrating the flow equation from the ultraviolet scale down to \(k=0\). The resulting effective action consists of local terms and nonlocal terms with unique coefficients.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is one of the most urgent problems in theoretical physics to understand quantum property of the gravitational system interacting with various matter fields. The Einstein gravity is non-renormalizable in perturbation theory. If one believes that gravity must be described by some quantum theory at some level, then we are led to expect that the theory will contain terms quadratic in curvatures which are necessarily generated by quantum effects, with coefficients of order unity. In fact, we expect to find in the action all possible diffeomorphism-invariant terms constructed with the metric and its derivatives. It had been shown long ago that if one includes such higher derivative terms, then the theory is perturbatively renormalizable [1]. The price one must pay is that perturbative unitarity is lost. The superstring theory is supposed to circumvent the problem, but it is still difficult to understand quantum geometric aspects of the spacetime physics in superstrings.
Another approach to get insight into the quantum effects of gravity is to use the functional renormalization group (FRG). It enables us to study the RG flow of infinitely many couplings as functions of a cutoff k. It has been used to study the ultraviolet (UV) behavior of gravity and establish the existence of a nontrivial fixed point (FP) which may be used to define a continuum limit [2,3,4]. To formulate this, one defines the effective average action (EAA) \(\Gamma _k\) by performing the path integral over field modes with the momentum scales equal or bigger than a scale given by a cutoff k [5, 6], and following the usual procedure of defining effective action. This EAA itself is not the usual effective action and it is still divergent in general in the UV limit. The k-dependence of the EAA is described by the FRG equation (FRGE)
where \(t=\ln k\), and \(R_k\) is a cutoff kernel which goes to zero when its argument z is greater than the cutoff scale \(k^2\). Because the FRGE only sees the variation of the EAA, it is free from the UV divergence and well defined in contrast to EAA. Technically this comes from the fact that \(\partial _t R_k\), which is inside the trace of FRGE, falls off fast in the UV. This FRGE describes the flow of the theory when the energy scale is changed. In this sense, it is also called flow equation.
We can fix initial point for the EAA at some UV scale \(\Lambda \) and identify it as the “bare” action of the theory. One can investigate how the EAA behaves in the limit \(\Lambda \rightarrow \infty \) by integrating the FRGE in the direction of larger k. If the flow reaches a FP, we may expect that all physical observables to be well defined, and the theory is UV-complete. Together with the assumption of finite dimensionality of the critical surface on which the putative FP lies, this is what is called asymptotic safety. There has been considerable evidence that the nontrivial FP exists in pure gravity with higher order terms and also gravity theory coupled to matter [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].
Most of the work so far focused on the existence of the UV FP, leading to the scenario of asymptotically safe gravity. There were also some works about the situation in the infrared (IR) regime [32,33,34] pertaining to solve the problems with infrared divergences. We also note that many of the interesting results amenable to observations happen at finite energy for which the problems of UV-completion are irrelevant provided some form of IR-UV decoupling holds (e.g. using Appelquist-Carazzone theorem for massive modes).
It is often considered that the EAA, which is obtained by integrating over the modes with scale larger than k, describes physical quantities around the energy scale k. However, there is a debate if the k-dependent EAA itself has physical meaning since the cutoff k is just a figurative energy scale used to cut off the path integral [35]. How do we then study physical aspects of the asymptotically UV-safe gravity? We note that it is the effective average action at \(k=0\), which is nothing but the quantum effective action as obtained in the standard quantum field theory, that contains information on the quantum effects on the physical quantities such as scattering amplitudes and transition probabilities at all energy scales.
It is thus significant to compute the effective action. The FRGE can be used as a tool to calculate the effective action nonperturbatively. For this purpose, we integrate the FRGE in the direction of small k and the infrared endpoint of the flow of EAA gives the quantum effective action \(\Gamma _0\). We should mention that this method of obtaining quantum effective action is not restricted only to asymptotic safe theories, but is valid for any quantum field theories. The advantage of this method, compared to calculating directly a functional integral, is that we never encounter divergences since the FRGE does not suffer from divergences and is well defined. Some examples have been discussed in [36, 37], in which gravity theory coupled to a scalar is considered among others. Here we would like to extend this calculation to the more general case of gravity coupled to gauge, Dirac and charged scalar fields. Integrating the flow, we can derive the nonlocal, finite parts of the effective action up to two powers of the gauge field strengths and curvatures of the metric. The usual method to calculate the rhs of the FRGE is to use the asymptotic expansion for the trace of the heat kernel coefficients, which gives only local expressions. To calculate nonlocal, finite parts of the effective action, we need a more sophisticated one which includes an infinite number of heat kernel coefficients. This expansion has been developed in [38,39,40,41]. An alternative derivation has been given in [42]. We use this nonlocal heat kernel expansion to calculate not only the local but also nonlocal parts of the effective action and to check them against standard computation using local heat kernel methods. We will see that these nonlocal terms have unique coefficients, but local terms are subject to renormalization and have arbitrary coefficients depending on the renormalization conditions. These unique nonlocal terms can be used to describe physical phenomena and obtain scattering amplitudes. They constitute a piece of generically genuine and universal information that we can extract in the effective field theory of gravitational interactions at low energies.
Nonlocal effective actions and their applications have been discussed in several works in different approaches. The nonlocal form of the anomaly-induced gravitational action was first indicated in [43]. The effective action was calculated perturbatively in the weak field limit using the covariant nonlocal expansion of the heat kernel in [44,45,46]. Nonlocal action from long distance fluctuations of massless particles in QED and generation of magnetic fields during inflation were also considered in [47]. In [48, 49], it was used to derive trace anomaly in QED and violation of equivalence principle. Refs. [50, 51] derived it using the Weyl anomaly, and discussed the generation of cosmological magnetic fields in the universe. Nonlocal effective gravitational actions have very interesting cosmological phenomenology such as explaining problems of dark matter [52], dark energy [52, 53] and inflation [54]. It has quite unusual classical features [55, 56]. A comprehensive review of its quantum properties can be found in [57].
The low-energy effective action has been studied in a number of papers. A nice review of this approach is given in [58]. In this approach, all independent terms compatible with the symmetries of the theory are written down in the order of increasing dimension [59]. It is important to sort out which interactions are important in the low energy. The coefficients of these terms may be calculated by perturbations on flat background. On the other hand, our effective action is equivalent to that obtained by integrating out the quantum fluctuations in the path integral on general backgrounds and is not just valid for low energy but for all energy scale. The one-loop effective action for pure gravity and gravity coupled to a scalar field is directly calculated using local and nonlocal heat kernel expansion [60, 61]. Attempt to give the approximate form of the effective action as the sum of Feynman diagrams is made in [62].
In this paper, we compute the effective action for the gravitational system coupled to some matter. In the gravitational sector, we restrict to a theory described by the Einstein action (Ricci scalar only) for simplicity, while a gravitational theory with higher derivatives is one of our future goals of an extension of this project. In the matter sector, we consider the action consisting of one abelian massless U(1) gauge field, one charged massive scalar field and a general number \(N_F\) of massive Dirac fermions coupled both to electromagnetism as well as to gravity. This is the simplest but quite general theory allowing us to see how the final result is affected by various fields. The reason for inclusion of only one abelian gauge field is because this is the only vector field that survives in the IR macroscopic limit (classically observable). On the other side, we consider an arbitrary number of fermions since there are plenty of them in Standard Model of particle physics and extensions thereof. Further generalization to include gauge fields in non-abelian gauge group, arbitrary numbers of fermions and scalars in various representations, and Yukawa interactions is a future goal.
This paper is organized as follows. In the next section, we first summarize the methodology of nonlocal heat kernel expansion and explain how to incorporate it in our calculation of the FRGE. The result is given in the form of a master formula. This formula requires the Hessian of the action for quantum fields (this is the operator of the second variational derivative of the action with respect to fluctuating fields, which we denoted by \(\frac{\delta ^2 \Gamma _k}{\delta \phi \delta \phi }\) in (1.1)). In Sect. 3, we calculate the Hessian in a mutually coupled system of Einstein gravity, electromagnetic (EM) gauge field, Dirac and charged scalar fields. In Sect. 4, we plug these results into the master formula to derive the FRGE, and integrate it (over k) from the UV scale \(k=\Lambda \) down to \(k=0\) to obtain the nonlocal terms with definite coefficients in the effective action \(\Gamma _0\). Section 5 is devoted to discussions. Some technical details are relegated to three appendices.
2 Nonlocal heat kernel expansion
Suppose that our Laplacian (or Hessian) takes the form
where \(\nabla \) is a covariant derivative with respect to all background fields and U is a non-derivative term. The main computation will be performed in a spacetime with Euclidean signature. We will need the trace of a following expression
In the above formula, \(\omega \) plays the role of the mass of the mode and \(R_k(z)\) is the cutoff function. The FRGE then has the form
where the functional trace (denoted by \({\mathrm{Tr}}\)) is both with respect to internal and external indices, so the spacetime dependence requires here also to take the volume integral. Introducing the Laplace transform
(2.3) reduces to
The commutator of the covariant derivatives \(\nabla \) gives the curvature tensor \({\varvec{\Omega }}_{\mu \nu }\) (depending on a specific representation on which these derivatives act):
We note that the tensor \({\varvec{\Omega }}_{\mu \nu }\) is antisymmetric and may have indices in particular matrix representation of internal indices. From standard (metric) Riemann tensor \(R_{\mu \nu \rho \sigma }\) using raising of indices with the inverse metric tensor \(g^{\mu \nu }\), we construct other curvature tensors, such as Ricci tensor \(R_{\mu \nu }\) and Ricci scalar (curvature scalar) R. Together with \(\mathbf{U}\) and \({\varvec{\Omega }}_{\mu \nu }\), these last three tensors constitute a set of generalized curvatures.
The nonlocal heat kernel expansion up to the quadratic order in generalized curvatures \({{{\mathcal {R}}}}=(\mathbf{U},{\varvec{\Omega }}_{\mu \nu },R_{\mu \nu \rho \sigma },R_{\mu \nu },R)\) is given by [42]
where the structure functions f’s are given by
Here the basic structure function (form-factor) f(x) reads
where we have also displayed the Maclaurin expansions for small x. The first constant terms in Eqs. (2.8)–(2.9) represent the local heat kernel expansion coefficients. The full nonlocal heat kernel has the infinite number of heat kernel coefficients, which can be collected in the form of nonlocal form-factors f(x), \(f_{Ric}(x)\), \(f_R(x)\), \(f_{RU}(x)\), \(f_U(x)\), \(f_\Omega (x)\). Substituting (2.7) into Eq. (2.5), we obtain
which is our master formula to derive the FRGE. In the above, we have used “small” traces \({\mathrm{tr}}(\ldots )\) to denote traces only in the internal space of indices. Here and in what follows, \(z=-\nabla ^2\) and we have defined
More explicitly, we have
where we have defined
To evaluate this, we first recall that
From this, we find
Using the definition (2.2) and the optimized cutoff [63]
in the first expression of (2.17), we find
where \({{\tilde{\omega }}}=\omega /k^2\). We then obtain
with \({{\tilde{z}}}=z/k^2\). Substituting these into (2.14), we obtain
We will use these results to derive the flow equation.
We note that the intermediate results of the RG flow depend slightly on the choice of the cutoff kernel function \(R_k(z)\). However, as discussed in [2, 3, 14, 64], the evidences for existence of FPs (realizing the idea of asymptotic safety in the UV) are independent of this choice and the scheme of regularization and renormalization. The same is also true in the \(k\rightarrow 0\) limit of the EAA, while the interpolating effective action \(\Gamma _k\) at finite \(k>0\) shows a bit of dependence. On the other hand, the nonlocal terms in the effective action \(\Gamma _0\) are universal and unambiguous and they do not rely on such details as the choice of the IR cutoff function. Here we chose the optimized cutoff function in (2.18) in order to have an analytic control over all functions and integrals involved in the process of taking functional traces in (2.3) and to have compact form for all intermediate expressions of the RG flow also in the case of finite k.
3 Hessian for gravity coupled to EM, Dirac and charged scalar fields
We consider the total action \(S_T\) of the system consisting of gravity coupled to EM (gauge), Dirac and charged scalar fields:
where \(S_H, S_V, S_f\) and \(S_S\) are the actions for the (Einstein) gravity, EM field \(V_\mu \), Dirac fermion \(\psi \) and a charged scalar field \(\phi \). Their explicit forms are given below.
To calculate the flow equation, we have to derive the Hessian in each sector, to which we now turn.
3.1 Hessian for graviton
Let us first consider the Einstein action (Ricci scalar of the metric g) together with the gauge fixing:
with \(g=\det (g_{\mu \nu })\) and where \(f_\mu \) is the gauge-fixing function
The quantum fluctuations are defined by
For simplicity, we set \(\kappa =1\) and consider \(d=4\) spacetime dimensions in what follows. Background quantities are denoted by bars over them. Separating the background and quantum fields (3.4), we find the Hessian \(\mathbf{H}_G\) in the following expression from the expansion of the action (3.2) to the second order in fluctuations \(h_{\mu \nu }\):
where
and where
Here the bracket on indices means symmetrization within the pairs of indices \((\mu ,\nu )\) and \((\alpha ,\beta )\) in the second term and within the pair \((\alpha ,\beta )\) in the third term in (3.8) (with the factor \(\frac{1}{2}\) included).
The diffeomorphism ghost action corresponding to the gauge fixing in (3.3) is
Hence we can calculate the ghost contribution to the flow equation with the vector-like Hessian \((\Delta _{gh})_{\mu \nu }=-{{\bar{g}}}_{\mu \nu }{{\bar{\nabla }}}^2-{{\bar{R}}}_{\mu \nu }\).
3.2 Gauge fields
The action for the gauge field is
where the U(1) (abelian) gauge field strength is given by
We note that the Christoffel symbols drop out from the antisymmetrized field strength, but it is convenient to recover the classical part when the derivatives acts on the gauge fields. The quantum fluctuations are defined as
and then the resulting perturbation of the field strength is
The part quadratic in the fluctuations \((h_{\mu \nu },A_\mu )\) of the action (3.10) under the volume integral is given by
We introduce the gauge fixing term
which contributes to the Hessian
In what follows, we set \(\alpha =1\). Collecting (3.14) and (3.16), we find that the gauge and gravitational contributions to the quadratic part of the action (3.10) is
where
with
where
is the unit matrix on the symmetric tensor with two indices. In various components of \(\mathbf{H}_V\) in Eqs. (3.19)–(3.21), symmetrization \(\mu \leftrightarrow \nu \), \(\alpha \leftrightarrow \beta \) and \((\mu ,\nu ) \leftrightarrow (\alpha ,\beta )\) should be understood. Note that \(\mathbf{U}_V\) is not symmetric (as a matrix). Naively one would expect that \(\mathbf{U}\) should be symmetric, but it is then not self-adjoint. Here we have chosen such that the Hessian is self-adjoint (as the operator acting between fluctuations and with a proper Hermitian complex scalar product in the field space). See Appendix A for more details.
The gauge ghost contribution to the Hessian consistent with the gauge fixing (3.16) is given by \(\Delta _{gh}^G=-{{\bar{\nabla }}}^2\). This is a scalar operator.
3.3 Dirac fields
The action we consider for Dirac fermions is
where the covariant derivatives acting on spinors are
with \(\omega _{\mu ab}\) being spin-connection coefficients and \( J^{ab}= \frac{1}{4}[\gamma ^a,\gamma ^b] \) the O(4) generators. From the action (3.23) and the definitions of covariant derivatives (3.25), one sees that the massive Dirac fermion (with mass \(m_F\)) is coupled minimally both to the gravitational and EM fields (via the fermionic electric charge \(e_F\)). We consider \(N_F\) fermions, but we can calculate the contribution for a single Dirac field and multiply it by \(N_F\) in the end.
We first show that we can express the fluctuation of the vierbein \(e^a_\mu \) in terms of that of the metric \(g_{\mu \nu }\) in (3.4). From the soldering relation \(g_{\mu \nu }=e_\mu ^a e_\nu ^b \eta _{ab}\), we find that we can choose [65]
where we denote
The inverse vierbein \(e^\mu _a\) and its expansion is given by
By the tetrad postulate
we can calculate the expansion of the spin-connection:
where
The Dirac field is decomposed as \(\psi \Rightarrow \psi +\chi \). (Here exclusively by bars over the spinorial quantities, we denote the Dirac conjugate of the spinors, not the background spinors). In this way, we can express the expansion of the Dirac action (3.23) to the quadratic order in fluctuations by only the variations of the covariant metric tensor \(h_{\mu \nu }\), gauge potential \(A_\mu \) and the Dirac field \(\chi \). We thus see that while we need to use vierbeins and spin-connections for the explicit construction of the action (3.23), we do not have to use the variation of \(e_\mu ^a\) nor \(\omega _\mu ^{ab}\) in the expansion since all fluctuations there are given in terms of the metric variations \(h_{\mu \nu }\).
We then find that the Dirac action (3.23) to the quadratic order in fluctuations (\(h_{\mu \nu },A_\mu ,\chi \)) is given under spacetime integral as
where \({{\bar{D}}}_\mu \) is the covariant derivative defined in (3.25) and restricted to the gravitational background \({{\bar{g}}}_{\mu \nu }\) and EM fields \({{\bar{A}}}_\mu \), and \(\gamma _{\alpha \beta \mu }\) is the antisymmetric product of Dirac gamma matrices. When we deal with neutral objects (not charged under EM group), we use only spacetime covariant background derivatives \({{\bar{\nabla }}}_\mu \).
In the Hessian (3.33), we have terms with fermion–fermion (\({{\bar{\chi }}}\)-\(\chi \)), boson-boson (h-h) and mixed (\(\chi \)-h with background \(\psi \)) fluctuations. Here we drop the mixed terms since they are intractable by the present methods of computation and moreover lead to highly nonlocal terms in the effective action. Let us then first discuss the fermion-fermion terms, and then come back to the boson–boson terms. The integration over Dirac field \(\chi \) in this sector yields the contribution to the effective action

Noting that  , the formula (3.34) can be rewritten as
, the formula (3.34) can be rewritten as

Now consider

Using the identity
and Bianchi identity for the Riemann tensor, we find

In this way, we have derived the so-called Lichnerowicz formula relating the square of the gauge-covariant Dirac operator acting on spinors to standard Bochner Laplacian acting on spinors treated as spacetime scalars shifted by various curvatures (in the internal and external spaces).
Hence the contribution (3.35) from fermion–fermion sector to the effective action turns out to be
We define
and use the regulator (2.18):
Then we have the contribution from Dirac fields to the FRG flow of the effective action
We can now use the technique of nonlocal heat kernel as described before. Noting that \({{\varvec{\Omega }}}_{\mu \nu } = [{{\bar{D}}}_\mu ,{{\bar{D}}}_\nu ] = -ie_F {{\bar{F}}}_{\mu \nu } +\frac{1}{4} {{\bar{R}}}_{\mu \nu }{}^{cd} \gamma _c \gamma _d\), (3.43) is cast into
with \(z=-{{\bar{D}}}_\mu ^2\). Internal traces that we will need are
We then find for (3.44)
where \(g_{Ric}, g_{R}, g_{RU}, g_{U}\) and \(g_\Omega \) are given in (2.14). We note that the term \(4m_F^{2}g_{U}m_F^{2}\) gives a constant under the volume integral in (3.48), but we keep it for completeness in our expression.
It should be noticed that by choosing the form of the kinetic operator \({{\varvec{\Delta }}}\) and \({\mathbf{U}}\) as in (3.41), we treated the mass term as an interaction. In this way we can parallel the treatment with the other massless gauge fields in the derivation of the effective action. This choice of the leading operator as \(z=-{{\bar{D}}}_\mu ^2\) changes slightly the shape of the cutoff function \(R_k(z)\) and the actual form of the flow at intermediate energy scales k. It corresponds to the choice of the cutoff of type I in gravitational theories [2, 14], and amounts to taking the massless propagator for fermions. This is a well-developed technique in renormalization theory and it is used, in particular, in QCD as mass-independent renormalization. In this case, quark mass is scheme-dependent quantity and it is then the most appropriate scheme. An alternative choice would be to take \(z=-{{\bar{D}}}_\mu ^2+m_F^2\) (realizing the cutoff of type II). When the mass interaction is fully resummed, the two schemes do agree. However, we find it better suited to use the massless scheme for fermions. For the effective action, the differences between two schemes are immaterial. The difference only shows up in the local terms. The reason for this is that nonlocal logarithmic universal terms in the effective action \(\Gamma _0\) are related to the expressions for the perturbative one-loop beta functions, and these beta functions in the UV limit are completely insensitive to mass terms. The fermionic contribution to the gravity is cosnsitent with [18].
We then come to the boson–boson terms in Eq. (3.33):
which should be written in a self-adjoint form. For this purpose, we check how terms behave under exchange of left and right fields and integration by parts under volume integral (cf. with Appendix A). The first term in (3.49) is transformed under the integration by parts as
due to complete antisymmetry of the product \(\gamma _{\alpha \beta \mu }\). No surface term is generated under the partial integration, and then it is clear that (3.50) is self-adjoint by itself under the exchange of fields and doing integration by parts.
We then put the quadratized action in (3.49) in the form:
where the Hessian in the matrix form is
These terms should be combined with other terms from gravity and gauge theory, and integrated over the fluctuation fields \(h_{\mu \nu }\) and gauge fields \(A_\mu \). We remark that in the bosonic terms in (3.49) fermionic fields appear only as backgrounds.
Explicitly the components of objects in (3.52) are given by
where
In the above, the symmetrization within each pair of indices \((\mu ,\nu )\) and \((\alpha ,\beta )\) is understood but not marked. Here we have also imposed self-adjointness, which is discussed in Appendix A.
3.4 Charged scalar
We consider charged scalar whose action is
where the covariant derivative on the scalar is
and where the invariant complex square of the field we write as \(|\phi |^2=\phi ^*\phi \). (By star in superscript, we denote complex conjugation of field.) It should be understood that when the covariant derivative in (3.57) acts on fields without charge, it is simply the gravitational covariant derivative \(\nabla _\mu \). When the derivative acts on a scalar quantity as here, it is simply a partial derivative (without spacetime connection coefficients).
Let us write the field as \(\phi ={{\bar{\phi }}}+\varphi \), the former being the background and the latter being a fluctuation. Then the quadratic action is
where bars on the covariant derivatives mean that they are made of background fields and the prime is the derivative with respect to \(|\phi |^2\) (not with respect to just \(\phi \)). This is put in the form
where the Hessian \(\mathbf{H}_S\) has the following expansion in order of derivatives
Here we use the “complex” basis discussed in the Appendix B. We find
where the various components of the \(\mathbf{U}_S\) tensor are given below
We note that similarly to the case of Dirac fermion, here we treat the mass of the scalar field (included in the scalar potential \(V=V(|\phi |^2)\)) as an interaction. In this way we realize cutoff of type I. For the scalar fluctuations, we are able to deal with all terms including mixed terms in (3.60)), hence our nonlocal contribution to the effective action is complete. In the next section, we show how to deal with all fluctuations in the scalar sector within nonlocal heat kernel technique.
3.5 Total Hessian
Collecting all the results for the Hessian (written in (3.5)–(3.8), (3.17)–(3.21), (3.52)–(3.55) and (3.59)–(3.64)), we get the bosonic part of the quadratic action of the total system. We can write it as
where we have expressed the bosonic fluctuations of quantum fields in a multiplet \((h^{\mu \nu }, A^\mu , \varphi ^*,\varphi )\), and
The components of the Hessian \(\mathbf{H}_T\) in derivative expansion are given as
where the components of the \(\mathbf{U}_T\) tensor are
Here symmetrization \(\mu \leftrightarrow \nu \), \(\alpha \leftrightarrow \beta \) and \((\mu ,\nu ) \leftrightarrow (\alpha ,\beta )\), if appropriate, should be understood.
It is convenient to extract an overall factor of \(\mathbf{K}_T\) (3.67) from the full Hessian \(\mathbf{H}_T\) and write it as
Using
which is the generalization of the gravitational DeWitt metric in field space, we find
In principle, in the tensors \(\mathbf{Y}\) and \(\mathbf{W}\) the indices are in natural matrix position (one index down – one index up) letting to perform traces (hence contractions) very naturally without usage of any metric tensor. In particular, all indices \(\alpha \) and \(\beta \) should be in superscripts. However, for notational simplicity, from displaying the matrix of \(\mathbf{W}\) tensor in (3.74) we do not write them in upper position, hoping that this will not lead to any confusion.
The explicit components of the \(\mathbf{W}\) tensor read
and other components of the \(\mathbf{W}\) tensor are the same as the corresponding components in \(\mathbf{U}_T\).
We next eliminate the first order term \(\mathbf{Y}^\delta {{\bar{D}}}_\delta \) in (3.71) by writing \(\tilde{\mathbf{D}}_\mu =\mathbf{1}{{\bar{D}}}_\mu -\mathbf{Y}_\mu \) following [37, 66]. Then \({{\varvec{\Delta }}}\) in (3.71) is rewritten as
where
Here
and
The explicit forms of the above components of the \(\mathbf{Y}_\delta \mathbf{Y}^\delta \) are given in Appendix C.1.
We note that the gauge- and spacetime-covariant shifted derivative \(\tilde{{\mathbf{D}}}_\mu \) is matrix-valued and constructed with backgrounds of the gauge and gravitational fields. By shifting the covariant derivative \({{\bar{D}}}_\mu \) to the new one \(\tilde{{\mathbf{D}}}_\mu \), we reduce the differential operator in (3.71) to the minimal form with leading symbol with two derivatives. The leading term with two derivatives is a square of the new covariant derivative \(\tilde{{\mathbf{D}}}_\mu \), the term with one derivative less is absent and finally all the other non-derivative operators (endomorphisms of the internal vector bundle) are collected in the operator \(\tilde{{\mathbf{W}}}\). Now the kinetic operator in (3.76) has precisely the form elucidated in (2.1), so the standard method of heat kernel technique can be applied here to take its functional trace.
For the components of the \(\tilde{{\mathbf{W}}}\) tensor, using (3.77) and (3.79), we find
Now we wish to calculate the commutator of the shifted covariant derivatives \(\tilde{{\mathbf{D}}}_\mu \). For this purpose the commutator of gauge-covariant derivatives \({{\bar{D}}}_\mu \) has to be found first. We give it in a matrix form using the general vector of bosonic fluctuations \(\Psi =(h_{\alpha \beta },A_\alpha ,\varphi ,\varphi ^*)^T\):
Using the commutation relations on particular types of fluctuations
we find
We have the general formula for the commutator \(\tilde{{{\varvec{\Omega }}}}_{\rho \sigma }\) of shifted covariant derivatives \(\tilde{{\mathbf{D}}}_\mu \):
and in particular for various tensors appearing above
and
where we also used the Bianchi identity
Finally, we write the components of the \(\tilde{{{\varvec{\Omega }}}}_{\rho \sigma }\) tensor in a matrix form
with the explicit formulas for all components given in Appendix C.2.
Since the Hessian \(\mathbf{H}_T\) of the total system has now the minimal form (2.1), we can use our master formula for FRGE (2.11) with identifications: \(\mathbf{U}=\tilde{{\mathbf{W}}}\) and \({{{\varvec{\Omega }}}}_{\rho \sigma }=\tilde{{{\varvec{\Omega }}}}_{\rho \sigma }\). For this we need to evaluate several traces in the internal spaces of fluctuations, while the functional traces were already done in formula (2.11). Therefore we need the traces of \(\tilde{{\mathbf{W}}}\), \(\tilde{\mathbf{W}}^2\) and \(\tilde{{{\varvec{\Omega }}}}^2=\tilde{{{\varvec{\Omega }}}}_{\rho \sigma }\tilde{{{\varvec{\Omega }}}}^{\rho \sigma }\). The results for them are summarized in Appendix C.3.
4 Effective action
Now we are ready to derive the flow equation based on Eq. (2.11). In this section, we drop bars on the fields since all quantities considered are built out of background field values and we will not need any field fluctuation.
We have one graviton, one real vector and one complex scalar (cf. (3.81) and above it), so in \(d=4\)
From our master formula (2.11), we get
In addition, we have the contributions from the coordinate reparametrization (gravitational) and gauge ghosts. The first one, based on (3.9), adds to (4.2)
The gauge ghost contributes
Finally we have a contribution from fermions in (3.48). All these contribute to the FRGE flow of the bosonic effective action \(\partial _t \Gamma ^{1-loop}_k \).
Plugging the results of the traces of \(\tilde{{\mathbf{W}}}, \tilde{{\mathbf{W}}}^2\) and \(\tilde{{{\varvec{\Omega }}}}^2\) in Eqs. (C.5), (C.6) and (C.7) from Appendix C.3 into (4.2) and collecting all these contributions (4.2)–(4.4) and (3.48), we get the flow equation of the effective action
where \(\Gamma ^{gem}_k, \Gamma ^{scalar}_k\) and \(\Gamma ^{fermion}_k\) are scale-dependent effective actions involving gravity and EM fields, scalars and fermions, respectively. Explicitly the flow of them is given by
where the structure functions \(g_i\) (for \(i=1,\ldots ,14\)) read
and for the flow of the action with scalars
where the structure functions \(g_i\) (for \(i=15,\ldots ,29\)) read
and the fermionic terms are
where the structure functions \(g_i\) (for \(i=30,\ldots ,4\)5) read
In deriving these results, we have to be careful in making partial integration because nonlocal operators are inserted between the factors in each of the terms above. To know precise positions, where to insert nonlocal operators in the form of functions \(g_i\), one must distinguish between left and right tensors, that is one needs to perform traces: \({\mathrm{tr}}\left( \tilde{{\mathbf{W}}}_L\tilde{{\mathbf{W}}}_R\right) \) and \({\mathrm{tr}}\left( \tilde{{{\varvec{\Omega }}}}_{L\rho \sigma }\tilde{{{\varvec{\Omega }}}}_R^{\rho \sigma }\right) \). Subsequently, one inserts \(g_i\) factors acting on a bracket collecting product of all right fields. The distinction between left and right fields here is symmetric and their roles can be reversed. This is reflected by performing integration by parts under spacetime volume integral and the fact that form-factors \(g_i\) are functions of the integration by parts-invariant gauge-covariant operator \(z=-D_\mu ^2\). We have also used Bianchi identities for the gauge field strengths and Riemann curvatures to simplify some terms.
Now our task is to integrate the flow equation (4.5) from the UV scale \(\Lambda \) down to zero. We first note that the \(g_a\) functions have the general form
and the coefficients are given in Table 1. As we will see in a moment, to obtain the effective action \(\Gamma _0\), it is enough to focus only on \(A_a\) coefficients. We can drop the term with the structure function \(g_2\) since it gives a constant after spacetime integration.
We can integrate the flow equation for \(g_a\) over k from \(k=0\) to \(k=\Lambda \) to obtain
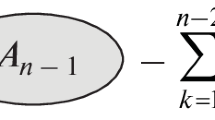
where
We find for large \(\Lambda \), for gravity and electromagnetism (cf. (4.6))
for scalar sector (cf. (4.8))
and for fermionic sector (cf. (4.10))
where we have introduced an arbitrary renormalization scale \(\mu \). These UV-divergences (when \(\Lambda \rightarrow \infty \)) can be subtracted by choosing \(G_{a,\Lambda }\) in (4.13) to eliminate the \(\Lambda \)-dependence. We set
where \(\gamma _a\) are arbitrary constants. Then the form-factors in (4.14) are
Thus the effective action has the local parts (4.15), (4.16) and (4.17) with the divergent coefficients replaced by arbitrary constants, and the following nonlocal parts with definite and universal coefficients:
We find the following three pieces of the effective action:
and
In preparing the above results (4.21)–(4.23), we used extensively commutation of covariant derivatives (3.82)–(3.84), Bianchi identities for Riemann and field strength tensors and the antisymmetric property of the product of three Dirac gamma matrices \(\gamma _{\mu \nu \rho }\). We also integrated by parts (where it was possible) to put the terms in the most symmetric form. (The operator \(\log \left( \frac{-D^2}{\mu ^2}\right) \) is always invariant under integration by parts.) Finally, in the scalar and fermionic sectors, we used the square of the gauge-covariant background derivative \(D_\mu \) as the argument of the logarithmic form-factors. This is certainly correct. However, in some cases when the operator acts on the fields in a right bracket, which all together are electromagnetically neutral, the EM background connection \(A_\mu \) completely drops out from \(D_\mu ^2\) and it is also fine to substitute \(\nabla _\mu ^2\). This was already done for all terms in (4.21) which from construction are uncharged.
The results (4.21)–(4.23) for the quantum effective action are written to the quadratic order in “generalized curvatures” \({{\mathcal {R}}}\). These generalized curvatures are matrices \(\tilde{{\mathbf{W}}}\), \(\tilde{ {\varvec{\Omega }}}_{\mu \nu }\) and the Riemann tensor \(R_{\mu \nu \rho \sigma }\) and its contractions. All terms in all components of \(\tilde{{\mathbf{W}}}\), \(\tilde{{\varvec{\Omega }}}_{\mu \nu }\) counts as one unit of generalized curvature.
Another remark is that according to the discussion in Sects. 2 and 3.5 , the argument of the logarithm in Eqs. (4.21)–(4.23) should be the two-derivative operator \(z=-\tilde{{\mathbf{D}}}_\mu ^2\), which is common for all fluctuations, divided by \(\mu ^2\). The nonlocal part of the effective action (4.19) have the same structure as in the local UV-divergences in (4.15), (4.16) and (4.17), with the factors of \(\log \left( \frac{\Lambda ^2}{\mu ^2}\right) \) replaced by \(\log \left( \frac{-D^2}{\mu ^2}\right) \). We also see that the nonlocal logarithmic pieces of the effective action depend only on \(A_a\) coefficients in structure functions \(g_a\) for each term counted by a different value of the index a. If one looks for a shortcut to get quickly the nonlocal terms in the effective action \(\Gamma _0\), then one can concentrate on \(A_a\) coefficients in the structure functions. One also notes that terms proportional to \(Q_2\) and \(Q_1\) in (4.2) do not contribute at all to nonlocal logarithmic terms of the effective action \(\Gamma _0\). Local operators in the effective action in (4.15), (4.16) and (4.17) are subject to renormalization and the coefficients of independent operators are arbitrary since they depend on the renormalization conditions. In contrast, the coefficients of the nonlocal terms are uniquely determined.
The effective action with the local and nonlocal terms is the main result of this paper.
5 Discussion
In this paper we have calculated the effective action in the gravity theory coupled to gauge, Dirac and charged scalar fields. In particular we have obtained its nonlocal part unambiguously. Most of the work so far on asymptotically safe gravity focused on the existence proof that there are UV FPs. However, the object directly connected to most important physical quantities is the effective action \(\Gamma _0\) (effective average action at \(k=0\)). We have used the FRGE and integrate it from high energy scale down to \(k=0\) to obtain the effective action. The nice property of this method is that there are no divergences in contrast to computing the functional integrals. We have shown that the resulting effective action has nonlocal terms with definite coefficients. The physical effects corresponding to nonlocal terms in the effective action are non-analytic in momentum, which are different from those generated by the local and analytic divergent terms. The local terms are affected by divergences and must be renormalized so that their coefficients depend on the renormalization conditions. The result on nonlocal terms can be used to calculate gravitational scattering amplitudes without ambiguity [67,68,69] and these predictions can be tested experimentally.
One could also evaluate the effective action perturbatively in the weak field limit using the covariant nonlocal expansion of the heat kernel in [44, 45]. The effective action in this framework was worked out in [46]. Similar results have been obtained in [48, 49] using Feynman diagrams. This result may be used to try to generate cosmological magnetic fields. This primordial magnetogenesis from anomalies relies on the effective action derived in the weak field approximation [47]. The result is valid in the regime in which the curvature satisfies the condition \(R^2 \ll \nabla ^2 R\). During the slow-roll inflation, the geometric curvature satisfies \(\nabla ^2 R \ll R^2\), while during matter domination we have \(\nabla ^2 R \sim R^2\). So to study primordial magnetogenesis reliably over a long range of cosmological evolution, it is necessary to go beyond the weak field approximation. The results in this case have been obtained for the effective action from the Weyl anomaly in the theory of gauge bosons interacting with Dirac fermion in curved backgrounds [50]. However, there the metric was assumed to be conformally flat. While this restriction has no problem in the application to Friedmann–Lemaître–Robertson–Walker metric, our result is valid for arbitrary backgrounds and quantum effects from gravity are also taken into account. The magnetogenesis has been discussed in [51] with negative conclusion. Our effective action has nonlocal terms with a similar structure, and could be used to see if the magnetic fields can be generated. It would be very interesting to study this problem with the effective action derived here which includes the quantum gravity effects.
Some comments are in order on the results for \(\Gamma _0\) in Eqs. (4.20)–(4.23). We have found so many terms in the total expression for the effective action, in comparison with quite a small number of terms present in the original action of the total system (in Sect. 3.5). We started out with Einsteinian gravitation and renormalizable matter models (of abelian gauge fields, fermions and scalars). There are many virtual processes that contribute to scattering amplitudes, which gives all possible terms. The only restriction is the reparametrization and gauge invariance. If this condition is satisfied, nothing forbids the invariant operators and the corresponding processes appear. This is true even if one starts with renormalizable or nonrenormalizable theories. The only difference between these theories is whether we would have divergent coefficients beyond those operators already present in the bare action.
It is known that in the perturbative framework (using for example Feynman diagrams as in [48, 49, 58, 59]), one gets the similar expression for the effective action of the model at the one-loop level. However, the procedure is different. There one isolates the perturbative UV-divergences, finds corresponding beta functions and renormalizes the theory by introducing an arbitrary energy scale of the renormalization point \(\mu \). Then the couplings of the theory are promoted from constants to scale-dependent one, the scale being represented by \(\mu \). But in the full effective action we have implicit independence on this \(\mu \) parameter, because the quantum effective action is RG transformation invariant. When the logarithmic UV-divergences are taken into consideration, the RG running of dimensionless couplings is logarithmic with the energy scale \(\mu \). The above-mentioned RG-invariance of the effective action is only achieved if we have very special nonlocal terms in the effective action built with the logarithm of the momentum. In covariant language, these nonlocal universal terms take the form with the insertion of nonlocal logarithmic form-factor of the gauge- and GR-covariant operator \(\log \left( \frac{-D^2}{\mu ^2}\right) \). In our case the terms under consideration are of the quadratic order in “generalized curvatures” \({{\mathcal {R}}}\), and the insertion of the nonlocal operator \(\log \left( \frac{-D^2}{\mu ^2}\right) \) is unambiguous. This is in accordance with the fact that we used nonlocal heat kernel expansion to the second order in curvatures \({{\mathcal {R}}}\) in Eq. (2.11); in the flow equations (4.6), (4.8) and (4.10), terms quadratic in \({{\mathcal {R}}}\) were multiplied by the functional \(Q_0[h_k]\), which is a dimensionless numerical constant, and in the Eqs. (4.15)–(4.17), the terms quadratic in curvatures \({{\mathcal {R}}}\) were all proportional to \(\log \left( \frac{\Lambda ^2}{\mu ^2}\right) \). It is consistent that perturbatively we would consider logarithmic UV-divergences in the Eqs. (4.15)–(4.17) related to local terms quadratic in curvatures. The form of the universal quadratic in curvatures \({{\mathcal {R}}}\) part of the nonlocal effective action is dictated by RG-invariance and should be read together with the scale-dependence (RG running) of couplings. Difference between one-loop effective action obtained by perturbation and that obtained from the FRGE is also discussed in [70, 71].
We emphasize that the main novelty of this work is the computation of nonlocal universal terms in the effective action \(\Gamma _0\) of the total system in Sect. 3.5 using the FRGE methods and integration of the RG flow equation. These results can be also viewed as listing of all one-loop UV-divergences for our total quantum system. These divergences are encoded in terms, which are at most quadratic in generalized curvatures \({{\mathcal {R}}}\).
Our results for the effective action \(\Gamma _0\) should be understood in certain expansion schemes. Let us concentrate on nonlocal universal terms which contain logarithmic form-factor of the covariant operator \(D^2\). Besides these terms, there are also some local higher curvature terms with universal (RG-independent) coefficients and local terms with coefficients dependent on the renormalization conditions. We performed a “generalized curvature” expansion coinciding with the scheme of heat kernel expansion. Our results are to the second order and we expect that higher orders in \({{\mathcal {R}}}\) exist too and they could be relevant for computation of various physical observables. For example, from the quadratic terms in \({{\mathcal {R}}}\) in \(\Gamma _0\), we can unambiguously derive the quantum finite corrections to the graviton polarization functions, but to know a precise form of 4-gravitons scattering amplitudes around flat spacetime, we would need to possess the knowledge of \(\Gamma _0\) to order quartic in curvatures \({{\mathcal {R}}}\). The curvature expansion is different from derivative expansion which is however a common practice for the effective field theory approaches. In our terms we have collected all powers of energy/momentum into covariant logarithmic form-factors of the operator \(D^2\). Within these approximation schemes and limitations, the results in (4.20)–(4.23) are complete in the sense that there are no other terms except those written and with the precise coefficients that we have determined. It is also an important problem which kind of terms may be generated at two-loop and beyond.
One can also ask a question about a possible extension of this type of computation for a model of renormalizable gravity in \(d=4\) spacetime dimensions by including higher curvature terms. Such terms may be relevant operators, so it is important to study the role of these terms in general RG flows. The first renormalizable model is due to Stelle [1] and contains generally covariant terms with \(R^2\) and \(R_{\mu \nu }^2\) (the \(R_{\mu \nu \rho \sigma }^2 \) term can be easily eliminated by using the Gauss-Bonnet identity valid in \(d=4\)). However, due to the higher derivative nature of operators in the gravitational sector, there is an issue with unitarity. Leaving this problem aside, we may still analyze beta functions of the couplings. Due to the renormalizability of this model of gravity coupled to matter [72,73,74], the number of UV-divergent terms is smaller. We note that in gravitational models, in which there are no perturbative UV-divergences (and they are UV-finite [75, 76]) by the above argumentation we will not find any logarithmic term in the effective action \(\Gamma _0\).
We have not included Yukawa couplings between fermions and scalar in our study. The reason is that the gauge invariance forbids Yukawa interactions between our scalar field and fermions because the charges do not match. However in more general situation, the Yukawa couplings may play significant role in the flow of the gravitational coupling and a scalar potential \(V(\phi )\) [65]. So it should be significant to extend our work in this direction. Other interesting subjects include studying quantum effects in other physical processes. For example, it would be of interest to use the quantum effective action to study if the quantum effects may tame the singularities in the blackholes and in the early universe, if they can be a rescue for the information paradox in the Hawking radiation process or whether there is any physical consequence in the observed gravitational waves.
We hope to return to these important subjects in the future.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study and no experimental data has been listed.]
References
K.S. Stelle, Renormalization of higher derivative quantum gravity. Phys. Rev. D 16, 953 (1977)
R. Percacci, An Introduction to Covariant Quantum Gravity and Asymptotic Safety (World Scientific, Singapore, 2017)
M. Reuter, F. Saueressig, Quantum Gravity and the Functional Renormalization Group: The Road towards Asymptotic Safety (Cambridge University Press, Cambridge, 2019)
A. Eichhorn, An asymptotically safe guide to quantum gravity and matter. Front. Astron. Space Sci. 5, 47 (2019). arXiv:1810.07615 [hep-th]
C. Wetterich, Exact evolution equation for the effective potential. Phys. Lett. B 301, 90 (1993)
T.R. Morris, The exact renormalization group and approximate solutions. Int. J. Mod. Phys. A 9, 2411 (1994). arXiv:hep-ph/9308265
M. Reuter, Nonperturbative evolution equation for quantum gravity. Phys. Rev. D 57, 971 (1998). arXiv:hep-th/9605030
D. Dou, R. Percacci, The running gravitational couplings. Class. Quant. Grav. 15, 3449 (1998). arXiv:hep-th/9707239
M. Reuter, F. Saueressig, Renormalization group flow of quantum gravity in the Einstein-Hilbert truncation. Phys. Rev. D 65, 065016 (2002). arXiv:hep-th/0110054
R. Percacci, D. Perini, Asymptotic safety of gravity coupled to matter. Phys. Rev. D 68, 044018 (2003). arXiv:hep-th/0304222
G. de Berredo-Peixoto, I.L. Shapiro, Conformal quantum gravity with the Gauss-Bonnet term. Phys. Rev. D 70, 044024 (2004). arXiv:hep-th/0307030
D.F. Litim, Fixed points of quantum gravity. Phys. Rev. Lett. 92, 201301 (2004). arXiv:hep-th/0312114
A. Codello, R. Percacci, Fixed points of higher derivative gravity. Phys. Rev. Lett. 97, 221301 (2006). arXiv:hep-th/0607128
A. Codello, R. Percacci, C. Rahmede, Investigating the ultraviolet properties of gravity with a Wilsonian renormalization group equation. Ann. Phys. 324, 414 (2009). arXiv:0805.2909 [hep-th]
D. Benedetti, P.F. Machado, F. Saueressig, Taming perturbative divergences in asymptotically safe gravity. Nucl. Phys. B 824, 168 (2010). arXiv:0902.4630 [hep-th]
M. Niedermaier, Gravitational fixed points and asymptotic safety from perturbation theory. Nucl. Phys. B 833, 226 (2010)
G. Narain, R. Percacci, Renormalization group flow in scalar-tensor theories. I. Class. Quant. Grav. 27, 075001 (2010). arXiv:0911.0386 [hep-th]
P. Dona, R. Percacci, Functional renormalization with fermions and tetrads. Phys. Rev. D 87, 045002 (2013). arXiv:1209.3649 [hep-th]
J.A. Dietz, T.R. Morris, Asymptotic safety in the f(R) approximation. JHEP 1301, 108 (2013). [arXiv:1211.0955 [hep-th]]
N. Ohta, R. Percacci, Higher derivative gravity and asymptotic safety in diverse dimensions. Class. Quant. Grav. 31, 015024 (2014). arXiv:1308.3398 [hep-th]
P. Donà, A. Eichhorn, R. Percacci, Matter matters in asymptotically safe quantum gravity. Phys. Rev. D 89, 084035 (2014). arXiv:1311.2898 [hep-th]
K. Falls, D. Litim, K. Nikolakopulos, C. Rahmede, Further evidence for asymptotic safety of quantum gravity. Phys. Rev. D 93, 104022 (2016). arXiv:1410.4815 [hep-th]
M. Demmel, F. Saueressig, O. Zanusso, RG flows of quantum Einstein gravity in the linear-geometric approximation. Ann. Phys. 359, 141 (2015). arXiv:1412.7207 [hep-th]
M. Demmel, F. Saueressig, O. Zanusso, RG flows of quantum Einstein gravity on maximally symmetric spaces. JHEP 1406, 026 (2014). arXiv:1401.5495 [hep-th]
N. Ohta, R. Percacci, Ultraviolet fixed points in conformal gravity and general quadratic theories. Class. Quant. Grav. 33, 035001 (2016). arXiv:1506.05526 [hep-th]
N. Ohta, R. Percacci, G.P. Vacca, Flow equation for \(f(R)\) gravity and some of its exact solutions. Phys. Rev. D 92, 061501 (2015). [arXiv:1507.00968 [hep-th]]
N. Ohta, R. Percacci, G.P. Vacca, Renormalization group equation and scaling solutions for f(R) gravity in exponential parametrization. Eur. Phys. J. C 76, 46 (2016). arXiv:1511.09393 [hep-th]
H. Gies, B. Knorr, S. Lippoldt, F. Saueressig, Gravitational two-loop counterterm is asymptotically safe. Phys. Rev. Lett. 116, 211302 (2016). arXiv:1601.01800 [hep-th]
T. Denz, J.M. Pawlowski, M. Reichert, Towards apparent convergence in asymptotically safe quantum gravity. Eur. Phys. J. C 78, 336 (2018). arXiv:1612.07315 [hep-th]
A. Eichhorn, S. Lippoldt, J.M. Pawlowski, M. Reichert, M. Schiffer, How perturbative is quantum gravity? Phys. Lett. B 792, 310 (2019). arXiv:1810.02828 [hep-th]
B. Knorr, C. Ripken, F. Saueressig, Form Factors in Asymptotic Safety: conceptual ideas and computational toolbox. Class. Quant. Grav. 36, 234001 (2019). arXiv:1907.02903 [hep-th]
N. Christiansen, D.F. Litim, J.M. Pawlowski, A. Rodigast, Fixed points and infrared completion of quantum gravity. Phys. Lett. B 728, 114 (2014). arXiv:1209.4038 [hep-th]
C. Wetterich, Infrared limit of quantum gravity. Phys. Rev. D 98, 026028 (2018). arXiv:1802.05947 [gr-qc]
P. Jizba, L. Rachwal, J. Knap, Infrared behavior of Weyl gravity: functional renormalization group approach. arXiv:1912.10271 [hep-th]
J.F. Donoghue, A Critique of the Asymptotic Safety Program. arXiv:1911.02967 [hep-th]
A. Satz, A. Codello, F.D. Mazzitelli, Low energy quantum gravity from the effective average action. Phys. Rev. D 82, 084011 (2010). arXiv:1006.380810 [hep-th]
A. Codello, R. Percacci, L. Rachwal, A. Tonero, Computing the effective action with the functional renormalization group. Eur. Phys. J. C 76, 226 (2016). arXiv:1505.03119 [hep-th]
A.O. Barvinsky, G.A. Vilkovisky, Beyond the Schwinger-Dewitt technique: converting loops into trees and in-in currents. Nucl. Phys. B 282, 163 (1987)
A.O. Barvinsky, G.A. Vilkovisky, Covariant perturbation theory. 2: Second order in the curvature. General algorithms. Nucl. Phys. B 333, 471 (1990)
I.G. Avramidi, The nonlocal structure of the one loop effective action via partial summation of the asymptotic expansion. Phys. Lett. B 236, 443 (1990)
I.G. Avramidi, The covariant technique for the calculation of the heat kernel asymptotic expansion. Phys. Lett. B 238, 92 (1990)
A. Codello, O. Zanusso, On the non-local heat kernel expansion. J. Math. Phys. 54, 013513 (2013). [arXiv:1203.2034 [math-ph]]
S. Deser, M.J. Duff, C.J. Isham, Nonlocal conformal anomalies. Nucl. Phys. B 111, 45 (1976)
A.O. Barvinsky, G.A. Vilkovisky, The generalized Schwinger-de Witt technique and the unique effective action in quantum gravity. Phys. Lett. 131B, 313 (1983)
A.O. Barvinsky, G.A. Vilkovisky, The generalized Schwinger-Dewitt technique in gauge theories and quantum gravity. Phys. Rep. 119, 1 (1985)
A.O. Barvinsky, Y.V. Gusev, G.A. Vilkovisky, V.V. Zhytnikov, The one loop effective action and trace anomaly in four-dimensions. Nucl. Phys. B 439, 561 (1995). arXiv:hep-th/9404187
B.K. El-Menoufi, Inflationary magnetogenesis and non-local actions: The conformal anomaly. JCAP 1602, 055 (2016). [arXiv:1511.02876 [gr-qc]]
J.F. Donoghue, B.K. El-Menoufi, QED trace anomaly, non-local Lagrangians and quantum equivalence principle violations. JHEP 1505, 118 (2015). arXiv:1503.06099 [hep-th]
J.F. Donoghue, B.K. El-Menoufi, Covariant non-local action for massless QED and the curvature expansion. JHEP 1510, 044 (2015). arXiv:1507.06321 [hep-th]
T. Bautista, A. Benevides, A. Dabholkar, Nonlocal quantum effective actions in Weyl-flat spacetimes. JHEP 1806, 055 (2018). arXiv:1711.00135 [hep-th]
A. Benevides, A. Dabholkar, T. Kobayashi, To \(B\) or not to \(B\): Primordial magnetic fields from Weyl anomaly. JHEP 1811, 039 (2018). arXiv:1808.08237 [hep-th]
A.O. Barvinsky, Dark energy and dark matter from nonlocal ghost-free gravity theory. Phys. Lett. B 710, 12 (2012). arXiv:1107.1463 [hep-th]
M. Maggiore, M. Mancarella, Nonlocal gravity and dark energy. Phys. Rev. D 90, 023005 (2014). arXiv:1402.0448 [hep-th]
A.S. Koshelev, L. Modesto, L. Rachwal, A.A. Starobinsky, Occurrence of exact \(R^2\) inflation in non-local UV-complete gravity. JHEP 1611, 067 (2016). arXiv:1604.03127 [hep-th]
R.P. Woodard, The case for nonlocal modifications of gravity. Universe 4, 88 (2018). arXiv:1807.01791 [gr-qc]
Y.D. Li, L. Modesto, L. Rachwal, Exact solutions and spacetime singularities in nonlocal gravity. JHEP 1512, 173 (2015). arXiv:1506.08619 [hep-th]
L. Modesto, L. Rachwal, Nonlocal quantum gravity: a review. Int. J. Mod. Phys. D 26, 1730020 (2017)
C. Burgess, Intro to Effective Field Theories and Inflation. arXiv:1711.10592 [hep-th]
M. Ruhdorfer, J. Serra, A. Weiler, Effective Field Theory of Gravity to All Orders. arXiv:1908.08050 [hep-ph]
A. Codello, R.K. Jain, On the covariant formalism of the effective field theory of gravity and leading order corrections. Class. Quant. Grav. 33, 225006 (2016). arXiv:1507.06308 [gr-qc]
A. Codello, R.K. Jain, On the covariant formalism of the effective field theory of gravity and its cosmological implications. Class. Quant. Grav. 34, 035015 (2017). arXiv:1507.07829 [astro-ph.CO]
B.S. DeWitt, Approximate effective action for quantum gravity. Phys. Rev. Lett. 47, 1647 (1981)
D.F. Litim, Optimized renormalization group flows. Phys. Rev. D 64, 105007 (2001). arXiv:hep-th/0103195
S. Nagy, B. Fazekas, Z. Peli, K. Sailer, I. Steib, Regulator dependence of fixed points in quantum Einstein gravity with \(R^2\) truncation. Class. Quant. Grav. 35, 055001 (2018). arXiv:1707.04934 [hep-th]
O. Zanusso, L. Zambelli, G.P. Vacca, R. Percacci, Gravitational corrections to Yukawa systems. Phys. Lett. B 689, 90 (2010). arXiv:0904.0938 [hep-th]
A.O. Barvinsky, A.Y. Kamenshchik, I.P. Karmazin, Renormalization group for nonrenormalizable theories: Einstein gravity with a scalar field. Phys. Rev. D 48, 3677 (1993). arXiv:gr-qc/9302007
J.F. Donoghue, Leading quantum correction to the Newtonian potential. Phys. Rev. Lett. 72, 2996 (1994). arXiv:gr-qc/9310024
N.E.J. Bjerrum-Bohr, J.F. Donoghue, B.R. Holstein, Quantum gravitational corrections to the nonrelativistic scattering potential of two masses. Phys. Rev. D 67, 084033 (2003). (Erratum: Phys. Rev. D 71 (2005) 069903). arXiv:hep-th/0211072
I.B. Khriplovich, G.G. Kirilin, Quantum long range interactions in general relativity. J. Exp. Theor. Phys. 98, 1063 (2004)
D.F. Litim, J.M. Pawlowski, Perturbation theory and renormalization group equations. Phys. Rev. D 65, 081701 (2002). arXiv:hep-th/0111191 [hep-th]
D.F. Litim, J.M. Pawlowski, Completeness and consistency of renormalisation group flows. Phys. Rev. D 66, 025030 (2002). arXiv:hep-th/0202188 [hep-th]
I.L. Buchbinder, S.D. Odintsov, I.L. Shapiro, Effective Action in Quantum Gravity (IOP Publishing Ltd., New York, 1992)
G. de Berredo-Peixoto, I.L. Shapiro, Higher derivative quantum gravity near four dimensions. Braz. J. Phys. 35, 1099 (2005)
I.L. Shapiro, P. Morais Teixeira, A. Wipf, On the functional renormalization group for the scalar field on curved background with non-minimal interaction. Eur. Phys. J. C 75, 262 (2015). arXiv:1503.00874 [hep-th]
L. Modesto, L. Rachwal, Super-renormalizable and finite gravitational theories. Nucl. Phys. B 889, 228 (2014). arXiv:1407.8036 [hep-th]
L. Modesto, L. Rachwal, Universally finite gravitational and gauge theories. Nucl. Phys. B 900, 147 (2015). arXiv:1503.00261 [hep-th]
Acknowledgements
We thank Roberto Percacci, Aleksandr Pinzul, Ilya Shapiro, Alberto Tonero, and Omar Zanusso for valuable discussions. This work was supported in part by the Grant-in-Aid for Scientific Research Fund of the JSPS (C) No. 16K05331. L.R. was supported from ESIF, EU Operational Programme Research, Development and Education No. CZ\(.02.2.69/0.0/0.0/16_{-}027/0008465\).
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Appendices
A Self-adjointness of the Hessian
When there are first derivative terms in the Hessian and the coefficients depend on the coordinates, there is an ambiguity in how to write the Hessian in the matrix form. We remove this ambiguity by imposing the self-adjointness condition. If we use the metric \({{{\mathcal {G}}}}\) in field space, the self-adjointness of the kinetic operator \(\Delta \) means that
In the usual case without first derivative terms, this requirement simply gives the symmetric matrix for \(\Delta \), but this is not true when there are first derivative terms.
We illustrate this by consideration of some simple examples. In the action (3.14), we have the terms with first derivative:
To clearly formulate this, it is necessary to distinguish the unprimed (left) and primed (right) fields. We rewrite this as
Here, in the second line of (A.3), we added the surface terms after the partial integration. This is the same as (A.2) if we identify the fields with and without prime upon partial integration. We get rid of the derivatives on the unprimed fields by partial integration and then what we get is
which is the same as (A.3) in which fields with and without primes are interchanged. Eq. (A.3) is written in the matrix form as in (3.18)–(3.21), which is therefore self-adjoint even though it does not look symmetric. It is important that in the process we use only integration by parts and do not exchange fields unawarely.
Another example is the \(h-\varphi \) mixing term in the action (3.58):
Let us rewrite (A.5) as
This is the same as (A.5) if we identify the fields with and without prime upon integration by parts. Upon this, we get
This is the same expression as (A.6) in which fields with and without primes are interchanged. Eq. (A.6) is written in the matrix form as in (3.60), which is again self-adjoint. Other terms are similar.
B Scalar basis
When we have a complex scalar \(\phi \), we have two different ways to represent it. One is to decompose the scalar field into two real fields
Suppose we have the action in terms of the real fields:
The path integrals over the complex scalar field \(\phi \) and its conjugate \(\phi ^*\) produce the factor \( (\det M)^{-1/2}\). Note that this matrix is of the size \(2\times 2\).
Now noting that
then (B.2) can be rewritten as
Though we have a “complex” field here, \(\psi ^\dagger \) and \(\psi \) are not independent (\(\phi \) and \(\phi ^*\) are independent). So the path integral over \(\psi \) yields
the same as the real field basis. We can use either basis whichever convenient. If the action has only \(\phi ^*\)-\(\phi \) terms, we may simply use action of the form \(\phi ^* M \phi \), but this is not the case with our action in section 3.4. In the text, we employ the “complex” basis.
C Explicit forms of tensors and their traces
1.1 C.1 Scalar \(\mathbf{Y}^2\)
Here we collect the explicit form of components of \(\mathbf{Y}^2\) in (3.79).
1.2 C.2 Tensor \({\tilde{\Omega }}_{\rho \sigma }\)
The components of \(\tilde{{{\varvec{\Omega }}}}_{\rho \sigma }\) in (3.90) are
Here it is understood that the antisymmetrization is made only for the indices \(\rho \) and \(\sigma \) and it has the weight 1/2. We have also used the relations
1.3 C.3 Traces of various tensors
In this part we collect internal traces of various tensors, which we needed in Sect. 4. In particular, they are essential information to compute explicitly results in formula (4.2).
We find that the trace of \(\tilde{{\mathbf{W}}}\) is
The trace of \(\tilde{{\mathbf{W}}}^2\) is
The trace of \(\tilde{{\varvec{\Omega }}}^2=\tilde{\varvec{\Omega }}_{\rho \sigma }\tilde{{\varvec{\Omega }}}^{\rho \sigma }\) is
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Ohta, N., Rachwał, L. Effective action from the functional renormalization group. Eur. Phys. J. C 80, 877 (2020). https://doi.org/10.1140/epjc/s10052-020-8325-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-8325-8