$U(1)_{B-L}$ extension of the standard model with $S_3$ symmetry

Abstract

We propose a renormalizable $B-L$ Standard Model (SM) extension based on $S_3$ symmetry which successfully accommodates the observed fermion mass spectra and flavor mixing patterns as well as the CP violating phases. The small masses for the light active neutrinos are generated through a type I seesaw mechanism. The obtained physical parameters in the lepton sector are well consistent with the global fit of neutrino oscillations (Esteban et al. in J High Energy Phys 01:106, 2019) for both normal and inverted neutrino mass orderings. The model also predicts effective neutrino mass parameters of ${\langle m_{ee}\rangle }= {1.02\times 10^{-2}}\,{\mathrm {eV}},\, m_{\beta }= {1.25}\times 10^{-2}\,{\mathrm {eV}}$ for normal hierarchy (NH) and ${\langle m_{ee}\rangle } ={5.03}\times 10^{-2}\, {\mathrm {eV}},\, m_{\beta } ={5.05}\times 10^{-2}\, {\mathrm {eV}}$ for inverted hierarchy (IH) which are all well consistent with the future large and ultra-low background liquid scintillator detectors which has been discussed in Ref. (Zhao et al. in Chin Phys C 41(5):053001, 2017) or the limit of the effective neutrino mass can be reached by the planning of future experiments. The model results are consistent with and successfully accommodate the recent experimental values of the physical observables of the quark sector, including the six quark masses, the quark mixing angles and the CP violating phase in the quark sector.

1 Introduction

Although highly successful in describing most of the elementary particle phenomena at low energy scale, the SM leaves many unresolved issues such as the large hierarchy of charged fermion masses, the fermion mixings, and the CP-violating phases, etc. Therefore, these issues can be considered as important evidences of physics beyond the SM.

Among the possible extensions of the SM, the one with an extra $U(1)_{B-L}$ gauge symmetry is one of promising extensions which has been considered in Refs. [1,2,3,4,5,6,7,8]. In this type of model, the presence of three right-handed neutrinos is essential to cancel the gauge and the mixed gauge-gravitational anomalies. However, it does not provide a natural explanation for fermion mixings.

Experimentally, the best-fit values for neutrino squared mass splittings, leptonic mixing angles and the Dirac CP violating phase, for both normal and inverted mass hierarchies with Super-Kamiokande atmospheric (wSK-atm) neutrino data, are given in Ref. [9]:

$$\begin{aligned}&\Delta m^2_{21}=7.39 \times 10^{-5} {{\mathrm {eV}}}^2,\quad \sin ^2\theta _{12}=0.310,\nonumber \\&\quad \sin ^2\theta _{23}=0.582,\nonumber \\&\Delta m^2_{31}= 2.525\times 10^{-3}{{\mathrm {eV}}}^2 \,{\mathrm { (NH)}},\nonumber \\&\quad \sin ^2\theta _{13}=0.02240\, {\mathrm { (NH)}}, \delta = 217^\circ \, {\mathrm {(NH)}},\nonumber \\&\Delta m^2_{32}= -2.512 \times 10^{-3}{{\mathrm {eV}}}^2 \,{\mathrm { (IH)}},\nonumber \\&\quad \sin ^2\theta _{13}=0.02263 \, {\mathrm {(IH)}},\, \delta = 280^\circ \,{\mathrm {(IH)}}. \end{aligned}$$

(1)

Table 1 Fermion and scalar contents of the model and the charge assignment ($\alpha =2,3$)

The discrete symmetry has revealed many outstanding advantages in explaining the observed pattern of SM fermionic masses and mixing angles given in Eq. (1). There have been many models based on discrete symmetries, see for instance, Refs. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. However, in most of these papers, the fermion masses and mixings are generated from non-renormalizable interactions or at loop levels. The renormalizable $B-L$ model with $S_3$ symmetry was first proposed by Gömez-Izquierdo and Mondragön [52], however, there are substantial differences between the work in Ref. [52] and our current work as follows¹: (a) Ref. [52] contains two other symmetries $Z_2$ and $Z^e_2$ compared to $S_3$ symmetry where the couplings ${\bar{L}} H e_{R}$ and ${\bar{L}} {\widetilde{H}} N$ are prevented by $Z^e_2$ to obtain diagonal charged and neutrinos Dirac mass matrices but it does not modify the Majorana mass matrix form; (b) in Ref. [52], the Yukawa coupling constant $y^q_2$ is assumed equal to zero ($a_q = 0$) which corresponds to an extra discrete symmetry (differs from the existing symmetries $Z_2$, $Z^e_2$ and $S_3$) is included to prohibit the Yukawa interaction term ${\bar{Q}}_{1L} H_3 d_{1R}+{\bar{Q}}_{2L} H_3 d_{2R}$; (c) in Ref. [52] the inverted and degenerate neutrino mass hierarchies were considered, however, the recent experimental data [9, 53] favors the inverted or normal hierarchy; (d) The Dirac CP-violating phase was also not predicted by [52]; (e) The quark mass matrices ${{\mathbb {M}}}_{u,d}$ in our model seem simpler in the sense that two entries “23” and “32” are vanished.

The aim of this paper is to construct the renormalizable $B-L$ extension of the SM. In this work, the first generation of quarks and leptons are put in ${{\underline{1}}}$ while the two others are put in ${{\underline{2}}}$ under $S_3$ symmetry. This paper is organized as follows. In Sect. 2 we present a simple SM extension by adding $U{(1)}_{B-L}$ and $S_3$ symmetries. In Sect. 3 we present the lepton sector of the model and introduce necessary Higgs fields responsible for lepton masses and mixings. Section 4 deals with quark mass and mixing. The implications of our model in the Higgs diphoton decay rate are analyzed in Sect. 5. We conclude in Sect. 6. Appendix A provides a brief description of the Clebsch–Gordan coefficients for the $S_3$ group.

2 The model

The electroweak sector of the SM is supplemented by the $S_3\otimes Z_4$ flavor symmetry and a gauge symmetry ${\mathrm {U}}(1)_{B-L}$. To the particle content, we add three right-handed neutrinos ($\nu _{iR}$), two $SU(2)_L$ scalar doublets $H^{\prime }, H^{\prime \prime }$ with $B-L=0$ put in ${{\underline{1}}}^{\prime }$ and ${{\underline{2}}}$ under $S_3$, respectively, and one flavon $\phi$ with $B-L=2$ put in ${{\underline{2}}}$ under $S_3$. The particle content of the model is then given in Table 1.

Since there are many Yukawa couplings in Higgs potential, it is easy to arrange a suitable Higgs potential. In order to generate the remarkable fermion mixing pattern, from the potential minimization conditions of the Higgs potential as presented in Appendix B, we choose the VEVs of scalar fields as follows

$$\begin{aligned} \langle H \rangle= & {} (0\,v_H)^T, \langle H^{\prime } \rangle =(0\,v_{H^{\prime }})^T, \langle H^{\prime \prime } \rangle =(\langle H^{\prime \prime }_1 \rangle , \langle H^{\prime \prime }_1 \rangle ), \nonumber \\ \langle H^{\prime \prime }_1 \rangle= & {} (0\,v_{H^{\prime \prime }})^T, \langle \phi \rangle =(\langle \phi _1 \rangle , \langle \phi _1 \rangle ), \langle \phi _1 \rangle =v_\phi . \end{aligned}$$

(2)

In order to show that the alignment in Eq. (2) is a automatical solution from the minimization conditions of $V_{\mathrm {\mathrm {total}}}$, in the system of minimization equations, let us put $v^*_{H}=v_{H},\, v^*_{H^{\prime }}=v_{H^{\prime }},\, v^*_{H^{\prime \prime }}=v_{H^{\prime \prime }}$ and $v^*_{\phi }=v_{\phi }$, which reduces to

$$\begin{aligned}&\mu _H^2 + 2 \lambda _H v_H^2 + (\lambda ^{H H^{\prime }}_{1} + \lambda ^{H H^{\prime }}_{2}) v_{H^{\prime }}^2 + 2 (\lambda ^{H H^{\prime \prime }}_1 \nonumber \\&\quad + \lambda ^{H H^{\prime \prime }}_2) v_{H^{\prime \prime }}^2 + 2 (\lambda ^{H \phi }_1 + \lambda ^{H \phi }_2) v_{\phi }^2=0, \end{aligned}$$

(3)

$$\begin{aligned}&\mu _{H^{\prime }}^2 + (\lambda ^{H H^{\prime }}_1 + \lambda ^{H H^{\prime }}_2) v_H^2 + 2 \left[ \lambda ^{H^{\prime }} v_{H^{\prime }}^2 \right. \nonumber \\&\quad \left. + (\lambda ^{H^{\prime } H^{\prime \prime }}_1 + \lambda ^{H^{\prime } H^{\prime \prime }}_2) v_{H^{\prime \prime }}^2 + (\lambda ^{H^{\prime } \phi }_1 + \lambda ^{H^{\prime } \phi }_2) v_{\phi }^2\right] =0, \end{aligned}$$

(4)

$$\begin{aligned}&\mu _{H^{\prime \prime }}^2 + (\lambda ^{H H^{\prime \prime }}_1 + \lambda ^{H H^{\prime \prime }}_2) v_H^2 + (\lambda ^{H^{\prime }H^{\prime \prime }}_1 + \lambda ^{H^{\prime }H^{\prime \prime }}_2) v_{H^{\prime }}^2 \nonumber \\&\quad + 2 (2 \lambda ^{H^{\prime \prime }}_1 + \lambda ^{H^{\prime \prime }}_3) v_{H^{\prime \prime }}^2 \nonumber \\&\quad + (2 \lambda ^{H^{\prime \prime }\phi }_1 + \lambda ^{H^{\prime \prime }\phi }_3 + 2 \lambda ^{H^{\prime \prime }\phi }_4 + \lambda ^{H^{\prime \prime }\phi }_6) v_{\phi }^2 {-\mu ^2_{SB}}=0, \end{aligned}$$

(5)

$$\begin{aligned}&\mu _{\phi }^2 + (\lambda ^{H\phi }_1 + \lambda ^{H\phi }_2) v_H^2 + (\lambda ^{H^{\prime }\phi }_1 +\lambda ^{H^{\prime }\phi }_2) v_{H^{\prime }}^2 \nonumber \\&\quad + (2 \lambda ^{H^{\prime \prime }\phi }_+ \lambda ^{H^{\prime \prime }\phi }_3 + 2 \lambda ^{H^{\prime }\phi }_4 +\lambda ^{H^{\prime }\phi }_6) v_{H^{\prime \prime }}^2 \nonumber \\&\quad + 2 (2 \lambda ^{\phi }_1 + \lambda ^{\phi }_3) v_{\phi }^2=0. \end{aligned}$$

(6)

The system of Eqs. (3)–(6) always give the solution ($v_H,\, v_{H^{\prime }},$$v_{H^{\prime \prime }}, v_\phi$) as chosen in Eq. (2). It is noted that this aligned is only one solution to have the desirable results.

Note for the low energy observables, but lowering that scale, for example at the TeV scale, will imply lower values for the neutrino Yukawa couplings needed to reproduce the tiny values of the light active neutrino masses. The scale of breaking of the $B-L$ symmetry does not have implications in the quark sector given that the only scalar field charged under this symmetry is a gauge singlet that only appear in the Yukawa terms for the right handed Majorana neutrinos. Independently on the magnitude of the $B-L$ breaking scale, the vacuum expectation values of the Higgs doublets should satisfy the relation $v^2_{H}+v^2_{H^{\prime }}+2v^2_{H^{\prime \prime }}=v^2$, with $v=246$ GeV, which is needed to correctly reproduce the measured values of the W and Z gauge boson masses. If the $B-L$/$S_3$ breaking scale is very high, some collider signatures that can be tested in the model are: the production of neutral scalar via gluon fusion mechanism, the associated production of a neutral scalar with a SM gauge boson (via Vector Boson Fusion or Drell–Yan mechanism), the associated production of a charged scalar with a SM gauge boson (via Vector Boson Fusion or Drell–Yan mechanism). Furthermore, flavor violating decay like $t\rightarrow hc$ (h being the 126 GeV Higgs), $h\rightarrow \mu \tau$, $\mu \rightarrow e\gamma$ can be use to constrain the model parameter space. Some low energy observables that can be used to constrain the model are the muon and electron anomalous magnetic moment, the oblique T and S parameters. Rather than avoiding, to make such process below the current experimental limits, some restrictions on the model parameter space need to be imposed, which could be constraints on the Yukawa couplings, on the mixing angles in the scalar sector and large masses for non SM scalars. Besides that, notice that our model has many free parameters, which allows us freedom to assume that the remaining scalars are sufficiently heavy to fulfill the current experimental bounds. Moreover, the loop effects of the heavy scalars contributing to precision observables can be suppressed by making an appropriate choice of the free parameters in the scalar potential. These adjustments do not affect the physical observables in the quark and lepton sectors, which are determined mainly by the Yukawa couplings. A detailed study of the phenomenology of the model is beyond the scope of this paper and is deferred for a future work.

3 Lepton masses and mixings

With the fermion content in Table 1 and the tensor products of $S_3$ group in Appendix A, the charged lepton masses can arise from the couplings of ${\bar{\psi }}_{(\alpha , 1) L} l_{(\alpha , 1)R}$ to scalars, where under $SU(3)_c\times SU(2)_L\times U(1)_Y\times U(1)_{B-L}\times S_3{\times Z_4}$ symmetry, ${\bar{\psi }}_{1L} l_{1R}$ transforms as $({\mathbf {1}}, {\mathbf {2}}, -1/2, 0, {{\underline{1}}, 1})$. Similarly, we have ${\bar{\psi }}_{\alpha L} l_{1 R}\sim ({\mathbf {1}}, {\mathbf {2}}, 1/2, 0, {{\underline{2}}, 1}),\, {\bar{\psi }}_{1 L} l_{\alpha R}\sim ({\mathbf {1}}, {\mathbf {2}}, 1/2, 0, {{\underline{2}}, 1})$ and ${\bar{\psi }}_{\alpha L} l_{\alpha R}\sim ({\mathbf {1}}, {\mathbf {2}}, 1/2, 0, {\underline{1}}+{\underline{1}}^{\prime }+{\underline{2}}, 1)$. Therefore, to generate masses for the charged leptons in the diagonal basis, we need two $SU(2)_L$ scalar fields H and $H^{\prime }$ respectively put in ${\underline{1}}$ and $1^{\prime }$ under $S_3$ as given in Table 1.

The Yukawa interactions in charged lepton sector are:

$$\begin{aligned} -{{\mathcal {L}}}^{clep}_{Y}= & {} h_1{\bar{\psi }}_{1L} H l_{1R} + h_2 \left( {\bar{\psi }}_{\alpha L} l_{\alpha R}\right) _{{{\underline{1}}}} H \nonumber \\&+\, h_3 \left( {\bar{\psi }}_{\alpha L} l_{\alpha R}\right) _{{{\underline{1}}^{\prime }}} H^{\prime }+ {\mathrm {H.c.}} \end{aligned}$$

(7)

With the help of Eqs. (7) and (2), the Lagrangian mass term of the charged leptons can be written in the form:

$$\begin{aligned} -{{\mathcal {L}}}^{\mathrm {mass}}_l=({\bar{l}}_{1L},{\bar{l}}_{2L},{\bar{l}}_{3L}) M_l (l_{1R},l_{2R},l_{3R})^T+ H. c, \end{aligned}$$

(8)

where

$$\begin{aligned} M_l= & {} {\mathrm {diag}}\left( h_1 v_H,\,\, h_2 v_H - h_3 v_{H^{\prime }}, \,\, h_2 v_H + h_3 v_{H^{\prime }} \right) \nonumber \\\equiv & {} {\mathrm {diag}}\left( m_e,\,\ m_\mu {,} \,\, m_\tau \right) , \end{aligned}$$

(9)

which has the diagonal form. Thus, the charged lepton diagonalization matrices are $U_{lL}= U_{lR}=1$ and the lepton mixing matrix depends only on that of the neutrino.

By comparing Eq. (9) with the experimental values for masses of the charged leptons given in Ref. [53], $m_e\simeq 0.51099 \,{\mathrm {MeV}}, m_\mu \simeq 105.65837\,{\mathrm {MeV}}, m_\tau \simeq 1776.86 \,{\mathrm {MeV}}$, we get² $h_1\sim 10^{-5}, h_2 \sim 10^{-2}, h_3\sim 10^{-2}$, i.e, $h_1 \ll h_2 \simeq h_3$.

The neutrino masses arise from the couplings of ${\bar{\psi }}_{i L} \nu _{j R}$ and ${\bar{\nu }}^c_{i R}\nu _{j R} \, (i,j=1,2,3)$ to scalars, where ${\bar{\psi }}_{\alpha L} \nu _{\alpha R} ({\bar{\nu }}^c_{\alpha R}\nu _{\alpha R})$, ${\bar{\psi }}_{\alpha L} \nu _{1 R}\, ({\bar{\nu }}^c_{\alpha R}\nu _{1 R})$ and ${\bar{\psi }}_{1 L} \nu _{1 R}\, ({\bar{\nu }}^c_{1 R}\nu _{1 R})$ transforms as $SU(2)_L$ doublets (singlets) and ${{\underline{1}}+{\underline{1}}^{\prime }+{\underline{2}}, {\underline{2}}}$ and ${{\underline{1}}}$ under $S_3$, respectively. For the known $SU(2)_L$ scalar doublets, available interactions are ${\bar{\psi }}_{1L} {\widetilde{H}} \nu _{1 R}$, $\left( {\bar{\psi }}_{\alpha L} \nu _{\alpha R}\right) _{{{\underline{1}}}}{\widetilde{H}}$ and $\left( {\bar{\psi }}_{\alpha L} \nu _{\alpha R}\right) _{{{\underline{1}}^{\prime }}} \widetilde{H^{\prime }}$ but they only generate Dirac mass terms. To generate Majorana mass terms for neutrinos we will therefore introduce one new $SU(2)_L$ singlets $\phi$ put in ${{\underline{2}}}$ under $S_3$ coupling to ${\bar{\psi }}_{1L}\nu _{1 L}$ and ${\bar{\psi }}_{\alpha L}\nu _{\alpha L}$.

The Yukawa interactions, which are invariant under all the symmetries of the model, in neutrino sector are:

$$\begin{aligned} -{{\mathcal {L}}}^{\nu }_{Y}= & {} \frac{x_1}{2} {\bar{\psi }}_{1 L} {\widetilde{H}} \nu _{1 R} +\frac{x_2}{2} \left( {\bar{\psi }}_{\alpha L} \nu _{\alpha R}\right) _{{{\underline{1}}}}{\widetilde{H}}\nonumber \\&+ \frac{x_3}{2} \left( {\bar{\psi }}_{\alpha L} \nu _{\alpha R}\right) _{{{\underline{1}}^{\prime }}} \widetilde{H^{\prime }}+\frac{y_1}{2} \left( {\bar{\nu }}^c_{\alpha R} \nu _{\alpha R}\right) _{{\underline{2}}}\phi \nonumber \\&+\frac{y_2}{2} \left( {\bar{\nu }}^c_{\alpha R} \nu _{1R}+{\bar{\nu }}^c_{1R}\nu _{\alpha R}\right) _{{\underline{2}}}\phi + {\mathrm {H.c.}} \end{aligned}$$

(10)

With the VEVs given in Eq. (2), we get the Dirac neutrino mass matrix ($M_D$) and the right-handed Majorana neutrino mass matrix ($M_R$) as follows

$$\begin{aligned} M_D= & {} {\mathrm {diag}}\left( a_D, b_{D}-c_D ,\, b_{D}+ c_D\right) , M_R\nonumber \\= & {} \left( \begin{array}{ccc} 0 &{} b_R &{} b_R \\ b_R &{} a_R &{} 0 \\ b_R &{} 0&{} a_R \\ \end{array} \right) , \end{aligned}$$

(11)

where

$$\begin{aligned} a_D= & {} x_1 v_{H}, b_D = x_2 v_{H}, c_D = x_3 v_{H'},\nonumber \\&a_R = y_1 v_\phi , b_R=y_2 v_\phi . \end{aligned}$$

(12)

The effective neutrino mass matrix, obtained through the type-I seesaw mechanism, reads:

$$\begin{aligned} {M}_{\mathrm {eff}}= & {} -M_D^T{M}_R^{-1}M_D=\left( \begin{array}{ccc} {{\mathcal {A}}}_0 &{} -{{\mathcal {B}}}_0 &{} -{{\mathcal {B}}}_0\\ -{{\mathcal {B}}}_0 &{} -{{\mathcal {C}}}_0 &{} {{\mathcal {C}}}_0 \\ -{{\mathcal {B}}}_0 &{} {{\mathcal {C}}}_0 &{} -{{\mathcal {C}}}_0 \\ \end{array} \right) \nonumber \\&+\left( \begin{array}{ccc} 0 &{} a_1 &{} -a_1\\ a_1 &{} -b_1+a_2 &{} -b_1 \\ -a_1 &{} -b_1 &{} -b_1-a_2 \\ \end{array} \right) \nonumber \\\equiv & {} M_0 +\delta M, \end{aligned}$$

(13)

where

$$\begin{aligned} {{\mathcal {A}}}_0= & {} \frac{a_D^2 a_R}{2 b_R^2},\quad {{\mathcal {B}}}_0=\frac{a_D b_D}{2 b_R},\quad {{\mathcal {C}}}_0 =\frac{b_D^2}{2 a_R}, \end{aligned}$$

(14)

$$\begin{aligned} a_1= & {} \frac{a_D c_D}{2 b_R},\quad a_2=\frac{b_D c_D}{a_R},\quad b_1= \frac{c_D^2}{2 a_R}. \end{aligned}$$

(15)

It is noted that ${{\mathcal {A}}}_0, {{\mathcal {B}}}_0$ and ${{\mathcal {C}}}_0$ given in Eq. (14) accommodated in the first matrix of Eq. (13) due to the contribution of H and $\phi$ only while the last term in Eq. (13) is deviation from the contribution of $H^{\prime }$ only. If there is no contribution of $H^{\prime }$, the deviations $a_{1,2}$ and $b_{1}$ will vanish and the matrix $M_{\mathrm {eff}}$ in (13) reduces to its first term which generates a $\mu -\tau$ mixing form. Thus, second term in (13) will take the role for a small deviation of $\theta _{13}$ and being responsible for the CP violating phase in the lepton sector.

The first matrix in Eq. (13) has three eigenvalues,

$$\begin{aligned} m^0_{1,2}= & {} \frac{1}{2} \left( {{\mathcal {A}}}_0\pm \sqrt{{{\mathcal {A}}}^2_0+8 {{\mathcal {B}}}_0^2}\right) ,\quad m^0_3=-2 {{\mathcal {C}}}_0, \end{aligned}$$

(16)

and the corresponding lepton mixing matrix takes the form:

$$\begin{aligned} {\mathbb {U}}_0 = \left( \begin{array}{ccc} \cos \theta &{}\sin \theta &{} 0 \\ -\frac{\sin \theta }{\sqrt{2}} &{}\frac{\cos \theta }{\sqrt{2}} &{} \frac{1}{\sqrt{2}} \\ -\frac{\sin \theta }{\sqrt{2}} &{}\frac{\cos \theta }{\sqrt{2}} &{} -\frac{1}{\sqrt{2}} \\ \end{array} \right) , \end{aligned}$$

(17)

where

$$\begin{aligned} \theta= & {} \arcsin \left( \frac{{\mathcal {K}}}{\sqrt{ {\mathcal {K}}^2+2}}\right) ,\quad {\mathcal {K}}=\frac{m^0_1-{{\mathcal {A}}}_0}{{{\mathcal {B}}}_0}=-\frac{m^0_2}{{{\mathcal {B}}}_0}, \end{aligned}$$

(18)

with ${{\mathcal {A}}}_0, {{\mathcal {B}}}_0$ and $m^0_{1,2}$ are defined in Eqs. (14) and (16), respectively.

The matrix ${\mathbb {U}}_0$ in Eq. (17) implies $\theta _{13}=0,\, \theta _{23}=\pi /4$ and $\theta _{12}=\theta$ which was rule out by the recent data.³ However, the contribution of the second term in Eq. (13) will improve this. Indeed, at the first order of perturbation theory, the second matrix in Eq. (13) contributes to both eigenvalues and eigenvectors. In this case, the neutrino masses are given as:

$$\begin{aligned}&m_{1} = m^0_1-2 b_1 \sin ^2\theta , m_{2}=m^0_2- 2b_1 \cos ^2\theta ,\nonumber \\&m_3=m^0_3, \end{aligned}$$

(19)

with $b_{1}$, $m^0_{1,2}$ and $\theta$ are given in Eqs. (15), (16) and (18), respectively. The corresponding lepton mixing matrix becomes:

$$\begin{aligned} {\mathbb {U}}= {\mathbb {U}}_0+\delta {\mathbb {U}}, \end{aligned}$$

(20)

where ${\mathbb {U}}_0$ is defined by (17) and $\delta {\mathbb {U}}$ has the following entries:

$$\begin{aligned} (\delta {\mathbb {U}})_{11}= & {} \frac{2 b_1 \sin ^2\theta \cos \theta }{m^0_1-m^0_2}, (\delta {\mathbb {U}})_{12}=\frac{2b_1\sin \theta \cos ^2\theta }{m^0_2-m^0_1},\nonumber \\ (\delta {\mathbb {U}})_{13}= & {} \frac{(a_2 \cos \theta + \sqrt{2} a_1 \sin \theta )\sin \theta }{m^0_3-m^0_2}\nonumber \\&+ \frac{(a_2 \sin \theta -\sqrt{2} a_1 \cos \theta )\cos \theta }{m^0_1 - m^0_3}, \nonumber \\ (\delta {\mathbb {U}})_{21}= & {} \frac{1}{\sqrt{2}}\left( \frac{ 2b_1 \cos ^2\theta \sin \theta }{m^0_1-m^0_2}+\frac{\sqrt{2} a_1 \cos \theta - a_2 \sin \theta }{m^0_1-m^0_3}\right) ,\nonumber \\ (\delta {\mathbb {U}})_{22}= & {} \frac{1}{\sqrt{2}}\left( \frac{ 2b_1 \cos \theta \sin ^2\theta }{m^0_1-m^0_2}+\frac{\sqrt{2} a_1 \sin \theta + a_2 \cos \theta }{m^0_2-m^0_3}\right) ,\nonumber \\ (\delta {\mathbb {U}})_{23}= & {} \frac{(m^0_2-m^0_1)a_1 \sin \theta \cos \theta }{(m^0_1-m^0_3)(m^0_2-m^0_3)}\nonumber \\&+\frac{a_2}{\sqrt{2}}\left( \frac{\cos ^2\theta }{m^0_3-m^0_2}+\frac{\sin ^2\theta }{m^0_3-m^0_1}\right) ,\nonumber \\ (\delta {\mathbb {U}})_{31}= & {} \frac{1}{\sqrt{2}}\left( \frac{ 2b_1 \cos ^2\theta \sin \theta }{m^0_1-m^0_2}+\frac{a_2 \sin \theta -\sqrt{2} a_1 \cos \theta }{m^0_1-m^0_3}\right) ,\nonumber \\ (\delta {\mathbb {U}})_{32}= & {} \frac{1}{\sqrt{2}}\left( \frac{ 2b_1 \cos \theta \sin ^2\theta }{m^0_1-m^0_2}-\frac{a_2 \cos \theta +\sqrt{2} a_1 \sin \theta }{m^0_2-m^0_3}\right) ,\nonumber \\&\quad (\delta {\mathbb {U}})_{33}=(\delta {\mathbb {U}})_{23}. \end{aligned}$$

(21)

In the three-neutrino framework, lepton mixing angles can be defined via the elements of the neutrino mixing matrix:

$$\begin{aligned} t_{12}= & {} \frac{|{\mathbb {U}}_{12}|}{|{\mathbb {U}}_{11}|},\quad t_{23}=\frac{|{\mathbb {U}}_{23}|}{|{\mathbb {U}}_{33}|},\quad s_{13}={\mathbb {U}}_{13} e^{i \delta }, \end{aligned}$$

(22)

where $t_{12}=s_{12}/c_{12}$, $t_{23}=s_{23}/c_{23}$, $c_{ij}=\cos \theta _{ij}$, $s_{ij}=\sin \theta _{ij}$ with $\theta _{12}$, $\theta _{23}$ and $\theta _{13}$, respectively, being the solar angle, atmospheric angle and the reactor angle and $\delta$ is the Dirac CP violating phase.

From Eqs. (17), (20)–(22), we found that, in both normal and inverted hierarchies, ${\mathbb {U}}_{11}$ and ${\mathbb {U}}_{12}$ depend only on two parameters $\theta , \theta _{12}$:

$$\begin{aligned} {\mathbb {U}}_{11}= & {} \left( \cos \theta + t_{12} \sin \theta \right) ^{-1},\nonumber \\ {\mathbb {U}}_{12}= & {} t_{12} \left( \cos \theta + t_{12} \sin \theta \right) ^{-1}. \end{aligned}$$

(23)

As pointed out in Ref. [9], at $3\sigma$ confidence level, ${\mathbb {U}}_{11} \in (0.797, \, 0.842)$. Thus, we get a value $\cos \theta ={0.831}$ (i.e., $t_{12}={0.670},\, \theta ={33.83}^\circ$) and ${\mathbb {U}}_{12} ={0.557}$, which is consistent with the best-fit value from the global analysis⁴ given in Ref. [9].

Fig. 1

$|{{\mathbb {U}}}_{k i}|$ $(k=2,3; j=1,2,3)$ as functions of $m^0_3$ with $m^0_3\in ({0.051, 0.052})\, {{\mathrm {eV}}}$ in the NH

Furthermore, Eqs. (17), (20)–(22) provide a solution:

$$\begin{aligned} a_1= & {} -\frac{1}{\sqrt{2}}\frac{(m^0_1 - m^0_3) (m^0_2-m^0_3) s_{13} e^{-i \delta }+a_2(m^0_1 - m^0_2) \sin \theta \cos \theta }{(m^0_1- m^0_3)\sin ^2\theta + (m^0_2 -m^0_3)\cos ^2\theta },\nonumber \\ b_1= & {} \frac{(m^0_1 - m^0_2) (\sin \theta -t_{12}\cos \theta )}{\sin (2\theta ) (\cos \theta +t_{12}\sin \theta )},\nonumber \\ a_2= & {} \left\{ \begin{array}{ll} \frac{\alpha - \sqrt{\beta }}{t^2_{23}-1}&{}\quad \hbox {for NH}, \\ \frac{\alpha + \sqrt{\beta }}{t^2_{23}-1}&{}\quad \hbox {for IH}, \end{array} \right. \end{aligned}$$

(24)

where

$$\begin{aligned} \alpha= & {} (t_{23}^2-1)(m^0_1 - m^0_2)\sin \theta \cos \theta s_{13}\cos \delta \nonumber \\&-(t_{23}^2+1)(m^0_1\sin ^2\theta +m^0_2\cos ^2\theta -m^0_3), \nonumber \\ \beta= & {} 4 t^2_{23}(m^0_1\sin ^2\theta +m^0_2\cos ^2\theta -m^0_3)^2\nonumber \\&-(t_{23}^2-1)^2(m^0_1 - m^0_2)^2\sin ^2\theta \cos ^2\theta s^2_{13}\sin ^2\delta . \end{aligned}$$

(25)

Although the global analysis in Ref. [58] shows a hint in favor of the NH over the inverted one at more than $3\sigma$ and the global analysis in Ref. [9] obtain a preference for NH at about $2\sigma$, but, it is the fact that the neutrino mass spectrum is currently unknown and it can be NH or IH depending on the sign of $\Delta m^2_{31}$ [53]. In the model under consideration, both NH and IH can be found in which the model parameters are in good agreement with the global analysis in Ref. [9].

Fig. 2

$\langle m_{ee}\rangle , m_\beta$ and $m^N_{light}$ as functions of $m^0_3$ with $m^0_3 \in ({0.051, 0.052})\, {{\mathrm {eV}}}$ in the NH

3.1 Normal spectrum

By taking the best-fit values for neutrino squared mass splittings, leptonic mixing angles and the Dirac CP violating phase for NH with Super-Kamiokande atmospheric neutrino data as given in Eq. (1), we get a solution⁵:

$$\begin{aligned} m^0_1= & {} {1.56}\sqrt{\alpha _1},\nonumber \\ m^0_2= & {} \frac{\left[ {7.85}\times 10^{-9}-{3.14}\times 10^{-6} (m^0_3)^2-{1.78}\sqrt{\beta _1}\right] \sqrt{\alpha _1}}{{3.39}\times 10^{-3}-{1.34} (m^0_3)^2}, \end{aligned}$$

(26)

where

$$\begin{aligned} \alpha _1= & {} -{1.04}\times 10^{-3}+ {0.411} (m^0_3)^2-{3.26}\times 10^{-7} \beta _1,\nonumber \\ \beta _1= & {} {8.52}\times 10^{-6}-{6.85}\times 10^{-3} (m^0_3)^2 + {1.38} (m^0_3)^4.\nonumber \\ \end{aligned}$$

(27)

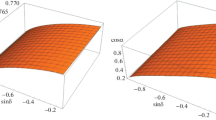
Now, ${{\mathbb {U}}}_{2i}$ and ${{\mathbb {U}}}_{3i}\, (i=1,2,3)$ depend only on $m^0_{3}$. In the NH, the estimated value of $m_3$ is [53] $m_3\simeq 0.0506 \, {{\mathrm {eV}}}$ thus we find an allowed region of $m^0_{3}$ that can reach the constraint on the absolute values of the entries of the lepton mixing matrix given in Ref. [9] which has been depicted in Fig. 1.

In the NH, $m_1< m_2<m_3$ thus $m_1\equiv m^N_{light}$ is the lightest neutrino mass. The effective neutrino masses governing the beta decay and neutrinoless double beta decay [59,60,61,62,63] $m_{\beta } =\left( \sum ^3_{i=1} \left| U_{ei}\right| ^2 m_i^2 \right) ^{1/2}, \langle m_{ee}\rangle = \left| \sum ^3_{i=1} U_{ei}^2 m_i \right|$ and $m^N_{light}$ as functions of $m^0_3$ has been plotted in Fig. 2.

In the case $m^0_3={0.051}\, {{\mathrm {eV}}}$ the other parameters are found in Table 2.

The absolute neutrino mass is found to be $\sum _{i=1}^3 m_i={7.2}\times 10^{-2} \,{{\mathrm {eV}}}$ which is well consistent with the strongest bound from cosmology, $\sum m_\nu < 0.078 \, {{\mathrm {eV}}}$ [64]. Furthermore, the effective neutrino masses $m_{\beta } ={1.25}\times 10^{-2}\,{{\mathrm {eV}}}$ and $\langle m_{ee}\rangle ={1.02\times 10^{-2}}\,{{\mathrm {eV}}}$ which are well consistent with the results in Ref. [65]. The magnitude of the elements of the leptonic mixing matrix in Eq. (20) then takes the form:

$$\begin{aligned} \left| {\mathbb {U}}^N \right| =\left( \begin{array}{c@{\quad }c@{\quad }c} 0.83{1}&{} 0.55{7}&{} 0.1{5} \\ 0.29{6}&{} 0.58{7}&{} 0.76{5} \\ 0.49{9}&{} 0.5{90}&{} 0.64{9} \\ \end{array}\right) , \end{aligned}$$

(28)

which is consistent with the constraint on the absolute values of the entries of the lepton mixing matrix given in Ref. [9]. The Jarlskog invariant is $J^N_{CP}=\mathrm {Im}({\mathbb {U}}_{23} {\mathbb {U}}^*_{13} {\mathbb {U}}_{12} {\mathbb {U}}^*_{22}) = -0.0{245}.$ The resulting effective neutrino mass parameter ${\langle m_{ee}\rangle }$ for normal hierarchy is below the upper bound arising from present $0\nu \beta \beta$ decay experiments. However, it is very well consistent with the future large and ultra-low background liquid scintillator detectors which has been discussed in Ref. [66] or the $\mathrm {meV}$ limit of the effective neutrino mass can be reached by the planning of future experiments [67,68,69,70,71,72,73,74].

Table 2 The model parameters in the case $m^0_3={0.051}\, {{\mathrm {eV}}}$ in NH

3.2 Inverted spectrum

Similar to the normal spectrum, taking the best-fit values of neutrino oscillation parameters for IH with Super-Kamiokande atmospheric neutrino data as given in Eq. (1), we get a solution⁶:

$$\begin{aligned} m^{0}_1= & {} -{1.5}\times 10^{-6} m^0_2 + {1.74}\sqrt{\alpha _2}, m^0_3 ={0.356}\sqrt{\beta _2}, \end{aligned}$$

(29)

with

$$\begin{aligned} \alpha _2= & {} {0.331} (m^0_2)^2- {2.45}\times 10^{-5},\nonumber \\ \beta _2= & {} -{1.98}\times 10^{-2}+ {7.88} (m^0_2)^2 -{2.83} \times 10^{-5} m^0_2\sqrt{\alpha _2}.\nonumber \\ \end{aligned}$$

(30)

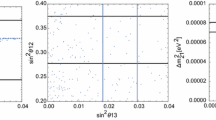
The elements of the lepton mixing matrix ${\mathbb {U}}^I_{2i}$ and ${\mathbb {U}}^{{I}}_{3i}\,(i=1,2,3)$ depend only on $m^0_{2}$. In the IH, the estimated value [53] of $m_2$ is $0.0504 \, {{\mathrm {eV}}}$ thus we find an allowed region of $m^0_{2}$ that can reach the constraint on the absolute values of the entries of the lepton mixing matrix given in Ref. [9] which has been depicted in Fig. 3.

Fig. 3

$|U_{k i}| \, (k=2,3; j=1,2,3)$ as functions of $m^0_2$ with $m^0_2\in ({0.051, 0.052})\, {{\mathrm {eV}}}$ in the IH

Fig. 4

$\langle m_{ee}\rangle , m_\beta$ and $m^I_{light}$ as functions of $m^0_2$ with $m^0_2 \in ({0.051, 0.052})\, {{\mathrm {eV}}}$ in the IH

In the IH, $m_3< m_1<m_2$ thus $m_3\equiv m^I_{light}$ is the lightest neutrino mass. The effective neutrino masses governing the beta decay and neutrinoless double beta decay and $m^I_{light}$ as functions of ${m^0_2}$ has been plotted in Fig. 4.

In the case $m^0_2={0.051}\, {{\mathrm {eV}}}$ the other parameters are found in Table 3.

The magnitude of the leptonic mixing matrix in Eq. (20) then takes the form:

$$\begin{aligned} \left| {\mathbb {U}}^I \right| =\left( \begin{array}{c@{\quad }c@{\quad }c} 0.83{1}&{} 0.55{7}&{} 0.1{5} \\ 0.38{7}&{} 0.53{2}&{} 0.76{5} \\ 0.4{2}&{} 0.64{9}&{} 0.64{9} \end{array}\right) , \end{aligned}$$

(31)

which is consistent with the constraint on the absolute values of the entries of the lepton mixing matrix given in Ref. [9]. The resulting effective neutrino mass parameter for inverted hierarchy is very well consistent with the future large and ultra-low background liquid scintillator detectors which has been discussed in Ref. [66] or the ${\mathrm {meV}}$ limit of the effective neutrino mass can be reached by the above mentioned future experiments [67,68,69,70,71,72,73,74].

4 Quark mass and mixing

The Yukawa interactions in quark sector are:

Table 3 Some model parameters in the case ${m^0_2=0.051\, {{\mathrm {eV}}}}$ in IH

$$\begin{aligned} -{{\mathcal {L}}}_{q}= & {} h_{1u} ({\bar{Q}}_{1 L} {\widetilde{H}})_{{{\underline{1}}}} u_{1 R} + h_{2u} ({\bar{Q}}_{\alpha L} {\widetilde{H}})_{{{\underline{2}}}} u_{\alpha R}\nonumber \\&+h_{3u} ({\bar{Q}}_{\alpha L}\widetilde{H^{\prime }})_{{{\underline{2}}}} u_{\alpha R}\nonumber \\&+h_{4u} ({\bar{Q}}_{1 L} {\widetilde{H}}^{\prime \prime })_{{{\underline{2}}}} u_{\alpha R} + h_{5u}({\bar{Q}}_{\alpha L} {\widetilde{H}}^{\prime \prime })_{{{\underline{1}}}} u_{1 R}\nonumber \\&+ h_{1d} ({\bar{Q}}_{1 L}H)_{{{\underline{1}}}} d_{1R}+h_{2d} ({\bar{Q}}_{\alpha L} H)_{{{\underline{2}}}} d_{\alpha R}\nonumber \\&+ h_{3d} ({\bar{Q}}_{\alpha L} H^{\prime })_{{{\underline{2}}}} d_{\alpha R} \nonumber \\&+ h_{4d} ({\bar{Q}}_{1 L} H^{\prime \prime })_{{{\underline{2}}}} d_{\alpha R}+h_{5d}({\bar{Q}}_{\alpha L} H^{\prime \prime })_{{{\underline{2}}}} d_{1R}+ {\mathrm {H.c.}} \nonumber \\ \end{aligned}$$

(32)

With the VEV alignments of $H, H^{\prime }$ and $H^{\prime \prime }$ in Eq. (2), the mass Lagrangian of quarks reads

$$\begin{aligned} -{{\mathcal {L}}}^{\mathrm {mass}}_q= & {} h_{1u} v^*_H {\bar{u}}_{1 L} u_{1R}+(h_{2u} v^*_H +h_{3u} v^*_{H^{\prime }}){\bar{u}}_{2 L} u_{2R}\nonumber \\&+(h_{3u} v^*_{H^{\prime }}-h_{2u} v^*_H){\bar{u}}_{3 L} u_{3R}\nonumber \\&+ h_{4u}v^*_{H^{\prime \prime }}({\bar{u}}_{1 L} u_{3 R}+{\bar{u}}_{1 L} u_{2 R}) \nonumber \\&+h_{5u}v^*_{H^{\prime \prime }}({\bar{u}}_{3L} u_{1R}+{\bar{u}}_{2L} u_{1R})\nonumber \\&+ h_{1d} v_H {\bar{d}}_{1 L} d_{1R} +(h_{2d} v_H +h_{3d} v_{H^{\prime }}){\bar{d}}_{2 L} d_{2R}\nonumber \\&+(h_{3d} v_{H^{\prime }}-h_{2d} v_H){\bar{d}}_{3 L} d_{3R}\nonumber \\&+h_{4d} v_{H^{\prime \prime }}({\bar{u}}_{1 L} d_{3 R}+{\bar{u}}_{1 L} d_{2 R}) \nonumber \\&+h_{5d} v_{H^{\prime \prime }}({\bar{u}}_{3L} d_{1R}+{\bar{u}}_{2L} d_{1R})+{\mathrm {H.c.}}\nonumber \\\equiv & {} ({\bar{u}}_{1L},{\bar{u}}_{2L},{\bar{u}}_{3L}) {\mathbb {M}}_u (u_{1R}, u_{2R}, u_{3R})^T\nonumber \\&+({\bar{d}}_{1L},{\bar{d}}_{2L},{\bar{d}}_{3L}) {\mathbb {M}}_d (d_{1R}, d_{2R}, d_{3R})^T+{\mathrm {H.c.,}}\nonumber \\ \end{aligned}$$

(33)

where ${\mathbb {M}}_{u}$ and ${\mathbb {M}}_{d}$ take the form:

$$\begin{aligned} {\mathbb {M}}_{u}= & {} \left( \begin{array}{ccc} a_{1u}&{} a_{4u} &{} a_{4u} \\ a_{5u}&{} a_{2u} + a_{3u}&{} 0 \\ a_{5u}&{} 0 &{} -a_{2u} + a_{3u} \end{array}\right) ,\nonumber \\ {\mathbb {M}}_{d}= & {} \left( \begin{array}{ccc} a_{1d}&{} a_{4d} &{} a_{4d} \\ a_{5d}&{}a_{2d} + a_{3d}&{} 0 \\ a_{5d}&{}0 &{}-a_{2d} + a_{3d} \end{array}\right) , \end{aligned}$$

(34)

with

$$\begin{aligned} a_{1u}= & {} h_{1u} v^*_H, a_{2u}= h_{2u} v^*_{H}, a_{3u}= h_{3u} v^*_{H^{\prime }},\nonumber \\&\quad a_{4u}= h_{4u} v^*_{H^{\prime \prime }}, a_{5u}= h_{5u} v^*_{H^{\prime \prime }}, \nonumber \\ a_{1d}= & {} h_{1d} v_H, a_{2d}= h_{2d} v_{H}, a_{3d}= h_{3d} v_{H^{\prime }},\nonumber \\&\quad a_{4d} = h_{4d} v_{H^{\prime \prime }}, a_{5d} = h_{5d} v_{H^{\prime \prime }}. \end{aligned}$$

(35)

It is noted that without contribution of $H^{\prime \prime }$, the matrices ${\mathbb {M}}_{u}, {\mathbb {M}}_{d}$ in Eq. (34) become diagonal ones, i.e, the quark mixing matrices are identity matrices, however, the quark masses can well fit to the experimental data given in Ref. [53].

The quark mass matrices satisfy the following relation:

$$\begin{aligned} M_qM^{\dagger }_q= & {} \left( \begin{array}{ccc} X_q &{} e^{i \theta _q} Y_q &{} e^{i \psi _q} Z_q \\ e^{-i \theta _q} Y_q &{} R_q &{} W_q \\ e^{i \psi _q} Z_q &{} W_q &{} S_q \\ \end{array} \right) , \end{aligned}$$

(36)

where

$$\begin{aligned} X_q= & {} x_{1q}^2+2 x_{4 q}^2,\quad W_q=x^2_{5q},\nonumber \\ e^{i \theta _q}Y_q= & {} e^{-i \left( \kappa _{2 q}-\kappa _{4 q}\right) } x_{2 q} x_{4 q}\nonumber \\&+e^{-i \left( \kappa _{3 q}-\kappa _{4 q}\right) } x_{3 q} x_{4 q}+e^{i \left( \kappa _{1q}-\kappa _{5 q}\right) } x_{1q} x_{5 q},\nonumber \\ e^{i \psi _q} Z_q= & {} -e^{-i \left( \kappa _{2 q}-\kappa _{4 q}\right) } x_{2 q} x_{4 q}+e^{-i \left( \kappa _{3 q}-\kappa _{4 q}\right) } x_{3 q} x_{4 q}\nonumber \\&+e^{i \left( \kappa _{1q}-\kappa _{5 q}\right) } x_{1q} x_{5 q},\nonumber \\ R_q= & {} x_{2 q}^2+2 \cos \left( \kappa _{2 q}-\kappa _{3 q}\right) x_{3 q} x_{2 q}+x_{3 q}^2+x_{5 q}^2,\nonumber \\ S_q= & {} x_{2 q}^2-2 \cos \left( \kappa _{2 q}-\kappa _{3 q}\right) x_{3 q} x_{2 q}+x_{3 q}^2+x_{5 q}^2.\nonumber \\ \end{aligned}$$

(37)

Here $q=u,d$, $x_{iq}=|a_{iq}|$, $\kappa _{iq}=\arg (a_{iq})$ $(i=1,2,\ldots ,5)$ and $X_q$, $Y_q$, $Z_q$, $W_q$, $R_q$ and $S_q$ are real parameters.

In order to fit the measured values of the SM quark masses and CKM parameters given in Refs. [53, 75] as shown in Tables 4 and 5,⁷ we proceed by solving the eigenvalue problem for the SM quark masses. The following solution has been found:

$$\begin{aligned} M_uM^{\dagger }_u= & {} \left( \begin{array}{ccc} 29751. &{} -1920.+761.398 i &{} 1.84494\, -2.91915 i \\ -1920.-761.398 i &{} 145.001 &{} -0.149911 \\ 1.84494\, +2.91915 i &{} -0.149911 &{} 0.0140043 \\ \end{array} \right) \hbox {GeV}^2,\nonumber \\ M_dM^{\dagger }_d= & {} \left( \begin{array}{ccc} 17.2562 &{} -1.79614+0.7086 i &{} 0.0134866\, +0.00200077 i \\ -1.79614-0.7086 i &{} 0.224489 &{} 0.000115589 \\ 0.0134866\, -0.00200077 i &{} 0.000115589 &{} 0.000346993 \\ \end{array} \right) \hbox {GeV}^2. \end{aligned}$$

(38)

Table 4 The best-fit results for quark masses and mixings taken from [76] and [53, 75], respectively. Note that the experimental values of the quark masses are given at the $M_Z$ scale

Table 5 The best-fit results for CKM parameters taken from Refs. [53, 75]

This show that our model is consistent with and successfully accommodate the experimental values of the physical observables of the quark sector: the six quark masses,the quark mixing angles and the CP violating phase in the quark sector.

5 Higgs diphoton decay rate

The decay rate for the $h\rightarrow \gamma \gamma$ process takes the form:

$$\begin{aligned}&\Gamma (h\rightarrow \gamma \gamma )\nonumber \\&\quad =\dfrac{\alpha _{em}^{2}m_{h}^{3}}{ 256\pi ^{3}v^{2}}\left| \sum _{f}a_{hff}N_{C}Q_{f}^{2}F_{1/2}(\rho _{f})+a_{hWW}F_{1}(\rho _{W})\right. \nonumber \\&\left. \qquad +\sum _{k=1,2,3}\frac{C_{hH_{k}^{\pm }H_{k}^{\mp }}v}{2m_{H_{k}^{\pm }}^{2}}F_{0}(\rho _{H_{k}^{\pm }})\right| ^{2}, \end{aligned}$$

(39)

Fig. 5

Correlation of the Higgs diphoton signal strength with the $a_{hWW}$ deviation factor from the SM Higgs-W gauge boson coupling

Fig. 6

Correlation of the Higgs diphoton signal strength with the charged scalar masses

where $\rho _{i}$ are the mass ratios $\rho _{i}=\frac{m_{h}^{2}}{4M_{i}^{2}}$ with $M_{i}=m_{f},M_{W}$; $\alpha _{em}$ is the fine structure constant; $N_{C}$ is the color factor ($N_{C}=1$ for leptons and $N_{C}=3$ for quarks) and $Q_{f}$ is the electric charge of the fermion in the loop. From the fermion-loop contributions we only consider the dominant top quark term. Furthermore, $C_{hH_{k}^{\pm }H_{k}^{\mp }}$ is the trilinear coupling between the SM-like Higgs and a pair of charged Higges, whereas $a_{htt}$ and $a_{hWW}$ are the deviation factors from the SM Higgs-top quark coupling and the SM Higgs-W gauge boson coupling, respectively (in the SM these factors are unity). Such deviation factors are close to unity in our model, which is a consequence of the numerical analysis of its scalar, Yukawa and gauge sectors.

Furthermore, $F_{1/2}(z)$ and $F_{1}(z)$ are the dimensionless loop factors for spin-1/2 and spin-1 particles running in the internal lines of the loops. They are given by:

$$\begin{aligned} F_{1/2}(z)&=2(z+(z-1)f(z))z^{-2}, \end{aligned}$$

(40)

$$\begin{aligned} F_{1}(z)&=-2(2z^{2}+3z+3(2z-1)f(z))z^{-2}, \end{aligned}$$

(41)

$$\begin{aligned} F_{0}(z)&=-(z-f(z))z^{-2}, \end{aligned}$$

(42)

with

$$\begin{aligned} f(z)=\left\{ \begin{array}{ll} \arcsin ^{2}\sqrt{2} &{} \quad \text {for}\ z\le 1 \\ -\frac{1}{4}\left( \ln \left( \frac{1+\sqrt{1-z^{-1}}}{1-\sqrt{1-z^{-1}} -i\pi }\right) ^{2}\right) &{} \quad \text {for}\ z>1 \end{array} \right. \end{aligned}$$

(43)

In order to study the implications of our model in the decay of the 126 GeV Higgs into a photon pair, one introduces the Higgs diphoton signal strength $R_{\gamma \gamma }$, which is defined as:

$$\begin{aligned} R_{\gamma \gamma }= & {} \frac{\sigma (pp\rightarrow h)\Gamma (h\rightarrow \gamma \gamma )}{\sigma (pp\rightarrow h)_{SM}\Gamma (h\rightarrow \gamma \gamma )_{SM}}\nonumber \\\simeq & {} a_{htt}^{2}\frac{\Gamma (h\rightarrow \gamma \gamma )}{\Gamma (h\rightarrow \gamma \gamma )_{SM}}. \end{aligned}$$

(44)

That Higgs diphoton signal strength, normalizes the $\gamma \gamma$ signal predicted by our model in relation to the one given by the SM. Here we have used the fact that in our model, single Higgs production is also dominated by gluon fusion as in the Standard Model.

The ratio $R_{\gamma \gamma }$ has been measured by CMS and ATLAS collaborations with the best fit signals [77, 78]:

$$\begin{aligned} R_{\gamma \gamma }^{CMS}=1.18_{-0.14}^{+0.17}\quad \text {and}\quad R_{\gamma \gamma }^{ATLAS}=0.96\pm 0.14. \end{aligned}$$

(45)

The correlations of the Higgs diphoton signal strength with the $a_{hWW}$ deviation factor from the SM Higgs-W gauge boson coupling and with charged scalar masses are shown in Figs. 5 and 6, respectively. Such correlations indicate that our model successfully accommodates the current Higgs diphoton decay rate constraints.

6 Conclusions

We have proposed a renormalizable $B-L$ standard model extension based on the $S_3$ symmetry which successfully accommodates the current data on SM fermion masses, fermionic mixing angles and CP violating phases of both quark and lepton sectors. The tiny values of the light active neutrino masses are generated through a type I seesaw mechanism. The obtained physical observables of the lepton sector are well consistent with the global fit of neutrino oscillation experiments [9] for both normal and inverted neutrino mass hierarchies. The model also predicts effective neutrino mass parameters of ${\langle m_{ee}\rangle }= {1.02\times 10^{-2}}\,{{\mathrm {eV}}},\, m_{\beta }= {1.25}\times 10^{-2}\,{{\mathrm {eV}}}$ for NH and ${\langle m_{ee}\rangle } ={5.03}\times 10^{-2}\, {{\mathrm {eV}}},\, m_{\beta } ={5.05}\times 10^{-2}\, {{\mathrm {eV}}}$ for IH which are all well consistent with the future large and ultra-low background liquid scintillator detectors which has been discussed in Ref. [66] or the limit of the effective neutrino mass can be reached by the planning of future experiments. The model results are consistent with and successfully accommodate the recent experimental values of the physical observables of the quark sector, including the six quark masses, the quark mixing angles and the CP violating phase in the quark sector. Finally, we have also shown that our model successfully accommodates the current Higgs diphoton decay rate constraints.

Appendices

Appendix A: The Clebsch–Gordan coefficients of $S _3$ group

$S_3$ is the permutation group of three objects, which is also the symmetry group of a equilateral triangle [51]. It has three irreducible representations denoted as 1, ${\underline{1}}^{\prime }$ and 2. We will work in the complex representation in which the conjugation rules are given by ${\underline{1}}^*(1^*)={\underline{1}}(1^*),\,\, {\underline{1}}^{'*}(1^*)={\underline{1}}^{\prime }(1^*),\,\, {\underline{2}}^*(1^*,2^*)={\underline{2}}(2^*,1^*)$, and the decomposition rules are

$$\begin{aligned} {\underline{1}}\otimes {\underline{1}}= & {} {\underline{1}}(11), {\underline{1}}^{\prime }\otimes {\underline{1}}^{\prime }={\underline{1}}(11), {\underline{1}}\otimes {\underline{1}}^{\prime }={\underline{1}}^{\prime }(11),\nonumber \\ {\underline{1}}\otimes {\underline{2}}= & {} {\underline{2}}(11,12), {\underline{1}}^{\prime }\otimes {\underline{2}}={\underline{2}}(11,-12),\nonumber \\ {\underline{2}} \otimes {\underline{2}}= & {} {\underline{1}}(12+21) \oplus {\underline{1}}^{\prime }(12-21) \oplus {\underline{2}}(22,11), \end{aligned}$$

(A1)

where the first and second factors in parentheses respectively indicate to the multiplet components of the first and second representations, respectively.

Appendix B: Higgs potential

The renormalizable potential invariant under all symmetries $SU(3)_C\otimes SU(2)_L\otimes U(1)_Y\otimes U(1)_{{B-L}}\otimes S_3{\otimes {Z_4}}$ is given by⁸:

$$\begin{aligned} V_{\mathrm {total}}= & {} V(H)+V(H^{\prime })+ V(H^{\prime \prime })+V(\phi )+V(H, H^{\prime })\nonumber \\&+{V_{SB}(H^{\prime \prime })}+V(H, H^{\prime \prime })+V(H, \phi )+ V(H^{\prime }, H^{\prime \prime })\nonumber \\&+V(H^{\prime }, \phi )+V(H^{\prime \prime }, \phi ), \end{aligned}$$

(B1)

where

$$\begin{aligned} V(H)= & {} \mu _{H}^2 H^\dagger H +\lambda ^{H}({H}^\dagger H)_{{\underline{1}}}({H}^\dagger H)_{{\underline{1}}},\nonumber \\ V(H^{\prime })= & {} V(H \rightarrow H^{\prime }), \end{aligned}$$

(B2)

$$\begin{aligned} V(H^{\prime \prime })= & {} \mu ^2_{H^{\prime \prime }} (H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{1}}} +\lambda ^{H^{\prime \prime }}_1 (H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{1}}}(H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{1}}} \nonumber \\&+ \lambda ^{H^{\prime \prime }}_2 (H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{1}}^{\prime }}(H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{1}}^{\prime }}\nonumber \\&+ \lambda ^{H^{\prime \prime }}_3 (H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{2}}}(H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{2}}}, \nonumber \\ V(\phi )= & {} V(H^{\prime \prime } \rightarrow \phi ), \end{aligned}$$

(B3)

$$\begin{aligned} V(H, H^{\prime })= & {} \lambda ^{H H^{\prime }}_1 (H^\dagger H)_{{\underline{1}}} (H^{'\dagger } H^{\prime })_{{\underline{1}}} \nonumber \\&+\lambda ^{H H^{\prime }}_2 (H^\dagger H^{\prime })_{{\underline{1}}^{\prime }} (H^{'\dagger } H)_{{\underline{1}}^{\prime }}, \end{aligned}$$

(B4)

$$\begin{aligned} V(H, H^{\prime \prime })= & {} \lambda ^{H H^{\prime \prime }}_1 (H^\dagger H)_{{\underline{1}}} (H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{1}}} \nonumber \\&+\lambda ^{H H^{\prime \prime }}_2 (H^\dagger H^{\prime \prime })_{{\underline{2}}} (H^{\prime \prime \dagger } H)_{{\underline{2}}}, \end{aligned}$$

(B5)

$$\begin{aligned} V(H, \phi )= & {} V(H, H^{\prime \prime } \rightarrow \phi ),\nonumber \\ V(H^{\prime },H^{\prime \prime })= & {} V(H\rightarrow H^{\prime }, H^{\prime \prime }),\nonumber \\ V(H^{\prime }, \phi )= & {} V(H\rightarrow H^{\prime }, \phi ), \end{aligned}$$

(B6)

$$\begin{aligned} V(H^{\prime \prime },\phi )= & {} \lambda ^{H^{\prime \prime }\phi }_1 (H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{1}}}(\phi ^\dagger \phi )_{{\underline{1}}} \nonumber \\&+ \lambda ^{H^{\prime \prime }\phi }_2 (H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{1}}^{\prime }}(\phi ^\dagger \phi )_{{\underline{1}}^{\prime }} \nonumber \\&+ \lambda ^{H^{\prime \prime }\phi }_3 (H^{\prime \prime \dagger } H^{\prime \prime })_{{\underline{2}}}(\phi ^\dagger \phi )_{{\underline{2}}}\nonumber \\&+\lambda ^{H^{\prime \prime }\phi }_4 (H^{\prime \prime \dagger } \phi )_{{\underline{1}}}(\phi ^\dagger H^{\prime \prime })_{{\underline{1}}}\nonumber \\&+\lambda ^{H^{\prime \prime }\phi }_5 (H^{\prime \prime \dagger } \phi )_{{\underline{1}}^{\prime }}(\phi ^\dagger H^{\prime \prime })_{{\underline{1}}^{\prime }}\nonumber \\&+\lambda ^{H^{\prime \prime }\phi }_6 (H^{\prime \prime \dagger } \phi )_{{\underline{2}}}(\phi ^\dagger H^{\prime \prime })_{{\underline{2}}}, \end{aligned}$$

(B7)

$$\begin{aligned} {V(H^{\prime \prime })_{SB}}&{=}&{-\mu ^2_{SB}\left( H^{\prime \prime }_1H^{\prime \prime \dagger }_2 +H^{\prime \prime }_2H^{\prime \prime \dagger }_1\right) ,} \end{aligned}$$

(B8)

where the $S_3$ soft-breaking mass term $V(H^{\prime \prime })_{SB}$ given by Eq. (B8) has been included to generate a non vanishing determinant for the squared mass matrix for the CP-even scalar fields. The scalars fields $H, H^{\prime }, H^{\prime \prime }$ and $\phi$ with their VEVs aligned in Eq. (2) is a solution from the minimization condition of $V_{\mathrm {total}}$ as shown in Sect. 2.