1 Introduction

The standard assumptions of homogeneity and isotropy (namely, the Cosmological Principle) have played an important role in modern cosmology [1]. A large number of cosmological observations such as the cosmic microwave background (CMB) radiation from the Wilkinson Microwave Anisotropy Probes (WMAP) [2, 3]. the statistics of the CMB temperature perturbation maps[4] and observations of large scale structure [5,6,7] generally [5] are in good agreement with \(\Lambda \)CDM model, known as concordance cosmological model [8]. Despite confirmation of \(\Lambda \)CDM model by many observational data, the model is also challenged by some studies [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40], (see also [23, 24] and references therein for more details). Therefore, for further evaluation of the the model, it is necessary to revisit the cosmological principle, by using recent Type Ia supernovae (SNIa) data [8, 27] among others. There is always a question whether a variety of new updated observational data confirms the universe to be isotropic on large scale,

Theoretically, apart from \(\Lambda \)CDM, there are a variety of models that question the isotropic nature of the universe. For example, a vector field may cause cosmic anisotropy and lead the comic to a direction-dependent dark energy [10]. The author of [13] used the hemisphere comparison method to fit the \(\Lambda \)CDM model (and \(\omega \)CDM model) to the supernovae data and detected a preferred axis at statistically significant level. Reference [16, 17] introduced a statistic based on the extreme value theory and applied it to the gold data set of SNIa. They showed that the data is consistent with isotropy and Gaussianity. Reference [20, 21] showed that peculiar velocities may generate dipole-like anisotropy, and maximizes the cosmic acceleration in one direction. By using Union2 observation, Ref. [25] has derived the angular covariance function of the standard candle magnitude fluctuations, but they did not find any angular scales where the covariance function deviates from 0 in a statistically significant manner. In contrast to these ”null-results”, Ref. [29] constructed a ”residual” statistic to search for the preferred direction in different slices of past light-cone, and they found that at low redshift \(z<0.5\) an isotropic model was not consistent with the SNIa data even at 2-3\(\sigma \). Reference [30] found that anisotropy was permitted both in the geometry of the universe and in the dark energy equation of state, if one takes the framework of an anisotropic Bianchi type I cosmological model and the presence of an anisotropic dark energy equation of state. By using 288 SNIa [18], Davis et al. [28] studied the effects of peculiar velocities, taking into consideration of our own peculiar motion, supernova’s motion and coherent bulk motion, and they found that it would cause a systematic shift \(\Delta \omega =0.02\) in the equation of state of dark energy if coherent velocities is neglected. These results are consistent with many other observations, such as the CMB dipole [9], large scale alignment in the QSO optical polarization data [11, 12] and large scale velocity flows [19]. Reference [26] obtained the average direction of the preferred axes as \((l,b)=(278^{\circ }\pm 26^{\circ },45^{\circ }\pm 27^{\circ })\). In Further analysis made by [35], have used different low-redshift \(z<0.2\) SNIa samples and employed the the Hubble parameter to quantify the anisotropy level, and the results showed that all the SNIa samples indicated an anisotropic direction at \(95\%\) confidence level. Recently the authors in [36,37,38,39,40] have used Pantheon dataset to find direction of the dipole in the galactic coordinate system. Recently, some studies have attempted to investigate various aspect of the isotropy of the universe by different catalogues [41,42,43,44].

In this paper, we are going to investigate the anisotropic assumption of the cosmological principle in \(\Lambda \)CDM and two alternative theories to General Relativity, well known as Chameleon and Teleparallel dark energy cosmological models. The authors in ([45,46,47,48,49,50,51,52,53,54,55]) extensively studied these two models. Recently, Chameleon cosmology has been revisited by many researchers to explain galaxy formation ([56]. On the other hand, it has been discussed that the gravitation wave detector could be used to detect the torsion from totally skew symmetric torsion waves in teleparallel gravity ([57]). These two cosmological models are always in favor for current experimental probes. In this paper, we are going to study these two models to search for possible maximum anisotropic direction of the universe using Union2, Pantheon and GRB data.

The paper is organized as follows. In the next section we give introduction both Chameleon and Teleparallel dark energy models. In Sect. 3 we explain the dark energy dipole method used in this paper. Section 4 describes the data used for this analysis. Section 5 is devoted to numerical results and discussion. We finally give a summary in Sect. 6.

2 The models

2.1 Chameleon model

We begin with the action of chameleon gravity given by,

$$\begin{aligned} S&=\int \left[ \frac{M^{2}_{pl}}{16\pi } R-\frac{1}{2}\phi _{\mu }\phi ^{\mu }+V(\phi )\right] \sqrt{-g}dx^{4}\nonumber \\&\quad +\int L_{m}(\Psi ^{(i)},g^{i}_{(\mu \nu )})dx^{4} \end{aligned}$$
(1)

where the matter fields \(\Psi ^{(i)}\) are coupled to scalar field \(\phi \) by \(g^{(i)}_{\mu \nu }=e^{\frac{2\beta _i\phi }{M_{pl}}}g_{\mu \nu }\). The \(\beta _{i}\) are dimensionless coupling constants, one for each matter species. In the following, we assume a single matter energy density component \(\rho _{m}\) with coupling \(\beta \). The variation of action (1) with respect to the metric in a spatially flat FRW cosmology yields the field equations,

$$\begin{aligned}&3H^{2}M^{2}_{pl}=\rho _{m}e^{\frac{\beta \phi }{M_{pl}}}+\frac{1}{2}\phi \dot{}^{2}+V(\phi ), \end{aligned}$$
(2)
$$\begin{aligned}&(2H\dot{}+3H^{2})M^{2}_{pl}=-\gamma \rho _{m}e^{\frac{\beta \phi }{M_{pl}}}-\frac{1}{2}\phi \dot{}^{2}+V(\phi ), \end{aligned}$$
(3)

where we assume a perfect fluid for matter field with \(p_{m}=\gamma \rho _{m}\). Also, variation of (1) with respect to scalar field \(\phi \) gives us the equation for chameleon field:

$$\begin{aligned} \phi \ddot{}+3H\phi \dot{}=-V\acute{}-\frac{\beta }{M_{pl}}\rho _{m}e^{\frac{\beta \phi }{M_{pl}}} \end{aligned}$$
(4)

where prime indicates differentiation with respect to \(\phi \). From Eqs. (2–4), one can easily obtain

$$\begin{aligned} \rho \dot{}_{m}+3H\rho _{m}(1+\gamma )=-3\gamma \frac{\beta }{M_{pl}}\rho _{m}\dot{\phi }. \end{aligned}$$
(5)

Integrating the above equation yields \(\rho _{m}=\frac{A}{e^{\frac{3\gamma \beta \phi }{M_{pl}}}}\frac{1}{a^{3(1+\gamma )}}\) where A is a constant of integration. In the following, by introducing dimensionless variables \(x=\frac{\phi \dot{}}{\sqrt{6}H M_{pl}}\), \( y=\frac{\rho _{m}e^{\frac{\beta \phi }{M_{pl}}}}{3H^{2}M^{2}_{pl}}\) and \(z=\frac{V}{3H^{2}M^{2}_{pl}}\), we obtain a new set of field equations as

$$\begin{aligned} x\acute{}= & {} -3x+\frac{3}{2}yx+3x^{3}-\frac{\sqrt{6}}{2}\beta y-\frac{\sqrt{6}}{2}\alpha z,\nonumber \\ y\acute{}= & {} -3y+3y^{2}+\sqrt{6}\beta x y+6x^{2}y,\\ z\acute{}= & {} z(\sqrt{6}\alpha x+y+6y^{2})\nonumber \end{aligned}$$
(6)

where prime from now on indicates derivative with respect to \(N = ln a\) and Friedmann constraint (2) becomes \(x^2+y+z=1\).

We also assume that the universe is filled with cold dark matter and \(V(\phi )=V_{0}e^{\frac{\alpha \phi }{M_{pl}}}\) where \(\alpha \) is dimensionless constants characterizing the slope of potential. In the new formulation we also obtain \(\frac{\dot{H}}{H^{2}}=\frac{-3y}{2}-3x^{2} \) and the equation of state for chameleon model as \(\omega _{ch}=2x^2+y-1\).

2.2 Interacting teleparallel dark energy

In teleparallel gravity, we assume a non-minimal coupling between a scalar sector and torsion scalar. We also consider an interaction between teleparallel dark energy and dark matter [58]. The action then simply reads

$$\begin{aligned}&S=\int d^{4}x h\left[ \frac{T}{2k^{2}}+ \frac{1}{2} \partial _{\mu }\phi \partial ^{\mu }\phi - V(\phi )+\xi f(\phi ) T\right] + S_{m},\nonumber \\ \end{aligned}$$
(7)

where T is the torsion, \(f(\phi )\) a function of scalar field \(\phi \), \(V(\phi )\) a potential, \(\xi \) coupling constant and \(S_{m}\) the action for matter field. The variation with respect to the tetrad field yields the coupled field equation

$$\begin{aligned}&2 \left( \frac{1}{k^{2}}+2 \xi f(\phi )\right) \left[ h^{-1} h^{a}_{\mu } \partial _{\sigma } \left( h h^{\tau }_{a} S^{\nu \sigma }_{\tau }\right) + T^{\tau }_{\mu \sigma } S^{\nu \sigma }_{\tau } \right. \nonumber \\&\left. + \frac{T}{4} \delta ^{\nu }_{\mu }\right] + 4 \xi S^{\nu \sigma }_{\mu } f_{,\phi } \partial _{\sigma } \phi + \left[ \frac{1}{2} \partial _{\mu } \phi \partial ^{\mu } \phi - V(\phi )\right] \delta ^{\nu }_{\mu } \nonumber \\&\quad - \partial _{\mu } \phi \partial ^{\nu } \phi = \Theta ^{\nu }_{\mu }, \end{aligned}$$
(8)

where \(S^{\nu \sigma }_{\tau }\) is the superpotential, \(\Theta ^{\nu }_{\mu }\) is the symmetric energy-momentum tensor and \(T^{\tau }_{\mu \sigma }\) is the torsion tensor. In flat FRW geometry where \(h^{a}_{\mu }(t)= diag(1,a(t), a(t), a(t))\), the non-zero components of the torsion tensor, contortion tensor and the superpotential are respectively

$$\begin{aligned}&T^{i}_{0j}= - T^{i}_{j0}= H \delta ^{i}_{j},\ \ K^{0i}_{j}= -K^{i0}_{j}= H \delta ^{i}_{j},\ \nonumber \\&\quad S^{i0}_{j}= -S^{0i}_{j}= H \delta ^{i}_{j}\ \ \end{aligned}$$
(9)

with \(i,j= 1, 2, 3.\) By imposing the above in (8), we obtain the Friedmann equations as

$$\begin{aligned}&H^2=\frac{\kappa ^2}{3}\left( \frac{1}{2} \dot{\phi }^{2}+ V(\phi )- 6\xi H^{2} f(\phi )+\rho _m\right) , \end{aligned}$$
(10)
$$\begin{aligned}&3H^2+2\dot{H}=-\kappa ^2\left( \frac{1}{2} \dot{\phi }^{2} -V(\phi ) + 4\xi H f_{,\phi }\dot{\phi } \right. \nonumber \\&\left. \quad + 6 \xi (3 H^{2}+2\dot{H}\right) f(\phi )+p_m). \end{aligned}$$
(11)

Here we also used the relation \(T=-6H^2\) for flat FRW geometry. With the same metric background, the variation of the action (7) with respect to scalar field yields

$$\begin{aligned} \ddot{\phi }+3H\dot{\phi }+V_{,\phi }+ 6 \xi f_{,\phi } H^{2}= -\sigma . \end{aligned}$$
(12)

where \(\sigma \) is the scalar charge corresponds to coupling between teleparallel dark energy and dark matter given by \(\delta S_{m}/ \delta \phi = -h \sigma \) [59,60,61,62,63,64,65]. Rewriting (12) in terms of the energy density and pressure \(\rho _{\phi }\) and \(p_{\phi }\) we find the continuity equation for the scalar field as

$$\begin{aligned} \dot{\rho }_{\phi }+ 3H \rho _{\phi } (1+\omega _{\phi })= -Q, \end{aligned}$$
(13)

whereas for matter we have

$$\begin{aligned} \dot{\rho }_{m}+ 3H \rho _{m} (1+\omega _{m})= Q. \end{aligned}$$
(14)

The term \(Q\equiv \dot{\phi }\sigma \) indicates the coupling between the two components. Also, we will define the barotropic index \(\gamma \equiv 1+ \omega _{m}\) such that \(1\le \gamma < 2\).

Of particular solutions in the study of cosmological scenarios are those in which the energy density of the scalar field mimics the background field energy density ie.e \(\rho _{\phi }= C\rho _{m}\), with C is a constant. Cosmological solutions which satisfy this condition are called scaling solutions and the cosmological coincidence problem can be alleviated in most dark energy models via these solutions [59,60,61,62,63,64]. To study the cosmological dynamics of the model, here we introduce the followings dimensionless variables

$$\begin{aligned}&\chi \equiv \frac{\kappa \dot{\phi }}{\sqrt{6}H}\ \ \ \ \eta \equiv \frac{\kappa \sqrt{V}}{\sqrt{3}H},\ \ \ \ \theta \equiv \kappa \sqrt{f},\ \ \ \ \nonumber \\&\quad \lambda \equiv -\frac{V_{,\phi }}{\kappa V},\ \ \ \ \alpha \equiv \frac{{f_{,\phi }}}{\sqrt{f}}. \end{aligned}$$
(15)

Using these variables we define

$$\begin{aligned} s\equiv -\frac{\dot{H}}{H^2} = \frac{-3\gamma \eta ^2 + 3(2-\gamma )\chi ^2+4\sqrt{6}\alpha \xi \theta \chi }{2(2\xi \theta ^2+1)} + \frac{3\gamma }{2},\nonumber \\ \end{aligned}$$
(16)

then, Eqs. (10) and (11) can be rewritten as a dynamical system of ordinary differential equations (ODE), namely

$$\begin{aligned}&\chi ^\prime = \frac{\sqrt{6}}{2}\lambda \eta ^2 - \sqrt{6}\alpha \xi \theta + \chi (s-3)- \hat{Q}, \end{aligned}$$
(17)
$$\begin{aligned}&\eta ^\prime = \left( s-\frac{\sqrt{6} \lambda \chi }{2}\right) \eta , \end{aligned}$$
(18)
$$\begin{aligned}&\theta ^\prime = \frac{\sqrt{6}\alpha \chi }{2}, \end{aligned}$$
(19)

where \(\hat{Q}\equiv \frac{\kappa Q}{\sqrt{6} H^2 \dot{\phi }}\). Without losing generality we assume that \(\xi =1\) and \(\lambda =const\). We also assume \(\gamma =1\) and \(f(\phi ) \propto \phi ^{2}\) such that \(\alpha = const\). From the coupling \( Q=\beta \kappa \rho _{m}\dot{\phi }\) we also find that \(\hat{Q}=\frac{\sqrt{6} \beta \Omega _{m}}{2}\). In terms of these dimensionless variables, the fractional energy densities \(\Omega \equiv (k^2 \rho )/(3H^2)\) for the scalar field is given by

$$\begin{aligned} \Omega _{\phi }= \eta ^2 + \chi ^2 - 2\theta ^2, \end{aligned}$$
(20)

Also, the equation of state of the field \(\omega _\phi = p_\phi / \rho _\phi \) reads

$$\begin{aligned} \omega _\phi = \frac{\chi ^2 - \eta ^2 + 4 \sqrt{\frac{2}{3}} \alpha \chi \theta + 2\left( 1-\frac{2}{3}s\right) \theta ^2}{(\eta ^2 + \chi ^2) -2 \theta ^2}. \end{aligned}$$
(21)

Finally we can define the effective equation of state for teleparallel gravity as \(\omega _{eff}= (p_m + p_\phi )/ (\rho _m + \rho _\phi )\) is given by

$$\begin{aligned} \omega _{tel}= -\eta ^2 +x\chi ^2 + 4 \sqrt{\frac{2}{3}} \alpha \chi \theta + 2 \left( 1- \frac{2}{3}s\right) \theta ^2. \end{aligned}$$
(22)

In the next section we best fit both Chameleon and teleparallel models parameters by using the observational data.

3 Dark energy dipole

An anisotropic repulsive dark energy will directly affect cosmic expansion and consequence leading to an anisotropic luminosity distance. This effect should be observable by the luminosity of SNIa. We calculate the isotropic background as dipole modulation. By using the luminosity distance we define the deviation from isotropic expansion as

$$\begin{aligned} \frac{\mu (\overrightarrow{z})-\mu ^{0}(z)}{\mu ^{0}(z)}=a(z)(\widehat{z}\cdot \widehat{n}). \end{aligned}$$
(23)

where \(\mu (\overrightarrow{z})\) is the true luminosity distance of the supernova, and in an isotropic background, the distance modulus is \(\mu ^{0}(z)\). \(a(z)(\widehat{z}\cdot \widehat{n})\) is the modulation part of the distance modulus, which shows the deviation from isotropic background. Generally. The \(\widehat{z}\) in (23) is the unit direction vector of the supernova, which can be expressed by using the Galactic coordinate system and \(\widehat{n}\) is the direction of dark energy dipole, which is the maximal expanding direction. In celestial coordinate system we have

$$\begin{aligned} \widehat{n}= (\cos \phi \sin \theta ,\sin \phi \sin \theta ,\cos \theta ) \end{aligned}$$
(24)

where \(\theta \in [0,\pi )\) and \(\phi \in [0,2\pi )\). The a(z) can be, in general, a complex function of the redshift, but here we assume a linear form as

$$\begin{aligned} a(z)=a_{0}+a_{1}z. \end{aligned}$$
(25)

where \(a_{0}\) and \(a_{1}\) are constants, representing the strength and time evolution of modulation. Accordingly, the theoretical distance modulus \(\mu _{th}\) is defined as

$$\begin{aligned}&\mu _{th}(z)=5 \log _{10}d_{L}(z)+ \mu _{0}, \ \ \ where \ \ \ \nonumber \\&\quad \mu _{0}=42.384-5\log _{10}h, \end{aligned}$$
(26)

where \( H_{0}=100h\) \(km.s^{-1}.Mpc^{-1}.\) is the current Hubble parameter We employ the Union2 dataset to constrain the anisotropic dark energy model. The directions to the SNIa we use here are given in Ref. [25], and are described in the equatorial coordinates (right ascension and declination). In order to make comparisons with other results, we convert these coordinates to the galactic coordinates (l, b) [25].

We further assume a completely independent experiment error between each measurement and so the covariance matrix can be simplified as the diagonal component, and the \(\chi ^{2}_{sn}\) can be written as

$$\begin{aligned} \chi ^{2}_{sn}= \sum _{i=1}^{557}\frac{\left[ \mu ^{obs}(z_{i})-\mu ^{th}(\overrightarrow{z_{i}})\right] ^{2}}{\sigma ^{2}(z_{i})}. \end{aligned}$$
(27)

where, \(\mu ^{obs}(z_{i})\) is the measured distance modulus from the Union2 data, and \(\mu ^{th}(\overrightarrow{z_{i}})\) is the direction-dependent theoretical distance modulus.

One can eliminate the nuisance parameter \(\mu _{0}\) by expanding \(\chi ^{2}_{sn}\) with respect to \(\mu _{0}\) [5]

$$\begin{aligned} \chi ^{2}_{sn}= A+ 2B\mu _{0}+ C\mu _{0}^{2}, \end{aligned}$$
(28)

where

$$\begin{aligned} A= & {} \sum _{i}\frac{\left[ \mu _{th}(z_{i};\mu _{0}=0)-\mu _{obs}(z_{i})\right] ^{2}}{\sigma ^{2}(z_{i})}, \end{aligned}$$
(29)
$$\begin{aligned} B= & {} \sum _{i}\frac{\left[ \mu _{th}(z_{i};\mu _{0}=0)-\mu _{obs}(z_{i})\right] }{\sigma ^{2}(z_{i})}, \end{aligned}$$
(30)
$$\begin{aligned} C= & {} \sum _{i}\frac{1}{\sigma ^{2}(z_{i})}. \end{aligned}$$
(31)

the \(\chi ^{2}_{sn}\) then has a minimum as

$$\begin{aligned} \widetilde{\chi } ^{2}_{sn}= A- B^{2}/C, \end{aligned}$$
(32)

which is independent of \(\mu _{0}\). This technique is equivalent to performing a uniform marginalization over \(\mu _{0}\) [5]. We will adopt \(\widetilde{\chi } ^{2}_{sn}\) as the goodness of fitting instead of \(\chi ^{2}_{sn}\).

One can easily calculate the likelihood function of each parameter by performing the Markov Chain Monte Carlo analysis. The parameters need to be constrained are \((a_{0}, a_{1}, \theta , \phi )\), where \((\theta , \phi )\) is the direction of modulation. We then convert \((\theta , \phi )\) into galactic coordinate (l, b).

Fig. 1
figure 1

The distance modulus \(\mu (z)\) vs. redshift best fitted with Union2, Pantheon and GRB data in Teleparallel, Chameleon and \(\Lambda \)CDM Models

Full size image

4 Data

In this paper we use three probes to testify our cosmological models with luminosity distance observation. The Union SNe Ia is an important probe to study the cosmic evolution. We use Union2 SNe Ia compilation with 557 SNe Ia within the redshift range \(0.015<z< 1.414\) [8]. The Pantheon sample is our second probe which which includes 1048 spectroscopically confirmed SNe Ia covering the redshift range \(0.01< z < 2.26\).

Recently, [66] released the Pantheon sample which includes 1048 spectroscopically confirmed SNe Ia covering the redshift range \(0.01< z < 2.26\). The original sample contains 276 SNe Ia discovered by the Pan- STARRS1 Medium Deep Survey, and other SNe Ia from SDSS, SNLS, various low-z and HST sub samples. The Pantheon data points are not uniformly distributed in the sky; half of them are located in the galactic south-east and most of them are at low redshifs

Our third probe is taken from gamma-ray bursts (GRBs) that are one of the most energetic phenomena in our Universe. The high luminosity makes them detectable out to high redshifts \(z = 8.1\) and can be considered as complementary cosmic probe to SN Ia and Pantheon. Therefore, it is considered as high redshift probe to study cosmic expansion and dark energy, star formation rate, the reionization epoch and the metal enrichment history of the Universe. The source of GRB data is available in [67]. Here we use GRB catalogue prepared by [68] which includes 67 GRB samples with positions described in the equatorial coordinates (right ascension and declination).

5 Result and discussion

5.1 Reconstructing luminosity distance

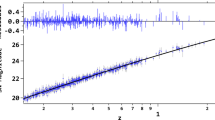
We best fit the luminosity distance with Chameleon, Teleparallel and \(\Lambda \)CDM dark energy models using Union2, Pantheon and GRB data (Fig. 1). As we see all models behave the same for Union2 up to \(z \simeq 1.4\) and Pantheon up to \(z \simeq 2.3\). However, for \(z>2.3\), without using GRB data, the Teleparallel dark energy model deviates widely whereas Chameleon and \(\Lambda \)CDM dark energy model stay in the same trajectory as fitted with both pantheon and GRB. This simply indicates that Chameleon and \(\Lambda \)CDM models are more consistent with the combined Union2, Pantheon and GRB data.

5.2 Cosmic anisotropy

In a second numerical analysis which is the main purpose of this paper, we calculate the maximum anisotropic direction for our models , employing Union2, Pantheon and GRB data. The result has been given in Table 1.

Table 1 Anisotropy
Full size table

As can be seen, we drive the constraints on anisotropic parameters, (\(a_0\), \(a_1\)), galactic coordinate, (l, b) and model parameters \(\alpha \), \(\beta \), \(\xi \), \(\Omega _{m}\), \(\lambda \) for Chameleon, Teleparallel dark energy and \(\Lambda \)CDM models, using Union2, pantheon and GRB data. we also analyse the Akaike information criteria, AIC, derived from frequentist probability and Bayesian information criteria, BIC, derived from Bayesian probability, to evaluate the performance of our models.

The AIC is defined as \(AIC = \chi ^2 + 2n\) ([70]) where n is the number of parameters of the model [71]. While \(\chi ^2\) is an standard measurement of the goodness of fit, AIC gives extra value by also taking into account the number of free parameters n in the model. Generally, models with too few parameters have higher \(\chi ^2\) known as underfitting, whereas those with too many fitting parameters known as overfitting suffer by larger n. The AIC compares two or more models, and gives a measure of confidence for the preferred model. Clearly, the better model that minimizes AIC is the one with fewer parameters, if the goodness of fit in the comparing models are not substantially different. From Table 1 we see that AIC in \(\Lambda \)CDM model and Chameleon model for different observational data is lower than Teleparallel dark energy model. This is because both \(\chi ^2\) and the number of free parameter in \(\Lambda \)CDM and Chameleon model is smaller that the corresponding Teleparallel dark energy model.

A better alternative to compare models is BIC, defined as \(BIC=\chi ^2+nlnN\), where N is the number of data points. Unlike AIC that is based on information theory, BIC is based on Bayesian statistics as a result of conventional Bayesian inference procedure. By assuming that prior to fitting, the models are equally favoured, from approximating the Bayes factor, BIC gives the predictive odds of the preferred model. Note that for large number of data points, N, BIC simply suppresses the possible overfitting problem if number of fitting parameters is also large. Therefore, for large N, one can not choose a Bayesian prior over the parameters in comparing models but can select the prior distribution over the choice of models ([70]) . This is to say that, though we assume an equal prior likelihood for each model, based on BIC value, yet one model can be preferred a priori over the other. With reference to Table 1, we observe that, typically, BIC is smaller in \(\Lambda \)CDM and Chameleon model over Teleparallel for different observation. This again confirms that both \(\Lambda \)CDM and Chameleon models are more favorable.

In Figs. 2, 3, 4 and 5, we plotted the maximum anisotropic deviation directions for Pantheon and \(Union2+GRB\). As can be seen, data distribution is more uniform in \(Union2+GRB \) compare to others. Therefore, one expect that the data analysis using both Union2 and GRB data would be less biased and more statistically rigorous.

Fig. 2
figure 2

Probability of dark energy dipole direction using \(2\times 10^{5}\) datapoints for Pantheon data . Left:Chameleon, Right:Teleparallel. White triangles denote Pantheon data

Full size image
Fig. 3
figure 3

Probability of dark energy dipole direction using \(2\times 10^{5}\) Union2 plus GRB data Blue and red triangles are Union2 and GRB data. Left:Chameleon, Right:Teleparallel

Full size image
Fig. 4
figure 4

Probability of dark energy dipole direction using \(2\times 10^{5}\) for \(\Lambda CDM\) Model Left:Union2+GRB data , Right:Pantheon data. White triangles denote Union2+GRB data

Full size image

A comparison between our work in this paper with other research groups have been provided in Table 2. The results show that maximum anisotropy for Union2 data in different research are very similar. Also for Pantheon data our result are compatible with previous studies using the same data. However, using combination of Union2 and GRB for our favored Chameleon model, the result is very close to \(\alpha \) dipole using \(Keck-VLT\) dataset which covering high redshift ranges. This, in particular, is illustrated in Fig. 5 that preferred direction of maximum anisotropy in the galactic coordinate system is sketched for both Union2-GRB and keck-VLT data points . Noting that the significance of the maximum direction of dipole in our computation is less than \(1\sigma \).

Fig. 5
figure 5

The \((1-\sigma )\) error on dark energy dipole in Chameleon model, using Union2 + GRB data in the galactic coordinate system compared with best-fitting \(\alpha \)-dipole (star). Blue and red triangles denote Union 2 and GRB data respectively

Full size image

6 Summary

There are evidence that universe expands in a preferred anisotropic direction. If such a cosmological axis exists, then universe undergoes an anisotropic expansion and the observed acceleration is maximized in one direction. The Union2 data are widely used as the standard candle to test possible anisotropy of the universe [10, 16, 17, 26, 29, 32, 68, 72, 77,78,79,80,81,82,83,84,85,86,87,88,89]. The consensus of these studies is that there is an asymmetry axis pointing in a preferred direction. In this paper, we perform a detailed analysis of the dark energy dipole using Union2, Pantheon and GRB data for three cosmological models; \(\Lambda \)CDM, Chameleon gravity and Teleparallel dark energy model. Testing possible anisotropy of the Universe beyond the standard cosmological model will provide some useful information to investigate that whether the maximum anisotropic direction is independent of isotropic dark energy models or not. This research shows that the maximum anisotropic direction in chameleon model is \((l = 128^{o}\pm 27^{o}\), \(b = 16.5^{o}\pm 14^{o})\) or equivalently \((l = 308^{o}\pm 27^{o}\), \(b = -16.5^{o}\pm 14^{o})\) and in teleparallel model is \((l = 128^{o}\pm 25^{o}\), \(b = 21^{o}\pm 20^{o})\) or equivalently \((l = 308^{o}\pm 27^{o}\), \(b = -21^{o}\pm 20^{o})\).

Table 2 Comparison of the maximum anisotropy for different dataset
Full size table

We observe that, by considering only Union2 data, the preferred direction of the anisotropy in both models are close to each other in comparison with \(\Lambda \)CDM as well as with those obtained in previous studies (Table 2). However, the degenerate behavior would be breaking at redshift \(z>1.4\) when we use higher redshift dataset such as GRB. This indicates that although Union2 dataset is important for the study of the expansion history of the Universe and the properties of dark energy, it covers only low redshift range (\( z< 1.4\)) of the sky, and therefore earlier evolution being largely unconstrained. Here, we also implement high-redshift probes, such as Pantheon and a combination of Union2 and GRB datadata to investigate the cosmic anisotropy. For pantheon data, the anisotropy in chameleon model is \( (l,b)=(270^{+20}_{-20},14^{+19}_{-57})\) which is compatible with previous studies. In particular it is close to [37] with \((l,b)=(282^{+47}_{-34}, 28^{+50}_{-1.7})\). Furthermore, by using a combination of Union2 and GRB, which produces a more uniform distribution of data over a wider range of redshift on the sky, we find the preferred anisotrpic direction at (\(l \approx 330^{o}\), \(b \approx -15^{o})\) in galactic coordinate) which is comparable with the values obtained in \(\alpha \)-dipole of keck-VLT dataset (\(l \approx 333^{o}\), \(b \approx -13^{o}))\). As discussed, the statistical analysis also favors \(\Lambda \)CDM and Chameleon cosmology over Teleparallel model. Finally, we may conclude that the discrepancy of the results in difference studies on cosmological anisotropy, apart from the cosmological model, can be related to the uniformality and volume of the dataset. Obviously, more uniformly distributed data in larger redshift range can help us to find more accurate direction for cosmic anisotropy.