1 Introduction

In modern cosmology one of the most challenging problems is to explain the late time acceleration of the Universe. The distance measurements of Supernova Type Ia (standard candle) observations [1, 2] revealed in 1998 that the expansion of the Universe is accelerating. Since then several other observations such as Cosmic Microwave Background Radiation observations (CMBR) [3,4,5,6,7], baryon acoustic oscillations measurements in galaxy power spectrum [8, 9], large scale structure studies [10,11,12] have also indicated this phenomenon of late time acceleration of the Universe. The general consensus is that a mysterious component called Dark Energy with negative pressure (opposite to gravity) is causing the late time acceleration of the Universe. The CMBR anisotropy measurements suggest that the Dark Energy accounts for about 68.5\(\%\) of the mass energy content of the present Universe.

As mentioned, the pressure acts opposite to that of gravity so as to accelerate the Universe in opposition to the tendency of an eventual gravitational collapse due to the mass present in the Universe. Several theoretical models have since been proposed for explaining the origin and nature of the mysterious Dark Energy and the consequent late time acceleration. There are attempts to interpret this Dark Energy by a cosmological constant \(\varLambda \) introduced in the Einstein’s equations and the Friedmann equations that follows for FRW cosmology [13,14,15,16,17,18] with Einstein equations. However from the point of view of particle physics the cosmological constant naturally arises as an energy density of the vacuum, but in such scenario one has to make a fine tuning of the theoretical result of order \(10^{121}\) [13, 19]. Cosmological constant \(\varLambda \) is also associated with another theoretical problem, namely the cosmic coincidence problem [20]. The quintessence Dark Energy [21] is generally realized by considering a scalar field \(\phi \) in a potential \(V(\phi )\) [22] and as time progresses \(\phi \) changes very slowly (slow roll). Various scalar field Dark Energy models have been studied in detail in literature [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82]. Other attempts to explain this late time acceleration includes modification of Einstein’s gravity in the large scale in the framework of theories of extra dimensions [83,84,85,86,87]. There are various proposals in the literature of higher dimensional models [88,89,90,91,92,93] to explain recent cosmic acceleration.

The Dark Energy and the inhomogeneities in the Dark Energy field are addressed by studying the Dark Energy perturbations [94, 95]. This is related to the perturbations of space time [96,97,98] as also the perturbations of the scalar field that may be considered to account for the Dark Energy. The study of cosmological perturbations is also important because the matter and other perturbations that are derived from a proposed theory have direct consequences in accounting for the matter power spectrum.

In the present work we investigate the late time acceleration by a scalar field namely Slotheon [99,100,101] field inspired by extra dimensional models. A Slotheon field arises out of the Dvali, Gabadadze and Porrati (DGP) [102] model related to brane world. The mechanism of the DGP model is such that gravity can be localised in a 4-dimensional brane and at short distance it looks like 4-dimensional while it weakens at large distance [103]. This property enables the DGP model for a description of the late time acceleration of the Universe, alternative to the conjecture of a positive cosmological constant and this could be possible by the modification of gravity at large horizon scale distance. At the limit when Planck mass \(M_{\mathrm{pl}} \rightarrow \infty \) and \(r_c \rightarrow \infty \), where \(r_c\) is a cross over scale for transition from 4-dimension to 5-dimension (1 extra dimension), this theory in the Minkowski space time can be described by a scalar field [103, 104], where the field obeys a shift symmetry (Galileon shift) [103]. Here the strong coupling scale of the DGP model given by \((r_c^2/M_{\mathrm{pl}})^{1/3}\) [103] remains fixed. A suitable scalar field that describes this symmetry when extended to the curved space time [105] is termed as Slotheon scalar field. We calculate in the present work the general relativistic perturbations [98, 106] for Slotheon field model and derive the analytical expressions for fractional matter density perturbation, fractional density perturbation of the Slotheon field considered and other relevant quantities. Evolution of these perturbations are also worked out and shown in detail in the present work. Finally the matter power spectrum for the Slotheon field is computed and shown.

Our calculations show that the Slotheon model favours more the \(\varLambda \)CDM model than the quintessence scenario. But \(\varLambda \)CDM does not deal with the fluctuations and subsequent inhomogeneities in Dark Energy. As these are relevant in horizon scale or beyond horizon scale, careful studies of power spectra at these scales are needed to look for such inhomogeneities. Although not observed yet, if the upcoming experiments such as SKA, LSST can probe such inhomogeneities then even though the \(\varLambda \)CDM model may not be useful, but the Slotheon model, which yields \(\varLambda \)CDM model results in non-perturbative limits, could be a viable model for Dark Energy.

This paper is organised as follows. In Sect. 2, we discuss the background evolution of the Universe for Slotheon field model. In Sect. 3 first order general relativistic perturbation equations and their solutions are given. Section 4 is devoted to the calculations for evolution of different perturbative quantities with time considering the Slotheon field. In Sect. 5 we investigate the effect of the Slotheon field on the matter power spectrum. Finally in Sect. 6 a summary and discussions are given.

2 Background evolution for Slotheon field

Slotheon field is a scalar field model inspired by a model in theories of extra dimensions, which is a class of modified gravity models and can be an alternative way to explain the late time acceleration of the Universe. As mentioned earlier, the Slotheon model follows from the DGP model with one extra dimension.

Writing down the DGP action in Minkowski space time in terms of a scalar field \(\pi \) (called the Galileon field) and then writing the equations of motion up to the second order derivative of \(\pi \) the theory is made free from the ghost degrees of freedom. The scalar field \(\pi \), which is called the Galileon field obeys a shift symmetry

$$\begin{aligned} \partial _\mu \pi \rightarrow \partial _\mu \pi + c_\mu \,\,, \end{aligned}$$
(1)

termed as Galileon shift symmetry. The Galileon shift symmetry in the flat Minkowski space time can also be given by \(\pi \rightarrow \pi + a + b_\mu x^\mu \), where a and \(b_\mu \) denote a constant and a constant vector respectively. The Slotheon field is obtained when the Galileon shift is extended to curved space time [105]. Here we consider this Slotheon field leads to the acceleration and Dark Energy of the Universe.

The formalism can be realised by considering the Lagrangian \( {\mathcal {L}} = -\frac{1}{2} g^{\mu \nu } \pi _{;\mu } \pi _{;\nu } + \frac{G^{\mu \nu }}{2M^2} \pi _{;\mu } \pi _{;\nu } \) (\(\pi _{;\mu }\) denotes the covariant derivative of \(\pi \), \(G_{\mu \nu }\) is the Einstein’s tensor while \(g_{\mu \nu }\) is the metric and M being an energy scale), which remains invariant under the shift \(\pi \rightarrow \pi + a + b_\mu x^\mu \) in curved space time. By adding standard Einstein-Hilbert term to the Lagrangian density \({\mathcal {L}}\) and a non trivial potential for \(\pi \), one obtains a rich gravitational theory, with some interesting properties. The field \(\pi \) moves slower in this theory than in the scalar field theory described by the Lagrangian \( {\mathcal {L}} = -\frac{1}{2} g^{\mu \nu } \pi _{;\mu } \pi _{;\nu } \) and hence \(\pi \) is called a Slotheon field.

The Slotheon action is given as [99]

$$\begin{aligned} S= & {} \int d^4x \sqrt{-g} \left[ \frac{1}{2} \left( M_{\mathrm{pl}}^2 R - \left( g^{\mu \nu } - \frac{ G^{\mu \nu }}{M^2} \right) \pi _{;\mu } \pi _{;\nu }\right) - V({\pi })\right] \nonumber \\&+S_m \left[ \psi _m; e^{2\beta \pi /M_\mathrm{pl}} g_{\mu \nu }\right] , \end{aligned}$$
(2)

where \( M_{\mathrm{pl}}^2 = \frac{1}{8 \pi G} \) is the reduced Planck mass, M is an energy scale and \(S_m\) is the action for the matter field and \(V(\pi )\) is the Slotheon potential for field \(\pi \). In the above R is the Ricci scalar, \(\psi _m\) is the matter field that couples to the field \(\pi \) with a dimensionless coupling constant \(\beta \). It can be noted here that without the term \(\frac{G^{\mu \nu }}{2M^2}\pi _{;\mu }\pi _{;\nu }\), the action of Eq. (2) is similar to the action of a standard quintessence scalar field [13]. Variations of this action with respect to the metric and the field \(\pi \) yield the following equations of motion respectively

$$\begin{aligned}&M_{\mathrm{pl}}^2 G_{\mu \nu } = T_{\mu \nu }^{(m)} + T_{\mu \nu }^{(\pi )}\,\,, \end{aligned}$$
(3)
$$\begin{aligned}&\Box \pi + \frac{1}{M^2}\left[ \frac{R}{2} \Box \pi - R^{\mu \nu } \pi _{;\mu \nu }\right] -V_\pi = -\frac{\beta }{M_{\mathrm{pl}}} T^{(m)}, \end{aligned}$$
(4)

where the derivative of potential \(V(\pi )\) with respect to \(\pi \) is given as \(V_\pi \) and \(T_{\mu \nu }^{(m)}\), \(T_{\mu \nu }^{(\pi )}\) are energy momentum tensors for dust like particles and for the field \(\pi \) respectively. In what follows we will not consider \(T_{\mu \nu }^{(r)}\) (energy momentum tensor for radiation) since the initial conditions adopted in the present work do not include the radiation dominated era as is described later. The tensor \(T^{(\pi )}_{\mu \nu }\) is given by

$$\begin{aligned} T_{\mu \nu }^{(\pi )}= & {} \pi _{;\mu } \pi _{;\nu } -\dfrac{1}{2} g_{\mu \nu } (\nabla \pi )^2 - g_{\mu \nu } V(\pi ) \nonumber \\&+ \frac{1}{M^2}\left( \frac{1}{2} \pi _{;\mu } \pi _{;\nu } R -2 \pi _{;\alpha } \pi _({_{;\mu } R_{\nu }^{\alpha }})\right. \nonumber \\&+\frac{1}{2}\pi _{;\alpha } \pi ^{;\alpha }G_{\mu \nu } - \pi ^{;\alpha } \pi ^{;\beta } R_{\mu \alpha \nu \beta } -\pi _{;\alpha \mu } \pi _{;\nu }^{\alpha } \nonumber \\&+ \pi _{;\mu \nu } \pi _{;\alpha }^{\alpha } \nonumber \\&\left. + \frac{1}{2} g_{\mu \nu }\left( \pi _{;\alpha \beta } \pi ^{;\alpha \beta } - (\pi _{;\alpha }^{\alpha })^2 + 2\pi _{;\alpha } \pi _{;\beta } R^{\alpha \beta }\right) \right) . \end{aligned}$$
(5)

In the above \(R^\alpha _\beta \) and \(R_{\mu \alpha \nu \beta }\) represent Ricci tensor and Riemann curvature tensor respectively. In spatially flat Friedmann Robertson Walker (FRW) background with the assumption that the coupling constant \(\beta =0\), the equations of motion take the form

$$\begin{aligned}&3 M_{\mathrm{pl}}^2 H^2 = \rho _m + \frac{{\dot{\pi }}^2}{2} + \frac{9 H^2 {\dot{\pi }}^2}{2M^2} + V(\pi )\,\,, \end{aligned}$$
(6)
$$\begin{aligned}&M_{\mathrm{pl}}^2 (2{\dot{H}} + 3H^2) = -\frac{{\dot{\pi }}^2}{2} +V(\pi ) + (2{\dot{H}} + 3H^2) \frac{ {\dot{\pi }}^2}{2M^2}\nonumber \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ + \frac{2 H{\dot{\pi }}\ddot{\pi }}{M^2}\,\,, \end{aligned}$$
(7)
$$\begin{aligned}&0 =\ddot{\pi } + 3H{\dot{\pi }} + \frac{3 H^2}{M^2}\left( \ddot{\pi } + 3H{\dot{\pi }} + \frac{2{\dot{H}}{\dot{\pi }}}{H}\right) + V_{\pi }\,\,. \end{aligned}$$
(8)

Here (and in what follows) \({\dot{Y}}\) represents derivative of Y with respect to time whereas \({\ddot{Y}}\) represents double derivative of Y with respect to time. It can be noted that \(\pi \) field is slower than a canonical scalar field and hence the name Slotheon. The slowing of the field is entirely due to gravitational interaction. In the present analysis we adopt an exponential form of the potential \(V(\pi )\) given by

$$\begin{aligned} V(\pi )=V_0 \mathrm{exp} \left( -\frac{\lambda \pi }{M_\mathrm{pl}}\right) \,\,, \end{aligned}$$
(9)

where \(\lambda \) is a constant.

3 Perturbations for the Slotheon field

In the present work the cosmological perturbations for both the Slotheon field and the matter are carried out in the longitudinal gauge or Newtonian gauge [107]. The scalar perturbed metric under this framework is given by [96, 106]

$$\begin{aligned} ds^2=-(1+2 \varPhi ) dt^2+a^2(t) (1+2 \varPsi ) \delta _{ij} dx^idx^j\,\,, \end{aligned}$$
(10)

where a(t) is the scale factor, \(\varPhi \) is gravitational potential and \(\varPsi \) is the perturbation in the spatial curvature. The anisotropic stress is assumed to be zero and therefore \(\varPhi =-\varPsi \) [107]. Under this circumstance the perturbed metric can be completely described by a single scalar variable \(\varPhi \). It is assumed that the baryonic matter, dark matter etc. can be described as perfect fluid so that the energy momentum tensor is written as

$$\begin{aligned} T^\mu _\nu = (\rho + p)u^\mu u_\nu + p \delta ^\mu _\nu \,\,, \end{aligned}$$
(11)

where \(\rho \), p, \(u_\mu \) are respectively the energy density, pressure density and four velocity of the fluid. The perturbations in these and the Slotheon field \(\pi \) are defined as

$$\begin{aligned} \rho (t ,\overrightarrow{x})= & {} {\bar{\rho }}(t) + \delta \rho (t ,\overrightarrow{x})\,\,, \end{aligned}$$
(12)
$$\begin{aligned} p(t ,\overrightarrow{x})= & {} {\bar{p}}(t) + \delta p(t ,\overrightarrow{x})\,\,, \end{aligned}$$
(13)
$$\begin{aligned} u^\mu= & {} {\bar{u}}^\mu + v^\mu \,\,, \end{aligned}$$
(14)
$$\begin{aligned} \pi (t ,\overrightarrow{x})= & {} {\bar{\pi }}(t) + \delta \pi (t ,\overrightarrow{x})\,\,. \end{aligned}$$
(15)

In the above \({\bar{\xi }}(t)\) ( where \(\xi (t,\overrightarrow{x})\equiv \rho (t,\overrightarrow{x})\), \(p(t, \overrightarrow{x})\), \({u}^\mu \), \({\pi }(t,\overrightarrow{x})\)) are the respective quantities for the homogeneous and isotropic background Universe and \(\delta \xi (t,\overrightarrow{x})\) denotes their respective perturbations. Note that \(v^\mu \) is perturbation of \(u^\mu \) in Eq. (14).

It is considered that perturbations are very small, therefore with \(\delta T^\mu _\nu \) to be the perturbation for \(T^\mu _\nu \) and using Eq. (11) one obtains, after neglecting second and higher order terms,

$$\begin{aligned} \delta T^0_0= & {} - \delta \rho \,\,, \end{aligned}$$
(16)
$$\begin{aligned} \delta T^0_i=-\delta T^i_0= & {} ({\bar{\rho }} + {\bar{p}})v^i \,\,, \end{aligned}$$
(17)
$$\begin{aligned} \delta T^i_j= & {} \delta p \delta ^i_j\,\,. \end{aligned}$$
(18)

For the Slotheon field tensor \(T_{\mu \nu }^{(\pi )}\), the perturbations \(\delta T^0_0\), \(\delta T^0_i\), \(\delta T^i_j\) are calculated using Eq. (5) and with Eqs. (16–18) we now have,

$$\begin{aligned}&\delta \rho _\pi =-\frac{1}{a^3 M^2}\left[ -a^3 M^2 \delta \pi V_\pi \right. \nonumber \\&~~~~~~~~~~+ {\dot{\pi }} \left( 2{\dot{a}} \nabla ^2(\delta \pi ) -\delta {\dot{\pi }}(a^3M^2 + 9 a {\dot{a}}^2) \right. \nonumber \\&~~~~\quad \quad \left. \left. + {\dot{\pi }} a \left( a^2 M^2 \varPhi -\nabla ^2 \varPhi + 9{\dot{a}}(a{\dot{\varPhi }}+2\varPhi {\dot{a}})\right) \right) \right] ,\nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned}&({\bar{\rho }}_\pi +{\bar{p}}_\pi ) v_i = -\frac{ {\dot{\pi }}}{a^2 M^2}\left[ -2 a \delta {\dot{\pi }} {\dot{a}} + \delta \pi (a^2 M^2 \right. \nonumber \\&\quad \quad \left. + 3 {\dot{a}}^2)+a(a{\dot{\varPhi }} + 3 \varPhi {\dot{a}}){\dot{\pi }}\right] \mid _{i}, \end{aligned}$$
(20)
$$\begin{aligned}&\delta p_\pi = \frac{1}{a^3 M^2}\left[ -a^3 M^2 \delta \pi V_\pi + {\dot{\pi }}\right. \nonumber \\&\quad \left( -2 a^2 \delta \ddot{\pi } {\dot{a}} + a (-a^2 M^2 \varPhi + a^2 \ddot{\varPhi } \right. \nonumber \\&\quad \quad \left. \left. +\nabla ^2 \varPhi -\varPhi _{ii}){\dot{\pi }}+{\dot{a}} (\nabla ^2(\delta \pi )-\delta \pi _{ii} \right. \right. \nonumber \\&\quad ~~~~+2 a (3 a {\dot{\varPhi }} + \varPhi {\dot{a}}){\dot{\pi }}) \nonumber \\&\quad \quad \left. \left. + a \delta {\dot{\pi }}(-{\dot{a}}^2+a(a M^2-2\ddot{a})) +4\varPhi {\dot{\pi }}\ddot{a} a^2 \right) \right. \nonumber \\&\quad \quad \left. +a(\nabla ^2\delta \pi -\delta \pi _{ii} - 2 a \delta {\dot{\pi }} {\dot{a}} + 2 a(a {\dot{\varPhi }}+4 \varPhi {\dot{a}}){\dot{\pi }})\ddot{\pi }\right] .\nonumber \\ \end{aligned}$$
(21)

In the above \(\delta \rho _\pi , v_i, \delta p_\pi \) are respectively the first order perturbed energy density, peculiar velocity and pressure density of the Slotheon field \(\pi \). Also in the above, the notation \(\mid _i\) signifies the covariant derivative with spatial coordinate \(x_i\) and \(\delta \pi _{ii}\), \(\varPhi _{ii}\) are the double covariant derivatives of \(\delta \pi \) and \(\varPhi \) respectively w.r.t the spatial co-ordinate \(x_i\).

3.1 Linearised perturbation equations

The perturbed Einstein’s equation is given by

$$\begin{aligned} \delta G^\mu _\nu =8 \pi G \delta T^\mu _\nu \,\,, \end{aligned}$$
(22)

where \(\delta G^\mu _\nu \) and \(\delta T^\mu _\nu \) are perturbed Einstein’s tensor and perturbed energy momentum tensor respectively. Solving Eq. (22) for the perturbed space time metric (Eq. (10)) we obtain the linearised Einstein’s equations. The equations can now be written in the Fourier space by suitable Fourier decompositions of \(\varPhi , \delta \rho _i, \delta p_i\) etc. and replacing \(\nabla ^2\) by \(-k^2\). The equations then take the form [107]

$$\begin{aligned}&3 H^2 \varPhi + 3 H {\dot{\varPhi }} + \frac{k^2 \varPhi }{a^2} = -4 \pi G \sum _i \delta \rho _i \,\,, \end{aligned}$$
(23)
$$\begin{aligned}&k^2({\dot{\varPhi }} + H \varPhi ) = 4 \pi G a\sum _i({\bar{\rho }}_i+{\bar{p}}_i)\theta _i \,\,, \end{aligned}$$
(24)
$$\begin{aligned}&\ddot{\varPhi } + 4 H {\dot{\varPhi }} +2{\dot{H}} \varPhi + 3 H^2 \varPhi = 4 \pi G \sum _i \delta p_i\,\,. \end{aligned}$$
(25)

It is to be mentioned here that for simplicity we have kept the notations of the quantities \(\varPhi , \delta \rho _i, \delta p_i\) etc. unchanged while writing them in the Fourier space. Here the summation over i represents the summation of the perturbations of the matter component (both dark matter and baryonic matter) and the perturbation of the Slotheon field. In what follows, matter perturbations are designated by subscript m and perturbations for Slotheon field are designated by subscript \(\pi \). Since dust like particles have negligible pressure fluctuations, only the Slotheon field contributes to the pressure density perturbations in this case. The velocity gradient \(\theta \) in the above takes the form \(\theta =i \overrightarrow{k}\cdot \overrightarrow{v}\) in the Fourier space, k being the wave number defined as \(k=\frac{2 \pi }{\lambda _p}\) with \(\lambda _p\) being the length scale of the perturbations. All perturbed quantities in the above equations correspond to the perturbations of the kth mode. The dynamical equation for \(\delta \pi \) can be obtained from the Slotheon action (Eq. (2)) for the perturbed space time metric (Eq. (10)), as

$$\begin{aligned}&\frac{1}{M^2}\left[ H{\dot{\pi }} \frac{k^2 \varPhi }{a} +18 \varPhi {\dot{a}}^3{\dot{\pi }} - 2 \ddot{a} k^2 \delta {\pi } +2 {\dot{a}} {\dot{\pi }} k^2 \varPhi -3{\dot{a}}^3 \delta {\dot{\pi }} \nonumber \right. \\&\quad + H^2 a (-k^2 \delta \pi )+\frac{{\dot{\pi }} k^2 {\dot{\varPhi }}}{a} - a^3 M^2 V_{\pi \pi } \delta \pi + 2 M^2 a^3 \varPhi (V_\pi +2\ddot{\pi }) \nonumber \\&\quad +4 a^3 M^2 {\dot{\pi }} {\dot{\varPhi }}+ {\dot{\pi }} a^3 k^2{\dot{\varPhi }} -a^3 M^2 \delta \ddot{\pi } + 36 a^2 \varPhi {\dot{\pi }} H \ddot{a} \nonumber \\&\quad + 18 \varPhi a^3 H^2 \ddot{\pi } - M^2 a k^2 \delta \pi +2 \ddot{\pi } a k^2 \varPhi -6 a^2 H \ddot{a} \delta {\dot{\pi }}\nonumber \\&\quad \left. + 30 a^3 H^2 {\dot{\pi }}{\dot{\varPhi }} +2 {\dot{\pi }} a k^2 {\dot{\varPhi }} -3 a^3 H^2 \delta \ddot{\pi } + 12 a^3 M^2 \varPhi H {\dot{\pi }} \right. \nonumber \\&\quad \left. + 6 {\dot{\pi }} a^2 \ddot{a} {\dot{\varPhi }}-a^3 H(3 M^2 \delta {\dot{\pi }} + 6 \ddot{\pi } {\dot{\varPhi }} - {\dot{\pi }} k^2 \varPhi - 6 {\dot{\pi }} \ddot{\varPhi })\right] . \end{aligned}$$
(26)

In the above \(V_{\pi \pi }\) is the double derivative of the potential \(V(\pi )\) with respect to \(\pi \).

Defining fractional density perturbation as

$$\begin{aligned} \delta = \frac{\delta \rho }{{\bar{\rho }}}\,\,, \end{aligned}$$
(27)

the quantity \(\delta \) is computed for matter as well as Slotheon field by using the Eqs. (23–26).

3.2 Dimensionless variables and initial conditions

In order to solve the perturbation equations numerically, one needs to define certain dimensionless variables and adopt certain well motivated initial conditions for these variables.

To this end the following dimensionless variables will be useful for solving the background equations (Eqs. 6–8) and the linearised perturbed equations (Eqs. 23–26).

$$\begin{aligned} x= & {} \dfrac{{\dot{\pi }}}{\sqrt{6}H M_{\mathrm{pl}}} \,\,, \end{aligned}$$
(28)
$$\begin{aligned} y= & {} \dfrac{\sqrt{V(\pi )}}{\sqrt{3} H M_{\mathrm{pl}}}\,\,, \end{aligned}$$
(29)
$$\begin{aligned} \lambda= & {} -M_{\mathrm{pl}} \dfrac{V_\pi }{V(\pi )}\,\,, \end{aligned}$$
(30)
$$\begin{aligned} \epsilon= & {} \dfrac{H^2}{2M^2}\,\,, \end{aligned}$$
(31)
$$\begin{aligned} q= & {} \frac{\delta \pi }{\dfrac{d\pi }{dN}}\,\,. \end{aligned}$$
(32)

In the above \(N=\mathrm{ln}(a)\) is the number of e-foldings. Using these dimensionless variables in the Eqs. (6–8) and Eqs. (23–26) the following autonomous system of equations are obtained,

$$\begin{aligned} \dfrac{dx}{dN}= & {} \frac{P}{\sqrt{6}}-x \frac{{\dot{H}}}{H^2}\,\,, \end{aligned}$$
(33)
$$\begin{aligned} \dfrac{dy}{dN}= & {} -y \left( \sqrt{\dfrac{3}{2}} \lambda x + \dfrac{{\dot{H}}}{H^2}\right) \,\,, \end{aligned}$$
(34)
$$\begin{aligned} \dfrac{d\epsilon }{dN}= & {} 2 \epsilon \dfrac{{\dot{H}}}{H^2}\,\,, \end{aligned}$$
(35)
$$\begin{aligned} \dfrac{d\lambda }{dN}= & {} \sqrt{6} x \lambda ^2 (1 - \varGamma )\,\,, \end{aligned}$$
(36)
$$\begin{aligned} \dfrac{dq}{dN}= & {} q_1\,\,, \end{aligned}$$
(37)
$$\begin{aligned} \dfrac{d\varPhi }{dN}= & {} \varPhi _1 \,\,, \end{aligned}$$
(38)
$$\begin{aligned} \dfrac{dq_1}{dN}= & {} \delta \pi _f-\frac{q {\dot{H}}}{x H^2} \dfrac{dx}{dN}- \frac{2 q_1}{x} \dfrac{dx}{dN} -q_1\frac{{\dot{H}}}{H^2}\,\,, \end{aligned}$$
(39)
$$\begin{aligned} \dfrac{d\varPhi _1}{dN}= & {} \frac{\delta p_f}{4\epsilon } -4 \varPhi _1-2 \frac{{\dot{H}}}{H^2}\varPhi -3\varPhi -\varPhi _1 \frac{{\dot{H}}}{H^2} \,\,, \end{aligned}$$
(40)

where \(\varGamma =\frac{V V_{\pi \pi }}{V_\pi ^2}\) and

$$\begin{aligned}&P =\frac{3 (12 \sqrt{6} x^3 \epsilon - 6 x^4 \beta \epsilon (1 + 18 \epsilon ) + y^2 \lambda + \beta (-1 + y^2))}{1 + 6 \epsilon (1 + x^2 (-1 + 18 \epsilon ))} \nonumber \\&+ \frac{3 \sqrt{6} x (-1 -6 \epsilon y^2))}{1 + 6 \epsilon (1 + x^2 (-1 + 18 \epsilon ))} \nonumber \\&+\frac{3x^2 (-6 y^2 \epsilon \lambda + \beta (1 - 6 \epsilon (-4 + y^2)))}{1 + 6 \epsilon (1 + x^2 (-1 + 18 \epsilon ))}\,\,, \end{aligned}$$
(41)
$$\begin{aligned}&\frac{{\dot{H}}}{H^2} = \frac{12 \sqrt{6} x^3 \beta \epsilon (1 + 18 \epsilon ) - 3 x^2 (1 + 6 \epsilon ) (1 + 18 \epsilon )}{2+12\epsilon (1+x^2(-1+18\epsilon ))} \nonumber \\&+ \frac{(1 + 6 \epsilon ) (-3 + 3 y^2)}{2+12\epsilon (1+x^2(-1+18\epsilon ))} \nonumber \\&+ \frac{12 \sqrt{6} x \epsilon (y^2 \lambda + \beta (-1 + y^2))}{2 + 12 \epsilon (1 + x^2 (-1 + 18 \epsilon ))}\,\,. \end{aligned}$$
(42)

As mentioned earlier, that the dimensionless coupling constant \(\beta =0\) in this work. The perturbation in pressure is calculated to be

$$\begin{aligned} \delta p_f= & {} \frac{\delta p_\pi }{M^4} = \frac{6 \sqrt{6} \lambda q x y^2 \epsilon }{1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1}} \\&\frac{ -4 \epsilon ^2 \left( \frac{{\dot{H}}}{H^2} x+\frac{dx}{dN}\right) \left( 6 x \left( 3 L q -3 L_i q - 8 \varPsi -2\varPsi _1 \right) \right) }{1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1}} \\&+\frac{4 \epsilon ^2 \left( \frac{{\dot{H}}}{H^2} x+\frac{dx}{dN}\right) \left( 12 (q \frac{dx}{dN}+ q_1 x)\right) }{1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1}} \\&+ \frac{12 x \epsilon \left( 24 \epsilon \frac{d\epsilon }{dN}+(6 \epsilon +1) (2 (3-2 \frac{{\dot{H}}}{H^2}) \epsilon +1)\right) \left( q \frac{dx}{dN}+ q_1 x \right) }{(6 \epsilon +1) (1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})} \\&-\frac{36 x \varPsi (2 \epsilon )^3 \left( a^2 L x+\frac{L x}{a^2}+2 (L \frac{dx}{dN}+3 x)\right) }{{(6 \epsilon +1) (1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})}} \\&-\frac{2 x \epsilon \left( 6 x \varPsi (2 \epsilon (72 \epsilon +19)+1)-72 L q x \epsilon (6 \epsilon +1)\right) }{{(6 \epsilon +1) (1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})}} \\&+\frac{2 x \epsilon \left( 8 \sqrt{6} \varPsi \epsilon (2 \sqrt{6} \frac{dx}{dN} (9 \epsilon +1)-3 \lambda y^2)\right) }{{(6 \alpha \epsilon +1) (1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})}} \\&-\frac{12 L x \varPsi _1 \epsilon }{a^2}-12 a^2 L x \varPsi _1 \epsilon \\&+\frac{3 q x \left( 4 L \frac{d\epsilon }{dN}+(6 \epsilon +1) \left( L_i-L\right) \right) 24 x \epsilon ^2}{(6 \epsilon +1)(1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})} \\&+\frac{x \varPsi \left( (6 \epsilon +1)\left( 2 +4 \frac{{\dot{H}}}{H^2}-3 L+3 L_i+4 \right) -72 \frac{d\epsilon }{dN}\right) 24 x \epsilon ^2}{(6 \epsilon +1)(1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})} \\&+\frac{2 \varPsi _1 \left( x (3 (\epsilon (6 -4 (L+7))-2 \frac{d\epsilon }{dN}+1)-4)+12 \frac{dx}{dN} \epsilon \right) 24 x \epsilon ^2}{(6 \epsilon +1)(1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})} \\&-\frac{32 a \epsilon ^2 \left( 2 (9 \varPsi \epsilon +\varPsi ) +3 (2 \epsilon ) (L \varPsi -\varPsi _1)\right) 6 a x^2}{a^2 (6 \epsilon +1(1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})} \\&+\frac{4 a \epsilon ^2 \left( (6 \epsilon +1)-24 \epsilon \right) \left( -2 \frac{{\dot{H}}}{H^2} \varPsi -3 \varPsi -4 \varPsi _1 \right) 6 a x^2}{a^2 (6 \epsilon +1)(1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})} \\&+\frac{8 a q \epsilon ^2 \left( -\frac{3 y^2}{\sqrt{6} x}\frac{d\lambda }{dN}+3 y^2 \lambda ^2 \right) 6 a x^2}{a^2 (6 \epsilon +1)(1-\frac{6 x^2 \epsilon -108 x^2 \epsilon ^2}{6 \epsilon +1})} \,\,. \end{aligned}$$

In the above \(L=\frac{k^2}{3 a^2 H^2}\) and \( L_i=\frac{k_i^2}{3 a^2 H^2}\), where \(k_i\) is the i th component (\(i=x,y,z\)) of k. Considering that the Universe is isotropic, we assume \(L_x=L_y=L_z=\frac{L}{3}\) for the present calculations. The perturbation in the Slotheon field is deduced as

$$\begin{aligned} \delta \pi _f= & {} \frac{\delta \ddot{\pi }}{H^2 \dfrac{d\pi }{dN}} \\= & {} \frac{6 \sqrt{6} \epsilon \left( L x \varPhi + a^4 L x \varPhi 6 a^2 x \varPhi +2 a^2 L \dfrac{dx}{dN} \varPhi \right) -3 a^2 \sqrt{6} L q x }{a^2 x \sqrt{6} (1 + 6 \epsilon )} \\&+\frac{ -6 a^2 \sqrt{6} L q x(3 \epsilon + \dfrac{d\epsilon }{dN})}{a^2 x \sqrt{6} (1 + 6 \epsilon )} \\&+ \frac{a^2\left( 4 \sqrt{6} \dfrac{dx}{dN} \varPhi (1+9\epsilon ) + 4 \sqrt{6} x \varPhi (2+9( \epsilon + \dfrac{d\epsilon }{dN}))-6 y^2 \lambda \varPhi \right) }{a^2 x \sqrt{6} (1 + 6 \epsilon )} \\&+ \frac{-3 a^2 \sqrt{6}\left( 1+2(3\epsilon + \dfrac{d\epsilon }{dN})\right) \left( q1 x+ q \dfrac{dx}{dN}\right) }{a^2 x \sqrt{6} (1 + 6 \epsilon )} \\&+\frac{\sqrt{6}\left( -6 x a^2 \varPhi _1(\frac{-{\dot{H}}}{H^2} +1) 2\epsilon \right) }{a^2 x \sqrt{6} (1 + 6 \epsilon )} \\&+ \frac{\sqrt{6}\left( 6\varPhi _1 L x \epsilon + 6 \varPhi _1 a^4 L x \epsilon \right) }{a^2 x \sqrt{6} (1 + 6 \epsilon )} \\&+ \frac{ \sqrt{6} \left( 2\varPhi _1 a^2 \left( 6\dfrac{dx}{dN} \epsilon +2 x + 6 x \epsilon (7+L)+ 3 x \dfrac{d\epsilon }{dN} \right) \right) }{a^2 x \sqrt{6} (1 + 6 \epsilon )} \\&+\frac{\sqrt{6}\left( a^2 x \varPhi (\frac{{\dot{H}}}{H^2} +1)(4+36 \epsilon +12 L\epsilon \right) }{a^2 x \sqrt{6} (1 + 6 \epsilon )} \\&+\frac{\sqrt{6} \left( a^2 q x (\frac{3 y^2}{\sqrt{6}x}\dfrac{d\lambda }{dN}-3 \lambda y^2)\right) }{a^2 x \sqrt{6} (1 + 6 \epsilon )} \\&+ \frac{12\sqrt{6} a^2 x \epsilon \left( \frac{\delta p_f}{4\epsilon } - 4 \varPhi _1 -2 \frac{{\dot{H}}}{H^2}\varPhi -3\varPhi \right) }{a^2 x \sqrt{6} (1 + 6 \epsilon )} \,\,. \end{aligned}$$

The Initial Conditions

The autonomous equations (Eqs. 33–40) are solved by adopting certain initial conditions for the background quantities as well as for the perturbed quantities. We choose the initial conditions at red shift \(z\simeq 1100\), i.e., at the early matter dominated Universe. We consider thawing Dark Energy models [108,109,110] for the Slotheon field. In a thawing model, the equation of state (EOS) \(\omega _\pi \) starts deviating from a frozen initial value of \(-1\) with the progress of time. The initial conditions for thawing model indicate that \(x_i\), the initial value of dimensionless quantity x (Eq. (28)), is close to zero. In this case we take a very small value of \(x_i\). The initial value \(y_i\) of y (Eq. (29)) is so chosen that the Dark Energy density parameter \(\varOmega _\pi \) and the matter density parameter \(\varOmega _m\) attain the values of around 0.69 and 0.31 respectively at the present epoch. The initial value \(\lambda _i\) of \(\lambda \) (Eq. (30)) that determines the slope of the potential \(V(\pi )\) is adopted to be 0.7. The initial value \(\epsilon _i\) of \(\epsilon \) (Eq. (31)) is treated as a parameter (it may be noted that the change in \(\epsilon _i\) in fact indicates the change in the energy scale M). The variable \(\epsilon \) contributes to the Slotheon term \(\dfrac{G^{\mu \nu }}{2M^2} \pi _{;\mu }\pi _{;\nu }\).

It is observed that when the initial value \(x_i \sim 0\) the results do not change significantly with the change of \(x_i\), whereas the results are very sensitive to the choice of \(y_i\). Noting that the dimensionless variable \(\epsilon \) related to the Hubble parameter \(H_0\) (as Eq. (31)), the initial values of \(\epsilon \) are so chosen that at the present epoch \(H_0\) attains a value of around 67.4 km \(\hbox {s}^{-1}\) \(\hbox {Mpc}^{-1}\) [111]. It is found that the mass scale M is very small i.e., around \(10^{-52}\) \(M_{\mathrm{Pl}}\). But as the value of Hubble parameter at the present epoch is of the order \(10^{-60} M_{\mathrm{Pl}}\), the mass scale M is quite large compared to Hubble parameter at the present epoch.

At a very early epoch of matter dominated Universe, there was no or negligible contribution of Dark Energy to the matter energy content of the Universe. In the present context, therefore Slotheon field had insignificant contribution at that era. In this work we adopt small values for \(q_i\) and \(q_{1i}\), where \(q_i\) and \(q_{1i}\) are the initial conditions for q (Eq. (32)) and \(q_1\) Eq (37) respectively. For choosing initial value of the gravitational potential we first write the Poisson’s equation for gravitational potential (in Fourier space \(\nabla ^2=-k^2\))

$$\begin{aligned} k^2 \varPhi = -4\pi G a^2 \sum _i {\bar{\rho }}_i \delta _i\,\,. \end{aligned}$$
(43)

Now in the early matter dominated epoch \(\varOmega _m=1\) and \(\varOmega _\pi =0\). Thus the initial condition of \(\varPhi \) can be obtained from the relation

$$\begin{aligned} \varPhi _i=-\frac{3}{2} \frac{H_i^2}{k^2} a_i^3\,\,, \end{aligned}$$
(44)

where \(\varPhi _i\) is the initial gravitational potential. In Eq. (44), it is considered that during matter dominated era matter density contrast \(\delta _m\) is proportional to a. It is known that during the matter dominated era, \(\varPhi \) is almost constant. Thus at this epoch \(\varPhi _1\) \((\varPhi _1=\frac{d\varPhi }{dN}\), Eq. (38))\(=\varPhi _{1i}=0\).

4 Numerical solutions and results

The autonomous system of equations (Eqs. 33–40) are solved numerically using the initial conditions mentioned above and considering an exponential form for the potential \(V(\pi )\) as given in Eq. (9).

4.1 Equation of state and density parameters

From the Einstein’s equations of the background space time (Eqs. 6–8), density parameter \(\varOmega _\pi (=\frac{{\bar{\rho }}_\pi }{\rho _c})\) of the field \(\pi \) and the matter density parameter \(\varOmega _m (=\frac{{\bar{\rho }}_m}{\rho _c}\), \(\rho _c\) being the critical density of the Universe) are obtained as

$$\begin{aligned} \varOmega _\pi= & {} y^2+x^2(1+18 \epsilon )\,\,, \end{aligned}$$
(45)
$$\begin{aligned} \varOmega _m= & {} 1-y^2-x^2(1+18 \epsilon )\,\,, \end{aligned}$$
(46)

where x, y etc. are defined in Eqs. (28–32). The effective EOS (\(\omega _\mathrm{eff}\)) is derived as

$$\begin{aligned} \omega _\mathrm{eff} = \frac{p_\mathrm{total}}{\rho _\mathrm{total}} = -1-\frac{2 {\dot{H}}}{3 H^2}\,\,, \end{aligned}$$
(47)

where \( p_\mathrm{total}=p_{m} +p_\pi \) and \( \rho _\mathrm{total} = \rho _{m} +\rho _\pi \). Hence for the flat FRW Universe, EOS \(\omega _\pi \) of the Slotheon field \(\pi \) takes the form

$$\begin{aligned} \omega _\pi =\frac{\omega _\mathrm{eff}}{\varOmega _\pi }\,\,. \end{aligned}$$
(48)

Using these equations, evolution of density parameters with scale factor a and the evolution of \(\omega _\pi \) with redshift z are calculated and the results are plotted in Fig. 1.

Fig. 1
figure 1

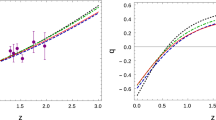
a Variations of dark energy density parameter (\(\varOmega _\pi \)) and matter density parameter (\(\varOmega _m\)) with scale factor a. b Variations of equation of state parameters of the Slotheon field for different \(\epsilon _i\), namely \(\epsilon _i=10^7, 2.5\times 10^7, 4.5\times 10^7, 6.5 \times 10^7\), with redshift z. Variation of the equation of state parameter of the standard quintessence field is also shown for comparison

Full size image

From Fig. 1a it is seen that \(\varOmega _m = 1\) and \(\varOmega _\pi =0\) at the early matter dominated Universe. As the Universe undergoes evolution with time (a increases) the matter density depletes whereas the Dark Energy density (the Slotheon field density in the present work) grows. The cross over of the two occurs at the epoch when \(a \sim 0.77\) after which Dark Energy component starts dominating over the matter component of the Universe. This may be noted that the value of redshift z at crossover point (\( a \sim 0.77\), Fig. 1a) is \(z \sim 0.3\). Thus the phenomenon of Dark Energy domination and the consequent late time acceleration of the Universe happens at a recent cosmological past. Also from Fig. 1a this can be seen that at the present epoch (\(a=1\)), \(\varOmega _\pi \simeq 0.69\) and \(\varOmega _m\simeq 0.31\).

In Fig. 1b the variations of the EOS \(\omega _\pi \) for the Slotheon field \(\pi \) with redshift z are shown for four different initial values of \(\epsilon \) chosen as \(\epsilon _i=10^7, 2.5\times 10^7, 4.5\times 10^7, 6.5 \times 10^7\). Similar variations for the standard quintessence field are also shown in the same figure for comparison. One can see from Fig. 1b that for higher values of \(\epsilon \) the nature of the variations of \(\omega _\pi \) with z tends to \(\varLambda \)CDM value of \(-1\) while they deviate from the nature expected from the quintessence model. This can be explained by the fact that the Slotheon term causes an extra slow roll to the scalar field \(\pi \) and hence the Slotheon scalar field has more affinity towards \(\varLambda \)CDM than the canonical scalar field without this term.

Fig. 2
figure 2

Evolutions of gravitational potentials with scale factor a for the Slotheon field for the three initial values of \(\epsilon \) namely \(2.5\times 10^7, 4.5\times 10^7, 6.5 \times 10^7\). Similar evolutions for standard quintessence field and \(\varLambda \)CDM model are also plotted for comparison

Full size image
Fig. 3
figure 3

Evolutions of density fluctuations of the Slotheon field for different initial values of the \(\epsilon \) ( \(\epsilon _i=2.5 \times 10^7, 4.5 \times 10^7, 6.5 \times 10^7\)) with scale factor a. For comparison such evolutions are also plotted considering standard quintessence model and \(\varLambda \)CDM model

Full size image

4.2 Density fluctuations of matter field and Slotheon field

We solve numerically the autonomous set of equations (Eqs. (33–40)) and obtain the variations of the gravitational potential \(\varPhi \), the density perturbation \(\delta _\pi \) of the Slotheon field and the matter density contrast \(\delta _m\) with the scale factor. The results are shown in Figs. 2, 3 and 4. For these calculations the adopted initial values of different quantities are discussed in sect 3.

In Fig. 2 the evolution of the gravitational potential \(\varPhi \) with the scale factor a are plotted for the three initial values of \(\epsilon \) namely \(2.5\times 10^7, 4.5\times 10^7, 6.5 \times 10^7\). Similar variations of \(\varPhi \) are also shown for the standard quintessence field for comparison. We also compute the evolution of gravitational potential \(\varPhi \) with a for the \(\varLambda \)CDM model and the results are plotted in the same figure (Fig. 2). From Fig. 2 it is observed that in the early matter dominated epoch, \(\varPhi \) is constant but as the Dark Energy component begins to contribute significantly, the gravitational potential suffers depletion. Note that in the early epoch when there is negligible contribution of the Dark Energy component, both the Slotheon and cosmological constant model behave identically in terms of the variation of \(\varPhi \) with a. But this is not so in later time when the Dark Energy component gradually increases. This is also to mention here that all the calculations in this section are done for different sizes of perturbations but as similar type of conclusions are drawn from each of the cases, here we only show the results for perturbation size \(5\times 10^2\) Mpc.

Fig. 4
figure 4

Evolutions of matter density fluctuations considering the Slotheon field for different initial values of \(\epsilon \), namely \(\epsilon _i=2.5 \times 10^7, 4.5 \times 10^7, 6.5 \times 10^7\), with scale factor a. Evolutions of matter density fluctuations with a, considering standard quintessence model and \(\varLambda \)CDM model are also plotted for comparison

Full size image

The density fluctuations \(\delta _\pi \) and \(\delta _m\) of Slotheon field \(\pi \) and matter respectively are calculated by using the linearised Einstein’s equations (Eqs. 23–26) in terms of the dimensionless variables given in Eqs. (28–32) and they are given as

$$\begin{aligned} \delta _\pi= & {} \frac{1}{\varOmega _\pi }\left( \sqrt{6} q \lambda y^2 x -24 q L \epsilon x^2 - 2 x^2 q_1 -2 q x \dfrac{dx}{dN} \right. \nonumber \\&\left. -36 x^2 \epsilon q_1 - 36 \epsilon q x \dfrac{dx}{dN} + 2 x^2\varPhi + 12 x^2 L \epsilon \varPhi \right. \nonumber \\&\left. +72 x^2\epsilon \varPhi + 36 x^2 \epsilon \dfrac{d\varPhi }{dN}\right) \,\,, \end{aligned}$$
(49)
$$\begin{aligned} \delta _m= & {} -\frac{1}{\varOmega _m}\left( 2 L \varPhi + 2 \varPhi + 2 \varPhi _1 \right) -\delta _\pi \frac{\varOmega _\pi }{\varOmega _m}\,\,. \end{aligned}$$
(50)

In Fig. 3 the perturbations \(\delta _\pi \) (perturbation of Dark Energy considered in this work) with a are plotted for \(\epsilon _i=2.5 \times 10^7, 4.5 \times 10^7, 6.5 \times 10^7\) (\(\epsilon _i \equiv \) initial value for \(\epsilon \)). As in Fig. 2, similar variations for standard quintessence field and \(\varLambda \)CDM are also shown for comparison. It can be observed from Fig. 3 that at the early matter dominated epoch, \(\delta _\pi \) is zero, as expected. But with time (higher scale factor) the perturbation of Dark Energy deviates from zero and gradually increases with the rise in the contribution of Dark Energy.

Figure 4 shows the evolution of matter density perturbation \(\delta _m\) with the scale factor a for the same initial values of \(\epsilon \) adopted in Fig. 2 and 3. Quintessence and \(\varLambda \)CDM results are also shown for comparison. Here too, at the initial stage \(\delta _m\) is small and grows almost linearly in the matter dominated epoch. Thus \(\delta _m \sim a\) in the matter dominated era. This growth appears to be depleted to some extent in the Dark Energy dominated epoch (\(a > 0.77\)). Note that \(\delta _m\) in the Slotheon model coincides with that of \(\varLambda \)CDM and standard quintessence models in the early Universe but they deviate more with time as a result of the increment of the Dark Energy contribution with time.

5 The effect of the Slotheon field on matter power spectrum

In this section we explore the effect of the Slotheon Dark Energy perturbations on the matter power spectrum of the Universe. We compute the matter power spectrum with the Slotheon field and compare it with the same obtained from \(\varLambda \)CDM model. For \(\varLambda \)CDM model, cosmological constant \(\varLambda \) is constant and there are no Dark Energy perturbations, but in the Slotheon model, with evolving equation of state \(\omega _\pi \), the Dark Energy perturbations play important role for the nature of the power spectrum.

Matter power spectrum is defined as the average of the modulus square of the matter density fluctuation \(\delta _m(k,a)\) and is given by [107]

$$\begin{aligned} Pm=\langle |\delta _m(k,a)|^2\rangle \,\,. \end{aligned}$$
(51)

We compute the matter power spectrum \(Pm_\mathrm{slotheon}\) for Slotheon field and that (\(Pm_{\varLambda \mathrm{CDM}}\)) for \(\varLambda \)CDM model using equations in Sect. 3 and Eqs. (49–50). We define a percentage suppression X for the Slotheon power spectrum with respect to the power spectrum obtained from \(\varLambda \)CDM model as

$$\begin{aligned} \frac{Pm_{\varLambda \mathrm{CDM}}-Pm_{\mathrm{slotheon}}}{Pm_{\varLambda \mathrm{CDM}}} \times 100 = \frac{\varDelta Pm}{Pm_{\varLambda \mathrm{CDM}}}\times 100=X\,\,. \end{aligned}$$
(52)
Fig. 5
figure 5

Variations of the suppressions for the Slotheon power spectrum w.r.t. the \(\varLambda \)CDM power spectrum, with wave number k. Variations are plotted for three different fixed initial values of \(\lambda \), namely \(\lambda _i=0.5, 0.7, 1\)

Full size image

In Fig. 5 we plot the variations of X with k for \(\epsilon _i=6.5 \times 10^7\) at redshift \(z=0\). Three such variations corresponding to three different fixed values of \(\lambda _i\), namely \(\lambda _i=0.5, 0.7, 1\), are shown in Fig. 5. From Fig. 5 it is seen that in general for lower values of k the percentage suppressions X is more which slowly diminishes as k increases. For example for \(\lambda _i=0.7\), the suppression \(X \sim 2\%\) for \(k=10^{-3}\) \(\hbox {Mpc}^{-1}\) but X is reduced to \(\sim 1.8\%\) when \(k=4 \times 10^{-2}\) \(\hbox {Mpc}^{-1}\). This scale dependence may indicate the fact that the Dark Energy inhomogeneities play an extra roll in large scales. This may be mentioned in the passing that for larger k values (around \(k > 0.1h\) \(\hbox {Mpc}^{-1}\)) non linearity sets in [112, 113] and linear perturbation treatment may not be useful. From Fig. 5 it can also be noted that X decreases with the decrease of \(\lambda _i\). It is expected because \(\lambda \) is related to the slope of the potential \(V(\pi )\) (Eq. (9)). Hence more \(\lambda _i\) decreases, more flat the potential \(V(\pi )\) tends to be and consequently approaches to \(\varLambda \)CDM model (which is based on a flat potential). It can also be mentioned from Fig. 5 that power spectrum for Slotheon field is not much different from \(\varLambda \)CDM power spectrum since the maximum suppression is only \(\sim 3.8\%\) even for \(\lambda _i=1\).

Hence Slotheon model behaviours are more akin to \(\varLambda \)CDM model (\(\varLambda \)CDM is a popular model to be used in power spectrum analysis) than the general quintessence one but any detection of the Dark Energy inhomogeneities will rule out the cosmological constant theory of Dark Energy but can not rule out the Slotheon field Dark Energy model.

6 Summary and discussions

The Dark Energy and late time acceleration of the Universe are addressed in this work by considering a type of scalar field, namely Slotheon scalar field, in a modified theory of gravity. Slotheon field is inspired by extra dimensional models at the dimensional cross over limit when Planck scale \(M_\mathrm{pl} \rightarrow \infty \) and the theory is extended to curved space time. In order to address the inhomogeneities of Dark Energy and their evolutions, quantities such as matter density fluctuations, the perturbations of the scalar field etc. are worked out in this paper. All the perturbation equations are then solved numerically.

The evolution of Dark Energy density \(\varOmega _\pi \) for the Slotheon scalar field \(\pi \) in the potential \(V(\pi )\) and the matter density \(\varOmega _m\) are calculated. The epoch of transition from matter dominated phase of the Universe to Dark Energy dominated phase (cross over epoch) is found to be at \(z \simeq 0.3\) for the Slotheon Dark Energy considered here. The evolution of Dark Energy equation of state (\(\omega _\pi \)) is also calculated. The Dark Energy in the Slotheon field is considered to be a thawing type Dark Energy.

The perturbation equations for the Slotheon field and matter are then derived with a suitable metric and from Einstein’s equations and they are solved numerically. This is done to study the evolution of Dark Energy density perturbations for the present case of Slotheon scalar field Dark Energy as well as evolution of matter perturbations in the same framework. These results are then compared with those for standard quintessence Dark Energy model of a scalar field and \(\varLambda \)CDM model for which the Dark Energy has a constant magnitude \(\varLambda \).

A crucial component for all the studies and calculations is to choose proper initial conditions for the dimensionless variables. In the present work all the choices of such initial conditions are justified with proper arguments. For evolution of gravitational potential and the evolution of matter perturbations, we find that although in the early Universe the results obtained with Slotheon model coincide with those of \(\varLambda \)CDM and general quintessence, they deviate away in later time. The Dark Energy density fluctuations deviate from zero with time as the Dark Energy density grows in the Universe. From the calculations and analyses in the present work it appears that the behaviour of Dark Energy from Slotheon model is more akin to the results of \(\varLambda \)CDM model than those from general quintessence model.

A discussion on the appearance of a fifth force for the case of the present Slotheon field model is in order. There may be a possibility that a fifth force may appear in case the scalar field \(\pi \) introduced in this work couples with matter. In this work it is considered that the Slotheon scalar field and the matter field are not coupled to each other. The coupling constant \(\beta \) is assumed to be 0 in this work. This is mentioned in page 3 (before equation (6)) of the present manuscript. Since there is no coupling between the Slotheon scalar field and the matter field, the fifth force does not arise in our work.

However for non zero values of the coupling \(\beta \), the fifth force constraints would be relevant. In reference [99] the authors have discussed this Slotheon field scenario (with same exponential form of the potential as adopted in this work), where the Slotheon scalar field is non-minimally coupled to the matter field. From the analysis of different observational data, the coupling \(\beta \) had been found to be constrained within a very small range of values for \(\beta \) (\(-0.05< \beta < 0.08\), Fig. 5 of Ref. [99]). Hence, as it is well within the observational constraints, it is justified to consider \(\beta =0\) in our work. In reference [99], the authors have also shown that, although the results obtained from the non-minimally coupled Slotheon scalar field model are different from the general relativistic results at large redshift (\(\mathrm{log}(1+z)>6\)) but they are same as General Relativity (GR) results for smaller redshifts. Thus ordinary GR is recovered in small redshifts in this Slotheon scenario.

In literature it has also been discussed that for DGP modification of gravity the Vainshtein effect is present locally and in these models, gravity is modified on large scales but preserved close to massive bodies due to the non-linearities of the kinetic terms of the scalar field (Refs. [114,115,116]). Since Slotheon model is derived from the DGP model and in fact is the extension of the Galileon model in curved space-time, the discussions regarding the fifth force in case of DGP model are also extended to Slotheon field and Slotheon field also preserves local gravity constranits. Moreover in Ref. [107], the authors have discussed the chameleon type mechanism for scalar field with general form of potential and showed that when the coupling between the scalar field and the matter field is \(<< 1\), the fifth force is suppressed relative to the gravitational force (same conclusions can be drawn from Ref. [117]). Now since as shown in Ref. [99] that for the Slotheon field the coupling \(\beta \) takes a very small constant value (\(-0.05< \beta < 0.08\) and not a function of the field) all over the spacetime, the model remains compatible with the local gravity constraints.

Recent LIGO detection of Gravitational Wave (GW) and the bounds obtained from such observations may also affect the types of Dark Energy models. From the observation of GW from the neutron star merger (GW 170817) the speed of the GW is constrained as [118]

$$\begin{aligned} -3 \times 10^{-15} \le \frac{c_T}{c_\gamma }-1 \le 7 \times 10^{-16}\,\,, \end{aligned}$$
(53)

where \(c_T\) denotes the GW phase velocity and \(c_\gamma \) the speed of light. This implies that GWs would travel luminally. Also the present LIGO bounds are for GWs at frequency \(10 - 100\) Hz [118], therefore the gravitational speed in this case is a function of the measured GWs’ frequency. In Ref. [118] with a specific scalar model of Dark Energy the authors show that GW sound speed tends to luminal at a frequency accessible to LIGO. The Horndeski scalar tensor theory can mimic modified gravity models arise from the decoupling limit of DGP [119]. The Galileon model or the present Slotheon model also follows from the decoupling limit of DGP. In such model of modified gravity the sound speed remains luminal (dispersion relation is modified at low frequencies [118]). Thus such models can not be ruled out after the GW 170817 phenomenon since for these models GW speeds at LIGO may very well remain luminal. Therefore the Slotheon Dark Energy model can not be ruled out using LIGO constraints from GW 170817. However with more possible GW data in future a more involved study of Slotheon model may be worth pursuing. But this is for posterity.

Thus from our calculations we may conclude that the results derived from the Slotheon model are more in agreement with \(\varLambda \)CDM model than those obtained from quintessence one. But perturbations and inhomogeneities in Dark Energy can not be addressed in \(\varLambda \)CDM framework. Possible existence of Dark Energy inhomogeneities are yet to be probed. This perturbations, if exist would be relevant in horizon scales. But with the up coming experiments like SKA, it may be possible in future to explore such inhomogeneities. Any signature of these perturbations could be decisive for the validity of \(\varLambda \)CDM model but the Slotheon model will continue to be valid and viable in such scenario, whose non-perturbative results are more similar to \(\varLambda \)CDM.