1 Introduction

Heavy meson decays can serve as a probe for New Physics (NP) beyond the Standard Model (SM). Of particular interest, CP violation in heavy mesons decays can discriminate between many extensions beyond SM physics that have new complex couplings of the new particles to quarks or leptons. These couplings provide the sources of the so called weak phases which are essential for having non vanishing CP violation. In the SM, complex couplings can arise only in the Cabibbo–Kobayashi–Maskawa (CKM) matrix describing the quark mixing [1, 2]. The couplings of the interactions of the charged quarks to \(W^\pm \) gauge bosons are proportional to the CKM matrix elements. Thus, with the presence of such interactions, CP violation can be generated in the SM. However, the CP violation in the SM is too small to account for the observed baryon asymmetry which plays an important role in the domination of matter in our local regions in the universe.

In the mesons sector, CP violation has been observed in the kaon and B mesons [3,4,5,6]. Regarding D mesons, the \(D^0 -{\bar{D}}^0\) mixing was discovered in 2007 after combining the results from BABAR [7], Belle [8] and CDF [9]. Later, the mixing has been observed at LHCb [10] and at Belle [11, 12]. Concerning direct CP violation in D meson decays, the direct CP asymmetry difference, \(\Delta A_{CP}\), between \(D^0\rightarrow \pi ^+\pi ^-\) and \(D^0\rightarrow K^+K^-\) is defined as

$$\begin{aligned} \Delta A_{CP} = A_{CP}(K^-K^+) - A_{CP}(\pi ^-\pi ^+) \end{aligned}$$
(1)

Measurement of \(\Delta A_{CP}\) was reported firstly in 2011 by the LHCb Collaboration [13] and later by CDF [14] and Belle [15]. The latest measurement of \(\Delta A_{CP}\), by LHCb collaboration, combined with the previous LHCb searches leads to a combined value [16]

$$\begin{aligned} \Delta A_{CP} = (-15.6 \pm 2.9) \times 10^{-4} \end{aligned}$$
(2)

This value is 5.3 standard deviations away from zero and hence confirms direct CPV in these particular weak decays of \(D^0\) meson. The result also inspires search for CP violation in other decay modes of D mesons and motivates further theoretical studies.

Two body non-leptonic D decays can be sorted into Cabibbo-Favored (CF), singly Cabibbo-suppressed (SCS) and Double Cabibbo Suppressed (DCS) according to the suppression factor \(\lambda \simeq |V_{us}| \simeq |V_{cd}|\) appears in their amplitudes. In the SM, previous studies showed that direct CP-asymmetry of order \(10^{-3}\) can be obtained for some SCS decay modes [17, 18]. For examples, the CP asymmetries of the decays \(D^0 \rightarrow K_s K^{*^0}\) and \(D^0 \rightarrow K_s {\bar{K}}^{*^0}\) were estimated to be as large as \( 3 \times 10^{-3}\) [18]. With more investigations in SCS decay modes, within SM also, a large CP-asymmetry of order \(10^{-2}\) was predicted for the mode \(D^0 \rightarrow K_s K_s\) [19]. Turning to the CF and DCS two body D decays, the asymmetries, within SM, are expected to be so tiny and of order \(\lesssim 10^{-9}\) for \(D^0 \rightarrow K^- \pi ^+ \) and \(D^0 \rightarrow K^+ \pi ^- \) as estimated in our earlier studies in Refs. [20, 21]. The result motivated us to explore, also in the same studies, NP effects in these decay processes where we showed that in some extensions of the SM sizable CP asymmetry of order \(10^{-2}\) can be obtained. In this work, we extend our studies in Refs. [20, 21] to explore direct CP violation in charged D decays to CF and DCS \(K\pi \) final states. In particular, we consider the CF mode \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\) and the DCS \(D^+ \rightarrow K^0 \pi ^+\) decay mode. The direct CP asymmetries of \(D^+ \rightarrow K^0({\bar{K}}^0) \pi ^+\) are expected to be different than those of \(D^0 \rightarrow K^\pm \pi ^\mp \) as the strong CP violating phases contributing to these processes have different origins. In our work in Ref. [20] we found that sizeable direct CP asymmetry of \(D^0 \rightarrow K^- \pi ^+\) can be generated in a specific new physics model namely, in non-manifest Left-Right Symmetric (LRS) model. In this study, we inspect if the model can still lead to sizeable CP asymmetries after taking into account the up to date constraints from collider physics, flavor physics, and low-energy precision measurements.

This paper is organized as follows: in Sect. 2, we derive the amplitudes of the \({\mathrm{CF}}\) and \({\mathrm{DCS}}\) non leptonic \(D^+ \rightarrow K^0({\bar{K}}^0) \pi ^+\) decays in the framework of the SM and give our estimations of their direct CP asymmetries. Motivated by the almost null values of the asymmetries, we extend the analysis to include two possible candidates of NP models. These NP candidates are based on the presence of new charged scalars in general two Higgs models and new charged bosons in no-manifest LRS. These models will be discussed in Sects. 3 and 4 respectively. Finally, we conclude in Sect. 5.

2 Direct CP asymmetry of \({\mathrm{CF}}\) and \({\mathrm{DCS}}\) non leptonic \(D^+ \rightarrow K \pi ^+\) decays in the standard model

In general the effective Lagrangian describing \({\mathrm{CF}}\) and \({\mathrm{DCS}}\) \(D^+ \rightarrow K \pi ^+\) decays can be expressed as

$$\begin{aligned} \mathcal{L}_{\mathrm{eff.}}= & {} {G_F\over \sqrt{2}}V_{c q}^*V_{u q'} \left[ \sum _{i,\ a} c_{1ab}^i \Bigg ({\bar{q}} \, \Gamma ^i \, c_a \Bigg ) \Bigg ({\bar{u}} \, \Gamma _i \, q'_b\Bigg )\right. \nonumber \\&\left. + \sum _{i,\ a} c_{2ab}^i \Bigg ({\bar{u}} \, \Gamma ^ic_a \Bigg )\, \Bigg ({\bar{q}} \, \Gamma _i \, q'_b \Bigg )\right] \end{aligned}$$
(3)

Here \(i=\) S, V and T stands for scalar (S), vectorial (V) and tensorial (T) operators respectively. The Latin indices \(a,\ b=L,\ R\) and \(q'_{L,\ R}=(1\mp \gamma _5)q\). In Eq. (3) \(q\ne q'\) where q and \(q'\) can be d or s down-type quarks. For \(\mathrm{CF}\) decays \(q =s \) and \(q' = d\) while for \(\mathrm DCS\) decays \(q =d \) and \(q' = s\).

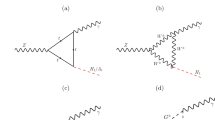
In the SM the contributions from tree-level and loop-level diagrams, shown in Fig.1, lead to the effective Hamiltonian that can be expressed as

$$\begin{aligned} \mathcal{H}^{SM}_{\mathrm{eff.}}= & {} {G_F\over \sqrt{2}}V_{c q}^*V_{u q'}\Bigg [c_1 \Bigg ( {\bar{q}} \gamma _\mu c_L\Bigg ) \Bigg ( {\bar{u}} \gamma ^\mu q'_L\Bigg ) \nonumber \\&+ c_2\Bigg ({\bar{u}} \gamma _\mu c_L \Bigg ) \Bigg ({\bar{q}} \gamma ^\mu q'_L\Bigg ) \Bigg ]+\mathrm{h.c.}\nonumber \\= & {} {G_F\over \sqrt{2}}V_{c q}^*V_{u q'}\left( c_1\, Q_1+c_2\, Q_2\right) +\mathrm{h.c.} \end{aligned}$$
(4)

In the framework of naive factorization approximation (NFA), the amplitude of the decay process under concern can be obtained using \(\mathcal{H}^{SM}_{\mathrm{eff.}}\) via

$$\begin{aligned} A^{SM}_{D^+\rightarrow K \pi ^+} = \langle K \pi ^+ | \mathcal{H}^{SM}_{\mathrm{eff.}} | D^+ \rangle \end{aligned}$$
(5)

Upon evaluating the matrix elements of the operators in Eq. (4), we obtain the amplitudes of the \(\mathrm{CF}\) decay mode \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\) and \(\mathrm DCS\) decay mode \(D^+ \rightarrow K^0 \pi ^+\) as

$$\begin{aligned} A^{SM}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}= & {} -i{G_F\over \sqrt{2}}V_{cs}^*V_{ud} \left[ (a_1+\Delta a^{s d}_1) X^{\pi ^+}_{D^+ {\bar{K}}^0} \right. \nonumber \\&\left. + (a_2+\Delta a^{s d}_2+\Delta a^{s d K^0}_2) X^{{\bar{K}}^0}_{D^+ \pi ^+} \right] ,\nonumber \\ A^{SM}_{D^+ \rightarrow K^0 \pi ^+}= & {} i{G_F\over \sqrt{2}}V_{cd}^*V_{us} \left[ (a_1+\Delta a^{d s}_1) X^{D^+}_{K^0\pi ^+} \right. \nonumber \\&\left. + (a_2+\Delta a^{d s}_2-\Delta a^{d s K^0}_2) X^{K^0}_{D^+ \pi ^+} \right] \end{aligned}$$
(6)

with \( X^{P_1}_{P_2P_3}\) is given by

$$\begin{aligned} X^{P_1}_{P_2P_3}= if_{P_1}\Delta _{P_2P_3}^2 F_0^{P_2P_3}(m_{P_1}^2),\ \Delta _{P_2P_3}^2=m_{P_2}^2-m_{P_3}^2 \end{aligned}$$
(7)

here \(f_{P}\) is the P meson decay constant and \(F_0^{P_2 P_3}\) is the form factor. In Eq. (6) the coefficients \(a_1 = c_1+ c_2/N_C \) and \(a_2=-( c_2+c_1/N_C)\), where \(N_C\) is the color number, account for the tree-level contributions to the amplitudes. These contributions originate from integrating out the \(W^\pm \) boson mediating the tree-level diagrams. On the other hand, and in the same equations, \(\Delta a^{s d, d s}_{1,2}\) and \(\Delta a^{s d K^0, d s K^0}_2 \) account for the contributions to the amplitudes originating from integrating out the \(W^\pm \) boson mediating the box and di-penguin diagrams in Fig. 1. Their expressions are given as

Fig. 1
figure 1

Feynman diagrams for DCS processes: left (right) di-penguins contribution (box) contribution. For CF processes we make the replacements \(d \leftrightarrow s\) in each diagram

Full size image
$$\begin{aligned} \Delta a^{s d}_1\simeq & {} -{G_Fm_W^2 V_{c D}^*V_{u D} V_{U s}^*V_{U d} f(x_U,\ x_D)\over 3 \sqrt{2}\ \pi ^2 } \nonumber \\&- {G_F \alpha _S V_{c D}^*V_{u D} V_{U s}^*V_{U d} K^2 E_0(m^2_D,K^2) E_0(m^2_U,K^2) \over 9\sqrt{2} \pi ^3 }, \nonumber \\ \Delta a^{s d K^0}_2\simeq & {} - {G_F \alpha _S V_{c D}^*V_{u D} V_{U s}^*V_{U d} m_{d} m_c \chi ^{K^0} E_0(m^2_D,K^2) E_0(m^2_U,K^2) \over 32\sqrt{2} \pi ^3}\nonumber \\ \Delta a^{s d}_2\simeq & {} -{G_Fm_W^2 V_{c D}^*V_{u D} V_{U s}^*V_{U d} f(x_U,\ x_D)\over \sqrt{2}\ \pi ^2 }, \nonumber \\ \Delta a^{d s}_1\simeq & {} -\frac{1}{\lambda ^2}\Delta a^{s d}_1\,\,\,\,\,\, \Delta a^{d s}_2 \simeq -\frac{1}{\lambda ^2}\Delta a^{s d}_2, \nonumber \\ \Delta a^{d s K^0}_2\simeq & {} -\frac{m_s}{m_d \lambda ^2}\Delta a^{s d K^0}_2 \end{aligned}$$
(8)

where \(K^2\) is the momentum flow through the gluon propagator and \(\chi ^{K^0} =m_{K^0}^2/(m_c\,m_s)\simeq 2\) and \(\lambda \simeq V_{us}\). In Eq.(8) U, D run over up-type and down-type quarks respectively, \(x_q=(m_q/m_W)^2\) and \(E_0(m^2_i,K^2)\) and \(f(x_U,x_D)\) are loop-functions originate from the box and di-penguin diagrams respectively. Non-vanishing direct CP asymmetry requires the presence of both weak CP violating phase and strong CP conserving phase. The required strong phase can be generated when the quark line in the loop can be put on its mass shell in the well-known BSS (Bander, Silverman, and Soni) mechanism [22]. A similar effect is known also for the penguin amplitudes of the singly-Cabibbo-suppressed charm decays as discussed in Ref. [23]. The loop-function function \(E_0(m^2_i,K^2)\) resulting from the di-penguin diagram in Fig.(1), is given as [22]

$$\begin{aligned} E_0(m^2_i,K^2)= & {} \int ^1_0 dx \, x(1-x)\ln \Bigg [ \frac{m^2_i}{K^2}- x(1-x)\Bigg ] \end{aligned}$$
(9)

In D meson system the momentum-squared of the gluon \(K^2\) is of order \(m^2_c\), a time-like, and and hence absorptive parts can be generated when light quarks such as d and s quarks run in the loop. This can be realized from Eq. (9) for \(K^2> \, 4 m^2_i \) where non-vanishing imaginary parts can be obtained. In fact the desired strong phase is proportional to \( Im\Bigg (E_0(m^2_d,K^2)-E_0(m^2_s,K^2)\Bigg )\equiv \kappa _{d s}\). In Fig. 2 we show the variation of \(\kappa _{d s}\) with the momentum flow through the gluon propagator \(K^2\). As can be seen from Eq.(8) that, the generated strong phases will be suppressed by a factor smaller than \(G_F \alpha _S /(9\sqrt{2} \pi ^3 )\simeq 9\times 10^{-9}\) indicating that BSS mechanism can not be the source of the strong phases in these decay modes. In fact this conclusion is also applied to all nonleptonic D meson decays into two mesons arising from the quark transition \(c\rightarrow u\, s\, d\). Consequently, and in the presence large weak phases, non vanishing direct CP violation in these decays can be only possible if other mechanisms for generating non small strong phases exist. Assuming the presence of such mechanisms, we investigate below how large can be the weak phases and thus the size of the direct CP asymmetry in the SM and in some of its extensions.

Fig. 2
figure 2

Variation of \(\kappa _{d s}\) with \(K^2\)

Full size image

In Refs. [24,25,26,27,28,29], an approach to study charm decays in a model-independent way, the so called the diagrammatic approach, was introduced. Within this approach, the amplitude is decomposed into parts corresponding to generic quark diagrams according to the topologies of weak interactions. For each one of these topological diagrams, the related magnitude and relative strong phase can be extracted from the data without making further assumptions, apart from flavor SU(3) symmetry [24]. Based on the extracted magnitudes and phases, many studies related to the investigation of direct CP violation in nonleptonic two-body D mesons decays were carried out in the literature [20, 21, 30,31,32,33,34,35]. In this approach the amplitudes of the \(\mathrm{CF}\) decay mode \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\) and \(\mathrm DCS\) decay mode \(D^+ \rightarrow K^0 \pi ^+\) as [24]

$$\begin{aligned} A_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}= & {} V_{cs}^*V_{ud}(T+C)\nonumber \\ {\mathcal A}_{D^+ \rightarrow K^0 \pi ^+}= & {} V^*_{cd}V_{us}(C''+A'') \end{aligned}$$
(10)

where the amplitudes T, \(C (C'')\) and \(A''\) represent the tree level color-allowed external W-emission quark diagram, the color-suppressed internal W-emission diagram and the W-annihilation diagram respectively. Their expressions in Naive Factorization Approximation (NFA) can be approximated as

$$\begin{aligned} T\simeq & {} {G_F\over \sqrt{2}} (a_1+\Delta a^{s d}_1) f_\pi m_D^2 F_0^{DK}(m_\pi ^2) \nonumber \\ C= & {} {G_F\over \sqrt{2}} (a_2+\Delta a^{s d}_2+\Delta a^{s d K^0}_2) f_K m_D^2 F_0^{D\pi }(m_K^2) \nonumber \\ C''\simeq & {} \frac{G_F}{\sqrt{2}} (a_1+\Delta a^{d s}_1) f_{D} m^2_K F^{K\pi }_0(m^2_{D})\nonumber \\ A''\simeq & {} \frac{G_F}{\sqrt{2}} (a_2+\Delta a^{d s}_2-\Delta a^{d s K^0}_2) f_K m^2_D F^{D\pi }_0(m^2_K) \end{aligned}$$
(11)

The direct CP asymmetries can be expressed as

$$\begin{aligned} A^{SM}_{CP} (D^+ \rightarrow {\bar{K}}^0 \pi ^+)= & {} {|A^{SM}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2-|{\bar{A}}^{SM}_{D^+ \rightarrow \bar{K}^0 \pi ^+}|^2 \over |A^{SM}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2+|{\bar{A}}^{SM}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2 }\nonumber \\\simeq & {} 2 r\sin (\alpha )\, \sin (\phi _2-\phi _1)\nonumber \\ A^{SM}_{CP} (D^+ \rightarrow K^0 \pi ^+)= & {} {|A^{SM}_{D^+ \rightarrow K^0 \pi ^+}|^2-|{\bar{A}}^{SM}_{D^+ \rightarrow K^0 \pi ^+}|^2 \over |A^{SM}_{D^+ \rightarrow K^0 \pi ^+}|^2+|\bar{A}^{SM}_{D^+ \rightarrow K^0 \pi ^+}|^2 } \nonumber \\\simeq & {} 2 r'\sin (\alpha ')\, \sin (\phi '_2-\phi '_1) \end{aligned}$$
(12)

where \(r=|C/T|\simeq 0.4\), \(r'=|A''/C''| \simeq 5.7\). The strong phases are defined through \(\alpha = \alpha _{C}- \alpha _{T}\) and \(\alpha '= \alpha _{A''}- \alpha _{C''}\) where the phases \(\alpha _{C}\), \(\alpha _{T}\), \(\alpha _{A''}\) and \(\alpha _{C''}\) are the strong phases of the amplitudes C and T, \(A''\) and \(C''\) respectively. The weak phases \(\phi _i\), and \(\phi '_i\), for \(i=1,2\) given in Eq.(12) can be estimated as

$$\begin{aligned} \phi _1= & {} \tan ^{-1}\Bigg ( \frac{|\Delta a^{s d}_1|\sin \Delta \phi _1}{a_1+|\Delta a^{s d}_1|\cos \Delta \phi _1}\Bigg ) \nonumber \\\simeq & {} \tan ^{-1}\Bigg ( \frac{|\Delta a^{s d}_1|\sin \Delta \phi _1}{a_1}\Bigg ) \nonumber \\ \phi _2= & {} \tan ^{-1}\Bigg ( \frac{|\Delta a^{s d}_2+\Delta a^{s d K^0}_2|\sin \Delta \phi _2}{a_2+|\Delta a^{s d}_2+\Delta a^{s d K^0}_2|\cos \Delta \phi _2}\Bigg ) \nonumber \\\simeq & {} \tan ^{-1}\Bigg ( \frac{|\Delta a^{s d}_2+\Delta a^{s d K^0}_2|\sin \Delta \phi _2}{a_2}\Bigg )\nonumber \\ \phi '_1= & {} \tan ^{-1}\Bigg ( \frac{|\Delta a^{ d s}_1|\sin \Delta \phi '_1}{a_1+|\Delta a^{d s}_1|\cos \Delta \phi '_1}\Bigg ) \nonumber \\\simeq & {} \tan ^{-1}\Bigg ( \frac{|\Delta a^{ d s}_1|\sin \Delta \phi '_1}{a_1}\Bigg )\nonumber \\ \phi _2= & {} \tan ^{-1}\Bigg ( \frac{|\Delta a^{d s }_2-\Delta a^{d s K^0}_2|\sin \Delta \phi '_2}{a_2+|\Delta a^{d s}_2-\Delta a^{d s K^0}_2|\cos \Delta \phi '_2}\Bigg ) \nonumber \\\simeq & {} \tan ^{-1}\Bigg ( \frac{|\Delta a^{d s }_2-\Delta a^{d s K^0}_2|\sin \Delta \phi '_2}{a_2}\Bigg ) \end{aligned}$$
(13)

where \(\Delta \phi _1\) and \(\Delta \phi _2\) (\(\Delta \phi '_1\) and \(\Delta \phi '_2\)) denote the weak phases of \(\Delta a^{s d}_1\) and \(\Delta a^{s d}_2+\Delta a^{s d K^0}_2\) (\(\Delta a^{d s}_1\) and \(\Delta a^{d s}_2-\Delta a^{d s K^0}_2\)) respectively. Using \(a_1= 1.2 \pm 0.1\) and \(a_2 = - 0.5 \pm 0.1\), we find that \(\sin (\phi _2-\phi _1) \simeq -2.0\times 10^{-10}\) and \(\sin (\phi '_2-\phi '_1) \simeq 4.8\times 10^{-9}\). Clearly, due to the so tiny weak phases, the asymmetries \(A^{SM}_{CP} (D^+ \rightarrow {\bar{K}}^0 \pi ^+)\) and \(A^{SM}_{CP} (D^+ \rightarrow K^0 \pi ^+)\) vanish in the SM, regarding how large are the required strong phases and the mechanisms generating them. In the following, we investigate the possibility of generating large weak phases in two extensions of the SM.

3 Models with charged Higgs contributions

Possible extensions of the SM include the two Higgs doublet models (2HDM) [36, 37]. Based on their couplings to quarks and leptons, these models can be classified into several types: type I, II or III and so on (for a review see Ref. [38]). Among these, 2HDM type III (2HDM III) is of a particular interest to our study. This can be attributed to the presence of complex couplings of Higgs to quarks. These couplings are relevant for generating the desired CP violating weak phases. In the literature, 2HDM III has gain interest as it can explain \(B\rightarrow D\tau \nu \), \(B\rightarrow D^*\tau \nu \) and \(B\rightarrow \tau \nu \) simultaneously while other types such as 2HDM I and 2HDM II cannot [39].

In 2HDM III the physical mass eigenstates are \(H_0\) (heavy CP-even Higgs), \(h_0\) (light CP-even Higgs) and \(A_0\) (CP-odd Higgs) and \(H^{\pm }\). In this model both Higgs doublets can couple to up-type and down-type quarks. As a consequence the couplings of the neutral Higgs mass eigenstates can induce flavor violation in Neutral Currents at tree-level. In the down sector these flavor violating couplings are stringently constrained from flavor changing neutral current processes [39, 40]. Thus in the following we consider only charged Higgs couplings to quarks that can be expressed as [39, 41]:

$$\begin{aligned} \mathcal {L}^{eff}_{H^\pm } {=} \bar{u}_f {\Gamma _{u_f d_i }^{H^\pm \,LR\,\mathrm {eff} } }P_R d_i H^+ {+} \bar{u}_f {\Gamma _{u_f d_i }^{H^\pm \,RL\,\mathrm {eff} } }P_L d_i H^++h.c.\, , \end{aligned}$$
(14)

where

$$\begin{aligned} {\Gamma _{u_f d_i }^{H^\pm \,LR\,\mathrm {eff} } }= & {} \sum \limits _{j = 1}^3 {\sin \beta \, V_{fj} \left( \frac{m_{d_i }}{v_d} \delta _{ji}- \epsilon ^{ d}_{ji}\tan \beta \right) , } \nonumber \\ {\Gamma _{u_f d_i }^{H^ \pm \,RL\,\mathrm {eff} } }= & {} \sum \limits _{j = 1}^3 {\cos \beta \, \left( \frac{m_{u_f }}{v_u} \delta _{jf}- \epsilon ^{ u\star }_{jf}\tan \beta \right) V_{ji}} \end{aligned}$$
(15)

Here \(v_u\) and \(v_d\) denote the vacuum expectations values of the neutral component of the Higgs doublets, tan \(\beta = v_u/v_d\) and V is the CKM matrix. Applying the Feynman-rules given in Eq. (14) allows us to calculate the contributions to the total amplitude originating from tree-level Charged Higgs mediation.

The contribution of charged Higgs to the effective Hamiltonian can be written as

$$\begin{aligned} Q^{H^\pm }_1= & {} (\bar{q} P_R c)(\bar{u} P_L q'),\nonumber \\ Q^{H^\pm }_2= & {} (\bar{q} P_L c)(\bar{u} P_R q'),\nonumber \\ Q^{H^\pm }_3= & {} (\bar{q} P_L c)(\bar{u} P_L q'),\nonumber \\ Q^{H^\pm }_4= & {} (\bar{q} P_R c)(\bar{u} P_R q'), \end{aligned}$$
(16)

where, as before, for \(\mathrm{CF}\) decays \(q =s \) and \(q' = d\) while for \(\mathrm DCS\) decays we have \(q =d \) and \(q' = s\). The Wilson coefficients \(C^H_i\), at the electroweak scale, can be expressed as

$$\begin{aligned} C^{H^\pm }_1= & {} \frac{\sqrt{2} }{ G_F V^*_{c q}V_{u q'} m^2_H} \Bigg (\sum \limits _{j = 1}^3 {\cos \beta \, V_{j q'} \left( \frac{m_u }{v_u} \delta _{j1}- \epsilon ^{ u\star }_{j1}\tan \beta \right) }\Bigg )\nonumber \\&\times \Bigg ( \sum \limits _{k= 1}^3 {\cos \beta \,V^{\star }_{k q}} \left( \frac{m_c}{v_u} \delta _{k2}-\epsilon ^{ u}_{k2}\tan \beta \right) \Bigg ),\nonumber \\ C^{H^\pm }_2= & {} \frac{\sqrt{2} }{ G_F V^*_{c q}V_{u q'} m^2_H} \Bigg (\sum \limits _{j = 1}^3 {\sin \beta \,V_{1j} \left( \frac{m_{q' }}{v_d} \delta _{j q'} - \epsilon ^{ d}_{j q'}\tan \beta \right) }\Bigg ) \nonumber \\&\times \Bigg ( \sum \limits _{k= 1}^3 {\sin \beta \,V^{\star }_{2k}} \left( \frac{m_{q}}{v_d} \delta _{k q}-\epsilon ^{ d\star }_{k q}\tan \beta \right) \Bigg ),\nonumber \\ C^{H^\pm }_3= & {} \frac{\sqrt{2} }{ G_F V^*_{c q}V_{u q'} m^2_H} \Bigg (\sum \limits _{j = 1}^3 {\cos \beta \, V_{j q'} \left( \frac{m_u }{v_u} \delta _{j1}- \epsilon ^{ u\star }_{j1}\tan \beta \right) }\Bigg ) \nonumber \\&\times \Bigg ( \sum \limits _{k= 1}^3 {\sin \beta \,V^{\star }_{2k}} \left( \frac{m_{q}}{v_d} \delta _{k q}-\epsilon ^{ d\star }_{k q}\tan \beta \right) \Bigg ),\nonumber \\ C^{H^\pm }_4= & {} \frac{\sqrt{2} }{ G_F V^*_{c q}V_{u q'} m^2_H}\Bigg ( \sum \limits _{k= 1}^3 {\cos \beta \,V^{\star }_{k q}} \left( \frac{m_c}{v_u} \delta _{k2}-\epsilon ^{ u}_{k2}\tan \beta \right) \Bigg )\nonumber \\&\times \Bigg (\sum \limits _{j = 1}^3 {\sin \beta \,V_{1j} \left( \frac{m_{q' }}{v_d} \delta _{j q'} - \epsilon ^{ d}_{j q'}\tan \beta \right) }\Bigg ) \end{aligned}$$
(17)

In order to evaluate the contributions of the charged Higgs to the amplitudes of the decay modes under consideration we need to discuss the restraints imposed on the flavor-changing parameters \(\epsilon ^{u,d}_{ij}\) appear in the expressions of \(C^{H^\pm }_i\) above. We consider first the down sector and discuss the possible constraints that can be imposed on \(\epsilon ^{d}_{ij}\). For the case \(i\ne j\), stringent bounds can be set on \(\epsilon ^{d}_{ij}\) from considering flavor changing neutral current (FCNC) processes due to the tree level neutral Higgs exchange [39, 40]. As a result, they cannot contribute significantly to the decay modes under investigation. Thus we are left with \(\epsilon ^{d}_{11}\), \(\epsilon ^{d}_{22}\) and \(\epsilon ^{d}_{33}\). The couplings \(\epsilon ^{d}_{11}\) and \(\epsilon ^{d}_{22}\) can be severely constrained by applying the naturalness criterion of ’t Hooft to the quark masses. In view of the criterion, the smallness of a quantity is only natural if a symmetry is gained in the limit in which this quantity is zero [39]. Consequently, it is unnatural to have large accidental cancellations without a symmetry forcing these cancellations. Applying the naturalness criterion to the quark masses leads to the bounds given as [40]

$$\begin{aligned} |v_{u(d)} \epsilon ^{d(u)}_{ij}|\le & {} \left| V^{CKM}_{ij}\right| \,\mathrm{max }\left[ m_{d_i(u_i)},m_{d_j(u_j)}\right] \,\,\,\,\, for\, i < j\nonumber \\ |v_{u(d)} \epsilon ^{d(u)}_{ij}|\le & {} \mathrm{max }\left[ m_{d_i(u_i)},m_{d_j(u_j)}\right] \, \,\,\,\,\, \,\,\,\,\, for\, i \ge j. \end{aligned}$$
(18)

Clearly, due to the smallness of the d and s quark masses, the constraints on \(\epsilon ^d_{11}\) and \(\epsilon ^d_{22}\) are so strong. Thus we are left with \(\epsilon ^d_{33}\) which is irrelevant to the decay modes we are interested in. Putting all together, we can safely neglect terms proportional to the couplings \(\epsilon ^{d}_{ij}\) in \(C^{H^\pm }_i\).

We turn now to discuss the constraints that can be set on the couplings \(\epsilon ^{u}_{ij}\). Again, applying the naturalness criterion of ’t Hooft to the u quark mass we find that, using second line of Eq. (18), the constraint on \(\epsilon ^u_{11}\) is so severe. As a result we can drop terms proportional to \(\epsilon ^{u}_{11}\) in \(C^{H^\pm }_i\). Thus, to a good approximation, we can finally write

$$\begin{aligned} C^{H^\pm }_1\simeq & {} -\frac{\sin 2\beta V_{3 q'} \epsilon ^{ u\star }_{31}}{\sqrt{2} \, G_F V^*_{c q}V_{u q'} m^2_H} \nonumber \\&\times \Bigg ( \frac{m_c}{v_u} V^{\star }_{2 q}-\epsilon ^{ u}_{22}\tan \beta V^{\star }_{2 q} -\epsilon ^{ u}_{32}\tan \beta V^{\star }_{3 q}\Bigg ),\nonumber \\ C^{H^\pm }_4\simeq & {} \frac{\sin 2\beta V_{1q'} m_{q' } }{ \sqrt{2} \, G_F V^*_{c q}V_{u q'} m^2_H v_d} \nonumber \\&\times \Bigg ( \frac{m_c}{v_u} V^{\star }_{2 q}-\epsilon ^{ u}_{22}\tan \beta V^{\star }_{2 q} -\epsilon ^{ u}_{32}\tan \beta V^{\star }_{3 q}\Bigg ),\nonumber \\ C^{H^\pm }_2\simeq & {} C^{H^\pm }_3 \simeq 0 \end{aligned}$$
(19)

where we have neglected the terms that are proportional to \(\epsilon ^{ u}_{12} \epsilon ^{ u\star }_{21}\) due to the strong constraint \(\mid \epsilon ^u_{12}\epsilon ^{u\,*}_{21}\mid \ < 2\times 10^{-8}\) from \(D-{\bar{D}}\) mixing [40]. Moreover, the bound also implies that \(\mid \epsilon ^u_{12,21}\mid < \sqrt{2}\times 10^{-4}\) in the absence of a symmetry that protect one of these parameters from being much smaller than the other one. As a consequence, we neglected terms proportional to \(\epsilon ^u_{12}\) in the above Wilson coefficients. We also neglected terms suppressed by the up quark mass.

We proceed now to calculate the amplitudes of the decay processes of interest. For \(\mathrm{CF}\) decay modes \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\), the total amplitude including Higgs contribution can be written as

$$\begin{aligned}&A^{SM+H^\pm }_{D^+ \rightarrow {\bar{K}}^0 \pi ^+} = -i{G_F\over \sqrt{2}}V_{cs}^*V_{ud} \left[ (a_1+\Delta a^{s d}_1+\Delta a^{H}_1) X^{\pi ^+}_{D^+{\bar{K}}^0}\right. \nonumber \\&\quad \left. + (a_2+\Delta a^{s d}_2+\Delta a^{s d K^0}_2+\Delta a^{H \,{\bar{K}}^0}_2) X^{{\bar{K}}^0}_{D^+ \pi ^+} \right] , \end{aligned}$$
(20)

with

$$\begin{aligned} \Delta a^{H}_1 = \chi ^{\pi ^+}(\mathcal C^H_1- \mathcal C^H_4),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Delta a^{H \,{\bar{K}}^0}_2 = \frac{1}{2N}\Bigg (\mathcal C^H_1-\chi ^{ K^0} \mathcal C^H_4\Bigg ) \end{aligned}$$
(21)

The quantities \(\mathcal C^H_{1.4}\) can be obtained from \(C^H_{1,4}\) by setting \(q=s\) and \(q'=d\) and

$$\begin{aligned} \chi ^{\pi ^+}\simeq & {} {m_{\pi }^2\over m_c\, m_d}\simeq 3 \end{aligned}$$
(22)

In the case of \(\mathrm{DCS}\) decay mode \(D^+ \rightarrow K^0 \pi ^+\), the total amplitude can be expressed as

$$\begin{aligned}&A^{SM+H^\pm }_{D^+ \rightarrow K^0 \pi ^+} = i{G_F\over \sqrt{2}}V_{cd}^*V_{us} \left[ (a_1+\Delta a^{d s}_1+\Delta a^{H\,D^+}_1) X^{D^+}_{K^0\pi ^+} \right. \nonumber \\&\quad \left. + (a_2+\Delta a^{d s}_2-\Delta a^{d s K^0}_2+\Delta a^{H\,K^0}_2) X^{K^0}_{D^+ \pi ^+} \right] , \end{aligned}$$
(23)

where

$$\begin{aligned} \Delta a^{H\,D^+}_1= & {} \chi ^{D^+}(\mathcal C'^H_1+ \mathcal C'^H_4), \nonumber \\ \Delta a^{H\,K^0}_2= & {} \frac{1}{2N}\Bigg (\mathcal C'^H_1-\chi ^{ K^0} \mathcal C'^H_4\Bigg ) \end{aligned}$$
(24)

The quantities \(\mathcal C'^H_{1.4}\) can be obtained from \(C^H_{1,4}\) by setting \(q=d\) and \(q'=s\) and

$$\begin{aligned} \chi ^{D^+} \simeq - {m_{D^+}^2\over m_c\, m_s} \simeq -28 , \end{aligned}$$
(25)

In a recent study a lower bound on the charged Higgs mass in 2HDM of Type II has been set after taking into account all relevant results from direct charged and neutral Higgs boson searches at LEP and the LHC, as well as the most recent constraints from flavour physics [42]. The bound reads \( m_{H^\pm }\gtrsim 600\) GeV independent of \(\tan \beta \). This bound should be also respected in 2HDM III [39]. For \(\tan \beta = 50\), \(m_H = 600\) GeV and keeping only dominant terms, after considering constraints imposed on the \(\epsilon ^{ q}_{i j}\) studied in details in Ref. [40], we find that

$$\begin{aligned} \Delta a^{H}_1\simeq & {} 0.001 \, \epsilon ^{ u}_{22} \nonumber \\ \Delta a^{H \,{\bar{K}}^0}_2\simeq & {} 0.0001\, \epsilon ^{ u}_{22}\nonumber \\ \Delta a^{H\,D^+}_1\simeq & {} 0.278 \, \epsilon ^{ u}_{22} \nonumber \\ \Delta a^{H \, K^0}_2\simeq & {} 0.003\, \epsilon ^{ u}_{22} \end{aligned}$$
(26)

We proceed now to discuss the constraints imposed on the coupling \(\,\epsilon ^{ u}_{22}\). The processes \(D_{(s)} \rightarrow \tau \nu \), \(D_{(s)} \rightarrow \mu \nu \) can constrain the real part of \(\,\epsilon ^{ u}_{22}\) while the constraints on the imaginary part of \(\,\epsilon ^{ u}_{22}\) are weak [40]. Regarding the imaginary part of \(\,\epsilon ^{ u}_{22}\) which is relevant for generating direct CP violation, and for \(m_{H^\pm } = 600\) GeV, \(\tan \beta =50\), the constraints from the electric dipole moment of the neutron reads \( -0.16 \lesssim \, Im(\epsilon ^{ u}_{22})\, \lesssim 0.16\) [40]. Other processes such as \(D-{\bar{D}}\) mixing and \(K-{\bar{K}}\) mixing can be used to set bounds on \(\,\epsilon ^{ u}_{22}\). However these bounds are weaker than the bounds obtained from \(D_{(s)} \rightarrow \tau \nu \), \(D_{(s)} \rightarrow \mu \nu \) and the electric dipole moment of the neutron [20, 40].

The real parts of \(\Delta a^{H}_1\) and \(\Delta a^{H}_2\) are expected to be much smaller than the SM contributions, \(a_1\) and \(a_2\), and hence we can safely neglect them and keep only the imaginary parts required for generating the weak phases.

The direct CP asymmetries of the CF decay mode \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\) and the \(\mathrm DCS\) decay mode \(D^+ \rightarrow K^0 \pi ^+\), after including Higgs contributions to the amplitudes in Eq.(11), can be expressed as

$$\begin{aligned}&A^{SM+H^\pm }_{CP} (D^+ \rightarrow {\bar{K}}^0 \pi ^+) \nonumber \\&\quad = {|A^{SM+H^\pm }_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2-|\bar{A}^{SM+H^\pm }_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2 \over |A^{SM+H^\pm }_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2+|\bar{A}^{SM+H^\pm }_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2 }\nonumber \\&\quad \simeq 2 r\sin (\alpha ^H)\, \sin (\phi ^{H}_2-\phi ^{H}_1)\nonumber \\&A^{SM+H}_{CP} (D^+ \rightarrow K^0 \pi ^+) \nonumber \\&\quad = {|A^{^{SM+H}}_{D^+ \rightarrow K^0 \pi ^+}|^2-|{\bar{A}}^{^{SM+H}}_{D^+ \rightarrow K^0 \pi ^+}|^2 \over |A^{^{SM+H}}_{D^+ \rightarrow K^0 \pi ^+}|^2+|\bar{A}^{^{SM+H}}_{D^+ \rightarrow K^0 \pi ^+}|^2 }\nonumber \\&\quad \simeq 2 r'\sin (\alpha '^H)\, \sin (\phi '^{H}_2-\phi '^{H}_1) \end{aligned}$$
(27)

The weak phases \(\phi ^{H}_i\) and \(\phi '^{H}_i\), \(i=1,2\), are defined through

$$\begin{aligned} \phi ^{H}_1\simeq & {} \tan ^{-1}\Bigg (\frac{|\Delta a^H_1|\sin \Delta \phi ^H_1}{a_1}\Bigg ) \nonumber \\ \phi ^{H}_2\simeq & {} \tan ^{-1}\Bigg (\frac{|\Delta a^{H \,{\bar{K}}^0}_2|\sin \Delta \phi ^H_2}{a_2}\Bigg )\nonumber \\ \phi '^{H}_1&\tan ^{-1}\Bigg (\frac{|\Delta a^{H D^+}_1|\sin \Delta \phi '^H_1}{a_1}\Bigg ) \nonumber \\ \phi '^{H}_2= & {} \tan ^{-1}\Bigg (\frac{|\Delta a^{H \, K^0}_2|\sin \Delta \phi '^H_2}{a_2}\Bigg ) \end{aligned}$$
(28)

where \(\Delta \phi ^{H}_1\) (\(\Delta \phi ^{H}_2\)) is the phase of \(\Delta a^{H}_1\) (\(\Delta a^{H \,\bar{K}^0}_2\)) while \(\Delta \phi '^{H}_1\) (\(\Delta \phi '^{H}_2\)) is the phase of \(\Delta a^{H D^+}_1\) (\(\Delta a^{H \, K^0}_2\)). Assuming maximum value of \(Im(\epsilon ^{ u}_{22})\), we find that \(\sin (\phi ^{H}_2-\phi ^{H}_1)\lesssim \mathcal {O}(10^{-4})\) and \(\sin (\phi '^{H}_2-\phi '^{H}_1)\lesssim \mathcal {O}(10^{-3})\) . Clearly, charged Higgs contributions can not enhance the direct CP asymmetry of the CF decay mode \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\) due to the tiny generated weak phases. On the other hand, with \(r'\simeq 5.7\), we find that \(|A^{SM+H}_{CP} (D^+ \rightarrow K^0 \pi ^+)| \lesssim \mathcal {O}(10^{-2})|\sin (\alpha '^H)|\) where \(\alpha '^H\) is the relative strong phase of the amplitudes \(A''\) and \(C''\) after including charged Higgs contributions. Based on the fit done in Ref. [24], we have \(|\sin (\alpha '^{fit})| \simeq 5\times 10^{-2}\) where \(\alpha '^{fit}\) is the value of the strong phases difference of the fitted amplitudes \(A''\) and \(C''\). This result indicates that \(|A^{SM+H}_{CP} (D^+ \rightarrow K^0 \pi ^+)|\lesssim \mathcal {O}(10^{-4})\). Hence we conclude that no sizable enhancement of the direct CP asymmetries of \(D^+ \rightarrow K^0 \pi ^+\), due to charged Higgs contributions, regardless the value of \(|\sin (\alpha '^H)|\).

It should be noted that the resultant tiny asymmetries, in both decay modes, is strongly dependent on the assumption of no fine-tuned cancellations in the Yukawa couplings contributing to fermion masses. If this assumption is relaxed, we can have contributions, to the amplitudes of the given decay process, from the terms proportional to \(\epsilon ^{ u}_{11}\), \(\epsilon ^{d}_{11}\) and \(\epsilon ^{d}_{22}\). The neutron electric dipole results in the bound \( |Im (\epsilon ^{ u}_{11})|\le 2.2\times 10^{-2} \) [40]. On the other hand, the ratios \(\mathcal {B} \Bigg (K\rightarrow \mu (e)\nu \Bigg )/\mathcal {B} \Bigg (\pi \rightarrow \mu (e)\nu \Bigg )\), where \(\mathcal {B} \) denotes the the branching ratio, yield the bound \( |Re (\epsilon ^{ d}_{22})|\le 1.0\times 10^{-3}\) [40]. Taking all this into account and assuming that the real and imaginary parts of \(\epsilon ^{d}_{11}\) have maximum values of \(\mathcal {O}(1)\), we find that the direct CP asymmetries of both decay modes can reach \(\mathcal {O}(10^{-1})\). This should be also the result for the CF decay mode \(D^0\rightarrow K^- \pi ^+\) studied in our early work in Ref. [20]. Up to date, no observation of such large asymmetry in D meson decays. As a consequence, large values of the real and the imaginary parts of \(\epsilon ^{d}_{11}\) are disfavored and consequently the related asymmetries.

4 A new charged gauge boson as left right models

In this section, we consider a new physics model based on the gauge group \(SU(2)_L \times SU(2)_R \times U(1)_{B-L}\) [43,44,45,46,47,48,49,50,51,52]. Assuming no mixing between \(W_L\) and \(W_R\) gauge bosons, the contributions from new diagrams, similar to the SM tree-level diagrams with \(W_L \) is replaced by a \(W_R\), to the effective Hamiltonian that governs \(D \rightarrow K \pi \) decays can be expressed as:

$$\begin{aligned}&\mathcal{H}_{\mathrm{LR}} = {G_F\over \sqrt{2}}\left( {g_R m_W\over g_L m_{W_R}}\right) ^2V_{R c q}^*V_{R u q'} \nonumber \\&\quad \Bigg [c_1'\Bigg ({\bar{q}} \gamma _\mu c_R\Bigg ) \Bigg (\bar{u}\gamma ^\mu q'_R\Bigg ) + c_2' ({\bar{u}} \gamma _\mu c_R{\bar{q}} \gamma ^\mu q'_R)\Bigg ]+\mathrm{h.c.}\nonumber \\ \end{aligned}$$
(29)

here \(g_{L}\) and \(g_{R}\) denote the gauge \(SU(2)_{L}\) and \(SU(2)_{R}\) couplings respectively and q and \(q'\) are different light down-type quarks. The masses \(m_W\) and \(m_{W_R}\) represent the \(SU(2)_{L}\) and \(SU(2)_{R}\) charged gauge boson masses respectively and \( V_R\) is the quark mixing matrix in the right sector in analogy to the CKM quark mixing matrix, \(V_{CKM }\equiv V\), in the left sector of the charged quark currents. ATLAS and CMS have set stringent limits on \(m_{ W_R}\), in the \(3.5-4.4 \) \( \mathrm{TeV}\) region based on their latest analyses with \(37\, {\mathrm{fb}}^{- 1}\) and \(35.9\, {\mathrm{fb}}^{- 1}\) luminosities, respectively, at \( \sqrt{s} = 13 \) \( \mathrm{TeV}\) [53,54,55,56,57,58]. These analyses rely on the assumptions that the model is manifestly left-right symmetric i.e. \(g_L = g_R\) and that \(V_R\) is either diagonal, or \(V_R = V\). Clearly, due to the stringent limits on \(m_{W_R}\) and the assumptions of \(V_R\), one expects that no sizeable CP asymmetry can be obtained in this class of left right symmetric models for both \(\mathrm{CF}\) and \(\mathrm DCS\) decay modes of \(D \rightarrow K \pi \) decays.

Previous studies showed that sizable CP asymmetries can be obtained in the Charm and muon sectors in a general left right symmetric model [20, 32, 59]. In this model, the mixing between the left and the right gauge bosons is allowed and the left-right symmetry is not manifest at unification scale. In order to estimate the CP asymmetries of the \(\mathrm{CF}\) and \(\mathrm{DCS}\) decay modes of \(D \rightarrow K \pi \) decays, in the framework of this model, we start by parameterizing the charged current mixing matrix as [32, 50, 60]

$$\begin{aligned} \left( \begin{array}{c} W^\pm _L \\ W^\pm _R \end{array}\right)= & {} \left( \begin{array}{cc} \cos \xi &{} -\sin \xi \\ \mathrm{e}^{i\omega }\sin \xi &{} \mathrm{e}^{i\omega }\cos \xi \end{array}\right) \left( \begin{array}{c} W^\pm _1 \\ W^\pm _2 \end{array}\right) \nonumber \\\simeq & {} \left( \begin{array}{cc} 1 &{} - \xi \\ \mathrm{e}^{i\omega }\xi &{} \mathrm{e}^{i\omega } \end{array}\right) \left( \begin{array}{c} W^\pm _1 \\ W^\pm _2 \end{array}\right) \end{aligned}$$
(30)

where \(\xi \) is a mixing angle, \(W^\pm _1\) and \(W^\pm _2\) are the mass eigenstates and \(\omega \) is a CP violating phase. Hence, the charged currents interaction in the quark sector can be expressed as

$$\begin{aligned} \mathcal{L}\simeq & {} -{1\over \sqrt{2}} {\bar{U}} \gamma _\mu \left( g_LVP_L+g_R\xi {\bar{V}}^RP_R\right) DW_1^\dagger \nonumber \\&- {1\over \sqrt{2}} {\bar{U}} \gamma _\mu \left( -g_L\xi VP_L+g_R\bar{V}^RP_R\right) DW_2^\dagger \end{aligned}$$
(31)

where \({\bar{V}}^R=\mathrm{e}^{i\omega }V^R\). Upon integrating out \(W_1\) in the usual way and neglecting \(W_2\) contributions, given its mass is much higher, we obtain the effective hamiltonian relevant to the \(\mathrm{CF}\) and \(\mathrm DCS\) \(D \rightarrow K \pi \) decays as:

$$\begin{aligned} \mathcal{H}^{q q'}_{\mathrm{eff.}}= & {} {4G_F\over \sqrt{2}}\Bigg \{c_1 \Bigg [\ \bar{q}\gamma _\mu \Bigg (V^*P_L+{g_R\over g_L}\xi \bar{V}^{R*}P_R \Bigg )_{c\, q} c \Bigg ] \nonumber \\&\Bigg [ \bar{u}\gamma ^\mu \Bigg (VP_L+{g_R\over g_L}\xi {\bar{V}}P_R \Bigg )_{u \, q'} q'\Bigg ] \nonumber \\&+ c_2 \Bigg [ {\bar{q}}_\alpha \gamma _\mu \Bigg (V^*P_L+{g_R\over g_L}\xi {\bar{V}}^{R*}P_R \Bigg )_{c\, q} c_\beta \Bigg ]\nonumber \\&\Bigg [\bar{u}_\beta \gamma ^\mu \Bigg (VP_L+{g_R\over g_L}\xi {\bar{V}}P_R \Bigg )_{u\, q'} q'_\alpha \Bigg ] \Bigg \}+\mathrm{h.}~\mathrm{c.} \end{aligned}$$
(32)

where \(\alpha ,\beta \) are color indices and \(q,q'\) are different light down-type quarks. The terms of the effective Hamiltonian proportional to \(\xi \) are:

$$\begin{aligned} \Delta \mathcal{H}^{q q'}_\mathrm{eff}\simeq & {} {G_F\over \sqrt{2}}{g_R\over g_L}\xi \left[ c_1{\bar{q}} \gamma _\mu V_{c \, q}^*c_L{\bar{u}} \gamma ^\mu {\bar{V}}^R_{u\,q'} q'_R\right. \nonumber \\&\left. + c_1 {\bar{q}} \gamma _\mu {\bar{V}}^{R*}_{c\,q} c_R {\bar{u}} \gamma ^\mu V_{u\,q'} q'_L \right. \nonumber \\&+ \left. c_2{\bar{q}}_\alpha \gamma _\mu V_{c\,q }^*c_{L\beta } \bar{u}_\beta \gamma ^\mu {\bar{V}}^R_{u\,q '} q'_{R\alpha }\right. \nonumber \\&\left. + c_2 \bar{q}_\alpha \gamma _\mu {\bar{V}}^{R*}_{c\,q } c_{R\beta } {\bar{u}}_\beta \gamma ^\mu V_{u\,q'} q'_{L\alpha } \right] +\mathrm{h.} \ \mathrm{c.} \end{aligned}$$
(33)

Upon evaluating the matrix elements of the operators in Eq. (33), we obtain the new contribution to the amplitude of the \(\mathrm{CF}\) decay mode \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\) by setting \(q=s\) and \(q'=d\)

$$\begin{aligned}&A^{LR}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+} = -{iG_F\over \sqrt{2}}{g_R\over g_L}\xi \left[ -c_1 V_{cs}^*{\bar{V}}^R_{ud} \left( X^{\pi ^+}_{D^+ {\bar{K}}^0} -{2\over N}\chi ^{K^0} X^{{\bar{K}}^0}_{D^+ \pi ^+} \right) \right. \nonumber \\&\quad \left. + c_1 {\bar{V}}^{R*}_{cs} V_{ud} \left( X^{\pi ^+}_{D^+ {\bar{K}}^0} - {2\over N}\chi ^{K^0} X^{{\bar{K}}^0}_{D^+ \pi ^+} \right) \right. \nonumber \\&\quad \left. -c_2 V_{cs}^*{\bar{V}}^R_{ud} \left( - 2\chi ^{K^0} X^{\bar{K}^0}_{D^+ \pi ^+} +{1\over N} X^{\pi ^+}_{D^+ {\bar{K}}^0} \right) \right. \nonumber \\&\quad \left. + c_2{\bar{V}}^{R*}_{cs}V_{ud} \left( -2 \chi ^{K^0} X^{{\bar{K}}^0}_{D^+ \pi ^+} +{1\over N} X^{\pi ^+}_{D^+ {\bar{K}}^0} \right) \right] \nonumber \\&\quad = {iG_F\over \sqrt{2}}{g_R\over g_L}\xi \left( V_{cs}^*\bar{V}^R_{ud}-{\bar{V}}^{R*}_{cs} V_{ud}\right) \left( a_1 X^{\pi ^+}_{D^+ {\bar{K}}^0} - 2\chi ^{K^0} a_2 X^{{\bar{K}}^0}_{D^+ \pi ^+} \right) \nonumber \\ \end{aligned}$$
(34)

and thus, the total amplitude including SM contribution can be written as

$$\begin{aligned} A^{SM+LR}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}\simeq & {} -i{G_F\over \sqrt{2}}V_{cs}^*V_{ud} \left[ (a_1+\Delta a^{s d}_1\Delta + a^{LR}_1) X^{\pi ^+}_{D^+ {\bar{K}}^0} \right. \nonumber \\&\left. + (a_2+\Delta a^{s d}_2+\Delta a^{s d K^0}_2+\Delta a^{LR \,{\bar{K}}^0}_2) X^{{\bar{K}}^0}_{D^+ \pi ^+} \right] ,\nonumber \\ \end{aligned}$$
(35)

with

$$\begin{aligned}&\Delta a^{LR}_1 \simeq - {g_R\over g_L }\xi \left( \bar{V}^R_{ud}-{\bar{V}}^{R*}_{cs} \right) a_1 ,\nonumber \\&\Delta a^{LR \,{\bar{K}}^0}_2 \simeq {2 g_R\over g_L }\xi \left( \bar{V}^R_{ud}-{\bar{V}}^{R*}_{cs} \right) \chi ^{K^0} a_2 \end{aligned}$$
(36)

The direct CP asymmetry of the CF decay mode \(D^+ \rightarrow \bar{K}^0 \pi ^+\), including the new contributions to the amplitudes in Eq. (11), can be expressed as

$$\begin{aligned}&A^{SM+LR}_{CP} (D^+ \rightarrow {\bar{K}}^0 \pi ^+) \nonumber \\&\quad = {|A^{^{SM+LR}}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2-|\bar{A}^{^{SM+LR}}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2 \over |A^{^{SM+LR}}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2+|\bar{A}^{^{SM+LR}}_{D^+ \rightarrow {\bar{K}}^0 \pi ^+}|^2 }\nonumber \\&\quad \simeq 2 r\,\sin (\alpha ^{LR})\, \sin (\phi ^{LR}_2-\phi ^{LR}_1) \end{aligned}$$
(37)

the weak phases \(\phi ^{LR}_1\) and \(\phi ^{LR}_2\) are defined through

$$\begin{aligned} \phi ^{LR}_1= & {} \tan ^{-1}\Bigg (\frac{|\Delta a^{LR}_1|\sin \Delta \phi ^{LR}_1}{a_1}\Bigg ) \nonumber \\ \phi ^{LR}_2= & {} \tan ^{-1}\Bigg (\frac{|\Delta a^{LR \,{\bar{K}}^0}_2|\sin \Delta \phi ^{LR}_2}{a_2}\Bigg ) \end{aligned}$$
(38)

where \(\Delta \phi ^{LR}_1\) and \(\Delta \phi ^{LR}_2\) are the phases of \(\Delta a^{LR}_1\) and \(\Delta a^{LR \,{\bar{K}}^0}_2\) respectively. We turn now to the \(\mathrm DCS\) decay mode \(D^+ \rightarrow K^0 \pi ^+\). Proceeding in a similar way as before and upon evaluating the matrix elements of the operators in Eq. (33) and setting \(q=d\) and \(q'=s\) we find that the new contribution to the amplitude can be expressed as

$$\begin{aligned}&A^{SM+LR}_{D^+ \rightarrow K^0 \pi ^+} = -{iG_F\over \sqrt{2}}{g_R\over g_L}\xi \left[ - c_1 V_{c d}^*{\bar{V}}^R_{u s} \right. \nonumber \\&\quad \times \left. \left( X^{D^+}_{K^0\pi ^+}-{2\over N}\chi ^{K^0} X^{K^0}_{D^+\pi ^+} \right) \right. \nonumber \\&\quad \left. + c_1 {\bar{V}}^{R*}_{c d} V_{u s} \left( X^{D^+}_{K^0\pi ^+}-{2\over N}\chi ^{K^0} X^{K^0}_{D^+\pi ^+} \right) \right. \nonumber \\&\quad \left. -c_2 V_{c d}^*{\bar{V}}^R_{u s} \left( - 2\chi ^{K^0} X^{DK^0}_{D^+\pi ^+}+{1\over N} X^{D^+}_{K^0\pi ^+} \right) \right. \nonumber \\&\quad \left. + c_2\bar{V}^{R*}_{c d}V_{u s} \left( - 2 \chi ^{K^0} X^{K^0}_{D^+\pi ^+}+{1\over N} X^{D^+}_{K^0\pi ^+}\right) \right] \nonumber \\&\quad = {iG_F\over \sqrt{2}}{g_R\over g_L}\xi \left( V_{c d}^*\bar{V}^R_{u s}-{\bar{V}}^{R*}_{c d} V_{u s}\right) \nonumber \\&\quad \times \left( a_1 X^{D^+}_{K^0\pi ^+}- 2\chi ^{K^0} a_2 X^{K^0}_{D^+\pi ^+} \right) \end{aligned}$$
(39)

Thus, the total amplitude after including SM contribution can be written as

$$\begin{aligned}&A^{SM+LR}_{D^+ \rightarrow K^0 \pi ^+} = i{G_F\over \sqrt{2}}V_{cd}^*V_{us} \left[ (a_1+\Delta a^{d s}_1+\Delta a'^{LR}_1) X^{D^+}_{K^0\pi ^+} \right. \nonumber \\&\quad \left. + (a_2+\Delta a^{d s}_2-\Delta a^{d s K^0}_2+\Delta a'^{LR\,K^0}_2) X^{K^0}_{D^+ \pi ^+} \right] , \end{aligned}$$
(40)

where

$$\begin{aligned}&\Delta a'^{LR}_1 \simeq {g_R\over g_L \lambda }\xi \left( {\bar{V}}^R_{u s}+{\bar{V}}^{R*}_{c d} \right) a_1 ,\nonumber \\&\Delta a'^{LR\,K^0}_2 \simeq - {2 g_R\over g_L \lambda }\xi \left( {\bar{V}}^R_{u s}+{\bar{V}}^{R*}_{c d} \right) \chi ^{K^0} a_2 \end{aligned}$$
(41)

with \(\lambda = V_{us}\). The direct CP asymmetry in this case, after including the new contributions to the amplitudes in Eq. (11), can be then expressed as

$$\begin{aligned}&A^{SM+LR}_{CP} (D^+ \rightarrow K^0 \pi ^+) \nonumber \\&\quad = {|A^{^{SM+LR}}_{D^+ \rightarrow K^0 \pi ^+}|^2-|\bar{A}^{^{SM+LR}}_{D^+ \rightarrow K^0 \pi ^+}|^2 \over |A^{^{SM+LR}}_{D^+ \rightarrow K^0 \pi ^+}|^2+|\bar{A}^{^{SM+LR}}_{D^+ \rightarrow K^0 \pi ^+}|^2 }\nonumber \\&\quad \simeq 2 r'\,\sin (\alpha '^{LR})\, \sin (\phi '^{LR}_2-\phi '^{LR}_1) \end{aligned}$$
(42)

where the weak phases \(\phi '^{LR}_1\) and \(\phi '^{LR}_2\) are defined through

$$\begin{aligned} \phi '^{LR}_1= & {} \tan ^{-1}\Bigg (\frac{|\Delta a'^{LR }_1|\sin \Delta \phi '^H_1}{a_1}\Bigg ) \nonumber \\ \phi '^{LR}_2= & {} \tan ^{-1}\Bigg (\frac{|\Delta a'^{LR \, K^0}_2|\sin \Delta \phi '^{LR}_2}{a_2}\Bigg ) \end{aligned}$$
(43)

where \(\Delta \phi '^{LR}_1\) and \(\Delta \phi '^{LR}_2\) are the phases of \(\Delta a^{LR}_1\) and \(\Delta a^{LR \, K^0}_2\) respectively.

In order to give estimations of the direct CP asymmetries in Eqs. (37, 42) we need to determine the allowed values of the left right mixing angle \(\xi \) and the elements of the matrix \({\bar{V}}^ R\) relevant to the decay processes under consideration. Information about the allowed values of the left right mixing angle \(\xi \) can be inferred from the measurement of the muon decay parameter \(\rho \), which governs the shape of the overall momentum spectrum, performed by the TWIST collaboration [61, 62]. This parameter is related to \(\xi \) via [61]:

$$\begin{aligned} \rho \simeq \frac{3}{4}\Bigg [1- 2\, \Bigg (\frac{g_R}{g_L} \xi \Bigg )^2\Bigg ] \end{aligned}$$
(44)

Defining \(\zeta = \frac{g_R}{g_L} \xi \) and for the TWIST value, from their latest global fit given in Table VII in Ref. [62], \(\rho = 0.74960 \pm 0.00019\) we obtain the allowed \(2 \sigma \) range of \(\zeta \)

$$\begin{aligned} \zeta \lesssim 2.3\times 10^{-2} \end{aligned}$$
(45)

We turn now to discuss the allowed values of the elements of the matrix \({\bar{V}}^R\) appear in Eqs. (36,41). These elements are \( {\bar{V}}^R_{ud}, {\bar{V}}^R_{cs}, {\bar{V}}^R_{us}\) and \({\bar{V}}^R_{cd}\). The real parts of these elements do not produce any weak CP violating phase required for generating direct CP asymmetry. In addition, their contributions to the amplitudes are suppressed by a factor \(\zeta \) and thus, to a good approximation, we can neglect them compared to the SM contributions. As a result, we only need to determine the allowed values of the imaginary parts of \( {\bar{V}}^R_{ud}, {\bar{V}}^R_{cs}, {\bar{V}}^R_{us}\) and \(\bar{V}^R_{cd}\).

In a recent study, the authors of Ref. [63] have listed the bounds from collider physics, flavor physics, and low-energy precision measurements on the complex couplings of the \(W^\pm \) boson to right-handed quarks. Particularly, these bounds are applied to the couplings in the left-right symmetric models that are generated from the mixing between the charged gauge bosons of the \(S U(2)_R\) and \(S U(2)_L\). As shown in Ref. [63], the experimental value of \((\epsilon '/ \epsilon )_K\) and the stringent bounds on the electric dipole moment of the neutron can lead to strong bounds on \( Im(\bar{V}^R_{ud})\) and \(Im({\bar{V}}^R_{us})\). From that study we find that \( Im({\bar{V}}^R_{ud})\) and \(Im({\bar{V}}^R_{us})\) can be as large as \(9\times 10^{-4}\) and \(2\times 10^{-4}\) respectively. Moreover, \(Im({\bar{V}}^R_{c d})\) can be as large as \(2\times 10^{-3}\) without violating the strongest bounds on the electric dipole moment of the neutron. The result of the study in Ref. [63] showed also that the dominant constraint on \(\zeta Im({\bar{V}}^R_{c s})\) results from the process \(K_L\rightarrow \pi ^0\, e^+\, e^ -\) and \(\zeta \, Im({\bar{V}}^R_{c s})\) can have a maximum allowed value \(7\times 10^{-3}\). This result shows that we can set \(Im(\bar{V}^R_{c s})\simeq {\mathcal O }(1)\) without violating the imposed constraints. Taking these values into account, we obtain \(\sin (\phi ^{LR}_2-\phi ^{LR}_1)\lesssim \mathcal {O}(10^{-2})\) and \(\sin (\phi '^{LR}_2-\phi '^{LR}_1)\lesssim \mathcal {O}(10^{-6})\). Clearly, the new weak phases in LRS models can only enhance the direct CP asymmetry of the \( \mathrm{CF}\) decay mode \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\). Moreover, with \(r\simeq 0.4\), we find that \(|A^{SM+LR}_{CP} (D^+ \rightarrow {\bar{K}}^0 \pi ^+) | \lesssim \mathcal {O}(10^{-2}) |\sin (\alpha ^{LR})|\) where \(\alpha ^{LR}\) is the relative strong phase of the amplitudes C, T after including the new contributions from LRS models discussed above. Using the results of the fit done in Ref. [24], we find that \(|\sin (\alpha ^{fit})| \simeq 0.5\) where \(\alpha ^{fit}\) is the value of the strong phases difference of the fitted amplitudes C and T. This result indicates that \(|A^{SM+LR}_{CP} (D^+ \rightarrow {\bar{K}}^0 \pi ^+)|\lesssim \mathcal {O}(10^{-3})\). Since, \(\alpha ^{LR}\) depends on the strong phases difference between SM and the new physics contributions, so better knowledge of the strong phases can help us to improve prediction on this CP asymmetry. Any observation of CP asymmetry in this channel will give us information not only on new physics but also on strong dynamics and strong phases.

5 Conclusion

In this work we have studied CP violation in charged decays of D meson. In particular, we have investigated the direct CP asymmetries of the Cabibbo favored non-leptonic \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\) and the doubly Cabibbo-suppressed decay mode \(D^+ \rightarrow K^0 \pi ^+\) within standard model, two Higgs doublet model with generic Yukawa structure and left right symmetric models.

In the standard model, we have shown that the generated weak phases at loop-level are so tiny leading to almost null direct CP asymmetries for both decay modes. This turn to be the case also regarding the predicted asymmetries in the two Higgs doublet model with generic Yukawa structure assuming no fine-tuned cancellations in the Yukawa couplings contributing to fermion masses. Relaxing this assumption can lead to direct CP asymmetries of \(\mathcal {O}(10^{-1})\) for real and imaginary parts of \(\epsilon ^{d}_{11}\) of \(\mathcal {O}(1)\). However, this is not favored due to the non observation of such large asymmetry in D meson decays.

Finally, we have shown that due to the strong constraints on the parameter space of the LRS models no sizable direct CP asymmetries can be achieved for the doubly Cabibbo-suppressed decay mode \(D^+ \rightarrow K^0 \pi ^+\). However, this is not the case for the Cabibbo favored non-leptonic \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\) decay mode, due to the presence of relatively large weak CP violating phases, where an upper bound on the direct CP asymmetry of \({\mathcal O } (10^{-3})\) can be obtained after respecting all relevant constraints on the parameter space of the model. The obtained result motivates search for direct CP violation in \(D^+ \rightarrow {\bar{K}}^0 \pi ^+\) at colliders as observing non zero direct CP asymmetry in this channel will shed light on new physics and also on the strong dynamics responsible for generating the strong phases. It is important to notice that, experimentally, the observed channel is \(D^+ \rightarrow {\bar{K}}_S \pi ^+\), so the new weak phases appearing in the D meson decay can interfere with the K oscillations enhancing the expected CP violation in this channel due to K meson oscillations.