1 Introduction

The inflationary paradigm is considered as a necessary part of the standard model of cosmology, since it provides the solution to the fundamental puzzles of the old Big Bang theory, such as the horizon, the flatness, and the monopole problems [2,3,4,5,6,7,8,9,10,11,12,13,14,15]. It can be achieved through various mechanisms, for instance through the introduction of a scalar inflaton field [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. Almost 20 years after the observational evidence of cosmic acceleration the cause of this phenomenon, labeled “dark energy”, remains an open question, which challenges the foundations of theoretical physics: why there is a large disagreement between the vacuum expectation value of the energy momentum tensor which comes from quantum field theory and the observable value of dark-energy density [34,35,36,37,38]. One way to parametrize dynamical dark energy is by using a scalar field or a “quintessence” model [39,40,41]. In such a way the cosmological constant gets replaced by a dark-energy fluid with a nearly constant density today [42,43,44,45,46]. For the slow-roll approximation the scalar field behaves as an effective dark energy. The form of the potential is clearly unknown and many different potentials have been studied and confronted with observations.

These two regimes of accelerated expansion are treated independently. However, it is both tempting and economical to think that there is a unique cause responsible for a quintessential inflation [47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76], which refers to unification of both concepts using a single scalar field. Consistency of the scenario requires that the new degree of freedom, namely the scalar field, should not interfere with the thermal history of the universe, and thereby it should be “invisible” for the entire evolution and reappear only around the present epoch, giving rise to late-time cosmic acceleration.

While the standard approach is to introduce some potential with slow-roll behavior, a successful model of quintessential inflation can be obtained from the ansatz of the slow-roll parameter as a function of the scale parameter itself (or the number of e-folds) [77,78,79], especially, with a Lorentzian ansatz [1]. Here we calculate the complete evolution of the universe from this ansatz.

The plan of the work is as follows: in Sect. 2 we introduce the ansatz for the slow-roll parameter and the corresponding inflationary observables. Section 3 finds the scalar potential that shows the same behavior. In Sect. 4 we introduce an example of a reheating mechanism. Section 5 calculates the expansion of the universe with matter fields. Finally Sect. 6 summarizes the results.

2 Lorentzian ansatz

In order to formulate an ansatz for the Hubble function that treats symmetrically both the early and the late times we use the Lorentzian function for the slow-roll parameter

$$\begin{aligned} \varepsilon (N) = \frac{\xi }{\pi }\frac{\varGamma /2 \, }{ N^2 + (\varGamma /2)^2} \end{aligned}$$
(1)

as a function of the number of e-folds, \(N = \log (a/a_i)\), where \(a_i\) is the scale parameter at some time (which we may choose as the initial state of the inflationary phase). \(\xi \) is the amplitude of the Lorentzian, \(\varGamma \) is the width of the Lorentzian. In that way the \(\varepsilon \) parameter increases from the initial value to 1 at the end of inflation; then continues to increase, peak and then decreases until it gets down to the value 1, and this represents the beginning of a the new dark-energy phase that will eventually dominate the late evolution of the universe. The upper panel of Fig. 1 presents the qualitative shape of this behavior.

The dominant energy condition yields another coefficients. The equation of state w is in the range \( |w| \le 1\). From the relation \(\varepsilon = \frac{3}{2}\left( w + 1\right) \) we obtain the bound \( 0 \le \varepsilon \le 3\). The ansatz for the vacuum energy evolution (1) is positive always, hence the lower bound is preserved. The largest value of the ansatz (1) is \(2 \xi /\pi \varGamma \). From the upper bound of \(\varepsilon \) we obtain the condition \(\varGamma < 2 \xi / 3\pi \).

In general, the calculation of the above observables requires a detailed perturbation analysis. Nevertheless, one can obtain approximate expressions by imposing the slow-roll assumptions, under which all inflationary information is encoded in the slow-roll parameters. In particular, one first introduces [80,81,82,83,84,85]

$$\begin{aligned} \varepsilon _{n+1} = \frac{{\text {d}}}{{\text {d}}N} \log |\varepsilon _n|, \end{aligned}$$
(2)

where \(\varepsilon _0\equiv H_{i}/H\) and n is a positive integer. The slow-roll parameters read

$$\begin{aligned} \varepsilon \equiv \varepsilon _1 = -\frac{H'}{H},\quad \varepsilon _2 = \frac{H''}{H'}-\frac{H'}{H}, \end{aligned}$$

and so on. From the first slow-roll parameter definition with the ansatz (1), we obtain the solution

$$\begin{aligned} H = \sqrt{\frac{\varLambda _0}{3}} \exp \left[ -\frac{\xi }{\pi }\tan ^{-1}\left( \frac{2 N}{\varGamma }\right) \right] . \end{aligned}$$
(3)

where \(\varLambda _0\) is an integration constant. The Hubble function interpolates from the inflationary values \(H_{-\infty }\) to the dark-energy value \(H_{+\infty }\) that corresponds to

$$\begin{aligned} H_{\pm } = \sqrt{\frac{\varLambda _0}{3}}\exp ^{\mp \xi /2}. \end{aligned}$$
(4)

The magnitude of the vacuum energy at the inflationary phase reads \(10^{-8} Mpl^4\), while the magnitude of the vacuum energy at the present slowly accelerated phase of the universe is \(10^{-120} Mpl^4\). From the Friedmann equations the values of the energy density is \(3H^2\) in the Planck scale. Therefore, the coefficients of the model are

$$\begin{aligned} \xi \approx 129,\quad \varLambda _0 = 1.7 \cdot 10^{-32} Mpl^4. \end{aligned}$$
(5)

We calculate the other slow-roll parameters using (2)

$$\begin{aligned} \varepsilon _2 = -\frac{8 N}{\varGamma ^2+4 N^2}, \quad \varepsilon _3 = \frac{1}{N}-\frac{8 N}{\varGamma ^2+4 N^2}. \end{aligned}$$
(6)

For \(\varGamma \rightarrow 0\) all of the slow-roll parameters with \(n \ge 3\) yield the value \(-1/N\). However, in the general case, all of the slow parameters have small values if the \(\varepsilon _2\) is small.

Fig. 1
figure 1

The upper panel shows the slow-roll parameter \(\varepsilon \) vs. the number of e-folds for the ansatz (1), in a logarithmic scale. The lower panel shows the corresponding Hubble function of the vacuum vs. the number of e-folds

Full size image

As usual inflation ends at a scale factor \(a_f\) where \(\varepsilon _1(a_f)=1\) and the slow-roll approximation breaks down. Therefore the end of inflation takes place when the number of e-folds reads

$$\begin{aligned} N_{f} = \pm \sqrt{\frac{\varGamma }{4 \pi } (2 \xi -\pi \varGamma )}. \end{aligned}$$
(7)

The negative value of \(N_{f}\) is the final state of the inflationary phase, while the positive value of \(N_f\) is the initial value of the slow-rolling dark energy at the late universe. Therefore, in order to calculate the inflationary observables, we must take the minus sign of \(N_{f}\). Consequently the initial \(N_i\) satisfies the condition \(N_f - N_i = {\mathscr {N}} \approx 50\)–60, where we impose \(60\,e\)-folds for the inflationary phase. Hence, the initial state of the inflationary phase reads

$$\begin{aligned} N_i = - \sqrt{\frac{\varGamma }{4 \pi } (2 \xi -\pi \varGamma )} - {\mathscr {N}}. \end{aligned}$$
(8)
Fig. 2
figure 2

The predicted scalar to tensor ratio r and the running \(\alpha _s\) vs. the primordial tilt \(n_s\) of the model. The observations are well within the Planck 2018 bounds

Full size image

The inflationary observables are expressed as [80,81,82,83,84,85]

$$\begin{aligned}&r \approx 16\varepsilon _1, \end{aligned}$$
(9)
$$\begin{aligned}&n_\mathrm {s} \approx 1-2\varepsilon _1-\varepsilon _2, \end{aligned}$$
(10)
$$\begin{aligned}&\alpha _\mathrm {s} \approx -2 \varepsilon _1\varepsilon _2-\varepsilon _2\varepsilon _3, \end{aligned}$$
(11)
$$\begin{aligned}&\begin{aligned} n_\mathrm {T} \approx -2\varepsilon _1, \end{aligned} \end{aligned}$$
(12)

where all quantities are calculated at \(N_{i}\). Therefore the tensor to scalar ratio and the primordial tilt give

$$\begin{aligned} r= & {} \frac{32 \varGamma \xi }{\pi \varGamma ^2+4 \pi N_i^2}, \end{aligned}$$
(13a)
$$\begin{aligned} n_s= & {} \frac{\pi \left( \varGamma ^2+4 N_i (N_i+2)\right) -4 \varGamma \xi }{\pi \left( \varGamma ^2+4 N_i^2\right) }, \end{aligned}$$
(13b)
$$\begin{aligned} \alpha _s= & {} \frac{8 \left( \pi \varGamma ^2-4 \pi N_i^2+4 \varGamma \xi N_i\right) }{\pi \left( \varGamma ^2+4 N_i^2\right) ^2}. \end{aligned}$$
(13c)

The power spectrum reads

$$\begin{aligned} \begin{aligned} A_s \approx \frac{H^2}{8\pi ^2 \varepsilon }. \end{aligned} \end{aligned}$$
(14)

For \(60\, e\)-folds and \(\varGamma = 0.1\) the observables read

$$\begin{aligned} r = 0.0076, \quad n_s = 0.961754. \end{aligned}$$
(15)

These values are in agreement with the latest 2018 Planck data [86, 87]

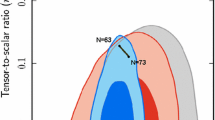
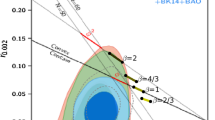
$$\begin{aligned} 0.95< n_s< 0.97, \quad r < 0.064. \end{aligned}$$
(16)

Figure 2 shows the predicted distribution of the observables [88]. We assume a uniform prior: \(N \in [50;70]\), \(\xi \in [100;200]\), \(\varGamma \in [0;1]\), with \(10^7\) samples. We find the posterior yields

$$\begin{aligned}&r = 0.045^{+0.065}_{-0.053}, \end{aligned}$$
(17)
$$\begin{aligned}&n_s = 0.9624^{+0.0087}_{-0.011}, \end{aligned}$$
(18)
$$\begin{aligned}&\alpha _s = -\left( 33^{+27}_{-30}\,\right) \cdot 10^{-5}, \end{aligned}$$
(19)
$$\begin{aligned}&\log \left( 10^{10} A_s\right) = 3.49 \pm 2.98 \,. \end{aligned}$$
(20)

The predicted distributions are in good agreement with the recent Planck values.

3 Scalar-field dynamics

The above ansatz is of general applicability in any inflation realization, whether this is driven by a scalar field or arises effectively from modified gravity, or from any other mechanism. In order to provide a more transparent picture let us consider a realization of these ideas in the context of a canonical scalar-field theory \(\phi \) moving in a potential \(V\left( \phi \right) \). We consider the action

$$\begin{aligned} {\mathscr {S}} = \int d^4x \sqrt{-g}\left[ \frac{M_{\text {Pl}}^2}{2}R-\frac{1}{2}\partial ^\mu \phi \partial _\mu \phi -V(\phi ) \right] \end{aligned}$$
(21)

with \(M_{\text {Pl}}\) the Planck mass, \(\phi \) the scalar field, and \(V(\phi )\) its potential. In the above action we have additionally considered the matter and radiation sectors \({\mathscr {S}}_{m}\) and \({\mathscr {S}}_{\gamma }\), respectively. These sectors can be neglected at the inflationary stage, however, they will gradually play an important role, giving rise to the standard thermal history of the universe and finally to the late-time accelerating phase. As usual, we focus on the case of a flat Friedmann–Robertson–Walker (FRW) geometry, with the metric

$$\begin{aligned} ds^2 = -dt^2 +a(t)^2\delta _{ij} dx^idx^j ~, \end{aligned}$$
(22)

where a(t) is the scale factor. The Friedman equations are given by

$$\begin{aligned} H^2 = \frac{8\pi G}{3}\left[ \frac{1}{2} \dot{\phi }^2 + V(\phi )\right] , \quad {\dot{H}} = -4\pi G\dot{\phi }^2, \end{aligned}$$
(23)

while the variation for the scalar field is

$$\begin{aligned} \ddot{\phi } + 3 H \dot{\phi } + V'(\phi ) = 0. \end{aligned}$$
(24)

Let us apply the ansatz in order to reconstruct a physical scalar-field potential that can generate the desirable inflationary observables. From the Friedmann equation (23), which holds in every scalar-field inflation, we extract the following solutions:

$$\begin{aligned} \phi = \int _{0}^{N} \sqrt{-2 \frac{H'}{H}} \, {\text {d}}N, \quad V(\phi ) = H H'+3 H^2, \end{aligned}$$
(25)

with \(8\pi G = 1\). From the integration of the Hubble parameter we get

$$\begin{aligned} N= & {} \frac{\varGamma }{2} \sinh \left( \sqrt{\frac{\pi }{\xi \varGamma }}\phi \right) , \end{aligned}$$
(26)
$$\begin{aligned} V(N)= & {} \varLambda _0 e^{-\frac{2 \xi }{\pi }\tan ^{-1}\left( \frac{2 N}{\varGamma }\right) } \left( 1-\frac{2 \varGamma \xi }{3 \pi \varGamma ^2+12 \pi N^2} \right) . \end{aligned}$$
(27)

Equation (26) cannot be inversed; in order to find \(N(\phi )\) and then through insertion into (26) to extract \(V(\phi )\) analytically we set

$$\begin{aligned} \begin{aligned} V(\phi ) = \varLambda _0 e^{-\frac{2 \xi }{\pi } \tan ^{-1}\left( \sinh x \right) } \left( 1-\frac{2 \xi }{3 \pi \varGamma } \text {sech}^2 x \right) , \end{aligned} \end{aligned}$$
(28)

with \(x \equiv \sqrt{\pi /\varGamma \xi } \phi \).

Figure 3 shows the scalar potential \(V(\phi )\). The universe in this picture begins with \(\phi \rightarrow \infty \) with a slow-roll behavior and goes to the left-hand side. After approaching the minimum the universe evolves with another slow-roll behavior that corresponds to the dark-energy epoch when \(\phi \rightarrow - \infty \). The asymptotic values of the potential are

$$\begin{aligned} V_{+\infty } = \varLambda _0 e^{\xi }, \quad V_{-\infty } = \varLambda _0 e^{-\xi } . \end{aligned}$$
(29)

Notice that this represents a see saw cosmological effect, that is, if \(\varLambda _0\) represents an intermediate scale, we see that making the inflationary scale big forces the present vacuum energy to be small. \(\varLambda _0\) represents the geometric average of the inflationary vacuum energy and the present dark-energy vacuum energies.

Fig. 3
figure 3

The corresponding scalar-field potential for the Lorentzian ansatz, with different values of \(\varGamma \): 0.1 red smooth line, 1 blue dashed line

Full size image

For the limits \(\varGamma \rightarrow 0\) the potential has a form of a step function for the two vacuum energies part. For the \(\varGamma \sim 1\) the potential approaches the form of tanh(x). Those features can be shown in Fig. 3.

See saw cosmological effects in modified measure theories with spontaneously broken scale invariance have been studied in [89,90,91]. Notice that in the case studied here the smallness of the vacuum energy in the late universe is correlated with a large energy in the early universe [89,90,91]. The small value of the vacuum energy in the late universe is related to a see saw formula (\(\sim f_1^2/f_2\)), where \(f_1\) is of the order of \(M_EW^4\) and \(f_2\) is of the order of \(M_\mathrm{{Planck}}^4\). In that case, however, both \(f_1\) and \(f_2\) are parameters defining a given flat region, so the see saw mechanisms are different.

4 Reheating

The quintessential inflation scenarios does not allow for the standard oscillating part that creates particles [92,93,94,95]. Therefore, in order to create particles we introduce a new scalar field \(\sigma \) whose mass is time dependent through the field \(\phi \). As an example:

$$\begin{aligned} m^2_\sigma = \mu ^2 \exp \left[ -2\frac{\alpha }{M_{\text {Pl}}} \phi \right] \end{aligned}$$
(30)

where \(\mu \) has the dimensions of mass and \(\alpha \) determines the coupling of the inflaton with the \(\sigma \) particles. Hence, the additional part of the action reads

$$\begin{aligned} {\mathscr {L}}_\sigma = -\frac{1}{2} g^{\mu \nu } \sigma _{,\mu } \sigma _{,\nu } - \frac{1}{2} m^2_\sigma \sigma ^2. \end{aligned}$$
(31)

The creation of the \(\sigma \) particles requires the time dependence of the inflaton field \(\phi \) [96]. The scalar field \(\phi \) evolves according to the slow-roll approximation up to the value \(\phi _\text {end} = -6.41\). From this value of \(\phi _\text {end}\) the inflaton falls into a state with a constant and approximately constant velocity at the flat region \(\dot{\phi }_0\) which can be calculated from the boundary conditions given at the end of inflation:

$$\begin{aligned} \dot{\phi }_0 =\sqrt{ \frac{\varGamma \xi }{\pi } }\frac{ H_0 e^{-\xi /2}}{N_{re}} \end{aligned}$$
(32)

where \(N_{re}\) is the number of e-foldings at the stage of reheating. The particle creation takes place when

$$\begin{aligned} |{\dot{m}}_\sigma |\, > m_\sigma ^2, \end{aligned}$$
(33)

which means it starts for

$$\begin{aligned} |{\dot{m}}_\sigma |\, \approx m_\sigma ^2. \end{aligned}$$
(34)

The condition yields

$$\begin{aligned} \phi \approx - \frac{1}{\alpha } \log \left( \alpha \frac{|\dot{\phi }_0|}{\mu }\right) . \end{aligned}$$
(35)

In order to estimate time creation of the \(\sigma \) particles, we divide the typical field value where the particle creation starts by the velocity

$$\begin{aligned} \varDelta t \sim - \phi /|\dot{\phi }_0| = \frac{1}{\alpha |\dot{\phi }_0| } \log \left( \alpha \frac{|\dot{\phi }_0|}{\mu }\right) . \end{aligned}$$
(36)

From the time duration one can calculate the density of particles in the phase space [96,97,98,99,100,101,102,103,104,105]:

$$\begin{aligned} n_k = \exp \left[ - \pi k^2 \varDelta t^2 \right] , \end{aligned}$$
(37)

where we neglect the mass \(m_\sigma \). k is the momentum of the particle produced. The integration over the momentum gives the density

$$\begin{aligned} n_\sigma = \frac{1}{2 \pi ^2} \int _{0}^{\infty } {\text {d}}k k^2 n_k = \frac{1}{8 \pi ^3} \left[ \frac{\alpha |\dot{\phi }_0|}{\log (\alpha \dot{\phi }_0/\mu )}\right] ^3 \end{aligned}$$
(38)

where we assume that the mass \(m_{\sigma }\) approaches zero, which is true for the specific dependence on the scalar field that we have chosen. This is the value for \(a = a_0\). In order to generalize this quantity for an arbitrary scale parameters we use the fact that the density deludes as \(\sim a^3\),

$$\begin{aligned} n_\sigma = \frac{1}{8 \pi ^3} \left( \frac{a_0}{a}\right) ^3 \left[ \frac{\alpha |\dot{\phi }_0|}{\log (\alpha \dot{\phi }_0/\mu )}\right] ^3. \end{aligned}$$
(39)

The energy density for the produced particles is

$$\begin{aligned} \rho _\sigma = \frac{1}{\left( 2\pi a\right) ^3} \int _{0}^{\infty }n_k \sqrt{k^2/a^2 + m_\sigma ^2} 4 \pi k^2 dk. \end{aligned}$$
(40)

For \(\alpha \) big enough the \( \sqrt{k^2/a^2}\) decays slower than \(m_\sigma ^2\) and the energy density of the sigma particles reads

$$\begin{aligned} \rho _\sigma = \left[ \frac{\alpha \dot{\phi }_0}{\sqrt{2}\pi \log \left[ \alpha \dot{\phi _0} / \mu \right] }\right] ^4 \frac{1}{a^4}, \end{aligned}$$
(41)

which behaves as radiation. In order to obtain a real thermal spectrum a thermalization process is required since the spectrum is not thermal. The thermalization should bring about all particle species [106,107,108]. This is just an example of how particles could be created after inflation. We now discuss some features that concern the evolution of the created matter that do not depend too much on the exact mechanism of particle creation. Similar calculations of particle creation for other quintessential inflationary models (obtained from spontaneous symmetry breaking of scale invariance) are being performed in [109], or based on a supergravity field redefinition [77].

5 Late-time expansion

This section discusses the qualitative behavior for the matter fields, which includes radiation and matter. The advantage of this model in comparison with most quintessence models is that the potential does not go to zero [42,43,44,45,46]. Instead, the potential approaches a small constant value that represents the cosmological constant. This means that our model is very close to the \(\varLambda \)CDM from early times, as opposed to other quintessential potential where the potential approaches zero for large values. But still we have two epochs. For example deviations from a constant value of the effective potential can produce problems with structure formation [110].

We start with the action

$$\begin{aligned} {\mathscr {S}}= & {} \int d^4x \sqrt{-g}\bigg [\frac{M_{\text {Pl}}^2}{2}R-\frac{1}{2}\partial ^\mu \phi \partial _\mu \phi -V(\phi ) \bigg ]\nonumber \\&+{\mathscr {S}}_\mathrm {m}+{\mathscr {S}}_\mathrm {r}. \end{aligned}$$
(42)

In flat Friedmann–Robertson–Walker (FRW) cosmology the two Friedmann equations read

$$\begin{aligned}&3H^2M_{\text {Pl}}^2 = \frac{1}{2}{\dot{\phi }}^2+V(\phi )+\rho _\mathrm {m}+\rho _\mathrm {r} \end{aligned}$$
(43)
$$\begin{aligned}&-\left( 2\dot{H}+3H^2\right) M_{\text {Pl}}^2 = \frac{1}{2}{\dot{\phi }}^2-V(\phi )+\frac{1}{3}\rho _\mathrm {r}, \end{aligned}$$
(44)

with

$$\begin{aligned} \ddot{\phi }+3H{\dot{\phi }} + V(\phi ) = 0\, , \end{aligned}$$
(45)

and the matter fields read

$$\begin{aligned} \rho _{m} = \frac{\varOmega _m^{0}}{a^3}, \quad \rho _{r} = \frac{\varOmega _r^{0}}{a^4}. \end{aligned}$$
(46)

Approximately, the exact solution in the absence of dust and radiation for the vacuum energy that we begin with can be used directly in the Friedmann equations. In order to present the thermal history of the universe in a more transparent way, we introduce the dimensionless density parameters for matter, radiation, and scalar field, respectively, given by

$$\begin{aligned} \varOmega _m= & {} \frac{\rho _m}{3H^2M_{\text {Pl}}^2} \, , \end{aligned}$$
(47)
$$\begin{aligned} \varOmega _r= & {} \frac{\rho _r}{3H^2M_{\text {Pl}}^2} \, , \end{aligned}$$
(48)
$$\begin{aligned} \varOmega _\phi= & {} \frac{\rho _\phi }{3H^2M_{\text {Pl}}^2} \, , \end{aligned}$$
(49)

where \(\rho _\phi =(1/2){\dot{\phi }}^2+V(\phi )\), and in Fig. 4 we depict their evolution as a function of the e-foldings. As we observe, we can reproduce the thermal history of the universe, starting from a scalar-field kinetic regime, then entering the radiation and matter regimes, and finally resulting in a late-time dark-energy dominated era. Finally, for completeness, in Fig. 4 we depict the corresponding behavior of the scalar-field equation of state parameter \(w_\phi \equiv p_\phi /\rho _\phi \), as well as of the effective equation of state parameter \(w_{\mathrm{eff}}\equiv p_{\mathrm{tot}}/\rho _{\mathrm{tot}}=-1-2{\dot{H}}/3H^2\). From this figure we verify that around the present era the potential term dominates over the kinetic one in the scalar-field energy density, which leads to a \(w_\phi \) around \(-1\).

Fig. 4
figure 4

The evolution of the energy densities for \(\varOmega _m = 0.3089\), \(\varOmega _\varLambda = 0.691\), \(\xi = 129\), \(\varGamma = 0.1\). The center of the Lorentzian is around \(N = -20\). Shortly after this point the radiation is created. The blue line is the energy density of the quintessential inflation. The red line is the energy density of the radiation, and the green line is for matter. In the lower panel the blue line describes the evolution of the scalar-field equation of states, and the blue dashed line is the total one

Full size image

Big Bang Nucleosynthesis (BBN) yields another constraint on the scalar inflaton model:

$$\begin{aligned} \varOmega _\phi (z \sim 10^{10}) \preceq 0.09. \end{aligned}$$
(50)

Considering the values \(\xi = 129,\varGamma = 0.1\) with the Planck values \(\varOmega _m = 0.3089\), \(\varOmega _\varLambda = 0.691\) yields \(\varOmega _\phi \sim 10^{-36}\), which is deep within the BBN constraint.

6 Conclusions

Here we formulate the slow-roll parameter of the inflaton field in a Lorentzian form. From that assumption all of the higher order slow-roll parameters are small and close to zero at the beginning of the inflationary period. Consequently, the inflationary observables agree with the recent Planck observations. The ratio between the inflationary and the late-time acceleration is determined by the value of \(\xi \approx 129\), and the width of the transition is determined by \(\varGamma \ll 10\).

In order to address in more detail in the scenario the matter fields contribution for the expansion of the universe, we address as an example a reheating mechanism that is designed to work for the smooth potential obtained in our quintessential inflationary scenario that relies on the fast time dependence of some additional particles coupled to the dilaton field instead of oscillations of the inflation potential (which do not exist).

Independently on how the matter is obtained, the further evolution of the matter and vacuum energy is quite distinguishable from other quintessential inflationary scenarios, since the inflationary potential approaches a constant instead of approaching zero. The models where the quintessential potential approaches zero have serious problems concerning structure formation; see for example [110, 111].

In the future it would be interesting to investigate different localized forms for the first slow-roll parameter. The Lorentzian form approaches a \(\delta \) function as \(\varGamma \rightarrow 0\). Therefore, different forms of \(\varepsilon \) that approach the delta function represent different transitions and forms of the inflationary and late-time vacuum energy. A Gaussian form for the \(\varepsilon \) parameter yields the same behavior.