1 Introduction

In recent years there has been a growing activity concerning the identification of integrable structures in four-dimensional gauge theories. This is mainly due to the interest that this subject has for the anti de Sitter/conformal field theory (AdS/CFT) conjecture [1,2,3,4]. After the seminal works in [5, 6], big progress has been made in the mapping of anomalous dimensions of gauge invariant Wilson operators in super Yang–Mills (SYM) theory to the spectrum of string theory in different backgrounds. A crucial step was to realize that the planar one-loop dilatation operator of \({{\mathcal {N}}} = 4\) SYM maps into the Hamiltonian of an integrable spin chain. The problem of finding anomalous dimensions translates then into the diagonalization of the corresponding Hamiltonian, and all the techniques developed for integrable systems become very useful in accomplishing this task. After those first results, the better understanding of the mapping has allowed more general results for larger orders in perturbation theory and for different sectors of the gauge and string theories (for an introduction to the field and a wider bibliography see [7]).

Nonetheless, two-dimensional integrable structures in four-dimensional gauge field theory appeared well before the AdS/CFT conjecture, in the region of high energy scattering in Quantum Chromodynamics (QCD). Non-Abelian gauge theories manifest interesting mathematical properties when they are investigated in terms of high energy scattering amplitudes in the Regge limit. This is the case of the SL(2,\({\mathbb {C}}\)) invariance [8] present in the impact parameter representation of QCD (and \({{\mathcal {N}}} = 4\) SYM) elastic scattering amplitudes evaluated in multi-Regge kinematics [9,10,11,12,13]. In this context the Balitsky-Fadin-Kuraev-Lipatov (BFKL) pomeron (with vacuum quantum numbers exchanged in the t-channel) can be interpreted as a bound state of two reggeized gluons where the Hamiltonian has an interesting operator representation [14] with holomorphic separability in coordinate space [15]. The iteration of the BFKL Hamiltonian in the s-channel, describing multiple reggeon exchanges in the generalized leading logarithmic approximation, defines the Bartels-Kwiecinski-Praszalowicz (BKP) equation [17, 18] and was found to have a hidden integrability [8, 15, 16, 19], being equivalent to a periodic spin chain of a XXX Heisenberg ferromagnet [20,21,22]. This was the first example of the existence of integrable systems in QCD. A similar integrable spin chain, an open one this time, was found in kinematical regions of n-point maximally helicity violating (MHV) and planar (\(N_c \rightarrow \infty \)) amplitudes in \({{\mathcal {N}}}=4\) SYM where Mandelstam cut contributions are maximally enhanced [23]. The importance of Mandelstam cuts in the complex angular momentum plane for \({{\mathcal {N}}}=4\) SYM MHV planar amplitudes was first realized in [24, 25] where corrections to the Bern-Dixon-Smirnov (BDS) iterative ansatz [26] for this class of amplitudes were found for the six-point amplitude at two loops.

There is an interesting connection between the integrable structures appearing in the calculation of the anomalous dimension of gauge invariant twist (scaling dimension minus Lorentz spin) two operators of spin M in \({{\mathcal {N}}}=4\) SYM, and in the multi-Regge kinematics. As it was shown in [27], the link to the BFKL equation appears upon analytically continuing the anomalous dimension function to complex values of M. In particular, the pomeron corresponds to the first singularity at \(M = \omega -1\), for small \(\omega \). The discrepancy between this result and the prediction obtained from the asymptotic Bethe ansatz was subsequently explained in [28] by the calculation of the corresponding wrapping corrections for the twist two operators.

The aim of the present work is to introduce a formal representation of the BFKL equation in matrix form which allows to investigate it in momentum space in a novel way. This framework is flexible enough to allow for modifications which tame the growth with energy of the BFKL evolution and which can be interpreted as an absorptive barrier for infrared modes. It is then shown how this approach, truncated in the ultraviolet, is closely related to the two-sites one-loop Hamiltonian of the sl(2) sector of the \({{\mathcal {N}}}=4\) SYM theory, in the double oscillator picture for operators of a given spin [29].

After this brief Introduction to the subject, in Sect. 2, a general discussion on the BFKL equation is provided, explaining the connection between the non-forward and forward limits. A novel discretization in virtuality space is described in detail, highlighting the role and physical interpretation of the shift and diagonal operators appearing in this representation. In Sect. 3 a square truncation of the BFKL discretization is introduced and the asymptotic behaviour of the corresponding eigensystem investigated. Section 4 is devoted to the study of a modification of the matrix Hamiltonian which reduces the influence of propagation into the infrared. In Sect. 5, known facts about Beisert’s representation of the non-compact SL(2) spin chain are introduced to set the ground for a comparison with the BFKL equation. Finally, some Conclusions are drawn.

2 Matrix representation

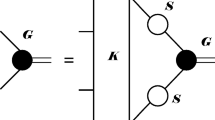
In this work the BFKL Hamiltonian is considered directly in two-dimensional transverse momentum space (\(\vec {k}\)), where other components have decoupled into an evolution variable (rapidity Y) which plays the role of time [9,10,11,12,13]. The four-point amplitude for off-shell reggeized gluons has the following momentum flow:

figure a

With this notation, the BFKL kernel for the pomeron channel has two contributions. The first one corresponds to \(\vec {k} = 0\), i.e., there is no propagator in the s-channel and can be written as

$$\begin{aligned}&``\mathrm{Reggeized ~Propagators}{\text {''}} \nonumber \\&\quad \simeq g^2 N_c \delta ^{(2)} \left( \vec {q}_1 - \vec {q}_1^{~'}\right) \delta ^{(2)} \left( \vec {q}_2 - \vec {q}_2^{~'}\right) \nonumber \\&\qquad \times \left( \int d^2 \vec {r} \frac{\vec {q}_1^{~2}}{\vec {r}^{~2} (\vec {q}_1 - \vec {r})^2} + \int d^2 \vec {r} \frac{\vec {q}_2^{~2}}{\vec {r}^{~2} (\vec {q}_2 - \vec {r})^2}\right) . \end{aligned}$$
(1)

The second piece has \(\vec {k} \ne 0\) and corresponds to squaring the Lipatov’s vertex, i.e.,

$$\begin{aligned}&``\mathrm{Emission}{\text {''}} \simeq \delta ^{(2)} \left( \vec {q}_1 + \vec {q}_2 - \vec {q}_1^{~'} - \vec {q}_2^{~'}\right) \frac{g^2 N_c }{\vec {q}_1^{~2} \vec {q}_1^{~'2}} \nonumber \\&\quad \times \left( \frac{\vec {q}_1^{~2} \vec {q}_2^{~'2}+\vec {q}_2^{~2} \vec {q}_1^{~'2}}{\vec {k}^{ 2}} - \left( \vec {q}_1 + \vec {q}_2 \right) ^2 \right) . \end{aligned}$$
(2)

After a Fourier transform of these two expressions, and complexifying the transverse momenta, Lipatov found the SL(2,\({\mathbb {C}}\)) invariance of this Hamiltonian [8]. In the present work, however, the focus lies on the forward limit, with zero momentum transfer \(\vec {q} = 0\). It is noteworthy that in this case the contribution from the “Reggeized Propagators” reads

$$\begin{aligned}&``\mathrm{Reggeized ~Propagators}{\text {''}} \nonumber \\&\quad \simeq 2 g^2 N_c \delta ^{(2)} \left( \vec {q}_1 - \vec {q}_1^{~'}\right) \int d^2 \vec {r} \frac{\vec {q}_1^{~2}}{\vec {r}^{~2} (\vec {q}_1 - \vec {r})^2}, \end{aligned}$$
(3)

while the “Emission” piece simplifies to

$$\begin{aligned} ``\mathrm{Emission}{\text {''}}\simeq & {} 2 \frac{g^2 N_c }{\vec {k}^{2}} = 2 \frac{g^2 N_c }{\left( \vec {q}_1 - \vec {q}_1^{~'}\right) ^{2}}. \end{aligned}$$
(4)

It is in this forward case that it truly represents a real emission since now the amplitude corresponds to the \(2 \rightarrow 3\) inelastic process. A further simplification is very convenient: to integrate over the azimuthal angle formed by the two transverse momenta \(\vec {q}_1\) and \(\vec {q}_1^{~'}\).

Once this is done the BFKL equation for forward scattering can be cast in the simple form

$$\begin{aligned} {\partial \varphi (Q^2,Y) \over \alpha \partial Y }= & {} \int _0^\infty {d q^2 \over |q^2-Q^2| } \left( \varphi (q^2,Y)\right. \nonumber \\&\left. - {2 \, \mathrm{min} (q^2,Q^2) \over q^2 + Q^2 } \varphi (Q^2,Y) \right) , \end{aligned}$$
(5)

where \(\alpha = \alpha _s N_c / \pi \), the integration takes place over the gluon virtuality \(q^2 (\equiv \vec {q}^{~2})\) and the correspondence with the previous notation is \(\vec {q}_1^{~2} = Q^2\) and \(\vec {q}_1^{~'2} = Q_0^2\). The term with \(\varphi (Q^2,Y)\) corresponds to Eq. (3) and the one with \(\varphi (q^2,Y)\) to Eq. (4). Since the forward limit has been taken, \(\varphi (Q^2,Y)\) is the cut reggeized gluon four-point function for a given rapidity Y with the initial condition \(\varphi (Q^2,Y=0) \sim \delta (Q^2-Q_0^2)\), and it corresponds to the sum of the squares of the \(2 \rightarrow 2 + n\) emissions amplitude over any number n of real gluon emissions.

To find the gluon Green’s function it is convenient to write Eq. (5) in the form

$$\begin{aligned} {\partial \varphi (Q^2,Y) \over \alpha \partial Y }= & {} \int _0^1 {d x \over 1-x } \left( \varphi (x \, Q^2,Y) \right. \nonumber \\&\left. + \frac{1}{x} \varphi \left( \frac{Q^2}{x},Y\right) - 2 \, \varphi (Q^2,Y) \right) , \end{aligned}$$
(6)

and then introduce a Mellin transform to obtain

$$\begin{aligned} \varphi (Q^2,Y)= & {} \int _{a - i \infty }^{a+i \infty } \frac{d \gamma }{ 2 \pi i} \left( {Q^2 \over Q_0^2}\right) ^{\gamma -1} e^{\alpha Y \chi (\gamma )}, \end{aligned}$$
(7)
$$\begin{aligned} \chi (\gamma )= & {} 2 \psi (1) - \psi (\gamma ) - \psi (1-\gamma ), \end{aligned}$$
(8)

with \(\psi \) being the digamma function and \(0<a<1\). It is well-known that, for asymptotically large values of the rapidity variable Y, this integral tends to

$$\begin{aligned} \varphi (Q^2,Y)\simeq & {} {e^{\alpha Y 4 \log {2}-\frac{t}{2} -{t^2 \over 56 \zeta (3) \alpha Y}} \over 2 \sqrt{14 \pi \zeta (3) \alpha Y}}, \end{aligned}$$
(9)

with \(t=\log {Q^2/Q_0^2}\). This implies the following diffusion equation for the function \(\phi = \varphi e^{t/2} / \pi \):

$$\begin{aligned} {\partial \phi \over \alpha \partial Y}= & {} 4 \log {2} \, \phi + 14 \zeta (3) {\partial ^2 \phi \over \partial t^2}, \end{aligned}$$
(10)

which shows that there exist two different flows for the virtualities of the t-channel gluons in the BFKL ladder: one towards the infrared (IR) and one towards the ultraviolet (UV). These IR/UV flows are symmetric since the eigenvalue function \(\chi (\gamma )\) is invariant under \(\gamma \leftrightarrow 1- \gamma \).

The space of virtualities can be discretized in Eq. (5) using \(q^2=n \,\Delta \), \(Q^2 = N \,\Delta \), \(dl^2 = \Delta \) and the notation \(\phi _n \equiv \varphi (n \,\Delta ,Y)\). It is then possible to write (with \(N= 1, \dots , \infty \))

$$\begin{aligned} \frac{\partial \phi _N}{\alpha \partial Y}= & {} \sum _{n=1}^{N-1} \frac{1}{N -n }\left( \phi _n - \frac{2 n }{N +n} \phi _N \right) \nonumber \\&+\sum _{n=N+1}^\infty \frac{1}{n - N} \left( \phi _n - \frac{2 N}{N + n}\phi _N\right) \nonumber \\\simeq & {} \sum _{n=1}^{N-1} \frac{\phi _n }{N -n }+\sum _{n=N+1}^\infty \frac{\phi _n }{n-N }- 2 h(N-1) \phi _N,\nonumber \\ \end{aligned}$$
(11)

where \(h (N) = \sum _{l=1}^N \frac{1}{l} = \psi (N+1)- \psi (1)\) is the harmonic number. This is a valid representation up to \({{\mathcal {O}}} \left( {\phi _N \over N }\right) \) terms, which are negligible at large N.

To find a matrix representation for the action of the kernel it is useful to introduce the N-dimensional vector \(\vec {\phi } \equiv (\phi _1,\phi _2, \dots , \phi _N)^t\), the extended \(\infty \)-dimensional vector \(\vec {\phi }_\infty \equiv (\phi _1,\phi _2, \dots , \phi _N, \dots )^t\) and write Eq. (11) in the form

$$\begin{aligned} \frac{\partial \vec {\phi }}{\alpha \partial Y}= & {} \hat{{\mathcal {H}}} \cdot \vec {\phi }_\infty , \end{aligned}$$
(12)

with the kernel being the following semi-infinite matrix with N rows and \(\infty \) columns:

$$\begin{aligned} \hat{{\mathcal {H}}}= & {} \left( \begin{array}{ccccccc} -2 h(0) &{} 1 &{} \frac{1}{2} &{} \frac{1}{3}&{} \frac{1}{4} &{} \frac{1}{5}&{}\cdots \\ 1&{} -2 h(1) &{} 1 &{} \frac{1}{2} &{} \frac{1}{3}&{} \frac{1}{4} &{}\cdots \\ \frac{1}{2}&{}1&{} - 2 h(2) &{} 1 &{} \frac{1}{2} &{} \frac{1}{3}&{} \cdots \\ \vdots &{}\vdots &{}\vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \frac{1}{N-1}&{}\frac{1}{N-2}&{}\cdots &{}1&{} -2 h(N-1) &{} 1 &{} \cdots \\ \end{array}\right) .\nonumber \\ \end{aligned}$$
(13)

In terms of components this is equivalent to

$$\begin{aligned} \left( \hat{{\mathcal {H}}}\right) _{i,j}= & {} \sum _{n=1}^{N-1} \frac{\delta _i^{j+n}}{n} + \sum _{n=1}^\infty \frac{\delta _{i+n}^j}{n} - 2 h(i-1) \delta _i^j, \end{aligned}$$
(14)

for \(1 \le i \le N, 1 \le j < \infty \). These matrix elements can be written in terms of the following shift operators:

$$\begin{aligned} \left( \hat{{\mathcal {S}}}_{\mathrm{IR}}\right) _{i,j} = \delta _i^{j+1} \, \, \, , \, \, \, \left( \hat{{\mathcal {S}}}_{\mathrm{UV}}\right) _{i,j} = \delta _{i+1}^j. \end{aligned}$$
(15)

Using the notation \(\left( \hat{{\mathcal {G}}} \right) _{i,j} = - 2 h(i-1) \delta _i^j\), the Hamiltonian becomes

$$\begin{aligned} \hat{{\mathcal {H}}}= & {} \sum _{n=1}^{N-1} \frac{(\hat{{\mathcal {S}}}_{\mathrm{IR}})^n}{n} + \sum _{n=1}^\infty \frac{(\hat{{\mathcal {S}}}_{\mathrm{UV}})^n}{n}+ \hat{{\mathcal {G}}}, \end{aligned}$$
(16)
$$\begin{aligned}= & {} - \sum _{n=N}^\infty \frac{\hat{{\mathcal {S}}}_{\mathrm{IR}}^n}{n} - \log {\left( 1-\hat{{\mathcal {S}}}_{\mathrm{IR}}\right) } - \log {\left( 1-\hat{{\mathcal {S}}}_{\mathrm{UV}}\right) } + \hat{{\mathcal {G}}}.\nonumber \\ \end{aligned}$$
(17)

The diffusion picture is then related to the action of this matrix on an initial condition of the form \(\sim \delta (Q^2-Q_0^2)\). Since \(Q_0^2 = N_0 \, \Delta \), the delta function corresponds to a single entry in the initial condition vector, i.e.

$$\begin{aligned} \vec {\phi }_0 \equiv \left( \phi ^0_1,\phi ^0_2, \dots , \phi ^0_N, \dots \right) ^t \, \, \, \, \, \, \mathrm{with} \, \, \, \, \, \, \phi ^0_i = \frac{\delta _i^{N_0}}{\Delta }. \end{aligned}$$
(18)

The action of the shift operators in the kernel translates the original single “cell” \(\phi ^0_i\) towards lower or higher entries in the vector. This corresponds to the emission of real gluons in the s-channel, which modify the virtuality of the t-channel reggeized gluons. The diagonal piece in the kernel corresponds to the generation of a rapidity gap in between gluon emissions. In order to illustrate this point, a matrix size \(N=50\) has been chosen and the matrix \(\hat{{\mathcal {H}}}\) has been applied to the initial condition vector \(\vec {\phi }_0\) with \(N_0=3\) shown in Fig. 1 (\(\Delta =1\) has been taken). The diffusion pattern can be seen in the resulting components of \(\hat{{\mathcal {H}}} \cdot \vec {\phi }_0\) in Fig. 2.

Fig. 1
figure 1

Initial condition vector \(\phi ^0_i = \frac{\delta _i^{N_0}}{\Delta }\) taking \(N_0 =3\) for \(\Delta = 1\) and \(N=50\)

Full size image
Fig. 2
figure 2

Action of \(\hat{{\mathcal {H}}}\) on \(\phi ^0_i = \frac{\delta _i^{N_0}}{\Delta }\) with \(N=50\) and \(N_0=3\)

Full size image

The continuum limit corresponds to \(N \rightarrow \infty \), \(\Delta \rightarrow 0\), while keeping \(N \Delta = Q^2\) fixed. In order to investigate this point in more detail one can rewrite Eqs. (11, 12) in the form

$$\begin{aligned} {\hat{{\mathcal {H}}}} \cdot \vec {\phi }_\infty= & {} \alpha \sum _{l=1}^\infty \left( \frac{(1- \delta _l^N)}{\left| l-N\right| } -2 h(N-1) \delta _l^N \right) \phi _l. \end{aligned}$$
(19)

To show that the \(N \rightarrow \infty \) limit of this equation does reproduce the continuum BFKL kernel it is useful to work with the representation used in Eq. (7), i.e.,

$$\begin{aligned} \chi _N(\gamma )= & {} \sum _{l=1}^\infty \left( \frac{(1- \delta _l^N)}{\left| l-N\right| } -2 h(N-1) \delta _l^N \right) \left( \frac{N}{l}\right) ^\gamma \nonumber \\= & {} \left( \sum _{l=1}^{N-1}-\sum _{l=N+1}^\infty \right) \frac{1}{N-l} \left( \frac{N}{l}\right) ^{\gamma } - \sum _{l=1}^{N-1}\frac{2}{l}. \end{aligned}$$
(20)

In Fig. 3 it is numerically shown that \(\lim _{N \rightarrow \infty }\chi _N (\gamma ) = \chi (\gamma )\) of Eq. (8) in the range \(0 \le \gamma \le 1\). The convergence in N is not uniform in this region since it is much faster for small values of \(\gamma \). Analytically, the continuum \(N \rightarrow \infty \) limit can be found using \(N = 1/ \Delta \) and \(l = x / \Delta \) with \(\Delta \rightarrow 0\) to obtain

$$\begin{aligned} \chi _\infty (\gamma )= & {} \int _0^1 \frac{dx}{1-x} \left( x^{-\gamma }+x^{\gamma -1}-2\right) = \chi (\gamma ). \end{aligned}$$
(21)
Fig. 3
figure 3

\(\chi _N (\gamma )\) coincides with the BFKL eigenvalue \(\chi (\gamma )\) at \(N \rightarrow \infty \)

Full size image

Let us finish this section by showing the behaviour of the gluon Green’s function in \(Q^2\) and Y space as obtained from Eq. (7). In Fig. 4 the values \(\alpha =Y=1\) and \(Q_0^2 = 3 \, \mathrm{GeV}^2\) have been taken, and the Green’s function for different regions in \(Q^2\), above and below the chosen \(Q_0^2\), has been plotted. In Fig. 5 \(Q^2\) is fixed at two different values and the growth with Y for \(\alpha =1\) has been shown. These plots will be useful for comparison with the results in Sect. 3.

Fig. 4
figure 4

(Anti-)Collinear behaviour of the gluon Green’s function in the BFKL equation

Full size image
Fig. 5
figure 5

The growth of the BFKL Green’s function with Y

Full size image

3 Asymptotic eigensystem in a square truncation

For the exponentiation of the Hamiltonian and its action on a given initial condition state it is needed to work with a square matrix. For this the square truncation of the BFKL matrix of the form

$$\begin{aligned} \left( \hat{{\mathcal {H}}}^{\mathrm{square}}\right) _{i,j}= & {} \sum _{n=1}^{N-1} \frac{\delta _i^{j+n}}{n} + \sum _{n=1}^{N-1} \frac{\delta _{i+n}^j}{n} - 2 h(i-1) \delta _i^j\nonumber \\ \end{aligned}$$
(22)

has been used for which it is possible to calculate the following vector (with \(\vec {\varphi }_0 \equiv (\varphi ^0_1,\varphi ^0_2, \dots , \varphi ^0_N)^t\) ):

$$\begin{aligned} \vec {\phi }= & {} e^{\alpha Y \hat{{\mathcal {H}}}^{\mathrm{square}}} \cdot \vec {\varphi }_0 \nonumber \\= & {} \left\{ 1 + \int _0^Y dy_1 \left( \alpha \hat{{\mathcal {H}}}^{\mathrm{square}} \right) \right. \nonumber \\&\left. + \int _0^Y dy_1 \left( \alpha \hat{{\mathcal {H}}}^{\mathrm{square}} \right) \int _0^{y_1} d y_2 \left( \alpha \hat{{\mathcal {H}}}^{\mathrm{square}} \right) \right. \nonumber \\&+ \left. \int _0^Y dy_1 \left( \alpha \hat{{\mathcal {H}}}^{\mathrm{square}} \right) \int _0^{y_1} d y_2 \left( \alpha \hat{{\mathcal {H}}}^{\mathrm{square}} \right) \right. \nonumber \\&\left. \times \int _0^{y_2} d y_3 \left( \alpha \hat{{\mathcal {H}}}^{\mathrm{square}} \right) + \cdots \right\} \cdot \vec {\varphi }_0, \end{aligned}$$
(23)

which corresponds to the solution of the equation

$$\begin{aligned} \frac{\partial \vec {\phi }}{\alpha \partial Y}= & {} {\hat{{\mathcal {H}}}}^{\mathrm{square}} \cdot \vec {\phi }. \end{aligned}$$
(24)

Note that one can act at both sides on \(\vec {\phi } \equiv (\phi _1,\phi _2, \dots , \phi _N)^t\), this is different to Eq. (12). More explicitly, in components, one can write

$$\begin{aligned} \frac{\partial \phi _j}{\alpha \partial Y}= & {} \sum _{l=1}^{N} \left( \frac{(1- \delta _l^j)}{\left| l-j\right| } -2 h(j-1) \delta _l^j \right) \phi _l. \end{aligned}$$
(25)

In the BFKL context each action of the Hamiltonian corresponds to a single gluon emission together with the creation of a Reggeized gluon in the t-channel which generates a gap in rapidity before having the next emission. In this way, powers of the Hamiltonian correspond to an increase in the gluon multiplicity. As one increases the product \(\alpha Y\) more terms in the sum (23) are needed to reach convergence. In order to study how this picture is realised when constructing the vector \(\vec {\phi }\) in the truncated BFKL case, in the present work the expression in Eq. (23) for a matrix of size \(N=50\) with an initial condition \(N_0=3\) (with \(\varphi _i^0= \delta _i^{N_0} \)) and a coupling \(\alpha =1\) has been calculated.

Fig. 6
figure 6

The growth of the vector \(\vec {\phi }\) with Y for a matrix size \(N=50\), vector components with \(n=3, 20\), and \(\alpha =1\)

Full size image

Then, a look at the \(n = 3, 20\) components of the resulting \(\vec {\phi }\) and the study of its dependence with Y is provided in Fig. 6. It can be seen that the behaviour is very similar to that of the BFKL gluon Green’s function in Fig. 5 but with a smaller growth in the truncated case (note that in BFKL the asymptotic growth corresponds to the Pomeron intercept 4 \(\log {(2)}\)).

It is possible to investigate how the asymptotic growth in the square truncation changes with the matrix size. Let us denote by \(\vec {\psi }_{L}^{(N)}\) the N eigenvectors of the \(N \times N\) matrix \(\hat{{\mathcal {H}}}^{\mathrm{square}}\), and by \(\lambda _L^{(N)}\), the corresponding eigenvalues. Since any initial condition vector can be expanded in the form \(\vec {\phi }_0 = \sum _{L=1}^N c_L^{(N)} \psi _L^{(N)}\), one can then write

$$\begin{aligned} \vec {\phi }= & {} e^{\alpha Y \hat{{\mathcal {H}}}^{\mathrm{square}}} \cdot \vec {\phi }_0 = \sum _{L=1}^N c_L^{(N)} e^{\alpha Y \lambda _L^{(N)}} \psi _L^{(N)}. \end{aligned}$$
(26)
Fig. 7
figure 7

Dependence of the eigenvalues on the matrix size N

Full size image
Fig. 8
figure 8

Dependence of the two largest eigenvalues on the matrix size N

Full size image

The spectrum of eigenvalues of the square matrix \(\hat{{\mathcal {H}}}^{\mathrm{square}}\) is shown in Fig. 7. It can be observed that there is always a largest positive eigenvalue, \(\lambda _{\mathrm{as}}^{(N)}\), with a gap with respect to the next one (see Fig. 8). This gap is not present for the lowest eigenvalues, which decrease as \(\sim -2\log {(N-2)}\) for large matrix sizes. Being the largest eigenvalue, \(\lambda _{\mathrm{as}}^{(N)}\) drives the \(\alpha Y \rightarrow \infty \) asymptotics:

$$\begin{aligned} \lim _{\alpha Y \rightarrow \infty } \vec {\phi }= & {} c_{\mathrm{as}}^{(N)} e^{\alpha Y \lambda _{\mathrm{as}}^{(N)}} \psi _{\mathrm{as}}^{(N)}. \end{aligned}$$
(27)

It is interesting to note that \(\lambda _{\mathrm{as}}^{(N)}\) grows very slowly with N in a way consistent with having its \(N \rightarrow \infty \) limit at the Pomeron intercept \(4 \log {(2)}\) (this has been confirmed up to N = 200000 where (N) the largest eigenvalue is 2.34). We should stress at this point that one should not expect that the square truncation of the BFKL matrix is the means of achieving a fast convergence towards the value 4 log(2). An example of a different approach with fast numerical convergence can be found in Ref. [30]. In the present context, Fig. 7 gives a proof of concept that it is consistent to study the eigenvalues of the square truncated BFKL matrix. If the asymptotic eigenstate \(\psi _{\mathrm{as}}^{(N)}\) is investigated one will find that the distribution of its components (see Fig. 9) is similar to that found for BFKL in Fig. 4. In this analysis \(N=100\) has been used, \(N_0=20\) and the coupling is \(\alpha =1\), but the features here discussed are generic. From the asymptotic expression in Eq. (9) one can extract the following logarithmic derivative

$$\begin{aligned} -2 Q^2 \frac{\partial }{\partial Q^2} \varphi \left( Q^2, Y\right)\simeq & {} 1+ \frac{1}{14 \alpha Y \zeta (3)} \log {\left( \frac{Q^2}{Q_0^2}\right) } \end{aligned}$$
(28)

It has been checked that the dominant eigenstate in the asymptotic limit \(\alpha Y \rightarrow \infty \) follows this behaviour with a logarithmic derivative going to one as the matrix size N increases. Numerically, it is much more complicated to capture the subasymptotic corrections since it is likely that a continuous of eigenstates contribute to them.

It is possible to study the multiplicity distribution (average number of iterations of the Hamiltonian for a given value of \(\alpha Y\) needed to reach convergence, in the QCD context this corresponds to the average number of emitted mini-jets for a fixed center-of-mass energy) in the asymptotic state by looking at the relative weight of the s different terms in the expansion \(e^{\alpha Y \lambda _{\mathrm{as}}^{(N)}} = \sum _{s=0}^\infty (\alpha Y \lambda _{\mathrm{as}}^{(N)})^s/s!\). This is shown for the \(n=40\) component (the results are independent of this choice) of the vector \(\vec {\phi }\) at different values of the rapidity variable \(Y=1,2,3\) in Fig. 10. A Poissonian-like distribution broadening is found with an increasing mean value as Y increases. These results should be compared to the similar ones (up to normalization) which are well-known to underly the BFKL dynamics as one increases Y (compare with, e.g., Fig. 1 in Ref. [31]).

Fig. 9
figure 9

The dominant eigenstate in the asymptotic \(\alpha Y \rightarrow \infty \) region

Full size image
Fig. 10
figure 10

Distribution in the number of iterations of the Hamiltonian for fixed \({\alpha }, N, n, Y\)

Full size image

4 Taming the energy growth by tampering with the infrared

It is possible to introduce modifications in the matrix representation here presented. In particular, it is tempting to impose an absorptive constraint (see for example [32]) in the sector of the kernel responsible for the evolution into infrared modes. A precise proposal reads as follows

$$\begin{aligned} {\partial \varphi (Q^2,Y) \over \alpha \partial Y }= & {} \int _0^\infty {d q^2 \over |q^2-Q^2| } \left[ \left( \left( \frac{q}{Q}\right) ^{2\kappa } \theta (Q-q)\right. \right. \nonumber \\&\left. \left. +\theta (q-Q)\right) \varphi (q^2,Y) \right. \nonumber \\&\left. - {2 \, \mathrm{min} (q^2,Q^2) \over q^2 + Q^2 } \varphi (Q^2,Y) \right] \, . \end{aligned}$$
(29)

For \(\kappa = 0\) the original symmetric evolution is recovered while for \(\kappa > 0\) a suppression of the diffusion into the infrared is imposed. This equation can be written in the form

$$\begin{aligned} {\partial \varphi (Q^2,Y) \over \alpha \partial Y }= & {} \int _0^1 {d x \over 1-x } \left( x^\kappa \varphi (x \, Q^2,Y) \right. \nonumber \\&\left. + \frac{1}{x} \varphi \left( \frac{Q^2}{x},Y\right) - 2 \, \varphi (Q^2,Y) \right) , \end{aligned}$$
(30)

with solution in the region \(0< \mathfrak {R}(\gamma ) < 1\)

$$\begin{aligned} \varphi (Q^2,Y)= & {} \int _{a - i \infty }^{a+i \infty } \frac{d \gamma }{ 2 \pi i} \left( {Q^2 \over Q_0^2}\right) ^{\gamma -1} e^{\alpha Y \chi _\kappa (\gamma )}, \end{aligned}$$
(31)
$$\begin{aligned} \chi _\kappa (\gamma )= & {} 2 \psi (1) - \psi (\gamma +\kappa ) - \psi (1-\gamma ). \end{aligned}$$
(32)

The discretised representation can be written as

$$\begin{aligned} \frac{\partial \phi _N}{\alpha \partial Y}= & {} \sum _{n=1}^{N-1} \left( \frac{n}{N}\right) ^\kappa \frac{\phi _n }{N -n }+\sum _{n=N+1}^\infty \frac{\phi _n }{n-N }- 2 h(N-1) \phi _N,\nonumber \\ \end{aligned}$$
(33)

with the corresponding matrix Hamiltonian being

$$\begin{aligned} \hat{\mathcal {H}}_\kappa = \begin{pmatrix} -2h(0) &{} 1 &{} \frac{1}{2} &{} \frac{1}{3} &{} \dots \\ 1 \left( \frac{1}{2}\right) ^\kappa &{} -2h(1) &{} 1 &{} \frac{1}{2} &{} \dots \\ \frac{1}{2} \left( \frac{1}{3}\right) ^\kappa &{} 1 \left( \frac{2}{3}\right) ^\kappa &{} -2h(2) &{} 1 &{} \dots \\ \frac{1}{3} \left( \frac{1}{4}\right) ^\kappa &{} \frac{1}{2} \left( \frac{2}{4}\right) ^\kappa &{} 1 \left( \frac{3}{4}\right) ^\kappa &{} -2h(3) &{} \dots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \frac{1}{N-1} \left( \frac{1}{N}\right) ^\kappa &{} \frac{1}{N-2} \left( \frac{2}{N}\right) ^\kappa &{} \frac{1}{N-3} \left( \frac{3}{N}\right) ^\kappa &{} \frac{1}{N-4} \left( \frac{4}{N}\right) ^\kappa &{} \dots \end{pmatrix}.\nonumber \\ \end{aligned}$$
(34)

The associated matrix elements are

$$\begin{aligned} \Big ( \hat{\mathcal {H}}_\kappa \Big )_{i,j}= & {} \sum _{n=1}^{N-1} \frac{\delta _i^{j+n}}{n} \Big ( \frac{j}{i} \Big )^\kappa + \sum _{n=N+1}^{\infty } \frac{\delta _{i+n}^j}{n} - 2h(i-1)\delta _i^j \nonumber \\= & {} \frac{1}{i-j} \Big ( \frac{j}{i} \Big )^\kappa \theta (i-j) + \frac{1}{j-i} \theta (j-i) \nonumber \\&-2h(i-1) \delta _i^j \, . \end{aligned}$$
(35)

It is now instructive to study the action of its square truncation on an initial condition vector with \(N_0=20\) and, again, \(N=50\), \(\Delta =1\). This is plotted in Fig. 11 for values of the new parameter \(\kappa =0,1,6\). When \(\kappa =0\) the usual BFKL behaviour for the Green’s function is obtained. As \(\kappa \) increases its value is strongly suppressed due to the infrared barrier introduced in the evolution kernel. As previously discussed, the asymptotic behaviour is governed by the spectrum of eigenvalues of the matrix Hamiltonian. This is shown in Fig. 12 where it can be seen how introducing \(\kappa =1\) makes the asymptotic eigenvalues decrease drastically. This includes the case of the largest eigenvalue whose dependence on \(\kappa \) is plotted, for a large matrix size of \(N=13000\), in Fig. 13. Since the largest eigenvalue rapidly tends to zero as \(\kappa \) increases, this limit can be considered as an effective method to generate an evolution with a weaker violation of the Froissart bound. There is an interesting interpretation of the spectrum shown in Fig. 12 when \(\kappa \rightarrow \infty \). In this limit the Hamiltonian becomes upper triangular and its eigenvalues correspond to the diagonal matrix elements, \(-2 h(i-1)\), with \(1 \le i \le N\). To illustrate this point, the behaviour of some of the eigenvalues as \(\kappa \) grows is given in Fig. 14.

Fig. 11
figure 11

Occupation number comparison for \(\kappa =0,1,6\). \(N_0=20\), \(N=50\), \(\Delta =1\)

Full size image
Fig. 12
figure 12

Eigenvalues comparison for \(\kappa =0\) and \(\kappa =1\). N goes up to 13000

Full size image
Fig. 13
figure 13

Largest eigenvalue of the Hamiltonian for a matrix size of \(N=13000\) and several values of \(\kappa \)

Full size image
Fig. 14
figure 14

Spectrum for a matrix size of N = 50 as \(\kappa \) increases

Full size image

To conclude this section, a brief study of the associated eigenvectors can be introduced. It is worth pointing out that the eigenvector linked to the largest eigenvalue is the only one with all its components being positive, as can be seen for a small matrix size with \(N=5\) and \(\kappa =0\), in Fig. 15. In this plot a second interesting feature appears: the secondary eigenvectors show oscillatory behaviour in their components. This implies that there exists a double mechanism to suppress the subleading eigenvalues: firstly, the fact that they are numerically smaller and, secondly, the destructive interference among their eigenvectors. These qualitative structure holds for large matrices and different values of \(\kappa \).

Fig. 15
figure 15

Eigenvector coefficients for \(\kappa =0\), \(N=5\)

Full size image

5 Matrix representation of the sl(2) spin chain Hamiltonian

As it was mentioned in the Introduction, there has been big progress in the understanding of the planar limit of the \({{\mathcal {N}}} = 4\) SYM dilatation operator by mapping it to the Hamiltonian of an integrable one-dimensional spin chain. The part of the theory of interest in this work is the non-compact bosonic sl(2) closed subsector where states are constructed with scalar fields \(\Phi \) (SO(6) Yang–Mills bosons) and their spacetime covariant derivatives \({{\mathcal {D}}} \Phi \), which scale under the sl(2) subgroup of the Lorentz group. The corresponding charges are related to the SO(4,2) group and to the SO(6) \({{\mathcal {R}}}\)-symmetry.

The commutation relations of the sl(2) subalgebra of the superconformal algebra are \(\left[ J^{(+)},J^{(-)} \right] = -2 J^{(3)}, \left[ J^{(3)},J^{(\pm )}\right] = \pm J^{(\pm )}\). The spin chain Hamiltonian representing the one-loop anomalous dimensions of \({{\mathcal {N}}} = 4\) SYM operators with spin \(S-1\) in the planar limit of the sl(2) sector reads

(36)

where \(\lambda = \frac{g^2 N_c}{8 \pi ^2}\) is the coupling. The notation in terms of harmonic oscillators \((a^\dagger )^n |0\rangle = \frac{1}{n!} ({{\mathcal {D}}})^n \Phi \) (with \(a |0\rangle = 0\), \(\left[ a,a^\dagger \right] =1\)), which corresponds to a site in a one-dimensional lattice (the total number of lattice sites is equal to the total \({{\mathcal {R}}}\)-charge), has been used. n indicates that a given site is in the n-th excited state with respect to the Tr\((\Phi ^2)\) vacuum. These excitations are classified in the spin \(s=-\frac{1}{2}\) representation of sl(2), which is infinite-dimensional. There is an overall trace in the operator cyclically ordering the different sites in the spin chain. Eq. (36) was introduced by Beisert in [29] and it corresponds to the nearest-neighbor one-loop Hamiltonian of an integrable XXX spin \(s= - \frac{1}{2}\) chain. More explicitly, this Hamiltonian is invariant under the sl(2) generators

$$\begin{aligned} J^{(+)}_{12}= & {} a^{\dagger }_1 \left( 1 + a^{\dagger }_1 a_1\right) + a^{\dagger }_2 \left( 1 + a^{\dagger }_2 a_2\right) , \end{aligned}$$
(37)
$$\begin{aligned} J^{(-)}_{12}= & {} a_1 + a_2, \end{aligned}$$
(38)
$$\begin{aligned} J^{(3)}_{12}= & {} 1 + a^{\dagger }_1 a_1 + a^{\dagger }_2 a_2. \end{aligned}$$
(39)

There is an interesting similarity between this spin chain representation and the square truncation of the BFKL equation. In order to find it it is needed to focus on a “slice” of the \(\hbox {XXX}_{-\frac{1}{2}}\) spin chain Hamiltonian characterized by \(S-N = N-1\). In this case the spin chain Hamiltonian acts on a diagonal state with the same number of derivatives in each oscillator (both are in the same \((N-1)\)-th excited state):

$$\begin{aligned}&{{\mathcal {H}}}_{1,2}^{\mathbf{sl}(2)} (a_1^+)^{N-1}(a_2^+)^{N-1} |00\rangle \nonumber \\&\quad = - \lambda \sum _{l=1}^{2N-1} \left( \frac{(1- \delta _l^N)}{\left| l-N\right| } -2 h(N-1) \delta _l^N \right) \nonumber \\&\qquad \times (a_1^+)^{l-1}(a_2^+)^{2N-1-l} |00\rangle . \end{aligned}$$
(40)

Let us now compare this expression with that for the square truncation of the BFKL Hamiltonian in Eq. (25). It is striking that the terms under the sum in Eqs. (40) and (25) are identical if one identifies \(\phi _l\) with \((a_1^+)^{l-1}(a_2^+)^{2N-1-l} |00\rangle \) and \(\alpha \) with \(- \lambda \). It should be stressed that in Eq. (36) the diagonal \(h(N-1)+h(S-N)\) terms coincide with those of BFKL only for \(S = 2 N -1\).

The main difference between the discretized-in-virtuality BFKL equation and the sl(2) spin chain projected on a diagonal state stems from the components with \(l \ge 2 N\) in Eq. (19) which are not present in Eq. (40). The corresponding matrices read

$$\begin{aligned} \hat{{\mathcal {H}}} = \left( \begin{array}{ccccc} -2 h(0) &{} 1 &{} \frac{1}{2} &{} \cdots &{}\frac{1}{N-1}\\ 1&{} - 2 h(1) &{} 1 &{}\cdots &{}\frac{1}{N-2}\\ \frac{1}{2}&{}1&{} -2 h (2) &{} \cdots &{}\frac{1}{N-3}\\ \vdots &{}\vdots &{}\vdots &{} \ddots &{}\vdots \\ \frac{1}{N-1}&{}\frac{1}{N-2}&{}\cdots &{} \cdots &{} -2 h (N-1)\\ \end{array}\right) _{\mathrm{XXX}_{-\frac{1}{2}}} \left. \begin{array}{ccc} \frac{1}{N} &{} \frac{1}{N+1} &{}\cdots \\ \frac{1}{N-1}&{} \frac{1}{N} &{}\cdots \\ \frac{1}{N-2}&{}\frac{1}{N-1}&{}\cdots \\ \vdots &{}\vdots &{}\ddots \\ 1&{}\frac{1}{2}&{}\cdots \\ \end{array}\right) _{\mathrm{BFKL}} \nonumber \\ \end{aligned}$$
(41)

However, the square truncation of the BFKL matrix coincides with the slice of the spin chain under study in this work.

Let us stress that the truncation of the BFKL kernel leads to a new evolution equation with different eigenvalues and a different Green’s function. In order to make this point more clear one can investigate the corresponding evolution equation in the continuum limit. We introduce a change of variables in Eq. (5), namely, \(q^2 \rightarrow l^2+ Q^2\) and in addition we change the upper limit of the integration from infinity to \({\bar{Q}}^2\) such that we finally have:

$$\begin{aligned} {\partial \varphi (Q^2,Y) \over \alpha \partial Y }= & {} \int _0^1 {d x \over 1-x } \left\{ \varphi (x \, Q^2,Y) \right. \nonumber \\&\left. + \frac{1}{x} \varphi \left( \frac{Q^2}{x},Y\right) - 2 \, \varphi (Q^2,Y) \right\} \nonumber \\&- \int _0^{\frac{Q^2}{Q^2+{{\bar{Q}}}^2}} {d x \over (1-x) x } \varphi \left( \frac{Q^2}{x},Y\right) \end{aligned}$$
(42)

where \({{\bar{Q}}}^2 \rightarrow \infty \) leads to the usual BFKL equation and \({{\bar{Q}}}^2 = Q^2\) to its square truncation in Eq. (25) with \(N \rightarrow \infty \). Making use of the representation for \(\varphi \) of Eq. (7) in Eq. (42) one obtains, in the \(0< \gamma < 1\) region, the following expression

$$\begin{aligned} \chi (\gamma )= & {} \frac{1}{\gamma } + 2 \sum _{L=1}^\infty \zeta (2 L +1) \gamma ^{2L} \nonumber \\&+ \sum _{L=1}^\infty \frac{1}{\gamma -L} \left( \frac{Q^2}{Q^2+{{\bar{Q}}}^2}\right) ^{L-\gamma }. \end{aligned}$$
(43)

This leads to a simple relation between the BFKL and the truncated BFKL kernels:

$$\begin{aligned} \chi ^{\mathrm{square}} (\gamma )= & {} \chi ^{\mathrm{BFKL}} (\gamma ) + \sum _{L=1}^\infty \frac{2^{\gamma -L}}{\gamma -L}. \end{aligned}$$
(44)

The main feature of this result is that the new term in \(\chi ^{\mathrm{square}}\) contains a pole at \(\gamma \rightarrow 1\) which cancels a similar one in \(\chi ^{\mathrm{BFKL}}\). The \(\gamma \rightarrow 0\) region only receives finite corrections. This can be seen in Fig. 16. The asymmetry in the square truncation of the kernel generates a different behaviour in the collinear \(Q>Q_0\) and anti-collinear \(Q<Q_0\) regions of the Green’s function \(\varphi (Q,Q_0,Y)\). This is explicitly shown in Fig. 17 where the Green’s function is shown for both equations for \(Q_0=1\) and \(\alpha Y=1\). Both solutions have a very different structure when \(Q<Q_0\), or \(N < N_0\) in the discretized version. Their behaviour is more similar in the asymptotic region \(Q \gg Q_0 (N \gg N_0)\) since there they share the same leading singularity at \(\gamma \rightarrow 0\):

$$\begin{aligned} \chi ^{\mathrm{BFKL}} (\gamma )= & {} \frac{1}{\gamma } + 2 \sum _{L=1}^\infty \zeta (2 L +1) \gamma ^{2L}, \end{aligned}$$
(45)
$$\begin{aligned} \chi ^{\mathrm{square}} (\gamma )= & {} \frac{1}{\gamma } + 2 \sum _{L=1}^\infty \zeta (2 L +1) \gamma ^{2L} \nonumber \\&- \sum _{m=0}^\infty \gamma ^m \sum _{n=0}^m \frac{(\log {2})^n}{n!} \mathrm{Li}_{1+m-n} \left( \frac{1}{2}\right) . \end{aligned}$$
(46)

It is worth pointing out that these kernels generate different leading \({{\mathcal {O}}}\left( (\alpha / \omega )^n\right) \) contributions to the anomalous dimension of twist-two operators with spin \(M=\omega -1\), for \(\omega \rightarrow 0\):

$$\begin{aligned} \gamma ^{\mathrm{BFKL}}_\omega =&\frac{\alpha }{\omega } + 2 \zeta (3) \left( \frac{\alpha }{\omega } \right) ^4 + 2 \zeta (5) \left( \frac{\alpha }{\omega } \right) ^6 + 12 \zeta (3)^2 \left( \frac{\alpha }{\omega } \right) ^7 +\dots , \nonumber \\ \gamma _\omega ^{\mathrm{square}} =&\frac{\alpha }{\omega } - \log {2} \left( \frac{\alpha }{\omega } \right) ^2 + \frac{1}{2} \left( (\log {2})^2 - \zeta (2) \right) \left( \frac{\alpha }{\omega } \right) ^3 \nonumber \\&+ \left( \frac{1}{3} (\log {2})^3 + \frac{3}{2} \zeta (2) \log {2}+ \frac{9}{8} \zeta (3) \right) \left( \frac{\alpha }{\omega } \right) ^4 + \cdots \end{aligned}$$
(47)

Let us conclude with some possible connections to other works like that in [33] where an expression as in Eq. (29) was found with \(\varphi \) corresponding there to the distribution of soft photons in a charged source, with no relation to high energy scattering in the Regge limit or the BFKL equation. A similar analysis can be applied in that context. From a more formal point of view, it is likely that a link can be found between the matrix representation of the sl(2) Hamiltonian here unveiled and the work in [34], where it was investigated how the discrete sinh-Gordon equation leads to the Toeplitz 2-Toda lattice. This new lattice has \(\tau \)-functions which are annihilated by operators living in a SL(2,\({\mathbb {Z}}\)) subalgebra of the Virasoro algebra, and have a very similar structure to Eq. (16) if the harmonic weights 1/n are identified with time variables in the IR/UV directions. It is on these time variables where the Virasoro operators act. Finally, in [35] a coherent state representation for the Hamiltonian of the spin chain with sl(2) symmetry was derived. The action of the Hamiltonian on the coherent states \(\vec {n}_1, \vec {n}_2\) then reads

$$\begin{aligned} \left<\vec {n}_1, \vec {n}_2 \right| {{\mathcal {H}}}_{1,2}^{\mathrm{sl}(2)} \left| \vec {n}_1, \vec {n}_2 \right>= & {} \log {\left( 1-\frac{(\vec {n}_1 - \vec {n}_2)^2}{4}\right) }, \end{aligned}$$
(48)

with \(\vec {n}_{1,2}\) living on a two-dimensional hyperboloid for sl(2). It will be interesting to study the relation of this work with the results here presented.

Fig. 16
figure 16

The BFKL and the truncated BFKL kernels in \(\gamma \) space

Full size image
Fig. 17
figure 17

Collinear behaviour of the BFKL and the truncated BFKL gluon Green’s functions

Full size image

6 Conclusions

In this work a semi-infinite matrix representation of the BFKL equation has been given in Eq. (13), together with its physical interpretation in terms of a diffusion process into infrared and ultraviolet regions of virtuality space. It has been found that the square truncation of the semi-infinite matrix in the BFKL equation and the action of the \(s=-\frac{1}{2}\) XXX spin chain Hamiltonian on a symmetric double copy of the harmonic oscillator share many common features. It was possible to make this connection by taking the original BFKL equation to its forward limit and averaging over the azimuthal angle dependence of its kernel. The remaining physical variable, which has been discretised to write the matrix representation, corresponds to the virtuality of exchanged gluons. The associated gluon Green’s function has been constructed using a square truncation of the BFKL matrix, by exponentiating it and acting on a general initial condition. It has been shown that in this case both systems manifest the same asymptotic behaviour. Finally, a modification of the t-channel gluon propagators in the infrared has been proposed as a simple mechanism to generate an evolution with a weaker violation of the Froissart bound by taming the exponential growth of the original evolution equation.