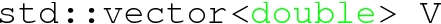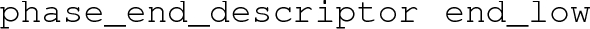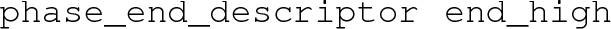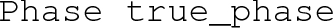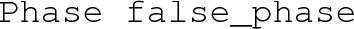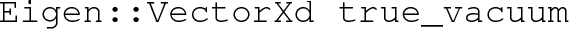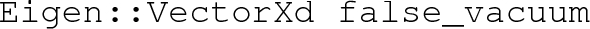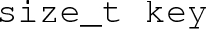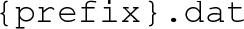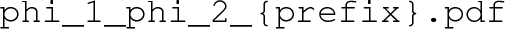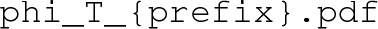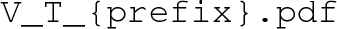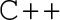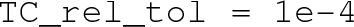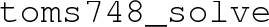Abstract
We present a C++ software package called PhaseTracer for mapping out cosmological phases, and potential transitions between them, for Standard Model extensions with any number of scalar fields. PhaseTracer traces the minima of effective potential as the temperature changes, and then calculates the critical temperatures, at which the minima are degenerate. PhaseTracer is constructed with modularity, flexibility and practicality in mind. It is fast and stable, and can receive potentials provided by other packages such as FlexibleSUSY. PhaseTracer can be useful analysing cosmological phase transitions which played an important role in the very early evolution of the Universe. If they were first order they could generate detectable gravitational waves and/or trigger electroweak baryogenesis to generate the observed matter anti-matter asymmetry of the Universe. The code can be obtained from https://github.com/PhaseTracer/PhaseTracer.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since some fundamental symmetries are expected to break in the early Universe the accompanying phase transitions are critical to our understanding of the phenomenon (see e.g. Ref. [1] for a review). These transitions occur when the system of scalar fields transits between two distinct minima, also called vacua, of the effective potential. If the vacua are separated by a barrier the transition is first order, and if the deeper minimum is charged a symmetry breaks spontaneously.
Finite temperature corrections to effective potentials result in important modifications to the free energy typically restoring spontaneously broken symmetries at high temperatures [2, 3]. Consequently, if a symmetry is broken at zero temperature, a phase transition probably occurred as the Universe cooled. We therefore expect that there was an electroweak phase transition associated with electroweak symmetry breaking. There may have been other phase transitions in the early Universe, such as one that breaks symmetries of a Grand Unified Theory (GUT) that embeds the Standard Model (SM) gauge groups into a unified gauge group [4,5,6,7,8]. Alternatively, other gauge groups may have broken at intermediate scales, for example, extra U(1) gauge groups that are fairly generic predictions of string theory [9,10,11,12,13,14] and can solve the \(\mu \)-problem of the Minimal Supersymmetric Standard Model (MSSM) [15,16,17]. These phase transitions played an important role in the evolution of the Universe and it is vital to understand their detailed mechanisms.
First order electroweak phase transitions are particularly interesting as they could help to satisfy Sakharov’s third condition for baryogenesis [18] – a departure from thermal equilibrium. Provided there is sufficient CP violation, they could trigger electroweak baryogenesis and explain the observed baryon asymmetry of the Universe (see e.g., Refs. [19,20,21,22] for reviews). Determining if an electroweak baryogenesis mechanism in a particular extension of the Standard Model can successfully predict the observed baryon asymmetry of the Universe is rather involved, as described by Refs. [19,20,21,22]. Nonetheless finding the critical temperature of the phase transition is a very important step in this calculation and many studies have focused on this and on the calculation of the order parameter of the first order phase transition (see for example Refs. [23,24,25,26]).
First order phase transitions also generate gravitational waves via collisions, sound waves and turbulence from expanding bubbles of a new phase (see e.g., Refs. [27,28,29,30]). The recent detection of gravitational waves [31,32,33,34,35] has opened a new window through which we can directly access physics beyond the Standard Model [36,37,38,39,40,41,42,43,44,45,46,47]. Gravitational waves accompanying first order phase transitions could be observable at current or future gravitational wave detectors, such as the Einstein Telescope [48], the Laser Interferometer Gravitational Wave Observatory (LIGO) [49], the Virgo interferometer [50], the Kamioka Gravitational-Wave Detector (KAGRA) [51], the Cosmic Explorer [52], the Laser Interferometer Space Antenna (LISA) [53], the Deci-hertz Interferometer Gravitational wave Observatory (DECIGO) [54], the Big Bang Observer (BBO) [55] or the Taiji program [56].
This would provide new tests of models beyond the SM (BSM), including electroweak baryogenesis, that are complementary to collider physics experiments and measurements of electric dipole moments (EDMs). Even if the energy scale associated with the phase transition is far higher than that which could be probed in any foreseeable collider experiments, gravitational wave detection is still a possibility. For example, it was shown in Ref. [57] that gravitational waves from the breakdown of a Pati–Salam group [4] at about \(10^5\,\text {GeV}\) can give rise to detectable signatures at the Einstein Telescope.
The gravitational wave spectrum is determined by thermal quantities such as the nucleation temperature (and rate) of the bubbles, \(T_n\), the latent heat released during the phase transition (relative to the radiation energy density of the plasma), \(\alpha \), the (inverse) duration of the transition, \(\beta \), and the velocity of the expanding bubble walls, \(v_w\). There are significant subtleties involved in calculating these and a variety of approaches have been taken in the literature [58,59,60,61,62]. Nonetheless, finding the first order phase transitions and their associated critical temperatures is an important step towards testable gravitational wave predictions.
To help study phase transitions and their associated phenomenology, we present PhaseTracer , a code to analyse the possible phases and phase transitions as the Universe cooled for any scalar potential. There are two other public codes with similar goals: CosmoTransitions [63] and BSMPT [64].Footnote 1 Our code is most similar to the former, which facilitated over a hundred studies. Compared to CosmoTransitions, the advantages of PhaseTracer are speed, as it is written in

rather than

; flexibility, as it can be linked to models in BSMPT and FlexibleSUSY [66,67,68]; robustness, as it includes a test-suite of known analytic and numerical results and correctly handles discrete symmetries; and lastly, active maintenance and development by several authors. Our code is public and we encourage contributions (such as repository pull requests) from the community.
BSMPT and PhaseTracer have different strategies for finding and tracing the temperature dependence of vacua. In the cases that we tested, however, PhaseTracer was able to identify more transitions than BSMPT. The public code Vevacious uses a numerical polyhedral homotopy continuation method, a powerful way to find all the roots of a system of polynomial equations, to identify vacua at zero temperature. This technique is more robust than the one used presently in PhaseTracer . However it requires the potential to be written in a special symbolic format and can only be used directly to find the tree-level minimum at zero temperature. After this, adjustments to the minima locations from one-loop Coleman-Weinberg corrections are then found using the MINUIT algorithms [69]. Minima at finite temperature are also found via MINUIT, using each minimum at zero temperature as a starting point and assuming that these two minima belong to the same phase, which is not always true.
With PhaseTracer our aim is to improve the calculation of phase transitions on several fronts. We intend to locate all minima at zero temperature and a high temperature and find the thermal phases of the potential by following the temperature dependence of the minima. We attempt to reliably distinguish phases during the evolution of the minima with temperature. We try to properly map the temperature dependence of all phases being aware that minima may appear and disappear with the temperature evolution. Finally, we aim to properly identify the potential transitions between the identified thermal phases including cases when the potential may have discrete symmetries.
The structure of our paper is as follows. In Sect. 2 we provide quickstart instructions for installing and running PhaseTracer . Then in Sect. 3 we describe the physics problem and our numerical methods to solve it, as well as presenting the zero- and finite-temperature corrections that we include in our calculations. After this we briefly describe the structure of the code in Sect. 4 before providing detailed instructions and examples on how to implement new models in Sect. 5. In Sect. 6 we provide an extensive set of example results and comparisons between PhaseTracer and other codes or analytic results. Finally in Sect. 7 we present our conclusions.
2 Quick start
2.1 Requirements
Building PhaseTracer requires the following:
A
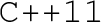
compatible compiler (tested with
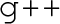
4.8.5 and higher, and
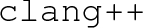
3.3)
CMake,Footnote 2 version 2.8.12 or higher.
The
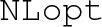
library,Footnote 3 version 2.4.1 or higher.
Eigen library,Footnote 4 version 3.1.0 or higher
Boost libraries,Footnote 5 version 1.53.0 or higher, specifically:
*
*
Our EffectivePotential library, which itself requires
The
library
On Ubuntu, they can be installed by

Furthermore, one of our example programs (

) uses a potential built with FlexibleSUSY. Our build script attempts to build FlexibleSUSY, but there are further dependencies; see the FlexibleSUSY manuals [66, 68] or the FlexibleSUSY README file for further details.
To visualize our results, our package includes plot scripts that require:
-
and the external modules
,
,
and
.
-
On Ubuntu, they can be installed by

Finally, for testing, we provide BSMPT programs that require
-
. If this is absent, it is built automatically but this requires the
and
build tools.
2.2 Downloading and running PhaseTracer
PhaseTracer can be obtained by doing,

where the master branch will have the latest stable version, and the development branch will have the latest in-development features.
To build PhaseTracer on a UNIX-like system with the Make build system installed as the default build tool, run at the command line:

The resulting library and executables are located in the

and

subdirectories of the main package directory, respectively. The built-in examples can be executed by running

The results described in Sect. 6 will be generated, including Fig. 3.
By default, the example

is not compiled, as it needs FlexibleSUSY. To build the

model, run at the command line:

Then the example can be executed by

Finally, by default comparisons with BSMPT are not compiled, but may be enabled by the

flag.
3 The physics problem
Our aim is to trace the minima of the effective potential for some arbitrary BSM physics theory, and find the critical temperatures for possible phase transitions between them. The first task is to construct the effective potential.
3.1 Constructing the effective potential
The effective potential typically includes the following contributions,
where \(V^\text {tree}\) is the tree-level potential expressed in terms of \(\overline{\text {MS}}\) parameters. The contribution \(\Delta V^{\text {1-loop}}\) stands for the one-loop zero temperature corrections to the effective potential, which in the \(R_\xi \) gauge are given by [70],
where the sums over \(\phi \), V and f represent sums over the scalar, vector and fermion fields respectively and we have introduced the renormalization scale, Q, the field dependent \(\overline{\text {MS}}\) mass eigenstates of the considered BSM theory \(m_i\), where there i stands for the BSM fields which are summed over, and finally \(n_i\), which gives the numbers of degrees of freedom for field i. With the potential constructed in this way we are assuming that the \(\overline{\text {MS}}\) parameters have been chosen or adjusted to fulfill the electroweak symmetry breaking conditions at the one-loop order, as would automatically be the case if one is obtaining them from a mass spectrum generator.
Please also note that if the parameters are input in a different scheme then one may need to modify these corrections, see e.g. section 3 of Ref. [71] for a review of the known one-loop corrections in the \(\overline{\text {MS}}\), \(\overline{\text {DR}}\) [72, 73] and \(\overline{\text {DR}}^\prime \) [74] schemes in the Landau gauge. One could also add counter-terms to the potentialFootnote 6 in (1), i.e. change \(V_\text {eff} \rightarrow V_\text {eff} + V_\text {c.t.}\) modifying the \(\overline{\text {MS}}\) scheme. This can be used to e.g. ensure that the one-loop zero temperature minimum matches the tree-level minimum and that the pole masses correspond to tree-level mass eigenstates.
The contribution \(\Delta V_T^{\text {1-loop}}\) is the one-loop finite-temperature correction to the effective potential and in the \(R_\xi \) gauge it is given by,

where \(J_\text {B}\) and \(J_\text {F}\) are the thermal functions,
The upper (lower) sign above applies for bosons (fermions). Strong Boltzmann suppression occurs in these thermal functions for \(m^2 \gg T^2\).
Finally if the Debye masses are provided then the daisy corrections can be included. Following the Arnold-Espinosa approach we include these in an additive potential of the form,
where in the first two terms we sum over the Higgs fields (including Goldstone bosons) and in the second two terms we sum over the massive gauge bosons. We use \({\overline{m}}^2\) to denote field-dependent mass eigenvalues that include Debye corrections. If there are no Debye corrections to the masses this contribution will vanish. We always take the real part of the potential, which deals with the possibility of tachyonic masses in (5). If Debye masses are not supplied by the user then this contribution will be neglected.
The effective potential presented is not gauge invariant [70, 75]. In our implementation, as described in Sect. 5, we allow the user to choose any \(R_\xi \) gauge for the calculation, allowing them to test variation in a variety of gauges. In future releases we plan to add additional methods to allow an alternative gauge-independent calculation based on the procedure in Ref. [70]. We also note that there are well-known problems associated with perturbative approaches near phase transitions [76, 77]. Nevertheless, lattice approaches are not currently a tractable alternative for phenomenological studies in arbitrary models of new physics.
3.2 Critical temperature and transition strengths
Having constructed a temperature dependent effective potential, we wish to trace its possible phases as the temperature changes. Tracing phases means tracking the temperature dependence of the minima of the effective potential. We will describe our method to do this in a separate section below. The result of this tracing are the phases of the potential, that is the locations of all minima as functions of temperature.
After we identified the phases of the potential we also wish to find critical temperatures at which the potential has degenerate minima. We define the critical temperature, \(T_C\), to be the temperature at which the potential has two degenerate minima,
Here \({x}_{\text {min}}\) and \({x}_{\text {min}}^\prime \) are two distinct minima in the field space, that is they are separated by a barrier. Without loss of generality we can assume that the deepest vacuum of the system was \({x}_{\text {min}}\) above \(T_C\). In most cases, below \(T_C\) the minima \({x}_{\text {min}}^\prime \) becomes the deepest vacuum. Just below the critical temperature, however, the system may remain at \({x}_{\text {min}}\), i.e., in a false vacuum. Somewhat below \(T_C\) the system may fluctuate over or tunnel through the barrier to the lower minimum, \({x}_{\text {min}}^\prime \), called the true vacuum [78,79,80].
We also define the quantity which is useful for characterising the strength of the transition,
and N is the number of scalar fields considered. By default all scalar fields in the potential are considered in the quadratic sum defining \(\Delta v(T)\), but as described later this may also be restricted, allowing, for example, one to output \(\gamma _\text {EW}\equiv (v_\text {EW} (T_c) - v_\text {EW}^\prime (T_C)) / T_C \) which may be more relevant for electroweak baryogenesis.
The strength of a first order phase transition can be a useful heuristic for assessing whether the phase transition is strong enough for a successful electroweak baryogenesis mechanism, with \(\gamma _\text {EW}> 1\) being a commonly applied rule of thumb. Similarly the strength of a first order phase transition also has an impact on the detectability of gravitational waves that are generated from the transition.
However it is important to note that for a full calculation of the baryon asymmetry of the Universe or gravitational wave spectra many other steps are required, which PhaseTracer alone does not take care of. For example another very important quantity, the so-called nucleation temperature can only be calculated by using PhaseTracer in combination with a cosmological bounce solver, such as BubbleProfiler [81], which calculates the bounce action for the potential at a given temperature. A first order transition proceeds via bubbles of broken phase nucleating in space-time. If these bubbles prove to be stable and grow, somewhat below \(T_C\) there will be a nucleation temperature, \(T_n\), at which the mean number of bubbles nucleated within the relevant space-time volume is one. For the early Universe the time of nucleation can be written as
where H is the Hubble parameter and \(\Gamma (T)\) is the nucleation rate per unit volume, which may be expressed as, \(\Gamma (T)= A(T)e^{-{S_E}/{T}}\) where \(S_E\) is the bounce action that can be obtained from a bounce solver. Ultimately, the physical problem becomes computing observable quantities – such as gravitational wave signatures or the baryon asymmetry of the Universe – using some of the above thermal properties of the transition. For reviews on how to do such calculations see e.g. Refs. [1, 20,21,22, 82, 83]. While PhaseTracer does not provide all of these quantities, the outputs of PhaseTracer , namely the phase structure and its temperature evolution, the critical temperatures and the strengths of the transitions, are important ingredients in such calculations and have quite broad utility.
3.3 Locating minima of the potential
We locate all minima of the potential at \(T = 0\) and \(T = 1000 \,\text {GeV}\) (which may be changed by

and

). To do so, we first generate a set of guesses by uniform sampling. We polish the guesses using local minimization and keep the unique minima. There are obviously more sophisticated techniques for global optimization that we do not implement. Nonetheless our method is fast and we have tested that it gives reliable results (see Sect. 6). If the performance of our implementation is a bottleneck or fails, we advise that a user implements techniques tailored to their particular physics problem or supplies guesses for the locations of the minima (

). After locating the minima at low and high temperature, we trace the high-temperature minima down in temperature, and the low-temperature minima up.
3.4 Tracing a minima
After identifying the minima, we trace them with temperature using

with an estimate of the derivative of the fields with respect to temperature,

Note that the minima, \({x}_{\text {min}}\), carries an implicit dependence on temperature, i.e., by \({x}_{\text {min}}\) we denote the trajectory of a minimum with temperature. We find the derivative by noting that

must vanish when evaluated along the trajectory of a minima, \({x}_{\text {min}}\), since by definition of the trajectory

for all temperatures, T, and all fields, \(x_i\). Thus we find the derivative in Eq. 9 by solving

This is implemented in

. The derivatives of the potential with respect to the fields and temperature are found by a finite difference method. We use it to predict the minima at temperature \(T_1 = T_0 + \Delta T\),
We polish this prediction with the

method to find \({x_1}_{\text {min}}\). Let us furthermore define a postdiction for \({x_0}_{\text {min}}\) in a similar manner,
Thus we trace a minimum in steps of \(\Delta T\) by guessing the minimum at temperature \(T_1 = T_0 + \Delta T\), polishing that guess, and iterating. We interrupt tracing if the step in temperature \(\Delta T\) is smaller than a user-specified level (changed by

) and if any of the following occurs:
We encounter a discontinuous jump in the minimum.
We define a discontinuous jump by a significant difference between the minima, \({x_1}_{\text {min}}\) and \({x_0}_{\text {min}}\), and a significant difference between a minima and its expected location, that is, between \({x_1}_{\text {min}}\) and \(x_{\text {predict}}\) or between \({x_0}_{\text {min}}\) and \(x_{\text {postdict}}\). A significant difference is defined by the absolute and relative tolerances,
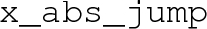
and
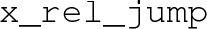
, that we use in Eq. 16. Their default values are shown in Table 1.
The minimum goes out of bounds or into a forbidden region of field space.
The Hessian is not positive semi-definite at what should be a minima. There is a possibility that the
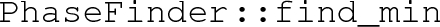
method may return a saddle point, instead of a local minimum. Thus if the Hessian at \(x_1\) has any negative eigenvalues then the phase ends.
The determinant of the Hessian matrix is zero, as this indicates that there is probably a transition. Note that this criteria (disabled by
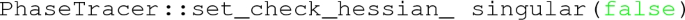
) can separate phases by first- and second-order transitions (without it, they are separated only by first-order ones).
If tracing isn’t interrupted, we stop once we reach the desired temperature. If a jump or the Hessian indicated that a phase ended, we check where the minimum went by finding and tracing the new minimum. For performance, before tracing a minimum, we check that it doesn’t belong to an existing known phase. This enables our method to efficiently trace intermediate phases that do not exist at the low or high temperature.
At each iteration, we re-evaluate the step size. If we find reason for interrupting tracing, we reduce the step size by a factor of two. If the guess of the minima, \(x_{\text {guess}}\) lay far away from the real minima, we reduce the step size by a factor of two; if not, we increase the step size by a factor of two. We define far away by the relevant absolute and relative tolerances,

and

, that we use in Eq. 16. Their default values are shown in Table 1.
Our strategy for tracing a minima relies on local optimization of a reasonable guess, found from Eq. 9. By default, we use a Nelder-Mead variant called subplex [84] implemented in

[85] as

. This can fail. If we are tracing a second-order phase transition, the minimum won’t change smoothly and thus our guess, based upon a first order Taylor expansion, may be poor. If the potential is pathological in the vicinity of the local minimum – e.g., particularly flat – the local optimization may fail even with a reasonable guess. Unfortunately, second-order transitions can present both problems simultaneously. In these cases, a phase may be incorrectly broken into two pieces that are discovered separately by the algorithm, since due to the discontinuity, tracing up and down can yield different results. The field values at the joint may be unreliable and the phases could slightly overlap.
To remedy this, note that we can predict first- and second-order transitions by singularities in the Hessian matrix in Eq. 12. For second-order transitions, a singular Hessian matrix means that there may be multiple solutions for the change in minimum with respect to temperature. The presence of multiple solutions for  indicates a possible jump discontinuity in
indicates a possible jump discontinuity in  at that temperature and thus a second-order transition. In cases in which a phase ends by a first order transition, on the other hand, two extrema – a minima and a barrier – merge into a double root. The Hessian matrix must vanish at a double root. Let us denote the magnitude of the smallest eigenvalue of the Hessian matrix at \({x}_{\text {min}}\) at temperature T by \({\lambda _T}_{\text {min}}\) and at zero temperature by \({\lambda _0}_{\text {min}}\). We judge the Hessian matrix to be singular if
at that temperature and thus a second-order transition. In cases in which a phase ends by a first order transition, on the other hand, two extrema – a minima and a barrier – merge into a double root. The Hessian matrix must vanish at a double root. Let us denote the magnitude of the smallest eigenvalue of the Hessian matrix at \({x}_{\text {min}}\) at temperature T by \({\lambda _T}_{\text {min}}\) and at zero temperature by \({\lambda _0}_{\text {min}}\). We judge the Hessian matrix to be singular if
where \(\epsilon _{\text {hess}}\) is a relative tolerance for this, stored in a member of the

class of PhaseTracer ,

. This has a default value of 0.01 which we recommend for most cases, but this may be reset by the user, via the method


. We use the smallest eigenvalue of the Hessian at zero temperature as an appropriate numerical scale, as if Eq. 15 is satisfied it means that there must be cancellations in the Hessian matrix caused by the finite-temperature corrections at that particular temperature. This partially alleviates the potential problems discussed in the previous paragraph.
3.5 Dealing with discrete symmetries
Discrete symmetries are common in scalar potentials. In a model with n discrete symmetries, each phase is potentially duplicated \(2^n\) times (though it may transform trivially under some transformations). The duplicates, however, cannot be ignored. Let us denote two phases by P and Q, which transform to \(P^\prime \) and \(Q^\prime \) by a discrete symmetry of the model. Suppose that at some critical temperature a transition from \(P \rightarrow Q\) is possible. The discrete symmetry means that the transitions \(P \rightarrow Q\) and \(P^\prime \rightarrow Q^\prime \) are equivalent, and that the transitions \(P \rightarrow Q^\prime \) and \(P^\prime \rightarrow Q\) are equivalent, but it does not mean that e.g., \(P \rightarrow Q\) and \(P \rightarrow Q^\prime \) are equivalent. In fact, in the presence of n discrete symmetries, each transition belongs to a set of up to \(2^n\) inequivalent “cousin” transitions.
Thus, to account for discrete symmetries efficiently, we allow a user to specify them if they want in the virtual

function. This insures that only one copy of a phase is traced, but all copies related by discrete symmetries are taken into account when calculating possible transitions. The function should return the result of each discrete symmetry on the set of fields, i.e., for n symmetries the returned

should have size n. We do not address global or local continuous symmetries, leaving it to a user to gauge fix them appropriately in their potential if they wish. See Sect. 6.2 for an example.
3.6 Finding possible first order transitions
Having identified the phases, we check for possible first order transitions (FOPTs) between them. For every pair of phases, we find the temperature interval in which they coexist. If the interval is non-vanishing and if the difference in potential between the two phases, \(\Delta V\), changes sign over the interval, we look for a critical temperature with a root-finding algorithm. By default, we assume there can be no more than one critical temperature between any two phases. This can be switched off by

and specifying the minimum separation between critical temperatures by e.g.,

. With these settings, we would look for critical temperatures in every \(1.5\,\text {GeV}\) interval in temperature in which the phases coexisted. The current default value for this setting is 1 GeV, based on experience with phase transitions that we have tested PhaseTracer on, i.e. the examples discussed in Sect. 6.
To check the validity of critical temperatures by eye, in

we provide a plotting routine that shows the potential along a straight line between the true and false minima at the critical temperature. We suggest that it is called as e.g.,

. For a genuine critical temperature, we should see degenerate minima separated by a barrier. We warn readers that we encountered cases in which numerical artefacts in the potential – e.g., small jump discontinuities in potentials that were constructed in a piece-wise manner – were located by our code and mistaken for minima. Thus, we advise checking a few transitions by eye if the potential contains any possible numerical pathologies.
4 PhaseTracer structure
The problem is divided into three steps: constructing the potential, finding phases and checking for critical temperatures between them. They are performed by the EffectivePotential library, and the

and

classes, respectively. The latter are implemented in the

and

files in the source code, respectively. The structure is illustrated in Fig. 1.
5 Implementing new models and running the code
5.1 The EffectivePotential library
New models are implemented in our EffectivePotential library, which provides pure virtual classes that represent a tree-level (

) and a one-loop effective potential (

). The latter automatically includes one-loop zero- and finite temperature corrections, as well as daisy corrections.
PhaseTracer comes with example models that publicly inherit from the pure virtual

class. The pure virtual classes make it easy to implement a new model. For example, we may implement the simple 1D model in Sect. 6.1 as,

We have overriden two pure virtual methods:

, the scalar potential as a function of the fields and the temperature, and

, the number of scalar fields in this problem. We have furthermore overridden the virtual method

, which ensures that our field always has non-negative values. In the implementation of this model packaged with PhaseTracer in

we furthermore implement analytic derivatives of the potential. In this simple example we are not including any additional perturbative corrections.
To include such perturbative corrections one can instead implement one-loop effective potentials through the pure virtual

class. For example, we may implement the 2D example in Sect. 6.2 as

This time we have overridden five methods of the pure virtual

class to define our model:

, the tree-level potential;

, the field-dependent scalar squared masses;

, the numbers of degrees of freedom for the scalars;

, the number of scalar fields (2) in this problem; and lastly,

, which returns the result of the model’s discrete symmetry, \(\phi \rightarrow -\phi \), on the fields.
The

class itself implements methods for the one-loop zero-temperature and finite-temperature corrections to the potential. Fermion and vector contributions are calculated if the methods

and

are implemented. By default, it works in the \(\xi =0\) (Landau) gauge, but this may be changed to any \(R_\xi \) gauge by the

method. Note, though, that it is up to the user to correctly implement the \(\xi \)-dependence of the scalar masses if they depart from \(\xi = 0\). Daisy contributions are added using the Arnold-Espinosa [86] method if Debye masses are supplied by implementing

. Furthermore, counter-terms can be added to the potential by overriding the virtual method

.
The only methods that must be overriden (i.e., that are pure virtual), however, are the tree-level potential and the number of scalar fields. The

and

methods aren’t compulsory – they default to one degree of freedom per scalar field and numerical estimates of the eigenvalues of the Hessian matrix of the tree-level potential, respectively. If you change the numbers of degrees of freedom, it is vital to change

too, as the order of the eigenvalues when found numerically won’t be stable and won’t correspond correctly to the intended degrees of freedom per scalar field. For this reason and for accuracy, wherever possible it is wise to implement derivatives and eigenvalues analytically. By default, there are no fermions or vectors in the model and the

method trivially returns the coordinates with no changes.
The

class automatically includes one-loop thermal corrections to the potential in (3). This requires an implementation of the thermal functions in (4). We interpolated them from a set of look-up tables generated from CosmoTransitions.
5.2 Running PhaseTracer
PhaseTracer may be called in an example program as follows (using the

as an example),

For a new model,

should be replaced with the name of the new model. The line

produces output about the phases with the format:

We see the number of phases found, and for each phase, the minimum and maximum temperature, the corresponding field values and potential, and an explanation about why the phase ended. In this case, the first phase ended at \(T = 1000\,\text {GeV}\) because that was the highest temperature under consideration (see

) and at \(T \approx 33\,\text {GeV}\) because the fields made a discontinuous jump. Each phase is numbered by a key, e.g.

.
The line

produces output about the transitions with the format:

We see the number of potential first order phase transitions, and for each one, the keys of the false and true phases (i.e.,

), followed by the true and false vacua at the critical temperature, information about which elements of the field changed in the transition, the critical temperature, transition strength \(\gamma \) ( or \(\gamma _\text {EW}\) if

is used) and difference in potential between the true and false vacua at the critical temperature. The latter serves as a sanity check: it should of course be close to zero.
5.2.1 The Phase and Transition objects
The objects containing this information may be accessed though

and

, which return a

of

and

objects, respectively. The

object is a

containing, amongst other things, the attributes:
-
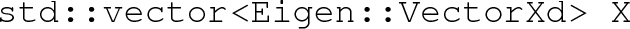
– The field values, \({x}_{\text {min}}\), through the phase
-
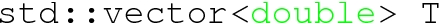
– The temperature, T, through the phase
-
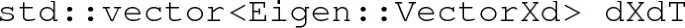
– The change in minima with respect to temperature,
 , through the phase
, through the phase -
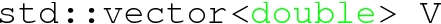
– The potential, \(V({x}_{\text {min}}, T)\), through the phase
-
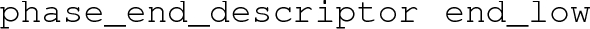
– The reason why the phase ended at the lowest temperature
-
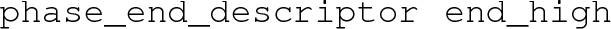
– The reason why the phase ended at the highest temperature
The

attributes are all ordered in ascending temperature. The

object, on the other hand, contains
-

– The critical temperature, \(T_C\)
-
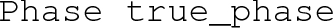
– The phase associated with the true vacuum
-
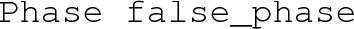
– The phase associated with the false vacuum
-
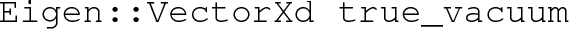
– The true vacuum at the critical temperature
-
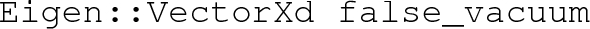
– The false vacuum at the critical temperature
-
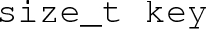
– The key indicating unique cousin transition.
For example, we may retrieve and print information about the first transition by

which would tell us the critical temperature of the first transition, and then print a summary of information about the true phase, the key corresponding to the true phase, and finally a summary of information about the transition.
5.2.2 Settings for finding phases and transitions
There are many adjustable settings that control the behavior of

and

objects, listed in Tables 1 and 2, respectively. They are altered by setters, i.e.,

methods, and read by

methods. The detailed usage of settings is introduced in Sect. 3 when we describe our algorithms of tracing phases and finding critical temperatures.
The attribute

in both

and

is the number of scalar fields charged under electroweak symmetry, which we assume are the first

scalar fields. By default

checks that the zero-temperature vacuum agrees with \(v = 246\,\text {GeV}\) only if a user sets

to a non-zero value. By default

calculates the transition strength \(\gamma \) using all scalar fields; it calculates \(\gamma _\text {EW}\) only if a user sets

.
When comparing floating point numbers, we typically check relative and absolute differences, i.e., our checks are of the form,

When tracing phases in temperature, we restrict the largest and smallest possible step sizes. The largest permissible step-size

is the minimum of

and the temperature interval multiplied by

. Similarly, the smallest permissible step-size

is the maximum one found from the relative and absolute settings.




5.3 Plotting results
The header

provides a function

that takes a

object and plots the phases, using

to construct file names for the resulting plots and data files:
-
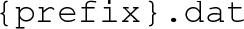
– Data file containing phases and transitions in a particular format
-
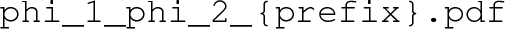
etc – The phases and transitions on plane of the first and second field, e.g., the left panel of Fig. 3
-
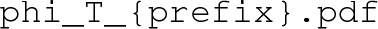
– The minima, \({x}_{\text {min}}\), versus temperature, T, for every phase, e.g., the right panel of Fig. 3
-
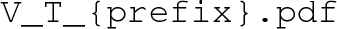
– The potential, \(V({x}_{\text {min}}, T)\), versus temperature, T, for every phase.
The plots are produced by the script

. To make plots with LaTeX fonts,  . Note that in models with discrete symmetries supplied by a user, the plots do not show cousin transitions (see Sect. 3.5).
. Note that in models with discrete symmetries supplied by a user, the plots do not show cousin transitions (see Sect. 3.5).
We furthermore provide  to check critical temperatures by plotting the minima between the true and false vacuum at the critical temperature – see Sect. 3.6 for further details.
to check critical temperatures by plotting the minima between the true and false vacuum at the critical temperature – see Sect. 3.6 for further details.
6 Examples/comparisons with existing codes and analytic solutions
6.1 One-dimensional test model
To exhibit the usage of PhaseTracer , we consider a one-dimensional potential,
for \(\phi \ge 0\) and \(\kappa < 0\) as a simple dummy model, without physical meaning. We consider the specific numerical constants,
The simplicity of the model means that it can be solved analytically, giving
with minima at 0 and \(-\kappa / (2\lambda ) = 50\) separated by a barrier at \(-\kappa / (4\lambda ) = 25\). We show the potential and the phase transition in Fig. 2. We find a numerical result of \(T_C = 59.1608\) with minima at \(4.92767\text {e}{-6}\) and 50.0003, i.e. the numerical result matches the exact analytic result up to at least six significant figures implying excellent agreement.Footnote 7 This result may be reproduced by

The argument –

– indicates that we want to produce debugging information including plots named

.
The one-dimensional potential at different temperatures (left) and the subsequent phase structure of the model (right). On the right panel, the lines show the field values at a particular minimum as a function of temperature. The arrows indicate that at that temperature the two phases linked by the arrows are degenerate and thus that a FOPT could occur in the direction of the arrow. The label x was autogenerated by our plotting code. In this example it stands for \(\phi \)
6.2 Two-dimensional test model
To compare the performance of PhaseTracer with CosmoTransitions, we adopt the test model with two scalar fields in CosmoTransitions. The tree-level potential is
The resulting field-dependent mass matrix for the pair of scalar fields isFootnote 8
Here \(m_1\), \(m_2\), v and \(\mu \) take the values listed in Table 1 of Ref. [63], i.e. \(120\,\text {GeV}\), \(50 \,\text {GeV}\), \(246 \,\text {GeV}\) and \(25 \,\text {GeV}\), respectively. In addition to the scalar fields in the tree-level potential, we add a scalar boson X with \(n_X=30\) degrees of freedom and the field-dependent mass
where \(Y_A^2=0.1\) and \(Y_B^2=0.15\). We set the renormalization scale in the one-loop potential to \(246 \,\text {GeV}\).
We compare our results against CosmoTransitions- 2.0.3 (at present the latest version) using its default settings.Footnote 9 After checking our implementation of the potential, by making sure we obtain exactly the same potential for given field values and temperature, we test the critical temperature and true and false vacuums found by our code. Our results may be reproduced by

The argument –

– indicates that we want to produce debugging information including plots named

.
We show in Table 3 that our results agree extremely wellFootnote 10 with CosmoTransitions for the critical temperature and field values for the first possible transition; however, our code is about 100 times faster for this problem.Footnote 11 The phase transitions in this problem are shown in Fig. 3. We see in the left panel a parametric plot of the two fields as functions of temperature. The distinct phases are shown by blue, orange and green colors, and the FOPT is shown by a black arrow. In the right panel, we see each field as a function of temperature.
Note, however, that PhaseTracer found two transitions whereas CosmoTransitions only found one. Due to the discrete symmetry, \(\phi \rightarrow -\phi \), there is in fact a cousin transition \((220.0, -150.0)\rightarrow (-263.5, -314.7)\) that accopanies the one found by CosmoTransitions (see Sect. 3.5). We always save all the transitions in the results, as we do not know a priori which transition has the greatest tunnelling probability. For this example, we calculated the bounce actions at \(T=100\,\text {GeV}\) using CosmoTransitions to be \(S_E=102659.3\) for \((224.5, -148.3)\rightarrow (275.3, 351.0)\) and \(S_E=1402952.5\) for \((224.5, -148.3)\rightarrow (-275.3, -351.0)\). In the CosmoTransitions example, the duplicated phase and thus the cousin transition is removed by forbidding \(\phi _1<0\) and it returns only the transition with the smaller action.Footnote 12 However, this appears to be a coincidence: forbidding \(\phi _2 < 0\) instead of \(\phi _1 < 0\) would result in CosmoTransitions finding only the transition with the larger actionFootnote 13. Note that in the automatically generated plots, such as Fig. 3, the symmetric cousin transitions are not shown, as their inclusion makes the plots hard to read.
Phase structure of the 2D test model. In the left panel, the changes in field values at a particular minimum with decreasing temperature are indicated by colored arrows in steps of \(\Delta T = 10 \,\text {GeV}\). The star represents a phase that does not change with temperature. The meaning of the right panel is same as the right panel in Fig. 2. The labels \(x_1\) and \(x_2\) were autogenerated by our plotting code. In this example they stand for \(\phi _1\) and \(\phi _2\), respectively
6.3 \({\mathbb {Z}}_2\) Scalar Singlet Model
As a more realistic two-dimensional example, we consider the \({\mathbb {Z}}_2\) scalar singlet extension of the SM. Unlike the SM, this model can accommodate a \(125\,\text {GeV}\) Higgs and a first order phase transition, as well as possibly providing a viable dark matter candidate. The potential consists of the ordinary SM Higgs potential and gauge- and \({\mathbb {Z}}_2\) invariant interactions involving a real singlet,
After EWSB, the real scalar obtains a tree-level mass \(m_S^2 = \mu ^2_s + \tfrac{1}{2} \lambda _{Hs} v^2\). We implement one-loop and daisy corrections to this tree-level potential. Under certain circumstances, a first order transition between an EW preserving and an EW breaking vacuum may be possible and the critical temperature can be found analytically; see, e.g., Ref. [36] for an analysis of the PTs in this model.
We reproduce the behaviour of the critical temperature as a function of \(\lambda _{Hs}\) and \(m_S\) that was found in Ref. [36] (see, e.g., Figure 1 of Ref. [36]) in Fig. 4. On the right panel, we show that the differences between numerical results from PhaseTracer and the analytic formulae are at most about \(0.01\%\). To reproduce it,

The first command scans the relevant parameter space and writes a data file named

that the second command plots in

.
6.4 Two-Higgs-Doublet Models
We next consider three Two-Higgs-Doublet Models (2HDMs) which are implemented in BSMPT. We do not reimplement their potentials; instead, we link PhaseTracer directly to the models implemented in BSMPT and directly call the BSMPT potentials. The general 2HDM tree-level scalar potential is
The two Higgs doublets take the form
where \(\rho _i\) and \(\eta _i\) \((i=1,2)\) represent the charged field components, \(\zeta _i\) and \(\psi _i\) \((i=1,2)\) indicate the neutral CP-even and CP-odd fields, and the VEVs \(v_i\) \((i=1,2,\mathrm{CB},\mathrm{CP})\) are real.
First, we consider the real, CP-conserving 2HDM (R2HDM) with the parameters
Second, we consider the complex, CP-violating 2HDM (C2HDM) with the parameters
Note that in this case we consider a complex phase for \(\lambda _5\). Lastly, we consider the Next-to-2HDM (N2HDM) with the parameters
Compared to the 2HDM models, this model contains an extra complex singlet with \({\mathbb {Z}}_2\) symmetric interactions,
The singlet field S is expanded as \(S=v_S+\zeta _S\) with \(v_S\) denoting singlet VEV.
To run our code on these models,

Note that these examples require BSMPT; see Sect. 2.2 for installation instructions. Regarding finding the critical temperature, our code is slower than BSMPT as we perform more checks and thoroughly map out the whole phase structure.
We show results from all three models with our code and BSMPT in Table 4. In BSMPT, the tolerance of the bisection method used to locate the \(T_C\) is \(0.01\,\text {GeV}\) , while our default relative precision

is 0.01%. Thus our results for R2HDM and C2HDM benchmark points are in agreement with that from BSMPT in the range of these errors. In addition, we find an extra group of transitions at \(T_C=161.205\,\text {GeV}\) for R2HDM, which is missed by BSMPT because it focuses only on the transition that starts in the symmetric vacuum. For the N2HDM benchmark point, the discrepancy of \(T_C\) is larger than the expected precision. This is related to the fact that BSMPT assumes that the false vacuum lies at the origin and with its default settings BSMPT misses the minimum around at (0, 0, 0, 0, 301.0) at \(T\simeq 121.00\,\text {GeV}\), mistakenly treating the minimum around at (0, 0, 32.5, 176.5, 297.1) as the deepest minima at that temperature.Footnote 14 By increasing the number of random starting points for finding multiple local minima in BSMPT, it finds this minima and agrees with our result, \(T_C=120.73\,\text {GeV}\), though the agreement may be partially an accident since the false vacuum does not lie at the origin, contrary to the assumption in BSMPT.
6.5 Next-to-Minimal Supersymmetric Standard Model
In Ref. [26] we explored the Next-to-Minimal Supersymmetric Standard Model (NMSSM) with a preliminary version of PhaseTracer . We include our NMSSM model (in which we match the NMSSM to a model with two-Higgs doublets and a singlet; see Ref. [26] for further details) as an example. The effective potential depends upon FlexibleSUSY (see Sect. 2.2 for the relevant installation instructions) for the matching conditions, tadpole equations and field-dependent masses. We show a benchmark point from this model in Fig. 5. To reproduce it,

which will solve this problem and produce the figures shown in Fig. 5 in files named

.
Phase structure of the NMSSM. The meanings of the upper panels and the lower left panel is same to the left panel of Fig. 3. The meanings of the right panel is similar to the right panel of Fig. 2. The dots represent transitions that do not change the corresponding field values. The labels \(x_1\), \(x_2\) and \(x_3\) were autogenerated by our plotting code. In this example they stand for \(h_u\), \(h_d\) and s, respectively
Because this model point is particularly pathological, there is a chance that PhaseTracer may miss Phase 4 and part of Phase 3 shown in Fig. 5. This is because at \(T=127.1\,\text {GeV}\), there exists a saddle point at \((h_u=0\,\text {GeV}, h_d=211.0\,\text {GeV}, s=0\,\text {GeV})\) near a minimum. When PhaseTracer traces the phases near this saddle point, it may correctly find the real minimum near the saddle point or mistake the saddle point for a minimum. In the latter case, when PhaseTracer discovers that the Hessian isn’t positive semi-definite, it stops tracing Phase 3 at the saddle point, and then will miss Phase 4. We will address this problem by improving the

method in a future version so that it cannot mistake saddle points for minima. The behaviour of PhaseTracer in these cases isn’t deterministic since it depends on random number generation for locating minima.
7 Conclusions
In this paper we have presented PhaseTracer , a fast and reliable

software package for finding the cosmological phases and the critical temperatures for phase transitions. For any user supplied potential, PhaseTracer first maps out all of the phases over the relevant temperature range.Footnote 15 Once the phases have been identified PhaseTracer checks each pair of phases to see if there may be a first order phase transition between them and calculates the critical temperature.
To do this PhaseTracer uses a similar algorithm to that of CosmoTransitions, but our implementation has a number of advantages: (i) PhaseTracer is orders of magnitude faster, as we have demonstrated in Sect. 6.2; (ii) PhaseTracer has been carefully designed to provide clear error information for cases where a solution cannot be found and has many adjustable settings which may be varied to find solutions in such cases; (iii) PhaseTracer will be maintained by an active team of developers (the authors of this manual) and is distributed with a suite of unit tests to validate the code and ensure results do not change unintentionally as the code evolves. In addition PhaseTracer has been designed so that it can be easily linked with FlexibleSUSY spectrum generators, making it easy to embed it in a much wider tool set for investigating the phenomenology of an arbitrary BSM extension. Furthermore we have also made it possible to link to potentials implemented in BSMPT, another tool for finding critical temperatures. This makes it possible for users to compare results in both BSMPT and PhaseTracer , as we have demonstrated for two Higgs doublet and two Higgs plus singlet extensions of the Standard Model in Sect. 6.4. This is particularly useful since BSMPT has a complementary approach, implementing a method that is simpler and faster, but finds exactly one transition that starts from the symmetric vacuum. Therefore BSMPT will miss other transitions and the transition it does find may not be in the cosmological history, while PhaseTracer will find all potential transitions.
With PhaseTracer it is therefore very easy to find the phases and critical temperatures of arbitrary Standard Model extensions. This is an important and useful tool for investigating both electroweak baryogenesis and gravitational waves, and can be used in thorough phenomenological investigations of realistic Standard Model extensions with many parameters, as we have demonstrated in Ref. [26] where an early prototype of PhaseTracer was used. Furthermore PhaseTracer is part of a wider goal to develop a set of tools that can be used to automatically calculate the baryon asymmetry of the Universe, predict the stochastic gravitational wave background from first order phase transitions and test this against observations from gravitational wave experiments.
Program Summary
Program title: PhaseTracer
Program obtainable from: https://github.com/PhaseTracer/PhaseTracer
Distribution format: tar.gz
Programming language: C++
Computer: Personal computer
Operating system: Tested on FreeBSD, Linux, Mac OS X
External routines: Boost library, Eigen library, NLopt library, AlgLib library
Typical running time: 0.01 (0.05) seconds for one (two) scalar fields
Nature of problem: Finding and tracing minima of a scalar potential
Solution method: Local optimisation of judicious guesses
Restrictions: Performance inevitably deteriorates for high numbers of scalar fields
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Our paper describes a code that is publicly available. There is no dataset associated with our paper.]
Notes
A
version of CosmoTransitions is adopted by Vevacious [65] but the latter is mainly set up to test whether or not the observed electroweak vacuum is unstable and should have transitioned to a deeper underlying minimum.
See http://cmake.org.
See http://www.boost.org.
By default, the counterterm potential is not included, but can be added to the potential, as described in Sect. 5.1 where we discuss the code implementation.
The agreement on \(T_C\) is often much better than the nominal relative precision,
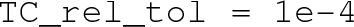
, as the
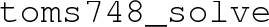
root-finding algorithm converges rapidly in many cases. However in principle it can be worse than the nominal precision, because there is uncertainty on the two minima.
We correct a typo for the off-diagonal elements in Ref. [63]. The typo was not present in the CosmoTransitions- 2.0.3 source code.
Note, however, that numerical results for this potential with CosmoTransitions- 2.0.3 are not consistent with results from previous versions of CosmoTransitions documented in Ref. [63].
In fact in this case they agree up to 9 significant figures, with default settings.
We computed timings of PhaseTracer in
using the average of 1000 repeats in
and
with a desktop with an Intel Core i7-6700 CPU @ 3.40GHz processor. For CosmoTransitions, we averaged the run time of
inside
of CosmoTransitions- 2.0.3 on the same machine.
In the code, it is \(\phi _1<-5\) to allow for slight inaccuracy in the location of the phase.
In fact, if \(\phi _2 < 0\) is forbidden, CosmoTransitions- 2.0.3 would only find Phase 2 shown in Fig. 3.
The results from PhaseTracer and BSMPT are all sensitive to the random number generation.
The upper and lower bound on the temperature is chosen by the user, though by default these are taken to be \(T=0\) and \(T=1\) TeV, which are the values relevant for electroweak phase transitions.
References
A. Mazumdar, G. White, Review of cosmic phase transitions: their significance and experimental signatures. Rep. Prog. Phys. 82, 076901 (2019). https://doi.org/10.1088/1361-6633/ab1f55. arXiv:1811.01948
D.A. Kirzhnits, Weinberg model in the hot universe. JETP Lett. 15, 529–531 (1972)
D.A. Kirzhnits, A.D. Linde, Macroscopic consequences of the weinberg model. Phys. Lett. 42B, 471–474 (1972). https://doi.org/10.1016/0370-2693(72)90109-8
J.C. Pati, A. Salam, Lepton number as the fourth color. Phys. Rev. D 10, 275–289 (1974). https://doi.org/10.1103/PhysRevD.11.703.2. (10.1103/PhysRevD.10.275)
H. Fritzsch, P. Minkowski, Unified interactions of leptons and hadrons. Ann. Phys. 93, 193–266 (1975). https://doi.org/10.1016/0003-4916(75)90211-0
H. Georgi, The state of the art-gauge theories. AIP Conf. Proc. 23, 575–582 (1975). https://doi.org/10.1063/1.2947450
F. Gursey, P. Ramond, P. Sikivie, A universal gauge theory model based on E6. Phys. Lett. 60B, 177–180 (1976). https://doi.org/10.1016/0370-2693(76)90417-2
H. Georgi, S.L. Glashow, Unity of all elementary particle forces. Phys. Rev. Lett. 32, 438–441 (1974). https://doi.org/10.1103/PhysRevLett.32.438
M. Cvetic, P. Langacker, New gauge bosons from string models. Mod. Phys. Lett. A 11, 1247–1262 (1996). https://doi.org/10.1142/S0217732396001260.. arXiv:hep-ph/9602424
M. Cvetic, P. Langacker, Z’ physics and supersymmetry. Adv. Ser. Direct. High Energy Phys. 18, 312–331 (1998). https://doi.org/10.1142/9789812839657_0012. arXiv:hep-ph/9707451
G. Cleaver, M. Cvetic, J.R. Espinosa, L.L. Everett, P. Langacker, J. Wang, Physics implications of flat directions in free fermionic superstring models 1. Mass spectrum and couplings. Phys. Rev. D 59, 055005 (1999). https://doi.org/10.1103/PhysRevD.59.055005. arXiv:hep-ph/9807479
G. Cleaver, M. Cvetic, J.R. Espinosa, L.L. Everett, P. Langacker, J. Wang, Physics implications of flat directions in free fermionic superstring models. 2. Renormalization group analysis. Phys. Rev. D 59, 115003 (1999). https://doi.org/10.1103/PhysRevD.59.115003. arXiv:hep-ph/9811355
P. Anastasopoulos, T.P.T. Dijkstra, E. Kiritsis, A.N. Schellekens, Orientifolds, hypercharge embeddings and the Standard Model. Nucl. Phys. B 759, 83–146 (2006). https://doi.org/10.1016/j.nuclphysb.2006.10.013. arXiv:hep-th/0605226
M. Cvetic, J. Halverson, P. Langacker, Implications of string constraints for exotic matter and Z’ s beyond the standard model. JHEP 11, 058 (2011). https://doi.org/10.1007/JHEP11(2011)058. arXiv:1108.5187
D. Suematsu, Y. Yamagishi, Radiative symmetry breaking in a supersymmetric model with an extra U(1). Int. J. Mod. Phys. A 10, 4521–4536 (1995). https://doi.org/10.1142/S0217751X95002096. arXiv:hep-ph/9411239
M. Cvetic, P. Langacker, Implications of Abelian extended gauge structures from string models. Phys. Rev. D 54, 3570–3579 (1996). https://doi.org/10.1103/PhysRevD.54.3570. arXiv:hep-ph/9511378
S.F. King, S. Moretti, R. Nevzorov, Theory and phenomenology of an exceptional supersymmetric standard model. Phys. Rev. D 73, 035009 (2006). https://doi.org/10.1103/PhysRevD.73.035009. arXiv:hep-ph/0510419
A.D. Sakharov, Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. https://inspirehep.net/literature/51345
A.G. Cohen, D.B. Kaplan, A.E. Nelson, Progress in electroweak baryogenesis. Ann. Rev. Nucl. Part. Sci. 43, 27–70 (1993). https://doi.org/10.1146/annurev.ns.43.120193.000331. arXiv:hep-ph/9302210
M. Trodden, Electroweak baryogenesis. Rev. Mod. Phys. 71, 1463–1500 (1999). https://doi.org/10.1103/RevModPhys.71.1463. arXiv:hep-ph/9803479
D.E. Morrissey, M.J. Ramsey-Musolf, Electroweak baryogenesis. New J. Phys. 14, 125003 (2012). https://doi.org/10.1088/1367-2630/14/12/125003. arXiv:1206.2942
G.A. White, A Pedagogical Introduction to Electroweak Baryogenesis. IOP Concise Physics (Morgan & Claypool, New York, 2016). https://doi.org/10.1088/978-1-6817-4457-5
C. Balazs, M. Carena, A. Freitas, C.E.M. Wagner, Phenomenology of the nMSSM from colliders to cosmology. JHEP 06, 066 (2007). https://doi.org/10.1088/1126-6708/2007/06/066. arXiv:0705.0431
C. Balázs, M. Carena, A. Menon, D.E. Morrissey, C.E.M. Wagner, Supersymmetric origin of matter. Phys. Rev. D 71, 075002 (2005). https://doi.org/10.1103/PhysRevD.71.075002. arXiv:hep-ph/0412264
Cs Balázs, A. Mazumdar, E. Pukartas, G. White, Baryogenesis, dark matter and inflation in the next-to-minimal supersymmetric standard model. JHEP 01, 073 (2014). https://doi.org/10.1007/JHEP01(2014)073. arXiv:1309.5091
P. Athron, C. Balazs, A. Fowlie, G. Pozzo, G. White, Y. Zhang, Strong first-order phase transitions in the NMSSM—a comprehensive survey. JHEP 11, 151 (2019). https://doi.org/10.1007/JHEP11(2019)151. arXiv:1908.11847
M. Maggiore, Gravitational wave experiments and early universe cosmology. Phys. Rep. 331, 283–367 (2000). https://doi.org/10.1016/S0370-1573(99)00102-7. arXiv:gr-qc/9909001
D.J. Weir, Gravitational waves from a first order electroweak phase transition: a brief review. Philos. Trans. R. Soc. Lond. A376, 20170126 (2018). https://doi.org/10.1098/rsta.2017.0126
T. Alanne, T. Hugle, M. Platscher, K. Schmitz, A fresh look at the gravitational-wave signal from cosmological phase transitions. JHEP 03, 004 (2020). https://doi.org/10.1007/JHEP03(2020)004. arXiv:1909.11356
K. Schmitz, New Sensitivity Curves for Gravitational-Wave Experiments. arXiv:2002.04615. https://inspirehep.net/literature/1779852
B.P. Abbott et al., LIGO Scientific, Virgo collaboration, Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016). https://doi.org/10.1103/PhysRevLett.116.061102. arXiv:1602.03837
B.P. Abbott et al., LIGO Scientific, Virgo collaboration, GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101 (2017). https://doi.org/10.1103/PhysRevLett.119.161101. arXiv:1710.05832
B.P. Abbott et al., LIGO Scientific, Virgo collaboration, GW151226: observation of gravitational waves from a 22-solar-mass binary black hole coalescence. Phys. Rev. Lett. 116, 241103 (2016). https://doi.org/10.1103/PhysRevLett.116.241103. arXiv:1606.04855
B.P. Abbott et al., LIGO Scientific, VIRGO collaboration, GW170104: observation of a 50-solar-mass binary black hole coalescence at redshift 0.2. Phys. Rev. Lett. 118, 221101 (2017). https://doi.org/10.1103/PhysRevLett.118.221101. arXiv:1706.01812
B.P. Abbott et al., LIGO Scientific, Virgo collaboration, GW170814: a three-detector observation of gravitational waves from a binary black hole coalescence. Phys. Rev. Lett. 119, 141101 (2017). https://doi.org/10.1103/PhysRevLett.119.141101. arXiv:1709.09660
V. Vaskonen, Electroweak baryogenesis and gravitational waves from a real scalar singlet. Phys. Rev. D 95, 123515 (2017). https://doi.org/10.1103/PhysRevD.95.123515. arXiv:1611.02073
A. Alves, T. Ghosh, H.-K. Guo, K. Sinha, D. Vagie, Collider and gravitational wave complementarity in exploring the singlet extension of the standard model. JHEP 04, 052 (2019). https://doi.org/10.1007/JHEP04(2019)052. arXiv:1812.09333
A. Alves, D. Gonçalves, T. Ghosh, H.-K. Guo, K. Sinha, Di-Higgs Production in the 4b Channel and Gravitational Wave Complementarity. arXiv:1909.05268
K. Hashino, M. Kakizaki, S. Kanemura, P. Ko, T. Matsui, Gravitational waves and Higgs boson couplings for exploring first order phase transition in the model with a singlet scalar field. Phys. Lett. B 766, 49–54 (2017). https://doi.org/10.1016/j.physletb.2016.12.052. arXiv:1609.00297
A. Beniwal, M. Lewicki, J.D. Wells, M. White, A.G. Williams, Gravitational wave, collider and dark matter signals from a scalar singlet electroweak baryogenesis. JHEP 08, 108 (2017). https://doi.org/10.1007/JHEP08(2017)108. arXiv:1702.06124
Z. Kang, P. Ko, T. Matsui, Strong first order EWPT & strong gravitational waves in Z\(_{3}\)-symmetric singlet scalar extension. JHEP 02, 115 (2018). https://doi.org/10.1007/JHEP02(2018)115. arXiv:1706.09721
A. Beniwal, M. Lewicki, M. White, A.G. Williams, Gravitational waves and electroweak baryogenesis in a global study of the extended scalar singlet model. JHEP 02, 183 (2019). https://doi.org/10.1007/JHEP02(2019)183. arXiv:1810.02380
D. Croon, T.E. Gonzalo, L. Graf, N. Košnik, G. White, GUT physics in the era of the LHC. Front. Phys. 7, 76 (2019). https://doi.org/10.3389/fphy.2019.00076. arXiv:1903.04977
P.S.B. Dev, A. Mazumdar, Probing the scale of new physics by advanced LIGO/VIRGO. Phys. Rev. D 93, 104001 (2016). https://doi.org/10.1103/PhysRevD.93.104001. arXiv:1602.04203
P.S.B. Dev, F. Ferrer, Y. Zhang, Y. Zhang, Gravitational waves from first-order phase transition in a simple axion-like particle model. JCAP 1911, 006 (2019). https://doi.org/10.1088/1475-7516/2019/11/006. arXiv:1905.00891
L. Bian, H.-K. Guo, Y. Wu, R. Zhou, Gravitational wave and collider searches for electroweak symmetry breaking patterns. Phys. Rev. D 101, 035011 (2020). https://doi.org/10.1103/PhysRevD.101.035011. arXiv:1906.11664
L. Bian, Y. Wu, K.-P. Xie, Electroweak phase transition with composite Higgs models: calculability, gravitational waves and collider searches. JHEP 12, 028 (2019). https://doi.org/10.1007/JHEP12(2019)028. arXiv:1909.02014
M. Punturo et al., The Einstein telescope: a third-generation gravitational wave observatory. Class. Quantum Grav. 27, 194002 (2010). https://doi.org/10.1088/0264-9381/27/19/194002
J. Aasi et al., LIGO Scientific collaboration, advanced LIGO. Class. Quantum Grav. 32, 074001 (2015). https://doi.org/10.1088/0264-9381/32/7/074001. arXiv:1411.4547
F. Acernese et al., VIRGO collaboration, Advanced Virgo: a second-generation interferometric gravitational wave detector. Class. Quantum Grav. 32, 024001 (2015). https://doi.org/10.1088/0264-9381/32/2/024001. arXiv:1408.3978
T. Akutsu et al., KAGRA collaboration, KAGRA: 2.5 generation interferometric gravitational wave detector. Nat. Astron. 3, 35–40 (2019). https://doi.org/10.1038/s41550-018-0658-y. arXiv:1811.08079
D. Reitze et al., Cosmic explorer: the U.S. contribution to gravitational-wave astronomy beyond LIGO. Bull. Am. Astron. Soc. 51, 035 (2019). arXiv:1907.04833
P. Amaro-Seoane, H. Audley, S. Babak, J. Baker, E. Barausse, P. Bender et al., Laser interferometer space antenna. arXiv:1702.00786
S. Kawamura et al., The Japanese space gravitational wave antenna DECIGO. Class. Quantum Grav. 23, S125–S132 (2006). https://doi.org/10.1088/0264-9381/23/8/S17
G.M. Harry, P. Fritschel, D.A. Shaddock, W. Folkner, E.S. Phinney, Laser interferometry for the big bang observer. Class. Quantum Grav. 23, 4887–4894 (2006). https://doi.org/10.1088/0264-9381/23/15/008. (10.1088/0264-9381/23/24/C01)
W.-R. Hu, Y.-L. Wu, The Taiji Program in Space for gravitational wave physics and the nature of gravity. Natl. Sci. Rev. 4, 685–686 (2017). https://doi.org/10.1093/nsr/nwx116
D. Croon, T.E. Gonzalo, G. White, Gravitational waves from a Pati–Salam phase transition. JHEP 02, 083 (2019). https://doi.org/10.1007/JHEP02(2019)083. arXiv:1812.02747
R. Apreda, M. Maggiore, A. Nicolis, A. Riotto, Gravitational waves from electroweak phase transitions. Nucl. Phys. B 631, 342–368 (2002). https://doi.org/10.1016/S0550-3213(02)00264-X. arXiv:gr-qc/0107033
L. Leitao, A. Megevand, A.D. Sanchez, Gravitational waves from the electroweak phase transition. JCAP 1210, 024 (2012). https://doi.org/10.1088/1475-7516/2012/10/024. arXiv:1205.3070
G.C. Dorsch, S.J. Huber, T. Konstandin, Bubble wall velocities in the Standard Model and beyond. JCAP 1812, 034 (2018). https://doi.org/10.1088/1475-7516/2018/12/034. arXiv:1809.04907
J. Ellis, M. Lewicki and J. M. No, On the Maximal Strength of a First-Order Electroweak Phase Transition and its Gravitational Wave Signal. arXiv:1809.08242
J. Ellis, M. Lewicki, J.M. No, V. Vaskonen, Gravitational wave energy budget in strongly supercooled phase transitions. JCAP 1906, 024 (2019). https://doi.org/10.1088/1475-7516/2019/06/024. arXiv:1903.09642
C.L. Wainwright, CosmoTransitions: computing cosmological phase transition temperatures and bubble profiles with multiple fields. Comput. Phys. Commun. 183, 2006–2013 (2012). https://doi.org/10.1016/j.cpc.2012.04.004. arXiv:1109.4189
P. Basler, M. Mühlleitner, BSMPT (Beyond the Standard Model Phase Transitions): a tool for the electroweak phase transition in extended Higgs sectors. Comput. Phys. Commun. 237, 62–85 (2019). https://doi.org/10.1016/j.cpc.2018.11.006. arXiv:1803.02846
J.E. Camargo-Molina, B. O’Leary, W. Porod, F. Staub, \({ Vevacious}\): a tool for finding the global minima of one-loop effective potentials with many scalars. Eur. Phys. J. C 73, 2588 (2013). https://doi.org/10.1140/epjc/s10052-013-2588-2. arXiv:1307.1477
P. Athron, J.-H. Park, D. Stöckinger, A. Voigt, FlexibleSUSY—a spectrum generator generator for supersymmetric models. Comput. Phys. Commun. 190, 139–172 (2015). https://doi.org/10.1016/j.cpc.2014.12.020. arXiv:1406.2319
P. Athron, J.-H. Park, T. Steudtner, D. Stöckinger, A. Voigt, Precise Higgs mass calculations in (non-)minimal supersymmetry at both high and low scales. JHEP 01, 079 (2017). https://doi.org/10.1007/JHEP01(2017)079. arXiv:1609.00371
P. Athron, M. Bach, D. Harries, T. Kwasnitza, J.-h. Park, D. Stöckinger et al., FlexibleSUSY 2.0: extensions to investigate the phenomenology of SUSY and non-SUSY models. Comput. Phys. Commun. 230(2018), 145–217. https://doi.org/10.1016/j.cpc.2018.04.016. arXiv:1710.03760
F. James, M. Roos, Minuit—a system for function minimization and analysis of the parameter errors and correlations. Comput. Phys. Commun. 10, 343–367 (1975). https://doi.org/10.1016/0010-4655(75)90039-9
H.H. Patel, M.J. Ramsey-Musolf, Baryon washout Electroweak phase transition, and perturbation theory. JHEP 07, 029 (2011). https://doi.org/10.1007/JHEP07(2011)029. arXiv:1101.4665
S.P. Martin, Two loop effective potential for a general renormalizable theory and softly broken supersymmetry. Phys. Rev. D 65, 116003 (2002). https://doi.org/10.1103/PhysRevD.65.116003. arXiv:hep-ph/0111209
W. Siegel, Supersymmetric dimensional regularization via dimensional reduction. Phys. Lett. 84B, 193–196 (1979). https://doi.org/10.1016/0370-2693(79)90282-X
D.M. Capper, D.R.T. Jones, P. van Nieuwenhuizen, Regularization by dimensional reduction of supersymmetric and nonsupersymmetric gauge theories. Nucl. Phys. B 167, 479–499 (1980). https://doi.org/10.1016/0550-3213(80)90244-8
I. Jack, D.R.T. Jones, S.P. Martin, M.T. Vaughn, Y. Yamada, Decoupling of the epsilon scalar mass in softly broken supersymmetry. Phys. Rev. D 50, R5481–R5483 (1994). https://doi.org/10.1103/PhysRevD.50.R5481. arXiv:hep-ph/9407291
M. Garny, T. Konstandin, On the gauge dependence of vacuum transitions at finite temperature. JHEP 07, 189 (2012). https://doi.org/10.1007/JHEP07(2012)189. arXiv:1205.3392
A.D. Linde, Infrared problem in thermodynamics of the Yang-Mills Gas. Phys. Lett. 96B, 289–292 (1980). https://doi.org/10.1016/0370-2693(80)90769-8
D.J. Gross, R.D. Pisarski, L.G. Yaffe, QCD and instantons at finite temperature. Rev. Mod. Phys. 53, 43 (1981). https://doi.org/10.1103/RevModPhys.53.43
S.R. Coleman, The fate of the false vacuum. 1. Semiclassical theory. Phys. Rev. D 15, 2929–2936 (1977). https://doi.org/10.1103/PhysRevD.15.2929. (10.1103/PhysRevD.16.1248)
C.G. Callan Jr., S.R. Coleman, The fate of the false vacuum. 2. First quantum corrections. Phys. Rev. D 16, 1762–1768 (1977). https://doi.org/10.1103/PhysRevD.16.1762
A.D. Linde, Fate of the false vacuum at finite temperature: theory and applications. Phys. Lett. 100B, 37–40 (1981). https://doi.org/10.1016/0370-2693(81)90281-1
P. Athron, C. Balázs, M. Bardsley, A. Fowlie, D. Harries, G. White, BubbleProfiler: finding the field profile and action for cosmological phase transitions. Comput. Phys. Commun. 244, 448–468 (2019). https://doi.org/10.1016/j.cpc.2019.05.017. arXiv:1901.03714
M. Quirós, Field theory at finite temperature and phase transitions. Acta Phys. Polon. B 38, 3661–3703 (2007)
C. Caprini et al., Detecting gravitational waves from cosmological phase transitions with LISA: an update. JCAP 3(2020), 24. https://doi.org/10.1088/1475-7516/2020/03/024. arXiv:1910.13125
T.H. Rowan, Functional stability analysis of numerical algorithms Tech. Rep., University of Texas (1990)
S.G. Johnson, The NLopt nonlinear-optimization package. https://nlopt.readthedocs.io/en/latest/Citing_NLopt/
P.B. Arnold, O. Espinosa, The effective potential and first order phase transitions: beyond leading-order. Phys. Rev. D 47, 3546 (1993). https://doi.org/10.1103/PhysRevD.47.3546. arXiv:hep-ph/9212235
Acknowledgements
We thank Graham White for advice and expertise passed on in other phase transition projects, Michael Bardsley for restructuring of our EffectivePotential library so that it will be easier in future to use this with PhaseTracer , and Giancarlo Pozzo for extensive early testing of the code. We also thank both Michael and Graham for crucial participation in our the wider goal of a complete package/set of codes for studying EWBG and GWs. The work of P.A. is supported by the Australian Research Council Future Fellowship Grant FT160100274. P.A. also acknowledges the hospitality of Nanjing Normal University while working on this manuscript. The work of C.B. and Y.Z. was supported by the Australian Research Council through the ARC Centre of Excellence for Particle Physics at the Tera-scale CE110001104. The work of P.A. and C.B. is also supported with the Australian Research Council Discovery Project Grant DP180102209.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Athron, P., Balázs, C., Fowlie, A. et al. PhaseTracer: tracing cosmological phases and calculating transition properties. Eur. Phys. J. C 80, 567 (2020). https://doi.org/10.1140/epjc/s10052-020-8035-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-8035-2




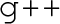
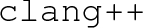
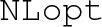
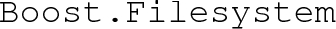
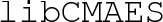
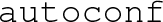
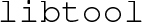
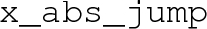
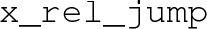
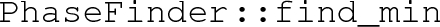
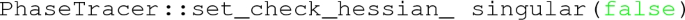

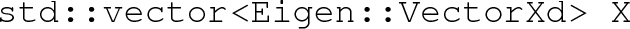
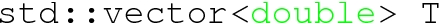
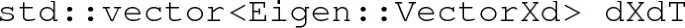
 , through the phase
, through the phase