1 Introduction

Direct detections of gravitational waves [1,2,3,4,5,6] and directly imaging the shadow of M87*, the supermassive black hole in the center of galaxy M87 [7,8,9,10,11,12], have not only shown that black holes are very common in the Universe, but also opened a new window to strong-field gravitational physics. A black hole is the simplest macroscopic object which one can obtain from the field equations of Einstein’s general relativity (GR). However, such a fundamental object is plagued with the existence of its event horizon and central singularity. The event horizon protects the singularity from exposure and disconnects the interior of the black hole from the exterior. This causes Hawking radiation, giving birth of the information-loss problem. The singularity is the place where GR becomes invalid. A quantum theory of gravity might be a cure, but no exact prescription is available yet. There are numerous ways to effectively remove the singularity, such as replacing it with a regular core [13,14,15,16], bouncing by the quantum pressure [17,18,19], and creating a quasi-black hole [20,21,22,23] (see Ref. [24] for a review). Alternatively, it might be possible to erase the event horizon by considering an exotic compact object which is more massive than a neutron star but without the event horizon [25] or a compact quantum object which exists due to the quantum dynamics [26]. Among the exotic compact objects, those with photon spheres are called ultracompact object s [25]. A number of proposals have been raised to realize these objects, such as whormholes [27, 28], fluid stars [29], boson stars [30], gravastars [31, 32], 2-2 holes [33], fuzzballs [34, 35], Planck stars [36] and nonlocal stars [37] (see Ref. [38] for a review).

In this work, we focus on a Lee-Wick ultracompact object. It is based on a new local higher derivative theory of gravity without real poles [39,40,41,42,43], which is consistent with the Lee-Wick model [44,45,46]. A black hole solution to the theory was currently found and proved to be non-singular [47]. Such a theory also permits a spacetime solution without the event horizon and central singularity but with the photon sphere, which might be treated as the Lee-Wick ultracompact object. While thermodynamics [47] and strong deflection gravitational lensing [48] of the Lee-Wick black hole were investigated, it is still unknown about physical properties and observational signature of the Lee-Wick ultracompact object, which are critical for searching and distinguishing such a horizonless object.

Through gravitational and electromagnetic waves, it is in principle possible to tell a ultracompact object from a black hole [38]. A telltale of the ultracompact object in gravitational waves observation is the late-time echoes in the ringdown phase [49,50,51,52,53]. However, the event rates for current ground-based gravitational wave detectors are low and the methods to filter the echoes out of noise are fledgling for now; next-generation ground-based and space-borne gravitational waves detectors might be more promising [25]. Therefore, in light of successful direct imaging M87* by the Event Horizon Telescope (EHT) [7], we will concentrate on investigating the behavior of the Lee-Wick ultracompact object on electromagnetic waves, especially strong deflection gravitational lensing and its unique signature.

In the strong deflection gravitational lensing by a black hole, the deflection angle can become much bigger than unity, producing a set of relativistic images in the outside of and very close to its photon sphere (unstable light ring) [54] and forming an escape cone of light, also known as “shadow”, inside the photon sphere [55] (see Refs. [56, 57] for reviews). EHT has directly measured the angular diameter of M87*’s shadow as \(42\pm 3\) microarcsecond (\(\mu \)as) [7,8,9,10,11,12]. Its efforts of directly imaging the shadow of the supermassive black hole in the Galactic Center, Sgr A*, are underway. Detecting relativistic images of black holes might also be feasible in the future, providing better understanding of black holes [58,59,60,61,62,63] and distinguishing various kinds of them [64,65,66,67,68,69,70,71,72,73,74].

An unparalleled property of the ultracompact object is the existence of an antiphoton sphere (stable light ring) inside the photon sphere [75, 76], which is not present at a black hole. Therefore, its strong deflection gravitational lensing is dramatically different from a black hole’s by having unique relativistic images inside the photon sphere. Although gravitational lensing by various horizonless objects, such as wormholes [77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93], naked singularities [94, 95], gravastars [96] and boson stars [97], have been widely studied, most of them paid less attention on the role of and resulting observables of the antiphoton sphere with a few exceptions: the gravitational lensing in the case where the antiphoton and photon spheres coincide was studied in the Majumdar-Papapetrou dihole spacetime [98] and an analytical approach to handle the strong deflection lensing by the antiphoton sphere of the ultracompact object was proposed [99].

In Sect. 2, the spacetime of a Lee-Wick ultracompact object will be briefly reviewed. We study its strong deflection gravitational lensing and resulting outer and inner relativistic images by using the methods of strong deflection limit respectively for the photon sphere [60, 63] and for the antiphoton sphere [99] in Sect. 3. In Sect. 4, taking Sgr A* and M87* as two ultracompact object s, we estimate their observables of the lensing, evaluate their observability and obtain a tentative bound on the UV scale for the ultracompact object based on the observation of M87* by EHT. In Sect. 5, we conclude and discuss our results.

2 Lee-Wick ultracompact object

The Modesto–Shapiro theory of gravity reads [39,40,41,42,43]

$$\begin{aligned} S=\frac{1}{8\pi G_N}\int d^4 x \sqrt{|g|}\left[ R+{\varLambda }^{-4} G_{\mu \nu }\square R^{\mu \nu }\right] , \end{aligned}$$
(1)

where \(G_N\) denotes the gravitational constant and \({\varLambda }\) is the UV scale. It is not necessary for \({\varLambda }\) to be comparable with the Planck mass. The static and spherically symmetric spacetime solution of a source with mass \(m_{\bullet }\) was found as (with \(G_N=c=1\)) [47]

$$\begin{aligned} \mathrm {d}s^2 = -A(r)\mathrm {d}t^2 +B(r)\mathrm {d}r^2 +C(r)\left( \mathrm {d}\theta ^2+\sin ^2{\theta }\mathrm {d}\phi ^2\right) ,\nonumber \\ \end{aligned}$$
(2)

where

$$\begin{aligned} A(r)= & {} [B(r)]^{-1} = 1-\frac{2m_{\bullet }}{r} f(\chi ), \end{aligned}$$
(3)
$$\begin{aligned} C(r)= & {} r^2, \end{aligned}$$
(4)

and

$$\begin{aligned} f(\chi )=1-e^{-\chi }\left[ (1+\chi )\cos {\chi }+\chi \sin {\chi }\right] , \end{aligned}$$
(5)

with

$$\begin{aligned} \chi = \frac{\sqrt{2}}{2} {\varLambda } r. \end{aligned}$$
(6)

For later convenience, we define that

$$\begin{aligned} x = \frac{r}{2 m_{\bullet }}\quad \mathrm {and} \quad \kappa = \sqrt{2} {\varLambda } m_{\bullet } \end{aligned}$$
(7)

which are scaled by the mass of the source and are dimensionless.

The (redefined) UV scale \(\kappa \) determines the existence of the event horizon(s) of the spacetime (2). When \(\kappa >\kappa _{\mathrm {h}}\approx 2.165\), it has two distinct event horizons; as \(\kappa =\kappa _{\mathrm {h}}\), they merge into one at \(r_{\mathrm {h}} = 2m_{\bullet }\,x_{\mathrm {h}}\) with \(x_{\mathrm {h}}\approx 0.953\); when \(\kappa <\kappa _{\mathrm {h}}\), it ends up no horizons. The spacetime with \(\kappa \ge \kappa _{\mathrm {h}}\) are called the Lee-Wick black hole [47].

The existence of the light ring(s) is also controlled by \(\kappa \). From the null geodesics of a photon in the equator (\(\theta =\pi /2\)) of the spacetime (2), we can have the equation of motion of its radial coordinate r as [63, 99]

$$\begin{aligned} A(r)B(r)\,\dot{r}^2 + L^2V_{\mathrm {eff}}(r) = E^2, \end{aligned}$$
(8)

where a dot means the derivative against the affine parameter, \(E=A(r)\dot{t}\) and \(L=C(r){\dot{\phi }}\) are the energy and angular momentum of the photon, and the effective potential per square of the angular momentum is

$$\begin{aligned} V_{\mathrm {eff}}(r) = \frac{A(r)}{C(r)}. \end{aligned}$$
(9)

A circular photon ring requires \(V'_{\mathrm {eff}}(r)=0\) and \(r>0\) where \('\) denotes the differentiation with respect to r. The unstable photon ring with \(V''_{\mathrm {eff}}(r)<0\) is usually called the photon sphere with the radius \(r_{\mathrm {m}} = 2 m_{\bullet }\, x_{\mathrm {m}}\) that is outside the event horizon (if exists); and the stable photon ring with \(V''_{\mathrm {eff}}(r)>0\) is called the antiphoton sphere with the radius \(r_{\mathrm {a}} = 2 m_{\bullet }\, x_{\mathrm {a}}\) [99].

We find that \(\kappa _{\mathrm {a}}\approx 1.763\) is the lower bound to ensure the existence of the antiphoton and photon spheres and when \(\kappa \rightarrow \kappa _{\mathrm {a}}\) these two spheres get close to each other and eventually vanish at \(\kappa =\kappa _{\mathrm {a}}\) and \(x_{\mathrm {a}}\approx 1.670\) due to \(V''_{\mathrm {eff}}=0\) at this point. For any \(\kappa < \kappa _{\mathrm {a}}\), no circular photon ring is allowable. We also find that \(\kappa _{\mathrm {h}}\) is the upper bound for the existence of the antiphoton sphere. In the case of \(\kappa \ge \kappa _{\mathrm {h}}\), the event horizon encloses the anti-photon sphere, making it ineffective, and only the photon sphere survives outside the event horizon. Therefore, for the horizonless case of the Lee-Wick spactime (2), its antiphoton and photon spheres exist as long as the UV scale satisfies

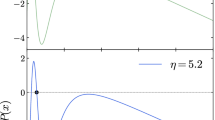
$$\begin{aligned} \kappa \in {\mathcal {D}}_{\mathrm {a}} =\{\kappa \,|\,\kappa _{\mathrm {a}}< \kappa < \kappa _{\mathrm {h}}\}. \end{aligned}$$
(10)

We call it a Lee-Wick ultracompact object. It has no event horizon and central singularity. Figure 1 shows A(x) and \(V_{\mathrm {eff}}\) for the Lee-Wick ultracompact object respectively in the top and bottom panels. It can be seen that, for a given \(\kappa \) belonging to the domain \({\mathcal {D}}_{\mathrm {a}}\), there exists no root of A(x) and \(V_{\mathrm {eff}}\) has two local extrema corresponding to the antiphoton and photon spheres. However, when \(\kappa =\kappa _{\mathrm {a}}\), neither of the local extrema exist for \(V_{\mathrm {eff}}\). The (dimensionless) radii of the antiphoton and photon spheres, \(x_{\mathrm {a}}\) and \(x_{\mathrm {m}}\), are shown in the top panel of Fig. 2, demonstrating that \(x_{\mathrm {m}}\) is bigger than \(x_{\mathrm {a}}\).

Fig. 1
figure 1

A(x) and \(V_{\mathrm {eff}}\) on \({\mathcal {D}}_{\mathrm {a}}\) are respectively shown in the top and bottom panels where \(x=(2m_{\bullet })^{-1}r\) and \(\kappa =\sqrt{2}{\varLambda } m_{\bullet }\). This domain ensures the existence of its antiphoton and photon spheres for the Lee-Wick horizonless ultracompact object

Full size image
Fig. 2
figure 2

It shows the positions of the antiphoton and photon spheres \(x_{\mathrm {a}}\) and \(x_{\mathrm {m}}\) in the top panel, the coefficients of the strong deflection limit \({\bar{a}}_+\) and \({\bar{a}}_-\) in the middle panel and \({\bar{b}}_+\) and \({\bar{b}}_-\) in the bottom panel

Full size image

3 Outer and inner relativistic images

In the strong deflection gravitational lensing, its deflection angle is much bigger than 1, resulting in a series of relativistic images by photons surrounding a compact object with n loops. A black hole with the event horizon and photon sphere forms the relativistic images outside the photon sphere but none inside. In contrast, a horizonless ultracompact object, such as the Lee-Wick one, can generate a series of relativistic images inside as well as those outside the photon sphere since it is possessed of both antiphoton and photon spheres.

For a light ray lensed by the Lee-Wick ultracompact object, its impact parameter u is

$$\begin{aligned} u^2=\frac{C(r_0)}{A(r_0)}, \end{aligned}$$
(11)

where \(r_0\) is the closet approach distance of the photon. Its deflection angle can be obtained as [58, 99, 100]

$$\begin{aligned} {\hat{\alpha }}(r_0) = - \pi + 2\int ^{\infty }_{r_0} \sqrt{ \frac{B(r)}{C(r)R(r)} } \mathrm {d}r, \end{aligned}$$
(12)

with

$$\begin{aligned} R(r) = \frac{C(r)}{C(r_0)} \frac{A(r_0)}{A(r)}-1. \end{aligned}$$
(13)

The radius of its photon sphere \(r_{\mathrm {m}}\) is given by the root of \(V'_{\mathrm {eff}}(r_{\mathrm {m}})=0\) with condition \(V''_{\mathrm {eff}}(r_{\mathrm {m}})<0\) while the radius of its antiphoton sphere \(r_{\mathrm {a}}\) is determined by the root of \(V'_{\mathrm {eff}}(r_{\mathrm {a}})=0\) with condition \(V''_{\mathrm {eff}}(r_{\mathrm {a}})>0\).

In the strong deflection limit generating the outer relativistic images, its deflection angle of a photon with \(r_0\gtrsim r_{\mathrm {m}}\) is [60, 63]

$$\begin{aligned}&{\hat{\alpha }}_+ (u) = - {\bar{a}}_{+} \log \bigg (\frac{u}{u_{\mathrm {m}}}-1\bigg ) +{\bar{b}}_{+} +{\mathcal {O}}[(u-u_{\mathrm {m}}) \nonumber \\&\quad \log (u-u_{\mathrm {m}})], \end{aligned}$$
(14)

where \(u_{\mathrm {m}}\) is the impact parameter evaluated at the photon sphere \(r_{\mathrm {m}}\) and

$$\begin{aligned} {\bar{a}}_{+}= & {} \sqrt{\frac{2}{A_{\mathrm {m}}C''_{\mathrm {m}}-A''_{\mathrm {m}}C_{\mathrm {m}}}}, \end{aligned}$$
(15)
$$\begin{aligned} {\bar{b}}_{+}= & {} {\bar{a}}_{+} \log \bigg [r_{\mathrm {m}}^2 \bigg ( \frac{C''_{\mathrm {m}}}{C_{\mathrm {m}}} - \frac{A''_{\mathrm {m}}}{A_{\mathrm {m}}} \bigg ) \bigg ] + I_{+}(r_{\mathrm {m}}) - \pi . \end{aligned}$$
(16)

Here, a quantity with subscript “\(\mathrm {m}\)” means its value at \(r_{\mathrm {m}}\), and we have

$$\begin{aligned} I_{+}(r_{\mathrm {m}}) = 2 \int _0^1 \bigg [\frac{r_{\mathrm {m}}}{(1-z)^2}\sqrt{\frac{ C_{\mathrm {m}}}{(A_{\mathrm {m}} C_{z}-A_{z} C_{\mathrm {m}})C_{z}}} {-}\frac{{\bar{a}}_{+}}{|z|} \bigg ] \mathrm {d}z,\nonumber \\ \end{aligned}$$
(17)

where

$$\begin{aligned} z=1-\frac{r_{\mathrm {m}}}{r}, \end{aligned}$$
(18)

and any function F with subscript z denotes

$$\begin{aligned} F_{z} \equiv F[r(z)] = F\left[ r_{\mathrm {m}}(1-z)^{-1}\right] . \end{aligned}$$
(19)

In the strong deflection limit, the Lee-Wick ultracompact object can also have the inner relativistic images inside the photon sphere if \(r_0 < r_{\mathrm {m}}\). The resulting deflection angle is [99]

$$\begin{aligned} {\hat{\alpha }}_- (u)= & {} - {\bar{a}}_{-} \log \bigg (\frac{u_{\mathrm {m}}^2}{u^2}-1\bigg ) +{\bar{b}}_{-}\nonumber \\&+{\mathcal {O}}\left[ (u^2_{\mathrm {m}}-u^2)\log (u^2_{\mathrm {m}}-u^2)\right] , \end{aligned}$$
(20)

where

$$\begin{aligned} {\bar{a}}_{-}= & {} 2 {\bar{a}}_{+}, \end{aligned}$$
(21)
$$\begin{aligned} {\bar{b}}_{-}= & {} 2{\bar{a}}_{+} \log \left[ 2r_{\mathrm {m}}^2 \left( \frac{C''_{\mathrm {m}}}{C_{\mathrm {m}}} - \frac{A''_{\mathrm {m}}}{A_{\mathrm {m}}} \right) \left( \frac{r_{\mathrm {m}}}{r_{\mathrm {c}}}-1\right) \right] \nonumber \\&+ I_{-}(r_{\mathrm {c}}) - \pi , \end{aligned}$$
(22)
$$\begin{aligned} I_{-}(r_{\mathrm {c}})= & {} 2 \int _{1-\frac{r_{\mathrm {m}}}{r_{\mathrm {c}}}}^1 \left[ \frac{r_{\mathrm {m}}}{(1-z)^2}\sqrt{\frac{ C_{\mathrm {c}}}{(A_{\mathrm {c}} C_{z}-A_{z} C_{\mathrm {c}}) C_{z}}} -\frac{{\bar{a}}_{+}}{|z|} \right] \mathrm {d}z.\nonumber \\ \end{aligned}$$
(23)

Here \(r_{\mathrm {c}}\) is defined as the root of \(V_{\mathrm {eff}}(r_{\mathrm {c}}) = V_{\mathrm {eff}}(r_{\mathrm {m}})\) and satisfies \(r_{\mathrm {c}} < r_{\mathrm {m}}\); and a function with subscript “\({\mathrm {c}}\)” means its value at \(r_{\mathrm {c}}\).

In the middle and bottom panels of Fig. 2, the coefficients of the strong deflection limit for the outer relativistic images \({\bar{a}}_+\) and \({\bar{b}}_+\) and those for the inner images \({\bar{a}}_-\) and \({\bar{b}}_-\) on the domain \({\mathcal {D}}_{\mathrm {a}}\) are shown. It is clear that \({\bar{a}}_{+}\) is a half of \({\bar{a}}_{-}\), see Eq. (21). When \(\kappa \approx \kappa _{\mathrm {a}}\), \({\bar{b}}_{-}\) is less than \({\bar{b}}_{+}\) by about a factor of 2; and for \(\kappa >1.790\), we have \({\bar{b}}_{-}>0>{\bar{b}}_{+}\). We can see that when \(\kappa \rightarrow \kappa _{\mathrm {a}}\), both \({\bar{a}}_{\pm }\) and \({\bar{b}}_{\pm }\) diverge. It happens because the antiphoton and photon spheres vanish at \(\kappa =\kappa _{\mathrm {a}}\), causing the strong deflection limit invalid, and there exists a point with \(V'_{\mathrm {eff}}(r_{\mathrm {m}}) = V''_{\mathrm {eff}}(r_{\mathrm {m}})=0\) (see the red curve in the bottom panel in Fig. 1), making \({\bar{a}}_{\pm }\) and \({\bar{b}}_{\pm }\) explode.

In order to obtain the observables of the outer and inner relativistic images, we adopt the lens equation as [58, 59, 101]

$$\begin{aligned} {\mathcal {B}}=\vartheta -\frac{D_{\mathrm {LS}}}{D_{\mathrm {OS}}}[{\hat{\alpha }}(\vartheta )-2n\pi ],\quad n\in {\mathbb {Z}}^+, \end{aligned}$$
(24)

where \({\mathcal {B}}\) is the angular position of the source, \(\vartheta \) is the angular position of the image, and \(D_{\mathrm {LS}}\) and \(D_{\mathrm {OS}}\) are respectively the distances from the lens to the source and from the observer to the source. It is assumed that the source, the lens and the observer are nearly aligned and both the source and observer are far from the lens. Therefore, \({\hat{\alpha }}(\vartheta )= {\hat{\alpha }}_+(u)\) for the outer relativistic image and \({\hat{\alpha }}(\vartheta )= {\hat{\alpha }}_-(u)\) for the inner image where \(u=\vartheta D_{\mathrm {OL}}\) and \(D_{\mathrm {OL}}\) is the distance from the observer to the lens. For a lensed image, its magnification \(\mu \) can be found as [102]

$$\begin{aligned} \mu (\vartheta ) = \bigg [ \frac{\sin {\mathcal {B}}(\vartheta )}{\sin \vartheta } \frac{\mathrm {d}{\mathcal {B}}(\vartheta )}{\mathrm {d}\vartheta }\bigg ]^{-1}. \end{aligned}$$
(25)

The position of the outer relativistic Einstein ring \(\vartheta ^0_{+n}\) with \({\hat{\alpha }}_+=2n\pi \) is [60]

$$\begin{aligned} \vartheta ^0_{+n} = \frac{u_m}{D_{\mathrm {OL}}}(1+e_{+n}) \end{aligned}$$
(26)

with

$$\begin{aligned} e_{+n} = \exp \bigg (\frac{{\bar{b}}_+-2n\pi }{{\bar{a}}_+} \bigg ), \end{aligned}$$
(27)

which leads to the apparent angular radius of the photon sphere as \(n\rightarrow \infty \)

$$\begin{aligned} \theta _{+\infty } \equiv \vartheta ^0_{+\infty } = \frac{u_m}{D_{\mathrm {OL}}}. \end{aligned}$$
(28)

The position of the outer relativistic image \(\vartheta _{+n}\) is [60]

$$\begin{aligned} \vartheta _{+n} = \vartheta ^0_{+n} + \frac{u_m e_{+n} D_{\mathrm {OS}}}{{\bar{a}}_{+} D_{\mathrm {LS}} D_{\mathrm {OL}} }({\mathcal {B}}-\vartheta ^0_{+n}) \end{aligned}$$
(29)

and its magnification is [60]

$$\begin{aligned} \mu _{+n} = \frac{u_m^2 D_{\mathrm {OS}}}{{\bar{a}}_+{\mathcal {B}}D_{\mathrm {OL}}^2 D_{\mathrm {LS}}} (1+e_{+n})e_{+n}. \end{aligned}$$
(30)

It can be found that if \(i>j>0\), then \(\vartheta _{+i}<\vartheta _{+j}\) and \(|\mu _{+i}|<|\mu _{+j}|\). The position of the inner relativistic Einstein ring \(\vartheta ^0_{-n}\) with \(\alpha _-=2n\pi \) is [99]

$$\begin{aligned} \vartheta ^0_{-n} = \frac{u_m}{D_{\mathrm {OL}} \sqrt{1+e_{-n}}} \end{aligned}$$
(31)

with

$$\begin{aligned} e_{-n} = \exp \bigg (\frac{{\bar{b}}_{-}-2n\pi }{{\bar{a}}_{-}} \bigg ) \end{aligned}$$
(32)

which gives the same angular radius of the photon sphere as the one for the outer relativistic images that

$$\begin{aligned} \theta _{-\infty } \equiv \vartheta ^0_{-\infty } = \frac{u_m}{D_{\mathrm {OL}}}. \end{aligned}$$
(33)

Hereafter, we will omit ± in the notation of the apparent size of the photon sphere for \(\theta _{\infty }= \theta _{\pm \infty }\). The position of the inner relativistic image \(\vartheta _{-n}\) is [99]

$$\begin{aligned} \vartheta _{-n} = \vartheta ^0_{-n} - \frac{u_m e_{-n} D_{\mathrm {OS}}}{2{\bar{a}}_{-} D_{\mathrm {LS}} D_{\mathrm {OL}} } \frac{({\mathcal {B}}-\vartheta ^0_{-n})}{(1+e_{-n})^{3/2}} \end{aligned}$$
(34)

and its magnification is [99]

$$\begin{aligned} \mu _{-n} = -\frac{u_m^2 D_{\mathrm {OS}}}{2{\bar{a}}_{-}{\mathcal {B}}D_{\mathrm {OL}}^2 D_{\mathrm {LS}}} \frac{e_{-n}}{(1+e_{-n})^2}. \end{aligned}$$
(35)

It can also be found that if \(-j<-i<0\), then \(\vartheta _{-i}<\vartheta _{-j}\) and \(|\mu _{-j}|<|\mu _{-i}|\).

If it is assumed that only the innermost and outermost relativistic images could be resolved and all of the remaining ones are packed together at the photon sphere \(\theta _{\infty }\), we can have separations among the relativistic images as

$$\begin{aligned} s_{i,j} \equiv \vartheta _{i}- \vartheta _{j}, \end{aligned}$$
(36)

and there brightness difference in the unit of magnitude as

$$\begin{aligned} {\varDelta } m_{i,j} \equiv 2.5\log _{10}\bigg (\frac{|\mu _i|}{|\mu _j|}\bigg ), \end{aligned}$$
(37)

where \(i,j=-1,\infty ,1\) respectively for the innermost relativistic image, the photon sphere and the outermost one. For the magnification of the photon sphere, it has contributions from both inner and outer relativistic images that

$$\begin{aligned} \mu _{\infty } = \sum _{j=2}^{\infty } (|\mu _{+j}|+|\mu _{-j}|). \end{aligned}$$
(38)

Therefore, we can have

$$\begin{aligned} s_{+1,\infty }= & {} \theta _{\infty } e_{+1} , \end{aligned}$$
(39)
$$\begin{aligned} s_{\infty ,-1}= & {} \theta _{\infty } \bigg (1 - \frac{1}{\sqrt{1+e_{-1}}} \bigg ), \end{aligned}$$
(40)
$$\begin{aligned} s_{+1,-1}= & {} \theta _{\infty } \bigg (1+e_{+1} - \frac{1}{\sqrt{1+e_{-1}}} \bigg ), \end{aligned}$$
(41)
$$\begin{aligned} {\varDelta } m_{+1,\infty }= & {} 2.5 \log _{10} [e_{+1}(1+e_{+1})] -2.5\log _{10} \nonumber \\&\times \left\{ \sum _{j=2}^{\infty } \left[ (1+e_{+j})e_{+j}+ {\frac{e_{-j}}{4(1+e_{-j})^2}} \right] \right\} ,\nonumber \\ \end{aligned}$$
(42)
$$\begin{aligned} {\varDelta } m_{-1,\infty }= & {} 2.5 \log _{10} \left[ \frac{e_{-1}}{4(1+e_{-1})^2} \right] -2.5\log _{10} \nonumber \\&\times \left\{ \sum _{j=2}^{\infty } \left[ (1+e_{+j})e_{+j} + \frac{e_{-j}}{4(1+e_{-j})^2}\right] \right\} \nonumber \\ \end{aligned}$$
(43)
$$\begin{aligned} {\varDelta } m_{+1,-1}= & {} 2.5\log _{10}\left[ 4\frac{e_{+1}}{e_{-1}} (1+e_{+1})(1+e_{-1})^2 \right] . \end{aligned}$$
(44)

Here, \(s_{+1,\infty }\), \(s_{\infty ,-1}\) and \(s_{+1,-1}\) are respectively the angular separations between the outermost relativistic image and the photon sphere, between the photon sphere and the innermost relativistic image and between the outermost and innermost images, while \({\varDelta } m_{+1,\infty }\), \({\varDelta } m_{-1,\infty }\) and \({\varDelta } m_{+1,-1}\) are respectively their brightness differences. The angular separations are dependent on \(\theta _{\infty }\) which relates to the mass and distance of the lens, while the brightness differences are dimensionless and irrelevant to these two quantities of the lens.

4 Observables for Sgr A* and M87*

For current capability of gravitational wave detection and astronomical observation, it is still hardly to distinguish a horizonless ultracompact object from a black hole [38]. Therefore, We hypothesize that Sgr A* and M87* were two Lee-Wick ultracompact object s with the mass \(M_{\mathrm {SgrA*}}=4.28\times 10^6\) \(M_{\odot }\) and the distance \(D_{\mathrm {OL,SgrA*}}=8.32\) kpc [103] and with \(M_{\mathrm {M87*}}=6.5\times 10^9\) \(M_{\odot }\) and \(D_{\mathrm {OL,M87*}}=16.9\) Mpc [12].

Their angular observables, including the apparent radius of the photon sphere \(\theta _{\infty }\) as well as the separations between the relativistic images \(s_{+1,\infty }\), \(s_{\infty ,-1}\) and \(s_{+1,-1}\), are shown in Fig. 3. On the domain \({\mathcal {D}}_{\mathrm {a}}\), \(\theta _{\infty }\) decreases with the increment of \(\kappa \). \(\theta _{\infty }\) for Sgr A* ranges from 29.7 to 31.1 \(\upmu \)as for the Lee-Wick ultracompact object, bigger than its value of 26.4 \(\mu \)as in the case of a Schwarzschild black hole; and \(\theta _{\infty }\) becomes 22.3–23.2 \(\upmu \)as for M87* whereas its value for the Schwarzschild black hole is 19.7 \(\upmu \)as. The angular separation between the outermost relativistic image and the photon sphere \(s_{+1,\infty }\) quickly reaches its peak values of 75 nanoarcsecond (nas) for Sgr A* and of 56 nas for M87* at \(\kappa \approx 1.780\) and then slowly decays to about 9 nas. By comparison, their corresponding values for the Schwarzschild black hole are 33.0 nas for Sgr A* and 24.7 nas for M87*. However, even at its peaks, \(s_{+1,\infty }\) is still far beyond the foreseen angular resolution of observation in the near future. In contrast, the angular separation between the innermost relativistic image and the photon sphere \(s_{\infty ,-1}\) is much bigger than \(s_{+1,\infty }\) and it can monotonically increase to 5.6 \(\mu \)as for Sgr A* and to 4.2 \(\mu \)as for M87* as \(\kappa \) approaches \(\kappa _{\mathrm {h}}\). These values are marginally with the current ability of EHT [7]. Since \(s_{+1,-1}=s_{+1,\infty }+s_{\infty ,-1}\) and \(s_{\infty ,-1}\gg s_{+1,\infty }\), we can have \(s_{+1,-1}\approx s_{\infty ,-1}\) and \(s_{+1,-1}\) have almost the same curves as those of \(s_{\infty ,-1}\) for Sgr A* and M87*.

Figure 4 shows the magnification-related observables which are the brightness differences between relativistic images \({\varDelta } m_{+1,\infty }\), \({\varDelta } m_{-1,\infty }\) and \({\varDelta } m_{+1,-1}\). Since the brightness differences do not depend on the mass and the distance of the lens, the two Lee-Wick ultracompact object s of Sgr A* and M87* share the same curves. The brightness difference between the outermost relativistic image and the others packaged at the photon sphere \({\varDelta } m_{+1,\infty }\) can reach about \(-0.8\) mag at \(\kappa \approx \kappa _{\mathrm {a}}\) and decrease to about \(-2.7\) mag at \(\kappa \approx \kappa _{\mathrm {h}}\), showing that the outermost one is fainter than the packaged one by at least 2 mag for \(1.879<\kappa <\kappa _{\mathrm {h}}\). By comparison, \({\varDelta } m_{+1,\infty }\) for the Schwarzschild black hole is 6.8 mag. The brightness difference between the innermost relativistic image and the packaged one at the photon sphere \({\varDelta } m_{-1,\infty }\) monotonically increases from about \(-1.3\) to 2.9 mag, demonstrating that the innermost one is brighter than the packaged one by at least 2 mag for \(1.839<\kappa <\kappa _{\mathrm {h}}\). The brightness difference between the outermost and innermost relativistic images \({\varDelta } m_{+1,-1}\) is simply \({\varDelta } m_{+1,\infty }-{\varDelta } m_{-1,\infty }\) and it indicates the innermost relativistic image is brighter than the outermost one by at least 2 mag for \(\kappa >1.771\) and by almost 5.7 mag at \(\kappa \approx \kappa _{\mathrm {h}}\). The curve of \({\varDelta } m_{+1,\infty }\) suggests that if it would have enough angular resolution to separate the outermost relativistic images from the photon sphere, the outermost image is fainter than the others packaged altogether by 2 mag and more, making them harder to detect, while \({\varDelta } m_{-1, \infty }\) and \({\varDelta } m_{+1,-1}\) show the innermost image is significantly brighter than both the packaged one at the photon sphere and the outermost one, rendering it a more promising signature of the ultracompact object to search.

For now, the only available measurement of these observables is the measured diameter of M87*’s shadow of \(42\pm 3\) \(\mu \)as [7]. If it is assumed that M87* is the Lee-Wick ultracompact object and its measured apparent size of shadow is determined by its innermost relativistic image, we can estimate a rough and tentative bound on \(\kappa \) as \(1.775\le \kappa \le 1.920\). If we further demand that the separation between the innermost image and the photon sphere is smaller than the uncertainty of the diameter of the shadow since no individual inner image is observed, it can narrow the bound down to \(1.775\le \kappa \le 1.855\) which leads to \(1.31\times 10^{-13}\) m\(^{-1}\le {\varLambda } \le 1.37\times 10^{-13}\) m\(^{-1}\). Note that, instead of \(\kappa \), \({\varLambda }\) parametrizes the Modesto–Shapiro theory of gravity so that even the same constraint on \(\kappa \) can give very different constraints on \({\varLambda }\) since Sgr A* and M87* have completely different masses. It is also worth mentioning that applying such a measurement to constrain the ultracompact object has to be proceeded with caution, because estimating properties of M87*’s shadow indispensably relies on the rotation of the central compact object and the general relativistic magnetohydrodynamics of plasma around it [12]. Both of them are absent in this work since the spacetime of a rotating Lee-Wick ultracompact object is still unknown and the general relativistic magnetohydrodynamics of plasma is computationally high-cost and beyond the scope of this work. Therefore, the bound on \(\kappa \) we have obtained is merely a hint for the Lee-Wick ultracompact object and not a genuine constraint on it.

Fig. 3
figure 3

The angular observables, the apparent radius of the photon sphere \(\theta _{\infty }\) as well as separation between relativistic images \(s_{+1,\infty }\), \(s_{\infty ,-1}\) and \(s_{+1,-1}\), are shown from top to bottom panels. When applicable, these observables for the ultracompact object (UCO) and for the Schwarzschild black hole (Sch) are both represented

Full size image
Fig. 4
figure 4

The magnification-related observables, the brightness differences between relativistic images \({\varDelta } m_{+1,\infty }\), \({\varDelta } m_{-1,\infty }\) and \({\varDelta } m_{+1,-1}\), are shown from top to bottom panels

Full size image

5 Conclusions and discussion

We study the strong deflection gravitational lensing by the Lee-Wick ultracompact object and obtain its observables, including the apparent radius of the photon sphere as well as the angular separations and the brightness differences between the relativistic images. Its unique feature is a series of relativistic images inside the photon sphere, which are absent for a black hole. By assuming that Sgr A* and M87* are two ultracompact object s, we show how these observables change with respect to the UV scale \(\kappa \) belonging to the domain \({\mathcal {D}}_{\mathrm {a}}\). We find that the apparent radius of the photon sphere for the Lee-Wick ultracompact object is bigger than the one for the Schwarzschild black hole with the same mass and distance. Although the angular separation between the outermost relativistic image and the others packaged at the photon sphere for the Lee-Wick ultracompact object can reach more than 50 nas at \(\kappa \approx 1.780\), which is two times bigger than the one for the Schwarzschild black hole, it is far beyond the foreseen technology, not to mention its considerable faintness. In contrast, the angular separation between the innermost relativistic image and the photon sphere for the Lee-Wick ultracompact object can increase to several \(\mu \)as marginally within the current ability and it is much brighter than both the packaged one at the photon sphere and the outermost one, making it as a very promising signature for the ultracompact object.

Based on the measured diameter for M87*’s shadow by EHT [7], a rough and tentative bound on the UV scale is estimated as \(1.775\le \kappa \le 1.855\) and \(1.31\times 10^{-13}\) m\(^{-1}\le {\varLambda } \le 1.37\times 10^{-13}\) m\(^{-1}\) for the ultracompact object by assuming that the apparent size of the shadow is determined by its innermost relativistic image and no individual inner image can be resolved by the current observation. It seems that \({\varLambda }\) might be too small to pass other tests of General Relativity and it might be expected to be much bigger than the TeV scale.

Such a Lee-Wick horizonless ultracompact object is a non-rotating one. Although the observation by EHT disfavors a irrotational black hole [7], it did not say anything about ultracompact object s. Even so, we expect that the rotation of the Lee-Wick ultracompact object will have an influence on the shadow; however, a detailed investigation on it has to wait until the metric of this rotating ultracompact object is available. Another critical ingredient is the general relativistic magnetohydrodynamics of plasma around the Lee-Wick ultracompact object, which is important to account for the asymmetric ring around M87* [11] and is also computationally high-cost. These two absent factors remind that the Lee-Wick horizonless ultracompact object can not be constrained in a self-consistent way by making direct use of the observed M87*’s shadow. This work provides some prediction of its strong deflection gravitational lensing signals and a hint of its horizonlessness and ultracompactness. In order to have a complete picture, more detailed studies about the effects of its rotation on the weak [104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120] and strong [121,122,123,124,125] deflection lensing as well as numerical simulations of general relativistic magnetohydrodynamics of plasma are required.