1 Introduction

The gravitational wave, which is theoretically predicted over 100 years ago, has been finally detected recently [1,2,3]. In the coming era of multi-messenger astrophysics, it requires searches for electromagnetic counterpart of the gravitational wave than ever before. Moreover, the gravitational wave is related to electromagnetic radiation closely. For instance, gravitational wave event GW-170817 is produced along with gamma-ray burst [3] and pulsar timing array is used to detect gravitational wave.

Pulsars, especially binary pulsars, one of the most possible electromagnetic counterparts of gravitational wave, are known as highly magnetized rotational stars in the space. Pulsars have been observed and investigated extensively for several decades. Rotation velocity of a pulsar could be observed precisely. It shows that pulsars would rotate slower as time goes by. In the canonical model, pulsar can be simply regarded as a rotational magnetic dipole. Loss of rotation energy is due to the magnetic dipole radiation [4, 5]. For a pulsar with moment of inertia I and magnetic dipole m, the evolution of rotation velocity \(\varOmega \) is described by the so-called spin-down equation,

$$\begin{aligned} {\dot{\varOmega }} = - \frac{2 m^2 \sin ^2 \theta }{3 I c^3} \varOmega ^3 \text {} \equiv - K \varOmega ^3, \end{aligned}$$
(1)

where \(\theta \) is magnetic inclination angle and c is speed of light. However, the spin-down equation does not describe the observed rotation velocity \(\varOmega \) well. The deviation of spin-down equation can be indicated by a dimensionless quantity, the so-called braking index,

$$\begin{aligned} n \equiv \frac{\ddot{\varOmega } \varOmega }{{\dot{\varOmega }}^2} . \end{aligned}$$
(2)

In the canonical model, the braking index equals to 3, while almost all observed braking indices are beyond 3 [6, 7]. The deviated braking indices indicate a modified spin-down equation.

In fact, various models were proposed to deal with the braking index problem. There are two major scenarios. The first scenario suggests that pulsars should have other kinds of radiation source besides the magnetic dipole radiation. And the second indicates that magnetic moment or moment of inertia of pulsars should evolve with time. In the first scenario, the expected radiation source might be gravitational quadrupole radiation [8,9,10], in which the pulsar is thought as an imperfect sphere. The energy radiation also can be caused by the outflow of relativistic particles in pulsar wind model [11,12,13], or fall-back disk around pulsars [14,15,16]. In the second scenario, the braking index can be given [6, 17] by,

$$\begin{aligned} n = 3 + \frac{\varOmega }{{\dot{\varOmega }}} \left( \frac{2 {\dot{M}}}{M} + \frac{2 {\dot{\theta }}}{\tan \theta } - \frac{{\dot{I}}}{I} \right) . \end{aligned}$$
(3)

The deviated braking indices turn to require physical origin for \({\dot{M}}\), \({\dot{\theta }}\) and \({\dot{I}}\). The magnetic moment, or the magnetic field, of pulsars might change with time due to Hall drift, Ohmic decay or other magnetic mechanism [18,19,20]. It was also studied statistically by providing phenomenological model for the evolution of magnetic field [21,22,23]. For the magnetic inclination angle, it might evolve with time tending to be in alignment or out of alignment because of the plasma in magnetosphere [24] or the rearrangement of pulsar components [25], respectively. The inertia of moment related to equation of state of the pulsars was also considered [26].

From these models, the deviated braking indices around 3 seem to be well understood. However, as Refs. [22, 27] pointed out, there are numerous braking indices beyond 3 over several orders of magnitude. Maybe, due to limitation of structure of pulsars or attributing to inaccuracy observation, the large braking indices are rarely explored. In this paper, we wish to be confronted with the braking index problem and focus on the large braking indices. In the ATFN pulsar catalogue (http://www.atnf.csiro.au/research/pulsar/psrcat/), there are 441 pulsars whose braking indices can be obtained. 32 of them have companions. We find that the 32 pulsars tend to have larger braking indices than that of the rest. The statistical result is shown in Fig. 1. It motivates us to consider that the gravitational field around pulsars might cause the large braking indices.

In this paper, we deal with braking index problem by proposing a modified spin-down equation based on a moving dipole potential [28]. In the modified spin-down equation, the braking indices increase with the accelerations of pulsars. We expect that the gravitational field around a pulsar might be the possible origin of the acceleration. The paper is organized as follows. In Sect. 2, we show the magnetic dipole radiation of a moving pulsar. In Sect. 3, we derive the braking indices via constructing the modified spin-down equation and provide estimation of the accelerations of pulsars. The main conclusions and discussions are summarized in final Sect. 4.

Fig. 1
figure 1

Probability distribution of braking indices for the pulsars. The light gray filled histogram is the braking indices of 32 pulsars with companions. The gray filled histogram is the braking indices of the rest 409 pulsars. The dark gray filled histogram is the cross region of these two kinds of pulsars

Full size image

2 Magnetic dipole radiation of a moving pulsar

In canonical model, the pulsars spin down due to the magnetic dipole radiation. Likewise, we only refer to the magnetic dipole radiation of pulsars. The difference is that we consider an accelerated pulsar based on a moving dipole potential [28]. The potential is of the form,

$$\begin{aligned} A_{\mu } (x) = \partial _{\nu } \left( \frac{Q^{ \nu }_{\mu }}{r^{\mu } u_{\mu }} \right) _\mathrm{{ret}}, \end{aligned}$$
(4)

where \(r^{\mu } = x^{\mu } - z^{\mu } (\tau )\), \(z^{\mu }\) is the position of the dipole, \(\partial _{\mu } \equiv \frac{\partial }{\partial x^{\mu }}\), \(u^{\mu } \equiv \frac{\mathrm{{d}} z^{\mu }}{\mathrm{{d}} \tau }\) and \(Q (\tau )^{ \nu }_{\mu } = u^{\nu } p_{\mu } - u_{\mu } p^{\nu } + \epsilon ^{\nu }_{ \mu \rho \sigma } u^{\rho } m^{\sigma }\). The \(p_{\mu }\) and \(m^{\sigma }\) are electric and magnetic dipole, respectively. Source terms are functions of \(\tau \) which is defined by the light cone condition,

$$\begin{aligned} r^{\mu } r_{\mu } = (x^{\mu } - z^{\mu } (\tau )) (x_{\mu } - z_{\mu } (\tau )) = 0. \end{aligned}$$
(5)

It implies \(z^0 = x^0 - \left| {\varvec{x}} - {\varvec{z}} \right| = x^0 - r\). Thus, the point dipole in the retard potential also can be represented as \( Q^{\mu } (\tau ) |_\mathrm{{ret}} \equiv Q^{\mu } (x^0 - r)\). The \(\tau \) is function of \(x^{\mu }\). One can calculate partial derivative of Eq. (5), the partial derivative of \(\tau \) referred to \(x^{\mu }\) is of the form,

$$\begin{aligned} \partial _{\mu } \tau = \frac{r_{\mu }}{r^{\lambda } u_{\lambda }}, \end{aligned}$$
(6)

Using Eqs. (4) and (6), we can obtain the electromagnetic field \(F_{\mu \nu }\) of the dipole,

$$\begin{aligned} F_{\mu \nu }= & {} \partial _{\mu } A_{\nu } - \partial _{\nu } A_{\mu } \nonumber \\= & {} \partial _{\mu } \partial _{\sigma } \left( \frac{Q^{ \sigma }_{\nu }}{r^{\lambda } u_{\lambda }} \right) - \partial _{\nu } \partial _{\sigma } \left( \frac{Q^{ \sigma }_{\mu }}{r^{\lambda } u_{\lambda \mu }} \right) \nonumber \\= & {} \frac{r_{\mu } r_{\sigma }}{(r^{\lambda } u_{\lambda })^3} {\ddot{Q}}_{\nu }^{ \sigma } + \left( \left( \frac{\eta _{\mu \sigma }}{(r^{\lambda } u_{\lambda })^2} - \frac{2 (u_{\sigma } r_{\mu } + r_{\sigma } u_{\mu })}{(r^{\lambda } u_{\lambda })^3} \right. \right. \nonumber \\&\left. \left. + \frac{3 u^2 r_{\sigma } r_{\mu }}{(r^{\lambda } u_{\lambda })^4} \right) \right. \nonumber \\&\left. - \frac{3 r_{\sigma } r_{\mu } r^{\kappa } a_{\kappa }}{(r^{\lambda } u_{\lambda })^4} \right) {\dot{Q}}_{\nu }^{ \sigma } \nonumber \\&+ \left( \left( \frac{u^2 \eta _{\sigma \mu }}{(r^{\lambda } u_{\lambda })^3} + \frac{3 u^4 r_{\sigma } r_{\mu }}{(r^{\lambda } u_{\lambda })^5} - \frac{3 u^2 (r_{\sigma } u_{\mu } + r_{\mu } u_{\sigma })}{(r^{\lambda } u_{\lambda })^4} \right) \right. \nonumber \\&+ \left( - \frac{a_{\sigma } r_{\mu } + r_{\sigma } a_{\mu }}{(r^{\lambda } u_{\lambda })^3} - \frac{(r^{\kappa } a_{\kappa }) \eta _{\sigma \mu }}{(r^{\lambda } u_{\lambda })^3} - \frac{6 (r^{\kappa } a_{\kappa }) u^2 r_{\sigma } r_{\mu }}{(r^{\lambda } u_{\lambda })^5} \right. \nonumber \\&\left. + \frac{3 (r^{\kappa } a_{\kappa }) (r_{\sigma } u_{\mu } + r_{\mu } u_{\sigma })}{(r^{\lambda } u_{\lambda })^4} \right) \nonumber \\&+ \left. \left( - \frac{(r^{\kappa } {\dot{a}}_{\kappa }) r_{\sigma } r_{\mu }}{(r^{\lambda } u_{\lambda })^4} + \frac{3 (r^{\kappa } a_{\kappa })^2 r_{\sigma } r_{\mu }}{(r^{\lambda } u_{\lambda })^5} \right) \right) Q_{\nu }^{ \sigma } \nonumber \\&- \left( \mathrm {permutation} \mathrm {of} \mu \mathrm {and} \nu \right) , \end{aligned}$$
(7)

where \(a^{\mu } \equiv \frac{\mathrm{{d}} u^{\mu }}{\mathrm{{d}} \tau }, {\dot{a}}^{\mu } \equiv \frac{\mathrm{{d}} a^{\mu }}{\mathrm{{d}} \tau }\) and \({\dot{Q}} \equiv \frac{\mathrm{{d}}}{\mathrm{{d}} \tau } Q\).

The construction of spin-down equation requires the form of electromagnetic radiation. For simplicity, we calculate the radiation in the moving frame adapted to \(u^{\mu }\). Namely, we set \(u = \left( c, {\varvec{0}} \right) \) in the electromagnetic field \(F_{\mu \nu }\). And changes of space-time metric are not considered. We would discuss it in the Sect. 4. In the reference frame of pulsars, the Eq. (7) can be simplified, such as \(r^{\mu } u_{\mu } = r^0 u_0 = - c r\) and the vanished electric dipole. By making using of normalization of 4-velocity \(u^{\mu } u_{\mu } = - c^2\), we know that the time component of acceleration is zero.

In classical electrodynamics, radiation of electromagnetic field is derived from the electromagnetic energy–momentum tensor,

$$\begin{aligned} T^{\mu }_{\nu }= & {} \frac{1}{4 \pi } \left( - F^{\mu }_{ \sigma } F^{\sigma }_{ \nu } + \frac{1}{4} \delta ^{\mu }_{\nu } F_{\sigma \rho } F^{\sigma \rho } \right) . \end{aligned}$$
(8)

And the radiation angular momentum, which is also the radiated electromagnetic torque, is calculated via the surface integral related to the spatial part of energy–momentum tensor at spatial infinity,

$$\begin{aligned} N^i= & {} - \oint _{S_{r \rightarrow \infty }} {\hat{r}}^j \mathrm{{d}}^2 \sigma \left( \epsilon ^i_{ k l} r^k T^l_j \right) \nonumber \\= & {} - \lim _{r \rightarrow \infty } \frac{1}{4 \pi } \oint _{S_r} \frac{r^j}{r} r^2 \mathrm{{d}} \varSigma \epsilon ^i_{ k l} r^k \left( \left\langle \mathrm{{Order} \mathrm {of} } \left( \frac{1}{r^2} \right) \right\rangle \right. \nonumber \\&\left. + \left\langle \mathrm{{Order} \mathrm {of} } \left( \frac{1}{r^3} \right) \right\rangle +{\mathcal {O}} \left( \frac{1}{r^4} \right) \right) \nonumber \\= & {} - \lim _{r \rightarrow \infty } \frac{1}{4 \pi } \oint _{S_r} \mathrm{{d}} \varSigma \left( 0 + r \epsilon ^i_{ k l} x^k x^j \left\langle \mathrm{{Order} \mathrm {of}} \frac{1}{r^3} \right\rangle \right) \nonumber \\= & {} - \frac{2}{3 c^3} (\dot{{\varvec{m}}} {\varvec{\times }} \ddot{{\varvec{m}}})^i - \frac{1}{c^5} \left( \frac{8}{15} a^i \dot{{\varvec{m}}} {\varvec{\cdot }} ({\varvec{a}} {\varvec{\times }} {\varvec{m}})^i \right. \nonumber \\&\left. + \frac{4}{15} {\varvec{a}} \cdot {\varvec{m}} ({\varvec{a}} {\varvec{\times }} \dot{{\varvec{m}}})^i - \frac{6}{5} {\varvec{a}} \cdot \dot{{\varvec{m}}} ({\varvec{a}} \times {\varvec{m}})^i \right. \nonumber \\&\left. - \frac{2}{15} \dot{{\varvec{a}}} \cdot {\varvec{m}} ({\varvec{a}} \times {\varvec{m}})^i - \frac{4}{15} (\dot{{\varvec{a}}} \times {\varvec{a}})^i m^2 \right) . \end{aligned}$$
(9)

The formula can be obtained without any ambiguities, although the calculation might be a bit cumbersome. Checking the case that \(a = {\dot{a}} = 0\), one can obtain the canonical spin-down equation using the radiation torque. And the braking index of the canonical spin-down is always 3. In the case that the acceleration \(\frac{a}{c\varOmega } \lesssim 1 \) and \(\frac{{\dot{a}}}{c\varOmega ^2} \lesssim 1\), the radiation energy of pulsars would not be affected too much. It would be shown in the next section that the accelerations of the case could still affect braking indices of pulsars in our model.

3 Braking index of accelerated pulsars

The spin-down equation describes time evolution of the rotation of a pulsar. In this section, we would construct a modified spin-down equation for an accelerated pulsar and study the corresponding braking indices.

Using conservation law of the energy momentum tensors, we know that loss of rotational angular momentum equals to the radiated electromagnetic torque. The modified spin-down equation is established as,

$$\begin{aligned} I \dot{{\varvec{\varOmega }}}= & {} {\varvec{N}}. \end{aligned}$$
(10)

For simplicity, we assume that the rotational magnetic dipole of a pulsar satisfies the equation,

$$\begin{aligned} \dot{{\varvec{m}}}= & {} {\varvec{\varOmega \times m}}, \end{aligned}$$
(11)

which means a pure rotation. For pulsars with companions, \({\dot{a}} \sim | P_b {\varvec{\times a}} | \ll a \varOmega \), where \(P_b\) is orbit period. In the torque Eq. (9), the \({\dot{a}}\) term is shown to be unimportant. Thus, we assume the pulsars undergoing nearly uniform accelerations. The electromagnetic torque is of the form,

$$\begin{aligned} {\varvec{N}}= & {} - \frac{2}{3 c^3} {\varvec{{\dot{m}} \times \ddot{m}}} \nonumber \\&- \frac{1}{c^5} \left( \frac{8}{15} {\varvec{a}}({\varvec{{\dot{m}} \cdot }} ({\varvec{a \times m}})) + \frac{4}{15} {\varvec{a \cdot m}} ({\varvec{a \times {\dot{m}}}}) \right. \nonumber \\&\left. - \frac{6 }{5} {\varvec{a \cdot {\dot{m}}}} ({\varvec{a \times m}}) \right) . \end{aligned}$$
(12)

Using the electromagnetic torque, we can write the modified spin-down equation as,

$$\begin{aligned} I {\varvec{{\dot{\varOmega }}}}= & {} - \frac{2}{3 c^3} {\varvec{{\dot{m}} \times \ddot{m}}} \nonumber \\&- \frac{1}{c^5} \left( \frac{8}{15} {\varvec{a}}({\varvec{{\dot{m}} \cdot }} ({\varvec{a \times m}})) + \frac{4}{15} {\varvec{a \cdot m}} ({\varvec{a \times {\dot{m}}}}) \right. \nonumber \\&\left. - \frac{6 }{5} {\varvec{a \cdot {\dot{m}}}} ({\varvec{a \times m}}) \right) . \end{aligned}$$
(13)

With the modified spin-down equation, we can calculate the braking index,

$$\begin{aligned} n= & {} \frac{| {\varvec{\varOmega }} | \frac{\mathrm{{d}}^2}{\mathrm{{d}} \tau ^2} | {\varvec{\varOmega }} |}{\left( \frac{\mathrm{{d}}}{\mathrm{{d}} \tau } | {\varvec{\varOmega }} | \right) ^2} = \frac{\varOmega ^2}{({\varvec{{\dot{\varOmega }} \cdot \varOmega }})^2} \frac{\mathrm{{d}}}{\mathrm{{d}} \tau } ({\varvec{{\dot{\varOmega }} \cdot \varOmega }}) - 1, \end{aligned}$$
(14)

where \(| {\varvec{\varOmega }} | \equiv \varOmega \). In principle, the braking index can be obtained by using Eqs. (11), (13) and (14). For the sake of intuition, we here would choose representable cases to tell the story. In these cases, the accelerations of pulsars are chosen to be parallel or vertical to the direction of rotation axes of pulsars.

3.1 Accelerations of pulsars parallel to direction of rotation axes

For the pulsars whose accelerations are parallel to the direction of \(\varOmega \), the modified spin-down equations can be simplified as,

$$\begin{aligned} {\varvec{{\dot{\varOmega }}}}= & {} - \frac{2}{3 I c^3} {\varvec{\varOmega }} ({\varvec{\varOmega \times m}})^2 - \frac{1}{I c^5} \left( \frac{8}{15} {\varvec{a}} ({\varvec{\varOmega \times m}}) {\varvec{\cdot }} ({\varvec{a \times m}}) \right. \nonumber \\&\left. + \frac{4}{15} ({\varvec{a \cdot m}}) ({\varvec{a \times }} ({\varvec{\varOmega \times m}})) \right) . \end{aligned}$$
(15)

The modified spin-down equation can be rewritten as,

$$\begin{aligned} {\dot{\varOmega }}= & {} - \frac{2}{3 I c^3} \varOmega ({\varvec{\varOmega \times m}})^2 \nonumber \\&- \frac{8}{15 I \varOmega c^5} ( {\varvec{a \cdot \varOmega }}) ({\varvec{\varOmega \times m}}) {\varvec{\cdot }} ({\varvec{a \times m}}) \nonumber \\= & {} - \frac{\varOmega m^2 \sin ^2 \theta }{I c^3} \left( \frac{2}{3} \varOmega ^2 + \frac{8 a^2}{15 c^2} \right) . \end{aligned}$$
(16)

In the case of \(a = 0\), the Eq. (16) reduces to the canonical spin-down equation (1). The magnetic inclination angle evolves with time satisfying the equation,

$$\begin{aligned} {\dot{\theta }} = \frac{\mathrm{{d}}}{\mathrm{{d}} \tau } \left( \arccos \left( \frac{\varOmega \cdot m}{\varOmega m} \right) \right) = \frac{4}{15 I c^5} a^2 m^2 \cos \theta \sin \theta .\nonumber \\ \end{aligned}$$
(17)

The differential equation can be solved analytically. Solution is of the form,

$$\begin{aligned} \cot \theta= & {} \cot \theta _0 e^{- \frac{4}{15} k b^2 \tau }, \end{aligned}$$
(18)

where \(k \equiv \frac{m^2}{I c^3} \mathrm{{and}} b \equiv \frac{a}{c}\). They are both constant parameters in our models. The Eq. (18) shows that the magnetic inclination angle evolves towards \(\theta = \frac{\pi }{2}\). The accelerations of this case could be the causes of oblique rotation of pulsars. Using Eqs. (14), (16) and (17), we obtain the braking indices,

$$\begin{aligned} n= & {} 3 - 2 \left( \frac{b}{\varOmega } \right) ^2 \left( \frac{1 + \frac{\cot ^2 \theta }{2}}{\frac{5}{4} + \left( \frac{b}{\varOmega } \right) ^2} \right) . \end{aligned}$$
(19)

In this case, the braking indices can’t be larger than 3. In the Fig. 2, we plot the braking index \(n (b, \theta )\) as function of acceleration b for fixed magnetic inclination angle \(\theta \). The braking indices decrease with the accelerations of pulsars. And the braking indices drop to a minimum value as the acceleration tends to infinity.

$$\begin{aligned} \lim _{b \rightarrow \infty } n= & {} 1 - \cot ^2 \theta . \end{aligned}$$
(20)
Fig. 2
figure 2

The braking indices are functions of accelerations of pulsars for fixed magnetic inclination angle. The accelerations of pulsars are parallel to direction of rotation axes

Full size image

In Fig. 3, we plot the braking index \(n (b, \theta )\) as function of magnetic inclination angle \(\theta \) for fixed acceleration b. It shows that the influence of acceleration would become significant, if the pulsars have small magnetic inclination angle. With the accelerations of this case, the large braking index can hardly be obtained.

Fig. 3
figure 3

The braking indices are functions of magnetic inclination angle for fixed acceleration. The accelerations of pulsars are parallel to direction of rotation axes

Full size image

3.2 Accelerations of pulsars vertical to direction of rotation axes

The other case is that the accelerations of pulsars are vertical to the direction of \(\varOmega \). In the case, the modified spin-down equation can be simplified as,

$$\begin{aligned} I {\varvec{{\dot{\varOmega }}}}= & {} - \frac{4 m^i}{9 I c^8} ({\varvec{\varOmega \cdot m}}) \alpha \beta - \frac{2}{3 c^3} {\varvec{\varOmega }} ({\varvec{\varOmega \times m}})^2 \nonumber \\&- \frac{1}{c^5} \left( - \frac{8}{15} {\varvec{a}} ({\varvec{\varOmega \cdot m}}) \alpha + \frac{4}{15} {\varvec{ \varOmega }} \alpha ^2 \right. \nonumber \\&\left. - \frac{6}{5} ({\varvec{a \times m}}) \beta \right) , \end{aligned}$$
(21)

where \(\alpha \equiv {\varvec{a \cdot m}}\), \(\beta \equiv {\varvec{a \cdot }} ({\varvec{\varOmega \times m}})\). The modified spin-down equation can be rewritten as,

$$\begin{aligned} {\dot{\varOmega }}= & {} - \frac{2 k}{3} \left( \frac{2}{3} k \left( \frac{b}{\varOmega } \right) ^2 \cos ^2 \theta {\hat{\alpha }} {\hat{\beta }} + \sin ^2 \theta \right) \varOmega ^3 \nonumber \\&- k b^2 \left( \frac{6}{5} {\hat{\beta }}^2 + \frac{4}{15} {\hat{\alpha }}^2 \right) \varOmega , \end{aligned}$$
(22)

where \({\hat{\alpha }} \equiv \frac{{\varvec{a \cdot m}}}{a m}\) and \({\hat{\beta }} \equiv \frac{{\varvec{a \cdot }} ({\varvec{\varOmega \times m}})}{a \varOmega m}\). For pulsars with \(\varOmega \sim 1 s^{- 1}\) and \({\dot{\varOmega }} \lesssim 10^{- 10} s^{- 2}\), it’s reasonable to use an approximation that \(k \varOmega \equiv \frac{m^2 \varOmega }{I c^3} \lesssim \frac{{\dot{\varOmega }}}{\varOmega ^2} \ll 1\). In the approximation, the modified spin-down equation can be simplified further as,

$$\begin{aligned} {\dot{\varOmega }}= & {} - \frac{2}{3} k \sin ^2 \theta \varOmega ^3 - k b^2 \left( \frac{6}{5} {\hat{\beta }}^2 + \frac{4}{15} {\hat{\alpha }}^2 \right) \varOmega . \end{aligned}$$
(23)

The magnetic inclination angle evolves with time satisfying the differential equation as follows,

$$\begin{aligned} {\dot{\theta }}= & {} - \frac{k b^2}{\tan \theta } \left( \frac{8}{15} {\hat{\alpha }}^2 - \frac{6}{5} {\hat{\beta }}^2 \right) . \end{aligned}$$
(24)

In the approximation, \({\hat{\alpha }}\) and \({\hat{\beta }}\) seem like trigonometric functions, since the differential equations referred to \({\hat{\alpha }}\) and \({\hat{\beta }}\) are given by

$$\begin{aligned} \dot{{\hat{\alpha }}}= & {} \varOmega {\hat{\beta }}, \end{aligned}$$
(25)
$$\begin{aligned} \dot{{\hat{\beta }}}= & {} - \varOmega {\hat{\alpha }}. \end{aligned}$$
(26)

The rotation velocity \(\varOmega \) of pulsars can be solved numerically with Eqs. (23)–(26) in principle. Fortunately, what we focus is the braking index, which can be obtained without solving these differential equations,

$$\begin{aligned} n= & {} \frac{21}{5} \frac{ b^2}{k \varOmega ^3} \frac{{\hat{\alpha }} {\hat{\beta }}}{\left( \sin ^2 \theta + \frac{3}{2} \left( \frac{b}{\varOmega } \right) ^2 \left( \frac{6}{5} {\hat{\beta }}^2 + \frac{4}{15} {\hat{\alpha }}^2 \right) \right) ^2} \nonumber \\&+ 3 + \left( \frac{b}{\varOmega } \right) ^2 f \left( \frac{b}{\varOmega }, \theta \right) +{\mathcal {O}} (k \varOmega ), \end{aligned}$$
(27)

where \(f \left( \frac{b}{\varOmega }, \theta \right) \sim 1\). The function f turns to be unimportant for the most situations, since \((k \varOmega )^{- 1} \gg 1\). The most interesting is that the positive or negative of n depends on \({\hat{\alpha }}\) and \({\hat{\beta }}\), which are related to position of pulsars and direction of the acceleration. Using Eqs. (25) and (26), we can obtain that \({\hat{\alpha }} = \sin \phi \) and \({\hat{\beta }} = \cos \phi \) approximately, where \(\phi \approx \varOmega \tau \). It leads to value of braking indices around the order of magnitude of \(\frac{b^2}{k \varOmega ^3}\). We rewrite the braking index in the term of \(b, \theta , k\) and \(\phi \) without the unimportant terms,

$$\begin{aligned} n= & {} \frac{21}{5} \frac{ b^2}{k \varOmega ^3} \frac{\sin \phi \cos \phi }{\left( \sin ^2 \theta + \frac{3}{2} \left( \frac{b}{\varOmega } \right) ^2 \left( \frac{6}{5} \cos ^2\phi + \frac{4}{15} \sin ^2\phi \right) \right) ^2} \nonumber \\&+ 3. \end{aligned}$$
(28)
Fig. 4
figure 4

The braking indices are functions of acceleration b for fixed magnetic inclination angle \(\theta \), moment of inertia, magnitude of magnetic dipole and \(\phi \). The accelerations of pulsars are vertical to direction of rotation axes

Full size image

In Fig. 4, we plot the \(n (b, \theta , k, \phi )\) as function of the acceleration b for fixed \(\theta , k\) and \(\phi \). The braking indices can be different from 3 when the acceleration \(a \approx 1 m \cdot s^{- 1}\). It indicates that the braking indices are more sensitive to the acceleration whose directions are vertical to the rotation velocity of pulsars. And in this case, the absolute value of braking indices increase with the acceleration. In Fig. 5, we plot the \(n (b, \theta , k, \phi )\) as function of the magnetic inclination angle \(\theta \) for fixed b, k and \(\phi \). It shows that the acceleration affect braking indices more apparently for alignment pulsars. The braking indices are also related to the k, namely, moment of inertia and magnetic dipole of pulsars. Pulsars with larger moment of inertia or smaller magnetic dipole would have larger braking indices.

Fig. 5
figure 5

The braking indices are functions of magnetic inclination angle \(\theta \) for fixed acceleration b, moment of inertia and magnitude of magnetic dipole and \(\phi \). The accelerations of pulsars are vertical to direction of rotation axes

Full size image

3.3 Order of magnitude estimation for the accelerations

It has been shown that the large braking index can be caused by acceleration of a pulsar in our model. In this section, we would provide the order of magnitude estimation of the acceleration. In the estimation, we assume that deviation of braking indices is completely caused by acceleration of pulsars. The pulsar timing data comes from ATNF pulsar catalogue.

When the direction of acceleration is vertical to the rotation velocity of pulsars, the braking indices can be changed more apparently than the other case. Therefore, we use Eq. (26) to estimate the accelerations of pulsars. As \(| {\hat{\alpha }} | \lesssim 1, | {\hat{\beta }} | \lesssim 1\) and \(| \sin \theta | \lesssim 1\), they turn to be unimportant for the braking index in the order of magnitude. The approximated Eq. (26) is reduced to the form,

$$\begin{aligned} | n - 3 |\approx & {} \frac{b^2}{k \varOmega ^3} . \end{aligned}$$
(29)

We consider the case that \(\frac{b}{\varOmega } \ll 1\), which leads to \(k \varOmega ^3 \approx {\dot{\varOmega }}\). In the approximation, we could estimate acceleration of pulsars completely with the pulsar timing data. The accelerations can be expressed as function of n and \(\varOmega \),

$$\begin{aligned} a\approx & {} c \sqrt{| (n - 3) {\dot{\varOmega }} |} . \end{aligned}$$
(30)
Fig. 6
figure 6

Cumulative distribution of estimated acceleration for the 32 pulsars with companions

Full size image

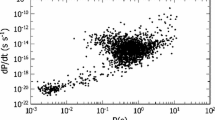
In Fig. 6, the accelerations of 32 pulsars with companions are shown. The estimated acceleration a ranges from \(10^2\) to \(10^6\) \(\mathrm {m\cdot s^{-2}}\). For most of binary systems, pulsars have accelerations around \(10^4 \mathrm {m\cdot s^{-2}}\). It’s the order of magnitude far away from the event horizon of black hole. In our model, the acceleration is covariant and involves the friction force. In the frame of a moving pulsar, one can show that the friction force equal to external force always. Thus, our results on acceleration could indicate the external force, maybe gravity we expected, experienced by pulsars. The estimated accelerations for the 441 pulsars are shown in Fig. 7. For the pulsars with braking indices less than 100, the braking index seems not correlation with acceleration. It indicates that, for the small braking indices, there might be other effect for the deviated braking indices as reviewed in the introduction. For larger braking indices, the accelerations of pulsars have positive correlation with the braking indices overall. And the pulsars with companions tend to have larger estimated acceleration than that of the rest as we expected. Our estimation is meaningful for the case that \(a \ll c \varOmega \sim 10^8 \mathrm {m\cdot s^{-2}}\), the pulsar (in the left-top of Fig. 7) with acceleration over \(10^8 \mathrm {m\cdot s^{-2}}\) should be excluded.

Fig. 7
figure 7

Correlations between the absolute value of braking index n and the estimated acceleration a

Full size image

4 Discussions and conclusions

In this paper, we discussed the possibility that acceleration motion of a pulsar can affect its magnetic dipole radiation. In detail, we derived the modified spin-down equation and showed that the accelerations of pulsars are closely related to the braking indices. It’s consistent with the statistical results in Fig. 1 that pulsars in binary systems tend to have larger braking indices.

Here, we only considered the most simple cases that the accelerations are along specific directions. As we known, it’s not realistic. In this sense, our results are preliminary and just give an order of magnitude estimation. The braking indices could be affected by acceleration motions of pulsars, only if the accelerations are larger than 1 m s\(^{-2}\).

We used the acceleration to indicate the external force experienced by a pulsar. However, the origin of the acceleration in our model still needs to be explored further, especially, for those pulsars without being marked as binaries. For the binaries, Keplerian parameters can be used to estimate the accelerations of pulsars via orbit period and mass of companions. The data of the accelerations can be obtained from ATNF pulsar catalogue. We found that the accelerations estimated from braking indices in our results is larger than that estimated by Keplerian parameters over several orders of magnitude. Of course, the acceleration experienced by a pulsar may be a combination of gravity from normal matter, dark matter and dark energy. In the future, we can test every component of the acceleration by more accurate observations.

As suggested by Lyne et al. [6] from observations, the braking indices that are beyond 3 over several orders of magnitude seem not very reliable. There might be problems from accuracy of \(\ddot{\varOmega }\) or dependence of fitting models. And in the ATNF pulsar catalogue, there aren’t data of \(\ddot{\varOmega }\) for most pulsars. This limits us to the 441 pulsars. With more accuracy observations in the future, the studies about the lager braking indices would be more meaningful.

We calculated the braking indices in local inertial frames adapted to the 4-velocity for a pulsar. Firstly, This frame is comoving with a pulsar. Namely, there are not translation motions of pulsars in the calculation. In this situation, the radiating angular momentums are clear from physical point of view. Secondly, it neglects the changes of metric for the reference frames. In the uniformly accelerating frames, the only difference of the metric could be \(g_{00}\) compared with the metric of Minkowski space-time, such as Rindler metric. The spatial part of energy–momentum tensors are nearly the same form as that in flat space-time. It indicates that our calculation might be valid at least in the case of uniform acceleration motion for a pulsar.