Abstract
The development of long baseline neutrino oscillation experiments with accelerators in Japan is reviewed. Accelerator experiments can optimize experimental conditions, such as the beam and the detector, as needed. The evidence of neutrino oscillations observed in atmospheric neutrinos was confirmed by the K2K experiment. The T2K experiment discovered the oscillation channel from a muon neutrino to an electron neutrino with the squared mass difference \(\varDelta m^2 \sim 2.5 \times 10^{-3}~\mathrm{eV}^2\), and presents a full analysis with all three flavor states of both neutrinos and anti-neutrinos. The three mixing angles, which quantify the mixing of the three neutrino states, have been measured. They are large compared to those of quarks, especially the mixing of the second and third generation which is nearly maximal. The T2K experiment has an ongoing program producing new results, and recently has shown a hint of CP violation in neutrinos. Future generation long baseline neutrino experiments beyond T2K are expected to clarify the relationship between flavor and mass, as well as measure possible CP violation in neutrino oscillations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Historical overview
The question of whether neutrinos are massless or massive has fascinated physicists for many years, for several reasons. Neutrino mass must be very small compared to other fermions, such as quarks and charged leptons. It has been known for decades that their masses had tight upper limits, but there was no compelling reason for them to be massless. On the contrary, the See–Saw mechanism naturally explains the extremely small neutrino mass by introducing ultra-high energy physics. Even further, without Grand Unification, finite Majorana neutrino masses are required for Baryogenesis in the universe [1].
From the point of view of Cosmology, a large mass of dark matter is required in the universe. In the 1990s, neutrinos with mass near the eV scale were thought to be a candidate of dark matter; due to the large number of primordial neutrinos expected in the Big Bang, massive neutrinos could have made up the critical mass of the universe. Later precision measurements of cosmic background radiation have shown that the dominant part of dark matter cannot be neutrinos [2, 3].
From the point of view of flavor physics, finite neutrino masses imply relationships between mass and flavor in analogy to the quark sector. In the quark sector, the corresponding studies have led to the Kobayashi–Maskawa theory of CP violation in neutral kaons.
During the late 1980s until early 1990s, there was a long-standing puzzle of deficiency of solar neutrinos, reported by the Homestake chlorine experiment [4]. The cause of the observed deficiency was not clear: it could have been due to problems in solar physics or problems in neutrino physics. In solar physics, the expected solar neutrino flux detected in the chlorine experiment was not from the main pp-chain fusion, but resulted from several nuclear reactions in the Sun. The prediction of neutrino rate depended on aspects of solar models and nuclear physics which might have missing pieces. The puzzle initiated a huge activity [5] with many experiments launched to study the solar neutrino flux in various energy regions, especially those from the main pp-chain fusion, where the neutrino flux can be predicted from thermal energy production with far fewer ambiguities. Neutrino oscillations were another possibility in neutrino physics. Finite neutrino mass introduces mass eigenstate of neutrinos in addition to the flavor eigenstates (\(\nu _e\), \(\nu _{\mu }\), and \(\nu _{\tau }\)), which correspond to the three kinds of charged leptons (e, \(\mu \), \(\tau \)). Co-existence of mass- and flavor-eigenstates causes neutrino oscillation, an analogous situation to the neutral kaon system, where co-existence of strangeness eigenstates (\(K^0\), \(\bar{K^0}\)) and mass eigenstates (\(K_L\), \(K_S\)) causes \(K^0 - \bar{K^0}\) oscillation. If \(\nu _e\) states from the sun change to other types of neutrinos (\(\nu _\mu \), \(\nu _\tau \)), the flux of \(\nu _e\) is reduced and \(\nu _\mu \) and \(\nu _\tau \) can only interact with electrons by neutral current interaction which has a much smaller rate, thus the observed deficiency of \(\nu _e\) can be explained. The solar neutrino deficiency suggests, if it is due to neutrino oscillation, the neutrino mass scale is much smaller than the eV scale. To study this mass scale, the experiment needs to have a long distance from the neutrino creation to its detection, due to slow oscillation. On the other hand, a neutrino scenario of dark matter requires masses near the eV scale. Because of the short oscillation length (\(\sim km\) scale for the mass square difference of \(\mathrm eV^2\) with neutrino energy of GeV), studies near the eV scale require high rejection power of \(\nu _{\mu }\) to look for small components of oscillation production in a \(\nu _{\mu }\) beam, since the wrong flavor components (other than \(\nu _{\mu }\)) in an accelerator neutrino beam are already known to be small. Short baseline experiments have been pursuing this direction [6, 7].
In 1988, the Kamiokande collaboration reported their first result on the atmospheric neutrino flux and showed a deficiency of the muon neutrinos (\(\nu _{\mu }\)), compared to the electron neutrino (\(\nu _e\)) events [8]. This could be interpreted as an indication of neutrino oscillation or could be due to an unknown cosmic ray process in the atmosphere, such as a process to produce more \(\nu _e\) than ordinary \(\pi \) and K production. Further studies were reported showing that the deficiency of \(\nu _{\mu }\) exists for neutrinos [9, 10], which comes from the direction below the horizon, which corresponds to a neutrino flight path between their creation and detection is on the order of 100 km. One of the critical measurements is to see that \(\nu _{\mu }\) from an accelerator shows the deficiency under similar conditions. This requires about 100 km baseline with a GeV neutrino beam, looking for the disappearance of \(\nu _{\mu }\).
The concept of a long baseline neutrino oscillation experiment with an accelerator neutrino beam was discussed by Masatoshi Koshiba at “A workshop for High Intensity facility in 1988” at Breckenridge, Colorado. This workshop was primarily concerned with the physics program at Fermilab in 1990, using the high intensity Main Injector accelerator. He discussed a large area water Cherenkov detector to extend high energy neutrino astronomy after discovering neutrinos from Supernova 1987A and using this detector as a far detector of a long baseline experiment with the FNAL Main Injector [11].
In Japan, construction of Super-Kamiokande started in 1991, with commissioning expected to begin in 1996, to extend various physics topics which were pioneered by the Kamiokande experiment. Super-Kamiokande has been one of the most massive detectors in the world with excellent detection capability of muons and electrons. There was also a 12 GeV proton synchrotron at KEK in Tsukuba, which was 250 km away from Kamioka. It was built in 1976 and the first high energy proton accelerator built in Japan after World War II. The 12 GeV proton energy was achieved through strong hard efforts by pioneering Japanese high energy physicists. Yoji Totsuka was leading the studies of neutrinos at Super-Kamiokande also with an accelerator beam, in addition to the cosmic neutrinos. He was the central figure of the K2K and T2K experiments from the very beginning as spokesperson of Super-Kamiokande and later as Director General of KEK. This was the starting point of the neutrino oscillation experiments with accelerator beams in Japan.
1.2 Neutrino oscillation formalism
Before introducing the long baseline neutrino oscillation experiments, we show the general formalism of neutrino oscillations assuming three flavors. Three types of neutrinos are assumed to have flavor eigenstates denoted by (\(\nu _e\), \(\nu _\mu \), \(\nu _\tau \)) and mass eigenstates denoted by (\(\nu _1\), \(\nu _2\), \(\nu _3\)). The flavor eigenstates are related to mass eigenstates by the 3x3 unitary matrix U,
The neutrino mixing matrix U can be parameterized by three angles (\(\theta _{12}\), \(\theta _{13}\), \(\theta _{23}\)) and one CP violation phases (\(\delta _{CP}\)) assuming a neutrino as a Dirac particle:
where \(c_{ij} = \cos \theta _{ij}\) and \(s_{ij} = \sin \theta _{ij}\).
Long baseline neutrino oscillation experiments with accelerators use a muon neutrino beam from a proton synchrotron. We study neutrino oscillation probabilities from muon neutrinos: \(P(\nu _\mu \rightarrow \nu _\mu ) \) in the disappearance channel and \(P(\nu _\mu \rightarrow \nu _e) \) in the appearance channel.
In the disappearance channel, the probability is expressed as
where L is the travel distance of the neutrino (baseline), E is the neutrino energy, and \(\varDelta m^2_{eff}\) incorporates effective leading dependences on the additional parameters \(\varDelta m^2_{21}\), \(\theta _{13}\), and \(\delta _{CP}\) as
Equation 2 can be rewritten to yield a form appropriate for the K2K and T2K experiments,
When a neutrino travels in the earth, it feels the potential of matter, by which the oscillation probability is affected. The matter effect serves to determine the so-called neutrino mass hierarchy, which is related to the sign of \(\varDelta m^2_{32(1)}\). In a long baseline experiment, the matter effect is not detectable in the disappearance channel, but in the appearance channel.
In the appearance channel, the oscillation probability in an approximate condition with energy \(E_\nu \) of \(O(1)\ \mathrm{GeV}\) traveling a distance of O(100) km is expressed [12, 13] as
where \(\varDelta _{ij}=\frac{\varDelta m^2_{ij} L}{4E_{\nu }}\), \(\alpha =\frac{\varDelta m^2_{12}}{\varDelta m^2_{31}} \sim 0.03\), \(A=\pm \frac{2E_{\nu }V}{\varDelta m^2_{31}}\sim \frac{E_{\nu } [\mathrm{\mathrm GeV}] \rho [\mathrm{\mathrm g}/\mathrm{cm}^3]}{30}\), V is a matter potential, and \(\rho \) is the earth density. With large \(\theta _{13}\) the dominant contribution is due to the first term, which depends also on \(\sin ^2\theta _{23}\). This dominant term can be calculated with \(\theta _{13}\) from reactor measurements and the \(\sin ^22\theta _{23}\) value from disappearance measurements. There is a two-fold ambiguity in \(\sin ^2\theta _{23}\), unless \(\theta _{23}=\pi /4\). The sign of the second term changes between neutrinos and anti-neutrinos, governing CP violation. The magnitude of CP violation is determined by the Jarlskog invariant [14]
The CP violating term is the interference of the oscillation amplitudes of \(\varDelta m^2_{23}\) and \(\varDelta m^2_{12}\). With the current best knowledge of oscillation parameters, the CP violation (second term) can be as large as \(\sim 30\)% of the first term.
The matter effects generate A dependence. The matter effect induces an effective neutrino mass to the \(\nu _e\) component and modifies the effective mixing angle for neutrinos propagating in matter. As a result, the oscillation length and effective mixing angle depend on the baseline. We call \(\varDelta m^2_{32} > 0\) as the normal mass hierarchy and \(\varDelta m^2_{32} < 0\) as the inverted one. The effect is an increased oscillation probability with the normal mass hierarchy for neutrinos. In the case of anti-neutrinos, it happens with the inverted hierarchy. In principle, measurements of the \(\nu _{e}\) appearance probability at two distances with the same L/E can isolate the matter effect.
2 The K2K experiment
2.1 Atmospheric neutrino anomaly observed in water Cherenkov detectors
Results on atmospheric-neutrinos available before K2K are summarized in Table 1. The quantity \((\mu /e)_{exp}\) is the ratio of muons to electrons produced by atmospheric neutrinos with energies of the order of a GeV, and measures the flux ratio of \(\nu _{\mu }\) to \(\nu _e\) to be compared with the Monte Carlo prediction, \((\mu /e)_{MC}\). In addition to the Kamiokande result [9], the IMB experiment [15], which used a water Cherenkov, has also an indication of the \(\nu _{\mu }\) deficit. On the other hand, results of tracking detectors FREJUS [16] and NUSEX [17] are consistent with the predictions, though they suffered from low statistics. The results from SOUDAN [18, 19] were still preliminary in 1995.
One explanation of the anomaly was that there was a problem with water Cherenkov separation of muons and electrons. For this reason, before proposing a long baseline neutrino experiment, the particle identification capability in the water Cherenkov detector was tested by a charged particle beam at KEK. The lepton identification is based on the sharpness (or fuzziness) of the Cherenkov ring image. Figure 1 shows a sample of single Cherenkov-ring events in K2K. The particle identification capability of the water Cherenkov detector was addressed by a test experiment with a charged particle beam at KEK-PS [20]. The investigated momentum region was between 100 and 500 MeV/c.
An event with a single \(\mu \)-like Cherenkov ring (top) and an event with an electro-magnetic shower-like ring (bottom) observed in K2K. The detector is a cylinder, lined with photomultiplier tubes. The center projection (unrolled cylinder) is the inner tank surface, and the projection in the upper left corner is the outer detector
A prototype water Cherenkov detector was set at the KEK PS K6 beamline in which charged particles were provided. Figure 2 shows the K6 beamline and the location of the detector. The K6 beamline consists of two bending magnets (D2, D3) and focusing quad magnets (Q7, Q8) with TOF and gas Cherenkov detectors for particle identification of the charged beam. This beamline provided the low energy secondary charged particles: pions, muons, and electrons with energies between 100 and 500 MeV, for the test of the water Cherenkov detector. An electron was identified by the time of flight (TOF) and gas Cherenkov detectors. A muon was identified by setting the second bending magnets to about 1/2 of the first bending magnet since the muon, which was emitted backward in the \(\pi \) rest frame, has an energy of \(m_{\mu }^2/m_{\pi }^2\times E_{\pi } \sim 0.5 E_{\pi }\). Figure 3 shows the TOF distribution at 500 MeV/c.
Figure 4 shows e-likelihood and \(\mu \)-likelihood at similar total Cherenkov light and Fig. 5 shows the result of misidentification probabilities for \(e\rightarrow \mu \) and \(\mu \rightarrow e\). It is evident that the mis-identification probabilities of about 1% level, are much smaller than the reported anomaly in atmospheric neutrino observations.
2.2 The oscillation physics to be explored by K2K
Kamiokande also measured the zenith angle dependence of the ratio \((\mu /e)_{exp}/(\mu /e)_{MC}\) for high energy neutrinos, where knowledge of the absolute initial flux was not necessary [10]. This is consistent with the picture where the different path lengths of the upward- and downward-going neutrinos produce different oscillation length. Figure 6 shows the path length of the neutrino from the creation in the atmosphere to the detection as a function of the zenith angle. The upward events are the interactions of neutrinos, which travel a substantial fraction of the earth diameter. On the other-hand, the downward events corresponding to neutrinos, which travel a distance on the order of an atmosphere thickness of several km. Figure 7 shows the ratio of \((\mu /e)_{exp}/(\mu /e)_{MC}\) as a function of the cosine of the zenith angle. Assuming 2-flavor mixing, the oscillation probability (P) from one neutrino to the other type is given by
Zenith angle distribution and comparison with an expectation without oscillation [10]
where E is the neutrino energy and L is the travel distance of the neutrino (baseline). Considering the fact that the dominant part of the atmospheric neutrinos are between sub-GeV and several GeV and the fact that the indicated deficiency starts near the horizon, the parameter region to be explored was in the \(\varDelta m^2\) region between \(10^{-2}\) and \(10^{-3}~\mathrm{eV}^2\). Also, the amount of the deficit increased as the zenith angle increased, to almost 0.5; this indicates a large neutrino mixing angle, \(\sin ^22\theta \sim 1\). The allowed parameter region under the assumption of neutrino oscillation is shown in Fig. 8 by Kamiokande [10]. The proposed accelerator-based experiment must be sensitive to small \(\varDelta m^2\) and look for a rather large effect, as opposed to accelerator programs searching for eV mass scales which require high background rejection. Instead, it required the highest possible intensity and the highest possible detector mass, since the event rate decreases as \(1/L^2\).
The 90% CL allowed neutrino-oscillation parameters as obtained from the multi-GeV data (thick curves). The allowed regions as obtained from the sub-GeV data are also shown by thick-dotted curves. The allowed regions as obtained by combining the sub- and multi-GeV data are also shown (shaded region). The best fit values are also shown by dash-crosses (sub-GeV data), full-crosses (multi-GeV data) and stars (sub- and multi-GeV data combined). The 90% CL excluded regions from the other experiments are also shown [10]
A feasibility study of the KEK-PS upgrade was performed in 1992–1993 [21]. The most critical aspect of the upgrade was to decrease beam losses, especially at the injection point and crossing transition energy point, to ensure sufficiently low radio-activity of the beam line. An important improvement was the introduction of white noise at the injection to ease the space charge effect. The planned upgrade of KEK-PS was achieved by rigorous efforts of the KEK accelerator department. Figure 9 shows the performance of the KEK-PS during the K2K experiment. The proton intensity per pulse was increased in the upgrade by more than a factor of two and the repetition rate was shortened to 0.5 Hz as shown in the feasibility study. In 5 years, it was possible to accumulate \(10^{20}\) protons on target.
The number of protons delivered to the production target in the period from June 1999 to November 2004. The horizontal axis corresponds to the date. The upper figure shows the total number of protons on target (POT) accumulated since June 1999, and the lower figure shows the per spill averaged in a day. In total, \(104.90\times 10^{18}\) protons were delivered during the entire period [22]
In the proposal, the flux was estimated, using the Sanford-Wang parametrization for the pion production cross section. The GHEISHA [23] package has been used for secondary interactions of produced pions in the material (target, horn, and air, etc.). This calculation was compared with the observed neutrino flux at BNL E734 [24] simulating their experimental setup. Without oscillation effects, 500 charged-current (CC) events were expected in the 22.5 kton fiducial volume of the Super-Kamiokande detector with \(10^{20}\) protons-on-target (POT), while in the near detector with a 1.7 ton fiducial volume, 8000 CC events were expected.
The KEK to Kamioka long-baseline neutrino oscillation experiment (K2K) was proposed in April 1995 [25, 26] and approved in 1996 at KEK as cooperation of three organizations: KEK, ICRR, and INS. The K2K collaboration started with three countries: Japan, the USA and Korea, and later included Canada, France, Italy, Poland, Russia, Spain, and Switzerland. The construction completed in 1999. Data were accumulated from 2000 to 2005. The complete description of the experiment can be found in the K2K final paper [22]. The experiment was proposed to be sensitive to the oscillations, \(\varDelta m^2 \ge 3\times 10^{-3} \mathrm{eV}^2\) and \(\sin ^22\theta \ge 0.1\), at more than the \(3\sigma \) confidence level. The goals were: (1) confirm the disappearance of \(\nu _{\mu }\) in accelerator neutrinos with similar distance and energy as Kamiokande atmospheric neutrino results and (2) to show the deficiency is due to neutrino oscillation. This could be shown by the energy dependence of the disappearance rate. The neutrino energy could be reconstructed by using charged current quasi-elastic neutrino interaction \(\nu _{\mu }+n\rightarrow \mu +p\) with two-body kinematics. With proper beam monitoring, it can be shown that either the \(\nu _{\mu }\) flux is decreased and/or the \(\nu _e\) flux is increased. If the \(\nu _{\mu } \rightarrow \nu _e\) oscillation causes the atmospheric neutrino anomaly, the \(\nu _{\mu }\) flux will be decreased and the \(\nu _e\) flux will be increased. With \(\nu _{\mu } \rightarrow \nu _{\tau }\) oscillation, the \(\nu _{\mu }\) flux would reduce while keeping the \(\nu _e\) flux unchanged.
2.3 K2K experimental design principle and challenges
The experimental principle of long baseline neutrino experiments with an accelerator beam and Super-Kamiokande, is summarized in this section.
Super-Kamiokande is the most massive neutrino detector in the world. The cosmic-ray background, which is especially difficult in a low counting-rate experiment, is negligible thanks to the underground site of the detector; there is no need for sending timing signals over long distances. The synchronization with the accelerator is required only in the analysis stage in terms of a common timing signal recorded at KEK and at Super-Kamiokande by a GPS time stamp at both locations.
The neutrino beam energy expected from KEK-PS is well suited to the Water-Cherenkov detector technique. Since the neutrino beam energy is typically 1 GeV, a large fraction of the neutrino reactions are either quasi-elastic or single-pion production, which are easily identified in a water-Cherenkov detector. An electron, which is the signal for \(\nu _{\mu }\rightarrow \nu _e\) oscillations, can be identified in the low-energy region, thanks to the small \(\pi ^0\) energy and low multiplicity of the events. Also, we do not expect hadronic jets that would otherwise swamp the electron signal.
In an accelerator beam compared to atmospheric neutrino production, the decay volume to produce neutrinos from \(\pi \) and K decays is much smaller than that of atmospheric neutrinos (on the order of 10 km, the thickness of earth atmosphere). This reduces the \(\mu \) decay probability, suppresses the \(\nu _e\) component to the order of percent level and makes an almost pure (\(\sim 99\%\) purity) \(\nu _{\mu }\) beam. The other advantage compared to atmospheric neutrinos is that the initial neutrino beam, before the oscillation, can be measured by placing a detector just after its production, which can monitor the \(\nu _{\mu }\) flux and the \(\nu _e\) contamination and measure the neutrino spectrum.
The experimental challenges are as follows. The oscillation effect to be searched for is the change of the neutrino spectrum over a long distance. One of the main points of the experiment is how precisely we predict the observed quantities at a far distance with and without oscillation effects. Then, the predictions should be compared with the observation.
Three pieces of information are needed. First, the neutrino spectrum at Super-Kamiokande must be predicted reliably. Second, the cross sections for low energy neutrinos in water must be modeled properly. Figure 10 shows the compilation (by the SOUDAN collaboration) of neutrino cross section measurements (see also the recent data in [27]). Finally, the detector response to the neutrino interactions must be taken into account due to different spectrum shapes that are expected in the near and far detectors.
In principle, the neutrino spectrum can be calculated, once the \(\pi ^{\pm }\) and \(K^{\pm }\) momentum and angular distributions in the decay volume are known. However, at the time of designing K2K, \(\pi \) production data at the relevant energy regions were only available for a thin target in a limited kinematic range. The Cho model [28] (a pion production model) with the Sanford–Wang formula [23, 29] is used to parameterize data . In addition, substantial effects must be taken into account to predict the neutrino flux. First, the production target (two interaction lengths of aluminum in K2K) is thick, that causes sizeable secondary interactions. Second, the horn focusing efficiency depends on the position of meson production along the beam axis. This depends on the proton beam profile, divergence, and attenuation of proton beam due to the total absorption cross section of 12 GeV proton and the target material.
Another difficulty is that the neutrino flux at two different locations does not scale as \((1/L)^2\) where L is the distance. This is because the acceptance of the two detectors are functions of the parent meson energy (angular divergence in the decay process), decay point (geometrical acceptance), and direction (focusing is not perfect, production of mesons is via strong interaction with \(\sim \)100MeV energy spread). Thus, the ratio of the neutrino fluxes at the far and near detectors (Far/Near ratio) depends on the energy of the neutrinos.
Furthermore, in the neutrino experiment, the observable is event rates, i.e. the product of neutrino flux and cross section as a function of the reconstructed neutrino energy. The predicted neutrino cross sections suffer from ambiguities due to low energy hadronic effects of target nucleons and cannot be calculated from first principles. Both cross section and flux must be determined simultaneously in a self-consistent way as described in Sect. 2.8.
2.4 K2K experimental setup
A schematic view of the K2K experiment is shown in Fig. 11. The figure shows the \(\pi \) and K production target, horn, pion monitor, decay volume, muon monitor and near detectors (ND). After 250 km of baseline, Super-Kamiokande (SK) locates and detects the neutrino events. Figure 12 shows the neutrino beam flux at ND and SK predicted by the MC simulation. The GPS information was used for identifying the accelerator produced events in SK. The fully contained events in the fiducial volume, which are used in the oscillation analysis of K2K, are selected and reconstructed by using the same methods as have been used in the atmospheric neutrino analysis. The GPS was also used for the alignment of the 250 km long experimental setup by a long-baseline GPS survey between KEK and Kamioka. The estimated precision of the beam orientation was 0.01 mrad, based on the accuracy (1 mm) of the GPS position survey.Footnote 1 The construction precision of the beam line and detectors at the near site were about 10 mm, that resulted in a precision of the beam orientation better than 0.1 mrad.
K2K neutrino beam flux at ND (left) and SK (right) predicted by the MC simulation [22]
2.4.1 Beam line components
For studies in a wide range of \(\varDelta m^2\), a wideband beam is most suitable. K2K adopted a horn magnet system to obtain the wideband beam with the highest possible intensity. A schematic view of the horn magnets is shown in Fig. 13.
First, the horn focuses a wide angular and momentum range of pions. At low energy, the production target must be inside of the horn magnet, because of the large angular distributions of produced pions. K2K used a 2 interaction length aluminum rod as the production target of the first horn. The aluminum target was used as the inner conductor of the horn, which reduced the radial size of the horn while maintaining a high magnetic field and containing the proton beam.
A large number of secondary charged particles, mainly pions, focused by the horn system enter the decay volume and decay to muons and neutrinos (\(\pi ^+ \rightarrow \mu ^+ + \nu _\mu \)). The momentum distributions of the pions, muons and neutrinos are shown in Fig. 14.
Schematic view of the two horn magnets. An electrical current of 250 kA is supplied to both horns, creating a toroidal magnetic field inside the horns. The production target, an aluminum rod of 66 cm in length and 3 cm in diameter is embedded inside the first horn magnet, which also plays the role of the inner conductor of the horn. The second horn is located 10.5 m downstream of the first horn
Energy distributions of the muons (left), pions (right top) and neutrinos (right bottom) from the pion decay in the K2K neutrino beam line after the horn focusing [30]. The shaded histograms correspond to the beam components with the muons above 5.5 GeV that are observed by MUMON
The muon profile from \(\pi \rightarrow \mu + \nu \) decay is measured by the muon monitor (MUMON) at the end of the decay volume after the beam dump. The muons measured by MUMON after the beam dump have energies above 5.5 GeV, thus their parents have more than 6 GeV. The muon profile measured by MUMON is used to monitor the neutrino beam direction. There are two methods to monitor the neutrino beam. One is by MUMON as mentioned and the other is the neutrino event distribution profile in ND. The reason for having two measurements of profiles is because of the two horn system. Low energy \(\pi \)’s are emitted at relatively large angles and are most efficiently focussed by the first horn. On the contrary, high energy \(\pi \)’s are emitted preferably in the forward direction, thus the second horn focusing effect is larger for higher energy pions. The relative alignment of the two horns must be monitored at both low and high energy. Otherwise, the possible misalignment of the two horns produces an artificial distortion of the neutrino spectrum, which may mimic neutrino oscillation.
The \(\pi ^{\pm }\) and \(K^{\pm }\) momentum and angular distributions in the decay volume were estimated based on two methods in K2K: an in-situ measurement by the pion monitor (PIMON) and from hadron production measurements by the CERN HARP experiment [31]. The in-situ measurement of the \(\pi ^{\pm }\) and \(K^{\pm }\) momentum and angular distribution was performed in PIMON. A schematic view of PIMON is shown in Fig. 16. The original idea was adapted from a technique used in the high energy \(\gamma \) ray astronomy. In some of the high \(\gamma \) ray searches from stars, the direction and the angular divergence of the air shower are measured, using air Cerenkov radiation with spherical mirror and array of photo-sensors at the focal plane of the mirror. Secondary particles from the production target are proton, \(\pi \), K and \(e^{\pm }\). Since the secondary proton energy must be below 12 GeV (incident energy) in K2K, a gas Cherenkov detector can be used, which is sensitive only to \(\pi ^{\pm }\) above 2 GeV/c (same \(\beta \) as 12 GeV proton) and \(e^{\pm }\). Furthermore, by changing the refractive index of the gas, a large part of the \(\pi ^{\pm }\) direction and momentum distribution can be extracted. Unfortunately, with a higher proton beam energy like T2K, where secondary particles contain much high energy proton up to 30 GeV, the PIMON approach is not possible.
2.4.2 Near detectors
Neutrinos are detected first by a set of near detectors (ND) located approximately 300 m from the neutrino production target and then by SK 250 km away. The ND consists of a 1 kton water Cherenkov detector (1KT) and a fine-grained detector system. The schematic view of ND is shown in Fig. 15. By having a water Cherenkov detector at the near site, the neutrino interaction cross section, nuclear final state interactions in the detector medium, the detector response to neutrino events, such as the muon identification efficiency and event type selection criteria, will cancel to first order in the far detector measurements. (There will remain effects due to the size of the detector, environment, etc.) The effects due to different spectrum shape in the near and the far detectors are estimated by having a fine grain tracking detector, which has a better capability of counting multiplicity of the high energy event component. A complete description of ND is in [22].
2.5 Neutrino flux prediction and the far-to-near flux ratio with hadron production data
2.5.1 Pion monitor: a in-situ measurement of the pion beam
The pion monitor (PIMON) was a gas Cherenkov imaging detector that consists of a gas vessel, a spherical mirror, and an array of 20 photo-multiplier tubes. The Cherenkov photons emitted by pions passing through the gas vessel are reflected toward and focused onto the PMT array by the spherical mirror. Then, the PMT array on the focal plane detects the image of Cherenkov photons. Thanks to the characteristics of the spherical mirror, photons propagating in the same direction are focused on the same position on the focal plane. Thus the spatial distribution is that of the direction of the Cherenkov light. The pion momentum distribution is also obtained from the size of the Cherenkov ring. Furthermore, a momentum scan can be done by modifying the refractive index of the inner gas at several points.
PIMON was operated periodically just downstream the horn magnets to measure the momentum (\(p_{\pi }\)) versus divergence (\(\theta _{\pi }\)) 2-dimensional distribution of pions entering the decay volume. As shown in Fig. 16, a pie-shaped mirror is used as the spherical mirror to measure only 1/30 part of the beam assuming azimuthal symmetry of the distribution. The top was aligned to be on the beam center. The reflection angle with respect to beam direction is \(30^{\circ }\).
A schematic view of the pion monitor (PIMON). PIMON consists of a gas vessel, a spherical mirror, and an array of 20 photo-multiplier tubes. The gas vessel is filled with freon gas R-318 (\(\mathrm{C}_4\mathrm{F}_8\)). A pie-shaped spherical mirror is set inside the gas vessel and Cherenkov right reflected by the mirror is directed to the array of photo-multiplier tubes which are set on the focal plane of the spherical mirror
An array of 20 PMTs (modified R5600-01Q made by Hamamatsu Corporation) is set 3 m away from the beam center to avoid beam associated radiation. The reflected photons are focused on the plane of the PMT array and detected by PMTs. They are arranged vertically with 35 mm intervals. The array can be moved by a half pitch of the interval along with the array, and hence 40 data points (one point for every 1.75 cm) are taken for Cherenkov light distribution. The relative gain among 20 PMTs was calibrated using a Xe lamp before the measurements. The gain ratio between neighboring PMTs was also checked using Cherenkov photons during the run. The error on the relative gain calibration is estimated to be 10% for June 1999 run and 5% for November 1999 run. The larger uncertainty in June 1999 was due to a saturation effect of PMTs, which was corrected by a 2nd polynomial function.
The gas vessel is filled with freon gas R-318 (\(\mathrm{C}_4\mathrm{F}_8\)). Its refractive index n is varied by changing the gas pressure using an external gas system. The data are taken at several refractive indices ranging between \(n=1.00024\!-\!1.00242\) to make PIMON sensitive to different pion momenta. Beyond \(n=1.00242\), the primary protons also emit Cherenkov photons which are a significant background. This corresponds to setting a momentum threshold of 2 GeV/c for pions.Footnote 2 The absolute refractive index is calibrated by the Cherenkov photon distribution from 12 GeV primary protons with the refractive index set at \(n=1.00294\).
For the background subtraction, beam associated radiation and electro-magnetic showers, which mainly come from the decay of neutral pions, \(\pi ^0\;\rightarrow \;2\gamma \), are considered. For the first category of background, a measurement with the mirror directed off from the direction of the PMT array is performed. For the electro-magnetic shower category, the subtraction is done by using the distribution measured at the lowest refractive index. After all the backgrounds are subtracted, the distribution of the Cherenkov light emitted from pions is obtained as shown in Fig. 17. The prediction of the beam Monte Carlo (MC) simulation is superimposed as well.
A \(\chi ^2\)-fitting is employed to extract \((p_\pi ,\theta _\pi )\) 2-dimensional distributions with various reflective indices. The \((p_\pi ,\theta _\pi )\)-plane is binned into \(5\times 10\) bins; 5 bins in \(p_\pi \) above 2 GeV/c with 1 GeV/c slice (the last bin is integrated over \(p_\pi >6\ \mathrm{GeV}/c\)) and 10 bins in \(\theta _\pi \) from \(-50\) to 50 mrad with 10 mrad slice. Templates of the Cherenkov light distributions emitted by pions in these bins are produced for each refractive index using an MC simulation. The weight of contribution from each bin was the fitting parameter. Figure 18 show the fit result.
The fit result of pion \((p_\pi ,\theta _\pi )\) distribution in November 1999 run. The top figure shows the resulting central value of the weighting parameters, and the bottom figure shows the estimated uncertainty on from the fit. The neutrino beam direction to SK from the target is defined as \(0^{\circ }\) (\(\theta _\pi = 0\)). The above pion angular distribution (and energy distribution) is affected by the detector acceptance (PIMON acceptance for the Cherenkov photons from the pions by using the pie-shaped spherical mirror in Fig. 16) that is not uniform over the angular distribution. It is the reason why the values in positive \(\theta _\pi \) is larger than ones in the negative \(\theta _\pi \) although they should be symmetric
The neutrino energy spectra at ND and SK are derived from the sum of the contributions of pions in each \((p_\pi ,\theta _\pi )\) bin in neutrino energy bins, which depend mainly on the pion kinematics and the geometry of the decay volume. The resulting ratio of the neutrino spectra at SK to that at the ND yields the far-to-near ratio correction. The shape of flux ratio reflects the profile of the neutrino flux
2.5.2 Neutrino flux prediction with the HARP measurements
The HARP experiment [31] was conducted in 2001 and 2002 in the CERN PS T9 beam-line, in order to study in a systematic and accurate way hadron production. The experiment studied a variety of produced hadrons (pions and kaons in particular) and with large phase space coverage, as a function of incident beam particle type (protons, pions), beam momentum (from 1.5 to 15 GeV/c), nuclear target material (from hydrogen to lead), and nuclear target thickness (from 2% to more than 100% hadronic interaction length fraction). Secondary tracks are efficiently reconstructed in the HARP forward spectrometer via a set of drift chambers located upstream and downstream with respect to a dipole magnet. Particle identification for forward tracks is obtained with a time-of-flight system, a Cherenkov threshold detector, and an electromagnetic calorimeter.
In particular, as part of the HARP program, the pion production measurement at the beam energy of 12 GeV on aluminum target was performed. In the forward region, the kinematical region of \(30<\theta _{\pi }<210\) mrad and \(0.75<p_{\pi }<6.5\) GeV/c was covered, which matches well with the pion production phase space to be responsible for the dominant fraction of the K2K neutrino beam flux.
The HARP results are adopted in the beam MC simulation to estimate the neutrino spectra at ND and SK. The calculated neutrino flux at the far and near sites in the absence of neutrino oscillation is shown in Fig. 19.
Relatively-normalized muon neutrino flux predictions at the near (top) and far (bottom) detectors. The empty circles with error bars show the central values and shape-only errors based on the HARP \(\pi ^+\) production measurement, the empty squares with shaded error boxes show the central values and errors from the pion monitor (PIMON) measurement, and the dotted histograms show the central values from the Cho-CERN compilation of older (non-HARP) \(\pi ^+\) production data. The PIMON predictions are normalized such that the integrated fluxes above 1 GeV neutrino energy match the HARP ones, at both the near and far detectors
The uncertainties in the flux prediction using HARP data are from primary interactions, primary proton beam optics, thick target effects such as secondary interactions of produced mesons, and the horn magnetic fields.
First, primary beam optics affect the effective interaction length of the target and material to be transversed by produced mesons before getting into the horn magnetic field. An uncertainty of 1.2 mm and 2.0 mrad in the mean transverse impact point on the target and in the mean injection angle, respectively, are assumed based on long-term beam stability studies [30].
Second, the contributions due to uncertainties in the multiplicity and kinematics of \(\pi ^+\) production in the proton-aluminum hadronic interactions, its interaction length, and the overall normalization of charged and neutral kaon production are considered as sources of the systematic uncertainties in the primary hadronic interactions. The HARP data were incorporated in terms of Sanford–Wang parameters. The uncertainties and correlations measured in HARP are propagated into flux uncertainties using standard error matrix propagation methods. An uncertainty of about 30% is assumed for the uncertainty in the proton-aluminum hadronic interaction length. The uncertainty in the overall charged and neutral kaon production normalization is assumed to be 50%.
Third, given the two-interaction length production target and other material present in the target area, such as the magnetic horns, re-interaction effects of the secondaries produced in primary hadronic interactions (e.g., \(\pi ^+\) absorption in aluminum) have an impact on the neutrino flux prediction. The systematic uncertainty is estimated by changing the hadron interaction models to describe secondary hadronic interactions in the beam MC simulation. In particular, we consider that the relatively large differences in the GCALOR/GFLUKA [32,33,34] and GHEISHA [35] models assumptions, also in comparison to available experimental data, are representative of the uncertainties associated with secondary hadronic interactions.
Finally, we estimate the uncertainties due to the imperfect knowledge of the magnetic field in the horn system. The uncertainties related to the magnetic field strength and to the field homogeneity in azimuth are taken into account. We assume a 10% uncertainty in the absolute field strength, which is well within the experimental uncertainty on the magnetic field strength and the horn current measured using inductive coils during the horn testing phase [36]. Furthermore, a periodic perturbation in azimuth of up to \(\pm 15\%\) amplitude with respect to the nominal field-strength is assumed as the uncertainty in the field homogeneity, which is also based on the experimental accuracy achieved in the measurement of the magnetic field mapping in azimuth during horn testing [37].
Prediction for the K2K muon neutrino far-to-near flux ratio in absence of oscillations. The empty circles with error bars show the central values and systematic errors on the muon neutrino flux predictions from the HARP \(\pi ^+\) production measurement discussed in the text, the empty squares with shaded error boxes show the central values and errors from the pion monitor measurement, and the dotted histograms show the central values from the Cho-CERN compilation of older (non-HARP) \(\pi ^+\) production data
2.5.3 Far-to-near flux ratio
The far-to-near flux ratio, \(\varPhi ^{\mathrm{SK}}/\varPhi ^{\mathrm{ND}}\), predicted by the HARP \(\pi ^+\) production measurement for primary hadronic interactions with the systematic error evaluation discussed in Sect. 2.5.2 in the absence of neutrino oscillations, is shown in Fig. 20 as a function of neutrino energy. The energy dependence of the far-to-near flux ratio is due to the acceptance difference between ND and SK with the divergence of the pion and neutrino beams. The ND has a larger acceptance for the off-axis beam described in Sect. 3.3, resulting in more low energy flux. In addition, the ND has a larger acceptance for the forward emitted neutrinos (\(\theta = 0\) in Eq. 15) in the pion decay where the pion beam has a divergence. This results in the more high energy neutrino flux at ND. We estimate that the flux ratio uncertainty in this analysis is at the 2–3% level below 1 GeV neutrino energy, while it is of the order of 4–9% above 1 GeV. As mentioned above, we find that the dominant contribution to the uncertainty in the far-to-near ratio comes from the HARP \(\pi ^+\) measurement itself. In particular, the uncertainty in the flux ratio prediction integrated over all neutrino energies is 2.0%, where the contribution of the HARP \(\pi ^+\) production uncertainty is 1.4%.
Figures 19 and 20 show the results of the extracted neutrino spectra and the far-to-near flux ratio from the PIMON data taken in November 1999. In the figures, the results from the HARP measurements and the predictions of the Beam-MC are also overlaid. The results of PIMON measurements are consistent with both of them, confirming the validity of the far-to-near estimations.
All three predictions on the far-to-near ratio are consistent with each other within their uncertainties. Among them, K2K used the one predicted by the HARP measurements in the neutrino oscillation analysis described in this paper. It gives the most accurate measurements on the hadron production.
The central values for the far-to-near flux ratio as a function of neutrino energy obtained from the HARP results of \(\pi ^+\) production, \(\overline{R}_{i}\), is given in Table 2, where the index i denotes an energy bin number. The total systematic uncertainties on the far-to-near flux ratio as a function of neutrino energy are given in Table 3, together with the uncertainty correlations among different energy bins, expressed in terms of the fractional error matrix \(\langle \delta R_i \delta R_j \rangle / (\overline{R}_i \overline{R}_j)\), where i, j label neutrino energy bins. The far-to-near central values and its error matrix are used in the analysis for neutrino oscillation.
2.6 Prediction of neutrino events at SK based on the measurements at ND
As already mentioned, knowledge of the neutrino flux itself is not precise enough to predict the events observed at SK. So, we use the combination of the far-to-near flux ratio (\(\varPhi ^{SK}/\varPhi ^{ND}\)) and the flux measurements at the near detector (\(\varPhi ^{ND}\)) for a prediction of the SK events. The neutrino spectrum at the near detector can be extracted from ND data with neutrino interaction models implemented in the NEUT library [38]. The expected events in SK will be generated by the same neutrino interaction models in NEUT, where some parameters were tuned in the ND measurements.
The near detector complex consists of a 1 kton water Cherenkov detector (1KT) and a fine-grained detector system. The schematic view of ND in K2K-IIbFootnote 3 is shown in Fig. 15. The 1KT has the same neutrino interaction target as that in SK, water. The detection efficiency is also similar to that in SK. At the same time, to complement the weaknesses of the water Cherenkov detector (such as detection of multi-particle final states), two tracking detectors were constructed (SciFi and SciBar).
The signatures of neutrino oscillation appear as a reduction in the number of observed \(\nu _{\mu }\) events and distortion in the \(\nu _{\mu }\) energy spectrum. To study the \(\nu _{\mu }\) energy spectrum, 1 ring \(\mu \)-like events (\(1R \mu \)) are used. The \(\nu _{\mu }\) energy can be reconstructed as \(E_\nu ^\mathrm{rec}\) for Charged-Current Quasi-Elastic (CC QE, \(\nu _\mu + n \rightarrow \mu + p\)) events. Neglecting Fermi momentum:
where \(m_N\), \(E_\mu \), \(m_\mu \), \(P_\mu \) and \(\theta _\mu \) are the nucleon mass, muon energy, the muon mass, the muon momentum and the scattering angle relative to the neutrino beam direction, respectively. The CCQE events have a signature of 1 ring \(\mu \)-like events (\(1R \mu \)), because most of the recoil protons are below the Cherenkov threshold of water. The background to this selection is due to charged current inelastic events (CC nonQE, \(\nu _\mu + N \rightarrow \mu + N + \pi 's\), where \(\pi \)’s are missed). Obviously, \(E_{\nu }\) with the CCQE assumption will be under-estimated for CC nonQE events. The issue is how to estimate the neutrino spectrum from the observed neutrino events in the presence of some contamination from CC nonQE events.
The event selection used to extract the spectrum is as follows. Figure 21 shows the likelihood distribution of the number of Cherenkov rings in K2K for both data and the MC simulation. The selection of a single ring is well reproduced by MC. Figure 22 shows the comparison of the distributions of the particle identification likelihood for data and the MC simulation for single ring events. The lepton identification capability is well understood. To measure the \(\mu \) energy, the events are required to be contained in the detector. The definition of the containment is checked as follows. Figure 23 shows the comparison of the distributions of the largest charge in a PMT for an event for data. Events that have a charge less than 200 photo-electrons (p.e.) are considered as Fully Contained (FC) events. The rest are partially contained (PC) events, because exiting particles emit Cherenkov light near the PMT around the exit point, which is likely to produce a large amount of light recorded by one PMT. Figure 24 shows the selection efficiency between all fiducial volume events and FC1R\(\mu \) events as a function of momentum.
The spectrum can be decomposed into overall normalization and its shape. The spectrum shape was obtained by fitting the observed two-dimensional distributions of \(p_{\mu }\) versus \(\theta _{\mu }\) for 1 ring \(\mu \)-like events (\(1R \mu \)) by a weighted sum of templates of CC QE and of CC nonQE, which were generated by the MC simulation for eight energy bins. The neutrino energies are divided into eight bins as shown in Table 4. Figure 25 shows the (\(p_{\mu }\), \(\theta _{\mu }\)) distribution for FC1R\(\mu \) events in the 1KT detector. For the MC expectation, the \((p_{\mu }, \theta _{\mu })\) distribution is prepared for each \(E_{\nu }\) bin and separately for CC QE and CC nonQE interactions; \(8\times 2\) distributions are prepared in total for each event sample. Some of the templates are shown in Fig. 26.
The spectrum shape is obtained by fitting the observed \((p_{\mu }, \theta _{\mu })\) distribution with sixteen templates that are prepared for eight neutrino energy bins and separately for QE and non-QE interactions. The fitting parameters are the neutrino energy spectrum parameters for eight energy bins (\(f^{\phi }_{1}\sim f^{\phi }_{8} \)), and a parameter, \(R_{nQE}\), representing the cross section ratio of CC nonQE to CC QE.
The contents in each \((p_{\mu }, \theta _{\mu })\) bin, \(N^{MC}_{i,j}\), are expressed with the 16 templates and the fitting parameters as,
where \(C_{norm}\), \(N^{MC(QE)}_{m,n,i}\) and \(N^{MC(nQE)}_{m,n,i}\) are a normalization parameter, the number of expected contents in (m,n)-th bin for QE interaction and nonQE interaction for i-th neutrino energy bin. The \(\chi ^{2}\) between the observed distributions, \(N^{data}_{m,n}\) , and the MC expectation, \(N^{MC}_{m,n}\), is calculated as:
where \(\epsilon \) is the fitting parameter for energy scale (nominally \(\sim \) 1), \(\sigma _{energy}\) is the estimated uncertainty of the energy scale (+3/-4%).
The measurements of other near detectors, SciFi and SciBar, are also included to calculate the total \(\chi ^{2}\). Finally, the set of fitting parameters (\(f^{\phi }_i, R_{nQE}\)) is found by minimizing the \(\chi ^{2}\) function. The best fit values, their error sizes and the correlations between them are listed in [22].
2.7 SK data
The SK events in K2K are collected from June 1999 to November 2004 as shown in Fig. 9. There is a gap of data taking period in 2002 because the SK detector had an accident of PMT explosion and the following repairing work. We called the former period as K2K-I and the latter as K2K-II. More detailed definitions are found in Table 5. In the periods of K2K-I and K2K-II, sub-periods (a, b, and c) are further defined with the experimental conditions. SK has full PMT photo-coverage of 40% (SK-I) in K2K-I and only 19% in K2K-II (SK-II).
The accelerator produced events in the SK detector are selected by using GPS information. The fully contained events in the fiducial volume, which are used in the oscillation analysis in K2K, are selected and reconstructed by using the similar methods used in the atmospheric neutrino analysis at SK.
Neutrino interactions from the accelerator are selected by comparing two Universal Time Coordinated time stamps from GPS, \(T_{KEK}\) for the KEK-PS beam spill start time and \(T_{SK}\) for the SK trigger time. The time difference \(\varDelta T = T_{SK} - T_{KEK} -TOF\), where TOF is a time of flight, is distributed from 0 and 1.1 \(\upmu \)s to match the width of the beam spill of the KEK-PS. The uncertainty of the synchronization for two sites is measured to be less than 200 nanosecond by using the atomic clock. Thus, \(\varDelta T\) for the K2K events are required to be from \(-0.2\) to 1.3 \(\upmu \)s.
In addition, the following cuts are required;
- (1)
no pre-activity within 30 \(\upmu \)s before the event to remove the decay electron events from cosmic muons which stopped in the detector before the beam window,
- (2)
no activity in the outer detector (Fully Contained event),
- (3)
no flashing PMT. A PMT sometimes begins to flash because of discharge around the dynode. These events have unique characteristics such as a timing distribution which is much broader than neutrino events and a repeated ring pattern,
- (4)
at least 30 MeV energy deposited assuming to be electron events in the inner detector,
- (5)
a reconstructed vertex point in the 22.5 kton fiducial volume, at least 2 m inside from the inner detector wall.
Table 6 shows the event reduction summary for K2K-I and K2K-II. The difference in the number of events after \(|\Delta \mathrm{T}|<500\mu \mathrm{s}\) cut comes from the difference of the detector trigger threshold for SK-1 and SK-2. In total, 112 accelerator-produced fully contained events are observed in the K2K experiment and 58 events are reconstructed as 1-ring \(\mu \)-like. Table 7 shows the event summary of observed events. Efficiency for these cuts is 77.2% for K2K-I and 77.9% for K2K-II. A major contribution of inefficiency comes from NC interaction events.
Figure 27 shows the \(\varDelta T\) distribution at each of the reduction steps. A clear peak at \(\varDelta T=0\) is seen after the fiducial volume cut. Three off-timing fully contained events are observed within \(\pm 500\mu \mathrm{s}\) timing window while two background events are expected from atmospheric neutrinos. Nine micro bunch structures can be seen clearly in the \(\varDelta T\) distribution with finer binning for all fully contained events in SK as shown in Fig. 28. Figure 29 shows the event rate as a function of POT. The event rate is consistent with the assumption that it is proportional to POT. A Kolmogorov–Smirnov (KS)-test to that assumption has a probability of 79%.
Systematic uncertainties on the estimation of \(\mathrm{N}_{\mathrm{SK}}\) and reconstructed neutrino energy in SK are evaluated using the atmospheric neutrinos as a control sample. Table 8 shows the systematic errors for \(\mathrm{N}_{\mathrm{SK}}\). The dominant uncertainty for \(\mathrm{N}_{\mathrm{SK}}\) comes from the vertex reconstruction in a fiducial volume. It is evaluated by comparing the number of events for atmospheric neutrino data with the MC expectation in the fiducial volume using the two different vertex reconstruction programs. Uncertainties in the neutrino interaction model from events in the different acceptances between ND and SK are also taken into account in the oscillation analysis. Systematic errors for the reconstructed neutrino energy spectrum from event reconstruction are shown in Table 9. Uncertainties coming from the ring counting and particle identification are evaluated by comparing the likelihood distribution for data and MC. Figures 30 and 31 show the ring counting and particle identification likelihood distributions of atmospheric neutrino data compared with the MC expectation in SK-II.
The MC expectation reproduces the data well. The uncertainties for the energy scale are also estimated by using cosmic ray muon, \(\pi ^0\) invariant mass, and decay electron samples. They are taken into account in the oscillation analysis (2.0% for K2K-I and 2.1% for K2K-II).
2.8 Oscillation analysis
The K2K data were taken over the period from June 1999 to November 2004, which is divided into five periods corresponding to different experimental configurations as shown in Table 5. The horn current was 200 kA (250 kA) and the diameter of the production target was 2 cm (3 cm) in the Ia (other) period. The SK PMTs were full density for Ia and Ib, but were half density for IIa, IIb, and IIc. The Lead–glass calorimeter was placed between the SciFi and MRD in Ia and Ib, which was replaced by the SciBar for IIa, IIb, and IIc periods. Only the first four layers of the SciBar detector were installed for IIa while it was complete for IIb and IIc. Furthermore, the water target in SciFi was replaced by aluminum rods during IIc. The numbers of protons delivered to the target and for the physics analysis are summarized in Table 5. In total, \(92.23\times 10^{18}\) POT are used in physics analysis.
Neutrino oscillation causes both a suppression in the total number of events observed at SK and distortion of the energy spectrum. Therefore, all of the beam-induced neutrino events observed within the fiducial volume of SK are used to measure the overall suppression and the subset of these events for which the incoming neutrino energy can be reconstructed (FC1R\(\mu \) events) are separately studied in order to study the spectral distortion.
The likelihood function is defined as the product of the likelihoods for the observed number of events in the SK fiducial volume (\( \mathcal {L}_{norm}\)), the shape of the \(E_{rec}\) spectrum (\(\mathcal {L}_{shape}\)) and a systematic constraint likelihood term (\(\mathcal {L}_{syst}\)) where they are varied within their uncertainties as,
We perform neutrino oscillation analysis in an assumption of two-flavor mixing. The oscillation parameters, (\(\sin ^22\theta , \varDelta m^2\)), are obtained by maximizing the likelihood function.
One-hundred twelve FC events and 58 FC1R\(\mu \) events are used in \(\mathcal {L}_{norm}\) and \(\mathcal {L}_{shape}\), respectively. The systematic parameters consist of the neutrino energy spectrum at ND, the far-to-near ratio, the neutrino cross section uncertainties, and SK energy scale and overall normalization. The expected number of events in SK with neutrino oscillation (\(N_{exp}\)) is calculated from the number of observed events in 1KT (\(N^{obs}_{1KT}\)) for oscillation parameters (\(\sin ^22\theta , \varDelta m^2\));
where \(N^{SK(1KT)}_{MC}\) is the expected number of events in MC as
The neutrino flux at SK (\(\varPhi ^{SK}\)) is predicted from ND analysis based on the flux at 1KT (\(\varPhi ^{1KT}\)) as
In the above expression, the neutrino oscillation probability is
and, \(R^{F/N}(E_\nu )\) is the near-to-far flux ratio based on HARP and Pion Monitor analysis, \(\sigma ^i (E_{\nu })\) is interaction cross section with water, ’i’ runs for CC QE, CC nonQE, and NC interactions constrained by ND data. The \(\epsilon _{SK}\) (\(\epsilon _{1KT}\)) is SK (1KT) detection efficiency of FC events, \(M_{SK}\) (\(M_{1KT})\) is the fiducial mass of SK (1KT), \(POT_{SK}\) (\(POT_{1KT})\) is the number of protons on target which corresponds to the analyzed data in SK (1KT) and \(C_{\nu _e}\) is the correction for the electron neutrino component in the neutrino beam estimated to be 0.996 by the MC simulation.
The normalization term, \(\mathcal {L}_{norm}\), is expressed in terms of a Poisson probability of the observe events (\(N_{obs}\)) where the expected number of events is \(N_{exp}\):
The shape term \( \mathcal {L}_{shape} \) is defined as the product of the probability for each FC\(1R\mu \) event to be observed at a reconstructed energy \(E_\nu ^{rec}\). The expected spectrum shape of reconstructed energy at SK is
where \(\epsilon ^{SK}_{1R\mu }(E_{\nu })\) is the detection efficiency of \(1R\mu \) events and \(r(E_\nu ;E_\nu ^{rec}) \) is the probability of reconstructing an event with true energy \(E_{\nu }\) as \(E_\nu ^{rec}\), based on neutrino interaction and detector simulation. The probability density function is
The systematic parameters are treated as fit parameters which are assumed to follow a Gaussian distribution and are constrained within the associated uncertainties. Details on the systematic errors are discussed in [22].
The number of FC events without neutrino oscillation is estimated to be \(158.4^{+9.4}_{-8.7}\). The major contribution to the uncertainty on the normalization (4.8%), is due to the fiducial volume uncertainty from the vertex reconstruction at both 1KT and SK.
2.9 Result
The results are summarized as follows;
The maximum likelihood points in the \(\sin ^{2}2\theta \) – \(\varDelta m^{2} \) space for all or physical regions are summarized in Table 10 with full and partial data sets.
The best fit point in the physical region is found to be at \((\sin ^{2}2\theta , \varDelta m^{2}) = (1.00, 2.8 \times 10^{-3} eV^{2})\). With the oscillation parameters, the expected number of events is 107.2, which agrees well with 112 observed within statistical uncertainty.
The observed \(E_{rec}\) distribution is shown in Fig. 32 with the expected distributions for the best-fit parameters, and the expectation without oscillations.
The consistency between the observed and fitted \(E_{rec}\) distributions is checked using a KS test. For the best fit parameters, the KS probability is 37%, while that for the null oscillation hypothesis is 0.07%. Thus, the observation is consistent with the oscillation hypothesis.
Although the point with the highest likelihood is outside of the physical region, \((\sin ^{2}2\theta , \varDelta m^{2}) = (1.2, 2.6\times 10^{-3} eV^{2})\), the probability that \(\sin ^{2}2\theta \ge 1.2\) if the true parameters are at the best fit physical parameters is 26.2%, based on MC virtual experiments.
The probability that the observations are due to a statistical fluctuation instead of neutrino oscillation is estimated by computing the log-likelihood ratio of the null oscillation case to the best fit point. The null oscillation probability is calculated to be 0.0015% (4.3\(\sigma \)). When only normalization (shape) information is used, the probability is 0.06% (0.42%).
The null oscillation probability was calculated separately for two periods of K2K-I and K2K-II. The probabilities for each sub-sample is summarized in Table 11.
Table 12 shows the effect of each systematic uncertainty on the null oscillation probability.
The effect is tested by applying each uncertainty individually. As shown in the table, the dominant contribution to the probabilities with the normalization information are from the far-to-near flux ratio and normalization error, while energy scale is the dominant error source for the probability with the \(E^{\mathrm {rec}}_{\mu }\) shape information.
Allowed region of oscillation parameters are evaluated based on the difference of log-likelihood between each point and the best fit point as
where \(\mathcal {L}_{\mathrm {max}}^{\mathrm {phys}}\) is the best fit point and \(\mathcal {L}(\sin ^22\theta ,\varDelta m^2)\) is the likelihood at \((\sin ^22\theta ,\varDelta m^2)\) with systematic parameters that maximize the likelihood at that point. Figure 33 is the allowed region corresponding to the 68%, 90% and 99% confidence levels (CL). They are defined to be \(\ln \mathcal {L}= \ln \mathcal {L}_{\mathrm {max}}^{\mathrm {phys}} - 1.37, -2.58 ~\mathrm {and}~-4.91\), respectively. These intervals are derived by using the 2-dimensional Gaussian approximation from the maximum in the unphysical region [39]. The 90% CL contour crosses the \(\sin ^{2}2\theta = 1\) axis at \(\varDelta m^{2} = 1.9~\mathrm {and}~3.5 \times 10^{-3}~eV^{2}\). Figure 34 shows the \(\ln \mathcal {L}_{\mathrm {max}}^\mathrm {phys} - \ln \mathcal {L}(\sin ^22\theta ,\varDelta m^2)\) distributions as a function of \(\sin ^{2}2\theta \) and \(\varDelta m^{2}\), with a slice at \(\varDelta m^{2} = 2.8 \times 10^{-3} eV^{2}\) and \(\sin ^{2}2\theta = 1.00\). Another consistency check was performed, by comparing the analyses using only the total number of events and only with shape analysis (Fig. 35). Also, the allowed regions calculated with only K2K-I/K2K-II data was checked for the consistency.
\(\ln \mathcal {L}_{\mathrm {max}}^{\mathrm {phys}} - {\ln \mathcal {L}}(\varDelta m^2,\sin ^22\theta )\) distribution as a function of \(\varDelta m^{2}\) (top) and \(\sin ^{2}2\theta \) (bottom), in which \(\ln \mathcal {L}_{\mathrm {max}}^{\mathrm {phys}}\) is the maximum value of \(\mathcal {L}\) in physical parameter region. The \(\sin ^{2}2\theta \) is set to be 1.00 in the top figure and \(\varDelta m^{2}\) is set to be \(2.76 \times 10^{-3} \mathrm {eV}^{2}\) in the bottom figure. Three horizontal lines correspond to the 68%, 90% and 99% CL interval from the bottom one, respectively
In conclusion, the K2K experiment, by using a neutrino beam derived from an accelerator proton beam, confirms neutrino oscillations first observed in atmospheric neutrinos.
3 The T2K experiment
T2K [40] is a second generation neutrino oscillation experiment, utilizing the new high-intensity proton accelerator in Japan: J-PARC. The name T2K comes from the initials of the “Tokai to (2) Kamioka” neutrino experiment. The neutrino program has been one of the main motivations of building a high-intensity proton synchrotron since the JHF (former name of J-PARC [41]) was first proposed in 1995. Possible neutrino experiments were first discussed in 1996 at the INSFootnote 4 symposium, and at JAERIFootnote 5 in 1997 at the JAERI workshop. Due to the rapid worldwide progress of neutrino physics, it became necessary to re-evaluate the physics goals for the next generation neutrino oscillation experiment. The JHF neutrino experiment-working group was formed in 1999 to formulate our strategy. The Expression of Interest was submitted to the JHF project team in January 2000. The first Letter of Intent was published in 2001 [42]. In 2002, two international workshops were held. The attendants included physicists from Canada, France, Italy, Korea, Russia, Spain, Switzerland, UK, and the USA, and an international working group was formed. The experiment was approved by MEXT (Ministry of Education, Culture, Sports, Science and Technology in Japan) in 2003 and the design and the construction started in 2004. This experiment is an international collaboration of Japan, Canada, France, Italy, Korea, Poland, Russia, Spain, Switzerland, UK, and the USA.
The main goals of T2K are to measure electron neutrino appearance in a predominantly \(\nu _{\mu }\) beam and to improve the precision of \(\nu _{\mu }\) disappearance parameters. The experiment has the following well-defined goals.
The mixing angle \(\theta _{13}\) is the last of the mixing angles in the three neutrino scheme as explained in Sect. 1.2. We already know that the other two mixings are large. One of the most burning questions was whether the third mixing angle is on the same order of magnitude or smaller by many orders of magnitudes. The observation of \(\nu _{\mu }\rightarrow \nu _e\) in the first stage of the experiment proved that \(\theta _{13}\) is not extremely small so that a future CP violation search becomes possible. The \(\nu _{\mu }\rightarrow \nu _e\) oscillation is an appearance channel driven by the sub-leading oscillation of \(\nu _{\mu }\) involving \(\varDelta m^2_{13}\). New developments in solar and reactor neutrino experiments (see reviews in [43, 44] and the SNO result [45]) indicate that \(\nu _{\mu }\) oscillates to \(\nu _e\) with a rather large mixing angle and \(\varDelta m^2_{12}\). This oscillation can compete with the \(\nu _{\mu }\) to \(\nu _e\) involving the mass squared difference of \(\varDelta m^2_{13}\). The former oscillation is suppressed by a small \(\varDelta m^2\) and the latter is suppressed by the small mixing angle, \(\theta _{13}\). Hence, the two processes can compete. This is one of the necessary conditions for a CP violation effect to be observable.
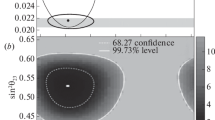
Before T2K and the new reactor experiments [46,47,48], the best upper limit was given by the CHOOZ experiment [49]. Figure 36 shows the spectrum and the comparison with expectation. Figure 37 shows the excluded region before T2K.
Measured spectrum by the CHOOZ experiment at the distance of 1 km with 425 GWth. [49]
Excluded region of \(\nu _e\) disappearance in reactor experiment by CHOOZ [49]
An upper limit of \(\sin ^22\theta _{13}<0.10\) with \(\varDelta m^2=2.5\times 10^{-3} \ \mathrm{eV}^2\) with 90% CL was set. A global analysis of neutrino oscillation data showed a hint of \(\theta _{13} > 0\) with 90% CL [50].
Figure 38 shows the excluded region of \(\nu _e\) appearance in K2K [51]. The upper limit was \(\sin ^22\theta _{13} <0.26\) at 90% CL at \(\varDelta m^2=2.8\times 10^{-3} \ \mathrm{eV}^2\) with the assumption of no CP violation, no matter effect and \(\theta _{23} = \pi /4\) (\(\sin ^22\theta _{13} = 2\sin ^22\theta _{\mu e}\)). The observed number of electron appearance candidates was 1 with 1.7 expected background, mainly from the high energy part of the neutrino spectrum. The reduction of background was crucial for the second generation experiment, in addition to increasing the intensity of the neutrino beam.
Excluded region of \(\nu _e\) appearance in K2K. The total observed number of electron appearance candidates is 1 with 1.7 expected background mainly from high energy neutrinos. The upper limit of \(\sin ^22\theta _{\mu e}<0.13\) at 90% CL with \( \Delta \ \mathrm{m}^2=2.8\times 10^{-3}\, \mathrm{eV}^2\)
Also, precision measurements of oscillation parameters in the \(\nu _{\mu }\) disappearance channel test how close to maximal the mixing between the second and third generations is.
3.1 Lessons from K2K
There are two major items to be improved in the second generation experiment, T2K. First is the beam power to search for the sub-leading oscillation channel as shown in Eq. 4. K2K already reached the radiation limit in the accelerator and beamline. The design of the new facility requires minimum beam loss and radio-activity generation in the accelerator and beamline. The second improvement is the suppression of backgrounds to the \(\nu _e\) appearance signal. The experiment must emphasize the capability of rejecting \(\pi ^0\) and multi-\(\pi \)’s, which fake the electron signal. Also, it is essential to be able to distinguish oscillated \(\nu _e\) signal from \(\nu _e\) contamination in the beam, which is expected at the few % level due to muon and kaon decays.
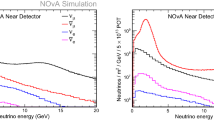
The contamination of FC1R\(\mu \) events in K2K due to inelastic (CC nonQE) is shown in Fig. 39. The hatched histogram is for CC nonQE in the MC simulation. We noticed that a large fraction of FC1R\(\mu \) are from CC nonQE where the \(\pi \) (mainly \(\pi ^{\pm }\)) is missed in the event reconstruction. For the \(\nu _e\) appearance search, neutral current \(\pi ^0\) production and multi-pion events constitute the main backgrounds. Figure 40 shows a schematic representation of low energy neutrino interactions. A major fraction of inelastic interactions is due to neutrinos with energy above 1 GeV. The new beam design should aim at suppressing the high energy part of the neutrino spectrum.
The reconstructed neutrino energy distribution for single Cherenkov ring events in K2K. The hatched histogram shows the MC simulation of CC nonQE events. There is a non-negligible contribution from inelastic charged current events (CC nonQE), where pions produced in the neutrino interaction are not recognized
3.2 Design of T2K
The following are the design goals of T2K.
\(E_{\nu }\) reconstruction: The charged current interaction is dominated by the CC QE interaction in the energy region below 1 GeV. This enables us to make a precise determination of the neutrino energy of both \(\nu _{\mu }\) and \(\nu _e\). The energy is calculated by the formula:
$$\begin{aligned} E_{\nu }= & {} \frac{m_N E_l - m_l^2/2}{m_N-E_l+p_l \cos \theta _l}, \end{aligned}$$(14)where \(m_N\) and \(m_l\) are the masses of the neutron and lepton (= e or \(\mu \)), \(E_l\), \(p_l\), and \(\theta _l\) are the energy, momentum, and angle of the lepton relative to the neutrino beam direction, respectively.
Neutrino beam energy The optimum sensitivity of the oscillation measurement can be achieved by tuning the neutrino beam energy to the oscillation maximum. The oscillation maximum will occur at neutrino energy, \(E_{\nu }\), about 0.6 GeV for the 295 km baseline, which is the distance between the new J-PARC accelerator and SK, with \(\Delta \mathrm{m}^2\sim 2.5\times 10^{-3}\mathrm{eV}^2\).
Background suppression The most efficient suppression may be achieved with a nearly monochromatic energy spectrum peaking around 0.6 GeV. This spectrum has another advantage, namely, the \(\nu _e\) appearance signal should be confined to a known energy region, which suppresses the background contribution from \(\nu _e\) contamination in the \(\nu _{\mu }\) beam. The small high energy component of the off-axis beam also improves the accuracy of the disappearance parameters. This is because the backgrounds in the \(\nu _{\mu }\) disappearance are small, leading to small \(E_{\nu }\) reconstruction bias.
Beam power The new accelerator is designed to have minimum beam loss in the injection and during acceleration through large aperture magnets and the “imaginary transition design” of the accelerator lattice [52]. The beamline, especially the entire area from target to decay volume must be carefully designed to use a high-intensity beam for a long period.
Basic principle The general T2K design follows the basic principles of K2K. This includes alignment and directional control/monitoring of the beam by \(\mu \) from \(\pi \rightarrow \mu \) decay and neutrino profile measurements. Near detectors are also placed in the direction of SK to normalize and to monitor the neutrino beam.
3.3 Off-axis beam
T2K uses an off-axis beam to accomplish the highest possible intensity of low energy neutrinos with only a small high-energy component in the spectrum. This idea was first proposed for the BNL long-baseline experiment [53]. Figure 41 shows the principle of the off-axis beam. The horn-focused secondary beam of \(\pi \) and K is pointed toward but not exactly to the detector, so that there is a small angle between the center of the beam and the detector location. The beam energy can be set by tuning the beam angle. The neutrino energy at an angle \(\theta \) relative to the \(\pi \) direction is
where \(E_{\pi }\), \(\gamma \), and \(\theta \) are the pion energy, the Lorentz factor of the pion ,and the angle between the direction of the secondary beam and the direction of the detector, respectively. The spectrum at the angle \(\theta \) has a Jacobian peak. Figures 42 and 43 show the expected neutrino energy spectra of charged current interactions in SK. In T2K, the angle is \(2.5^{\circ }\), the resultant peak energy is around 0.6 GeV. A small high energy tail remains as a result of imperfect focusing of the secondary particles.
Comparison of \(\nu _e\) and \(\nu _\mu \) spectra for the \(2^\circ \) off-axis beam. The solid (black) histogram is \(\nu _\mu \) and the dashed (red) one is \(\nu _e\). The hatched area is a contribution from the kaon decay. The low energy \(\nu _e\) component is due to \(\mu \) from \(\pi \) decay
The suppression of the high energy tail by the T2K off-axis beam is demonstrated in Fig. 44 as compared with the K2K case in Fig. 39, where the reconstructed \(\nu _{\mu }\) energy distributions for single muon events without oscillation are shown from simulated data. A feature of the off-axis beam is that pions with almost any energy contribute to neutrinos with a given energy \(E_{\nu }\). This is an advantage for the oscillation signal search with the higher neutrino flux. However, a disadvantage is caused by the feature that different energy pions contribute differently to the near and far detector neutrino flux. The secondary particle distribution must be known in a wide energy range to calculate the flux at the near and far detectors. Another issue is that neutrino oscillation leads to a major fraction of the \(\nu _{\mu }\) beam disappearing at the far detector due to the kinematics of the narrowband beam and the large mixing of \(\nu _\mu \) to \(\nu _\tau \) oscillations with negligible cross section of \(\tau \) production in CC interactions. T2K relies on the data from the CERN NA61 experiment that measures \(\pi \) and K production from 30 GeV protons on Carbon [54].
The reconstructed neutrino energy of single muon events in the simulation for T2K without oscillation. Comparing with the K2K case in Fig. 39, the inelastic contamination is much smaller with the T2K off-axis beam due to the reduced high energy tail
3.4 New accelerator at J-PARC and neutrino beamline
A high power proton accelerator complex was constructed by a collaboration of JAEA (Japan Atomic Energy Association) and KEK (High Energy Accelerator Research Organization) in Tokai village, Ibaraki, Japan. The name J-PARC stands for the Japanese Proton Accelerator Research Complex.
Figure 45 shows the layout of the J-PARC facility consisting of a 400 MeV linac, 3 GeV 1 MW rapid cycling (25 Hz) synchrotron (RCS), and 0.75 MW 50 GeV proton synchrotron main ring (MR). The research at J-PARC covers a wide range of fields from biology to high energy physics. The design intensity of the MR is \(3.3\times 10^{14}\) protons/pulse (ppp) at a repetition rate of 0.285 Hz (3.5 s period) at 50 GeV and higher repetition rate at lower energy, resulting in a beam power of 0.75 MW. The spill width is \(\sim \)5.2 \(\upmu \)s. The distance is 295 km between J-PARC at Tokai and Super-Kamiokande at Kamioka. Given the 295 km baseline, the neutrino energy is tuned to a peak at \(\sim 0.6\ \mathrm{GeV}\), which corresponds to \(\varDelta m^2\) at \(2.5 \times 10^{-3}~\mathrm{eV}^2\). The facility started with 180 MeV energy in the linac and 30 GeV proton energy in the MR. The commissioning of RCS started in September 2007, and the MR commissioning completed in 2009. The linac was upgraded to 400 MeV in 2014, the RCS achieved 1 MW operation for a short time (not physics run), and the power of the MR reached 500 kW with 30 GeV proton energy for neutrino experiments.
The proton beam is fast-extracted from the MR in a single turn and transported to the production target. The layout of the neutrino beamline in the J-PARC facility is illustrated in Fig. 46. The protons are extracted toward the inside of the MR ring and are bent by 90\(^\circ \) to the SK direction by the transport line with a radius of curvature of 110 m. Superconducting magnets are used for the transport line. The secondary pions and kaons from the target are focused by horns, and decay in flight into neutrinos in a decay volume (DV) 110 m long. The DV is designed to accommodate the beam of \(2.5 \sim 3^\circ \) off-axis angle. The beam dump is placed at the end of the DV and stops particles other than neutrinos and muons. The dump consists of graphite blocks of about 3.15 m thickness followed by iron plates with 2.5 m total thickness. The muons penetrating the DV are absorbed in the soil in front of the near detector.
The whole volume from target to beam dump is filled with helium gas. Figure 47 shows a cut-out view of the beamline. The design of the beamline is dictated by the beam power (thermal shock and high radiation). Examples of the critical issues of the operation of a high power beam facility include thermal shock wave, heat generation by ionization losses of charged particles, and generation of radio-activity.
The thermal shock and heat generation in the target forced us to use graphite for the target and the beam dump core. The production target is a graphite rod of 26 mm diameter and 90 cm long (corresponding to 2 interaction lengths). About 80% of incoming protons interact in the target. At the design intensity, the target receives 58 kJ/spill energy deposit by ionization losses of charged particles and it causes a thermal shock stress of \(\sim \)7 MPa. The heat is removed by forced-flow helium gas and the stress is confirmed to be a factor 3 less than the strength of the graphite. The helium cooling is used because of the expected high energy deposit and to avoid boiling vapor. The target is followed by three electromagnetic horns operated at \(\pm 250~\mathrm{kA}\)Footnote 6 pulsed current to focus either positively or negatively charged secondaries in the forward direction. They are cooled by water spray to remove the Joule heat and deposited energy by charged particles.
The operation also generates radioactive water and air. The expected radioactive water is 13 GBq/(3 weeks) and has to be diluted to less than 30 Bq/cc for disposal. This requires many tanks, ion exchange filters, and a backup loop. The cooling of the target by helium generates 7 GBq /(3 weeks) radioactive He (must be diluted <5 mBq/cc to dispose of). The production cross-section of tritium in He is 1/10 of air. The air contamination in the He vessel needs to be less than 10 ppm. Temperature rise and thermal shock limit the beam power to approximately 2 MW proton beam. Another limit comes from the aluminum horn, the graphite target, and the Ti vacuum window mechanical stability. Substantial R&D and experience are needed to go substantially beyond this limit.
3.5 Monitoring of secondary particles
A muon monitor is placed just after the beam dump to monitor the intensity and the profile of muons which pass through the beam dump spill-by-spill, just like in K2K. High energy muons of \(>5.5\ \mathrm{GeV}\) can penetrate the beam dump and reach the muon monitor. The secondary \(\pi \) beam direction was monitored to better than 1 mrad. accuracy.
T2K also uses a multi-horn system, so the direction of both high energy and low energy secondary particles should be monitored. As in K2K, the low energy part is monitored by detecting the neutrino event profile distribution with a large lever arm. Figure 48 shows the array of iron-scintillator sandwich detectors (INGRID) used to monitor the neutrino profile. The secondary beam direction and efficiency of generating neutrinos/protons are measured much better than 1 mrad and 0.7%, respectively.
3.6 Near detector at 280 m from the target (ND280)
To minimize the uncertainty of neutrino cross-sections and event selection in the oscillation analysis, a water Cherenkov detector in ND is an ideal detector, as in K2K. In T2K, we cannot use a water Cherenkov detector for the following reasons. Since there is no division in the detector and the Cherenkov angle is typically as large as \(42^\circ \), a single event occupies a large fraction of the detector. This limits the neutrino rate to be less than 1 event/pulse. Also, since the vertex must be a few meters away from the front surface of the PMT array, the usable fiducial volume inside the total volume is small in a small detector. In K2K, 50 tons in a total mass of 1000 tons were used for the fiducial. The only solution may be to place it at a relatively large distance (about a km away from the target). At the starting time at least, T2K decided not to put a near detector outside of the J-PARC site.
Instead, T2K has a fine grain tracking detector as its near detector (Fig. 49), measuring neutrino interactions at 280 m from the target [55]. This off-axis detector aims to measure the muon neutrino energy spectrum, contamination of electron neutrinos, and neutrino interactions with a similar energy spectrum at SK. The detector consists of two fine-grained scintillator trackers (FGDs), three Time Projection Chambers (TPCs), Pb/Scintillator Sandwich \(\pi ^0\) detector (P0D) and Electro-magnetic calorimeter (ECal) inside the large volume dipole magnet with a 0.2 T magnetic field. The Muon Range detectors (SMRD) are also inserted in the iron yoke of the magnet. The interaction points of neutrinos are measured by FGD and P0D; charged particles from the interaction are measured by the TPCs; electrons and \(\gamma \) rays measured by the ECal; muons are identified by SMRD. One FGD (FGD1) consists of only the scintillator modules and the other (FGD2) contains the water modules in addition to scintillator. FGD2 is used to study neutrino interactions on water. The identification of charged particles is performed by FGDs and TPCs. A typical event display of ND280 is shown in Fig. 50. For a demonstration of the performance, the dE/dX measurement as a function of the momentum by TPCs is shown in Fig. 51.
Fine-Grained scintillator detector (FGD) and TPC comprise the tracking system. The \(\pi ^0\) detector (P0D) is a sandwich of water bag, lead, and scintillator tracking system. The whole detector is inside a large aperture magnet, which is instrumented with scintillators. This magnet was used for the UA1 and NOMAD experiments and donated by CERN
A typical events display of neutrino interaction in ND280 [55]
Distribution of the energy loss as a function of the momentum for negatively (top) and positively (bottom) charged particles produced in neutrino interactions, compared to the expected curves for muons, electrons, protons and pions [55]
3.7 T2K results
In this section we describe the performance of the T2K experiment and the results obtained. The major result is the discovery of electron neutrino appearance from the muon neutrino beam. In addition, many neutrino cross section results are provided as well as the precise measurements of oscillation parameters. At present, an investigation of CP violation is focused more.
3.7.1 Neutrino beam production and Beam data-taking
T2K physics data-taking started in January 2010 and continues in 2020 and beyond. The data-taking history is shown in Fig. 52. A maximum beam power of 500 kW was recorded in 2018. Data-taking was interrupted twice for about a year: once on March 11, 2011 by the Great East Japan Earthquake, and once on May 23, 2013 due to an incident at the J-PARC Hadron Experimental Facility. The neutrino event rate and neutrino beam directions were carefully monitored by MUMON and INGRID as shown in Fig. 53. The long-standing beam monitoring guarantees a high quality of the neutrino beam for analysis.
T2K can be operated with both neutrino and anti-neutrino beams by changing the polarity of the horn current. Figure 54 shows the prediction of the neutrino and anti-neutrino beam flux [56] at SK. In neutrino beam production, the flux is dominated by muon neutrinos with a small irreducible contamination of electron neutrinos (a few % level), referred to as “beam \(\nu _e\)”. The beam \(\nu _e\) component is a major background when searching for electron neutrino appearance. In anti-neutrino beam production, the flux is dominated by anti-muon neutrinos with a \(\sim 10\)% fraction of muon neutrinos called the “wrong-sign component”. The fraction of electron neutrinos is small.
Prediction of the T2K flux for neutrinos (top) and antineutrinos (bottom) at SK [56]. The flux above \(E_\nu = 10\ \mathrm{GeV}\) is not shown; the flux is simulated up to \(E_\nu = 30\ \mathrm{GeV}\)
3.7.2 Discovery of electron neutrino appearance from muon neutrinos
In the initial data set of \(1.43 \times 10^{20}\) POT accumulated by March 2011 corresponding to 6.5% of the present data, the first time evidence of non-zero \(\theta _{13}\) was reported [57] by observing \(\nu _\mu \rightarrow \nu _e\) appearance. The probability of \(\nu _\mu \rightarrow \nu _e\) oscillation is dominated by the leading term of \(\sin ^22\theta _{13}\) as shown in Eq. 4, and it is affected by the term with \(J_{CP}\) where the CP violation phase \(\delta _{\mathrm {CP}}\) and the mass ordering are important.
Six electron neutrino events were observed in SK, compared to \(1.5 \pm 0.3\) expected events assuming \(\theta _{13}=0\). The probability to observe six or more candidate events is \(7 \times 10^{-3}\), corresponding to a \(2.5 \sigma \) significance. The event display of an electron neutrino candidate event is shown in Fig. 55.
The reconstructed neutrino energy of six events is shown in Fig. 56. Six observed electron neutrino events are consistent with the appearance of electron neutrinos due to non-zero \(\theta _{13}\). To be precise, the result corresponds to a confidence interval of \(0.03 (0.04)< \sin ^2 2\theta _{13} < 0.28 (0.34)\) at the 90% CL for \(\sin ^2 2 \theta _{23}=1.0\), \(|\varDelta m^2_{23}| = 2.4 \times 10^{-3}~\mathrm{eV}^2\), and \(\delta _{CP}=0\) for normal (inverted) mass hierarchy. This was the first evidence of non-zero \(\theta _{13}\) at \(2.5 \sigma \) significance.
By collecting more data, \(\nu _\mu \rightarrow \nu _e\) oscillation was well established in 2013 with \(6.57 \times 10^{20}\) POT [58]. Twenty-eight electron candidate events were observed in SK with \(4.92\pm 0.55\) expected background events, corresponding to a \(7.3 \sigma \) significance. As an analysis update, a newly developed algorithm was applied to suppress the background events which contain \(\pi ^0 \rightarrow 2 \gamma \) decays, where one of the photons is not reconstructed. The details of the new event selection are found in [59]. The number of observed and expected events is shown in Table 13.
The observed number of events, 28, is consistent with or slightly higher than the expectation of 21.6 with \(\sin ^2 2\theta _{13} = 0.10\) and \(\delta _{\mathrm {CP}}=0\). The higher number may indicate CP violation (\(\delta _{\mathrm {CP}} \ne 0\)). The best fit value of \(\theta _{13}\) is evaluated to be \(\sin ^2 2 \theta _{13} = 0.140 \pm 0.038 (0.170 \pm 0.045)\) in the case of normal (inverted) hierarchy with a 68% C.L. by fixing the other oscillation parameters: \(\sin ^2 2 \theta _{12} = 0.306\), \(\varDelta m_{21}= 7.6 \times 10^{-5}\ \mathrm{eV}^2\), \(\sin ^2 \theta _{23}=0.5\), \(|\varDelta m^2_{32}|=2.4\times 10^{-3}\) eV\(^{2}\), and \(\delta _{\mathrm {CP}}=0\). The electron momentum versus angle distribution is shown in Fig. 57, and is used to extract the best fit values of the oscillation parameters \(\sin ^2 2 \theta _{13} \) and \(\delta _{\mathrm {CP}}\).
The electron momentum versus angle distribution for 28 single-ring electron events with the MC expectation in [58]. The best fit value of \(\sin ^2 2 \theta _{13} = 0.140\) in the normal hierarchy case is used for the expectation
The allowed regions for \(\sin ^2 2 \theta _{13}\) as a function of \(\delta _{\mathrm {CP}}\) are evaluated as shown in Fig. 58, where the values of \(\sin ^2 \theta _{23}\) and \(\varDelta m^2_{32}\) are varied in the fit with the constraint from [60]. In order to be sensitive to \(\delta _{\mathrm {CP}}\), we adopt the PDG2012 value of \(\theta _{13} = 0.098 \pm 0.013\) from reactor experiments [61]. The fit \(-2 \varDelta \ln L\) as a function of \(\delta _{\mathrm {CP}}\) is extracted as shown in Fig. 59. The T2K measurement together with the reactor \(\theta _{13}\) value prefers \(\delta _{\mathrm {CP}} = - \pi /2\) with an exclusion of \(0.19 \pi< \delta _{\mathrm {CP}}< 0.80 \pi ~(-\pi< \delta _{\mathrm {CP}}<- 0.97 \pi \text{ and } -0.04 \pi< \delta _{\mathrm {CP}} < \pi )\) with normal (inverted) hierarchy at the 90% CL. This may be the first hint of CP violation in neutrinos.
The allowed regions for \(\sin ^2 2 \theta _{13}\) as a function of \(\delta _{\mathrm {CP}}\) in the normal (top) and inverted (bottom) mass hierarchy case from [58]. The value of \(\theta _{13}\) from reactor experiments in PDG2012 is shown as the shaded region
The \(-2 \varDelta \ln L\) value as a function of \(\delta _{\mathrm {CP}}\) with the reactor \(\theta _{13}\) constraint for normal and inverted hierarchies from [58]. The likelihood is marginalized over \(\theta _{13}\), \(\theta _{23}\) and \(\varDelta m^2_{32}\). The 90% CL is evaluated using the Feldman–Cousins method, where the \(\delta _{\mathrm {CP}}\) regions with values above the 90% CL lines are excluded
3.7.3 Oscillation analysis
a. Introduction
Hereafter, we present the full oscillation analysis results mainly using data from T2K Run 1-7 [62]. In addition, we also show the recent CP violation result with data from T2K Run 1-8 [63].
The oscillation analysis is conducted by comparing the observations at the far detector with the predictions including the oscillation effects. We precisely predict the neutrino event rate and the energy spectrum at the far detector from the measurements by ND280. We explain the ND280 measurements and how the measurements constrain the uncertainties on the neutrino beam flux and cross sections. The neutrino interaction generator libraries NEUT [38] is used to simulate neutrino interactions in both ND280 and SK. The uncertainties of neutrino interactions in NEUT is primarily determined by external data. Similarly, the neutrino beam flux is simulated by the T2K library with external data introduced in Sect. 3.3. Both uncertainties of neutrino interactions and the beam flux are further constrained by the ND280 measurements. Then, we describe the SK selection to make the event samples in the oscillation analysis. We explain the extraction of the oscillation parameters by fitting the observables with the predictions where all types of uncertainties are properly taken into account. We summarize the final results at the end.
b. ND280 measurements with flux and cross-section tuning
The ND280 measurements have mainly two purposes. One is for the oscillation analysis where the uncertainties on the neutrino beam flux and cross sections are constrained. For this purpose, neutrino and anti-neutrino CC interaction events with a muon are selected since the oscillation effects appear only in the CC interaction with neutrino flavor identification.Footnote 7 The other ND280 purpose is to measure the neutrino cross sections precisely.
ND280 is a magnetized tracking detector as introduced in Sect. 3.6. Neutrinos interacting in FGDs are detected and the tracks from the interaction vertices are reconstructed in TPC operated with the 0.2 T magnetic field. The momenta of charged particles are measured from the track curvatures. We identify a negative muon (\(\mu ^-\)) as the highest negative momentum track in each event originating in FGDs. A positive muon (\(\mu ^+\)) is identified as the highest positive momentum track only in anti-neutrino beam mode. The energy loss of the muon candidate track in TPC is required to be consistent with a muon (see Fig. 51). The energy loss of the charged track in TPC is also used to identify a pion and a proton. The TPC PID and TPC performance are described in more detail in [64].
The events are categorized by the number of pions accompanying the interaction. In the neutrino beam mode, three sample categories containing a negative muon are used: CC-\(0\pi \), CC-\(1\pi ^+\) and CC-other. The CC-\(0\pi \) sample is dominated by CC QE interactions, the CC-\(1\pi ^+\) sample by CC single-\(\pi \) production, and the CC-other sample by CC multi-\(\pi \) production and deep inelastic scattering (DIS). In anti-neutrino beam mode, four sample categories are selected using the charge of the muon and the number of tracks: CC\(\mu ^-\)-1-track, CC\(\mu ^-\)-N-track, CC\(\mu ^+\)-1-track and CC\(\mu ^+\)-N-track. The CC\(\mu ^-\)-1-track sample is dominated by CC QE neutrino interactions, the CC\(\mu ^+\)-1-track by CC QE anti-neutrino interactions, the CC\(\mu ^-\)-N-track by neutrino CC inelastic scattering, and CC\(\mu ^+\)-N-track by anti-neutrino CC inelastic scattering. The events are further categorized by the interactions at FGD1 consisting of scintillators only and FGD2 with a water target between scintillator trackers. By using FGD2, we extract the neutrino cross sections on water, while cross sections on scintillator are measured by FGD1. For each of the selected samples, the numbers of observed events are summarized in Table 14. The small number of events is observed in anti-neutrino beam mode because of the small cross section and the small data set.Footnote 8 In the anti-neutrino beam mode the contamination of wrong-sign neutrinos is expected to be approximately 30%, while the wrong-sign contamination in neutrino mode is only about 4%. The momentum distributions of the CC-\(0\pi \) samples in neutrino beam mode are shown in Fig. 60. More distributions are found in [62]
Muon momentum distributions of the neutrino beam mode CC-\(0\pi \) samples in FGD1 [62]. The dots are data, and the histograms are the predictions by simulation before flux+cross section tuning is applied (Pre-fit). The ratio of data to the prediction is shown in the bottom plot
By using the ND280 measurements, the flux and cross-section models are constrained. A sophisticated analysis is developed to fit the flux and cross-section parameters using the muon momentum and angular distribution data of \(14 \{=(3+4) \times 2\}\) ND280 samples, which correspond to the 3 samples in neutrino mode and the 4 samples in anti-neutrino mode for both FGD1 and FGD2 summarized in Table 14. The flux parameters are for \(\nu _\mu \), \(\overline{\nu }_\mu \), \(\nu _e\) and \(\overline{\nu }_e\) fluxes for both neutrino and anti-neutrino beam modes. The cross-section parameters are used in the modeling of CC QE, multi-nucleon CC interactions, CC single \(\pi \) resonance production, CC/NC coherent \(\pi \) production, NC \(\gamma \) production, Fermi momentum and nucleon binding energy, and final state interactions. The details of the parameterization are found in [62]. Figure 61 shows the result of the flux tuning and Fig. 62 shows that of the cross section parameters. The neutrino cross sections as a function of energy, with an error band corresponding to the uncertainty on the neutrino cross sections due to the error parameters, are shown in Fig. 63. The T2K ND280 measurements improved considerably the understanding of neutrino cross sections in low energy (\(\sim \)1 GeV). The flux parameters at ND280 are fitted together with the cross-section parameters and are used to produce a full correlation matrix with the flux parameters at SK. The correlation matrix of the SK flux and cross-section parameters is shown in Fig. 64. The parameters and uncertainties from Fig. 64 are used in the oscillation analysis described in the following sections.
Energy-dependent neutrino cross-sections divided by energy. The bands are the uncertainties of the model predictions after fitting to the ND280 data. The dashed lines are the prediction of the original model before fitting. Neutrino cross-sections (top) and anti-neutrino cross-sections (bottom) are shown
The correlation matrix of the SK flux and cross section parameters. Parameters \(1 \sim 25\) correspond to the \(\nu _\mu \) flux (1–11), \(\overline{\nu }_\mu \) flux (12–16), \(\nu _e\) flux (17–23), and \(\overline{\nu }_e\) flux (24–25) in neutrino beam mode, parameters \(26 \sim 50\) correspond to \(\nu _\mu \) flux (26–30), \(\overline{\nu }_\mu \) flux (31–41), \(\nu _e\) flux (42–43), and \(\overline{\nu }_e\) flux (44–50) in anti-neutrino beam mode, and parameters \(51 \sim 65\) are cross section parameters
c. SK measurements
The analysis of SK events continues and improves the analyses in the past. T2K events are selected by requiring the coincidence of the event time at SK with the accelerator spill timing added to the time of flight (TOF) of neutrinos from Tokai to Kamioka. Figure 65 shows the time difference (\(\varDelta T_0\)) between the neutrino observation and production with the TOF offset. In Fig. 65, we observe the beam events at \(\varDelta T_0=0\) by a simple selection of Fully-Contained (FC) events with visible energy greater than 30 MeV. The events with \(\varDelta T_0 \ne 0\) are background from atmospheric neutrinos. Figure 66 shows the \(\varDelta T_0\) distribution around 0, where we observe eight bunches due to the accelerator timing structure. From these figures, we can imagine the small number of non-beam background events.
The time difference (\(\varDelta T_0\)) between the neutrino observation and production after subtracting the TOF offset during T2K Run 1-7 [62]. The histograms are stacked
\(\varDelta T_0\) distribution zooming in around 0 showing the accelerator bunch structure [62]
After the timing cut, we select Fully-Contained (FC) Fiducial-Volume (FV) events with a single Cherenkov ring reconstructed. The Cherenkov ring is identified as either an electron-type or a muon-type ring.
Electron neutrino events are further selected by requiring one electron-type ring, a visible energy greater than 100 MeV, no decay electron observed, a reconstructed energy less than 1250 MeV, and not \(\pi ^0\)-like. The not \(\pi ^0\)-like cut is designed to remove events with two photons from a \(\pi ^0\) decay. The details of this cut, called fiTQun, are found in [65]. With \(7.48 \times 10^{20}\) POT neutrino data and \(7.47 \times 10^{20}\) POT anti-neutrino data, we find 32 electron neutrino events with the expected efficiency of 65.6% and 4 anti-electron neutrino events with the efficiency of 70.8%. The predicted numbers of events with \(\delta _{CP}=-\pi /2\) were calculated to be 28.55 events for neutrinos and 6.28 events for anti-neutrinos in the case of normal mass hierarchy. In addition, a new event sample using electron neutrino events with one decay electron is added in neutrino beam mode. The single electron-ring selection predominantly consists of electron neutrino CC interactions. One decay electron could come from a \(\pi \rightarrow \mu \rightarrow e\) pion decay where the pion Cherenkov ring is invisible due to low pion momentum. So, electron neutrino events with one decay electron are predominantly electron neutrino CC single \(\pi \) production events. This sample is called e-like+1\(\pi ^+\). We observe 5 e-like+1\(\pi ^+\) events in neutrino beam mode, with an expectation of 3.14 events. Figure 67 shows the reconstructed neutrino energy distributions of electron neutrino events for both neutrino and anti-neutrino beams. The energy distributions are consistent with electron neutrino appearance.
Muon neutrino events are selected by requiring one muon-like ring, a momentum greater than \(200~\mathrm{MeV}/\mathrm{c}\) and the number of decay electrons to be less than or equal to 1. We observe 135 muon neutrino events with the expectation of 137.76 in neutrino beam mode, and 66 muon neutrino events with the expectation of 68.26 in anti-neutrino beam mode. The selection efficiency after requiring FCFV is calculated to be 90.5% for neutrinos in neutrino beam mode and 95.6% for anti-neutrinos in anti-neutrino beam mode. Figure 68 shows the reconstructed neutrino energy distributions of muon neutrino events in neutrino beam mode and anti-neutrino beam mode. As a result of neutrino oscillations, the energy spectra of muon neutrinos deviate greatly from the original off-axis beam spectra. The observation is consistent with the maximum disappearance of muon neutrinos.
In summary, we use five samples in SK for the oscillation analysis. The numbers of observed events and the MC expectations are summarized in Table 15.
d. Results
In the oscillation analysis, we extract the oscillation parameters by comparing the observations at SK with the expectations. The expected number of events in SK in each lepton momentum and angular bin \((p_k, \theta _k)\) for all five samples are expressed as
where \(P_{\nu _j \rightarrow \nu _k} \) is the oscillation probability, \(\varPhi ^{SK}_{j} \) is the expected neutrino flux at SK, \(\sigma _k\) is cross-section, \(\epsilon \) is the detector efficiency and \(M_{SK}\) is the mass of SK. \(\varPhi ^{SK}_{j} \) and \(\sigma _k\) are predicted based on near detector measurements. The oscillation parameters \(\theta _{12}\) and \(\varDelta m^2_{12}\) are fixed to the values given in PDG2015 [66]: \(\sin ^{2}2\theta _{12}=0.846\), \(\varDelta m^2_{12}=7.53\times 10^{-5}\) eV\(^{2}\). The oscillation parameters are extracted by simultaneously fitting all \(\nu _e\) and \(\nu _\mu \) data samples in neutrino beam mode and anti-neutrino beam mode, summarized in Table 15. The comparison of the observations with the expectations is evaluated by the \(\varDelta \log L\) method. Another fit based on a Markov Chain Monte Carlo (MCMC) is also used as an alternative analysis method.
The predictions of the number of SK events and their uncertainties are calculated based on ND280 constraints. Figure 69 shows the expected energy spectra of electron neutrino events and anti-neutrino events in SK. The original prediction before the constraints by near detector data and the size of the uncertainties are also shown. Figure 70 shows the expected energy spectra of muon events in SK for both neutrino and anti-neutrino beams with the original predictions before the constraints by near detector data and the size of the uncertainties. Table 16 shows the systematic uncertainties on the predicted event rates at SK. The size of the systematic error on the number of events for each sample is 5–6% except for the e-like+1\(\pi ^+\) sample (\(\sim \)15%). The largest error source is the uncertainty due to the flux+cross sections, even after the ND280 constraint. Without constraints by the ND280 measurements, the error size increases up to 12–14%.
By minimizing \(- \varDelta \ln L\), we measure the oscillation parameters \(\delta _{\mathrm {CP}}\), \(\sin ^2 \theta _{13}\), \(\sin ^2 \theta _{23}\), and \(\varDelta m^2_{32(13)}\). The best fit values and 1D confidence intervals of \(\delta _{\mathrm {CP}}\) and \(\sin ^2 \theta _{13}\) under the constant \(\varDelta \chi ^2 (\equiv -2 \varDelta \ln L)\) approximation are shown in Table 17. The result of \(\sin ^2 \theta _{13}\) is consistent with the more precise value measured by reactor \(\theta _{13}\) experiments as given in PDG 2015 [66]. Figure 71 shows one-dimensional \(\varDelta \chi ^2\) distributions of \(\delta _{\mathrm {CP}}\) and \(\sin ^2 \theta _{13}\). Figure 72 shows the two-dimensional \(\varDelta \chi ^2\) contour of \(\sin ^2 \theta _{13}\) versus \(\delta _{\mathrm {CP}}\).
Hereafter, we constrain the value of \(\theta _{13}\) to \(\sin ^2 2 \theta _{13} = 0.085 \pm 0.005\) from [66] measured by reactor experiments because it is more precise than the measurement by T2K. We perform an oscillation analysis with this \(\theta _{13}\) constraint. The best fit values of the parameters are obtained as shown in Table 18. With the \(\theta _{13}\) constraint, we obtain more precise measurements, especially for \(\delta _{\mathrm {CP}}\).
Figure 73 shows the 90% constant \(\varDelta \chi ^2\) surface in the \(\sin ^2 \theta _{23} - \varDelta m^2_{32}\) plane in the case of normal mass ordering. The measurements of the parameters \(\sin ^2 \theta _{23}\) and \(\varDelta m^2_{32}\) by T2K are one of the most precise today. The T2K result is consistent with other measurements as shown in Fig. 73, although the MINOS and NOvA measurements [69, 70] have some tension with T2K. The NOvA and T2K collaborations are jointly investigating the source of the tension.
In 2018, we updated the CP violation result by adding the T2K Run 8 data-set, using data corresponding to a total exposure of \(14.7 \times 10^{20}\) POT in neutrino mode. With the new data-set, we observed 89 electron neutrino candidate events in total, while 67.5 are expected for \(\delta _{\mathrm {CP}}=0\) and normal mass ordering. Figure 74 shows one-dimensional \(\varDelta \chi ^2\) distributions of \(\delta _{\mathrm {CP}}\). The Feldman-Cousins method with critical \(\varDelta \chi ^2\) values is used to calculate the \(2 \sigma \) confidence level. The improved measurement of \(\delta _{\mathrm {CP}}\) shows an indication of CP violation, and the obtained \(2 \sigma \) confidence interval for \(\delta _{\mathrm {CP}}\) does not include the CP-conserving cases (\(\delta _{\mathrm {CP}}=0, \pi \)).
The primary oscillation results presented so far are based on the frequentist approach. We also adopt the Bayesian approach by using a MCMC technique where we evaluate the posterior probability marginalized over nuisance parameters. The results by the MCMC are consistent with the primary results [62]. Figure 75 shows the marginal posterior probability in each two-parameter space, together with the one-dimensional posterior probability densities. The posterior probabilities for the mass orderings and \(\sin ^2 \theta _{23}\) octant are also evaluated as shown in Table 19. The results slightly prefer the normal mass ordering with \(\sin ^2 \theta _{23}>0.5\).
The 1D \(-2 \varDelta \ln L\) distributions as a function of \(\delta _{\mathrm {CP}}\) for normal (black) and inverted (red) mass ordering using the reactor \(\theta _{13}\) value in the PDG 2016 [67]. The vertical lines show the corresponding allowed \(2 \sigma \) confidence intervals evaluated by the Feldman–Cousins method
Two-dimensional histograms of the marginal posterior probability with a 90% (\(1 \sigma \)) credible interval given by the white solid (dashed) lines [62]. The one-dimensional histograms represent the posterior probability density where all other parameters are marginalized. The blue areas are the \(1 \sigma \) (dark), 90% (medium), and 95% (light) credible intervals
3.7.4 Other measurements
In addition to neutrino oscillation studies, T2K conducts various measurements of neutrino-nucleus cross-sections by using both the ND280 and SK detectors. The measurements are important to understand neutrino-nucleus interactions and to model them better, which would impact on a reduction of the systematic uncertainties of neutrino oscillation measurements shown in Table 16.
The cross-sections measured in T2K are summarized in Table 20. In the beginning, T2K measured the muon neutrino Charged Current (CC) inclusive cross sections with the T2K off-axis near detector (ND280) [73] and the on-axis near detector (INGRID) [74] as a first step. Later, these analyses became more sophisticated and were able to measure exclusive channels, such as CC-QE [75, 76], CC with no pion [77], CC 1\(\pi \) production [78], and CC-coherent \(\pi \) [79] including the energy-dependence of some cross sections. The nuclear-dependence was also intensively studied. At the position of the on-axis near detector, two new detectors, one with a plastic (CH) target and the other with a water (\(\mathrm{H}_2\mathrm{O}\)) target, were installed to measure cross sections on different target materials. By using these detectors with INGRID, which has an iron target, the CC inclusive cross sections on iron, plastic, and water targets, and the ratios of cross sections were measured. With ND280, the electron neutrino CC inclusive cross sections were measured [80, 81] using the powerful particle identification performance of the TPC and ECal. In the analysis described in [81], the electron neutrino contamination in the beam is measured relative to the prediction by simulation. The measurement is also divided into two contributions: electron neutrinos from kaon decays and from muon decays. The Neutral Current (NC) nuclear de-excitation gamma-ray production cross-section in neutrino-oxygen interactions was also studied [82, 83] using the far detector, Super-Kamiokande. The NC nuclear de-excitation gamma-ray production process is considered a serious background from atmospheric neutrinos when we search for a signal of Supernova relic neutrinos. From year 2014 onward, an anti-neutrino beam was available to study CP violation in neutrino oscillations. The anti-neutrino beam was also utilized to measure anti-neutrino cross sections [84, 85].
As an advanced analysis, final-state proton multiplicities, muon and proton kinematics, and their correlations in charged-current pion-less neutrino interactions are measured by the ND280 detector in its plastic scintillator (C8H8) target [86]. Thanks to the exploration of the proton kinematics and imbalances between the proton and muon kinematics, the results offer a novel probe of the nuclear-medium effects most pertinent to (sub-)GeV neutrino-nucleus interactions.
All of the results are compared to predictions by the neutrino interaction generator libraries NEUT [38] and GENIE [87], and are used to improve the models in those libraries. T2K advanced the measurements of neutrino and anti-neutrino cross sections and contributed to improving the theoretical models useful for future CP violation measurements.
3.7.5 Search for new physics
Besides measurements of neutrino oscillations and neutrino-nucleus cross sections, T2K has performed searches for physics beyond the standard model.
Most data from the studies of neutrino oscillations are consistent with the three flavor paradigm. However, some experiments have reported deviations from the three flavor scheme that could be explained by a fourth neutrino with a mass difference \(\varDelta m^2 \sim 1\ \mathrm{\mathrm eV}^2\) from the three standard neutrinos. A search for light sterile neutrinos was carried out using the long-baseline T2K beam data at SK [94]. In addition to the standard samples described in Sect. 3.7.3, neutral-current interaction samples are also used to enhance the sensitivity to sterile mixing. No evidence of sterile neutrino mixing in the \(3 + 1\) model was found from a simultaneous fit to the CC muon, electron, and NC samples. We set the most stringent limit on the sterile oscillation amplitude \(\sin ^2 \theta _{24}\) for the sterile neutrino mass splitting \(\varDelta m^2_{41}<3 \times 10^{-3}\ \mathrm{\mathrm eV}^2\). Another search for sterile neutrinos was also conducted using short-baseline data from ND280 with a limited sensitivity [95].
Motivated by neutrino mass generation mechanisms such as the see-saw mechanism, right-handed heavy neutrinos are predicted. In the T2K beam, heavy neutrinos can be produced from kaon decays and then subsequently decay in ND280. The decays of \(N \rightarrow l_\alpha ^{\pm } \pi ^\mp \) and \(N \rightarrow l_\alpha ^{\pm } l_\beta ^{\mp } \nu \) (\(\alpha , \beta = e, \mu \)) are searched for using the ND280 TPC, where the background was reduced to less than two events [96]. No excess was observed, setting the upper limits on the mixing elements of heavy neutrinos to electron-, muon-, and tau- flavored currents (\(U^2_e\), \(U^2_\mu \), \(U^2_\tau \)), e.g., \(U^2_e<10^{-9}\) at the 90% C.L. for a heavy neutrino mass of 390 \(\mathrm{\mathrm MeV/c}^2\).
An extension of the Standard Model allows Lorentz and CPT violations. The effect of such violations could be observed as sidereal modulations in the neutrino event rate. Using a large amount of neutrino data collected by INGRID, sidereal modulations were checked [97]. No signal was observed and T2K sets limits on associated Lorentz and CPT-violating terms from the extension of the Standard Model. The results imply Lorentz and CPT violations are suppressed by a factor of more than \(10^{20}\) at the GeV scale.
3.7.6 Summary of T2K results
A new oscillation channel, \(\nu _\mu \rightarrow \nu _e\), with a mass difference \(\varDelta m^2 \sim 2.5 \times 10^{-3}\ \mathrm{\mathrm eV}^2\) was discovered by T2K. The \(\nu _\mu \rightarrow \nu _e\) oscillation is a consequence of nonzero \(\theta _{13}\) and affects the CP violation phase \(\delta _{\mathrm {CP}}\) in the three-generation scheme. The T2K results indicate CP violation at 2 \(\sigma \) confidence level and prefer the normal mass ordering. The most precise measurements of neutrino oscillation parameters \(\theta _{23}\) and \(\varDelta m^2_{23}\) are also reported. In addition to the three-generation neutrino oscillation, T2K provides many measurements of neutrino-nucleus cross-sections and search for new physics beyond the standard model such as a heavy neutral lepton, fourth-generation scheme, CPT violation, etc..
At the time beginning of 2020 when writing this summary, T2K has collected \(22.3 \times 10^{20}\) POT data (\(14.7 \times 10^{20}\) POT in neutrino beam mode and \(7.6 \times 10^{20}\) POT in anti-neutrino beam mode) [63], which corresponds to 29% of the approved POT goal (\(7.8 \times 10^{21}\) POT). We continue data taking and keep producing interesting physics results until the next-generation experiment, Hyper-Kamiokande, comes in operation.
4 Prospect of T2K
The future T2K running focusses on investigating the issue of CP violation. There is a plan to upgrade the J-PARC accelerator in order to increase the repetition rate of the acceleration cycle by installing a new power supply system. With the upgrade scheduled in 2021, the beam power of J-PARC will reach 750 kW or higher. The J-PARC accelerator has the potential to achieve an even higher beam power, up to 1300 kW. The T2K collaboration proposes to search for neutrino CP violation with a sensitivity of \(3 \sigma \) in the case of maximum CP violation by extending the T2K run with a total of \(20 \times 10^{21}\) POT [98]. The T2K neutrino beamline will also be upgraded to accept the 1300 kW high-power beam [99]. Figure 76 shows the expected POT for T2K with the J-PARC and T2K beamline upgrades. With the upgraded accelerator and improvements to the analysis, T2K could reach \(3 \sigma \) sensitivity to neutrino CP violation with \(\sim 15 \times 10^{21}\) POT as shown in Fig. 77. The T2K near detector is also being upgraded to extend and improve its acceptance for particles produced in neutrino interactions [100]. There is a great chance to investigate the existing hint of neutrino CP violation and to establish its existence in the near future.
Expected POT with an extension of T2K. [98]
The sensitivity of T2K as a function of data accumulation (POT) with analysis improvements [98]
5 Summary and outlook
The discovery of neutrino oscillations has opened a new field and has generated a great impact both experimentally and theoretically. The series of experiments, SK [43], SNO [101], KamLAND [44], K2K, MINOS [102], and T2K confirmed the existence of neutrino oscillations and unraveled several outstanding properties. The neutrino oscillations are described by three mixing angles, CP phase and mass squared differences with the three-generation neutrino scheme. There are two distinct values for the mass difference, showing that neutrino mass has at least two, most likely three nonzero values. As presented in this review, the K2K experiment discovered neutrino oscillations in the KEK neutrino beam and precisely determined one of the mass squared difference, \(\varDelta m^2_{23}=m^2_{3}-m^2_{2}\sim 2.5\times 10^{-3}\ \mathrm{\mathrm eV}^{2}\). The succeeding T2K experiment discovered oscillations between \(\nu _{\mu }\) and \(\nu _e\). This is evidence of non-zero \(\theta _{13}\). The \(\nu _{\mu } \rightarrow \nu _e\) oscillation involves all three mass eigenstates, and the study of possible CP violation in the lepton sector becomes reality. At present (2020), the T2K experiment sees a hint of CP violation in neutrino oscillations at \(2 \sigma \) confidence level.
We face new and urgent questions in neutrino physics: Mass hierarchy, Octant ambiguity, Unitarity, and CP violation. Addressing these questions requires new experiments with higher precision. In fact, this will be achieved by two new large projects: the recently approved Hyper-Kamiokande (Hyper-K) project [103] in Japan, the successor of the SK and T2K experiments, and the new experiment DUNE [104] in the USA. The Hyper-K has a 260 kton water tank in which the 190 kton of fiducial volume, ten times larger than that of SK is used for the detection of neutrinos. With the larger mass and improving instruments, Hyper-K has much better sensitivity to neutrino oscillations, neutrino astronomy, nucleon decay, etc. With the upgraded J-PARC, we explore neutrino CP violation with more than \(5\ \sigma \) sensitivity and search for new physics beyond the three-generation scheme. To probe the GUT, the sensitivity of the proton decay will be improved by a factor of 10 up to the lifetime of \(10^{35}\) years or longer for the \(p \rightarrow e^+ \pi ^0\) decay mode and \(3 \times 10^{34}\) years for \(p \rightarrow \bar{\nu } K^+\). Hyper-K has a great discovery potential of the proton decay with many decay channels. Hyper-K is also a unique observatory of neutrino astronomy and studies of astroparticle physics, such as dark matter, using neutrinos.
In conclusion, neutrino research has a rich future program and promises a major impact on particle physics and cosmology.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: I review two experiments: K2K and T2K in this paper. K2K is old, and the data are not available. For T2K, some data are found in https://t2k-experiment.org/publications/.]
Notes
The precision of the beam orientation was estimated with the position accuracy of two locations with the distance of about 100 m for the K2K neutrino beam line at KEK.
The corresponding kaon flux above the 2 GeV/c pion threshold is negligible.
K2K-IIb is defined in Table 5.
INS is Institute of Nuclear Study in the University of Tokyo. It became a part of KEK in 1997.
JAERI is Japan Atomic Energy Research Institute. It became a part of JAEA (Japan Atomic Energy Agency) in 2005.
The design value is 320 kA.
Although the NC interaction is important to understand the background events in the oscillation analysis, external data are used to constrain the NC interaction.
The ND280 data in neutrino beam mode is \(5.81 \times 10^{20}\) POT, and data in anti-neutrino is \(2.84 \times 10^{20}\) POT.
References
M. Fukugita, T. Yanagida, Phys. Lett. B 174, 45 (1986)
C.L. Bennett et al., Astrophys. J. 464, L1 (1996)
G. Hinshaw et al., WMAP collaboration. Astrophys. J. Suppl. 208, 19 (2013)
B.T. Cleveland, T. Daily, R. Davis Jr., J.R. Distel, K. Lande, C.K. Lee, P.S. Wildenhain, J. Ullman, Astrophys. J. 496, 505 (1998)
D.H. Perkins, Eur. Phys. J. H 39(5), 505 (2014)
E. Eskut et al., CHORUS collaboration. Nucl. Instrum. Meth. A 401, 7 (1997)
J. Altegoer et al., NOMAD collaboration. Nucl. Instrum. Meth. A 404, 96 (1998)
K.S. Hirata et al., Kamiokande-II collaboration. Phys. Lett. B 205, 416 (1988)
K.S. Hirata et al., Kamiokande-II collaboration. Phys. Lett. B 280, 146 (1992)
Y. Fukuda et al., Kamiokande collaboration. Phys. Lett. B 335, 237 (1994)
M. Koshiba, Summary report on long baseline neutrino oscillation, in Workshop on Physics at the Main Injector (to be followed by Fermilab Annual Users Meeting May 19–20), 16–18 May 1989. Batavia, Illinois
A. Cervera, A. Donini, M.B. Gavela, J.J.G. Cadenas, P. Hernandez, O. Mena, S. Rigolin, Nucl. Phys. B 579, 17 (2000). [Erratum-ibid. B 593, 731 (2001)]
M. Freund, Phys. Rev. D 64, 053003 (2001)
C. Jarlskog, Phys. Rev. Lett. 55, 1039 (1985)
D. Casper et al., Phys. Rev. Lett. 66, 2561 (1991)
C. Berger et al., Frejus collaboration. Phys. Lett. B 227, 489 (1989)
M. Aglietta et al., NUSEX collaboration. Europhys. Lett. 8, 611 (1989)
M.C. Goodman, Soudan-2 collaboration. Nucl. Phys. Proc. Suppl. 38, 337 (1995)
W.W.M. Allison et al., Phys. Lett. B 391, 491 (1997). https://doi.org/10.1016/S0370-2693(96)01609-7. arXiv:hep-ex/9611007
S. Kasuga et al., Phys. Lett. B 374, 238 (1996)
K. Nishikawa, textit A Possible long baseline neutrino oscillation experiment using KEK PS and Super-Kamiokande, in INS-Rep.-924, April 1992, KEK Preprint 93–55
M.H. Ahn et al., K2K collaboration. Phys. Rev. D 74, 072003 (2006)
J.R. Sanford, C.L. Wang, Brookhaven National Laboratory, AGS internal report, PRINT-67-1023, BNL-11299, BNL-11479) (unpublished)
L.A. Ahrens et al., Phys. Rev. D 34, 75 (1986)
K. Nishikawa et al. KEK-PS E362 (K2K) proposal
K. Nishikawa, Nucl. Phys. Proc. Suppl. 59, 289 (1997)
J.A. Formaggio, G.P. Zeller, Rev. Mod. Phys. 84, 1307 (2012)
Y. Cho et al., Phys. Rev. D 4, 1967 (1971)
C.L. Wang, Phys. Rev. Lett. 25, 1068 (1970)
T. Inagaki. Measurement of the Disappearance of Muon Neutrino in 250 km Long Base Line Experiment. https://www-he.scphys.kyoto-u.ac.jp/theses/doctor/inagaki_dt.pdf (2001)
M.G. Catanesi et al., HARP collaboration. Nucl. Phys. B 732, 1 (2006)
T.A. Gabriel, J.D. Amburgey, B.L. Bishop, CALOR: A Monte Carlo Program Package for the Design and Analysis of Calorimeter Systems, in ORNL/TM-5619
C. Zeitnitz, T.A. Gabriel, Nucl. Instrum. Meth. A 349, 106 (1994)
A. Fasso, A. Ferrari, J. Ranft, P.R. Sala, Conf. Proc. C 9309194, 493 (1993)
H. Fesefeldt, The Simulation of Hadronic Showers: Physics and Applications, in PITHA-85-02
M. Kohama. http://ppwww.phys.sci.kobe-u.ac.jp/seminar/pdf/kohama-mron.pdf (1997) (in Japanese)
T. Maruyama, First Observation of Accelerator origin Neutrino Beam after passing through 250 km of Earth. http://hdl.handle.net/10097/38809 (2000)
Y. Hayato, Acta Phys. Polon. B 40, 2477 (2009)
S. Eidelman et al., Particle data group. Phys. Lett. B 592(1–4), 1 (2004)
K. Nishikawa et al. J-PARC E11 (T2K) proposal. http://j-parc.jp/researcher/Hadron/ en/pac_0606/pdf/p11-Nishikawa.pdf
Y. Itow et al. T2K collaboration. https://arxiv.org/abs/hep-ex/0106019
Y. Suzuki, Eur. Phys. J. C 79(4), 298 (2019)
A. Suzuki, Eur. Phys. J. C 74(10), 3094 (2014)
Q.R. Ahmad et al., SNO collaboration. Phys. Rev. Lett. 89, 011302 (2002)
Y. Abe et al., Double Chooz collaboration. Phys. Rev. Lett. 108, 131801 (2012)
F.P. An et al., Daya Bay collaboration. Phys. Rev. Lett. 108, 171803 (2012)
J.K. Ahn et al. RENO collaboration. Phys. Rev. Lett. 108, 191802 (2012)
M. Apollonio et al., CHOOZ collaboration. Eur. Phys. J. C 27, 331 (2003)
G.L. Fogli, E. Lisi, A. Marrone, A. Palazzo, A.M. Rotunno, Phys. Rev. Lett. 101, 141801 (2008)
S. Yamamoto et al., K2K collaboration. Phys. Rev. Lett. 96, 181801 (2006)
High-intensity Proton Accelerator Project Team. Accelerator Technical Design Report for High-intensity Proton Accelerator Facility Project, J-PARC”, JAERI-Tech 2003-044, KEK Report 2002-13. https://jopss.jaea.go.jp/ pdfdata/JAERI-Tech-2003-044.pdf
J. Anderson et al. The 9th Lake Louise Winter School, TRI-PP-94-34 (1994)
N. Abgrall et al., NA61/SHINE collaboration. Eur. Phys. J. C 76(11), 617 (2016)
K. Abe et al., T2K collaboration. Nucl. Instrum. Meth. A 659, 106 (2011)
K. Abe et al., T2K collaboration. Phys. Rev. D 87, 012001 (2013)
K. Abe et al., T2K collaboration. Phys. Rev. Lett. 107, 041801 (2011)
K. Abe et al., T2K collaboration. Phys. Rev. Lett. 112, 061802 (2014)
K. Abe et al., T2K collaboration. Phys. Rev. D 88(3), 032002 (2013)
K. Abe et al., T2K collaboration. Phys. Rev. Lett. 111(21), 211803 (2013)
J. Beringer et al., Particle Data Group collaboration. Phys. Rev. D 86, 010001 (2012)
K. Abe et al., T2K collaboration. Phys. Rev. D 96(9), 092006 (2017). (Erratum: [Phys. Rev. D 98, no. 1, 019902 (2018)])
K. Abe et al., T2K collaboration. Phys. Rev. Lett. 121(17), 171802 (2018)
N. Abgrall et al., T2K ND280 TPC collaboration. Nucl. Instrum. Meth. A 637, 25 (2011)
R.B. Patterson, E.M. Laird, Y. Liu, P.D. Meyers, I. Stancu, H.A. Tanaka, Nucl. Instrum. Meth. A 608, 206 (2009)
K.A. Olive et al., Particle Data Group. Chin. Phys. C 38, 090001 (2014)
C. Patrignani et al., Particle Data group. Chin. Phys. C 40(10), 100001 (2016). https://doi.org/10.1088/1674-1137/40/10/100001
E.G. Fuller, Phys. Rep. 127, 187 (1985)
P. Adamson et al., NOvA collaboration. Phys. Rev. Lett. 118(15), 151802 (2017)
P. Adamson et al., MINOS collaboration. Phys. Rev. Lett. 110(25), 251801 (2013)
R. Wendell, Super-Kamiokande collaboration. PoS ICRC 2015, 1062 (2016)
M.G. Aartsen et al., Nucl. Phys. B 908, 161 (2016)
K. Abe et al., T2K collaboration. Phys. Rev. D 87, 092003 (2013)
K. Abe et al., T2K collaboration. Phys. Rev. D 90(5), 052010 (2014)
K. Abe et al., T2K collaboration. Phys. Rev. D 92(11), 112003 (2015)
K. Abe et al., T2K collaboration. Phys. Rev. D 91(11), 112002 (2015)
K. Abe et al., T2K collaboration. Phys. Rev. D 93(11), 112012 (2016)
K. Abe et al., T2K collaboration. Phys. Rev. D 95(1), 012010 (2017)
K. Abe et al., T2K collaboration. Phys. Rev. Lett. 117(19), 192501 (2016)
K. Abe et al., T2K collaboration. Phys. Rev. Lett. 113(24), 241803 (2014)
K. Abe et al., T2K collaboration. Phys. Rev. D 89(9), 092003 (2014). [Addendum-ibid. D 89, no. 9, 099902 (2014)] [Erratum-ibid. D 89, no. 9, 099902 (2014)]
K. Abe et al., T2K collaboration. Phys. Rev. D 90(7), 072012 (2014)
K. Abe et al., T2K collaboration. Phys. Rev. D 100(11), 112009 (2019)
K. Abe et al., T2K collaboration. Phys. Rev. D 96(5), 052001 (2017)
K. Abe et al. T2K collaboration. arXiv:1908.10249 [hep-ex]
K. Abe et al., T2K collaboration. Phys. Rev. D 98(3), 032003 (2018)
C. Andreopoulos, A. Bell, D. Bhattacharya, F. Cavanna, J. Dobson, S. Dytman, H. Gallagher, P. Guzowski et al., Nucl. Instrum. Meth. A 614, 87 (2010). arXiv:0905.2517 [hep-ph]
K. Abe et al. T2K collaboration. arXiv:1904.09611 [hep-ex]
K. Abe et al., T2K collaboration. Phys. Rev. D 98, 012004 (2018)
K. Abe et al., T2K collaboration. Phys. Rev. D 97(1), 012001 (2018)
K. Abe et al., T2K collaboration. Phys. Rev. D 93(7), 072002 (2016)
K. Abe et al., T2K collaboration. J. Phys. G 46(8), 08LT01 (2019)
K. Abe et al., T2K collaboration. Phys. Rev. D 97(3), 032002 (2018)
K. Abe et al., T2K collaboration. Phys. Rev. D 99(7), 071103 (2019)
K. Abe et al., T2K collaboration. Phys. Rev. D 91, 051102 (2015)
K. Abe et al., T2K collaboration. Phys. Rev. D 100(5), 052006 (2019)
K. Abe et al., T2K collaboration. Phys. Rev. D 95(11), 111101 (2017)
K. Abe et al. T2K collaboration. arXiv:1609.04111 [hep-ex]
K. Abe et al. T2K collaboration and J-PARC Neutrino Facility Group. arXiv:1908.05141 [physics.ins-det]
K. Abe et al. T2K collaboration. arXiv:1901.03750 [physics.ins-det]
B. Aharmim et al., SNO collaboration. Phys. Rev. C 88, 025501 (2013)
P. Adamson et al. MINOS collaboration. Phys. Rev. D 77, 072002 (2008). https://doi.org/10.1103/PhysRevD.77.072002. arXiv:0711.0769 [hep-ex]
K. Abe et al. Hyper-Kamiokande collaboration. arXiv:1805.04163 [physics.ins-det]
R. Acciarri et al. DUNE collaboration. arXiv:1601.05471 [physics.ins-det]
Acknowledgements
The former KEK Director General, H. Sugawara, made long baseline experiments a reality in Japan. The Kamiokande experiment led by Prof. Masatoshi Koshiba was the start of a series of experiments in Kamioka. We also thank the KEK accelerator group, the J-PARC accelerator group and all K2K and T2K collaborators. My coauthor, Koichiro Nishikawa, was the founder of the K2K experiment and the first spokesperson of the T2K experiment. He deceased during the write up of this review. Koichiro was a marvelous colleague and a dear friend of mine.
Author information
Authors and Affiliations
Corresponding author
Additional information
Deceased: Koichiro Nishikawa.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Nakaya, T., Nishikawa, K. Long baseline neutrino oscillation experiments with accelerators in Japan. Eur. Phys. J. C 80, 344 (2020). https://doi.org/10.1140/epjc/s10052-020-7906-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-7906-x