1 Introduction

Currently, a large number of cosmological inflationary models are being studied on the basis of various types of exotic matter [1,2,3] and modifications of Einstein’s theory of gravity [4,5,6,7,8]. These models of the early universe can be considered as a development of the first cosmological inflation models based on the evolution of a certain scalar field and Einstein’s gravity [9,10,11,12,13,14,15,16]. The reasons for modifying the original inflationary models are the need to build a quantum theory of gravity [17] and explain the repeated accelerated expansion of the universe in the present era [18, 19].

One of the first modifications of GR is the scalar–tensor gravity theories [20, 21]. This type of modified gravity theories successfully solves the problems of constructing consistent scenarios for the evolution of the early universe and its repeated accelerated expansion. It should also be noted that the speed of propagation of gravitational waves in the case of scalar–tensor theories of gravitation is equal to the speed of light in vacuum, as in the case of Einstein’s gravity [22, 23], which corresponds to recent measurements of the characteristics of gravitational waves from black holes and neutron stars mergers [24].

There are various types of scalar–tensor theories of gravity, one of which is the case of non-minimal coupling of a material scalar field and curvature. The construction of inflationary scenarios based on these theories of gravity has been carried out in many studies using exact and approximate solutions of the equations of cosmological dynamics [20, 21, 25,26,27,28,29]. The main criterion for the correctness of the constructed models of the early universe based on the inflationary paradigm is the compliance of the spectral parameters of cosmological disturbances with the observational constraints obtained from measurements of the anisotropy and polarization of CMB [30].

We note that the main parameters characterizing the type of cosmological model of the early universe are the potential of a scalar field \(V(\phi )\), the non-minimal coupling function \(F(\phi )\), which determines the physical processes that occur at the inflationary stage, and the Hubble parameter H(t) corresponding to the dynamics of accelerated expansion. Therefore, it is possible to determine the relations between these parameters that gives the models corresponding to the observational data for some class of cosmological models.

In this paper, we study cosmological models based on the relation \(H=\lambda \sqrt{F}\) with exponential power-law (EPL) dynamics \(H(t)=\frac{m}{t}+\lambda \). This case is interesting in that it is a combination of de Sitter and Friedmann solutions, which implies a transition between these stages under certain conditions.

The determination of a priori given relations between the parameters of cosmological models or “ansatzes” is often used to analyze them both for the case of Einstein gravity [16, 31,32,33] and its modifications [34,35,36,37,38]. On the one hand, the use of ansatzes makes it possible to obtain exact analytical solutions of the dynamic equations, on the other hand, on the basis of this method it is possible to single out cases that have the correct physical interpretation.

As example of such an approach, we can mention the models of cosmological inflation with “constant roll” based on GR, f(R)-gravity and scalar–tensor gravity [32,33,34,35]. It is also possible to give many other examples of the use of anasatzes to construct and analyze the cosmological models (for example, see [16, 31, 36,37,38]).

The physical content of the relation \(H=\lambda \sqrt{F}\) in the inflationary models based on GSTG is that the non-minimal coupling of a scalar field and curvature, otherwise the deviations from Einstein gravity, induce the corresponding deviations from a pure exponential expansion and the deviations of its potential from the constant [27]. Also, for any potential of a scalar field in these models, the observational constraints on the spectral parameters of cosmological perturbations will be satisfied. Thus, the initial problem of analyzing inflationary models in this case is reduced to reconstructing the parameters of the scalar–tensor gravity theory and the evolution of the scalar field for a known potential, which is the main objective of this article.

The article is organized as follows. In Sect. 2 we represent the action of the GSTG model and its connection to GR with a scalar field. The dynamic equations in the Friedmann–Robertson–Walker metric for GSTG are displayed. Section 3 contains the choice of the quadratic connection between Hubble parameter and coupling function of the specific kind, which then is applied for obtaining a general form of the solution for the exponential power-law expansion. Accelerated period, exit from early inflation and the second accelerated expansion stage are studied for such expansion. The exact solutions for a generalized polynomial potential and for its partial cases (polynomial and exponential) are represented in Sect. 4. All cosmological parameters are defined by the choice of one generating function \(\Psi (\phi )\) for these EPL inflationary models. In Sect. 5 we represent the reconstructed models from physically motivated potentials, namely the Higgs, Higgs–Starobinsky, Coleman–Weinberg and massive scalar field potentials. Section 6 is devoted to a calculation of the cosmological parameters for the model under consideration and contains the proof of the satisfaction of the model’s prediction against observational restrictions. As a result, we find that the EPL-models based on the GSTG under consideration correspond to observational constraints on the parameters of cosmological perturbation for any \(m>0\) and we estimated the value of the parameter \(\lambda \) as well. In Sect. 7 we summarize the results of our investigation.

2 The model and cosmology equations

The generalized scalar–tensor theory is described by the action [20, 21]

$$\begin{aligned} S_\mathrm{(STG)}= & {} \int d^4x\sqrt{-g}\Big [\frac{1}{2}F(\phi ) R \nonumber \\&- \frac{\omega (\phi )}{2}g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu } \phi - V(\phi )\Big ] +S^{(m)}, \end{aligned}$$
(1)
$$\begin{aligned} S^{(m)}= & {} \int d^4x\sqrt{-g} {{\mathcal {L}}}^{(m)}, \end{aligned}$$
(2)

where the Einstein gravitational constant \( \kappa =1\), g is the determinant of the space-time metric tensor \(g_{\mu \nu }\), \(\phi \) is a scalar field with the potential \(V=V(\phi )\), \(\omega (\phi )\) and \(F(\phi )\) are differentiable functions of \(\phi \) which define the type of gravity theory, R is the Ricci scalar of the space-time, and \({{\mathcal {L}}}^{(m)}\) the Lagrangian of the matter. In the present article we will study the case of vacuum solutions for the model (1) suggesting that \( S^{(m)}=0\).

The action of the scalar field Einstein gravity is

$$\begin{aligned} S_{(GR)}= & {} \int d^4x\sqrt{-g}\nonumber \\&\times \left[ \frac{R}{2} - \frac{1}{2}g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu } \phi -V(\phi )\right] . \end{aligned}$$
(3)

Let us remind the reader that the scalar field \(\phi \) is a gravitational field in the action (1), while the scalar field \(\phi \) in the action (3) is the source of the gravitation and it is a non-gravitational (material) field.

Considering the gravitational and scalar field equations of the models (1) and (3) in the Friedman universe we use the choice of natural units, including \( \kappa =1\). Therefore we could not distinguish between gravitational and non-gravitational (material) scalar fields. Thus, the solutions of the model’s equations should be related to the subsequent situation. That is, from the physical point of view, the solutions will correspond to different theories of gravity.

Let as note also that the cosmological constant \(\Lambda \) can be extracted from the constant part of the potential \(V(\phi )\); therefore we did not include it in the actions (1) and (3).

To describe a homogeneous and isotropic universe we chose the Friedmann–Robertson–Walker (FRW) metric in the form

$$\begin{aligned} \mathrm{d}s^2= & {} -\mathrm{d}t^2+a^2(t)\Biggl (\frac{\mathrm{d} r^2}{1-k r^2}\nonumber \\&+r^2 \left( \mathrm{d}\theta ^2+\sin ^2\theta d\varphi ^2\right) \Biggr ), \end{aligned}$$
(4)

where a(t) is a scale factor, the constant k is the indicator of universe’s type: \( k>0,~k=0,~k<0 \) are associated with closed, spatially-flat, and open universes, respectively.

The cosmological dynamic equations for the STG theory (1) in a spatially-flat FRW metric are [22]

$$\begin{aligned} E_{1}\equiv & {} 3FH^{2}+3H{\dot{F}}-\frac{\omega }{2}{\dot{\phi }}^{2}-V(\phi )=0, \end{aligned}$$
(5)
$$\begin{aligned} E_{2}\equiv & {} 3FH^{2}+2H{\dot{F}}+2F{\dot{H}}+{\ddot{F}}\nonumber \\&+\frac{\omega }{2}{\dot{\phi }}^{2}-V(\phi )=0, \end{aligned}$$
(6)
$$\begin{aligned} E_{3}\equiv & {} \omega \ddot{\phi } + 3\omega H{\dot{\phi }} +\frac{1}{2}{\dot{\phi }}^{2}\omega '_{\phi }+V'_{\phi }-6H^{2}F'_{\phi }\nonumber \\&-3{\dot{H}}F'_{\phi }= 0, \end{aligned}$$
(7)

where a dot represents a derivative with respect to the cosmic time t, \(H \equiv {\dot{a}}/a\) is the Hubble parameter and the prime denotes a derivative w.r.t. the scalar field, for example: \(F'_{\phi } = \partial F/\partial \phi \).

From the Bianchi identities one has

$$\begin{aligned} {\dot{\phi }}E_{3}+{\dot{E}}_{1}+3H(E_{1}-E_{2})=0; \end{aligned}$$
(8)

thus, only two of Eqs. (5)–(7) are independent. For this reason, the scalar field Eq. (7) can be derived from Eqs. (5)–(6); these completely describe the cosmological dynamics and we will deal with the GSTG gravity equations only. We have

$$\begin{aligned}&3FH^{2}+3H{\dot{F}}=\frac{\omega (\phi )}{2}{\dot{\phi }}^{2}+V(\phi ), \end{aligned}$$
(9)
$$\begin{aligned}&H{\dot{F}}-2F{\dot{H}}-{\ddot{F}}=\omega (\phi ){\dot{\phi }}^{2}. \end{aligned}$$
(10)

We will refer to Eqs. (9)–(10) as the GSTG cosmology equations.

If \(F=1\) Eqs. (9)–(10) are reduced to those for scalar field Friedmann (inflationary) cosmology from GR,

$$\begin{aligned}&3H^{2}=\frac{\omega (\phi )}{2}{\dot{\phi }}^{2}+V(\phi ), \end{aligned}$$
(11)
$$\begin{aligned}&\omega (\phi ){\dot{\phi }}^{2}=-2{\dot{H}}, \end{aligned}$$
(12)

where we can choose \(\omega =1\) or redefine a scalar field as \(\psi =\int \sqrt{\omega (\phi )}d\phi \).

Therefore, one can consider the GR cosmology equations (11)–(12) as a partial case of the GSTG dynamic equations (9)–(10). The partial solutions of the equations (11)–(12) are de Sitter ones, namely \(\phi =\mathrm{const}\), \(H=\lambda =\mathrm{const}\), and \(V=3\lambda ^{2}=\mathrm{const}\), which correspond to exponential expansion of the universe. In our approach, we associate these solutions with Einstein gravity and consider the non-minimal coupling of a scalar field and curvature as the source of the deviations from the de Sitter cosmological model.

3 The quadratic connection between Hubble parameter and coupling function

The quadratic connection between Hubble parameter \(H(\phi )\) and the function \(F(\phi )\) of the non-minimal interaction to gravity for the first time has been proposed in the form \(H=\lambda \sqrt{F}\) with \(\lambda > 0\) [27]. Such an approach gave the possibility for a detailed study of the inflation with a power-law Hubble parameter.

Let us consider the generalization of such a method with a representation of the GSTG cosmology equations based on the following connection: \(H=\pm \lambda \sqrt{F}\) with \(H(t)=f(t)+\lambda \), where \(\lambda >0\) for positive sign and \(\lambda <0\) for negative sign; f(t) is a \( \mathcal {C}^2\) function of the cosmic time. As a result, one can derive from the definition of F(t) and Eqs. (9)–(10) the system

$$\begin{aligned} F(t)= & {} \left( 1+\frac{f(t)}{\lambda }\right) ^2, \end{aligned}$$
(13)
$$\begin{aligned} V(\phi (t))= & {} \frac{1}{\lambda ^{2}}\left[ 3(f(t)+\lambda )^{4}\nonumber \right. \nonumber \\&\left. +6(f(t)+\lambda )^{2}{\dot{f}} +{\dot{f}}^{2}+(f(t)+\lambda )\ddot{f}\right] ,\nonumber \\ \end{aligned}$$
(14)
$$\begin{aligned} \omega (\phi (t)){\dot{\phi }}^{2}= & {} -\frac{2}{\lambda ^{2}}\left[ {\dot{f}}^{2}+(f(t)+\lambda )\ddot{f}\right] . \end{aligned}$$
(15)

As a very wide inflationary evolution of the scale factor we consider the exponential power-law (EPL) expansion \(H(t)=\frac{m}{t}+\lambda \) or \(f(t)=\frac{m}{t}\). Let us describe the parameters of cosmological models for this case.

3.1 The parameters of cosmological models for EPL expansion

We may find the solutions in terms of the cosmic time for the EPL expansion from Eqs. (13)–(15):

$$\begin{aligned} F(\phi (t))=\sum ^{2}_{k=0}A_{k}t^{-k}=F_{0}+F_{1}+F_{2}, \end{aligned}$$
(16)

where \(A_{0}=1\), \(A_{1}=\frac{2m}{\lambda }\), \(A_{2}=\frac{m^{2}}{\lambda ^{2}}\);

$$\begin{aligned} X=-\frac{1}{2}\omega (\phi (t)){\dot{\phi }}^{2}=\sum ^{4}_{k=3}B_{k}t^{-k}=X_{3}+X_{4}, \end{aligned}$$
(17)

where \(B_{3}=\frac{2m}{\lambda }\) and \(B_{4}=\frac{3m^{2}}{\lambda ^{2}}\). We have

$$\begin{aligned} V(\phi (t))=\sum ^{4}_{k=0}C_{k}t^{-k}=V_{0}+V_{1}+V_{2}+V_{3}+V_{4}, \end{aligned}$$
(18)

where

$$\begin{aligned} C_{0}= & {} 3\lambda ^{2},~~~~C_{1}=12m\lambda ,~~~~C_{2}=6m(3m-1),\\ C_{3}= & {} \frac{2m}{\lambda }(6m^{2}-6m+1),~~~\\ C_{4}= & {} \frac{3m^{2}}{\lambda ^{2}}(m^{2}-2m+1). \end{aligned}$$

Therefore, one can consider the inflation on two time scales: from \(k=0\) to \(k=2\), which is governed by the non-minimal coupling \(F(\phi )\gg V(\phi )\) for \(|\lambda |\ll 1\), and from \(k=3\) to \(k=4\) which is governed, in the general case, by the kinetic energy X and the potential \(V(\phi )\). Also, we note that the condition \(m\gg 1\) corresponds to the regime of the potential dominance \(V(\phi )\gg X\). This division into different time intervals corresponds to the inflationary stage only in the considered models. From the proposed analysis it follows that the difference between this type of inflation and the standard one [9,10,11,12,13,14,15,16] is the presence of the stage of predominance of a non-minimum coupling at the beginning of the inflation. Now, we consider the exponential power-law (EPL) cosmological dynamics including the stages beyond the initial inflationary one on the basis of the analysis of the universe’s relative acceleration.

It is interesting to note that when k runs from \(k=0\) to \(k=2\) we have a non-minimal coupling F in the action (12) \(S_\mathrm{(STG)}\) but the kinetic part \( X=-\frac{1}{2}\omega (\phi (t)){\dot{\phi }}^{2}\) is absent. In the case when k runs from \(k=3\) to \(k=4\) we have the kinetic part X but the non-minimal coupling F is absent. It is evident that the potential is present for all k.

3.2 Accelerated period in EPL inflation

The scale factor of EPL inflation is

$$\begin{aligned} a(t)=a_s t^m e^{\lambda t},~a_s=\mathrm{const}. \end{aligned}$$
(19)

Then the relative acceleration Q(t) is

$$\begin{aligned} Q(t):= \frac{\ddot{a}(t)}{a(t)}= m(m-1)z^2+2\lambda m z +\lambda ^2,~~z=1/t. \end{aligned}$$
(20)

The roots of the quadratic trinomial of the right hand side are

$$\begin{aligned} z_1=-\frac{\lambda }{\sqrt{m}+m},~~ z_2=\frac{\lambda }{\sqrt{m}-m}. \end{aligned}$$
(21)

That is, for cosmic time t we have

$$\begin{aligned} t_1=-\frac{\sqrt{m}+m}{\lambda },~~ t_2=\frac{\sqrt{m}-m}{\lambda }. \end{aligned}$$
(22)

To analyze the dynamics, taking into account the condition \(|\lambda |\ll 1\), we will consider the normalized constant parameter \({\tilde{\lambda }}=\lambda \times 10^{-6}\).

We have a positive acceleration in the following cases:

  • \({\tilde{\lambda }}>0,~m>1\), then \( z_1<0,~z_2<0\), and for positive z or t acceleration period is \( z\in (0, \infty )\). Thus we have eternal inflation during the period \(t \in (0, \infty )\).

  • \( {\tilde{\lambda }}>0,~0<m<1\) then \( z_1<0,~z_2>0\). We have acceleration during the period \( z \in (0, z_2)\). It means that we have acceleration during the period \( t \in (t_2, \infty )\).

  • \({\tilde{\lambda }}<0,~m>1\). We have two periods of accelerated expansion: \( z\in (0, z_1)\), which corresponds to \( t \in (t_1, \infty )\), and \( z\in (z_2, \infty )\) or \(t \in (0, t_2)\).

  • \( {\tilde{\lambda }}<0,~0<m<1\). We have \(z_1>0,~z_2<0\) and \(t_1>0,~t_2<0\), respectively. For positive t we have accelerating period \( z\in (0, z_1)\), which corresponds to \( t \in (t_1, \infty )\).

Fig. 1
figure 1

The relative acceleration Q of the universe’s expansion for different values of the parameters \({\tilde{\lambda }}=\lambda \times 10^{-6}\) and m

Full size image

It is interesting to note the case when we have two accelerating periods, i.e. when \({\tilde{\lambda }}<0,~m>1\). Effectively the early inflation takes place for \({\tilde{\lambda }}=-1,~m=1.8\) during the period \(t\in (0,~0.458)\); the later inflation occurs when \(t\ge 3.142.\)

In Fig. 1 one can see two stages of the universe’s acceleration (for different parameters m and \({\tilde{\lambda }}\)), and that the expansion of the early inflation is faster than the later one. Between these two stages, the universe expands without acceleration. Thus, the EPL-dynamics (19) with \({\tilde{\lambda }}<0\) and \(m>1\) corresponds to the correct change in the stages of the universe’s expansion.

The dependencies of potential and kinetic energies on time are described by Eqs. (17) and (18). Graphical representations on Figs. 2 and 3 show the behavior of potential and kinetic energies for different values of \({\tilde{\lambda }}\) and m during both inflationary periods. One can see that during the deceleration period the kinetic energy is crossing the phantom zone. Figure 4 demonstrates the influence of a non-minimal interaction. Let us note that for early inflation (\(t\in (0,~0.458)\), for \({\tilde{\lambda }}=-1,~m=1.8\)) the influence of the non-minimal interaction is very high. For the later inflation F(t) becomes much smaller.

Fig. 2
figure 2

Potential energy for different values of \({\tilde{\lambda }}<0\) and \(m>1\)

Full size image
Fig. 3
figure 3

Kinetic energy for different values of \({\tilde{\lambda }}<0\) and \(m>1\)

Full size image
Fig. 4
figure 4

F(t) for different values of \({\tilde{\lambda }}<0\) and \(m>1\)

Full size image

4 The exact solutions for generalized polynomial potential

Now, we consider the following equation:

$$\begin{aligned} t^{-1}\equiv \Psi (\phi ), \end{aligned}$$
(23)

where \(\Psi (\phi )\) is some function of a scalar field. The evolution of the scalar field \(\phi =\phi (t)\) can be defined by the choice of the function \(\Psi (\phi )\).

Thus, form Eq. (18) one has the generalized polynomial potential

$$\begin{aligned} V(\phi )= & {} 3\lambda ^{2}+\delta V(\phi ),~~~~~\nonumber \\ \delta V(\phi )\equiv & {} \sum ^{4}_{k=1}C_{k}[\Psi (\phi )]^{k}, \end{aligned}$$
(24)

with corresponding coupling function, which we define from (16):

$$\begin{aligned} F(\phi )= & {} 1+\delta F(\phi ),~~~~~\nonumber \\ \delta F(\phi )\equiv & {} \sum ^{2}_{k=1}A_{k}[\Psi (\phi )]^{k}, \end{aligned}$$
(25)

and the kinetic function

$$\begin{aligned} \omega (\phi )= & {} -\frac{2}{U(\phi )}\sum ^{4}_{k=3}B_{k}[\Psi (\phi )]^{k},~~~~~\nonumber \\ {\dot{\phi }}^{2}\equiv & {} U(\phi ), \end{aligned}$$
(26)

which can be obtained from Eq. (17).

The term \(\delta V\) in potential (24) can be interpreted as corrections in the low-energy limit of the effective theory of quantum gravity [17, 39], which is induced in this case by the non-minimal coupling \(\delta F(\phi )\) of a scalar field and curvature.

Also, we note that the potential of the scalar field depends on the rate of the expansion of the universe, namely

  • for \(m=0\) one has the flat potential \(V=V_{0}=3\lambda ^{2}=\mathrm{const}\),

  • for \(m=1/3\) one has \(V_{2}=0\),

  • for \(m=\frac{1}{2}\left( 1\pm \frac{1}{\sqrt{3}}\right) \) one has \(V_{3}=0\),

  • for \(m=1\) one has \(V_{4}=0\),

  • for other values of the parameter m all components \(V_{k}\ne 0\).

Thus, one can generate the exact cosmological solutions for the case of the generalized polynomial potential by the choice of the generating function \(\Psi (\phi )\). Let us consider some exact solutions for the inflationary models based in this approach.

4.1 The model with polynomial potential

For this case, we consider the following generating function:

$$\begin{aligned} \Psi (\phi )=\left( \frac{\phi }{\alpha }\right) ^{1/\beta }, \end{aligned}$$
(27)

where \(\alpha \) and \(\beta \) are arbitrary constants.

From Eq. (23) one can find the evolution of the scalar field and the function \(U(\phi )={\dot{\phi }}^{2}\) from its definition:

$$\begin{aligned} \phi (t)= & {} \alpha t^{-\beta },~~~~~\nonumber \\ U(\phi )= & {} -\alpha \beta \left( \frac{\phi }{\alpha }\right) ^{\frac{1+\beta }{\beta }}. \end{aligned}$$
(28)

From the expression for the generating function (27) and equation (24) one has the polynomial potential

$$\begin{aligned} V(\phi )=3\lambda ^{2}+\sum ^{4}_{k=1}C_{k}\left( \frac{\phi }{\alpha }\right) ^{k/\beta }, \end{aligned}$$
(29)

the non-minimal coupling function from Eq. (25),

$$\begin{aligned} F(\phi )= & {} \left[ 1+\frac{m}{\lambda }\left( \frac{\phi }{\alpha }\right) ^{1/\beta }\,\right] ^{2}\nonumber \\= & {} 1+\sum ^{2}_{k=1}A_{k}\left( \frac{\phi }{\alpha }\right) ^{k/\beta }, \end{aligned}$$
(30)

and the kinetic function from (26)

$$\begin{aligned} \omega (\phi )= & {} \frac{2}{\alpha \beta }\sum ^{4}_{k=3}B_{k}\left( \frac{\phi }{\alpha }\right) ^{\frac{k-\beta -1}{\beta }}. \end{aligned}$$
(31)

The polynomial potentials (29) are considered in the context of the effective quantum gravity theory in Refs. [17, 39]. Thus, we reconstructed the parameters (30)–(31) of the scalar–tensor gravity theory for this type of potentials in the inflationary models under consideration.

4.2 The model with exponential potential

Let us study a logarithmic evolution of the scalar field, which often appears in standard Friedmann cosmology [31]:

$$\begin{aligned} \phi (t)=\beta \ln t, \end{aligned}$$
(32)

this case corresponds to the choice of the generating function \(\Psi (\phi )=\exp \left( -\phi /\beta \right) \) and \(U(\phi )=\beta ^{2}\exp \left( -2\phi /\beta \right) \).

With the proposal of (32) we have the expansion on exponents with the same coefficients as in Eqs. (16)–(18):

$$\begin{aligned} V(\phi )=3\lambda ^{2}+\sum ^{4}_{k=1}C_{k}\exp \left( -\frac{k}{\beta }\phi \right) , \end{aligned}$$
(33)

a non-minimal coupling function

$$\begin{aligned} F(\phi )=1+\sum ^{2}_{k=1}A_{k}\exp \left( -\frac{k}{\beta }\phi \right) , \end{aligned}$$
(34)

and the kinetic function

$$\begin{aligned} \omega (\phi )=-\frac{2}{\beta ^{2}}\sum ^{4}_{k=3}B_{k}\exp \left( \frac{2-k}{\beta }\phi \right) . \end{aligned}$$
(35)

The model of quintessential inflation with the potential (33) on the basis of Einstein gravity was considered earlier in Ref. [40].

5 Inflationary stage for physically motivated potential

Now we consider another view on the problem, different from that described in Sect. 4 where we had started, in fact, from the known evolution of a scalar field. Here we changed the situation and looked for an algorithm which gives us the possibility to find the parameters of scalar–tensor gravity which give exact solutions for a given physical potential. The algorithm is demonstrated on the Higgs potential in the following subsection. Note that the form of the potential does not influence the function of the non-minimal coupling F(t).

Due to the fact that the scalar field potential is of key importance for determining physical processes at the stage of cosmological inflation, it is precisely the potential \(V(\phi )\) that is specified for constructing models of the early universe. The form of the scalar field potential is determined from elementary particle physics, quantum field theory, and theories of unifying fundamental interactions, such as supersymmetric theories and string theories in the context of the inflationary paradigm [17]. We will call the potentials of a scalar field associated with these mechanisms physical potentials. Physical mechanisms corresponding to a large number of inflationary potentials were considered in the review [39].

5.1 The solution for Higgs potential

Let us use Eq. (18) to find the scalar field dependence on time. The Higgs potential we take in the standard physical form [39, 41]:

$$\begin{aligned} V(\phi )=\frac{\lambda _H}{4}\left( \phi ^2-v^2 \right) ^2, \end{aligned}$$
(36)

where \(\lambda _{H}\) is the Higgs coupling constant and v is the vacuum expectation value of the Higgs field.

Denoting the right hand side of (18) as T(1/t) one can obtain

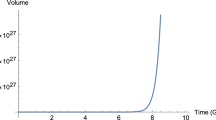
$$\begin{aligned} \phi = \pm \sqrt{v^2+\frac{2}{\sqrt{\lambda _H}}\sqrt{T(1/t)}}. \end{aligned}$$
(37)

This solution for the scalar field is demonstrated in Fig. 5. Because of the plus–minus sign before the square root we have two branches in the picture, and gaps when the function under the square root is negative.

Fig. 5
figure 5

Evolution of scalar field for Higgs potential for \({\tilde{\lambda }}=-1\), \(m=1.8\). Zeros of the T(1/t) are 0.263, 0.941, 2.213, 3.783

Full size image

Then, calculating \({\dot{\phi }}^2\)

$$\begin{aligned} {\dot{\phi }}^2= & {} \frac{1}{4\lambda _H T(1/t)}\\&\left( v^2+ \frac{2}{\sqrt{\lambda _H}}\sqrt{T(1/t)}\right) ^{-1} {\dot{T}}^2 \end{aligned}$$

and inserting the result in (17), one can define the kinetic function \(\omega (\phi (t))\).

Figure 6 demonstrates the change of kinetic function \(\omega \) during allowable periods for real solutions of the scalar field and for different values of \({\tilde{\lambda }}<0\) and \(m>1\). The function \(\omega (t)\) (when \(m=1.8\), \({\tilde{\lambda }} = -1\)) tends to \( - \infty \) when \(t \rightarrow 1.216 \).

Fig. 6
figure 6

Kinetic function \(\omega \) for different values of \({\tilde{\lambda }}<0\) and \(m>1\)

Full size image

5.2 The solution for Higgs–Starobinsky potential

We consider the approximated Higgs potential [39, 41,42,43]

$$\begin{aligned} V(\phi )=V_0\left( 1-\exp \left[ -\frac{2\phi }{\sqrt{6}M_P}\right] \right) ^2,~~~V_0=\mathrm{const}, \end{aligned}$$
(38)

which is the analog of Starobinsky one (see [41] and the literature quoted therein),

$$\begin{aligned} V(\phi )=\frac{3}{4}m^2_{*}M_P^2\left( 1-\exp \left[ -\frac{2\phi }{\sqrt{6}M_P}\right] \right) ^2, \end{aligned}$$
(39)

where \(m_{*}\) is the mass of a scalar field; also, we consider \(M^{-2}_P=1\) in the chosen system of units.

Once again, equating the potential (38) to T(1/t) we have

$$\begin{aligned} \phi =-\sqrt{3/2}\ln \mid 1 \mp \sqrt{T(1/t)/V_0}\mid . \end{aligned}$$
(40)

The general form of the Higgs–Starobinsky potential is well known and we display in Fig. 7 the evolution of the scalar field for different values of \({\tilde{\lambda }}<0\) and \(m>1\). Note that during the later evolution the scalar field varies very slowly.

Fig. 7
figure 7

Evolution of scalar field for Higgs–Starobinsky potential for different values of \({\tilde{\lambda }}<0\) and \(m>1\)

Full size image

Because there are negative zones for the square root in the logarithm’s argument we get a few gaps and the function is tending to infinity when the logarithm’s argument tends to zero.

5.3 The solution for Coleman–Weinberg potential

The scalar field dependence on t for the Coleman–Weinberg potential [39],

$$\begin{aligned} V(\phi )= \alpha \phi ^4\left( \ln \left( \frac{\phi }{v_\phi }\right) -\frac{1}{4}\right) + \frac{\alpha }{4}v_\phi ^4, \end{aligned}$$
(41)

can be extracted from the equation

$$\begin{aligned} \phi ^4 \left( \ln \left( \frac{\phi }{v_\phi }\right) -1/4\right) =T(1/t)/\alpha - \frac{1}{4}v_\phi ^4. \end{aligned}$$
(42)

Note that it is rather difficult to represent the diagram of Coleman–Weinberg potential in physical units.

5.4 Massive scalar field

The exact solution for a massive scalar field for GR cosmology can be represented by the following formula [39]:

$$\begin{aligned} V(\phi )=\frac{1}{2}m^2\phi ^2-V_*. \end{aligned}$$
(43)

Equating the potential (43) with T(1/t) one can find

$$\begin{aligned} \phi (t) = \pm \frac{\sqrt{2}}{m}\sqrt{T(1/t)+V_*}. \end{aligned}$$
(44)

Using our method we can find the generalized scalar–tensor gravity admitting the exact solutions with \(V_*=0\), which is impossible for GR cosmology.

The function \(F(\phi )\) of the non-minimal interaction to gravity cannot be represented in an analytical way. The same relates to the kinetic energy X and the kinetic function \(\omega \). The evolution of the massive scalar field for different values of \({\tilde{\lambda }}<0\) and \(m>1\) is displayed in Fig. 8.

Fig. 8
figure 8

Evolution of massive scalar field for different values of \({\tilde{\lambda }}<0\) and \(m>1\)

Full size image

6 Parameters of cosmological perturbations

Now, we calculate the parameters of the cosmological perturbations to check the correspondence of the inflationary models under consideration of the observational constraints which are obtained from the PLANCK observations [30] of the cosmic microwave background (CMB) radiation.

In accordance with the theory of cosmological perturbations, during the stage of inflation, quantum fluctuations of the scalar field generate the corresponding perturbations of the space-time metric. To the linear order of perturbation theory, the observed anisotropy and polarization of the CMB are explained by the action of two types of perturbations, namely, scalar and tensor perturbations (relic gravitational waves). The third type of perturbations, namely vector perturbations, quickly decay in the process of accelerated expansion of the early universe.

Thus, an estimation of the anisotropy of CMB gives corresponding restrictions on the values of the spectral parameters of cosmological perturbations, which according to modern observations are [30]

$$\begin{aligned}&{{\mathcal {P}}}_{S}=2.1\times 10^{-9}, \end{aligned}$$
(45)
$$\begin{aligned}&n_{S}=0.9663\pm 0.0041, \end{aligned}$$
(46)
$$\begin{aligned}&r<0.065~~~\text {(Planck 2018/BICEP2/Keck-Array)}. \end{aligned}$$
(47)

In Ref. [27] the expressions of the parameters of cosmological perturbations for the inflationary models under consideration on the crossing of the Hubble radius (\(k=aH\)) were obtained in the following form:

$$\begin{aligned} {{\mathcal {P}}}_{S}= & {} \frac{\lambda ^{2}}{16\pi ^{2}\epsilon (\epsilon -\delta )},~~~~~\nonumber \\ {{\mathcal {P}}}_{T}= & {} \frac{2\lambda ^{2}}{\pi ^{2}},~~~ r\simeq 32\epsilon (\epsilon -\delta ), \end{aligned}$$
(48)
$$\begin{aligned} n_{S}\simeq & {} 1+2\epsilon \delta -4\epsilon +2\delta +(1-\epsilon )\nonumber \\&\times \left( \frac{\epsilon \delta -\xi }{\epsilon -\delta }\right) ,~~~~~n_{T}=0, \end{aligned}$$
(49)

where

$$\begin{aligned} \epsilon= & {} -\frac{{\dot{H}}}{H^{2}},~~~\quad \delta =-\frac{{\ddot{H}}}{2H{\dot{H}}},~~~\quad \xi =\epsilon \delta -\frac{1}{H}{\dot{\delta }}, \end{aligned}$$
(50)

are the slow-roll parameters.

The slow-roll conditions for this type of inflation are satisfied when [27]

$$\begin{aligned} \delta _{F}=\frac{{\dot{F}}}{HF}=\frac{2{\dot{H}}}{H^{2}}=-2\epsilon \ll 1. \end{aligned}$$
(51)

For EPL inflation \(H(t)=\frac{m}{t}+\lambda \) one has

$$\begin{aligned} \delta= & {} \frac{1}{\left( m+\lambda t\right) },\quad \epsilon = m\delta ^{2},~~~\xi =\delta ^{2},~~~m>0. \end{aligned}$$
(52)

Thus, we obtain

$$\begin{aligned} {{\mathcal {P}}}_{S}= & {} \frac{2\lambda ^{2}}{\pi ^{2}r}, \quad {{\mathcal {P}}}_{T}=\frac{2\lambda ^{2}}{\pi ^{2}}, \end{aligned}$$
(53)
$$\begin{aligned} r\simeq & {} 32m\delta ^{3}(m\delta -1), ~~~~~\nonumber \\ n_{S}\simeq & {} 1+3\delta -5m\delta ^{2}. \end{aligned}$$
(54)

From (54) we obtain the following dependence:

$$\begin{aligned} r= & {} \frac{2}{625m^{2}}\left[ \left( -3+\sqrt{20m(1-n_{S})+9}\right) ^{3}\right. \nonumber \\&\times \left. \left( 7+\sqrt{20m(1-n_{S})+9}\right) \right] . \end{aligned}$$
(55)
Fig. 9
figure 9

The dependence \(r=r(n_{S})\) for different values of the constant parameter: \(m_{1}=\frac{1}{2}\left( 1-\frac{1}{\sqrt{3}}\right) \), \(m_{2}=\frac{1}{3}\), \(m_{3}=\frac{1}{2}\left( 1+\frac{1}{\sqrt{3}}\right) \), \(m_{4}=1\), \(m_{5}=1.8\) and for \(m\rightarrow \infty \)

Full size image

Also, from (55) one finds that for the spectral index of scalar perturbations \(n_{S}=0.9663\pm 0.0041\) the condition \(r<0.065\) is satisfied for any positive value of the parameter m. In Fig. 9 the dependence \(r=r(n_{S})\) for different values of the constant parameter m is shown.

For \(m\rightarrow \infty \) from Eq. (55) we obtain

$$\begin{aligned} r_{\infty }=\frac{32}{25}\left( n_{S}-1\right) ^{2}, \end{aligned}$$
(56)

and for the pure de Sitter exponential expansion with \(m=0\) and the tensor-to-scalar ratio \(r\rightarrow 0\). Also, we note that from (52) one has \(\delta (m\rightarrow \infty )=0\) and \(\epsilon (m\rightarrow \infty )=0\), i.e. the slow-roll condition (51) is fulfilled for this case, and, therefore, we can use Eq. (55) to calculate the tensor-to-scalar ratio.

After substituting the minimal value of the spectral index of scalar perturbations \(n_{S}=0.9663- 0.0041=0.9622\) into Eq. (56) one has \(r_{\infty (\mathrm{max})}=0.0018\). Therefore, the possible values of the tensor-to-scalar ratio in these models are \(r\in (0,0.0018)\), which corresponds to the observational constraint (47).

Also, we find the e-fold number

$$\begin{aligned} N=\int ^{t_{e}}_{t_{i}}H(t)\mathrm{d}t=m\ln \left( \frac{t_{e}}{t_{i}}\right) +\lambda (t_{e}-t_{i})\approx 60, \end{aligned}$$
(57)

where \(t_{i}\) and \(t_{e}\) are the times of the beginning and the end of the inflation.

Thus, the tensor-to-scalar ratio in considering models for realistic values of the parameter \(m\ne \infty \) can be estimated as \(r\sim 10^{-4}\) and from the condition \({{\mathcal {P}}}_{S}=\frac{2\lambda ^{2}}{\pi ^{2}r}=2.1\times 10^{-9}\) one has \(\lambda ^{2}\sim 10^{-12}\).

Also, we note that the power spectrum of the tensor perturbations (relic gravitational waves) is constant on the crossing of the Hubble radius:

$$\begin{aligned} {{\mathcal {P}}}_{ T}=\frac{2\lambda ^{2}}{\pi ^{2}}\approx \frac{2}{\pi ^{2}}\times 10^{-12}=\mathrm{const}, \end{aligned}$$
(58)

and the amplitude of the relic gravitational waves \({{\mathcal {A}}}_{ T}={{\mathcal {P}}}^{1/2}_{ T}\approx \frac{\sqrt{2}}{\pi }\times 10^{-6}\).

Thus, in this case, the models of cosmological inflation for any potential (24) defined by an arbitrary generating function \(\Psi (\phi )\) will satisfy the observational restrictions on the values of the cosmological perturbation parameters.

In such a way we showed that the cosmological models based on the quadratic connection between Hubble parameter and coupling function, \(H=\lambda \sqrt{F}\), with exponential power-law dynamics \(H(t)=\frac{m}{t}+\lambda \), correspond to observational constraints on the parameter of cosmological perturbations for any potential of a scalar field and any expansion rate of the universe.

7 Conclusion

In this paper, we examined cosmological inflationary models with an EPL expansion of the early universe based on scalar–tensor gravity theories implying a non-minimal coupling of the scalar field and curvature. To comply with these models with observational restrictions on the values of the spectral parameters of cosmological perturbations, we considered the quadratic relationship between the non-minimal coupling function and the Hubble parameter \(H\propto \sqrt{F}\).

The first result of the proposed approach was the possibility of comparing the values of the potential of the scalar field, its kinetic energy, and the function of the non-minimal coupling at different time scales. This feature is based on a polynomial representation of all model’s parameters (16)–(18). This result allows us to determine the nature of the inflationary process by the dominance of some component in the considered models. Namely, we obtained a mode of the predominance of non-minimal coupling \(F\gg V\) for the times from \(k=0\) to \(k=2\) and potential \(V\gg X\) for the times from \(k=3\) to \(k=4\).

The second result is the possibility of constructing exact cosmological solutions for generalized polynomial potentials based on the choice of one generating function \(\Psi (\phi )\) from Eqs. (23)–(26). The examples of exact solutions are given in Sect. 4. Further, the dependences of the kinetic energy of the scalar field and its potential on the cosmic time for various physical potentials and \(m\sim 1\) were considered.

The third result is that this class of models corresponds to observational restrictions on the values of the parameters of cosmological perturbations for any potentials of a scalar field and any expansion rate of the universe. Based on observational restrictions on the value of the power spectrum of scalar perturbations and the tensor-to-scalar ratio (45)–(47), we estimated the value of the free model’s parameter as \(\lambda ^{2}\sim 10^{-12}\).

Thus, the proposed approach allows one to consider phenomenologically correct models of the early universe and compare the parameters of scalar–tensor gravity theories for different physical potentials, which makes it possible to make a consistent analysis for many inflationary models.

The development of the proposed approach is the analysis of higher orders corrections to the potential,

$$\begin{aligned} V(\phi )= & {} 3\lambda ^{2}+\sum ^{4}_{k=1}C_{k}[\Psi (\phi )]^{k}\\&+\sum ^{\infty }_{k=5}{\tilde{C}}_{k}[{\tilde{\Psi }}(\phi )]^{k}, \end{aligned}$$

which can be induced by non-minimal coupling of a scalar field with higher curvature terms, for example, with the Gauss–Bonnet scalar [29, 44,45,46,47,48].

Thus, in this approach, the non-minimal coupling of the scalar field and scalar curvature R defines a segment of a more general polynomial potential, which can be reconstructed for cosmological models that satisfy observational constraints on the values of cosmological perturbation parameters and the requirement for the correct change of the stages of the universe’s expansion.