1 Introduction

The embedding class I condition is a versatile and simple tool, which can be considered an auxiliary condition to solve Einstein’s field equations. Staged by Karmarkar [1], this condition generally applies to any n-dimensional (pseudo)-Riemannian space-time. In short, this technique says that a n-dimensional (pseudo)-Riemannian manifold can be embedded into a pseudo-Euclidean \(n+p\)-dimensional space, where p denotes the class of the embedded manifold. Since general relativity works on a 4-dimensional manifold a spherically symmetric and static space-time described by a Riemaniann variety with Lorentzian metric can be embedded within a 5-diemensional pseudo-Euclidean space, then the submerged manifold is of class I. For the aforementioned case the derivation of the class I condition made by Karmarkar reads

$$\begin{aligned} R_{rtrt}=\frac{R_{r\theta r\theta }R_{\phi t\phi t}+R_{r\theta \theta t}R_{r\phi \phi t}}{R_{\theta \phi \theta \phi }}. \end{aligned}$$
(1)

The above relationship between the Riemann tensor components is valid only if \(R_{\theta \phi \theta \phi }\ne 0\) [2]. As we will see in the following, the components of the Riemann tensor engaged in expression (1) lead to a beautiful and simple relationship between the metric potentials \(\nu \) and \(\lambda \) that determine the geometry of the space-time under study. For the resolution of the field equations in the context of general relativity, this relationship is very helpful, given that in the context of compact solutions such as the modeling of neutron stars, whose material content is described by an imperfect fluid, the number of unknowns exceeds the number of equations. Specifically one has five unknowns: the geometry \(\{\nu ,\lambda \}\) and the matter content \(\{\rho ,p_{r},p_{t}\}\). Then, with the imposition of a suitable ansatz for \(\nu \) or \(\lambda \) the class I condition leads to the determination of the modeling geometry, whereby the thermodynamic variables that characterize the model are obtained by inserting the resulting geometry into the field equations. Therefore the problem is mathematically solved.

Due to the great difficulty involved in solving the general relativity field equations, during the last years the conspiracy of class I has been widely used in the study on modeling compact structures with anisotropic matter distribution [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. As we mentioned earlier this technology solves the problem in the mathematical sense, however the challenge is even greater since such models must be physically admissible to represent a realistic situation. In a simpler context a compact configuration can be made of a perfect fluid matter distribution \(p=p_{r}=p_{t}\), which greatly reduces the resolution of the field equations. Nevertheless, the work by Lake and Delgaty [38] showed that not all models built on the assumption of a perfect fluid distribution are admissible from the physical point of view. The inclusion of local anisotropies \(\Delta \equiv p_{t}-p_{t}\) in the stellar interior has a long history and has been thoroughly studied [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]. Due to extreme internal density and strong gravity within self-gravitating compact object indicates that pressure may not be equal, i.e., there exist two different kinds of interior pressures, namely the radial and tangential pressure [41, 67]. Such kind of compact object may be developed to study the phase transitions and distributions containing the combination of two fluids [68, 69]. Lemaître [70] first pointed out this outcome in the stellar structure and evolution of compact objects. Later on, Bowers and Liang [39] revived the interesting study of anisotropic relativistic matter distributions in general relativity. Using the generalization of the equation of hydrostatic equilibrium, they created a static spherically symmetric stellar structure and investigated the modifications in the surface redshift and gravitational mass. Through the theoretical studies, Ruderman in [71] jagged that nuclear matter tends to become anisotropic in nature at very high densities of order of \(10^{15}\) g/cm\(^3\). For a massive compact star model, they had considered that both pressures (radial and tangential) might be differ to each other. In this situation, many different opinions have been presented for the presence of anisotropy in the stellar compact objects such as by the existence of different kinds of phase transitions [72], the occurrence of solid core, combination of two fluids, presence of type 3A superfluid [73] or by other different physical aspects. Nowadays, several works have been done for anisotropic stellar models in different context [32, 74,75,76,77, 79].

In this direction, recently a novel method was developed to generate anisotropic solutions to Einstein’s field equations [80,81,82,83,84,85,86,87,88,89,90]. The so-called gravitational decoupling by minimal geometric deformation (MGD) was designed to extend solutions driven by an isotropic matter distribution to anisotropic domains. This scheme not only modifies the material content of the object, also deforms its geometry in such a way that the symmetry of the solution is preserved. These last two years the amount of works available in the literature using this method has grown considerably. Applications range from stellar interiors, black holes and modified gravity theories, to name a few [78, 91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116]. What is more, the MGD inverse problem ı.e, given an anisotropic solution it is possible to know the isotropic counterpart, was developed in [117] and the extended case, that is, deformation on both metric potentials was worked in [118].

Recently, class I condition has been used within the framework of MGD [119]. In that work, a space-time has been generated using the embedding technique and then deformed by applying MGD. In this sense, the proposal of this article is not only to extend solutions to scenarios dominated by anisotropic matter. The fundamental idea is to use Karmarkar’s condition as a generator of MGD, which in turn allows to determine the components of the new material sector responsible for the anisotropic behavior inside the compact structure. As examples we have considered the uncharged Adler–Finch–Skea solution [120, 121] to be re-anizotropized using the described methodology and a hybrid obtained by using the temporal metric potential corresponding to Kuchowicz space-time [122] which was worked in [13]. It is worth mentioning that the Adler–Finch–Skea solution was already obtained in the framework of class I scheme, as well as the hybrid formed by Kuchowicz metric potential. Furthermore, in both cases the matter distribution corresponds to an anisotropic charged one (see [28] and [29] for further details). However, in this case we have taken only the geometry of such solutions. To produce the profiles of the energy–density, radial and tangential pressures, anisotropy factor, velocities of the pressure waves, stability and balance mechanism we have used the observational data corresponding to the compact objects [123] 4U 1538-52, SMC X-1 and LMC X-4 for model 1 (Adler–Finch–Skea) and Cen X-3 for model 2 (Kuchowicz). The article is organized as follows: Sec. 2 presents in brief the class I approach and the gravitational decoupling by means of minimal geometric deformation. In Sect. 3 the anistoropic stellar interior solution is provided. Next in Sect. 4 are analyzed the main results and finally in Sect. 5 some remarks are reported.

Throughout the article we shall use the mostly negative signature \(\{+,-,-,-\}\).

2 Class I and MGD schemes revisited

2.1 Embedding class I

A space-time is said to be of class I ı.e, admits to be embedded into a 5-dimensional pseudo-Euclidean space, if there exist a second fundamental form symmetric tensor \(K_{\sigma \gamma }=K_{\gamma \sigma }\) satisfying the Gauss–Codazzi equations

$$\begin{aligned} R_{\sigma \gamma \beta \omega }= & {} \epsilon \left( K_{\sigma \beta }K_{\gamma \omega }-K_{\sigma \omega }K_{\gamma \beta }\right) , \end{aligned}$$
(2)
$$\begin{aligned} \nabla _{\beta }K_{\sigma \gamma }= & {} \nabla _{\gamma }K_{\sigma ,\beta }, \end{aligned}$$
(3)

where \(\epsilon =\pm \) (according to the normal to the manifold being time-like “–” or space-like “+”), \(R_{\sigma \gamma \beta \omega }\) is the Riemann tensor and \(\nabla _{\omega }\) the affine connection associated to the metric tensor \(g_{\gamma \beta }\), \(\nabla _{\gamma }g_{\beta \omega }=0\).

Regarding the spherically symmetric and static space-time given in Schwarzschild like coordinates \(x=\{t,r,\theta ,\phi \}\) by

$$\begin{aligned} ds^{2}=e^{\nu }dt^{2}-e^{\lambda }dr^{2}-r^{2} \left( d\theta ^{2}+sin^{2}\theta d\phi ^{2}\right) , \end{aligned}$$
(4)

the only non trivial components of the symmetric tensor \(K_{\sigma \gamma }\) are: \(K_{tt}\), \(K_{rr}\), \(K_{\theta \theta }=sin^{2}\theta \,K_{\phi \phi }\) and \(K_{tr}=K_{rt}\). By inserting these components into (2) one arrives to

$$\begin{aligned} R_{rtrt}=\frac{R_{r\theta r\theta }R_{\phi t\phi t}+R_{r\theta \theta t}R_{r\phi \phi t}}{R_{\theta \phi \theta \phi }}. \end{aligned}$$
(5)

The Riemann tensor components compromised in the previous condition and associated to the line element (4) are

$$\begin{aligned} R_{rtrt}= & {} -e^{\nu }\left( \frac{\nu ^{\prime \prime }}{2}-\frac{\lambda ^{\prime }\nu ^{\prime }}{4}+\frac{\nu ^{\prime 2}}{4}\right) , \end{aligned}$$
(6)
$$\begin{aligned} R_{\theta \phi \theta \phi }= & {} -e^{-\lambda }r^{2}\sin ^{2}\theta \left( e^{\lambda }-1\right) , \end{aligned}$$
(7)
$$\begin{aligned} R_{\phi t \phi t}= & {} -\frac{r}{2}\nu ^{\prime }e^{\nu -\lambda }\sin ^{2}\theta , \end{aligned}$$
(8)
$$\begin{aligned} R_{r \theta r\theta }= & {} -\frac{r}{2}\lambda ^{\prime }, \end{aligned}$$
(9)
$$\begin{aligned} R_{r\phi \phi t}&=0 \end{aligned}$$
(10)
$$\begin{aligned} R_{r\theta \theta t}&=0. \end{aligned}$$
(11)

Next, replacing (6)–(11) in Eq. (5) we obtain the following differential equation

$$\begin{aligned} 2\frac{\nu ^{\prime \prime }}{\nu ^{\prime }}+\nu ^{\prime } =\frac{\lambda ^{\prime }e^{\lambda }}{e^{\lambda }-1}, \end{aligned}$$
(12)

with \(e^{\lambda }\ne 1\), from where

$$\begin{aligned} e^{\lambda }=1+A\nu ^{\prime 2}e^{\nu }, \end{aligned}$$
(13)

being A an integration constant. Equation (12) also can be solved to express the metric potential \(\nu \) in terms of \(\lambda \) as follows

$$\begin{aligned} e^{\nu }=\left[ B+C\int \sqrt{e^{\lambda }-1}dr\right] ^{2}, \end{aligned}$$
(14)

where B and C are integration constants.

2.2 Gravitational decoupling by MGD

Minimal geometric deformation (MGD from now on) approach is a novel tool useful to generate anisotropic solutions of the Einstein field equations starting from an isotropic (anisotropic) one [90]. In general, there are many ways to introduce local anisotropies. In this regard we will focus on the case where the shear term of the energy–momentum tensor is taken to be null. Hence, the anisotropic behaviour appears when \(p_t - p_r \ne 0\). In order to produce the aforementioned anisotropies, it is necessary to introduce an extra gravitational source which, in principle, can be e.g. a scalar, vectorial or tensorial field. This extra source is coupled to the energy–momentum tensor associated to the seed solution. The effective energy–momentum tensor can be defined as follows [90, 124]

$$\begin{aligned} {T}_{\mu \nu } \equiv {\tilde{T}}_{\mu \nu } + \alpha \theta _{\mu \nu }, \end{aligned}$$
(15)

where \({\tilde{T}}_{\mu \nu }\) corresponds to a perfect fluid given by

$$\begin{aligned} {\tilde{T}}_{\mu \nu }=\left( {\tilde{\rho }}+{\tilde{p}}\right) \chi _{\mu }\chi _{\nu }-{\tilde{p}}g_{\mu \nu }, \end{aligned}$$
(16)

being \(\chi ^{\mu }=e^{-\nu /2}\delta ^{\mu }_{\ t}\) the time-like four velocity of the fluid satisfying \(\chi ^{\mu }\chi _{\mu }=1\), \({\tilde{\rho }}\) the isotropic energy–density and \({\tilde{p}}\) the isotropic pressure. The new field \(\theta _{\mu \nu }\) encodes the anisotropies introduced into the system. Now, the Einstein field equations

$$\begin{aligned} G_{\mu \nu }\equiv R_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }=-\frac{8\pi G}{c^{4}}T_{\mu \nu }, \end{aligned}$$
(17)

associated with the geometry (4) and the matter distribution (15) explicitly reads

$$\begin{aligned} 8\pi {\rho }= & {} \frac{1}{r^2}-e^{-\lambda }\left( \frac{1}{r^2}-\frac{\lambda ^{\prime }}{r}\right) , \end{aligned}$$
(18)
$$\begin{aligned} 8\pi {p}_{r}= & {} -\frac{1}{r^2}+e^{-\lambda }\left( \frac{1}{r^2}+\frac{\nu ^{\prime }}{r}\right) , \end{aligned}$$
(19)
$$\begin{aligned} 8\pi {p}_{t}= & {} \frac{1}{4}e^{-\lambda }\left( 2\nu ^{\prime \prime }+\nu ^{\prime 2}-\lambda ^{\prime }\nu ^{\prime }+2\frac{\nu ^{\prime }-\lambda ^{\prime }}{r}\right) , \end{aligned}$$
(20)

where the primes denote differentiation with respect to the radial coordinate r. Besides, hereinafter we shall employ geometrized relativistic units where \(G=c=1\). The full diffeomorphims symmetry entails the conservation of the energy–momentum tensor

$$\begin{aligned} \nabla _{\mu }T^{\mu }_{\nu }=0, \end{aligned}$$
(21)

which reads

$$\begin{aligned} \begin{aligned}&{\tilde{p}}^{\prime } + \frac{1}{2}\nu ^{\prime } \left( {\tilde{p}} + {\tilde{\rho }}\right) - \alpha H(\theta _i^i) =0, \end{aligned} \end{aligned}$$
(22)

where the function \(H(\theta _i^i)\) encodes the corresponding anisotropies and it is defined as:

$$\begin{aligned} H(\theta _i^i) \equiv \left( \theta ^{r}_{r} \right) ^{\prime } + \frac{1}{2}\nu ^{\prime } \left( \theta ^{r}_{r}-\theta ^{t}_{t} \right) + \frac{2}{r} \left( \theta ^{r}_{r}-\theta ^{\varphi }_{\varphi }\right) . \end{aligned}$$
(23)

The above expression (22) is a linear combination of Eqs. (18)–(20), where we have defined

$$\begin{aligned} {\rho }\equiv & {} {\tilde{\rho }}+\alpha \theta ^{ t}_{t} \end{aligned}$$
(24)
$$\begin{aligned} {p}_{r}\equiv & {} {\tilde{p}}-\alpha \theta ^{r}_{r} \end{aligned}$$
(25)
$$\begin{aligned} {p}_{t}\equiv & {} {\tilde{p}}-\alpha \theta ^{ \varphi }_{\varphi }. \end{aligned}$$
(26)

It is essential to point out that the inclusion of \(\theta \)-term introduces anisotropies if \(\theta ^{r}_{r}\ne \theta ^{\varphi }_{\varphi }\) only. Thus the effective anisotropy is defined in the usual manner, namely:

$$\begin{aligned} \Delta \equiv {p}_{t}-{p}_{r}=\alpha \left( \theta ^{r}_{r}- \theta ^{\varphi }_{\varphi }\right) . \end{aligned}$$
(27)

Naturally, we recover a perfect fluid when \(\alpha \) is taken to be zero. On the other hand if the seed solution already contains anisotropies inside the matter content the energy–momentum tensor is described by an imperfect fluid distribution as follows

$$\begin{aligned} {\tilde{T}}_{\mu \nu }=\left( {\tilde{\rho }} +{\tilde{p}}_{t}\right) \chi _{\mu }\chi _{\nu } -g_{\mu \nu }{\tilde{p}}_{t}+\left( {\tilde{p}}_{r} -{\tilde{p}}_{t}\right) u_{\mu }u_{\nu }, \end{aligned}$$
(28)

with \({\bar{p}}_{r}\) and \({\bar{p}}_{t}\) being the pressure waves in the principal directions ı.e, the radial and tangential ones respectively. The four-velocity of the above fluid distribution is characterized by the time-like vector \(\chi ^{\nu }\). Moreover \(u^{\nu }\) is a unit space-like vector in the radial direction (orthogonal to \(\chi ^{\nu }\)). In that case (27) becomes to

$$\begin{aligned} \Delta \equiv {\tilde{p}}_{t}-{\tilde{p}}_{r}+\alpha \left( \theta ^{r}_{r}-\theta ^{\varphi }_{\varphi }\right) . \end{aligned}$$
(29)

So, in this case the extra term \(\alpha \left( \theta ^{r}_{r}-\theta ^{\varphi }_{\varphi }\right) \) introduces a stronger anisotropic behaviour into the matter distribution. This serves to improve the stability and equilibrium mechanism. In general, it is not trivial to obtain analytic solutions of the Einstein field equations in the context of interior solutions, ı.e., relativistic stars. To find a tractable exact solution, albeit recent, a popular alternatives is the gravitational decoupling via the MGD approach. The crucial point of this technique relies on the following map:

$$\begin{aligned} \text {e}^{\nu (r)}\mapsto & {} e^{\nu (r)}+\alpha h(r) \end{aligned}$$
(30)
$$\begin{aligned} \text {e}^{-\lambda (r)}\mapsto & {} \mu (r)+\alpha f(r), \end{aligned}$$
(31)

in which we deform minimally the \(g_{tt}\) and \(g_{rr}\) components of the metric. The later maps deform the metric components by the inclusion of certain unknown functions h(r) and f(r). At this level, it is noticeable remark that the corresponding deformations are purely radial. The later feature remains the spherical symmetry of the solution. The so-called MGD corresponds to set \(h(r)=0\) with \(f(r)\ne 0\), or \(h(r)\ne 0\) with \(f(r)=0\). The first case maintain the deformation in the radial component only, which means that any temporal deformation is excluded. In light of this, the anisotropic tensor \(\theta _{\mu \nu }\) is produced by the radial deformation (31).

The system of differential equations can be split under the replacement (31). Thus, the field equations are naturally decoupled in two set: i) the first set satisfies Einstein field equations, and correspond to the isotropic (anisotropic) case, namely \(\alpha = 0\), and it is given by

$$\begin{aligned} 8\pi {\tilde{\rho }}= & {} \frac{1}{r^{2}}-\frac{\mu }{r^{2}} -\frac{\mu ^{\prime }}{r} \end{aligned}$$
(32)
$$\begin{aligned} 8\pi {\tilde{p}}= & {} -\frac{1}{r^{2}}+\mu \left( \frac{1}{r^{2}} +\frac{\nu ^{\prime }}{r}\right) \end{aligned}$$
(33)
$$\begin{aligned} 8\pi {\tilde{p}}= & {} \frac{\mu }{4}\left( 2\nu ^{\prime \prime } +\nu ^{\prime 2}+2\frac{\nu ^{\prime }}{r}\right) +\frac{\mu ^{\prime }}{4}\left( \nu ^{\prime }+\frac{2}{r}\right) , \end{aligned}$$
(34)

along with the following conservation equation

$$\begin{aligned} {\tilde{p}}^{\prime } + \frac{1}{2}\nu ^{\prime } \left( {\tilde{p}} + {\tilde{\rho }}\right) =0, \end{aligned}$$
(35)

and ii) the second set of equations corresponds to the \(\theta \)-sector which is obtained when we turn on \(\alpha \). Thus, the equations for the later sector are:

$$\begin{aligned} 8\pi \theta ^{t}_{t}= & {} -\frac{f}{r^{2}}-\frac{f^{\prime }}{r} \end{aligned}$$
(36)
$$\begin{aligned} 8\pi \theta ^{r}_{r}= & {} -f\left( \frac{1}{r^{2}}+\frac{\nu ^{\prime }}{r}\right) \end{aligned}$$
(37)
$$\begin{aligned} 8\pi \theta ^{\varphi }_{\varphi }= & {} -\frac{f}{4}\left( 2\nu ^{\prime \prime } +\nu ^{\prime 2}+2\frac{\nu ^{\prime }}{r}\right) -\frac{f^{\prime }}{4}\left( \nu ^{\prime }+\frac{2}{r}\right) . \end{aligned}$$
(38)

The corresponding conservation equation associated to the \(\theta \)-sector is computed to be

$$\begin{aligned} \left( \theta ^{r}_{r}\right) ^{\prime }-\frac{1}{2}\nu ^{\prime } \left( \theta ^{t}_{t}-\theta ^{r}_{r}\right) -\frac{2}{r}\left( \theta ^{\varphi }_{\varphi }-\theta ^{r}_{r}\right) =0. \end{aligned}$$
(39)

It is important to remark that the above equation is precisely the essential point to use the MGD approach, given that it guarantees that the energy interchange is pure gravitational only. At this stage it should be noted that if the seed solution is anisotropic the pressure in the left hand side of Eqs. (33)–(34) must be replaced by \({\tilde{p}}_{r}\) and \({\tilde{p}}_{t}\), respectively. Moreover, the conservation equation is modified to

$$\begin{aligned} {\tilde{p}}^{\prime }_{r} + \frac{1}{2}\nu ^{\prime } \left( {\tilde{p}}_{r} + {\tilde{\rho }}\right) +\frac{2}{r}\left( {\tilde{p}}_{r} -{\tilde{p}}_{t}\right) =0. \end{aligned}$$
(40)

3 Anisotropic stellar interiors

In this section we provide two examples of anisotropic stellar interiors. Specifically, we re-anisotropize the Adler–Finch–Skea model previously obtained in [28] and second one was worked in Maurya et al. [29] (although in these works the solutions include electric charge we will take only the geometrical description).

To do so the embedding class I technology is combining with the MGD machinery to generate the deformation function f(r). Putting together Eqs. (12) and (31) one arrives to

$$\begin{aligned} \alpha f^{\prime }(r)+\mu ^{\prime }(r)= & {} \bigg [2\frac{\nu ^{\prime \prime }(r)}{\nu ^{\prime }(r)}+\nu ^{\prime }(r)\bigg ]\bigg [\mu ^{2}(r) +2\alpha \mu (r) f(r)\nonumber \\&+\alpha ^{2}f^{2}(r)-\mu (r)-\alpha f(r)\bigg ]. \end{aligned}$$
(41)

In principle this first order non-linear differential equation (41) in f(r) looks to complicated, however it is possible to integrate this equation for specific choice of \(\nu (r)\) and \(\mu (r)\). It should be remembered that the seed solution corresponds to a solution of the Einstein field equations with anisotropic matter distribution which was obtained using the Karmarkar condition (13). A (almost complete) list of such solutions can be found in [6]. Although some solutions have a fairly complex geometry, the differential equation (41) can be solved in most cases, except for some exceptions where the seed solution is described by very complex metric functions, such as hypergeometric functions. Moreover in the works [125,126,127,128], it was proved that in the modelling of realistic compact objects, the gravitational potential \(\nu (0)=\text {finite and constant}\), \(\nu ^{\prime }(0)=0\) and \(\nu ^{\prime \prime }(0)>0\). On the other hand, the radial pressure and the energy density must be positive and continuous within the compact objects which yields \(r>2\,m(r)\) [129, 130]. Then from \(p_r \ge 0\) with \(r>2\,m(r)\), it follows that \(\nu ^{\prime }(0)\ne 0\). This implies that generic function \(\nu (r)\) attains its regular minimum at centre and increasing monotonically function of r. Also we ensure that the another obtained gravitational potential \(e^{\lambda (r)}\) should be the form \(e^{\lambda (r)}=1+O(r^2)\) near at \(r=0\). By keeping all above mathematical and physical points in our mind we have chosen two different space-time to modeling compact structures, which are given below.

3.1 Model 1

To find the decoupler function f(r) we impose the following class I seed space-time

$$\begin{aligned} \nu (r)= & {} \text {Ln}\left[ \left( A+Br^{2}\right) ^{2}\right] , \end{aligned}$$
(42)
$$\begin{aligned} \mu (r)= & {} \frac{1}{1+Cr^{2}}. \end{aligned}$$
(43)

From Eqs. (42)–(43) it can be clearly observed that this space-time is fulfilling the physical and mathematical requirements mentioned above (see Fig. 1). Moreover, the matter content inside the stellar interior described by the above geometry is given by

$$\begin{aligned} {\tilde{\rho }}= & {} \frac{C\left( Cr^{2}+3\right) }{8\pi \left( Cr^{2} +1\right) ^{2}}, \end{aligned}$$
(44)
$$\begin{aligned} {\tilde{p}}_{r}= & {} \frac{4B-BCr^{2}-AC}{8\pi \left( Br^{2} +A\right) \left( Cr^{2}+1\right) }, \end{aligned}$$
(45)
$$\begin{aligned} {\tilde{p}}_{t}= & {} \frac{4B+BCr^{2}-AC}{8\pi \left( Br^{2} +A\right) \left( Cr^{2}+1\right) ^{2}}, \end{aligned}$$
(46)

where the constants B and C have units of \([\text {length}]^{-2}\) and A is dimensionless. So, the decoupler function obtained from (41) using Eqs. (43)–(42) is

$$\begin{aligned} f(r)=\frac{Cr^{2}}{\left( 1+Cr^{2}\right) \left( \alpha +CF+FC^{2}r^{2}\right) }, \end{aligned}$$
(47)

being F an integration constant with units \([\text {length}]^{2}\). As it is observed at \(r=0\) the deformation function f(r) is zero. furthermore, it is dimensionless. So, the deformed space-time reads

$$\begin{aligned} ds^{2}= & {} -\left( A+Br^{2}\right) ^{2}dt^{2}+\bigg (\frac{1}{1+Cr^{2}}\nonumber \\&+\frac{\alpha Cr^{2}}{\left( 1+Cr^{2}\right) \left( \alpha +CF +FC^{2}r^{2}\right) }\bigg )^{-1}dr^{2}+r^{2}d\Omega ^{2}.\nonumber \\ \end{aligned}$$
(48)

Now, by inserting Eq. (47) into the set of Eqs. (36)–(38) provide the following expressions for the \(\theta \)-sector components

$$\begin{aligned} \theta ^{t}_{t}= & {} \frac{\alpha C\left( FC^{3}r^{4}-2FC^{2}r^{2}-\alpha Cr^{2}-CF-3\alpha \right) }{8\pi \left( FC^{3}r^{4}+2FC^{2}r^{2}+\alpha Cr^{2}+CF+\alpha \right) ^{2}}, \end{aligned}$$
(49)
$$\begin{aligned} \theta ^{r}_{r}= & {} \frac{-\alpha C\left( 5Br^{2}+A\right) }{8\pi \left( FC^{3}r^{4}+2FC^{2}r^{2}+\alpha Cr^{2}+CF+\alpha \right) \left( A+Br^{2}\right) }, \end{aligned}$$
(50)
$$\begin{aligned} \theta ^{\varphi }_{\varphi }= & {} \frac{C}{8\pi \left( FC^{3}r^{4}+2FC^{2}r^{2}+\alpha Cr^{2}+CF+\alpha \right) ^{2}\left( A+Br^{2}\right) }\nonumber \\&\times \bigg (FBC^{3}r^{6}+AFC^{3}r^{4}-8BFC^{2}r^{4}-4\alpha BCr^{4}-7BCFr^{2} \nonumber \\&-7\alpha Br^{2}-ACF-\alpha A \bigg ). \end{aligned}$$
(51)

So, by virtue of Eqs. (45), (46), (50) and (51) the anisotropic factor (29) is given by

$$\begin{aligned} \Delta (r)=\frac{FC^{2}r^{2}\left[ CF\left( AC +B\left( Cr^{2}-2\right) \right) -2\alpha B\right] }{8\pi \left[ A+Br^{2}\right] \left[ CF\left( 1+Cr^{2}\right) +\alpha \right] ^{2}}. \end{aligned}$$
(52)

As can be seen at the center \(r=0\) of the compact star (52) is vanishing ı.e, \(\Delta (0)=0\) as it is required.

3.2 Model 2

In order to find the decoupler function f(r) for the model 2, we impose the following another class I seed space-time

$$\begin{aligned} \nu (r)= & {} A+Br^{2}, \end{aligned}$$
(53)
$$\begin{aligned} \mu (r)= & {} \frac{1}{1+C\,r^{2}\,e^{A+Br^2}}. \end{aligned}$$
(54)

Again it is observed that from From Eqs. (53)–(54) the space-time is satisfying the physical and mathematical requirements mentioned above (see Fig. 5). The matter content inside the stellar model 2 can be described using the above geometry as follows,

$$\begin{aligned} {\tilde{\rho }}= & {} \frac{C\,e^{A+Br^2}(3+2Br^2+C\,r^2\,e^{A+Br^2}}{8\pi \left( 1+C\,r^{2}\,e^{A+Br^2}\right) ^{2}}, \end{aligned}$$
(55)
$$\begin{aligned} {\tilde{p}}_{r}= & {} \frac{2B-C\,e^{A+Br^2}}{8\pi \left( 1+C\,r^{2}\,e^{A+Br^2}\right) }, \end{aligned}$$
(56)
$$\begin{aligned} {\tilde{p}}_{t}= & {} \frac{2B-C\,e^{A+Br^2}+B^2\,r^2}{8\pi \left( 1+C\,r^{2}\,e^{A+Br^2}\right) ^{2}}, \end{aligned}$$
(57)

where the constants B and C have same units as \([\text {length}]^{-2}\) while A is dimensionless. Then from (41), the decoupler function f(r) can be obtained by using Eqs. (54)–(53) as,

$$\begin{aligned} f(r)=\frac{C\,r^{2}\,e^{A+Br^2}}{\left( 1+C\,r^{2}\,e^{A+Br^2}\right) \,\left( \alpha +C\,e^{A}\,F+FC^{2}r^{2}\,e^{2A+Br^2}\right) },\nonumber \\ \end{aligned}$$
(58)

being F an integration constant with units \([\text {length}]^{2}\). As it is observed at \(r=0\) the deformation function f(r) is zero, and has no dimension. Then the deformed space-time for the Model 2 can be read as,

$$\begin{aligned} \begin{aligned} ds^{2}=&\,e^{A+Br^{2}}dt^{2}-r^{2}d\Omega ^{2}-\left( \frac{1}{1+C\,r^{2}\,e^{A+Br^2}}\right. \\&\left. +\alpha \frac{C\,r^{2}\,e^{A+Br^2}\,\big (1+C\,r^{2}\,e^{A+Br^2}\big )^{-1}}{\left( \alpha +C\,e^{A}\,F+FC^{2}r^{2}\,e^{2A+Br^2}\right) }\right) ^{-1}dr^{2}. \end{aligned} \end{aligned}$$
(59)

Now, by plugging Eq. (55) into the set of Eqs. (36)–(38) which yield the following expressions for the \(\theta \)-sector components

$$\begin{aligned} \theta ^{t}_{t}= & {} \frac{C\,e^{A+Br^2}\,\big [C^3\,e^{3A+2Br^2}F\,r^4-\theta _{1}(r)-C\,r^2\,\theta _2(r)\big ]}{8\pi \,(1+C\,r^{2}\,e^{A+Br^2})^2\,\big [C\,e^{A}\,F\,(1+C\,r^{2}\,e^{A+Br^2})+\alpha \big ]^2}, \end{aligned}$$
(60)
$$\begin{aligned} \theta ^{r}_{r}= & {} \frac{-C\,e^{A+Br^2}\,(1+2\,B\,r^2)}{8\pi \,(1+C\,r^{2}\,e^{A+Br^2})\,\big [C\,e^{A}\,F\,(1+C\,r^{2}\,e^{A+Br^2})+\alpha \big ]}, \end{aligned}$$
(61)
$$\begin{aligned} \theta ^{\varphi }_{\varphi }= & {} \frac{C\,e^{A+Br^2}\,\big [C^3\,e^{3A+2Br^2}F\,r^4-\theta _{3}(r)-BC\,r^4\,\theta _4(r)\big ]}{8\pi \,(1+C\,r^{2}\,e^{A+Br^2})^2\,\big [C\,e^{A}\,F\,(1+C\,r^{2}\,e^{A+Br^2})+\alpha \big ]^2} \end{aligned}$$
(62)

where,

\(\theta _1(r)=(3+2Br^2)\,(C\,e^{A}\,F+\alpha )\),

\(\theta _2(r)=e^{A+Br^2}\,(2\,C\,e^{A}+\alpha )\),

\(\theta _3(r)=[1+2Br^2\,(2+Br^2)]\,(C\,e^{A}\,F+\alpha )\),

\(\theta _4(r)=(2+B\,r^2)\,e^{A+Br^2}\,(2\,C\,e^{A}+\alpha )\).

Then, from Eqs. (56), (61) and (62) the anisotropic factor (29) is given by

$$\begin{aligned} \Delta (r)=\frac{r^2\,\big [C^2\,e^{2A+Br^2}\,F-B\,(C\,e^{A}\,F +\alpha )\big ]^2}{8\pi \,\big [C\,e^{A}\,F\,(1+C\,r^{2}\,e^{A+Br^2})+\alpha \big ]^2}. \end{aligned}$$
(63)

It can be clearly noted that the anisotropy, given in Eq. (63), vanishes at the center of the compact star i.e. \(\Delta (0)=0\) at \(r=0\) which is required for physical acceptability.

4 Physical analysis

The feasibility of any model describing the interior of a compact object representing realistic structures such as neutron stars must satisfy some requirements to be physically and mathematically admissible [40, 56]

  • The metric potentials, namely \(e^{\nu }\) and \(e^{\lambda }\) must be free from singularities, finite and monotone increasing functions with increasing radius. Besides, \(e^{\nu (0)}>0\) and \(e^{\lambda (0)}=1\).

  • The main thermodynamic variables, namely \(\{\rho ,p_{r},p_{t}\}\) should be strictly positive functions at every point inside the configuration.

  • The behavior of the thermodynamic observables responds to a monotonically decreasing one ı.e, their maximum values are attained at the center of the object reaching their minimum at the surface.

  • Both the radial and tangential pressure coincide at the center. Moreover, at the boundary the radial pressure must vanish and the tangential one not necessarily is.

  • Inside the compact static structure the velocity of the pressure waves in the principal direction of the sphere must be less than the speed of light \(c=1\) in order to preserve causality condition: \(0\le v^{2}_{r}=\frac{dp_{r}}{d\rho }<1\) and \(0\le v^{2}_{t}=\frac{dp_{t}}{d\rho }<1\).

  • The energy–momentum tensor has to satisfy simultaneously the following conditions: \(\rho -p_{r}-2p_{t}\ge 0\) and \(\rho +p_{r}+2p_{t}\ge 0\).

Fig. 1
figure 1

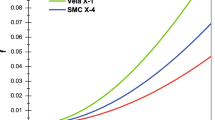
The trend of metric potential against the radial coordinate r/R for \(C=0.2\) km\(^{-2}\), \(\alpha =0.008 {\text {km}}\) and different values mentioned in Table 1 for compact objects 4U 1538-52, SMC X-1 and LMC X-4

Full size image

In addition to meet the above requirements, at the boundary \(\Sigma :r=R\) the model describing the stellar interior \({\mathcal {M}}^{-}\) should be joined in a smoothly way with the corresponding exterior space-time \({\mathcal {M}}^{+}\). As we are dealing with an uncharged anisotropic fluid sphere, in principle the outer manifold is described by the vacuum space-time ı.e, external Schwarzschild solution. Nevertheless, the inclusion of the \(\theta \)-sector into the matter field could in principle modify both the geometry and the matter content of the outer manifold. In this situation the compact structure will be not immersed in vacuum space-time anymore. In this case the compact object can remain embedded into a vacuum space-time whether the contributions coming from the \(\theta \)-sector are assumed to be confined within the stellar interior only [90]. Thereby the outer manifold \({\mathcal {M}}^{+}\) is given by [131]

$$\begin{aligned} ds^{2}{=}\left( 1{-}\frac{2M_{\text {Sch}}}{r}\right) dt^{2} {-}\left( 1{-}\frac{2M_{\text {Sch}}}{r}\right) ^{-1}dr^{2}-r^{2}d\Omega ^{2},\nonumber \\ \end{aligned}$$
(64)

being \(M_{\text {Sch}}\) the Schwarzschild mass which coincides with the total mass M of the object at the boundary \(\Sigma \). Then, to match the inner manifold \({\mathcal {M}}^{-}\) with the external one \({\mathcal {M}}^{+}\) we apply the Israel-Darmois junction conditions procedure [132, 133]. This procedure dictates the continuity of the first and second fundamental form across the surface \(\Sigma \). The first fundamental form says that the intrinsic geometry described by the metric tensor \(g_{\mu \nu }\) induced by \({\mathcal {M}}^{-}\) and \({\mathcal {M}}^{+}\) on the interface meets

$$\begin{aligned} g^{-}_{tt}|_{r=R}=g^{+}_{tt}|_{r=R} \quad \text{ and } \quad g^{-}_{rr}|_{r=R}=g^{+}_{rr}|_{r=R} \end{aligned}$$
(65)

and the second fundamental form related with the extrinsic geometry described by the extrinsic curvature tensor \(k_{ij}\) (Latin indices run over on spatial coordinates) says

$$\begin{aligned} p_{r}(r=R)=\left[ {\tilde{p}}_{r}(r) -\alpha \theta ^{r}_{r}(r)\right] |_{r=R}=0, \end{aligned}$$
(66)

and

$$\begin{aligned} M_{\text {Sch}}=M=m(R)=4\pi \int _0^R \left[ {\tilde{\rho }}+\alpha \theta ^{t}_{t}\right] r^{2}dr. \end{aligned}$$
(67)

The expression (66) is obtained from the continuity of \(k_{rr}\) while (67) comes from the continuity of \(k_{\theta \theta }\) and \(k_{\phi \phi }\).

4.1 Junction conditions model 1

Fig. 2
figure 2

The trend of pressures (radial and tangential) (top left), density (top right), anisotropy (bottom left) and velocity (bottom right) against the radial coordinate r/R for \(C=0.2\) km\(^{-2}\), and \(\alpha =0.008\) for compact objects 4U 1538-52, SMC X-1 and LMC X-4

Full size image
Fig. 3
figure 3

The trend of energy conditions (left panel) and adiabatic index (right panel) against the radial coordinate r/R for \(C=0.2\, {\text {km}}^{-2}\) \(\alpha =0.008\) and different values mentioned in Table 1 for compact objects 4U 1538-52, SMC X-1 and LMC X-4

Full size image
Fig. 4
figure 4

The trend of TOV equation against the radial coordinate r/R for same parameter values \(C=0.2\) km\(^{-2}\), \(\alpha =0.008\) and different values mentioned in Table 1 for compact objects 4U 1538-52 (top left), SMC X-1 (top right) and LMC X-4 (bottom)

Full size image
Fig. 5
figure 5

The trend of metric functions \(e^{\lambda }\) (left), and \(e^{\nu }\) (right) against the radial coordinate r/R for various values of B and different \(\alpha =-0.3,~0.1\) and 0.3 for compact object Cen X-3

Full size image
Fig. 6
figure 6

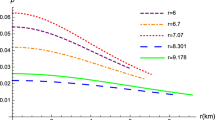
The trend of pressures (radial and tangential) (top left), density (top right), anisotropy (bottom left) and velocity (bottom right) against the radial coordinate r/R for different B displayed in Table 3 and \(\alpha =-0.3,~0.1\) and 0.3 for compact object Cen X-3

Full size image
Fig. 7
figure 7

The trend of energy conditions (left panel) and adiabatic index (right panel) against the radial coordinate r/R for different values of parameter B exhibited in Table 3 and different \(\alpha =-0.3,~0.1\) and 0.3 for compact object Cen X-3

Full size image
Fig. 8
figure 8

The trend of TOV equation against the radial coordinate r/R for different values of constants B mentioned in Table 3 and different \(\alpha =-0.3\) (top left), 0.1(top right) and 0.3 (bottom) for compact object Cen X-3

Full size image

Next from Eqs. (48), (64) and (65) one obtains

$$\begin{aligned}&\left( A+BR^{2}\right) ^{2}=1-\frac{2M}{R}, \end{aligned}$$
(68)
$$\begin{aligned}&\frac{1}{1+CR^{2}} +\frac{\alpha CR^{2}}{\left( 1+CR^{2}\right) \left( \alpha +CF+FC^{2}R^{2}\right) } \nonumber \\&\quad =1-\frac{2M}{R}, \end{aligned}$$
(69)

and from expressions (45), (50) and (66)

$$\begin{aligned} F=\frac{4B\alpha }{C\left( AC-4B+BCR^{2}\right) }. \end{aligned}$$
(70)

After some algebra Eqs. (68)–(70) can be combined to provide

$$\begin{aligned} F= & {} \frac{2M\alpha }{C\left( CR^{3}-2M-2MCR^{2}\right) } \end{aligned}$$
(71)
$$\begin{aligned} B= & {} \frac{M}{2\sqrt{R^{5}}\sqrt{R-2M}} \end{aligned}$$
(72)
$$\begin{aligned} A= & {} \frac{2R-5M}{2\sqrt{R}\sqrt{R-2M}}. \end{aligned}$$
(73)

Equations (71)–(73) are the necessary conditions to determine the constants parameters that characterize the model. In Table 1 are displayed the resulting numerical values for A, B and F by considering the data for the mass and radius corresponding to the compact objects 4U 1538-52, LMC X-4 and SMC X-1 [123] along with \(C=0.2 [\text {km}^{-2}]\) and \(\alpha =0.08\). As can be seen from the matching condition it is evident that the constant parameters A, B and F depend on \(\{R,M,C,\alpha \}\). What is more the physical behaviour of the main quantities such as \(\rho \), \(p_{r}\), \(p_{t}\) and \(\Delta \) depend on the set \(\{A, B, C, F, \alpha \}\). Nevertheless, as C, \(\alpha \), M and R are fixed by hand, then the physical behaviour of the model entirely depends on \(\{R,M,C,\alpha \}\). So, as the metric potentials must be increasing functions with increasing radial coordinate r, then from Eq. (42) it follows that both A and B must have the same sign. Besides, the conditions \(\rho (0)>0\) and \(p_{r}(0)>0\) must be satisfied. So, from Eqs. (24), (25), (44), (45), (49) and (50) one obtains

$$\begin{aligned} \rho (0)= & {} \frac{3C^{2}F}{8\pi \left( CF+\alpha \right) }>0, \end{aligned}$$
(74)
$$\begin{aligned} p_{r}(0)= & {} \frac{4BCF-AFC^{2}+4B\alpha }{8\pi \left( CF+\alpha \right) }>0. \end{aligned}$$
(75)

From (74) one gets

$$\begin{aligned} F>0 \quad \text{ and }\quad CF+\alpha >0 , \end{aligned}$$
(76)

or

$$\begin{aligned} F<0 \quad \text{ and }\quad CF+\alpha <0, \end{aligned}$$
(77)

in order to assure a positive defined density throughout the compact configuration. Now, from (75) and Zeldovich’s condition \(p_{r}(0)/\rho (0)\le 1\) one has

$$\begin{aligned} \frac{FC^{2}}{4\left( CF+\alpha \right) }<\frac{B}{A}\le \frac{FC^{2}}{\left( CF+\alpha \right) }. \end{aligned}$$
(78)

Based on the previous discussion the inequality (78) is true iff

$$\begin{aligned} CF+\alpha>0 \Rightarrow \alpha >-CF, \end{aligned}$$
(79)

or

$$\begin{aligned} CF+\alpha<0 \Rightarrow \alpha<-CF\Rightarrow \alpha <C|F|. \end{aligned}$$
(80)

On the other hand, if the \(\theta \)-sector is turned off ı.e, \(\alpha =0\) which implies \(F=0\) the seed solution is recovered. In particular, for this model from Eq. (24) it is observed that C must be a strictly positive quantity in order to have a physical relevant density \(\rho \) describing a compact object. Of course, if \(\alpha \) and F are zero the values of the constants A and B will change in magnitude but they still have the same sign. So, in conclusion despite the solution was modified the sign of the constant C does not change. This means that in general the deformed solution accepts negative values for the \(\alpha \) parameter restricted to the condition (79) or (80), being the resulting solution admissible from the physical and mathematical point of view.

4.2 Junction conditions model 2

Similarly to the model 1 we use the boundary conditions as before, obtaining the following equations for the first fundamental form

$$\begin{aligned}&e^{A+BR^{2}}=1-\frac{2M}{R}, \end{aligned}$$
(81)
$$\begin{aligned}&\frac{\alpha C\,r^{2}\,e^{A+Br^2}}{\left( 1+C\,r^{2}\,e^{A+Br^2}\right) \,\left( \alpha +C\,e^{A}\,F+FC^{2}r^{2}\,e^{2A+Br^2}\right) } \nonumber \\&\quad +\frac{1}{1+C\,r^{2}\,e^{A+Br^2}} =1-\frac{2M}{R}, \end{aligned}$$
(82)

and for the second fundamental form one gets

$$\begin{aligned} F=\frac{2B\alpha }{e^{A}C\left( Ce^{A+Br^{2}}-2B\right) }. \end{aligned}$$
(83)

In this case we have taken as free parameters the constant B and \(\alpha \). Besides, the mass M and radius R were fixed by using the numerical data corresponding to the compact star Cen X-3. In Table 3 are depicted the resulting values for the remaining constant parameters that characterize the solution. It should be noted that the constant A depends only on the mass M and radius R. This is because Eq. (81) corresponds to the continuity of the temporal metric potential across the boundary \(\Sigma \) which remains the same under MGD due to the deformation enters via the radial metric potential into the space-time.

From Figs. 1, 2 (upper panels), 5 and 6 (top panels) it is evident that the inner geometry is completely regular throughout the stellar interior and the main salient thermodynamic variables satisfy the aforementioned requirements to describe a realistic compact structure from the astrophysical point of view. Furthermore, the radial pressure \(p_{r}\) vanishes at the surface of the structure and the tangential \(p_{t}\) one dominates at all points. As it is observed in Figs. 2 and 6 (top panels) both \(p_{r}\) and \(p_{t}\) drift apart towards the surface inducing an and anisotropic behaviour in the stellar interior. What is more the anisotropy factor \(\Delta \) increases monotonically towards the boundary remaining finite and continuous in the interior as can be seen from Figs. 2 and 6 (lower left panel). This fact reveals the presence of an attractive force in nature within the compact object. This force helps to counteract the gravitational gradient which sustains the stability and balance of the system against radial disturbances. In Figs. 2 and 6 (lower right panels) it is appreciated that the matter distribution respects causality condition and it is described by a well behaved energy–momentum tensor (see left panels in Figs. 3, 7). The former is an important subject regarding the study of compact structures. Indeed a bounded and finite sound speed of the pressure waves in the principal directions of the fluid sphere says that any sign travelling inside the structure cannot exceed the speed of light. On the other hand the trend of the constraints imposed on energy–momentum tensor are satisfied everywhere. This corroborates that the matter distribution threading the stellar interior is positive defined. So, in conclusion the resulting model could serve to describe realistic compact objects such as neutron stars.

4.3 Stability and hydrostatic balance

To complement the above requirements it is also important analyze the stability and hydrostatic equilibrium of the system. To study the former we have considered to analyze the behaviour of the relativistic adiabatic index \(\Gamma \) in the radial direction. This is so because under the presence of local anisotropies a spherically symmetric system is affected only in the radial direction against an eventual gravitational collapse.

Table 1 The numerical values of constant parameters A, B and F with \(C=0.2 \,[\text {km}^{-2}]\) and \(\alpha =0.08\)
Full size table
Table 2 The numerical values of constant parameters A, B and F with \(C=0.2 \,[\text {km}^{-2}]\) and \(\alpha =0.08\)
Full size table
Table 3 The numerical values of constant parameters A, C and F for different values of the constants B and \(\alpha \) with the data corresponding to the compact object Cen X-3 (Rawls  et  al. [123]): \(R=9.178\) [km] and \(M=1.49 M_{\odot }\)
Full size table

In the arena of classical isotropic matter distribution (Newtonian fluid spheres) the collapsing condition corresponds to \(\Gamma <4/3\) [40, 48]. In the framework of relativistic fluid spheres the situation involves some extra terms which can be seen as corrections to the previous condition [49, 50],

$$\begin{aligned} \Gamma <\frac{4}{3}+\left[ \frac{1}{3}\kappa \frac{\rho _{0}p_{r0}}{|p^{\prime }_{r0}|}r +\frac{4}{3}\frac{\left( p_{t0}-p_{r0}\right) }{|p^{\prime }_{r0}|r} \right] _{max} \end{aligned}$$
(84)

where \(\rho _{0}\), \(p_{r0}\) and \(p_{t0}\) are the initial density, radial and tangential pressure when the fluid is in static equilibrium. The second term in the right hand side represents the relativistic corrections to the Newtonian perfect fluid and the third term is the contribution due to anisotropy. It is clear from (84) that if we have a non-relativistic perfect fluid matter distribution the bracket vanishes and we recast the collapsing Newtonian limit \(\Gamma <4/3\). In this regard, Heintzmann and Hillebrandt [40] showed that in the presence of a positive an increasing anisotropy factor \(\Delta =p_{t}-p_{r}>0\), the stability condition for a relativistic compact object is given by \(\Gamma >4/3\), that is so because positive anisotropy factor may slow down the growth of instability. Nevertheless, relativistic correction to the adiabatic index \(\Gamma \) could introduce some instabilities inside the star [134, 135]. To overcome this issue in [136] was proposed a more strict condition on the adiabatic index \(\Gamma \). This condition claim the existence of a critical value for the adiabatic index \(\Gamma _{\text {crit}}\). To have a stable structure, this critical value depends on the amplitude of the Lagrangian displacement from equilibrium and the compactness factor \(u\equiv M/R\). The amplitude of the Lagrangian displacement is characterized by the parameter \(\xi \), so taking particular a form of this parameter the critical relativistic adiabatic index is given by

$$\begin{aligned} \Gamma _{\text {crit}}=\frac{4}{3}+\frac{19}{21}u, \end{aligned}$$
(85)

where the stability condition becomes \(\Gamma \ge \Gamma _{\text {crit}}\). To compute the adiabatic relativistic index \(\Gamma \) one has the following expression

$$\begin{aligned} \Gamma =\frac{\rho +p_{r}}{p_{r}}\frac{dp_{r}}{d\rho }. \end{aligned}$$
(86)

Figures 3 (right panel) and 7 (right panel) shown that \(\Gamma >\Gamma _{crit}\) everywhere within the stellar interior, hence the models 1 and 2 are stable under radial perturbation induced by the anisotropic behaviour. In Tables 2 and 3 are depicted the numerical values of the central relativistic adiabatic index for each model, where clearly the mentioned condition is satisfied.

The other important study is related with the hydrostatic equilibrium under different forces, namely the hydrostatic \(F_{h}\), the gravitational \(F_{g}\) and the anisotropic \(F_{a}\) forces. To accomplish this analysis we have considered the following modified Tolman–Oppeneheimer–Volkoff (TOV) equation,

$$\begin{aligned} \begin{aligned}&{\tilde{p}}^{\prime } + \frac{1}{2}\nu ^{\prime } \left( {\tilde{p}} + {\tilde{\rho }}\right) \\&\quad -\alpha \left[ \left( \theta ^{r}_{r}\right) ^{\prime } + \frac{1}{2}\nu ^{\prime } \left( \theta ^{r}_{r}-\theta ^{t}_{t} \right) + \frac{2}{r} \left( \theta ^{r}_{r}-\theta ^{\varphi }_{\varphi }\right) \right] =0. \end{aligned} \end{aligned}$$
(87)

It is clear that in the case \(\alpha =0\) the familiar TOV [137, 138] in the context of relativistic isotropic models is recovered. From Figs. 4 and 8 it is observed that the system is in equilibrium under the mentioned forces. As said earlier the anisotorpic force is repulsive in nature. Then the gravitational gradient is counteracts by the action of the hydrostatic and anisotropic forces. This prevents the system to collapse below its Schwarzschild radius onto a point singularity. Moreover, after some point inside the stellar interior the anisotropic force dominates the hydrostatic one showing the preponderance that local anisotropies have in the balance on the configuration.

5 Concluding remarks

In this paper, we have combined the class I approach and gravitational decoupling methodology by means of minimal geometric deformation to generate anisotropic interior solutions. The main component of this technology is that we have implemented the class I condition as generator of minimal geometric deformation functions f(r). To obtain the decoupler function f(r) we have tested our approach by setting two different class I space-time solutions, namely Adler–Finch–Skea solution (model 1) and Kuchowicz solution (model 2). As it is well known in the framework of gravitational decoupling the \(\theta \)-sector is completely determine once the \(\nu (r)\) metric potential and the decoupler function f(r) are specified. Although the generating equation (41) of decoupler functions looks quite complex, it can be solved once the seed geometry has been proposed. This approach offers a new possibility to find deformation functions f(r) in the light of gravitational decoupling in addition with previous works [90, 92,93,94,95,96] where the mimic constraint scheme was used to generate f(r) or imposing a suitable f(r) as was done in [103, 119].

It is worth mentioning that we have tested the viability of the resulting models to describe compact objects supporting by an anisotropic matter distribution, analyzing all the necessary criteria that any admissible compact structure must satisfy in order to represent a realistic neutron or quark star. In this concern we have checked the behaviour of the geometric structure as well as of the main thermodynamic variables inside of the compact configuration, causality condition, the trend of the energy–momentum tensor, stability by means of relativistic adibatic index and hydrostatic balance by using the modified Tolman-Oppenheimer-Volkoff equation. All this analysis is supported by Figs. 1, 2, 3, 4, 5, 6, 7 and 8 for both, model 1 and 2 where it is clear that the obtained solutions satisfy all the requirements to be an acceptable models capable to describe realistic compact structures. Moreover, as Tables 1, 2 and 3 exhibit we have used real data to obtain the constant and physical parameters that characterized the solution. Specifically, we have imposed the mass and radius for some known compact configurations, namely 4U 1538-52, SMC X-1 and LMC X-4 for model 1 and Cen X-3 for model 2.