1 Introduction

Although there is no doubt of the beauty and the overall correctness of the General Relativity [1,2,3], the theory suffers from a number of shortcomings [4,5,6,7,8] which could be addressed by extensions, provided by the Extended Theories of Gravity (ETGs), of the Einstein’s proposal. Apart from the cosmological arguments on the need of looking for modified theories of gravity [9,10,11,12,13,14,15,16], there are also indications coming from astrophysics strengthening reasons for searching for the alternatives. In the light of the very recent observation of the pulsar PSR J2215+5135 with the mass \(M_1=2.27^{+0.17}_{-0.15}M_\odot \) for the neutron star [17] putting in trouble exotic forms of matter (hyperons or deconfined quarks) and the previous discoveries of the massive neutron stars as \(2.01\pm 0.04M_\odot \) (PSR J0348+0432) [18], and \(1.97\pm 0.04M_\odot \) (PSR J1614-2230) [19], the ETGs [20, 21] allow to exceed the maximal mass of \(2M_\odot \) demonstrated by GR without introducing exotic components.

Roughly speaking, in the ETGs one changes the geometric part of the action which can be achieved by, for example, generalizing the Einstein–Hilbert action Lagrangian density to an arbitrary function of the scalar curvature (f(R) gravity [8, 11, 22,23,24,25,26,27,28,29]), by adding minimally or non-minimally coupled scalar field [30, 31], or by assuming that physical constants are not actually constants [32,33,34]. For a more detailed discussion, see [35].

In the present paper we are interested in the \(f({\hat{R}})\) Palatini gravity under the Ehlers–Pirani–Schild (EPS) interpretation, which in more detail was discussed in [36,37,38]. The Palatini formulation of \(f({{\hat{R}}})\) gravity has advantages with respect to the metric one since the field equations are second-order differential equations for the metric g while in the metric formulation we deal with the fourth-order equations. Since we are interested in stars, it should be mentioned that astrophysical objects have been already widely discussed in the context of Palatini gravity: studies on black holes can be found in [39,40,41,42,43,44,45], on wormholes in [46,47,48,49], and on neutron stars in [50,51,52,53,54,55,56,57,58,59,60,61].

Let us just briefly recall the Palatini formalism which assumes that the spacetime geometry is described by two independent structures: a class of Lorentzian metrics which are conformally related to each other, and a connection which later on, as a dynamical feature of the action, will turn out to be a Levi–Civita connection with respect to a metric conformally related to the metric g. Thus, we consider a standard action of the \(f({{\hat{R}}})\) gravity of the form

$$\begin{aligned} S=S_{\text {g}}+S_{\text {m}}=\frac{1}{2\kappa }\int \sqrt{-g}f({\hat{R}}) d^4 x+S_{\text {m}}(g_{\mu \nu },\psi _m), \end{aligned}$$
(1)

where \({\hat{R}}={\hat{R}}^{\mu \nu }g_{\mu \nu }\) is the Palatini-Ricci scalar constructed using two independent objects, the connection \({\tilde{\Gamma }}\) and the metric g. The variation with respect to the metric g and the independent connection \({\tilde{\Gamma }}\) is given, respectively, by the formulas

$$\begin{aligned} f'({\hat{R}}){\hat{R}}_{\mu \nu }-\frac{1}{2}f({\hat{R}})g_{\mu \nu }=\,&\kappa T_{\mu \nu }, \end{aligned}$$
(2)
$$\begin{aligned} {\hat{\nabla }}_\beta (\sqrt{-g}f'({\hat{R}})g^{\mu \nu })=\,&0, \end{aligned}$$
(3)

where \(T_{\mu \nu }\) is the energy momentum tensor and \(f'({\hat{R}})=df/d{\hat{R}}\).

Equations (3) imply that the connection \({\hat{\nabla }}_\beta \) is the Levi–Civita connection of the conformal metric h (up to a projection, for the detailed discussion see e.g., [62]):

$$\begin{aligned} h_{\mu \nu }=f'({\hat{R}})g_{\mu \nu }. \end{aligned}$$
(4)

Let us observe that Palatini gravity is equivalent to GR when one considers the linear function f of the form \(f({{\hat{R}}})={{\hat{R}}}-2\Lambda \), and the independent connection turns out to be Levi–Civita connection of the metric g.

We are going to use here the following interesting fact: the equations in question can be rewritten [25] in the terms of the conformal metric \( h_{\mu \nu }\) [63, 64] and the scalar field defined as \(\Phi =f'({\hat{R}})\):

$$\begin{aligned}&{\bar{R}}_{\mu \nu } - \frac{1}{2} h_{\mu \nu } {\bar{R}} =\kappa {\bar{T}}_{\mu \nu }-\frac{1}{2} h_{\mu \nu } {\bar{U}}(\Phi ) \end{aligned}$$
(5a)
$$\begin{aligned}&\Phi {\bar{R}} - (\Phi ^2\,({\bar{U}}(\Phi ))^\prime =0, \end{aligned}$$
(5b)

where the bar quantities are defined as follows: \({\bar{U}}(\Phi )=({\hat{R}}\Phi -f({\hat{R}}))/\Phi ^2\), and the appropriate energy momentum tensor reads \({\bar{T}}_{\mu \nu }=\Phi ^{-1}T_{\mu \nu }\). One should also bear in mind that \({{\hat{R}}}_{\mu \nu }={\bar{R}}_{\mu \nu }, {\bar{R}}= h^{\mu \nu }{\bar{R}}_{\mu \nu }=\Phi ^{-1} {{\hat{R}}}\) and \(h_{\mu \nu }{\bar{R}}=\ g_{\mu \nu }{{\hat{R}}}\). The above equations are field equations of the scalar-tensor action for the metric \(h_{\mu \nu }\) and (non-dynamical) scalar field \(\Phi \).

We will now focus on the spherical-symmetric spacetime whose g-metric is given by

$$\begin{aligned} ds^2=-B(r)dt^2+A(r)dr^2+r^2 d\theta ^2+r^2\sin ^2\theta d\varphi ^2 \end{aligned}$$
(6)

while the conformal metric is given by (4). Solving the equations in the Einstein frame, using the properties and the interpretation of the Palatini gravity it was shown [54, 65] that the generalized Tolman–Oppenheimer–Volkoff (TOV) equations read

$$\begin{aligned} \left( \frac{\Pi }{\Phi ({r})^2}\right) '&=-\frac{G{\tilde{A}}{\mathcal {M}}}{r^2} \left( \frac{Q+\Pi }{\Phi ({r})^2}\right) \left( 1+\frac{4\pi r^3\frac{\Pi }{\Phi ({r})^2}}{{\mathcal {M}}}\right) \end{aligned}$$
(7)
$$\begin{aligned} {\mathcal {M}}(r)&= \int ^r_0 4\pi {\tilde{r}}^2\frac{Q({\tilde{r}})}{\Phi ({\tilde{r}})^2} d{\tilde{r}}, \end{aligned}$$
(8)

where the generalized energy density Q and the pressure \(\Pi \) are defined as

$$\begin{aligned} \bar{Q}= & {} {\bar{\rho }}+\frac{1}{2}\bar{U}=\frac{\rho }{\Phi ^2}+\frac{U}{2\Phi ^2}= \frac{Q}{\Phi ^2}, \end{aligned}$$
(9a)
$$\begin{aligned} {\bar{\Pi }}= & {} \bar{p}-\frac{1}{2}\bar{U}=\frac{p}{\Phi ^2}-\frac{U}{2\Phi ^2}= \frac{\Pi }{\Phi ^2}. \end{aligned}$$
(9b)

Recall that \(\bar{U}\) and \(\Phi \) depend on the choice of the model we are interested in. Let us notice that the r-coordinate as well as \({{\tilde{A}}}\) are objects from the Einstein frame thus one applies the conformal transformation:

$$\begin{aligned} r^2\rightarrow \Phi (r) r^2,\quad {{\tilde{A}}} = \Phi (r)^{-1} A(r). \end{aligned}$$
(10)

In what follows we will focus on the Starobinsky model \(f({{\hat{R}}})={{\hat{R}}}+\beta {{\hat{R}}}^2\) [11] considered in [66] in the context of the Lane–Emden equation. The generalized versions of Lane–Emden equation were already studied in [66,67,68,69,70,71, 74, 75], and some of them were obtained from the generalized TOV equations [65, 76,77,78,79,80,81,82,83].

We follow the Weinberg convention [84], and hence the signature of the metric is \((-+++)\) while \(\kappa =-8\pi G/c^4\).

Given the prominent role played by exact solutions and exactly solvable models in modern physics, see e.g., [85, 86] and references therein, it is natural to look for exact solutions of the generalized Lane–Emden equation introduced in [66] in the context of Palatini gravity. In the next section we present such solutions for two cases: that of an incompressible star (\(n=0\)), when the solution coincides with a well-known one, and that of a neutron star (\(n=1\)), when the solution we found is, to the best of our knowledge, new. In Sect. 3 the physical implications of this new solution are explored using both analytical and numerical techniques, and Sect. 4 contains discussion.

2 Exact solutions of the Lane–Emden equation

The standard Lane–Emden equation coming from the Newtonian limit of the GR equilibrium equations (TOV equations) and polytropic equation of state \(p=K\rho ^\gamma \), where K and \(\gamma \) are polytropic parameters, has the following form:

$$\begin{aligned} \frac{1}{\xi ^2}\frac{d}{d\xi }\left( \xi ^2\frac{d\theta }{d\xi }\right) +\theta ^n=0; \end{aligned}$$
(11)

here \(n=\frac{1}{\gamma -1}\).

Recall the relation among dimensionless quantities appearing in (11) and the physical ones:

$$\begin{aligned} r&=r_c{\xi },\quad \rho =\rho _c\theta ^n,\quad p=p_c\theta ^{n+1}, \end{aligned}$$
(12)
$$\begin{aligned} r^2_c&=\frac{(n+1)p_c}{4\pi G\rho ^2_c}, \end{aligned}$$
(13)

where \(p_c\) and \(\rho _c\) are central pressure and energy density, respectively.

Equation (11) is known to possess three exact solutions for \(n=\{0,1,5\}\) and, generally speaking, it proved pretty much impossible to find exact solutions of the generalized Lane–Emden equations considered in [67,68,69,70,71, 74, 75]. Thus, for other values of n or in the case of generalized Lane–Emden equations, the approximate and/or numerical methods were applied in order to examine the properties of stars.

As shown in [66], the generalized Lane–Emden equation for the Starobinsky Lagrangian \(f({{\hat{R}}})={{\hat{R}}}+\beta {{\hat{R}}}^2\) in the Einstein frame is given by

$$\begin{aligned} \frac{1}{\bar{\xi }}\frac{d^2}{d\bar{\xi }^2}\left( \left[ 1+\frac{2\alpha }{n+1} \theta ^n\right] \bar{\xi }\theta \right) =-\theta ^n, \end{aligned}$$
(14)

where \(\alpha =\kappa c^2\beta \rho _c\), with \(\rho _c\) being a central density. The extra term including \(\alpha \) occurring in (14) comes from the potential U appearing in (5a) and definitions (9) whose form depends on the Lagrangian. The details of the derivation can be found in [66].

Under the conformal transformation \(\bar{\xi }^2=\Phi \xi ^2\), where \(\Phi =1+2\alpha \theta ^n\), the above equation takes the form

$$\begin{aligned} \xi ^2\theta ^n\Phi +\displaystyle \frac{\Phi ^{-1/2}}{1+\frac{1}{2} \xi \Phi _{\xi }/\Phi }\displaystyle \frac{d}{d\xi }\left( \displaystyle \frac{\xi ^2\Phi ^{3/2}}{1+\frac{1}{2} \xi \Phi _{\xi }/\Phi }\displaystyle \frac{d\theta }{d\xi } \right) =0. \end{aligned}$$
(15)

An approximation of (15) was analyzed from the perspective of finding the numerical solutions in [66]. Notice that for \(\alpha =0\) we have \(\Phi =1\) and (15) boils down to (11).

Now note that for \(n=0\) equation (14) becomes linear,

$$\begin{aligned} \frac{1}{\bar{\xi }}\frac{d^2}{d\bar{\xi }^2}\left( \left[ 1+2\alpha \right] \bar{\xi }\theta \right) =-1, \end{aligned}$$
(16)

and its general solution is readily found to read

$$\begin{aligned} \theta =-\displaystyle \frac{\bar{\xi }^2}{6(1+2\alpha )}+C_0+\frac{C_1}{\bar{\xi }}, \end{aligned}$$
(17)

where \(C_i\) are arbitrary constants.

The transformation \(\bar{\xi }^2=\Phi \xi ^2\) in this case amounts to a rescaling \(\bar{\xi }=(1+2\alpha )^{1/2}\xi \), so the general solution of (15) for \(n=0\) reads

$$\begin{aligned} \theta =-\displaystyle \frac{\xi ^2}{6}+C_0+\frac{C_1}{\xi }, \end{aligned}$$
(18)

where we have rescaled \(C_1\) for the sake of convenience.

If \(C_1\ne 0\) then this solution has singularity at \(\xi =0\), which is unphysical, so we should assume that \(C_1=0\). Upon further imposing the boundary conditions in the Jordan frame, \(\theta (0)=1\), \(\theta '(0)=0\), we find that (18) becomes

$$\begin{aligned} \theta =-\displaystyle \frac{\xi ^2}{6}+1. \end{aligned}$$
(19)

Notice that it has the same form as the solution of the standard Lane–Emden equation (11) for \(n=0\) describing incompressible stars, and for this reason it has been discussed in many textbooks (see e.g., [84]).

Our key observation now is that for \(n=1\) the generalized Lane–Emden equation (15) has an exact solution

$$\begin{aligned} \theta =\frac{15-\xi ^2}{2\alpha (10+\xi ^2)}, \end{aligned}$$
(20)

which appears to be new and can be employed to describe a Newtonian neutron star.

3 Newtonian neutron star in Palatini gravity

As we have already mentioned, the solutions of the Lane–Emden equation have to satisfy the boundary conditions, namely \(\theta (0)=1\) and \(\theta '(0)=0\). The solution (20) for \(n=1\) turns out to satisfy them only if \(\alpha =\frac{3}{4}\).

This value lies in the allowed range \(\alpha >-1/2\). Indeed, because of the boundary condition \(\theta (0)=1\) the conformal factor \(\Phi \) for \(\xi =0\) takes the value \(1+2\alpha \). Now, for \(\alpha =-1/2\) this value becomes zero which is not allowed since the conformal factor may not change sign, cf. [66] for details. Moreover, the numerical analysis in [66] also indicates that the values of \(\alpha \) smaller than \(-1/2\) are unphysical.

This means that when we assume that the value of the central density of an average neutron star is \(\rho _c\sim 8 \times 10^{17}\;\frac{\text {kg}}{\text {m}^3}\), the Starobinsky parameter is found to be

$$\begin{aligned} \beta \sim -5.02978 \times 10^6\text {m}^2. \end{aligned}$$
(21)

Let us recall that \(\alpha =\kappa c^2 \beta \rho _c\) and because of the Weinberg’s convention (\(\kappa =-8\pi G/c^4\)) that we follow throughout the paper, \(\kappa \) introduces a minus to the definition of the parameter \(\alpha \). Therefore, for positive \(\alpha \) we deal with a negative value of the Starobinsky parameter \(\beta \). In order for the solution (20) to describe a polytropic (with \(n=1\)) star, one obtains \(\alpha =3/4\) which immediately gives values of the parameter \(\beta \), which however will depend on a type of stars. Thus, the denser star, the larger absolute value of the Starobinsky parameter. This example also demonstrates how the theories of Palatini family are sensitive to the local energy density distribution [60].

Now we are able to find the star’s mass, radius, and central density. Recall that by introducing the dimensionless quantities [84, 87]:

$$\begin{aligned} \omega _n&:=-\xi ^2\frac{d\theta }{d\xi }\mid _{\xi =\xi _R}, \end{aligned}$$
(22)
$$\begin{aligned} \gamma _n&:=(4\pi )^\frac{1}{n-3}(n+1)^\frac{n}{3-n}\omega _n^\frac{n-1}{3-n}\xi _R, \end{aligned}$$
(23)
$$\begin{aligned} \delta _n&:=-\frac{\xi _R}{3\frac{d\theta }{d\xi }\mid _{\xi =\xi _R}}. \end{aligned}$$
(24)

we can write down the star’s mass, the mass-radius relation, central density, and temperature, in the form

$$\begin{aligned} M&=4\pi r_c^3\rho _c\omega _n, \end{aligned}$$
(25)
$$\begin{aligned} R&=\gamma _n\left( \frac{K}{G}\right) ^\frac{n}{3-n}M^\frac{n-1}{n-3}\xi _R, \end{aligned}$$
(26)
$$\begin{aligned} \rho _c&=\delta _n\left( \frac{3M}{4\pi R^3}\right) , \end{aligned}$$
(27)
$$\begin{aligned} T&=\frac{K\mu }{k_B}\rho _c^\frac{1}{n}\theta , \end{aligned}$$
(28)

where the last equation for the temperature profile is given under the assumption that the gas is ideal with the equation of state \(T=\frac{k_B\rho T}{\mu }\), with \(k_B\) and \(\mu \) being the Boltzmann constant and mean molecular weight, respectively.

However, let us notice that the above quantities were defined for the General Relativity setting. Since we wish to apply them to the Palatini gravity, we must keep in mind that the above expressions are the ones in Einstein frame. Thus, the quantities \(\omega _n\) and \(\delta _n\) should be rewritten, see Eqs. (31) and (32) below; notice that the mass (8) is still written in the Einstein frame because the r-coordinate comes from the conformal metric h. This can be directly verified by applying the generalized Lane–Emden equation (15) to (8) while taking into account that the conformal transformation in the case of Starobinsky model preserves the polytropic equation of state for small values of p [61]. Thus, in the case of Palatini gravity we should have written

$$\begin{aligned} \omega _n&:=-{\bar{\xi }}^2\frac{d\theta }{d{\bar{\xi }}}\mid _{\xi =\xi _R}, \end{aligned}$$
(29)
$$\begin{aligned} \delta _n&:=-\frac{{\bar{\xi }}_R}{3\frac{d\theta }{d{\bar{\xi }}}\mid _{\xi =\xi _R}}. \end{aligned}$$
(30)

Then, applying the conformal transformation relation \({\bar{\xi }}^2=\Phi \xi ^2\), we find that

$$\begin{aligned} \omega _n&=-\frac{\xi ^2\Phi ^\frac{3}{2}}{1+\frac{1}{2}\xi \frac{\Phi _\xi }{\Phi }} \frac{d\theta }{d\xi }\mid _{\xi =\xi _R}, \end{aligned}$$
(31)
$$\begin{aligned} \delta _n&=-\frac{\xi _R}{3\frac{\Phi ^{-\frac{1}{2}}}{1+\frac{1}{2}\xi \frac{\Phi _\xi }{\Phi }}\frac{d\theta }{d\xi }\mid _{\xi =\xi _R}}. \end{aligned}$$
(32)

Now we are able to calculate the physical values of the star’s mass. Moreover, since the solution for \(n=1\) in the case of the standard Lane–Emden equation is known, \(\theta _{N}=\frac{\sin {\xi }}{\xi }\), we can compare Newtonian neutron stars in the two models. Here and below we will denote the solution and values obtained from the standard Lane–Emden equation by the subscript N.

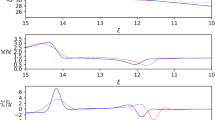
We plot the solutions in Fig. 1. Notice that Fig. 1 also represents the dimensionless temperature profile as \(T\sim \theta \).

Fig. 1
figure 1

Plots of the exact solutions for the case \(n=1\). The dashed curve represents the solution \(\theta =\frac{\sin {\xi }}{\xi }\) of the standard equation while the continuous curve is the solution of the Palatini one, \(\theta =\frac{15-\xi ^2}{2\alpha (10+\xi ^2)}\), with \(\alpha =3/4\). The solution for \(n=0\), which is the same for both cases, is given by the dotted curve

Full size image

The neutron star’s radius \(\xi _R\) is defined by the first zero of the solution, \(\theta (\xi _R)=0\), and hence we find that \(\xi _R=\sqrt{15}\) while \(\omega _1\sim 3.87\), and \(\delta _1=5\). Therefore, we can immediately compare the masses and radii of the stars

$$\begin{aligned} \frac{M}{M_N}=\frac{\omega _1}{\omega _N}\sim 1.23,\;\;\frac{R}{R_N}\sim 1.23,\;\;\frac{\rho }{\rho _N}\sim 0.99 \end{aligned}$$
(33)

where we have used \((\xi _R)_N=\pi \) and \(\omega _N=\pi \) [84].

Let us notice a very important result here: Since one describes the low mass brown dwarfs, that is, the stars with the masses \(M\lesssim 4 \times 10^{-3}M_\odot \), by the polytropic models with \(n=1\), we may easily compare the result coming from Palatini gravity with the one from GR. From (26) we see that the radius for \(n=1\) is independent of the star’s mass

$$\begin{aligned} R=\gamma _{n=1}\left( \frac{K}{G}\right) ^\frac{1}{2} \end{aligned}$$
(34)

whose value in the case of GR is \(\approx 0.1R_\odot \) being close to the observed value [71]. However, in the modified gravity, because the polytropic constant K is independent of the theory of gravity one deals with

$$\begin{aligned} R^{\text {modified}}=0.1\frac{\gamma _{n=1}^{\text {modified}}}{\gamma _{n=1}^{\text {GR}}}R_\odot \end{aligned}$$
(35)

and thus immediately we have in our case that the radius of a low mass dwarf star is \(\approx 0.123R_\odot \). This can be compared to the measurements of the mass-radius relation for such objects as soon as for example GAIA survays will release the data [72, 73].

4 Conclusions

We have found two exact solutions for \(n=0\) and \(n=1\) of the modified Lane–Emden equation (15) using the Einstein–Jordan frame correspondence [88,89,90,91], keeping in mind that physical properties of the star such as mass and radius are the ones appearing in Jordan frame, which we demonstrated clearly in the discussion preceding the formulas (29) and (30). We have not examined the result for \(n=0\) since it would describe an incompressible star. We should notice that the latter solution has exactly the same form as the solution of the standard Lane–Emden equation. However, the case of the Newtonian neutron star (the solution for \(n=1\)), although being just a toy model, shows that one deals with the stellar objects bigger than the stars of the pure GR models. Let us also stress that in this work we have used the exact formula for obtaining the star’s mass, that is, Eqs. (25) and (31), in contrast to the previous work [66] where an approximate formula for mass was used. Moreover, with the result on the radius of a low mass dwarf star which is also modelled by the polytropic EoS with \(n=1\) we have shown that the theory can be probed thanks to the observation of such objects. The modification introduced by Palatini gravity changes the value of their radii with respect to the GR one and hence the theories could be distinguished from one another.

We expect that the examination of the full relativistic theory, described by the modified TOV Eqs. (7) and (8), will also provide a similar conclusion, that is, that the Palatini star is larger and heavier for the negative Starobinsky parameter \(\beta \) (positive \(\alpha \) parameter), without a need of introducing exotic matter in their internal structure. It should be clarified here that the result was obtained for the negative Starobinsky parameter \(\beta \): the parameter \(\alpha \) appearing in the modified Lane–Emden equation consists of the constant \(\kappa \), which had been defined to be negative.

Moreover, requiring that the solution (20) has to satisfy the boundary conditions accompanying the Lane–Emden equation, we obtained the exact value of the parameter \(\alpha =\frac{3}{4}\) which led to the fact that the Starobinsky parameter is negative and of the order \(10^6 \text {m}^2\) under the assumption of the central energy density \(\rho _c\sim 8 \times 10^{17}\frac{\text {kg}}{\text {m}^3}\).

Let us also mention a discussion in [90] that in the Palatini theories (for example, \(f({{\hat{R}}})\) gravity and Born–Infeld inspired gravity, cf. e.g., [98,99,100,101]) the energy density must be continuous and differentiable function in order to avoid divergences in the field equations. This comes from the fact that one obtains \({{\hat{R}}}={{\hat{R}}}(\rho )\) which appears in the conformal function \(\Phi \) taking part in the conformal transformation which includes the derivatives of \(\rho \).

Therefore, we would like to conclude that the Palatini gravity is a viable alternative to General Relativity since it passes Solar System tests (vacuum solutions are equivalent to General Relativity with cosmological constant) [92,93,94], introduces inflation preserving late time accelerated expansion [63, 64, 96, 97], gives clues on the Dark Matter problem [102], and provides conditions for existence of stable relativistic stars [54] that are similar to General Relativity.