Analytic derivation of the photon structure function $F^{\gamma }_{2} (x,Q^{2})$ at the leading order and the next-to-leading order approximations based on the Laplace transform method

Abstract

In this paper, we present the analytical solutions, based on the Laplace transform method, for the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi evolution equations of the photon at the leading order (LO) and next-to-leading order (NLO) approximations in perturbative QCD. Using these solutions, we derive the singlet, non-singlet, gluon, and photon distribution functions of the photon and also the photon structure function $F^{\gamma }_{2} (x,Q^{2})$ at the LO and NLO approximations. We show that the resulting distribution functions are in agreement with the results of the parameterization model formulated by Gluck, Reya, and Vogt (GRV) (Phys Rev D 46(5):1973, 1992). Moreover, our numerical results of $F^{\gamma }_{2} (x,Q^{2})$ are comparable with the results achieved by Aurenche, Fontannaz, and Guillet (AFG) (Eur Phys J C Part Fields 44(3):395–409, 2005) and also with the experimental data released by the L3, DELPHI, OPAL, ALEPH and PLUTO collaborations.

1 Introduction

In the electromagnetic (EM) interactions, the photon mediates the EM force between EM charged objects. If the photon, in these kinds of interactions, fluctuates into a charged fermion–antifermion pair and one of them interacts with a gauge boson, then the parton structure of the photon is revealed. When fermions are a lepton–antilepton pair, the interaction process can be calculated in the framework QED, but if they are a quark–antiquark pair, this process is described in the framework of QCD. The calculations in the framework of QCD are complicated, because the spectrum of fluctuations is richer. In the photoproduction process, therefore, both the QCD and the QED contributions have to be taken into account in the calculations. There are two types of photons in the interactions: the direct photon and the resolved photon. The direct photon takes part in hard interactions and its structure is not revealed, but the resolved photon first fluctuates into a hadronic state and its structure is revealed. The resolved photon includes two contributions, point-like and hadronic-like, which must be taken into account in the calculations of the structure function and the cross section [1]. In deep inelastic scattering, the results of the photon structure function $F^{\gamma }_{2} (x,Q^{2})$ have been reported by the large electron–positron collider (LEP) [2,3,4,5,6,7] and the electron–proton collider HERA [8,9,10].

After observing the photon structure function in different interactions, theorists have been interested in studying such a structure function. Since the photoproduction processes are susceptible to the properties of the photon itself, the electron–positron and the electron–proton colliders at low energy regions can be used as useful tools for probing the photon structure like that of the proton. On the other hand, there are many differences between the hadronic structure function and the photon structure function. For example, at low $Q^{2}$, the hadronic structure function decreases but the photon structure function grows even without considering the QCD corrections [1, 11].

So far, the photon structure function has been suggested by various theoretical methods: Aurenche et al. [12] obtained the photon structure function beyond the leading logarithm approximation. They modified the hadronic component by taking into account the MS factorization scheme. By fitting all the available data on the photon structure function, Gordon and Storrow [13] determined the parton distribution functions of the photon. In fact, they attempted to update these functions by constraining the input gluon distributions through fitting them to TRISTAN jet data; Vieira and Storrow [14] obtained the quark distribution functions of the photon and the photon structure function using the ansatz of Rossi [15] generating regularized asymptotic solutions to the inhomogeneous Altarelli–Parisi equations; Kolanoski and Zerwas [16] calculated the total cross section for hadron production by two photons. They presented the photon structure function at LO and NLO by the quark parton model and the vector meson dominance model; Berger [17] calculated the photon structure function at LO and NLO based on the operator product expansion and gave a unified picture of the hadronic and point-like pieces. He obtained the point-like contribution of the photon structure function in the MS scheme and the hadronic-like contribution from the vector meson dominance model.

To obtain the parton distribution functions at higher energies than the initial scale $Q_{0}^{2}$, one can use the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) evolution equations [18, 19]. The DGLAP evolution equations are a set of coupled integro-differential equations that give the parton distribution functions in perturbative QCD.

Recently, the QCD DGLAP evolution equations of the proton at LO and NLO have been solved by using the Laplace transform [20,21,22,23] and the Mellin transform methods [24, 25] and have consequently yielded the proton structure function and singlet, non-singlet, and gluon distribution functions inside the proton. Furthermore, utilizing these methods, one can solve the QCD$\otimes$QED DGLAP equations at LO and NLO [26, 27]. In these equations, the QED corrections are considered in the QCD calculations. Such corrections are critical and affect the distribution and structure functions and consequently modify the cross section of processes. In Refs. [26, 27], it has been shown that the photon contribution at high x is comparable with t and b quark contributions in the proton [26, 28].

In this paper, we apply the Laplace transform method to solve the QCD$\otimes$QED evolution equations of the photon at LO and NLO QCD and also at LO QED. On this basis, we extract the singlet, gluon, and photon distribution functions of the photon at the scale $Q^{2}$ as follows:

$$\begin{aligned} F^{\gamma }_{s}(x,Q^{2})= & {} {\mathcal {F}}(F_{s0}^{\gamma }(x), G_{0}^{\gamma }(x), M_{0}^{\gamma }(x),F_{ns0}^{\gamma }(x)), \end{aligned}$$

(1)

$$\begin{aligned} G^{\gamma }(x,Q^{2})= & {} {\mathcal {G}}(F_{s0}^{\gamma }(x), G_{0}^{\gamma }(x), M_{0}^{\gamma }(x),F_{ns0}^{\gamma }(x)), \end{aligned}$$

(2)

$$\begin{aligned} M^{\gamma }(x,Q^{2})= & {} {\mathcal {M}}(F_{s0}^{\gamma }(x), G_{0}^{\gamma }(x), M_{0}^{\gamma }(x),F_{ns0}^{\gamma }(x)), \end{aligned}$$

(3)

where $F_{s0}^{\gamma }(x)$, $F_{ns0}^{\gamma }(x)$, $G^{\gamma }_{0}(x)$, and $M^{\gamma }_{0}(x)$ are the singlet, non-singlet, gluon, and photon distribution functions at the initial scale $Q_{0}^{2}$, respectively. In the above equations, the functions ${\mathcal {F}}$, ${\mathcal {G}}$ and ${\mathcal {M}}$ can be obtained by using the splitting functions $P_{qq}(x,Q^{2})$, $P_{qg}(x,Q^{2})$, $P_{gg}(x,Q^{2})$, $P_{q\gamma }(x,Q^{2})$, $P_{\gamma q}(x,Q^{2})$, and $P_{\gamma \gamma }(x,Q^{2})$ and the distribution functions at the initial scale. Moreover, using the singlet and non-singlet distribution functions, one can get the photon structure function at different scales $Q^{2}$.

The rest of the present paper is organized as follows: In Sect. 2, we present general solutions for decoupling the QCD$\otimes$QED DGLAP evolution equations of the photon at LO in both QCD and QED by applying the Laplace transform method. In Sect. 3, we use the same method to calculate the QCD$\otimes$QED DGLAP evolution equations at NLO QCD and LO QED. In Sect. 4, we also present an analytical solution of the non-singlet sector of the photon structure function based on the Laplace transform method. In Sect. 5, the numerical results of the photon structure function, obtained by the Laplace transform method, are compared with the available L3 [2, 3], OPAL [4, 5], DELPHI [6], ALEPH [7] and PLUTO [29] data as well as the GRV [30] and AFG [31] results. Also in this section, we compare the results of the singlet, non-singlet, and gluon distribution functions of the photon with the GRV results [30]. At the end of this section, we present the photon distribution function of the photon and show a comparison of this distribution function with the s-quark and c-quark distribution functions at NLO adopted from the GRV results. Appendix A gives a brief explanation of the Laplace and the Mellin transforms. In Appendix B, we present the functions of a set of coefficients in the Laplace s space, which are dependent on the splitting functions.

2 Master formula for the LO corrections

The QCD$\otimes$QED DGLAP evolution equations of the photon for the parton density functions of the quark, antiquark, gluon, and photon obey the following inhomogeneous equations, respectively [1, 32]:

$$\begin{aligned}&\frac{\partial q_{i}^{\gamma }(x,Q^{2})}{\partial \ln Q^{2}}=\frac{\alpha _{s}(Q^{2})}{2\pi }\left\{ \sum _{k=1}^{n_{f}}[P_{q_{i}q_{k}}(x)\otimes q_{k}^{\gamma }(x,Q^{2})\nonumber \right. \\&\quad \left. +P_{q_{i}{\bar{q}}_{k}}(x)\otimes {\bar{q}}_{k}^{\gamma }(x,Q^{2})]+P_{q_{i}g}(x)\otimes g^{\gamma }(x,Q^{2})\right\} \nonumber \\&\quad +\frac{\alpha _{e}(Q^{2})}{2\pi } e_{i}^{2}P_{q_{i}\gamma }(x)\otimes \gamma ^{\gamma }(x,Q^{2}),\nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned}&\frac{\partial {\bar{q}}_{i}^{\gamma }(x,Q^{2})}{\partial \ln Q^{2}}=\frac{\alpha _{s}(Q^{2})}{2\pi }\left\{ \sum _{k=1}^{n_{f}}[P_{{\bar{q}}_{i}q_{k}}(x)\otimes q_{k}^{\gamma }(x,Q^{2})\nonumber \right. \\&\left. \quad +P_{{\bar{q}}_{i}{\bar{q}}_{k}}(x)\otimes {\bar{q}}_{k}^{\gamma }(x,Q^{2})]+P_{{\bar{q}}_{i}g}(x)\otimes g^{\gamma }(x,Q^{2})\right\} \nonumber \\&\quad + \frac{\alpha _{e}(Q^{2})}{2\pi } e_{i}^{2}P_{{\bar{q}}_{i}\gamma }(x)\otimes \gamma ^{\gamma }(x,Q^{2}), \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial g^{\gamma }(x,Q^{2})}{\partial \ln Q^{2}}=\frac{\alpha _{s}(Q^{2})}{2\pi }\left\{ \sum _{k=1}^{n_{f}}[P_{gq_{k}}(x)\otimes q_{k}^{\gamma }(x,Q^{2})\nonumber \right. \\&\quad \left. +P_{g{\bar{q}}_{k}}(x){\bar{q}}_{k}^{\gamma }(x,Q^{2})]+P_{gg}(x)\otimes g(x,Q^{2})\right\} \nonumber \\&\quad + \frac{\alpha _{e}(Q^{2})}{2\pi } P_{g\gamma }(x)\otimes \gamma ^{\gamma }(x,Q^{2}), \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\partial \gamma ^{\gamma }(x,Q^{2})}{\partial \ln Q^{2}}=\frac{\alpha _{e}(Q^{2})}{2\pi }\left\{ \sum _{k=1}^{n_{f}}e_{i}^{2} [P_{\gamma q_{k}}(x)\otimes q_{k}^{\gamma }(x,Q^{2})\nonumber \right. \\&\quad \left. +P_{\gamma {\bar{q}}_{k}}(x)\otimes {\bar{q}}_{k}^{\gamma }(x,Q^{2})]+P_{\gamma g}\otimes g^{\gamma }(x,Q^{2})\right\} \nonumber \\&\quad +\frac{\alpha _{e}(Q^{2})}{2\pi }P_{\gamma \gamma }(x)\otimes \gamma ^{\gamma }(x,Q^{2}). \end{aligned}$$

(7)

These equations include the QCD corrections in the QED calculations. In the above equations, $q_{i}^{\gamma }$, ${\bar{q}}_{i}^{\gamma }$, $g^{\gamma }$, and $\gamma ^{\gamma }$ represent the quark, antiquark, gluon, and photon parton density functions of the photon, respectively. The $P_{i,j}(x)$ are the Altarelli–Parisi splitting kernels at one loop correction, which are defined as follows:

$$\begin{aligned}&P_{qq}^{LO}=\frac{4}{3}\frac{1+x^{2}}{(1-x)_{+}}+2\delta (1-x) , \nonumber \\&P_{qg}^{LO}=\frac{1}{2}\left( x^{2}+(1-x)^{2}\right) ,\nonumber \\&P_{gq}^{LO}=\frac{4}{3}\left( \frac{1+(1-x)^{2}}{x}\right) ,\nonumber \\&P_{gg}^{LO}=6\left( \frac{1-x}{x}+\frac{x}{(1-x)_{+}}+x(1-x)\right) \nonumber \\&\qquad \qquad + \left( \frac{11}{2}-\frac{n_{f}}{3}\right) \delta (1-x),\nonumber \\&P_{{\bar{q}}{\bar{q}}}^{LO}=P_{qq}^{LO},\ \ \ \ P_{{\bar{q}}g}^{LO}=P_{qg}^{LO},\ \ \ \ P_{{\bar{q}} \gamma }^{LO}\nonumber \\&\qquad \quad =P_{q \gamma }^{LO},\ \ \ \ P_{g\gamma }^{LO}=P_{\gamma g}^{LO}=0\nonumber \\&P_{\gamma q}^{LO}=C_{F}^{-1} P_{gq}^{LO}, \ \ \ P_{q \gamma }^{LO}=T_{R}^{-1}P_{qg}^{LO},\ \ \ P_{\gamma \gamma }^{LO}\nonumber \\&\qquad \quad =-\frac{2}{3}\sum _{i}e_{i}^{2}\delta (1-x), \end{aligned}$$

(8)

where $n_{f}$ denotes the number of active massless flavors, $C_{F}=\frac{4}{3}$, and $T_{R}=\frac{1}{2}$. It should be noted that, at LO, $P_{g\gamma }=P_{\gamma g}=0$ due to the missing photon–gluon coupling, but these splitting functions at NLO are not zero [33]. By summing Eqs. (4) and (5) and using $F^{\gamma }_{2}=\langle e^{2}\rangle F^{\gamma }_{s}+F^{\gamma }_{ns}$, we can write

$$\begin{aligned} \frac{\partial F^{\gamma }_{s}(x,Q^{2})}{\partial \ln Q^{2}}= & {} \frac{\alpha _{s}^{LO}(Q^{2})}{2\pi }\left\{ P_{qq}^{LO}(x)\otimes F^{\gamma }_{s}(x,Q^{2})\nonumber \right. \\&\left. +2n_{f}P_{qg}^{LO}\otimes G^{\gamma }(x,Q^{2})\right\} \nonumber \\&+\frac{\alpha _{e}(Q^{2})}{2\pi } 2A P_{q\gamma }^{LO}(x)\otimes M^{\gamma }(x,Q^{2}), \end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial G^{\gamma }(x,Q^{2})}{\partial \ln Q^{2}}= & {} \frac{\alpha _{s}^{LO}(Q^{2})}{2\pi }\left\{ P_{gq}^{LO}(x)\otimes F^{\gamma }_{s}(x,Q^{2})\nonumber \right. \\&\left. +P_{gg}^{LO}\otimes G^{\gamma }(x,Q^{2})\right\} , \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial M^{\gamma }(x,Q^{2})}{\partial \ln Q^{2}}= & {} \frac{\alpha _{e}(Q^{2})}{2\pi }\left\{ P_{\gamma q}^{LO}(x)\otimes [\langle e^{2}\rangle F^{\gamma }_{s} (x,Q^{2})\nonumber \right. \\&\left. +F^{\gamma }_{ns}]+P_{\gamma \gamma }^{LO}\otimes M^{\gamma }(x,Q^{2})\right\} , \end{aligned}$$

(11)

where $F^{\gamma }_{s}=\sum _{k=1}^{n_{f}}x\left( q_{k}^{\gamma }+{\bar{q}}_{k}^{\gamma }\right)$, $G^{\gamma }=xg^{\gamma }$, $M^{\gamma }=x\gamma ^{\gamma }$, and $F^{\gamma }_{ns}=\sum _{k=1}^{n_{f}}\left( e_{q_{k}}^{2}-\langle e^{2}\rangle \right) x\left( q_{k}+{\bar{q}}_{k}\right)$ are the singlet, gluon, non-singlet, and photon distribution functions, respectively. Here, $A=\sum _{k=1}^{n_{f}}e_{q_{k}}^{2}$ and $\left\langle e^{2} \right\rangle =\frac{1}{n_{f}}\sum _{k=1}^{n_{f}}e_{q_{k}}^{2}$. In Eqs. (9)–(11), the symbol $\otimes$ represents the convolution integral given in Appendix A.

Equations (9)–(11) have the same structure as those mentioned in Ref. [26]. However, in the present paper, there are three main differences between our calculations and those done in Ref. [26]: First, in our work, the contributions of ${\tilde{P}}_{qq}$ and ${\tilde{P}}_{{\bar{q}}{\bar{q}}}$ are zero in the evolution functions of the photon. Second, the non-singlet contribution of the photon structure function is considered here in solving these equations, while it has not been included in Ref. [26]. Third, in Ref. [26], the proton structure function has been obtained only at high $Q^{2}$ and x smaller than 0.1, whereas, here, the photon structure function is computable for all of x and $Q^{2}$ ranges.

As shown in Refs. [20,21,22], the Laplace transform ${\mathcal {L}}$ of the convolution factors is simply the ordinary product of the Laplace space of the factors. Thus, in order to make Eqs. (9)–(11) easily solvable, we transform these equations to the Laplace space. To do this, we apply the variable changes $x{\equiv }\exp (-v)$ and $y{\equiv }\exp (-\omega )$ together with the Laplace transform (a brief explanation of this transform and its reverse is given in Appendix A), as a result of which we have

$$\begin{aligned} f(s,Q^{2})= & {} {\mathcal {L}}\left[ {\hat{F}}_{s}^{\gamma }(v,Q^{2});s\right] =\int _{0}^{\infty }{\hat{F}}_{s}^{\gamma }(v, Q^{2})e^{-sv}dv,\nonumber \\ g(s,Q^{2})= & {} {\mathcal {L}}\left[ {\hat{G}}^{\gamma }(v,Q^{2});s\right] ,\nonumber \\ m(s,Q^{2})= & {} {\mathcal {L}}\left[ {\hat{M}}^{\gamma }(v,Q^{2});s\right] ,\nonumber \\ f_{ns}(s,Q^{2})= & {} {\mathcal {L}}\left[ {\hat{F}}_{ns}^{\gamma }(v,Q^{2});s\right] , \end{aligned}$$

(12)

where we used the following notations:

$$\begin{aligned} {\hat{F}}_{s}(v,Q^{2})\equiv & {} F^{\gamma }_{s}(e^{-v},Q^{2}), \ {\hat{G}}(v,Q^{2}) \equiv G^{\gamma }(e^{-v},Q^{2}),\nonumber \\ {\hat{M}}(v,Q^{2})\equiv & {} M^{\gamma }(e^{-v},Q^{2}),\ {\hat{F}}_{ns}(v,Q^{2}) \equiv F^{\gamma }_{ns}(e^{-v},Q^{2}),\nonumber \\ \end{aligned}$$

(13)

and then the Laplace transform converts Eqs. (9)–(11) into three coupled ordinary first-order differential equations in s space which can be written as

Table 1 The percentage relative errors of exact and approximate values of Eqs. (26)–(28)

$$\begin{aligned} \frac{\partial f}{\partial \ln Q^{2}}(s,Q^{2})= & {} \frac{\alpha _{s}^{LO}(Q^{2})}{4\pi }\nonumber \\&\quad \times \left[ \Phi _{f}^{LO}(s)f(s,Q^{2})+\Theta _{f}^{LO}(s)g(s,Q^{2})\right] \nonumber \\&\quad +\frac{\alpha _{e}(Q^{2})}{4\pi }\Omega _{f}^{LO}(s)m(s,Q^{2}), \end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial g}{\partial \ln Q^{2}}(s,Q^{2})= & {} \frac{\alpha _{s}^{LO}(Q^{2})}{4\pi }\Phi _{g}^{LO}(s)g(s,Q^{2})\nonumber \\&\quad +\frac{\alpha _{s}^{LO}(Q^{2})}{4\pi }\Theta _{g}^{LO}(s)f(s,Q^{2}), \end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial m}{\partial \ln Q^{2}}(s,Q^{2})= & {} \frac{\alpha _{e}(Q^{2})}{4\pi }\left[ \Omega _{\gamma }^{LO}(s)m(s,Q^{2})\nonumber \right. \\&\left. \quad +\Upsilon _{\gamma }^{LO}(s)f(s,Q^{2})\nonumber \right. \\&\left. \quad +\Upsilon _{ns\gamma }^{LO}(s)f_{ns}(s,Q^{2})\right] , \end{aligned}$$

(16)

where the coefficients $\Phi ^{LO}$, $\Psi ^{LO}$, $\Omega ^{LO}$, and $\Upsilon ^{LO}$ are the LO splitting functions in the Laplace space s [22]:

$$\begin{aligned} \Phi _{f}^{LO}\left( s\right)= & {} 4-\frac{8}{3}\left( \frac{1}{s+1}+\frac{1}{s+2}+2\left( \psi (s+1)+\gamma _{E}\right) \right) , \nonumber \\\end{aligned}$$

(17)

$$\begin{aligned} \Theta _{f}^{LO}\left( s\right)= & {} 2n_{f}\left( \frac{1}{s+1}-\frac{2}{s+2}+\frac{2}{s+3}\right) , \end{aligned}$$

(18)

$$\begin{aligned} \Upsilon _{f}^{LO}\left( s\right)= & {} \frac{5}{24}\Phi _{f}^{LO}\left( s\right) ,\nonumber \\ \Omega _{f}^{LO}\left( s\right)= & {} \frac{A}{n_{f}}\Theta _{f}^{LO}\left( s\right) , \end{aligned}$$

(19)

$$\begin{aligned} \Phi _{g}^{LO}\left( s\right)= & {} \frac{33-2n_{f}}{3}\nonumber \\&+12\left( \frac{1}{s}-\frac{2}{s+1}+\frac{1}{s+2}\nonumber \right. \\&\left. -\frac{1}{s+3}-\psi (s+1)-\gamma _{E}\right) , \end{aligned}$$

(20)

$$\begin{aligned} \Theta _{g}^{LO}\left( s\right)= & {} \frac{8}{3}\left( \frac{2}{s}-\frac{2}{s+1}+\frac{1}{s+2}\right) , \end{aligned}$$

(21)

$$\begin{aligned} \Omega _{f}^{LO}\left( s\right)= & {} \frac{A}{n_{f}}\Theta _{f}^{LO}\left( s\right) ,\nonumber \\ \Omega _{\gamma }^{LO}\left( s\right)= & {} -\frac{4A}{3}, \ \ \ \Upsilon _{\gamma }^{LO}\left( s\right) =\frac{3\langle e^{2}\rangle }{4}\Theta _{g}^{LO}\left( s\right) ,\nonumber \\ \Upsilon _{ns\gamma }^{LO}\left( s\right)= & {} \frac{3}{4}\Theta _{g}^{LO}\left( s\right) , \end{aligned}$$

(22)

where $\psi$ is the digamma function and $\gamma _{E}$ is the Euler constant. By introducing the new variable $\tau$ as $\frac{\partial \tau (Q^{2})}{\partial \ln (Q^{2})}=\frac{\alpha _{s}(Q^{2})}{4\pi }$, the coupled first-order differential Eqs. (14)–(16) in s space can be rewritten as

$$\begin{aligned} \frac{\partial f}{\partial \tau }(s,\tau )= & {} \Phi _{f}^{LO}(s)f(s,\tau )+\Theta _{f}^{LO}(s)g(s,\tau )\nonumber \\&+\frac{\alpha _{e}(Q^{2})}{\alpha _{s}^{LO}(Q^{2})}\Omega _{f}^{LO}(s)m(s,\tau ), \end{aligned}$$

(23)

$$\begin{aligned} \frac{\partial g}{\partial \tau }(s,\tau )= & {} \Phi _{g}^{LO}(s)g(s,\tau )+\Theta _{g}^{LO}(s)f(s,\tau ), \end{aligned}$$

(24)

$$\begin{aligned} \frac{\partial m}{\partial \tau }(s,\tau )= & {} \frac{\alpha _{e}(Q^{2})}{\alpha _{s}^{LO}(Q^{2})}\nonumber \\&\quad \times \left( \Omega _{m}^{LO}(s)m(s,\tau )+\Upsilon _{\gamma }^{LO}(s)f(s,\tau )\nonumber \right. \\&\quad \left. +\Upsilon _{ns\gamma }^{LO}(s)f^{ns}(s,\tau )\right) . \end{aligned}$$

(25)

To make calculations easier at the LO and NLO approximations, we consider the following expressions [20, 26]:

$$\begin{aligned} \frac{\alpha _{e}(Q^{2})}{\alpha _{s}^{LO}(Q^{2})}\approx & {} a_{10}+a_{11}\exp (b_{11}\tau ), \end{aligned}$$

(26)

$$\begin{aligned} \frac{\alpha _{e}(Q^{2})}{\alpha _{s}^{NLO}(Q^{2})}\approx & {} a_{20}+a_{21}\exp (b_{21}\tau ), \end{aligned}$$

(27)

$$\begin{aligned} \frac{\alpha _{s}^{NLO}(Q^{2})}{4\pi }\approx & {} a_{30}+a_{31}\exp (-b_{31}\tau ), \end{aligned}$$

(28)

where the constants $a_{ij}$ and $b_{ij}$ can be obtained by the fitting functions [26]. The percentage relative errors of Eqs. (26)–(28) are given in Table 1. As can be seen, the maximum value of these percentages is less than $2.5\%$. The coefficients $a_{ij}$ and $b_{ij}$ in Eqs. (26)–(28) are determined within a few percent accuracy.

To solve the QCD$\otimes$QED evolution equations at LO, we need to transform Eqs. (23)–(25) a second time, this time from $\tau$ space to u space. Therefore, in u space and s space, we have

$$\begin{aligned}&u {\mathsf {F}}(s,u)-f_{0}(s)=\Phi _{f}^{LO}(s){\mathsf {F}}(s,u)+\Theta _{f}^{LO}(s){\mathsf {G}}(s,u)\nonumber \\&\quad + \Omega _{f}^{LO}(s)\left( a_{10}{\mathsf {M}}(s,u)+a_{11}{\mathsf {M}}(s,u-b_{11})\right) , \end{aligned}$$

(29)

$$\begin{aligned}&u{\mathsf {G}}(s,u)-g_{0}(s)=\Phi _{g}^{LO}(s){\mathsf {G}}(s,u)\nonumber \\&\quad +\Theta _{g}^{LO}(s){\mathsf {F}}(s,u), \end{aligned}$$

(30)

$$\begin{aligned}&u{\mathsf {M}}(s,u)-\gamma _{0}(s)=\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \left( a_{10}{\mathsf {M}}(s,u)+a_{11}{\mathsf {M}}(s,u-b_{11})\right) +\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad \left( a_{10}{\mathsf {F}}(s,u)+a_{11}{\mathsf {F}}(s,u-b_{11})\right) \nonumber \\&\quad +\Upsilon _{ns\gamma }^{LO}(s)\left( a_{10}{\mathsf {F}}_{ns}(s,u)+a_{11}{\mathsf {F}}_{ns}(s,u-b_{11})\right) , \end{aligned}$$

(31)

where the Laplace transforms are as follows:

$$\begin{aligned} {\mathsf {H}}(s,u)= & {} {\mathcal {L}}\left[ h(s,\tau );u\right] ,\nonumber \\ {\mathsf {H}}(s,u-c)= & {} {\mathcal {L}}\left[ h(s,\tau )\exp (c\tau );u\right] ,\nonumber \\ {\mathsf {H}}(s,u+c)= & {} {\mathcal {L}}\left[ h(s,\tau )\exp (-c\tau );u\right] . \end{aligned}$$

(32)

To solve Eqs. (29)–(31), we consider the parameter $a_{11}$ as an expansion parameter. On this basis, the solutions of Eqs. (29)–(31) can be obtained as three power series of the parameter $a_{11}$. Since this parameter is much smaller than one, we use these power series only up to the second sentence. For example, in the interval $3\le Q^{2}<20$, we have $a_{11} = 0.0109$. Then the second sentence is about two orders of magnitude larger than the third sentence. By setting $a_{11}=0$ in Eqs. (29)–(31), the first approximation of the function $\frac{\alpha _{e}(Q^{2})}{\alpha _{s}^{LO}(Q^{2})}$ leads to

$$\begin{aligned}&\left( u-\Phi _{f}^{LO}(s)\right) {\mathsf {F}}_{1}(s,u)-\Theta _{f}^{LO}(s){\mathsf {G}}_{1}(s,u)\nonumber \\&\quad -\Omega _{f}^{LO}(s)a_{10}{\mathsf {M}}_{1}(s,u)=f_{0}(s), \end{aligned}$$

(33)

$$\begin{aligned}&\left( u-\Phi _{g}^{LO}(s)\right) {\mathsf {G}}_{1}(s,u)\nonumber \\&\quad +\Theta _{g}^{LO}(s){\mathsf {F}}_{1}(s,u)=g_{0}(s), \end{aligned}$$

(34)

$$\begin{aligned}&\left( u-\Omega _{\gamma }^{LO}(s)a_{10}\right) {\mathsf {M}}_{1}(s,u)\nonumber \\&\quad -\Upsilon _{\gamma }^{LO}a_{10}{\mathsf {F}}_{1}(s,u)\nonumber \\&\quad -\Upsilon _{ns\gamma }^{LO}a_{10}{\mathsf {F}}_{ns}(s,u)=\gamma _{0}(s). \end{aligned}$$

(35)

One can easily solve Eqs. (33)–(35) and obtain the functions ${\mathsf {F}}_{1}$, ${\mathsf {G}}_{1}$, and ${\mathsf {M}}_{1}$ as follows:

$$\begin{aligned}&{\mathsf {F}}_{1}^{LO}(s,u)=A_{1}^{LO}f_{0}(s)+A_{2}^{LO}g_{0}(s)\nonumber \\&\quad +A_{3}^{LO}m_{0}(s)+A_{4}^{LO}F_{ns}(s,u), \end{aligned}$$

(36)

$$\begin{aligned}&{\mathsf {G}}_{1}^{LO}(s,u)=B_{1}^{LO}f_{0}(s)+B_{2}^{LO}g_{0}(s)\nonumber \\&\quad +B_{3}^{LO}m_{0}(s)+B_{4}^{LO}F_{ns}(s,u), \end{aligned}$$

(37)

$$\begin{aligned}&{\mathsf {M}}_{1}^{LO}(s,u)=C_{1}^{LO}f_{0}(s)+C_{2}^{LO}g_{0}(s)\nonumber \\&\quad +C_{3}^{LO}m_{0}(s)+C_{4}^{LO}F_{ns}(s,u), \end{aligned}$$

(38)

where the coefficients $A_{i}$, $B_{i}$, and $C_{i}$ (with $i=1...4$) are the functions of s and u given in Appendix B. Equations (36)–(38) are not the final solutions of the QCD$\otimes$QED evolution equations at LO. In fact, they are just used in the second approximation. We resolve Eqs. (29)–(31) to obtain the second approximation ($a_{11}\ne 0$) of the ${\mathsf {F}}$, ${\mathsf {G}}$, and ${\mathsf {M}}$ functions. Then, by repeating the above processes, we have

$$\begin{aligned}&\left( u-\Phi _{f}^{LO}(s)\right) {\mathsf {F}}_{2}(s,u)-\Theta _{f}^{LO}(s){\mathsf {G}}_{2}(s,u)\nonumber \\&\quad -\Omega _{f}^{LO}(s)a_{10}{\mathsf {M}}_{2}(s,u)=f_{0}{'}(s), \end{aligned}$$

(39)

$$\begin{aligned}&\left( u-\Phi _{g}^{LO}(s)\right) {\mathsf {G}}_{2}(s,u)\nonumber \\&\quad -\Theta _{g}^{LO}(s){\mathsf {F}}_{2}(s,u)=g_{0}(s), \end{aligned}$$

(40)

$$\begin{aligned}&\left( u-\Omega _{\gamma }^{LO}(s)a_{10}\right) {\mathsf {M}}_{2}(s,u)\nonumber \\&\quad -\Upsilon _{\gamma }^{LO}a_{10}{\mathsf {F}}_{2}(s,u)\nonumber \\&\quad -\Upsilon _{ns\gamma }^{LO}a_{10}{\mathsf {F}}_{ns}(s,u)=m_{0}^{'}(s), \end{aligned}$$

(41)

where ${\mathsf {F}}_{2}$, ${\mathsf {G}}_{2}$, and ${\mathsf {M}}_{2}$ are the distribution functions of the photon in s and u spaces at LO in the second approximation. Also, $f_{0}{'}$ and $m_{0}{'}$ are

$$\begin{aligned} f_{0}{'}(s)= & {} f_{0}(s)+a_{11}\Omega _{f}^{LO}(s){\mathsf {M}}_{1}(s,u-b_{11}), \end{aligned}$$

(42)

$$\begin{aligned} m_{0}{'}(s)= & {} m_{0}(s)+a_{11}\left( \Omega _{\gamma }^{LO}(s){\mathsf {M}}_{1}(s,u-b_{11})\nonumber \right. \\&\left. +\Upsilon _{\gamma }^{LO}(s){\mathsf {F}}_{1}(s,u-b_{11})\nonumber \right. \\&\left. +\Upsilon _{ns\gamma }^{LO}(s){\mathsf {F}}_{ns}(s,u-b_{11})\right) . \end{aligned}$$

(43)

Similar to the first approximation ($a_{11}=0$), the functions ${\mathsf {F}}_{2}$, ${\mathsf {G}}_{2}$ and ${\mathsf {M}}_{2}$ are easily obtained as follows:

$$\begin{aligned}&{\mathsf {F}}_{2}^{LO}(s,u)=A{'}_{1}^{LO}f_{0}(s)+A{'}_{2}^{LO}g_{0}(s)+A{'}_{3}^{LO}m_{0}(s)\nonumber \\&\quad +A{'}_{4}^{LO}F^{ns}(s,u)+A{'}_{5}^{LO}F^{ns}(s,u-b_{11}), \end{aligned}$$

(44)

$$\begin{aligned}&{\mathsf {G}}_{2}^{LO}(s,u)=B{'}_{1}^{LO}f_{0}(s)+B{'}_{2}^{LO}g_{0}(s)+B{'}_{3}^{LO}m_{0}(s)\nonumber \\&\quad +B{'}_{4}^{LO}F^{ns}(s,u)+B{'}_{5}^{LO}F^{ns}(s,u-b_{11}), \end{aligned}$$

(45)

$$\begin{aligned}&{\mathsf {M}}_{2}^{LO}(s,u)=C{'}_{1}^{LO}f_{0}(s)+C{'}_{2}^{LO}g_{0}(s)+C{'}_{3}^{LO}m_{0}(s)\nonumber \\&\quad +C{'}_{4}^{LO}F^{ns}(s,u)+C{'}_{5}^{LO}F^{ns}(s,u-b_{11}), \end{aligned}$$

(46)

where $A{'}_{i}$, $B{'}_{i}$, and $C{'}_{i}$ (with $i=1...5$) are given in Appendix B.

3 Master formula for the NLO corrections

In this section, we intend to extend our calculations to the NLO approximation for the distribution functions of the photon. The QCD$\otimes$QED evolution equations of the photon at NLO QCD can be written as

$$\begin{aligned}&\frac{\partial F^{\gamma }_{s}(x,Q^{2})}{\partial \ln Q^{2}}=\frac{\alpha _{s}^{NLO}(Q^{2})}{2\pi }\nonumber \\&\quad \times \Bigg [\left( P_{qq}^{LO}(x)+\frac{\alpha _{s}^{NLO}(Q^{2})}{2\pi }P_{qq}^{NLO}(x)\right) \nonumber \\&\quad \otimes F^{\gamma }_{s}(x,Q^{2})+2n_{f}\bigg (P_{qg}^{LO}(x)\nonumber \\&\quad +\frac{\alpha _{s}^{NLO}(Q^{2})}{2\pi }P_{qg}^{NLO}(x)\bigg ) G^{\gamma }(x,Q^{2})\Bigg ]\nonumber \\&\quad +\frac{\alpha _{e}(Q^{2})}{2\pi }\bigg [2A P_{q\gamma }^{LO}(x)\otimes M^{\gamma }(x,Q^{2})\bigg ], \end{aligned}$$

(47)

$$\begin{aligned}&\frac{\partial G^{\gamma }(x,Q^{2})}{\partial \ln Q^{2}}=\frac{\alpha _{s}^{NLO}(Q^{2})}{2\pi }\nonumber \\&\quad \times \bigg [\left( P_{gq}^{LO}(x)+\frac{\alpha _{s}^{NLO}(Q^{2})}{2\pi }P_{gq}^{NLO}(x)\right) \nonumber \\&\quad \otimes F^{\gamma }_{s}(x,Q^{2})+\bigg (P_{gg}^{LO}(x)\nonumber \\&\quad +\frac{\alpha _{s}^{NLO}(Q^{2})}{2\pi }P_{gg}^{NLO}(x)\bigg ) G^{\gamma }(x,Q^{2})\bigg ], \end{aligned}$$

(48)

$$\begin{aligned}&\frac{\partial M^{\gamma }(x,Q^{2})}{\partial \ln Q^{2}}=\frac{\alpha _{e}(Q^{2})}{2\pi }\nonumber \\&\quad \times \bigg [ P_{\gamma q}^{LO}(x)\otimes \left[ \langle e^{2}\rangle F^{\gamma }_{s}(x,Q^{2})+F^{\gamma }_{ns}(x,Q^{2})\right] \nonumber \\&\quad +P_{\gamma \gamma }^{LO}\otimes M^{\gamma }(x,Q^{2})\bigg ]. \end{aligned}$$

(49)

Fig. 1

A comparison of the singlet distribution function of the photon extracted by Eq. (68) in scales $Q^{2}= 10.8, 12, 15.3,$ 76.4, 120, and 780 GeV$^{2}$ at the LO and NLO approximations with the GRV results

Fig. 2

The ratio $\frac{F^{\gamma }_{s}(GRV)}{F^{\gamma }_{s}(Theory)}$ at LO and NLO

Fig. 3

The gluon distribution function of the photon at scales $Q^{2}= 10, 20, 100$ and 1000 GeV$^{2}$ in LO and NLO in comparison with the GRV results

Fig. 4

The ratio $\frac{G^{\gamma }(GRV)}{G^{\gamma }(Theory)}$ at LO and NLO

Fig. 5

A comparison of the non-singlet distribution function $F_{ns}^{\gamma }$ of the photon at LO and NLO with the GRV results

Fig. 6

The ratio $\frac{F^{\gamma }_{ns}(GRV)}{F^{\gamma }_{ns}(Theory)}$ at LO and NLO

Fig. 7

A comparison of the photon structure function $F_{2}^{\gamma }$ at LO and NLO with L3, DLPHI, and OPAL data as well as with the GRV results

Fig. 8

A comparison of the photon structure function $F_{2}^{\gamma }$ at different initial scales $Q_{0}^{2}=1\mathrm{GeV}^{2}$ and $Q_{0}^{2}=0.3\mathrm{GeV}^{2}$ in LO and NLO with PLUTO, L3, and ALEPH data as well as with the AFG results at $Q_{0}^{2}=1\mathrm{GeV}^{2}$ in NLO

Fig. 9

The photon distribution function at scales $Q^{2}= 5, 10, 20,$ 50, 100, and 1000 GeV$^{2}$ in LO and NLO in comparison with the c-quark and s-quark distribution functions of the photon at NLO provided by the GRV results

To solve Eqs. (47)–(49), again we need the Laplace transform from v (${\equiv }\ln \frac{1}{x}$) and $\tau$ ($=\frac{1}{4\pi }\int ^{Q^{2}}_{Q_{0}^{2}}\alpha _{s}(Q{'}^{2})d \ln (Q{'}^{2})$) to the s and u spaces, respectively. In this regard, the solutions of the evolution equations of the photon at NLO can be converted to

$$\begin{aligned}&u {\mathsf {F}}(s,u)-f_{0}(s)=\Phi _{f}^{LO}(s){\mathsf {F}}(s,u)\nonumber \\&\quad +\Theta _{f}^{LO}(s){\mathsf {G}}(s,u)+\Phi _{f}^{NLO}(s)\nonumber \\&\quad \times \left( a_{30}{\mathsf {F}}(s,u)+a_{31}{\mathsf {F}}(s,u+b_{31})\right) \nonumber \\&\quad +\Theta _{f}^{NLO}(s)\left( a_{30}{\mathsf {G}}(s,u)+a_{31}{\mathsf {G}}(s,u+b_{31})\right) \nonumber \\&\quad +\Omega _{f}^{LO}(s)\left( a_{20}{\mathsf {M}}(s,u)+a_{21}{\mathsf {M}}(s,u-b_{21})\right) , \end{aligned}$$

(50)

$$\begin{aligned}&u{\mathsf {G}}(s,u)-g_{0}(s)=\Phi _{g}^{LO}(s){\mathsf {G}}(s,u)+\Theta _{g}^{LO}(s){\mathsf {F}}(s,u)\nonumber \\&\quad +\Theta _{g}^{NLO}(s)\big (a_{30}{\mathsf {F}}(s,u)+a_{31}{\mathsf {F}}(s,u+b_{31})\big )\nonumber \\&\quad + \Phi _{g}^{NLO}(s)\left( a_{30}{\mathsf {G}}(s,u)+a_{31}{\mathsf {G}}(s,u+b_{31})\right) , \end{aligned}$$

(51)

$$\begin{aligned}&u{\mathsf {M}}(s,u)-m_{0}(s)=\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \times \left( a_{20}{\mathsf {M}}(s,u)+a_{21}{\mathsf {M}}(s,u-b_{21})\right) \nonumber \\&\quad +\Upsilon _{\gamma }^{LO}(s)\left( a_{20}{\mathsf {F}}(s,u)+a_{21}{\mathsf {F}}(s,u-b_{21})\right) \nonumber \\&\quad +\Upsilon _{ns\gamma }^{LO}(s)\left( a_{20}{\mathsf {F}}_{ns}(s,u)+a_{21}{\mathsf {F}}_{ns}(s,u-b_{21})\right) , \end{aligned}$$

(52)

where the coefficients $\Phi _{f}^{NLO}$, $\Theta _{f}^{NLO}$, $\Phi _{g}^{NLO}$, and $\Theta _{g}^{NLO}$ are the NLO splitting functions in the Laplace space s derived in Ref. [34]. Since $a_{21}$ and $a_{31}$ are smaller than one, they can be used as expansion parameters. Therefore, by setting $a_{21}=0$ and $a_{31}=0$ in Eqs. (50)–(52), these equations can be rewritten at NLO as follows:

$$\begin{aligned}&\left( u-\Phi _{f}^{LO}(s)-a_{30}\Phi _{f}^{NLO}(s)\right) {\mathsf {F}}_{1}(s,u)\nonumber \\&\quad -\left( \Theta _{f}^{LO}(s)+a_{30}\Theta _{f}^{NLO}(s)\right) {\mathsf {G}}_{1}(s,u)\nonumber \\&\quad -a_{20}\Omega _{f}^{LO}(s){\mathsf {M}}_{1}(s,u)=f_{0}(s), \end{aligned}$$

(53)

$$\begin{aligned}&\left( u-\Phi _{g}^{LO}(s)-a_{30}\Phi _{g}^{NLO}(s)\right) {\mathsf {G}}_{1}(s,u)\nonumber \\&\quad -\left( \Theta _{g}^{LO}(s)+a_{30}\Theta _{g}^{NLO}(s)\right) {\mathsf {F}}_{1}(s,u)=g_{0}(s), \end{aligned}$$

(54)

$$\begin{aligned}&\left( u-a_{20}\Omega _{\gamma }^{LO}(s)\right) {\mathsf {M}}_{1}(s,u)\nonumber \\&\quad -a_{20}\Upsilon _{\gamma }^{LO}{\mathsf {F}}_{1}(s,u)-a_{20}\Upsilon _{ns\gamma }^{LO}{\mathsf {F}}_{ns}(s,u)=m_{0}(s). \end{aligned}$$

(55)

By solving Eqs. (53)–(55), one can obtain the gluon ${\mathsf {G}}_{1}$, singlet ${\mathsf {F}}_{1}$, and photon ${\mathsf {M}}_{1}$ distribution functions in the first approximation at NLO:

$$\begin{aligned}&{\mathsf {F}}_{1}^{NLO}(s,u)=A_{1}^{NLO}f_{0}(s)+A_{2}^{NLO}g_{0}(s)\nonumber \\&\quad +A_{3}^{NLO}m_{0}(s)+A_{4}^{NLO}{\mathsf {F}}_{ns}(s,u), \end{aligned}$$

(56)

$$\begin{aligned}&{\mathsf {G}}_{1}^{NLO}(s,u)=B_{1}^{NLO}f_{0}(s)+B_{2}^{NLO}g_{0}(s)\nonumber \\&\quad +B_{3}^{NLO}m_{0}(s)+B_{4}^{NLO}{\mathsf {F}}_{ns}(s,u), \end{aligned}$$

(57)

$$\begin{aligned}&{\mathsf {M}}_{1}^{NLO}(s,u)=C_{1}^{NLO}f_{0}(s)+C_{2}^{NLO}g_{0}(s)\nonumber \\&\quad +C_{3}^{NLO}m_{0}(s)+C_{4}^{NLO}{\mathsf {F}}_{ns}(s,u), \end{aligned}$$

(58)

where the coefficients $A_{i}^{NLO}$, $B_{i}^{NLO}$, and $C_{i}^{NLO}$ (with $i=1...4$) are given in Appendix B. At this stage, it is not necessary to invert Eqs. (56)–(58) to v and $\tau$ spaces. In fact, they are just used in the second approximation as an initial function. To obtain the next approximation ($a_{21}\ne 0,\ a_{31}\ne 0$) of the functions ${\mathsf {F}}$, ${\mathsf {G}}$, and ${\mathsf {M}}$, we use the transforms ${\mathsf {F}}_{1}\rightarrow {\mathsf {F}}_{2}$, ${\mathsf {G}}_{1}\rightarrow {\mathsf {G}}_{2}$, and ${\mathsf {M}}_{1}\rightarrow {\mathsf {M}}_{2}$ and also replace $f_{0}$, $g_{0}$, and $m_{0}$ with $f_{0}{'}$, $g_{0}{'}$, and $m_{0}{'}$ in Eqs. (53)–(55), respectively. Thus, we have

$$\begin{aligned}&\left( u-\Phi _{f}^{LO}(s)-a_{30}\Phi _{f}^{NLO}(s)\right) {\mathsf {F}}_{2}(s,u)\nonumber \\&\quad -\left( \Theta _{f}^{LO}(s)+a_{30}\Theta _{f}^{NLO}(s)\right) {\mathsf {G}}_{2}(s,u)\nonumber \\&\quad -a_{20}\Omega _{f}^{LO}(s){\mathsf {M}}_{2}(s,u)=f_{0}{'}(s), \end{aligned}$$

(59)

$$\begin{aligned}&\left( u-\Phi _{g}^{LO}(s)-a_{30}\Phi _{g}^{NLO}(s)\right) {\mathsf {G}}_{2}(s,u)\nonumber \\&\quad -\left( \Theta _{g}^{LO}(s)+a_{30}\Theta _{g}^{NLO}(s)\right) {\mathsf {F}}_{2}(s,u)=g_{0}{'}(s), \end{aligned}$$

(60)

$$\begin{aligned}&\left( u-a_{20}\Omega _{\gamma }^{LO}(s)\right) {\mathsf {M}}_{2}(s,u)\nonumber \\&\quad -a_{20}\Upsilon _{\gamma }^{LO}{\mathsf {F}}_{2}(s,u) -a_{20}\Upsilon _{ns\gamma }^{LO}{\mathsf {F}}_{ns}(s,u)=m_{0}{'}(s),\nonumber \\ \end{aligned}$$

(61)

where

$$\begin{aligned}&f_{0}{'}(s,u)=f_{0}(s)+a_{21}\Omega _{f}^{LO}(s){\mathsf {M}}_{1}(s,u-b_{21})\nonumber \\&\quad +a_{31}\left( \Phi _{f}^{NLO}{\mathsf {F}}_{1}(s,u+b_{31})\nonumber \right. \\&\left. \quad +\Theta _{f}^{NLO}(s){\mathsf {G}}_{1}(s,u+b_{31})\right) \end{aligned}$$

(62)

$$\begin{aligned}&g_{0}{'}(s,u)=g_{0}(s)+a_{31}\left( \Theta _{g}^{NLO}{\mathsf {F}}_{1}(s,u+b_{31})\nonumber \right. \\&\left. \quad +\Phi _{f}^{NLO}(s){\mathsf {G}}_{1}(s,u+b_{31})\right) \end{aligned}$$

(63)

$$\begin{aligned}&m_{0}{'}(s,u)=m_{0}(s)+a_{21}\left( \Omega _{\gamma }^{LO}(s){\mathsf {M}}_{1}(s,u-b_{21})\nonumber \right. \\&\quad +\Upsilon _{\gamma }^{LO}(s){\mathsf {F}}_{1}(s,u-b_{21})\nonumber \\&\left. \quad +\Upsilon _{ns\gamma }^{LO}(s){\mathsf {F}}_{ns}(s,u-b_{21})\right) . \end{aligned}$$

(64)

By solving Eqs. (59)–(61), one can obtain the functions ${\mathsf {F}}_{2}$, ${\mathsf {G}}_{2}$, and ${\mathsf {M}}_{2}$ as follows:

$$\begin{aligned}&{\mathsf {F}}_{2}^{NLO}(s,u)=A{'}_{1}^{NLO}f_{0}(s)+A{'}_{2}^{NLO}g_{0}(s)\nonumber \\&\quad +A{'}_{3}^{NLO}m_{0}(s)+A{'}_{4}^{NLO}{\mathsf {F}}_{ns}(s,u)\nonumber \\&\quad +A{'}_{5}^{NLO}{\mathsf {F}}_{ns}(s,u-b_{21}), \end{aligned}$$

(65)

$$\begin{aligned}&{\mathsf {G}}_{2}^{NLO}(s,u)=B{'}_{1}^{NLO}f_{0}(s)+B{'}_{2}^{NLO}g_{0}(s)\nonumber \\&\quad +B{'}_{3}^{NLO}m_{0}(s)+B{'}_{4}^{NLO}{\mathsf {F}}_{ns}(s,u)\nonumber \\&\quad +B{'}_{5}^{NLO}{\mathsf {F}}_{ns}(s,u-b_{21}), \end{aligned}$$

(66)

$$\begin{aligned}&{\mathsf {M}}_{2}^{NLO}(s,u)=C{'}_{1}^{NLO}f_{0}(s)+C{'}_{2}^{NLO}g_{0}(s)\nonumber \\&\quad +C{'}_{3}^{NLO}m_{0}(s)+C{'}_{4}^{NLO}{\mathsf {F}}_{ns}(s,u)\nonumber \\&\quad +C{'}_{5}^{NLO}{\mathsf {F}}_{ns}(s,u-b_{21}), \end{aligned}$$

(67)

where the coefficients $A{'}_{i}^{NLO}$, $B{'}_{i}^{NLO}$, and $C{'}_{i}^{NLO}$ (with $i=1...5$) are given in Appendix B.

The functions obtained in Eqs. (44)–(46) and Eqs. (65)–(67) are in the Laplace spaces s and u. To get the final equations, we have to return them to the usual spaces, namely the v and $\tau$ spaces. For this purpose, we use the Laplace inverse transform and the convolution integral (see Appendix A). Therefore, the distribution functions are obtained as follows:

$$\begin{aligned} {\hat{F}}^{\gamma n}_{s}(v,\tau )= & {} \int _{0}^{v}K_{f1}^{n}\left( v,w,\tau \right) {\hat{F}}_{0s}^{\gamma n}\left( w\right) \mathrm{d}w\nonumber \\&+\int _{0}^{v}K_{f2}^{n}\left( v,w,\tau \right) {\hat{G}}_{0}^{\gamma n}\left( w\right) \mathrm{d}w\nonumber \\&+ \int _{0}^{v}K_{f3}^{n}\left( v,w,\tau \right) {\hat{M}}^{\gamma n}_{0}\left( w\right) \mathrm{d}w\nonumber \\&+K_{f4}^{n}\left( v,\tau \right) , \end{aligned}$$

(68)

$$\begin{aligned} {\hat{G}}^{\gamma n}(v,\tau )= & {} \int _{0}^{v}K_{g1}^{n}\left( v,w,\tau \right) {\hat{F}}_{0s}^{\gamma n}\left( w\right) \mathrm{d}w\nonumber \\&+\int _{0}^{v}K_{g2}^{n}\left( v,w,\tau \right) {\hat{G}}_{0}^{\gamma n}\left( w\right) \mathrm{d}w\nonumber \\&+\int _{0}^{v}K_{g3}^{n}\left( v,w,\tau \right) {\hat{M}}_{0}^{\gamma n}\left( w\right) \mathrm{d}w\nonumber \\&+K_{g4}^{n}\left( v,\tau \right) , \end{aligned}$$

(69)

$$\begin{aligned} {\hat{M}}^{n}(v,\tau )= & {} \int _{0}^{v}K_{\gamma 1}^{n}\left( v,w,\tau \right) {\hat{F}}_{0s}^{\gamma n}\left( w\right) \mathrm{d}w\nonumber \\&+\int _{0}^{v}K_{\gamma 2}^{n}\left( v,w,\tau \right) {\hat{G}}_{0}^{\gamma n}\left( w\right) \mathrm{d}w\nonumber \\&+\int _{0}^{v}K_{\gamma 3}^{n}\left( v,w,\tau \right) {\hat{M}}^{\gamma n}_{0}\left( w\right) \mathrm{d}w\nonumber \\&+K_{\gamma 4}^{n}\left( v,\tau \right) , \ \ \ \ \ n=LO \ \text{ or }\ NLO, \end{aligned}$$

(70)

where the kernels $K_{ij}$ (with $i=f, g, \gamma$ and $j=1, 2, 3, 4$) in $\tau$ and v spaces are

$$\begin{aligned} K_{fk}^{n}(v, \tau )= & {} {\mathcal {L}}^{-1}\left[ A_{k}{'}^{n}(s,u);\tau ;v\right] ,\nonumber \\ K_{gk}^{n}(v, \tau )= & {} {\mathcal {L}}^{-1}\left[ B_{k}{'}^{n}(s,u);\tau ;v\right] ,\nonumber \\ K_{\gamma k}^{n}(v, \tau )= & {} {\mathcal {L}}^{-1}\left[ C_{k}{'}^{n}(s,u);\tau ;v\right] , \nonumber \\ K_{f4}^{n}(v,\tau )= & {} {\mathcal {L}}^{-1}\left[ A_{4}{'}^{n}{\mathsf {F}}^{ns}(s,u) +A_{5}{'}^{n}{\mathsf {F}}^{ns}(s,u-b_{21});\tau ;v\right] ,\nonumber \\ K_{g4}^{n}(v,\tau )= & {} {\mathcal {L}}^{-1}\left[ B_{4}{'}^{n}{\mathsf {F}}^{ns}(s,u) +B_{5}{'}^{n}{\mathsf {F}}^{ns}(s,u-b_{21});\tau ;v\right] ,\nonumber \\ K_{\gamma 4}^{n}(v,\tau )= & {} {\mathcal {L}}^{-1}\left[ C_{4}{'}^{n}{\mathsf {F}}^{ns}(s,u)\nonumber \right. \\&\left. +C_{5}{'}^{n}{\mathsf {F}}^{ns}(s,u-b_{21});\tau ;v\right] ,\nonumber \\&\ \ k=1, 2, 3 \ \ \text{ and } \ \ n=LO \ \text{ or }\ NLO. \end{aligned}$$

(71)

To get the numerical results of Eqs. (68)–(70), we need to know the distribution functions at the initial scale. For this aim, we use the fitted results of GRV [30] at the initial scale $Q_{0}^{2}=1GeV^{2}$ for $F^{\gamma }_{0s}$ and $G^{\gamma }_{0}$. On the other hand, since $\int _{0}^{1} u^{\gamma }_{0}(x)\mathrm{d}x=0.65$, $\int _{0}^{1} d^{\gamma }_{0}(x)\mathrm{d}x=0.52$, and $\int _{0}^{1} s^{\gamma }_{0}(x)\mathrm{d}x=0.11$, in a good approximation, we take the photon starting distributions as in the following equation:

$$\begin{aligned}&\gamma ^{\gamma }(x,Q^{2}_{0})=\frac{\alpha _{e}(Q^{2})}{2\pi }\nonumber \\&\qquad \times \left[ \frac{4}{9}\ln \left( \frac{Q^{2}_{0}}{m_{u}^{2}}\right) u^{\gamma }_{0}(x)+ \frac{1}{9}\ln \left( \frac{Q^{2}_{0}}{m_{d}^{2}}\right) d^{\gamma }_{0}(x)\right] \nonumber \\&\qquad \otimes \frac{1-(1-x)^{2}}{x}. \end{aligned}$$

(72)

Note that the above equation for the photon distribution function of the photon is similar to the photon distribution function of the proton which is obtained in Ref. [28].

4 The non-singlet sector

In this section, we provide the solution of the non-singlet distribution function by using the Laplace transform method at LO QED and LO QCD as well as at LO QED and NLO QCD. The QED$\otimes$QCD evolution equation for the non-singlet density function of the photon is as follows [32]:

$$\begin{aligned} \frac{\partial q_{ins}^{\gamma }(x,Q^{2})}{\partial \ln Q^{2}}= & {} \frac{\alpha _{e}(Q^{2})}{2\pi }e_{i}^{2}a(x)\nonumber \\&+\frac{\alpha _{s}(Q^{2})}{2\pi }P_{qqns}(x)\otimes q_{ins}^{\gamma }(x,Q^{2}), \end{aligned}$$

(73)

where the kernel $P_{qqns}$ is the non-singlet splitting function and a(x) describes the $\gamma \rightarrow q{\bar{q}}$ splitting. By using $F^{\gamma }_{ns}=\sum _{k=1}^{n_{f}}\left( e_{q_{k}}^{2}-\langle e^{2}\rangle \right) x\left[ q_{k}+{\bar{q}}_{k}\right]$, as introduced in Ref. [1] and Eq. (73), one can write the non-singlet distribution functions at LO and NLO as follows:

$$\begin{aligned}&\frac{4\pi }{\alpha _{s}(Q^{2})}\frac{\partial F_{ns}^{ LO\gamma }(x,Q^{2})}{\partial \ln Q^{2}}=\frac{\alpha _{e}(Q^{2})}{\alpha _{s}(Q^{2})}Z_{ns}(x)\nonumber \\&\quad + P_{qqns}^{LO}(x)\otimes F_{ns}^{LO\gamma }(x,Q^{2}), \end{aligned}$$

(74)

$$\begin{aligned}&\frac{4\pi }{\alpha _{s}(Q^{2})}\frac{\partial F_{ns}^{NLO\gamma }(x,Q^{2})}{\partial \ln Q^{2}}=\frac{\alpha _{e}(Q^{2})}{\alpha _{s}(Q^{2})}Z_{ns}(x)\nonumber \\&\quad + \left( P_{qqns}^{LO}(x)+\frac{\alpha _{s}(Q^{2})}{4\pi }P_{qqns}^{NLO}(x)\right) \nonumber \\&\quad \otimes F_{ns}^{NLO\gamma }(x,Q^{2}), \end{aligned}$$

(75)

where the kernel $Z_{ns}(x)$ is

$$\begin{aligned} Z_{ns}(x)=\sum _{k=1}^{n_{f}} 2e_{q_{k}}^{2}\left( e_{q_{k}}^{2}-\langle e^{2}\rangle \right) P_{q\gamma }^{LO}(x). \end{aligned}$$

(76)

Using the convolution integral, the relation $\frac{\partial \tau (Q^{2})}{\partial \ln (Q^{2})}=\frac{\alpha _{s}(Q^{2})}{4\pi }$ and also the change variables $x \equiv \exp (-v)$ and $y \equiv \exp (-w)$, we can convert Eqs. (74) and (75) as follows:

$$\begin{aligned}&\frac{\partial {\hat{F}}_{ns}^{LO\gamma }(v,\tau )}{\partial \tau }=\frac{\alpha _{e}(\tau )}{\alpha _{s}(\tau )}{\hat{Z}}_{ns}(v)\nonumber \\&\quad + \int _{0}^{v}{\hat{P}}_{qqns}^{LO}(v-w) {\hat{F}}_{ns}^{LO\gamma }(w,\tau )\exp (w-v)\mathrm{d}w, \end{aligned}$$

(77)

$$\begin{aligned}&\frac{\partial {\hat{F}}_{ns}^{NLO\gamma }(v,\tau )}{\partial \tau }=\frac{\alpha _{e}(\tau )}{\alpha _{s}(\tau )}{\hat{Z}}_{ns}(v)\nonumber \\&\quad + \int _{0}^{v}\left( {\hat{P}}_{qqns}^{LO}(v-w)+\frac{\alpha _{s}(\tau )}{4\pi }{\hat{P}}_{qq ns}^{NLO}(v-w)\right) \nonumber \\&\quad {\hat{F}}_{ns}^{NLO\gamma }(w,\tau )\exp (w-v)\mathrm{d}w. \end{aligned}$$

(78)

To solve Eqs. (77) and (78), we need to use the Laplace transform from the v and $\tau$ spaces to the s and u spaces, respectively. On this basis, Eq. (77) is converted to a first-order differential equation, whose solution is as follows:

$$\begin{aligned} {\mathsf {F}}_{ns}^{LO}(s,u)= k_{1ns}^{LO}(s,u)f_{0}^{ns}(s)+k_{2ns}^{LO}(s,u)z(s). \end{aligned}$$

(79)

Similarly, Eq. (78) is also converted to an ordinary first-order differential equation, whose solution in the first approximation $\frac{\alpha _{s}^{NLO}(Q^{2})}{4\pi }$ ($a_{31}=0$) is

$$\begin{aligned} {\mathsf {F}}_{ns}^{NLO1}(s,u)= & {} \frac{u^{2}-b_{21}u}{u(u-b_{21})(u-\Phi _{qq ns}^{LO}-a_{31}\Phi _{qqns}^{NLO})}f_{0}^{ns}(s)\nonumber \\&+\frac{\left( a_{20}u+a_{21}u-a_{20}b_{21}\right) }{u(u-b_{21})(u-\Phi _{qq ns}^{LO}-a_{31}\Phi _{qqns}^{NLO})}z(s) \end{aligned}$$

(80)

and in the second approximation

$$\begin{aligned} {\mathsf {F}}_{ns}^{NLO2}(s,u)= & {} k_{1ns}^{NLO}(s,u)f_{0}^{ns}(s)\nonumber \\&+k_{2ns}^{NLO}(s,u)f_{0}^{ns}(s)z(s). \end{aligned}$$

(81)

Note that to obtain Eqs. (80) and (81), we use Eq. (28). Taking all the above into consideration, the non-singlet distribution function $F_{ns}^{\gamma }(v,\tau )$ at LO and NLO can be obtained:

$$\begin{aligned} {\hat{F}}_{ns}^{\gamma i}(v,\tau )= & {} \int _{0}^{v}K_{1ns}^{i}\left( v,w,\tau \right) {\hat{F}}_{0ns}^{\gamma i}\left( w\right) \mathrm{d}w\nonumber \\&+\int _{0}^{v}K_{2ns}^{i}\left( v,w,\tau \right) {\hat{Z}}_{ns}\left( w\right) \mathrm{d}w ,\nonumber \\&i=LO\ \text{ or }\ NLO, \end{aligned}$$

(82)

where the kernel $K_{jns}^{i}={\mathcal {L}}^{-1}\left[ {\mathcal {L}}^{-1}\left[ k_{jns}^{i}(s,u);\tau \right] ;v\right]$ and the kernels $k_{jns}^{i}(s,\tau )$ are presented in Appendix B. For the numerical investigation of Eq. (82), we apply the non-singlet distribution of the photon at the initial scale, $F^{\gamma }_{ns}(x,Q^{2}_{0})$, which is obtained from the fitted results of GRV [30]. Finally, recalling that $v \equiv \ ln(1/x)$ and $\tau =\frac{1}{4\pi }\int ^{Q^{2}}_{Q_{0}^{2}}\alpha _{s}(Q{'}^{2})d \ln (Q{'}^{2})$, one can convert Eqs. (68)–(70) and Eq. (82) back into the usual spaces, i.e. the Bjorken-x and virtuality $Q^{2}$.

5 Results and conclusion

In the previous sections, we obtained the singlet, non-singlet, gluon, and photon distribution functions of the photon at the LO and NLO approximations by using the Laplace transform method. In this section, we shall present the numerical results which can be extracted from these functions. For the verification of our solutions, we compare our numerical results of the photon structure function with L3, OPAL, DELPHI, PLUTO, and ALEPH data and also our numerical results of the different kinds of distribution functions of the photon at the arbitrary scale $Q^{2}$ with those from the GRV results.

The results of Eq. (68) are depicted in Fig. 1. It indicates the evolution of the singlet distribution function of the photon at scales $Q^{2}=10.8, 12, 15.3, 76.4, 120$, and 780 GeV$^{2}$. In this figure, the solid and dash lines present the solution which is resulted from the Laplace transform method at NLO and LO, respectively, and also the dot lines show the GRV results [30] at LO and NLO. In order for the difference between our results and the GRV results to be more visible, we display the ratio $\frac{F_{s}^{\gamma }(GRV)}{ F_{s}^{\gamma }(Theory)}$ for different scales at LO and NLO in Fig. 2. As can be seen in this figure, the maximum ratio at high x is about 20%. Note that all the figures discussed in this section, the colored bands represent the error caused by Eqs. (26)–(28).

Figure 3 shows the results of the gluon distribution function $G(x,Q^{2}) = x g(x,Q^{2})$ of the photon and their comparison with the LO and NLO analyses of the GRV results [30] at scales $Q^{2}=10, 20, 100$, and 1000 GeV$^{2}$. Figure 4 displays the ratio $\frac{G^{\gamma }(GRV)}{ G^{\gamma }(Theory)}$ for different scales. As can be seen in this figure, this rate has a more incremental slope at NLO than LO. Despite this fact, at both approximations, the maximum ratio in this figure is about 25%.

In Fig. 5, a detailed comparison is shown for the non-singlet distribution function of the photon at LO and NLO, extracted by Eq. (82). Indeed, in this figure, our analytical solution based on the Laplace transform method is presented for the non-singlet sector and compared with the GRV results [30] at scales $Q^{2}=10.8,12,15.3,76.4,120$, and 780 $GeV^{2}$. We depicted the ratio $\frac{F_{ns}^{\gamma }(GRV)}{ F_{ns}^{\gamma }(Theory)}$ in Fig. 6. The maximum ratio in this figure is about 18%.

From Figs. 1, 2, 3, 4, 5 and 6, the results of analytical solutions for all the singlet, non-singlet, and gluon distribution functions clearly show agreement over a wide range of x and $Q^{2}$ variables with the GRV results.

As a numerical illustration for our analytical approach to the study of the photon structure function $F_{2}^{\gamma }(x,Q^{2})$ at the LO and NLO approximations, we compared our results with the photon structure function obtained from GRV and depicted them in Fig. 7. Also, a comparison with the LEP-L3 data [2, 3] at $Q^{2}=10.8, 15.3$, and 120 GeV$^{2}$ has been shown there. In the LEP-L3 data, the total systematic error is calculated from the quadratic sum of the systematic error and the additional systematic error due to the dependence on the Monte Carlo model. Moreover, in Fig. 7, we showed a comparison of the photon structure function with the LEP-OPAL data [4, 5] at scales $Q^{2}=10.8, 12, 76.4$, and 780 GeV$^{2}$. Note that the OPAL data is only calculated with the systematic error. Finally, in this figure, our findings are compared with the LEP-DELPHI data [6] at scale $Q^{2}=12$ GeV$^{2}$, in which the total error has been calculated from the quadratic sum of the statistical error and the systematic error. At the end of the presentation of the results for the photon structure function, in Fig. 8, we presented the results of the photon structure function at different initial scales $Q_{0}^{2}=0.3$ and 1 GeV$^{2}$ and compared them with the PLUTO [29], L3 [3], and ALEPH [7] data as well as with the AFG results [31] at the initial scale $Q_{0}^{2}=1$ GeV$^2$. It is also noteworthy that the photon structure function increases by decreasing the initial scale, as shown in Fig. 8. For comparison, in Ref. [31], this increase at the peak of the figures is about 20%, but in our results, it is around 25%.

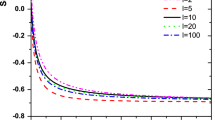
In Fig. 9, we plotted the photon distribution function obtained from Eq. (70) at LO and NLO in energy scales $Q^{2}=5,10,20,50,100$ and 1000 GeV$^{2}$. Knowing that the photon distribution function has not been presented in the new data, we compared it with the s-quark and c-quark distribution functions of the photon at NLO provided by the GRV results. This distribution of the photon can be presented as a prediction of the DGLAP evolution equations.

Table 2 $\chi ^{2}$-values for Our results and the GRV results

Table 3 $\chi ^{2}$-values for Our results and the AFG results

In Tables 2 and 3, we presented our results, with notation “Our”, of $\chi ^{2}$-values, derived from our calculations and the experimental data and compared them with the resulting $\chi ^{2}$-values of GRV and AFG. As can be seen in Table 2, our results at LO are in better agreement with experimental data than those obtained by GRV. However, at NLO, our results are only in agreement with the L3 and DELPHI data, which are again better than the GRV results achieved through the parametrization model. On the other hand, Table 3 shows the $\chi ^{2}$-values of our results and the AFG results. Indeed, as shown, there is not much difference between these two results except for the experimental data released by the ALEPH collaboration. As illustrated, our analytical solutions for the photon structure function over a wide range of x and $Q^{2}$ values are in good agreement, especially at LO, with the experimental data provided by L3, OPAL, DELPHI, and PLUTO collaborations.

In conclusion, in this paper, we utilized the Laplace transform method for decoupling of the QCD$\otimes$QED DGLAP evolution equations and extracted the singlet $F^{\gamma }_{s}(x,Q^{2})$, non-singlet $F^{\gamma }_{ns}(x,Q^{2})$, gluon $G^{\gamma }(x,Q^{2})$, and photon $M^{\gamma }(x,Q^{2})$ distribution functions of the photon. The calculations are done in the LO QED and the LO and NLO QCD approximations. These functions are general and require only knowledge of $F^{\gamma }_{s0}$, $G^{\gamma }_{s0}$, $F^{\gamma }_{ns0}$ and $M^{\gamma }_{s0}$ at the starting value $Q^{2}_{0}$ for the evolution. In the present paper, we also calculated the photon structure function $F^{\gamma }_{2} (x,Q^{2})$ using the Laplace transform method at the different values of $Q^{2}$, derived from singlet $F^{\gamma }_{s} (x,Q^{2})$ and non-singlet $F^{\gamma }_{ns} (x,Q^{2})$ distribution functions. The solutions seem to be right, because the distribution functions of the photon and the photon structure function are in agreement with those from the available experimental data as well as with other parameterization models.

Appendices

Appendix A

The Laplace integral is a powerful tool, formulated like the power series and Fourier series, to solve a wide variety of initial value problems. This integral was originally investigated in the pursuit of purely mathematical aims. The strategy is to transform the difficult differential equations into simple algebra problems (for a comprehensive discussion, see Ref. [35]). For a function F(x) defined on $0\le x<\infty$, the corresponding Laplace transform f(s) can be obtained by the following integral:

$$\begin{aligned} f(s)={\mathcal {L}}\lbrace F(x);s\rbrace =\int _{0}^{\infty } e^{-sx}F(x)\mathrm{d}x, \end{aligned}$$

(A.1)

where the parameter s may be real-valued or complex-valued and ${\mathcal {L}}$ is called the Laplace transform operator. The sufficient conditions for the existence of a Laplace transform of F(x) to f(s), for all $s > a$, are

• (1) F(x) be piecewise continuous in every finite interval $0\le x\le N$ for any $N> 0$,

• (2) $\vert F (x)\vert \le K e^{ax}$ when $x \ge M$, for any real constant $a\in \mathrm I\!R$, $K>0$, and $M>0$.

Furthermore, the inverse Laplace transform of a function f(s) is defined as follows:

$$\begin{aligned} F(x)={\mathcal {L}}^{-1} \lbrace f(s);x\rbrace =\frac{1}{2\pi i}\int _{\sigma -i\infty }^{\sigma +i\infty }f(s)e^{sx}, \end{aligned}$$

(A.2)

where ${\mathcal {L}}^{-1}$ is called the inverse Laplace transform operator and $\sigma$ is a real number so that the contour path of the integration is in the region of convergence of f(s). The conditions for the existence of an inverse Laplace transform of f(s) to F(x) are as follows:

• (1) $\lim _{s\rightarrow \infty }f(s)=0$

• (2) $\lim _{s\rightarrow \infty }s f(s)=$ finite.

The Mellin transform is a basic tool for analyzing the behavior of a function because of its scale invariance property. Indeed, this scale invariance property is analogous to the Fourier transform’s shift-invariance property (for a comprehensive discussion, see Ref. [36]). The Mellin transform of an integrable function F(x) on $(0,\infty )$ is defined as follows:

$$\begin{aligned} f(n)={\mathsf {M}}\lbrace F(x);n\rbrace =\int _{0}^{\infty }F(x)x^{n-1}\mathrm{d}x, \end{aligned}$$

(A.3)

where ${\mathsf {M}}$ is called the Mellin transform operator. This integral exists for all cases of complex n in the open strip $(a,b)=\lbrace n: n=\sigma +i\mu :a<\sigma <b\rbrace$. By substituting $x=e^{-t}$ in Eq. (A.3), a two-sided or two one-sided Laplace integrals are created as follows:

$$\begin{aligned} f(n)= & {} \int _{-\infty }^{\infty }F(e^{-t})e^{-tn}\mathrm{d}t\nonumber \\= & {} \int _{0}^{\infty }F(e^{-t})e^{tn}\mathrm{d}t+\int _{0}^{\infty }F(e^{t})e^{-(-tn)}\mathrm{d}t. \end{aligned}$$

(A.4)

Also, the inverse Mellin transform is defined as

$$\begin{aligned} F(x)={\mathsf {M}}^{-1}\lbrace f(n);x\rbrace =\frac{1}{2\pi i}\int _{c-i\infty }^{c+i\infty }f(n)x^{-n}, \end{aligned}$$

(A.5)

where $c \in (a,b)$ is any real number and ${\mathsf {M}}^{-1}$ is called the inverse Mellin transform operator. This integral exists when:

• (1) f(n) is regular in the infinite strip $a<\sigma <b$ and, for any arbitrary small positive $\epsilon$, $f(n)\rightarrow 0$ in the strip $a+\epsilon \le \sigma \le b+\epsilon$ as $\mu \rightarrow \pm \infty$.

• (2) $\int _{-\infty }^{\infty }f(\sigma +i\mu )d\mu$ for each value of $\sigma \in (a,b)$ is convergent and integrable.

In this paper, we used the following property in our calculations to simplify the equations:

$$\begin{aligned}&{\mathcal {L}}\left\{ \int _{0}^{y}H(x)B(y-x)\mathrm{d}x;s\right\} \nonumber \\&\quad ={\mathcal {L}}\left\{ H(x)\otimes B(x);s\right\} \nonumber \\&\quad ={\mathcal {L}}\left\{ H(x);s\right\} {\mathcal {L}}\left\{ B(y);s\right\} , \end{aligned}$$

(A.6)

where H(x) and B(x) are arbitrary functions and $H(x)\otimes B(x)$ is known as the convolution integral of H(x) and B(x).

Appendix B

In Eqs. (36)–(38), the coefficients $A^{LO}_{i}$, $B^{LO}_{i}$, and $C^{LO}_{i}$ (with $i=1\dots 4$) are as follows:

$$\begin{aligned}&A_{1}^{LO}(s,u)=\bigg [\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{10}-\Omega _{\gamma }^{LO}(s)a_{10}u\nonumber \\&\quad -\Phi _{g}^{LO}(s)u+u^2\bigg ]/H_{1},\nonumber \\&A_{2}^{LO}(s,u)=\bigg [-\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)a_{10}\nonumber \\&\quad +\Theta _{f}^{LO}(s)u\bigg ]/H1,\nonumber \\&A_{3}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}u\bigg ]/H1,\nonumber \\&A_{4}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}^2\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}^2u\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H{1}, \end{aligned}$$

(B.1)

$$\begin{aligned}&B_{1}^{LO}(s,u)=\bigg [-\Omega _{\gamma }^{LO}(s)\Theta _{g}^{LO}(s)a_{10}\nonumber \\&\quad +\Theta _{g}^{LO}(s)u\bigg ]/H_{1},\nonumber \\&B_{2}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)a_{10}^2\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)a_{10}-\Omega _{\gamma }^{LO}(s)a_{10}u\nonumber \\&\quad -\Phi _{f}^{LO}(s)u+u^2\bigg ]/H_{1},\nonumber \\&B_{3}^{LOO}(s,u)=\bigg [\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{10}\bigg ]/H_{1},\nonumber \\&B_{4}^{LO}(s,u)=\bigg [\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{10}^2\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{1}, \end{aligned}$$

(B.2)

$$\begin{aligned}&C_{1}^{LO}(s,u)=\bigg [-\Phi _{g}^{LO}(s)a_{10}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad +a_{10}u\Upsilon _{\gamma }^{LO}(s)\bigg ]/H_{1},\nonumber \\&C_{2}^{LO}(s,u)=\bigg [\Theta _{f}^{LO}(s)a_{10}\Upsilon _{\gamma }^{LO}(s)\bigg ]/H_{1},\nonumber \\&C_{3}^{LO}(s,u)=\bigg [\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)-\Phi _{f}^{LO}(s)u\nonumber \\&\quad -\Phi _{g}^{LO}(s)u-\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)+u^2\bigg ]/H_{1},\nonumber \\&C_{4}^{LO}(s,u)=\bigg [\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{f}^{LO}(s)a_{10}u\Upsilon _{ns\gamma }^{LO}(s)-\Phi _{g}^{LO}(s)a_{10}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{10}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +a_{10}u^2\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{1}, \end{aligned}$$

(B.3)

where

$$\begin{aligned}&H_{1}=\bigg [\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}^2\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad -\Omega _{f}^{LO}(s)a_{10}^2u\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}\\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)a_{10}u\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{10}u\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{10}\\&\quad -\Omega _{\gamma }^{LO}(s)a_{10}u^2+\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)u\nonumber \\&\quad -\Phi _{f}^{LO}(s)u^2-\Phi _{g}^{LO}(s)u^2\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)u+u^3\bigg ]. \end{aligned}$$

In Eqs. (44)–(46), the coefficients $A{'}^{LO}_{i}$, $B{'}^{LO}_{i}$, and $C{'}^{LO}_{i}$ (with $i=1\dots 5$) are as follows:

$$\begin{aligned}&A{'}_{1}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}a_{11}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad A_{1}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}a11u\Upsilon _{\gamma }^{LO}(s)A_{1}(s,u-b_{11})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{11}uC_{1}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{11}u^2C_{1}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{10}\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)a_{10}u-\Phi _{g}^{LO}(s)u+u^2\bigg ]/H_{2},\nonumber \\&A{'}_{2}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}a_{11}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad a_{21}[u-b_{11}]\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}a_{11}u\Upsilon _{\gamma }^{LO}(s)a_{21}[u-b_{11}]\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{11}uC_{2}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{11}u^2C_{2}^{LO}(s,u-b_{11})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)a_{10}\nonumber \\&\quad +\Theta _{f}^{LO}(s)u\bigg ]/H_{2},\nonumber \\&A{'}_{3}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}a_{11}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad A_{3}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}a_{11}u\Upsilon _{\gamma }^{LO}(s)A_{3}^{LO}(s,u-b_{11})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{11}uC_{3}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{11}u^2C_{3}^{LO}(s,u-b_{11})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}u\bigg ]/H_{2},\nonumber \\&A{'}_{4}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}^2\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}^2u\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{2},\nonumber \\&A{'}_{5}^{LO}(s,u)=\bigg [-A_{4}^{LO}(s,u-b_{11})\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)\nonumber \\&\quad a_{10}a_{11}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad +A_{4}^{LO}(s,u-b_{11})\Omega _{f}^{LO}(s)a_{10}a_{11}u\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad -C41\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{11}u+C41\Omega _{f}^{LO}(s)a_{11}u^2\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}a_{11}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}a_{11}u\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{2}, \end{aligned}$$

(B.4)

$$\begin{aligned}&B{'}_{1}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \Theta _{g}^{LO}(s)a_{10}a_{11}C_{1}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{11}uC_{1}^{LO}(s,u-b_{11})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{g}^{LO}(s)a_{10}+\Theta _{g}^{LO}(s)u\bigg ]/H_{2},\nonumber \\&B{'}_{2}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \Theta _{g}^{LO}(s)a_{10}a_{11}C_{2}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{11}uC_{2}^{LO}(s,u-b_{11})\nonumber \\&\quad -\Omega _{f}^{LO}(s)a_{10}^2\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)a_{10}\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)a_{10}u-\Phi _{f}^{LO}(s)u+u^2\bigg ]/H_{2},\nonumber \\&B{'}_{3}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \Theta _{g}^{LO}(s)a_{10}a_{11}C_{3}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{11}uC_{3}^{LO}(s,u-b_{11})\bigg ]/H_{2},\nonumber \\&B{'}_{4}^{LO}(s,u)=\bigg [\Omega _{f}^{LO}(s)\nonumber \\&\quad \Theta _{g}^{LO}(s)a_{10}^2\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{2},\nonumber \\&B{'}_{5}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \Theta _{g}^{LO}(s)a_{10}a_{11}C_{4}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{11}uC_{4}^{LO}(s,u-b_{11})\bigg ]/H_{2}, \end{aligned}$$

(B.5)

$$\begin{aligned}&C{'}_{1}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}a_{11}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)C_{1}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}a_{11}u\Upsilon _{\gamma }^{LO}(s)C_{1}^{LO}(s,u-b_{11})\nonumber \\&\quad -\Phi _{g}^{LO}(s)a_{10}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad +a_{10}u\Upsilon _{\gamma }^{LO}(s)\bigg ]/H_{2},\nonumber \\&C{'}_{2}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}a_{11}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)C_{2}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}a_{11}u\Upsilon _{\gamma }^{LO}(s)C_{2}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Theta _{f}^{LO}(s)a_{10}\Upsilon _{\gamma }^{LO}(s)\bigg ]/H_{2},\nonumber \\&C{'}_{3}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}a_{11}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)C_{3}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}a_{11}u\Upsilon _{\gamma }^{LO}(s)C_{3}^{LO}(s,u-b_{11})\bigg ]/H_{2},\nonumber \\&C{'}_{4}^{LO}(s,u)=\bigg [\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{f}^{LO}(s)a_{10}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{g}^{LO}(s)a_{10}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{10}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +a_{10}u^2\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{2},\nonumber \\&C{'}_{5}^{LO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}a_{11}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)C_{4}^{LO}(s,u-b_{11})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{10}a_{11}u\Upsilon _{\gamma }^{LO}(s)C_{4}^{LO}(s,u-b_{11})\bigg ]/H_{2}, \end{aligned}$$

(B.6)

where

$$\begin{aligned} H_{2}= & {} \bigg [\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}^2\Upsilon _{\gamma }^{LO}(s)\nonumber \\&-\Omega _{f}^{LO}(s)a_{10}^2u\Upsilon _{\gamma }^{LO}(s)\nonumber \\&-\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{10}\\&+\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)a_{10}u\nonumber \\&+\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{10}u+\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{10}\nonumber \\&-\Omega _{\gamma }^{LO}(s)a_{10}u^2\\&+\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)u-\Phi _{f}^{LO}(s)u^2\nonumber \\&-\Phi _{g}^{LO}(s)u^2-\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)u+u^3\bigg ]. \end{aligned}$$

In Eqs. (56)–(58), the coefficients $A^{NLO}_{i}$, $B^{NLO}_{i}$, and $C^{NLO}_{i}$ (with $i=1\dots 4$) are as follows:

$$\begin{aligned}&A_{1}^{NLO}(s,u)=\bigg [\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{20}\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)a_{20}u-\Phi _{g}^{NLO}(s)a_{30}u\nonumber \\&\quad -\Phi _{g}^{LO}(s)u+u^2\bigg ]/H_{3},\nonumber \\&A_{2}^{NLO}(s,u)=\bigg [-\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)a_{20}\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{30}u+\Theta _{f}^{LO}(s)u\bigg ]/H_{3},\nonumber \\&A_{3}^{NLO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{20}u\bigg ]/H_{3},\nonumber \\&A_{4}^{NLO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}^2a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}^2\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{20}^2u\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{3}, \end{aligned}$$

(B.7)

$$\begin{aligned}&B_{1}^{NLO}(s,u)=\bigg [-\Omega _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{g}^{LO}(s)a_{20}+\Theta _{g}^{NLO}(s)a_{30}u+\Theta _{g}^{LO}(s)u\bigg ]/H_{3},\nonumber \\&B_{2}^{NLO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)a_{20}^2\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)a_{20}-\Omega _{\gamma }^{LO}(s)a_{20}u\nonumber \\&\quad -\Phi _{f}^{NLO}(s)a_{30}u-\Phi _{f}^{LO}(s)u+u^2\bigg ]H_{3},\nonumber \\&B_{3}^{NLO}(s,u)=\bigg [\Omega _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{20}\bigg ]H_{3},\nonumber \\&B_{4}^{NLO}(s,u)=\bigg [\Omega _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}^2a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{20}^2\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{3}, \end{aligned}$$

(B.8)

$$\begin{aligned}&C_{1}^{NLO}(s,u)=\bigg [-\Phi _{g}^{NLO}(s)a_{20}a_{30}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{g}^{LO}(s)a_{20}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad +a_{20}u\Upsilon _{\gamma }^{LO}(s)\bigg ]/H_{3},\nonumber \\&C_{2}^{NLO}(s,u)=\bigg [\Theta _{f}^{NLO}(s)a_{20}a_{30}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad +\Theta _{f}^{LO}(s)a_{20}\Upsilon _{\gamma }^{LO}(s)\bigg ]/H_{3},\nonumber \\&C_{3}^{NLO}(s,u)=\bigg [\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{30}^2\nonumber \\&\quad -\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{30}^2\nonumber \\&\quad +\Phi _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{30}\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{30}\nonumber \\&\quad -\Phi _{f}^{NLO}(s)a_{30}u-\Phi _{g}^{NLO}(s)a_{30}u\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{30}\nonumber \\&\quad -\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{30}\nonumber \\&\quad +\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)\nonumber \\&\quad -\Phi _{f}^{LO}(s)u-\Phi _{g}^{LO}(s)u\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)+u^2\bigg ]/H_{3},\nonumber \\&C_{4}^{NLO}(s,u)=\bigg [\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}^2\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}^2\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Phi _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{f}^{NLO}(s)a_{20}a_{30}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{g}^{NLO}(s)a_{20}a_{30}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{20}a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{f}^{LO}(s)a_{20}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{g}^{LO}(s)a_{20}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{20}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +a_{20}u^2\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{3}, \end{aligned}$$

(B.9)

where

$$\begin{aligned}&H_{3}=\bigg [\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}^2a_{30}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{20}a_{30}\\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{30}\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad -\Phi _{f}^{LO}(s)u^2-\Phi _{g}^{LO}(s)u^2+(-\Phi _{f}^{NLO}(s)\\&\quad \times \Phi _{g}^{NLO}(s)a_{20}a_{30}^2\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}^2)\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad +(-\Phi _{f}^{NLO}(s)a_{30}-\Phi _{g}^{NLO}(s)a_{30})u^2\nonumber \\&\quad +(\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{30}^2\\&\quad -\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{30}^2)u+u^3\nonumber \\&\quad +(\Phi _{f}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad +\Phi _{g}^{NLO}(s)a_{20}a_{30})\Omega _{\gamma }^{LO}(s)u\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}^2\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad -\Omega _{f}^{LO}(s)a_{20}^2u\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}+\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)a_{20}u\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{20}u+\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\\&\quad \times \Theta _{g}^{LO}(s)a_{20}+\Phi _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{30}u\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{30}u\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{30}u-\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{30}u\\&\quad -\Omega _{\gamma }^{LO}(s)a_{20}u^2+\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)u\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)u\bigg ]. \end{aligned}$$

Moreover, in Eqs. (65)–(67), the coefficients $A{'}^{NLO}_{i}$, $B{'}^{NLO}_{i}$, and $C{'}^{NLO}_{i}$ (with $i=1 \dots 5$) are as follows:

$$\begin{aligned}&A{'}^{NLO}_{1}(s,u)=\bigg [\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{31}u^2B_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{21}u^2C_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{31}u^2A_{1}^{NLO}(s,u+b_{31})+u^2\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{20}-\Omega _{\gamma }^{LO}(s)a_{20}u\nonumber \\&\quad -\Phi _{g}^{NLO}(s)a_{30}u+\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)\nonumber \\&\quad \times a_{31}uB_{1}^{NLO}(s,u+b_{31})+\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{31}u\nonumber \\&\quad A_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{31}uA_{1}^{NLO}(s,u+b_{31})-\Phi _{g}^{LO}(s)\nonumber \\&\quad \times \Theta _{f}^{NLO}(s)a_{31}uB_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{21}uC_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{20}a_{31}\nonumber \\&\quad \times B_{1}^{NLO}(s,u+b_{31})-\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{31}\nonumber \\&\quad A_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{30}a_{31}uA_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{30}a_{31}uB_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}B_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}uB_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{20}a_{21}C_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \times a_{20}a_{21}uC_{1}^{NLO}(s,u-b_{21})-\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)\nonumber \\&\quad a_{30}a_{31}uB_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{21}a_{30}uC_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{30}a_{31}uA_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{31}A_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{31}uA_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}a_{31}\nonumber \\&\quad A_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{30}a_{31}A_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}\nonumber \\&\quad B_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{30}a_{31}B_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{21}a_{30}\nonumber \\&\quad C_{1}^{NLO}(s,u-b_{21})\nonumber \end{aligned}$$

$$\begin{aligned}&\quad -\Phi _{g}^{LO}(s)u\bigg ]/H_{4},\nonumber \\&A{'}^{NLO}_{2}(s,u)=\bigg [-\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{31}u^2B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{21}u^2C_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{31}u^2a_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)a_{20}\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{30}u+\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{31}u\nonumber \\&\quad B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{31}ua_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{31}ua_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)a_{31}uB_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{21}uC_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{20}a_{31}B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{31}a_{2}^{NLO}(s,u+b_{31})+\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad a_{30}a_{31}ua_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{30}a_{31}uB_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{31}a_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)a_{20}a_{31}ua_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{31}B_{2}^{NLO}(s,u+b_{31})-\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}u\nonumber \\&\quad B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{20}a_{21}C_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)a_{20}a_{21}uC_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{30}a_{31}uB_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{21}a_{30}u\nonumber \\&\quad \times C_{2}^{NLO}(s,u-b_{21})-\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{30}a_{31}u\nonumber \\&\quad a_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{21}a_{30}C_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}a_{31}a_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}a_{31}a_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \times \Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{LO}(s)u\bigg ]/H_{4},\nonumber \\&A{'}^{NLO}_{3}(s,u)=\bigg [\Phi _{f}^{NLO}(s)a_{31}u^2A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{31}u^2B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{21}u^2C_{3}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{31}uB_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{31}uA_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{21}uC_{3}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{31}uA_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)a_{31}uB_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{20}a_{31}\nonumber \\&\quad \times B_{3}^{NLO}(s,u+b_{31})-\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{31}A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{30}a_{31}uB_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{30}a_{31}uA_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{31}A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{31}uA_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}uB_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{20}a_{21}C_{3}^{NLO}(s,u-b_{21})\nonumber \end{aligned}$$

$$\begin{aligned}&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s) a_{20}a_{21}uC_{3}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)\nonumber \\&\quad \times a_{30}a_{31}uA_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{30}a_{31}uB_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{21}a_{30}uC_{3}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s) a_{20}a_{21}a_{30}C_{3}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}a_{31}A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}a_{31}A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}\nonumber \\&\quad B_{3}^{NLO}(s,u+b_{31})\bigg ]/H_{4},\nonumber \\&A{'}^{NLO}_{4}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}^2a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}^2\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{20}^2u\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{4},\nonumber \\&A{'}^{NLO}_{5}(s,u)=\bigg [\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{21}a_{30}\nonumber \\&\quad C_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{20}a_{21}C_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)a_{20}a_{21}uC_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{21}a_{30}uC_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{21}uC_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{21}u^2C_{4}^{NLO}(s,u-b_{21})\bigg ]/H_{4},\nonumber \\&A{'}^{NLO}_{6}(s,u)=\bigg [\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}a_{31}\nonumber \\&\quad A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)\nonumber \\&\quad a_{20}a_{30}a_{31}\nonumber \\&\quad \times B_{4}^{NLO}(s,u+b_{31})+\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)\nonumber \\&\quad a_{20}a_{30}a_{31}B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}a_{31}\nonumber \\&\quad \times A_{4}^{NLO}(s,u+b_{31})+\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\nonumber \\&\quad \Phi _{g}^{LO}(s)a_{20}a_{31}A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{20}a_{31}B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)a_{20}a_{31}uA_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{31}A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}uB_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{30}a_{31}uA_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{30}a_{31}uB_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{30}a_{31}uB_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{30}a_{31}uA_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{31}uA_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{31}uB_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{31}u^2A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)a_{31}uB_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{31}uA_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{31}u^2B_{4}^{NLO}(s,u+b_{31})\bigg ]/H_{4},\\&B{'}_{1}^{NLO}(s,u)=\bigg [\Theta _{g}^{LO}(s)u\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{31}B_{1}^{NLO}(s,u+b_{31})u^2\nonumber \\&\quad +\Theta _{g}^{NLO}(s)a_{31}A_{1}^{NLO}(s,u+b_{31})u^2\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{30}-\Omega _{\gamma }^{LO}(s)\Theta _{g}^{LO}(s)a_{20}\nonumber \\&\quad +\Theta _{g}^{NLO}(s)a_{30}u\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{31}uB_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{31}u\nonumber \end{aligned}$$

(B.10)

$$\begin{aligned}&\quad \times A_{1}^{NLO}(s,u+b_{31})-\Theta _{g}^{NLO}(s)a_{31}\nonumber \\&\quad A_{1}^{NLO}(s,u+b_{31})\Phi _{f}^{LO}(s)u\nonumber \\&\quad -\Phi _{f}^{NLO}(s)^2a_{31}B_{1}^{NLO}(s,u+b_{31})a_{30}u\nonumber \\&\quad -\Phi _{f}^{NLO}(s)a_{31}\nonumber \\&\quad \times B_{1}^{NLO}(s,u+b_{31})\Phi _{f}^{LO}(s)u\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{21}uC_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{20}a_{31}\nonumber \\&\quad A_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{20}a_{31}\nonumber \\&\quad B_{1}^{NLO}(s,u+b_{31})+a_{20}\Theta _{g}^{NLO}(s)a_{31}\nonumber \\&\quad A_{1}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\nonumber \\&\quad +a_{20}\Phi _{f}^{NLO}(s)^2a_{31}B_{1}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)a_{30}\nonumber \\&\quad +a_{20}\Phi _{f}^{NLO}(s)a_{31}B_{1}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Theta _{g}^{LO}(s)a_{20}a_{21}C_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad -a_{20}^2\Upsilon _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)a_{31}B_{1}^{NLO}(s,u+b_{31})\Omega _{f}^{LO}(s)\nonumber \\&\quad -a_{20}\Theta _{g}^{NLO}(s)a_{31}A_{1}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)u\nonumber \\&\quad -a_{20}\Phi _{f}^{NLO}(s)a_{31}B_{1}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)u\nonumber \\&\quad -a_{20}^2\Upsilon _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)a_{31}A_{1}^{NLO}(s,u+b_{31})\Omega _{f}^{LO}(s)\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{21}a_{30}uC_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{30}a_{31}uB_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad a_{20}a_{21}a_{30}C_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad a_{20}a_{30}a_{31}B_{1}^{NLO}(s,u+b_{31})\bigg ]/H_{4},\nonumber \\&B{'}_{2}^{NLO}(s,u)=\bigg [\Theta _{g}^{NLO}(s)a_{31}A_{2}^{NLO}(s,u+b_{31})u^2\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{31}B_{2}^{NLO}(s,u+b_{31})u^2\nonumber \\&\quad +a_{20}\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)a_{30}+u^2\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)a_{20}u-a_{20}^2\Upsilon _{\gamma }^{LO}(s)\Omega _{f}^{LO}(s)\nonumber \\&\quad +a_{20}\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\nonumber \\&\quad -\Phi _{f}^{NLO}(s)a_{30}u+\Phi _{f}^{NLO}(s)\nonumber \\&\quad \Theta _{g}^{LO}(s)a_{31}uA_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{31}u\nonumber \\&\quad B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Theta _{g}^{NLO}(s)a_{31}a_{2}^{NLO}(s,u+b_{31})\Phi _{f}^{LO}(s)u\nonumber \\&\quad -\Phi _{f}^{NLO}(s)^2a_{31}B_{2}^{NLO}(s,u+b_{31})a_{30}u\nonumber \\&\quad -\Phi _{f}^{NLO}(s)a_{31}B_{2}^{NLO}(s,u+b_{31})\Phi _{f}^{LO}(s)u\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{21}uC_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{20}a_{31}\nonumber \\&\quad \times A_{2}^{NLO}(s,u+b_{31})-\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)\nonumber \\&\quad a_{20}a_{31}B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +a_{20}\Theta _{g}^{NLO}(s)a_{31}A_{2}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\nonumber \\&\quad +a_{20}\Phi _{f}^{NLO}(s)^2a_{31}B_{2}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)a_{30}\nonumber \\&\quad +a_{20}\Phi _{f}^{NLO}(s)a_{31}B_{2}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Theta _{g}^{LO}(s)a_{20}a_{21}C_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad -a_{20}^2\Upsilon _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)a_{31}B_{2}^{NLO}(s,u+b_{31})\Omega _{f}^{LO}(s)\nonumber \\&\quad -a_{20}\Theta _{g}^{NLO}(s)a_{31}A_{2}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)u\nonumber \\&\quad -a_{20}\Phi _{f}^{NLO}(s)a_{31}B_{2}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)u\nonumber \\&\quad -a_{20}^2\Upsilon _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)a_{31}A_{2}^{NLO}(s,u+b_{31})\Omega _{f}^{LO}(s)\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{21}a_{30}uC_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{30}a_{31}uB_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{21}a_{30}C_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}a_{31}B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{f}^{LO}(s)u\bigg ]/H_{4},\nonumber \end{aligned}$$

$$\begin{aligned}&\quad B{'}_{3}^{NLO}(s,u)=\bigg [\Theta _{g}^{NLO}(s)a_{31}A_{3}^{NLO}(s,u+b_{31})u^2\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{31}B_{3}^{NLO}(s,u+b_{31})u^2\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{31}u\nonumber \\&\quad \times A_{3}^{NLO}(s,u+b_{31})+\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{31}u\nonumber \\&\quad B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)^2a_{31}B_{3}^{NLO}(s,u+b_{31})a_{30}u\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)\nonumber \\&\quad \times a_{21}uC_{3}^{NLO}(s,u-b_{21})-\Theta _{g}^{NLO}(s)a_{31}\nonumber \\&\quad A_{3}^{NLO}(s,u+b_{31})\Phi _{f}^{LO}(s)u\nonumber \\&\quad -\Phi _{f}^{NLO}(s)a_{31}B_{3}^{NLO}(s,u+b_{31})\Phi _{f}^{LO}(s)u\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \times \Phi _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{20}a_{31}A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{20}a_{31}B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +a_{20}\Theta _{g}^{NLO}(s)a_{31}\nonumber \\&\quad \times A_{3}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\nonumber \\&\quad +a_{20}\Phi _{f}^{NLO}(s)^2a_{31}B_{3}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)a_{30}\nonumber \\&\quad +a_{20}\Phi _{f}^{NLO}(s)a_{31}B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad \times \Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)-\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\nonumber \\&\quad \Theta _{g}^{LO}(s)a_{20}a_{21}C_{3}^{NLO}(s,u-b_{21})\nonumber \\&\quad -a_{20}^2\Upsilon _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)a_{31}A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad \times \Omega _{f}^{LO}(s)\nonumber \\&\quad -a_{20}^2\Upsilon _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)a_{31}B_{3}^{NLO}(s,u+b_{31})\Omega _{f}^{LO}(s)\nonumber \\&\quad -a_{20}\Theta _{g}^{NLO}(s)a_{31}A_{3}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)u\nonumber \\&\quad -a_{20}\Phi _{f}^{NLO}(s)a_{31}B_{3}^{NLO}(s,u+b_{31})\Omega _{\gamma }^{LO}(s)u\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{21}a_{30}uC_{3}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad \times a_{30}a_{31}uB_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{21}\nonumber \\&\quad \times a_{30}C_{3}^{NLO}(s,u-b_{21})-\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad a_{20}a_{30}a_{31}B_{3}^{NLO}(s,u+b_{31})\bigg ]/H_{4},\nonumber \\&B{'}_{4}^{NLO}(s,u)=\bigg [\Omega _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}^2a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{20}^2\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{4},\nonumber \\&B{'}_{5}^{NLO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{21}a_{30}\nonumber \\&\quad C_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Omega _{\gamma }^{LO}(s)\Theta _{g}^{LO}(s)a_{20}a_{21}C_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{21}a_{30}uC_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{21}uC_{4}^{NLO}(s,u-b_{21})\bigg ]/H_{4},\nonumber \\&B{'}_{6}^{NLO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{f}^{NLO}(s)a_{20}^2a_{31}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}^2a_{31}\Upsilon _{\gamma }^{LO}(s)A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)^2a_{20}a_{30}a_{31}B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}a_{31}B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\Phi _{f}^{NLO}(s)a_{20}a_{31}B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{31}\nonumber \\&\quad A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{20}a_{31}\nonumber \\&\quad A_{4}^{NLO}(s,u+b_{31})-\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)a_{20}a_{31}u\nonumber \\&\quad B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\nonumber \\&\quad \times \Theta _{g}^{LO}(s)a_{20}a_{31}B_{4}^{NLO}(s,u+b_{31})\nonumber \end{aligned}$$

$$\begin{aligned}&\quad -\Omega _{\gamma }^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{31}uA_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)^2a_{30}a_{31}uB_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{30}a_{31}uB_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{f}^{LO}(s)\Phi _{f}^{NLO}(s)a_{31}uB_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{31}u\nonumber \\&\quad \times A_{4}^{NLO}(s,u+b_{31})+\Phi _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{31}u\nonumber \\&\quad A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{31}u^2B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)\nonumber \\&\quad \times a_{31}uB_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{g}^{NLO}(s)a_{31}u^2A_{4}^{NLO}(s,u+b_{31})\bigg ]/H_{4},\\&C{'}_{1}^{NLO}(s,u)=\bigg [-a_{20}\Upsilon _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)a_{30}\nonumber \\&\quad -a_{20}\Upsilon _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)\nonumber \\&\quad +a_{20}\Upsilon _{\gamma }^{LO}(s)u\nonumber \\&\quad +\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad \times A_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}a_{21}\Upsilon _{\gamma }^{LO}(s)C_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{20}a_{21}u\Upsilon _{\gamma }^{LO}(s)C_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)A_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{20}a_{31}u\Upsilon _{\gamma }^{LO}(s)A_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{20}a_{31}u\Upsilon _{\gamma }^{LO}(s)B_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad \times B_{1}^{NLO}(s,u+b_{31})-\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{21}a_{30}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)C_{1}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}a_{31}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad \times A_{1}^{NLO}(s,u+b_{31})-\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)B_{1}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad \times B_{1}^{NLO}(s,u+b_{31})+\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)A_{1}^{NLO}(s,u+b_{31})\bigg ]/H_{4},\nonumber \\&C{'}_{2}^{NLO}(s,u)=\bigg [a_{20}\Upsilon _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)a_{30}\nonumber \\&\quad +a_{20}\Upsilon _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\nonumber \\&\quad +\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad a_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}a_{21}\Upsilon _{\gamma }^{LO}(s)C_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{20}a_{21}u\Upsilon _{\gamma }^{LO}(s)C_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}\nonumber \\&\quad \times a_{31}\Upsilon _{\gamma }^{LO}(s)a_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{20}a_{31}u\Upsilon _{\gamma }^{LO}(s)a_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad \times B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{20}a_{31}u\Upsilon _{\gamma }^{LO}(s)B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{21}a_{30}\Upsilon _{\gamma }^{LO}(s)C_{2}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)a_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{2}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}a_{31}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)a_{2}^{NLO}(s,u+b_{31})\bigg ]/H_{4},\nonumber \end{aligned}$$

(B.11)

$$\begin{aligned}&C{'}_{3}^{NLO}(s,u)=\bigg [\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}a_{21}\Upsilon _{\gamma }^{LO}(s)C_{3}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{20}a_{21}u\Upsilon _{\gamma }^{LO}(s)C_{3}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{31}\nonumber \\&\quad \times \Upsilon _{\gamma }^{LO}(s)A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{20}a_{31}u\Upsilon _{\gamma }^{LO}(s)A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{20}a_{31}u\Upsilon _{\gamma }^{LO}(s)B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{21}a_{30}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad C_{3}^{NLO}(s,u-b_{21})-\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)A_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{3}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad A_{3}^{NLO}(s,u+b_{31})\bigg ]/H_{4},\nonumber \\&C{'}_{4}^{NLO}(s,u)=\bigg [\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}^2\Upsilon _{ns\gamma }^{LO}(s)ns\nonumber \\&\quad -\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}^2\Upsilon _{ns\gamma }^{LO}(s)ns\nonumber \\&\quad +\Phi _{f}^{LO}(s)\Phi _{g}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{30}\Upsilon _{ns\gamma }^{LO}(s)+\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{f}^{NLO}(s)a_{20}a_{30}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{g}^{NLO}(s)a_{20}a_{30}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{20}a_{30}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{f}^{LO}(s)a_{20}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Phi _{g}^{LO}(s)a_{20}u\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{20}\Upsilon _{ns\gamma }^{LO}(s)\nonumber \\&\quad +a_{20}u^2\Upsilon _{ns\gamma }^{LO}(s)\bigg ]/H_{4},\nonumber \\&C{'}_{5}^{NLO}(s,u)=\bigg [-\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{21}a_{30}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)C_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad -\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}a_{21}\Upsilon _{\gamma }^{LO}(s)C_{4}^{NLO}(s,u-b_{21})\nonumber \\&\quad +\Omega _{f}^{LO}(s)a_{20}a_{21}u\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad C_{4}^{NLO}(s,u-b_{21})\bigg ]/H_{4},\nonumber \\&C{'}_{6}^{NLO}(s,u)=\bigg [-\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)\nonumber \\&\quad a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad \times B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{NLO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}a_{31}\Upsilon _{\gamma }^{LO}(s)\nonumber \\&\quad \times A_{4}^{NLO}(s,u+b_{31})-\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{31}\nonumber \\&\quad \Upsilon _{\gamma }^{LO}(s)A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)\Theta _{f}^{LO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Phi _{f}^{NLO}(s)a_{20}a_{31}u\Upsilon _{\gamma }^{LO}(s)A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad -\Phi _{g}^{LO}(s)\Theta _{f}^{NLO}(s)a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)B_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)\nonumber \\&\quad \times a_{20}a_{31}\Upsilon _{\gamma }^{LO}(s)A_{4}^{NLO}(s,u+b_{31})\nonumber \\&\quad +\Theta _{f}^{NLO}(s)a_{20}a_{31}u\Upsilon _{\gamma }^{LO}(s)B_{4}^{NLO}(s,u+b_{31})\bigg ]/H_{4}, \end{aligned}$$

(B.12)

where

$$\begin{aligned}&H_{4}=\bigg [\Omega _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}^2a_{30}\Upsilon _{\gamma }^{LO}\\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}^2\\&\quad +\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}^2\\&\quad +\Omega _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}^2\Upsilon _{\gamma }^{LO}\\&\quad -\Omega _{f}^{LO}(s)a_{20}^2uO\Upsilon _{\gamma }^{LO}\\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}\\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{20}a_{30}\\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{NLO}(s)a_{20}a_{30}u\\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{NLO}(s)a_{20}a_{30}u\\&\quad +\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{20}a_{30}\\&\quad +\Omega _{\gamma }^{LO}(s)\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)\\&\quad \times a_{20}a_{30}+\Phi _{f}^{NLO}(s)\Phi _{g}^{NLO}(s)a_{30}^2u\\&\quad -\Theta _{f}^{NLO}(s)\Theta _{g}^{NLO}(s)a_{30}^2u\\&\quad -\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)a_{20}\\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{f}^{LO}(s)a_{20}u\\&\quad +\Omega _{\gamma }^{LO}(s)\Phi _{g}^{LO}(s)a_{20}u\\&\quad +\Omega _{\gamma }^{LO}(s)\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)a_{20}\\&\quad -\Omega _{\gamma }^{LO}(s)a_{20}u^2+\Phi _{f}^{LO}(s)\Phi _{g}^{NLO}(s)a_{30}u\\&\quad +\Phi _{f}^{NLO}(s)\Phi _{g}^{LO}(s)a_{30}u\\&\quad -\Phi _{f}^{NLO}(s)a_{30}u^2-\Phi _{g}^{NLO}(s)a_{30}u^2\\&\quad -\Theta _{f}^{LO}(s)\Theta _{g}^{NLO}(s)a_{30}u\\&\quad -\Theta _{f}^{NLO}(s)\Theta _{g}^{LO}(s)a_{30}u\\&\quad +\Phi _{f}^{LO}(s)\Phi _{g}^{LO}(s)u-\Phi _{f}^{LO}(s)u^2\\&\quad -\Phi _{g}^{LO}(s)u^2-\Theta _{f}^{LO}(s)\Theta _{g}^{LO}(s)u+u^3\bigg ]. \end{aligned}$$

In Eqs. (79) and (81), the non-singlet solution coefficients $k_{1ns}^{LO}$, $k_{2ns}^{LO}$, $k_{1ns}^{NLO}$ and $k_{2ns}^{NLO}$, are as follows:

$$\begin{aligned}&k_{1ns}^{LO}(s,u)=\frac{u^{2}-b_{11}u}{u(u-b_{11})(u-\Phi _{qqns}^{LO}(s))},\nonumber \\&k_{2ns}^{LO}(s,u)=\frac{\left( a_{10}u+a_{11}u-a_{10}b_{11}\right) }{u(u-b_{11})(u-\Phi _{qqns}^{LO}(s))},\nonumber \\&k_{1ns}^{NLO}(s,u)=-\bigg [a_{30}b_{21}^2b_{31}\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad +a_{30}b_{21}^2\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad -a_{30}b_{21}b_{31}^2\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad -3a_{30}b_{21}b_{31}\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad -2a_{30}b_{21}\Phi _{qqns}^{NLO}(s)u^3\nonumber \\&\quad +a_{30}b_{31}^2\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad +2a_{30}b_{31}\Phi _{qqns}^{NLO}(s)u^3+a_{30}\Phi _{qqns}^{NLO}(s)u^4\nonumber \\&\quad -a_{31}b_{21}^2b_{31}\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad -a_{31}b_{21}^2\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad +a_{31}b_{21}b_{31}^2\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad +3a_{31}b_{21}b_{31}\Phi _{qqns}^{NLO}(s)u^2+2a_{31}b_{21}\Phi _{qqns}^{NLO}(s)u^3\nonumber \\&\quad -a_{31}b_{31}^2\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad -2a_{31}b_{31}\Phi _{qqns}^{NLO}(s)u^3\nonumber \\&\quad -a_{31}\Phi _{qqns}^{NLO}(s)u^4-b_{21}^2b_{31}^2u+b_{21}^2b_{31}\Phi _{qqns}^{LO}(s)u\nonumber \\&\quad -2b_{21}^2b_{31}u^2+b_{21}^2\Phi _{qqns}^{LO}(s)u^2\nonumber \\&\quad -b_{21}^2u^3+b_{21}b_{31}^3u\nonumber \\&\quad -b_{21}b_{31}^2\Phi _{qqns}^{LO}(s)u +4b_{21}b_{31}^2u^2-3b_{21}b_{31}\Phi _{qqns}^{LO}(s)u^2\nonumber \\&\quad +5b_{21}b_{31}u^3-2b_{21}\Phi _{qqns}^{LO}(s)u^3+2b_{21}u^4\nonumber \\&\quad -b_{31}^3u^2+b_{31}^2\Phi _{qqns}^{LO}(s)u^2\nonumber \\&\quad -3b_{31}^2u^3+2b_{31}\Phi _{qqns}^{LO}(s)u^3-3b_{31}u^4\nonumber \\&\quad +\Phi _{qqns}^{LO}(s)u^4-u^5]/H_{5},\nonumber \\&k_{2ns}^{NLO}(s,u)=-\bigg [a_{20}a_{30}b_{21}^2b_{31}\Phi _{qqns}^{NLO}(s)\nonumber \\&\quad +a_{20}a_{30}b_{21}^2\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad -a_{20}a_{30}b_{21}b_{31}^2\Phi _{qqns}^{NLO}(s)\nonumber \\&\quad -3a_{20}a_{30}b_{21}b_{31}\nonumber \\&\quad \times \Phi _{qqns}^{NLO}(s)u-2a_{20}a_{30}b_{21}\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad +a_{20}a_{30}b_{31}^2\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad +2a_{20}a_{30}b_{31}\Phi _{qqns}^{NLO}(s)u^2+a_{20}a_{30}\nonumber \\&\quad \times \Phi _{qqns}^{NLO}(s)u^3-a_{20}a_{31}b_{21}^2\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad +a_{20}a_{31}b_{21}b_{31}\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad +2a_{20}a_{31}b_{21}\Phi _{qqns}^{NLO}(s)u^2-a_{20}a_{31}b_{31}\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad -a_{20}a_{31}\Phi _{qqns}^{NLO}(s)u^3-a_{21}a_{30}b_{21}b_{31}\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad -a_{21}a_{30}b_{21}\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad +a_{21}a_{30}b_{31}^2\Phi _{qqns}^{NLO}(s)u+2a_{21}a_{30}b_{31}\nonumber \\&\quad \times \Phi _{qqns}^{NLO}(s)u^2+a_{21}a_{30}\Phi _{qqns}^{NLO}(s)u^3\nonumber \\&\quad +a_{21}a_{31}b_{21}b_{31}\Phi _{qqns}^{NLO}(s)u\nonumber \\&\quad +a_{21}a_{31}b_{21}\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad -a_{21}a_{31}b_{31}\Phi _{qqns}^{NLO}(s)u^2\nonumber \\&\quad -a_{21}a_{31}\Phi _{qqns}^{NLO}(s)u^3-a_{20}b_{21}^2b_{31}^2\nonumber \\&\quad +a_{20}b_{21}^2b_{31}\Phi _{qqns}^{LO}(s)-2a_{20}b_{21}^2b_{31}u\nonumber \\&\quad +a_{20}b_{21}^2\Phi _{qqns}^{LO}(s)u-a_{20}b_{21}^2u^2+a_{20}b_{21}b_{31}^3\nonumber \\&\quad -a_{20}b_{21}b_{31}^2\Phi _{qqns}^{LO}(s)+4a_{20}b_{21}b_{31}^2u\nonumber \\&\quad -3a_{20}b_{21}b_{31}\Phi _{qqns}^{LO}(s)u+5a_{20}b_{21}b_{31}u^2\nonumber \\&\quad -2a_{20}b_{21}\Phi _{qqns}^{LO}(s)u^2+2a_{20}b_{21}u^3-a_{20}b_{31}^3u\nonumber \\&\quad +a_{20}b_{31}^2\Phi _{qqns}^{LO}(s)u-3a_{20}b_{31}^2u^2\nonumber \\&\quad +2a_{20}b_{31}\Phi _{qqns}^{LO}(s)u^2-3a_{20}b_{31}u^3\nonumber \\&\quad +a_{20}\Phi _{qqns}^{LO}(s)u^3-a_{20}u^4+a_{21}b_{21}b_{31}^2u-a_{21}b_{21}b_{31}\nonumber \\&\quad \times \Phi _{qqns}^{LO}(s)u+2a_{21}b_{21}b_{31}u^2\nonumber \\&\quad -a_{21}b_{21}\Phi _{qqns}^{LO}(s)u^2+a_{21}b_{21}u^3-a_{21}b_{31}^3u\nonumber \\&\quad +a_{21}b_{31}^2\Phi _{qqns}^{LO}(s)u-3a_{21}b_{31}^2u^2\nonumber \\&\quad +2a_{21}b_{31}\Phi _{qqns}^{LO}(s)u^2-3a_{21}b_{31}u^3\nonumber \\&\quad +a_{21}\Phi _{qqns}^{LO}(s)u^3-a_{21}u^4\bigg ]/H_{5}, \end{aligned}$$

(B.13)

where

$$\begin{aligned} H_{5}= & {} (u+b_{31})(-u-b_{31}+b_{21})(a_{30}\Phi _{qqns}^{NLO}(s)\nonumber \\&-b_{31}+\Phi _{qqns}^{LO}(s)-u)u(-u+b_{21})(a_{30}\Phi _{qqns}^{NLO}(s)\nonumber \\&+\Phi _{qqns}^{LO}(s)-u). \end{aligned}$$